
Piramide - Egipt.
Matematika v Egiptu je bila 2000 let pret Kr. že dobro razvita veda. Na nivoju, kot se ga danes učimo v osnovni šoli in deloma v srednji. Egipčni so matematiko zapisovali in učili s pomočjo problemov - kot primere, ki jih je potrebno posnemati. Matematika je bila predvsem uporabna veda.
Egipčani so uporabljali dva številska sistema - enega za pisanje na kamen, drugega za pisanje na papir. Oba sta bila zasnovana na številu deset. Prvi je uporabljal različne simbole za potence števila deset. Mnogokratnike posamezne potence so nato prikazovali s ponavljanjem ustreznega simbola tolikrat, kot je bilo treba.
Osnovni aritmetični operaciji sta bili seštevanje in podvajanje. Za množenje in deljenje so uporabljali domiselno metodo, ki je temeljila na podvajanju. Uporabljali so pojem "n-tega dela". Govorili so o tretjini, četrtini (1/4). Našemu ulomku 3/5 bi rekli "polovica in desetina" (1/2 + 1/10 = 3/5). Na Rhindovem papirusu je podvojitev petine (2/5) prikazana kot vsota tretjine in petnajstine (1/3 + 1/15 = 2/5). A stroka še zmeraj ni čisto enotna glede egipčanske matematike.
Znali so reševati preproste linearne enačbe.
Znali so določiti približek ploščine, površine in prostornine nekaterih geometrijskih likov, teles (krogov, polobel, valjev, prisekane kvadratne piramide, ...). Ploščino kroga s premerom 'd = 2r' so računali s približkom (8d/9)2 = (16r/9)2, kar je v resnici precej dober približek. Kvadrat razmerja (16/9) je zelo blizu številu PI = 3,141592654..., saj velja ( (16/9)2 = 256/81 = 3,160493827 ).
Seveda pa je končna ocena o pomenu in metodah egipčanske matematike zavita v skrivnost minulih tisočletij.
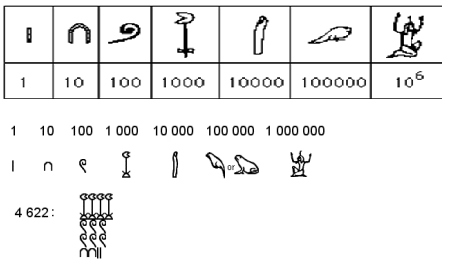
Egipčanske številke - hireoglifi in primer zapisa števila 4622. Tak zapis so uporabljali kar okrog 2000 let - pozneje so zapis poenostavili.

Nekaj primerov egipčanskih ulomkov.

Ahmesovi zapisi matematike ali Rhindov papirus, spada med najstarejše ohranjene matematične zapise (Egipat, okrog 1600 pred Kr.). Na njem je napisanih 54 problemov. Podani so izračuni ulomkov, volumnov nekaterih teles, ... Recimo volumen valja, ki so ga dokaj uspešno ocenili z izrazom: V = h[(1 - 1/9)d]2. Matematična vsebina papirusa je prepis vsaj 200 let starejšega teksta - neznanega avtorja. Svečeniki starega Egipta so hranili take zapise kot posebno skrivnost - v znanju je moč. Leta 1858 ga je v Luksorju našel Alexander Henry Rhind, škotski starinar in preprodajalec egiptovskih relikvij.
_-_Google_Art_Project.jpg)
"Veliki babilonski zigurat" - stolp (okrog 600 pred Kr.). Slika je umetniška podoba Pietra Bruegela iz leta 1563. Babilonski stolp je skoraj zagotovo bil višji od piramid v Gizi. Komaj leta 1889 je Eifflov stolp v Parizu presegel dimenzije - višino ZIGGURATA babilonskega. Takih zgradb (piramid, 200 m visokih stolpov, itn) se zagotovo ni dalo graditi brez osnov geometrije - matematike, statike. Ime Babilon izhaja iz besede babilli, ki pa pomeni božja vrata.
Sumerci so po letu 3000 pr. Kr. razvili zapleten sistem merskih enot. Po letu 2600 pr. Kr. so na glinaste tablice že zapisovali tabele za množenje in se ukvarjali z geometrijskimi nalogami in problemi z deljenjem. Iz tega obdobja so tudi najstarejši sledovi babilonskih številk.

Mezopotamske, babilonske številke so se razvile nekje 2000 pred Kr. Žgali so jih v glinene tablice.
Babilonci, znani po svojih astronomskih opazovanjih in izračunih, h katerim je pripomogel tudi abakus, ki so ga izumili sami, so za mnoge namene uporabljali šestdesetiški številski sistem z osnovo 60, katerega so nasledili od Sumercev ali Akadcev. Dediščina šestdesetiškega sistema se je ohranila do danes pri merjenju kotov in časa: krog ima 360°, 60° merijo notranji koti v enakostraničnem trikotniku, ura ima 60 minut in minuta 60 sekund. Število 60 je po teoriji superiorno zelo sestavljeno število (prejšnje in nasledje število sta 12 in 120), ki je bilo izbrano zaradi njegove prvorazredne faktorizacije 2x2x3x5, zaradi katere je deljivo s števili 1, 2, 3, 4, 5, 6, 10, 12, 15, 20 in 30. Cela števila in ulomki so se zapisovali enako. Decimalna vejica se ni pisala, ampak jo je bilo treba razbrati iz konteksta.
Takratna ocena leta je bila zelo blizu vrednosti 360 dni (6X60). Zdi se, da je to število, poleg že naštetih prednosti osnove 60, močno vplivalo na bodoči razvoj geometrije, matematike. Recimo, da smo krog razdelili na 360 ločnih stopinj.
Babilonci niso imeli niti znaka niti koncepta za število nič. Četudi so razumeli idejo ničnosti, nanjo niso gledali kot na število, ampak na manjkajoče število. Namesto ničle so sprva uporabljali presledek, katerega so kasneje zamenjali s simbolom


Babilonski zapis števil.
Poleg tega so, za razliko od Egipčanov in Rimljanov, uvedli sistem mestnih vrednosti, v katerem vrednost številke ni odvisna samo od nje same, ampak tudi od njene lege v zapisu števila. Sistem je bil precej podoben sodobnemu desetiškemu sistemu. Vrednosti mest so padale od leve proti desni, tako da se je na primer število 734 zapisalo s 7·100 + 3·10 + 4.

Babilonska glinasta tablica YBC 7289: na diagonali je zapisana približna vrednost kvadratnega korena števila 2, točna na štiri šestdesetiške digite 1 24 51 10 (1 + 24/60 + 51/602 + 10/603 = 1,41421296... ) oziroma sedem desetiških digitov. Na tablici je izračun dolžine diagonale kvadrata s stranico 30. Rezultat je 42 25 35 oziroma 1,41421296x30 = 42,4263888...
Babilonci so poleg aritmetičnih izračunov razvili tudi algebrske metode za reševanje enačb. Tudi pri njih so si pomagali s tabelami že izračunanih vrednosti. Za reševanje kvadratnih enačb so uporabljali standardno kvadratno obliko enačbe.
Za število PI so uporabljali soliden približek 25/8 = 3,125, napaka 0,5 percentov. Pitagorov in Talesov izrek (obodni kot trikotnika nad premerom krožnice je pravi, premer je hipotenuza) so poznali 1000 let pred starimi Grki.
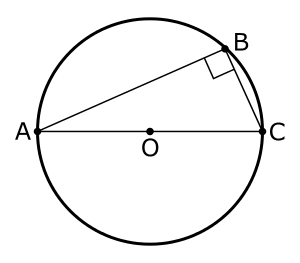
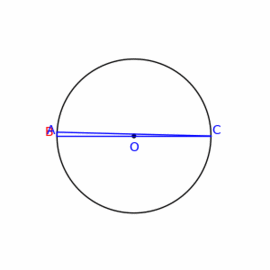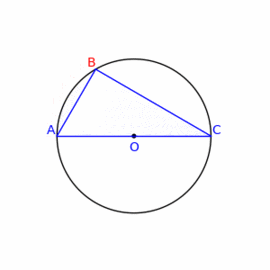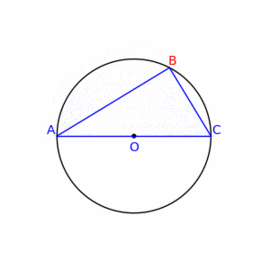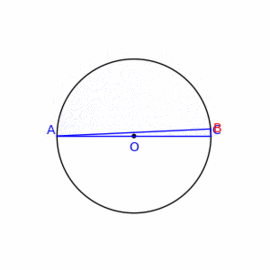
Talesov izrek - obodni kot trikotnika nad premerom krožnice je pravi, premer je hipotenuza.

Chichen Itza - severno majevsko mesto.

Zapis števil pri Majih. Zapis števil se je v srednji Ameriki razvil že 1000 pred Kr., Maji so ga dopolnili in dodali ničlo - zagotovo že leta 357 po Kr.

Majevski zapis števil iz "Dresdenskega Codexa".
Predkolumbovska civilizacija Majev je uporabljala sistem številčenja z osnovo do 20 (uporabljali so dvajsetiški sistem). Poznali so tudi ničlo, ki so jo Babilonci vpeljali zelo pozno.
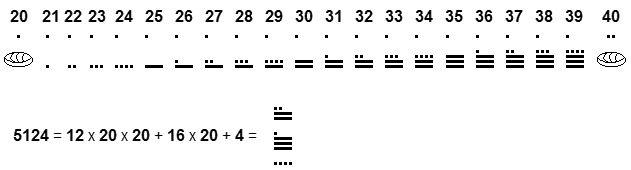

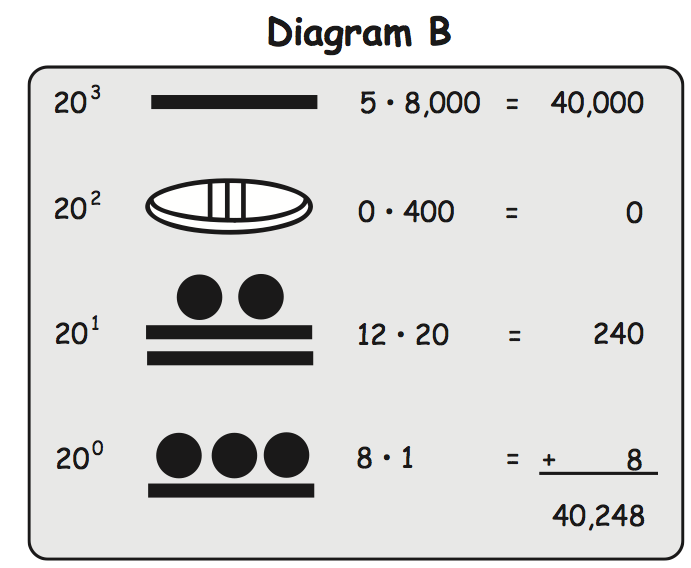
Majevski zapis števil večjih od 19.

Princip računanja Majev.

Stare številke antične Grčije in primer zapisa števila 4672.

V 4. stoletju pred Kr. pa so pomen števil dali kar črkam abecede (alfabetski sistem). Izbrali so spet znake samo za nekatera števila . Znake za ostala pa so sestavili iz njih. Da so ločili črke in pisane besede od številk, so številkam dodali črtico. Število tri tisoč sedemstooseminosemdeset je sestavljeno iz števil: tri tisoč, sedemsto, osemdeset in osem. Tako so Grki zmanjšali število potrebnih znakov. Vsa števila do sto so lahko označili s številkami, ki so jih sestavili iz osemnajstih osnovnih znakov. Za oznako števil do tisoč so potrebovali sedemindvajset znakov.
Ptolemaj je v drugem stoletju uporabljal vrednost za PI = 377/120 = 3,141667, kar je prva vrednost natančna na tri decimalke.
Matematiki so stari Grki dali novo dimenzijo, saj se takrat začne razvoj abstraktne matematike, ki nima zgolj neposredne praktične uporabe. Zasnovali so aksiomatski pristop k matematiki. Grki so najbolj razvijali geometrijo in algebro. Matematika je za Grke osnova vsega, tako da so na vhodu v Platonovo Akademijo napisali: "Naj ne vstopa, kdor ne zna geometrije". Evklid iz Aleksandrije (325–265 pr. Kr.) je napisal enega najbolj znamenitih matematičnih učbenikov v zgodovini človeštva - izdal ga je pod naslovom "Elementi". To je matematična knjiga, ki je bila najboljši učbenik na področju geometrije do 19. stoletja, do Carla Friedricha Gaußa, Hilberta, ..., ko se pojavijo prvi resnejši neevklidski opisi geometrije.
Kaj trdi Evklid.
Evklidovi Elementi se začenjajo z naslednjimi petimi postulati, aksiomi (zapisano v sodobnem matematičnem jeziku):
a) Skozi poljubni dve točki poteka točno ena premica.
b) Premica je neomejena - lahko jo podaljšamo v neskončnost.
c) Za katerokoli daljico obstaja krožnica, ki ima to daljico za polmer in eno od krajišč za središče.
d) Vsi pravi koti so med sabo skladni.
f) Če poljubni premici sekamo s tretjo premico (prečnico) in je vsota notranjih kotov na eni strani prečnice manjša od dveh pravih kotov, potem se dani premici sekata na tej strani prečnice.

Peti postulat: če je alfa + beta < 180°, se premici h in k sekata v točki S.
Peti postulat je nekoliko nerodno formuliran. Poznejši matematiki so ga nadomestili z aksiomom o vzporednici, ki je razumljivejši, po matematičnem pomenu pa je enakovreden:
Skozi poljubno točko T, ki ne leži na premici p, poteka točno ena vzporednica k premici p.
Ti aksiomi se še danes učijo v srednji šoli. Evklidovi Elementi ne vsebujejo le geometrije, ampak tudi kar precej teorije števil in elementarno geometrijsko algebro. V glavnem gre za sistematične predstavitve dosežkov različnih starejših grških matematikov in seveda izročila Babiloncev in ostalih ljudstev. Svoja spoznanja je dodal tudi sam Evklid.
Elementi so izjemna knjiga, študirana in občudovana od vsega začetka in poleg biblije na Zahodu najbolj citirana knjiga. Nobena druga ni imela takega znanstvenega vpliva, saj je celih dva tisoč let prevladovala pri pouku geometrije. Od leta 1482, ko je bila prvič natisnjena, je izšlo preko 1000 modernih izdaj, vendar temelječih na kasnejših predelavah. Nobenega originala Evklidovih Elementov namreč niso našli - samo prepise.

Ohranjen kos Evklidovih Elementov, najden v Oksirhinku v Egiptu, izvira iz okoli leta 100.
Uganke iz antične zgodovine
-----------------------------------
Vedež iz apolonovega svetišča na otoku Delosu je prerokoval ljudstvu v Atenah, da se bo rešilo kuge, če bodo njegov oltar v obliki kocke povečali tako, da bo njegova prostornina dvakrat večja od prvotne. Najbrž so delski problem zaupali Platonu, ki ga je predložil geometrom v svoji Akademiji. Dejansko so se s podvojitvijo kocke ukvarjali številni grški matematiki (Menhmus, Arhitras, Evdoks, Eratosten, Papus, Diokles, Hipokrat) - in tudi prišli do rešitve. Vendar pa noben od njih ni rešil naloge z evklidskim orodjem, ker to ni mogoče. Jedro problema je namreč v konstrukciji števila 21/3, ki ni mogoča z evklidskim orodjem. Trden dokaz, da to ni mogoče, so matematiki našli šele v 19. stoletju. Origami (pregibanje s papirjem) pa omogoča konstruirati naravna števila, racionalna števila, njihove kvadratne korene in števila oblike a + a1/2 in tudi števila oblike 21/3.
Znana je tudi zgodba matematično neukega grškega pesnika. Pisal je o kralju Minosu, ki ni bil zadovoljen z grobnico svojega sina Glavka. Zahteval je dvakrat večjo grobnico in napačno sklepal, da je to mogoče doseči s podvojitvijo vseh njenih dimenzij. To napako so nato reševali matematiki ...
Kako so s prepogibanjem papirja rešili starogrške uganke komaj pred nedavnim, si preberite v članku: "Origami - osnove".
Odlika tega sistema je enostavna vizualna predstavitev števil, ki se jih hitro naučimo (vsaj majhne številke).
Ima pa sistem zapisa rimskih stevil svoje omejitve, je brez decimalnih številk, večje število znakov za veliko številko (ali pa bi morali najti nove znake), sistem rimskih števil ne pozna ničle.
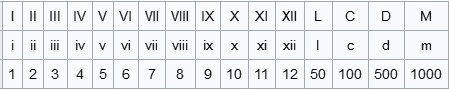
Pretvorba med rimskimi in hindujsko-arabskimi številkami.

Primer zapisa večjih vrednosti in seštevanja z rimskimi številkami.


Yang Hui je že v 13. stoletju zapisal trikotnik števil (Pascalov trikotnik). Iz trikotnika se razbere tudi zapis kitajskih števil. V resnici bi bilo bolj pošteno ta trikotnik imenovati Yangov (Jangov) ali Kitajski trikotnik.

Animacija "Yangovega - Pascalovega" trikotnika števil. Trikotnik nastane, če se v vsaki vrstici od zunaj začne z enicami in se sešteva sosednji števili, vsoto pa se napiše pod njima. Na ta način se lahko hitro izračuna binomske koeficiente brez uporabe ulomkov ali množenj.

Hindujsko-arabske številke - danes v nekoliko modificirani obliki splošno sprejet matematični zapis števil. V bistvu so te številke nastale v Indiji med leti 300 do 700 po Kr., v Evropo pa so prišle preko arabskih knjig.
