Fizikalni eksperimenti na spletu, nekateri izračuni, razlage, animacije

Zbirka povezav se dopolnjuje!

  1. Cartesian diver
    (kartezični plavač)

  2. Eksperimenti v mikrogravitaciji
    (a)

  3. Eksperimenti v mikrogravitaciji
    (b)

  4. breztežnost v prosto padajoči plastenki polni vode z lahko žogico pripeto na vijačno vzmet - genialno
    (stran 295)

  5. Stacked ball drop physics
    (prožni trki med masivnimi in lahkimi telesi - teorija)

  6. Stacked ball drop physics
    (prožni trki med masivnimi in lahkimi telesi - primer in primerjava s supernovo)

  7. Stacked ball drop physics
    (prožni trki med masivnimi (V hitrost) in lahkimi telesi (v hitrost) - v številkah, v' je hitrost lahkega telesa po prožnem trku z masivnim telesom: v' = 2V - v)

  8. acceleration of a yo-yo and tension in the string
    (pospešek igračke jojo in sila v vrvici)

  9. Yoyo Pulled Along the Ground
    (pospešek igračke jojo na ravnem, vrvico vlečemo vodoravno)

  10. Yo-Yo: Rolling, sliding, pulling
    (pospešek igračke jojo na ravnem, vrvico vlečemo poševno)

  11. Solid Cylinder Rolling Down an Incline
    (pospešek kotalečega se valja po klancu)

  12. Elongation of a bar due to its Own weight (A)
    (podaljšanje palice zaradi lastne teže).
    ali Elongation of a bar due to its Own weight (B)

  13. Elongation of a bar due to its Own weight (C)
    (stožec ...)

  14. Geometríjska vrsta
    Člen geometrijske vrste k je manjši od 1:
    k<1
    - vsota geometrijske vrste s je: s = k^0 + k^1 + k^2 + k^3 + ... + k^n = 1 + k^1 + k^2 + k^3 + ... + k^n, kjer potenca n zavzema vrednosti od 0 do neskončno, poiščimo vsoto, velja:
    - vsota ks = k^1 + k^2 + k^3 + ... + k^n
    Razlika obeh vrst je: s - ks = 1, sledi končni rezultat vsote s:
    s = 1/(1 - k)
    Vsota vrste (ak^n ), kjer lahko izpostavimo vrednost a, je s = a/(1 - k).
    Če se n začne z n = 1, potem velja s = ak + ak^2 + ak^3 + ... + ak^n: s = a*k*(k^(1-1) + k^(2-1) + k^(3-1) + ... + k^(n-1)) = vsota ak(k^(n-1)) = ak/(1 - k)
    PRIMER 1:
    SUM(n=1, infinity) (-3)^(n-1)/4^(n-2) - determine whether the series is convergent or divergent. If it is convergent, and its sum. (geometríjska vrsta)


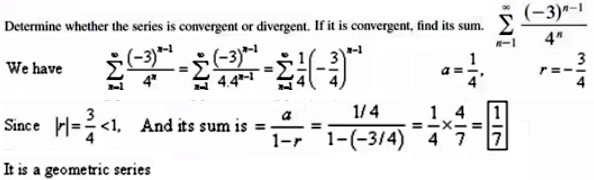
    PRIMER 2:
    sestavljena vrsta, vsota ( 6^(n-2)/8^n - 3^(n+1)/8^n ) od n=1 do n = neskončno (uporabimo enačbo s = ak/(1 - k) ), naprej pa zapišimo vsoto obeh vrst:
    vsota ( 6^(n-2)/8^n ) - vsota (3^(n+1)/8^n ), velja:
    prvi člen, vsota ( 6^(n-2)/8^n ) = vsota (1/36)( 6^n/8^n ) = vsota (1/36)( 3^n/4^n ) = vsota (1/48)( 3^(n-1)/4^(n-1) ) = (1/48)( 1/(1 - 3/4)),
    za drugi del vrste velja:
    vsota ( 3^(n+1)/8^n ) = vsota (9/8)((3^(n-1)/8^(n-1) ) = (9/8)((1/(1 - 3/8 ), če setavimo oba dela vrste dobimo:
    s = (1/48)( 1/(1 - 3/4)) - (9/8)((1/(1 - 3/8 ) = 1/12 - 9/5 = -103/60 = -1.716666666666 ...

  15. Zakaj je x na 0 enako 1: x^0 = 1?
    --------------------------------------------
    Dokaz ćez palec!
    Poglejmo n-ti koren šetvila x. Koren x(1/n) = x^(1/n) = ?, če n gre proti neskončno, gre potenca 1/n proti 0,
    n-ti koren (če n večamo) vsakega števila gre tako proti 1, tudi če je število 1>x>=0x.
    ZATO VELJA: x^0 = 1.
    Velja tudi 1/x^(1/n) = (1/x)^(1/n) = 1, če n in x gre proti neskončno, limitirata 1/x in 1/n proti 0, velja rorej 0^0 = 1.
    Primeri, ki to nakazujejo:
    121^(1/9) = 1.703807779
    121^(1/18) = 1.305299881
    122^(1/27) = 1.19473775
    123^(1/36) = 1.143017606
    124^(1/45) = 1.113064885
    --------------------------------
    0.01^(1/9) = 0.59948425
    0.01^(1/18) = 0.774263683
    0.01^(1/27) = 0.843190929
    0.01^(1/27) = 0.879922544
    0.01^(1/45) = 0.902725178

    n=100000000, zato velja 1/100000000 = 0.00000001
    x=0.00000001, velja (0.00000001)^(1/100000000) = 0.999999816 ali (1/100000000)^(1/100000000) = 0.999999816
    x=100000000, velja (100000000)^(1/100000000) = 1.000000184
    -----------------------------------------------------------------------------
    Dokaz s pomočjo geometrijske vrste za 0^0 = 1. Če x<1, velja za vsoto vrste s:
    s = x^0 + x^1 + x^2 + x^3 + ... + x^n = 1/(1 - x)
    IN če je x = 0, velja s = 0^0 + 0 + ... = 1/(1 - 0), od koder sledi 0^0 = 1/(1 - 0) = 1


  16. ()



    Za astronomski krožek: ZORKO Vičar


    RFC-822: Zorko.Vicar@guest.arnes.si

    Nazaj na domačo stran.

    Valid HTML 4.0!