Pojasnilo
Prispevek je dopolnjeno gradivo, ki so ga uporabljali dijaki med vajami pri izbirnem predmetu fizika (naravoslovna gimnazija, leto 1992/1993). Program PCvista je že nekoliko zastarel a sama logika obdelave astronomskih CCD posnetkov je ostala enaka.

CCD ( Charge Coupled Device ) je danes najbolj popularen detektor za potrebe astronomije. Poleg astronomije ga uporabljajo tudi druge vede, ki potrebujejo visoko občutljiv ploskovni detektor vidne svetlobe z linearnim odzivom. Dodatna prednost CCD-ja je v tem, da podatke zajemamo v digitalni obliki.

Naloga:

1) Analiza nekaj tipičnih posnetkov s CCD kamero.
2) Spoznati računalniško predstavitev modela masivne homogene zvezde in izdelava teoretičnega H-R diagrama.
3) Analiza CCD opazovanj odprte zvezdne kopice s ciljem dobiti eksperimentalni H-R diagram.

šIRšI OKVIR
Preden se lotimo ukazov PCviste, je potrebno pojasniti osnovne pojme iz astronomije. Ponavadi v srednjih šolah astronomijo zanemarjamo, zato učencem nista znana pojma sij-magnituda in H-R diagram; ker sta ključna za našo nalogo, ju je potrebno na kratko pojasniti. Na tem mestu nima smisla razglabljati o začetku vesolja - prapok, tudi ne iskati odgovorov ali je vesolje odprto ali zaprto... Omejimo se na tisto, kar nam je dostopno s srednješolsko fiziko.

Kdo torej povzroča vsa ta burna dogajanja v vesolju : visoki tlaki, temperature, kopičenje ogromnih mas, močni elektromagnetni valovi, močna magnetna polja, eksplozije zvezd, ukrivljanje žarkov - gravitacijske leče, da ne govorimo o črnih luknjah...?

Problema se lotimo kar se da preprosto, in sicer začnimo kar doma na Zemlji z vprašanjem : "Kaj nas zadržuje na Zemlji?" Newton in Einstein sta našla odgovor v sili gravitacije. Newtonova empirična enačba za privlačno gravitacijsko silo med dvema točkastima telesoma (z masama m1 in m2) na razdalji r, se glasi:

Zamislimo si kar se da preprost model vesolja, oziroma fiziko zvezd. Vzemimo oblak vodika, masa naj bo nekaj Sončevih mas (vodik smo izbrali zato, ker ga je v vesolju največ - kako so to ugotovili?). Plin je redek, vendar se začne gostiti. Kaj ga gosti? Znotraj oblaka je zbrana velika masa, ki z lastno silo gravitacije krči oblak plina, gostota se veča, tlak narašča, temperatura narašča...! Zvezda (zvezde) se rojeva. Postavi se vprašanje, zakaj naraščanje T, r, P ne gre v "neskončnost". Odgovor bomo poiskali kar pri odbojnih silah med atomi in v sevalnem tlaku, ki se sprosti pri zlivanju (fuziji) lažjih, recimo vodikovih, jeder v težja jedra, npr. helij (fuzijo znamo sprožiti tudi na Zemlji, vendar na žalost zaenkrat samo v nekontrolirani obliki eksplozije vodikove bombe).

Počakaj, poučni animaciji.

Pred očmi astronomov se rojevajo nove zvezde in "umirajo" stare (nimajo več jedrskega goriva). Meritve, ki so nam dostopne, potrjujejo naš modelček, ki išče ravnovesje med gravitacijsko in jedrsko energijo.

Zdaj bi vsaj v grobem znali pojasniti odkod zvezdam (galaksijam) visoki tlaki, temperature, ogromne sevalne moči... Marsikaj smo zanemarili, recimo vpliv mase na življenje zvezd itd., vendar nam gre tukaj predvsem za preprost model - princip.

Dimenzije v vesolju so glede na Zemljo ekstremne, saj ocenjujejo velikost vesolja na 15 milijard svetlobnih let, to je 1,4 x 10²⁶ m in starost na 15 milijard let. Kljub nepredstavljivim dimenzijam in omejeni ločljivosti inštrumentov se da iz dobljenih podatkov dovolj prepričljivo sklepati o dogajanjih v vesolju.

Osnovni instrument je oko. Že stari Grki (Hiparh, Ptolomej) so razdelili zvezde po siju oziroma magnitudi - to je fiziološka enota za sij. Najsvetlejše so imenovali zvezde prve magnitude (m=1 m), komaj vidne pa šeste magnitude (m=6 m). Da bi stara razdelitev zvezd po njihovem siju ostala v veljavi in tudi fizikalno bolj praktično uporabna, so preko meritev poiskali zvezo med sijem in gostosto svetlobnega toka zvezde. Rezultat je naslednji: sija dveh zvezd m1 in m2 in gostoti svetlobnega toka, gostoti izseva (j=P/S) j1 in j2, ki ga ti zvezdi pošiljata na Zemljo, so povezani z empirično enačbo:

Kako so prišli, do te pomembne povezave. Poglejmo si spodnjo tabelo meritev.

Meritve:
m2-m1       1      2      3      4      5     6    10   15    20    25
j1/j2       2,512  6,13  15,85  39,81 100   251,2  104   106   108  1010 
----------------------------------------------------------------
Povezave:
(j1/j2)(m2-m1)  2,512  2,5122 2,5123 2,5124 2,5125 2,5125  ... 
log(j1/j2)    0,4    0,8    1,2    1,6    2     2,4    ...
0,4*(m2-m1)   0,4*1  0,4*2  0,4*3  0,4*4  0,4*5 0,4*6  ...

Prve meritve segajo v leto 1856. Pogson je takrat odkril, da so zvezde prve magnitude približno 100 krat svetlejše od zvezd šeste magnitude (j1(m=1)/j2(m=6)=100). Tako so vpeljali nov sistem magnitud, ki temelji na definiciji, da razlika petih magnitud ustreza natanko stokratnemu razmerju med gostotama izseva. Da so lahko v sistem vključili tudi zelo svetle zvezde, planete, Luno, Sonce, komete, utrinke ..., so skalo razširili še na negativna števila. Sirij ima po tej razvrstitvi magnitudo okrog minus 1,5 (-1,5). S tem so sicer nekoliko porušili staro razvrstitev zvezd, a praktično skoraj ohranili vrednosti starih meritev sija. Še beseda o meritvah in iskanju povezave med sijem in gostoto izseva, to je namreč drugi del, ki krona meritve. Ustavimo se pri bolj poznanem občutku, oglejmo si sluh. Že pri sluhu se je pokazalo, da človeški senzor za sluh (uho) ni linearen, če se gostota energijskega toka zvoka podvoji, se fiziološki občutek za (glasnost) jakost zvoka ne podvoji, ampak se logaritemsko zaduši (glasnost=10*log(j/j0) [fonov], nekateri pravijo decibeli, j0=10^-12W/m²). S tem je narava omogočila, da slišimo šelestenje listaja in normalni zvok, katerih razmerje gostot energiskih tokov (j1/j2) je lahko tudi neverjetnih 1(w/m²)/10^-11(w/m²)=10¹¹, razmerje v občutku glasnosti, ki ga zaznamo z ušesom pa je samo log(10¹²)/log(10)=12 (razlika v glasnosti pa 120fonov-10fonov = 110 fonov). Seveda je fiziološki občutek za glasnost odvisen še od frekvence.

Vrnimo se k očesu in pogojem nočnega neba, saj so razmere čez dan drugačne. Občutek sija bomo obravnavali grobo, brez upoštevanja valovne dolžine, zenice, receptorjev itd. Oko reagira najbrž podobno kot uho, saj vidimo ponoči zelo šibke zvezdice (j(m=6)=10^-10W/m²) in recimo svetlo Luno ob ščipu (j(m=-12,7)=3*10^-3W/m²). Razmerje med gostotama svetlobnega toka je približno 100000, razlika med magnitudama pa 18,7. Človeška čutila so torej načeloma logaritemska in enak sklep velja za oko. Iz tabele meritev za občutek sija glede na gostoto svetlobnega toka in iz obdelave pod črto razberemo povezavo: m2-m1=2,5*log(j1/j2), oziroma j1/j2=10^{-0,4(m1 -m2)}. Seveda se danes pojavljajo utemeljene pripombe na račun "izpeljane" povezave, ki je vezana na določene zgodovinske danosti, pomanjkljivosti in nenatančnosti, a o tem kdaj drugič.

Zvezda, ki pošilja na Zemljo gostoto svetlobnega toka 0,98 x10^-8 W/m² ima sij +1m. Najsvetlejše telo na nebu je Sonce, ima sij -26,8m, med ostalimi zvezdami pa prednjači Sirij -1,5m. Seveda sij ni fizikalna mera za izsev zvezde, sij je poleg izseva odvisen še od oddaljenosti zvezde in spektra v katerem zvezda najmočneje seva. Oko namreč ni enako občutljivo na vse valovne dolžine. Če je vizualna magnituda, recimo Sirija, negativna, kar pomeni, da je zvezda zelo svetla, to ne pomeni, da je tudi njen izsev energije največji. Mnoge zvezde imajo veliko večji izsev od Sirija a manjši sij, (magnitudo) ker so dosti dlje od Sirija (da ne govorimo o Soncu). Zadrego so rešili tako, da so vpeljali absolutno magnitudo (to je sij zvezde na razdalji 10pc=32,6sv.l.=308,4X10¹²km, s tem so rešili problem razdalje), hkrati pa so vpeljali bolometrično magnitudo (ime pove, da sij določijo preko absorbcije črnega telesa, ki ni odvisen od valovne dolžine elektromagnetnega valovanja, s tem so rešili problem človeškega očesa, ki selektivno zazna samo vidni del elektromagnetnega valovanja). Vpeljali so tudi absolutno bolometrično magnitudo.

Danes merimo sij s fotometri. Naš fotometer je kar CCD kamera, in zato bo računalnik podal kar inštrumentalno magnitudo - med njo, absolutno magnitudo in fiziološko obstaja matematična povezava (glej prispevek o določanju magnitude s pomočjo CCD kamere).

FOTOMETRIJA

Astronomi so uvedli natančno merjenje magnitud (sija) skozi tri filtre UVB (U=ultravioletni, B=modri in V=vizualni ali filter, ki ustreza občutljivosti človeškega očesa). Postopek se imenuje fotometrija. Ponavadi se v fokus teleskopa postavi CCD kamera, z UVB filtri.
B-V=CI je barvni indeks (razlika magnitud med modrim in vizualnim filtrom)
U filter prepušča ultravioletne valovne dolzine 360nm in več
B filter prepusca (okrog) 380nm do 550nm
V filter prepusca (okrog) 500nm do 650nm
Razlika magnitud B-V=CI se imenuje barvni indeks in je mera za temperaturo zvezde (barvo zvezde) in spektralni tip. L je izsev (energijski tok zvezde P v Wattih (W))
------------
L = kR²T_eff⁴ je Stefanov zakon
kR²=4*p*s*R²
s= 5,769*10^-8Wm^-2K^-1 je Stefanova konstanta
R=polmer zvezde
T_eff=efektivna temperatura površine zvezde.
------------
Bolometrična magnituda je vizualna magnituda s prišteto korekcijo bolometra:
m_bol=m+BC
M_bol=M+BC absolutna bolometrična magnituda
B-V=CI je barvni indeks (razlika magnitud med modrim in vizualnim filtrom)
U filter prepušča ultravioletne valovne dolzine 360nm in več
B filter prepusca (okrog) 380nm do 550nm
V filter prepusca (okrog) 500nm do 650nm

Da obstaja zveza med temperaturo in razliko filtriranih magnitud B-V, je dovolj groba špekulacija na podlagi empirične formule (j1/j2 = 10^{-0,4(m1 -m2)}). Če pišemo namesto jB/jV razmerje, ki ga poda Stefanov zakon jB/jV=(TB/TV)⁴ » 10^{-0,4(mB -mV)} in izraz logaritmiramo, dobimo iskano povezavo med razliko magnitud in temperaturo. Barvam (filtriranim magnitudam) smo nekritično pripisali različne temperature, kar ni bilo korektno, je pa razmislek v pomoč za razumevanje principa moderne fotometrije. Oglej si tudi spodnja grafa, ki sta izjemno pomembna za razumevanje principa fotometrije.

Empirične povezave med CI, M_bol in T_eff

Gospod Cameron Reed, Alma College (Michigan) je v članku z naslovom
"The Composite Observational-Theoretical HR Diagram"
v reviji kanadske astronomske kraljeve družbe (The Royal Astronomical Society of Canada)
Februar/Marc 1998, Volume92 Number 1 [669] stran 36,
podal empirično povezavo med M_bol in CI glede na temperaturo T_eff.

• B-V = -3.684 log(T) + 14.551
  za log(T) < 3.961
• B-V = 0.344 [log(T)]² -3.402 log(T) +8.037
  za log(T) >3.961
• BC = -8.499 [log(T)- 4]⁴ + 13.421[log(T)- 4]³- 8.131[log(T)- 4]² - 3.901 [log(T)- 4] - 0.438

Zdaj, ko smo v grobem spoznali sij, si poglejmo osnovne značilnosti H-R diagrama (slika 1, spodaj).

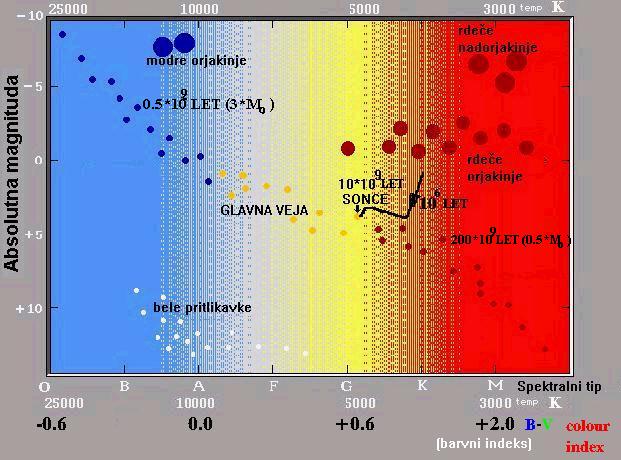
Slika 1a. Hertzsprung-Russellov diagram.

Slika 1b. Spektralni tipi zvezd.

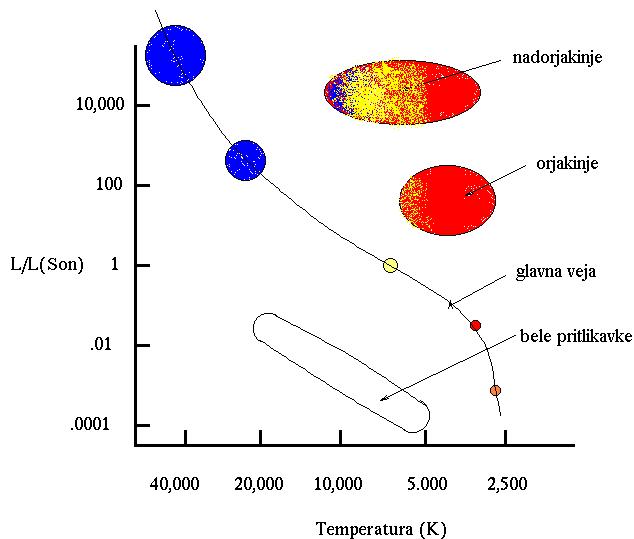
Slika 1c. Še en preprosta predstavitev H-R diagrama.

H-R diagram

H-R diagram je skrajšano ime za Hertzsprung-Russellov diagram. Na absciso nanašamo ponavadi temperaturo (ali njen logaritem) na površini zvezde (lahko pa tudi spektralni tip ali pa barvni indeks B-V, to je razlika med magnitudama modrega in vizualnega-zelenega filtra). Na ordinato pa ponavadi nanašamo relativni izsev (P/Po ali njegov logaritem) - to je relativni energijski tok glede na Sonce, lahko pa tudi nanašamo absolutno magnitudo, ali magnitudo dobljeno skozi vizualni filter (V). Večina zvezd leži na diagonali (na glavni veji) H_R diagrama. Da bomo lažje razumeli H-R diagram, si oglejmo preprost model nastanka in življenja zvezd. Kdaj zvezda pride na glavno vejo? Zvezda je ponavadi plinasta rzbeljena krogla, ki zaradi velike mase (Sonce ima maso Mo=2*10³⁰kg), gravitacijsko stiska notranje dele do te mere, da temperatura (v središču je temperatura 10*10⁶K ali več) in tlak narasteta do te mere, da steče zlivanje jeder, ki omogoča tako velike izseve zvezd. Zakaj nastane iz oblaka plina in prahu zvezda? Da se nek oblak plina začne krčiti, mora biti izpolnjen pogoj, da je vsota kinetične in potencialne energije manjša od nič (Wk+Wp<0). Če predpostavimo atome na robu takega oblaka, potem mora veljati za večino teh atomov mv²/2-GmM/R<0, M je masa oblaka, m masa atoma. Ker pa je temperatura povezana s kinetično energijo (mv²/2=3kT/2), sta za nastanek zvzde odločilna Temperatura in masa posameznega plinskega, oz. prašnega oblaka. Poglejmo še pogoj, kdaj telo (recimo satelit) kroži okrog vesoljskega telesa M, saj vemo, da je takrat energija manjša od nič. Pogoj za kroženje je: mv²/R=GMm/R² ==> Wk=mv²/2=GMm/2R=-Wp/2, ==> 2Wk+Wp=0 Iz zadnje povezave lahko sklepamo, da mora biti za nastanek zvezde izpolnjen pogoj: 2Wk+WpŁ0
To je tako imenovan virialni teorem za gravitacijsko vezanost sistemov v vesolju. Oglejmo si masiven plinski in prašni oblak (recimo Sončeve mase) nekje v vesolju. Recimo, da je vsota obeh energij oblaka nič (Wk+Wp=0). Molekule in atomi v oblaku zaradi trkov sevajo in s tem se jim manjša temperatura, oziroma kinetična energija, kar spet pomeni, da se bo oblak začel krčiti in segrevati. Kdaj torej pride do zametka zvezde? Protozvezda je ime gmote plina s površinsko temeperaturo okrog 3000 kelvinov (v plinu še ne potekajo jedrske reakcije) iz katere bo nastala prava zvezda. Protozvezde sevajo v infrardečem in so zelo velike (100 ali več polmerov Sonca), zato imajo kljub skromni temperaturi, vlike izseve (premisli razmerje P/Po=(R/Ro)²(T/To)⁴). Lahko tudi rečemo, da se zvezda krči, dokler je hidrostatični tlak večji od tlaka plina (približek: rGM/2R>rkT/mo, to je Jeansov pogoj nestabilnosti za krčenje zvezde). Koliko časa traja krčenje oblaka od protozvzde, do glavne veje, ko stečejo jedrske reakcije, je odvisno predvsem od mase zvezde. Sonce je rabilo od protozvezde do glavne veje nekaj milijonov let, zvezda s pol manjšo maso okrog 10 milijonov let, zvezda s petkratno maso sonca pa samo okrog 10000 let, saj ima v tem primeru gravitacija veliko večji vpliv. Ko zvezda doseže glavno vejo (po zapleteni teoretični krivulji), se v njej začne zlivanje, v glavnem vodikovih, jeder, njena starost je takrat nič, temperatura v jedru zvezde pa 10 ali več milijonov kelvinov, tlak pa okrog 1015Pa.

Večina zvezd leži (v obdobju ravnovesnega stanju, takoj po končanju krčenja oblaka, ko se začne zlivanje vodika in ostalih jeder) na glavni veji (diagonali), tudi Sonce (že skoraj 5 milijard let in bo še toliko časa). Zvezde z visoko temperaturo in velikim izsevom so zelo masivne in obratno (do približne odvisnosti izseva od mase lahko pridemo s špekulacijo (uporabimo zvezo za sevanje črnega telesa), da je P µ T⁴ , temperatura na površju pa je povezana s temperaturo jedra, ki pa je sorazmerna z maso M, Tc µ moGM/Rk (hidrostatični tlak je p=rgh==>p=rGM/R, tlak v plinu je P=rkT/mo), kar nam da približno oceno, da je isev sorazmeren z maso na 4, v resnici je izsev sorazmeren z maso zvezde na 3.5, P µ M^3,5). Če smo bolj dosledni, ugotovimo, da je potenca v resnici odvisna od mase zvezd in zelo niha. Nekateri deli diagrama so prazni, kar pomeni, da so nekatere faze v razvoju zvezd zelo hitre (eksplozije nov, supernov, hiter prehod v fazo rdečih orjakinj, to je napihovanje po končanju zlivanja jeder ...). Na diagramu tudi opazimo, da imajo nekatere zvezde visoko temperaturo in majhen energijski tok P. Kako naj to pojasnimo? Predpostavimo, da zvezde sevajo po Stefanovem zakonu (kar se izkaže kot dober približek) : j=P/S = sT⁴ Iz te predpostavke sledi, da imajo te zvezde majhen polmer (majhno površino) saj velja :
P = 4pr²sT⁴.
Imenujemo jih bele pritlikavke in večina zvezd (tudi naše Sonce, ko bo porabilo jedrsko gorivo), bo končalo kot bela pritlikavka. Bele jih imenujemo zato, ker oddajajo belo svetlobo, ki je posledica visoke temperature. Opazimo pa tudi zvezde s temperaturo od 3000 K do 6000 K z velikim energijskim tokom P. To so ponavadi relativne stare zvezde (zvezde po prvi ravnovesni fazi zlivanja jeder, rdeče orjakinje), ki imajo (po Stefanu) velik polmer. Delijo se v rdeče orjakinje, nadorjakinje (zelo velik izsev), podorjakinje z relativno majhnim energijskim tokom P, izsevom. Lega zvezd na H-R diagramu je odvisna od starosti, mase in kemijske sestave zvezd.

Kako nastanejo rdeče orjakinje? V sredici zvezde prej ali slej zmanjka vodika. Tako kot peč, ki je ne nalagamo, se sredica zvezde, v kateri je zmanjkalo vodika, ohladi. Zaradi tega pride do dveh pojavov. Sredica se zaradi gravitacije sesede in se segreje do višje temperature kot jo je imela prej. Površinske plasti krčenju ne morejo slediti in močno sevanje sredice jih pripravi do tega, da se gibljejo navzven. Zvezda se zdaj premakne iz glavne veje navzgor proti desni po H-R diagramu. Zvezda se zelo poveča in seva rdečo svetlobo, ker so se površinske plasti ohladile. Izsev se poveča, čeprav je temperatura površja padla, a se je površina močno povečala. Po dovolj dolgem času se površinske plasti izgubijo v vesolju in preostane sredica prejšnje zvezde. V rdeči orjakinji se zaradi krčenja jedra vname helij. Koliko faz zlivanj se ponovi in s tem tudi nastali elementi, je odvisno od mase zvezde. Vodik izgoreva v helij, helij v berilij in skupaj v ogljik, ogljik izgoreva v neon in potem v kisik, kisik v silicij ... Zlivanje težjih jeder v še težje zahteve vse višje temperature, ki se pojavljajo v masivnejših zvezdah in pri eksplozijah nov in supernov. Vsi težki elementi so rezultat zlivanja jeder v sredicah zvezd in eksplozijah. To je tudi material, iz katerega smo nastali ljudje.

Pot zvezde v H-R diagramu je torej zelo zapletena. Če pogledamo H-R diagram kopice zvezd, kjer so zvezde enako stare a različnih mas, bomo preko prehoda (kolena2) iz glavne veje desno navzgor, lahko sklepali na starost kopice. Zakaj? Zvezde v kolenu ravnokar zapuščajo glavno vejo in so torej pokurile jedrsko zalogo energije. Ker pa poznamo čas, ki ga prebijejo zvezde določenih mas na glavni veji, je to že hkrati starost kopice. Recimo kopica, ki ima koleno v legi Sonca, z absolutno magnitudo okrog +4,8 je stara približno 10 milijard let, saj vemo, da bo Sonce vztrajalo na glavni veji skupaj 10 milijard let. H-R diagram je torej izredno uporaben, za določanje starosti zvezdnih kopic.

Poglejmo, kako bi izračunali, koliko časa Sonce ohranja enak izsev. Odgovor je, dokler poteka zlivanje jeder, predpostavimo, da je Sonce sestavljeno v glavnem iz vodika. Vemo, da gre pri, zlivanju vodika v helij, slabih 8% mase v energijo (mc²), ki Soncu omogoča konstanten izsev. Poglejmo, kolikšen delež se sprosti v eni sekundi, izsev Sonca v sekundi je:
Dmc²/s=4*10²⁶J/s ==> Dm=4*10²⁶J/(9*10¹⁶)(m/s)²=4,44*10⁹kg.
Koliko časa bo potrebno, da se pokuri ves vodik?

to=0.08Mo/Dm=0,08*2*10³⁰kg/4,44*10⁹kg=3,6*10¹⁸s=10¹¹let=10 milijard let
Velja tudi: t µ M/PµM/M^3,5 µ M^-2,5

Poglejmo, zakaj masivnejše zvezde hitreje pokurijo zalogo jedrske energije, hitreje zapustijo glavno vejo, uporabimo že poznani zvezi, P µ M^3,5, tµ M^-2,5?

P µ M^3,5 ==> t/to=(Mo/M)^2,5
Primer, za zvezdo z maso 4Mo:
t=to(1/4)^2,5=(1/32)to=življenje_Sonca/32.
Rezultat je presenetljiv.


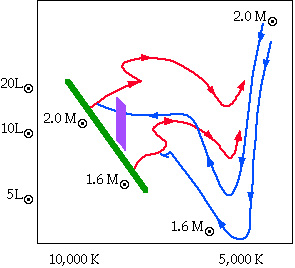
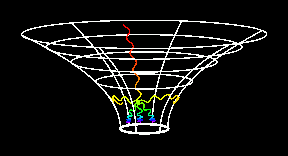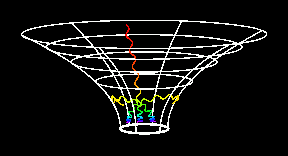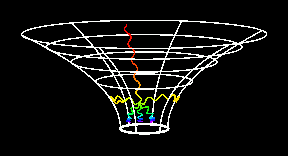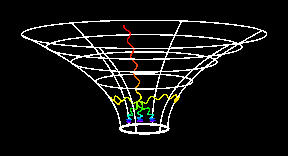
Na sliki sta primera razvoja zvezd z masama 1,6 in 2,0 Sončeve mase. Modra krivulja predstavlja pot in čas prehoda od protozvezde do glavne veje, imenuje se Hayashi-jeva sled. Zelena krivulja predstavlja glavno vejo, kjer zvezda preživi največ časa. Na glavni veji zvezde v jedrih zlivajo vodik v helij. Po koncu zlivanja se zvezda začne širiti in se premakne iz glavne veje desno navzgor v področje rdečih orjakinj. Bolj masivne zvezde ostanejo na glavni veji manj časa (gravitacije bolj stiska jedra, termonuklearne reakcije potekajo hitreje) in hkrati postanejo zelo velike rdeče zvezde (nadorjakinje). Masivne zvezde recimo lahko preživijo na glavni veji manj kot milijardo let (površinska temperatura 20 000K ali več), lažje pa prebivajo na glavni veji celo 10¹² let (površinska temperatura 3000K ali manj). Glej tudi:
http://www.geocities.com/CapeCanaveral/8851/hr.html


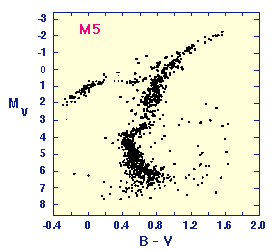
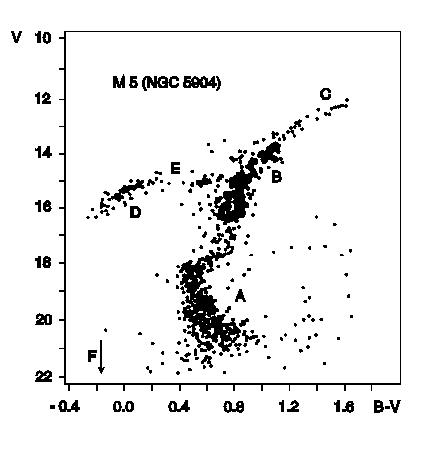
H-R diagram krogelne kopice M5. Ker so zvezde zapustile glavno vejo pri absolutni magnitudi okrog vrednosti za Sonce, predvidevamo, da je kopica M5 stara okrog 10 milijard let, toliko časa namreč zvezde velikosti Sonca vztrajajo na glavni veji. Vse masivnejše zvezde zapustijo glavno vejo že prej.
Desna slika, legenda oznak:

(A): Glavna veja (Main Sequence).

(B): Veja-področje rdečih orjakinj (Red Giant Branch).

(C): Območje Helijevih bliščev (Helium flash occurs here).

(D): Vodoravna-horizontalan veja (Horizontal Branch (HB)).

(E): Schwarzschildovo območje (Schwarzschild space in the HB).

(F): Bele pritlikavke, pod puščico (White Dwarfs (below the arrow)).

Na kratko omenimo še kefeide, to so zvezde, ki se periodično širijo in krčijo in zato tudi utripajo (spreminjajo sij). Izjemno pomemben podatek je ta, da je perioda utripanja mera za povprečen izsev zvezde. Kefeide se zato uporabljajo kot standardni svetilniki za določanje razdalj v naši galaksiji in razdalj do nam bližnjih galaksij. Kefeide so del zadnje faze razvoja masivnih zvezd po izstopu iz glavne veje, v H-R diagramu je to tako imenovano področje nestabilnosti. Eden izmed modelov pravi, da je zvezda nestabilna zaradi helija (helijev ventil), v zunanjih plasteh masivnih zvezd. Ko je zvezda v fazi krčenja, temperatura narašča in izsev se poveča, zunanje plasti postanejo bolj prozorne. Hkrati pa se začne helij ionizirati (izgubi en elektron), zaradi ionizacije se temperatura helija ne viša. V območju ioniziranega helija postane stisnjen helij precej neprozoren (ovira) za svetlobo. Helij tako postane zanka (zaprt ventil) za izsev, kar povzroči, da se ovojnica zvezde začne napihovati (razširjati). V fazi širjenja temperatura pada, elektroni in ioni helija se rekonbinirajo, plin postane boj prepusten, hkrati pa se pri rekonbinaciji sproti od prej nakopičena energija. Ovojnica zvezde zato spet zečne krčiti. Proces se tako periodično ponavlja.
Oglej si tudi poglavje o kefeidah, kjer se iz grafa lepo razbere fazne zamike med sijem, hitrostjo, polmerom in temperaturo utripajoče zvezde.

Zveza med magnitudo in periodo je logaritemska. Z grobim premislekom izpeljimo povezavo med magnitudo in periodo. Recimo, da zelo poenostavimo izpeljavo nihajnega časa pulzirajoče zvezde in sklepamo, da veljajo pri zvezdi in matematičnem nihalu približno enake zakonitosti (nihajni čas nihala je : to=2p(l/g)^1/2). Za g vstavimo GM/R ², za l pa kar polmer R. Tako dobimo naslednjo zvezo:

to=2p(R³/GM)^1/2 ==> tor^1/2=(3p/G)^1/2=3.74*10⁵kg^1/2m^-3/2s

Naša groba špekulacija je dala presenetljivo dober rezultat. Ker je izsev P funkcija mase (P µ M^3,5), in ker je magnituda logaritemsko povezana z izsevom ( log(j1/j2)=-0,4(m1-m2) ), masa pa sorazmerna z gostoto (gostota pa je funkcija periode utripanja to), lahko sklepamo na logaritemsko povezavo med magnitudo in periodo utripanja kefeide. Meritve potrjujejo prav to hipotezo. Oglej si prispevek o kefeidah.

Končni fazi v razvoju zvezd sta ponavadi dve : bela pritlikavka ali nevtronska zvezda.

Gostota bele pritlikavke je tako velika, da bi imel z njeno snovjo napolnjen nahrbtnik maso kot lokomotiva. Na Zemlji ne poznamo snovi, ki bi imela tako pošastno gostoto. V jedrih navadnih zvezd potekajo jedrske reakcije, ki vzdržujejo visoko temperaturo in visok tlak. Po našem modelu pa ta vzdržuje ravnotežje gravitacijskemu pritisku zunanjega dela, ki hoče zvezdo stisniti. Ko jedrske reakcije v jedru ponehujejo (ko zmanjka goriva), gravitacijske sile vedno bolj stiskajo zvezdo, dokler ne dosežejo stanja, ki je značilno za bele pritlikavke. Povprečna gostota belih pritlikavk je 10⁶ do 10¹⁰kg/dm3. Če pa je masa zvezde (jedra, ki ostane od rdeče orjakinje) nekoliko večja od mase Sonca, se krčenje zvezde ne zaustavi pri stanju, ki ustreza belim pritlikavkam, temveč šele v tako imenovanem nevtronskem stanju - nevtronska zvezda. V nevtronski zvezdi se pri zrušitvi zvezde (eksplozija supernove - tako eksplozijo so Kitajci leta 1054 opazovali v ozvezdju Bika, tudi podnevi) protoni in elektroni združijo v nevtrone:

n je nevtrino, kateri je najverjetneje odgovoren (radialni tok nevtrinov z veliko energijo) za odstranitev zvezdne ovojnice. Gostota nevtronskih zvezd je od 10¹³ do 10¹⁵kg/dm³. Nevtronska zvezda je kot velikansko atomsko jedro, ki jo v glavnem sestavljajo nevtroni, vsebuje pa tudi primesi protonov, elektronov in drugih delcev. Pri eksploziji supernove se atmosfera zvezde napihne (zaradi velike energije nevtrinov) in njeni plini brizgnejo na vse strani s hitrostjo več 100km/s. Rakova meglica je med najmočnejšimi viri radijskega sevanja, kozmičnih in rentgenskih žarkov na nebu, seva tudi polarizirano vidno svetlobo.

Februarja 1987 so astronomi prvič po skoraj štiristo letih opazili supernovo, ki jo je bilo mogoče videti s prostim očesom. Supernova, ki je dobila oznako 1987A, je ležala v velikem Magellanovem oblaku v oddaljenosti 170 tisoč svetlobnih let. Pred 170 tisoč leti je eksplodirala zvezda velikanka, ki so jo pred eksplozijo opazovali pod oznako Sanduleak - 69^o202. Kaj takega se je v zgodovini astronomije primerilo prvič. še več. V dveh velikih merilnikih, s kakršnimi poskušajo globoko pod zemljo zaznati radioaktivni razpad protona, so zasledili sunek nevtrinov ali antinevtrinov; osem jih je bilo v ZDA in enajst na Japonskem. Po treh mesecih je zvezda sevala močneje kot 200 milijonov Sonc, potem se je sij zmanjšal. Proučevanje svetlobe in nevtrinov ali antinevtrinov iz supernove 1987A je prispevalo k razumevanju veličastnega pojava. Glej sliko.

O črnih luknjah samo toliko : to bi naj bile zvezde z ogromno maso in gostoto (masa bi naj presegala 10 Sončevih mas), tako da gravitacija ne pusti, da bi kakršnokoli valovanje zapustilo njeno "površino", od tod ime črna luknja. če bi Sonce kolapsiralo v črno luknjo, bi se radij Sonca zmanjšal od 6,96 x 10⁵ km na 3km (špekulativna izpeljava "polmera" črne luknje iz pogoja, da je vsota kinetične in potencialne energije "fotona" nič, mf*c²/2-Gmf*m/R=0, ==> R=2Gm/c²). Gostota bi znašala 10¹⁶kg/dm³.

Zdaj, ko smo se zelo površno in z velikimi poenostavitvami seznanili s H-R diagramom (ta diagram je zelo poučen, je življenjepis zvezd, o njem se pišejo debele knjige), moramo opozoriti še na to, da bo naš H-R diagram nastal preko dveh posnetkov iste zvezdne kopice. Prvi posnetek je narejen z B filtrom (prepušča modro svetlobo), drugi pa z V filtrom (prepušča zeleno svetlobo). Razlika magnitud B-V je funkcija temperature, energijski tok P=j*S pa je funkcija magnitude, merjene skozi V filter, saj velja

(dj/dl=(2phc²/l⁵)(e^hc/lkT-1)^-1)

Iz zadnje enačbe se da pokazati, da je H-R diagram mogoče izluščiti iz funkcije V od (B-V).

SLIKA H-R DIAGRAMA

Nalogi tudi prilagamo nekaj zanimivih slik in karto neba vidnega iz naših krajev, da bi si lažje predsavljali, kje ležijo meglice, prikazane na CCD posnetkih. Lepo bi bilo, če bi to preprosto karto tudi kdaj zvečer uporabili.

Kako deluje CCD kamera

Osnova elektronskega beleženja slik je tako imenovani CCD čip, ki ga namestimo v goriščno ravnino teleskopa. Fotoni z astronomskih objektov skozi prozoren zgornji pokrov čipa vstopajo v silicijevo rezino in tam povzročajo fotoefekt (slika 2). Izkoristek tega procesa je dokaj dober, saj do 80% fotonov z valovnimi dolžinami med 400 in 1100nm povzroči prehod elektrona v prevodni pas. To je mnogo bolje kot pri filmu, kjer je izkoristek največ nekaj procentov. Mesto nastanka elektrona nam pove izvor ustreznega fotona. število elektronov na določenem mestu je sorazmerno s tokom padlih fotonov in tako s sijem ustreznega objekta. Za kvantitativne meritve astrnomskih objektov v goriščni ravnini moramo med ekspozicijo preprečiti izgubljanje ali morebitno potovanje elektronov po čipu. Elektronom moramo onenogočiti, da bi se vrnili nazaj v prejšnje vezano stanje. Poleg tega ne smemo dopustiti, da bi se razlezli po čipu in tako razmazali podrobnosti na sliki. Za oboje poskrbi napetost, ki jo priključimo med žicami na zgornji strani in med spodnjo stranjo silicijeve rezine. Elektroni se nabirajo v potencialnih jamah pod žicami, mesta, kamor bi se elektroni lahko vezali, pa električno polje potisne v notranjost silicija. Kanali, ki so zapolnjeni s snovjo, po kateri se prosto elektroni ne morejo gibati, so nanizani v pravokotni smeri glede na žice in elektronom preprečujejo tudi potovanje vzdolž žic. Tako dosežemo, da nas elektroni v prevodnem pasu "počakajo" na mestu svojega nastanka vse do trenutka, ko ekspozicijo končamo in preberemo, koliko in kje se jih je nabralo. To je dalo detektorju tudi ime : CCD je kratica za angleško skovanko Charge Coupled Device; v tem primeru je naboj vezan na električno polje žic. Po koncu ekspozicije s preklapljanjem napetosti na žicah elektrone najprej "zapeljemo" na rob silicijeve rezine, tam pa naboj s kondenzatorjem spremenimo v napetost, ga digitaliziramo in po hitri povezavi sporočimo računalniku. Informacija o osvetlitvi posamezne točke, to je pravokotnega območja med sosednjima kanaloma in pod ustrezno žico, je tako takoj po branju že zapisana v računalnikov spomin. CCD detektor je torej ploskovni detektor z nekaj sto tisoč točkami, ki pokrivajo površino okrog 2cm².

Prednosti CCD detektorja v primerjavi s filmom je veliko. Računalnik prebere naboj na CCD čipu v nekaj sekundah (v video kameri, kjer je potrebna manjša točnost pri branju, celo v 1/25 sekunde). Sliko lahko takoj prikažemo na zaslonu in se odločimo, če sta bili dolžina ekspozicije in centriranje objekta pravšnji ali pa bomo posnetek takoj ponovili. Zamudno razvijanje filma tako odpade.

Ker je število elektronov v prevodnem pasu sorazmerno številu vpadnih fotonov, je zato za razliko od filma odziv CCD detektorja linearen. Ob tem ima CCD detektor zelo velik dinamični obseg, to je razmerje med najmanjšo in največjo možno zabeleženo intenziteto. Na posnetku Oriona je to razmerje kar 1:15000. (Oglej si sliko m42 na monitorju.) Tako lahko na istem posnetku zabeležimo temne robne dele meglice ter zelo svetel osrednji Trapez. Kaj takega na filmu zaradi mnogo manjšega dinamičnega obsega ne bi bilo mogoče; če bi hoteli slikati celo meglico, bi bil Trapez presvetljen, ob dovolj kratki ekspoziciji za slikanje Trapeza pa ne bi videli temnih zunanjih delov meglice.

Kot boste videli med vajo, deluje slika Orionove meglice zelo naravno. Predel v temnem spodnjem kotu slike meglice nam to nazorno kaže (slika 3). Zabeleženi odčitki nihajo le zaradi relativno majhnega števila fotonov, ki so med ekspozicijo zadeli detektor. Prihajanje fotonov na detektor je naključen proces. Pri 100 pričakovanih fotonih na določeni točki jih pri posamezni ekspoziciji preštejemo nekaj več ali manj, vendar je razlika do 100 redkokdaj večja od (100)^1/2=10. Tej vrsti napak, ki jim pravimo fotonski šum, se ne moremo izogniti pri nobenem detektorju. Ostalim vrstam napak, kot je neželjeno vzbujanje elektronov v prevodni pas zaradi previsoke temperature detektorja ali napakam zaradi nenatančnega branja zbranega naboja, pa se izognemo tako, da detektor hladimo z več vzporednimi Peltierovimi členi na približno 200 K ter da naboj beremo dovolj počasi.

Do sedaj smo govorili le o prednostih CCD detektorja. Ima pa tudi eno pomanjkljivost: CCD čipi imajo relativno majhno površino, ki je občutljiva za svetlobo, tako da pokrijejo le majhen del goriščne ravnine teleskopa. Zato še vedno uporabljajo fotografske plošče kadar želijo hkrati posneti velik kos nebesnega svoda. Ne smemo pa pozabiti, da je slika, dobljena s CCD detektorjem, takoj na voljo v digitalni obliki in jo takoj lahko začnemo obdelovati: sliki lahko povečamo kontrast, izmerimo sij, pozicijo in velikost objektov, seštejemo in kvantitativno primerjamo posamezne slike istega objekta med seboj. Vse to gre pri filmu veliko težje : pri razvijanju moramo z zamudnim postopkom digitalizirati sliko, ki je na filmu zapisana kot kemijska reakcija zrnc. Tudi po razvitju imamo precej težav zaradi majhnega dinamičnega obsega zapisa in zaradi pogostih napak v zrnatosti filma. Tako tudi objekte, ki na nebu zavzamejo relativno velik prostorski kot, raje "pokrijejo" z mozaikom več CCD posnetkov kot pa da bi uporabili film.

Avtomatski 25 centimeterski teleskop, ki so ga razvili na astronomsko geofizikalnem observatoriju ( AGO ), se je izkazal kot zanesljiv tovrstni instument ( glej astronomske efemeride Naše nebo 1992). Pri zasukih teleskopa večjih od 90o je napaka okrog 5', pri zasukih manjših od 1o pa le do 10". Ker je vidno polje CCD detektorja na tem teleskopu precej večje ( 10'x15'), je problem iskanja objektov na nebu rešen.

Temni objekti zahtevajo kljub veliki občutljivosti CCD detektorja dolge ekspozicijske čase. Med trajanjem osvetlitve sledi teleskop navideznemu vrtenju neba, tako da se slika astronomskih objektov na CCD detektorju ne razmaže. Pri polurni osvetlitvi se mora teleskop obrniti za 7,5o, to je za 7,5x60x60"=27000". Slika bo ostra, če teleskop pri tem zasuku ne bo zgrešil za več kot kako ločno sekundo. Take natančnosti ne zmorejo še tako natančno izdelani mehanski deli. Zato je potrebno napake pri sledenju sproti preverjati in odpravljati. Najenostavnejša rešitev je, da pravilnost sledenja spremljamo s pomožnim daljnogledom, ki je pritrjen na glavnega. Kako svetlo zvezdo v bližini opazovanega objekta nastavimo na nitni križ, napake pri sledenju pa sproti popravljamo s komandami za krmiljenje obeh motorjev na teleskopovih oseh. Nerodno je le, da moramo ves čas ekspozicije stati ob okularju, pa še naša sodba o velikosti potrebnega popravka sledenja je precej negotova. Sodobnejši način aktivnega sledenja, ki ga uporabljajo na AGO, je mnogo natančnejši in za opazovalca manj naporen. Namesto opazovalca opravi nalogo manjša CCD kamera, ki jo namestimo v goriščno ravnino pomožnega teleskopa. Med trajanjem osvetlitve na glavnem teleskopu naredimo z manjšim teleskopom dolgo serijo nekajsekundnih CCD posnetkov okrog svetle zvezde. Po vsakem posnetku računalnik analizira ali je slika svetle zvezde še vedno na istem mestu ter po potrebi pošlje ustrezne ukaze motorjem.

Avtomatski teleskop današnjega časa je precej zapleten: dva CCD detektorja, dva računalnika, dva koračna motorja, računanje pozicij objektov v danem trenutku, sprotna analiza in popravljanje napak pri sledenju, ... , pravzaprav je avtomatski teleskop vrsta natančnega robota. Natančnega v tem primeru pomeni, da bi iz Ljubljane lahko ob lepem vremenu slikali Aljažev stolp na Triglavu.

PCvista

CCD posnetek astronomskega objekta vsebuje ogromno informacij : Tipično je njegov zapis dolg nekaj kBytov. Tako v eni noči ponavadi posnamemo za nekaj 10 MBytov gradiva. Ena osnovnih funkcij vsakega programa za analizo CCD astronomskih slik je zato redukcija te velike količine informacij na znosno količino astronomsko zanimivih lastnosti merjenega objekta. Pred tem je treba z vsakega posnetka odstraniti instrumentalne napake, ki nastanejo pri prehodu svetlobe skozi teleskop in njeni registraciji na CCD-ju. Kljub njeni pomembnosti te prve stopnje obdelave v pričujočih nalogah ne boste srečali. Delo je zamudno in ni toliko zanimivo.

V svetu je v uporabi več programskih paketov za obdelavo astronomskih slik, ki so si podobni v začetnih fazah obdelave posnetkov, razlikujejo pa se po izpopolnjenosti orodij za končno obdelavo fotometričnih oziroma spektroskopskih meritev. Naštejemo lahko : IRAF, STDAS, VISTO ( ki je bila razvita na več kalifornijskih univerzah ), v Evropi pa največ uporabljajo Midas. To so veliki programski paketi s po nekaj sto tisoč vrsticami kode. Marsikateremu programerju je lahko za zgled, da so ti paketi nekomercialni in jih je zato mogoče dobiti zastonj ali pa proti simbolični odškodnini.

PCvista je edini kvalitetni program za digitalno obdelavo astronomskih slik, ki teče na PC računalnikih.

PCvista : najpomembnejši ukazi

To je le kratek uvod v uporabo PCviste. Med obdelavo si pomagajte z ukazom: HELP ukaz, oziroma HELP, ki nam našteje vse možne ukaze.

Najprej gremo v delovni direktorij (napišemo : cd zvezde). Ko smo v zvezdah, inicializiramo - poženemo PCvisto z ukazom: pcvista . Ko se zaslon umiri, smo v DOS-u, vendar računalnik pozna 37 dodatnih ukazov, ki sestavljajo programski paket PCvista. Najpomembnejši so naslednji:

POZOR : Ukaze najprej samo preberite (prvih šest lahko sproti preizkusite), uporabili jih boste šele pri analizi CCD posnetkov in pri H-R diagramu.

1 A
je ukaz, ki vas iz grafičnega preseli nazaj v tekstovni način. Toplo ga priporočamo pred startom kakršnegakoli editorja ali drugega programa, ki ni vključen v Pcvisto.

2 BUFFERS slika ( recimo buffers m42 )
izpiše osnovne podatke o sliki (v našem primeru o sliki m42), ki je zapisana v datoteki slika.fts (v našem primeru v datoteki m42.fts). To so npr. njena velikost, ime objekta ter kdo, kdaj in kje jo je posnel.

2 TV slika (spet si izberimo m42, zato bi naš ukaz izgledal tv m42)
pokaže sliko na zaslonu. Intenziteta osvetlitev na določeni točki slike je prikazana z ustrezno barvo s palete 16 barv, ki jih lahko prikaže PC-jev zaslon. Vse točke, ki imajo intenziteto osvetlitve nižjo od minimum, so pobarvane z barvo 1; vse točke z intenziteto večjo od minimum $+$ razpon pa z barvo 16. Vmes je barvna skala linearna. Ukaz TV slika razpon minimum ( recimo tv m42 400 200 ZOOM=3 ) nam omogoča ročno nastavitev področja intenzitet, ki ga bomo ogledovali. Pogosto je potreben dodatni parameter ZOOM. V našem primeru bomo videli trikrat povečano sliko ( ZOOM=3 ), ki je spravljena v datoteki m42.fts, pri čemer bo barvna skala pokrila območje intenzitet med 200 in 600 enotami. Dodatni parameter BOX=n omeji prikaz slike na izraz ( boks ), ki je definiran pod številko n. Glej ukaz št. 6!

4 COLOR
paleta nam omogoča izbor barvne palete. Palete imajo trenutno naslednja imena : vga-wrmb (white, red, magenta, blue), vga-heat (rdeče oranžno rumeni toni), vga-bw (črno bela), vga-wb (belo črna), vga-rain (še ena barvasta).

5 CURSOR
je ukaz, ki omogoča pregledovanje intenzitet posameznih točk na sliki, ki smo jo prikazali z ukazom TV slika. Po sliki se premikamo s puščicami (kurzorji). Tipka Insert hitrost premikanja kurzorja spremeni iz 10 v 1 točko oz. obratno. Pregledovanje s kurzorjem zaključimo s pritiskom na tipko Enter ali Return. Pri premikanju po ekranu s kurzorjem se pod sliko izpišejo koordinate in intenziteta trenutne točke.

6 BOX n INT (recimo box 5 int)
omogoča interaktivno definicijo boksa (izreza) s številko n. Pred tem moramo sliko prikazati z ukazom TV slika ( recimo spet tv m42 ). Potek je naslednji : ko izberemo boks, pritisnemo Enter in se pojavi nekje na sliki križec (+), potem s kurzorji križec premaknemo v sredo območja, ki ga želimo opazovati, nato pritisnemo Enter, nakar pa še s pritiski na kurzorje definiramo velikost območja (naredimo okence), ki ga želimo opazovati, na koncu pa okence potrdimo s tipko Enter, s tem smo definirali boks n. Ko je boks n definiran, lahko veliko ukazov (npr. prikaz analize slike) poženemo le na tako definiranem izrazu, če ukazu dodamo parameter BOX=n (recimo tv m42 box=5 300 100 zoom=3 , za začetek lahko razpon (300) minimum (100) izpustimo). Včasih je bolje koordinate boksa vtipkati neposredno :
BOX n nc=st.stolpcev nr=st.vrstic cc=sred.stolpec cr=sred.cvrstica. Ukaz BOX n DEL definicijo boksa n zopet izniči. če dobiš na zaslonu drugačno sliko kot si jo definiral z boksom, potem to pomeni, da je boks s to številko že nekdo definiral, vendar na drugem območju, zato ta boks uniči ali pa definiraj novega.

7 PL
je ukaz, ki požene interaktivni komandni jezik za risanje grafov. Podatke zajema iz stolpično urejenih ascii datotek. Tipično zaporedje ukazov za izris preprostega grafa, če imamo spravljene vrednosti abscis v stolpcu 1, vrednosti ordinat pa v stolpcu 2 ascii datoteke z imenom podatki.dat, je naslednja: pl, data podatki.dat, xcolumn 1, ycolumn 2, limits, erase, box, connect. če bi namesto conect uporabili points, bi namesto linije narisali ločene točke. Dodatni ukazi omogočajo risanje oznak, povečevanje, barvanje, tiskanje... V DOS se vrnemo z ukazom end .

8 COL slika n ( recimo col m42 112 )
nariše graf intenzitet v stolpcu n slike slika.fts. Ukaz nas ne vrne v DOS ampak ostanemo v PL okolju. če nam skala grafa ni všeč, ga lahko modificiramo. Tipični ukazi za to so : limits x1 x2 y1 y2, erase, box, connect, kjer so x1, x2, y1, y2 nove meje za absciso in ordinato. V DOS se vrnemo z ukazom end. Pozor : lahko se zgodi, da sta vlogi stolpcev in vrstic zamenjani - to preverimo z ukazom CURSOR, glej točko 5. Z ukazom limits se lahko s kurzorji pomikamo po diagramu in odčitavamo ordinate in intenziteto - "sij". Pozor col.bat in row.bat sta komandni proceduri, narejeni na FNT in nista del pcviste, ponavadi sta v mapi s slikami (recimo zvezde).

9 ROW slika n
nariše graf intenzitet v vrstici n slike slika.fts. Ostali komentarji in opozorila so enaki kot pri ukazu COL, glej točko 8.

10 NEBO slika (recimo nebo ohpb34m)
izračuna vrednost neba (- ozadja) na sliki slika.fts. Ta ukaz pravilno oceni tudi tipično napako (standardno deviacijo) za točke, ki pripadajo ozadju. Ta ukaz morate izvesti pred uporabo ukaza STARS na izbrani sliki. POZOR : ukaze nebo, stars, gphot, identify boste uporabili samo na dveh posnetkih, to sta ohpv17m in ohpb34m!

11 STARS slika show outfile=ime (recimo stars ohpv17m show outfile=zvezdav)
poišče zvezde na sliki slika.fts (v našem primeru na sliki ohpv17m), ki smo jo prej ukazali z ukazom tv (v našem primeru tv ohpv17m). Pozicije zvezd sproti označuje na zaslonu, rezultate pa spravlja v datoteko ime (v našem primeru v datoteko zvezdav). Možno je uporabiti tudi ukaz box=n. Pred ukazom stars morate pognati ukaz nebo, glej točko 10.

12 GPHOT slika infile=vhodno ime outfile=izhodno ime verbose (recimo gphot ohpv17m infile=zvezdav outfile=podatkiv verbose)
izračuna fotometrično intenziteto (magnitudo) zvezd na sliki slika.fts. (Pazite, izhodno ime ukaza stars je vhodno ime ukaza gphot.) To naredi tako, da izračuna kakšen Gaussov profil se najbolje prilega opazovani zvezdi (izračuna standardno deviacijo $\sigma$ za sij in jo primerja z že znanimi standardi). Pozicije zvezd preberi iz datoteke vhodno ime (rezultat ukaza STARS), rezultate pa shrani v datoteko izhodno ime (v našem primeru v datoteko podatkiv). Opcija verbose pomeni, da bo rezultate sproti izpisoval tudi na zaslon. To je uporabno, ker se program včasih računsko zatakne. Obvestila tipa sqrt domain error so nepomembna. Tudi ogromne formalne napake izračunanih intenzitet (magnitud), ki jih javlja program, so brez pomena. Huje pa je, če pride do runtime error. V tem primeru (po ukazu A) s primernim editorjem (recimo s pcshell) preglejte vhodno datoteko ter izbrišite zvezdo, pri kateri se je računalniku zataknilo ("fitanje" Gaussovih profilov je nelinearen proces, ki numerično ni preprost, zato je po izkušnjah eno zvezdo bolje izgubiti kot pa jo narobe pofitati). Zvezda, ki jo morate izbrisati, je v vhodni datoteki označena z zvezdico. če imate čas, pa je boljše, da še enkrat poženete ukaz STARS...

13 IDENTIFY
požene program, ki omogoča avtmatsko medsebojno identifikacijo zvezd na dveh podobnih posnetkih (v našem primeru na posnetkoma ohpv17m in ohpb34m). Ukaz je uporaben zlasti pri risanju H-R diagrama odprte zvezdne kopice. Denimo, da imamo v datoteki podatkiv spravljene rezultate GPHOT fotometrije kopice v V pasu, v datoteki podatkib pa ustrezne rezultate za B pas. Ko nas program vpraša po imenih teh dveh datotek in datoteke za končne rezultate (sami si izberite ime), mu moramo povedati še kakšen je relativni premik med obema slikama - ta nastane zaradi nenatančnosti instrumentov . Tega najlaže preberemo s primerjavo koordinat na ustreznih gphod datotekah (z ustreznim editorjem). Premiki so za različne zvezde rahlo različni, kljub temu pa so tolerance relativno majhne. če je npr. premik v x(=prvi) koordinati med B in V posnetkom tipično +1 točko, bo primerno območje za Dx do 3 (izberi toleranco do 10). Ko se na ekranu izpiše : x pozicija v B-x pozicija v V naj bo med A in B. Potem napišite
A : 0
B : 10
Nato pritisnete Enter in enako ponovite še za y os. Izhodna datoteka ima naslednjo strukturo :
stolpec 1 :
identifikacijska številka zvezde v datoteki podatkiv,
stolpec 2 :
x koordinata iz datoteke podatkiv,
stolpec 3 :
y koordinata iz datoteke podatkiv,
stolpec 4 :
magnituda ( npr. V ) iz datoteke podatkiv,
stolpec 5:
magnituda ( npr. B ) iz datoteke podatkiv,
stolpec 6:
razlika magnitud (npr. B-V) v datotekah podatkib in podatkiv.
V primeru, da pride med izvajanjem ukaza do runtime error napake, je vzrok najverjetneje napaka v eni od vhodnih datotek. Preglej ju z editorjem in ju popravi ( ponavadi se kakšen klicaj znajde na nepravem mestu ).

Analiza nekaj značilnih posnetkov s CCD kamero

Pri vsaki sliki s pomočjo ukaza za risanje intenzitet v vrsticah - stolpcih (ukaza 8, 9) natiskajte po en diagram z ukazom HARDCOPY .

Natiskaj tudi naslednjih 5 slik s tipko Print Screen , seveda morate biti v grafičnem načinu delovanja, kar dosežete (preden narišete sliko na ekran) z ukazom GRAPHICS.

V tem delu naloge slik ne bomo analizirali, ampak se bomo naučili, kako si jih ogledamo, jih identificiramo in preberemo z njih osnovne informacije o posnetem astronomskem objektu. Pravo analizo posnetkov bomo odložili do naslednje naloge (H-R diagram odprte zvezdne kopice).

Ogledali si bomo 5 posnetkov, ki so bili posneti januarja 1991 z novim CCD sistemom na astronomskem observatoriju na Golovcu. To so posnetki petih znanih astronomskih objektov : Orionove meglice, Konjske glave, Rakovice, spiralne galaksije NGC 2903 ter galaksije vidne s prostim očesom v Andromedi M31. Vsi posnetki so bili narejeni brez barvnih filtrov skozi 10-inčni avtomatski teleskop, ki je delo domačih strokovnjakov. CCD pokrije vidno polje velikosti 10'x16'.

Posnetki so že delno obdelani, to pomeni, da so s kalibracijo z ravnim poljem odstranjene instrumentalne napake zaradi odbojev svetlobe v teleskopu in različne občutljivosti posameznih delov CCD-ja.

Obdelava posnetkov

Pri ogledovanju posnetkov uporabite vse ukaze od 1 do 9 ( TV, COLOR, CURSOR, BOX, COL, ROW, LIMITS, ... ). Obvezno si vse uporabljene ukaze ( in njihove parametre ) takoj zapišite na list. Brez tega boste pozabili katere variante vrednosti parametrov ste že preizkusili in kaj hitro boste vedno znova npr. z neuporabnim kontrastom risali sliko na zaslonu.

Orionova meglica (datoteka m42.fts)
Najprej morate pognati delovni direktorij ( napišite cd zvezde ), nato poženite še PCvisto ( napišite kar pcvista ), nakar z ukazom tv slika ( v našem primeru tv m42 ) narišete sliko na zaslon. Preizkusite različne barvne palete z ukazom COLOR ( če imate črno-beli VGA zaslon, ta ukaz izpustite ). Slika vam je morda všeč, vendar se njena prava lepota skriva drugje. Orinova meglica je emisijska meglica, ki jo osvetljujejo 4 zvezde v sredini meglice, ki jim pravimo Trapez. če ste se kdaj preizkusili z amatersko astro fotografijo, veste, da je nedosegljiv izziv hkrati posneti temna zunanja območja in izredno svetle zvezde v Trapezu. S CCD kamero je to zaradi njenega izjemnega dinamičnega obsega mogoče. Občutek za dinamični obseg posnetka boste najlaže dobili tako, da boste sliko najprej narisali s TV ukazom z razponom 100 in minimumom okrog 25 enot. Osrednja območja meglice so presvetljena, lepo pa se vidijo temne strukture daleč na obrobju meglice. Nato ponavljajte ukaz TV, tako da ob istem razponu višate vrednost minimuma za npr. 100 enot. Območje dobrega kontrasta se počasi seli proti osrednjim območjem meglice. čudovito ! Kakšen razpon in minimum je primeren za gledanje osrednjega Trapeza ?

Lahko identificirate posamezne od štirih zvezd ? Kje je na naši sliki sever, kje vzhod? Z ukazom CURSOR ugotovi, kolikšna je razlika med intenziteto zunanjih območij meglice in ozadjem ter koliko nad ozadjem sega vrh najsvetlejše zvezde Trapeza. Kolikšen je torej dinamični obseg tega posnetka ? Ta obseg obvezno zabeleži. Na sliki 2 si oglej kje leži Orion.

Konjska glava ( datoteka konjgl.fts )
Leži v Orionu, je verjetno najbolj znana med absorbcijskimi meglicami ( narišemo jo z ukazom tv konjgl ). Svetla emisijska območja v ozadju delno prekriva temna meglica, ki ima obliko konjske glave. Meglica je v resnici rdeče barve, zato bo videti najbolj naravno, če boste uporabljali barvno paleto vga-heat. Obliko Konjske glave boste po risanju z ukazom tv prepoznali brez težav. Vendar videz vara. Nivo osvetlitve predelov v Konjski glavi je le za malenkost nižji od nivoja osvetlitve emisijskih predelov. To preverite z ukazoma ROW in COL ! Enega od teh diagramov natiskajte. Kaj lahko sklepate o nivoju šuma Golovškega CCD sistema ?

Rakovica ( datoteka rakflip.fts )
Leži v Biku ( nariši jo z ukazom tv rakflip ), je ostanek eksplozije super nove, ki so jo Kitajci opazili leta 1054. Ob eksploziji je večino snovi odneslo navzven. Del prvotne zvezde pa se je skrčil v izredno gosto nevtronsko zvezdo, ki jo danes opazimo kot pulzar s periodo 0,033 sekunde.

Koristno je, če s parametrom BOX pri ukazu TV prikažete le območje meglice. Ali lahko ugotovite približno lokacijo pulzarja ?

NGC 2903 ( datoteka ngc2903.fts )
je spiralna galaksija v ozvezdju Leva ( sliko boste najbrž znali zdaj narisati brez dodatnih navodil ). Kot pri vseh spiralnih galaksijah je snov v njenih zunanjih delih zbrana v tankem disku. Lahko ugotovite, kakšen je kot med ravnino diska in nebesno kroglo ? S primerno nastavitvijo kontrasta si oglejte tudi turbulentne notranje predele te galaksije.

M 31 ( datoteka m31.fts )
Edina galaksija vidna s prostim očesom iz naših krajev ( vidna le pozimi v Andromedi ). Od nas je oddaljena 2,16x10¹⁹ km. Podobna je naši galaksiji, glej slike na strani 5 in 6. 3 in 4. Ali bi znal pokazati na sliki, kje približno bi se nahajalo naše Sonce glede na središče galaksije, če bi bila to slika Rimske ceste ? Premer naše galaksije je 25000pc ( pc beri parsek, to je ena izmed astronomskih enot, 1pc=30,84x10¹²km=206000 razdalj od Zemlje do Sonca=3,26 svetlobnih let ). Ali veš, da Sonce potuje okrog središča galaksije s hitrostjo 250 km/s in en obhod traja 2x10⁸let?

Preglejte še vse ostale posnetke, imena boste našli z ukazom dir .fts. Imena si izpišite v zvezek ! Priporočamo vam sliko galaksije ngc4565.

Kratko navodilo za uporabo programa "Model masivne homogene zvezde"

Potrebne datoteke - programi : velzv.exe, velzv.pl

Uvod

Program izračuna osnovne fizikalne lastnosti in notranjo strukturo zvezde s homogeno kemijsko sestavo in maso med eno in desetimi Sončevimi masami (Mo=3x10³⁰ kg - Mo je masa Sonca, vse količine,ki se nanašajo na Sonce, so označene z indeksom o). Z njim lahko izračunamo lego zvezd na glavni veji H-R diagrama : za zvezde z različnimi masami ( vendar običajno podobno kemijsko sestavo) narišemo njihov izsev kot funkcijo površinske temperature (P = 4pr²sT⁴).

Program rešuje sistem sklopljenih nelinearnih diferencialnih enačb zvezdne strukture ob ustreznih robnih pogojih v centru in na površini. Pri tem se drži metode, ki jo je prvi opisal M. Schwarzschild v knjigi Structure and Evolution of the Stars (Princeton University Press, 1958). Kot lahko sklepate že po letnici izdaje te knjige, je naš model relativno preprost. Kasnejši razvoj tega področja je omogočil obravnavo kemijsko nehomogenih zvezd, ki nastanejo zaradi zlivanja lažjih elementov v težje v njihovih sredicah ter obravnavo termično in dinamično nestabilnih faz v razvoju zvezd. Taki modeli so računsko zahtevni ( nekaj 10 ur Cray X-MP CPU časa v primerjavi z 1,6 sekunde CPU časa na Vax-u UEK2 za naš program ). Kljub temu pa tudi pričujoči program omogoča študij lastnosti zvezd na glavni veji H-R diagrama.

Tehnični opis

Ko boste prebrali navodila, poženete diagram z ukazom velzv , seveda moramo biti v delovnem direktoriju zvezde.

Program nas najprej vpraša po vhodnih parametrih ( masi, radiju, procentu vodika in procentu helija - omejitve v izbiri nam sporoči program, vsak izbran parameter potrdimo s tipko Enter ). Dobra začetna ocena za radij zvezde v enotah radija Sonca je enaka kvadratnemu korenu iz njene mase ( v enotah Mo). Nato program začne z iskanjem rešitev enačb zvezdne strukture. Da se pokazati, da imajo enačbe zvezdne strukture skupaj z enačbo stanja in robnimi pogoji ob poznani masi in sestavi zvezde eno samo rešitev. Nerodno je le, da se v ovojnici masivnih zvezd energija prenaša s sevanjem, v jedru pa s konvekcijo. Sistema enačb sta dokaj različna. Program zato rešuje enačbe jedra iz središča navzven, enačbe ovojnice pa s površine navznoter. Na meji med jedroma in ovojnico je treba rešitvi pravilno stakniti. Tehnično gledano mora imeti parameter, ki ga je Schwartzschild imenoval C, tako vrednost, da bo parameter število sečišč enak 1.

Po izpisu osnovnih fizikalnih parametrov zvezde na zaslon (ne v datoteko!) naredi program tri nove datoteke z imeni temper.zv, tlak.zv in pldata.pl . ( POZOR : Fizikalne parametre - lastnosti modela si zapišite v zvezek, saj se ne zapišejo v nobeno datoteko, potrebovali jih boste za risanje H-R diagrama ). Prvi dve sta ASCII tabeli radiale odvisnosti temperature in tlaka. Slednja vsebuje nekatere podatke za risanje grafov. če se v naprej vstavljeni radij zvezde močno razlikuje od na koncu izračunanega, poženi program znova z novim radijem.

Radialno odvisnost temperature in tlaka narišemo z ukazom pl velzv ( Prej moramo pognati PCvisto z ukazom PCvista ter po možnosti nastviti barve z ukazom color vga-wrmb ). Radialne odvisnosti gostote program ne nariše, vendar oblike te krivulje ni težko uganiti. Strmina radialne odvisnosti gostote bi bila vedno med položnejšo temperaturo in bolj strmo tlakovno krivuljo, saj povsod v zvezdi kar dobro velja enačba idealnega plina rµp/T (delež sevalnega tlaka je povsod majhen).

Program ( graf ) zapustimo z ukazom end . Preden zapustite program ( graf ), natisnite graf ( zaslon ) z ukazom hardcopy .

če hočete ohraniti grafe radialnih potekov temperature in tlaka za kasneje, preimenujte ustrezne tri datoteke pred ponovnim startom Pascalovega programa. To lahko naredite npr. s Pctools ali s Tp. pascalom, Notepadom ...

Za risanje H-R diagrama si izberi 10 mas od 1,1 do 9,9 Sončnih mas, korak naj bo med 0,5 in 1. Na ordinato H-R diagrama nanašaj log(P/Po)
(P = 4pr²sT⁴, s=5,67x10^-8W/m²K⁴, Po=3,9x10²⁶W). Na absciso nanašaj temperaturo v kelvinih, začetek diagrama pa naj se začne z najvišjo temperaturo, tako kot je označeno na sliki 1.

H-R diagram odprte zvezdne kopice

Potrebne datoteke : ohpv17m.fts, ohpb34m.fts, hrdiag.pl

Uvod

Zdaj, ko ste spoznali, koliko dela nam vzame ročno računanje in risanje H-R diagrama, pa poglejmo, kako to naredi računalnik za konkretno gručo zvezd.

V okviru te naloge bomo narisali H-R diagram odprte zvezdne kopice NGC 6819. želimo preveriti, da je lega večine zvezd na takem diagramu v bližini črte, ki ji pravimo glavna veja. Tako "opazovalno" glavno vejo bomo nato primerjali s "teoretično", ki jo dobimo kot rezultat druge naloge ( Model homogene zvezde ). Poleg tega bomo z opazovalnim H-R diagramom lahko identificirali zvezde, ki pripadajo rdečim orjakinjam ter "modrim vsiljivcem" ( blue stragglers ).

Opazovalni podatki so bili posneti v juliju 1990 na 1,2-meterskem teleskopu Newtnovega tipa na Observatoire d'Haute Provence v Franciji. Prednost tega teleskopa je veliko vidno polje ( 5'x7' ). To so do sedaj najnatančnejši posnetki osrednjega območja te kopice. Prvi posnetek ( ohpv17m.fts ) je 17-minutna ekspozicija te kopice skozi V filter, drugi ( ohpb34m.fts ) pa 34-minutni posnetek skozi B filter. Posnetkov skozi U filter v naši nalogi ne bomo potrebovali. Oba posnetka sta že delno obdelana : z njih so odstranjene instrumentalne napake, tako da je zabeležena intenziteta linearna funkcija osvetlitve . Nekaj problemov s saturacijo je le pri najsvetlejših zvezdah posnetih v V filtru, vendar ta problem za naše namene ni pomemben.

Potek obdelave

H-R diagram je graf, v katerem rišemo (kot je bilo rečeno že v uvodu) V magnitudo zvezd v odvisnosti od razlike med njihovo B in V magnitudo (B-V). Torej moramo poznati navidezne sije zvezd skozi pasovna filtra V in B. To meritev moramo narediti za čimveč zvezd, saj lahko drugače napake v meritvi V magnitude, zlasti pa razlike med B in V magnitudo, sliko popolnoma razmažejo. Ker so opazovanja v V pasu točnejša od tistih v B, začnimo z analizo posnetka skozi V filter (datoteka ohpv17m.fts). Najprej je na mestu nasvet :
Na list si sproti pišite vse ukaze, ki ste jih uporabili. Beležite tudi delne rezultate, zlasti pa imena datotek, kjer imate delne rezultate spravljene. Brez dobrega "knjigovodstva" se vsaka obdelava slik hitro sprevrže v spraševanje - kaj sedaj delamo, ki pa največkrat ostane brez pravega odgovora.

Po začetni nastavitvi sistema (inicializaciji sistema, izboru palete - glej navodila za program PCvista) si najprej ogledamo sliko z ukazom tv ohpv17m. Verjetno ste presenečeni, koliko zvezd se lahko znajde na koščku neba z velikostjo 5'x7' ! Očitno je zvezd preveč da bi jih lahko merili ročno, zato si bomo pomagali z ukazi za fotometrično analizo bogatih zvezdnih polj (ukazi od 10 do 13). V ta namen moramo najprej določiti pozicije zvezd na našem posnetku. Računalnik bo imel za zvezdo vsako ojačitev, ki bo za neko minimalno razliko presegala običajen nivo neba (ozadja). Poleg tega bo preveril, da ojačitev ni nezvezdnega izvora : biti mora približno enakomerno razmazana na vse strani ter ne prestrma (kozmični žarek) in ne prepoložna (difuzen objekt, npr. meglica ali galaksija). Preden se lotimo te naloge, moramo dobro poznati nivo ozadja (neba). Tega izračunamo z ukazom 10, to je ukaz NEBO...

Sedaj začnemo z iskanjem zvezd in njihovih lokacij. Najprej sliko z ukazom TV... narišemo v primerni barvni skali (če imamo črnobeli monitor tega ne naredimo), nato pa poženemo ukaz 11, to je STARS... če se nam zdi, da gre delo prepočasi, lahko iskanje dodatno omejimo na določen izrez slike (uporabimo dodaten parameter BOX=n). Vendar manjši izrez pomeni manj zvezd in zato slabši končni H-R diagram, torej če je dovolj časa, raje uporabite ukaz stars na celotnem posnetku.

Lege zvezd sedaj poznamo, ne poznamo pa njihovega sija (magnitude). To naredi ukaz 12 ( to je GPHOT... ), ki skuša vsako ojačitev, ki jo je ukaz STARS označil kot zvezdo, pofitati z Gaussovim profilom.

Analiza posnetkov v V filtru je tako končana, saj za nekaj sto zvezd poznamo njihove V magnitude. To niso navidezne V magnitude zvezd, ampak njihove ti. instrumentalne magnitude. Obe vrsti magnitud se razlikujeta le za konstanto, ki je odvisna od ekspozicijskega časa, velikosti teleskopa, izkoristka teleskopa, CCD detektorja in prosojnosti neba. Konstanto bi lahko določili s primerjavo instrumentalnih in navideznih magnitud standardnih zvezd, to je zvezd, katerih navidezno magnitudo poznamo iz neodvisnih meritev. Tudi v našem polju je nekaj takih zvezd, vendar te kalibracije ne bomo naredili : zanima nas le odvisnost relativne V magnitude zvezd od njihove relativne B-V magnitude, zato premiki za konstanto v tem primeru niso pomembni.

Isti postopek ponovimo še za posnetek skozi B filter (datoteka ohpb34m.fts). Seveda morate biti previdni, da ne bi slučajno uporabljali enakih imen za vhodne in izhodne datoteke, če smo recimo pri V filtru uporabili imeni zvezdav in podatkiv , je prav, da za B filter uporabimo imeni zvezdab in podatkib (glej točko 13). Ker zvezde, ki smo jih izmerili na V in B posnetkih niso nujno iste, moramo ugotoviti, katere zvezde si medsebojno ustrezajo in izračunati njihovo B-V magnitudo. To naredimo z ukazom 13, to je IDENTIFY... Identifikacija temelji na dejstvu, da je transformacija med legami zvezd na obeh posnetkih preprosta translacija (z določenim tolerančnim faktorjem).

Ukaz IDENTIFY nam naredi ascii datoteko, v kateri so (poleg ostalega) tabelirane instrumentalne V in B-V magnitude posameznih zvezd. Preostane le, da te rezultate predstavimo v obliki H-R diagrama. To naredimo z ukazom PL , ki nas postavi v okolje za interaktivno risanje grafov. Do cilja bomo prišli najhitreje, če bomo vtipkali ukaz data datoteka.pod (tu pod izrazom datoteka stoji ime datoteke, ki smo si ga izbrali pri ukazu identify za datoteko z rezultati) in naslednji ukaz je input hrdiag, ki izvede ukazano datoteko, ki nariše končni graf. V PL okolju po potrebi še opravimo skaliranje in popravimo izgled grafa. Graf obvezno natisnemo z ukazom hardcopy .

Interpretacija

če ste naredili analizo dovolj skrbno, na H-R diagramu ni težko prepoznati glavne veje. Morda veste, zakaj je linija dobljene opazovalne glavne veje v V(B-V) grafu skoraj navpična, v teoretičnem P(T) pa je nagnjena (zvezde z višjim izsevom imajo višjo efektivno temperaturo) ?

Glavna veja je močno razmazana zlasti za temne zvezde ( velika vrednost magnitude V ). To je seveda posledica merskih napak. Morda veste, v kateri smeri so napake pozicij zvezd večje : v navpični ( V magnituda) ali v vodoravni ( B - V magnituda) ?

Nekatere zvezde očitno ne pripadajo glavni veji H-R diagrama. Lahko identificirate, katere zvezde pripadajo rdečim orjakinjam, katere modrim vsiljicem, katere pa verjetno niso članice kopice ( ampak so le naključno v istem vidnem polju ) ?

Vredno je omeniti še dve zanimivosti dobljenega H-R diagrama. Glavna veja je pri določeni V magnitudi "preščipnjena", rdeče orjakinje pa so v diagrammu zbrane v strnjeni črti. Oboje se sklada z rezultati teoretičnih modelov.

Na koncu je na mestu kratek komentar k naši obdelavi. Prav bi bilo, če bi pri vsaki stopnji obdelave naredili mnogo dodatnih preverjanj. Le tako bi lahko zagotovili, da je vsaka točka končnega H-R diagrama na pravem mestu (v okviru eksperimentalne napake).

Z dodatnimi testi bi izločili zvezde, ki niso članice kopice, instrumentalne magnitude bi pretvorili v navidezne in končno določili diferencialno absorbcijo, oddaljenost in starost zvezdne kopice. žal pa taka obdelava ene noči opazovanj s CCD kamero zahteva vsaj teden dni za njihovo obdelavo.

Literatura : \\
Skripta za uporabo PCviste ( Seminar iz astronomije za profesorje fizike, februar 1991) \\
Astronomical Image Display for IBM PC`s or Compatibles (M. Richmond, R. Treffers ; University of California, Berkeley;1989) \\
Andrej čadež, Fizika zvezd, D.M.F. in A. SRS, Lj. 1979 \\
F. Avsec, M. Prosen, Astronomija, D.Z.S., Lj. 1975 \\
J. Strnad, Prapok Prasnov Požene v Dir, D.Z.S., Lj. 1988 \\
V. Vujnovič, Astronomija 1 in 2, š.K., Zagreb 1990 \\
T. Zwitter, B. Dintinjana, Slikanje astronomskih objektov s CCD kamero, Presek 4, Lj. 1992 _

Zorko Vičar

-original 1992/93, dopolnjeno leta 2001.

Do sedaj je to stran obiskalo ljudi.

Nazaj na domačo stran.