

 Vsebina te strani se v okviru časa in ustreznega gradiva dopolnjuje.
Vsebina te strani se v okviru časa in ustreznega gradiva dopolnjuje.
Izračunaj mejno magnitudo (ali premer objektiva teleskopa, če poznaš mejno magnitudo) s spodnjo formo. Vtipkaj premer objektiva v mm, klikni in dobil boš mejno magnitudo teleskopa.
GEOMETRIJA NASTANKA SLIKE IN POVEČAVA
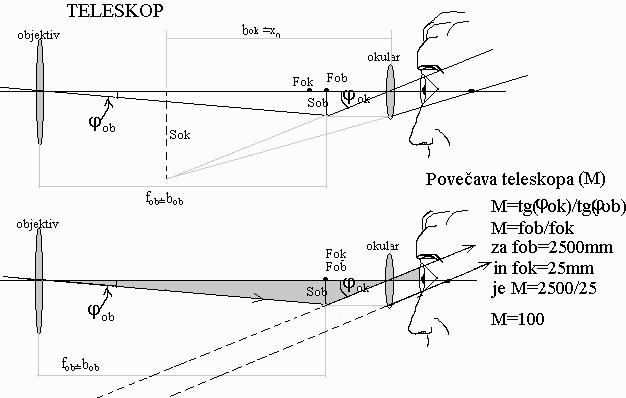
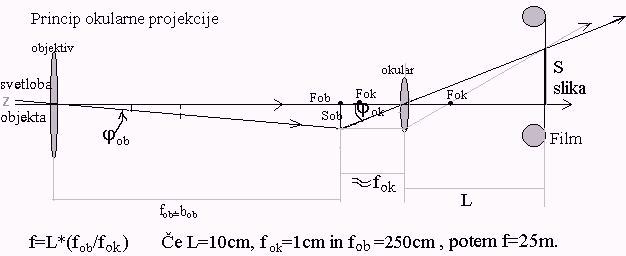
| a)________ |
b)________ |
zorni kot φ je podan v ločnih sekundah ["] in minutah [']
max.φ min.φ
Merkur 15" 5"
Venera 60" 10"
Mars 25" 3"
Jupiter 50" 30"
Saturn 20" 15"
(Sat. obroč) 40"
Uran 3,6"
Neptun 1,5"
Luna 30'
Sonce 30'
Izpeljava mejne magnitude teleskopa!
Najprej stavek o Pogsonu, ki je raziskoval subjektivne človeške občutke
glede svetlosti zvezd (sij, magnituda m), glede na fizikalne meritve
gostote svetlobnega toka j = energije/(čas*površina) = d(dE/dt)/dS = dL/dS, ki jih pomerimo
pri dani zvezdi.
Pogson je delal na observatorijih v Angliji in Indiji.
Do leta 1847 je izračunal tira dveh kometov.
Leta 1850 je pokazal, da je povprečna zvezda z navideznim sijem
1m (prve magnitude) približno stokrat svetlejša od povprečne zvezde, z magnitudo 6m,
ki je po Hiparhu še vidna s prostim očesom.
Empirična povezava
med magnitudo in gostoto energijskega toka
je "Pogsonov zakon":
j1/j2 = 10-0,4(m1-m2) = 10-2(m1-m2)/5
Sledi izpeljava mejne magnitude teleskopa za odprtino očesne zenice 6 mm
in mejno magnitudo očesa 6m (še opomba - mnogi uporabljajo višje vrednosti
za mejno magnitudo,
tja do 7m ali pri zenici odprtine 7 mm).
VELJA
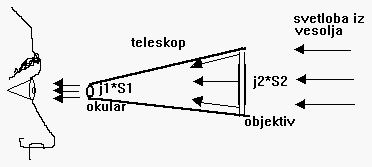
d1=dzenice=d=6mm,
m1=močesa=6,
D2=D=Dteleskopa,
m2=m=mobjekta,
-ker (j1*Sočesa=j2*Sobjektiva ali j1*d2*π/4 =j2*D2*π/4 ), to pomeni, da v teleskop prihaja tista mejna gostota energijskega toka j2 , ki se v teleskopu zgosti na j1, energijski tok pa se pri tem ohranja (primerjava vodovodne cevi, ki se zoži, skoznjo teče enak vodni tok le hitrost se v ožjem delu poveča, v1*S1=v2*S2)
-iz razmisleka sledi (D/d)2=10-2(m1-m)/5,
po logaritmiranju dobimo
m=5*log(D/d)+m1
-sledi končni izraz m=5*log
(D)-5*log6+6≈ 2+5*log(D)
Še opomba - večinoma se uporabljajo formule,
ki dajo višje vrednosti, za 0.7 pa tudi do 1.7, recimo:
m=3.7+5*log(10)(D),
ali (že omenili na začetku)
m=4.5+4.4*log(10)(D),
a mi bomo ostali pri zmernejši oceni.
V nekaterih knjigah, ki jih pišejo praktiki, pa so to oceno še znižali
za pol magnitude:
m=1.5+5*log(10)(D)
- kar je, če D podamo v cm: m=6.5+5*log(10)(D)
Morebiti ja zadnja enačba za večino opazovalcev (povprečje)
še najbolj realna (vas ne razočara, ko testirate
vašo optiko)!
Za astronomski krožek: ZORKO Vičar
Komentarji so zaželjeni.
E-POŠTA, RFC-822: Zorko.Vicar@guest.arnes.si