Kako "bel" je v resnici sneg v temi (?)

Bil je dokaj jasen ponedeljek - temperature okrog ničle, a ker je rahlo pihalo, se je zdelo, da je zelo mrzlo. Kljub kopreni in relativno skromnemu "siingu", Luna pa je bila že čez polovico, smo pokukali proti Orionu (proti meglicama M42, M43) in si zaželeli še h in hi Perzeja, oziroma razsuti kopici dvojčici NGC 869 in NGC 884 v Perzeju. Najprej smo ugotovili, da teleskop ni kolimiran - Klemen je to hitro uredil. A zaradi nemirnega ozračja, slika še zmeraj ni bila ravno ostra - do povečav okrog 70x je še kar šlo ... Pomerili smo še svetlost neba - SQM (Sky Quality Meter ) je pokazal sij neba okrog 18 mag/arc-sec² (pričakovano slabo). Nad obzorje Ljubljane pa samo izmerili zgolj okrog 16 mag/arc-sec², v zenitu pa nekaj več kot 18 mag/arc-sec². Ljubljana je nebo pričakovano še dodatno osvetlila zaradi odboja od snega in delno zaradi novoletne razsvetljave.
Po meritvah mejnega sija pa smo ugotovili, da smo "žrtve" fenomena optične prevare. Sneg na terasi šole se nam je namreč zdel tako bel, kot že dolgo ne in seveda svetlejši od neba, tudi svetlobne kupole nad Ljubljano. Na sneg je pošiljala svetlobo Luna in žal svetlobno onesnaženje (terasa je sicer dvignjena nad večino direktnih svetlobnih onesnaževalcev, a tukaj so odboji in sipanje svetlobe), ter seveda naravna svetloba samega nočnega neba (zvezd, planetov ...).
A ko je Andrej pomeril svetlost snega na terasi, je le ta znašala kar 18 mag/arc-sec² - enako kot nebo? Kako je to mogoče, ali je res temu tako, zakaj ta iluzija o izjemno svetlem snegu? Logično je, da je sneg blizu mejne magnitude neba, a možgani, oči so govorile drugače (vsem se je zdelo, da je sneg svetlejši od neba, tudi od neba nad Ljubljano). Andrej je skočil v observatorij po ogledalo iz grafoskopa (koliko let še že ne uporablja ta naprava naše mladosti?). Hkrati je pogledal tla (preko ogledala približno pod kotom 45 ° glede na horizont) in nebo. V tem primeru, glejte slike - je bilo očitno, da je nad Ljubljano (tik nad horizontom) slika snega v zrcalu precej temnejša od neba - torej SQM ne laže. Martin pa je špegel dvignil še nekje do pasu Oriona in sedaj sta se svetlosti neba in tal pokritih s snegom izenačili (kot da bi ogledalo čudežno izginilo v zvezdnem oboku - "magic", res impresiven prizor). Ko smo ogledalo dvignili proti zenitu, pa je bilo ogledalo (slika tal) pričakovano svetlejše od neba. Izjemno preprosta, a lepa, vaja med iskanjem odgovora, kako "bel" je v resnici sneg v temi!?
Iz samih fotografij - ki (v glavnem) ne lažejo, se opazi, da je svetlost snega v vidni svetlobi skoraj enaka svetlosti neba nad 40 ° višine. A naše oči so nas hotele prepričati, da je sneg po katerem tacamo, veliko svetlejši od neba - a to je bila le optična prevara (iluzija).


Hkratno opazovanje neba in tal preko zrcal.




Leva slika nazorno pokaže (pozitiv in negativ), da so zasnežena tla enako temna kot nebo nad 40 ° višine, horizont pa je zaradi svetlobnega onesnaženja precej svetlejši (kar dokazuje slika tal v ogledalu). Na zgornji desni sliki ogledalo čudežno izgine v Orionu, zasnežena tla in nebo sta eno (kakor na Zemlji, tako na Nebu).
Do teh zanimivih primerjav pa je prišlo, ker smo imeli občutek, da so zasnežena tla veliko svetlejša od katerega koli dela neba, a temu še zdaleč ni tako.

Košček zasneženih tal (kvadratek) je 3x prilepljen na levi strani slike:
* tik nad horizontom (kjer se opazi, da so zasnežena tla bistveno temnejša),
* na višini okrog 45 ° (kjer skoraj izgine)
* in blizu 90 °, kjer so tla nekoliko svetlejša od neba blizu zenita (vpliv lokalne razsvetljave na povišano svetlost tal)!
Enak efekt dobimo z ogledalom - kar je veliko bolj prepričljivo in pedagoško učinkovito.

Trak (zgoraj desno) je po vsej dolžini in širini enake barve, svetlosti - a na različno svetli površini se zdi različnih odtenkov.
Zakaj tako zaznavamo? Morebiti s tako iluzijo navidezno povečamo kontrast, ki nam je pomagal preživeti v realnem (naravnem) svetu, kjer nas obdaja polno odtenkov barv, senc, živih bitij, pregrad, prepadov, sten, rastlin, rek, raznih drugih ovir.
A kot ljubitelji astronomije, bomo pristavili tudi svoj piskrček in zatrdili, da nam je narava dala to izjemno zmožnost zaznavanja kontrastov (tudi iluzij) zato, da lažje prepoznamo prekrasne vzorce nočnega neba, Rimsko cesto, razsute kopice, meglice, komete, utrinke, v mislih tvorimo ozvezdja po katerih potujejo planeti (nebesni potepuhi) ... Tudi, če temu ni tako, pa vendar deluje!
To presenečenje smo doživeli tudi na terasi gimnazije Šentvid ob ocenjevanju svetlosti snega napram svetlosti neba. Enko temen sneg, kot je nebo, se nam je zdel na ozadju temnejše okolice precej svetlejši od neba.




Zorko Vičar
Jan. 2022

----------------------DODATEK--------------------------

Teden dni pozneje 17. jan. 2022, ob praktično polni Luni, je bil sneg pričakovano še bolj osvetljen od od Lune odbite Sončeve svetlobe in svetlost snega se je izenačila z nebom že na višini okrog 15 °. Višje na nebu so bila zasnežena tla veliko svetlejša od neba, kljub polni Luni. Ob polni Luni je torej snežna površina tako svetla, kot nebo nad horizontom nad Ljubljano, gledano iz Šentvida, to je okrog 16 mag/arc-sec².

V resnici je SQM 17. 1. 2022 pokazal nad Ljubljano mejno magnitudo zgolj okrog 15,5 mag/arc-sec², zasnežena tla pa so imele vrednost okrog 16.5, kar je precej svetleje kot ob prvem krajcu 18 mag/arc-sec² pred tednom dni. Nebo v zenitu je še zmeraj omogočalo mejno magnitudo dobrih 18 mag/arc-sec², kljub polni Luni. A meritve z SQM so morale potekati v senci Lunine svetlobe, sicer je stranski vpad Lunine svetlobe na senzor SQM-a zbil mejno magnitudo Zenita skoraj na 17 mag/arc-sec².

Polna Luna v naših krajih povzroča osvetljenost tal do okrog E = 0,3 lx (odvisno od višine Lune in stanja atmosfere, večinoma se privzame od 0,05–0,1 lx). Svetlost, ki jo zazna naše oko, pa je odvisna od same površine, sneg ima zagotovo največjo odbojnost, kar od 0,8 do 0,9. Pri 555 nm valovne dolžine (zelena svetloba - pri kateri je oko najbolj občutljivo na energijski tok in njegove spremembe) velja: 683.002 lx = 1 W/m². Iz tega podatka zgolj grobo ocenimo s koliko W/m² so tla osvetljena (zaradi polne Lune). Gostota energijskega toka Lunine svetlobe ob Zemlji je velikostnega reda 0.3 lx (1/683.002 lx) W/m² = 0.00044 W/m² - gre res za grobo oceno.

Primerjajmo ta rezultat s Pogsonovim zakonom. Vesoljsko telo, od katerega prihaja na Zemljo svetlobni tok z gostoto j₂ = 2.52 * 10^-8 W/m², ima sij magnitude 0, kar zapišemo kot m2 = 0. Magnituda polne Lune je okrog m1 = -12,8 m. Ocenimo gostote svetlobnega gostote iz Pogsonovega zakona ( j₁/j₂=10^-0,4(m1-m2) ) znaša za j₁ = 0.0033 W/m² (velja za vrh atmosfere). To je okrog 400000 krat manj od gostote svetlobnega toka Sonca na vrh atmosfere. Računa se torej nekoliko razhajata, a je prvi z luxi le grob približek. Veliko je seveda odvisno tudi od ge. širine in seveda od oddaljenosti Lune, od pogojev v atmosferi, odbojnosti.

Še primerjava s Soncem, ki na vrh atmosfere pošlje okrog 1361 W/m² svetlobnega toka (do tal pride precej manj, odvisno seveda tudi ge. širine in stanja atmosfere, albeda). Delež svetlobe odbite s polne Lune na Zemljo je torej zanemarljiv ( 400000 krat manjši od Sončeve), a naše oči (možgani) tudi pokrajino obsijano zaradi polne Lune, zelo dobro zaznajo (še posebej ob snežni odeji).

Še ocena svetlosti površine snega L zaradi polne Lune s pomočjo kalkulatorja in formule, ki povezuje meritve SQM-a s svetlostjo, spet se uporabi Pogsonov zakon
(velja: L = 10.8*10⁴ * 10^{-0.4(vrednost v mag/arcsec^2)} [cd/m^-2]):
http://unihedron.com/projects/darksky/magconv.php?ACTION=SOLVE&txtMAGSQA=16.5
Če za sneg vstavimo izmerjen sij 16.5 mag/arc-sec², dobimo svetlost površine snega L = 2.7 10^-2 cd/m^-2. Če v grobem sklepamo, da se od snega večino svetlobe odbije, potem lahko zaokrožimo, da je osvetljenost zaradi polne Lune 17. jan 2022 ob 21. h bila večja od E = 0,03 lx. Razmišljajmo naprej in poiščimo boljšo oceno. Za idealno difuzno površino (sneg se temu približa - Lambertov reflektor) z odbojnostjo 'a' velja med svetlostjo površine L in osvetljenostjo površine E povezava:
L = E*a/π (Lambertov zakon).
od koder sledi E = Lπ/a. Za albedo a = 0.8 sledi ocena osvetljenosti tal s polno Luno:
E = 0.027*3.14/0.8 lx = 0,11 lx,
kar pa že ustreza teoretičnim vrednostim.
Tako smo preko snežne odeje, polne Lune in meritev mejne magnitude preko SQM instrumenta dokaj verodostojno ocenili osvetljenost E površine tal zaradi polne Lune. Zelo poučna vaja.


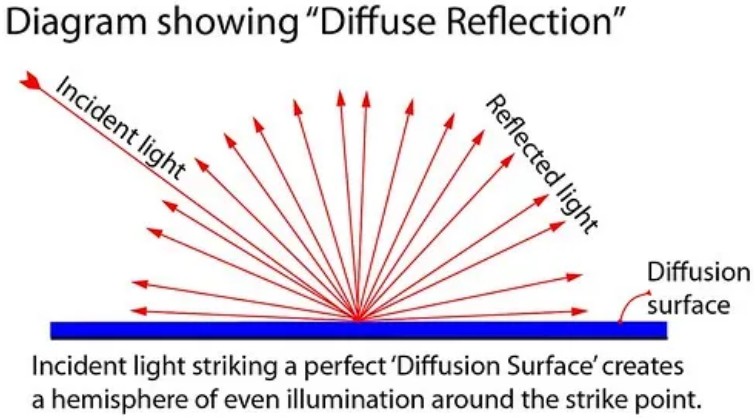
Idealna difuzna površina v vse smeri enakomerno sipa, odbija vpadno svetlobo (sneg se temu približa, odboji svetlobe v kristalih v vse smeri - Lambertov reflektor).

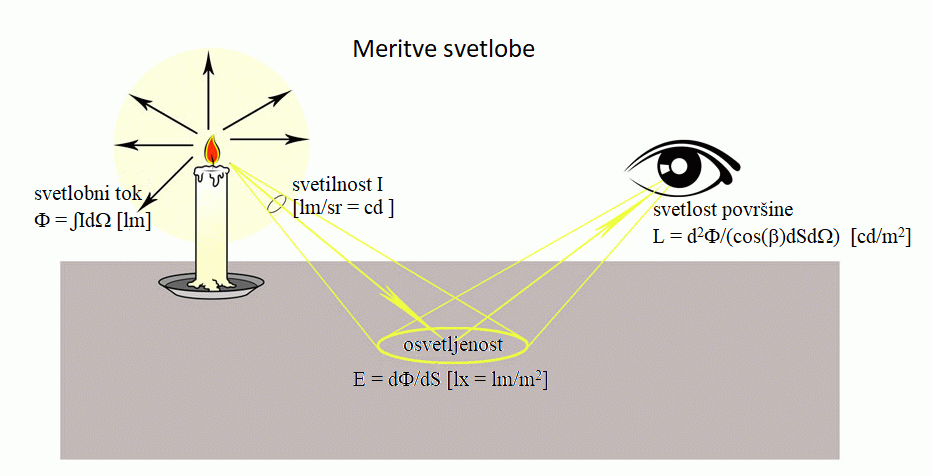
Slika: Ponovitev fotometrije preko preproste sheme goreče sveče:
- svetlobni tok Φ = ∫IdΩ [lm] (fiz. prim. količina P - enota W),
- svetilnost I [lm/sr = cd],
- osvetljenost E = dΦ/dS [lx = lm/m² = cd*sr/m²] (fiz. prim. količina j = P/S - enota W/m²),
- svetlost površine (ali svetila) L = d²Φ/(cos(β)dSdΩ) [lm/(sr*m²) = cd/m²].
Gostota svetlobnega toka »j« ima enoto W/m² in primerljiva fotometrična količina osvetljenost E ima enoto lm/m² = lx – povezava med njima je odvisna od valovne dolžine. Recimo za 555 nm valovne dolžine (zelena svetloba - pri kateri je oko najbolj občutljivo na energijski tok in njegove spremembe) velja: 683.002 lx = 1 W/m².

To noč (17. jan. 2022) sem testiral SQM še za mejne vrednosti - v smeri polne Lune, sij je padel nekaj pod 15 mag/arc-sec², na kopnih kamnitih tleh je SQM pokazal 19 mag/arc-sec² (na snegu pa pričakovano zgolj 16.5), v observatoriju brez luči - kjer pa je SQM dolgo zbiral fotone - zato sem ga usmeril proti lini observatorija in je tako (z zadnjimi močmi) pokazal fiktivno mejno magnitudo 23,4 mag/arc-sec². Tako sem določil mejne vrednosti naprave SQM. Po 12 letih torej senzor SQM-a še zmeraj deluje korektno.

------------------------------------