Exercise for Kepler's Laws
Before you begin, everyone in the group needs to make a cover sheet. Be sure to include your name, your section, today's date, this assignment, and the other members of your group. Leave enough space to write a few things on the cover page.
For the rest of this worksheet, you will need to have assigned tasks and take turns "mousing." This can be done at the end of the sections on each law. Chose now who will start as mouse driver. The other tasks in the group will be the recorder (the one to fill in the work sheet), and one or more archivers to take detailed notes.
Go to the Solar System Collaboratory Home Page at the hyperlink listed above. Hit one of the Enter Website links. This will open several new windows. Hit the link to enter the Kepler's Laws module. You should now see four links - one to each of Kepler's three laws, and one to a dial-an-orbit application. We will be spending much of the time in the dial-an-orbit application.
Kepler's First Law
Mouse driver ____________________________
Follow the First Law link. As soon as you enter this page, move the eccentricity slider to 0.5. (The initial orbit shown on the page does NOT have an eccentricity of zero!) Now click on "Give me a Hint" to read about the first law.
1. Write out Kepler's First Law.
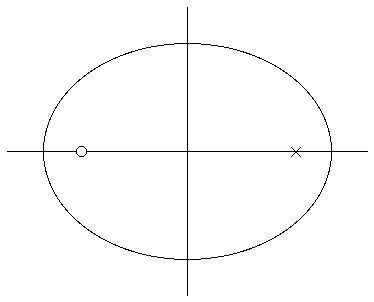
2. Use the information on the Hints page and on the Show Me the Math page to label the following information on the ellipse shown below.
a. Major Axis b. Semi-Major Axis c. Minor Axis
d. Semi-Minor Axis e. Focus #1 with the "sun" f. Focus #2 with the "X"
g. Perihelion (Periapsis) h. Aphelion (Apoapsis)

3. In a real orbit, what is at the focus #2? __________________________
Now go to the dial-an-orbit application. In this application, the sun is always at the origin (i.e. x=0,y=0). Enter the following values for location and velocity of the orbiting planet and then press the SELECT button. For accuracy, enter the values in the initial position and initial speed windows using the keyboard. Note that each small tick mark represents 10 units of length. Answer the questions about the resulting orbit.
Orbit #1:
4. Did you start the orbit at periapsis or at apoapsis? __________________________
5. Where does orbit #1 cross the x axis again? __________________________
(This will be the distance from the sun at
that point.)
6. What is the Major axis of this orbit? __________________________
7. What is the Semi-major axis of this orbit? __________________________
8. Where is the second, empty, focus? __________________________
9. What is the distance between the two foci (focuses)? __________________________
Use the pause button and the time increments shown below the picture to measure the period of the orbit.
10. What is the period of this orbit? __________________________
The eccentricity of an ellipse is defined as the ratio of the distance between the foci to the major axis.
eccentricity = (distance between the foci)÷(major axis)
11. What is the eccentricity of orbit #1? __________________________
Orbit #2:
13. Where is the second, empty, focus? __________________________
14. What is the distance between the two foci (focuses)? __________________________
15. What is the period of this orbit? __________________________
16. What is the eccentricity of orbit #2? __________________________
Orbit #3:
18. Where is the second, empty, focus? __________________________
19. What is the distance between the two foci (focuses)? __________________________
20. What is the period of this orbit? __________________________
21. What is the eccentricity of orbit #3? __________________________
22. This ellipse has a special shape. What is this shape? __________________________
Go back to the First Law page. Browse through the planets and find:
23. What planet has the highest eccentricity? __________________________
24. What is that eccentricity? __________________________
25. What is the eccentricity of Earth's orbit? __________________________
Kepler's Second Law
New Mouse Driver ____________________________
Follow the Second Law link. Look at the Hints page and the Show me the Math page.
26. Write out Kepler's Second Law.
Go back to the Dial an Orbit application.
Orbit #1:
Now you will try to recreate orbit #1, but from a different starting location. Remember that when the satellite gets to the location given above, it will have the same velocity.
Start the planet at:
x = -160Your orbit #1 should have crossed the axis here. The -160 is the distance from the sun at that location in the orbit. Be sure to use the negative sign in the calculations below. Use trial and error to find the velocity, vy, that will give you the same orbit (semi-major axis and period) as orbit #1 in the First Law exercise. Be sure that the planet orbits in the same direction as in the First Law exercise.
y = 0
vx = 0
27. vy = ____________________
28. Which speed is faster, periapsis or apoapsis? ___________________________
Look at the starting conditions in the First Law section for the periapsis distance and velocity.
29. For orbit #1, what is the product of the distance at periapsis times the velocity at periapsis? ___________________________
30. For orbit #1, what is the product of the distance at apoapsis times the velocity at apoapsis? ________________________________
31. There may be a small bit of rounding error, but are these numbers the same? ___________________
Orbit #2:
Start the planet at (x=-130,y=0, and vx=0). Find the velocity, vy, that will give you the same orbit (semi-major axis, period, and direction) as orbit #2 in the First Law exercises.
32. vy = ________________________
33. For orbit #2, what is the product of the speed at periapsis times the distance at periapsis? ________________________________
34. For orbit #2, what is the product of the speed at apoapsis times the distance at apoapsis? ________________________________
35. There may be a small bit of rounding error, but are these numbers the same? ________________________________
Orbit #3:
36. Knowing the special situation for orbit #3, would you expect the speed to vary anywhere? ________________________________
Kepler's Third Law
New Mouse Driver ____________________________
Follow the Third Law link. Look at the Hints page.
37. Write out Kepler's Third Law.
38. Using INTEGER exponent buttons, run through all
the available integer combinations (1/1, 1/2,..., 1/9; 2/1, 2/2,..., 2/9;
3/1, 3/2,... 3/9;...). Which combinations give you a good fit to the data?
(There will be several that give you a good fit.)
39. Although there are many pairs of exponents that
seem to fit the data equally well, why do you think Kepler formulated his
third law as he did?
40. The period of Halley's comet is 76 years. From the graph, what is the semi-major axis of Halley's comet? __________________________
41. Look at the answers to the earlier exercises. How do the semi-major axes of orbits #1, #2, and #3 compare? __________________________
42. From Kepler's Third Law, how would you expect the periods of orbits #1, #2, and #3 to compare? __________________________________
In the Dial-an-orbit application, start the planet at (x=30, y=0, and vx=0). Find the velocity, vy, that will give you the same semi-major axis as the orbits in the First Law exercises.
43. vy = ____________________
44. How would you expect the period of this orbit
to compare to the others?
In the Dial-an-orbit application, start the planet at (x=90, y=0, and vx=0). Find the velocity, vy, that will give you a semi-major axis of 150.
45. vy = ____________________
46. How would you expect the period of this orbit
to compare to the others?
In the Dial-an-orbit application, start the planet at (x=60, y=0, and vx=0). Find the velocity, vy, that will give you a semi-major axis of 80.
47. vy = ____________________
48. How would you expect the period of this orbit
to compare to the others?
Before turning in this exercise, everyone needs to write out all of Kepler's Laws on their cover page.