"The sun must not catch up the moon, nor does the night outstrip the day.
Each one is travelling in an orbit with its own motion"
(Al Qur'an 36:40)
"the sun and the moon (are subjected) to calculations"
(Al Qur'an
55:5)
This page provides a QBASIC program for calculating a rough position for the Moon, given your location and the date and time (UT). The program listing below gives the geocentric longitude and latitude of the Moon's centre, plus the geocentric and topocentric right ascension and declination, as well as the lunar parallax. The program is a 'test bed' for a programmable calculator program - the aim is to spend less time in front of computer screens!
The method used is based on a trigonometric series for the longitude, latitude and parallax of the Moon found on page D46 of the 1997 Astronomical Almanac. The position of the Moon in the sky can be predicted to within a third of its apparent diameter of the 'true' position as found using sophisticated methods.
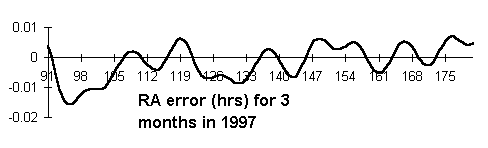
I have compared the results obtained with this BASIC program (modified so as to direct output to a file) with topographic positions produced by Monzur Ahmed's Mooncalc program, and with geocentric positions taken from the NASA Twelve Year Planetary Ephemeris. The results suggest that short term errors are less than 0.015 Hours in RA and 0.12 degrees in declination. This is better than claimed in the Astronomical Almanac.
A similar series exists for the position of the Sun, and this will be added soon to allow calculations of the phase, position angle and parallactic angle of the Moon.
Below is the QBASIC listing for the Moon position program. The program is not 'optimised' at all, and is designed to be easy to read and adapt for other languages including the limited syntax found on programmable calculators.
The user is prompted for the latitude and longitude of their location, and the year, month, day and time in UT for which the Moon's position is wanted. The longitude is given in decimal degrees, with West negative.
The output produced by a trial session is shown after the BASIC listing. Note
that you will need to alter the values of glong and
glat to reflect your own location.
The easiest way to transfer the listing into QBASIC would be to use
copy and paste into a text editor such as Notepad (or SimpleText),
from where the listing can be saved with a .BAS file extension.
' ********************************************************** ' Moon positions to a quarter of a degree on the sky ' From page D76 of Astronomical Almanac ' ' max RA error 97 (seconds of time), rms error 22 secs ' max dec error 811 arcseconds, rms error 224 arcseconds ' compared to Integrated Computer Ephemeris for 18.6 years ' either side of J2000 ' ' definitions and functions ' DEFDBL A-Z pi = 4 * ATN(1) twopi = 2 * pi degs = 180 / pi rads = pi / 180 ' ' FNday only works between 1901 to 2099 - see Meeus chapter 7 ' DEF FNday (y, m, d, h) = 367 * y - 7 * (y + (m + 9) \ 12) \ 4 + 275 * m \ 9 + d - 730531.5 + h / 24 ' ' the atn2 function below returns an angle in the range 0 to two pi ' depending on the signs of x and y. ' DEF FNatn2 (y, x) a = ATN(y / x) IF x < 0 THEN a = a + pi IF (y < 0) AND (x > 0) THEN a = a + twopi FNatn2 = a END DEF ' ' the function below returns the true integer part, ' even for negative numbers ' DEF FNrange (x) = x - INT(x / twopi) * twopi ' CLS ' ' get the date and planet number from the user ' INPUT " lat : ", glat INPUT " long : ", glong INPUT " year : ", y INPUT " month : ", m INPUT " day : ", day INPUT "hour UT : ", h INPUT " minute : ", mins h = h + mins / 60 d = FNday(y, m, day, h) t = d / 36525 ' ' calculate the geocentric longitude ' writing the coefficients in the series as angles in rads ' would save 29 multiplications per position! ' l = FNrange(rads * (218.32# + 481267.883# * t)) l = l + rads * 6.29# * SIN(FNrange((134.9# + 477198.85# * t) * rads)) l = l - rads * 1.27# * SIN(FNrange((259.2# - 413335.38# * t) * rads)) l = l + rads * .66# * SIN(FNrange((235.7# + 890534.23# * t) * rads)) l = l + rads * .21# * SIN(FNrange((269.9# + 954397.7# * t) * rads)) l = l - rads * .19# * SIN(FNrange((357.5# + 35999.05# * t) * rads)) l = l - rads * .11# * SIN(FNrange((186.6# + 966404.05# * t) * rads)) l = FNrange(l) ' ' calculate the geocentric latitude ' bm = rads * 5.13# * SIN(FNrange((93.3# + 483202.03# * t) * rads)) bm = bm + rads * .28# * SIN(FNrange((228.2# + 960400.87# * t) * rads)) bm = bm - rads * .28# * SIN(FNrange((318.3# + 6003.18# * t) * rads)) bm = bm - rads * .17# * SIN(FNrange((217.6# - 407332.2# * t) * rads)) ' ' get the parallax ' gp = .9508 * rads gp = gp + rads * .0518# * COS(FNrange((134.9# + 477198.85# * t) * rads)) gp = gp + rads * .0095# * COS(FNrange((259.2# - 413335.38# * t) * rads)) gp = gp + rads * .0078# * COS(FNrange((235.7# + 890534.23# * t) * rads)) gp = gp + rads * .0028# * COS(FNrange((269.9# + 954397.7# * t) * rads)) ' ' from the parallax, get the semidiameter and the radius vector ' sdia = .2725 * gp rm = 1 / (SIN(gp)) xg = rm * COS(l) * COS(bm) yg = rm * SIN(l) * COS(bm) zg = rm * SIN(bm) ' ' rotate to equatorial coords ' obliquity of ecliptic ' ecl = (23.4393 - 3.563E-07 * d) * rads xe = xg ye = yg * COS(ecl) - zg * SIN(ecl) ze = yg * SIN(ecl) + zg * COS(ecl) ' ' geocentric RA and Dec ' ra = FNatn2(ye, xe) dec = ATN(ze / SQR(xe * xe + ye * ye)) ' ' topocentric RA and DEC (spherical earth) ' Local Siderial Time in degrees ' lst = 100.46 + .985647352# * d + h * 15 + glong glat = glat * rads glong = glong * rads lst = FNrange(lst * rads) xtop = xe - COS(glat) * COS(lst) ytop = ye - COS(glat) * SIN(lst) ztop = ze - SIN(glat) rtop = SQR(xtop * xtop + ytop * ytop + ztop * ztop) ratop = FNatn2(ytop, xtop) dectop = ATN(ztop / SQR(xtop * xtop + ytop * ytop)) ' ' topocentric distance ' rmtop = SQR(xtop * xtop + ytop * ytop + ztop * ztop) ' ' print output in readable form - the 'formatting strings' ' only work with Microsoft basics and FirstBas compiler ' remove them for other basics. ' PRINT pr1$ = "\ \ ###.### ###.###" pr2$ = "\ \ #######.####" PRINT USING pr2$; "days from J2000 ....................... "; d PRINT USING pr1$; "geocentric ecliptic coords (l,b) ...... "; l * degs; bm * degs PRINT USING pr2$; "lunar parallax (deg) .................. "; gp * degs PRINT USING pr2$; "diameter (arcmin) ..................... "; sdia * degs * 60 * 2 PRINT USING pr2$; "geocentric distance (lun dia) ......... "; rm PRINT USING pr2$; "equator of date (deg) ................. "; ecl * degs PRINT USING pr1$; "geocentric equatorial coords (ra, dec). "; ra * degs / 15; dec * degs PRINT USING pr2$; "local siderial time (hrs) ............. "; lst * degs / 24 PRINT USING pr1$; "topocentric equatorial coords (ra, dec) "; ratop * degs / 15; dectop * degs PRINT USING pr2$; "topocentric lunar distance (lun dia) .. "; rmtop END '*********************************************************************************************
Here is the output of a sample session. Finding the position of the Moon for 11:56 UT on August 9th 1998, as seen from Birmingham UK. Note that only the first three decimal places of angle are actually meaningful! This is an approximate method!
lat : -1.91667 long : 52.5 year : 1998 month : 8 day : 9 hour UT : 11 minute : 56 days from J2000 ....................... -510.0028 geocentric ecliptic coords (l,b) ...... 335.206 -0.244 lunar parallax (deg) .................. 0.9909 diameter (arcmin) ..................... 32.4039 geocentric distance (lun dia) ......... 57.8223 equator of date (deg) ................. 23.4395 geocentric equatorial coords (ra, dec). 22.475 -9.830 local siderial time (hrs) ............. 7.8865 topocentric equatorial coords (ra, dec) 22.510 -9.656 topocentric lunar distance (lun dia) .. 58.6530
For comparison, Mooncalc (by Monzur Ahmed) gives the following positions for the Moon.
BIRMINGHAM 52:30N 1:55W TZ:0.0 Height:236m Geo Refrac OFF Julian Day Number: 2451034.5 Date: Sun 9 Aug 1998 JD of Conjunction: 2451018.0728 Time: 11h 56m 00s UT Apparent Sunrise: 4h 39m 47s UT Apparent Sunset: 19h 45m 27s UT ---------------------------------1 of 4---------------------------------- Moon Alt: -43.721 -43d 43m 17s Moon Azi: 328.781 328d 46m 52s Moon Dec: -9.909 -9d 54m 31s Moon RA: 22.481 22h 28m 51s Sun Alt: 53.172 53d 10m 20s Sun Azi: 173.100 173d 05m 59s Sun Dec: 15.830 15d 49m 46s Sun RA: 9.277 9h 16m 37s Rel Alt: -96.894 -96d 53m 37s Rel Azi: 155.681 155d 40m 53s Elongation 161.440 161d 26m 23s Moon Age: 406.19h 16D 22H 11M Phase:0.9741 Width:31.57m Semi-Diam:0.270 Earth-Moon Dist:368652.93km ------------------------------------------------------------------------- Moon Rise: 20h 29m 33s UT Azimuth: 104d 09m 30s Moon Set: 6h 14m 09s UT Azimuth: 251d 47m 14s Sunrise-Moonrise: 15h 49m 46s Sunset-Moonset: -13h 31m 18s ------------------------------------------------------------------------- New Moon: 23 July 1998 13h 44m 48s TD Full Moon: 9 July 1998 16h 01m 53s TD -------------------------------------------------------------------------
On this occasion, the method is different from Mooncalc by a third of a minute of time (about 5 arcmin) in RA and about 5 arcminutes in DEC. The results can be worse than this, see the following section.
I compared geocentric positions produced by the method shown here with a
three month set of daily geocentric positions taken from the NASA Twelve Year
Planetary Ephemeris. I took the error in each coordinate as 'TYPE - low
precision method' and then plotted the errors as a time series against day
number for RA and for DEC using a spreadsheet. 
The main features of the RA error graph are;
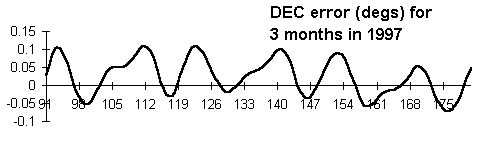
The main features of the DEC error are;
I then compared the topocentric positions adjusted for refraction obtained with Mooncalc and with the method shown here for each hour on April 13th 1997. By comparing the approximate method with refraction adjusted positions, I am attempting to compare the position of the Moon as observed against the stars with the position predicted by the low precision method.
The results for a complete day are shown in the table below. The topocentric RA and DEC produced by Mooncalc are listed in columns 2 and 3, and the estimates produced by the program given here are in columns 4 and 5. Column 6 shows the RA error, defined as (error=Mooncalc - estimate). Column 7 shows the RA error in degrees for comparison with the DEC error in column 8. The *'s show when the Moon is above the horizon.
April 13th 1997 Mooncalc D46 Error UT RA Dec RA Dec RA RA degs DEC 0 6.218 17.413 6.228 17.391 -0.01 -0.15 0.022 1 6.258 17.363 6.268 17.34 -0.01 -0.15 0.023 2 6.301 17.317 6.311 17.294 -0.01 -0.15 0.023 3 6.346 17.278 6.355 17.254 -0.009 -0.135 0.024 4 6.391 17.246 6.401 17.222 -0.01 -0.15 0.024 5 6.438 17.224 6.447 17.197 -0.009 -0.135 0.027 6 6.484 17.21 6.493 17.183 -0.009 -0.135 0.027 7 6.53 17.205 6.539 17.177 -0.009 -0.135 0.028 8 6.575 17.208 6.584 17.178 -0.009 -0.135 0.03 9 6.618 17.217 6.627 17.186 -0.009 -0.135 0.031 10* 6.658 17.231 6.667 17.199 -0.009 -0.135 0.032 11* 6.697 17.247 6.706 17.214 -0.009 -0.135 0.033 12* 6.733 17.263 6.742 17.228 -0.009 -0.135 0.035 13* 6.766 17.275 6.775 17.24 -0.009 -0.135 0.035 14* 6.797 17.281 6.806 17.246 -0.009 -0.135 0.035 15* 6.826 17.28 6.835 17.243 -0.009 -0.135 0.037 16* 6.853 17.268 6.862 17.231 -0.009 -0.135 0.037 17* 6.88 17.244 6.888 17.207 -0.008 -0.12 0.037 18* 6.905 17.209 6.914 17.171 -0.009 -0.135 0.038 19* 6.932 17.161 6.94 17.122 -0.008 -0.12 0.039 20* 6.959 17.102 6.967 17.063 -0.008 -0.12 0.039 21* 6.987 17.034 6.995 16.993 -0.008 -0.12 0.041 22* 7.017 16.957 7.026 16.916 -0.009 -0.135 0.041 23* 7.05 16.874 7.058 16.833 -0.008 -0.12 0.041 24* 7.085 16.789 7.093 16.747 -0.008 -0.12 0.042
As you can see, the errors are getting larger in DEC and smaller in RA throughout the day. These changes are probably part of a larger periodic error variation over time. There is not any sudden change in error value near Moonrise.
[Root ]
Last Modified 8th August 1998
Keith Burnett