S POMOČJO PARALAKSE


V najini raziskovalni nalogi sva določila oddaljenost Saturna od Sonca s pomočjo paralakse. Uporabila sva podatke za rektascenzijo in deklinacijo, ki sva jih dobila iz računalniškega programa. Naredila sva tudi meritve, s pomočjo katerih sva sama določila premik Saturna na zvezdnem nebu. Meritve temeljijo na slikanju in na natančnem vnašanju v nebesno karto, iz katere sva nato odčitala podatke za Ra in Dec.
Paralakso uporabljamo ponavadi za mirujoča telesa, zato je določanje oddaljenosti težje, saj se Saturn giblje. Saturnovo gibanje sva morala odšteti od skupnega gibanja Zemlje in Saturna. Nato sva to gibanje vnesla v graf in določila točke, ki so potrebne za izračun paralakse. Za končno rešitev sva dobila razdaljo Saturna do Sonca, ki se zelo dobro ujema z dejansko, napaka ni večja od 2%. Nalogo sva podprla tudi z veliko slikovnega materiala, ki sva ga večino tudi sama posnela ali narisala.
SUMMARY
We have determined in this research work the distance from the Sun to the planet Saturn with parallax method. The data for declination and right ascension was obtained from computer program. We also measured the shifts of Saturn on the night sky with the photograph method and sky maps.
The parallax is usually applied for the standstill objects, but Saturn has own motion. We substracted the Saturn's mean movement from the way caused by the motion of the Earthbound viewer and the Saturn's motion. Results were inserted to the graph and parallax's angle was read from the curve (ellipse). On the end it was easy to calculate the distance from the Sun to the Saturn. Calculaton is really good and the relative error is about 2 %.
|
|
 |
 |
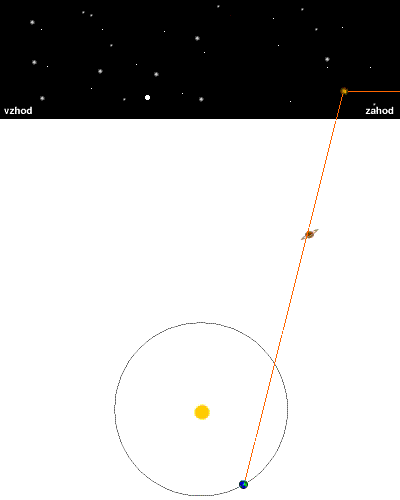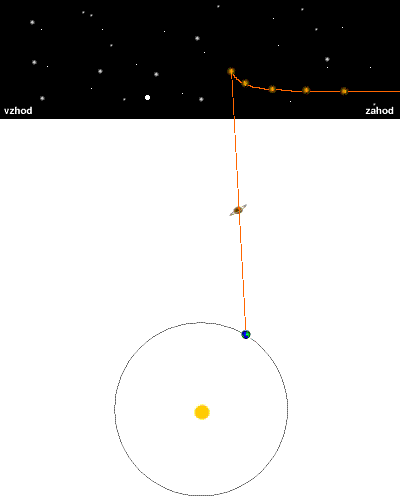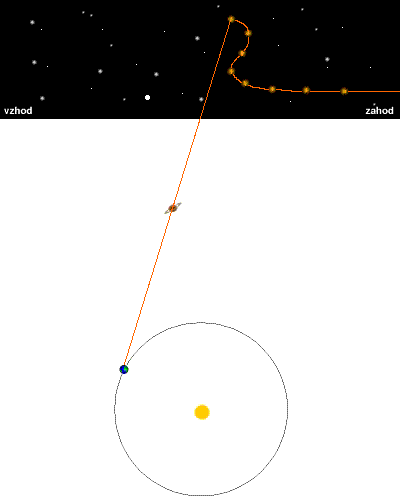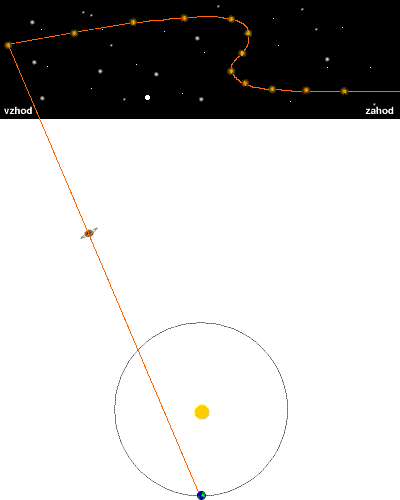
Brez odstetega gibanja |
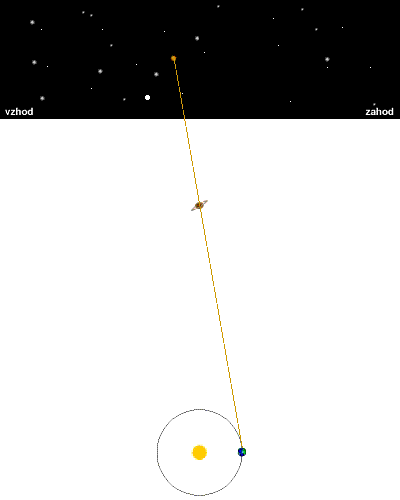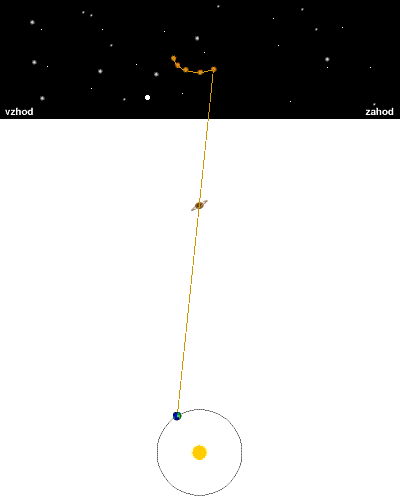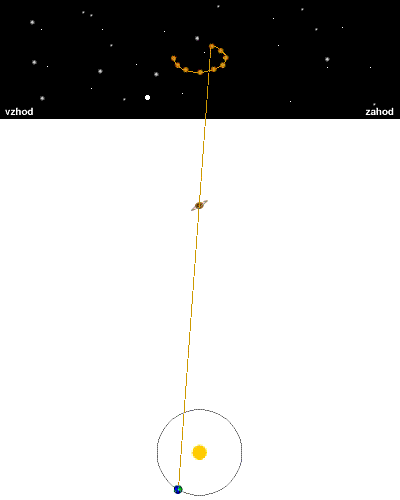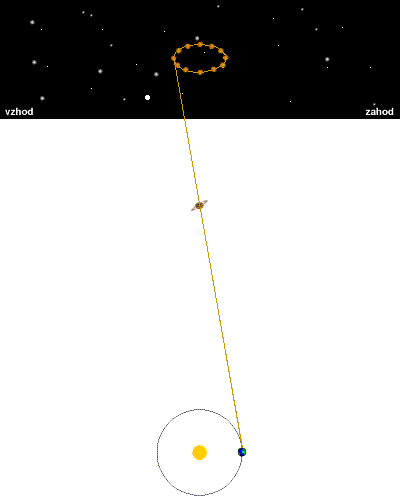
Z odstetim gibanjem |
PARALAKSA
Kaj je paralaksa?
Za začetek si oglejmo preprost primer paralakse: iztegnimo roko,
dvignimo palec, zaprimo levo oko in se obrnimo proti oddaljeni steni.
Na steni si izberimo objekt, na primer stikalo za luč. Zapomnimo si položaj
palca glede na stikalo. Zaprimo sedaj desno oko in poglejmo palec z levim
očesom. Pri tem lahko opazimo, da se je lega palca glede na stikalo
spremenila. Do tega pride zato, ker se je premaknilo opazovališče.
To je osnovni princip paralakse, pri čemer imenujemo razdaljo med levim
in desnim očesom baza. Če poznamo bazo in izmerimo kot, za katerega se je
navidezno premaknil prst glede na stikalo, lahko izračunamo oddaljenost
prsta od stikala. Premik prsta glede na stikalo lahko povečamo, če prst
približamo očesu, s katerim gledamo, ali če je razmik med enim in drugim
opazovališčem večji.
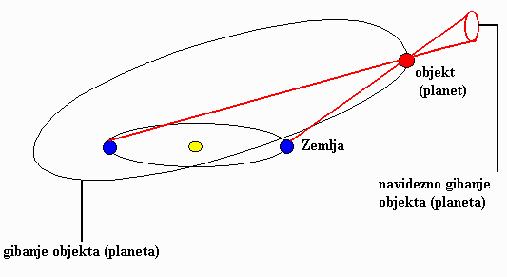
V astronomiji je računanje oddaljenosti prsta enako računanju oddaljenosti opazovanega objekta: Lune, planeta, bližnje zvezde. Namesto stikala na steni imamo ozadje mnogo bolj oddaljenih zvezd, ki nam služijo za nepremične oblekte, od katerih merimo premik izbranega bližnjega objekta.
Paralaksi bi lahko rekli tudi navidezni premik dveh različno oddaljenih objektov glede na ozadje, če jih opazujemo pod različnimi koti. V astronomiji ima merjenje paralakse za osnovo veliko polos tira Zemlje okoli Sonca in rabi za določitev oddaljenosti Soncu najbližjih zvezd. To osnovo imenujemo baza. Za druge bližje objekte je ta baza lahko manjša. Za Luno, na primer, zadostuje že nekaj tisoč kilometrov. Lahko pa določimo tudi oddaljenost zunanjih planetov našega osončja od Sonca. Primerni objekti za računanje paralakse so Saturn, Uran, Neptun in Pluton, ki so zelo oddaljeni od Zemlje in Sonca in se gibljejo razmeroma počasi in zato potrebujejo dalj časa, da obkrožijo Sonce.
Na spodnji sliki lahko vidimo, kako bi lahko izračunali oddaljenost smreke s
pomočjo paralakse. Premik opazovalca pomeni hkrati premik smreke na
oddaljenem obzorju.

Spodnja slika prikazuje navidezno pot mirujočega objekta po nebesni krogli,
če ta objekt ne leži v osi ekliptike in ne v njeni ravnini. Pot je elipsa.
Če telo leži v osi ekliptike, je pot skoraj krožnica, če leži v ravnini
ekliptike, pa je pot kar lok, za male kote privzamemo, da je pot premica.
Naslednja slika prikazuje, kako izračunamo paralakso za mirujoči objekt (zvezda).
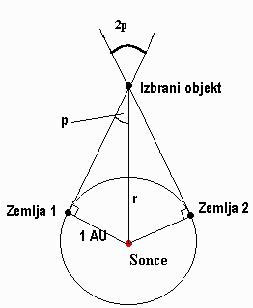
Formula se torej glasi:
r = 1ae/sin(p)
Kako je paralaksa odvisna od oddaljenosti, nam kaže spodnja
animacija. Ker so zvezde zelo daleč, najbližje so oddaljene več kot
4 svetlobna leta, je pralaksa zvezd zelo majhna, manj kot ločno sekundo.
To je tudi razlog, da so se mnogi znanstveniki toliko časa držali
geocentričnega modela vesolja, saj tako majhnih kotov na nebu, vse do
19. stoletja, niso znali meriti. Ker paralakse niso opazili, so tudi
Zemljo imeli za mirujoče telo v vesolju.
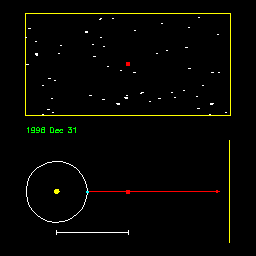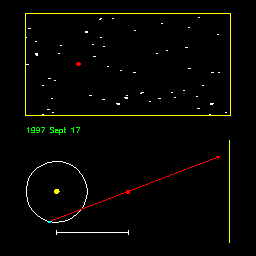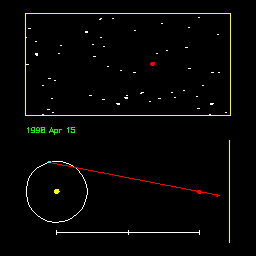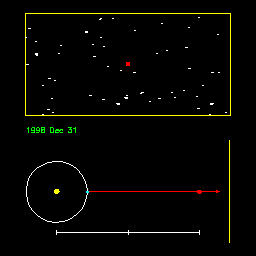


Sledi slika nebesne karte, na katero so vrisane pozicije Saturna med
zvezdami (rdeče pike). Če nimamo podatkov za rektascenzijo in deklinacijo,
si lahko pomagamo s to karto, in sicer tako, da iz fotografij nanašamo
lego objekta (Saturna) v karto.
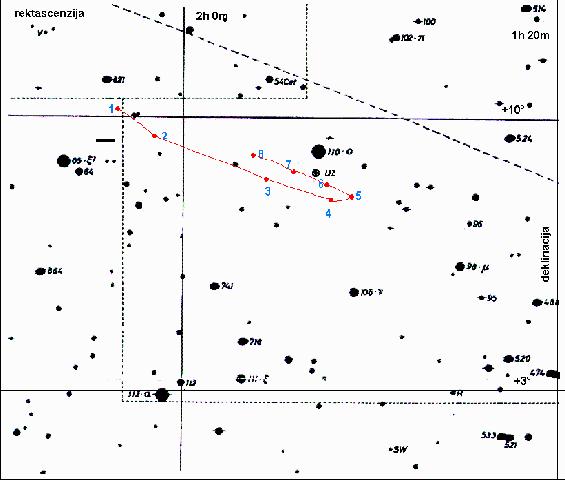
št. slike datum RA - h m s DEC-st. ' '' 1 6.8.1998 2 07 17 10 10 01 2 24.9.1998 2 02 55 9 34 39 3 5.11.1998 1 50 59 8 27 40 4 3.12.1998 1 44 11 7 54 24 5 8.1.1999 1 41 57 7 52 14 6 29.1.1999 1 44 44 8 14 28 7 12.2.1999 1 48 08 8 37 29 8 26.2.1999 1 52 35 9 05 45
Odšteto gibanje Saturna
Kot sva napisala že v uvodu, je za računanje paralakse potrebno
lastno Saturnovo gibanje odšteti, zato ker je paralaksa namenjena računanju
razdalje do mirujočega objekta. Odštejmo torej Saturnovo gibanje od
skupnega gibaja Zemlje in Saturna. Ker si meritve sledijo v enakomernih časovnih
intervalih, bomo letno gibanje saturna delili s številom časovnih
intervalov in tako dobili povprečen lasten premik Saturna na interval. Te lastne
premike pa bomo odšteli od dejanskih premikov, kot jih izmerimo iz Zemlje.
Za to uporabimo naslednje izraze (D je delta, oz. razlika):
...za rektascenzijo:
a1i' =a1i-i*Da/n
(2)
...za deklinacijo
d1i'=d1i-i*Dd/n
a1i in d1i označujeta še neodšteto gibanje, torej takšno kot v resnici
je do časovnega intervala i.
i*Da/n in i*Dd/n predstavljata lastno gibanje Saturna do časovnega
intervala i.
a1i' in d1i' označujeta, kakšen položaj bi imel Saturn (gledano z Zemlje),
če bi miroval do časovnega intervala i.
Podatki za RA in DEC so na vsak sedmi dan v letu.
n=365/7 -- 52 torej i teče od 1 do 52. To številko sva malo priredila.
Za i sva vzela od 0 do 52 za n prav tako 52, za graf in za Da in Dd
sva vzela razliko med 53 in 1. To pa zato, da bi bila izračun in graf
bolj natančna. Da in Dd sta razliki med začetno in končno rektascenzijo
ter začetno in končno deklinacijo.
N je število datumov (točk na grafu), torej 52.
Da = 91515 "- 47790 " = 43725 "
Dd = 28092 "- 10665 " = 17427 "
Tukaj je primer računanja za i = 1:
a1' = 47790 " - 1*43725 "/52 = 46949,13 "
d1' = 10665 " - 1*17427 "/52 = 10329,87 "
Izračuna je narejen na podlagi podatkov za leto 1998 s programom Excel: Podatki za retakscenzijo in deklinacijo Saturna so v spodnji tabeli.
i datum RAC DEC h m s st. ' '' 1 1.1.98 0 53 6 2 57 45 2 8.1.98 0 53 58 3 5 12 3 15.1.98 0 55 9 3 14 32 4 22.1.98 0 56 37 3 25 38 5 29.1.98 0 58 22 3 38 21 6 5.2.98 1 0 23 3 52 32 7 12.2.98 1 2 38 4 8 2 8 19.2.98 1 5 6 4 24 38 9 26.2.98 1 7 45 4 42 13 10 5.3.98 1 10 34 5 0 35 11 12.3.98 1 13 32 5 19 34 12 19.3.98 1 16 37 5 39 0 13 26.3.98 1 19 48 5 58 44 14 2.4.98 1 23 3 6 18 35 15 9.4.98 1 26 20 6 38 24 16 16.4.98 1 29 39 6 58 3 17 23.4.98 1 32 58 7 17 23 18 30.4.98 1 36 16 7 36 16 19 7.5.98 1 39 31 7 54 34 20 14.5.98 1 42 41 8 12 9 21 21.5.98 1 45 46 8 28 55 22 28.5.98 1 48 45 8 44 44 23 4.6.98 1 51 35 8 59 30 24 11.6.98 1 54 15 9 13 6 25 18.6.98 1 56 44 9 25 27 26 25.6.98 1 59 1 9 36 27 27 2.7.98 2 1 5 9 46 1 28 9.7.98 2 2 53 9 54 4 29 16.7.98 2 4 26 10 0 33 30 23.7.98 2 5 41 10 5 24 31 30.7.98 2 6 39 10 8 34 32 6.8.98 2 7 17 10 10 1 33 13.8.98 2 7 37 10 9 45 34 20.8.98 2 7 36 10 7 47 35 27.8.98 2 7 16 10 4 7 36 3.9.98 2 6 37 9 58 52 37 10.9.98 2 5 39 9 52 6 38 17.9.98 2 4 25 9 43 59 39 24.9.98 2 2 55 9 34 39 40 1.10.98 2 1 11 9 24 20 41 8.10.98 1 59 18 9 13 18 42 15.10.98 1 57 16 9 1 48 43 22.10.98 1 55 10 8 50 9 44 29.10.98 1 53 3 8 38 40 45 5.11.98 1 50 59 8 27 40 46 12.11.98 1 49 1 8 17 28 47 19.11.98 1 47 11 8 8 21 48 26.11.98 1 45 34 8 0 35 49 3.12.98 1 44 11 7 54 24 50 10.12.98 1 43 5 7 49 58 51 17.12.98 1 42 18 7 47 24 52 24.12.98 1 41 49 7 46 48 53 31.12.98 1 41 41 7 48 12 Vse podatke sva pretvorila v ločne sekunde (˝). Pretvorniki so: 1stopinja=60' in 1'=60" 1stopinja =60*60" 1h = 60*60s in 1h = 15*3600˝
Sledi graf neodštetega gibanja. To je gibanje,
ki ga vidimo z Zemlje. Vanj sta vključena Saturnovo in Zemljino gibanje.
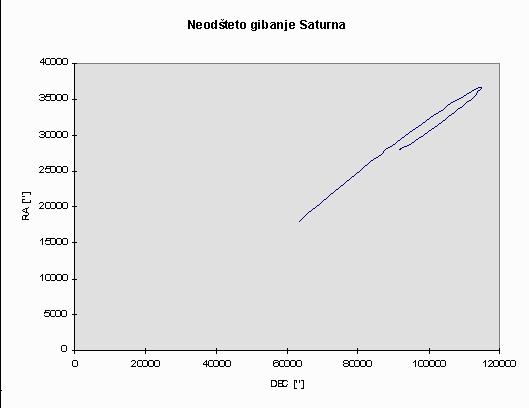
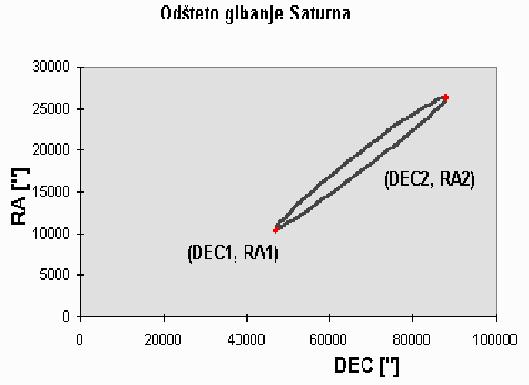
Iz grafa za odšteto gibanje določimo skrajni točki elipse in izračunamo veliko os (na grafu označeni rdeče).
RA ["] DEC ["] DEC1, DEC2 87918,17 26314,1 RA1, RA2 46888,27 10329,87 odšteto 41029,9 = Da1' 15984,23 = Dd1'Odčitke vstavimo v formulo za izračun paralakse p, uporabili smo Pitagorov izrek.
Ra in Dec delimo s 3600. 3600 je pretvornik. Da1' = 41029,9°/3600=11,4° Dd1' = 15984,23°/3600=4,4° p = (koren(149,32°))/2 p = 12,22°/2 p = 6,11° Paralaksa je torej 6,11°. Sedaj moramo izračunati še oddaljenost Saturna od Sonca po že izpeljani zvezi. r = 1ae/sin(p) R je razdalja od Sonca do Saturna v astronomskih enotah (ae). r = 1ae/sin(6,11°) = 1ae/0,106437614 = 9,4ae Napako, ki lahko nastane zaradi več dejavnikov, sva ocenila na približno dva odstotka. Ti dejavniki so: · nenatančnost pri odčitavanju podatkov iz grafa · gostota meritev je omejena · Saturn ni vedno enako oddaljen od Sonca in Zemlje. Rezultat, ki sva ga izračunala, je 9,4AE, t.j. 1406,24 milijonov km oziroma 78,1 svetlobnih minut. 1 svetlobna minuta = 3*10E8m/s*60s = 1,8*10E10m = 18*10E6 km Zanimalo naju je, koliko sva se približala dejanski oddaljenosti Saturna od Sonca. To izračunamo tako, da od najinega rezultata odštejemo dejansko razdaljo in vse skupaj delimo z dejansko razdaljo. Odstopanje v odstotkih je: 9,4 - 9.54/9,54 = 0,0015 ali 1,5% (4)Rezultat je, glede na preprostost metode, izjemen.
Spodnji animaciji pojasnjujeta bistvo naloge. Poženi osvežitev (refresh) za ponoven zagon animacije.
Prikaz paralakse Saturna
Mentor: Zorko Vičar
Avtorja: Peter Novak, Mitja Šiška
Astronomski krožek Gimnazije Šentvid, april 1999.
Nazaj na domačo stran.