



V raziskovalni nalogi z naslovom Sončeva aktivnost sem obravnaval površinske pojave na Soncu, kot so pege in bakle ter povezavo med vremenom in Sončevo aktivnostjo. Sonce sem opazoval s teleskopom in ga vsakič tudi skiciral na karirast papir. S tem sem dobil dovolj podatkov, da sem lahko preveril že znane ugotovitve.Rezultati naloge so me presenetili, saj sem ugotovil in preveril mnogo stvari, kot so Wolfovo število, pojavljanje in razvoj peg, število peg v skupinah. Najpomembnejša pa je nepreverjena ugotovitev, da Sončeva aktivnost neposredno vpliva na razvoj vremena na Zemlji.
Raziskovalna naloga se dotika predvsem astronomije in meteorologije. Namen naloge je raziskati vpliv Sončeve aktivnosti na vreme. Poleg tega naloga vsebuje tudi raziskave na področju Sončeve aktivnosti, ki se kaže predvsem v pojavih kot so pege, bakle, protuberance, itd. Torej lahko na splošno rečemo, da se naloga ukvarja predvsem s Soncem in vremenom.
1.2 DOSEDANJE RAZISKAVE NA TEM PODROČJU
Že dolgo časa je znano, da je Sonce eden glavnih ustvarjalcev vremena
na Zemlji. Predvsem je znano, da Sončeva aktivnost vidno vpliva na vreme
v daljšem časovnem obdobju. Najbolj znan primer je prav gotovo mala
ledena doba v letih 1645-1715. V tem času ni bilo Sončeve aktivnosti,
zato je temperatura na Zemlji padla, vendar v povprečju le za 0,6 °C. A
to je pomenilo velik padec temperature, saj je v tem obdobju, v vrsti
ostrih zim reka Temza v Londonu pogosto zamrznila . Astronom dr. John
Eddy je leta 1977 odkril, da je bilo v zadnjih 3000 letih Sonce aktivno
le 300 let [1]. To pomeni, da imamo prebivalci Evrope izredno veliko
srečo, da zdaj živimo ravno v obdobju Sončeve aktivnosti.
Astronomske spremembe so tudi zelo pomemben dejavnik
spreminjanja klime. Na njih je svojo znano teorijo klimatskih
sprememb zasnoval srbski astronom in klimatolog Milankovič. Precesija
(spreminjanje nagiba osi vrtenja glede na ravnino ekliptike) zaradi
delovanja privlačnosti Sonca in Lune je danes taka, da se bo nagib
prevesil na drugo stran (od sedanjih +23,5° na -23,5°) v naslednjih
13000 letih. Nutacija zato, ker se os vrtenja ne ujema povsem z
geometrijsko osjo Zemlje (na polu se razlikujeta za okrog 10 km) in
zato, ker Luna ne kroži povsem po ekliptiki, precesiji dodaja dodatna
nihanja s periodo 18,6 let. Tudi orbita okrog Sonca se počasi spreminja.
To velja za položaj dvižnega vozla, položaj perihelija , ekscentričnost
elipse itd. Posledica tega je spreminjanje osončenja. Zato so bili v
preteklosti posamezni deli Zemlji različno osončeni.
Izračun osončenja za zadnji 200000 let in prihodnjih 50000 let kaže,
da so v tako dolgem obdobju na marsikaterem predelu Zemlje povsem normalne
spremembe celo za kakih 200 do 250 MJm-2 na kvadratni meter. Vidimo, da
to pomeni pri 45° geografske širine fluktuacije za okrog ±5% glede na
dolgodobno (milijarda let) povprečje v teh geografskih širinah.
Značilne so periode teh fluktuacij: 40000 let zaradi spreminjanja
nagiba osi vrtenja Zemlje in 19000 let ter 23000 let zaradi njene
precesije (torej simetrično na severno in južno poloblo: kadar je na eni
topleje pozimi, je na drugi topleje poleti in obratno), in 60000 do 150000
let za vso Zemljo zaradi sprememb tirnice okrog Sonca.
Primerjava z značilnimi usedlinami posameznih organizmov v nekaterih
geoloških vrtinah potrjujejo pomembnost astronomskih vplivov na klimo.
Astronomski faktorji so glavni vzrok za pojav ledenih dob, pa spet
toplejših in hladnejših obdobij. Zdaj je vsa Zemlja v medledenem obdobju.
Zaradi astronomskih vzrokov naj bi se naslednja tisočletja
spet hladila [6].
Poleg vremena področje raziskovalne naloge zajema tudi Sončevo
aktivnost samo. Na tem področju so astronomi že davno ugotovili, da se
tako število, kot ploščina peg, kot tudi položaj peg spreminjajo v
enajstletnem ciklu Sončeve aktivnosti. Ponavadi se v bližini peg pojavljajo
bakle, ki so prav tako posledica Sončeve aktivnosti. Kot je že prej
omenjeno, se aktivnost spreminja. En cikel traja približno enajst let.
Ob maksimumu je peg največ, pojavljajo se v bližini ekvatorja.
Okoli minimuma pa je običajno peg zelo malo oziroma nič, pojavljajo se
tudi 40 in več stopinj stran od ekvatorja.
1.3 NAMEN RAZISKOVALNE NALOGE
Osnovni problem, s katerim se ukvarja raziskovalna naloga je vpliv
Sonca na vreme v krajšem časovnem obdobju (meseci ali celo dnevi). Večina
dela je bilo opazovanje Sonca s teleskopom tipa Newton skozi zaščitno folijo
Mylar. S pomočjo skic Sonca sem izračunal približne koordinate skupin peg,
nato pa sem z metodo poskušanja ugotavljal povezavo med vremenom in
Sončevo aktivnostjo.Pričakujem neko povezavo med Sončevo aktivnostjo in
vremenom za krajše časovno obdobje. Med drugim pričakujem tudi to, da se
pege pojavljajo samo na določenih heliografskih širinah.
2.2 Izračun Wolfovega števila
Prvo kar sem po opazovanjih naredil je bil izračun Wolfovega števila.
Za izračun je bilo potrebno prešteti vse pege in določiti korekcijske
faktorje. Wolfovo število se izračuna po formuli:
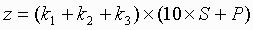 (1)
(1)Ocena opazovalnih pogojev Popravek K2 1 (povsem mirno ozračje) 0,01 2 (zelo dobri pogoji) 0,03 3 (srednje dobri pogoji) 0,05 4 (dokaj slabi pogoji) 0,07 5 (slabi pogoji) 0,09 6 (zelo slabi pogoji) 0,11Tabela 1: Vrednosti korekcijskega faktorja K2 za popravek Wolfovega števila zaradi seeinga
Kot je razvidno iz tabele ta faktor kar precej prispeva k končni vrednosti Wolfovega števila. Tretji faktor, K3, je še najmanj pomemben, ker je največja možna vrednost le tega 0,04. Spodnja tabela prikazuje vrednosti tega faktorja v odvisnosti od vidljivosti.
Opazovalni pogoji Popravek K3 Jasno 0,00 rahla meglica 0,01 meglica 0,02 gostejša meglica 0,03 megla 0,04Tabela 2: Vrednosti korekcijskega faktorja K3 za popravek Wolfovega števila zaradi vidljivosti.
Kot vidimo so vsi faktorji pomembni za končni izračun Wolfovega števila,
še posebej če je to večje od 100. Za primer vzemimo opazovanje dne 9.
avgusta 1998. Ta dan je bilo na Soncu veliko peg. Na moji risbi sem
naštel 52 peg, razporejenih v 6 skupin (1 multipolarno, 1 bipolarno in
štiri unipolarne). Če popravkov ne bi upošteval bi za vrednost Wolfovega
števila dobil 112. Pogoji na ta dan so bili dobri, saj je bil seeing 2.
stopnje, vendar pa je bila rahla meglica. Iz zgornjih tabel in vrednosti
faktorja K1 lahko enostavno izračunamo vrednost Wolfovega števila:
Z=(1,12+0,03+0,01)X(6X10+52)=129,92 (2)Sedaj vidimo, da je razlika kar precejšnja. Drugače je razlika še posebej velika v vetrovnih ali rahlo oblačnih dnevih [2].
2.3 Računanje koordinat skupin peg
Sončeve pege se praviloma pojavljajo le na določenih heliografskih
širinah. Zato je v raziskovalni nalogi vključena raziskava o glavnih
značilnostih skupin peg. Ta del vsebuje precej računanja, zato mi je vzel
največ časa.
Za računanje potrebujemo tudi kar nekaj podatkov, ki so težje dostopni.
To so predvsem podatki o legi Sončeve osi. To lego opišemo s tremi
parametri: P, B0, L0 . Prvi nam pove vrednost pozicijskega kota navidezne
lege Sončeve osi, ki ga štejemo pozitivno od severne točke na robu Sonca
proti vzhodu. Največji možni vrednosti le-tega sta 26,3°. B0 je koordinata,
ki nam pove heliografsko širino, L0 pa heliografsko dolžino središča
navidezne Sončeve ploskvice [3].
Podatke, ki sem jih vstavil v tabele, sem obdelal s pomočjo Microsoft
Excela. Vsaka tabela vsebuje 13 različnih parametrov. V prvem stolpcu sta
datum in čas opazovanja, pri čemer sem čas v urah in minutah na risbah
pretvoril v del dneva. Vsi navedeni časi so v univerzalnem času (UT). Od 2.
do 4. stolpca si sledijo P, B0 in L0 . Vrednosti sem dobil z linearno
interpolacijo vrednosti, ki jih navaja revija Naše nebo [3].
Naslednji dva stolpca predstavljata koordinate središča skupin peg,
vendar samo če so unipolarne. Pri bipolarnih in multipolarnih skupinah so
navedene koordinate za središča skrajnih večjih peg. Parameter x je
pozitiven v smeri proti zahodu, y v smeri proti severu. Pri tem je
potrebno omeniti, da je zahod na Soncu tam, kjer pege zahajajo. Vse
vrednosti teh dveh koordinat sem določil s pomočjo risb. Enota za vse tri
parametre je navidezni polmer Sončeve ploskvice.
Od 7. do 9. stolpca so vrednosti za x0, y0 in d0. To so dejanske
vrednosti za x in y na Sončevi površini. D0 je oddaljenost od navideznega
središča Sončeve ploskvice in se izračuna po formuli:
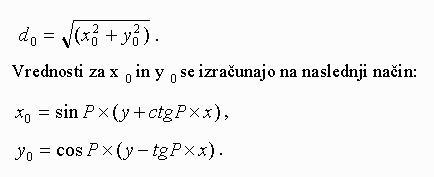 (3)(4)(5)
(3)(4)(5)
Izpeljavo le teh pojasnjuje slika.
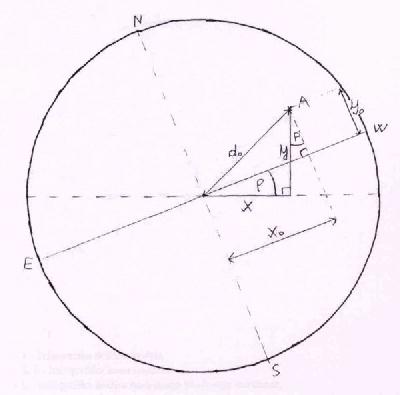
Slika 1: Osnovne koordinate na Sončevi ploskvici

Naslednja slika prikazuje vse koordinate na Sončevi ploskvici.
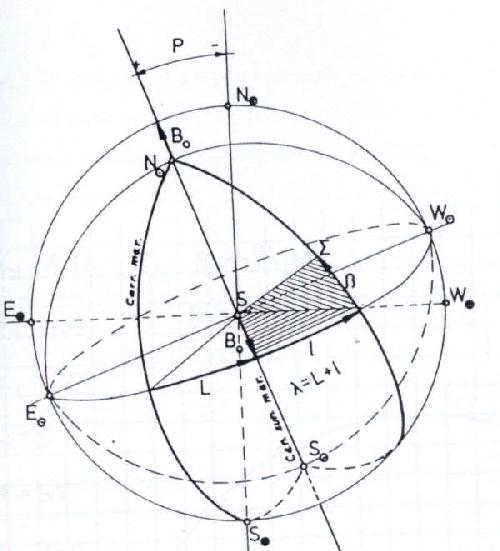

V zadnjem stolpcu so podatki o številu peg, ki pripadajo posamezni
skupini peg v opazovanem trenutku [4].
Vsi zgoraj omenjeni parametri in vrednosti so zbrani v 47 tabelah,
ki so dosegljive na Internet astronomski strani Gimnazije Šentvid.
V tabelah so vse skupine, za katere je dovolj podatkov. Skupine spadajo
v obdobje junij 1998- januar 1999. Vsaka tabela vsebuje podatke o skupini
peg za najmanj tri dni. Levo spodaj pod tabelo se nahaja legenda, desno pa
osnovni podatki o skupini peg. Poleg povprečne vrednosti so navedena tudi
odstopanja. Dodatno je navedena življenjska doba, če jo je bilo moč
izračunati in tip skupine.
Povprečno heliografsko širino in dolžino, kotno dolžino in število
peg sem izračunal tako, da sem vzel aritmetično sredino vseh vrednosti v
tabeli. Edino tam, kjer so v eni tabeli zbrane vrednosti skupine, ki je
deloma bipolarna, deloma unipolarna sem za povprečno vrednost kotne dolžine
vzel aritmetično sredino vrednosti, ki so večje od nič. Odstopanja so
standardne deviacije vrednosti v tabeli. Za lažjo predstavo je na naslednji
strani risba Sončevega površja.
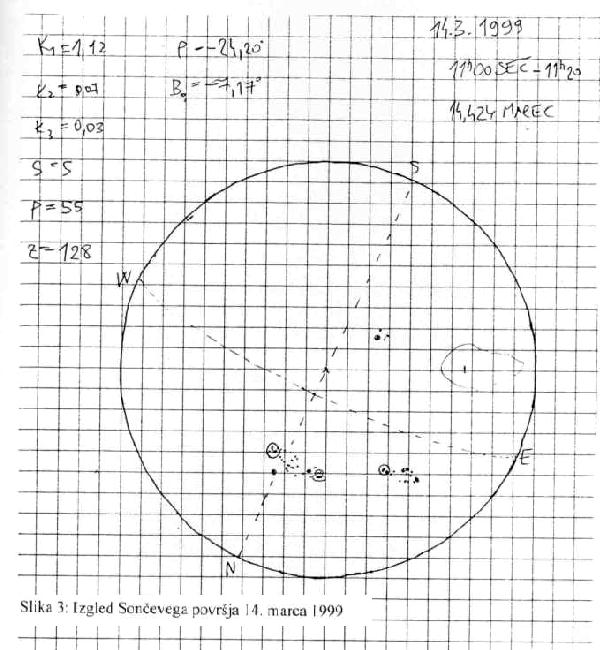
Slika 3: Izgled Sončevega površja 14. marca 1999.
Na zgornji sliki je moč opaziti veliko število peg,
ki so narisane kot črne pike. Nekatere obdaja polsenca, ki je
označena kot črta okoli peg. Veliko polje znotraj neprekinjene črte na
jugovzhodu Sončeve ploskvice predstavlja področje velikega števila bakel.
Spodaj je primer tabele, gre za tabelo o skupini peg številka 17.
Dan P B0 L0 x y x0 y0 d0 Heli.š. Hel. dol. K.d. Š.p. 17,396 avg. 16,70 6,74 147,43 -0,510 -0,630 -0,6695 -0,4569 0,8106 -22,84 100,84 0 1 18,406 avg. 17,05 6,79 134,08 -0,400 -0,600 -0,5583 -0,4563 0,7211 -21,99 97,06 0 2 19,438 avg. 17,38 6,83 120,44 -0,150 -0,600 -0,3224 -0,5278 0,6185 -25,74 99,47 0 1 21,424 avg. 17,97 6,90 94,20 0,105 -0,550 -0,0698 -0,5556 0,5599 -27,13 89,70 0 1 Legenda: Podatki o skupini peg: Povpr. vred. Od. P-Pozicijski kot Sončeve osi Heliografska širina: -24,4 st. 2,4 B0-Heliografska širina središča navidezne Sončeve Heliografska dolžina: 96,8 st. 5,0 ploskvice Kotna dolžina: 0,0 st. 0,0 L0-Heliogr. Dolžina središča navidezne Sončeve ploskvice Št. peg: 1 1 x-koordinata na risbah Sonca Življenjska doba: ? dni y-koordinata na risbah Sonca Tip: unipolarna skupina, tipa H Tabela 3: Podatki o skupini peg številka 172.4 Iskanje povezav med Sončevo aktivnostjo in vremenom
3. REZULTATI
3.1 Wolfovo število
Wolfovo število je zelo primerno za določanje aktivnosti Sonca. Obstajajo izračuni le-tega za dobrih 300 let. Sam sem izračunal Wolfovo število s pomočjo svojih risb Sonca. Wolfovo število sem izračunal za skoraj 90 dni v obdobju junij 1998- marec 1999. Izračuni se povečini dobro ujemajo s tistimi, ki jih objavlja Sunspot Index Data Center v Bruslju. Kot primer navajam vrednosti Wolfovega števila za meseca julij in avgust 1998:
Datum Moj izračun WŠ-ja Dokončna vrednost WŠ-ja 1. julij 1998 119 94 2. julij 129 95 5. julij 78 94 6. julij 56 74 9. julij 29 32 10. julij 57 49 11. julij 57 57 13. julij 38 44 16. julij 73 67 17. julij 51 59 29. julij 70 74 31. julij 75 68 2. avgust 68 76 9. avgust 129 125 12. avgust 125 121 14. avgust 78 94 17. avgust 91 87 18. avgust 104 83 19. avgust 119 101 21. avgust 117 89 30. avgust 145 117 31. avgust 129 109 Povprečno 88 86 Tabela 4: Wolfovo število v juliju in avgustu 1998.
Iz tabele je razvidno, da se mesečne vrednosti dobro ujemajo.
Dnevna neujemanja so posledica opazovalnih pogojev, različnega teleskopa
in seveda opazovalca. Povprečni odklon znaša 15 %, drugače pa ni nikoli
večji od 36 %.
Mesečne vrednosti so najbolj cenjene, ker povejo Sončevo aktivnost
celega Sonca (Sonce se okrog svoje osi zavrti v dobrih 27 dnevih).
Naslednja tabela prikazuje primerjavo mojih izračunanih vrednosti in
začasnih vrednosti, ki jih objavlja Sunspot Index Data Center v Bruslju.
Vendar so notri samo vrednosti tistih dni, ki so v mojih risbah.
Mesec Moj izračun WŠ-ja Začasna vrednost WŠ-ja Junij 63 69 Julij 69 67 Avgust 111 101 September 108 83 Oktober 57 59 November 82 71 Tabela 5: Mesečne vrednosti Wolfovega števila v letu 1998Iz tabele je razvidno, da se vrednosti za mesece junij, julij in oktober kar dobro ujemajo.
3.2 Površina peg
Poleg Wolfovega števila je zanimivo opazovati velikost peg.
Z opazovanji sem ugotovil, da imajo pege premer od 1000 pa do okoli
80000 km. Največ peg ima premere od 5000 do 20000 km. Največje pege so
bile vidne tudi s prostim očesom. Te pege spadajo v tipa F in G.
3.3 Bakle
Bakle so poleg peg edini pojav na Soncu, ki ga je možno opazovati
brez posebnih sredstev. Pojavljajo se okoli peg, najbolj izrazite so pred
in po nastanku peg. Vidijo se le proti robu Sončeve ploskvice in to zaradi
pojava robne zatemnitve. Bakle so za okoli 400 K bolj vroče od okolice,
zato so videti svetlejše. Območja, kjer se pojavljajo bakle so velika od
okoli 10 do okoli 10 km , kar predstavlja od nekaj promilov do nekaj
odstotkov površine navidezne Sončeve ploskvice.
3.4 Heliografska širina skupin peg
Druga najpomembnejša tema raziskovalne naloge je bila določiti,
na katerih širinah se pege pojavljajo. 47 tabel je bilo dovolj, da
sem ugotovil, da so se pege v tem obdobju pojavljale na heliografskih
širnah okoli 21° južno in okoli 18° severno. Vse skupine so bile oddaljene
od 5° pa tja do 35° od ekvatorja. Tudi porazdelitev po poloblah je dokaj
enakomerna. Na severni polobli je bilo 22 od 47 skupin, na južni pa 25
skupin peg. Vse navedene ugotovitve sem tudi pričakoval.
3.5. Kotna dolžina skupin peg
Pomemben faktor za ocenjevanje tipa skupine peg je prav gotovo
kotna dolžina. Kotna dolžina je kotna razdalja po longitudi med dvema
glavnima pegama v bipolarni skupini. Samo tipi A, H in J imajo kotno
dolžino 0°, ker tem skupinam pripadajo samo unipolarne skupine.
Povprečna kotna dolžina ostalih skupin je okoli 8,5°. Najmanjše skupine
imajo kotno dolžino kakih 4°, največje pa presegajo tudi 15° ( do 17° ).
3.6 Tipi skupin peg
Skupine peg delimo na devet razredov po züriški klasifikaciji.
To so razredi A, B, C, D, E, F, G, H in J [5]. Zato sem se odločil da
raziščem, koliko skupin spada v vsak navedeni tip. Spodnja tabela
prikazuje zastopanost skupin v posameznih tipih.
Tip skupine Zastopanost (%) A 12 B 8 C 7 D 10 E 4 F 5 G 5 H 35 J 14 Tabela 6: Zastopanost skupin peg za posamezni tip.Takoj je jasno, da prevladujejo tipi H, J, A in D. Predvsem izstopa tip H, kamor spadajo srednje velike ali velike pege s polsenco in majhnim številom okoliških peg. Zato sklepam, da razvite skupine peg najdalj časa pripadajo tipu H.
3.7 Število peg v skupinah
Število peg je v skupinah zelo različno. Odločil sem se, da
izračunam koliko peg ima povprečna skupina. Za 11 cm reflektor velja,
da je povprečno število peg v skupini 5. K temu prispeva precejšen delež
skupin z eno samo pego. V povprečju je 10 % skupin, ki vsebujejo vsaj 20
peg. V času opazovanj sem opazil nekaj skupin z več kot 30 pegami.
Iz tega sklepam, da se vsako leto okrog maksimuma aktivnosti pojavi
skupina peg z več kot 50 pegami.
3.8 Življenjska doba peg
Kot vse druge stvari imajo tudi Sončeve pege omejeno trajanje.
V literaturi lahko zasledimo, da pege živijo od nekaj ur pa do več mesecev.
Zato sem se odločil, da raziščem ali je morda življenjska doba povezano
s katero od lastnosti skupin peg. Na voljo nisem imel prav veliko podatkov,
vendar sem ugotovil, da se večje skupine peg na Soncu vidijo ponavadi v
dveh ali celo več sinodskih rotacijah. Najdlje živeče skupine so v tem
polletnem obdobju imele življenjske dobe okoli 80 dni. Povprečna
življenjska doba se giblje od 20 do 40 dni. Opazil sem tudi nekaj skupin
z življenjsko dobo manjšo od 10 dni. Predvsem tiste skupine, ki imajo
majhno razvitost (samo do tipa A,B,C ali D) živijo največ kak mesec.
Skupine, ki so tipa E ali F pa ponavadi živijo več kot mesec, včasih tudi
več mesecev. Na podlagi opazovanj, bi z gotovostjo rekel, da bolj razvite
skupine, z večjimi pegami živijo dlje kot ostale.
3.9 Povezava med vremenom in Sončevo aktivnostjo
3.9.1 Povezava med klimo in aktivnostjo Sonca
Kot je v uvodu že omenjeno so meteorologi že davno dokazali, da Sončeva aktivnost dolgoročno vpliva na vreme. Zato se s tem področjem nisem kaj dosti ukvarjal, uspel sem ugotoviti le, da mesečna oziroma letna aktivnost nista kaj dosti povezana z temperaturo, količino padavin, dolžino trajanja snežne odeje in drugimi podobnimi meteorološkimi parametri. Vse to sem ugotavljal s pomočjo podatkov o temperaturi, količini padavin, sončnim obsevanjem, itn. za meteorološki opazovalnici Triglav Kredarica in Ljubljana-Bežigrad za obdobje 1967-1999. To se mi zdi precej logično, saj ne morejo vsi kraji na Zemlji odstopati za enako vrednost v temperaturi, količini padavin, sončnemu obsevanju, itn., ker na vreme vpliva veliko dejavnikov.
3.9.2 Povezava med vremenom (kratkoročno) in aktivnostjo
Najpomembnejša naloga, s katero se ukvarja raziskovalna naloga je prav
gotovo povezava med trenutnim vremenskim stanjem in trenutno aktivnostjo
Sonca. Kot je napisano že v vsebini, sem se odločil da poiščem skupne
točke med položaji največje magnetne aktivnosti (mlade in srednje stare
skupine peg in bakle) in vremenskim stanjem v Evropi, severni Afriki
in Turčiji. Ugotovitve so me presenetile, saj sem našel dokaj dobro
povezavo med tema dvema stvarema.
Sončeve površino, ki je obrnjena k nam,
razdelimo na južno in severno poloblo ter še obe na vzhodno in
zahodno polovico, tako da dobimo štiri enake dele. Če v severovzhodni
četrtini ni aktivnosti (ni bakel in peg) potem je skoraj zagotovo, da
se azorski anticiklon v istem času razširi nad Iberski polotok, zahodno
Sredozemlje, delom Francije in nad Maroko ter Alžirijo. V zimskem času se
v primeru da na zahodni strani Sonca ni aktivnosti razširi sibirski
anticiklon. Islandski ciklon pa je najbolj dejaven takrat, ko na južni
polovici kar mrgoli peg in bakel. Tak primer je druga polovica septembra
leta 1998.
Sonce potrebuje 27 dni (gledano z Zemlje), da se zavrti okoli lastne
osi. Ker se pege ravno tako hitro gibljejo, je čas trajanja istega ciklona
ali anticiklona omejen na dva tedna. To pomeni, da nobena vremenska
situacija ne ostane nespremenjena za več kot 2 tedna.
Problem, ki nastane pri tej teoriji je predvsem ta, da v
času minimuma skoraj ni aktivnosti, kar pomeni, da teorija v
tem času ne drži, tako kot je omenjeno zgoraj. Zato mislim, da
je Sončeva aktivnost na njegovi površini posledica nemirne notranjosti,
kar pomeni, da imajo pege temelje v večjih Sončevih globinah. Seveda se
zavedam, da moja sklepanja temeljijo na prekratkem časovnem nizu opazovanj,
in da sem se omejil zgolj na Sonce.
Tabele s številom Sončevih peg za raziskovalno nalogo Sončeva aktivnost (1998/99) so v zapakirani datoteki pege98.zip.
Še nekaj besed o vrtenju Sonca.
Če merimo premik peg vsak dan, lahko za primerjavo tudi
izračunamo kolikšen del (w ) celotnega kroga
(360o) opiše pega na dan na določeni heliografski
širini v enem dnevu.
Empirična enačba se glasi:
w = 1/26( 1 -
(1/8)sin2b - (1/6)sin4b )
Pri tem je (b )
heliografska širina.
Na 20o pega v enem dnevu opiše 37,8 10-3
celotnega kroga,
torej celoten krog opiše v 26,4 dneh. Iz meritev in iz računa lahko
določimo napako, odstopanje. Odstopanja so tipično okrog enega dneva.
Avtor naloge in tabel: Gregor Vertačnik, Gimnazija Šentvid-Ljubljana
Mentor: Zorko Vičar
Do sedaj je to stran obiskalo
ljudi.
Nazaj na domačo stran.