Ploščina poligona na krogli



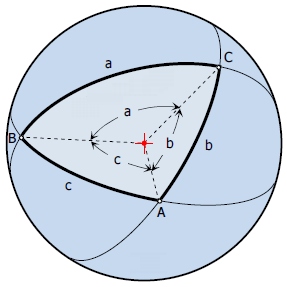
Ploščina (Area) trikotnika na sferi (vsako ploščino poligona lahko razdelimo na trikotnike - to je naša metoda.
Računamo podobno kot na ravnini, kjer seštevamo ploščine trapezov, tudi tokrat upoštevamo predznak posamezne ploščine, ki ga da razlika ge_dol[i]- ge_dol[j]. Le da v tem primeru seštevamo vsote ploščin trikotnikov, ki jih dajo trikotni pod-poligoni zaporednih točk na sferi, recimo glede na južni pol { (ge_si[i], ge_si[j]); (ge_dol[i], ge_dol[j]); (-90,0) }. 
    a   
  B----C 
  c\  /b 
    \/   
     A
Za polmer Zemlje privzamemo R = 6378.1370 km). Kako do ploščine trikotnika na sferi:

A, B, C = so koti sferičnega trikotnika (angles of spherical triangle in degrees)
E = sferični je eksces trikotnika (spherical excess of triangle), E = A + B + C - 180
- ostale formule za pomoč pri izračunu vrednosti E (other formula for the spherical excess E)
a, b, c = stranice sferičnega trikotnika v kotnih enotah (sides of spherical triangle)
s=(a+b+c)/2
tan(E/4) = sqrt(tan(s/2)*tan((s-a)/2)*tan((s-b)/2)*tan((s-c)/2))
Area_površina = pi*R^2*E/180



Ploščina poligona na sferi (O): km^2 | m^2 - z Reset se začne nov poligon (tri točke dajo ploščina - AREA - trikotnika.


Vnesi točke poligona na sferi preko ge. širine in dolžine v stopinjah, primer spodaj.

- IZ ZGORNJEGA OKNA IN KOORDINAT SE RAČUNA PLOŠČINO POLIGONA NA SFERI, razmejitev med podatki je znak '|' .

Geografska dolžina se meri od 0 do 180 ° in od 0 do -180 °. Geografska širina se meri od 0 do 90 ° in od 0 do -90 °. Kotne funkcije (v kombinaciji) so lahko zaradi natančnosti nestabilne pri skrajnih mejah 0, 90, 180, -180 °. Spodaj je primer, kako določimo polovico površino Zemlje z vrednostmi rahlo pod mejami ge. širine 90 °. S poligonom pod skrajnimi točkami, pa aplikacija deluje stabilno. Ne smemo pa pozabiti, da Zemlja ni čisto okrogla - je geoid.
KRAJ_1 | 89.999| 180|
KRAJ_3 | 0| 180|
KRAJ_3 | -89.999| 180|
KRAJ_3 | 0| 0|

Bolje je uporabiti vrednosti, ki so zamaknjene
KRAJ_1 | 45| 0|
KRAJ_3 | 45| 180|
KRAJ_3 | -45| 180|
KRAJ_3 | -45| 0|


  • Podoben interaktivni kalkulator, a s klikanjem po površini Zemlje in računanjem razdalj ter površin poligonov, je na strani:
    g-map - isce kraje in izpisuje koordinate ...

    Zorko V., 25. jun. 2019