ap-1 - 1
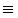 0 (mod p)
0 (mod p)
2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97, 101, 103, 107, 109, 113,
127, 131, 137, 139, 149, 151, 157, 163, 167, 173,
179, 181, 191, 193, 197, 199, 211, 223, 227, 229,
233, 239, 241, 251, 257, 263, 269, 271, 277, 281,
283, 293, 307, 311, 313, 317, 331, 337, 347, 349,
353, 359, 367, 373, 379, 383, 389, 397, 401, 409,
419, 421, 431, 433, 439, 443, 449, 457, 461, 463,
467, 479, 487, 491, 499, 503, 509, 521, 523, 541,
547, 557, 563, 569, 571, 577, 587, 593, 599, 601,
607, 613, 617, 619, 631, 641, 643, 647, 653, 659,
661, 673, 677, 683, 691, 701, 709, 719, 727, 733,
739, 743, 751, 757, 761, 769, 773, 787, 797, 809,
811, 821, 823, 827, 829, 839, 853, 857, 859, 863,
877, 881, 883, 887, 907, 911, 919, 929, 937, 941,
947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013,
1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069,
1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151,
1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223,
1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291,
1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373,
1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451,
1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511,
1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583,
1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657,
1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733,
1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811,
1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889,
1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987,
1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053,
2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129,
2131, 2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213,
2221, 2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287,
2293, 2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357,
2371, 2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423,
2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531,
2539, 2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617,
2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687,
2689, 2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741,
2749, 2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819,
2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903,
2909, 2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999,
3001, 3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079,
3083, 3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181,
3187, 3191, 3203, 3209, 3217, 3221, 3229, 3251, 3253, 3257,
3259, 3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331,
3343, 3347, 3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413,
3433, 3449, 3457, 3461, 3463, 3467, 3469, 3491, 3499, 3511,
3517, 3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571,
3581, 3583, 3593, 3607, 3613, 3617, 3623, 3631, 3637, 3643,
3659, 3671, 3673, 3677, 3691, 3697, 3701, 3709, 3719, 3727,
3733, 3739, 3761, 3767, 3769, 3779, 3793, 3797, 3803, 3821,
3823, 3833, 3847, 3851, 3853, 3863, 3877, 3881, 3889, 3907,
3911, 3917, 3919, 3923, 3929, 3931, 3943, 3947, 3967, 3989,
4001, 4003, 4007, 4013, 4019, 4021, 4027, 4049, 4051, 4057,
4073, 4079, 4091, 4093, 4099, 4111, 4127, 4129, 4133, 4139,
4153, 4157, 4159, 4177, 4201, 4211, 4217, 4219, 4229, 4231,
4241, 4243, 4253, 4259, 4261, 4271, 4273, 4283, 4289, 4297,
4327, 4337, 4339, 4349, 4357, 4363, 4373, 4391, 4397, 4409,
4421, 4423, 4441, 4447, 4451, 4457, 4463, 4481, 4483, 4493,
4507, 4513, 4517, 4519, 4523, 4547, 4549, 4561, 4567, 4583,
4591, 4597, 4603, 4621, 4637, 4639, 4643, 4649, 4651, 4657,
4663, 4673, 4679, 4691, 4703, 4721, 4723, 4729, 4733, 4751,
4759, 4783, 4787, 4789, 4793, 4799, 4801, 4813, 4817, 4831,
4861, 4871, 4877, 4889, 4903, 4909, 4919, 4931, 4933, 4937,
4943, 4951, 4957, 4967, 4969, 4973, 4987, 4993, 4999, 5003,
5009, 5011, 5021, 5023, 5039, 5051, 5059, 5077, 5081, 5087,
5099, 5101, 5107, 5113, 5119, 5147, 5153, 5167, 5171, 5179,
5189, 5197, 5209, 5227, 5231, 5233, 5237, 5261, 5273, 5279,
5281, 5297, 5303, 5309, 5323, 5333, 5347, 5351, 5381, 5387,
5393, 5399, 5407, 5413, 5417, 5419, 5431, 5437, 5441, 5443,
5449, 5471, 5477, 5479, 5483, 5501, 5503, 5507, 5519, 5521,
5527, 5531, 5557, 5563, 5569, 5573, 5581, 5591, 5623, 5639,
5641, 5647, 5651, 5653, 5657, 5659, 5669, 5683, 5689, 5693,
5701, 5711, 5717, 5737, 5741, 5743, 5749, 5779, 5783, 5791,
5801, 5807, 5813, 5821, 5827, 5839, 5843, 5849, 5851, 5857,
5861, 5867, 5869, 5879, 5881, 5897, 5903, 5923, 5927, 5939,
5953, 5981, 5987, 6007, 6011, 6029, 6037, 6043, 6047, 6053,
6067, 6073, 6079, 6089, 6091, 6101, 6113, 6121, 6131, 6133,
6143, 6151, 6163, 6173, 6197, 6199, 6203, 6211, 6217, 6221,
6229, 6247, 6257, 6263, 6269, 6271, 6277, 6287, 6299, 6301,
6311, 6317, 6323, 6329, 6337, 6343, 6353, 6359, 6361, 6367,
6373, 6379, 6389, 6397, 6421, 6427, 6449, 6451, 6469, 6473,
6481, 6491, 6521, 6529, 6547, 6551, 6553, 6563, 6569, 6571,
6577, 6581, 6599, 6607, 6619, 6637, 6653, 6659, 6661, 6673,
6679, 6689, 6691, 6701, 6703, 6709, 6719, 6733, 6737, 6761,
6763, 6779, 6781, 6791, 6793, 6803, 6823, 6827, 6829, 6833,
6841, 6857, 6863, 6869, 6871, 6883, 6899, 6907, 6911, 6917,
6947, 6949, 6959, 6961, 6967, 6971, 6977, 6983, 6991, 6997,
7001, 7013, 7019, 7027, 7039, 7043, 7057, 7069, 7079, 7103,
7109, 7121, 7127, 7129, 7151, 7159, 7177, 7187, 7193, 7207,
7211, 7213, 7219, 7229, 7237, 7243, 7247, 7253, 7283, 7297,
7307, 7309, 7321, 7331, 7333, 7349, 7351, 7369, 7393, 7411,
7417, 7433, 7451, 7457, 7459, 7477, 7481, 7487, 7489, 7499,
7507, 7517, 7523, 7529, 7537, 7541, 7547, 7549, 7559, 7561,
7573, 7577, 7583, 7589, 7591, 7603, 7607, 7621, 7639, 7643,
7649, 7669, 7673, 7681, 7687, 7691, 7699, 7703, 7717, 7723,
7727, 7741, 7753, 7757, 7759, 7789, 7793, 7817, 7823, 7829,
7841, 7853, 7867, 7873, 7877, 7879, 7883, 7901, 7907, 7919
V teoriji računske zahtevnosti algoritmov se problemi uvrščajo v različne težavnostne razrede glede na to, koliko resursov je potrebnih za rešitev (n.pr. časa reševanja, korakov v algoritmu, velikosti spomina računalnika itd.). Najlažji problemi so tisti, za katere obstaja algoritem, s katerim pridemo do rešitve v času, ki je omejen z neko fiksno potenco dolžine vhoda (s polinomom) - ti spadajo v razred P (polynomial time class).
Naslednji razred je NP (nondeterministic polynomial time class). Za te probleme se da v času, omejenem s polinomom, preveriti, ali je neka rešitev pravilna, medtem ko se časa, potrebnega za rešitev, ne da omejiti s polinomom.
Primer problema iz razreda NP: Hitro lahko preverimo, ali je sestavljanka (jigsaw puzzle) pravilno sestavljena - za vsak košček pogledamo sosednje, za kar potrebujemo približno (število sosednjih koščkov) x (število koščkov sestavljanke) enot časa. Pri reševanju pa imamo toliko kombinacij, da ni mogoče najti algoritma, ki bi imel število korakov omejeno z neko fiksno potenco števila koščkov.
Verjamemo, da sta razreda P in NP različna, ni pa dokazano. Pravzaprav je za dokaz tega razpisana nagrada v višini milijon dolarjev.
Predpostavki pri RSA sta, da spada razstavljanje velikega števila v razred NP, iskanje velikega praštevila pa v razred P.
Drugo predpostavko so avgusta letos (2002) dokazali trije indijski znanstveniki M. Agrawal, N. Kayal, and N. Saxena v članku PRIMES is in P.
Iz "malega Fermat-ovega izreka" so izpeljali algoritem, s katerim ugotovimo, ali je število n praštevilo v času, ki je omejen s polinomsko funkcijo dolžine števila n:
O(N)12f(log N).
To je velik teoretičen dosežek, ali pa bo tudi praktično uporaben, je zaenkrat težko reči.
V praksi bomo še naprej uporabljali sedaj uveljavljene postopke:
V zadnjih 30 letih so predstavili več postopkov, ki temeljijo na "malem Fermat-ovem izreku":
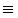 0 (mod p)
0 (mod p)
Če enačba velja za vsa števila a (a < p), je izpolnjen potreben pogoj za to, da je število p praštevilo, žal pa ni zadosten. Obstajajo namreč števila, ki pogoj izpolnjujejo, pa niso praštevila (Carmichaelova števila, n.pr. 561).
Število, ki naj bi bilo praštevilo, mora biti liho, in ga lahko zapišemo v obliki
Iz tega se da izpeljati sklep, da je p praštevilo z veliko verjetnostjo glede na osnovo a, če velja
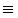 1 (mod p)
ali ad.2r
1 (mod p)
ali ad.2r 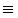 -1 (mod p),
kjer je r večji ali enak 0 in manjši od s (test Rabin - Miller).
-1 (mod p),
kjer je r večji ali enak 0 in manjši od s (test Rabin - Miller).
Če število ne ustreza testu, je gotovo sestavljeno, v nasprotnem primeru pa je verjetnost napake 1/4t, kjer t pomeni število ponovitev testa za različne osnove. Število, ki ustreza testu za 6 osnov, bi torej z verjetnostjo 1/46 = 0,00024 bilo sestavljeno število. Napaka se manjša z večanjem števila p. Pri 256-bitnem številu p ocenjujejo verjetnost napake na 1/251 pri 6 testih. Za običajno uporabo je taka možnost napake sprejemljiva.
V praksi je postopek takle:
 ad (mod n)
ad (mod n)
 -1 (mod n), sledi, da je n praštevilo in konec testa, sicer pa se vrnemo v zanko (z).
-1 (mod n), sledi, da je n praštevilo in konec testa, sicer pa se vrnemo v zanko (z).
Več o iskanju praštevil: Primality Proving
Oktober 2002