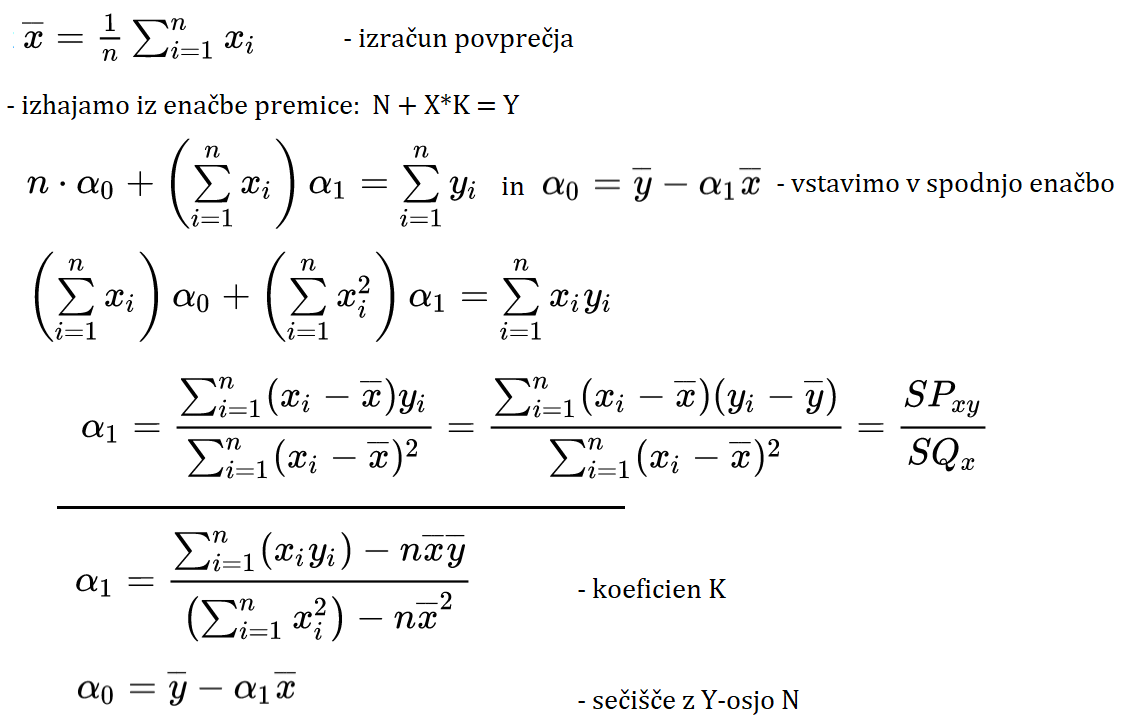Izracun linearne, kvadratne, kubne in eksponentne regresijske - preproste osnove
Zakaj metoda najmanjših kvadratov?
Še beseda o linearni regresiji
Regresija meri odvisnost dveh slučajnih spremenljivk - kakšen vpliv ima ena na drugo.
Na populaciji merimo 2 podatka, zanima nas vrsta odvisnosti med slučajnima spremenljivkama.
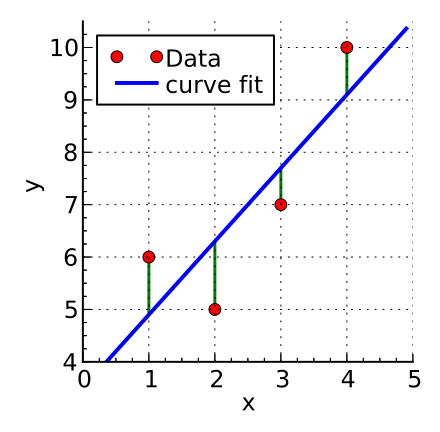
Razsevni grafikon spremenljivk x in y in graf linearna regresije - premice.
Glede na to, kako bi krivulja »morala izgledati«, začnemo graditi krivuljo, ki se bo najbolje prilegala
(da bo imela čim višjo korelacijo r).
Le redko je graf linearen,
a ker nas velikokrat zanima le linearni trend - v prvem približku torej poiščemo linearno regresijo.
Pri linearni regresiji torej iščemo strmino premice (trend 'K') in presečišče z Y osjo, to (presečišče ) naj bo označeno s črko 'N'.
Y = K*X + N
Postopek je naslednji:
- nn je število povezav med pari X in Y (točk na grafu),
- Seštejemo spremenljivke, njihove vse produkte (indeks i teče od 1 do nn, oz. od 0 do nn-1),
sum_x += 1*x[i];
sum_y += 1*y[i];
sum_xy += (x[i]*y[i]);
sum_xx += (x[i]*x[i]);
sum_yy += (y[i]*y[i]);
Izračunamo korelacijo, naklon K in N presečišče Y osi premice:
korelacija=(nn*sum_xy - sum_x*sum_y)/Math.sqrt((nn*sum_xx-sum_x*sum_x)*(nn*sum_yy-sum_y*sum_y));
K = (nn*sum_xy - sum_x*sum_y)/(nn*sum_xx - sum_x*sum_x);
N = (1*sum_y - k*sum_x)/nn;
Parametra K in N izberemo torej po metodi najmanjših kvadratov tako,
da minimiziramo Y = K*X + N (pogledamo za vsako meritev koliko daleč navpično (Yi) leži od premice (Y),
vsota kvadratov vseh razlik pa mora biti najmanjša).
Zakaj metoda najmanjših kvadratov?
Ker je vsota razlik teoretične krivulje Y in meritev Yi na kvadrat
prvi pogoj, ki da pri odvajanju zadostno število enačb, glede na število iskanih končnih konstant.
Spodaj so podani teoretični koraki, postopek.
Velja:
s=vsota(a1Xi + ao - Yi)2 = minimalna (odvajamo in odvod mora biti nič)
Odvajamo torej po K in N, oziroma po a1 in ao.
ds/da1 = 2vsota(a1Xi + ao - Yi)a1Xi = 0
ds/dao = 2vsota(a1Xi + ao - Yi)1 = 0
Tako velja:
nao + vsota(a1Xi) = vsota(Yi), izraz delimo z n od koder sledi ==>
ao = Y_pov - a1X_pov
( saj vemo, da je X_pov = vsota(Xi)/n, enaka logika velja za Y_pov )
- in še
vsota(Xi)ao + a1vosta(Xi)2 = vsota(Yi*Xi)
Spodaj je postopek simbolno matematično korektno zapisan.
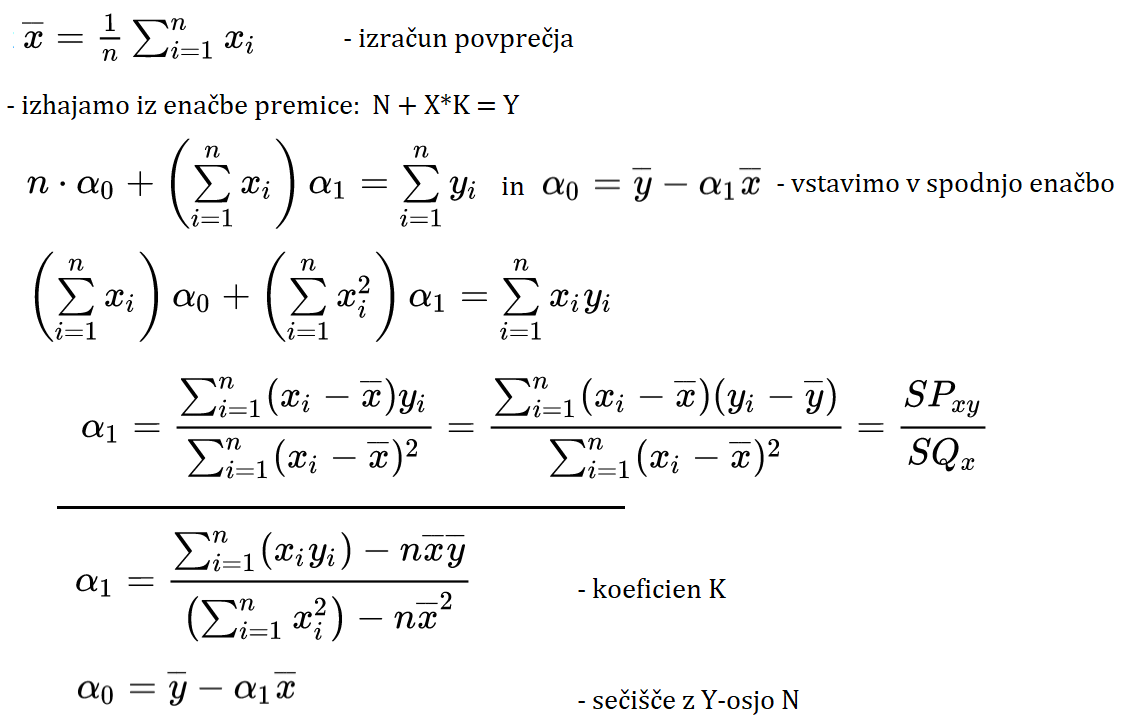
--------------------------------------------------------------------------------------------------
Še preprost način izpeljave in izračuna kvadratne in kubne regresije!
## Quadrat Regression y = ax^2 + bx +c - osnovna enacba
# -------------------------------
# n je stevilo vseh x sov, Xi je iti x
# s=vsota(aXi^2 + bXi +c - Yi)^2 - metoda najmanjsih kvadratov
# ds/da=ds/db=ds/dc=0
# vsota(Xi^4)a + vsota(Xi^3)b + vsota(Xi^2)c = vsota ((Xi^2)yi)
# vsota(Xi^3)a + vsota(Xi^2)b + vsota(Xi)c = vsota ((Xi)yi)
# vsota(Xi^2)a + vsota(Xi)b + nc = vsota (yi)
#--------------------------------------------------------
# A1=vsota(Xi^4) B1=vsota(Xi^3) C1=vsota(Xi^2)
# C2=vsota(Xi) U1=vsota ((Xi^2)yi) U2=vsota ((Xi)yi)
# U3=vsota (yi) n je stevilo vseh x sov, n>=3
#-------------------------------------------------------------
# A1a+B1b+C1c=U1
# B1a+C1b+C2c=U2
# C1a+C2b+nc =U31
# sistem treh enacb iz katerih poiscemo a, b in c
# iz spodnje izrazis a, in vstavis v srednjo in izrazis b v odvisnosti od c
# z B1 pomnozis zgornjo in z B1 srednjo
# in zgornji odstejes in v razliko vstavis b in iz
# te enacbe potegnes c
# nato pa se dobis b in na koncu a
# ----------------sledijo enacbe-----------------------
# $E=$C1*$C1-$C2*$B1;
# $K=$n*$B1-$C2*$C1;
# $H=$U2*$C1 - $B1*$U3;
# $J=$E*($U1*$B1 - $U2*$A1);
# $czg= $J - $B1*$B1*$H + $C1*$A1*$H;
# $csp=$B1*$B1*$K + $C1*$B1*$E - $C1*$A1*$K - $C2*$A1*$E;
# $c = $czg/$csp;
# $b =($U2*$C1 -$C1*$C2*$c + $B1*$n*$c - $B1*$U3)/$E;
# $a = ($U3 - $C2*$b -$n*$c)/$C1;
# TO JE TO !!!!!!!!!!!!
###################### kubna regresija #################################
###################### kubna regresija #################################
###################### kubna regresija #################################
## Cube Regression y = ax^3 + bx^2 + cx + d - osnovna enacba
# -------------------------------------------------------------------
# n je stevilo vseh x sov, Xi je iti x
# s=vsota(axi^3 + bxi^2 + cxi + d - Yi)^2 - metoda najmanjsih kvadratov, pri odvajanju bomo množenje z 2 kar spustili, kot da bi delili z 2 ...
# ds/da=ds/db=ds/dc=ds/dd=0
# ds/da = vsota(axi^3 + bxi^2 + cxi + d - Yi)xi^3=0
# ds/db = vsota(axi^3 + bxi^2 + cxi + d - Yi)xi^2=0
# ds/dc = vsota(axi^3 + bxi^2 + cxi + d - Yi)xi=0
# ds/dd = vsota(axi^3 + bxi^2 + cxi + d - Yi)=0
# vsota(Xi^6)a + vsota(Xi^5)b + vsota(Xi^4)c +vsota(Xi^3)d= vsota ((Xi^3)yi)
# vsota(Xi^5)a + vsota(Xi^4)b + vsota(Xi^3)c +vsota(Xi^2)d= vsota ((Xi^2)yi)
# vsota(Xi^4)a + vsota(Xi^3)b + vsota(Xi^2)c +vsota(Xi)d= vsota (Xiyi)
# vsota(Xi^3)a + vsota(Xi^2)b + vsota(Xi)c + nd = vsota (yi)
#
#-------------------------------------------------------------
# E=vsota(Xi^6) F=vsota(Xi^5) G=vsota(Xi^4)
# H=vsota(Xi^3) I=vsota(Xi^2) J=vsota(Xi)
# K4=vsota ((Xi^3)yi) K3=vsota ((Xi^2)yi) K2=vsota ((Xiyi) K1=vsota (yi)
# n je stevilo vseh x sov, n>=4
#-------------------------------------------------------------
# Ea+Fb+Gc+Hd=K4
# Fa+Gb+Hc+Id=K3
# Ga+Hb+Ic+Jd=K2
# Ha+Ib+Jc+nd=K1
# poznam vse st., ki so predstavljene z velikimi crkami
# To je sistem štirih enacb iz katerih poisčemo a, b, c in d
# iz spodnje izrazis a, in vstavis v eno visje in izrazis b* v odvisnosti od c in d
# z F pomnozis zgornjo in z E eno nizje
# in zgornji odstejes in v razliko vstavis b (kot fun c in d) in iz
# te enacbe potegnes c v odvisnosti od d ki ga vstavis v b*
# odstejes srednji dve in vanju vstavis b* in c, od koder izrazis d
# nato gres po vrsti nazaj, tako dobis d, c, b in a
# ----------------sledijo enacbe-----------------------
# $T=$H*$H-$G*$I;
# $Z=$K2*$H-$G*$K1;
# $W=$G*$J - $I*$H;
# $R=$G*$n - $J*$H;
# $N=$F*$F - $G*$E;
# $O=$G*$F - $H*$E;
# $P=$H*$F - $I*$E;
# $S=$K4*$F - $K3*$E;
# $A_A=$R*$N + $P*$T;
# $B_B=$N*$W + $O*$T;
# $D_D=$S*$T - $N*$Z;
# $G_G=$D_D/$B_B; $H_H=$A_A/$B_B;
# $U_U=$W*$G_G + $Z;
# $F_F=$R-$W*$H_H;
# $X_X=$U_U/$T; $H_H=$F_F/$T;
# $S_S=$G*$G - $H*$F;
# $C_C=$H*$G - $I*$F;
# $M_M=$I*$G - $J*$F;
# $K_K=$K3*$G - $K2*$F;
# $d= ($K_K-$S_S*$X_X-$G_G*$C_C)/($Y_Y*$S_S-$H_H*$C_C+$M_M);
# $c= ($D_D-$d*$A_A)/$B_B;
# $b= ($c*$W+$d*$R+$Z)/$T;
# $a= ($K1-$b*$I-$c*$J-$n*$d)/$H;
# TO JE TO ZA: Y ∝ X*X*X ... !!!!!!!!!!!!
# E=vsota(Xi^6) F=vsota(Xi^5) G=vsota(Xi^4)
# H=vsota(Xi^3) I=vsota(Xi^2) J=vsota(Xi)
# K4=vsota ((Xi^3)yi) K3=vsota ((Xi^2)yi) K2=vsota ((Xiyi) K1=vsota (yi)
# n je stevilo vseh x sov, n>=4
#-------------------------------------------------------------
# Ea+Fb+Gc+Hd=K4
# Fa+Gb+Hc+Id=K3
# Ga+Hb+Ic+Jd=K2
# Ha+Ib+Jc+nd=K1
-----------------------------------------------------------------------
Opozorilo - za polinome višje stopnje od 3, pa je smiselno
za reševenja sistem linearnih enačb uporabiti Gaussovo eliminacijsko metodo,
preko razširjene matrike A[i, j] ==> m x n.
Recimo, da je cilj najti in opisati množico rešitev naslednjega sistema linearnih enačb:
2 x + y - z = 8 ( L 1 )
- 3 x - y + 2 z = - 11 ( L 2 )
- 2 x + y + 2 z = - 3 ( L 3 )
Spodnja tabela je postopek zmanjševanja vrstic, ki se hkrati uporablja za sistem enačb
in z njim povezano razširjeno matriko. V praksi sistemov običajno ne obravnavamo v smislu enačb,
temveč uporabljamo razširjeno matriko, ki je bolj primerna za računalniške algoritme.
Postopek zmanjševanja vrstic je mogoče povzeti na naslednji način: odstranite x iz vseh enačb pod
L1 in nato odstranite y iz vseh enačb pod L2. To bo sistem postavilo v trikotno obliko. Nato je z uporabo
povratne substitucije mogoče rešiti vsako neznanko.
Matrika se postopoma pretvori v obliko ešalona (imenovana tudi trikotna oblika, pod diagonalo so ničle)!
 Kot je razloženo zgoraj, Gaussova eliminacija pretvori dano m × n matriko A v matriko v obliki
vrstnega ešalona (na koncu je diagonala različna od nič).
V naslednji psevdokodi A[i, j] označuje vnos matrike A v vrstici i in stolpcu j z indeksi, ki se začnejo z 1.
Transformacija se izvede na mestu, kar pomeni, da je prvotna matrika izgubljena, ker jo postopoma nadomesti
oblika vrsta-ešalon (vrsta - trikotnik, pod diagonalo so ničle).
h := 1 /* Initialization of the pivot row (inicializacija, vzpostavitev "vrtilne-prenosne vrstice") */
k := 1 /* Initialization of the pivot column */
while h ≤ m and k ≤ n
/* Find the k-th pivot: */
i_max := argmax (i = h ... m, abs(A[i, k]))
if A[i_max, k] = 0
/* No pivot in this column, pass to next column */
k := k + 1
else
swap rows(h, i_max)
/* Do for all rows below pivot: */
for i = h + 1 ... m:
f := A[i, k] / A[h, k]
/* Fill with zeros the lower part of pivot column: */
A[i, k] := 0
/* Do for all remaining elements in current row: */
for j = k + 1 ... n:
A[i, j] := A[i, j] - A[h, j] * f
/* Increase pivot row and column */
h := h + 1
k := k + 1
*** Uporabi JavaScript aplikacijo za reševanje sistema linearnih enačb preko matrike.
###################### eksponentna regresija #################################
###################### eksponentna regresija #################################
###################### eksponentna regresija #################################
Eksponentna regresija na podatkih:
Kot je razloženo zgoraj, Gaussova eliminacija pretvori dano m × n matriko A v matriko v obliki
vrstnega ešalona (na koncu je diagonala različna od nič).
V naslednji psevdokodi A[i, j] označuje vnos matrike A v vrstici i in stolpcu j z indeksi, ki se začnejo z 1.
Transformacija se izvede na mestu, kar pomeni, da je prvotna matrika izgubljena, ker jo postopoma nadomesti
oblika vrsta-ešalon (vrsta - trikotnik, pod diagonalo so ničle).
h := 1 /* Initialization of the pivot row (inicializacija, vzpostavitev "vrtilne-prenosne vrstice") */
k := 1 /* Initialization of the pivot column */
while h ≤ m and k ≤ n
/* Find the k-th pivot: */
i_max := argmax (i = h ... m, abs(A[i, k]))
if A[i_max, k] = 0
/* No pivot in this column, pass to next column */
k := k + 1
else
swap rows(h, i_max)
/* Do for all rows below pivot: */
for i = h + 1 ... m:
f := A[i, k] / A[h, k]
/* Fill with zeros the lower part of pivot column: */
A[i, k] := 0
/* Do for all remaining elements in current row: */
for j = k + 1 ... n:
A[i, j] := A[i, j] - A[h, j] * f
/* Increase pivot row and column */
h := h + 1
k := k + 1
*** Uporabi JavaScript aplikacijo za reševanje sistema linearnih enačb preko matrike.
###################### eksponentna regresija #################################
###################### eksponentna regresija #################################
###################### eksponentna regresija #################################
Eksponentna regresija na podatkih:
y = a*eb*x.
Zdi se zahtevna naloga - a v tem primeru obstaja dokaj preprosta rešitev
preko pogosto uporabljene matematične metode - linearizacije.
V tem primeru bomo torej linearizirali funkcijo z logaritmiranjem in
tako preko linearne regresije določili člena a in b.
Velja: ln y = ln a + bx
Iščemo torej člena a in b za logaritem meritev Yi.
In naj bo Yl = ln y in tako velja
Yl = ln a + bx = A + bx.
Postopek je sedaj enak kot pri linearni regresiji, le da na koncu velja,
ko izračunamo člena a in b
(velja a = exp(A) ):
y = aebx.
Spet s korelacijo R določimo odstopanje teoretične fitane funkcije od meritev - če je blizu 1,
je torej izbira eksponentne funkcije smiselna!
Nazaj
 Kot je razloženo zgoraj, Gaussova eliminacija pretvori dano m × n matriko A v matriko v obliki
vrstnega ešalona (na koncu je diagonala različna od nič).
V naslednji psevdokodi A[i, j] označuje vnos matrike A v vrstici i in stolpcu j z indeksi, ki se začnejo z 1.
Transformacija se izvede na mestu, kar pomeni, da je prvotna matrika izgubljena, ker jo postopoma nadomesti
oblika vrsta-ešalon (vrsta - trikotnik, pod diagonalo so ničle).
h := 1 /* Initialization of the pivot row (inicializacija, vzpostavitev "vrtilne-prenosne vrstice") */
k := 1 /* Initialization of the pivot column */
while h ≤ m and k ≤ n
/* Find the k-th pivot: */
i_max := argmax (i = h ... m, abs(A[i, k]))
if A[i_max, k] = 0
/* No pivot in this column, pass to next column */
k := k + 1
else
swap rows(h, i_max)
/* Do for all rows below pivot: */
for i = h + 1 ... m:
f := A[i, k] / A[h, k]
/* Fill with zeros the lower part of pivot column: */
A[i, k] := 0
/* Do for all remaining elements in current row: */
for j = k + 1 ... n:
A[i, j] := A[i, j] - A[h, j] * f
/* Increase pivot row and column */
h := h + 1
k := k + 1
*** Uporabi JavaScript aplikacijo za reševanje sistema linearnih enačb preko matrike.
###################### eksponentna regresija #################################
###################### eksponentna regresija #################################
###################### eksponentna regresija #################################
Eksponentna regresija na podatkih:
Kot je razloženo zgoraj, Gaussova eliminacija pretvori dano m × n matriko A v matriko v obliki
vrstnega ešalona (na koncu je diagonala različna od nič).
V naslednji psevdokodi A[i, j] označuje vnos matrike A v vrstici i in stolpcu j z indeksi, ki se začnejo z 1.
Transformacija se izvede na mestu, kar pomeni, da je prvotna matrika izgubljena, ker jo postopoma nadomesti
oblika vrsta-ešalon (vrsta - trikotnik, pod diagonalo so ničle).
h := 1 /* Initialization of the pivot row (inicializacija, vzpostavitev "vrtilne-prenosne vrstice") */
k := 1 /* Initialization of the pivot column */
while h ≤ m and k ≤ n
/* Find the k-th pivot: */
i_max := argmax (i = h ... m, abs(A[i, k]))
if A[i_max, k] = 0
/* No pivot in this column, pass to next column */
k := k + 1
else
swap rows(h, i_max)
/* Do for all rows below pivot: */
for i = h + 1 ... m:
f := A[i, k] / A[h, k]
/* Fill with zeros the lower part of pivot column: */
A[i, k] := 0
/* Do for all remaining elements in current row: */
for j = k + 1 ... n:
A[i, j] := A[i, j] - A[h, j] * f
/* Increase pivot row and column */
h := h + 1
k := k + 1
*** Uporabi JavaScript aplikacijo za reševanje sistema linearnih enačb preko matrike.
###################### eksponentna regresija #################################
###################### eksponentna regresija #################################
###################### eksponentna regresija #################################
Eksponentna regresija na podatkih: