Gimnazije Šentvid, seminar_1999 IZ ASTRONOMIJE, ASTROFOTOGRAFIJA.

Seminar 1999

Vsebina te strani se v okviru časa in ustreznega gradiva dopolnjuje.
ČASI, FILMI,
TABELE,
ASTROFOTOGRAFIJA ...
 t=(f/D)2/(XISO*K)
Osvetljenost filma

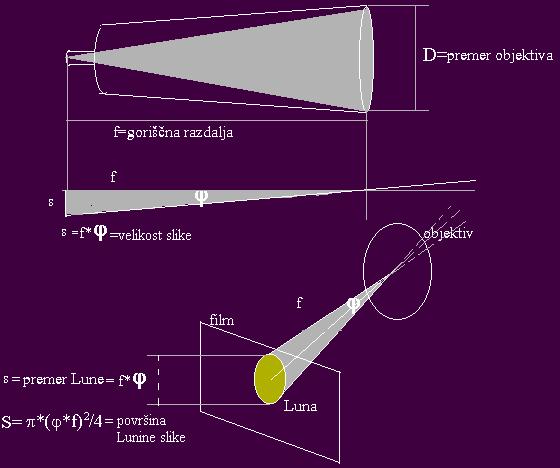
Izkaže se, da je za svetlost slike (ali tudi osvetljenost filma, očesa …) izjemno pomembna (odločilna) zaslonka. Poglejmo preprosto izpeljavo. Površina objekta na filmu je ponavadi sorazmerna s kvadratom velikosti slike, za primer Lune (glej sliko) velja:

S=π*(φ*f)2/4

Svetlobni tok P, ki prispe skozi vhodno odprtino teleskopa , je kar j*(D2*π/4). J je gostota svetlobnega toka objekta. Ves ta svetlobni tok se porazdeli po površini slike na filmu. Če iščemo povprečno osvetljenost filma (recimo s sliko Lune), potem velja (privzamimo, da so žarki skoraj pravokotni na film):

j(osvetljenost filma s sliko Lune) =P/S =j*(D2*π/4) /((φ*f)2*π/4) = konst*(D/f)2=
=konst*(1/zaslonka)2

Konstanta je tukaj mišljena le za točno določen objekt, gostota svetlobnega toka zelo oddaljenih vesoljskih teles in zorni kot se namreč zelo počasi spreminjata. Enačbo lahko posplošimo. Iz enačbe za osvetljenost filma ("osvetljenost slike") je razvidno, da je le ta odvisna od gostote svetlobnega toka z objekta, obratne vrednosti kvadrata zornega polja (na nobeno od teh količin ne moremo vplivati) in od razmerja med premerom in goriščem teleskopa na kvadrat. Razmerje D/f ponavadi imenujemo relativna odprtina. Zaslonka ali tudi f-vrednost pa je definirana ravno obratno, je f/D. Vrednost zaslonk (f/D) je na objektivih fotoaparatov ponavadi zapisana s sledečimi vrednostmi: 2,8 4 5,6 8 11 16. Če bomo opazovali šibke objekte (meglice, galaksije, kopice), si želimo čim več zbrane svetlobe, torej teleskope velikih premerov. Toda to ni dovolj, kot vidimo je sama osvetljenost odvisna od kvadrata relativne odprtine (D/f) in če kupimo teleskope relativno dolgih gorišč (recimo zaslonke nad 10), pomeni, da bomo imeli v zornem polju teleskopa sicer relativno velike objekte, a na žalost svetlobno šibke, medle. To je tudi glavni problem poceni 5 ali 6 centimetrskih teleskopov, ki ponujajo bajne povečave (tudi nekaj 100X, ki so ponavadi tudi v neskladju z ločljivostjo teleskopov), in ki nam razen Lune, Sonca in planetov, ne omogočajo opazovanj večine ostalih megleničastih objektov ("deep sky" objektov). Ljudje pa, ker smo neuki, pademo na trik in kupujemo "povečave", namesto da bi kupovali svetlobno zmogljive teleskope (velik premer objektiva, vsaj 8cm in zaslonka 10 ali manj). Poglejmo kakšna je pravzaprav sploh razlika, če slikamo recimo Luno z zaslonko 10, enkrat s teleobjektivom z goriščem 100 mm in enkrat s teleskopom (teleobjektivom) z goriščem 1000mm. Luna slikana z enakim filmom in enkimi časi bo na posnetkih narejenimi s teleskopom enako svetla, kot na posnetkih narejenimi s teleobjektivom, glej enačbo za osvetljenost. Kakšna je torej razlika? Slika narejena s teleskopom je spodobno velika (1m goriščne razdalje nam da Luno veliko slabih f*φ=1000mm*30*p/(180*60)=9 mm). Luna slikana skozi teleobjektiv 100mm pa bo velika le slab milimeter.




Ker je :
j(osvetljenost filma s sliko Lune) =P/S =j*(D2*π/4) /((φ*f)2*π/4) = konst*(D/f)2=konst*(1/zaslonka)2

SKLEPAMO, DA ZA KVALITETNO EKSPONIRAN (OSVETLJEN) FILM VELJA, DA JE kvocient med številom fotonov in površino zmeraj približno enak. To dosežemo s primernim časom in zaslonko, glede na gostoto vpadnega svetlobnega toka j in glede na zorni kot φ:

(število fotonov)/(površinska enota)=kon.*(D/f)2*t
(v kon. je med drugim zapopaden tudi zorni kot in j)

Ker je posnetek uporaben le, če pade na film zadostno število fotonov na površinsko enoto, velja, da je število fotonov vsekakor premosorazmerno produktu ekspozicijskega časa (t) in osvetljenosti filma (j). Ker je osvetljenost premosorazmerna relativni odprtini (D/f) na kvadrat, bo torej čas snemanja sorazmeren kvadratu zaslonke (f/D). Iz navedenih dejstev sledi, da bo v splošnem čas osvetlitve obratno sorazmeren z občutljivostjo filma (enota ISO), gostoto svetlobnega toka in sorazmeren s kvadratom zornega kota. Vsekakor je pomembna tudi valovna dolžina oziroma spekter vpadne svetlobe in občutljivost filma po valovnih dolžinah. Zorni kot, gostoto svetlobnega toka in še ostale vplive bomo združili v konstanto K=konstnta*j/φ2. Enačba, ki seldi ima naslednjo obliko:
t=(f/D)2/(XISO*K)
Vrednost zaslonk (f/D) je na objektivih fotoaparatov ponavadi zapisana s sledečimi vrednostmi: 2,8 4 5,6 8 11 16. Zdaj tudi vemo zakaj? Kvadrati navedenih vrednosti linearno naraščajo in vsak kvadrat je od prejšnjega večji za 2X. To pomeni, da če zaslonko povečamo recimo od 2,8 na 4, moramo čas ekspozicije podvojiti.
Formula in maske za izračun (oceno) časa pri snemanju nebesnih objektov.
-----------------------------
t=(f/D)2/(XISO*K)

K     je konstanta (odvisna od telesa)
XISO  občutljivost filma (ISO)
f/D   zaslonka (razmerje med goriščno razdaljo in 
      premerom vhodne odprtine-objektiva)

-------------------------------------------------------------------

K za različna telesa Sončevega sistema.


Luna



































				
				      K
mlada Luna (ozek srp)		      10
4 ali 24 dni stara Luna		      20
prvi ali zadnji krajec		      40
10 ali 18 dni stara Luna	      80
polna Luna			      220
delni mrk			      20
popolni mrk			      0,005
pepelnato siva Luna (neosvetljen del) 0,01



Planeti		  Srednja vrednost 	
                  K  
Venera	200-800	  500		
Mars	50	   50 (120)		
Jupiter	20-40	   40		
Saturn	10	   10		

Sonce			
t=(f/D)*(f/D)/(XISO*K)			
0.01% filter			
K=70 000 000
Časi za Luno:
Ekspozicijski čas t=(f/D)2/(XISO*K)=
K=10 K=20 K=40 K=80 K=220 K=20 K=0.005 K=0.01









(f/D) 2/ XISO *K s (-vrednost 1/t )
Časi za Saturn:
Ekspozicijski čas t=(f/D)2/(XISO*K)=

(f/D) 2/ K*(ISO) s (-vrednost 1/t )
Časi za Jupiter:
(f/D) 2/ K*(ISO) s (-vrednost 1/t )
Časi za Mars:
(f/D) 2/ K*(ISO) s (-vrednost 1/t )
Časi za Merkur:
(f/D) 2/ K*(ISO) s (-vrednost 1/t )
Časi za Venero:
(f/D) 2/ K*(ISO) s (-vrednost 1/t )

Graf in razpredelnica za izbiro časa pri slikanju planetov, pri danima zaslonki in filmu.

Trikotnik: Lunina, Saturn Venera; posnela Milica Pribošič, film 400 ISO, marec 1999.

Za astronomski krožek: ZORKO Vičar

Komentarji so zaželjeni.
E-POŠTA, RFC-822: Zorko.Vicar@guest.arnes.si

Nazaj na seminar.
Nazaj na domačo stran.