

1) INTRODUCTION
It is possible that compact stars might possess strong magnetic fields. If the magnetic flux is conserved during the course of stelar evolution, then the field B will scale with radius R as B ∝ 1/R2. Thus, in transition form the main sequence (R≈ 109m) to the white-dwarf stage (R≈ 3*106m), an initial surface field of 0.001T could grow to 102T. Our problem is how to discover magnetic compact stars?
We know that magnetic field splits energy levels of atoms and can also inffluence the polarization of the emitted light. This effects are the key for the detection of magnetic fields on stars.
2) SPLITTING OF ENERGY LEWELS OR ZEEMAN EFFECT
a) In weak magnetic fields, i.e. in fields that are considerably weaker than typical atomic fields (B≤ 0,1T), the atom responds to the external field as whole (LS coupling), and the energy level splitting can be described by the anomalous Zeeman effect.
EM=En+g(h/2π) eoBMJ/(2m) (1)
Here En is energy without magnetic field, J is the quantum number of total angular momentum, MJ the magnetic quantum number and g the Lande factor
g=1+( J(J+1)+S(S+1)-L(L+1) )/(2J(J+1))
The selection rule for allowed transitions between the levels of different terms is Δ MJ=0 (π components) and Δ MJ=±1 (σ ± components). σ ± means right and left hand circular polarization and π linear polarization.
b) Zeeman effect in strong magnetic field (0,01≤ B≤ 10T). This so called Pashen-Back effect is the result of the decoupling of L and S. The energies, (EM) of split levels are now given by
EM=En+g(h/2π) eoB(ML+2MS)/(2m) (2)
where ML is the orbital magnetic quantum number and MS is the spin magnetic quantum number. The selection rules require: Δ ML=0, ± 1; Δ MS=0
c) Quadratic Zeeman effect
if the magnetic flux is conserved in gravitational collapse, it is expected that white dwarfs an neutron stars will have magnetic fields between 102 and 108 T. For these very large field strengths, the quadratic Zeeman effect is expected to dominate over the linear effect. One gets a theoretical description by also including the quadratic terms in the Hamiltonian,
χ ∧ =( P∧ +eorxB/2 )2/(2m) + eoB· S∧ /m (3)
Where S∧ is the spin operator (attention, the vectors are written down in bold face). For B=(0,0,B) the Hamiltonian can be written as
χ ∧ =P∧ 2/(2m) +eoB(L∧ Z + 2SZ∧ )/(2m) + eo2 B2r2(sin (ϑ ))2/(8m) (4)
where r and ϑ are polar coordinats with respect to the field direction. The second term in χ∧ is responsible for the linear effect (2) and the last term causes the quadratic Zeeman effect. This effect produces a displacement Δλ of spectral lines towards shorter wavelengths. The displacement for hydrogen has been computed by Van Vleck (1932) and by Jenkins and Segre (1932) and can be expressed as follows:
Δ λ q = - eo2 B2rb2λ 2n4(1+ml2)/(8mhc) (5)
where eo2rb2/(8mhc)=4,5 10-5 (1/T2m). Due to this steep dependence of the quantum number n of the upper level, the quadratic effect becomes important even at relatively low magnetic fields; for example at B=103T the Hβ line is shifted by 5,44nm due to the quadratic effect which is quite comparable to the 10nm due to the linear contribution.
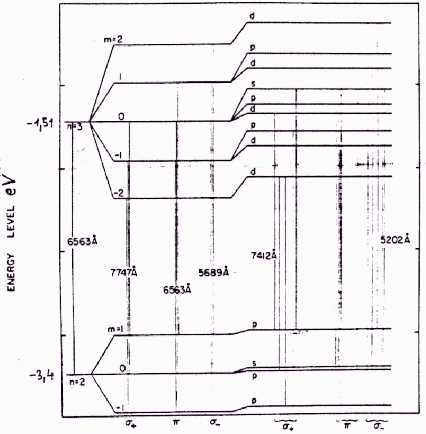
Figure 1.
The Zeeman splitting of Hα
at B=5 103T. The energy level shifts are shown first as computed from the linear term alone, whereas in the second step the quadratic effect is included. The permitted transitions are indicated by lines connecting the horizontal energy levels and are spaced horizontally in proportion to their wavelengths.
The energy levels were calculated from the analytic expression of Homada and Nakamura (1973).
By quadratic effect σ ± and π component has not the same wavelengths like by linear effect. Note that the multiplicity of levels becomes quite complex. It will be seen that each component of the classical triplet splits into five subcomponents.
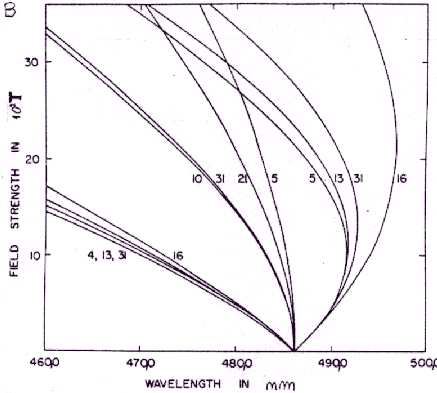
Figure 2.
The Zeeman splitting of Hβ
in fields up to 3,6 103 T. The wavelengts are interpolated
from Kemic's tables (1974).
3) A MODEL OF CIRCULARLY POLARIZED THERMAL EMITTER
We want to show that circular polarization must accompany any emission of eletronic origin from a thermal source in magnetic field. As the prototype of the radiating systems we take a collection of eletronic harmonic oscillators. We supposed that all the oscillators are sustained in thermal equilibrium at uniform temperature T, through nonradiative interactions with a thermostat (which, for example, might be the store of kinetic energy of atoms in a gas).
The radiating system is immersed in a uniform magnetic field B=(0,0,B). The Hamiltonian for the oscillator is:
H=(P-eA)2/(2m)+Kr2/2 (6)
Since mv=p-eA, the Hamiltonian can also be written as
H=mv2/2+Kr2/2 (6a)
The classicals equation of motion is:
m(d2r/dt2)=-Kr+e(dr/dt)xB (7)
We can split equation (7) in z and (x,y) plane, because the magnetic field B influences only on (x,y) part of motion in z direction is independet from motion in (x,y) plane. In the (x,y) plane we have
d2ρ /dt2=-ω 2ρ+2Ω (dρ/dt)xk (7a)
where k is the unit vector along z direction, ω =(K/m)1/2 is the oscilator frequency and Ω =eB/(2m) is Zeeman frequency.
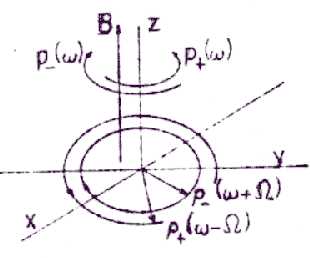
Figure 3.
The two circularly "polarized" components of the general
orbit r(t) of a harmonic oscillator in a magnetic field,
projected in the (x,y) plane.
Equation (7a) has two solutions:
ρ ± (t)=ρ ± (cos(ω ± t+Φ ± ), ± sin(ω ± t+Φ ± )) (7b)
-which are right-and left-hand circular orbits. The frequencies are (the + orbit has lower frequency if the charge is positive):
ω ± =(ω 2+Ω 2)1/2± Ω (8)
Generaly ρ (t)=ρ +(t)+ρ -(t). We can split the Hamiltonian (6) into z and (x,y) part of the Hamiltonian is:
Hx,y=((ω 2+ω 2-)ρ 2+ + (ω 2+ω 2+)ρ 2-)/(2m)
The equipartition theorem now predicts kT/2 for each quadratic term in Hamiltonian, thus:
(ω 2+ω 2+)<ρ 2->/(2m)=(ω 2+ω 2-)<ρ 2+>/(2m)=kT (9)
<ρ ± 2>=2kT/(m(ω 2+ω 2±)) (9a)
The eletronic-dipole emission power is proportional to a2ω 4 , where a is the amplitude of the dipole momentum. If a2=<ρ ± 2> then we use equation (9a) and we get for the power emitted by electron circuling in positive and negative direction (with frequency ω ± ):
P± (ω ± )=eo2<ρ ± 2>ω 4±/(12π ε oco3)=α 2kTω 4± /(m(ω 2+ω 2± )) (10)
Or, if we express according to (8) in terms of ω and Ω we get:
P± (ω ± )=α kTω 3/(m(ω ± Ω ))= P(ω )ω /(ω ± Ω ) (10a)
If we are observing the emission in the direction of the magnetic field, then the electron circling in the positive direction will radiate photons which are right-hand circularly polarized and the electron moving opposite will be oppositely polarized. The fractional polarization of light observed in this direction is thus:
q(ω )=(P+(ω )-P-(ω )) /(P+(ω )+P-(ω ))=-Ω /ω =-eB/(2mω ) (11)
This result is valied if Zeeman frequency is low enough so that (h/2π) Ω <<kT.
4. OBSERVATIONAL RESULTS
Strong circular polarization, 1-3%, has been discovered in visible light from the "peculiar" white dwarf GRW-70o 8247. To first-order the polarization of magnetoemission along the B field is given by (11), or in terms of wavelength q(ω )=-Ω /ω =-Ω λ /(c2π ), where Ω is the Zeeman frequency, i.e. the inclination of the q(λ ) is proportional to the magnetic field. The magnetic field deduced in this way from figure 4 is B=(1,2 ± 0,3) 103T.
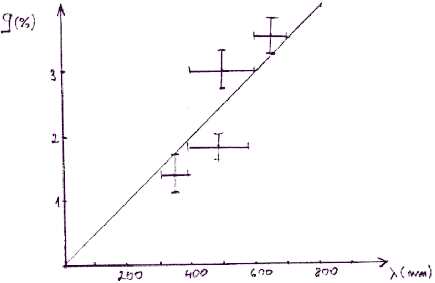
Figure 4.
Circular polarization, in percent, of light from the white dwarf
GRW 70o 8247. Horizontal bars indicate the approximate
wavelengths passbands. The straight line is the theoretical
q(λ
) for B=1,2 103T.
This star has also a very interesting spectrum, which consists of two or three absorbtion bands. The magnetic field of 103T displaces the central (π ) component of the Hγ line to λ =413.5nm and Hδ to λ =365nm, which is the location, where the dips are actually observed.
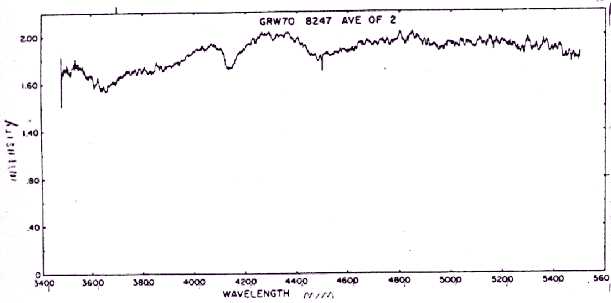
Figure 5.
Spectrum of the white dwarf GRW 70o 8247.
The next example is the white dwarf (L 795-7=Feig 7). This star has a rich spectrum of hydrogen and helium Zeeman components. The absorbtion features are identified with Zeeman components of HeI(π )(λ1=587,6 and λ2=667,8nm) and Hα, all in a field of 1,8 103T. All three lines correspond to transitions between n=2 and n=3, and have therefore a weak (Δ λq=2nm) quadratic shift. It should be pointed out that a very uniform magnetic field must exist over a large part of the star to give such a well resolved Zeeman pattern.
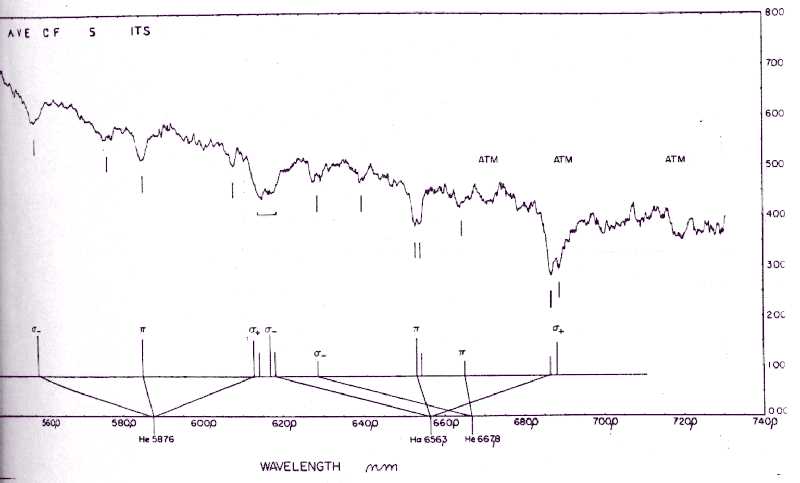
Figure 6.
Spectrum of white dwarf L 795-7=Feig 7 show Zeeman splitting
of Hα
and HeI(λ1=587,6
and λ2=667,6nm).
We can see the linear and also the quadratic Zeeman effect.
The spectrum on figure 7 shows the variabylity that has the same period - this period is 2,2, hours.
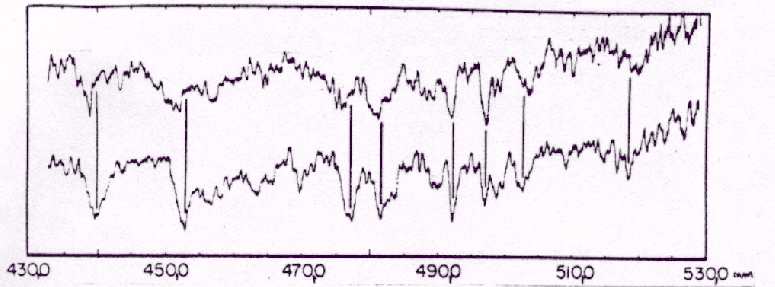
Figure 7.
The upper spectrum is fitted by a field 2 103T;
the lower by 1,8 103T.
REFERENCES
J. Č. Kemp - Circular polarization of thermal radiation in a magnetic field, Ap. J. 162 (1970), 172-174
J. R. P. Angel - Magnetism in white dwarfs, Ap. J. 216 (1977) 1-8
Mentor -A. Čadež
Pripravil (seminar) Zorko Vičar
FNT Ljubljana, 1986
sym