Dobili se bomo ob 17:30 v observatoriju Gimnazije Šentvid, Prušnikova 98, 1000 Ljubljana. Kateri datum bo izbran bo seveda odločilo vreme, vsekakor pa se 4 ure (od 14. ure naprej) pred odhodom od doma slišimo po telefonu ali elektronski pošti. Moj telefon je (061) 324 563, e-naslov je zorko.vicar@guest.arnes.si. Na žalost se mi je po elektronski pošti javilo samo 7 udeležencev, čeprav je načeloma oddalo naslove 14 udeležencev.

IZJEME Če slučajno kdo na izbran dan ne bi imel časa, se lahko načeloma zanj dogovorim za nek drug termin. To naj bo prej izjema kot pravilo. Bi pa za večjo skupino (vsaj štirje) bil pripravljen narediti izjemo za kateri koli dan (jasna noč in Luna ni polna) med tednom, razen v ponedeljek. To posebno željo mi lahko sporočite po telefonu (vsaj štirje) ali e-pošti, obvezno mi morate oddati vaše tel. številke, da vas obvestim o našem srečanju.

Veliko potrpljenja in enkrat nam bo uspelo.
21.10. 1999
Lep pozdrav, Zorko Vičar
=================================================================
Dodatek

1. Upam, da vam 7 Messierjevih objektov ne dela preglavic. Poleg znanega naslova na Internetu lahko uporabite kot literaturo tudi revijo Spika ali katero koli tujo ali domačo literaturo o M objektih. Vaš tekst naj bo tak, da bi ga lahko z veseljem prebirali tako učenci kot tudi vsi ostali. V zadnji Spiki je izšel lep članek o zvezdnih kopicah in ga lahko s pridom uporabite.

2. Če imate čas in pogoje lahko že do našega srečanja sami fotografirate vrtenje neba (aparat na stojalu, čas na B, recimo vsaj 15 minut, ponavadi snemamo severni del neba, ni pa nujno, objektiv naj bo 50mm ali manj, film: 100, 200 ali 400 ISO). Prav tako lahko, če imate čas in pogoje, postavite pred objektiv uklonsko mrežico. Med vrtenjem neba le ta ukloni sled zvezde v spekter. Zvezda naj bo svetla in po možnosti osamljena. Uporabite teleobjektive in mrežice z nekaj 100 raz na mm. Postavite mrežico pred objektiv tako (kar s samolepilnim trakom), da bo mreža približno vzporedna s potjo zvezde. Časi naj bodo okrog 5 do 10 minut, še prej pa se prepričajte, če imate v iskalu fotoaparata zvezdo in njen spekter. Tisti, ki imate teleskop in Spiko lahko skicirate Jupitrove lune in jih poimensko določite.

3. V nadaljevanju sledi še nekaj informacij o teleskopih in o tem, kako poiščemo nam najbližjo galaksijo M31 v Andromedi (samo za tiste, ki tega še nikoli niso storili).

"Pot" do galaksije v Andromedi.

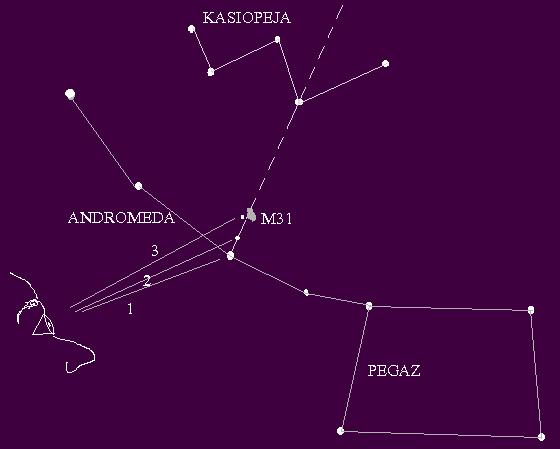
Skica ozvezdij Kasiopeja, Pegaz in Andromeda, s katero si pomagajte pri iskanju nam najbližje galaksije v Andromedi M31. Uporabite navaden daljnogled in sledite skici od poti 1 do 3. M31 se kaže kot medel madež do katerega nas pripelje "premica" 3. M31 ima veliko zorno polje skoraj 3 stopinje. Lahko jo fotografirate s stojala, objektivi 50 ali več mm, čas ekspozicije okrog minute, film 200 ali več ISO.

Še nekaj besed o relativni odprtini teleskopa, zaslonki, osvetljenosti filma, sliki …

Ponovimo:

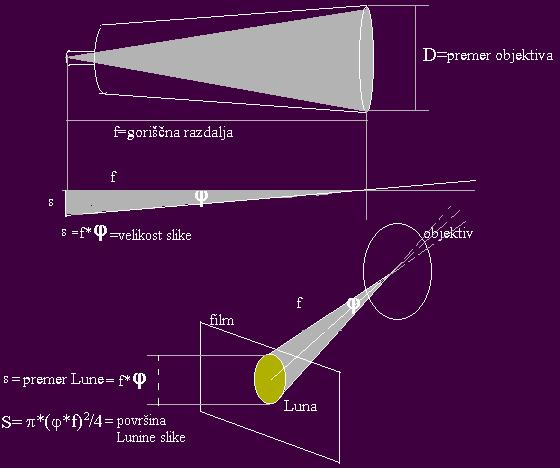
Kaj pomeni, če na teleskopu piše 10" (f/6,3)? To bi lahko tudi zapisal kot: D (f/zaslonka). D je premer objektiva, f goriščna razdalja teleskopa (objektiva), zaslonka pa je razmerje med goriščem in premerom (f /D). Gorišče teleskopa lahko torej zapišem tudi kot: f=D*zaslonka. 10" (f/6,3) pomeni torej, da je premer objektiva (teleskopa) D=10"=25,4cm, zaslonka 6,3 in gorišče f=D*zaslonka=160cm. Zakaj ponavadi podajo proizvajalci zaslonko in premer teleskopa, ne pa tudi gorišča? Izkaže se, da je za svetlost slike (ali tudi osvetljenost filma, očesa …) izjemno pomembna (odločilna) zaslonka. Poglejmo preprosto izpeljavo. Površina objekta na filmu je ponavadi sorazmerna s kvadratom velikosti slike, za primer Lune (glej sliko) velja:

S=p*(j*f)²/4

Svetlobni tok P, ki prispe skozi vhodno odprtino teleskopa , je kar j*(D²*p/4). J je gostota svetlobnega toka objekta. Ves ta svetlobni tok se porazdeli po površini slike na filmu. Če iščemo povprečno osvetljenost filma (recimo s sliko Lune), potem velja (privzamimo, da so žarki skoraj pravokotni na film):

j_{(filma s sliko Lune)} =P/S =j*(D²*p/4) /((j*f)²*p/4) = konst*(D/f)²=
=konst*(1/zaslonka)²

Konstanta je tukaj mišljena le za točno določen objekt, gostota svetlobnega toka zelo oddaljenih vesoljskih teles in zorni kot se namreč zelo počasi spreminjata. Enačbo lahko posplošimo. Iz enačbe za osvetljenost filma ("osvetljenost slike") je razvidno, da je le ta odvisna od gostote svetlobnega toka z objekta, obratne vrednosti kvadrata zornega polja (na nobeno od teh količin ne moremo vplivati) in od razmerja med premerom in goriščem teleskopa na kvadrat. Razmerje D/f ponavadi imenujemo relativna odprtina. Zaslonka ali tudi f-vrednost pa je definirana ravno obratno, je f/D. Vrednost zaslonk (f/D) je na objektivih fotoaparatov ponavadi zapisana s sledečimi vrednostmi: 2,8 4 5,6 8 11 16. Če bomo opazovali šibke objekte (meglice, galaksije, kopice), si želimo čim več zbrane svetlobe, torej teleskope velikih premerov. Toda to ni dovolj, kot vidimo je sama osvetljenost odvisna od kvadrata relativne odprtine (D/f) in če kupimo teleskope relativno dolgih gorišč (recimo zaslonke nad 10), pomeni, da bomo imeli v zornem polju teleskopa sicer relativno velike objekte, a na žalost svetlobno šibke, medle. To je tudi glavni problem poceni 5 ali 6 centimetrskih teleskopov, ki ponujajo bajne povečave (tudi nekaj 100X, ki so ponavadi tudi v neskladju z ločljivostjo teleskopov), in ki nam razen Lune, Sonca in planetov, ne omogočajo opazovanj večine ostalih megleničastih objektov ("deep sky" objektov). Ljudje pa, ker smo neuki, pademo na trik in kupujemo "povečave", namesto da bi kupovali svetlobno zmogljive teleskope (velik premer objektiva, vsaj 8cm in zaslonka 10 ali manj). Poglejmo kakšna je pravzaprav sploh razlika, če slikamo recimo Luno z zaslonko 10, enkrat s teleobjektivom z goriščem 100 mm in enkrat s teleskopom (teleobjektivom) z goriščem 1000mm. Luna slikana z enakim filmom in enkimi časi bo na posnetkih narejenimi s teleskopom enako svetla, kot na posnetkih narejenimi s teleobjektivom, glej enačbo za osvetljenost. Kakšna je torej razlika? Slika narejena s teleskopom je spodobno velika (1m goriščne razdalje nam da Luno veliko slabih f*j=1000mm*30*p/(180*60)=9 mm). Luna slikana skozi teleobjektiv 100mm pa bo velika le slab milimeter.

Še enkrat,
če boste kupili teleskop, priporočam velik premer objektiva, 8 ali več centimetrov in zaslonko f/D=10 ali manj.

Mejna povečava teleskopa.

Velikokrat smo pozorni samo na možne povečave teleskopa (M=fob/fok) hkrati pa pozabljamo, da povečava ponavadi ni odločilna za uspešno delo s teleskopom, in da je omejena. Kako določimo še smiselno povečavo teleskopa? Odgovor bomo poiskali v ločljivosti teleskopa in očesa. Povečava teleskopa ni zgolj kvocient med goriščno razdaljo teleskopa in okularja, ampak se za to zvezo skriva predvsem razmerje (tangensov) kotov pod katerima vidimo neko telo s protim očesom in skozi teleskop, ki bistveno poveča zorno polje (zdi se kot, da smo se predmetu približali). Tako oko kot teleskop pa imata nek mejni kot (kot ločjivosti), ki ju omejuje. Ločljivost optičnih naprav je vezana na valovno dolžino svetlobe in na premer odprtine, skozi katero prihajajo žarki (mejni kot je j_o= 0,61*l/R=1,22*l /D»l/D). Ločljivost očesa je okrog ene ločne minute (1", kar ustreza valovni dolžini okrog 500nm in zenici 2mm). Dveh teles ne ločimo, če sta narazen za manj kot ločno minuto. Iz povedanega sledi. Povečava teleskopa ne sme presegati vrednosti, ki kot ločjivosti teleskopa poveča na ločljivost človeškega očesa. Če opazujemo z večjimi povečavami, se sicer slika v okularju veča, a postaja nejasna, saj opazujemo kote (podrobnosti), ki so zaradi uklona na vhodni odprtini teleskopa nejasni. Nejasnosti pa opazimo, ker smo kot ločljivosti teleskopa povečali čez mejni kot ločljivosti očesa. Mejno ločljivost lahko zapišemo tudi z enačbo:
Mmejna= j_{o_očesa}/j_{o_teleskopa}
Vstavimo v enačbo vrednosti, premer D teleskopa naj ostane neznanka, za premer zenice vstavimo vrednost 2mm, saj le ta odprtina ustreza ločljivosti očesa. Potrebno je povdariti, da so fotoreceotorji v mrežnici očesa toliko narazen, da omogočajo ločljivost 1", očitno sta se fizika in fiziologija očesa v evoluciji ujeli.
Mmejna= j_{o_očesa}/j_{o_teleskopa} »(l/Dzenice)/(l/D)=D/Dzenice=D/2mm

Izpeljava je dala izjemno preprost rezultat in ponavadi se še zadovoljimo z dvojno (ali celo trojno) vrednostjo izpeljanega rezultata. Ponavadi so še smiselne tiste povečave, ki so enake vrednosti premera objektiva v mm (D/1mm):
M_{še_uporabna}=D/1mm
Teleskopi 200 mm premera še dajo dokaj dobro sliko, pri 200 kratni povečavi. Teleskopi s premerom 400 mm ali več sicer omogočajo nekaj 100-kratne povečave, a pri povečavah večjih od 300 ponavadi že nastopijo hude motnje zaradi loma svetlobe v zraku ("migetanje zraka"). Vsak podatek na 5 centimetrskih teleskopih o nekajstokratni povečavi je zavajajoča bedarija. V trgovinah z optično opremo je takih nesmislov in zavajanj na pretek.

Primerjava ni čisto dobra, a vendar, če "umetniško" sliko opazujemo preblizu, vidimo samo emulzijo (koščke barve) in slika zato ni nič bolje vidna, ravno obratno, vidimo le brezoblični košček in ne celote.

25.10.1999
E-POŠTA, RFC-822: Zorko.Vicar@guest.arnes.si