Ali matematika in fizika v šoli vesta druga za drugo?

 

Določene neusklajenosti med poukom matematike in fizike bodo zaradi narave obeh predmetov zmeraj prisotne. Vprašanje je le, če smo storili dovolj, da bi zmanjšali neskladnosti, nesinhronosti med obema predmetoma. Sama matematična spretnost pa je pomembna tudi za večino ostalih predmetov. Prispevek je dobronamerno kritičen, podaja pa tudi nekatere možne rešitve.  

 

Več kot 10 let obiskujemo šolo, kaj in koliko se naučimo, ali smo primerljivi z ostalimi kulturami? Nekaj o tem nam povedo mednarodne primerjave, mednarodna tekmovanja (olimpiade), soočenje raziskovalnih nalog, število patentov, gospodarska razvitost, pa na nek način tudi naše življenje, standard, vitalnost naše kulture, itn. Primerjalne študije ne kažejo prav dobrega rezultata, seveda pa smo še zmeraj nekje blizu evropskim standardom, a kako dolgo? Drugo vprašanje pa je, zakaj nismo zraven in ali smo sploh kdaj bili? Ko omenjamo primerjalne študije, imamo v mislih Mednarodne raziskave znanja matematike in naravoslovja nasploh, TIMSS 2003 (Trends in International Mathematics and Science Study). TIMSS 2003 je potekala v letih 2001-2004 kot skupen projekt 51 držav članic Mednarodne zveze za proučevanje učinkov izobraževanja, IEA (International Association for Evaluation of Educational Achievement). Povzetek bi bil nekako takšen. TIMSS dokazuje, da le malo slovenskih učencev dosega višje nivoje znanja, in da jih veliko ne doseže niti najnižjega nivoja, kar nas uvršča na rep evropskih držav. Naši učenci so sicer praktično povsod dosegli boljši rezultat kot leta 1995, a drugi so napredovali hitreje kot mi. Nekaj težav je v interpretaciji, ker smo v reformi osnovne šole. Mednarodna raziskava PISA – Programme for International Student Assessment,   kaže podobne rezultate. Raziskava bo potekala tudi leta 2006. Samo dva primera dobrih rezultatov nam dokaj sorodnih okolij. Dvakrat zapored je bila Finska PISA zmagovalec. Bavarska pa se je po zadnji PISA študiji zelo dobro odrezala v matematiki, saj bavarski 15-letniki spadajo v sam svetovni vrh.

 

Vrnimo se k naslovu. Naslovna dilema že sama po sebi meri na nezanemarljivo hibo, tudi ali predvsem srednjega šolstva. Zdi se namreč, da je nekaj temeljnih metodoloških in učno programskih napak vgrajenih v pouk dveh temeljnih naravoslovnih predmetov, enako si upam trditi za večino ostalih predmetov. Na kratko, naš koncept šole je daleč od optimalnega, od zadovoljivega. Zakaj je tako, je   vprašanje, ki je zelo pomembno, a ga tukaj ne bomo odpirali. Posvetimo se raje argumentom naslovne dileme, ki jih delno potrjujejo že omenjene raziskave   - ali matematika in fizika v šoli vesta druga za drugo?

 

Problem simbolov in spremenljivk.

Kar nekaj indicev kaže na to, da matematika živi precej izolirano pot v učnem procesu (nekaj podobnega velja za večino ostalih predmetov), je skoraj ne zanimajo dileme uporabe pri drugih predmetih (se jim izogiba). Zdi se, da je zelo srečna s svojim abstraktnim naborom spremenljivk (x, y, z, a, b, c, r, a, b, g, itn), učenci pa so (smo bili) tudi veseli, da se naučijo nekaj aksiomov, nekaj receptov za premetavanje simbolčkov po zvezkih in kontrolkah, ne da bi se večina sploh zavedala, čemu to služi, da bi v resnici globlje razumeli kaj počnejo. Seveda je tak način dela navidezno lažji, tako za učitelje kot za učence. A na koncu je rezultat nekoliko manj uporaben in življenje težje. Naši učenci imajo celo občutek, da obvladajo matematiko (to kažejo ankete, že omenjene primerjalne raziskave pa so seveda neugodne za naše šole), a ko se soočijo z uporabo matematike pri drugih predmetih, v življenju, so mnogi zgubljeni – kot otroci brez staršev.

 

Navedimo nekaj primerov. Mnogokrat dijaki pri fiziki brez večjih težav zapišejo fizikalni problem v obliki enačbe in zdi se, da je s tem rešitev že blizu. A to ne drži. Pogosto se zalomi prav pri matematični razrešitvi enačbe. Učitelj je sedaj v zadregi, dijak si načeloma zasluži kar visoko oceno, a kaj, ko ne pride do rezultata. Če učitelj dojame dilemo, prosi dijaka, da spremenljivko zapiše z zloglasnim simbolom x in dijak po tem koraku ponavadi postane rdeč in hkrati vesel (zave se trivialnosti procesa), premetavanje x-ov pa seveda strese iz rokava ( ta del matematike je torej izpolnil poslanstvo ). Odštevanje, deljenje, izpostavljanje, obračanje enačb z x simbolom, jim ponavadi gre od rok. Matematika v lastni abstraktni obrtni formi torej da, v življenju, z množico ostalih spremenljivk, pa ne. Oglejmo si primer iskanja geostacionarne orbite satelitov. Če že dijak pravilno nastavi pogoj, kdaj satelit kroži po geostacionarni orbiti (centripetalna sila na satelit mase m je enaka sili teže na razdalji r od središča Zemlje z maso M, obhodni čas t_o je en dan: m*r*(2*p/t_o)² = G*M*m/r² ), se pa mnogim ustavi prav pri razrešitvi enačbe. Preprosto iz enačbe ne znajo izraziti iskane neznanke, razdalje r. Če jim recimo v tej zadregi sugeriramo, naj namesto r pišejo x, ali pa jim celo zapišemo izraz a*x=b/x², bodo brez težav izrazili x=(b/a)^1/3. Zdi se, da je to majhen problem, in da se ta dilema razreši že zgolj z nekaj primeri, ali pa da se naprti vsa teža te "majhne" zagate na učitelje fizike. Fiziki pa ja morajo biti didaktično tako dobri, da bodo ta prehod uporabe matematike v fiziki izpeljali en, dva, tri - gladko. Pa praksa ni čisto taka. Pri fiziki je problem tudi izjemno skromen fond ur. Tudi če matematika zaščiti svoje polje delovanja s teorijo, da je matematika čista veda, sama sebi namen, pa se tudi sama matematika hitro ujame v past. Malokateri matematik, ki se rad igra (tudi meni je bila ta igra všeč) s premetavanjem x-ov po tabli, upa v kontrolni nalogi podati naloge z netipičnimi simboli, recimo s spremenljivko U, ali kaj podobnega. Podzavestno čuti, da bo kontrolna naloga izpadla precej slabše, in da bodo mnogi učenci kar debelo gledali. Matematika se kdaj tudi sma ne more izogniti ostalim simbolom, realnim problemom, recimo pri računanju ekstremov z odvodi (četrti letnik). Primer, kdaj bo pri danih pogojih volumen bazena največji, je že lahko tak. Takrat se ponavadi zalomi, saj učenci s težavo dojamejo, da je spremenljivka lahko še kaj drugega kot x ali y.

 

Preseganje dileme, posplošitev pojma spremenljivke na primerih.

Matematika ima precej ur in na koncu poglavij bi si lahko vzela čas, da po teoriji in seveda   nujnem drilu, recimo s simboli x,y, itn, vsako poglavje obdela še s spremenljivkami, ki so simbolno del ostalih ved, življenja. Lep primer je reševanje kvadratne enačbe, ki živi z x, a, b in c in je učenci ponavadi v fiziki ali morebiti kje drugje, ne prepoznajo, čeprav jo formalno celo prav zapišejo. Pojem spremenljivke postane živ šele, ko ga dojamemo na poljubnem simbolu in na poljubnem problemu. Učenci bodo znali narisati graf kvadratne funkcije y=x², imajo pa recimo težave pri risanju grafa poti v odvisnosti od časa pri enakomerno pospešenem gibanju (s=a*t²/2, če se pa pot poda s simbolom x, je še huje, saj x za dijake sploh nima enote). O tem, da že v naprej sklepamo, kako bo potekal graf, trend, odvisnost, ko imamo pred sabo nek poljuben matematični izraz, se premalo sliši. Zanimiva je zagata, ko mediji poročajo, recimo o eksponentni rasti te ali one panoge, spremenljivke, logaritemski odvisnosti, sorazmernosti, obratni sorazmernosti, korelaciji itn, pa mnogi, ki imajo končano srednjo šolo, nimajo prave predstave, kaj to pomeni. Seveda vsi vsega nikoli ne bomo razumeli in poznali, a kulture se razlikujejo ravno po tem, koliko vzgoja in šola ljudi pripravita na izzive časa, koliko jih izobrazita. Morebiti je pred leti v tej smeri kar simpatičen korak naredil prof. France Križanič, ki je v matematičnem učbeniku za srednje šole vključil kar nekaj fizikalno obarvanih nalog in razlag. Nekateri primeri bodo v nadaljevanju še podrobneje ponazorili možna prepletanja med matematiko in fiziko.

 

 

 

Časovni razkorak, neusklajenost, med matematiko in fiziko.

Vemo, da fizika že na začetku potrebuje matematična znanja, ki jih matematika, tudi če bi hotela, ne more sočasno posredovati učencem. Poglejmo nekatere asinhronosti. Problem je recimo že s funkcijami, ponavadi učenci na začetku poznajo zgolj linearno. Vektorji in trigonometrija - kotne funkcije,  so naslednja taka zagata, ki pa jo delno lahko rešimo s podobnimi trikotniki itn, a vendar na tak način izgubimo priložnost, da poglavja iz mehanike obdelamo dovolj temeljito – univerzalno. Naslednji tak zamik predstavljajo ostale nelinearne funkcije, funkcije več spremenljivk, sistem več algebraičnih enačb itn - s temi pojmi se učenci prej srečajo pri fiziki kot pri matematiki - da problema diferencialnega računa in limit (hitrost, pospešek) tukaj ne omenjamo. Iz gimnazijskih časov, drugi letnik, mi je ostala v spominu fizikalna naloga iz Kvaternika, rešitev katere je vodila preko kvadratne enačbe. Redkim, ki smo se naloge lotili, se je zdelo, da smo malo neumni, ker smo se vrteli v krogu - tudi sami podatki niso bili tako izbrani, da bi enačbo lahko razrešili z razstavljanjem. Sploh pa nismo bili navajani, poučeni, da bi lahko fizikalna naloga imela dve rešitvi, kaj šele, da bi eno rešitev zavrgli. Nakar so nam kolegi iz tretjega letnika, sovozači na avtobusu, povedali, da naj počakamo na čas, ko bomo pri matematiki obravnavali kvadratno enačbo. To so bili časi, ko se je fizika v gimnaziji začela v drugem letniku, pa smo bili še zmeraj zelo navzkriž z matematiko. Posebna zgodba so že omenjeni vektorji, brez katerih v fiziki ne prideš daleč. Učenci v zmedi pogosto računajo z vektorji tako kot s skalarji. Še o osnovni šoli. V osmem razredu devetletke se pri ravnovesju sil (ta snov se obravnava okrog novega leta) v nalogah že pojavljajo pravokotni trikotniki, z jasnim namenom, da se probleme rešujejo tudi s pomočjo Pitagorovega izreka. Ker le tega še ne poznajo, učencem, razen pri enakostraničnem trikotniku, ne ostane druga pot, kot da vse naloge rešujejo grafično, preko merila. To sicer ni narobe, a izpusti se priložnost za popolnejšo, univerzalnejšo obravnavo snovi. Reforma osnovne šole torej tudi takih neskladij ni rešila.  

 

Našteli smo nekaj poznanih razhajanj, a kako izboljšati sinhronost med obema predmetoma? Ena od delnih rešitev bi lahko bila, za srednje šole - mnogim poznana še iz mladosti - da se fizika preseli v drugi letnik. Sklicevanje na osnovno šolo, kjer naj bi učenci dobili dovolj široko znanje iz matematike, ni najboljši argument. Druga možnost je, da matematiki in fiziki še bolje uskladijo predmetnik – a to je najbrž tako zapleteno, kot razpletanje gordijskega vozla. Določen napredek bi lahko bil, da se pri matematiki, na koncu poglavij, znanje utrdi na primerih iz fizike in ostalih predmetov. Nekaj predlogov sledi v nadaljevanju.

 

Pomen razumevanja in povezovanja

Ali je pomembno snov razumeti ali zgolj uporabljati? Dobro je, če smo dobri obrtniki, računarji, a če se pojavi pred nami nek nov problem, je za rešitev potrebno tudi razumevanje. Marsikdaj se nam odpre globlje razumevanje, če neko, recimo matematično orodje, uporabimo še v kateri izmed ostalih strok. Pomen dojemanja bomo ilustrirali na nekaj primerih.

 

Primer stožnic - ko se pri matematiki obravnava stožnice, se da na koncu poglavja pridobljeno znanje elegantno uporabiti pri nebesni mehaniki. Naš planet, naše življenje teče po elipsi, kometi pa lahko potujejo pod vplivom gravitacije Sonca tudi po hiperboli ali paraboli. Tudi vodoravni in poševni met opišemo s parabolo. Zagata je, da učenci pri fiziki slišijo prvi Keplerjev zakon še preden pri matematiki obravnavajo elipso in pri nebesni mehaniki tako zmeraj računajo zgolj naloge, kjer se eliptični tir nebesnega telesa poenostavi v krožnico. V matematični kontrolki se tako lahko poda nalogo, kjer nastopa elipsa, recimo za Halleyev komet. Primerov je dovolj tudi iz ostalih poglavij in tako prepletanje bi bilo dobrodošlo. Potrebno pa je paziti na razlike med obema predmetoma, fizikalni del (problem) naloge - v matematični kontrolki - ne sme biti preveč zapleteno zastavljen.

 

 

Uporaba logaritmov. Logaritmi se v srednji šoli zdijo čisto matematično »mehanično« orodje za lažje računanje, zraven pa narišemo še kakšen graf. Pri tem poglavju bi lahko vključili razlago in računske primere odzivanja človeških čutil, ki signale dušijo logaritemsko in s tem povečajo razpon zaznavanja. Uho in zvočno valovanje sta povezana logaritemsko, kar nam pomaga, da slišimo tako prišepetavanje v šoli, kot razločimo različne zvoke v neznosnem mestnem hrupu. Oko pa poveča razpon zaznavnosti med šibko in močno svetlobo, lep primer so porazdelitve zvezd po magnitudah. Še o dojemanju logaritmov . Spomnim se pogovorov, tudi z odličnjaki, ki so priznali, da so sicer uporabo logaritemskih tablic obrtniško imeli v malem prstu, a še zdaleč niso razumeli kaj je osnova, zakaj so logaritmi dobri, kje je smisel logaritmov. Bili so veseli, da so dobili odlično oceno. To, da je zadaj računanje s potencami s skupno osnovo, da nam logaritmi znižajo stopnjo računske operacije, pri množenju seštejemo logaritma (potenci), pri deljenju odštejemo logaritma (potenci), potenciranje poenostavimo v množenje eksponenta in logaritma osnove itn, da na tak način hitreje in enostavneje ročno računamo z večjimi števili, to razumevanje ni ostalo ali pa nikoli ni bilo v zavesti večine. Da so bile Vegove tablice 150 let matematični »bestseller« do uvedbe računalnikov, prav zaradi lažjega računanja, o tem nismo slišali prav nič. Ko ljudje spoznajo ozadje logaritmov, ponavadi izjavijo kaj v stilu: »Super, to je dobra finta, sedaj vsaj vemo, zakaj je bil J.Vega svoje čase tak »frajer.« Danes nam sicer kalkulatorji in računalniki znajo poračunati poljubno zapletene računske operacije, a tisti, ki razume ozadje logaritemskih tablic, bo tudi brez kalkulatorja znal izvrednotiti številsko zapletene operacije.  

 

Še nekaj besed o pouku fizike in težavah znotraj nje. Fizika nasploh velja za enega težjih predmetov. Profesorji ponavadi ta problem razrešijo tako, da (ob pomanjkanju ur) od večine populacije ne zahtevajo kaj dosti več kot osnovne definicije, lažje naloge, nekateri pa celo spustijo cela poglavja. Pri tako skromnem fondu ur jih je kar za razumeti. Kjer pa so profesorji nepopustljivi, pa velja fizika za najtežji naravoslovni predmet. Kratkoročno lahko zahteva po globjem razumevanju fizikalnih procesov povzroči kar nekaj nezadovoljstva med učenci, a se nam ta nepopularna strogost obrestuje na dolgi rok. Zakaj? Fizikalno izobraženega in razmišljujočega človeka imajo rade vse stroke. Fizika od nas zahteva kar nekaj nivojev in spretnosti: poznavanje pojava, meritve, matematični opis, rešitve - uporaba. Vse stopnje so zelo zelo zahtevne in zahtevajo veliko znanja, poznavanje merilne tehnike, danes tudi računalniških orodij, razumevanja matematike in na nek način veliko izkušenj, občutke za naravne procese, opazovanja, meritve, načrtovanje, povezovanje v celoto. Povedano bomo delno osvetlili še preko vzorčne naloge.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

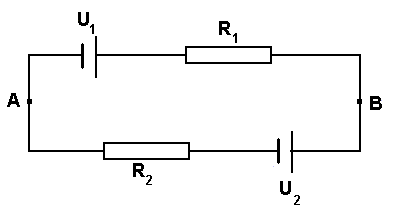
Fenomen naloge z dvema zaporedno vezanima upornikoma in napetostnima viroma (naloga iz učbenika R. Kladnika, Fizika za tehniške usmeritve 2), ki je zahtevala izračun toka v vezju in napetosti med točkama A in B. Te naloge ni rešil prav noben dijak enega izmed četrtih razredov srednje šole za elektrotehniko, razen dijaka, ki je ponavljal. Torej dijaki elektrotehniške smeri, ki so 4 leta poslušali razne strokovne predmete iz ust različnih profesorjev, so bili pri tej nalogi, iz srednješolskega učbenika, nemočni. Sicer so vsi nekaj računali, a brez vsake logične uporabe drugega Kirchhoffovega zakona. Dijaki so dejali, da imajo naloge z upori in baterijami v malem prstu, da so to poglavje pri pouku fizike jemali tako, kot da bi se spet desetič učili abecede. Tudi se jim ni zdelo potrebno še kaj vaditi iz učbenika za fiziko. Če bi bil to prvi letnik in en profesor, bi človek brez težav zvalil krivdo na profesorja, a ker se je to zgodilo v četrtem razredu strokovne šole, se zdi, da je nekaj narobe v konceptu in didaktiki naših šol. V tem primeru je tudi nadvse poučen dijak ponavljalec, ki bi po logiki moral biti eden redkih, ki te naloge ne bi pravilno rešil, a je bilo ravno obratno. Dejal je, da je z inštruktorjem šel skozi vse naloge iz učbenika (ostali seveda tega niso počeli), in da sedaj marsikaj razume. Ni malokrat, ko recimo dijaki na popravnih izpitih blestijo, ker jih inštruirajo res dobri strokovnjaki, ker jim morebiti tak individualni način dela bolj ustreza, ker uporabljajo učbenik, in ker bi radi snov razumeli. Na tem mestu je tudi simptomatična zloglasna neuporaba učbenikov pri učenju. To je slovenski sindrom, ki nas veliko stane. V pogovoru s kolegi smo nekako ugotovili, da tudi mi nismo uporabljali učbenikov. Učitelji niso kazali potrebe, da bi nas pripravili do uporabe, mi pa se tudi nismo zavedali, da so učbeniki lahko zelo koristni. Fotokopirnice danes obilno služijo, ker mnogi dijaki (tudi študentje) kopirajo predavanja vrlih marljivih deklic, ki lepo in vestno pišejo predavanja (v zadnjem času se tudi na Internetu pojavljajo slabe kopije). To je zelo narobe. Učbenik (lahko tudi Internetni) bi moral biti prvi učitelj, profesor pa tisti, ki bi pomagal pri razumevanju in dodatni razlagi. Učbeniki so ponavadi tudi bolj interdisciplinarni kot sam pouk in bi uporaba učbenikov v določeni meri pomagala k razrešitvi naslovne dileme.

 

Analizirajmo še problemček, ki nekako sodi tako v fiziko kot v matematiko ali pa še na druga področja, recimo v kmetijstvo, ekonomijo, načrtovanje proizvodnje. Zdi se mi, da se na njem da delno sklepati o uspešnosti naših šol. Prišel sem v kontakt z učencem osmega razreda, ki se je pripravljal za sprejemne izpite. Prosil me je, če mu rešim problem iz matematične zbirke nalog, kateremu tudi njegov inštruktor (dipl. ing.) ni bil kos. Naloga je bila na prvi pogled prav banalna. Gre pa nekako takole.

Oče s starim traktorjem zorje celotno njivo v ts=2 urah, sin pa z novim potrebuje tn=1 uro. Odločila sta se, da bosta pa tokrat začela orati njivo s starim in novim traktorjem sočasno. V kolikšnem času t bosta zorala njivo? Pot do rešitve lahko vodi preko različnih, a podobnih razmislekov. Rešitev se lahko sklicuje na časovni delež, ki ga opravi vsak od obeh oračev in je vsota 1 (t/ts +  t/tn=1), ali na »hitrost« oranja ( (njiva/ts)*t+(njiva/tn)*t=njiva) ), itn. Učenec je bil ob rešitvi prav zadovoljen, le v glavo mu ni šlo, zakaj se tega že sam ni spomnil. On je namreč oba časa seštel in delil z dva, kar je seveda absurd, ki pa ga mnogi (večina) ne prepoznajo. Sam tudi ni dojel, zakaj je njegovo razmišljanje napačno, tudi prvi inštruktor ne. Naloga je torej izjemno simpatična in kako so se z njo spopadli gimnazijci? Tudi pri njih je bil rezultat precej porazen. Le nekaj dijakov je bilo nalogi kos. Naloga je logično enaka problemu, po kolikšnem času se srečata avtomobila, če se istočasno odpravita na pot, prvi recimo iz Maribora, drugi iz Celja. Starejši avto iz Maribora porabi 2 uri za pot do Celja, novejši avto iz Celja pa eno uro do Maribora. Obstaja še različica, da imamo podani obe hitrosti in razdaljo. Logično so to povsem enake naloge. Učenci se ponavadi srečajo pri fiziki z zadnjo varianto in jo tudi načeloma rešijo, oziroma na nek ozek način tudi razumejo, a posplošitev na problem dveh traktorjev itn, je za veliko večino pretrd oreh. Taka naloga je pomembna tudi za izračune ekonomskih prognoz, recimo za primere, ko imamo v nek proces vključenih več delavcev, strokovnjakov z različnimi sposobnostmi. Nalogo takega tipa priporočam za testiranje dijakov, kjer se bo pokazalo, v kolikšni meri so sposobni sami izračunati trajanje nekega procesa, kjer nastopa več akterjev z različnimi hitrostmi opravljanja nalog.     

 

Primerov nedojemanja oziroma neprepoznavanja matematike je v fiziki in drugje približno toliko, kot je poglavij v matematiki, saj matematika v veliki meri črpa izzive iz realnosti ali zaradi realnosti. Tukaj bodo nemara didaktiki pripomnili, da je povezovanje znanj in uporaba le teh, najvišja stopnja znanja in razumevanja. Da, a v naših šolah je tega povezovanja najbrž premalo. Kvečjemu se matematiki in fiziki kdaj pa kdaj sporečejo, češ da fiziki preveč poenostavljajo, in da s tem delajo škodo matematiki ali pa, da prehitevajo matematiko. Prav te težave pa bi lahko bile enkraten izziv za soočenje z dilemo, da se pravzaprav učimo za to, da bomo to znanje tudi znali uporabljati. Življenje ni zgolj matematika, fizika itn, v šoli so predmeti ločeni zaradi zahtevnosti različnih strok, a na koncu in že vmes, mora potekati postopek povezovanja, drugače šola postane neučinkovita, s tem pa za sabo potegne ogromno problemov. Zakaj nam mnogi očitajo, da ne znamo misliti - ker od učencev ne zahtevamo dovolj mišljenja, jih ne urimo. Logično mišljenje, povezovanje, je na začetku zahtevno in se ga zato izogibamo, zahteva tudi nekaj časa, a razumevanje ljudem ostane v glavi dlje časa kot učenje receptov in jim koristi več kot vse učenje na pamet. To izjavljajo tudi otroci, ki se po določenih letih vračajo iz tujine v Slovenijo, v naše šole. Zelo težko se navadijo na naš sistem, večinoma golega memoriranja in še posebej se čudijo razširjenosti »plonkanja«. A to je že drug problem, vrnimo se nazaj k pouku. Če torej enkrat že razumeš rešitev problema, bo večja verjetnost, da boš podoben problem, čeprav si ga pozabil, še kdaj v življenju rešil - razumel, kot če nikoli (med izobraževanjem) nisi prišel do rešitve z razumevanjem, ni bilo časa za tak pristop, ker je učni načrt zahteval goro poglavij ... Tudi če imamo prvaka iz logike, še to ne pomeni, da se bo ta učenec znašel v tem svetu. Če mladih ne soočimo z izzivi, zagatami realnega sveta, jih bodo težko pozneje sami prepoznali.

 

Omenimo še znano »šalo«, uganko, ki je zelo poučna, ker od človeka zahteva, da preskoči šolski mehanicistični način razmišljanja in se spomni na vsakdanje življenje, ki pa je bližje fiziki. Enkrat so gimnazijci reševali, kot dodatno nalogo, problem, koliko časa se suši 5 hlač, če se ene sušijo pol ure. K nalogi je bila podana skica z vrvico, na kateri visi 5 hlač. Večina dijakov ni padala na trik, a nekaj, tudi zelo dobrih, dijakov je postalo rdečih, ko so spoznali, kako neumnost so ustrelili, ko so podzavestno, mehanično množili 5*0.5h.  

 

Informatika kot povezovalec med predmeti.

Predmet, ki bi lahko delno povezoval ostale, je recimo informatika, kjer pa je pri sramotnih 2 urah na teden zgolj v enem letu, prioritetno učenje Worda. Tako živimo v času informatike, ki je v naših šolah praktično ni, po drugi strani pa z izbirnimi vsebinami zapravljamo dragocene ure. Če bi otroci vsaj kaj slišali o Excelu – Basicu, Accessu, SQLu, če ostanemo zgolj pri Microsoftovih orodjih, bi vsaj malo »povohali« pot do modernih orodij, baz, osnov programiranja, predstavitev podatkov, statistike itn. Celo študentje naravoslovnih smeri so začudeni, ko se recimo v službah srečajo z SQL jezikom, bazami podatkov, s skriptnimi jeziki, kot da bi padli z Marsa. Če hočemo postati konkurenčni, moramo povečati težo informatike, računalništva. Tako bodo lahko tudi profesorji ostalih predmetov učencem omogočili računalniško uporabo različnih znanj. Tudi Internetne html predstavitve različnih predmetov so skrajno skromne. Zakaj še zmeraj ostajamo pri matematiki in fiziki zgolj pri kredi (flomastru) in tabli (vsaj tako je na večini šol, vsa čast izjemam, tudi sam imam otroke na različnih stopnjah)? V razumni meri je potrebno učencem omogočiti tudi elektronske učbenike in delno tudi predstavitev snovi z računalniškimi simulacijami. Zdi se, kot da prav ignoriramo izjemna moderna orodja, znanja, tehnologije. Tem tehnologijam sta prav matematika in fizika postavila temelje. Tudi interaktivni testi so lahko zelo simpatični, vsaj za vajo. Z njimi bi lahko profesorji in učenci zelo enostavno kontrolirali svoje znanje in napredek, saj ti rezultati v hipu kar butnejo v glavo. Komunikacija in pomoč med strokovnimi službami in šolami bi lahko bila sedaj res učinkovita.

 

Zagotovo so mnenja o zastopanosti informatike deljena, mnogi so zadovoljni z dvema urama. A izkušnje, pogovori z učitelji informatike in realne potrebe v življenju, so v prid povečanja teže tega predmeta. Predlagana rezerva je v izbirnih vsebinah in še kje.

 

Še nekaj besed o računalniško vodenih eksperimentih. Veliko truda je bilo vloženega, že v začetku devetdesetih let, v računalniško vodenje fizikalnih meritev, eksperimentov. Primer takega učila sta pri nas merilno krmilna sistema CMS-S1 in CMC-S2 (Kocjančič, 1991) za IBM PC in združljive računalnike, ki se lahko uporabljata za merjenje različnih fizikalnih količin (električna napetost in tok, temperatura, osvetljenost, pH itn.), vodenje eksperimentov, procesov in robotov, regulacije itn. To je bil res odličen domač didaktični pripomoček (veliko raziskovalnih nalog je bilo narejenih s tem kompletom), ki ga v zadnjih letih delno nadomešča tuj komplet Vernier. V naravoslovnih programih so večino teh vaj izvajali učenci sami, danes je, zaradi skrčenja števila ur fizike, skrčen tudi program teh vaj, razen pri fiziki kot maturitetnem izbirnem predmetu. Take vaje so seveda več vredne kot vse računalniške animacije realnosti, a zaradi že omenjenih razlogov z njimi ni moč pokriti vseh vsebin. Rešitve lahko iščemo tudi v povečanju števila ur fizike, vsaj za eno uro, kot je bilo to v starih gimnazijah pred usmerjenim izobraževanjem, da ne omenjamo zelo dobrih naravoslovnih gimnazij iz prve polovice devetdesetih. Računalniške simulacije so torej v danih razmerah zaradi dosegljivosti, če so pa interaktivne, pa še toliko bolj, zelo dobrodošel didaktični pripomoček. Tudi vsi ostali ljudje, ki niso direktno vključeni v izobraževanje, se lahki iz njih marsikaj naučijo. Tako se veča izobraževalna moč države. Najslabše je, če ni ne praktičnih vaj, ne simulacij, ne interaktivnih testov.

 

Zaključek.

Vsi vsega nikoli ne bomo razumeli in znali. Prav pa je, da bi nas šola učila   določenih logičnih veščin, ki jih lahko nato uporabljamo na več področjih. Morebiti je šah dober primer, kako in kaj naj bi počela šola. Vsekakor je potrebno otroka naučiti začetne postavitve figur na šahovsko polje, pravil premikanja in jemanja figur po poljih, logiko šaha in mata. Dobro jim je pokazati tudi nekaj zanimivih otvoritev in partij. A brez dobrega treninga šahovske igre bo vse formalno znanje neuporabno. Seveda ne moremo pričakovati, da bo v razredu 15 punc igralo kot šahovska princesa Judith Polgar in fantje kot Milan Vidmar. A ko se soočimo z ekipami drugih šol, narodov, bo do izraza prišlo prav naše razumevanje šahovske igre, ki smo jo pridobili z dobrim in permanentnim treningom. Naša šola nekako pride do prve faze, nato pa že hiti na nova poglavja, teme in na koncu je precej manj uspeha kot bi si želeli, čeprav smo kot roboti vsrkavali množico informacij. V 13 letih se da veliko trenirati in hkrati tudi obdelati dovolj snovi. Brez razumevanja snovi in široke uporabe znanja šola ostaja abstraktni relikt odvečnosti in teženja.

 

Problem naših šol je tudi dvojni protislovni elitizem talentov, zaradi katerih pomembna večina izpade »butasta«, hkrati pa zanemarjamo talente. Sliši se ostro, a argumentacija sledi. Mnogokrat se profesorjem zdi odveč (ali se jim ne dovoli) trenirati večino. Argument je v stilu, pametni že razumejo, ostali pa so tako in tako »butasti kmetje«. To je huda zabloda, »butasta« večina namreč drži vsakdanji svet pokonci, in če je ta večina zanemarjena, trpi celotna država (gospodarstvo, uporaba novih tehnologij, medijev, kultura, itn). Hkrati pa, razen veselja, da talentirani zlahka dojamejo snov, za njih ne storimo dovolj, da bi lahko zares razvijali svoje sposobnosti (saj poznate tisto, za uspeh, za rešitev problema, je potrebno 5 % talenta in 95 % dela). Didaktike za delo s talentiranimi pri nas še ni ali pa so njeni učinki skromni. Tudi spoznanja, da je vsakdo za kaj talentiran in vreden, še nismo vzeli. Če imamo razne strokovne svete, zavode, SAZU, vlade, itn, za kaj - jih imamo prav za to, da kaj premaknejo na bolje. Po svetu je veliko primerjalnih didaktičnih, šolskih, kulturnih smeri. Tudi nivo naših strokovnjakov je zaenkrat še tak, da brez težav prepoznajo, kaj je boljše in kaj je slabše od naše trenutne prakse, le začeti je treba, dobiti morajo zeleno luč. Veliko lahko storimo sami, a primerjava z drugimi zmeraj prav pride in se je ne smemo sramovati.

 

Ljubljana, december 2005

 

 

Odziv 1

[...] Članek sodi na področje didaktike matematike in fizike v srednji šoli. Avtor na podlagi primerov skuša pokazati, da prevladujoči pristopi pri poučevanju matematike dijakov ne usposabljajo v zadostni meri za suvereno uporabo matematike v drugih vedah, predvsem v fiziki. [...] Verjamem pa, da je tema zanimiva in vredna obravnave in objave ...

 

Naj dodam, da že v načelu podpiram objavo člankov s ‘pedagoško’ vsebino v [...]. Pri poučevanju matematike in fizike je vrsta perečih problemov, ki jih je potrebno natančno opredeliti in se v čim širšem krogu pogovoriti o možnostih za njihovo odpravljanje. [...] bi bil primeren forum za tovrstno razpravo.

 

Poučen je tisti del prispevka, v katerem so navedene značilne težave pri prevajanju fizikalnih problemov v matematični jezik, pri razumevanju matematično formuliranega problema in pri njegovem reševanju.  Predlagam, da se ta del razširi in morda doda kakšne predloge za spoprijemanje s temi težavami. Koristno bi bilo, če bi poleg zadreg z zapisom spremenljivk in neznak omenil še kakšne druge, npr. primere neusklajenega obravnavanja snovi (ko se pri fiziki potrebuje kaj, kar pri matematiki še ni bilo obdelano -  vektorji in podobno). Ostanejo naj tudi odstavki o povezavi z informatiko (lahko podkrepljeni s konkretnimi primeri), o težavah z razumevanje nestandardnih nalog (električni krog), o različnih obrazih iste naloge (traktoristi) ter zaključna dva odstavka.

 

[…] komentar o uporabi učbenikov se mi je zdel zanimiv, a nekako ne sodi v koncept članka. Morda pa bi lahko bil iztočnica za kako drugo razpravo?

 

 

Odziv 2

[…] Izkušnje s študenti v prvih letnikih in primerjave z drugimi državami kažejo, da je računalniška pismenost pri nas na razmeroma visokem nivoju (k temu je veliko pripomoglo dolgoletno usmerjanje sredstev resornega ministrstva v t.i. računalniško opismenjevanje). Zato je zahteva po »enormnem povečanju teže informatike in računalništva« neresna.

[…]

Članek se loteva aktualne problematike, o kateri bi morali konstruktivno razmišljati tudi drugi učitelji. […] O tej temi smo na široko razpravljali tudi na Okrogli mizi o pouku fizike, februarja letos, na Pedagoški fakulteti. Vsi so se strinjali, da obstajajo določeni objektivni problemi, ki jih bo potrebno reševati sistemsko, številni učitelji pa so tudi povedali, da so omenjene probleme v veliki meri rešili s pogovorom (med učiteljem fizike in matematike), na osebni ravni.