Spremenljivke

SUPERNOVE, NOVE, SPREMENLJIVKE ...


  1. VSNET (An International Mailing List of Variable Stars)

  2. www.aavso.org     (AAVSO)
  3. Please visit the International Supernovae Network (I.S.N.) web pages.
  4. Supernova Links
  5. Klasifikacija (taxonomya) supernov.
  6. More about the Schwarzschild Geometry
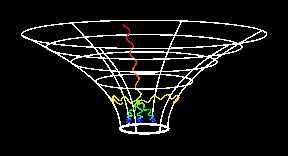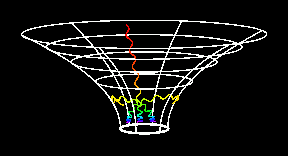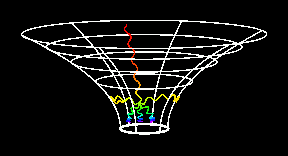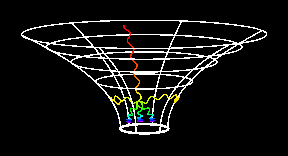
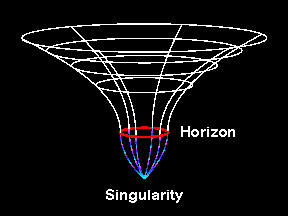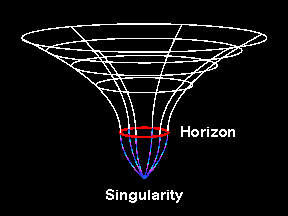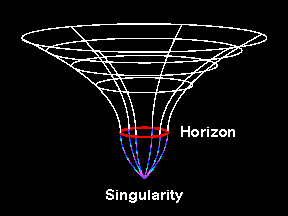
    Schwarzschild metric

    Schwarzschild's geometry is described by the metric (in units where the speed of light is one, c = 1)
    ds2 = - ( 1 - rs / r ) dt2 + ( 1 - rs / r )-1 dr2 + r2 do2  .
    The quantity ds denotes the invariant spacetime interval, an absolute measure of the distance between two events in space and time, t is a `universal' time coordinate, r is the circumferential radius, defined so that the circumference of a sphere at radius r is 2 pi r, and do is an interval of spherical solid angle.


Do sedaj je to stran obiskalo veliko ljudi.
števci www.izmenjava.com

Za astronomski krožek: ZORKO Vičar

E-POŠTA, RFC-822: Zorko.Vicar@guest.arnes.si

Nazaj na domačo stran.