Koliko časa mine med ponovnim srečanjem dveh planetov?

Koliko časa mine med ponovnim srečanjem dveh planetov (konjunkcijama)?

Priblizno na 20 let se Saturn in Jupiter navidezno na nebu srečta, zakaj?

Da bo problem bolj domač, se tukaj kaže spomniti na ples urnih kazalcev, saj poznate pesmico:
"Dolgi Luka, kratki Miha, čudna dva možica, noč in dan po eni nogi v krogu se vrtita (lovita) ...".
Rešujemo torej uganko, kdaj se bosta planeta (kazalca spet srečala).

Pa začnimo z analogijo dohitevanja počasnejšega avta. KDAJ HITREJŠI AVTO "A" DOHITI POČASNEJŠEGA "B", če speljeta hkrati in je med njima na začetku razdalja "d"? Pomagajmo si s podnjo skico.


                       Xa = Va*t                   
                                                   točka srečanja
Va--------->----------------------------------------*
========================Vb-->-----------------------*
            d                          Xb = Vb*t

V času srečanja t prepelje avto A pot Xa = Va*t, avto B pa Xb = Vb*t.
Pot Xa je vsota poti Xb in razdalje d, velja: Xa = d + Xb.
Povedano zberemo v spodnjih enačbah in izrazimo iskani čas t.

Xa = d + Xb
Va*t = d + Vb*t
Va*t - Vb*t = d
(Va - Vb)*t = d
t = d/(Va - Vb)     - to je torej čas, ko a dohiti vozilo b  !!!

----------------------------------

In kje ima ta primer povezavo recimo z Jupitrom in Saturnom?
V bistvu je to enak problem, le da ga bomo izrazili z obhodnima časoma planetov in s kotnima hitrostima.
Podajmo najprej zaokrožena obhodna časa T za Jupiter (Tj) in Saturn (Ts).
Ts = 30 let
Tj = 12 let

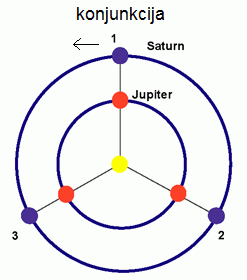
Ko sta planeta poravnana, lahko rečemo, da hitrejši zaostaja za počasnejšim za cel krog ali za 2pi.
NA KOLIKO LET SE TOREJ SRECATA?
Podobno kot pri avtomobilih zapišimo - tokrat kote - hitrosti in kot, ki ga opiše hitrejši do ponovnega srečanja je: kot_jup = 2pi + kot_sat. Kot se izračuna kot produkt kotne hitrosti in časa, recimo kot_jup = t*2pi/Tj. Spodaj je izpeljava časa srečanja t.

kotna_hitrost_J = 2pi/Tj
kotna_hitrost_S = 2pi/Ts

kot_jup = 2pi + kot_sat

t*2pi/Tj = 2pi + t*2pi/Ts                 - pokrajšamo 2pi

t/Tj = 1 + t/Ts

t/Tj -  t/Ts = 1 


t*(1/Tj -  1/Ts) = 1 

t*(Ts-Tj)/(Tj*Ts) = 1 

t = Tj*Ts/(Ts-Tj)    - to je torej čas ponovnega srečanja  !!!
-----------------------------------------------

Še izračun za Jupiter in Saturn:

t = 30*12let/(30-12) = 30*12let/18 = 30*2let/3 = 10*2let = 20 let    - TO JE TO

Recimo, da je 12 letni učenec Bojan leta 1961 pri Kunaverjevem astronomskem krožku opazoval srečanje Jupitra in Saturna. Koliko je bil star Bojan, ko sta se planeta spet srečala? Lahko preveriš recimo s programom Stellarium. Naši izračuni so zaokroženi!
-----------------------------------------------

Še primer za urni in minutni kazalec.

Recimo, da začnemo opazovati, ko sta kazalca poravnana skupaj (zagotovo vemo, da sta ob 12:00), potem lahko rečemo, da je razdalja med njima cel obseg, izraženo v kotu je to 2*p.

Tm = 1h  - obhodni čas minutnega kazalca.

Tu = 12h - obhodni čas urnega kazalca

t = Tm*Tu/(Tu-Tm) = 12/11 h = 01:05:25,27 ...

Preverite, če opazujemo prvo srečanje obeh kazalcev po 12. uri, je to približno 5 min in 27 s čez 13. uro.

Še posnetki Lovljenja Jupitra in Saturna iz leta 2000: http://www2.arnes.si/~gljsentvid10/raz9900/ani4.htm