Uganke, miselne zvijače

NEKAJ UGANK

1. Einstein-ova uganka
|
| Kdo ima ribo ?
|
| Einstein je dejal, da 98% populacije na svetu ne reši te uganke.
|
| Preizkusi se in izvedel boš, če spadaš med izbrana 2% !!!
|-----------------------------------------------------------------------------------------|
|
|
| Imamo 5 hiš v 5 različnih barvah v vrsti.
| V vsaki hiši živi oseba druge narodnosti.
| 5 lastnikov pije določeno znamko pijače, kadijo določeno znamko cigaret in imajo
| svoje ljubljenčke.
| Noben lastnik nima enakega ljubljenčka, ne kadi iste znamke cigaret in ne pije iste
| pijače kot drugi.
|
| Drugi podatki:
| 1. Britanec živi v rdeči hiši.
|
| 2. Šved ima psa.
|
| 3. Danec pije čaj.
|
| 4. Zelena hiša je takoj na levo od bele.
|
| 5. Lastnik zelene hiše pije kavo.
|
| 6. Lastnik, ki kadi Pall Mall redi ptiče.
|
| 7. Lastnik rumene hiše kadi Dunhill.
|
| 8. Lastnik, ki živi v srednji hiši, pije mleko.
|
| 9. Norvežan živi v prvi hiši.
|
| 10. Lastnik, ki kadi Blends, živi zraven osebe, ki ima mačko.
|
| 11. Lastnik konja živi zraven osebe, ki kadi Dunhill.
|
| 12. Oseba, ki kadi Bluemasters, pije pivo.
|
| 13. Nemec kadi Prince.
|
| 14. Norvežan živi zraven modre hiše.
|
| 15. Oseba, ki kadi Blends, živi zraven osebe, ki pije vodo

Kako ugotoviti, katero od treh stikal prižge luč
v sobi, če le enkrat lahko greš v sobo? Ko prideš
ven, boš vrata zaprl in povedal rešitev.
Pomoč, nekaj znanja iz fizike ne bo škodilo.

Na križišču sta brata, eden laže, eden pa ne. Kako
bo popotnik vprašal enega od njiju (s katerim vprašanjem),
da bo dobil nedvoumno informacijo, katera od dveh poti
vodi v Ljubljano? Popotnik ve samo to, da eden od njiju laže,
ne ve pa kateri.

Pred smrtno obsodbo ti rablji ponudijo še
zadnjo možnost za rešitev, ki pa je v resnici navidezno
nerešljiva past, a prav ta past, če jo pravilno rešiš,
ti lahko zagotovo reši življenje.
"Izvoljeni" oblastniki se ljudstvu pred giljotino pohvalijo,
da imaš še zadnjo možnost oprostitve in sicer, če izmed
dveh klobukov izbereš tistega, pod katerim ni žogice.
Rablji v resnici ne želijo
tvoje pomilostitve, zato ti nastavijo pod vsak klobuk
po eno žogico. Ti pa zato slučajno izveš, kako boš
ukrepal, da ostaneš živ? Rešitev je nadvse poučna in
uporabna v vsakdanjem življenju
(življenju, ki nikomur ne prizanaša).

------------------------------------------------------------------
------------------------------------------------------------------
------------------------------------------------------------------

II. Uganke in opičji triki (nekaj ugank Raymonda Smullyana,
Poznate naslov te knjige?)

A. Nekaj dobrih starih ugank
Začeli bomo s starimi ugankami, ki so zabavale že več generacij.
Nekatere od njih morda že poznate, vendar sem vanje vpletel nekaj
novih zank.

4. Čigavo sliko gledam?
Ta uganka je bila zelo priljubljena, ko sem bil otrok, danes
pa je, kot kaže, nekoliko manj znana. Zanimivo je, da nanjo večina
ljudi odgovori narobe in kljub vsem dokazom vztraja pri tem, da ima
prav. Spominjam se, da smo se pred približno petdesetimi leti v neki
družbi o tem prepirali ure in ure in da tisti, ki so imeli prav,
preprosto niso mogli prepričati ostalih. Problem je takle. Neki
moški je gledal portret. Nekdo ga je vprašal: "Čigavo sliko pa
gledaš?" Odgovoril je: "Bratov in sester nimam, a oče tega moža je
sin mojega očeta." (Z "očetom tega moža" je seveda mislil očeta
moškega na sliki.)
Čigavo slikoje gledal?

5.
Predstavljajte si, da bi v gornjem primeru mož odgovoril:
"Bratov in sester nimam , a sin tega možaje sin mojega očeta."

6. Kaj se zgodi, če neustavljiva topovska krogla zadene
nepremični steber?

Toje še en problem iz mojega otroštva, ki mi je zelo všeč.
Z neustavljivo topovsko kroglo mislimo kroglo, ki podre vse,
kar se znajde na njeni poti. Z nepremičnim stebrom mislimo steber,
ki ga nobena stvar ne more podreti. Kaj se torej zgodi, če neustavljiva
topovska krogla zadene nepremični steber?

7.
Naslednji problem je zelo preprost in ga morda poznate.
V predalu v temni sobi imam 24 rdečih in 24 modrih nogavic,
Katero je najmanjše število nogavic, ki jih moram potegniti
iz predala, da bom imel v roki vsaj dve nogavici iste barve?

8.
Še eno vprašanje o nogavicah: predstavljajte si, da imam v predalu
nekaj modrih in enako število rdečih nogavic. Predstavljajte si, da
se izkaže, daje najmanjše število nogavic, ki jih moram izvleči iz
predala, da bi gotovo dobil vsaj en par iste barve, enako najmanjšemu
številu nogavic, ki jih moram potegniti, da bi gotovo dobil vsaj dve
nogavici različne barve. Koliko nogavic je v predalu?

9.
Še ena dobro znana logična uganka: recimo, da je prebivalcev
New Yorka več kot las na glavi kateregakoli prebivalca tega
mesta in da nobeden od meščanov ni popolnoma plešast - ali iz
tega nujno sledi, da morata obstajati vsaj dva prebivalca z
natančno enakim številom las?

Poglejmo še različico te uganke. V Mestu so resnična naslednja dejstva:

(1) Nobena dva meščana nimata natančno enakega števila las.
(2) Noben prebivalec nima točno 518 las.
(3) V mestuje več prebivalcev, kotje las na glavi kateregakoli prebivalca.
Kateroje največje možno število prebivalcev Mesta?

10. Kdo je morilec?
Zgodba govori o karavani, ki je potovala skozi Saharo. Neke noči so
postavili šotore. Naše glavne osebe so A, B in C. Oseba A je sovražila
osebo C. Odločila se je, da jo bo umorila, in sicer tako, da bo v njeno
čutaro nasula strup (ta čutara je edini vir vode osebe C). Ne glede na
to se je tudi oseba B odločila, da bo umorila osebo C, tako da bo
(oseba B se ni zavedala, da je voda osebe C že zastrupljena) v čutaro
osebe C izvrtala luknjico in bo voda počasi iztekla. Oseba C je nekaj
dni kasneje umrla od žeje. Vprašanje je: kdo je morilec - oseba A ali B?
Lahko rečemo, da je morilka oseba B, ker oseba C ni popila strupa,
torej bi umrla tudi, če oseba A ne bi zastrupila vode. Lahko pa tudi
rečemo, da je prava morilka oseba A, ker dejanje osebe B ni vplivalo
na smrt osebe C. Takoj ko je oseba A zastrupila vodo, je bila oseba
C pogubljena, torej bi umrla tudi, če oseba B ne bi izvrtala luknjice.
Katero razmišljanjeje pravilno?

Naj vam povem šalo o drvarju, ki je iskal službo v taboru gozdarjev.
Delovodja mu je rekel: "Ne vem če bo tole rava služba za vas. Mi namreč
podiramo drevesa." , p
Drvar je odgovoril: "Prav to delam tudi jaz." "Dobro," je rekel delovodja,
"tu je sekira, pa poglejmo, koliko časa potrebujete, da posekate tole
drevo." Drvar je odšel k drevesu in ga podrl z enim zamahom.
Delovodja je začudeno rekel: "Podrite še tistole veliko drevo.
" Drvar je šel k drevesu in ga - tresk, tresk - v dveh zamahih
posekal. "Krasno!" je vzkliknil delovodja. "Seveda vas bom najel!
Zanima me le, kje ste se naučili takole sekati?" "Oh," je skromno
odvrnil drvar, "veliko sem vadil v gozdu Sahara."
Delovodja je malce pomislil; "Mislite - v puščavi Sahara." "Ja,"je rekel
drvar, "puščavaje pa zdaj."

11. Še ena pravniška
Dvema možema so sodili za umor. Porota je enega od njiju spoznala
za krivega, drugega pa za nedolžnega. Sodnik se je obrnil h krivemu
in mu rekel: "Tole je najbolj čuden primer, kar sem jih kdajkoli
obravnaval. Čeprav je vaša krivda dokazana, mi zakon nalaga, da
vas spustim."
Kako bi lahko to razložili?

12. Dva človeka
Dva človeka sta sedela na podrtem deblu - veliki in mali.
Mali človek je bil sin velikega, veliki pa ni bil oče malega.
Kako lahko to razložimo?

13. Ura, ki se je ustavila
Prijetna stara uganka: neki mož je bil brez ročne ure,
imel pa je natančno stensko uro, ki jo je od časa do časa
pozabil naviti. Ko se mu je to nekoč spet zgodilo, je odšel
k prijatelju, pri njem preživel večer, se vrnil domov in
naravnal uro. Kakoje lahko to naredil, ne da bi vnaprej
vedel, koliko časaje bil zdoma?

14. Še o medvedu
Pri tem problemu je zanimivo to, da ga je večina
ljudi že slišala in pozna odgovor, vendar ga ne zna razložiti.
Čeprav torej mislite, da odgovor poznate, se prepričajte in
poglejte v rešitve.

Mož stoji 100 korakov južno od medveda. Naredi 100 korakov proti
vzhodu, se obrne proti severu, ustreli proti severu in zadene medveda.
Kakšne barveje bil ta medved?

B Opičji triki .
Na začetku se kar nisem mogel odločiti, kakšen naslov naj dam tej
knjigi; razmišljal sem o naslovih "Zabavna logika", "Logične
rekreacije in zabava" in drugih, vendar nisem bil preveč zadovoljen.
Potem sem pogledal v slovar, Geslo °sprostitev" me je napotilo k
odstavku 840,2 z naslovom "Zabava". Naletel sem na veliko izbiro
gesel: veselost, zabava, slavje, sreča, razposajenost, šala, burka,
bedastoča, maškarada. V naslednjem odstavku pa sem našel še: igranje,
hrupna igra, hudomušnost, norčija, objestnost, opičji trik.
Ko sem zagledal geslo "opičji trik", sem se zasmejal in rekel
ženi: "Hej, morda pa bi moral dati tej knjigi
naslov 'Opičji triki"'. Ta naslov bi bil res zabaven,
vendar bi, če bi ga uporabil za celo knjigo, bralca prav
lahko zavedel. Večji del te knjige bi namreč težko označili
za opičje trike. Kljub temu pa ta naslov, kot bo bralec kmalu
sam ugotovil, odlično pristaja temu poglavju.

15. Problem z dvema kovancema
Dva kovanca skupaj dasta 3 tolarje, pa eden od njiju ni kovanec za en
tolar. Katera kovanca sta to?

16.
Vprašanje za tiste, ki se spoznajo na katoliško vero. Morda veste
tole: ali katoliška cerkev dovoljuje, da se moški poroči s sestro
svoje vdove?

17.
Neki možje stanoval v 25. nadstropju 30-nadstropne stolpnice.
Vsakojutro (razen ob sobotah in nedeljah) je vstopil v dvigalo,
izstopil v pritličju in odšel na delo. Zvečer se je vrnil domov,
vstopil v dvigalo, izstopil v 24. nadstropju in po stopnicah
odkorakal do svojega stanovanja.
Zakaj je izstopil v štiriindvajsetem in ne v petindvajsetem nadstropju?

18. Slovnično vprašanje
Vprašanje za tiste, ki jih skrbi pravilna raba jezika: ali je bolj
pravilno reči "Rumenjakje bel" ali "Rumenjakje beli"?

19. Hitrostni problem
Vlak odpelje iz Maribora v Ljubljano. Uro kasneje odpelje vlak
iz Ljubljane v Maribor. Oba vlaka vozita z natančno enako hitrostjo.
Kateri bo bližje Mariboru, ko se bosta srečala?

20. Vprašanje naklona
Streha neke hiše ima neenak naklon: polovica strehe se spušča pod
kotom 60 stopinj, druga polovica pa pod kotom 70 stopinj. Recimo,
da petelin znese jajce prav na vrhu strehe. Na katero stran bojajce padlo?

21. Koliko devetic?
V neki ulici je sto stavb. Stanovalci so poklicali uslužbenca z občine,
da bi stavbe označil s številkami od 1 do 100. Ali si brez papirja in
svinčnika lahko zamislite, koliko devetic bo potreboval?

22. Krog
Polž potrebuje uro in pol, da preleze krog v smeri urinega kazalca;
ko leze v nasprotni smeri, pa potrebuje za isti krog le 90 minut.
Od kod ta razlika?

23. Vprašanje mednarodnega prava
Letalo se zruši točno na meji med ZDA in Kanado. V kateri državi bodo
pokopali preživele?

24. Kako bi lahko to razložili?
Gospod Smith in njegov sin Artur sta se peljala z avtom. Imela sta
prometno nesrečo; oče je bil na mestu mrtev, sina pa so v kritičnem
stanju pripeljali v bolnišnico. Operirati bi ga moral kirurg. Njegove
besede pa so bile: "Ne morem operirati, to je moj sin Artur."
Kako bi to razložili?

25. Zdaj pa...
Še tole: poznate naslov te knjige?

RESITVE
4. Presenetljivo veliko ljudi napačno trdi, da moški gleda svojo
fotografijo. Vživijo se v vlogo moškega, ki gleda sliko in razmišljajo
takole: "Če nimam bratov in sester, potem moram biti očetov sin jaz sam.
Torej gledam svojo sliko."
Njihova prva predpostavkaje gotovo pravilna: če nimam niti bratov niti
sester, potem sem očetov sin seveda jaz sam. Vendar iz tega še ne sledi,
da je "Jaz" tudi odgovor na naše vprašanje. Če bi bila druga predpostavka
problema "Ta mož je sin mojega očeta", bi bil odgovor "Jaz". Vendar te
predpostavke v problemu ni, pač pa piše: "Oče tega moža je sin mojega
očeta." Iz tega sledi, da sem oče tega moža jaz (ker sem jaz sin mojega
očeta). Če pa sem oče tega možajaz sam, potem mora biti ta mož moj sin.
Torej se pravilna rešitev problema glasi, da moški gleda sliko svojega
sina.
Če kakega skeptičnega bralca še nisem prepričal (mislim, da mnogih med
vami nisem), mu bo pomagalo, če si problem ogleda z bolj grafičnega
stališča:
(1) Oče tega moža je sin mojega očeta.
Če nerodno zvezo "sin mojega očeta" nadomestimo z "jaz", dobimo:
(2) Oče tega moža sem jaz.
Sem vas prepričal?

5. Odgovor na drugi problem, "Bratov in sester nimam, a sin tega
moža je sin mojega očeta", .I~, da moški gleda sliko svojega očeta.

6. Dani pogoji problema so logično protislovni. Logično je nemogoče,
da bi obstajala oba, neustavljiva topovska krogla in nepremični steber.
Če bi obstajala neustavljiva topovska krogla, bi po definiciji podrla
vsak steber na svoji poti, torej nepremični steber ne bi mogel obstajati.
Če pa bi obstajal nepremični steber, ga nobena topovska krogla ne bi mogla
podreti, torej neustavljiva topovska krogla ne bi mogla obstajati. Obstoj
neustavljive topovske krogle sam po sebi ni logično protisloven, kakor ni
logično protisloven niti obstoj nepremičnega stebra. Če pa trdimo, da
obstajata oba, potem zaidemo v protislovje. Problem pravzaprav ni
bistveno drugačen, kot če bi vas vprašal:
"Obstajata dva moža, John in Jack. Johnje višji od Jacka in Jackje višji
od Johna. Kako mi lahko to razložite?"
Najboljši odgovor bi bil: "Lažete ali pa se motite."

7. Najbolj pogost napačen odgovor je "25". Če bi bilo vprašanje
"Katero je najmanjše število nogavic, ki jih moram potegniti iz predala,
da bom imel v roki vsaj dve nogavici različnih barv?", bi bil pravilni
odgovor "25". Vendar sprašujem po vsaj dveh nogavicah iste barve.
Pravilni odgovor je "tri". Če iz predala potegnem tri nogavice, so
lahko vse tri iste barve (torej imam v roki prav gotovo dve nogavici
iste barve) ali pa sta dve nogavici iste barve, tretja pa drugačne in
tudi v tem primeru imam v roki dve nogavici iste barve.

8. Odgovor je: štiri.

9. Odgovor na prvo vprašanje je "Da". Da nam bo lažje, predpostavimo,
da ima New York natančno 8 milijonov prebivalcev. Če bi imel vsak meščan
različno število las, bi dobili 8 milijonov različnih pozitivnih števil,
od katerih bi bilo vsako manjše od 8 milijonov. To je nemogoče!
Odgovor na drugo vprašanje je: 518. Da bi to dokazali, predpostavimo,
da imamo več kot S18 prebivalcev, recimo 520. Potem dobimo S20 različnih
števil, vsa man.jša od S20 in nobeno enako 518. To pa je nemogoče:
obstaja natančno S20 različnih števil (vključno z ničlo) manjših od 520,
torej obstaja samo S 19 števil različnih od S 18, ki so manjša od 520.
Slučajno pa mora biti eden od prebivalcev Mesta popolnoma plešast. Zakaj?

10. Prav res dvomim, da lahko katerokoli rešitev razglasimo za pravilno
ali napačno. Bojim se, da so pri problemih tega tipa vse rešitve enako
dobre. Osebno mislim, da je A tista oseba, ki bi jo morali obtožiti za
smrt osebe C. Če bi bil jaz branilec osebe B, bi svojo obrambo naslonil
na dve dejstvi:
(1) Če nekomu odstranimo zastrupljeno vodo, ga s tem na noben način ne
umorimo.
(2) Dejanje osebe B je osebi A verjetno le podaljšalo življenje (čeprav
to ni bil namen osebe B), ker se zaradi strupa umre prej kot zaradi žeje.
Branilec osebe A pa bi lahko ugovarjal: "Kako lahko kdorkoli pri zdravi
pameti obsodi osebo A, če oseba C strupa sploh ni popila?" Problem je
res težak. Še bolj ga zaplete dejstvo, da nanj lahko gledamo z moralnega,
pravnega ali pa čisto znanstvenega stališča, ki vključuje tudi pojem
povzročitve.
Z moralnega stališča sta oba moža kriva namere uboja, vendar je obsodba
za dejanski umor dosti bolj drastična.
Ne vem, kako bi odločil zakon, če bi na zadevo gledali s pravnega stališča.
Morda bi različne porote odločile različno. Kar se tiče znanstvenega
stališča, že sam pojem povzročitve zastavlja mnogo problemov. Mislim,
da bi o tej uganki lahko napisali celo knjigo.

11. Obsojenca sta bila siamska dvojčka.

12. Veliki človekje bila mati malega človeka.

13. Ko je mož odšel iz svoje hiše, je navil uro in si zapomnil,
koliko je kazala. Ko je prišel k prijatelju, si je zapomnil čas
prihoda in čas odhoda. Na ta način je vedel, koliko časa je prebil
pri prijatelju. Ko se je vrnil domov, je pogledal na uro in tako vedel,
koliko časa je bil zdoma. Ko je odštel od tega čas, ki ga je prebil pri
prijatelju, je vedel, koliko časa je porabil za pot tja in nazaj.
Polovico tega časa je prištel uri, ko je zapustil prijatelja in tako
vedel, kolikoje bila ura v trenutku, koje prišel domov.

14. Medved mora biti bel polarni medved. Običajni razlog, ki ga
ljudje navajajo, je, da je medved moral stati na severnem tečju.
To je ena možnost, ne pa edina. Če gledamo s severnega tečaja, so
vse smeri proti jugu. Če torej medved stoji na severnem polu, mož
pa ,je l00 korakov južno od njega in naredi 100 korakov proti vzhodu,
se bo, ko se bo obrnil proti severu, spet obrnil proti severnemu polu.
Kot sem že rekel, pa to ni edina rešitev. Pravzaprav obstaja neskončno
število rešitev. Ena od njih bi lahko bila tale: mož je zelo blizu
južnemu tečaju, nekje na polarnem krogu z obsegom natančno 100 korakov,
medved pa stoji 100 korakov severno od njega. Če torej mož naredi
100 korakov proti vzhodu, bo obhodil ves krog in se znašel na mestu,
od koderje odšel. To je druga rešitev. Mož bi lahko stal tudi na mestu
kjer ima polarni krog obseg natančno SO korakov. Če bi naredil 100 ,
korakov, bi ga obhodil dvakrat in se spet znašel na istem mestu. Ali
pa bi bil še malo bližje južnemu polu, na mestu, kjer bi obseg znašal
tretjino od 100 korakov, krog bi obhodil trikrat in se vrnil na
izhodiščno mesto. In tako dalje za vsako naravno število n. Torej
na zemlji res obstaja neskončno število mest, ki izpolnjujejo dane
pogoje. Sevedaje v vsaki od teh rešitev medved zadosti blizu sevememu
ali južnemu polu, da ga lahko imamo za polarnega medveda. Obstaja pa
meglena možnost, da bi kako hudobno človeško bitje na severni pol
nalašč pripeljalo rjavega medveda - samo zato, da bi razjezilo avtorja
tega problema.

15.
Pravilni odgovor je: kovanec za I tolar in kovanec za 2 tolarja.
Eden od njiju, namreč kovanec za 2 tolarja, ni kovanec za 1 tolar.

16. Kako pa se lahko mrtev človek poroči s komerkoli?

17. Bil je pritlikavec in ni mogel doseči gumba za 25. nadstropje.
Neki moj znanec (ki očitno ne slovi ravno po tem, da bi zelo dobro
pripovedoval šale), je to šalo povedal na zabavi, na kateri sem bil
tudi jaz. Začel je takole: "V petindvajsetem nadstropju neke stolpnice
je živel pritlikavec..."

18. Pravzapravje rumenjak rumen. 19.
Oba vlaka sta bila očitno enako oddaljena od Maribora, ko sta se srečala.

20. Petelini ne nesejojajc.

21.Dvajset.

22.Nobene razlike ni: ura in pol je natančno toliko kot devetdeset minut.

23.Res bi si težko želeli pokopati preživele!

24.Kirurgje bila mati Arturja Smitha.

25.Žal se prav zdajle ne morem spomniti naslova te knjige.
Vendar ne skrbite - prepričan sem, da se ga bom slejkoprej spet spomnil.

IIl. Vitezi in oprode
A Otok vitezov in oprod .
O otoku, na katerem nekateri prebivalci, imenovani vitezi, vedno govore
resnico, drugi, imenovani oprode, pa vedno lažejo, obstaja veliko ugank.
Predpostaviti moramo, daje vsak prebivalec otoka ali vitez ali oproda.
Najprej vam bom povedal znano uganko te vrste, nato pa bom nadaljeval z
ugankami, ki sem si jih sam
izmislil.

26.
Trije prebivalci otoka, osebe A, B in C, so skupaj stali v vrtu. Mimo je
prišel tujec in vprašal osebo A: "Ali ste vitez ali oproda?" Oseba A mu je
odgovorila, vendar precej nerazločno, tako da tujec ni razumel njenega
odgovora. Nato je tujec vprašal osebo B: "Kaj je rekla oseba A?" Oseba
B je odvrnila: "Oseba A je rekla, da je oproda." Takrat se je vmešal še
tretji, oseba C, in rekel: "Ne verjemite osebi B. Laže!" Vprašam vas:
kaj sta osebi B in C?

27.
Ko sem naletel na prejšnji problem, je mojo pozornost takoj pritegnilo
dejstvo, da oseba C pravzaprav deluje kot nekakšen privesek. To pomeni,
da lahko vsak, takoj ko oseba B spregovori, ugotovi, da laže. Naslednja
različica to značilnost problema odpravi. Predpostavimo, da tujec, namesto
da bi osebo A vprašal po njenem poreklu, vpraša: "Koliko vitezov
je med vami?" Oseba A spet odgovori nerazločno. Zato tujec vpraša
osebo B: "Kaj je rekla oseba A?" Oseba B odgovori: "0seba A je rekla,
da je med nami natanko en vitez." Oseba C pa pravi: "Ne verjemite
osebi B. Laže!"
Kaj pa sta zdaj osebi B in C?

28.
V tem problemu nastopata samo dve osebi: A in B. Vsaka od njiju je bodisi
vitez ali pa oproda. Oseba A trdi: "Vsaj eden od najuje oproda."
Kaj sta osebi A in B?

29. Predstavljajmo si, da oseba A pravi: "Sem oproda ali pa je B vitez."
Kaj sta osebi A in B?

RESITVE
26. Nemogoče je, da bi kdorkoli, vitez ali oproda, rekel "Jaz sem oproda",
ker vitez ne bi napak trdil, da je oproda, oproda pa ne bi po resnici izdal
svojega stanu. Zato oseba A ni nikoli rekla, da je oproda.
Oseba B je lagala, ko je trdila, da je oseba A zase rekla,
da je oproda. Torej je oseba B oproda. Kerje oseba C izjavila,
da oseba B laže inje oseba B res lagala, je oseba C govorila resnico,
torej je vitez. Tako je oseba B oproda, oseba C pa vitez. Ne moremo vedeti,
kaj je oseba A.

27. Odgovorje enak kot pri prejšnjem problemu, čepravje sklepanje malce
drugačno.
Prva stvar, ki jo moramo upoštevati, je, da sta osebi B in C
različnega stanu, ker oseba B nasprotuje osebi C. Ena od njijuje vitez,
druga pa oproda. Če bi bila oseba A vitez, bi bila prisotna dva viteza
in oseba A ne bi lagala, daje prisoten samo eden. Če pa bi bila oseba A
oproda, potem bi bilo res, da je prisoten natančno en vitez, vendar
oseba A kot oproda tega ne bi mogla izjaviti po resnici. Zato oseba A
ne bi mogla trditi, da je med njimi en vitez. Oseba B je narobe podala
izjavo osebe A inje oproda, oseba C pa vitez.

28. Predpostavimo, da je oseba A oproda. Potem je trditev
"Vsaj eden od naju je oproda" napačna (ker oprode vedno lažejo),
torej sta obe osebi viteza. Če bi bila oseba A oproda, bi morala
biti hkrati tudi vitez, kar je nemogoče. Zato oseba A ni oproda,
ampak vitez. Njena
trditev mora biti resnična, eden od njijuje torej res oproda.
Kerje oseba A vitez, mora biti oproda oseba B. Tako je oseba A
vitez, oseba B pa oproda.

29. Ta problem je dober uvod v logiko disjunkcije. Če imamo dani
katerikoli trditvi p, g, potem izjava '~ ali g" pomeni, da je vsaj
ena od trditev p, g resnična (lahko pa tudi obe). Če bi bila
trditev "p ali g" napačna, bi bili napačni obe trditvi p, g.
Če bi, na primer, rekel "Dežuje ali pa sneži" in bi bila moja trditev
napačna, bi bilo napačno oboje: da dežuje in da sneži. Tako se v logiki
uporablja "ali" in tako ga bomo uporabljali tudi v tej knjigi.
V vsakdanjem življenju se včasih uporablja tako, da lahko držita
obe možnosti, včasih pa tako, da se izjavi med seboj izključujeta
in velja torej samo ena možnost. Če, na primer,
rečem: "Poročil se bom z Beti ali pa se bom poročil z
Jano," je povsem jasno, da ena možnost izključuje drugo
in da se ne bom poročil z obema. Če pa na fakulteti zahtevajo,
naj študent vpiše predavanja iz n~aternatike ali predavanja iz
tujega jezika, ga gotovo ne bodo izključili, če bo vpisal oboje.
Tako rabo "ali" imenujemo vključevalna.
I)isjunktivna zveza "to ali ono" pa ima še drugo pomembno lastnost.
Opazujmo zvezo "p ali ~~".~Predpostavimo, da je trditev resnična. Če
je trditev p napačna, mora biti q resnična (ker j~ resnična vsaj ena
od trditev in mora biti, če je p napačna, resnična trditev g).
Predstavljajte si, da je res, da dežuje ali pa sneži, in je trditev,
da dežuje, napačna. Torej mora biti res, da sneži.
Zdaj pa bomo ti dve načeli tudi uporabili. Oseba A je podala trditev
disjunktivnega tipa "Sem oproda ali pa je oseba B vitez". Recimo, da
je oseba A oproda. Potem mora biti njena trditev napačna. To pomeni,
da ni res niti to, da je oseba A oproda, niti to, da je oseba B vitez.
Če bi bila oseba A oproda, bi iz tega sledilo, da ni oproda, kar bi
bilo nesmiselno. Zato roora biti oseba A vitez.
Tako smo torej ugotovili, da je oseba A vitez. Zato je njena trditev
resnična: drži vsaj ena od rnožnosti:
(1) oseba A je oproda,
(2) oseba B je vitez.
Ker je prva možnost napačna (oseba A je vitez),
mora biti resnična druga možnost: torej je oseba B vitez.
Osebi A in E sta obe viteza.

KONEC ugank Raymonda Smullyana
------------------------------------------------------------------
------------------------------------------------------------------
------------------------------------------------------------------

S tremi tehtanji ugotovi, katera groglica je med 12 - imi lažja ali težja
(samo ena ni po teži enaka ostalim, navidez pa so enake)?

\______/ \______/
|_________________|
____________/\_____________O O O O O O O O O O O O______

Z eno potezo (premikom vžigalice)
naredi štiri trikotnike.

S števili od 1 do 9 sestavi matriko 3X3, da bo vsota
vsake vsrtice in kolone posebj ter obeh diagonal
enaka 15. Eno številoko lahko uporabiš samo enkrat.

15 15
|_|_|_|15
|_|_|_|15
|_|_|_|15
15 15 15

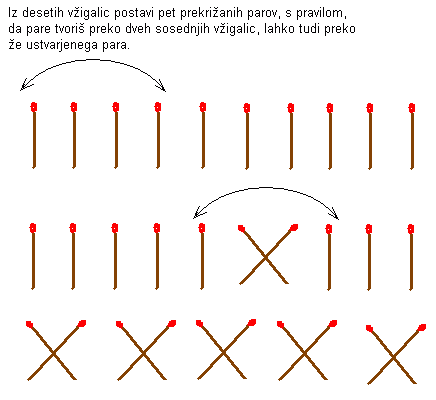Iz desetih vžigalic postavi pet prekrižanih parov, s pravilom,
da pare tvoriš preko dveh sosednjih vžigalic, lahko tudi preko
že ustvarjenega para.

Glej tudi članek - KRATKOČASNE VŽIGALICE

Test inteligence

...

Nazaj na domačo stran.