GEOMETRIJA ZEMLJINE SENCE,
Lunin mrk

O izjemnem pomenu Luninih mrkov za antične mislece, astronome pri merjenju, oz. oceni razdalje do Lune, delno Sonca, velikosti Lune, delno Sonca, smo v Spiki pisali že februarja leta 2000 – »ANTIKA IN MRKI«, tudi v januarski Spiki 2018 v članku »Iskanje odgovorov, kateri fizikalni opis sveta je primernejši« (o periodi sarosa). O uporabi (zlorabi) mrka v ekonomske in politične namene pa si lahko več preberete na strani: http://www2.arnes.si/~gljsentvid10/mrki_zgo_pregled.html

Vsak Luni mrk v medijih pospremi stavek, da je Luna med mrkom vidna v oranžno-rdečih odtenkih, ker atmosfera lomi svetlobo v geometrijsko senco Zemlje. A podrobnejših izračunov na omenjeno tematiko ni ravno na pretek. Naredimo tokrat - s preprostimi geometrijskimi orodji in fiziko loma - korak naprej. Vrnimo se k zadnjemu mrku 27. 7. 2018 in ga opišmo s stališča osvetljenosti Lune in same geometrije loma žarkov v atmosferi Zemlje.

Še prej pa dva odstavka o opazovanju in druženju na tersi Gimnazije Šentvid – Ljubljana. Zbralo se nas je blizu 30 navdušencev iz U3, popotnikov po ZDA 2017, dijakov, učiteljev, članov ADV, Šentvidčanov, ljubiteljev astronomije, mrkov, narave nasploh ... - za čas počitnic, in ker opazovanja nismo uradno najavili, v bistvu zelo veliko. Od ZDA ekipe 2017 se nas je zbralo 11 (to je kar 2/3). Tudi šolski čebelar je prišel nahranit čebele na teraso - tako da je bilo doživetje mrka in narave popolno. Uporabili smo 2 teleskopa (Ciko - Dobson 30 cm, f/5 in Newton 20 cm, f/5 na montaži EQ5 pro goto iz MLA2009) ter vse daljnoglede. Zelo prav sta nam prišli novi pridobitvi iz spodnjega cenovnega razreda, stojalo za daljnogled Paragon-Plus in daljnogled SkyMaster 20X80. Odlično sta opravila svojo nalogo. Novo translacijsko stojalo so opazovalci lahko brez zapletov prilagodili različnim višinam, a hkrati niso izgubili Lune iz polja daljnogleda. Vidno polje je v daljnogledu SkyMaster 20x80 pričakovano zelo razkošno - 3,7 °, povečava 20x pa tudi že pokaže kar veliko podrobnosti na sami Luni. Bilo je zelo prijetno druženje, tako da so nekateri (tudi zaradi obujanja spominov iz naših potovanj) skoraj zamudili na začetek vzhoda Lune. Astronomija in potovanja - "potovanja v nebesne daljave" in po Zemlji - zbližujeta ljudi, tudi zaradi mrkov ...

Lunin mrk 27. jul. 2018 na Šentvidu - kombinirana "češko-ameriška" ekipa (Praga - Casper). "To ni razred 3.c."

Ker se je mrk začel v mraku, na opazovalce najprej ni naredil večjega vtisa. T. i. rdeča Luna (da ne govorimo o medijskem pretiravanju, ko so cel da nabijali o krvavi Luni ...) je bila prej siva - oranžno bleda (bila je tudi nizko nad obzorjem, nekaj koprene je odbito svetlobo od Lune dodatno slabilo). Proti koncu mrka (popolne faze - nekaj čez 23. uro) pa se je Luna dovolj dvignila nad horizont in bil je že astronomski mrak, da je zažarela v vsej svoji zamračeni lepoti v odtenkih rdeče. Nekateri so ob koncu popolne faze dobili asociacijo na lanski diamantni prstan pri Sončevem mrku – imenitna in slikovita primerjava.

Najlepši prizor je bil ob koncu popolne faze (ko se pojavi neke vrste Lunin diamantni prstan - kot se je slikovito izrazila Urša). Foto: Zorko Vičar.

Zahod Sonca blizu Triglava na dan mrka. Še zanimivost - od Lune odbita svetloba nazaj na Zemljo je že prej (pred 2.6 sekunde) prečkala atmosfero Zemlje (to je svetloba na sliki) in se je med mrkom spet vrnila, recimo delno tudi v "naše oči" ob pogledu na zamračeno Luno (Šentvid 27. 7. 2018, foto: Zorko Vičar).

Imenitno vzdušje na terasi Gimnazije Šentvid – Lj. med Luninim mrkom 27. 7. 2018. Na nebu zamračena Luno, pod njo Mars, žal pa tudi sipana svetloba preosvetljene Ljubljane. Foto: Martin Gladović.

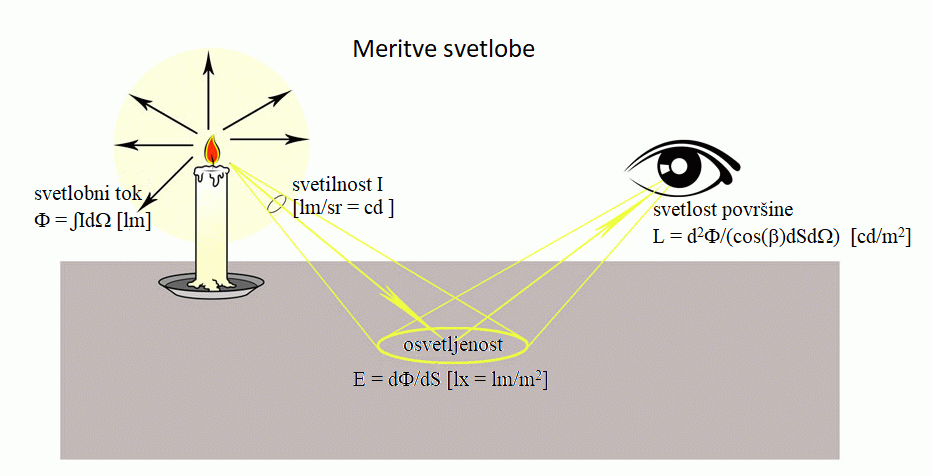
Slika: Ponovitev fotometrije preko preproste sheme goreče sveče:
- svetlobni tok Φ = ∫IdΩ [lm],
- svetilnost I [lm/sr = cd],
- osvetljenost E = dΦ/dS [lx = lm/m² = cd*sr/m²],
- svetlost površine (ali svetila) L = d²Φ/(cos(β)dSdΩ) [lm/(sr*m²) = cd/m²].
Gostota svetlobnega toka »j« ima enoto W/m² in primerljiva fotometrična količina osvetljenost E ima enoto lm/m² = lx – povezava med njima je odvisna od valovne dolžine. Recimo za 555 nm valovne dolžine (zelena svetloba - pri kateri je oko najbolj občutljivo na energijski tok in njegove spremembe) velja: 683.002 lx = 1 W/m².

Dr. Mitja R. je ocenil osvetljenost Lune med popolno fazo mrka na okrog 0,1 lx (to je bila zgolj primerjava z okolico - iz ocenjene svetlosti sklepamo na osvetljenost). Še malo fizike (definicij fizioloških količin) preden se posvetimo pomenu te ocene – pomagajte si sliko.
Diferencial svetlobnega toka dΦ se izračuna preko produkta svetilnosti I in diferenciala prostorskega kota dΦ z enoto sr (sr je steradian, za sfero velja naslednja povezava za polni prostorski kot Ω = S/r² = 4π sr). Enota za svetilnost I je lm/sr = cd (kandela). Končna enačba za svetlobni tok je torej Φ = ∫IdΩ - to je integral (vsota) svetilnosti po prostorskem kotu. Svetlobni tok Φ ima torej enoto lm (lumen). Svetlost svetila (ali poljubne površine) L = d²Φ/(cos(β)dSdΩ) ima enoto lm/(sr*m²) = cd/m² (kjer je Ω že omenjni prostorski kot, β pa kot med normalo na površino svetila in kotom opazovanja). Svetlost L ima kdaj tudi oznako B. Osvetljenost je svetlobi tok porazdeljen po dani površini in je definiran kot E = dΦ/dS, enota je že omenjeni luks, kar se zapiše kot lx = lm/m². Ta količina se tudi meri in je predpisana, recimo za javne prostore, pisarne, hodnike, učilnice ... Primer - svetlobni tok Φ = 1000 lm (lumnov), ki osvetljuje površino enega kvadratnega metra, daje osvetljenost E = 1000 luksov (lx = lm/m² = cd*sr/m²). Kadar pa ta isti svetlobni tok osvetljuje površino 10 kvadratnih metrov, pa je osvetljenost E = 100 lx. Klasična žarnica z močjo 100 W izseva pri omrežni napetost 230 V okrog Φ =1400 lumnov svetlobnega toka (kar je na sferi površine S = 1 m² = 4*πr² enako E = Φ/S = 1400 lx, če sveti v vse smeri enakomerno - kot točkasto svetilo). Povezava med fizikalno enoto za energijsko gostoto toka svetlobe (gostota svetlobnega toka »j« ima enoto W/m²) in fotometrično enoto lm/m² = lx je odvisna od valovne dolžine. Recimo za 555 nm valovne dolžine (zelena svetloba - pri kateri je oko najbolj občutljivo na energijski tok in njegove spremembe) velja: 683.002 lx = 1 W/m². Vrnimo se k oceni osvetljenosti Lune.
Ocena 0.1 lx torej pomeni osvetljeno belo površino s 100 W žarnico na razdalji blizu r = 33 m, če le ta seva v vse smeri enako (E₁/E₂ = r²₁/r²₂ - zato velja r = ((1 m²/(4*π))*(1400 lx/0,1 lx))^1/2 = 33 m). Luna je tako med mrkom (po oceni) izgledala svetla kot bela površina na razdalji dobrih 30 m vstran od klasične 100 W žarnice.

Svetlost Lune (ki jo zaznajo naše oči) je seveda odvisna od stanja atmosfere, višine Lune, seveda tudi od razdalj Zemlja-Luna, Sonce - Zemlja ...
S koliko luksi pa je osvetljena Zemlja med mrkom, zaradi od Lunine odbite svetlobe? Vprašanja, s koliko luksi osvetljuje Luna Zemljo, se lahko lotimo preko magnitude. V astronomiji namreč pogosto uporabljamo oceno sija nebesnih teles preko vizualne magnitude in tukaj nam pride prav Pogsonov zakon, ki povezuje magnitudi in osvetljenosti (lahko gostoti svetlobnega toka) iz dveh virov, nebesnih teles:
E₁/E₂ = 10^{-0.4(m1 - m2)}.
V tem primeru velja naslednja povezava med osvetljenostjo tal (E_v) in magnitudo (m_v):
m_v = -14.18 - 2.5*log(E_v).
Polna Luna v zenitu v tropskih krajih povzroča osvetljenost tal E = 1 lx, v naših krajih pa le okrog 0,3 lx. Magnituda Lune med mrkom je bila temnejša od m_v = -10 (groba ocena je okrog -3, to je pričakovana vrednost med popolnimi mrki, kdaj tudi blizu -2), kar da za osvetljenost Zemlje (tal) okrog E_v = 0,00002 lx zaradi odbite svetlobe od Lune na Zemljo (primerjava - zvezda Sirij osvetljuje Zemljo z 0,00001 lx). Še zanimivost - vsa odbita svetloba nazaj na Zemljo je že prej (pred 2.6 sekunde) prečkala atmosfero Zemlje in se je sedaj spet vrnila, recimo delno tudi v "naše oči". Sploh tale mrk je bil zanimiv, poseben, saj se je začel že nekoliko pred vzidom Lune - in smo kot opazovalci bili v tistem pasu Zemljine atmosfere, ki je lomila svetlobo na Luno (delno tudi naše razpršene sence ...).
Sonce ob jasnem dnevu osvetljuje Zemljo z okrog 10000 lx (brez direktnega obseva, direktno pa z 32000–130000 lx) in nekaj podobnega lahko sklepamo za Luno (150 milijonov km je približna oddaljenost obeh teles od Sonca). Del te svetlobe se tudi odbije proti Zemlji. To odbito svetlobo pri polni Luni zaznamo kot magnitudo -12,6. Če sklepamo na linearno povezavo (površine ostanejo enake, le energijski tok svetlobe se zmanjša) je groba ocena osvetljenosti Lune med mrkom (zaradi loma svetlobe v atmosferi Zemlje proti Luni) okrog 10 lx (velja ocena: E_Lm = 100000 lx*0.00002 lx/0.3 lx = 6,6 lx). To je približno toliko, kot so osvetljena tla v zgodnjem mraku in ta rezultat se zdi kar pričakovan (svetloba mraka na Luni) ter hkrati dober test naših ocen. A marsikaj smo zanemarili - še enkrat, gre za velikostni red osvetljenosti Zemlje in Lune med mrkom. Če pa upoštevamo za odbojnost Lune vrednost 0.12, se ocena osvetljenosti Lune med mrkom poveča skoraj za 10x (saj velja razmerje 1/0.12), grobo zaokroženo na okrog 100 lx (odvisno od mrka, določeni viri, izračuni, navajajo tudi vrednosti nekaj 100 lx). Torej je v resnici osvetljenost večja kot ob mraku na Zemlji – zakaj? Ker se svetloba fokusira (združuje iz roba Zemlje) na Luni. To pomeni, da bi se po Luni ob mrku pri 100 lx lahko sprehajali veliko elegantneje, kot se sprehajamo po Zemlji ob polni Luni pri 0,3 lx Lunine svetlobe. Zgolj za primerjavo - s 100 lx so recimo osvetljeni hodniki javnih prostorov.
Doslej še noben človek ni bil prisoten na Luni med Luninim mrkom, ko bi hkrati lahko opazoval Sončev mrk zaradi sočasnega Zemljinega prekritja Sonca. Tak Sončev mrk - gledan iz Lune - bi trajal sicer več kot uro in pol, vau - na Zemlji jih lahko občudujemo le nekaj minut - a Zemlja bi večji del časa prekrivala notranji del korone. A vseeno se noben ne bi odrekel taki možnosti opazovanja Sončevega mrka iz Lune. Zorni kot Zemlje iz Lune je 1,9 °, to je skoraj 4x več kot je navidezno veliko Sonce. Vseeno pa bi znali biti robni svetlobni efekti v Zemljini atmosferi res izjemni (žarki med gorami, odboji od oceanov, od snega na polih, mavrični presek atmosfere), v kombinaciji z morebitno korono na začetku in koncu mrka pa kar nepredstavljivi. Stali pa bi na "rahlo rdeči preprogi" - na površini z odtenki rdeče obarvane Lune (v skafandru seveda ali v kakem bivanjskem modulu). Ker Luna nima atmosfere, nas ta osvetljenost površine Lune med mrkom ne bi smela preveč motiti pri opazovanju zvezdnega neba.

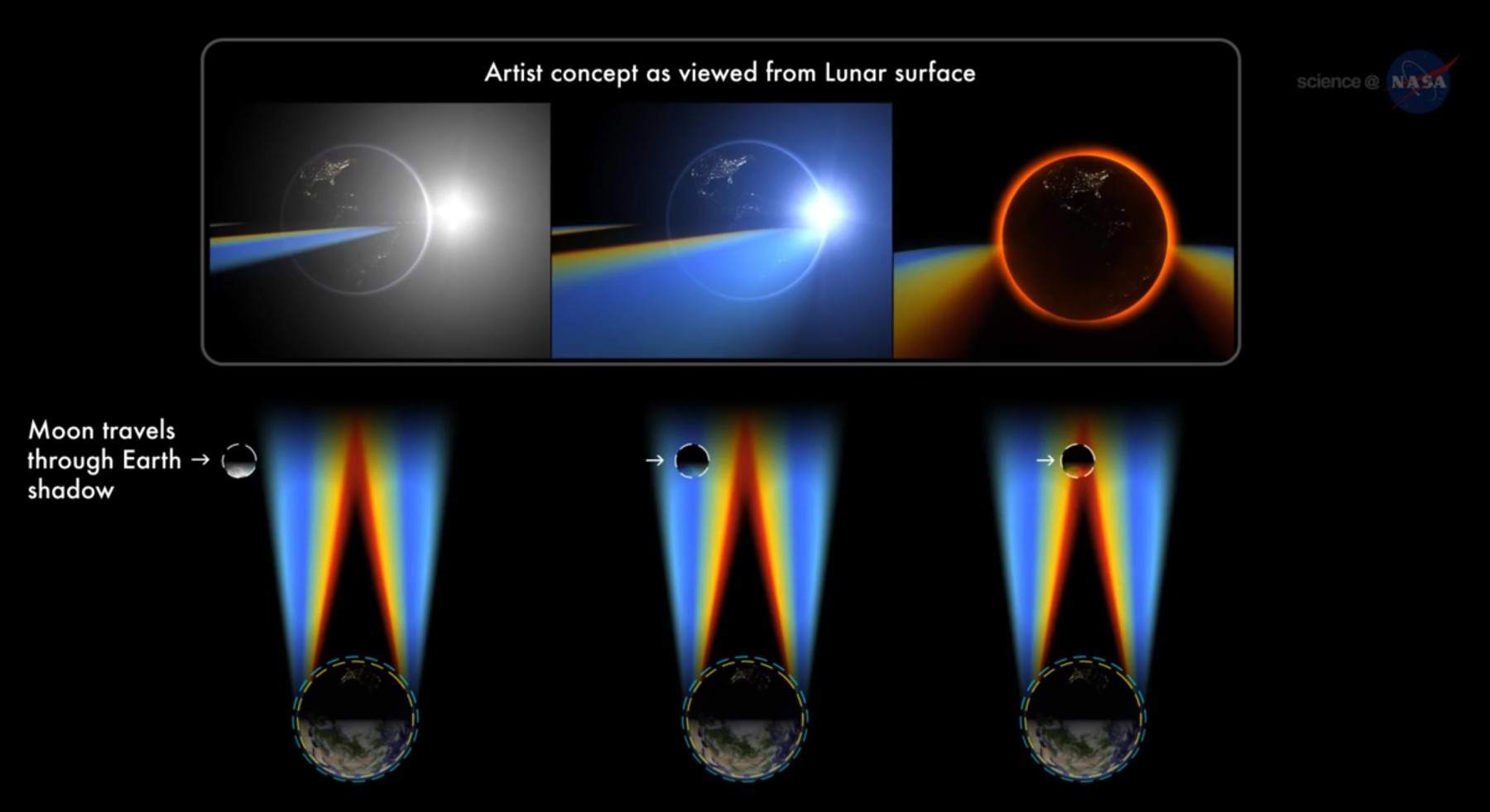
Pogled iz Lune proti Zemlji s Soncem v ozadju - oranžna obroba je atmosfera, ki prepušča samo oranžno-rdeč spekter (ostala svetloba se večinoma že prej sipa, filtrira - najbolj modra – to je umetniška podoba). Ali iz Mednarodne vesoljske postaje ne doživijo Sončevega mrka 16 x na dan? Ne - ker je MVP praktično tik nad Zemljo (okrog 400 km) in od tam vzhod in zahod Sonca nista radikalno drugačna kot iz Zemlje (rob Zemlje, atmosfera, zasveti zaradi sipane svetlobe s Sonca in tako recimo ni moč videti korone). Iz 60x bolj oddaljene Lune pa se gostota svetlobnega toka iz ozračja zelo zmanjša (s kvadratom razdalje za sipano svetlobo) - in kakšen bi bil v resnici prizor prekritja Sonca z Zemljo iz Lune (ob začetku in koncu mrka je morebiti vsaj delno vidna korona nad rdečo obrobo Zemlje, vmes pa zgolj rdeč obroč (to je svetleča Zemljina atmosfera) v smeri Sonca, okrog pa zvezde, planeti, kakšen komet …?) – vsekakor privlačen izziv? Iz misij Apollo 11 in 12 je nekaj posnetkov zakritja Sonca, a ne iz Lune – le med letom (zakritje Sonca z Luno in z Zemljo): http://www.collectspace.com/news/news-081617a-total-solar-eclipse-from-space-astronauts.html

Umetniška podoba delnega Sončevega mrka iz Lune.

Pot svetlobe s Sonca tik nad površino Zemlje

Vemo, da se v ozračju najmočneje sipa modra svetloba, zato čez dan vidimo nebo kot modrino. Ko je Sonce nizko nad obzorjem (in žarki potujejo do nas skozi debelejšo plast atmosfere) pa je modre svetlobe zmeraj manj - rdeče pa še kar veliko – zakaj (?). Rdeča svetloba ima v vidnem delu EM spektra najdaljšo valovno dolžino in se tako lahko tudi najdlje prebije skozi plasti ozračja (o tem seveda odloča tudi sestava ozračja) - tudi do naših oči - hkrati pa na nasprotni strani tudi zapusti Zemljino atmosfero in se zaradi rahlega loma svetlobe (kot na prizmi) zbira v senci Zemlje, kjer osvetljuje tudi Luno ob Luninem mrku (zemljina atmosfera je neke vrste leča - a iz plina). Zato ob mrku lahko sploh vidimo Luno in to v odtenkih rdeče barve. Če bi sestava ozračja bila drugačna, bi lahko Luna ob mrku bila tudi nekoliko drugačne barve - enako zarja.

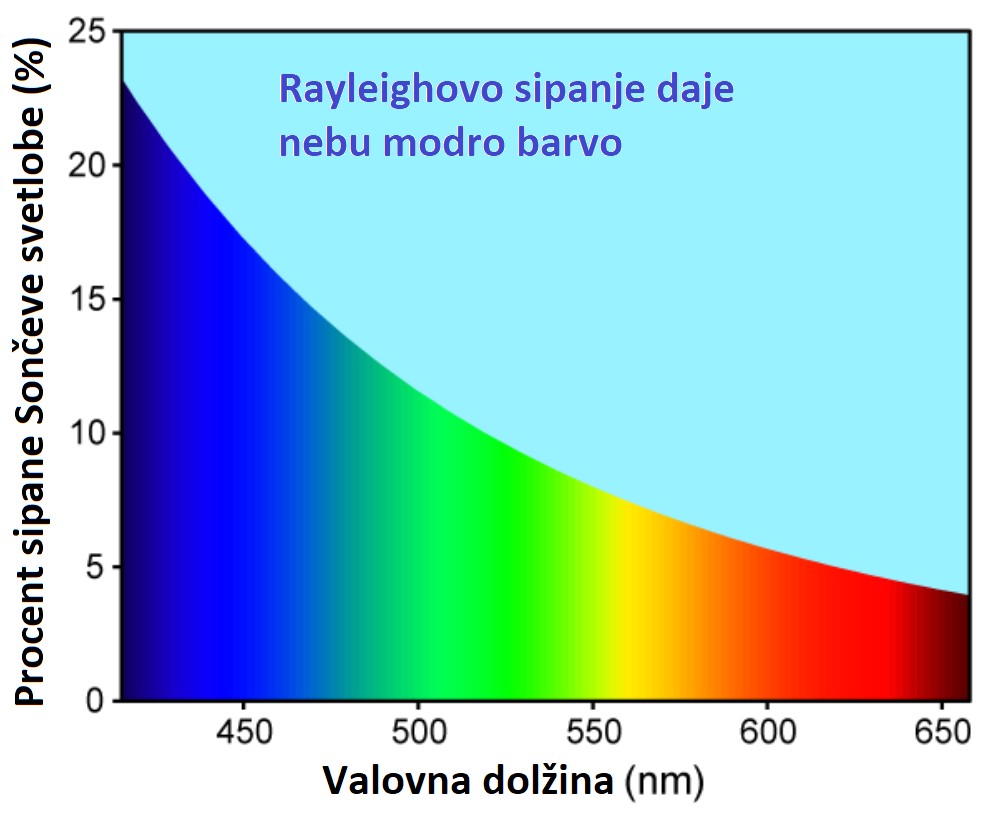
Rayleighovo sipanje se pojavi, ko so delci precej manjši od valovne dolžine svetlobe. Delež sipane svetlobe I/I_o glede na valovno dolžino λ je sorazmerna s premerom delcev (d) na šesto potenco in obratno sorazmerna s četrto potenco valovne dolžine (λ):
I/I_o ∝ d⁶/λ⁴.
Pri molekulah pa je odvisnost glede na valovno dolžino še zmeraj obratno sorazmerna s četrto potenco valovne dolžine (λ), a sorazmerna s kvadratom parametra polarnosti α:
I/I_o ∝ α²/λ⁴.
V obeh primerih torej velja, da se bo modra svetloba veliko bolj razpršila kot pa rdeča svetloba.
Za dušik (N₂ – v zraku ga je 78 % - to je prostorski delež) znaša absorpcijski presek na molekulo σ = 5,1 • 10^-31 m² pri valovni dolžini 532 nm (zelena svetloba). To pomeni, da bo pri normalnem zračnem tlaku (2•10m²⁵ molekul/m³ dušika) razpršen 2•10²⁵ molekul/m³ * 5,1 • 10^-31 m² = 10^-5 del svetlobe po vsakem metru poti svetlobe.
Na 100 km bi pri istih pogojih tako zelena svetloba bila že popolnoma filtrirana - modra pa že prej (a gostota plinov v atmosferi eksponentno pada z višino, zato filtracija ni tako intenzivna).

Rayleighovo sipanje se lepo izraža ob zahodu Sonca - do nas na obzorju prodre oranžno rdeča svetloba - ostale barve so zaradi sipanja že filtrirane (dolga pot skozi atmosfero). Modrina neba pa se zazna v plasteh atmosfere bližje zenitu, kjer je pot žarkov skozi atmosfero krajša kot tik nad obzorjem.

Sipana svetloba je tudi polarizirana. Modre svetlobe je zato več polarizirane kot ostalih barv in zgornji sliki to evidentno dokazujeta. Levi motiv je slikan brez polarizatorja, zato tudi odtenki rumene in oranžne. Na desni je isti motiv slikan z linearnim polarizatorjem - ki zato prepušča več modre svetlobe in na sliki je tako poudarjena modrina neba brez izrazitih odtenkov rumene na oblakih, na cesti ...

Še drug primerjalni motiv - brez in s polarizatorjem - Kamniške Alpe 29. 3. 2019. Foto: Vičar Z. (skozi polarizacijska očala, sonce sije iz leve).
Tretji primerjalni motiv - brez in s polarizatorjem - Kamniške Alpe marca 2019 iz Ljubljane. Foto: Vičar Z. (skozi polarizacijska očala, sonce sije iz leve).

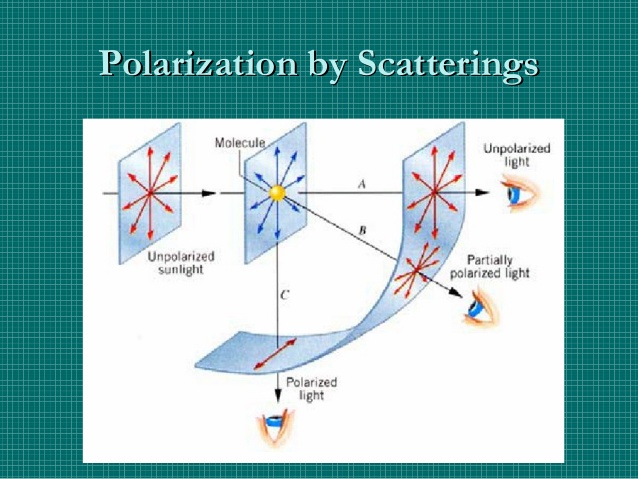
Princip polarizacije svetlobe v atmosferi. Polarizacija je očitna pri kotu 90 ° na smer Sončevih žarkov. Svetloba (električno polje) zaniha električne delce pravokotno na smer širjena in delci zato sevajo v ravnini nihanja - zato je oddano valovanje polarizirano v smeri 90 ° na vpadne žarke. To lahko preverite z vrtenjem polarizacijskih sončnih očal (ali glave …) - dobra in enostavna vaja (v določeni legi, pravokotno na vpadne žarke, sem vam nebo nekoliko zatemni).

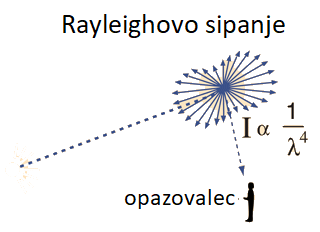
Shema sipanja svetlobe v atmosferi Zemlje. Rdeča svetloba (λ = 700 nm) se skoraj 10 krat manj sipa kot vijolična (λ = 400 nm) saj velja I/I_o ∝ 1/λ⁴, od koder sledi ((700 nm/400 nm)⁴ = 9,4).

Satelitski posnetek krasno prikazuje sipalni presek atmosfere Zemlje ob vzhodu Sonca nad Pacifikom. Tik nad morjem prodira rdeča svetloba (po daljši poti, kjer je modra svetloba že filtrirana), višje dominira (krajša pot žarkov) modra svetloba, ki se najizraziteje sipa.
Še beseda o sliki. Sonce bo kmalu "vzšlo" nad južnim Pacifikom. Fotografiral član posadke 35. misije na Mednarodni vesoljski postaji med 4. in 5. uro po lokalnem času, 5. maja 2013. Vesoljska postaja je bila v na -27,4 ° južne zemljepisne širine in 110,1 ° zahodne dolžine nad Zemljo, nekaj sto kilometrov vzhodno od Velikonočnih otokov.
Image Credit: NASA
Vir: https://www.nasa.gov/multimedia/imagegallery/image_feature_2505.html

Še ena izmed zgovornih slik svetlobnega profila atmosfere ob zahodu Sonca iz Mednarodne vesoljske postaje. Rdeči odtenki segajo v stratosfero, nad 15 km nadmorske višine. V troposferi je zbrane kar dobre 3/4 mase atmosfere in prav tukaj se lomi večina rdeče (nefiltrirane svetlobe) v Zemljino senco. Nad troposfero je namreč lomni količnik že zelo blizu 1. Image Credit: NASA

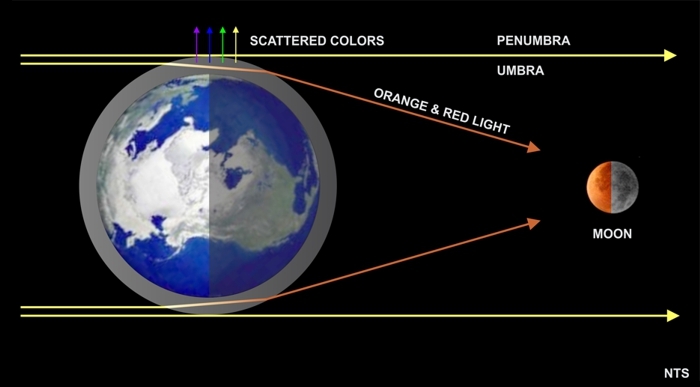
Groba slika loma svetlobe v atmosferi Zemlje (prehod je v resnici zvezen).

V Zemljino senco se proti osi Zemlja - Sonce večinoma lomita rdeča in oranžna neabsorbirana svetloba. Lomni količnik atmosfere pri tleh je n = 1,000292.

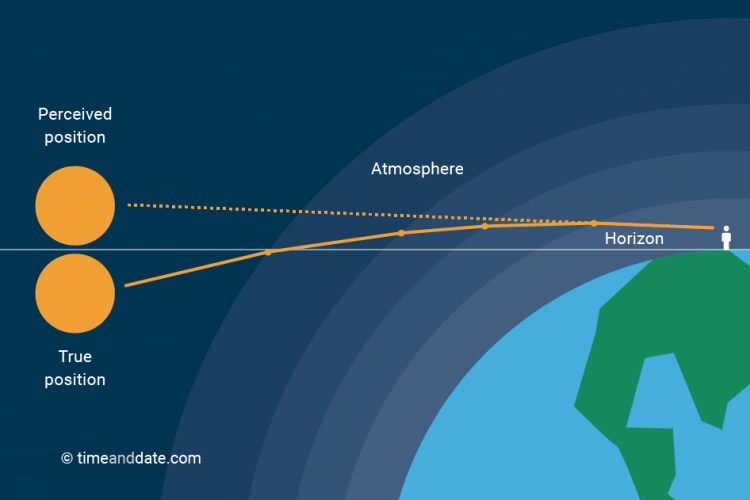
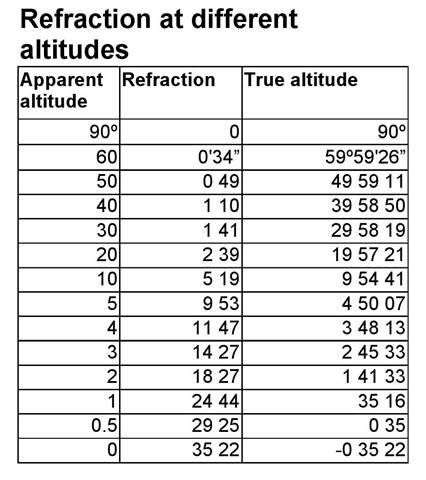
Skica poti žarka skozi atmosfero in tabela kotov loma glede na višino svetlobnega vira - od 0 (horizont) do 90 ° (zenit). Tri četrtine atmosfere se nahaja do višine 11 km (znotraj troposfere). Kljub zelo redki atmosferi nad troposfero, pa le ta še do 120 km nadmorske višine - preko trenja - vpliva na satelite. Kot loma na horizont zaradi atmosfere je nekje: φ_r = - 35' 22''. To pomeni, da so zvezde, recimo Sonce, že pod matematičnim horizontom za - 35' 22'', ko jih zaradi loma svetlobe v atmosferi vidimo ravno na horizontu. Ko svetloba Sonca potuje naprej in zapusti atmosfero Zemlje, se na drugi polovici poti lomi še za enak kot. Celoten zasuk žarka je torej blizu φ_II = 2φ_r = 1° 10' 44'. To bo hkrati naš glavni podatek pri oceni poti - geometrije rdeče svetlobe - v geometrijski senci Zemlje.

Ker je Sonce precej veliko napram Zemlji in nam je tudi relativno blizu, bomo morali upoštevati za kot presečišča osi Sonce-Zemlja z lomljenimi žarki še naklon žarkov iz skrajnih točk Sonca in seveda vmes (s celotne površine dela Sonca, od koder žarki potujejo v smeri Zemlje - za mrk so relevantni tisti, ki zadenejo atmosfero na robu Zemlje glede na smer proti Luni). Tako bomo dobili dokaj realno sliko, zakaj je Luna med mrkom videti točno določene barve (oranžno-rdeča) in ne drugačne. Navedene informacije o lomu svetlobe tako že podajajo osnovne smernice geometrije poteka svetlobe v Zemljini senci, ki tudi bistveno določajo podobo Luninega mrka. Seveda, vsaka dodatna pot svetlobe skozi atmosfero, le to slabi – veliko je odvisno od stanja atmosfere, vremena, geografske širine, tudi onesnaženosti ozračja zaradi izpustov gorenja (oksidacije) fosilnih goriv, peščenih viharjev, vulkanske aktivnosti ...

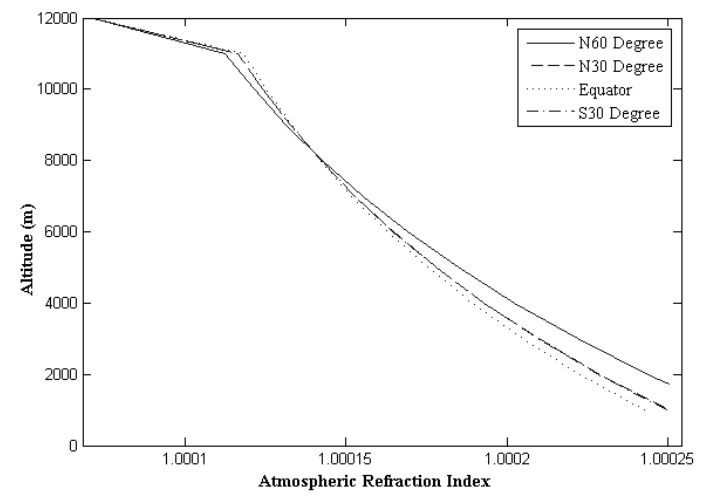
Lomni količnik pada z višino - zelo približno (za del troposfere) po naslednji povezavi: n = 1+0.000292*e-z/7000. Kjer je 'z' nadmorska višina. V resnici je potrebno upoštevati temperaturo, geografsko širino, vlažnost, profil atmosfere, tlak, nadmorsko višino, itn. Enačb za oceno lomnega količnika zraka in računanje kota loma (navidezne višine nebesnih objektov) je več. Še zanimiv premislek – ocena. Že na višini Kredarice pade lomni količnik zraka iz zaokrožene vrednosti 1,0003, kar na 1,0002 (to je za 1/3 vrednosti nad 1) – kar dodatno potrjuje upravičenost observatorijev na visokih nadmorskih višinah in zakaj je nebo v višinah večinoma zelo »mirno«. Med opazovanji planetov se tako zazna veliko več podrobnosti – in že skoraj moti izjemna mirnost slike. Ko sem prvič opazoval planete s Kredarice (2515), je mirnost slike bila zame popolno presenečenje (kot da bi se težko navadil na dobre pogoje).

Kot loma v ozračju na horizont, ki je za nas relevanten, je pod matematičnim horizontom – in sicer približno za:
φ_r = - 35' 22''.
To pomeni, da bomo videli Luno in Sonce na horizontu, čeprav sta še ali že 35' 22'' pod matematičnim horizontom (njuna velikost na nebu je približno 30'). Tako tudi dan traja dlje in zato enakonočje ni na začetku pomladi in jeseni (ampak kdaj?). Ta kot bomo, kot smo že omenili, tudi uporabili pri računanje loma Sončeve svetlobe v senco Zemlje – spodnjega rdečega žarka.

Ocena lege »gorišč« rdeče svetlobe v senci Zemlje

Najprej ocenimo polovični kot vrha stožca, ki ga tvori senca Zemlje (brez ozračja) zaradi obsevanja Sonca. Pomagajmo si s sliko skrajnih žarkov, ki določajo popolno geometrijsko senco.

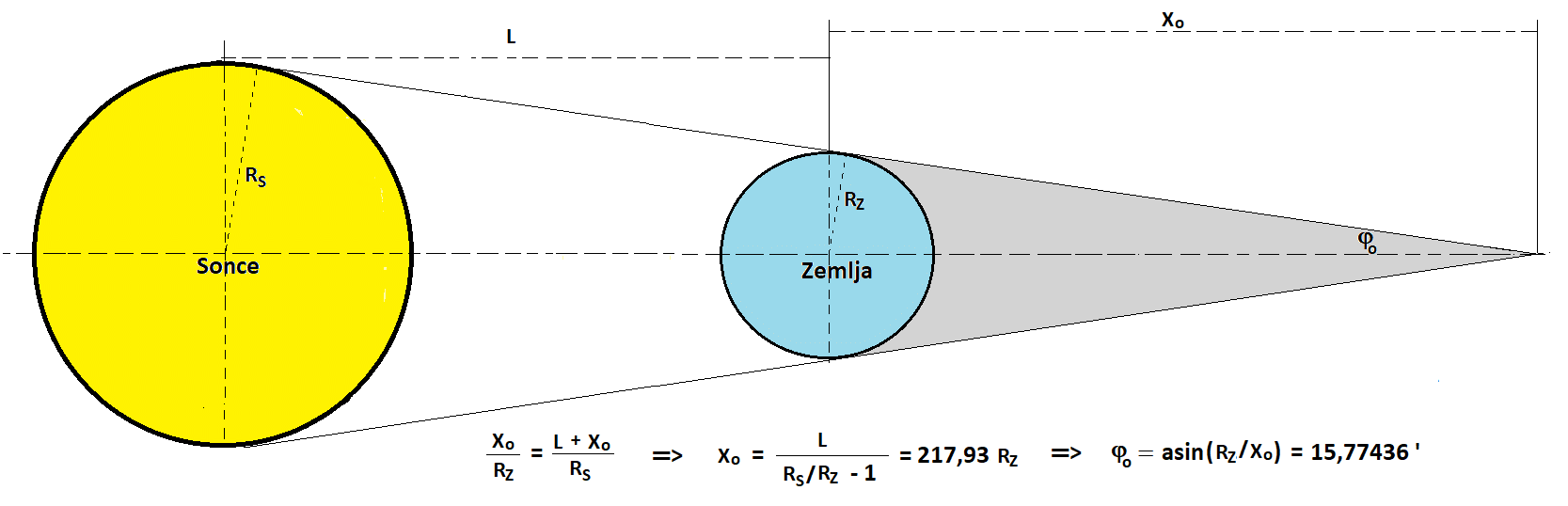
Geometrija Zemljine sence (brez ozračja), ki jo tvori Sonce. Ko vanjo na svoji orbiti vstopi Luna, smo priča čudovitemu nebesnemu pojavu, Luninemu mrku. Luno pa med mrkom lahko opazujemo zaradi loma svetlobe v atmosferi Zemlje v njeno senco - ta pojav razkrivajo slike, ki sledijo. Polovični kot stožca je φ_o = 15,774'. Razmerja velikosti teles, kotov, preslikav in razdalj na sliki niso realna - so podana zgolj za ponazoritev geometrije.

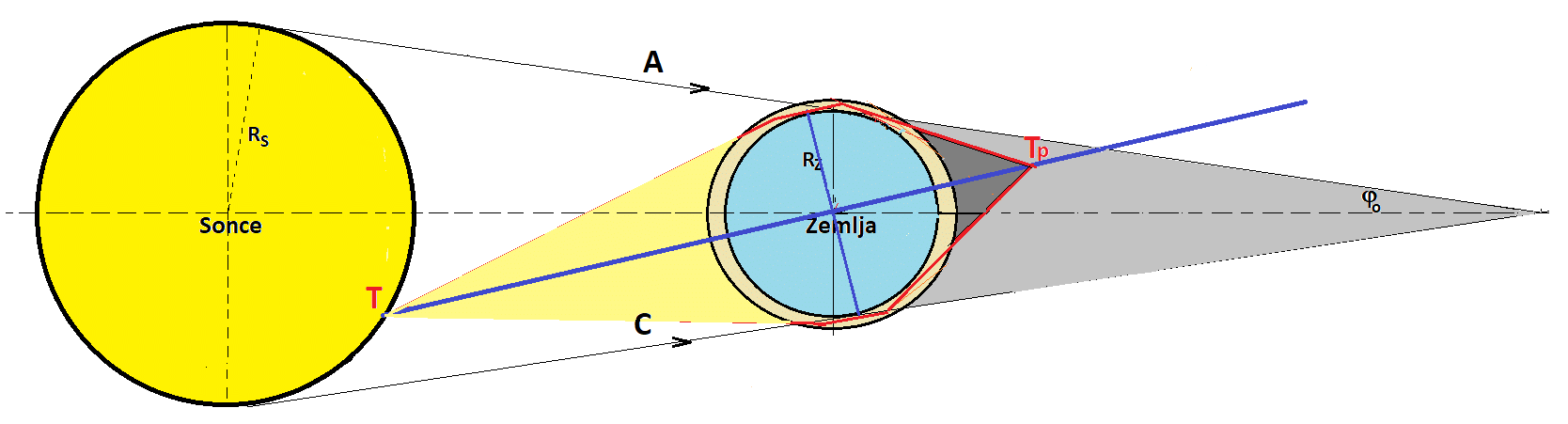
Preslikava točke T na Soncu skozi atmosfero Zemlje v točko T_p v geometrijsko senco Zemlje. Če bi hoteli dobiti korektno sliko loma svetlobe v senco Zemlje, bi morali geometrijo loma izračunati za vsako točko površine Sonca, s katere žarki zadenejo rob Zemlje. A za oceno loma svetlobe v senco Zemlje bosta dovolj skrajna žarka in prečni (diagonalni) žarek, vsi ostali žarki bodo znotraj šopa omenjenih žarkov v opazovani presečni ravnini. Ostali žarki izven presečne ravnine so zavrteni okrog točke preslikave – vsi žarki v smeri trenutne lege Lune obarvajo njeno površino med mrkom v oranžno - rdeče odtenke. Seveda je to le preslikava za najnižje žarke, tik ob površini Zemlje, ostali žarki se lomijo manj in zato nastanejo preslikave dlje od Zemlje!
Razmerja velikosti teles, kotov, preslikav in razdalj na sliki niso realna - so podana zgolj za ponazoritev geometrije.

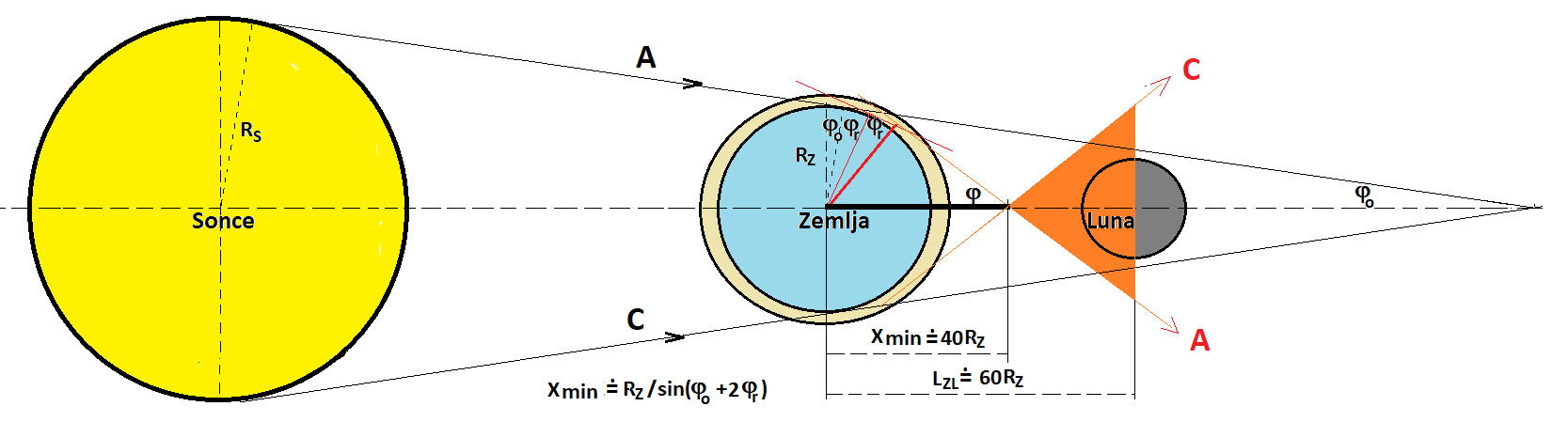
Lom svetlobe v atmosferi v geometrijsko senco Zemlje – najnižji žarek. Refrakcija svetlobe pod horizont na nadmorski višini 0 m je okrog φ_r = - 35' 22". Ko svetloba Sonca potuje naprej in zapusti atmosfero Zemlje, se lomi še za enak kot. Glede na os, ki povezuje središči Zemlje in Sonca, je celoten zasuk robnih žarkov A in C v povprečju φ = φ_o + 2φ_r = 86,50769601 ' = 1,441794934 °.
Kot φ_o = 15,8 ločnih sekund prispeva sama zveznica Sonce-Zemlja, ki povezuje oba robova (to je polovični kot vrha stožca sence). Prvi fokus atmosfere Zemlje za rdečo svetlobo je v točki križanja žarkov A in C v geometrijski senci Zemlje (na razdalji x_min od središča Zemlje).
Razmerja velikosti teles, kotov, preslikav in razdalj na sliki niso realna - so podana zgolj za ponazoritev geometrije.

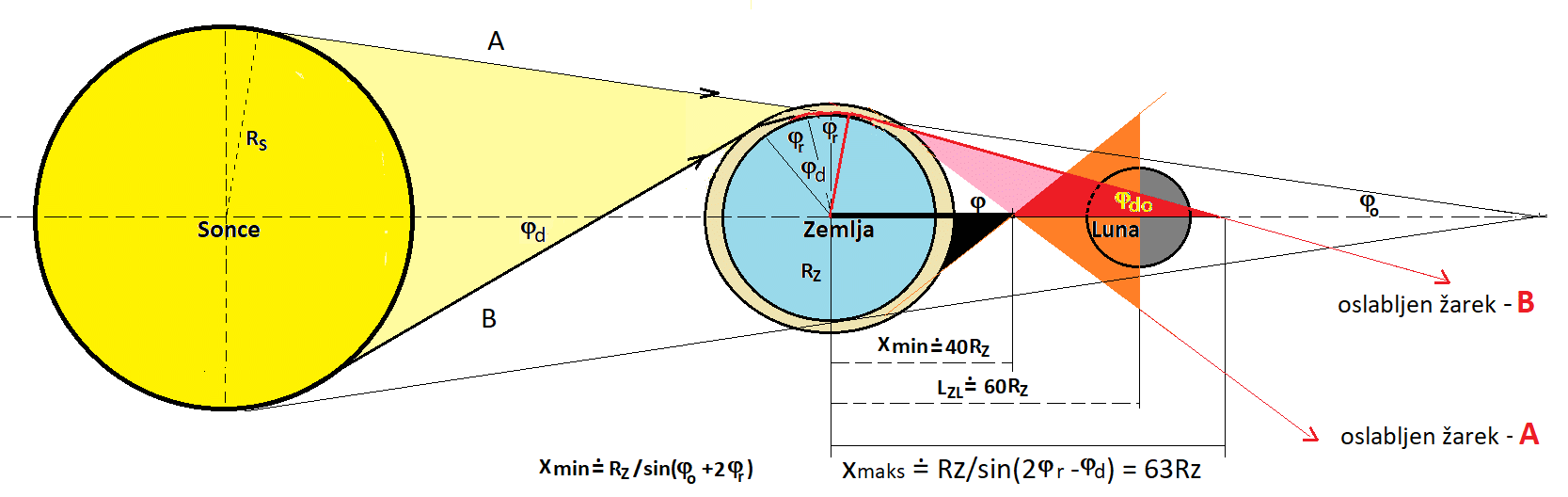
Dopolnjena slika loma žarkov v atmosferi Zemlje z obema skrajnima "goriščema" za rdečo barvo. Rdeča barva se porazdeli med obema skrajnima žarkoma A in B označenima s puščicami (zavrtenima za 2π okrog osi Sonce-Zemlja) in dejansko osvetli celotni del Lune, ki ga vidimo iz Zemlje ob mrku. Izven področja rdeče svetlobe pa se prebijejo tudi nekateri žarki krajših valovnih dolžin (oranžna, rumena, zelena, modra ... barva) ter osvetljujejo rob Lune (te barve večinoma opazimo ob začetku in koncu Luninega mrka – a niso zelo izrazite). Črno obarvano polje in simetrična površina na drugi strani osi Sonce-Zemlja, je popolna senca Zemlje napram Soncu. V ta prostor zaidejo le fotoni zvezd, med Luninim mrkom pa tudi rdeča svetloba odbita od Lune. Rdeča barva spodnjega žarka tako seka os Sonce-Zemlja najbližje pri razdalji 40 Rz od središča Zemlje in najdlje 63 Rz - sredina je blizu 52 Rz. To je tudi blizu efektivne goriščne razdalje Zemlje (f_at = 49 Rz), ki ga tvori njena atmosfera (deluje kot leča) - za žarke iz neskončnosti. Nekateri izračuni (zgolj za rob kroglaste leče z upoštevanjem sferične aberacije - glejte članek prof. Mitje Rosine - Svetlost Lune ob mrku - Presek 6, š. l. 1999/2000) dajo nekoliko manjšo vrednost 47 Rz, odvisno od robnih pogojev. Razmerja velikosti teles, kotov, preslikav in razdalj na sliki niso realna - so podana zgolj za ponazoritev geometrije.

Tlak z višino pada eksponentno - če je na nivoju morja zračni tlak okrog 1013 hPa, je na Kredarici vrednost tlaka okrog 748 hPa. Tako je večino zraka (molekul in atomov, ki sestavljajo plinski plašč Zemlje) zgoščenega do višine 20 km, do 11 km kar 3/4 mase. Pri računanju loma svetlobe po prehodu skozi atmosfero Zemlje (računanju fokusa atmosfere Zemlje) je torej smiselno privzeti za efektivni polmer loma svetlobe kar polmer Zemlje - gre seveda za ocene spodnjega žarka. Za minimalno goriščno razdaljo rdeče svetlobe (razdaljo x_min od središča zemlje), kjer se zbira rdeča svetloba iz roba Sonca (glejte sliko, žarek A) lomljena v atmosferi Zemlje, velja naslednja povezava:
x_min = Rz/sin(φ_o + 2*φ_r) = 40 Rz
Tudi če povečano polmer za 20 km, je to še zmeraj zgolj znotraj nekaj procentov same ocene lege fokusa.

Svetloba, ki se približa Zemlji na 10 km se lomi približno za 10 ločnih minut (podatek iz spletnega kalkulatorja), kar da za x_min_h10km okrog 100 Rz. Ta svetloba pa že zgreši Luno v geometrijskem središču Zemljine sence (a jo močneje osvetli v fazi začetka ali konca mrka). Višje pa lomni količnik kmalu pade blizu vrednosti 1 in tako se krajših valovnih dolžin (modre svetlobe) prebije precej manj v Zemljino senco, kot same rdeče svetlobe v spodnjih plasteh atmosfere. Bolj se bližamo robu Zemljine sence, večja bo gostota lomljene svetlobe, saj se z višino žarkov nad morjem manjša absorpcija (filtriranje) svetlobe. Ob mrku je tako del Lune, ki je bližji robu Zemljine geometrijske sence, svetlejši.

Če upoštevamo svetlobo iz nasprotnega roba Sonca na rob Zemlje (diagonalne žarke φ_d = asin((Rz +Rs)/L = 16,066 '), glejte sliko, žarek B) pa je drugi skrajni fokus pri sečišču žarka pod kotom φ_do = 2*φ_r - φ_d = 54,667 ':
x_maks = Rz/sin(2*φ_r - φ_d) = 63 Rz.
Vemo pa, da je Luna v povprečju oddaljena za okrog 60 polmerov Zemlje od samega središča Zemlje. To pomeni, da je prvi fokus rdeče svetlobe (križanje žarkov A in C) približno 20 Rz pred Luno, drugi fokus (določata ga presečišče med žarkom B in osjo Sonce - Zemlja) pa že nekoliko za Luno (3Rz), kar pomeni, da se rdeča svetloba med mrkom razprši po celotni površini Lune. Polovični kot, ki ga Luna oklepa na razdalji s prvim goriščem je α = asin(RL/(LZL - x_min)) = 23,5'. Ta kot je precej manjši od kota φ = φ_o + 2*φ_r, kar pomeni, da je res celotna Luna med centralnim (popolnim) mrkom znotraj snopa svetlobe rdeče (delno oranžne) barve. Seveda je na robu sence tudi več zelene in modre barve (ki se prebije skozi zgornje redkejše plasti atmosfere Zemlje in delno lomi). Tako lahko na robu Lune, sploh proti koncu ali pred začetkom popolnega mrka zaznamo tako odtenke zelene, modre in ostalih barv. Vse je seveda odvisno od stanja atmosfere med samim mrkom - vremena na obroču atmosfere, ki lomi žarke v senco in na Luno. Vemo, da je atmosfera podvržena tudi plimovanju - vsi našteti dejavniki lahko vplivajo na robne pogoje poteka mrka.

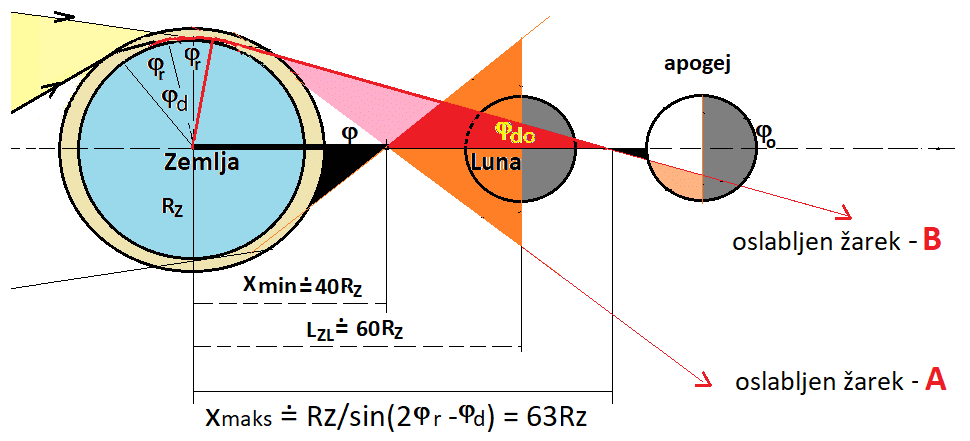
Če je Luna med mrkom v apogeju (odzemlju) in potuje čez centralni pas Zemljine sence, je tam del površine Lune precej manj osvetljen (črno polje ob Luni v apogeju).

Računi se lahko ponovijo na skrajnih točkah orbite Lune, perigej (zaokrožena razdalja Zemlja-Luna je 57 polmerov Zemlje) in apogej (zaokrožena razdalja Zemlja-Luna je 64 polmerov Zemlje). Vidimo, da če je Luna ob mrku v apogeju (zaokrožena razdalja Zemlja-Luna je v tem primeru 64 polmerov Zemlje), pade skrajna goriščna točka nekoliko pred Luno (nekaj je odvisno tudi od razdalje Zemlja-Sonce). Kar pomeni, da je v tem primeru ta del Lune (pri centralnem mrku), še nekoliko manj osvetljen (v popolni senci najnižjih lomljenih žarkov, narišite si skico). Lahko bi govorili o neke vrsti kolobarjastem Luninem mrku (ker je Luna daleč, jo v takem primeru imenujejo tudi mikro Luna) - a o tem pojavu ni zaznamkov, saj je ta površina razmeroma majhna. Se pa opazi na spodnji modelski sliki mrka. Ta temnejši del mrka namreč še zmeraj doseže kar nekaj svetlobe, ki se manj lomi na višjih plasteh ozračja. Ta zatemnitev se morebiti opazi na animaciji:
https://apod.fmf.uni-lj.si/ap190120.html (VIR: APOD)

Prav pri zadnjem Luninem mrku je bila Luna blizu apogeja in je potovala praktično čez središče Zemljine Sence. Rahla centralna zatemnitev (»senca na Luni«) je označen z rumeno puščico na spodnji modelski sliki mrka.

Ker je Luna blizu apogeja nekoliko počasnejša (Keplerjevi zakoni - zadaj je ohranitev vrtilne količine), je tudi mrk v tem primeru nekoliko daljši. Mrk 27. 7. 2018 je tako trajal kar 1h 43 min (primarno pa zaradi tega, ker je bil praktično centralen), to je samo 4 minute manj kot je možen najdaljši teoretični mrk. Potrebno je upoštevati še, da se v tem primeru tudi premer sence nekoliko spremeni (Luna potuje bližje vrhu stožca), a upoštevati je potrebno tudi razdaljo Sonce - Zemlja, ki nekoliko vpliva na višino stožca Zemljine sence in s tem na dolžino mrka. Razdalja Zemlja-Luna je bila tokrat 63.64 Rz, Razdalja Sonce - Zemlja pa 1,0155 AE. Zemlja je bila v afeliju (odsončju) 6. julija 2018 (na razdalji 1,0167 AE). V tem primeru so torej bili izpolnjeni praktično vsi pogoji za dolg in temen Lunin mrk s centralno zatemnitvijo - označena z rumeno puščico.

Slika dokaj verodostojno (z namerno preveč poudarjenimi barvami) kaže na porazdelitev in atmosferski lom različnih valovnih dolžin (barv) znotraj Zemljine sence - kar bistveno določa prečudovit pojav Luninega mrka. Hkrati pa slika nazorno kaže, da kdaj nenavadne barve (modra, zelena ...) na Luni med mrkom niso zgolj naša domišljija.

V resnici je zelo malo meritev geometrije in fotometrije Luninega mrka – kar pa je hkrati lepa priložnost za zanimive še neopravljene raziskave, meritve!

Če je za ogled popolnega Sončevega mrka večinoma potrebno potovati zelo daleč (kar ni slabo, je pa kar drago), so pa Lunini mrki zelo socialni – vsak jih lahko vsakih nekaj let opazuje praktično iz domačega dvorišča. In tukaj se ponujajo dobre vaje tako za študente, kot za dijake in osnovnošolce – večinoma sta dovolj že daljnogled, fotoaparat in analiza slik.


Krvava Luna z modrim pasom (dodatek 2021)
Avtorstvo slike: Angel Yu
Pojasnilo: Kaj povzroči, da modri pas med Luninim mrkom prečka Luno? Modri pas je resničen, vendar ga je običajno težko videti. Predstavljena HDR slika Luninega mrka iz prejšnjega tedna, posneta iz Yanchenga na Kitajskem, je bila digitalno obdelana, da se izenači svetlost Lune in poudarijo barve. Siva barva spodaj desno je naravna barva Lune, osvetljene neposredno od Sonca. Zgornja leva stran Lune ni neposredno osvetljena od Sonca, ker je zakrita v Zemljini senci. Vendar je rahlo osvetljena s sončno svetlobo, ki je šla globoko skozi Zemljino atmosfero. Ta del Lune je rdeč in poimenovan krvava Luna, iz istega razloga, kot so na Zemlji sončni zahodi rdeči: ker zrak bolj siplje modro svetlobo kot rdečo. Nenavaden modri pas je drugačen -- njegovo barvo ustvari sončna svetloba, ki je prešla visoko skozi Zemljino atmosfero, kjer ozon bolje absorbira rdečo svetlobo kot modro.

Lepo priložnost za vaje in podrobnejše analize ponuja že kar popolni jutranji Lunin mrk 21. januarja 2019 v letu, ko Mednarodna astronomska zveza praznuje 100 let (MAZ100 ali IAU100).

V letu 2019 bo veljalo geslo Pod enim nebom in v njem IAU načrtuje več aktivnosti skozi celo leto – podobno kot v Mednarodnem letu astronomije 2009.
PREDLOG - POBUDA
Lepo bi bilo, če bi vse šole v eni noči po celotni Sloveniji naredile za učence (učitelje, starše in občane iz okolice šol, popotnike, za vse generacije, tudi ostarele ...) osnovna Galilejeva astronomska opazovanja izpred 410 let (Lunina mrka, mlada Luna, planeti, nekaj svetlejših megličastih objektov ...). Večina šol ima namreč iz MLA2009 solidno astronomsko opremo in je prav, da se te opreme ne ustraši in jo uporabi ob praznovanju IAU100 - Pod enim nebom (zagotovo bi šolam pomagala astronomska društva, univerze, posamezniki ...). Ali nam bo torej uspelo prebuditi astronomsko Slovenijo?

Zorko Vičar
Šentvid – Lj., avgust 2018 (objavljeno januarja 2019 v Bojanovi SPIKI)

http://astronomska-revija-spika.si/spika-januar-2019/

Spika, januar 2019

Objavil Bojan Kambič dne 7. 1. 2019 Spika 2019
Januarske Spike se bodo najbolj razveselili tisti, ki noči radi preživljajo pod nočnim nebom. Tone nas popelje v globine ozvezdja Trikotnik, ki ga večina pozna le po imenu in morda po galaksiji M 33. A v njem je veliko več od tega … Poglejte!
Da pa januarskega Luninega mrka ne boste le pogledali, je poskrbel Zorko Vičar s poglobljeno študijo geometrije Zemljine sence. Ko jo boste prebrali, boste lahko prijateljem in znancem, ki bodo opazovali z vami, strokovno razložili, kaj se dogaja med mrkom in zakaj je Luna takih barv, kot je. Članek je napisan tako poljudno, da ga bodo razumeli tudi učitelji po osnovnih in srednjih šolah.
Naša nemška kolega, ki nas že nekaj Spik zapored vabita k opazovanjem, sta tokrat izbrala Zvezdno kopico s srcem in školjko z biserom. Poglejte, kaj se skriva za tem naslovom! In tu je še Andrej Guštin (ta Spikin izgubljeni sin), ki vam v drugem delu serije o začetniški astrofotografiji tokrat nazorno pokaže, kako lahko testirate optiko svojih objektivov in preverite, ali so uporabni za zvezde.
Vsem, ki mislite, da ste že vrhunski astrofotografi, pa je rokavico tokrat vrgel naš Matej s fantastično Andromedino galaksijo, ki krasi naslovnico tokratne Spike. Seveda vas k opazovanju vabijo tudi lunatiki in Ljubo Juvan, ki je pri nas zadolžen za komete.
Ko pa boste izpod mrzle zimske noči prijetno utrujeni prišli na toplo, vas čaka še razmišljanje o velikih možeh, ki so ta naš voz astronomije povlekli iz srednjeveškega blata. Tokrat je na vrsti Leibnitz in njegov odnos do Descartesa in Newtona. Vrhunsko!
In še preden boste prišli do konca, bo pred vami že nova, februarska Spika!

Nazaj na članke.
Nazaj na aktualno stran.
Nazaj na domačo stran.