.gif)



.gif) |
 |
 |
 |
Zgodovina in mrki – vsebina, ki je naše izobraževanje ne pokriva
Mrki so bili za razvoj astronomije ključnega pomena. Babilonci (Kaldejci) so zabeležili vse mrke po letu 747 pr. Kr. (verjetno že prej). Kot smo že omenili, so odkrili tudi periodo sarosa, ki je omogočila napovedovanje Sončevih mrkov, seveda tudi Luninih. Letošnji saros 145 ima 77 mrkov in ti trajajo v obdobju 1370 let. Začetek sarosa 145 je 4. jan. 1639 na severni polobli in konec 17. apr. 3009 na južni polobli.
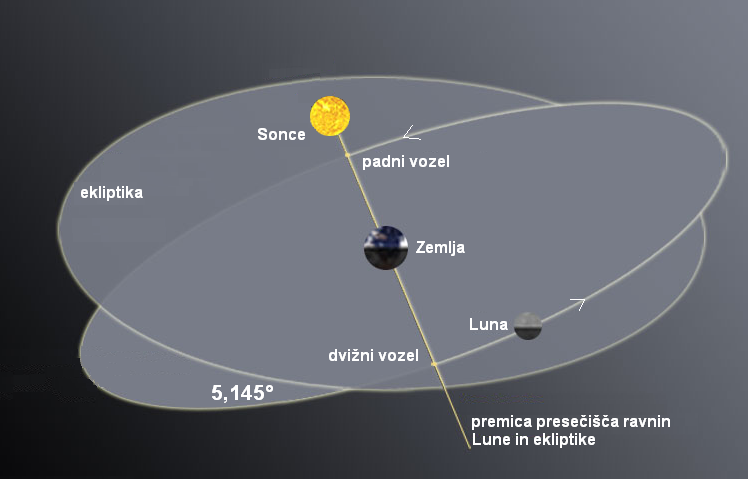
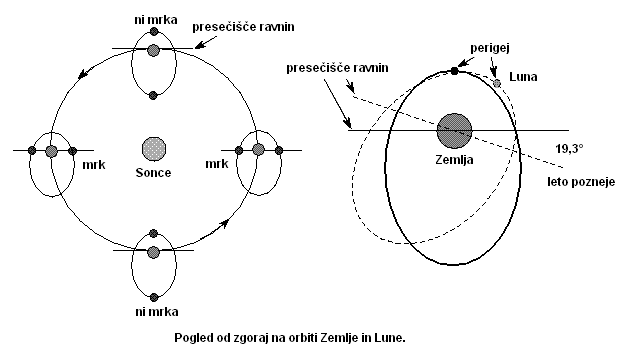
Slika: Ko presečišče ravnine ekliptike in ravnine potovanja Lune (okrog Zemlje)
kaže proti Soncu, nastane:
- ali Sončev mrk, če je Luna v padnem vozlu (descending node),
- ali Lunin mrk, če je Luna v dvižnem vozlu (ascending node).
V tem primeru na sliki je Luna izven vozlov in ni mrka.
Dinamika vseh treh teles je še toliko zanimivejša,
ker ravnina poti Lune okrog Zemlje precedira (precesira) – presečišče
obeh ravnin se zato premika (suče). Razmerja teles na sliki so zgolj informativna.
Mrki 145. sarosa pa se dogajajo v dvižnem vozlu Lune (ascending node).
Še logika periode saros(a)
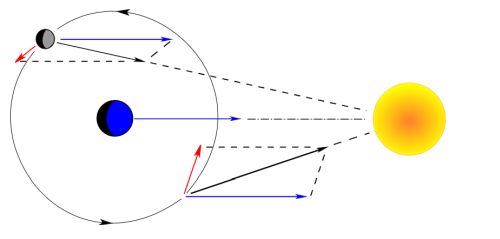
Precesija je pojav, pri katerem vrtilna os (vrtilna količina) telesa spremeni svojo smer v prostoru pod vplivom navora rezultante zunanjih sil.
Lunina orbita ima dve pomembni precesijski gibanji - precesijo apside, perigeja (prizemlja) in precesijo orbite Lune okrog Zemlje - precesija vozlov.
Lunino precesijo povzročajo motnje, ki jih povzroča plimski vpliv Sonca. Na sliki imamo prikazan vektor centralne sile Sonca na Zemljo (modra barva) in
še vektorja na Luno ob različnih legah na orbiti (črna barva) - takoj opazimo, da te sile niso vzporedne in od tukaj tudi navor na orbito Lune
okrog Zemlje in tako se dogaja precesija. Še bolj raznoliko vektorsko sliko bi dobili, če bi narisali še vektorje centralne sile Zemlje na Luno in vektorje
sile Sonca na Luno.
Ravnina Lunine orbite okrog Zemlje je nagnjena za 5,145° glede na ekliptiko (na ravnino potovanja Zemlje okrog Sonca),
hkrati pa orbita Lune še precedira s časom obhoda 18,612 let. Presečišče ravnin Lune in Ekliptike imenujemo vozel
(dvižni in padni vozel),
ki tudi, zaradi precesije, potuje. Pojav mrka je odvisen od treh ciklov:
- od obdobja, v katerem se spreminjajo Lunine mene
(vsem nam poznani sinodski mesec S=29,530589 dni),
- od časa, ko Luna prehaja skozi vozel obeh ravnin, to je nodularni ali
drakonsi mesec
N=27,212221 dni - zaradi precesije Lunine tirnice,
za kot 19.3549 ° na leto v nasprotni smeri gibanja Lune (glej sliko),
je nekoliko krajši od dolžine siderskega meseca – to je obrata za 360 °,
- in časa, ko Sonce prehaja skozi isto vozlišče Lune
(eklipsno ali drakonsko leto D=346,620075883 dni, to leto je krajše od tropskega,
ker se Lunin vozel suče -
zaradi precesije potuje).
Zmnožki naravnih števil in sinodskih mesecev, drakonskih mesecev in drakonskih let skoraj sovpadajo (lahko bi rekli, da poiščemo najmanjši skupni večkratnik), če velja:
223*S = 242*N = 19*D
6585,32 d = 6585,36 d = 6585,78 d
V tem času pa se ponovi tudi mnogokratnik anomalističnega meseca (A = 27,55455 dni), čas prehoda Lune iz perigeja v perigej, ki je daljši od siderskega meseca, saj ravnina Lunine orbite precedira za kot 19.3549 ° na leto v nasprotni smeri gibanja Lune (glej sliko).
239*A = 27,55455 d = 6585.54 d
Perioda je pomembna, ker lega Lune na orbiti (tudi) odloča o dolžini mrka (če je Luna v perigeju - prizemlju, je mrk daljši). Zato si je nekaj bližnjih mrkov istega sarosa tudi zelo podobnih po trajanju (recimo mrka 1999 in 2017, približno 2 minuti in pol).
V izračunanem obdobju se torej spet približno ponovi lega Zemlje, Lune, Sonca na premici mrka (ali blizu, saj so telesa razsežna in ni nujna točna poravnava), ki leži v smeri presečišča ravnin gibanja Lune in gibanja Zemlje. To je 18 tropskih let in 11,3 dni (ali 10,3 dni) in znaša 6585,66 dni. To je torej perioda sarosa, ko se ponavljajo Sončevi mrki – in večinoma tudi Lunini mrki. V enem koledarskem letu se lahko zgodijo največ štirje Sončevi mrki (Luninih in Sončevih pa skupaj 7). Na dolgi rok je, skupaj z delnimi mrki (tudi s temi v polsenci Zemlje), Sončevih in Luninih mrkov približno enako. Lunini jih celo nekoliko presegajo – če pa izpustimo Lunine mrke v polsenci (penumbri), pa je več Sončevih mrkov. Lunin mrk zgolj v polsenci se komaj opazi – del Lune blizu umbre (popolne sence), je morebiti nekoliko temnejši.
Naloga iskanja ponovitve mrka (saros) je podobna, kot če rešujemo uganko, kdaj bodo spet urni, minutni in sekundni kazalec na uri poravnani. Vemo, da so recimo ob 12. h. Privzamimo, da je enota minuta, ki traja 60 s (sekundni kazalec torej naredi obrat za 360° v 1 min, minutni v 60 min, urni pa v 12*60 min). Tako iščemo enakost za zmnožke a*min = b*60min = c*12*60min. Členi so: c = 1, b = 12 in a = 12*60. Če bi pa ura tekla z napako, pa bi bili členi nekoliko drugačni, glede na pravi čas.
Še nekoliko bolj preprosta vaja - kdaj se spet srečata urni in minutni kazalec po 12. uri - pomemben je princip.
Velja:
1/T = 1/Tm -1/Tu
T = Tm*Tu/(Tu-Tm) = 12/11 h
Preverite, če opazujemo prvo srečanje obeh kazalcev po 12. uri, je to približno 5 min in 27 s čez 13. uro.
Do ponovnega srečanja na poziciji 12 bo prišlo po enem obratu urnega kazalca in 11 časovnih intervalih srečanja obeh kazalcev (11*T = 11*12/11 = 12 ur). Pomebna ugotovitev, za srečanje na isti poziciji mora torej miniti celo število intervalov srečanj in celo število obhodov počasnejšega telesa (11*T = 1*Tu).
Saj poznate pesmico, uganko: "Dolgi Luka, kratki Miha, čudna dva možica, noč in dan po eni nogi v krogu se vrtita (lovita) ...".
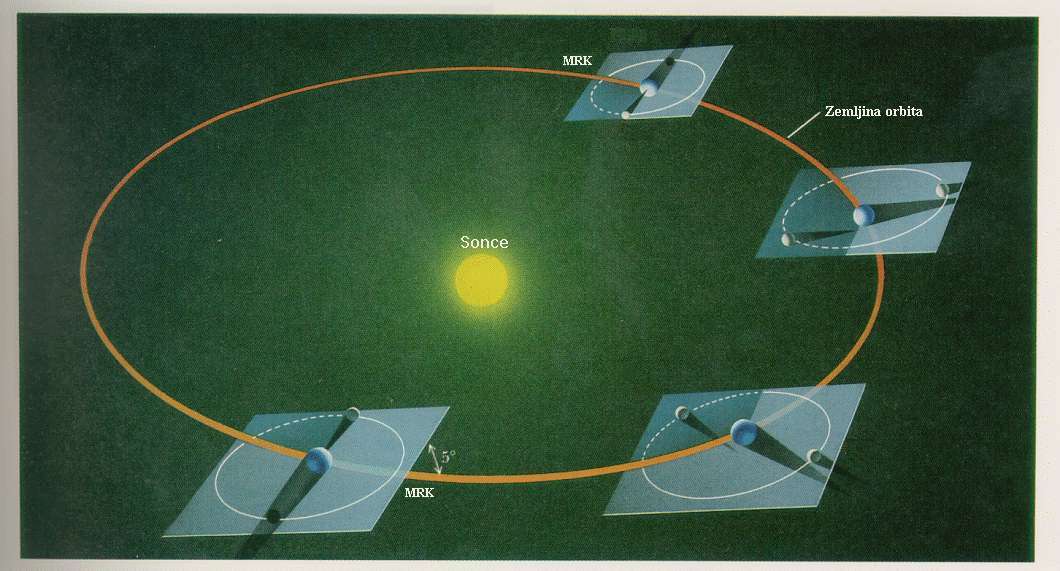
Slika: Slika nazorno prikazuje pogoje za nastanek Luninih in Sončevih mrkov.
* A za napovedovanje točne poti mrkov, je saros premalo. J. Kepler je v letih 1609 - 1619 odkril zakone nebesne mehanike in s tem omogočil točne izračune dogodkov v Osončju
– tudi poteke mrkov (kdaj, kje). Seveda so njegove zakone matematično in fizikalno nadgradili njegovi nasledniki, to so R. Hooke, E. Halley, I. Newton,
a resnični oče moderne nebesne mehanike in gravitacije je vsekakor izjemen J. Kepler.
Izračuni so seveda odvisni od natančnosti vhodnih spremenljivk –
tukaj so določene težave, saj se recimo dan daljša, itn. Kdaj je potrebno upoštevati
tudi popravke, ki jih klasična mehanika ne zna opisati in tukaj nam priskoči na pomoč
splošna teorija
relativnosti (precesija perihelija). S to tematiko
se še srečamo pri uklonu svetlobe ob masivnih zvezdah.
KAJ VSE SO NAM MRKI OMOGOČILI?
* V antiki so, s pomočjo kotov, razmerij senc, časa trajanja Luninih mrkov, določili velikost in razdaljo do Lune in ocenili velikost ter razdaljo do Sonca (Aristotel, Aristarh, Hiparh, ...), to je bil izjemen uspeh – glejte članek Antika in mrki (Spika, februar 2000).
* Med Sončevim mrkom (med slikanjem emisijskega spektra Sončeve korone) v Indiji je 18. 8. 1868 Jules Janssen odkrili element helij, žlahtni plin 42He (v laboratoriju na Zemlji je bil helij detektiran leta 1895 – odkril ga je W. Ramsay). Helios v grščini pomeni Sonce. Helij je tudi glavni produkt zlivanja ioniziranega vodika v sredici Sonca. Pri tem procesu se sprosti ogromno energija (E = Δm*C2 - razlika v masi elementov pred fuzijo in po njej, pomnožena s kvadratom hitrosti svetlobe), ki omogoča, da Sonce stabilno sveti že 5 milijard let in nam tako omogoča življenje. Ime helij je torej še kako posrečeno – no, izvor energije zvezd (fuzijo) in nastanek težkih elementov smo dojeli veliko pozneje. Helij je pričakovano drugi najpogostejši element v vesolju (večinoma je nastal, za razliko od ostalih masivnejših atomov, že po prvi nukleosintezi kamlu po velikem poku - ko je temperatura vesolja padla na okrog 1010 K - heliju tako tudi pravimo pepel velikega poka). Seveda so tudi vsi ostali elementi do železa večinoma produkt fuzije v zvezdah, težji pa so posledica eksplozij supernov, trkov. Veliko težkih elementov kot so zlato, platina, uran, plutonij, jod, tudi delno železo, itn nastane pri brutalnih trkih nevtronskih zvezd – letos so tak trk potrdili tudi preko gravitacijskih valov – izjemno (zaznala observatorija LIGO in Virgo – s senzorji, laserskimi interferometri, teorijo gravitacijskih valov, trki črnih lukenj, se v Sloveniji ukvarja dr. Andrej Čadež). Do sedaj smo take trke zaznavali samo preko GRB - kratkih izbruhov sevanja gama (po katerih se lahko zgodi eksplozija imenovana kilonova, ki je tip supernove, po svetlosti 1000 krat klasična nova – v Sloveniji se z gama izbruhi ukvarja dr. Andreja Gomboc). Veliki pok, nove, supernove, kilonove, trki - kakšen gromozanski »kraval« se je torej že zdavnaj moral zgoditi v vesolju, da smo ljudje sploh lahko nastali. V nas in ostalih živih bitjih je namreč poleg večinskega vodika (nastal je tik po »velikem poku«) in kisika, še veliko ogljika, dušika (to so sestavni deli DNK - aminokislin), natrija, fosforja, kalcija, tudi železa, joda, ... mi ljudje pa bi kdaj dali prav vse za zlato, odšli v Ameriko, Afriko ..., se ugonobili z uranom ...
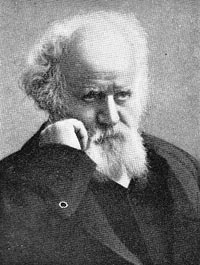

Slika: Levo Jules Janssen, desno Helijeva rumena crta valovne dolžine 587.562 nm je takoj za zeleno
barvo – slikano med mrkom, vir: APOD.
To je emisijski spekter Sončeve korone.
* Eno ključnih potrditev splošne teorije relativnosti je omogočil Sončev mrk 1919
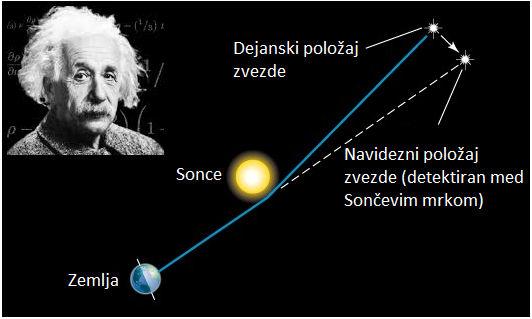
Slika: Kot odklona žarka iz prvotne smeri tik ob Soncu je po Einsteinu: ϑ = 4GM/(c2R) = 1,75 ''
(če bo »slučajno« kdo od bralcev računal odmik, je rezultat potrebno iz radianov spremeniti v ločne sekunde:
M = 1,99*1030 kg je masa Sonca, R = 695700000 m polmer Sonca,
c = 299792458 m/s = 3*108 m/s hitrost svetlobe, G=6,67408*10-11 m3·kg-1·s-2 gravitacijska konstanta). Izvor razmerij med količinami v formuli se da celo v srednji šoli do neke mere pojasniti, a samo do polovice Einsteinovega rezultata, preko poti fotona po hiperboli mimo Sonca. Nekaj podobnega, napako polovične vrednosti, je Einstein naredil leta 1911 in že drugi pred njim (Soldner), a je enačbo, preko splošne teorije relativnosti, korigiral leta 1915. O odklonu svetlobnih žarkov v gravitacijskem polju (zaradi teže) so razmišljali že mnogi pred Einsteinom – Newton, Laplace, Cavendish je izvedel račun, a brez objave. Prvi izračun odklona žarka v gravitacijskem polju Sonca pa je leta 1804 objavil že omenjeni nemški fizik in astronom Johhan Soldner.
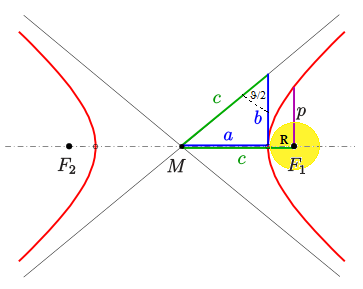
Slika: Hiperbola (rdeči krivulji na grafu) je lahko pot delca, telesa z maso (m) -
recimo kometa - v gravitacijskem polju masivnega sfernega lupinasto homogenega objekta – recimo
zvezde z maso (M). Pogoj je, da ima delec skupno energijo večjo od nič. Zapišimo energijo delca z maso m in hitrostjo v, ko sta središči teles oddaljeni za (r) – vsota kinetične in potencialne energije je:
E = Ek + Ep = mv2/2 – GmM/r. Enačba hiperbole je: x2/a2 - y2/b2 = 1 (a in b sta polosi).
Enačbo lahko tudi zapišemo kot: y=±(b/a)(x2 - a2)1/2.
Enačba asimptot hiperbole je: y=±bx/a (to sta premici, ki se sekata med temenoma in se pri veliki vrednosti spremenljivke x zelo približata krivulji hiperbole). Iz slike lahko razberemo, da je zvezda v gorišču hiperbole, da je razdalja od središča zvezde do temena hiperbole enaka c-a. Za c velja: c = (a2 + b2)1/2. Razdalja od središča zvezde do asimptote (pravokotnica nanjo) je kar b – izpeljite sami – pomembna je za določitev vrtilne količine, ko je objekt (recimo foton) zelo oddaljen. Ekscentričnost hiperbole je: e=(a2+b2)1/2/a; parameter p (semi-latus rectum – tangenta temena, v gorišču pa razdalja do krivulje) pa ima vrednost: p = b2/a. Toliko torej rabimo vedeti o hiperboli, da lahko izvedemo klasični račun odklon žarka ob zvezdi – žal 2x napačen. A vaja je zelo poučna in nas hkrati popelje do razmišljanja o principih splošne relativnosti.
Poglejmo na kratko, kaj nam torej ponuja Newtonov klasični opis potovanja svetlobe ob zvezdi. Za delec, ki ima vsoto potencialne in kinetične energije večjo od nič velja, da potuje po hiperboli (x2/a2 - y2/b2 = 1) – recimo v bližini zvezde, ki je v gorišču hiperbole.
Zapišimo energijski zakon za tak primer: E=Ek+Ep=GmM/(2a) > 0, v neskončnosti je energija zgolj kinetična mv2/2 [potencialna energija Ep = -GmM/r = -GmM/∞ = 0 je v neskončnosti namreč 0].
Parameter a je glavna polos: 2a je razdalja med temenoma hiperbole. Nakažimo še pot do
zelo pomembnega izraza za celotno mehanično energijo: E = Ek + Ep = mv2/2 – GmM/r = GmM/(2a).
Zapišimo energijo, ko je telo najbližje zvezdi – v temenu:
E1 = mv12/2 - GmM/(c - a); v neskončnosti pa velja:
E2 = mv22/2 - GmM/∞ = mv22/2.
Vrtilna količina v temenu je: L1 = mv1(c - a); v neskončnosti pa kar: L2 = mv2b.
Ker obravnavamo sistem brez zunanjih navorov in sil, se ohranjata tako vrtilna količina kot energija teles.
Poznamo torej dve enačbi - za energijo in vrtilno količino
(E1 = E2 in L1 = L2) z dvema neznankama
(hitrosti v1 in v2):
mv12/2 - GmM/(c - a) = mv22/2
mv1(c - a) = mv2b
Iz enačb recimo izrazimo v2
(sami se potrudite, upoštevajte, da je c2 = a2 +b2,
prvi delni rezultat je: v22 = GM/a),
vrednost kvadrata hitrosti vstavimo v izraz za energijo v neskončnosti
in končni rezultat je zelo preprost:
E = Ek + Ep = mv22/2 = GmM/(2a)
Vrnimo se k uklonu svetlobe - kako je s fotoni, kvanti svelobe v gravitaciji? S fotoni so, po definiciji gravitacijske sile (F = Gm1m2/r2, ki deluje le med masnimi delci m1 in m2), v Newtonovi mehaniki problemi, saj nimajo mase – in kako bi torej gravitacija sploh lahko delovala na nemasne delce? A mnogi so to protislovje nekako čarovniško preskočili in fotonu pripisali virtualno maso mf = E/c2 = hν/c2. Vsekakor ima svetloba, glede na Sonce, energijo večjo od nič, saj nam drugače Sonce ne bi pošiljalo izsevane energije (drugače bi bilo, če bi »živeli« v bližini črne luknje) ... Fotoni torej potujejo po hiperboli (naj bi). In odklon svetlobe od prvotne smeri bi naj ustrezal kar enačbam asimptot hiperbole (y=±bx/a). Kot odklona asimptote hiperbole od tangente temena se izpelje kar iz razmerja polosi, glejte sliko:
tan(ϑ/2) = a/b.
Ker po energijskem zakonu velja, da ima delec daleč vstran od centralne zvezde z maso M le
kinetično energijo E = mv2/2 = GmM/(2a), in če privzamemo, da je hitrost
v enaka kar hitrosti svetlobe c (saj iščemo pot fotona), dobimo za parameter a vrednost:
a = GM/c2.
Poiščimo še parameter b. Če foton potuje čisto blizu površine zvezde, ki je v
gorišču hiperbole, velja za najbližjo razdaljo »zvezda – foton«, da je ta kar enaka polmeru zvezde R:
R = c – a = ae – a
Ker je R = c – a = (a2+b2)1/2 – a, lahko iz zadnje enačbe izrazimo polos
b = ((R + a)2 - a2)1/2. A ker je polos a = GM/c2 veliko manjša od polosi b (pri Soncu se namreč ne opazi velikih odklonov svetlobe), se na koncu izkaže
(ker je a = GM/c2 = 1475,7 m in je a/R = 2,1*10-6, in ker je b>p>R, lahko pri vrednotenju polosi b, razmerje a/R zanemarimo), da je parameter b v realnosti za fotone kar
enak polmeru zvezde R. Velja za zvezde podobne Soncu, b = R((1 + a/R)2 – a2/R2)1/2
= R((1 +0)2 – 0)1/2 = R, pri masivnih kompaktnih zvezdah ta približek ne velja.
Klasična enačba odklona žarka ob Soncu je torej za
a = GM/c2 in b = R kar:
tan(ϑ/2) = a/b = GM/(c2R)
Ker so odkloni majhni (tan(ϑ/2) ≈ ϑ/2), velja:
ϑ/2 = GM/(c2R)
Celoten kot odklona bi torej naj bil:
ϑ = 2GM/(c2R) = 0,875 '' (???)
A rezultat je za 2x premajhen (pravilen izraz je: ϑ = 4GM/(c2R) = 1,75 ''),
zato so pri enačbi vprašaji. To je lahko dobra vaja, ki mladim pusti misliti, zakaj klasična
Newtonova fizika tukaj odpove in kaj se skriva za splošno teorijo relativnosti ...?!
Če bo urednik za, lahko posvetimo še kakšen tekst splošni teoriji
relativnosti (Če bo napisan
dovolj poljudno, je urednik vedno za! Op. ur.).
Tako čez palec premislimo vsaj o eni napaki, ki smo jo naredili pri računanju odklona
fotona ob zvezdi.
V primeru, ko imamo opravka z delci visokih hitrosti ali celo s svetlobo, moramo upoštevati relativistično mehaniko, enačbe (kinetično energijo za masni delec Ek = mc2(γ -1), za foton pa recimo zveze p = E/c = hν/c = h/λ). Seveda - teh predpostavk klasičen pristop ne vključuje [ γ = 1/(1 - (v/c)2)1/2 je Lorentzov faktor].
Odmik svetlobe od prvotne smeri ob zvezdi lahko izračunamo tudi po znani enačbi za kot med asimptotami (velja za hiperbolo):
δ = 2sin-1(1/e)
e=(a2+b2)1/2/a - je ekscentričnost (parametra a in b pa moramo izračunati enako kot smo že pokazali, iz ohranitve energije in vrtilne količine). Rezultat bo seveda enako napačen za svetlobo in hitre delce kot smo že izračunali in po krajšanju majhnih količin je tudi končna enačba enaka
(ϑ = δ = 2GM/(c2R) = 0,875 '' (???)).
Med Sončevim mrkom, 29. maja leta 1919, je Einsteinovo napoved (1.75 loč. sekunde) odklona žarka zaradi gravitacije (bolje, zaradi ukrivljenosti prostora-časa) potrdil (približno) Sir Arthur Eddington (izjemen dosežek). Potrditev je tudi matematiki dala nov zagon glede izjemne uporabnosti neevklidske geometrije.
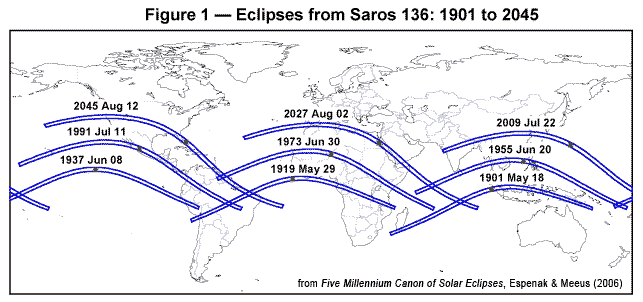
Slika: Poti popolnih Sončevih mrkov, ki pripadajo sarosu 136 – zelo nazoren
prikaz dinamike mrkov v sarosu. Temu sarosu je pripadal tudi mrk Eddingtonove
potrditve Einsteinove splošne teorije relativnosti (29. maj 1919) – fotografiranje
odklona žarkov oddaljenih zvezd ob Soncu. Tudi mrk iz 22. jul. 2009 – ki se je na
Kitajskem žal skril za oblake - je del cikla sarosa 136. Mrk sarosa 136 pa
se bo spet pokazal 2. avg. 2027, tudi na poti čez bližnji Gibraltar – vredno ogleda.
Trenutno so mrki sarosa 136 zelo dolgi – trajajo dobrih 6 minut.
Luna pa je ob S. mrkih serije 136 v padnem vozlu (descending node).
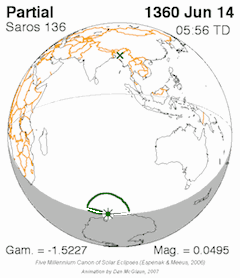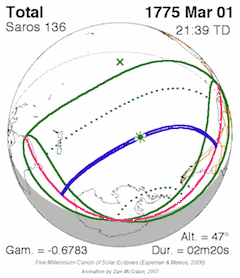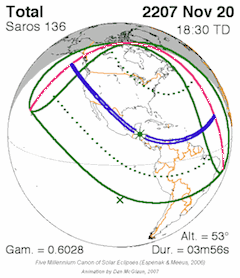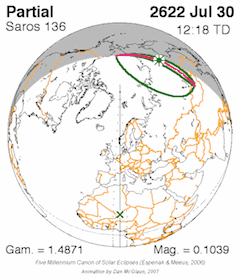
Vir:
https://en.wikipedia.org/wiki/Saros_(astronomy)
Sončevi mrki se pojavljajo v tem primeru v bližini padnega vozla Lune (descending node).
Sorodnim mrkom pa se doda tudi številka serije (sarosa).
Prvi mrk te serije (136) se začne
na južnem delu Zemlje in pot mrka se
z vsakim
naslednjim mrkom pomakne nekoliko
proti severu.
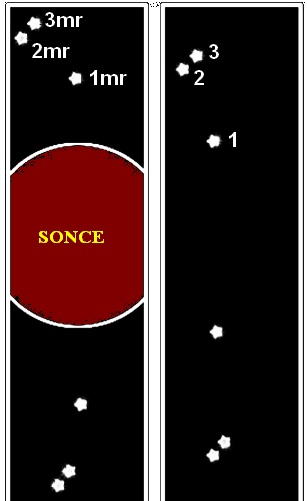
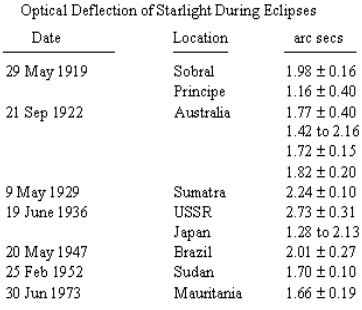
Slika: Položaj zvezd med in po mrku. Odmik med mrkom je 1.75 loč. sekunde, to je pričakovana vrednost
za zvezde tik ob Soncu. Tabela desno kaže na težave pri meritvah odklona svetlobe – tudi med mrki po letu 1919.

Slika: Napoved Eddingtonovega odkritja. Credit: Illustrated London News (1919). Eddingtonovi odpravi sta slikali mrk iz otoka Principe (zahodna Afrika) in iz kraja Sobral (Brazilija) – nikjer ni bilo ravno idealno vreme.

Slika: Fotografija mrka 29. 5. 1919, negativ – na njej se komaj opazi zvezde in njihov premik (črtici desno zgoraj). Mrk se je zgodil blizu Plejad in Hijad – kar je bilo idealno, saj je tam nebo bogato posejano z zvezdami. Tudi sam Eddington nekoliko dvomi o odkritju: » ... one can say with certainty that the effect (at the solar limb) lies between 0.87” and 1.74” ... «, pripomnil je še, da gre zgolj za preliminarne meritve, in da bo dokončna vrednost odklona zvezd naknadno določena.

Slika: Oprema uporabljena med mrkom 29. 5. 1919 v kraju Sobral, Brazilija.
Credit SSPL, via Getty Images.
Sliko mrka so v teleskop usmerili z ogledalom - tako
imenovanim heliostatom, kar je nazorno vidno iz fotografije postavitve opreme.
Še zgodovinsko ozadje in dvomi glede Eddingtonovih meritev
Eddington je bil angleški, Einstein pa nemški pacifist. Eddington je hotel Einsteinu
nekako pomagati – tudi preko potrditve odklona svetlobe zvezd med mrkom. To je bil hkrati ČAS NOVEGA UPANJA PO HUDI SVETOVNI VOJNI ... A Eddington je bil glede verodostojnosti
meritev precej na majavih temeljih (odmik zvezd od Sonca je bil manjši od velikosti zvezde na sliki, pri nekaterih v napačno smer – proti Soncu). A na koncu so drugi potrdili to, kar je on naredil
precej čez palec (v kontekstu časa) - bolj iz prijateljstva in želje pomagati novi teoriji k življenju – kot pa iz neoporečne analize (dokaj neposrečenih) slik. A tudi J. Kepler je pred 400 leti verjel Galileju na pisano besedo (drug od drugega sta bila oddaljena dobrih 1000 km, Praga - Padova). Verjel je, da je Galilei v resnici videl Jupitrove lune, in da potujejo okrog planeta (čeprav Galileju tega noben »kolega« iz univerze ni hotel potrditi). Zakaj, ker je J. Kepler zaupal svoji mehaniki.
Lorentz pravi glede Eddingtonovih meritev naslednje: “Verjetno lahko verjamemo (glede na obseg ugotovljenega odklona), da odklon svetlobe v Sončevi atmosferi sploh ni relevanten pojav [to je bil namreč glavni argumenti za dvom], ampak je v resnici zaznan odklon zaradi gravitacije same. To je vsekakor eden od najimenitnejših
rezultatov, ki jih je znanost kdaj dosegla in lahko smo izjemno zadovoljni.”
Na srečo lahko danes bolj natančne meritve opravimo v radijskih valovnih dolžinah, zlasti s pomočjo kvazarjev in mrk ni več nujni pogoj za take meritve. Analiza leta 2004, v kateri je bilo obdelanih več kot 2 milijona opazovanj VLBI (Very Long Baseline Interferometry), da razmerje med dejansko opazovanimi odkloni in odkloni, ki jih predvideva splošna relativnost, kar 0,99992 ± 0,00023 (izjemna natančnost). Tako je bila dramatična napoved iz leta 1919 tudi retroaktivno utemeljena.
Enega prvih poskusov slikanja mrka in detekcije odklona svetlobe bi naj izvedel že Erwin Finlay-Freundlich, iz Astronomskega observatorija Berlin. Freundlich se je leta 1914 (to je še pred Einsteinovim pravilnim izračunom odklona svetlobe) odpravil slikat mrk na Krim, vendar se je prej začela prva svetovna vojna. Preden je prišlo do mrka, je bil aretiran kot vohun (a že po nekaj dneh so ga Rusi internirali nazaj v Nemčijo). Tudi ekipa iz observatorija Lick v Kaliforniji ni uspela pripotovati na krimski mrk - a je tako deževalo. Njihovo kamero so, kljub zamudi, zaplenili Rusi in tako ni bilo odprave na mrk v Venezuelo leta 1916.
Po Eddingtonovi objavi "uspešnih" meritev odklona svetlobe ob Soncu (med mrkom 1919), je Einstein takoj postal svetovna ikona - genij - iz zmedenega skuštranega znanstvenika so ga mediji preobrazili v superzvezdo sveta znanosti – v »preroka«. A mnoge temelje novi fiziki, kot se razbere iz zgodovine znanosti, so postavili že številni raziskovalci pred njim. Podobno kot je Newtonu trasiral pot že J. Kepler in delno R. Hooke, pa še kdo ...
Če sklenemo – mrki so nam v veliko pomoč pri iskanju položaja Zemlje in človeka v vesolju in hkrati pri iskanju odgovorov, kateri fizikalni opis sveta je primernejši:
– ali klasični Newtonov opis sveta, v katerem vladajo absolutni linearni čas v prostoru treh dimenzij in hipna sila gravitacije vezana zgolj na maso, ki določa dinamiko vesolja in teles v njem,
– ali Einsteinov opis sveta, kjer masa-energija ukrivljata prostor-čas štirih dimenzij (gravitacija je smo posledica ukrivljenosti, gravitacijski pospešek in pospeševanje nekega sistema sta ekvivalentna), kjer sta čas in merjenje razdalj vezana na opazovalca in ukrivljenost prostor-časa (večja je ukrivljenost, recimo zaradi velike mase, gravitacije – počasneje teče čas – čas je tudi odvisen od relativne hitrosti), tudi o dinamiki teles in svetlobe odloča ukrivljenost prostor-časa, gravitacijska motnja potuje s hitrostjo svetlobe (posledica so gravitacijski valovi – letos je za detekcijo valov bila podeljena Nobelova nagrada), hitrost svetlobe pa je hkrati zgornja meja za pošiljanje informacij, energije po prostor-času; koncept ukrivljenega prostor-časa tudi elegantno razreši dilemo, zakaj se lahko nemasni delec (foton) krivo giblje po vesolju, razloži gravitacijsko lečenje.
Geometrija mrka, ocena širine sence, hitrost in smer mrka, trajanje mrka, energijska bilanca, določanje razdalj med Luno, Zemljo, Soncem, razmerja med dimenzijami teles, bodočnost mrkov glede na oddaljevanje Lune – upočasnjevanje rotacije Zemlje, spektroskopija korone, opazovanje Sonca nasploh, potrditev splošne teorije relativnosti ... - vsaj nekatere od omenjenih vsebin bi lahko našle prostor v učnih programih srednjih šol, delno osnovnih, tudi v nekaterih študijskih programih.
Mrki so torej veličastni eksperimenti, ki jih narava »mimo proračuna» pripravi za nas – na nas je le, da jih opazujemo in vključimo v šolske programe.
To je še en razlog, da se vidimo na naslednjem mrku.
Šentvid, jan. 2018
Zorko Vičar