

Slike:

Komet C/2002 C1 Ikeya-Zhang posnet 11.3.2002, teleskop LX200, 10",f/6.3, CCD ST7, 30 s, ob 19:05.

Komet C/2002 C1 Ikeya-Zhang posnet 11.3.2002, teleskop LX200, 10",f/6.3, CCD ST7, 60 s, ob 19:09.

Komet C/2002 C1 Ikeya-Zhang posnet 11.3.2002, teleskop LX200, 10",f/6.3, CCD ST7, 60 s, ob 19:12:50.

Komet C/2002 C1 Ikeya-Zhang posnet 11.3.2002, teleskop LX200, 10",f/6.3, CCD ST7, 120 s, ob 19:21.

Komet C/2002 C1 Ikeya-Zhang posnet 11.3.2002, teleskop LX200, 10",f/6.3, CCD ST7, 120 s, ob 19:37.

Komet C/2002 C1 Ikeya-Zhang posnet 11.3.2002, teleskop LX200, 10",f/6.3, CCD ST7, 30 s, ob 19:55.
Spremna beseda.
O prelepem kometu C/2002 C1 Ikeya-Zhang ste najbrž že vse slišali. *Ali res, glej dodatek? Tudi na
Gimnaziji Šentvid smo se ob jasni noči - mraku 11. 3. 2002 odločili, da kljub neugodni legi kometa,
naredimo nekaj testnih CCD posnetkov in ni nam bilo žal. Kljub izjemno skromni višini, komet je bil
namreč na začetku snemanja le okrog 16 stopinj nad zahodnim obzorjem (mestnimi lučmi), ob koncu
snemanja pa le še 6 stopinj, se je komet razkril v mnogih podrobnostih, v vsej svoji lepoti, na
izjemno jasnem, čistem nočnem nebu. Podrobnosti v repu kometa se krasno razločijo in žametni
prehodi med prameni repa so vse prisotne izjemno navdušili. Tudi pogled skozi daljnogled oz.
teleskop ni dosti zaostajal za CCD posnetki. Nauk - šolski astronomi, preosvetljenost urbanih
okolij ne sme biti izgovor, da ne opazujemo in slikamo nebesnih objektov, ne bojte se mestne
svetlobe, čeprav se seveda astronomi z njo nikoli ne bomo popolnoma sprijaznili.
Pri snemanju so bili prisotni: Kristina Meršak, Rok Mališnik, Nina Pogačnik, Zorko Vičar, Klemen
Blokar, Matija Kastelic, Gregor Vertačnik, Nejc Dolinšek, Nejc Janež, Igor in Mitja Šiška, Matjaž
Alič, Peter Mihor, Dejan Kolarič, David Božič.
Za Astronomski krožek Gimnazije Šentvid, Zorko Vičar
*Dodatek.
Ko sem zapisal prvi stavek spremne besede, sem še enkrat pogledal v zadnji dve Spiki in glej ga
zlomka, o kometu C/2002 C1 Ikeya-Zhang res piše kar nekaj, a zdi se mi, da bi le bilo dobro dodati
še kakšen stavek in mogoče še "posladek" za uporabo v šoli. O zgodovini kometa bi dodal samo tole,
da je bil viden že leta 1661 in najbrž leta 1273 in tudi 877. Leta 1661 so že poznali osnove
mehanike gibanj teles v Sončevem sistemu (Keplerjevi zakoni) in meritve orbite kometa so bile
že toliko natančne, da so lahko danes brez težav ugotovili, da gre za že videni povratni komet
(C/1661 C1). To je s 309 meritvami potrdil, 25. februarja 2002, Brian G. Marsden
(Smithsonian Astrophysical Observatory). Zdi se, da je ta komet prvi s tako dolgo
povratno dobo (~340 let), ki je bil že večkrat opazovan. Vsi ostali kometi s še daljšimi
povratnimi dobami so bili, glede na dosegljive zgodovinske vire, opazovani samo enkrat.
Pa še nekaj računanja, "posladek".
Srednješolci pri fiziki že v drugem letniku spoznajo energijski zakon in pogoje, kdaj se vsota
kinetične in potencialne energije ohranja ( - energija se ohranja, ko je delo vseh zunanjih sil,
razen dela teže, enako 0, za planete velja W=Wk+Wp=mv2/2-GMm/r = konst).
Pri matematiki pa
ponavadi v tretjem letniku že obdelajo elipso
(x2/a2+y2/b2=1).
To dvoje se da lepo združiti in
uporabiti pri oceni nekaterih spremenljivk kometa. Zakaj je to dobro? Če že za drugo ne, se
učenci vsaj enkrat srečajo s sočasno, sinhrono uporabo tako matematike kot fizike, ne pa da
slišijo prvi Keplerjev zakon, pa nimajo pojma o elipsi in pri nebesni mehaniki tako zmeraj
računajo samo naloge, kjer se eliptični tir nebesnega telesa poenostavi v krožnico. Pri matematiki
pa jim elipsa služi zgolj kot še en lik, ki ga je potrebno poznati za maturo, nič pa se ne zavedajo,
da pravzaprav tudi naš planet in mi skupaj z njim, potujemo okrog Sonca po elipsi. Seveda tukaj ne bomo
obdelali kompleksnih merilnih in matematičnih metod za določitev tira nebesnega objekta, ampak si bomo ogledali,
kako lahko uporabimo "neke čudne" oznake in številke, to so elementi tira telesa, ki jih najdemo na Internetnih
straneh o kometih, asteroidih ... Ti elementi tira so že rezultat obdelav na desetine ali stotine meritev, z
večine profesionalnih observatorijev.
Konkretno lahko recimo na Internet strani
"http://cfa-www.harvard.edu/iau/Ephemerides/Comets/2002C1.html" o kometu C/2002 C1 Ikeya-Zhang najdemo naslednje podatke:
e =0.990027, Incl.=28.1217o, q=0.507085 AE, Node(an)=93.3677o, Peri.(w)=34.6718o.
Med podatki je še nekaj parametrov, vsekakor sta med njimi tudi datum in čas prehoda skozi perihelij Tp (Perihelion passage)
in srednja anomalija ( Mean anomaly, M=(G*Mson/a3)1/2(t-T)=E-e*sin(E), ** glej izpeljavo na koncu),
ki je merilo za čas, normiran v kotnih enotah.
Srednja anomalija torej izraža čas in je za točno določitev lege kometa na orbiti nepogrešljiva, a najbrž presega vsebino in
želje tega prispevka in bomo skušali shajati brez nje.
Kaj pomenijo posamezne kratice in kako si jih lahko predstavljamo, si lahko ogledate v nadaljnjem tekstu podprtim s slikami.
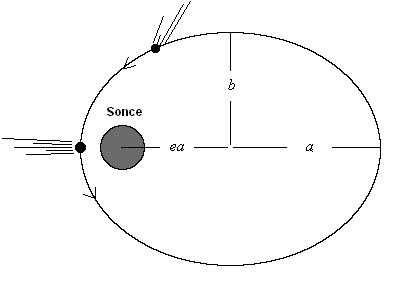 |  |
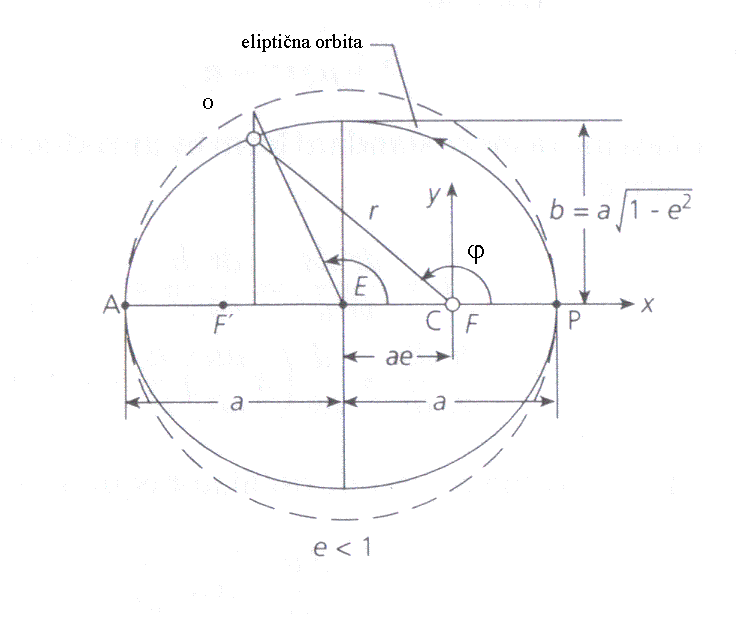
Eliptični tir kometa (levo zgoraj), Sonce je v enem izmed dveh gorišč elipse, a je
velika in b mala polos elipse.
Ekscentričnost elipse e je definirana kot e=(a2-b2)1/2/a in
zavzema vrednosti med 0 in 1 (0 <= e < 1).
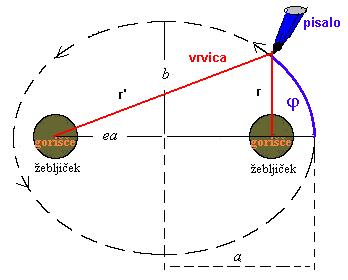
Slika desno zgoraj prikazuje, kako najlažje učencem predstavimo naravo elipse.
Recimo, na ploščo iz plute položimo list,
vanj zapičimo dva žebljička, med njima napeljemo vrvico, jo s pisalom napnemo,
in vlečemo krivuljo, rezultat je elipsa. Žebljička
predstavljata gorišči elipse. Iz geometrije na skici velja, da je vsota r'+r konstantna, je
enaka dolžini vrvice in vsota izražena z veliko polosjo elipse
znaša r'+r=2a. Sedaj nam ne bo težko izračunati razdalje med središčem in
goriščem ((a2-b2)1/2=e*a). Tudi izpeljava klasičnega,
kanoničnega, zapisa enačbe elipse (x2/a2+y2/b2=1)
nam ne sme povzročati težav,
v astronomiji pa nam največkrat pride prav stožnična
oblika v polarnih koordinatah: r=a(1-e2)/(1+e*cos(φ)).
Nakažimo korake izpeljave obeh enčab.
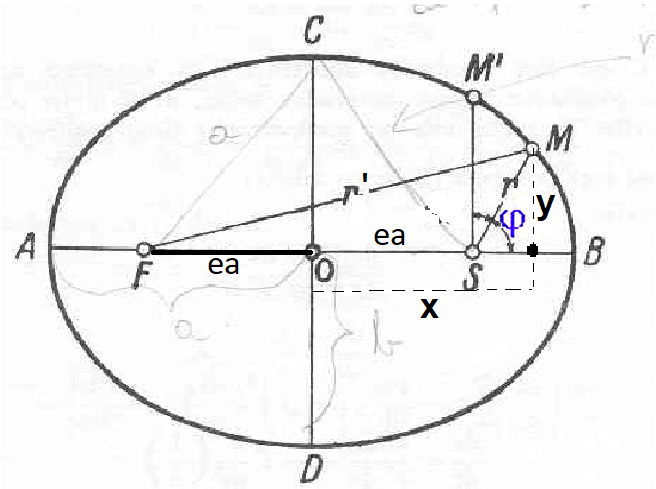
Iz slike razberemo:
e=(a2-b2)1/2/a, oziroma a2-b2 = (e*a)2
r' + r = 2a
r2 = (x - e*a)2 + y2
r'2 = (x + e*a)2 + y2
x = e*a + r*cos(φ)
---------------------------------------------------
Ker sta r' in r neznanki, zapišemo enačno r' + r = 2a v obliki
r' = 2a - r in jo kvadriramo, od to sledi.
r'2 = 4a2 - 4a*r + r2
za r'2 in r2 vstavimo že zapisane izraze izražene z x, y in e*a.
(x + e*a)2 + y2 = 4a2 - 4a*r + (x - e*a)2 + y2
- od koder sledi,
x2 + 2x*e*a + (e*a)2 + y2 = 4a2 - 4a*r +
x2 - 2x*e*a + (e*a)2 + y2
- odštejemo kar je levo in desno enakega (x2, y2, (e*a)2),
po krajšanju z a in 4 tako ostane,
r = a - e*x
Ker iščemo kanonično obliko enačbe (z x, y in a, b), kvadriramo zadnjo enačbo in vanjo vstavimo r izražen z x in y ter e*a.
r2 = a2 - 2a*e*x + (e*x)2
x2 - 2x*e*a + (e*a)2 + y2 = a2 - 2x*e*a + (e*x)2
- preoblikujemo enačbo in tako ostane:
x2 + y2 - (e*x)2 = a2 - (e*a)2
- za e2 vstavimo (a2-b2)/a2,
od koder dobimo,
x2 + y2 - x2(a2-b2)/a2
= a2 - a2(a2-b2)/a2
- izraz pomnožimo z a2, odštejemo kar se da ..., tako ostane:
a2x2 + a2y2
- x2a2 + x2b2 = a4
- a2(a2 - b2 )
- sledi,
b2x2 + a2y2
=
a2b2
- enačbo delimo s produktom a2b2 in tako dobimo
končno kanonično obliko enačbe:
| x2/a2 + y2/b2 = 1 |
| r=a(1-e2)/(1+e*cos(φ)) |
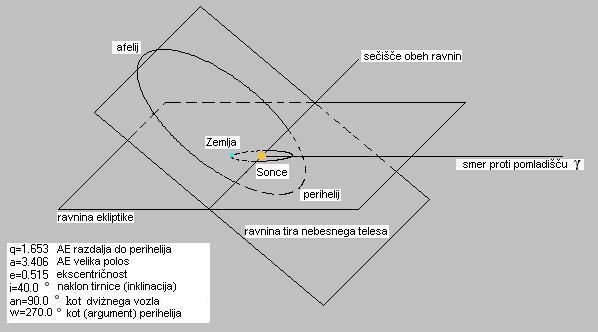
Slika ponazarja dogajanje na dveh nebesnih ravninah in sicer na ravnini ekliptike, po kateri
potuje naš planet in na ravnini, po kateri recimo potuje komet.
Ravnini se sekata, Sonce leži na sečišču ravnin in hkrati v gorišču obeh tirov. Da si lahko
prostorsko predstavljamo nek objekt v našem osončju in mu tudi sledimo,
moramo poznati elemente tira, orbite. Vrednosti elementov na sliki so take, da bi bila
predstava čim lažja. Kratica AE je astronomska enota (srednja razdalja Zemlja-Sonce
in znaša 149 597 870 km = 499,006 sv.s). Določiti moramo naslednje elemente:
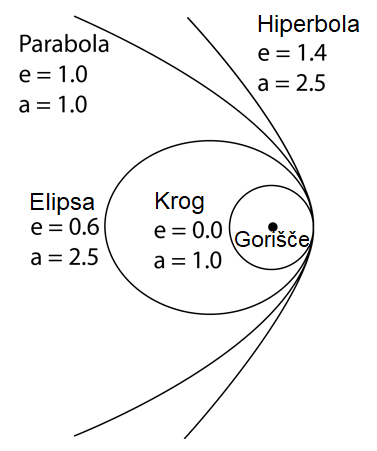
- i naklon tira ali inklinacijo (inclination), kot med ravninama
- e ekscentričnost elipse (orbital eccentricity) e=(a2-b2)1/2/a
- a veliko polos elipse (semimajor axis ), ali pa q razdaljo med Soncem in perihelijem (perihelion
passage distance), q = a-ea = a(1-e)
- node ali (an) kot dvižnega vozla (ascending node), to je kot med pomladiščem
(premico Sonce - pomladišče) in presečiščem obeh ravnin.
- w ali (Peri.) kot perihelija, argument perihelija (argument of perihelion), to je kot med
sečiščem ravnin in perihelijem (premico Sonce - perihelij)
- za dinamiko telesa je potrebno poznati še Tp (perihelion passage), to je čas prehoda
skozi perihelij in srednjo anomalijo M (Mean anomaly).
K naštetim parametrom se zaradi motenj dodajo še nekateri, zmeraj pa moramo tudi
upoštevati, da pomladišče zaradi precesije Zemlje neprestano spreminja lego,
potuje po nebu. Tako se tudi koordinate, oziroma nekateri elementi tira, stalno spreminjajo.
Zato se zmeraj doda informacija za katero obdobje (epoho) podatki veljajo.
Da bi si lažje predstavljali elemente tira kometa C/2002 C1 Ikeya-Zhang, se poigrajte
z Internet stranjo:
http://home.wxs.nl/~dmsweb/video/orbit.html
ali pa si oglejte spodnjo sliko, ki je rezultat takega privlačnega igranja.
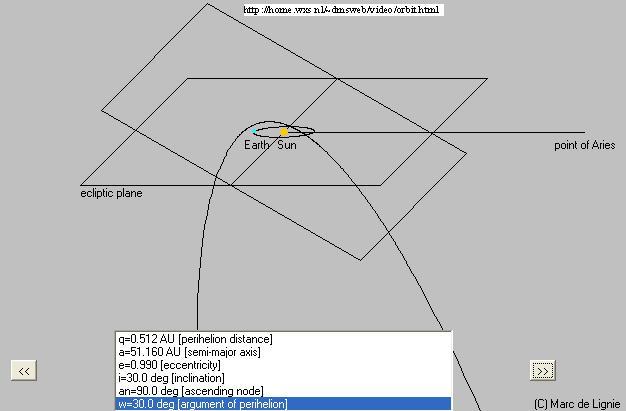
Zgornji sliki primerjaj med sabo, tako boš dobil prostorski občutek za pomen elementov tira,
pri določitvi poti nebesnih objektov. Sliko smo dobili tako, da smo v
Java program vstavili elemente tira, ki so zelo blizu vrednostim za komet
C/2002 C1 Ikeya-Zhang.(program dopušča le približne vrednosti). Program je na:
http://home.wxs.nl/~dmsweb/video/orbit.html.
Vrnimo se zdaj k naši računski vaji. Iz elementov tira lahko izračunamo kar nekaj količin.
1) Podani imamo vrednosti q in e, zveza med a, e in q je (glej sliko elipse):
q = a-ea = a(1-e).
Če vstavimo Internetne podatke v izraz a=q/(1-e), dobimo za velikost glavne osi vrednost
a = 50.85 AE (AE je astronomska enota). Za primerjavo, Pluton je od
Sonca povprečno oddaljen okrog 39,5 AE. Največja razdalja kometa od Sonca je torej
a+(a-q) in znaša več kot 100 AE, kar je daleč onstran trenutno znanega
planetnega roba, daleč onkraj Plutonove orbite.
2) Mala polos elipse znaša b=a(1-e2)1/2=7,16 AE. Za primerjavo,
razdalja Jupiter - Sonce v
povprečju znaša 5,2 AE. Zdaj že imamo dovolj podatkov, da lahko
v zmanjšanem merilu skiciramo orbito kometa, dobili bomo francosko štruco, s Soncem zelo
blizu krajčka.
3) Iz tretjega Keplerjevega zakona izračunajmo še obhodni čas kometa. Ta zakon povezuje veliko
polos elipse a in obhodni čas T, povezava je naslednja: a3/T2 = konst.,
za Sončev sistem kar dobro velja a3/T2 = 1(AE)3/1leto2.
T2=a3/konst=(leto2/AE3)*(q/(1-e))3,
če vstavimo podatke v enačbo, dobimo po korenjenju za
obhodni čas kometa vrednost T = 362,56 let. Ta vrednost se kar dobro ujema
s časom, ki je potekel od leta 1661, ko je bil komet nazadnje viden, oziroma s časi med leti:
877, 1273, 1661. Seveda na tirnico kometa vplivajo tudi planeti s svojo gravitacijo,
kar se tudi pozna na spremembi obhodnega časa.
Še pripomba na tretji Keplerjev zakon. Ta zakon je le približek, a za komete, ki imajo
majhno maso glede na Sonce, zelo dobro velja. Newton je zakon z vpeljavo
osnovnih zakonov mehanike in gravitacije izpopolnil. Dopolnjen zakon se glasi:
T2=a3(4p2/(G(m1+m2)) ), m1 in m2 sta masi teles, ki sta
gravitacijsko vezani. V našem
primeru ena masa pripada Soncu, druga pa zelo majhnemu kometu (glede na Sonce),
tako da lahko maso kometa brez zadržkov zanemarimo in uporabimo originalni
Keplerjev izraz.
4) Poglejmo še, kaj lahko potegnemo iz energijskega zakona (potrebovali bomo naslednje podatke:
M=2*1030 kg je masa Sonca, m je masa kometa,
G = 6.672*10-11 Nm2kg-2 je gravitacijska konstanta).
Potencialna energija v afeliju je Wpa = -GmM/(a+ea), v periheliju pa Wpp = -GmM/(a-ea).
Kinetična energija v afeliju je Wka = mva2/2, v
periheliju pa Wkp = mvp2/2,
Celotna energija kometa je W = Wp + Wk = -GmM/(2a), izpeljava sledi na koncu, točka 5.
Iz zgornjih povezav lahko izračunamo hitrosti v afeliju va in periheliju vp.
Zvezi sta: mva2/2 = GmM/(a+ea) - GmM/(2a),
mvp2/2 = GmM/(a-ea) - GmM/(2a).
Izraza poenostavimo: va2=(GM/a)((1-e)/(1+e)), vp2=(GM/a)((1+e)/(1-e)).
Za hitrost v afeliju dobimo vrednost va = 296 m/s v periheliju pa
vp = 59086 m/s » 59 km/s. V periheliju je hitrost res ogromna. Za primerjavo, hitrost
potovanja Zemlje
okrog Sonca znaša približno 30 km/s. Zemlja je očitno najhitrejše in najcenejše prevozno
sredstvo, ki si ga sploh lahko privoščimo.
Vrnimo se h kometom. Hitrost kometa ni odvisna od njegove mase in orbiti kometa
vztrajno sledijo tudi masivnejši prašni delci, ki predvsem zaradi Sončevega vetra
in posledično izbruhov, odpadajo od kometa. Povratni komet se tako z vsakim povratkom v
prisončje zmanjša, lahko pa tudi razpade (komet Shumaker-Levy je ob srečanju z
Jupitrom pod vplivom plimskih sil razpadel in leta 1994 padel na Jupiter, »lep dogodek«).
Sledenje prašnih delcev orbiti kometa in (morebitno) Zemljino sekanje kometove orbite,
sta tudi vzroka za vsakoletno periodično ponavljanje meteorjev (utrinkov). Če Zemlja seka
glavo razpadlega kometa, pa pride celo do meteorskega dežja ali nevihte. Hitrosti,
s katerimi priletijo prašni delci v atmosfero Zemlje, so odvisne od smeri vpada. Hitrosti
so tako lahko celo manjše od same hitrosti Zemlje (hitrosti se odštejeta), večinoma pa so
večje. Mogoče so najbolj znani roj Perzeidi (10.-12. avgust), relativna hitrost Perzeidov
glede na Zemljo je okrog 59 km/s.
Perzeidi so ostanki kometa Swift Tuttle - 1862 III (Doomsday-Comet, komet sodnega dne).
5) Rekli smo, da je energija nebesnega telesa, ki periodično potuje okrog Sonca kar
W = Wp + Wk = -GmM/(2a). Nakažimo, kako pridemo do te povezave.
Do rezultata se dokopljemo preko izjemno pomembnega izreka o ohranitvi vrtilne količine.
Na žalost se to poglavje v srednji šoli ponavadi preskoči (na hitro,
vrtilna količina za točkasto telo je vmr=hitrost*masa*ročica, za perihelij in afelij velja:
vpm(a-ea)= vam(a+ea)). Če vrtilne količine ne poznamo, pa si lahko pomagamo z
drugim Keplerjevim zakonom, ki pravi, da se ploščinska hitrost telesa (kometa) ohranja.
Ali drugače, zveznica Sonce-komet opiše v enakih časih enake ploščine.
Iz zadnje trditve, po kratki miselni telovadbi, pridemo do naslednje povezave:
vp(a-ea)= va(a+ea), kar pa je enak rezultat kot pri uporabi zakona o ohranitvi
vrtilne količine.
Dejansko je drugi Keplerjev zakon le posledica ohranitve vrtilne količine.
Zdaj bo pa lažje, imamo dve neznanki (va in vp) in tudi dve enačbi, recimo da najprej
izrazimo hitrost perihelija vp = va(1+e)/(1-e). Hitrost vp vstavimo v enačbo za ohranitev
energije W = mva2/2 - GmM/(a+ea) = mvp2/2-GmM/(a-ea) in iz nje
izrazimo hitrost v afeliju va
(dobimo: va2=GM(1-e)/(a+ae) ). Rešitev za va2 vstavimo nazaj v energijsko
enačbo, jo poenostavimo in končno prisopihamo do željene rešitve:
W = Wp + Wk = mva2/2 - GmM/(a+ea) = GM(1-e)/(2(a+ae)) - GmM/(a+ea) = -GmM/(2a).
Izrazimo še vrtilno količino z veliko polosjo a in ekscentričnostjo e.
Vrtilna količina v afeliju je:
L = mva*a(1+e) in še kvadrat: L2 = m2va2*(a+ae)2
Izrazimo še kinetični del energije mva2 z vrtilno količino L:
mva2/2 = L2/(2m(a+ae)2) - ta zapis vstavimo v polno energijo W.
Wp + Wk = mva2/2 - GmM/(a+ea) = -GmM/(2a)
Tako dobimo naslednji izraz:
L2/(2m(a+ae)2) - GmM/(a+ea) = -GmM/(2a)
Izrazimo L2:
L2 = (2m(a+ae)2)*(GmM/(a+ea) -GmM/(2a))
= GMm2(a2(1+e)2)(2/(2a))*(2 - e - 1)/(1 + e)
= GMm2a(1 + e)(1 - e)
Končna poezava med vrilno količino L, masama teles M in m, veliko polosjo
a (včasih jo označimo tudi z A)
in ekscentričnostjo e, je:
L2 = GMm2a(1 - e2) = GMm2A(1 - e2)
Ta izraz pride prav recimo pri računanju precesije perihelija:
δφ = 6πG2M2m2/(c2L2)
= 6πGM/(c2A(1 - e2))
Za telesi m in M, ki imata primerljivi masi, upoštevamo reduciano maso
μ = mM/(m + M)
(kar je korekno, ker velja
splošno za vsa razmerja velikosti teles m in M) in
upoštevamo še doplonjen izaz za vrtilno količino L z reducirano maso μ, velja
[ L2 = Gμ2(M + m)A(1 - e2) ]
, tako dobimo za precesijo perihelija dopolnjeno univerzalno enačbo:
δφ = 6πG2M2m2/(c2L2)
= 6πG(M + m)/(c2A(1 - e2))
Več o precesiji perihelija planetov najdete
na strani:
Zakaj astronomija
- in zakaj tudi v šoli? (XIII)
Oglejte si tudi - izpeljava Keplerjevih zakonov, uporaba Laplace–Runge–Lenz vektorja
Sedaj bi lahko še nadaljevali, recimo zapisali hitrost v poljubni točki
v=((G*M/a)*((2*a/r)-1))1/2 .
S pomočjo enačbe elipse (r=a(1-e2)/(1+e*cos(φ)) )
in z uporabo srednje anomalije
(cos(φ)=(cos(E)-e)/(1-e*cos(E)),
sin(φ)=sin(E)*(1-e*e)1/2/(1-e*cos(E))
), bi lahko enačbi orbite priredili
časovno odvisnost,
ki je uporabna za programiranje, animacije ... Vsa ta matematika pa že presega meje
prispevka, z njo se lahko poprime kak programer. Na
http://www2.arnes.si/guest/gljsentvid10/okni.html je nekaj animacij napisanih zgolj v
Javascript-jeziku, kjer so
bile testirane enačbe iz teksta.
Seveda tukaj nismo nič komentirali, da če je telo gravitacijsko vezano, je njegova energija
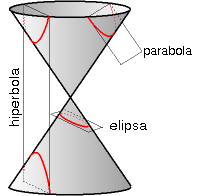
negativna (W=-GmM/(2a), gibanje po elipsi ali krožnici), če je energija 0, se telo
giblje po paraboli (Wk = -Wp), in če je energija večja od 0, se telo giblje po hiperboli.
Marsikaj je v prispevku privzeto in poenostavljeno. Nekaj osnov, potrebnega znanja,
bi morali pridobiti v srednji šoli, sicer pa so podrobnejše izpeljave lahko predmet nekega
drugega prispevka. Vsekakor pa taki računi ne bi smeli predstavljati večjih težav nekomu,
ki se kiti z maturo in na nek način bi osnove nebesne mehanike morale biti sestavni del pouka.
Ali je taka tudi realnost naših šol?
Vsak tak astronomski dogodek bi lahko bil vključen v pouk matematike in fizike, recimo z osnovnimi izračuni o orbiti, hitrostih, s primerjavami ...
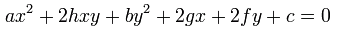
Nazaj na domačo
stran.