Naslednja poglavja so za nekoliko zahtevnejše bralce ali pa tudi ne (odvisno, kaj vas zanima)!
Večina vsebin se dotika povezave med osnovnimi delci narave,
skrivnosti izvora atomov, bodočnosti in dinamike vesolja in čudeža
življenja, ki je povezano z dolgotrajno preobrazbo Zemlje (zorenjem našega planeta).
Vmes pa skočimo še v svet fizike velikih hitrosti in kvantnih delcev, brez katere se težko razloži
fenomen
osnovnih pojavov v nas in okrog nas. Podane so tudi vaje iz astronomije,
ki jih lahko izvede vsaka šola - tudi, če se zgolj preko preprostih
razlag pouči učence o fiziki, ki nam razkriva vesolje kot ga zaznamo s prostim očesom
ali skozi teleskope in spektroskope, fotografije ...!
Preden se dotaknemo današnjih oblik življenja, zgradbe celice, dihanja in prenosa energije v celice,
se vprašajmo, zakaj najbrž življenje
ni nastalo takoj po velikem poku - začetku vesolja?
Razen vodika in večine helija
po velikem poku ni bilo kaj veliko ostalih elementov (zgolj nekaj litija,
zanemarljivo število težjih elementov kot so berilij, bor … ).
Oglejte si poglavje -
nekaj razvojnih stopenj vesolja, nastanek atomov (H, He: 75%/25%), Higgsova vloga,
Heisenbergova nedoločenost.
Zakaj pa sam vodik in helij najbrž nista - v obdobju, ko je temperatura vesolja padla na cca 20 K
in so se tvorili prvi nevtralni atomi in zvezde, preprosti planeti ... - tvorila preprostega življenja?
Ker je sam helij žlahtni plin in se ne veže rad v molekule (elektronegativnost ima zelo majhno [sploh se je ne da oceniti] napram
recimo kisiku, ki jo ima 3,5 po Paulingovi lestvici). Helij je najmanj reaktiven izmed vseh elementov - tako ima tališče
pri -272,20 °C (pri 2,5 MPa). Torej se ubogi vodik ni imel s kom povezati v kako
molekulo. Raznolikost atomov je na začetku vesolja bila res pičla (vodik in žlahtni samosvoj vase zaprt samotar helij),
da bi lahko govorili o kakem življenju, strukturah organskih molekul, kot jih poznamo danes (ko je že eksplodiralo
kar nekaj generacij supernov in vsaj delno obogatilo vesolje s težjimi elementi: dušik, kisik, ogljik, fosfor, železo ...).
Če je torej že nastalo (nastaja) kako življenje iz vodika in helija, je to pri zelo nizkih temperaturah (pod minus 270 °C)
- kjer je energijska bilanca
pri kemijskih reakcijah zelo skromna ... Govorimo torej zgolj o hipotezi, ki pa je zelo dobra osnova za razmišljanje,
kaj vse rabimo v vesolju, da tam nekje na nekem majhnem planetu ob skromni zvezdi nastane čudež, ki ga imenujemo življenje.
Kratka zgodovina nastanka težkih elementov, tudi atomov našega telesa. V središču zvezd,
kot smo že omenili, se torej tlak in temperatura povečata (v Soncu na 15 milijonov K)
do te mere, da se recimo protoni, v kombinaciji z nevtroni, zbližajo do razdalje,
ko prevlada močna jedrska sila nad odbojno silo med pozitivnimi protoni in se tako
vodikova jedra zlivajo v helijeva (2 nevtrona in 2 protona združena v jedru helija
tehtata nekaj manj kot pred reakcijo, pred združitvijo – razlika je Δm. Kot že rečeno - to
lastnost imenujemo tudi masni defekt, ki pa sprosti ogromno energijo E = Δmc2. Tako recimo
Sonce lahko stabilno sveti milijarde let in torej zvezda kar sama vzdržuje visoko temperaturo
in tlak nasproti lastni teži zvezde – zvezda tako ne ugasne, se ne sesede). Ko se pridela
zadosten delež helijevih jeder in začne primanjkovati vodikovih, se začne zvezda sesedati,
tlak in temperatura v sredici spet naraščata. Če tlak in temperatura (okrog 100 milijonov K)
v središču dosežeta primerne vrednosti, stečejo še bolj zapletene reakcije, ko se helij nadalje
pretvarja v ogljikova, kisikova in dušikova jedra (steče t. i. dušikov-kisikov-ogljikov cikel
– to je hkrati kemijski začetek cikla potencialnega življenja na planetih, naših nebesnih
potepuhih, ki se znajdejo ob pravem času na pravem kraju – kot se je to zgodilo nam ob Soncu,
ki recimo beremo Spiko ...).
Vse elemente v vesolju (razen vodika in večine helija - ki sta nastala kmalu po velikem poku)
so v svojih sredicah pridelale zvezde.
Če se zaradi dovolj velike mase (zvezde z začetno maso okrog 10 M☉
in več) temperatura v sredici dvigne na nekaj milijard K, pa nastajajo atomska jedra do velikosti
železa. Železo je (bomo razložili zakaj) tako imenovani končni produkt (vsi težji elementi od
železa, tudi zlato, so nastali, nastajajo ob trkih zvezd, ob eksplozijah supernov). Zelo masivna
zvezda je tako po notranji zgradbi podobna čebuli - iz železovega središča navzven imamo naslednje
plasti: silicijevo, dušikovo, kisikovo, ogljikovo, helijevo, v zunanji plasti zvezde pa vodikovo
plast. Končna faza zvezde večje od 1,4 M☉
je po eksploziji supernove nevtronska zvezda (elektroni
in protoni se zaradi velikih sil stisnejo v nevtrone – jedro take zvezde je velik sestavljen
nevtron). Pri večjih masah, nekaj Sončevih, pa se lahko tvori tudi črna luknja, s katere po
definiciji tudi svetlobe ne uide (M —r— hν, izpeljava po domače, preko energije delca za drugo
kozmično hitrost ob zvezdi z maso M, na razdalji r, velja:
mv2/2 – GmM/r = 0 => r = 2GM/v2 =>
kaj pa, če je ta delec foton svetlobe, potem velja Schwrzschildov polmer dogodkovnega horizonta
črne luknje rs = 2GM/c2, od tega polmera proti središču ni več moč ujeti 'odhajajoče' svetlobe, informacij,
kaj se dogaja v črni luknji, idejo je podal že John Michell leta 1783), zato črno luknjo opazimo
le posredno, ko iz okolice preko akrecijskega diska (teoretično telo, črna luknja, z »neskončno«
gostoto - singularnost) srka vase materijo iz okolice (v rotacijskem disku padajoče materije se
zaradi trenja in sproščene energije zazna tudi rentgensko sevanje, močno magnetno polje in posledično
polarizacija ...).
Sledi nekaj osnov astrofizike - popestrenih s slikami,
ki nam strnjeno razkrivajo različne tipe zvezd, njihove življenjske poti, zaključne
faze in načine, kako precej enostavno, preko spektrov, določimo sestavo oddaljenih zvezd in njihove
okolice.
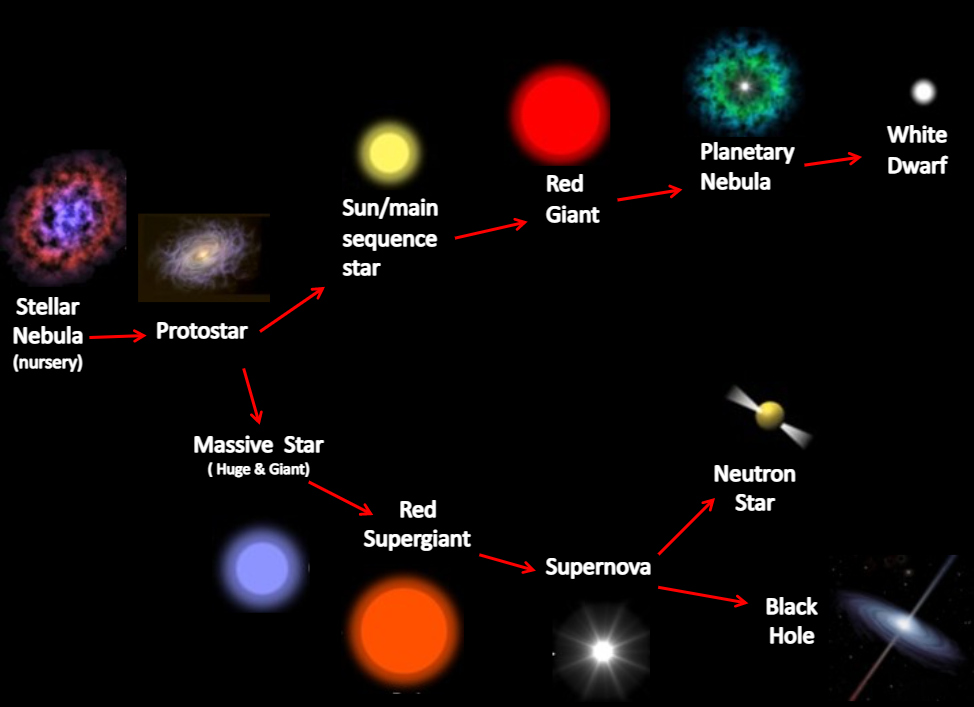
Razvojne faze lahkih in masivnejših zvezd so precej različne. Masivnejše zvezde tudi
veliko prej (manj kot v 5 milijardah let) pridejo do končne faze – supernove (nevtronske
zvezde ali črne luknje) – zato masivnejše zvezde najbrž niso primerne za planetne sisteme
primerne za razvoj visoko razvitega življenja. Dolgožive zvezde (10 milijard let in več)
podobne Soncu pa so tozadevno veliko obetavnejše, kar se tiče naseljivih kamnitih planetov.
Masivnejše zvezde pa so z nukleosintezo težjih elementov in izmetom le teh med eksplozijami
(med eksplozijami nastajajo tudi težji elementi od železa), omogočile nastanek zvezd prve
generacije, recimo kot je Sonce, bogatih s težkimi elementi, kar omogoča nastanek
kamnitih planetov.
Heliju in ostalim težjim elementom, ki nastanejo v zvezdah
in pri eksplozijah ter trkih zvezd
pravimo tudi fuzijski pepel
(ogljik C, kisik O, dušik N, fosfor P, kalcij Ca ... do železa Fe
nastanejo v zvezdah - naprej do zlata Au ali aurum, urana U ...
ti elementi pa nastanejo med eksplozijami, trki zvezd).
Ker pa so mnogi prej našteti kemijski elementi tudi
gradniki življenja, nas samih, seveda tudi planetov (potepuhov), bomo mi
ta proces opisali bolj slikovito, celostno. In sicer brez vsakega
dvoma lahko trdimo, da so zvezde »Groharjevi sejalci življenja«,
preko fuzije seveda, ki pa jo omogoča gravitacija.
V nastanku kemijskih elementov se tako
nujno povežeta gravitacija, sila velikih teles in sila, ki tvori atome,
to je močna jedrska sila, ki veže nukleone (protone in nevtrone) v atomska jedra.
Ta proces je potrebno nujno razlagati celostno, v paru: gravitacija - nukleosinteza.
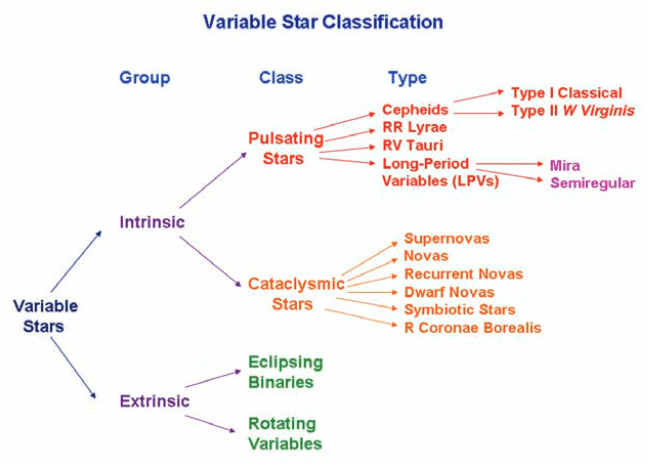
Klasifikacija spremenljivih zvezd! V resnici se vsaka zvezda od svojega nastanka
pa do zadnje faze razvoja – ko se, zaradi porabe lažjih atomskih jeder,
v sredicah zvezd preneha nukleosinteza atomskih jeder in pride do burnega
kolapsa – cel čas nekoliko spreminja (spreminja se izsev, tudi Soncu,
temperatura, velikost, prihaja do nihanj - pulziranja, tukaj so še dvojne
zvezde, akrecija, trki, končna faza v obliki nov, supernov ... ).
Le zvezde mase okrog Sončeve ali nekoliko manjše (in zvezde prve populacije),
se zdijo dovolj stabilne – majhne spremembe izseva, kar okrog 10 milijard
let dolga stabilna nukleosinteza – da lahko v svoji orbiti gostijo potencialne
kamnite planete (potepuhe), kjer se postopoma razvijejo pogoji za kompleksnejše
oblike življenja (po približno štirih milijardah let).
Vir slike: https://chandra.harvard.edu/graphics/edu/earth_scientist_stars.pdf

Barve planetarne Obročaste meglice (M57 v Liri) proti zvezdam ali kako enostavno
določiti kemijsko sestavo meglice. To izjemno poučno in hkrati enostavno vajo lahko
naredi vsak učitelj s pomočjo učencev in z uporabo uklonske mrežice, teleskopa
in navadnega fotoaparata. Razklonjena Obročasta meglica je na sliki vidna le nekajkrat,
saj oddaja vidno svetlobo zgolj v nekaj barvah (kot recimo vzbujeni plin v laboratoriju, recimo vodik –
take vaje so se včasih delale v naravoslovnih oddelkih gimnazij). Dve najizrazitejši barvi
meglice sta rdeča (zaradi vodika) in modra (zaradi kisika). Ti se na levi strani od
središča slike pojavita kot skoraj prekrivajoči se sliki v rdeči in modri barvi.
Slika desno od sredine pa prikazuje meglico v kombinaciji barv, kot jo vidimo običajno, oziroma jo ujame
fotoaparat nameščen na teleskop.
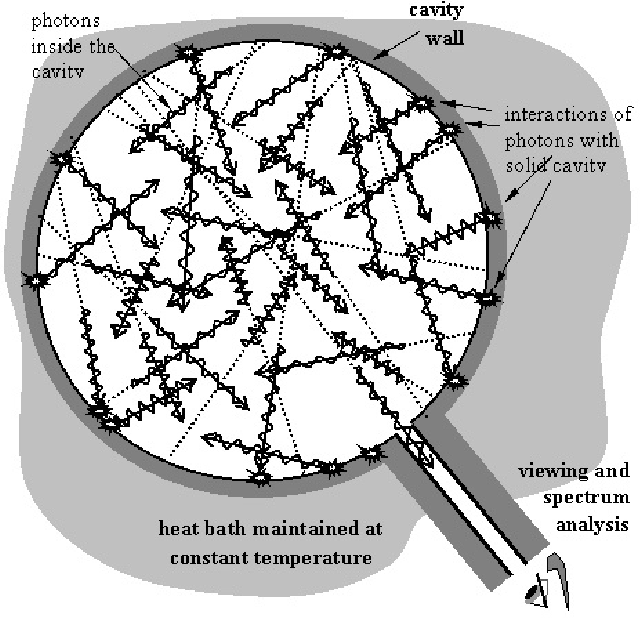
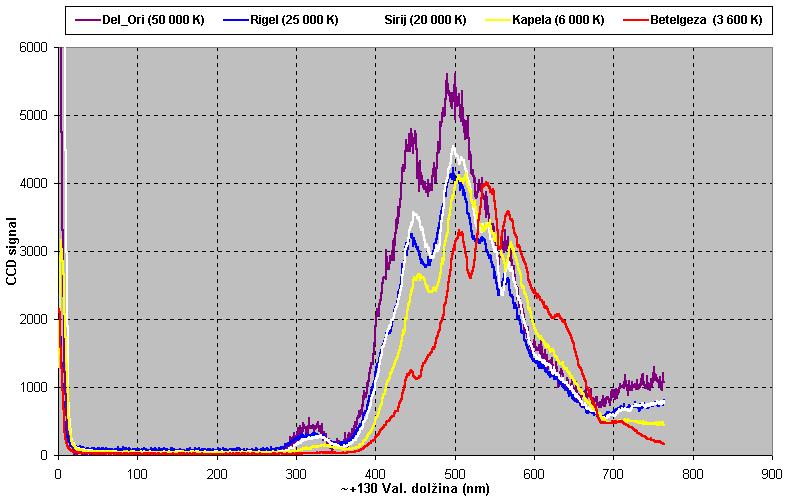
Spektri zvezd pa so skoraj zvezni (opazijo se absorpcijske črte), saj oddajajo večino svoje
svetlobe v barvah po vsem vidnem spektru (sevajo kot črno telo). Te barve torej ustvarjajo
skoraj neprekinjeno črto, zato se zvezde pojavijo v spremstvu večbarvnih črt. Razklon
(disperzija) svetlobe objekta v barve je znanstveno zelo koristna metoda, ki lahko razkrije
kemijsko sestavo objekta, njegovo hitrost in oddaljenost. To vajo pa lahko naredi tudi vsak učenec.
Vir slike: apod.
Čudovito planetarno meglico M57 lahko z učenci tudi opazujemo v ozvezdju Lire,
s teleskopi premera 150 mm ali več, kar od pozne pomladi pa do zime. Na sredi
meglice je bela pritlikavka (ki se v amaterskih teleskopih ne zazna, razen na posnetkih)
– tak konec zvezde čaka tudi naše Sonce.
Spodaj je shema najpreprostejšega spektrografa
na uklonsko mrežico brez reže (t. i. »slitless spectrograph«),
ki pa vseeno zmore didaktično tako
izjemne slike (posnetke spektrov), kot je recimo ta iz strani APOD. Sledi tudi preprosta
slikovna razlaga metod, za analizo oddaljenih zvezd (atomske sestave, temperature, mase,
hitrosti, starosti zvezd).
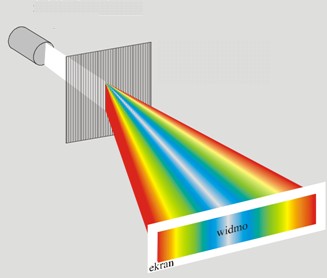
Uklonska mrežica razdeli svetlobo po barvah, najbolj se uklonijo daljše valovne dolžine (rdeča).
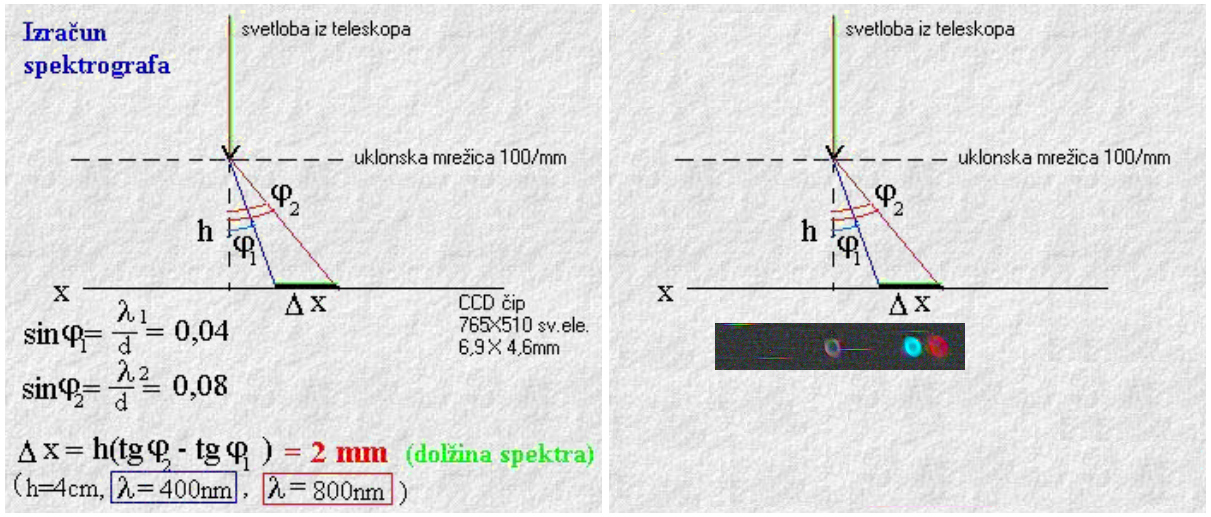
Shema in izračun "slitless spectrographa" (brez reže), pred leti izdelanega na Šentvidu. Naredi
ga lahko vsakdo, ki ima možnost namestiti digitalni fotoaparat na teleskop, pred
detektor svetlobe (recimo nekaj cm pred fotočip - v odprtino fokuserja) pa
namestimo uklonsko mrežico (mi smo uporabili mrežico s 100 režami na mm –
ima jo vsaka šola v fizikalnem kabinetu) – in to je vse kar rabimo. Pred leti
smo uporabili CCD kamero, ki pa je seveda večina šol nima. Prej se še poučimo o
gostoti svetlobnih elementov foto čipa, malo poračunamo, testiramo in v pol ure,
izjemno učinkovit in praktično zastonj, spektrograf že deluje. Z njim lahko
posnamemo absorpcijske spektre zvezd (začuda tudi emisijske spektre nekaterih meglic).
Kot bomo videli spodaj, lahko potrdimo tudi Planckov in Wienove zakon. Zagotovo si
šole ne morejo privoščiti dragih astronomskih spektrografov - "slitless spectrograph"
(brez reže)
pa za pedagoške namene čisto zadostuje. Ločljivost take naprave je skromna -
za zvezde tipično nekaj nanometrov – a za prikaz bistva ta podatek ni relevanten.
(za prikaz absorpcijskih spektrov zvezd, emisijskih spektrov nekaterih meglic,
potrditev Planckovega in Wienovega zakona to zadostuje). Uklonsko mrežico lahko
učenci uporabijo tudi direktno preko opazovanja plinskih svetilk (vidijo
multiplicirano sliko svetilke, uklonjeno po emisijskem spektru svetlečega plina).
Princip delovanja takega preprostega spektrografa pa lahko učencem pokažemo kar
preko projekcije svetilke na bel zaslon z navadno lupo in uklonsko mrežico.
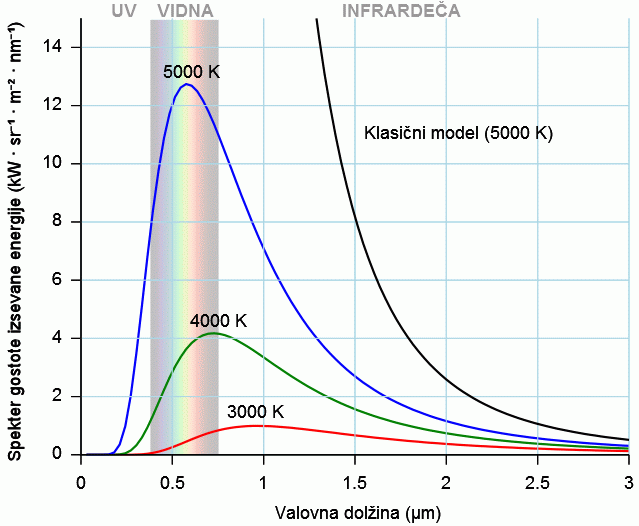
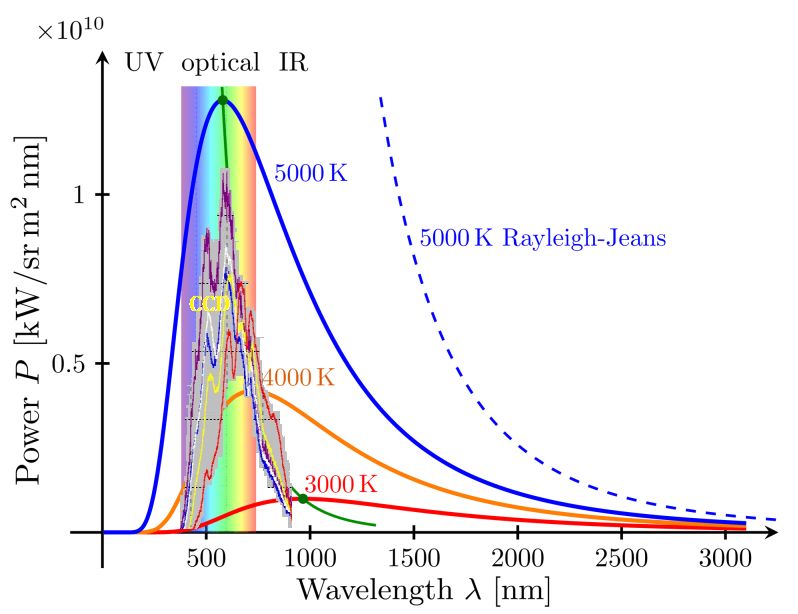
Graf zgoraj ponazarja porazdelitev gostote toplotnega izseva po valovnih
dolžinah za idealna črna telesa z različnimi temperaturami. Tako porazdelitev najbolje
opisuje (že omenjeni) Planckov zakon. Lege maksimumov (in pripadajoče valovne
dolžine) izseva pa določa temperatura, kar opiše Wienov zakon
(λ*T=2897Kµm).
Danes Stefanov zakon o sevanju črnega telesa (j = σT4)
izpeljujemo iz
Planckovega zakona.
Spektralna gostota (po valovnih dolžinah) črnega telesa
je po Planckovem zakonu enaka:
dj/dλ = (2πhc2/λ5)(ehc/(λkT) - 1)-1
– lahko tudi sami narišete.
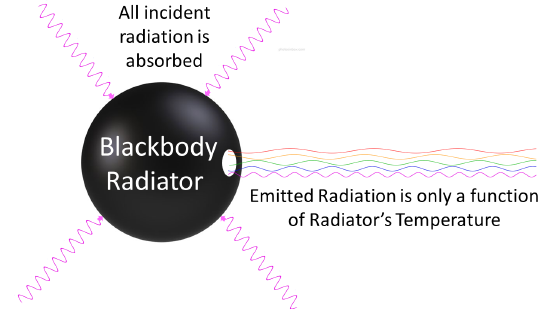
Planckova enačba predvideva, da bo črno telo sevalo energijo pri vseh frekvencah, uporabna pa je le,
če se pri meritvah upošteva dovolj veliko število fotonov. Sevalno polje črnega telesa se lahko
predstavlja kot fotonski plin, v katerem bo ta gostota energijskega toka ena od termodinamskih
spremenljivk plina. Vzor mu je bila Boltzmannova verjetnostna porazdelitev (tudi Maxwell-Boltzmannova),
ki je osnova kinetične teorije plinov, kjer se recimo natančno opiše porazdelitev kinetične energije
delcev plina (od tam tudi eksponent).
Ta zakon nam zelo pomaga pri študiju sevanja zvezd – določanje spektralnih
tipov in površinske temperature zvezd.
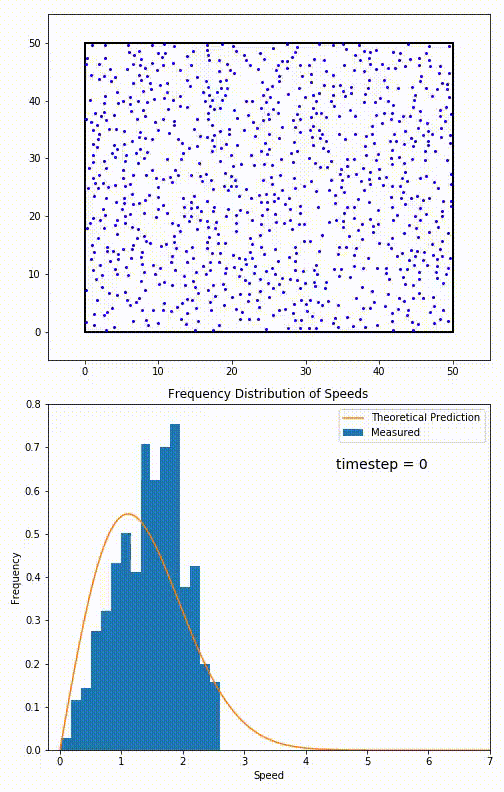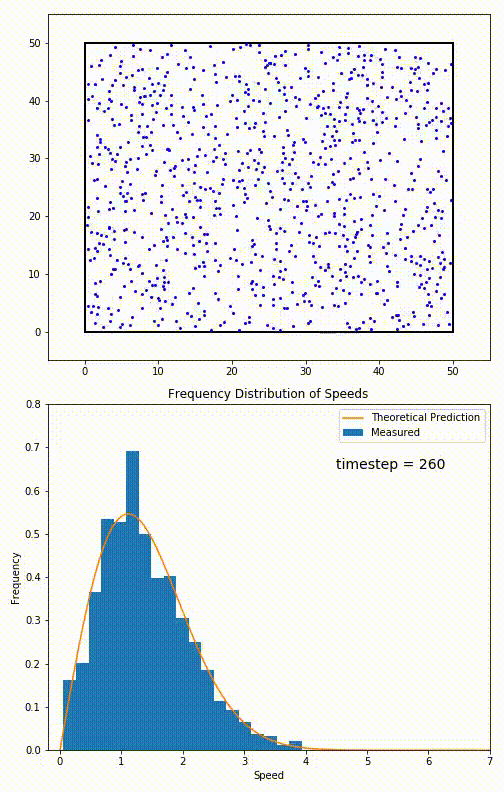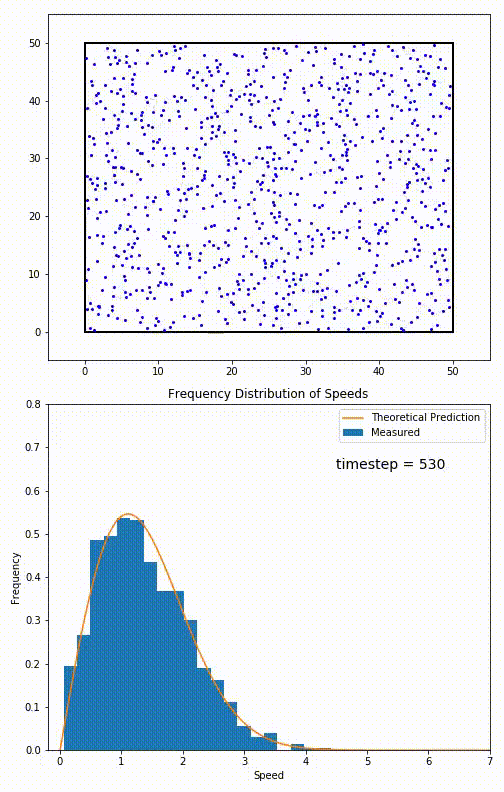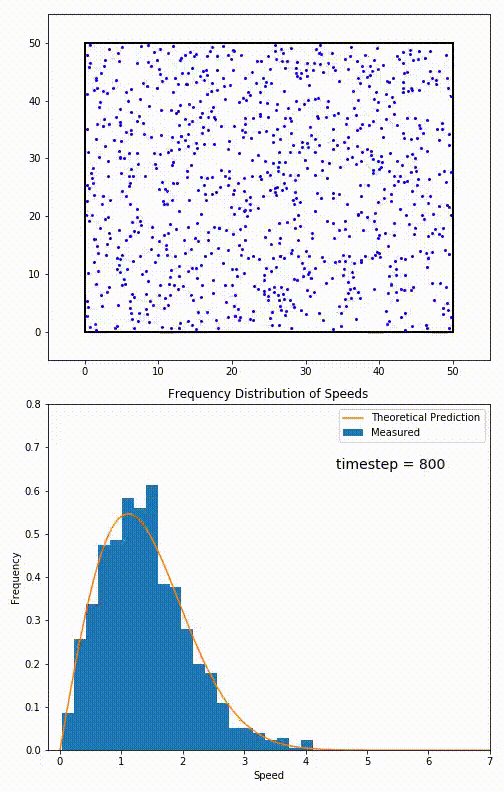
Simulacija 2D plina, ki ga zelo dobro opisuje Maxwell–Boltzmannova porazdelitev hitrosti delcev plina.
Za delce, omejene na gibanje v ravnini, je porazdelitev hitrosti podana s povezavo:
Ta porazdelitev se uporablja za opisovanje sistemov v ravnovesju (s = v). Vendar se večina sistemov
ne začne v svojem ravnotežnem stanju. Razvoj sistema proti njegovemu ravnotežnemu stanju ureja Boltzmannova enačba.
Nakažimo pot do Planckovega zakona
 |  |
 |
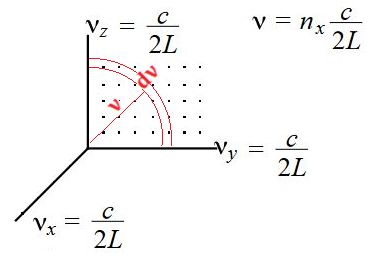
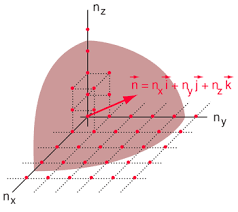


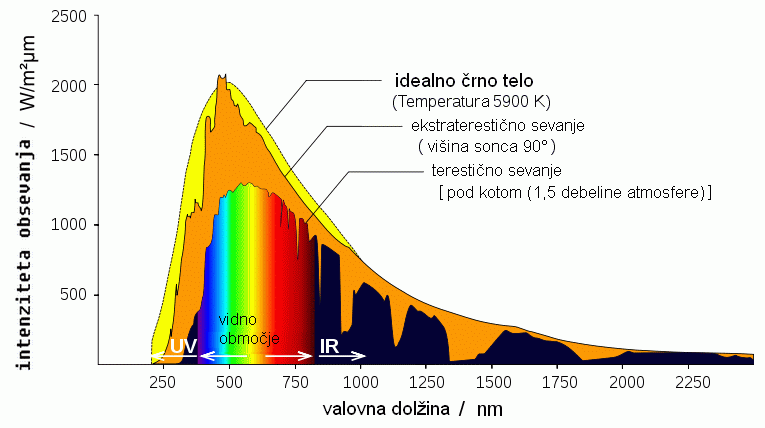
Energija terestičnih Sončevih žarkov (tistih, ki se prebijejo do površine Zemlje
skozi atmosfero) je najizrazitejša pri valovnih dolžinah, ki so značilne za rumeno in
zeleno barvo. Evolucija je naredila tako, da so tudi naše oči najbolj občutljive na
ti dve barvi. Nanometer
(nm = 10-9m)
je enota za merjenje valovnih dolžin, recimo svetlobe
(valovne dolžine, ki jih zaznamo ljudje, so od približno 380 do 780 nm). Spekter Sonca,
kot ga detektiramo na površini Zemlje, je kombinacija vplivov Sončeve ionosfere in
zemeljske atmosfere. Projekcija sevanja Sonca (poljubne zvezde) na film ali čip nam
razkrije svetlobni spekter, ki je poln temnih absorpcijskih črt (te črte so posledice
absorpcije ionosfere Sonca, delno pa tudi atmosfere Zemlje). Iz absorpcijskih črt
tako tudi detektiramo pline, ki obdajajo Sonce in so tudi del samega Sonca – slika
spodaj. Iz zamika črt proti rdeči ali modri barvi (iz Dopplerjevega pojava) pa lahko
določimo tudi hitrosti zvezd in ali se od nas oddaljujejo ali se nam približujejo.
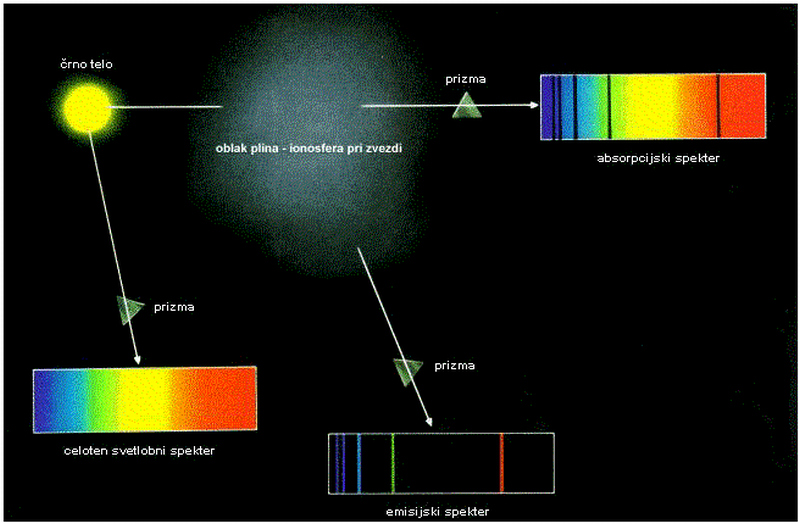
Nastanek emisijskega in absorpcijskega spektra (preprosta shematska razlaga,
svetlobo nam seveda v spekter lahko lomi tudi prizma). Emisijski spekter se
lahko posname recimo za planetarno meglico M57 (emisijske spektre si lahko
ogledamo ali posnamemo tudi za različne pline kar v šolskem laboratoriju in
tako umerimo naš spektrograf). Absorpcijske črte (rahle zatemnitve spektra)
pa lahko učenci zelo enostavno opazujejo kar pri Soncu – dovolj je že ozka
reža (lahko priprta vrata) in uklonska mrežica (lahko prizma), zrcalo za usmeritev
Sončevih žarkov na režo, ter zatemnjena soba z belim zaslonom, kamor se projicira
spekter.
 |  |
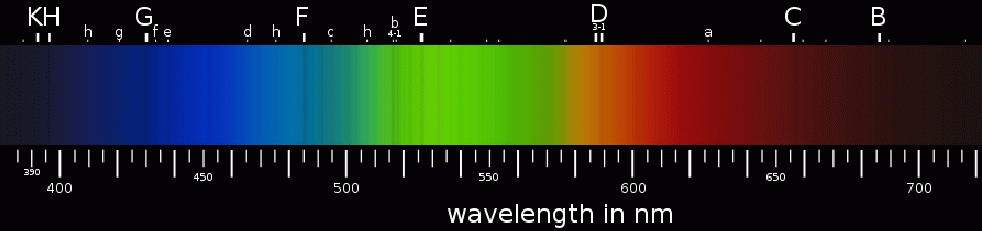
O (≥ 30,000 K - modra, ≥ 16 M☉) – H črte šibke, B (10,000–30,000 K - modro-bela, 2.1–16 M☉) – H črte srednje, A (7,500–10,000 K - bela, 1.4–2.1 M☉) – H črte močne, F (6,000–7,500 K - rumeno-bela, 1.04–1.4 M☉) – H črte srednje, G (5,200–6,000 K - rumena, Sonce, 0.8–1.04 M☉) – H črte šibke, K (3,700–5,200 K - rumeno-oranžna, 0.45–0.8 M☉) – H črte precej šibke, M (2,400–3,700 K - rdeče-oranžna, 0.08–0.45 M☉) – H črte precej šibke.
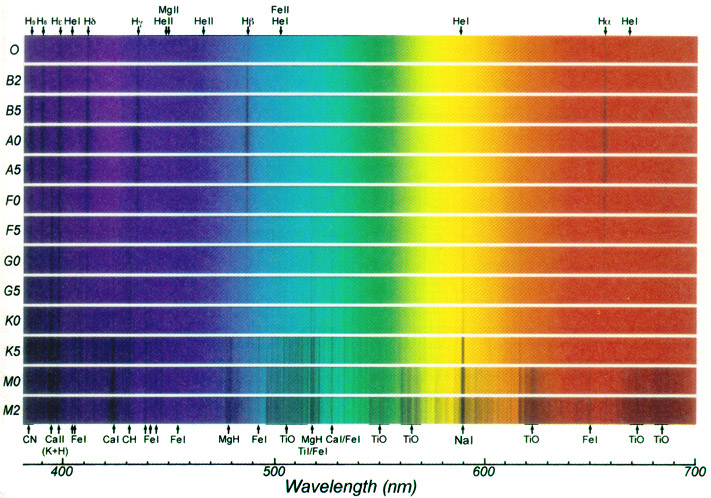
Znotraj vsakega od prvotnih sedmih zvezdnih razredov je gospa Annie Jump
Cannon določila še podrazrede (podtipe), oštevilčene od 0 do 9. Zvezda na
sredini med območjem F0 in G0 je zvezda tipa F5. Manjše številke podtipov so
bolj vroče zvezde v razredu. Sonce je zvezda tipa G2 s površinsko temperaturo
5800 K. Slika prikazuje spektralne značilnosti različnih zvezdnih razredov s podtipi.
Kako si pa recimo zapomnite 7 osnovnih tipov zvezd po temperaturah
in barvah (O, B, A, F, G, K, M) - recimo kar preko začetnic besed
prikupne fraze v angleščini:
"Oh, Be A Fine Girl, Kiss Me"
Rumeno Sonce spada v G tip - je torej "Girl" - s površinsko temperaturo
okrog 5769 K. Temperaturo površine Sonca je že leta 1879 pravilno izračunal naš rojak fizik Jožef Stefan
- kot prvi na svetu iz lastnega zakona o toplotnem sevanju teles.
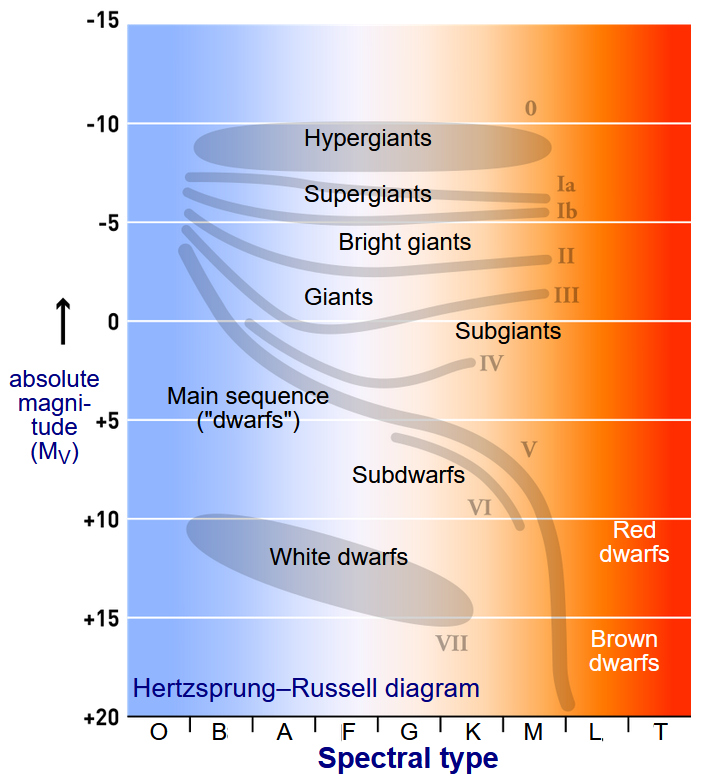
Hertzsprung-Russllov diagram je med astronomi zelo priljubljen prikaz
obnašanja bogate družine različno velikih in različno starih zvezd predstavljenih
na ravnini, kjer X os predstavlja površinsko temperaturo zvezd ali kar osnovne tipe
(O, B, A, F, G, K, M, dodana sta še tipa L in T za hladne pritlikavke).
Y os pa podaja njihovo absolutno magnitudo (sij) - absolutna magnituda Mv
je v astronomiji po definiciji sij zvezde, kot bi ga pomerili na oddaljenosti
10 parsekov (32,6 svetlobnih let). Na diagramu izstopa glavna veja – kjer se
zvezde nahajajo, ko v njihovih sredicah poteka fuzija (zlivanje lažjih v težja jedra).
Sonce bo vsega skupaj preživelo okrog 10 milijard let na glavni veji – to je spektralni
tip G. Nato se bo Sonce povečalo (napihnilo) in šlo v H-R diagramu desno navzgor
(tip - nekoliko hladnejša rdeča orjakinja), nakar se bo Sonce skrčilo (odvrglo
zunanje plasti – planetarna meglica) in se preselilo levo navzdol med bele (vroče)
pritlikavke. Zvezda z 10 masami Sonca (tip B) pa na glavni veji preživi zgolj
t = 1010(1/10)2,5 let = 32 milijonov let
(planeti v okolici take zvezde bodo težko razvili življenje podobno našemu na
Zemlji – recimo razvoj vretenčarjev, primatov). H-R diagram je odigral veliko vlogo pri
oceni starosti vesolja!
Ko recimo pomerimo sije in temperature zvezd neke kroglaste kopice zvezd in jih vnesemo v H-R diagram, lahko približno določimo starost kopice (različno velike zvezde se namreč porazdelijo po časovni skali stabilnega izseva, ki jo določa glavna veja in tam, kjer zvezde zapuščajo glavno vejo, koleno – zasuk v desno - se razbere starost in to iz znane enačbe t = 1010(M☉/M)2.5 let – to enačbo smo opisali že v Spiki 11, 2020).
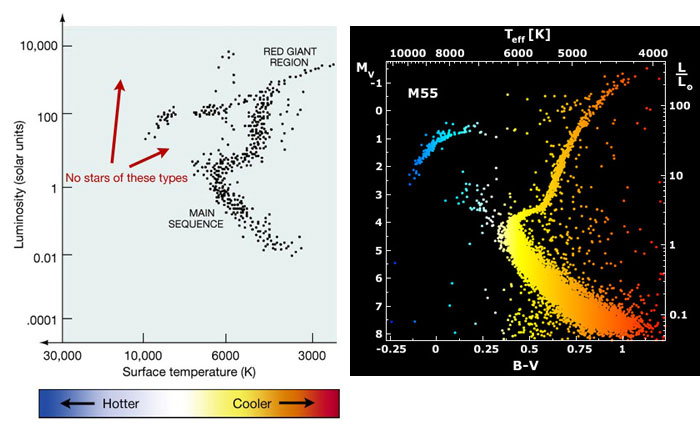
Kroglasta kopica M55 v Strelcu se v H-R diagramu lomi nekje pri masi Sonca – kopica
je torej stara vsaj toliko kot je življenjska doba Sonca na glavni veji. Izkazalo se
je, da je stara vsaj 12,3 milijarde let (blizu starosti vesolja) – da se lomi pri 0,92
mase Sonca. Starost vesolja se lahko ocenjuje tako preko kroglastih kopic
(najstarejši objekti), kot preko kozmologije (merjenja Hubble-Lemaîtrove konstante,
Dopplerjevega pojava) – obe oceni se kar dobro ujemata (kozmološka ocena je seveda
bližje resnici). Pred desetletji, ko metode merjenj še niso bile dodelane, se
je protislovno zdelo, da so kroglaste kopice v haloju naše Galaksije celo »starejše«
od vesolja (sin starejši od očeta - to je seveda bil nonsens, ki pa je zelo pripomogel
k izboljšanju metod določanja spektralnih tipov, temperatur zvezd, mas, oddaljenosti).
Ker je
Jožef Stefan iz meritev izluščil svoj znameniti zakon (20. marca 1879) o toplotnem
sevanju teles j = σT4, pa še nakažimo, kako
s pomočjo Planckova porazdelitve sevanja dobimo ta rezultat, velja:
j
= ∫(2πhc2/λ5)(ehc/(λkT) - 1)-1dλ.
Vpeljemo novo spremenljivko x = hc/(λkT), oziroma 1/λ = kTx/(hc), od koder velja dx = -hcdλ/(λ2kT),
v tem primeru integralna enačba dobi obliko j =
-(2πk4T4/(h3c2) )∫x3(ex - 1)-1dx.
Ker je integral ∫x3(ex - 1)-1dx = -π4/15, integrirali
smo v mejah 0 < λ
< ∞ (oziroma za x pa veljata meji ∞ < x
< 0), dobimo končni rezultat:
j = -(2πk4T4/(h3c2) )(-π4/15)
= 2π5k4T4/(15h3c2) = σT4.
Stefanova konstanta je: σ = 2π5k4/(15h3c2).
Izjemen uspeh Teoretične fizike v povezavi z meritvami !!!
V tej verigi do uspeha je igral pomembno vlogo torej tudi
Jožef Stefan,
ki je kot otrok delal pri očetu mlinarju. Zaradi nošnje vreč je imel povešeno ramo.
Mama je bila nepismena, a jo je študent Jožef naučil brati in pisati - izjemna gesta.
Na Dunaju je postal takrat najmlajši redni profesor, sodelavci in študentje so ga imeli izredno radi.
Bil je tudi mentor Ludwigu Boltzmannu.

Omenimo še, da je 1879 Jožef Štefan prvi na svetu (s pomočjo lastnega zakona o toplotnem sevanju teles
j = σT4)
pravilno določil temperaturo površine
Sonca To = 5775.9 K (Sonce je Zemlji najbližja zvezda, razbeljena plinasta
krogla - v resnici je iz plazme, zmesi ločenih atomskih jeder in elektronov),
ki nam daje praktično vse - energijo, ki jo porabljamo za rast, življenje,
je tudi gonilo vremena - vodnega kroga, določa seveda, kar je bistveno in smo že omenili,
tudi temperaturo planeta. Če bi bili nekoliko bližje ali dlje od Sonca, bi nam
bilo ali prevroče ali premrzlo in ...
Stefan je zakon o sevanju objavil 20. marca 1879 v članku
"O odnosu med toplotnim ravnovesjem in temperaturo"
(Über die Beziehung zwischen der Wärmestrahlung und der Temperatur)
v Poročilih z zasedanj dunajske Akademije znanosti.
Stefan je za izpeljavo uporabil Tyndallove (John) podatke,
kjer pa je temperature pretvoril v absolutne.
Štefan je že dojel pomen kinetične
teorije plinov in posledično uporabil absolutno temperaturo (vsako pospešeno gibanje
električnih delcev, kar trki v snovi so, povzroči sevanje em valov,
ki je seveda odvisno od temperature).
Če povzamemo zgodbo o toplotnem sevanju,
ki je posledica pospešenega gibanja električnih delcev in
kvantnih pojavov (termičnega gibanje gradnikov teles) - v vseolju pa
lokalno viša temperaturo gravitacija, ki recimo zgošča (stiska)
prah in pline v vroče zvezde!
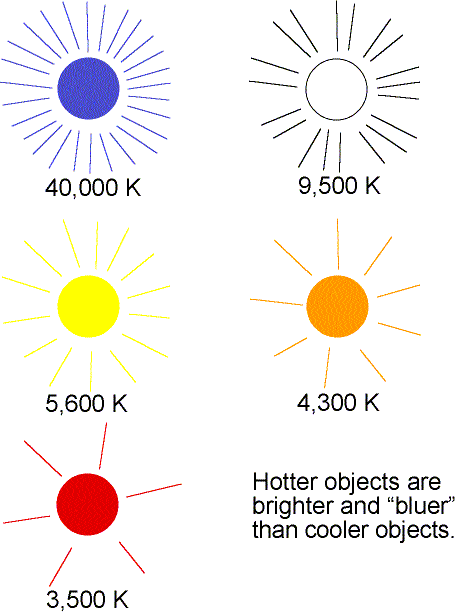
Vroče zvezde so svetlejše in bolj modre, kot hladne, ki so bolj rdeče.
Vmes so oranžne, rumene in bele.
Wilhelm Wien (živel 1864 - 1928) je odkril, da je vrh krivulje toplotnega spektra,
λmaksimuma. v nanometrih, povezan s temperaturo preko povezave
λmaksimuma = 2.9 × 106 / temperatura (v K) ali tudi
λ*T=2897Kµm.
To preprosto razmerje je zdaj znano kot Wienov zakon.
Z uporabo tega boste ugotovili, da hladni predmeti, kot so avtomobili,
rastline in ljudje, sevajo večino svoje energije v infrardečem sevanju.
Zelo hladni predmeti sevajo predvsem v radijskem pasu.
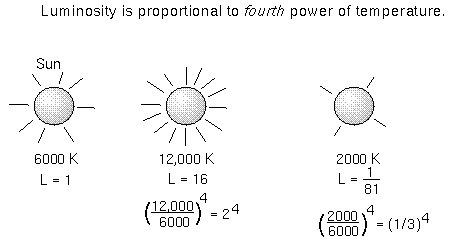
Ko seštejete vso energijo vseh kvadratnih metrov na površini predmeta, recimo zvezde,
dobite svetilnost (luminosity L ali tudi oznaka P) --- skupno količino energije,
ki jo vsako sekundo odda predmet.
Svetlost (L) = (skupna površina S) × (σ × temperatura4).
Če bi bilo naše Sonce samo dvakrat bolj vroče, kot je zdaj,
bi proizvedlo 24 = 16-krat več energije kot zdaj!
Ta zakon je prvi odkril slovenski Fizik Jožef Stefan (1835 - 1893).
Izsev Sonca je PSon = LSon = Lo = 4πRo2 jo
= 4πRo2 jna_Zemlji(AE/Ro)2 =
4πRo2 σ × To4 = 3.827×1026 W.
Gostota svetlobnega toka (energijskega toka, Sonce namreč seva tudi v
ostalih valovnih dolžinah) s površine Sonca je
jna_Soncu = σ × To4 = Lo/(4πRo2) =
jna_Zemlji(AE/Ro)2
= (1/0.00464912637)2 * 1371 W/m2 = 63430006 W/m2
= 63.43 milijonov vatov na kvadratni meter.
Polmer Sonca je približno Ro = 6.96 108 m = 0.00464912637 AE
≈ 109 Zemljinih polmerov.
Na vrh Zemljine atmosfere pa pade v povprečju
gostota svetlobnega toka s Sonca (seveda že razredčena, saj pada
z 1/R2):
jna_Zemlji = Lo/(4πAE2) = 1371 W/m2.
AE je astronomska enota, to je razdalja Zemlja - Sonce in znaša približno
AE = 150 106 km.
Na tej razdalji se je torej lahko razvilo življenje na planetu Zemlja, pri
vpadni gostoti svetlobnega toka j = 1371 W/m2.
Ko iščemo življenja drugje v vesolju, upoštevamo ta dva podatka
(na kateri razdalji od zvezde je gostota svetlobnega toka približno j =
1371 W/m2).
Vir slike: https://www.astronomynotes.com/light/s4.htm

Fizik, dr. Jožef Stefan (* 24. marec 1835, Sveti Peter pri Žrelcu, sedaj predel Celovca,
† 7. januar 1893, Dunaj). Odkrije znameniti zakon (Stefanov) o sevanju toplotnih teles:
j = P/S = L/S = σ × T4 - tako leta
1879 tudi prvi na svetu pravilno izračuna površinsko temperaturo (5776 K) našega Sonca,
zvezde, ki nam daje vse, to je življenje ... Globok priklon Jožefu Stefanu.
J. Stefan je poznal gostoto energijskega toka Sonca na Zemlji
( jna_Zemlji
= 1371 W/m2 - to vrednost smo ljudje seveda izmerili),
poznal je razdaljo Zemlja - Sonce,
to je astronomsko enoto AE in polmer Ro Sonca (oboje smo izmerili in
tudi poračunali
s pomočjo Keplerjevih zakonov); iz analiz meritev pa je zapisal
svoj znameniti zakon o toplotnem sevanju teles
j = L/S = σ × T4 .
Privzel je, da Sonce seva blizu črnega telesa in iz podatkov torej poračunal
površinsko temperaturo Sonca:
To = (jna_Soncu/ σ)1/4
= (jna_Zemlji(AE/Ro)2/σ)1/4 = 5776 K
Izjemen dosežek mlinarjevega sina in nepismene mame!
* Glej tudi:
Kalkulator JS - temperature planeta glede na razdaljo do zvezde, izsev zvezde, odbojnost, emisivnost planeta.
Ali obstaja kaka posebna dinamika nastajanja zvezd?
Odgovor je - JA OBSTAJA.
Vsekakor je na začetku po velikem poku bilo vesolje prevroče in hitrosti prevelike, da bi lahko gravitacija prevladala nad sredobežnimi
kinetičnimi energijami posameznih osnovnih gradnikov vesolja (nukleoni nastanejo
cca po 0.0001 s po velikem poku, helijeva jedra nastanejo po dobri minuti, nevtralni atomi pa
nastanejo po okrog 380 000 letih od rojstva vesolja, ko temperatura pada na okrog 3000 K). Tako so prve zvezde nastale komaj cca
100 milijonov let po velikem poku, ko je temperatura vesolja padla na cca 15 K. Galaksije pa so se začele oblikovati, ko je vesolje bilo
staro blizu pol milijarde let. S kopičenjem okoliške snovi so galaksije postajale večje in z veliko več novimi zvezdami in zato
tudi svetlejše. Toda pred štirimi milijardami let se je rojevanje zvezd začelo upočasnjevati. Danes,
po cca 13.8 milijarde let od rojstva vesolja, so galaksije relativno mirna področja (domovi za ostarele), kjer se glede na
začetno obdobje, tvori malo novih zvezd.
Ena od hipotez pripisuje to upočasnitev zvezdnim vetrovom, ki so, ko so galaksije postale dovolj naseljene z zvezdami, postali
tako močni, da so le ti začeli razbijati oblake plinov, ki bi jih potencialno gravitacija lahko
krčila v nove zvezde.
Za rojevanje zvezd torej potrebujemo hladne, dovolj goste oblake plinov, prahu. To pa pri prisotnosti močnih zvezdnih
vetrov ni mogoče. Poleg razbijanja večjih struktur oblakov, ti vetrovi celo grejejo sam plin.
Hkrati pa se tako lahko tvorijo določene spojine v medzvezdnem prostoru, recimo vodni led, ogljikov monoksid, dioksid, metanol, amonijak
(NH3)
ali formaldehid (CH2O) - tako lahko nastanejo aminokisline.
Ta teorija je še v preverjanju. A zvezde vsekakor ne nastajajo več tako hitro kot včasih.
Kaj to pomeni za nastanek novih planetnih sistemov in novega življenja?
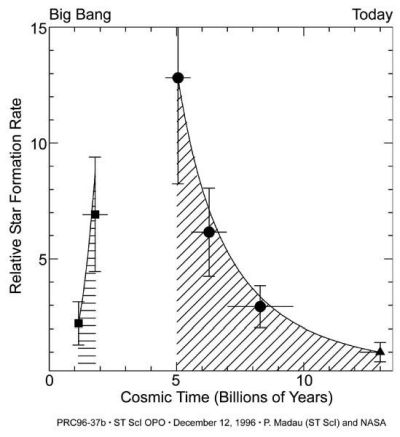
Zgornji graf prikazuje zgodovino hitrosti nastajanja zvezd v zadnjih cca 12 milijardah let - kmalu po rojstvu vesolja do danes (leto 1996).
Graf temelji na opazovanjih oddaljenih galaksij, ki so jih izvedli vesoljski teleskop Hubble in zemeljski observatoriji.
Navpična os podaja vrednosti za srednjo hitrost nastajanja zvezd kot večkratnike današnje hitrosti (vrednost enote je danes 1).
Podatki kažejo, da je bila ta stopnja morda celo 15-krat večja od današnje vrednosti. Vodoravna os prikazuje čas
v milijardah let, od velikega poka do danes.
Hubblovi podatki prikazujejo strm porast stopnje nastajanja zvezd, ki se je zgodil kmalu po velikem poku.
Zemeljski podatki pa kažejo,
da se je hitrost nastajanja zvezd strmo zmanjšala od pred približno 9 milijardami let do danes. Ni še nobenih opazovanj,
ki bi zapolnila vrzel med tema dvema nizoma podatkov, kjer bi se pobočja združila in oblikovala vrh aktivnosti rojstva zvezd.
To področje raziskav se je seveda nadaljevalo ..., spodaj so zadnje ocene in porazdelitve nastajanja zvezd skozi čas vesolja.
Vir:
https://science.nasa.gov/asset/hubble/second-graph-tracing-the-history-of-the-rate-of-star-formation/
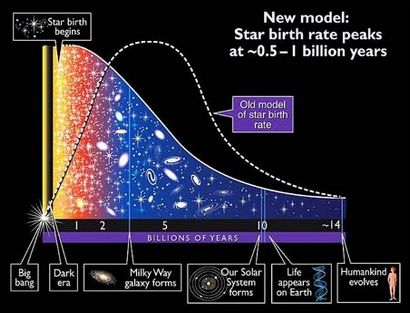
Graf prikazuje razvoj vesolja od samega začetka, torej od velikega poka, do razvoja človeštva - starejši in novejši model.
Avtorske pravice: A. Feild (STScI), 2019
Vir:
https://sci.esa.int/web/hubble/-/29330-star-formation-rate-since-the-big-bang
Še poučen članek iz:
https://www.astronomy.com/science/i-read-that-once-every-second-somewhere-in-the-universe-a-massive-star-ends-its-life-as-a-supernova-how-does-that-compare-to-the-rate-of-new-star-formation/
Pebral sem, da enkrat na sekundo, nekje v vesolju ogromna zvezda konča svoje življenje kot supernova.
Kako se pa ta podatek navezuje s stopnjo nastajanja novih zvezd?
Peter Hoffman, Bellmore, Združene države Amerike
S pomočjo ekipe za astronomijo | Objavljeno: 29. december 2014 | Nazadnje posodobljeno dne 18. maja 2023
Zvezde so se v zgodnjem vesolju tvorile z veliko višjo stopnjo rojevanja kot danes, vendar se rast ni ustavila.
V povprečju galaksije vsako leto rodijo več zvezd kot je eksplozij supernov.
Oglejmo si hitrost nastajanja novih zvezd v Galaksiji, ki nam je najbližja, smo del nje - v naši Rimski cesti.
Tehnologija omogoča astronomom,
da vidijo posamezne zvezde Rimske ceste, tako da lahko preštejejo vsa sonca (zvezde), merijo njihovo starost in merijo svetlost
(ki je povezana z njihovimi masami). Pred nekaj leti so znanstveniki uporabili vesoljski teleskop Spitzer za preučevanje
ravnine (diska) Rimske ceste - kjer se oblikujejo skoraj vse nove zvezde - in ugotovili stopnjo rodnosti od 0,68 do 1,45 sončeve
mase na leto. Raziskovalci običajno pravijo, da naša galaksija vsako leto pretvori material enega Sonca v novo zvezdo.
Če predpostavimo skupno stopnjo eksplozij supernov na sekundo, to pomeni, da se na leto zgodi skoraj
32 milijonov eksplozij teh masivnih
zvezd v galaksijah vidnega vesolja.
Te supernove izvirajo iz zvezd med približno 10 in 50-kratno Sončevo maso. Ta stopnja kaže,
da je v te supernove vsako leto vključenih približno 320 do 1,6 milijarde sončevih mas. Toda ta vrednost velja za
opazljivo vesolje, ki je ogromno.
Iz globokih opazovanj Hubblovega vesoljskega teleskopa - poleg računalniških simulacij kozmičnih struktur - astronomi
sklepajo, da je vesolje v svoji zgodovini oblikovalo od 100 do 500 milijard galaksij (Za naš preprostost izračun
uporabimo 100 milijard.). Če ima vsaka od teh galaksij ali je imela, stopnjo nastajanja
zvezd približno enega Sonca na leto, to pomeni, da pretvorijo desetine ali stotine več snovi v zvezde,
kot je supernov, ki eksplodirajo in nekaj mase odvržejo v vesolje.
Seveda je vesolje nekoliko bolj zapleteno,
kot namiguje osnovna matematika.
Nekatere galaksije, kot so medsebojno delujoče galaksije in galaksije z izbruhi zvezd, vsako leto tvorijo od
10 do 1000 sončnih mas zvezd, medtem ko druge, kot recimo stare eliptične, ne morejo več tvoriti zvezd. Poleg tega,
ko je bilo vesolje staro približno 3 milijarde let, so galaksije ustvarjale zvezde veliko hitreje kot danes.
Ko povprečimo prejšnje visoke stopnje nastajanja zvezd z današnjimi vrednostmi, še vedno dobimo stopnjo nastajanja zvezd,
ki je višja od stopnje supernov, kar je smiselno:
vse ustvarjene zvezde niso takega tipa, mase, da eksplodirajo kot supernove. Namesto tega sledijo
široki distribuciji in zvezde z nižjo maso so veliko pogostejše od zelo masivnih.
Ko izračunamo povprečje prejšnjih visokih stopenj nastajanja zvezd z današnjimi vrednostmi, še vedno dobimo stopnjo nastajanja zvezd,
ki je višja od stopnje eksplozij supernov, kar je logično: niso vse formirane zvezde takšne, da eksplodirajo.
Zvezde sledijo široki porazdelitvi in zvezde z nižjo maso so veliko pogostejše od zvezd z veliko maso (tudi naše Sonce je precej
skromne mase - kar omogoča Soncu dolgo fuzijo, cca 10 milijard let in s tem Sonce omogoča tudi razvoj življenja na Zemlji).
Liz Kruesi

Kvarke so odkrili preko sipanja elektronov na nukleonih, recimo v samem protonu –
eksperimenti Roberta Hofstadterja so dokazali, da proton ni točkasto telo
(Hofstadterjev članek iz leta 1956, objavljenem v reviji Reviews of Modern Physics,
"Electron Scattering and Nuclear Structure - Elektronsko sipanje in jedrska struktura".).
Preko oblike sipalnega diagrama so ugotovili, da so gluoni nosilci močne sile med kvarki,
in da hkrati nastajajo v protonu kratkoživi pari kvark-antikvark. Silo med kvarki
se ponazori z izmenjavo gluonov (poenostavljeno povedano, to niso prosti delci,
ampak delujejo kot neke vrste vzmeti, lepilo ali glue – po tem izrazu so gluoni
tudi dobili ime). Med samimi protoni, nevtroni, torej vsemi nukleoni v jedru pa
se izmenjujejo pioni
(mezoni, ki so tudi sestavljeni iz kvarka in antikvarka - ki pa ni nujno antidelec prisotnega kvarka, slika spodaj).
Te sile razložimo podobno kot podajanje žoge med šolarji (in žoga šolarje na nek
način tudi veže skupaj) in to (žoganje) je možno le do določene razdalje –
do katere tudi deluje močna sila. Povejmo torej, da je kvantna mehanika bolj
logična od klasične mehanike, saj klasična mehanika predpostavi, da sile kar
tako delujejo na daljavo. V resnici pa je torej zadaj zmeraj nek delec kot
nosilec sile ..., primer s podajanjem žoge je vsekakor odlična prispodoba
za razumevanje osnovnih sil. V okviru QED (quantum electrodynamics) nabiti
delci (recimo protoni) medsebojno delujejo z izmenjavo »virtualnih« fotonov,
ki pa ne obstajajo zunaj interakcije in so le nosilci sile. Še preprost primer.
Recimo pri pojemanju hitrosti elektrona v električnem polju (zaviranju), elektron
oddaja elektromagnetno valovanje – in to (elektromagnetno valovanje) lahko posredno
razumemo tudi kot delce polja. Kot recimo lahko električne delce pospešujemo
z laserskimi žarki ali ostalimi viri fotonov. Iz tega pojavnega in merljivega
fenomena se je na nek način rodila ideja o kvantizaciji elektromagnetnega polja -
Paul A. M. Dirac 1927 (matematični zapis je pričakovano nekoliko zapleten).
Od tu naprej se je ideja razširila na opis vseh osnovnih delcev in povezav med
njimi (recimo hadronov, to je protonov in nevtronov, ki so sestavljeni iz treh
kvarkov), kot neke vrste valovnih paketov in naenkrat je povezava med energijo in maso
(E = mc2)
postala v resnici samoumevna – kar pa se tudi direktno odraža v nukleosintezi težjih
atomov v zvezdah in pri meritvah nastalih delcev ob trkih delcev (hadronov) v
pospeševalnikih (CERN). Trenutno velja, da je le kakšen procent sveta atomov
moč pripisati klasični masi, recimo kvarkom (pa še za te ni jasno ali imajo zares
maso), vsa ostala »masa«, ki jo tehtamo s tehtnicami, je v resnici vezavna energija
kvarkov preko gluonov in notranja kinetična energija kvarkov, tudi nukleonov. Večina
hadronske »mase« torej prihaja iz gluonov, ki vežejo kvarke, ne pa iz samih kvarkov.
Čeprav so gluoni sami po sebi brez mase, imajo energijo - natančneje, kvantno
kromodinamično vezavno energijo (QCBE) - in prav ta tako bistveno prispeva k
celotni masi hadrona (recimo protona). Primer, proton ima maso približno
938 MeV/c2,
od tega preostala masa njegovih treh valenčnih kvarkov prispeva le približno
9 MeV/c2
(to je slab procent); večino preostale mase
(E/c2)
lahko, kot smo že omenili,
pripišemo energiji polja gluonov, ki so brez mase in kinetični energiji kvarkov.
Kako je z maso kvarkov, še ni dokončno dorečeno. V QCD se kvarki štejejo za
točkovne entitete z velikostjo nič. Od leta 2014 eksperimentalni dokazi kažejo,
da je kvark zagotovo manjši od 10-19 metra. Trenutno poznamo 6 kvarkov
(u, d, c, s, t, b).

»Mase« vseh 6 kvarkov ponazorjene z različno velikimi barvnimi krogci
(to so ocene). V spodnjem levem kotu sta prikazana proton (siv krogec)
in elektron (rdeč) – kot skala, zgolj za primerjavo. 'Top quark' (t)
je največji in ima maso ~173 GeV/c2. u (up) in d (down) kvark tvorita
protone in nevtrone – nukleone atomov. Tukaj so še s (strange),
c (charm) in b (bottom) kvarki.


Skica prikazuje zelo strnjen povzetek interakcij med subatomskimi delci,
opisan s standardnim modelom delcev (to so nedeljivi delci, zato se imenujejo
tudi osnovni delci narave, vesolja). Od teh delcev nam je domač recimo foton (svetloba),
malo manj elektron (e), a sestavlja (iz šole nam vsem znane) atome in še manj so
nam poznani kvarki (recimo u, d), a ti sestavljajo protone (uud) in nevtrone (ddu),
ki sestavljajo jedra atomov. Te tri kvarke (dveh tipov u in d) »lepijo« v protone
in nevtrone gluoni. Vse ostale delce narave se torej da sestaviti iz teh osnovnih
gradnikov narave – prikazanih na shemi (posamezni osnovni delci se seveda delijo
v podskupine). Higgsov bozon nam daje (je dal) maso (Higgsov bozon, delec - po
P. Higgsu - je bil uveden v standardno teorijo delcev in sil (1964), da bi razložili,
kako je bila med tvorbo vesolja porušena elektrošibka simetrija in je tako nastalo več
subatomskih delcev kot antidelcev (antimaterije) in zakaj imajo delci sploh maso – nastali so,
ker jih je upočasnilo Higgsovo polje; Higgsov bozon je torej nosilec polja,
ki v zgodnjem izredno vročem vesolju pripravi kvarke do sodelovanja, jih upočasni
in s tem gre del energije v maso – materijo po zvezi E/c2). V zgornji tabeli pa
nista omenjena hipotetična X in Y bozona – ki bi naj povezovala kvarke z leptoni
(kot je pozitron), kar bi naj omogočalo kršitev ohranjanja barionskega števila in
s tem omogočalo razpad protona. Barion (izhaja iz grščine in pomeni težek) je delec,
ki ga sestavlja liho število kvarkov, vsaj trije (kvark ima kvantno barionsko
število B = 1/3), recimo proton in nevtron imata barionsko število 1,
ker imata tri kvarke ( B = 1/3 + 1/3 + 1/3 = 1 ). Ohranjanje barionsko
števila pomeni, da je vsota vseh barionskih števil pred in po interakciji enako.
X in Y bozon pa bi lahko pri razpadu protona kršila to pravilo (kaj bi to pomenilo
za vesolje?). Še opis vloge W in Z bozonov. Šíbka jedrska síla omogoča razpad,
da se en delec pretvori v drugega. Recimo, da gre za pretvorbo nevtrona v proton
in delec ß- (elektron) ter
(νe) antinevtrino (ta pretvorba se imenuje tudi razpad
beta:
n => p + e- + νe).
V kvantni mehaniki ima vsaka sila svoje polje in delce, ki posredujejo to silo –
v tem primeru se imenujeta ta delca W in Z bozon (šíbka jedrska síla ima kratek doseg,
krajšega od močne jedrske sile, znotraj nukleona 10-18 m).
Vemo pa, da sta proton in
nevtron nadalje sestavljena iz kvarkov, torej gre pri razpadu nevtrona pravzaprav za
to, da se eden od kvarkov d, ki sestavlja nevtron, pretvori v kvark u, pri čemer nastane
bozon W- (pretvorba d kvarka v
u: d => W- + u ).
Sila in delec inflacije
Mnogi fiziki kot gonilo začetne inflatorne rasti vesolja korektno (glede na teorijo prenosa sil preko polj
in nosilcev polj) predlagajo novo
temeljno silo z lastnim poljem, posredovano z delcem, imenovanim inflaton (torej še en potencialni bozon).
Spet drugi predlagajo več polj z več delci. Čas bo pokazal, kdo ima prav, če sploh.
Kot smo že omenili, se posamezni osnovni delci delijo še v podskupine.
* Elementarni ali osnovi bozoni, ki prenašajo sile so: Higgsov bozon, foton, gluoni, Z in W± bozona,
morda obstaja še
šesti bozon graviton. Vsi našteti delci so odgovorni za osnovne interakcije - so
nosilci
sil (vse smo omenili že v uvodnem članku o silah)! Vsi bozoni imajo celoštevilčni
spin: 0 (Higgsov bozon), 1 (fotoni, gluoni), 2 (graviton - ni še potrjen) ...
Imenovani so po indijskem fiziku Satjendri Natu Boseju. Vsi osnovni delci so bodisi bozoni,
bodisi fermioni. Ponovimo še enkrat – da so v standardnem modelu delcev osnovni ali elementarni bozoni nosilci
osnovnih interakcij - sil.
Še opozorilo o sestavljenih nosilcih sil - to so mezoni (sestavljeni iz kvarka in antikvarka).
Mezoni igrajo ključno vlogo v močnih interakcijah, saj so nosilci močne sile, ki deluje med hadroni (med protoni in nevtroni - jih vežejo
v atomska jedra, ti mezoni se imenujejo tudi pioni, rho mezoni, omega mezoni)
in tukaj so tudi mezoni z imenom kaoni, ki so del šibkih interakcij ... A mezoni niso osnovni gradniki snovi!
Mezoni torej tudi niso osnovni nosilci močne sile (to so gluoni, ki delujejo med kvarki), vendar so nosilci močne sile na ravni hadronov.
To pomeni, da mezoni prenašajo močno interakcijo, ki veže nukleone (protone in nevtrone) znotraj jedra.
Obstajajo tudi sestavljeni bozoni iz fermionov (kompozitni delci), ki imajo celoštevilčni
spin, a ti sestavljeni bozoni niso nosilci sil - recimo izotop vodika devterij še tudi šteje med bozone, ker ima spin 1,
a ni nosilec sile. Bozoni se lahko "zgrnejo" v isto kvantno stanje - ne upoštevajo Paulijevega izključitvenega načela.
Več sledi.
* Potem so tukaj fermioni – nimajo celega spina (za razliko od bozonov) – fermioni so
podvrženi Paulijevemu izključítvenemu načelu, ki pravi, da recimo fermiona v atomu
ne moreta istočasno zasesti istega kvantnega stanja. Skupno model delcev razlikuje
24 različnih fermionov - šest kvarkov z eksotičnimi imeni (recimo, da jih poimenujemo:
gor - up, dol - down, čudnost - strange ali s, čar - charm ali c, vrh - top ali t
in dno - bottom ali b) in
šest leptonov (elektron, elektronski nevtrino, mion, mionski nevtrino, tau lepton in
tau nevtrino) skupaj z ustreznimi antidelci.
Še opozorilo o sestavljenih fermionih.
Delci, sestavljeni iz lihega števila
osnovnih fermionov, so prav tako fermioni (na primer proton, nevtron, tritijevo
atomsko
jedro 3H, helijevo jedro 3He, ogljikovo jedro 13C).
Delci iz sodega števila fermionov (kompozitni delci)
pa so tudi bozoni, a ne osnovni, ki prenašajo sile (na primer jedro devterija
2H - saj ima proton spin 1/2 in nevtron 1/2 in je tako skupni spin devterija 1, tukaj so še
helijevo jedro 4He [v parih se spin izniči in 2 protona imata tako skupaj spin 0,
2 nevtrona pa torej tudi imata skupaj spin 0], ogljikovo jedro 12C tudi spada med bozone,
tudi 16O ..., tudi molekula H2 je sestavljen bozon - a to niso osnovni,
elementarni bozoni, ki prenašajo sile - ti so našteti na začetku).
V atomski fiziki in kvantni optiki se ulovijo in ohladijo bozonski atomi za kvantne eksperimente / Bose-Einsteinov kondenzat(BEC).
Vsa znana snov v današnjem vesolju je sestavljena iz fermionov:
leptonov in barionov
(barioni pa
so vrsta sestavljenih subatomskih delcev,
ki vsebujejo liho število kvarkov - veže jih močna jedrska sila, vsaj 3, recimo proton, nevtron - torej masivni delci vsakdanjega sveta).
Še o leptonih (grško leptos - lahek). Lepton je osnovni delec s spinom 1/2, ki ne sodeluje v močni sili.
Lahko je nabit (npr. elektron) ali nevtralen (npr. nevtrino).
Sodeluje v elektromagnetni, šibki in gravitacijski sili. Imajo maso, spadajo tudi v družino fermionov.
Prisotnost leptonov v naravi
Prva generacija
Elektron (e):
- nahaja se v atomih,
- pomemben v elektriki,
- nastane recimo z beta razpadom.
Elektronski nevtrino (νe):
- nastane z beta razpadom
(pričakovano se
sprosti veliko nevtrinov tudi
pri eksplozijah supernov,
prehod protonov v nevtrone
e- + p => νe + n
).
Druga generacija
Mion (μ):
- se pojavlja v velikem številu
z vpadom kozmičnih delcev
v zgornje plasti ozračja.
Mionski nevtrino (νμ):
- se pojavi v jedrskih reaktorjih,
- nastane, že omenili, ob vstopu kozmičnih delcev
v zgornje plasti ozračja.
Tretja generacija
Tau lepton (τ):
- do sedaj detektiran samo
v laboratorijih (pričakovano bi naj bil
pogost delec takoj po velikem poku).
Tau nevtrino (ντ):
- do sedaj detektiran samo
v laboratorijih.
Pripadjoči nevtrini (νe, νμ, ντ) so tudi leptoni.
Še zanimivost.
Vsako sekundo gre skozi naše telo na milijarde nevtrinov (iz Sonca in iz ostalih delov vesolja),
a praktično noben ne reagira z našo materijo. Ogromno nevtrinov se sprosti ob eksplozijah supernov.
Še ocena: potrebna bi bila svinčena krogla premera kar cca 1 svetlobno leto, da bi en nevtrino trčil v enega od atomov
v enem letu preleta te krogle! Razlog je v sami naravi nevtrina, saj
nevtrini sodelujejo samo v šibki jedrski sili (in gravitaciji), ki je pa izjemno šibka in zelo, zelo kratkega dosega,
le cca 10-18 m, to je na velikostnem redu kvarka.
To je povzetek trenutnih splošno sprejetih fizikalnih modelov in meritev osnovnih
nedeljivih delcev, ter nekaj povezav med njimi (kako recimo kvarki in gluoni gradijo naš pojavni
svet preko protonov in nevtronov). A če kaj berete, recimo Spiko, je še kar nekaj kandidatov za
osnovne delce, recimo zloglasni aksioni ali morebiti WIMPi (Weakly interacting massive particles),
eden od njiju bi naj bil nosilec
skrivnostne temne snovi – recimo, da aksionom trenutno kaže nekoliko bolje (SPIKA 5, 2023) …
Še beseda o hadronih - omenili smo jih na začetku poglavja.
V fiziki delcev je hadron
(starogrško in romanizirano pomeni hadrós "krepak, debel")
sestavljen subatomski delec.
Sestavljen je iz dveh ali več kvarkov,
ki jih skupaj drži močna interakcija. So analogni molekulam,
ki jih skupaj drži električna sila.
Večina mase navadne snovi izvira iz dveh hadronov: protona in nevtrona,
medtem ko je večina mase protonov in nevtronov posledica vezavne energije
njihovih sestavnih kvarkov, zaradi delovanja močne sile.
Tako smo, kar se da strnjeno, opisali (glejte naslov) ključno zgodbo našega sveta.
Osnovne nedeljive delce vesolja in posebej, tudi iz šole, vsem poznana nukleona proton
ter nevtron (sestavljena iz treh kvarkov), ki tvorita, skupaj z elektroni, atome, molekule,
naš spoznavni svet, nas same, tudi naše umsko »vesolje«.
Osnovni delci se imajo torej pri določenih pogojih zelo radi.

V resnici se imajo kvarki, nukleoni in atomi radi – ta preprosta prispodoba je
marsikateremu otroku približala svet atomov in molekul.

Grafi razvoja vesolja glede na čas, temperaturo in energijo: t (Planckov »prvi«
čas 10-44 s),
T (začetna temperatura 1032 K)
in E = kBT (začetna energija 1019 GeV)
- t, T, E
grafi so izjemno učinkovita in strnjena metoda za učenje osnov
kozmologije in hkrati fizike osnovnih delcev. Oboje, svet
osnovnih delcev in svet velikih teles je že od samega začetka
vesolja povezan v celoto – simbolično kot otrok in mama, ko enega
brez drugega ni (otroka zagledamo po rojstvu, kot delce po inflaciji).
V najzgodnejših časih vesolja bi naj sevanje imelo toliko energije,
da bi po Einsteinovi enačbi
E = mc2
spontano nastajali pari materije in antimaterije (recimo e- in e+)
in se spet pretvorili (anihilirali) v gama svetlobo – v to idilo pa
baje poseže »božji« delec - Higgsov bozon, več sledi. Na vrhu grafa razvoja
vesolja je podano še poglavje »POSPEŠEVALNIKI«, ki kaže, do katerih energij,
sil in časov smo preko trkov delcev v pospeševalnikih že potrdili klasični model
razširjajočega se vesolja. S pospeševalniki smo prišli do starosti vesolja nekje
10-10 s (neverjeten uspeh), do ekstremne temperature 1015 K
in do energije okrog 102 GeV (ko so se osnovne sile že ločile
in smo tik pred začetkom njihovega delovanja – recimo druženju
kvarkov, zaradi močne sile, v protone in nevtrone). Ta graf torej
tudi dokaj solidno utemeljuje upravičenost gradnje velikih in dragih
pospeševalnikov – trkalnikov delcev. Je ena od mnogih predstavitev, predvsem
zgodnjega vesolja, glede na delce in interakcijo med njimi skozi čas-prostor,
temperaturo prostora in energijo - recimo kinetično energijo Planckove mase.
Trenutno je ta energija pri temperaturi vesolja 2,7 K na grafu ocenjena na
E = kBT = 2,7 K*8,61733 10-5 eV/K = 2,3 10-4 eV = 2,3 10-13 GeV
(kdaj pa se poda tudi energija svetlobe
E = hc/λ,
z valovno dolžino vrha
Planckovega sevanja črnega telesa pri dani temperaturi; Wienov zakon:
λmaks=b/T; ko velja
E = hc/λ = hcT/b.
Skala ni linearna – poudarek je torej na času od velikega poka,
do nastanka atomov –
V 380000 let.
Če razvrstimo zaokrožene zaloge energij, ki se nahajajo v osnovnih delcih
in njihovih sestavnih delih, tudi preko enačbe E = mc2 za nukleone (Higgsov
bozon ki je dal maso elektronom, kvarkom, W, Z bozonom … ima energijo okrog
125,09 GeV,
W in Z bozona pa okrog 80,4 GeV in 91,2 GeV,
proton okrog 938.3 MeV, ionizacija vodika okrog 13,6 eV in Helija okrog 24,6 eV,
ocena temperature glede na energijo je kar
T = E/kB) in podatke primerjamo na skali energije razvoja vesolja
(v GeV), ter si ogledamo nastale delce, lahko razberemo zakaj in kdaj
so se delci sploh lahko začeli pojavljati in združevati v svet nukleonov
in nato atomov (atom je jedro z elektronskim oblakom), nato v molekule ...,
bo ta graf naenkrat postal zelo domač, poveden za razumevanje razburljivega
dogajanja v vesolju skozi čas, do nas! Higgsov bozon je (naj bi bil) odgovoren
za prekinitev simetrije med delci in antidelci – inflacija vesolja.
Ko je temperatura padla na okrog 1010 K so se še pred tvorbo zvezd lahko zlivali
protoni in nevtroni v devterij in tudi že v helijeva jedra z dvema nevtronoma
in dvema protonoma (sevanje je bilo že toliko razredčeno, da ni razbijalo helijevih jeder).
Heliju tako tudi pravimo pepel velikega poka (nastalo je še nekaj litija in zelo malo ostalih elementov).
Zato je danes v grobem razmerje med helijem in vodikom v prid vodika, ki ga je okrog
75 % in helija okrog 25% - velja za področja, kjer ni novega fuzijskega helija,
ki nastaja v zvezdah (danes so v povprečju razmerja 25 % helij, 73 % vodik in
2 % ostali kemijski elementi). To se je zgodilo, ko je vesolje bilo staro
dobro minuto, takrat je bilo razmerje med protoni in nevtroni že okrog 7:1
v prid protonom – pred tem (pri višjih temperaturah je veljalo
n + e- <==> νe + p in
n + νe <==> p + e-
)
je bilo nevtronov in protonov približno enako (po padcu temperature pa so mnogi
nevtroni razpadli v protone, beta minus razpad zaradi šibke jedrske sile - prosti
nevtroni so nestabilni s povprečno življenjsko dobo le 880 sekund). V tem primeru
(recimo v nekem delčku vesolja) je od prvotnih 14 protonov in 2 nevtronov ostalo
12 protonov ter en helij in noben prost nevtron, saj se v helij vežeta dva protona
in 2 nevtrona – razmerje v atomskih masah je torej 12:4 (ali 75 %/25% v procentih
v prid vodika – razmerje pa seveda velja za celotno vesolje). To je na sliki
razvoja vesolja (zgoraj) področje, kjer piše zlivanje protonov in nevtronov.
V tem obdobju nastane (poleg 4He, tritija
3H, devterija 2He) še nekaj litija s
3 protoni in 4 nevtroni (7Li iz 4He in
3He, a 3He je bilo zelo malo). Ko
je nastal stabilen helij je bila temperatura vesolja že prenizka (gre za širjenje
vesolja), oziroma ni bilo dovolj časa, da bi iz različnih ostalih jeder nastalo
še kaj veliko ostalih težjih elementov (približno 0,01% je nastalo še devterija
in helija-3, v sledovih še (komaj okrog 10-10) litija in zanemarljivo število težjih
elementov kot so berilij, bor …). Vsa ostala nastala jedra iz helija so bila na začetku
vesolja večinoma nestabilna in so takoj razpadla – nakar je kmalu temperatura zelo padla
– gre za širjenje vesolja …, to je razlika glede na fuzijo v zvezdah.
Če preletimo zgornji graf po velikem poku in inflaciji vesolja, je trenutni scenarij
naslednji - temperatura vesolja je odločala o nastanku prvih nukleonov (po 0,0001
sekunde, temperatura pade na 1012 K), v nadaljevanju razvoja vesolja je pričakovano
temperatura odločala tudi o nastanku atomskih jeder (po nekaj minutah, ko temperatura
pade pod
1010 K),
sledijo nevtralni atomi (po okrog 380 000 letih, temperatura pada na okrog 3000 K),
nato nastopijo zvezde (gravitacija prevzame vajeti v roke in že okrog 100 milijonov
let po velikem poku se pojavijo prve zvezde), pojavijo se tudi planeti, kmalu tudi
galaksije (prve se pojavijo že po okrog 400 milijonih let po velikem poku,
temperatura sevanja ozadja pade 475 milijonov let po velikem poku na vrednosti okrog 19 k,
danes na 2,7 K).
Ko so nastale prve zvezde in galaksije so se v vesolju prižgale luči (zvezde oddajajo svetlobo, tudi UV)
- takrat se je zgodila ponovna ionizacija
(reonizacije) vodika, helija in svetloba se je potem lahko skoraj neovirano širila po vesolju.
Vesolje postane 10 % prosojno za svetlobo 475 milijonov let po velikem poku in v obdobju
250 milijonov let je vesolje postalo skoraj povsem ionizirano in tako prozorno za vidno svetlobo.
Iz tega obdobja vidimo tudi prve galaksije (z = 11, JW zazna že z = 12) - prej je bil prostor
za vidno svetlobo neviden (doba teme) - saj so atomi svetlobi preprečevali neovirano potovanje -
komaj nastajajoče zvezde (razlog je gravitacija, ki združuje vodik in helij in temna snov,
ki tvorbo zvezde pospeši) so ustvarile dovolj velik izsev, energije, da so počasi ionizirale atome.
Po nastanku atomov in pred nastankom zvezd, je prevladovala infrardeča svetloba,
ki jo je zadrževala atomska megla vodika in helija
(kot recimo, če v zimskih mesecih zjutraj
pogledamo s Krvavca na Ljubljansko kotlino, večinoma vidimo meglo, ki nam zastira pogled na
Ljubljano, Šmarno goro ..., ko pa Sončevi žarki s svojo energijo razbijejo meglo,
postane Ljubljanska kotlina prosojna in svetloba neovirano potuje
med nami in dolino).
Po nastanku zvezd, galaksij pa pridemo do našega bistva -
nastanejo Sonce, planeti in na Zemlji nastane tudi življenja pred okrog 4 milijardami let (za katerega
pričakujemo, da se je razvilo še kje v naši Galaksiji, tudi v ostalih). A moderni
človek se pojavi komaj pred kakimi 200 000 leti, načrtno generirane elektromagnetne
signale pa znamo v vesolje pošiljati komaj dobrih 100 let. Da je vesolje veliko
milijarde svetlobnih let (da vesolje torej ni zgolj naša Galaksija - Rimska
cesta premera 100 000 sv. l.) pa smo se prepričali pred komaj slabimi 100 leti
(preko sija utripajočih zvezd kefeid smo najprej ugotovili, da je nam sosednja
galaksija M31 daleč vsaj milijon sv. l. – danes vemo, da je oddaljena okrog 2,5 milijona sv. l.).
Nebesno mehaniko pa nam je razkril Kepler pred 400 leti. Velik problem vseh naših modelov
je merjenje razdalj v vesolju …!!!
Ravno preko merjenj razdalj s supernovami tipa Ia, smo na prehodu iz 2. v 3. tisočletje
začudeno ugotovili, da ne samo, da s vesolje širi, ampak se širi celo pospešeno.
Pospešek mu daje na novo vpeljana temna energija, ki nasprotuje gravitaciji ...
Če dodamo še malo naše poezije, ki tokrat ni Prešernova - Janez Vesel Koseski pravi:
"Zakon nature je tak, da z majhnega raste veliko."
Velja torej tudi za vesolje.
Zadnji tak velik uspeh in hkrati napor je izstrelitev (25. dec. 2021) novega izjemnega vesoljskega
teleskopa James Webb v Lagrangevo točko L2 (6,5 m premera - sestavljen je iz 18 zrcal, šesterokotnikov
velikosti 1,32 metra, v raketo so zrcala zložili na principu origamija). Za razliko od Hubbla,
ki vesolje opazuje v bližnjem ultravijoličnem, vidnem in bližnje infrardečem delu
(0,1–1,0 μm)
spektra, pa JWST opazuje v območju s krajšimi valovnimi dolžinami, od dolgovalovne
vidne svetlobe (rdeče) do srednje infrardečega sevanja (0,6–28,3 μm) - to je svetloba
v obdobju teme vesolja (čas med 380 000 let do okrog 400 milijonov let po velikem poku,
ko temperatura pade iz 3000 K na okrog 60 K, od valovnih dolžin sevanja 970 nm do okrog 50 μm).
Tako lahko zazna objekte z visokim Dopplerjevim rdečim premikom z ≈ 20, ki
so za Hubbla prestari, prešibki, oz. preveč oddaljeni. Relativni Dopplerjev
premik (z = Δλ/λ ) valovnih dolžin svetlobe zaradi premikanja s hitrostjo
v, je v splošnem 1 + z = ( (1 + v/c)/(1 - v/c) )1/2,
c je hitrost svetlobe. Hubble teoretično vidi Dopplerjev premik
z ≈ 11,1, to je približno
400 milijonov let po velikem poku, J. Webb teleskop pa vidi v same zgodnje začetke vesolja,
zagotovo več kot 13,5 milijarde let nazaj, teoretično celo približno 180 milijonov
let po velikem poku, za z ≈ 20. Torej teoretično je z = 20
dovolj, da vidimo prve galaksije (≈ 270 milijonov let) in zgodnje zvezde
(≈ 100 do 180 milijonov let
po velikem poku)
Prvi Webbovi posnetki so glede ločljivosti in števila zaznanih šibkih objektov,
zvezdic, naravnost fascinantni (kot da bi človeštvu operirali sivo mreno – toliko
več šibkih objektov razločno zaznamo). Skratka – ne bo nam dolgčas.

Teleskop James Webb (desno) vidi veliko dlje (rdeči premik Z = 20) proti
začetku vesolja, kot teleskop Hubble (z = 11,1), ki vidi okrog 13,4 milijarde let nazaj.
J. Webb pa vidi v same zgodnje začetke vesolja,
zagotovo več kot 13,5 milijarde let nazaj, teoretično celo približno 180 milijonov
let po velikem poku, za z ≈ 20. Torej teoretično je z = 20
dovolj, da vidimo prve galaksije (≈ 270 milijonov let) in zgodnje zvezde
(≈ 100 do 180 milijonov let
po velikem poku).
Za izračune lahko
uporabite kozmološki kalkulator, vstavite rdeči premik 'z' in izberite ravno ali odprto vesolje,
spreminjate lahko tudi gostoto:
https://www.astro.ucla.edu/%7Ewright/CosmoCalc.html
(ali kalkulator lokalno).
Temperatura se večji del časa širjenja vesolja spreminja po enačbi, ki jo bomo izpeljali,
sedaj jo le zapišimo in uporabimo:
T=To(to/t)2/3
Če pa se vprašamo zgolj po oceni, kolikšna je bila temperatura T mladega vesolja komaj
t = 100 sekund po velikem poku, ko se je že tvoril helij (zgolj jedro) v razmerju z vodikom
H/He = 75 %/25 % (prva kratka fuzija), pa nam zgornja približna enačba
( T=T0(to/t)2/3 – ta enačba zagotovo več ne velja za vesolje mlajše od sekunde,
tudi za ocene ne) vrne kar pravilen velikostni red (1010 K) iz grafa. Za čas to torej
privzemimo starost vesolja to = 13.8 milijard let, za t seveda t = 100 s, za trenutno
temperaturo vesolja pa To = 2,725 K. Velja torej:
T = 2,725 K*(13,8*109*365*24*3600/100)2/3
= 72636844432 K = 7 1010 K
Dobili smo pričakovan rezultat - kot je podan na grafu.
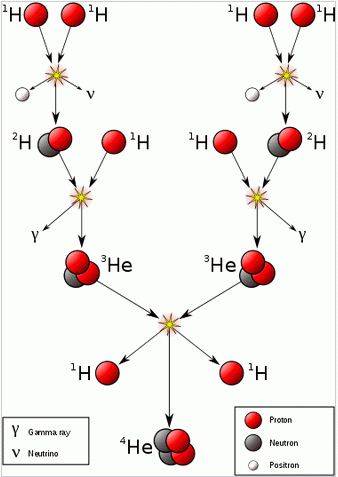
V bistvu nam številčnost vodika in helija pomaga modelirati hitrost širjenja zgodnjega
vesolja. Če bi se širilo hitreje, bi bilo več nevtronov in tako več helija. Če pa počasneje,
bi več prostih nevtronov razpadlo že pred točko stabilnosti devterija (devterij – proton z
nevtronom – je vmesni člen reakcije do helija) in bi bilo tako manj helija. To razmerje vodika
in helija je res velik adut v rokah teorije velikega poka.
Modeliranje proizvodnje helija in
razmerja vodik-helij predvideva tudi druga jedra, zlasti
7Li, 2H (devterij),
3H (triton) in
3He. Te opažene številke hkrati ustrezajo modelu velikega poka v ozkem razponu. Poleg tega
razmerja helij/vodik - zelo občutljivega testa za model velikega poka, je pa temperatura
mikrovalovnega ozadja tudi izrazito povezana s tremi vrstami nevtrinov (elektronski nevtrino
(νe), mionski nevtrino (νμ),
tau nevtrino (ντ) tudi
direktno, kot lego kocke pašejo v trenutno
vrednost temperature mikrovalovnega ozadja TCMB = 2,725 K – in
še ena napoved, temperatura današnjega
kozmičnega nevtrinskega ozadja je TCNB = 1,96 K ± 0,02 K,
kar je tudi blizu teoretičnemu izrazu
TCNB = TCMB(4/11)1/3 – tako
veliki pok tudi preko sevanja nevtrinov postaja vedno bolj trden model).
Tudi samo razmerje med številom barionov in fotonov je bilo eden od prispevkov odkritja sevanja
ozadja 2,725 K (barion je delec, ki ga sestavljajo vsaj trije kvarki, liho število, recimo protoni,
nevtroni, delci delta, lambda …). Te meritve so omogočile izračun gostote energije fotonov v vesolju,
ocena gostote barionov pa je dala barionsko/fotonsko razmerje približno 10-9
(fotoni so torej
prevladovali in onemogočali tvorbo elektronskih oblakov ob jedrih). To so torej trdni argumenti
za stanje v mladem vesolju - starem nekaj minut.
Večino ostalih težjih elementov naknadno tvorijo vroče zvezde iz plazme preko fuzije – do železa,
ostali težji elementi pa se tvorijo pri eksplozijah supernov in trkih zvezd. Nehomogenosti v
mladem vesolju danes pojasnujemo s prisotnostjo temne snovi, ki je omogočila razvoj galaksij,
zvezd – izmerjeno pospešeno širjenje vesolja pa temni energiji, ki danes v vesolju po deležu
celo prevladuje. Glejte spodnjo sliko (ki se ponovi še v naslednjih poglavjih). Strnjen graf
razvoja vesolja bomo še večkrat komentirali.
Še enkrat naredimo nekaj izračunov - ocen - tema je pomembna.
Pri visokih začetnih temperaturah vesolja (to pomeni velik
kT) je razmerje nevtronov in protonov bilo
n/p ≈ 1, to pomeni, da je bilo
skoraj enako število nevtronov in protonov.
Ko se vesolje ohlaja (nižja
T), začne naraščati število protonov, saj so lažji.
Ko temperatura pade pod približno 0.8 MeV, se reakcije, ki pretvarjajo n in p, upočasnijo - razmerje "zamrzne".
V zgodnjem vesolju (T = 1032 K ≈ ∞) so bili torej nevtroni in protoni v termičnem ravnovesju (e-Δmc2/(kT)
≈ e-Δmc2/(k∞) = 1 ), in njuno številsko razmerje je
določeno z Boltzmannovo porazdelitvijo.
Približna enačba za razmerje med nevtroni in protoni n/p je:
n/p ≈ e-Δmc2/(kT)
Zakaj v enačbi nastopa izraz Δmc2?
Ker zelo poenostavljeno velja En - Ep ≈ (mn - mp)c2 + (Ekin_n - Ekin_p)
≈ (mn - mpp)c2,
Saj sta kinetični energiji (Ekin_n in Ekin_p) protonov in nevtronov praktično enaki?
V resnici bi morali uporabiti enačbo E2 = m2c4 + p2c2,
a na koncu bi dobili enak rezultat.
Δmc2 ≈ 1.29 MeV - je torej energijska razlika med nevtronom in protonom v začetku vesolja
kT - temperatura vesolja (v energijskih enotah – MeV)
Pri temperaturi T ≈ 0.8 MeV/k, kar je okoli 1 sekunda po velikem poku:
n/p ≈ e-1.29/0.8 ≈
e-1.6125 ≈ 0.199 ≈ 1/5
Vendar se do začetka nukleosinteze (pri kT ≈ 0.1 MeV)
nekaj nevtronov že razpade, zato se realno razmerje zmanjša na približno:
n/p ≈ 1/7
Zakaj je to pomembno?
Ker vsak atom helija-4 potrebuje 2 nevtrona, količina helija je direktno odvisna
od začetnega n/p razmerja. Ostali protoni (ki ne gredo v helij) ostanejo - kot vodik.
Ker je helij sestavljen iz 4 nukleonov, iz dveh protonov in nevtronov (imata ker praktično enaki masi),
velja:
1/7 = 2/14, od koder sledi po začetni nukleosintezi številsko razmerje med helijem in protoni
NHe/Np = 1/12
in
od tod velja masno razmerje v prid protonov (vodika):
mHe/mH = 4/12 = 25/75
Kljub nukleosintezi v zvezdah to razmerje na globalni skali vesolja še zmeraj ostaja skoraj enako ...,
lokalno, recimo na kamnitih planetih (Zemlja, Mars, Merkur, Venera) pa je močno v prid težjih elementov.
Na Zemlji v prid kisika in ogljika - od tod obilno ogljikovodikov, dihamo kisik ...
Očetje nukleosinteze velikega poka so:
George Gamow zagovarja, da je vroč začetek vesolja osnova za nukleosintezo velikega poka BBN (Big Bang nukleosintezi),
Ralph Alpher poda izračune tvorbe elementov po Velikem poku 1948 (skupaj z njegovim
mentorjem Gamowom),
Robert Herman napove mikrovalovno sevanje ozadja CMB (Cosmic Microwave Background) in tako podpore BBN.
Leta 1965 sta Arno Penzias in Robert Wilson (po naključju!) zaznala nenavadno mikrovalovno šumenje,
ki je prihajalo od vsepovsod.
Nista vedela, da sta odkrila ostanek svetlobe iz Velikega poka.
Za to odkritje sta leta 1978 prejela Nobelovo nagrado.
Tudi sestava Sonca je še zmeraj blizu razmerja mHe/mH = 4/12 = 25/75.
To razmerje je veličastno dokazala že 1925
Cecilia Payne-Gaposchkin (rojena Cecilia Helena Payne, 1900 – 1979).
Bila ameriška astronomka in astrofizičarka britanskega rodu.
Več si preberite na strani:
Leto kvantne mehanike (IYQ2025) - oglejte si spekter življenja.
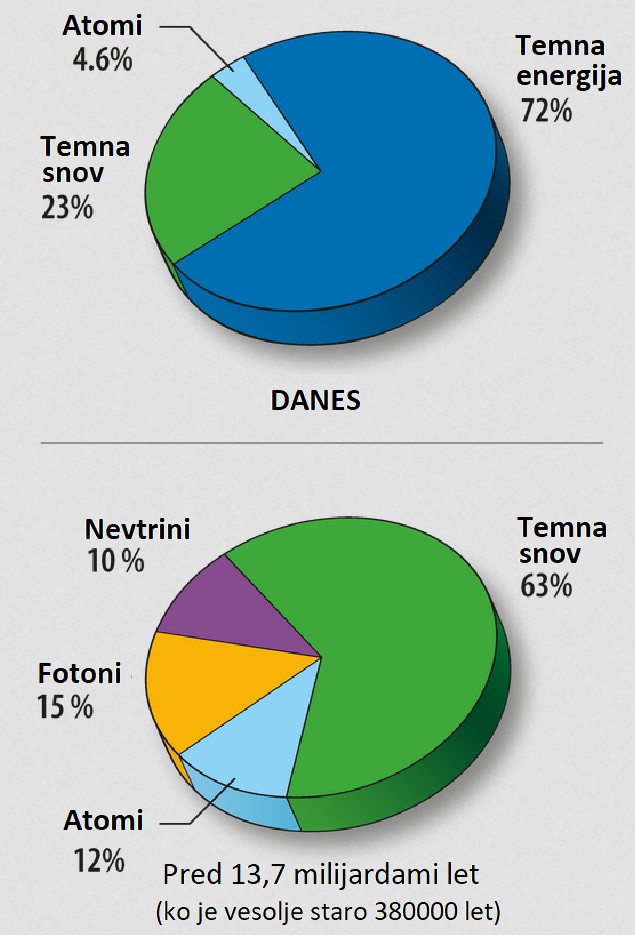
Grafa prikazujeta relativno sestavo gostote energije vesolja danes in na začetku.
Da lahko z opazovanjem določimo položaj telesa, ga moramo osvetliti in sprejeti od njega odbito
svetlobo. Zaradi uklona ali sipanja svetlobnega žarka (odvisno od velikosti delca in valovne
dolžine) pa lahko položaj telesa (recimo elektrona) določimo le na valovno dolžino natančno.
Zato lahko zapišemo, da je nedoločenost položaja telesa približno enaka valovni dolžini svetlobe
(Δx ≈ λ)
s katero gledamo telo (recimo elektron). Z zmanjšanjem valovne dolžine svetlobe lahko
tako sicer natančneje določimo položaj zahtevanega delca, vendar v tem primeru povečamo energijo
svetlobe, fotonov (E = hν = hc/λ) – in tudi gibalno količino
p = h/λ (glede gibalne količine svetlobe, izpeljave, glejte poglavje
"Fizika
velikih hitrosti in pospeškov, zelo pomembno poglavje za razumevanje pojavov v vesolju";
- čez palec pa se splača kar na tem mestu razložiti izraz p = h/λ; in sicer izhajajmo iz dejstva,
da je klasična kinetična energija delca sorazmerna s produktom gibalne količine
in hitrosti: E ∝ mv2 = mvv = pv, pri elektromagnetnem valovanju hitrosti c,
recimo pri fotonih svetlobe
pa direktno velja za energijo enakost med prduktom gibalne količine in hitrosti E = pc; od koder sledi, da
je gibalna količina fotona kar: p = E/c = hν/c = h/λ; h je Planckova konstanta).
Z zmanjšanjem valovne dolžine svetlobe pa torej
opazovan delec med »trkom« tudi izraziteje spremeni svojo gibalno količino
(v primerjavi z začetno), tako da je ni mogoče povsem natančno določiti
(za nedoločenost gibalne količine tako približno velja
Δp ≈ h/λ, produkt
ΔpΔx
bo tako sorazmeren s Planckovo konstanto h=6,62607015·10-34 Js).
S povečanjem frekvence svetlobe sicer zmanjšamo valovno dolžino (in tako povečamo natančnost
lege Δx), a se izgubi natančnost merjenja hitrosti (gibalne količine). S povečanjem valovne
dolžine pa se izgubi natančnost določanja položaja.
Povejmo še, da v angleški literaturi gibalno količino (p = mv) poimenujejo "momentum", oznaka
'p' pa prihaja od latinske besede "pellere" ("push, drive"; potisk, pogon, gibanje ...).
Heisenberg je leta 1925 razvil matrično mehaniko, prvi dosledni kvantnomehanski formalizem.
To, da so njegovi izračuni matrični (Heisenberg je imel komaj 23 let), mu razkrije Max Born.
Njegov cilj je bil razviti teorijo, ki temelji samo na opazljivih količinah,
kot so spektralne črte, frekvence, ne pa na "neopazljivih" konceptih, kot so recimo Bohrove vprašljive tirnice elektronov.
Uvedel je nemoteče opazovanje in delal z matematičnimi količinami kot so matrike (npr. matrika za položaj, hitrost delca itd.),
ki ne komutirajo, kar vodi do Heisenbergovega načela nedoločenosti. Kaj to pomeni?
Če najprej izmerimo lego x in nato gibalno količino p, dobimo drugačen rezultat, kot če merimo v obratnem vrstnem redu,
a razlika je zmeraj
ih/(2π),
torej ni nič - kar pa neposredno vodi do Heisenbergovega načela nedoločenosti - leto 1927:
Δp·Δx ≥ h/(4π)

Kanonično komutativno pravilo za spremembo položaja q in gibalne količine (momenta) p - dveh spremenljivk delca,
1927. pq - qp = h /(2 πi). Heisenbergovo načelo nedoločenosti, negotovostni, 1927.
V matrični mehaniki je matematična formulacija kvantne mehanike,
vsak par ne-komutativnih sebi-adjungiranih operaterjev, ki predstavljajo opazljive spremenljivke,
podvržen podobnim mejam negotovosti.
Poglejmo preprost primer komutiranja operatorjev položaja
x in gibalne količine
p.
Če je komutator dveh operatorjev neničeln, pomeni, da teh količin ni mogoče hkrati natančno
izmeriti (npr. položaj in gibalna količina).
Komutatorji so povezani z dinamiko sistemov
( prek Heisenbergove enačbe gibanja, kjer je ℏ = h/(2π) reducirana Planckova konstanta):
dA/dt = [A,H]/(iℏ) + ∂A/∂t
Oziroma v doslednejšem zapisu:
dAH(t)/dt = [AH(t),HH(t)]/(iℏ) + (∂AS/∂t)H
Členi v enčbi so:
AH(t) - opazovana količina (operator) v Heisenbergovi sliki,
HH(t) - Hamiltonian v Heisenbergovi sliki (pogosto enak kot v Schrödingerjevi, če je časovno neodvisen)
(∂AS/∂t)H - eksplicitna časovna odvisnost operatorja v Schrödingerjevi sliki,
prenesenega v Heisenbergovo sliko (z uporabo istega U(t)).
--------------------------------------
Kjer je: U(t) = e-iHt/ℏ in inverz: U†(t) = eiHt/ℏ
Pretvorba med obema slikama ( Heisenbergovo 'H' in Schrödingerjevo 'S' )
je torej:
AH(t) = U†(t)AS(t)U(t)
Primer: Operator položaja x
- za prost delec (brez potenciala) je Hamiltonianom: H = p2/(2m)
Operator položaja v Schrödingerjevi sliki je xs. Potem je operator v Heisenbergovi sliki:
xH(t) = U†(t)xS(t)U(t)
S pomočjo komutatorjev lahko pokažemo, da se operator razvije kot:
xH(t) = xs(t) + pS/m
Kjer je pS = -iℏ∂/∂x operator za gibalno količino (moment) v Schrödingerjevi sliki,
ki deluje na valovno funkcijo Ψ(x,t).
Kjer spet velja: pH(t) = U†(t)pS(t)U(t)
(ker je klsaično hitrost enaka v = p/m in torej xH(t) = xs(t) + pS/m
ustreza klasični enačbi gibanja za prost delec, kjer je lega: x = xo + v*t )
Povejmo še razliko med valovnima funkcijama Schrödingerjeve in Heisenbergove slike opisa sveta kvantne mehanike:
ΨS(x,t) - valovna funkcija v Schrödingerjevi sliki se razvija s časom (t).
ΨH(x) - valovna funkcija v Heisenbergovi sliki je fiksna v času.
Velja še ΨS(x,t) = <x|Ψ(t)> - več sledi.
Zato tudi velja:
|ΨH(x)> = |ΨS(0)>
Operatorje bomo torej tukaj pisali v poševnem fontu (Italic), recimo
x in
px, komutator dveh operatorjev pa bo [x, px]. Večinoma
pa jih pišejo s strešico ^, recimo:
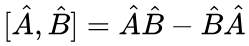
V prostorsko-časovni predstavitvi valovne funkcije, recimo elektrona, velja zapis:
Ψ(x,t) =
Aei(px/ℏ – Et/ℏ) = Ae– iEt/ℏΨ(x)
Zgolj v prostorski predstavitvi (kjer delce opišemo kot funkcije x lege
Ψ(x), sta, kot je zapisano v poglavju
o valovni funkciji, operatorja definirana na naslednji način.
Operator položaja:
x Ψ(x) = x·Ψ(x)
Operator gibalne količine:
pxΨ = -iℏ∂Ψ(x)/∂x
Glejte poglavje :
Delčna in valovna narava osnovnih kvantnih delcev.
To sta osnovna operatorja kvantne mehanike v pozicijski (krajevni) predstavitvi.
Izračunajmo komutator [x, px]Ψ(x).
Po definiciji komutatorja velja:
[x, px]Ψ(x) = x(pxΨ(x)) - px(xΨ(x))
Na koncu uporabimo splošno matematično pravilo.
V kvantni mehaniki obstaja splošna neenakost, ki pravi:
ΔA·ΔB ≥ |<[A,B]>|/2
Ta zgornja formula izhaja iz matematike kvantne mehanike, natančneje iz Schwarzove neenakosti
(tudi Cauchy–Schwarzova neenakost).
Valovno funkcijo Ψ(x) v dokazu pišemo kar kot Ψ.
x(pxΨ) = x(-iℏ∂Ψ/∂x) = -ixℏ∂Ψ/∂x
px(xΨ) = -iℏ∂(xΨ)/∂x = -iℏ(1*Ψ + x∂Ψ/∂x)
Tako velja, ker je ∂x/∂x = 1:
[x, px]Ψ
= -ixℏ∂Ψ/∂x - ( -iℏ(1*Ψ + x∂Ψ/∂x) ) = iℏΨ
Valovno funkcijo Ψ na obeh straneh okrajšamo in tako dobimo izraz za komutator dveh operatorjev
x in px.
[x, px] = iℏ
Ker velja:
ΔA·ΔB ≥ |<[A,B]>|/2, oziroma Δx·Δp ≥ |<[x,p]>|/2
Je končni rezultat kar Heisenbergovo načelo nedoločenosti:
Δx·Δp ≥ ℏ/2 ali Δx·Δp ≥ h/(4π)
Ta zapis v sebi skriva globoko resnico - recimo, da ni vseeno katero količino pomerimo prej (x ali p,
lego ali gibalno količino, obakrat vplivamo na obe količini, kako, sledi v nadaljevanju, a vseeno obstaja spodnja
limita h/(4π), ki smo jo ravno izračunali).
Velja pa tudi, da je komutator na py, torej za pravokotno smer pričakovano enak 0 (saj velja ∂x/∂y = 0):
[x, py]Ψ(x)
= -ixℏ∂Ψ(x)/∂y - ( -iℏ(0*Ψ(x) + x∂Ψ(x)/∂y) )
= (-ixℏ∂/∂y + xiℏ∂/∂y) Ψ(x)
= 0
Za vajo in razumevanje Heisenbergove enačbe gibanja ( dA/dt = [A,H]/(iℏ) + ∂A/∂t )
si oglejmo še
Hamiltonian in sicer energijo sistema glede na položaj x
in gibalno količino p, brez potenciala, torej se kvantni delec (recimo elektron) giblje prosto:
H = p2/(2m)
Heisenbergova enačba za
x,
če se sam operator A ne spreminja s časom velja
∂A/∂t = 0,,
je potem:
dx/dt = [x,H]/(iℏ)
Not vstavimo člen za energijo preko operatorja H = p2/(2m)
dx/dt = [x,H]/(iℏ) = [x,p2/(2m)]/(iℏ) = [x,p2]/(iℏ2m)
Velja tudi:
[x,p2/(2m)] = [x,p2]/(2m)
Izračunamo komutator [x, p2]:
[x, p2] = p[x, p] + [x, p]p =
piℏ + iℏp = 2iℏp
Tako dobimo:
[x,H] = [x, p2/(2m)] = 2iℏp/(2m) = iℏp/m
Končni rezultat je:
dx/dt = [x,H]/(iℏ) = (1/(iℏ))iℏp/m = p/m
To je pa enačba za hitrost v klasični mehaniki glede na gibalno količino v = p/m.
Še Heisenbergova enačba za operator gibalne količine, rabimo torej [p,H].
dp/dt = [p, H]/(iℏ) = [p, p2/(2m)]/(iℏ) = [p, p2]/(iℏ2m)
Spet smo torej privzeli Hamiltonian
H = p2/(2m).
Komutator je:
[p, p2] = 0 => [p, H] = 0 => dp/dt = 0
To pomeni: gibalna količina se ne spreminja s časom ( dp/dt = 0 )
– kar je logično za prost delec brez sile (torej brez potenciala).
To sta bili preprosti vaji za razumevanje Heisenbergove enačbe gibanja, kjer je komutator ključen:
dA/dt = [A,H]/(iℏ) + ∂A/∂t
Heisenbergov princip nedoločenosti se da res slikovito in enostavno prikazati "eksperimentalno - računsko"
na primeru delca (delcev), ki gre skozi ozko režo (tej širino lahko spreminjamo, s tem
pa tudi nedoločenost lege in gibalne količine). Vajo lahko izvedemo v razredu.
Ta vaja je zelo dober pedagoški primer,
kako se negotovost v položaju in gibanju preračunljivo povežeta (Δp·Δx ≥ h/(4π)).

Pri ozki spodnji reži širine w1 pridobimo informacijo o legi valovanja (nedoločenost Δx1 ≈ w1),
a izgubimo na komponenti gibalne količine v x smeri (nedoločenost Δp1x).
Pri širši zgornji reži širine w2 je uklon manjši, a je večja nedoločenost lege fotona, elektrona (Δx2 ≈ w2).
Velja, če:
w2 > w1
potem
Δp1x > Δp2x in Δx2 > Δx1.
Produkt obeh nedoločenosti ΔpΔx pa je kar velikostnega reda Planckove konstante h
- kot je že predvideval W. Heisenberg. Pa to še
dokažimo.
Skozi režo širine
w pošljemo delce (elektrone, fotone ...).
Delce lahko lociramo na širino reže.
Negotovost v legi je torej kar
Δx ≈ w.
Ko gre delec skozi režo, zaradi uklona spremeni svojo smer (poznan pojav tudi iz klasične fizike)
— to pomeni, da ni več natančno določen v smeri gibanja, kar vrne fizikalno negotovost v gibalni količini smeri x,
kar zapišemo kot
Δpx
(prečno na gibanje).
Uklonski vzorec za režo širine
w
in valovno dolžino
λ
ima prvi minimum pri kotu:
α ≈ λ/w
Pojasnilo, zgornja enačba velja samo za uklon na eni reži
(Znotraj reže širine
w
si lahko predstavljamo nešteto točk, ki sevajo valove (Huygensovo načelo).
Ko gledamo, pod katerim kotom
α se valovi iz različnih delov reže med seboj izničijo, velja pogoj, da mora
njihova razlika v poti doseči celotno valovno dolžino - to je drugače kot
pri dveh režah - pri dveh režah pa velja pogoj polovice valovne dolžine).
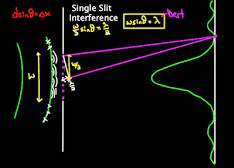
Uklon na eni reži širine w - podobno velja za uklone na objektivih ...
Če poznamo gibalno količino delca:
p = h/λ
potem je prečna komponenta (v smeri
x, zaradi uklona):
Δpx ≈ p·α = (h/λ)·(λ/w) = h/w
Obe oceni vstavimo v Heisenbergovo enačbo
Δx·Δpx ≈ w·h/w = h
Torej:
Δx·Δpx ≈ h ≥ h/(4π)
Kar pa ustreza Heisenbergovemu načelu nedoločenosti!
Kaj pomeni ta rezultat?
Ožja reža pomeni večjo negotovost v prečni komponenti gibalne količine (kar vrne širši vzorec na zaslonu - slika spodaj).
Torej ni mogoče narediti reže, ki bi ti dala natančno lego in natančno smer hkrati,
saj velja Δx·Δpx ≈ h.
Povedano se lepo razbere iz spodnjih slik.

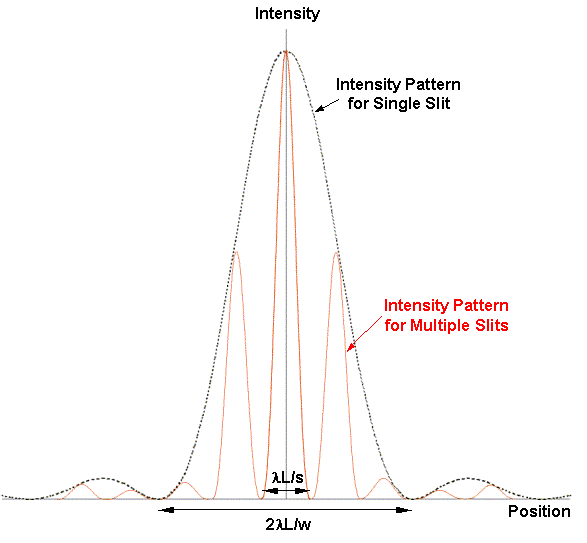
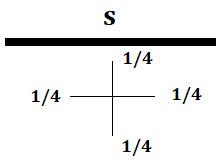
Iz zgornje slike razberemo, da lahko uklonske vzorce ustvari ena sama reža ali dve in več rež ('slits').
Za dve ozki reži na razdalji d sedaj velja, da je Δx ≈ d. Račun se ponovi.
A v tem primeru se zazna še ena zanimivost.
Če merimo, skozi katero režo gre delec (npr. detektor ob vsaki reži),
sicer pridobimo informacijo o položaju delca, ki je sedaj
Δx ≈ d, kar je razdalja med režama (majhna negotovost).
A s tem neizogibno zmotimo njegovo gibalno količino, to pomeni, da se valovna narava izgubi
in interferenčni vzorec izgine.
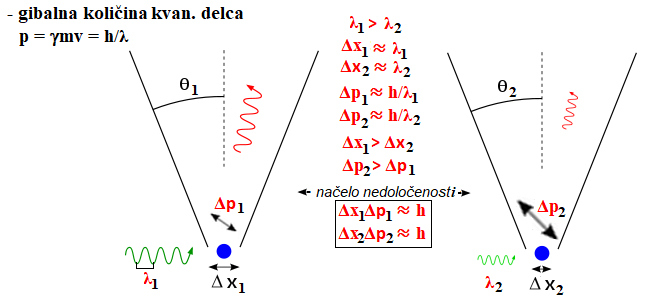
Heisenbergov mikroskop, miselni eksperiment – shema za razumevanje načela nedoločenosti
(znotraj stožca se nahaja odbiti – emitiran – foton in tudi gibalna količina; nedoločenost obeh:
foton zaniha elektron in ga hkrati premakne iz lege). To je kvantna lastnost samega opazovanega
sistema in se mu tudi z uporabo popolnih merilnih instrumentov ni mogoče izogniti.
Bolj natančno merimo položaj
(Δx ≈ λ), manj natančno merimo hitrost, torej gibalno količino
(Δp ≈ h/λ) in obratno.
To lastnost (nedoločenost) je leta 1927 odkril nemški fizik Werner Heisenberg in je običajno
definirana kot:
ΔpΔx ≥ h/(4π)
Če upoštevamo, da je E = hν = hc/λ = pc in da je Δt ≈ Δx/c,
pridemo še do naslednje oblike
nedoločenosti:
ΔEΔt ≥ h/(4π),
ki povezuje nedoločenost energijskega stanja delca ΔE v času Δt trka (uklona ali sipanja)
svetlobe. Če obrnemo logiko, da opazovan elektron vrne foton nazaj v prostor - prehod elektrona
iz višjega na nižji energijski nivo se zgodi v času, ki je nedoločen na
Δt ≥ h/(ΔE4π) –
odloča torej nedoločenost energije (in obratno). Ta energijski zapis je za mnoge sporen,
sploh glede časa, a se vseeno velikokrat sklicujejo nanj – govori o morebitnih začetkih
vesolja (načelo nedoločenosti nam posredno sporoča, da si je moč energijo iz ničesar
sposoditi, če se le ta dovolj hitro 'povrne'). Koncept opisa stanja nekega delca zgolj
preko verjetnosti, čeprav se zdi protisloven, je temeljnega pomena. Heisenbergovo načelo
nedoločenosti
ΔpΔx ≥ h/(4π) je popolnoma spremenilo pogled na svet (nekateri so se ga
razveselili – da ni vse določeno – drugi ga niso nikoli sprejeli, ker nam nedoločenost postavlja omejitve;
"kdo pa si želi omejitev, znanstveniki najmanj - a vendar so temelj našega sveta!").
Veliko je bilo torej nasprotovanj, saj to načelo nasprotuje determinističnim dogmam stare
klasične fizike (ko smo še upali, da bomo nekoč lahko vse natančno izmerili, izračunali,
napovedali v naprej – a temu nikoli ne bo tako; nekateri so v tem videli konec fizike,
drugi šele pravi začetek). Začelo se je obdobje verjetnostnega pristopa k kvantni fiziki
in postavilo mejo eksperimentalni natančnosti. Ta korak, zgolj verjetnostni opis sveta
atomskih delcev, je Einstein videl le kot začasno rešitev – njegov argument je bil:
»Bog
je morda prebrisan, vendar ni zloben.«.
Maxu Bornu pa je napisal, da je zagotovo prepričan,
da on (Bog) ne kocka. N. Bohr pa mu je odvrnil, da naj vendar ne ukazuje Bogu. No – (skoraj)
vsi so se sklicevali na Boga ... in vsak je verjel, da je na njegovi strani. Tudi, če ima
Einstein prav (da v ozadju ni kockanja), nam to nič ne pomaga pri opisu, meritvah sveta –
zmeraj nas bo spremljala nedoločenost lege in gibalne količine. V astronomiji (v svetu velikih
teles) nam postavlja omejitve tako hitrost svetlobe (opazujemo lahko le končno vidno obzorje
vesolja, od koder nas je še dohitela svetloba iz preteklosti), kot tudi ločljivost samih inštrumentov,
tudi zaradi uklona svetlobe ... Velja preprosta trditev - zmeraj le snov (recimo človek) gleda, opazuje
drugo snov - večinoma prejema odbito valovanje ali direktno izsevano valovanje od druge snovi – in valovanju se
lahko valovna dolžina premakne zaradi Dopplerja in gravitacijskega premika (tudi gravitacijskih
valov), na valovanje vpliva tudi vmesna snov, sipanje, uklon ... A tisto kar šteje, niso zgolj omejitve (recimo
načelo nedoločenosti, zgolj verjetnostna porazdelitev delcev v prostoru in času), šteje to,
da se zavedamo obnašanja snovi, valovanj, naštetih omejitev (a le te tudi nosijo s sabo tudi zelo
dragocene informacije), in da iz »nepopolnega« sveta potegnemo čim več koristnih informacij
pri iskanju resnice o nas in svetu. In že do sedaj smo bili nepričakovano zelo, zelo uspešni
(a čaka nas še ogromno presenečenj) – in prav je, da se to res imenitno in prigarano znanje
prenese na mlade – tudi preko šol (da se nit vedenj in radovednosti iz preteklosti v bodočnost
ne prekine – kot se je žal že večkrat prekinila po svetu in tudi v Sloveniji).
Obstaja luštna šala na tematiko principa nedoločenosti
gibalne količine in lege. Takole "se je zgodilo".
Bohr s "pametnim" mobilcem telefonira Heisenbergu, ki ravno drvi z avtom
v službo. Bohr ga poheca, da je na sledi njegovemu telefonu in mu tako pove njegovo natančno prekoračitev hitrosti.
A Heisenberg se odzove kot pravi fizik: "U, sedaj ko si mi povedal, kako hitro se peljem, pa ne vem kje sem, čisto sem zgubljen!"
Načelo nedoločenosti s sabo prinaša veliko zanimivih ocen – z njim bomo ocenili kinetično
energijo kvarkov v nukleonih (proton, nevtron). Proton je sestavljen iz dveh U (up) kvarkov
(2,4 MeV/c2 vsak) in enega D (down) kvarka (5,0 MeV/c2, najdemo različne ocene mase ...),
a to je le 1%
celotne mase (938.272 MeV/c2) protona – kje se torej skriva ostala masa (ne bi
verjeli, večinoma v kinetični energiji kvarkov in v energiji delcev polja prenosa močne jedrske
sile, to je v gluonih, ki so tudi brez mase, a vežejo kvarke v protone, nevtrone, posredno tudi
protone in nevtrone v jedra atomov).
Meritve in trenutni izračuni določajo štiri različne prispevke k masi protonov, od katerih več
kot 90% v celoti izvira iz dinamike kvarkov in gluonov – to so: kvarkov kondenzat (~ 9%),
kinetična energija treh kvarkov (~ 32% - bomo izračunali), energija gluonskega polja močne
jedrske sile (~ 37%) in anomalen gluonski prispevek (~ 23%). Le 1 procent materije se (najbrž)
skriva v kvarkih – ČE sploh.
Eergijo kvarka v protonu spet ocenimo preko načela nedoločenosti. Proton je sestavljen
iz treh kvarkov – za nedoločenost lege privzamemo kar dvojni premer protona
okrog 2d = 2 fm = 2 10-15 m
(to pomeni delno radialno
in tangentno gibanje kvarkov, saj
kvarki niso strogo omejeni na velikost protona,
ampak se gibajo v večjem obsegu zaradi močne interakcije z gluoni in drugimi kvarki). Sedaj
privzamemo za gibalno količino že kar znan Heisenbergov izraz
p ≈ h/(4π2d) in za kinetično energijo Ek ≈
pc (ker je mirovna
masa kvarka zelo majhna, velja pc >>
mqc2).
Kinetična energija enega kvarka je tako ocenjena
kar na okrog 100 MeV. Za vsoto treh kvarkov pa na okrog 300 MeV – kar je že zelo blizu 1/3 mirovne
energije protona mpc2 = 938.272 MeV. Torej nas že ta ocena pripelje do sklepa, da je
pri protonih, nevtronih zelo malo mirovne mase. Masa atomov se v resnici izraža iz kinetične
energije kvarkov (Ek/c2) in v energiji delcev polja močne jedrske sile, v gluonih –
ki so tudi brez mase (njihov energija skupaj je cca 600 MeV).
Delčna in valovna narava osnovnih delcev, valovna funkcija, vodikov atom, Bohrov model
Da je prva polovica 20. stoletja res obrnila znanost na glavo, pove tudi nepričakovano odkrita
lastnost osnovni delcev, to je dvojna narava kvantnih delcev - da se torej obnašajo tudi kot
valovanje, interferirajo in jim tako lahko tudi pripišemo valovno dolžino
(λ = h/p). Ker
lahko elektronu zelo povečamo gibalno količino in s tem skrajšamo valovno dolžino – so to
lastnost kmalu uporabili za elektronski mikroskop – ki dosega velike povečave (ločljivot
je sorazmerna z valovno dolžino). Louis de Broglie že leta 1924 pokaže na to dvojno naravo
gibanja kvantnih delcev z maso (recimo elektronov), ki jih lahko obravnavamo tudi kot valovanje.
De Broglie pravilno zapiše tudi njihovo valovno dolžino kot kvocient Planckove konstante in
gibalne količine:
λ = h/(mv),
pri visokih hitrostih velja relativistični izraz
λ = h/(γmv) = h(1 – v2/c2)1/2)/(mv).
Temu so se nekateri na začetku posmehovali, a so resni eksperimentatorji kmalu potrdili
pravilnost njegovega razmišljanja (ideja se je rodila zaradi kvantizacije energijskih
nivojev atomov). Povejmo še, da si danes brez elektronskega mikroskopa ne moremo predstavljati
raziskav celic, genskega zapisa, nasploh moderne znanosti ...

|
|
Schrödingerjev pristop - opis kvantnih delcev s pomočjo valovne funkcije
Poskušajmo se približati duhu vrhunca matematičnega zapisa lege delca v kvantni mehaniki
(vesolje, svet velikih teles in osnovnih delcev sta eno). Za prosti elektron brez zunanjih
sil veljata že znani zvezi za gibalno količino p = h/λ in za energijo približno
E ≈ hν = ℏω ,
kjer je ℏ = h/(2π).
Zakaj velja zveza E ≈ ℏω (?) -
če se elektron zelo približa svetlobni hitrosti velja, da je člen
(c2m)
zanemarljiv napram polni energiji γc2m hitrega elektrona in zato enačbo
E2 = (c2m)2 + (cp)2
poenostavimo v E ≈ cp = ch/λ = hν =2πνh/(2π) = ℏω,
glejte poglavje
"Fizika
velikih hitrosti in pospeškov, zelo pomembno poglavje za razumevanje pojavov v vesolju".
V tem primeru se
prosti gibajoči elektron obnaša kot harmonično valovanje [velja enačba iz srednje šole
y = Acos(kx - ωt) = Acos(2πx/λ - ωt)
– osnove fizike, valovni vektor k = 2π/λ]
in valovna funkcija se zapiše z gibalno količino p in energijo E kot navadno
linearno valovanje v x smeri:
Ψ(x,t) = Acos(kx - ωt) = Acos(2πx/λ - ωt) = Acos(px/ℏ – Et/ℏ).
Za valovno dolžino
λ in ω smo torej privzeli že znani osnovni povezavi (p = h/λ in E = ℏω).
Za valovni vektor k velja torej povezava k = p/ℏ. Zapišimo se gibalno količino delca
p = mv in kinetično energijo E = mv2/2 = p2/(2m), od koder sledi, da je gibalna količina
p = (2mE)1/2. Tako za valovni vektor k velja izraz:
k = p/ℏ = (2mE)1/2/ℏ - velja za gibanje delca izven potenciala.
Če gibajočemu prostemu elektronu (brez zunanjih sil, potencialov) pripišemo klasično harmonično
valovno funkcijo
Ψ(x,t) = Acos(2πx/λ - ωt) = Acos(px/ℏ – Et/ℏ),
tako je sklepal De Broglie,
je to idealizirana prispodoba klasične mehanike (»kjer se ne kocka«).
Take valovne funkcije poznamo iz valovanj na vodi, pri struni ... iz srednje šole
(pove nam odmik vala od ravnovesne lege v točki x in času t, lahko pa tudi z odvajanjem izračunamo
hitrost in pospešek vala, seveda tudi energijo). Kako pa je v kvantni mehaniki?
Če pa kvantnemu delcu (elektronu) hočemo pomeriti lego (da preverimo
pravilnost valovne funkcije), smo zagotovo primorani upoštevati
Heisenbergovo načelo nedoločenosti (to je »kockanje«): ΔpΔx ≥ h/(4π).
Za kvantni zapis uporabimo Eulerjevo povezavo za zapis kotnih funkcij
eix = cos(x) + i*sin(x),
ki nas pripelje do valovne funkcije
Ψ(x,t) =
Aei(px/ℏ – Et/ℏ) = Ae– iEt/ℏΨ(x)
(ta funkcija je prikladnejša pri opisu kvantnega valovanja – pri
odvodih se praktično ne spremeni, ima še druge prednosti pri računanju verjetnosti).
Eulerjeva formula je torej zelo priročen način, da se povežeta eksponentna funkcija in
trigonometrične funkcije (sinus in kosinus),
ki opisujejo valovno naravo sistema. Brez kompleksnih števil pa bi bil
matematični opis teh pojavov tudi precej bolj zapleten, še posebej pri merjenjih in obravnavi
superpozicij
(kvantni sistem obstaja v več stanjih hkrati - kombinacija različnih možnosti - ko pa pomerimo recimo
elektron, bo ta vstopil v eno izmed možnih stanj)
in interferenc
(interferenca se lahko zgodi samo, če imamo superpozicijo različnih možnosti - recimo interferenca
gibajočih elektronov ali svetlobe na režah).
Ta srednješolska funkcija nam bo zelo pomagala pri razumevanju De Broglie –
Einstein – Schrödingerjeve matematike opisa lege kvantnih delcev v času in
prostoru.
Podajmo primer interference na dveh režah, ki ga že poznamo iz klasične fizike.
Interferenca nastane, ko imamo več poti (ali stanj), skozi katere lahko sistem preide
in te poti valovanj interferirajo med seboj. Rezultat je, da se verjetnostni vzorec, ki ga opazimo na koncu,
lahko poveča (konstruktivna interferenca) ali zmanjša (destruktivna interferenca), odvisno od faznega zamika med potmi.
Poglejmo, kako to izgleda pri eksperimentu na dveh režah, kjer imamo dve poti, skozi kateri lahko delci (recimo elektroni)
potujejo.
Za ta preprost primer bomo uporabili kompleksna števila, Schrödingerjev zapis, torej Eulerjevo
notacijo in pokazali, kako interferirata dve poti elektronov (privzeli bomo poenostavitev in izraz
(2πx/λ - ωt) zapisali kar kot kot φ - ja, v resnici je to kot).
Recimo, da imamo dve poti: P1 in P2. Valovni funkciji za obe poti bosta zapisani v kompleksni obliki
(kot smo že omenili, kot dve enaki sinusni valovanji z različnimi amplitudami A in B):
Ψ1 = A eiφ1 in Ψ2 = B eiφ2
Pri teh dveh valovanjih poznamo
A in B amplitudi za poti P1 in P2,
φ1 in φ2 pa sta fazi teh poti (višina in zamik valov v dani točki).
Skupna valovna funkcija je superpozicija,
ko se poti P1 in P2 združijo in se valovni funkciji prekrivata, je:
Ψ = Ψ1 + Ψ2 =
A eiφ1 + B eiφ2
- opisuje valovno funkcijo sistema — torej, potencialno stanje, dokler ga ne izmeriš.
Ko izračunamo verjetnost, dobimo interferenco, ki je enaka kvadratu skupne valovne funkcije, tako dobimo:
|Ψ|2 =
|A eiφ1 + B eiφ2|2
Ta izračun lahko izrazimo v naslednji poenostavitvi:
|Ψ|2 = A2 + B2 + 2AB cos(φ1 - φ2)
Konstruktivna interferenca nastane, če je fazni razmik φ1 - φ2 = 0 (ali večkratnik 2π,
ko je razlika poti valovanj 0 ali λ, oziroma mλ, m je celo število ),
amplitudi se seštejeta, kar poveča verjetnost, da bomo opazili določen izid.
|Ψ|2 = A2 + B2 + 2AB
Destruktivna interferenca nastane, če je fazni razmik
φ1 - φ2 = π (ali neparni večkratnik π,
ko je razlika poti valovanj λ/2 ali (2n + 1)λ/2, n je celo število )
potem se amplitudi odštejeta, kar zmanjša verjetnost za opazovanje določenega izida.
|Ψ|2 = A2 + B2 - 2AB
Najprej podajmo klasično sliko valovanja.
Če sta amplitudi A in B enaki, potem pri konstruktivni interferenci dobimo
vrednost za |Ψ|2 = A2 + A2 + 2AA = 4A2,
kar pomeni, da je amplituda skupnega valovanja |Ψ| = 2A.
Pri destruktivni interferenci pa dobimo (če A = B)
vrednost za |Ψ|2 = A2 + A2 - 2AA = 0,
kar pomeni, da je amplituda skupnega valovanja |Ψ| = 0 - valovanji se v tej točki odštejeta.
Ta dva rezultata sta poznana iz klasične fizike.
Kako pa je z interpretacijo v kvantni mehaniki?
Pri elektronih pa to pomeni, da v teh točkah, smereh, kjer velja |Ψ|2 = 0, skoraj zagotovo ne bomo zaznali elektronov.
Pri maksimalni vrednosti |Ψ|2 pa, da jih bomo najverjetneje zaznali.
V kvantni mehaniki kvadrat valovne funkcije (v tem primeru superpozicije dveh stanj)
|Ψ|2 ni gostota delcev (ali amplituda), ampak verjetnost (pravilneje verjetnostna gostota) za delec, recimo elektron.
V resnici je potrebno valovne funkcije (in njihove koeficiente A, B) normirati,
če hočemo, da superpozicija predstavlja veljavno kvantno stanje, saj velja za verjetnost, kje se nahaja delec,
za vse kote ali smeri dx, razdalje, da je le ta:
verjetnost = ∫|Ψ|2dx = 1.
Lahko še podamo analogijo
z glasbo.
Vemo, da z ušesi ne vidimo oblike zvočnega vala.
Kar slišimo, je rezultat interference, jakosti, frekvenc, itn, zvočnega valovanja.
Podobno v kvantni mehaniki ne “vidimo”
valovne funkcije Ψ(x,t), ampak zaznavamo učinke,
ki izvirajo iz nje (npr. interferenca |Ψ|2, verjetnost, energijske vrednosti).
Po tem uvodu in vaji pa si poglejmo še parcialne odvode valovne funkcije
Ψ(x,t) =
Aei(px/ℏ – Et/ℏ) = Ae– iEt/ℏΨ(x)
po času in kraju za naš prosti elektron (amplitudi A bomo zgolj začasno pripisali vrednost 1,
kasneje se bo v osnovni obliki Schrödingerjeve enačbe pokrajšala):
∂Ψ/∂x = (ip/ℏ)Ψ
in
∂Ψ/∂t = (-iE/ℏ)Ψ
Izrazimo še gibalno količino p in energijo E - če obe strani pomnožimo z iℏ velja:
-iℏ∂Ψ/∂x = pΨ
in
iℏ∂Ψ/∂t = EΨ
- zagotovo se spomnimo, da velja za kompleksno število (imaginarno enoto) i2 = -1,
- od tukaj potegnemo operatorja (ukaza za izračun) za gibalno
količino in energijo:
p = -iℏ∂/∂x
in
E = iℏ∂/∂t .
Ker se kinetična energija izraža s kvadratom
gibalne količine [ Ek = mv2/2 = p2/(2m) ], bomo rabili še dugi odvod
valovne funkcije po koordinati, kraju. Izvedimo torej drugi odvod, da dobimo p2:
∂2Ψ/∂x2 = (-p2/ℏ2)Ψ
Vse povedano združimo v skupno diferencialno enačbo opisa kvantnih delcev,
ki se obnašajo tudi kot valovanje.
Za prosto gibajoč delec velja energija E = mv2/2 = p2/(2m),
za valovanje pa E = hν = ℏω. Če izenačimo obe energiji, povežemo
tako valovno, kot delčno naravo kvantnih delcev preko povezave
ℏω = E = p2/(2m) in uporabimo operatorje
p = -iℏ∂/∂x in E = iℏ∂/∂t . Tako tudi
dobimo kar znamenito Schrödingerjevo diferencialno enačbo za prosti delec v eni dimenziji:
iℏ∂Ψ/∂t = -(ℏ2/(2m)) ∂2Ψ/∂x2
Diferencialna enačba torej hkrati povezuje kar obe naravi kvantnih delcev (tako valovno, kot delčno).Tako smo se približali duhu De Broglie – Einstein – Schrödingerjevih razmišljanj!
Takoj povejmo, da ima Schrödingerjeva diferencialna enačba podobno vlogo kot drugi Newtonov zakon v klasični fiziki mdv/dt = F, ki nam opiše x lego mase m v času t (kar pa lahko zapišemo tudi preko energije). Mi smo za zdaj obravnavali le prost elektron, a večinoma elektrone (delce) srečamo vezane s silo v kristale, v atome, molekule ... – torej so v nekem potencialu - to pa opisuje Hamiltonov operator na desni strani enačbe iℏ∂Ψ/∂t = -( (ℏ2/(2m)) ∂2Ψ/∂x2 ) = HΨ (mi smo vpeljali le operator za kinetično energijo H = -(ℏ2/(2m)) ∂2/∂x2 ). H je torej oznaka za Hamiltonov operator, klasično izhaja iz vsote kinetične in potencialne energije: H = Ek + Ep = p2/(2m) + V(t,r), recimo za klasični vzmetni (harnonični) oscilator velja funkcija H = mv2/2 + kx2/2, od koder sledi analogija za hamiltonov operator H = -(ℏ2∇2/(2m) + V(t,r) na Schrödingerjevi valovni funkciji Ψ, kjer je ∇2 = ∂2/∂x2 + ∂2/∂y2 + ∂2/∂z2 Laplaceov operator (∇ ali nabla). Naša preprosta sklepanja o valovanju prostega elektrona nam torej pomagajo pri razumevanju Schrödingerjeve diferencialne enačbe in valovne funkcije, kot rešitev le te. Einstein je videl v teh razmišljanjih in enačbah le prehodno matematiko in prehodno opisovanje sveta osnovnih delcev (zanj Bog ne kocka). Splošna oblika Schrödingerjeve diferencialne enačbe je torej:
iℏ∂Ψ/∂t = HΨ ali tudi EΨ = HΨ
Končna splošna oblika Schrödingerjeve valovne funkcije v prostoru je:
Ψn(r,t) =
A e– iEnt/ℏΨn(r)
in je tako postala osnova opisa gibanja v kvantni fiziki.
Oznaka r je sedaj krajevni vektor v prostoru (zamenjali smo torej eno dimenzijo x s prostorom
r, kar v osnovi zapišemo s tremi pravokotnimi koordinatami: x, y, z
- lahko pa tudi s cilindičnimi, sferičnimi koordinatami ...).
Seveda predvidevamo več kvantnih stanj z oznako n, to je glavno kvantno število.
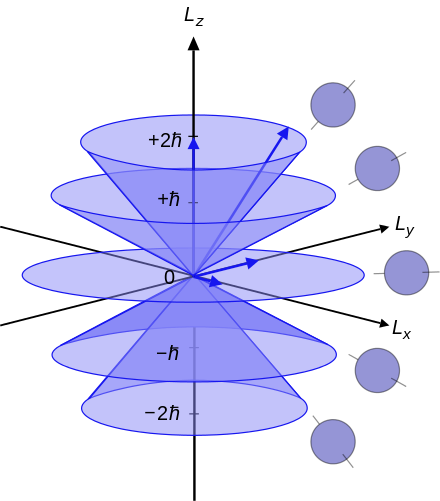

Vektorski model vrtilne količine L preko
kvantnega števila ml za azimutno (orbitalno) kvantno število l = 2 (levo).
Vektorska predstavitev celotne vrtilne količine (orbitalne L in spinske S) J = L + S (desno).
Lahko pa imamo, slika zgoraj, še magnetno kvantno število (večinoma ga označeno z m,
oziroma ml = ±l, to je "črka l") - zaradi "kroženja" elektrona (vrtilna količina
je torej tudi kvantizirana, ml predstavlja projekcijo vrtline količine L s kvantnim številom
l na smer zunanjega mmagnetnega polja), poznamo tudi tirno magnetno
kvantno število "l" zaradi vrtenja okrog skupnega težišča - pomembno je recimo tudi pri molekulah.
Potem poznamo še magnetno spinsko kvantno število s -
recimo zaradi "rotacije" elektrona okrog lastne središčne osi, lastna vrtilna količina
(s = 1/2 za elektron in v atomu lahko zavzame dve vrednosti ms = ±1/2).
Vrtilne količine se vektorsko seštevajo, seveda z upoštevanjem kvantnih števil - slika zgoraj.
Poudarimo še enkrat,
da je to le splošni zapis valovne funcije, kjer ji krajevni del
Ψn(r), tudi energijo En,
določa potencial – zunanje sile. Najti specifično rešitev valovne funkcije,
katero določajo zunanje sile
(potenciali) pa seveda ni enostavno - razen za preproste primere (harmonični
oscilator, vodikov atom, prosti delec). A te osnovne rešitve nam pomagajo
pri numeričnih metodah iskanja obnašanja kompleksnejših sistemov (atomi z večjim številom
elektronov, molekule, kristali, različna agregatna stanja snovi ...).
Amplitudo A se pri valovni funkciji lahko piše kot Ψon ali tudi an ...,
odvisno od vira.
Produkt valovne funkcije
ΨΨ
pa nam da
verjetnostno gostoto za lokacijo delca
(tega tudi Schrödinger na začetku ni vedel). Velja pa seveda, da je verjetnost
1, če integriramo po celotnem prostoru
∫ΨΨd3r = 1.
Valovna funkcija Ψ
je torej normirana na verjetnost 1 preko integrala produkta
ΨΨ
po celotnem prostoru. Torej je delec zagotovo del našega sistema (verjetnost 1),
ne vemo pa točno kje je – govorimo le o verjetnosti lege (v skladu s Heisenbergomin
načelom nedoločenosti in kockanjem ...
V enačbi je
En
lastna vrednost
energijskega stanja (lastna vrednost energije) in seveda ni poljubna.
Vsaki lastni vrednosti energije En pripada ena rešitev Schrödingerjeve
diferencialne
enačbe - to je lastna valovna funkcija Ψn(r,t).
Diskretni energijski
nivoji kvantnih delcev (recimo nukleonov, atomov, molekul in
oddanih ali absorbiranih fotonov) so prstni odtisi vesolja, ki nam
omogočajo preučevanje oddaljenih svetov, zvezd, planetov, galaksij,
začetkov vesolja, samo dinamiko vesolja ...
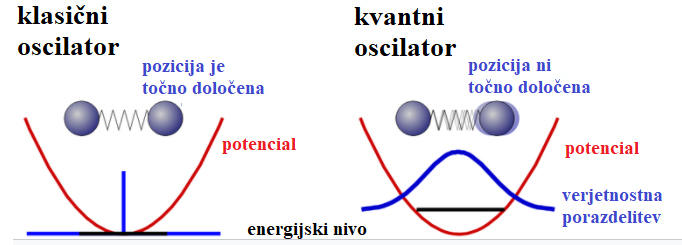
Primerjava med klasičnim in kvantno mehanskim oscilatorjem. Pri klasičnem (levo)
so možne vse vrednosti energij, tudi nič, enako velja za lego, gibalno količino.
Pri kvantnem oscilatorju desno, zaradi Heisenbergovega načela nedoločenosti
( ΔpΔx ≥ h/(4π) ),
to ni mogoče (energija 0 ni mogoča,
Eo = ℏω/2),
govori se le o energiji ničelne točke
(ki je na desni nekoliko dvignjena črta znotraj paraboličnega potenciala
kx2/2)
ali nihanju okrog ničelne točke (kjer je verjetnostna gostota,
da se nahaja delec, največja - pri osnovni energiji
Eo = ℏω/2). V teoriji kvantnega polja to vodi do nihanj
(fluktuacij) vakuuma – nekateri vidijo v tem začetek vesolja.
Več sledi.
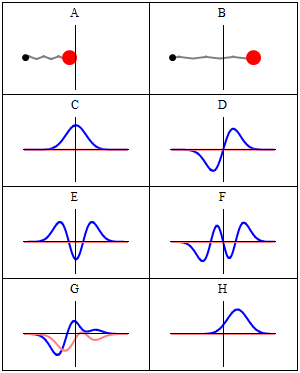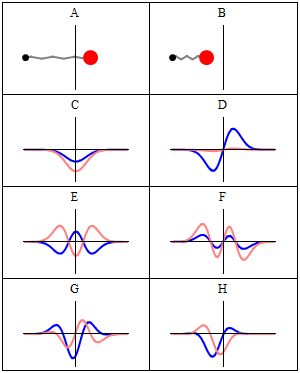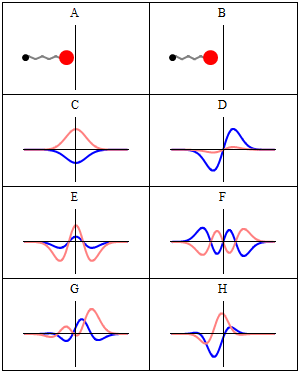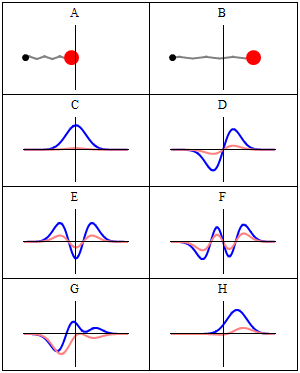
Harmonični oscilator v klasični mehaniki (A - B) in kvantni mehaniki (C - H).
Primerjava konceptov klasičnega in kvantnega harmoničnega oscilatorja za en sam delec brez spina.
Procesa se zelo razlikujeta. Klasični proces (A–B) je predstavljen kot gibanje delca po trajektoriji.
Kvantni proces (C–H) nima takšne trajektorije. Namesto tega je predstavljen kot val;
tukaj navpična os prikazuje realni (modri) in imaginarni (rdeči) del valovne funkcije.
Slike (C–F) prikazujejo štiri različne rešitve Schrödingerjeve enačbe za stoječe valovanje.
Slike (G–H) prikazujejo dve različni valovni funkciji, ki sta rešitvi Schrödingerjeve enačbe,
vendar ne za stoječa valovanja.

Vsak od teh treh grafov je valovna funkcija, ki ustreza časovno
odvisni Schrödingerjevi enačbi za harmonični oscilator
(klasični harmonični oscilator:
H = mv2/2 + kx2/2,
oziroma za kvantni zapis; iℏ∂Ψ/∂t = HΨ).
Levo: Realni del (modri) in imaginarni del (rdeči)
valovne funkcije. Desno: porazdelitev verjetnosti lege delca za dano
valovno funkcijo na določenem položaju. Zgornji dve vrstici sta primera
stacionarnih stanj, ki ustrezajo stoječim valovom (verjetnost porazdelitve
lege je simetrična). Spodnja vrstica je primer stanja, ki ni stacionarno
(motnja – ni simetrije). Desni stolpec prikazuje, zakaj stacionarna
stanja nosijo to ime.
Hamiltonov operator za harmonični oscilator je
H = -ℏ2∇2/(2m) + mω2x2/2
saj velja, da je maksimalna kinetična energija enaka maksimalni prožnostni
kx2/2 = mω2x2/2.
Schrödingerjeva enačba povezuje delčno in valovno naravo
kvantnih sistemov
iℏ∂Ψ/∂t = HΨ ,
od koder sledi za stacionarno stanje izraz:
EnΨ =
-ℏ2∇2Ψ/(2m) + mω2x2Ψ/2
rešitev je za valovno funkcijo
Ψn(x)
precej zapletena (kot je sicer reševanje
diferencialnih enačb zapleteno, kdaj je tudi odvisno od navdiha, intuicije, izkušenj),
rešitev je:
Ψn(x) = ( mω/(πℏ))1/4
(1/(2nn!)1/2)
ℋn
( x(mω/ℏ)1/2 )
e-mωx2/(2ℏ)
-
ℋn
so Hermitovi polinomi
Za lastna energijska stanja velja:
En = ωℏ(n + 1/2)
Prvo stanje energije
( Eo = ωℏ/2 )
lahko uganemo že iz oblike potenciala
kx2/2 = mω2x2/2.
Za osnovno stanje n=0 velja:
Ψo(x) = ( mω/(πℏ))1/4e-mωx2/(2ℏ)
, dobimo Gaussovo krivuljo,
glej graf, kjer se na dnu razbere Gaussovo porazdelitev -
in znotraj tega vala lahko sklepamo na lego delca, recimo elektrona.
Verjetnost se izračuna kot
∫ΨΨdx = ∫
( mω/(πℏ))1/4e-mωx2/(2ℏ)
( mω/(πℏ))1/4e-mωx2/(2ℏ)
dx =
( mω/(πℏ))1/2∫e-mωx2/ℏdx
,
ker je integral ∫e-ax2dx = (π/a)1/2,
velja, da je inetgral od -∞ do +∞ pričakovano enak
( mω/(πℏ))1/2∫e-mωx2/ℏdx
= 1. V kvantni mehaniki torej
ni samo kockanje, je pa seveda prisotna določena negotovost, ki
pa jo znamo poračunat (podobno, kot je naše življenje nekoliko
negotovo, zato pa je tudi zanimivo, če se tega zavedamo ...).
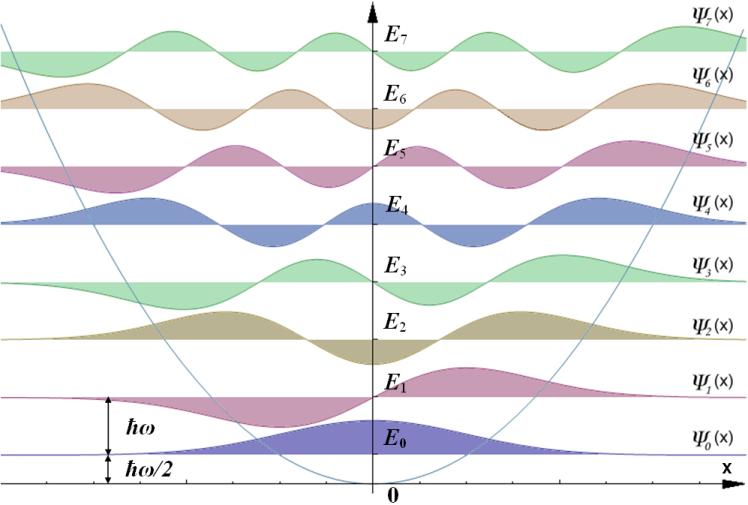
Potek valovne funkcije kvantnega harmoničnega oscilatorja za različne
energijske vrednosti. Za osnovno stanje n=0 velja:
Ψo(x) = ( mω/(πℏ))1/4e-mωx2/(2ℏ)
, dobimo Gaussovo krivuljo.
Primeri harmoničnih oscilatorjev v naravi
Primeri harmoničnih oscilatorjev v naravi Harmonski oscilator je pomemben modelski sistem v kvantni fiziki, saj je eden redkih zaprtih rešljivih sistemov kvantne mehanike (torej brez približkov in numeričnih metod). Z njim lahko razložimo številna fizična dejstva. V molekularni fiziki omogoča modelski približek povezav med atomi (v molekule) in tako omogoča napoved spektrov vibracij (zelo, zelo pomembno tudi za astronomijo, pri določanju vrste molekul na eksoplanetih, itn). To lahko ponazorimo tako, da prikažemo vez skozi dve masni točki (dva atoma), ki sta med seboj povezana z »vzmetjo« (harmonski potencial V ≈ kx2/2) in zato med seboj nihata.

Harmonični oscilator je dober približek, vsaj za nizke vibracijske
energije molekul.
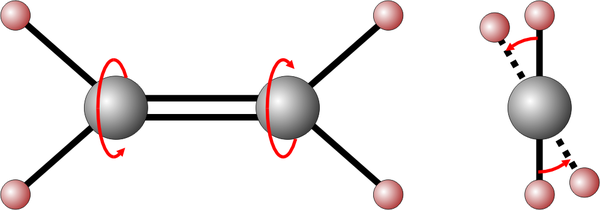
Drugi primer je torzijska vibracija molekule etena (etilena C2H4).
Pri tem se dvojna vez tako rekoč zvije in dva atoma vodika med vrtenjem
nihata drug proti drugemu.
V sodobni atomski fiziki se atomi in ioni, ki jih je treba pregledati, analizirati, v ta namen ujamejo in ohladijo v ionske pasti ali optične pasti (atomi se ujamejo v polju nič znotraj presečišča šibkega kvadropolarnega prostorsko spreminjajočega se magnetnega polja in šestih krožno polariziranih laserskih žarkov - to je lasersko hlajenje na samo nekaj milijonink Kelvina ) - seveda za potrebe višje ločljivosti meritev. Poleg tega je v takih primerih mogoče raziskati različna fazna stanja snovi (npr. Bose-Einsteinovi kondenzati, Fermijevi kondenzati). Takšne pasti imajo kot prvi približek parabolični potencial (harmonski potencial V ≈ kx2/2). Tako lahko delce v teh primerih opišemo tudi z modelom kvantno-mehanskega harmoničnega oscilatorja.
V fiziki trdnih snovi pa opisuje Einsteinov model metodo za izračun prispevka mrežnih vibracij (fononov) k toplotni kapaciteti kristalne trdne snovi. To je osnova opisa trdne snovi, ki jo modelsko sestavlja N kvantnih harmoničnih oscilatorjev, od katerih lahko vsak niha neodvisno v treh smereh.
Osnovni gradnik v svetu atomov je vodikov atom Kvantna mehanika seveda primarno išče rešitve za pojasnitev svetlobnih spektrov atomov – za energijske nivoje elektronskih oblakov in tudi za kemijske lastnosti elementov. Za vajo zgolj nastavimo Schrödingerjevo enačbo za najpreprostejši atom – to je vodikov. Vse teče podobno kot pri prostem elektronu ali harmoničnem oscilatorju, le ta je potencialna energija tokrat Colombova V = -epee/(4πεor). Za maso elektrona m pa vstavimo reducirano maso μ = mM/(m+M), M je masa protona, m je masa elektrona (tako računamo gibanje okrog masnega centra – kot pri Keplerjevih zakonih). Klasični Hamilton je H = p2/(2m) + V = p2/(2μ) – e2/(4πεor), od koder sledi analogija za hamiltonov operator H = -ℏ2∇2/(2μ) – e2/(4πεor). Zapišimo še Schrödingerjevo enačbo:
iℏ∂Ψ/∂t = HΨ
iℏ∂Ψ/∂t = ( -ℏ2∇2/(2μ)
– e2/(4πεor) )Ψ
A poiskati rešitev valovne funkcije
Ψ
že za najbolj preprost atom, zahteva kar nekaj spretnosti
(saj moramo upoštevati veliko kvantnih stanj in števil – energijskih stanj elektrona …).
Spodaj je podana zgolj slika verjetnostne gostote Ψ*Ψ lege elektrona. Splošna rešitev
je precej zapletena, podajmo pa le valovno funkcijo (neodvisno od časa) za osnovno
kvantno stanje atoma v sfernih koordinatah
Ψnlm(r,ϑ,φ) = Ψ100
= (z3/(πa3))1/2 e-zr/a,
potem za stanje
n=2, l=1, m=0 velja:
Ψ210 = (z3/(32πa3))1/2 (zr/a)
e-zr/(2a) cos(ϑ),
kjer velja
En
= - z2mee4/(2(4πεonℏ)2)
= - (e2/(4πεo))(z2/(2an2))
a = 4πεoℏ2/(mee2)
= ℏ/(mecα) – je Bohrov radij
( α = e2/(4πεoℏc)
je konstanta fine strukture)
Vodikov atom v različnih kvantnih stanjih. Slika prikazuje različne verjetnostne gostote
Ψ*Ψ lege elektrona skozi ravnino xz za elektron ob protonu pri različnih kvantnih številih
n, l, m
(desna kolona so vrednosti glavnega kvantnega števila n (1, 2, 3)
– to število je vpeljal že Bohr; glavno magnetno kvantno število je za
vse m = 0; črka s pomeni magnetno azimutno (orbitalno ali tirno) kvantno število l = 0, p pomeni l = 1,
d pomeni l = 2). Bolj je barva svetla, večja je verjetnost za lego elektrona.
Za osnovno kvantno stanje atoma v sfernih koordinatah je valovna funkcija
Ψnlm(r,ϑ,φ) = Ψ100
= (z3/(πa3))1/2 e-zr/a
(slika levo zgoraj velja za produkt Ψ100*Ψ100).
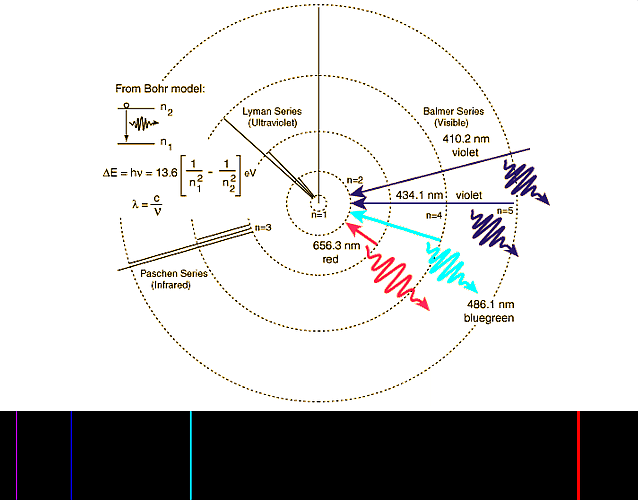
Slika prikazuje vmesni, sedaj že presežen Bohrov model vodikovega atoma,
ki pa je pravilno napovedal valovne dolžine spektralnih črt in je tako vseeno
zelo usmeril bodoči razvoj fizike, tudi astronomije. V čem je problem zgolj
klasičnega modela s kroženjem elektrona okrog jedra? Ker je kroženje pospešeno
gibanje in povzroča sevanje, bi tako elektroni kmalu izgubili energijo in bi po
spirali padli na protone (ljudje bi se zmanjšali na stotino mm ..., ter cel
svet v enakem razmerju). Vemo pa, da se to ne zgodi.
Povzetek mehanike osnovnih delcev
Dotaknimo se še stabilnosti (velikosti) sveta atomov pri zmernih temperaturah (recimo,
ki omogočajo življenje). Veliko je vprašanj na temo, kako to, da elektroni ne padejo
na protone – saj se oboji vendar privlačijo (kot prvo, pri takem padcu bi se sprostila
nerealna neskončna energija – vemo pa, da kaj takega vesolje ne premore, kaj šele atomi).
Najprej so poskušali to zagato rešiti s kroženjem elektronov okrog jedra (kot planeti
okrog Sonca) – a ker je kroženje pospešeno gibanje in povzroča izrazito sevanje,
bi tako elektroni kmalu izgubili energijo in bi po spirali padli na protone (ljudje
bi se recimo zmanjšali le na stotino mm ..., cel svet v enakem razmerju). A temu
ni tako! Veliko je bilo razmišljanj in idej o tem problemu. Na koncu se izkaže,
da če se elektron zelo približa jedru, se pojavi neke vrste odboj, ki ga vrže nazaj
v ravnovesno lego (to nam seveda kažejo tudi same dimenzije atomov), a to lahko tudi
razložimo z energijskim zakonom, z nekoliko dopolnjeno klasično vsoto kinetične in
potencialne energije – kateri poiščemo minimalno vrednost, a hkrati upoštevamo še
valovno naravo delcev (to dopolnitev slike, modela atomov, iz meritev sveta kvantnih
delcev, je predlagal De Broglie). V izraz za gibalno količino elektrona vstavimo kar
valovno povezavo, ki jo je predlagal De Broglie
p = h/λ , kjer je en val kar enak
obsegu »orbite«
λ = 2πr,
od koder sledi za gibalno količino:
p = h/(2πr) = ℏ/r. Zakaj
pa atom ne seva (čeprav še zmeraj govorimo o gibalni količini in tudi o pospešenem
gibanju), morebiti pa seva, a na drugačen način - zdi se, kot da si v resnici
v ravnovesnem stanju proton in elektron stalno izmenjujeta delce elektromagnetnega polje
– to je (virtualne) fotone (in tako se bilanca oddanih in prejetih fotonov uravnoteži).
Do enakega rezultata za gibalno količino (kar je zelo pomembno) pridemo tudi preko načela
netoločenosti, kjer velja
rp = ℏ,
ko sklepamo na verjetnost lege elektrona nekje znotraj
krogle polmera r (to je ocena velikosti atoma). Če pogledamo vsoto konetične in potencialne
energije in poiščemo njen odvod, ter lego ničle odvoda, potem dobimo za minimum energije radij
rmin =
a = 4πεoℏ2/(mee2)
= ℏ/(mecα)
– to je Bohrov radij. Zakaj iščemo minimum celotne energije,
ker se zmeraj delec ali večje telo, nahaja (ali stremi) v točki z najnižjo energijo – primer:
ko smo se kot otroci sankali, smo se čez čas zmeraj ustavili na dnu kotanje –
princip je enak kot pri elektronu v atomu. Poglejmo še izračun povedanega
(upoštevajmo še valovno naravo elektrona za gibalno količino
p = ℏ/r).
Zapišimo energijo
E = Ek + Ep = p2/(2m)
– e2/(4πεor)
= ℏ2/(2mr2) – e2/(4πεor),
poiščemo odvod dE/dr = 0, za minimum energije po odvajanju sledi pogoj, enačba:
-2ℏ2/(2mr3) + e2/(4πεor2) = 0.
Izrazimo še lego r minimalne energije in tako dobimo že
zapisan rezultat:
r = rmin = a =
4πεoℏ2/(mee2)
= ℏ/(mecα) = 5.29×10-11 m.
In to je ocenjena velikost atoma tudi znotraj molekularne vezane strukture
vodika (premer okrog 0.1 nm). Uporabili smo torej klasično delčno in valovno
naravo elektrona. Sedaj pa tudi ŽE vemo, da kvantni delci v osnovnem stanju
nikoli nimajo vsote kinetične in potencialne energije nič, če so vezani
(recimo Ek = p2/(2m) ≠ 0)
– saj bi potem delci izgubili valovno naravo.
Simbolično lahko rečemo, da so kvantni delci
»nekaj živega – srce jim nikoli ne neha biti –
so valovni paketi« in prav ta narava jim recimo
omogoča tvorbo atomov preko izmenjave fotonov
(izjemno domiselna modelska rešitev za svet kvantnih
delcev, atomov ... – trenutno še ni junaka, ki bi jo uspel nadgraditi).
Kinetična energija elektrona z bližanjem protonu narašča hitreje
(1/r2),
kot se spreminja potencialna energija (1/r) – elektron se torej ne dovoli ujeti
protonu (razen v nevtronskih zvezdah – oziroma pri razpadu nekaterih atomov
(recimo rubidija v kripton), pri Augerjevem efektu, ko elektron iz notranje
K lupine pade v jedro in proton spremeni v nevtron – pri tem drug elektron,
ki gre sedaj na delno prosto lupino K, izseva rentgensko svetlobo ali pa odda
energijo višje ležečemu elektronu – Augerjev elektron – ki zapusti novonastali
atom, tako nastane ion; novo atomsko jedro pa preide v stabilno stanje večinoma
z gama izsevom). Fotone (virtualne) - delce prenosa sile - pa si proton in
elektron izmenjujeta znotraj elektromagnetnega polja – to je torej teorija
prilagojena meritvam ..., kot zmeraj v fiziki. Virtualne fotone je bolje
razumeti kot vzbujena osnovna kvantna stanja kvantnih polj - ti delci
so "začasni" v smislu, da se pojavijo pri prenosu sil in jih upoštevamo
pri izračunih interakcij, samih sil (bilanca izmenjave fotonov,
recimo elektron – proton, je torej v ravnovesju in tako z razlago stabilnosti
atoma ne kršimo pravil o izgubi energije zaradi elektromagnetnega sevanja samega
polja). Tudi energija elektrona je v osnovnem stanju, pri jedru atoma, različna
od nič in zato lahko tudi oddaja in prejema delce polja, delce sil –
to je virtualne fotone - oboje je torej povezano, osnovna ali vzbujena stanja
in izmenjava fotonov. Je v bistvu eno, je pogojeno – od nič različna energija
kvantih delcev v osnovnih stanjih in seveda obvezna izmenjava fotonov (v teoriji
je to izraženo preko Feynmanovih diagramov).
Tunelski pojav - zelo pomemben tudi za fuzijo v zvezdah !!!
 | 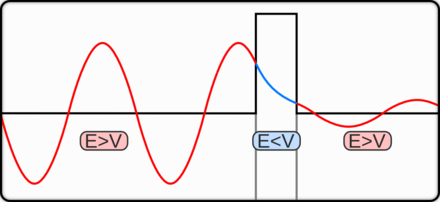
|
Poglejmo ali nas razmislek o izmenjavi bozonov fotonov pripelje do Coulombovega zakona ali nas masa bozonov pripelje do dosega šibke jedrske sile in masa bozonov pionov do velikosti atomskega jedra ali se da pokazati, da so kvarki v protonu in nevtronu le procentek energije (mase) obeh ključnih nukleonov - ostalo je energija nemasnih bozonov gluonov!?
Od fotonov kot nosilcev elektromagnetne sile do Coulombovega zakona
Lahko si predstavljamo, da če recimo elektrona (oznaka e ali q) izmenjujeta fotone energije E, se bo celotna energija para elektronov spremenila za količino, ki je približno sorazmerna tej energiji – kar povzroča elektrostatično interakcijsko silo. A virtualni fotoni morajo potovati na razdalji r in to lahko počnejo le s svetlobno hitrostjo. Se pravi, v času, ki je enak Δt = r/c. Načelo negotovosti, nedoločenosti določa ( ΔE Δt ≈ ℏ, dvojko smo izpustili, ker gre za ocene), da bo energija navideznih fotonov reda velikosti ΔE ≈ ℏ/Δt. Za čas vstavimo Δt = r/c in energija interakcije bo torej:
ΔE = k·ℏ·c/r
k je konstanta, ki jo dajo meritve.
Ker iščemo silo, jo lahko izpeljimo preko zapisane energije in razdalje r, ko velja,
da je sila odvod energije:
F = dE/dr, od tod dobimo silo F ∝ 1/r2:
F = -k·ℏ·c/r2.
To je izjemno pomemben razmislek, rezultat,
ki da odvisnost 1/r2.
Sila elektrostatične interakcije se zato zmanjšuje s kvadratom razdalje –
o tem pa nam govori že dolgo znani Coulombov zakon:
F = e1·e2/(4πεor2)
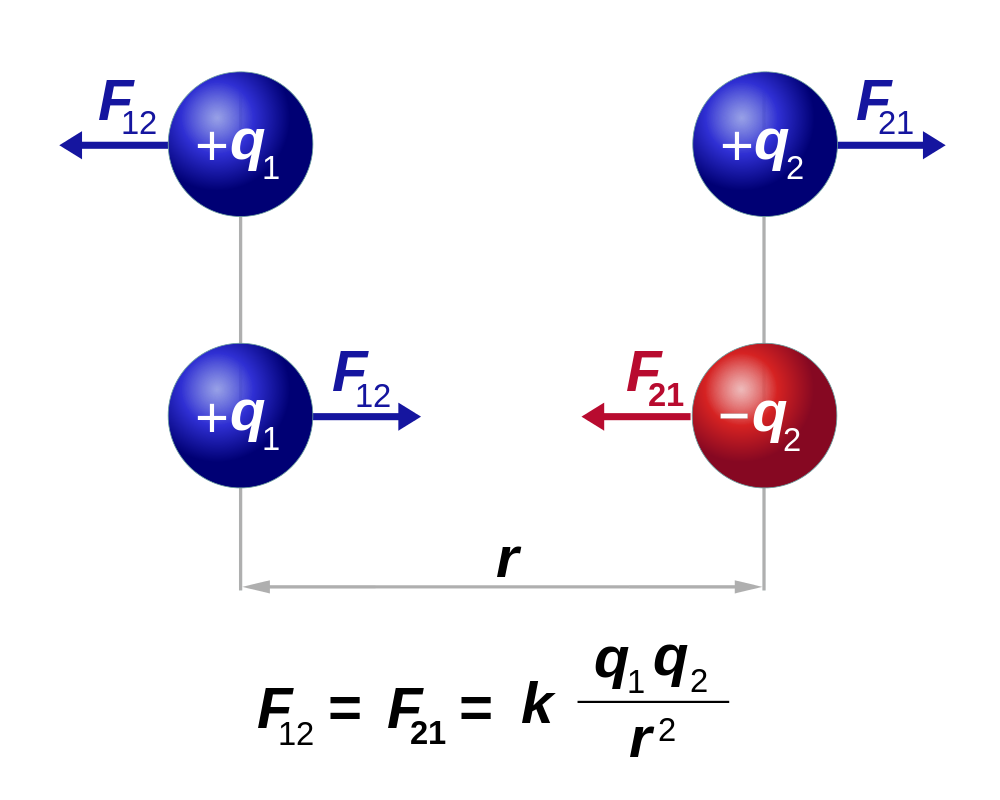


Te sile, recimo odbojne, lahko razložimo podobno kot sile med podajanjem žoge med šolarji - recimo na ledu to lahko prej opazimo
(ali na dveh čolnih), da se s podajanjem žoge
igralca odrivata - oddaljujeta.
Pri privlačni sili pa se zdi, kot da prvi meče žoge vstran od drugega, drugi pa te žoge
prejme v smeri proti prvemu.
Pri privlačni sili se zdi morebiti kdaj boljši koncept napete vrvi ali elastike med tekmovalcema,
ko se preko vrvi vlečeta vsak sebi in je vrv tako prenašalka privlačne sile.
A to so le prispodobe - ki pa lahko vseeno, sploh na začetku, zelo pomagajo
pri osnovnih konceptih razlage pojavnega sveta.
Izkaže še, da je k = 0,007.
To je dokaj poenostavljena izpeljava Coulombove sile iz
fotonov kot nosilcev elektrostatične (elektromagnetne) sile –
a koncept izpeljave
je sledil osnovni ideji o nosilcih sil in rezultat je zelo, zelo poučen
(vrne nam kar Coulombov zakon).
Doseg W in Z bozonov šibke sile
V primeru jedrske interakcije pa je delec prenosa sile masiven (poglejmo Z in W bozona –
recimo razpad beta [-], povzroči, da nevtron odda elektron znotraj razdalje 10-18 m
in tako nastaneta prost elektron, proton in še elektronski antinevtrino
n => p + e- + νe).
Pri razpadu nevtrona pravzaprav gre za to, da se eden od kvarkov d,
ki sestavlja nevtron pretvori v kvark u, pri čemer nastane bozon W-:
d => W- + u .
Ali znamo oceniti to kratko razdaljo delovanja 10-18 m šibke jedrske sile,
delca prenosa sile pa sta Z in W bozona (ki hitro razpadeta)? Bozoni so
bistveno težji od elektrona. Razdalja, ki jo lahko ti delci preletijo,
zaradi kratkoživosti, ni več poljubna. Dejansko njihova energija ne more biti manjša od
E = mc2.
Zato je njihov čas obstoja v najboljšem primeru reda velikosti
Δt = ℏ/ΔE = ℏ/mc2.
In ker masni delci šibke jedrske sile ne morejo potovati hitreje od svetlobe,
bodo lahko potovali le na kratke razdalje ΔL. Ko velja maksimalna pot
ΔL = Δt·c = ℏ/(mc).
Na primer, bozon Z ima maso približno 91,19 GeV, W pa 80,38 GeV.
To mu daje razdaljo delovanja reda
ΔL = ℏ/(mc) ≈ 2·10-18 m – pričakovano torej znotraj nukleona (nevtrona).
To je razdalja, ki smo jo iskali in pričakovali – deluje na nivoju kvarkov
(saj gre za pretvorbo d kvarka v u, nevtron sestavljajo kvarki
u, d, d, proton pa u, u, d).
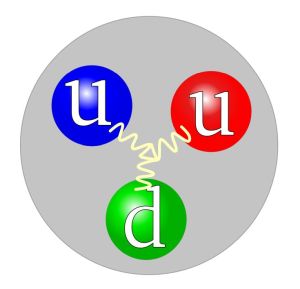
Proton sestavljajo kvarki u, u, d. Simbolične vzmeti so geometrijska prispodoba
gluonov – brezmasnih delcev močne jedrske sile, ki vežejo kvarke v nevtrone, protone, v pione ...
Doseg pionov – nosilcev sil med protoni in nevtroni
Pioni, ki prenašajo močno jedrsko silo med nukleoni (med protoni in nevtroni v atomskem jedru)
imajo energijo (maso) nad 100 MeV, recimo pion π± ima maso 139,57018 MeV, in ta podatek,
dobljen iz meritev, da doseg piona
ΔL = Δt·c = ℏ/(mc)
okrog 10-15 m. Kar pa je (pričakovano)
velikost atomskega jedra!!!
Preprost in grob dokaz - zakaj so kvarki po masi (energiji) neznatni in je masni svet
protislovno praktično
"prazen" ?
Še grobi oceni energije gluona recimo znotraj protona (oziroma posredno ocena 'mirovne' mase kvarka),
kjer bomo predpostavili,
da tri valovne dolžine povežejo tri kvarke (gluone bomo
torej predpostavili kot valovanje s hitrostjo c na obodu kroga s premerom d):
3λ ≈ πd. Kjer je d približno en fm
= 10-15 m (velikost protona). Kar da za valovno dolžino λ ≈ πd/3.
Kar vrne za grobo oceno energije gluona(ov):
E = hν = hc/λ = 3hc/(πd) =
3*4.135667696*10-15 eV·Hz-1*3 108m/( π*10 -15 m s) =
1 184 781 522 eV
≈ 1000 Mev (dober GeV).
Ker je masa protona 938.27208816 MeV/c2, to pomeni,
da je naša ocena bila nekoliko pretirana, ampak velikostni red pravilen.
Še druga ocena energije gluonov v protonu.
Če pa izvedemo oceno energije gluonov (spet)
preko nedoločenosti ΔpΔx ≈ h/(4π),
a tokrat privzamemo za nedoločenost lege Δx = d = 1 fm kar velikost protona, potem je gibalna količina gluona
v nukleonu [ p = h/(4πd) ]
in tako lahko zapišemo energijo gluona kot E = pc. Tako dobimo realnejšo končno oceno energije
za 3 gluone (ki vežejo tri kvarke):
E = 3pc = 3*h/(4πd)
= 600 MeV.
K temu lahko dodamo še oceno kinetične energije treh kvarkov, ki smo jo že
ocenili na okrog 300 MeV.
Iz teh ocenen izhaja, da morajo kvarki imeti zelo majhno vztrajnostno maso, "mirovno" energijo.
Korektni izračuni in meritve to tudi dokazujejo - kvarki predstavljajo le kak
procent mase protona, nevtrona. Naš svet je torej skoraj prazen v kontekstu
energije nemasnih gluonov - nosilcev sil in "masno" zelo skromnih kvarkov,
sestavnih gradnikov nukleonov. Masa je torej v glavnem skrita v energiji E nemasnih nosilcev sil in kinetični energiji
lahkih kvarkov:
m = E/c2.
Masa (mirovna) vseh treh kvarkov v protonu je le okrog 9 MeV/c2
(up okrog 2.3 in down okrog 4.8 MeV/c2).
Gre zgolj za ocene ..., tudi zgolj nedoločenost kvarkov da (logično)
podobne vrednosti (eno oceno kinetične energije kvarkov smo že podali zgoraj, ta je
okrog 300 MeV), a kvarki imajo tudi še
mirovno maso. Vrednosti energij protonov in nevtronov se v večji meri pripišejo nemasnim gluonom, tudi izmerijo ... (tudi sipalne slike,
preko obstreljevanja nukleonov z elektroni,
kažejo kvarke, slika zgoraj, kot da bi bili povezani z gluonskimi "vzmetmi").
Enačbo E = pc za nesnovni delec bomo še spoznali v poglavju:
Fizika velikih hitrosti in pospeškov, zelo pomembno poglavje za razumevanje pojavov v vesolju.
Drugače pa se v teoretčni fiziki ta problem rešuje s Feynmanovimi popotnimi integrali
(Feynman path integrals) - iskanje vseh možnih trajektorij za izračun kvantne amplitude med
delci.
Masni defekt, ki se pojavlja pri fuziji (nukleosintezi)
v sredicah zvezd,
se v fundamentalnem opisu najbolj odraža kot
majhno zmanjšanje energije gluonskega polja,
a to ni lokalna sprememba znotraj enega nukleona,
temveč kolektivni efekt vezanega jedra
(recimo dveh protonov in dveh nevtronov v heliju).
Pri zlitju protonov in nevtronov se ta “izgubljena” masa pojavi kot
energija fotonov (γ - sevanje) ter
kinetična energija delcev (jedra, elektronov, nevtrinov …).
Še zgolj čisti teoetični energijski pogled.
Ko se jedro oblikuje, se delci vežejo v nižjo energijsko stanje,
razlika v energiji se oddaja navzven,
zato ima končno jedro manjšo maso.
Večina mase nukleona torej ne prihaja iz mase kvarkov,
ampak iz energije gibanja in polj (QCD!).
Groba energijska razdelitev:
Približno:
≈ 1–2 % masa kvarkov
≈ 30–40 % kinetična energija kvarkov
≈ 40–50 % gluonska energija
≈ 10 % morje kvarkov + vezavna energija
(številke so odvisne od definicije in skale v QCD)
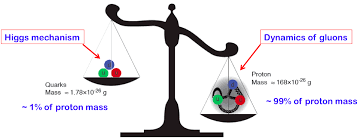
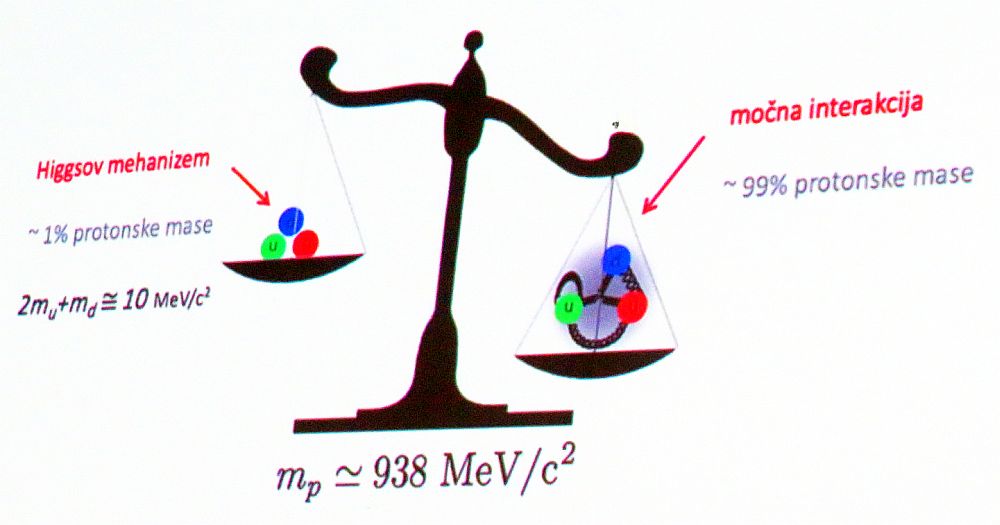
Simbolna slika, ki nazorno kaže, da je večino mase (ki jo tehtamo) v energiji nemasnih gluonov
(m = Egluonov/c2), ki lepijo kvarke
v protone, nevtrone ...
Nevtroni imajo nekoliko večjo maso od protonov, ker imajo tudi kvarki d nekoliko večjo maso od u.
Proton je sestavljen iz kvarkov u, u, d, nevtron pa trije kvarki u, d, d.
Masa (mirovna) vseh treh kvarkov v protonu je 938.27208816 MeV/c2, to je okrog 9 MeV/c2
(kvark up ima maso okrog 2.3 in down okrog 4.8 MeV/c2). Masa nevtrona je
1.674927471 x 10-27 kg ali 939565413.3 eV/c2.
Tako smo delno nakazali dosege delcev sil, katerih velik pomen smo omenili v uvodu
ciklusa razmišljanj o pomenu astronomije (pojasnili smo doseg elektromagnetne sile,
šibke jedrske sile pri razpadih in močne jedrske sile med nukleoni, ki tvorijo atome,
naš svet). To je koncept, ki ga zagotovo lahko razumejo dijakinje in dijaki naravoslovnih
gimnazij – bi ga morali v šoli absorbirati, saj govori o naših gradnikih (to torej niso atomi,
ampak subatomski osnovni delci vesolja in nosilci sil in čas je, da se ta snov uvede
v gimnazije – za večino dijakov pozneje več ne bo priložnosti, da bi ujeli osnovna
vedenja o zgradbi nas samih in vesolja).
Doseg gluonov, nosilcev močne jedrske sile med kvarki.
Gluoni delujejo znotraj nukleonov (proton, nevtron), pionov ...,
med kvarki na razdalji velikosti atomskega jedra 10-15 m
in znotraj te razdalje je sila konstantna (kar je za svet
velikih teles nenavadno, recimo kot pri raztezanju žvečilnega gumija ...),
energija pa se posledično veča z razdaljo r, tako velja za potencial
V = konst*r.
Ko se kvarka preveč oddaljita – se dovedena energija manifestira
v novih dveh parih kvarkov (slika spodaj).
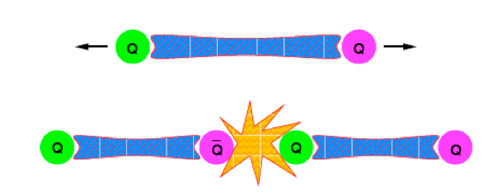
Ko se kvarka preveč oddaljita – se dovedena energija manifestira
v novih dveh parih kvarkov.
Pri nosilcih gravitacijske sile (gravitonih) smo še pri ugibanjih o njihovi naravi. Čeprav zaenkrat velja, da so gravitoni brez mase, bi pa še vedno nosili energijo, tako kot vsi drugi kvantni delci. Fotonsko energijo in energijo gluona prenašajo tudi delci brez mase. Ni pa jasno, katere spremenljivke bi lahko določile energijo gravitona, količino energije, ki jo nosi en sam graviton. Druga možnost je, da so morebiti gravitoni delci z maso. Analiza gravitacijskih valov je dala novo zgornjo mejo mase gravitonov. Comptonova valovna dolžina (λ = h/(mc)) gravitona je najmanj 1,6 × 1016 m ali približno 1,6 svetlobnih let, kar ustreza zelo majhni masi gravitona, največ 7,7 × 10-23 eV/c2. To razmerje med valovno dolžino in masno energijo se izračuna s pomočjo Planck-Einsteinove relacije (E = hc/λ), torej iz iste formule, ki elektromagnetno valovno dolžino povezuje z energijo fotona.
O tem, kje se kvantni delci nahajajo (recimo elektron) pa zapišemo z že omenjeno verjetnostjo preko valovne funkcije (∫ΨΨd3r). Sedaj tudi vemo, zakaj absolutna temperaturna ničla ni mogoča, ker kvantnih delcev ni brez gibanja – kvanti so kot otroci, brez dirkanja ne obstajajo ..., tudi za otroke zgolj simbolično velja ΔxΔp ≥ h/(4π). To prvič spoznate, ko otrok shodi in ga veselo postavite na tla in v trenutku nepozornosti že izgine iz vašega vidnega polja - groza - in pojavi se prvinski strah, huda zagata ... (zagotovo veste le, de je otrok nekje na tem svetu, upate, da je vsaj v vaši ulici, in da ga najdete preden pride socialna služba ...). Spomnimo se še na naš uvod v astronomijo – začeli smo ga z osnovnimi silami in z nosilci (delci) prenosa sil – in kvantne mehanike ni brez nosilcev sil.
Kvantni delci se čutijo recimo preko izmenjave fotonov (simbolična slika) –
to je tudi izvor električne sile med protonom in elektronom. Hkratna
'skrivnostna' delčna in valovna narava kvantnih delcev in dejstvo,
da lahko govorimo le o verjetnostni lege delca in njegovi hitrosti
(o nedoločenosti gibalne količine in lege) – pa je pred stoletjem
povzročilo zelo burne odzive takratnih eminentnih znanstvenikov.
Te dileme bi lahko strnili v Einsteinovo vprašanje - ali
Bog (narava) kocka? Zagotovo se kockanje zdi na nivoju osnovnih delcev dokaj
utemeljena prispodoba – na nivoju sestavljanja atomov v svet velikih teles,
pa je ta svet precej bolj predvidljiv, a ne čisto in je zato hkrati
skrivnostno čudežen.
Einstein, Podolsky in Rosen so predpostavljali skrite spremenljivke
(hidden variables), ki v naprej določajo stanje kvantnega delca (spin, pri svetlobi polarizacijo ...).
Verjeli so, da je kvantna mehanika le začasen pomanjkljiv opis narave, dokler ne najdemo
skritih spremenljivk.
Bell pa je dokazal, da skrtih sprmenljivk ni in torej velja kvantna mehanika kot pravilen
opis narave (svet vodijo naključja in ne skrite spremenljivke - če
pa obstajajo x spremenljivke, pa imajo spet kvantno naravo).
Bell je pred tem sam verjel, da obstajajo skrite spremenljivke.
Še aplikacija naključij na biologijo, na mutacije,
ki spreminjajo živa bitja. Vse mutacije ne vodijo k napredku. A nekatere mutacije pomagajo bitjem
preživeti v novih okoliščinah in temu pravimo - prednostno naključje.
Na to temo velja izrek: "Bog kocka, vendar šteje samo uspehe."
O tem pričata vesolje (naš dom) in mi sami – enkratnost in urejenost čudeža življenja preko atomov in hkrati njegova krhkost (ko nam kdaj koristi zgolj še teorija kaosa za napovedovanje mnogih pojavov, od razumevanja narave življenja, opisa vremena, razvoja galaksij, zvezdnih sistemov s planeti ...). Če je astronomija - Keplerjeva izjemno natančna nebesna mehanika (napovedovanje mrkov, konjunkcij, okultacij nebesnih teles, načrtovanje vesoljskih poletov ...) - človeku dala upanje, da bo kmalu lahko razumeli in do potankosti opisal ta naš prekrasni svet - pa smo dokaj kmalu tudi spoznali, da je že vremenska napoved pretrd oreh za še tako dobre modele in računalniške (nevronske) mreže ... Zakaj je bil Kepler tako uspešen (?), zato, ker je skoraj zmeraj obravnaval gibanje dve teles, ki se (po masi in obliki) ne spreminjata zelo hitro in se gibljeta praktično v praznem prostoru (spremljal je gibanje planeta in Sonca). A svet molekul, življenja, oceanov, naše atmosfere, vremena ... je veliko kompleksnejši kot svet dveh vesoljskih teles in ta kompleksen sveta atomov se opisuje statistično (vremenski modeli) preko tlaka (ki pomeni neko povprečje trkov delcev z neko površino), s temperaturo (ki spet pomeni neko povprečno kinetično energijo atomov in molekul), z Newtonovim zakonom, energijskim zakonom - termodinamična energijska enačba, z zakoni ohranitve mase, pretokov - kontinuitetne enačbe, gibalne količine, vrtilne količine, seveda se upošteva plinski zakon …, tukaj so torej Navier-Stokesove enačbe za gibanje tekočin, s Coriolisovim sistemskim pospeškom na vrteči se Zemlji, z opazovanimi sistemi, kjer so robni pogoji zmeraj variabilni (temperatura, tlak, gostota, hitrost vetrov, tukaj so viskoznost, oceani, trenje, gorske pregrade, kopno, vlaga v zraku, reflektivnost tal, vplivi iz vesolja, variabilno obsevanje ...). Dandanes je ločljivost najboljših globalnih modelov približno 10 km, lokalni (»naš« ALADIN) pa ima ločljivost okrog 4 km (ta podatek in recimo časovni korak 5 min sam po sebi pove, da napovedljivost vremena po nekaj dneh ni več zanesljiva – tudi kdaj za en dan ne - spomnimo se hudih poplav jeseni 2012, ki so bile napovedane za Notranjsko, zgodile pa so se na Štajerskem, tudi na Dravskem polju - tudi zaradi izpustov vode iz jezov avstrijskih hidroelektrarn ...). Vrnimo se na veliko skalo - zagotovo tudi sam Kepler odpove, ko naredimo natančnejše meritve, tukaj je relativistični prispevek k precesiji perihelija (elipsa planeta se počasi suka in opiše cvet), seveda pa motnje ostalih planetov, plimovanje, precesije perihelijev ... zelo zapletejo napovedi lege planetov na dolgi časovni skali (a ni tako hudo, kot recimo pri meteorologiji). Napoved časovnega razvoja bioloških sistemov pa je po svoje še bolj zapleten, zaradi vpliva okolice, tudi mutacij, genetike – in recimo »svobodne« volje možganov.
To - kar je naredil Einstein preko tenzorskih enačb polja za opis vesolja,
je Schrödinger naredil za opis gibanja v svetu osnovnih delcev preko
diferencialne enačbe gibanja (upošteval je delčno in valovno naravo kvantov)
in njene ustrezne rešitve - valovne funkcije Ψ. Einstein in seveda večina
sodobnikov, se je zanimala tako za svet velikih teles, za vesolje, kot za
svet osnovnih delcev (kvantni svet), za gradnike, ki nas sestavljajo.
In oba svetova sta povezana – sta eno. Omenjeno povezanost sveta velikih
teles in kvantnih delcev posebej dojamemo pri raziskovanju rojstva vesolja
– ko se rodijo tudi osnovni delci, sile, tudi nosilci, delci sil – ki
na nek način tudi pospešujejo vesolje ... In matematiki opisa obeh
svetov se dokaj prepletata – iščemo dinamiko, lego teles (metriko) in
seveda energije. Veliki svet je sestavljen iz zidakov osnovnih kvantnih
delcev narave in veliko kvantnih delcev na kupu (v zvezdi) tvori,
zaradi lastne težnosti, nove sestavljanke masivnih atomov (elemente: C, O, N, P, Fe, Ca, Na, K ...), ki pa so
direktno naši gradniki (gradniki planetov, Zemlje in življenja na njej).
Če smo malo slikoviti, nedoločenost kvantov (recimo kvarkov v protonih, nevtronih,
nedoločenost elektronov ...) v vsakdanjem kruhu in vodi,
ki ju dnevno zaužijemo, nikakor ne vpliva na to, na gotovost,
da bi NE vedeli, kaj sta kruh in voda (kako pomembna), da brez njiju telo in možgani ne morejo delovati.
In ko prebiramo zapise starih ljudstev, recimo poezijo ali astronomijo
(recimo vedenje o periodi ponovitve mrkov saros izpred 1000-e let), čutimo, razumemo naše prednike
(brez vsakega vpliva principa nedoločenosti iz sveta kvantov)
tako dobro,
kot recimo razumemo mamo ali očeta, ko nam naročita, da pospravimo kuhinjo ... po dobrem kosilu.
Kvantana fizika je torej pomembna za svet osnovnih gradnikov, a svet velikih teles zato ni negotov
v smislu nezmožnosti logičnih zaporedij, dogodkov (vsi zakoni narave,
ki jih opisujeta fizika, astronomija, veljajo univerzalno) - kar pričata vesolje samo, njegov razvoj
in seveda razvoj življenja ... Seveda pa obstaja izrazita povezava med svetom velikih teles
in dogajanjem v svetu osnovnih delcev. To se posebej odraža v razvoju življenja, fotosinteza
je izrazit kvantni pojav in seveda tudi same mutacije genov ...,
podobno lahko torej sklepamo pri odločitvah, delovanju
samih možganov, živčevja, telesa kot takega ...
Na nivoju atomov, fotonov, se že dolgo razmišlja, da bi kvantno stanje (recimo atomov) direktno uporabili kot zapis računalniških stanj (0, 1). Pričakuje se, da bo tako komunikacija med »qubiti« (teoretično) veliko hitrejša, kot to omogoča trenutna polprevodniška tehnologija naparevanja matrik stikal (tranzistorjev – kjer je tudi osnova kvantna mehanika, a medij prenosa je dokaj velik kontakt, plasti) – kjer čas računanja procesorjev tako upočasnjuje električni upor. Najbolj razširjen model je kvantno vezje, ki temelji na kvantnem bitu ali "qubitu" (quantum bit), ki je nekoliko podoben bitu v klasičnem računalniku – a je zelo svojeglav. Qubit je namreč lahko v kvantnem stanju 1 ali 0 ali v superpoziciji 1 in 0 stanj (to pomeni, da lahko delec zavzema vsa možna kvantna stanja istočasno). Na prvi pogled se zdi - da je tako stikalo neuporabno (prispodoba - »hkrati prijazna, a tudi neprijazna tašča«). A obstaja rešitev! Ko je stanje kvantnega delca izmerjeno - pa je zares v stanju 0 ali 1 (ko taščo srečamo, »je torej zgolj prijazna ali neprijazna«). A verjetnost obeh izidov je žal odvisna od kvantnega stanja qubita tik pred meritvijo (»torej ni vseeno kdaj obiščemo taščo – ker se njeno razpoloženje spreminja sproti, tako da stanja časovno žal ne moremo določiti v naprej – da bi recimo zmeraj naleteli na prijazno stanje - a ko se srečamo s taščo, takoj zvemo, kaj nas čaka«). Ta nedoločenost stanja je eden večjih problemov kvantnih računalnikov – tudi časovna nestabilnost.
Opišimo primer tribitnega registra v klasičnem računalniku - stanje računalnika, torej tranzistorjev
v kateremkoli trenutku je lahko eno od 23 = 8 stanj, zapišimo jih:
000; 001; 010; 011; 100; 101; 110; 111, zagotovo vemo, da mora biti ta računalnik v enem od teh
stanj in je skupna verjetnost vseh stanj enaka 1.
Po drugi strani pa so lahko v kvantnih računalnikih qubiti hkrati
v večih od teh stanj. Torej, če predstavimo stanja kvantnih računalnikov z 8 znaki:
a, b, c, d, e, f, g, h, potem njihovi kvadrati dejansko
predstavljajo verjetnost za vsako posamezno vrednost,
vsota teh verjetnosti pa je 1, torej sedaj velja:
|a|2 +
|b|2 + |c|2 + |d|2 + |e|2 +
|f|2 + |g|2 + |h|2 = 1
.
Če bi klasični računalnik izvedel n operacij,
bi teoretično lahko naredili z enakim številom »qubitov« na kvantnem računalniku KAR
2n operacij v istem časovnem intervalu,
to pomeni, da sta prirast zmogljivosti in hitrosti takšnega računalnika vsaj teoretično eksponentna.
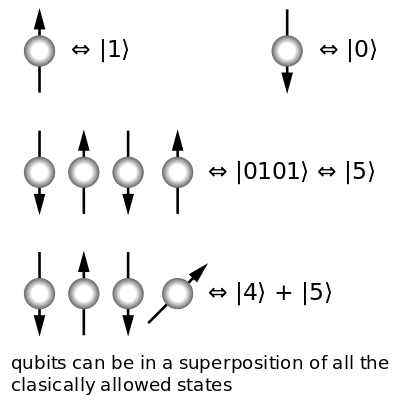
»Qubiti« so sestavljeni iz kontroliranih kvantnih delcev in mehanizmov za nadzor
(npr. naprave, ki ujamejo delce in jih pretvorijo iz enega stanja v drugo).
Slika prikazuje
metode nadzora, recimo za vsoto števil preko kontrole kvantnih delcev na podlagi kvantnega potenciala
»qubitov«.
V zadnjih letih so že uspeli zgraditi majhne kvantne računalnike, razvoj pa se nadaljuje. Številne službe po svetu vlagajo velika sredstva v razvoj kvantnega računalništva za potrebe kriptografije – razbijanja varnostnih digitalnih ključev (algoritmov šifriranj). Problem kvantnih procesorjev je tudi – da morajo biti pričakovano hlajeni na zelo nizke temperature. Trenutno nekateri kvantni računalniki zahtevajo, da se njihovi qubiti ohladijo zgolj na 20 milikelvinov, da se prepreči dekoherenca (sprememba stanj – saj veste, trki med delci so odvisni od temperature mv2 ∝ kT in s tem tudi sprememba energij, nestabilnost kvantnih stanj). In še ena zagata nas utruja, študija iz leta 2020 trdi, da lahko žal tudi ionizirajoče sevanje, kot so kozmični žarki, kljub nizki temperaturi povzroči, da nekateri sistemi v milisekundah spremenijo stanje - se »odklopijo«. Kot kozmični delci, sevanja, v živih bitjih povzročajo mutacije, se podobno dogaja v svetu umetne inteligence – v svetu procesorjev. V opisu narave računalnikov tako še enkrat opazimo izjemno povezanost globokega vesolja in življenja, dogajanja na Zemlji – tudi preko (ne)stabilnosti procesorskih tehnologij. Splošno prepričanje je, da bomo lahko, če bo mogoče zgraditi večje kvantne računalnike, nekatere probleme reševali veliko hitreje kot klasični računalniki (da bomo računske operacije, ki sedaj teoretično zahtevajo leta časa, rešili v kašnem dnevu). Tako bodo osnovni kvantni delci narave (v računalnikih) lahko tudi reševali zelo zahtevne simulacije začetkov vesolja - torej tudi samega sebe, njihovega nastanka, rojstva. In kaj nam bodo povedali rezultati fizikalno-kozmoloških modelov pognanih v super kvantnih računalnikih? Komaj čakamo na njihove odgovore – recimo, koliko danes tavamo v napačnih prepričanjih, modelih, glede nastanka vesolja, osnovnih delcev, se motimo v razlagi izvora skrivnostnega življenja … ali pa tudi ne? Nekateri pa bolj stavijo na računalniške nevronske mreže – ki bi nam naj (preko učenja) še bolje pomagale pri razlagi sveta – tudi pri razlagi, napovedih bodočnosti (pri upravljanju) trenutno še naše edinstvene Zemlje.
Kvantni delci se obnašajo zelo samosvoje – čutijo tudi stanja oddaljenih sosedov, če so nekoč
bili skupaj, prepleteni (recimo polarizacijo ali spin - smer vrtilne količine - če ga spremeni
sosed, ga tudi jaz – pojav »nam je znan iz vsakdanjega sosedskega življenja …«, tukaj je še,
že omenjena, skoraj hipna sprememba polarizacije fotonov) – ta pojav imenujemo tudi kvantna
teleportacija. Prvi eksperiment 1993 je potekal tako – da se je vhodni snop svetlobe po prehodu
skozi kristal razdelil v dva stožca – ki sta bila tako kvantno povezana, prepletena (Quantum entanglement).
Pomerili so
spremembo polarizacije - če se je la ta spremenila na enem snopu, se je tudi na drugem (recimo
pri ponovnem prehodu enega od žarkov skozi kristal in ponovni razdelitvi svetlobe). A bo mogoč
tudi kvantni teleportacijski internet (ali celo vpliv na naše nevrone – pod določenimi pogoji
prepletenosti)?
Še pojasnilo – da ne bo kake pomote – medtem, ko je teleportacija v znanstveni fantastiki
pogosto prikazana kot sredstvo za hipen prenos fizičnih predmetov, tudi ljudi, z ene lokacije
na drugo (to seveda ne gre ...), pa resnična kvantna teleportacija prenaša samo (zgolj)
kvantne informacije.
Poleg tega pošiljatelj morda ne ve lokacije prejemnika in ne ve,
katero določeno kvantno stanje bo prenešeno. Imena znanstvenikov povezana s tem izjemnim
pojavom (tudi najbrž v bodočih računalnikih) so Einstein-Podolsky-Rosen, potem CH Bennett,
G. Brassard, C. Crépeau, R. Jozsa, A. Peres in WK Wootters, ki so leta 1993 uporabili
dvojne komunikacijske metode za pošiljanje / prejemanje kvantnih informacij. Leta
1997 so eksperimentalno teleportacijo izvedli dve raziskovalni skupini pod vodstvom
Sanduja Popescuja in Antona Zeilingerja. Eksperimentalne kvantne teleportacije so bile
opravljene s stanji osnovnih delcev - vključno s fotoni, atomi, elektroni in superprevodnimi
tokokrogi - tudi seveda na večjih razdaljah. Najdaljša razdalja uspešne teleportacije
je bila 1400 km - skupine Jian-Wei Pana z uporabo satelita Micius za vesoljsko kvantno
teleportacijo. Kvantna teleportacija lahko tudi zmanjša napake povezane z zanesljivostjo
kvantnih izračunov, pri razporeditvi stanja logičnih vrat – qubitov.
A bo nekoč mogoč tudi kvantni teleportacijski internet (ali celo vpliv na naše nevrone –
pod določenimi pogoji prepletenosti)?
Ali je morebiti kvantna teleportacija rešitev »nerešljivega« problema, kako sploh komunicirati
z oddaljenimi civilizacijami (pošiljanje elektromagnetnih valov traja predolgo) –
kaj pa preko teleportacije na nivoju »stare« svetlobe (recimo na nivoju mikrovalov ozadja,
ki so bili nekoč kvantno prepleteni)! Zelo vznemirljivo! Mikrovalovi nam trenutno razkrivajo
zgodovino vesolja – ali bi lahko preko njih tudi komunicirali (problem so začetna stanja ali
bi jih lahko dešifrirali)? Še enkrat - zelo vznemirljivo! (idejo o komunikaciji s
tujimi oddaljenimi bitji preko teleportacije z mikrovalovi kozmičnega
sevanja ozadja je zapisal Zoro Vičar - s pridržkom, beri spodnjo opombo,
pomlad 2021).
----------------------------------------------
Še opomba glede komunikacije z mikrovalovi kozmičnega ozadja.
Problem vseh teh idej je, da rabiš pri kvantni teleportaciji še klasični kanal,
ki je omejen na hitrost svetlobe. Z njim preneseš informacijo o meritvi primarnega
kvantnega stanja A, ki ga šele potem lahko izvede oddaljen prepleten kvantni sistem
B. Oba sta potem neuporabna za bodoče informacije, komunikacije - prenos stanja.
Če hočeš več takih prenosov, moraš imeti več parov prepletenih kvantnih sistemov,
recimo fotonov. Vsaka meritev namreč pomeni, da po meritvi,
več ne poznaš stanja prepletenega para.
Tudi, če bi mikrovalovno ozadje vsebovalo kako kodiranje informacij (oddaljene
civilizacije z dodatno polarizacijo mikrovalov),
bi to veljalo le za dani trenutek oddaje signalov, oziroma za stanje vesolja, recimo
na začetku - ko postane vesolje transparentno za prasevanje.
Iz tega tudi črpamo zgodovino vesolja - kozmološki model.
Zmeraj torej rabimo še klasični kanal, ki je 'žal' omejen na hitrost svetlobe
in tako je hipna teleportacija zgolj iluzija znanstvene fantastike -
ki pa seveda ima svoj čar.
Glejte tudi izračune za
izjemen teleskop s SONCEM kot gravitacijsko lečo (možnost neposrednega snemanja eksoplanetov ... ).
Še vesela novica na tematiko teleportacije - kvantne prepletenosti!

Nobelova nagrada za fiziko gre letos (2022) v roke treh znanstvenikom – Francozu Alainu Aspectu,
Američanu Johnu F. Clauserju in Avstrijcu Antonu Zeilingerju, ki se ukvarjajo s proučevanjem
kvantne mehanike, je odločila Kraljeva švedska akademija znanosti.
Nagrado so prejeli "za eksperimente s prepletenimi fotoni, določanje kršitev Bellovih neenačb
in odkritja na področju kvantne informatike".
Kvantna znanost bi lahko odprla nova področja uporabe računalnikov ter zmožnosti obdelave ogromnih
količin podatkov. Ločeno delo treh letošnjih (2022) Nobelovih nagrajencev je izpopolnilo teorije,
o katerih so znanstveniki, kot je Albert Einstein, razmišljali že desetletja.
Še dileme okrog kvantne fizike, ki jih je zmeraj manj.
Morda je naš opis sveta s kvantno mehaniko nepopoln,
ko govorimo o tem, da delec nima stanja,
dokler ga z meritvijo ne prisilimo v izbiro. Z drugimi besedami, morda obstajajo skrite spremenljivke,
ki jih ne poznamo, a že ves čas določajo, katero stanje bo delec pokazal ob meritvi. Vprašanje se
zdi filozofsko - je drevo padlo, dokler tega ni nihče opazil? Površno bi dejali, da je vseeno -
a to ne drži. John Steward Bell si je izmisli eksperiment, ki je doživel več variacij, kako to preveriti.
Izvesti je možno eksperiment, ki nedvoumno pokaže, ali imajo kvantni delci skrite spremenljivke (in torej
nič naključnosti) ali pa stanje res zavzamejo šele ob meritvi in to ni eksplicitno napovedljivo
(lahko pa vnaprej poznamo verjetnosti, torej dogajanje v ansamblu delcev). Eksperimenti so pokazali,
da je Bellova neenakost drži - svet nima skritih spremenljivk, svet je naključen.
“Vsakdo, ki ga kvantna fizika ni pretresla, je ni razumel.” (Niels Bohr) - vir: kvarkadabra
Einstein, Podolsky in Rosen (kratiza za imena je kar EPR) niso trdili, da kvantna mehanika ni dobra fizikalna teorija, ki ne bi znala pravilno napovedati dogajanja v naravi. Dokazati so poskušali le, da (še) ne da popolnega opisa narave. Verjeli so, da poleg valovne funkcije obstaja še neka skrita količina, s poznavanjem katere bi lahko vsak naravni sistem opisali v celoti in do potankosti točno predvideli njegovo prihodnost, če bi le poznali tudi zakone, po katerih se spreminja. Količina ima pridevnik skrita, ker se (skoraj) nikomur ne sanja, kako bi z njo računali ali jo merili.
Bell je pokazal, da bi lokalne skrite spremenljivke povzročile nestrinjanje z napovedmi QM (kvantne mehanike) v določenih posebnih primerih. Torej Bellov izrek temelji na EPR. Scenariji s skritimi spremenljivkami postavljajo kritično zahtevo, ki ni bila očitna. 30 let po EPR je Bell razkril to zahtevo, ki se imenuje Bellova neenakost.
John Bell je predlagal posplošitev EPR/Bohmovega miselnega poskusa: Namesto fiksne postavitve merilcev elektronovega in pozitronovega spina je predlagal vrtljive merilce, ki bi jih lahko zavrteli v poljubno smer okoli osi gibanja elektrona. Najprej bi merili komponento elektronovega spina v smeri npr. vektorja a, kar z drugimi besedami pomeni, da bi detektor zasukali v smer a. Podobno bi detektor za spin pozitrona zasukali v smer b (slika). Da bo bolj enostavno, vzemimo za enoto meritve spina kar ℏ/2 Vsak detektor lahko registrira pri prehodu elektrona ali pozitrona le dve možnosti: +1 za spin gor in -1 za spin dol v smeri detektorja. Tabela zapisov meritev za več zaporednih razpadov π0 (pion) bi lahko izgledala takole:
| elektron | pozitron | produkt |
| -1 | +1 | -1 |
| +1 | +1 | +1 |
| +1 | -1 | -1 |
| +1 | +1 | +1 |
| -1 | -1 | +1 |
| … | … | … |
Iz meritev nato izračunamo povprečje produkta spinov za dano orientacijo detektorjev, in novo količino imenujmo P(a,b). Za primer, ko sta vektorja a in b enaka (a = b), dobimo staro EPR različico eksperimenta. Tu je ena meritev zmeraj +1, druga pa -1, kar vedno pripelje do produkta -1, zato je povprečje:
P(a,a) = -1
Antiparalelna detektorja (a = –b) imata iz podobnih razlogov zmeraj produkt +1, zato:
P(a,-a) = +1
Za poljubno orientacijo spinov teorija kvantne mehanike napove povprečje:
P(a,b) = –aˇb
Pri tem predstavlja pika med a in b skalarni produkt vektorjev. Bell je dokazal, da je takšen rezultat nemogoč za vsako lokalno teorijo s skritimi spremenljivkami. Podrobni izpeljavi tu ne bomo sledili, orisali bomo samo nekaj najpomembnejših elementov.
Slika - Bellova verzija poskusa EPR. Detektorja lahko poljubno vrtimo.
Predpostavimo, da je za “popoln” opis sistema elektrona/pozitrona potrebna vpeljava nove
skrite spremenljivke q. Le-ta se na nam nepoznan način spreminja od enega razpada piona do drugega.
Naprej predpostavimo, da je izid meritve na elektronu neodvisen od orientacije (b) detektorja
za pozitron, ki ga eksperimentator lahko izbere šele tik pred vstopom pozitrona v detektor,
tako da se zaradi končne hitrosti potovanja informacij (omejitev s svetlobo hitrostjo) detektorja
med seboj ne moreta uskladiti – predpostavka lokalnosti. Ker poznamo skrito spremenljivko, lahko
točno napovemo izid meritve spina na elektronu A (a,q) in na pozitronu B(b,q).
Obe napovedi lahko zavzameta le vrednosti +-1.
S pomočjo krajšega računa je prišel Bell do ugotovitve, da velja za
lokalno teorijo s skritimi spremenljivkami naslednja neenakost,
ki je danes znana pod imenom Bellova neenakost:
![]()
Že bežen premislek pa nam pove, da napoved običajne kvantne mehanike (P(a,b) = -a(b) krši Bellovo neenakost. Poglejmo primer treh orientacij za oba detektorja, ki so zamaknjene za kot 45. Kvantna mehanika zanje napove povprečja meritev:
P(a,b) = 0 (skalarni produkt vektorjev a in b),
P(a,c) = P(b,c) = -21/2/2 = -0.707
Toda:
0 - (-21/2/2) ≰ 1 - 21/2/2
Vir: https://en.wikipedia.org/wiki/Bell%27s_theorem
Primer orientacije detektorjev, ki pokaže kršitev Bellove neenakosti za kvantno mehaniko.
A John Clauser se je z Bellovo neenakostjo ukvarjal že v 60. letih kot študent in kasneje je s tremi raziskovalci predlagal realistični eksperiment, ki bi jo preveril. Leta 1972 je z meritvami parov kvantno prepletenih fotonov neizpodbitno dokazal, torej, da je Bellova neenakost kršena. Svet ni popolnoma predvidljiv. Eksperiment je imel nekaj pomanjkljivosti, ki pa jih je kasneje odpravil Alain Aspect. Izboljšal je način za vzbujanje atomov, tako da so izsevali več prepletenih fotonov. Prav tako je izpopolnil način, s katerim je preprečil, da bi sistem oddajal kakšne informacije, ki bi lahko vplivale na meritve.
V kvantnem svetu lahko s prepletenimi delci naredimo kup bizarnih eksperimentov. Eden izmed njih je že omenjena kvantna teleportacija, s katero prenesemo (sicer nepoznano) stanje na tretji delec.
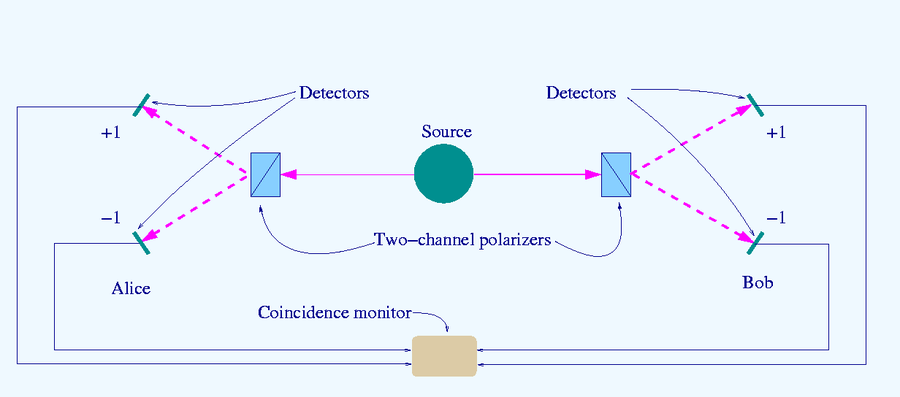
Shema "dvokanalnega" Bellovega testa.
Vir S proizvaja pare "fotonov", poslanih v nasprotnih smereh. Vsak foton naleti na
dvokanalni polarizator, katerega orientacijo (a ali b) lahko nastavi eksperimentator.
Zaznava prihajajoče signale iz vsakega kanala in koincidenčni monitor
prešteje sovpadanja štirih vrst (++, --, +- in -+).
Zgodovina in dokaz z enostavno matematiko (With Easy Math)
Leta 1935 je Albert Einstein sodeloval z Borisom Podolskim in Nathanom Rosenom, da bi objavil
članek, ki se zdaj preprosto omenja z začetnicami njegovih treh avtorjev: EPR (1).
V bistvu so ugotovili (bolje sklepali),
da je kvantna mehanika (QM) nepopolna, ker obstajajo tako imenovane "skrite spremenljivke", ki morajo pojasniti
vsaj nekaj negotovosti, ki je del QM. Skrite spremenljivke pomenijo, da obstajajo mikroskopske lastnosti
temeljnih delcev, ki jih ne moremo neposredno opazovati s testiranjem, morda zaradi tehnoloških omejitev,
ki morda v prihodnosti ne bodo obstajale. tj. morda preprosto potrebujemo večji mikroskop, da vidimo podrobnosti
dogajanja na najmanjši ravni. A ker jih ne moremo opazovati, so morda zdaj "skriti" - toda če bi o njih takrat vedeli
več, bi to morda pojasnilo sicer skrivnostno obnašanje delcev.
Heisenbergov princip negotovosti (HUP), ključna komponenta kvantne mehanike, pravi, da teh spremenljivk
ni le neopazljivo; preprosto ne obstajajo zunaj konteksta opazovanja. To odstopa od našega vsakdanjega pogleda na realnost.
EPR je imel preprosto, a močno definicijo tega, kar so imenovali "element resničnosti":
ČE je mogoče opazovano lastnost sistema napovedati z absolutno gotovostjo (100 %),
ne da bi motili ta sistem, POTEM mora ustrezati elementu resničnosti. Preprosta in
jedrnata definicija, seveda. In takšen, s katerim bi le malokdo trdil. To definicijo
bomo uporabili v našem dokazu Bellovega izreka.
EPR je zagotovil dokaz, ki v bistvu pravi: ali obstajajo skrite spremenljivke, ALI
atributi delcev (kot so položaj, hitrost, energija, polarizacija itd.) niso resnični
in definirani, dokler jih ne opazujemo. Ta del je splošno sprejet in je preprosto
razširitev HUP. EPR je tudi dejal, da ker je "nerazumno" verjeti, da ti atributi
delcev zahtevajo opazovanje, da postanejo resnični, zato morajo obstajati skrite
spremenljivke. Einstein je rekel: "Mislim, da mora imeti delec ločeno realnost,
neodvisno od meritev. To je: elektron ima vrtenje, lokacijo in tako naprej, tudi
če se ne meri. Rad mislim, da je luna tam, tudi če Ne gledam tega." Ta drugi del
EPR so nekateri sprejeli, drugi pa zavrnili, vključno z Bellom.
Navsezadnje QM dejansko pravi, da opazovanje oblikuje resničnost - in to se lahko zgodi
tudi v resnici! Nenavadno stališče, seveda, ki pa ni v nasprotju z dejstvi.
S tega stališča je Bell šel še dlje: pokazal je, da bi lokalne skrite spremenljivke
povzročile nestrinjanje z napovedmi QM v določenih posebnih primerih. Torej Bellov
izrek temelji na EPR. Scenariji s skritimi spremenljivkami postavljajo kritično
zahtevo, ki ni bila očitna. 30 let po EPR je Bell razkril to zahtevo, ki se
imenuje Bellova neenakost.
...
Polarizacija fotona
Oglejmo si primer polarizacije svetlobe. Delec svetlobe se imenuje foton. Večina
fotonov
je linearno polariziranih in to polarizacijo je mogoče opazovati (izmeriti)
z uporabo
polarizacijskega filtra ali polarizacijskega kristala. Polarizacijska
sončna očala uporabljajo to polarizacijsko lastnost
kot osnovo za svoje delovanje.
Praviloma bo polovica vse NAKLJUČNO polarizirane svetlobe
prešla skozi polarizacijski
filter. Drugo polovico bo filter odbil/absorbiral. To velja ne
glede na usmerjenost
filtra. Na splošno lahko filter nastavite pod katerimkoli kotom
od 0 stopinj do
360 stopinj - to pomeni, da ga lahko
poljubno vrtite v krogu. Ti učinki so vidni
tudi, če je vir
svetlobe tako šibek, da preide le en foton naenkrat! Ko gre kateri
koli foton skozi polarizacijsko lečo, bo njegova polarizacija nato natančno
poravnana z
lečo (tudi če prej ni bila).
Recimo, da obravnavamo en delec (foton) svetlobe.
Postavimo preprosto vprašanje:
ali ima določeno polarizacijo pri naslednjih treh kotih: 0
stopinj (A),
120 stopinj (B) in 240 stopinj (C)? Glede na dokument
EPR njegova polarizacija
pod temi 3 koti ustreza dejanskim elementom realnosti, ČE
jih je mogoče z
gotovostjo predvideti brez motenj v sistemu. To je
mogoče potrditi s konvencionalno optiko:
vsak foton z znano polarizacijo (recimo 0
stopinj) lahko pozneje preveri drug polarizator
pri enaki nastavitvi kota. Predvideni rezultat
(100-odstotna gotovost) je, da bo imel
foton v tem poznejšem času enako
polarizacijo, kar je znano že približno 200 let
(Malus, 1809). V nadaljevanju
morajo A, B in C posamezno ustrezati elementom realnosti
v skladu z
definicijo EPR. (Pravzaprav bo vsaka polarizacija kota prestala
ta preizkus posebej.)
Nato pridemo
do vprašanja v vrednosti 64.000 $: ali A, B in C ustrezajo
HKRATNIM
elementom realnosti? Vidite, test, ki smo ga opisali zgoraj, deluje samo
za en
kot naenkrat. A, B ali C lahko testiramo enega za
drugim, ni pa načina, da bi
testirali vse 3 hkrati. Toda glede
na EPR element realnosti obstaja neodvisno
od dejanja opazovanja. tj. vsi elementi
realnosti imajo v vsakem trenutku
določene vrednosti, TUDI ČE NJIHOVIH VREDNOSTI NE
POZNAMO. Pravzaprav EPR pravi,
da bi bilo vsako drugo stališče nerazumno. Torej
morajo imeti koti A, B in
C istočasno dokončne odgovore na vprašanja
o svojih polarizacijah - tudi če
jih ni mogoče poznati. Torej je
lahko pri kotu A skrita spremenljivka A; in
pri kotu B imamo
skrito spremenljivko B; in pod kotom C imamo skrito spremenljivko C.
Če bi le imeli orodja, bi morda lahko želeli, da bi nekoč
lahko hkrati opazovali skrite
spremenljivke A, B in C enega samega fotona.
Tukaj si želimo predstavljati, da tudi če
se dejanske vrednosti fotonovih "skritih
spremenljivk" zdijo muhaste ali naključne,
morajo biti NEKAJ.
Ali pa ne! Poglejmo, kam
nas pripelje ta na videz razumna predpostavka. Dokaz obsega
manj kot ducat
odstavkov z eno tabelo. In ENOSTAVNA MATEMATIKA, ki ji lahko sledi vsak!
...
Slika
1:
Ne moremo razložiti, zakaj polarizacija fotona zavzame vrednosti, ki jih ima pri
nastavitvah kota A, B in C. Lahko pa jo naknadno izmerimo s
polarizatorjem pri eni nastavitvi, v nekaterih primerih pa jo lahko predvidimo za
eno nastavitev vnaprej. Barve se ujemajo s stolpci v tabeli 1 spodaj.
(Po dogovoru poravnava 0 stopinj ustreza ravnini navzgor.)
Dokaz
a. PREDPOSTAVITE, da ima foton
hkrati 3 resnične skrite spremenljivke A, B in C pod koti 0
stopinj, 120 stopinj in 240 stopinj glede na zgornji diagram. Te 3
skrite spremenljivke, če obstajajo, bi ustrezale sočasnim elementom realnosti, povezanim z merljivimi
polarizacijskimi atributi fotona pri merilnih nastavitvah A, B in C. Z drugimi
besedami, vsaka skrita spremenljivka nam daje odgovor na vprašanje "ali bo ta
foton šel skozi polarizacijsko lečo, nastavljeno pod določenim kotom?" Verjetno so te informacije
NEKAKO kodirane zagotovo v fotonu v času, ko je ustvarjen (nekako kot
nabor navodil) in na noben način NISO odvisne od same polarizacijske leče
(na katero naletimo pozneje).
To je PRVA in primarna predpostavka, ki jo potrebujemo
za Bellov izrek. To je tudi minimalna definicija katere koli teorije skritih
spremenljivk. To predpostavko imenujem "zvonov resničnost". In... ta predpostavka je enaka predpostavki,
da je Luna tam, ko nihče ne pogleda. Navsezadnje preprosto pravimo, da
so odgovori na 3 vprašanja "Kakšna je polarizacija fotona pri: 0, 120
in 240 stopinj?" obstajajo neodvisno od tega, da jih dejansko vidimo. Če
ima foton določene sočasne vrednosti za te 3 nastavitve polarizacije, potem morajo
ustrezati 8 primerom ([1]...[8]), predstavljenim v tabeli 1 spodaj. Naša prva predpostavka
je torej, da je resničnost neodvisna od opazovanja, in preverili bomo, ali
ta predpostavka drži.
b. Zdaj bomo postavili še eno preprosto vprašanje: če smo
izmerili polarizacijo pri katerem koli od treh kotov, kakšna je verjetnost, da
se bo sosednja meritev pri enem od drugih dveh kotov ujemala z
rezultati prvega? Če bi na primer poznali polarizacijo pri A, kakšna je
verjetnost, da bi bil primer B enak? Ali če bi poznali polarizacijo pri
B, kakšna je verjetnost, da bi bil primer C enak? Ali če bi
poznali polarizacijo pri C, kakšna je verjetnost, da bi bil primer A enak?
Zgoraj
je treba upoštevati le tri pare kotov: A in B (temu bomo
rekli [AB]); B in C (temu bomo rekli [BC]); in nazadnje A
in C (temu bomo rekli [AC]). Če sta A in B dala
enake vrednosti (bodisi oba + ali oba -), potem se [AB]=ujema in
temu bomo rekli "1". Če sta A in B dala različni vrednosti
(eden a + in drugi a -), potem je [AB]=neujemajoče se in
temu bomo rekli "0". Enako za [BC] in [AC]. Če upoštevate vse
permutacije tega, kaj so lahko A, B in C, pridete do naslednje
tabele:
....
Prevod glave tabele spodaj:
Primer |A=0 stopinj| B=120 stopinj | C=240 stopinj | [AB] | [BC] | [AC] | Vsota [AB]+[BC]+[AC] |
Povprečje ([AB]+[BC]+[AC]/3)
| Case | A=0 degrees | B=120 degrees | C=240 degrees | [AB] | [BC] | [AC] | Sum [AB]+[BC]+[AC] | Average ([AB]+[BC]+[AC]/3) |
| [1] | A+ | B+ | C+ | 1 (++) | 1 (++) | 1 (++) | 3 | 1.000 |
| [2] | A+ | B+ | C- | 1 (++) | 0 | 0 | 1 | 0.333 |
| [3] | A+ | B- | C+ | 0 | 0 | 1 (++) | 1 | 0.333 |
| [4] | A+ | B- | C- | 0 | 1 (--) | 0 | 1 | 0.333 |
| [5] | A- | B+ | C+ | 0 | 1 (++) | 0 | 1 | 0.333 |
| [6] | A- | B+ | C- | 0 | 0 | 1 (--) | 1 | 0.333 |
| [7] | A- | B- | C+ | 1 (--) | 0 | 0 | 1 | 0.333 |
| [8] | A- | B- | C- | 1 (--) | 1 (--) | 1 (--) | 3 | 1.000 |
Še odlomki iz teksta:
"Dr. Anton Zeilinger (z Dunaja), pionir kvantne mehanike, o teleportaciji
in nesmiselnosti vnaprejšnjega iskanja uporabnosti raziskav."
(Delo 2016, bil je gost Instituta Jožef Stefan)
https://old.delo.si/znanje/znanost/kandidat-za-nobelovca-o-radovednosti-ki-ga-zene.html
Eno samo naključje
V kvantni mehaniki ne potrebujemo več nobene povezave, da uresničimo hipen prenos informacije, pojasnjuje. »To je resnično zanimiv dosežek, ki kaže, da moramo morda na novo razmišljati o tem, kaj sploh je prostor, kaj prostor pomeni in ali sta prostor tu in prostor drugje v resnici res ločena, kot ju dojemamo z naše perspektive.«
Morda bomo torej morali spremeniti našo predstavo o prostoru, toda tu, pravi dr. Zeilinger, presenečenj ni in ni konec. Teleportacija odpira še en zanimiv koncept – koncept naključnosti.
»Zdaj spoznavamo, da ne označuje le pomanjkanja kontrole, ampak je ta koncept temeljni koncept našega sveta. V resnici je naš svet eno samo naključje. In to je res vznemirljivo … Kaže, da ne moremo najti vzroka, zakaj se nekaj dogaja … Preprosto se pač zgodi.«
Mar to pomeni, da nas ta dosežek sooča s spoznanjem, da zdaj vemo celo manj, kot smo vedeli pred tem dosežkom?
»No, rekel bi, da vemo veliko več, a kadar vemo več, odkrivamo tudi meje našega znanja. In to je zanimivo, kajti zavedanje meja nas gotovo spodbuja k razmišljanju in iskanju poti, kako te meje preseči. Mogoče so za temi mejami nove ideje, ki jih še nismo odkrili,« razmišlja dr. Zeilinger.
Pa je te meje mogoče preseči?
»Seveda. Empirična znanost je razmeroma mlada. Imamo jo šele 300 ali 400 let, to je malenkostni del dobe človeškega obstoja. Zelo neverjetno je, da bi že dokončno odkrili, kaj je naš svet. Ogromno je še stvari, o katerih ne vemo kaj dosti,« pravi dr. Zeilinger.
Ko že govori o mejah – ali vidi tudi meje teleportacije? »Teleportacija je metoda komuniciranja, metoda pošiljanja informacij v prostem prostoru, in sicer informacij iz enega kvantnega računalnika v drug kvantni računalnik daleč, daleč stran,« odgovarja profesor Zeilinger. In doda, da sam v prihodnosti vidi kvantni internet.
Na poti do takega interneta pa morajo najprej premagati razdalje in močno povečati stopnjo prenosa podatkov. Ta je za zdaj v kvantnem računalništvu še vedno izjemno nizka, poudari. A to sta zanj le tehnična izziva, ne pa izziv znanja. Skratka, po besedah dr. Zeilingerja »praktični izziv, ki ga bo mogoče preseči z drugimi metodami. Prepričan sem, da ga je mogoče preseči.«
.......................
Samodejno se postavi vprašanje: in kaj bomo imeli od tega?
»Ah, uporabnost – vedno me sprašujejo po uporabnosti, a na to ni mogoče odgovoriti. Seveda sem prepričan, da bomo imeli kvantni internet, ki bo omogočal veliko hitrejši tok informacij. Kaj vse se bo še razvilo, pa je težko napovedati. Poglejte, kako je bilo z laserjem. Ko so ga razvijali in razvili, ni nihče niti slutil, da bodo nekoč s tem povezani skenerji v supermarketih, zgoščenke ali operacije oči. Vse to je prišlo veliko pozneje. V vsej zgodovini človeštva se je tako dogajalo. Vsaka nova tehnologija je odprla pot številnim novim aplikacijam, ki jih na začetku niso niti slutili. Enako se bo zgodilo s teleportacijo,« zatrjuje dr. Zeilinger.
A zakaj se je lotil raziskovanja prav tega področja? »Zgolj iz radovednosti,« odgovori brez razmišljanja. »V temeljih bi bilo absolutno narobe utemeljiti temeljno raziskavo z navajanjem uporabnih možnosti. To bi bila velika napaka. Celo velika podjetja, kakršen je Microsoft, to razumejo. V znanost vlagajo veliko denarja, na stotine milijonov dolarjev in evrov, čeprav nimajo nikakršnega zagotovila, kakšna bo njihova uporabnost.«
Moč radovednosti
Posebej v kvantno mehaniko so ga zvabile napovedi kvantnih fizikov o individualnih delcih, ki so se takrat zdele v nasprotju z vsakršno intuicijo. V eksperimentih še niso bile preverjene. Anton Zeilinger se je po doktoratu iz fizike na dunajski univerzi leta 1971, takrat komaj 26-leten, videl prav v tej eksperimentalni smeri. Pa je ta do zdaj potešila njegovo znanstveno radovednost – ali so vprašanja še ostala?
»Ah, še vedno je veliko nerešenih vprašanj,« zamišljeno odkimava. »Več ko vemo, bolj vemo, česa vsega še ne vemo … Je pa zanimivo, čedalje bolj.«
.......................
Prednost Evrope
Tu je v dobrih 40 letih dosegel ogromno, toliko, da že nekaj let velja za zelo verjetnega dobitnika Nobelove nagrade. A že brez nje v Avstriji velja za osebnost, ki utegne Dunaju vsaj delno povrniti sijaj, kakršnega je to mesto imelo v znanosti vse do začetka druge svetovne vojne. Takrat so zaradi politike iz številnih institucij izključili izjemne znanstvenike židovskega rodu, ki so emigrirali v ZDA.
Tja je želja po raziskovanju zvabila tudi dr. Zeilingerja (štiri leta je delal na znamenitem MIT pri poznejšem dobitniku Nobelove nagrade prof. C. G. Schullu in še danes sodeluje kot gostujoči profesor), toda evropski način življenja mu je bil bližji – kljub zapeljivim ponudbam se je vrnil v Avstrijo. S seboj pa je že takrat prinesel spoznanja, kaj prenesti iz sicer zelo različnega ameriškega izobraževalnega sistema v evropskega.
Plod njegove zamisli in organizacije je tako (verjetno po vzoru MIT) IST Austria (Institute of Science and Technology Austria), ustanova za mednarodne temeljne podoktorske raziskave v naravoslovju in tehnologiji, ki v Klosterneuburg na severozahodnem obrobju Dunaja že nekaj let privablja vrhunske znanstvenike z vsega sveta.
Se mu zdi, da Evropa v znanosti zdaj dohiteva ZDA? »Na nekaterih področjih smo celo pred ZDA. Na primer na mojem, v kvantni mehaniki in kvantni informatiki. Nekateri od prvih eksperimentov na tem področju so bili narejeni v Evropi. Prav gotovo smo torej enakovredni ameriški znanosti, če ne celo malo pred njo. A zatika se pri prenosu temeljnega znanja v tehnologijo, v aplikacijo. Tu ima Evropa težave.«
Konservativna evropska industrija
Zakaj? Po mnenju profesorja Zeilingerja je največja slabost v Evropi konservativnost velike industrije. Ta je v ZDA veliko bolj pripravljena tvegati in v znanost vlaga neprimerno več kot industrija v Evropi. Prav več denarja pa je tisto, kar zagotavlja najboljšim univerzam v ZDA vrhunskost.
In Kitajska? Ta bo njegov partner pri naskoku na novi rekord v kvantni teleportaciji, kar nedvomno kaže, da se Kitajska prebija med vodilne znanstvene sile. Kako ji je to uspelo?
»Po eni strani zaradi denarja, ki ga v znanost vlagajo res veliko. Po drugi strani pa so na Kitajskem zelo uspešni pri privabljanju domačih znanstvenikov po svetu nazaj domov, saj jim zagotovijo sredstva za dobre raziskave.«
Ali v Evropi na tem področju storimo dovolj? »Nikoli ne moremo reči, da smo storili dovolj. A trudimo se; v Nemčiji so pri tem uspešni, prav tako smo v Avstriji. Še vedno pa bi marsikje lahko naredili več,« meni dr. Zeilinger.
Tokrat je bil v Ljubljani prvič – in upa, da ne zadnjič. »Imamo veliko skupnega in tudi podobni
smo si, ločuje nas le jezik,« nam je ob koncu pogovora zaupal pionir teleportacije. In ker
uspešno premaguje rekordne razdalje pri prenosu znanja, ni neutemeljeno upati, da bomo presegli
tudi jezikovne.
Generalna pripomba.
Problem vseh teh idej je, da rabiš pri kvantni teleportaciji
še klasični kanal, ki je omejen na hitrost svetlobe. Z njim preneseš
informacijo o meritvi primarnega kvantnega stanja A, ki ga šele
potem lahko izvede oddaljen prepleten kvantni sistem B. Oba sta potem
neuporabna za bodoče informacije, komunikacije - prenos stanja.
Če hočeš več takih prenosov, moraš imeti več parov prepletenih
kvantnih sistemov, recimo fotonov. Vsaka meritev namreč pomeni, da po meritvi, več
ne poznaš stanja prepletenega para.
Glede komunikacije z mikrovalovi kozmičnega ozadja.
Tudi, če bi mikrovalovno ozadje vsebovalo kako kodiranje informacij (oddaljene
civilizacije z dodatno polarizacijo mikrovalov),
bi to veljalo le za dani trenutek oddaje signalov, oziroma za stanje vesolja, recimo
na začetku - ko postane vesolje transparentno za prasevanje.
Iz tega tudi črpamo zgodovino vesolja - kozmološki model.
Zmeraj torej rabimo še klasični kanal, ki je 'žal' omejen na hitrost svetlobe
in tako je hipna teleportacija zgolj iluzija znanstvene fantastike -
ki pa seveda ima svoj čar.
Tudi hitrost interneta zato ne bo večja, morebiti varnejša.
Kvantni računalniki pa so zmoglivejši. Zakaj?
Klasični računalnik dela z biti (0 ali 1).
Kvantni računalnik pa deluje preko
superpozicije kvantnih stanj.
Kubiti so lahko 0 in 1 hkrati (dokler jih ne izmerimo).
To pomeni, da kvantni računalnik lahko računa več možnosti naenkrat, ne ene po ene.
Ni ravno “paralelizem” kot pri večjedrnih CPU-jih, ampak še bolj eksotično.
Prednost = superpozicija + prepletenost + interferenca (da dobimo pravilno stanje).
Kvantna prepletenost pa je nujna za kvantno prednost, varnost.
Še enkrat opišimo primer tribitnega registra v klasičnem računalniku - stanje računalnika, torej tranzistorjev
v kateremkoli trenutku je lahko eno od 23 = 8 stanj, zapišimo jih:
000; 001; 010; 011; 100; 101; 110; 111, zagotovo vemo, da mora biti ta računalnik v enem od teh
stanj in je skupna verjetnost vseh stanj enaka 1.
Po drugi strani pa so lahko v kvantnih računalnikih qubiti hkrati
v večih od teh stanj. Torej, če predstavimo stanja kvantnih računalnikov z 8 znaki:
a, b, c, d, e, f, g, h, potem njihovi kvadrati dejansko
predstavljajo verjetnost za vsako posamezno vrednost,
vsota teh verjetnosti pa je 1, torej sedaj velja:
|a|2 +
|b|2 + |c|2 + |d|2 + |e|2 +
|f|2 + |g|2 + |h|2 = 1
.
Če bi klasični računalnik izvedel n operacij,
bi teoretično lahko naredili z enakim številom »qubitov« na kvantnem računalniku KAR
2n operacij v istem časovnem intervalu,
to pomeni, da sta prirast zmogljivosti in hitrosti takšnega računalnika vsaj teoretično eksponentna.
Skrivnost začetka vesolja (osnovne sile - "Božji delec")
- zakaj toliko besed o valovanju, kvantih in Heisenbergovem načelu nedoločenosti
Začetek vesolja je enigma, a večkrat si pomagamo prav z znanim Heisenbergovim načelom nedoločenosti za čas in energijo ( ΔE Δt ≥ h/(4π) ). Načelo nedoločenosti nam posredno sporoča, da si je moč energijo iz ničesar sposoditi, če se le ta dovolj hitro 'povrne'. Ko kvantna fluktuacija povzroči nastanek energijskega paketa delcev in antidelcev ( ΔE ≥ h/(4πΔt) ), več podobnih sinhronih dogodkov, se iz tega morebiti rodi (pri zlomu simetrije v prid delcev, recimo, da je 10 milijard protonov našlo antiprotone ter se izničilo in spremenilo v žarke gama [to sevanje še danes zaznamo v obliki mikrovalov ozadja, vesolje se širi], en sam pa je ostal brez para in tako naprej, iz teh ostankov od ostankov pa smo tudi nastali ljudje ...) samo vesolje. Konceptualni problem je lahko nedoločenost časa, od kod bi se vzel ... A smo torej kvantna fluktuacija, ki še mora vrniti sposojeno energijo – lahko da, saj nič ni večnega, razen zakonov narave, ki jih še ne poznamo ravno dovolj in ne vseh. Iz splošne teorije relativnosti izhaja še en zelo vzpodbuden razmislek – oziroma kar iz zadnjih meritev pospešenega širjenja vesolja. Gre za navezavo na temno energijo, ki pospešeno siri vesolje. In kako je s to skrivnostno energijo (katere posledice smo izmerili komaj leta 1998), v primeru, ko še ni bilo delcev – torej na začetku vesolja. Po analogiji prožnostne energije vzmeti, ki recimo sorazmerno z x2 potiska vzmet narazen (govorimo o energiji kx2/2), zapišimo energijo na delec zaradi temne energije EΛ = Λmc2R2/6, ki pospešeno širi naše vesolje (je torej sorazmerna z R2). Ta energija je torej sorazmerna z velikostjo vesolja na kvadrat R2 in s kozmološko konstanto Λ ter je normirana s členom c2/6 (kar pa izhaja iz enačb splošne relativnosti). Če zapišemo polno klasično energijo (Ekin + Epot + EΛ), nam ostaneta samo zadnja dva člena: -GM/R + Λc2R2/6 = 0. Delcev na začetku vesolja še ni, zato kinetični del energije odpade. Za teoretično maso (M = E/c2) vakuuma vstavimo produkt gostote in volumna M = ρV = ρ4πR3/3 (vakuumu namreč pripišemo kvantne fluktuacije, so seveda merljive), ostane nam torej izraz Gρ4πR3/(3R) = Λc2R2/6, od koder sledi gostota vakuuma:
ρvak = Λc2/(8πG)
- ocena je ρvak = 5,9 10-27 kg/m3
- za Λ ≈ 1.1056 10-52 m-2 , je vrednost gostote 3,5 protonov
na m3 (pričakovana
vrednost glede na kritično gostoto).
Prav enaka enačba se izpelje tudi iz tenzorskih enačb splošne relativnosti – bomo nakazali.
Zadnja enačba predstavlja torej tako imenovano gostoto vakuuma (naj se sliši še tako čudno,
a v vakuumu se, kot smo že omenili, stalno dogajajo fluktuacije, pari delec-antidelec, ...)
in je to hkrati tudi drugi tak matematični zapis, poleg Heisenbergovega načela nedoločenosti
[ ΔE Δt ≥ h/(4π) ],
v katerem se skriva možna razlaga začetka vesolja (načelo nedoločenosti nam posredno sporoča,
da si je moč energijo iz ničesar sposoditi, če se le ta dovolj hitro 'povrne'). Scenarij
je torej kratek:
pospešeno širjenje prostor-časa (fluktuacije, pari delec-antidelec, porušitev simetrije v
prid delcev – in sedaj že lahko rečemo, da smo bivajoči ...). Ali sta končni enačbi upravičeni
pri razlagi začetka vesolja – »ko še ni bilo časa (ali pač med kvantnimi fluktuacijami)« -
pa je drugo vprašanje. A ideje o začetkih vesolja štejejo – tudi če so negotove.
Sploh pa še naprej ostane (problem) razlaga – zakaj je narava (fizika) taka kot je in zakaj
sploh JE - obstaja (fluktuacije so lahko le posledica in ne razlog nastanka vesolja)?
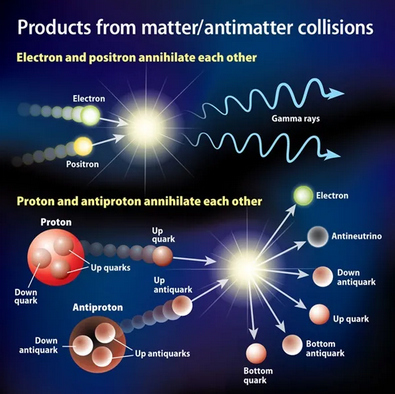
Pri zlomu simetrije
v prid delcev, recimo,
da je 10 milijard protonov našlo antiprotone ter se izničilo in spremenilo v žarke gama
[to sevanje še danes zaznamo v obliki mikrovalov ozadja, vesolje se širi in prvotne valovne dolžine gama
žarkov so se zelo podaljšale], en sam proton pa je ostal brez para in tako naprej do naslednjega delca protona, elektrona, ...,
iz teh ostankov od ostankov pa smo tudi nastali ljudje ..., prej vesolje z zvezdami, planeti ...

Barionska asimetrija (BAU, baryon asymmetry of the universe) fizike delcev
eksperimentalno kaže
veliko prevlado snovi nad antimaterijo v vesolju.
V fizikalni kozmologiji je tako eden večjih problemov barionska asimetrija, znana tudi
kot problem asimetrije materije in antimaterije -
to je neravnovesje glede barionske snovi (vrsti snovi, ki jo doživljamo, vidimo v vsakdanjem življenju,
ki tvori naše atome)
in antibarionske snovi
v opazljivem vesolju.
Niti standardni model fizike delcev, niti teorija splošne relativnosti ne
nudita smiselne razlage, zakaj bi moralo biti tako, in naravna predpostavka je,
da je vesolje nevtralno z vsemi ohranjenimi naboji. Veliki pok bi moral
proizvesti enake količine materije in antimaterije. Ker se zdi, da ni bilo tako,
je verjetno, da so nekateri fizikalni zakoni delovali drugače ali, da za materijo
in antimaterijo niso obstajali. Obstaja več konkurenčnih hipotez, ki pojasnjujejo
neravnovesje materije in antimaterije, ki je povzročilo bariogenezo
(v prid vesolja, ki ga živimo). Trenutno torej še ni
enotne teorije, ki bi pojasnila pojav, ki je bil opisan kot
"ena največjih skrivnosti v fiziki".
V fiziki delcev je kršitev CP ali CP-simetrije
(CP-symmetry or charge conjugation parity symmetry):
kombinacija C-simetrije (nabojna konjugacijska simetrija) in P-simetrije (paritetna simetrija).
CP-simetrija navaja, da bi morali biti zakoni fizike enaki, če delec zamenjamo s svojim antidelcem
(C-simetrija), medtem ko so njegove prostorske koordinate obrnjene ("zrcalna" ali P-simetrija).
Simetrija C pomeni simetrijo fizikalnih zakonov pri transformacijah,
ki predstavljajo spremembo električnega naboja. Elektromagnetizem,
gravitacija in močne interakcije sledijo simetriji C, šibke
interakcije pa jo kršijo v veliki meri.
Simetrija CP pomeni simetrijo (obnašanje) fizikalnih količin pri
transformacijah, ki jih sestavljata dve operaciji: sprememba naboja
(oznaka C) in zrcaljenje (oznaka P). To pomeni, da spremenimo delec
v njegov antidelec (sprememba naboja) in nastalo situacijo zrcalimo
(spremenimo predznak vsem trem koordinatam) preko neke točke.
Simetrija CP je tako kombinacija dveh simetrij: simetrije P in simetrije C.
Po transformaciji CP elektron s spinom navzgor postane pozitron (antidelec elektrona)
s spinom navzdol.
Odkritje kršitve CP leta 1964 pri razpadih nevtralnih kaonov je prineslo Nobelovo nagrado
za fiziko leta 1980 odkriteljema, to sta bila Jamesa Cronina in Vala Fitcha.
V vesolju se tako ne ohranja niti simetrija C niti simetrija P.
Primer je že omenjen razpad kaonov. V veliko primerih s simetrijo CP povezujemo
tudi simetrijo CPT, ki vključuje še obrat časa. Običajno pa za simetrijo
CP privzamemo, da vsebuje tudi čas.
Razlika v hitrosti nastajanja materije in antimaterije.
Ena od bolj sprejemljivih torij je generiranje barionske
asimetrije - kršitev simetrije paritete naboja - je proces, da se materija
generira z drugačno hitrostjo kot njegova antimaterija in to bi se naj dogajalo
ob rojstvu vesolja - veliki pok.
Interakcije izven toplotnega ravnovesja
V scenariju neravnovesnega razpada se zdi, da mora biti
hitrost reakcije, ki povzroči barionsko asimetrijo, manjša od hitrosti
širjenja vesolja. V tej situaciji delci in njihovi ustrezni antidelci ne
dosežejo toplotnega ravnovesja zaradi hitre ekspanzije,
ki zmanjša pojav anihilacije parov.
Še o meritvah
barionske asimetrije (BAU, baryon asymmetry of the universe), ki kaže
veliko prevlado snovi nad antimaterijo v vesolju.
Je eden najpomembnejših pojavov, ki jih je še treba razumeti v fiziki delcev,
ker ga ni mogoče razložiti s standardnim modelom.
Barionsko asimetrijo določamo peko razmerja:
η = (nB - nAB)/nγ > 0
- ko velja,
==> nB >> nAB
- kjer je nB število barionov kot merilo količine snovi,
- nAB je število antibarionov (antidelcev barionov) kot merilo količine antimaterije,
- nγ je število gama fotonov nastalih ob anihilaciji materije in antimaterije.
Opazovana številčna vrednost je:
η = ( 6,14 ± 0,25 ) · 10-10
Najnatančnejši način do danes je bil določitev iz sevanja kozmičnega ozadja
iz satelitskih podatkov WMAP.
Sedaj tudi vidimo, od kod razmerje, sklepanje, da je
da je 10 milijard protonov našlo antiprotone ter se izničilo in spremenilo v žarke gama,
en sam proton pa je ostal brez para in tako naprej do naslednjega delca.
Po modelu velikega poka se je snov ločila od sevanja kozmičnega ozadja
(CBR - cosmic background radiation) pri temperaturi približno 3000 kelvinov,
kar ustreza povprečni kinetični energiji 3000 K/(10,08×103 K/eV) = 0,3 eV.
Po ločitvi snovi od sevanja skupno število fotonov CBR ostane konstantno. Zato se zaradi
širjenja prostora-časa gostota fotonov zmanjša.
Zanima nas torej
število gama fotonov (nγ) nastalih ob anihilaciji materije in antimaterije
(model praktično predvideva, da je današnje mikrovalovno sevanje ozadja nastalo
zaradi gama fotonov, ki se pojavijo ob anihilaciji skoraj vse materije z antimaterijo
[prehod materije in antimaterije v svetlobo Eγ = mc2 = hν] na
začetku vesolja - zaradi širjenja vesolja pa
se je efektivna temperatura sevanja, vesolja - energija prvotnih fotonov - zmanjšala pod 3 K).
Gostoto (γ) fotonov nγ
= Nγ/V z energijo <E>γ = hν bomo dobili iz enačbe,
ki smo jo že delno
izpeljali pri Planckovem zakonu:
<E>dN/V = hνdN/V =
(8πhν3/c3)dν/(ehν/(kT) - 1)
Gostota fotonov pri
ravnotežni temperaturi T na kubični centimeter je torej podana z
nγ = Nγ/V =
∫ (8πν2/c3)dν/(ehν/(kT) - 1)
Vpeljemo novo spremenljivko x = hν/(kT), velja dx = hdν/(kT) ... po zamenjavi
dobimo spodnjo enačbo in jo integriramo od 0 do ∞:
nγ = Nγ/V = (
8π(kT/(hc))3 )∫x2(ex - 1)-1dx
=
(
8π(kT/(hc))3 )2ζ(3)
≈ 20,3(T/1K)3 cm-3
'k' je Boltzmannova konstanta, h Planckova konstanta, c je hitrost svetlobe
v vakuumu ter ζ(3), ki je Apéryjeva konstanta
[ζ(3) = 1.202056903159594285399738161511449990764986292].
Pri trenutni temperaturi fotonov CBR 2,725 K to ustreza
gostoti fotonov nγ
okoli 411 fotonov CBR na kubični centimeter.
Ker je število fotonov na kubni cm relativno skromno, se zdi,
da parameter asimetrije η, kot je definiran zgoraj,
ni ravno "dober" parameter. Namesto tega se kot prednostni parameter asimetrije kdaj
uporablja gostoto entropije s,
ηs = (nB - nAB)/s
- ker je gostota entropije vesolja ostala razmeroma konstantna skozi
večino njegovega razvoja. Entropijska gostota je
s = entropija/volumen = (p + ρ)/T = 2π2g*(T)T3/45
Trenutno je s = 7,04nγ.
Kjer so p in ρ tlak in gostota iz tenzorja gostote energije
Tμν in g* kot efektivnim številom prostostnih stopinj
za "brezmasne" delce (kolikor velja mc2 << kT) pri temperaturi T.
***
Še ena všečna manj verjetna ideja o nastanku vesolja - in sicer,
da obstaja območje vesolja (t. i. zrcalno vesolje) kjer prevladuje antimaterija.

Špekulacija brez temeljev v meritvah -
veliki pok bi naj ustvaril par vesolje-antivesolje, naše vesolje teče naprej
v času, medtem ko naš zrcalni dvojnik teče nazaj.
Še ena drzna možnost, ki razlaga navidezne barionske asimetrije je, da sta materija
in antimaterija v bistvu ločeni v različnih, zelo oddaljenih regijah vesolja.
Prvotno so mislili, da nastanek galaksij antimaterije pojasnjuje barionsko asimetrijo,
saj se od daleč atomi antimaterije ne razlikujejo od atomov snovi;
oba proizvajata svetlobo (fotone) na enak način. Vzdolž meje med območji
snovi (materije) in antimaterije pa bi bilo mogoče zaznati anihilacijo (in posledično
generiranje sevanja gama), odvisno od njene oddaljenosti ter gostote snovi
in antimaterije. Takšne meje, če obstajajo, bi verjetno ležale v
globokem medgalaktičnem prostoru. Gostota snovi v medgalaktičnem
prostoru je razmeroma dobro ugotovljena in znaša približno en atom na kubični meter.
Ob predpostavki, da je to tipična gostota v bližini meje,
je mogoče izračunati svetilnost žarkov gama mejne interakcijske cone.
A nobena takšna območja niso bila odkrita, vendar je 30 let raziskav
postavilo meje, kako daleč bi lahko bila taka območja. Na podlagi takšnih analiz
se zdaj zdi malo verjetno, da bi v kateri koli regiji v opazljivem
vesolju prevladovala antimaterija.
Še nekaj teorije o "zrcalnem" vesolju.
Stanje vesolja, kakršno je, ne krši simetrije CPT, tako bi lahko Veliki pok obravnavali
kot dvostranski dogodek - tako klasično kot kvantnomehansko, sestavljen iz para vesolje-antivesolje.
To pomeni, da je to vesolje slika naboja (C), paritete (P) in časa (T) anti-vesolja.
Ta par je izšel iz obdobij velikega poka in ne neposredno v vročo dobo, v kateri
prevladuje sevanje. Protivesolje bi se vrnilo v preteklost iz velikega poka in bi
ob tem postalo večje, v njem pa bi prevladovala tudi antimaterija. Njegove prostorske
lastnosti so obrnjene v primerjavi s tistimi v našem vesolju, kar je podobno ustvarjanju
parov elektron-pozitron v vakuumu. Ta model, ki so ga razvili fiziki iz Inštituta za
teoretično fiziko Perimeter v Kanadi, predlaga, da so temperaturna nihanja v kozmičnem
mikrovalovnem ozadju (CMB) posledica kvantno-mehanske narave prostora-časa v bližini
singularnosti velikega poka. To pomeni, da bi točka v prihodnosti našega vesolja
in točka v daljni preteklosti protivesolja zagotovili fiksne klasične točke, medtem
ko bi vse možne kvantno temelječe permutacije obstajale vmes.
Kvantna negotovost povzroči, da vesolje in protivesolje nista natančni zrcalni sliki drug drugega.
Ta model ni pokazal, ali lahko reproducira nekatera opažanja v zvezi s scenarijem
inflacije, kot je razlaga enotnosti kozmosa v veliki skali. Vendar pa zagotavlja
naravno in preprosto razlago temne snovi. Takšen par vesolje-protivesolje bi proizvedel
veliko število supertežkih nevtrinov, znanih tudi kot sterilni nevtrini. Ti nevtrini
so lahko tudi vir nedavno opaženih izbruhov visokoenergijskih kozmičnih žarkov.
V definiciji gostote vakuuma pa torej tudi problem začetnega časa v Heisenbergovem načelu nedoločenosti ni več tako čuden, nerazumljiv. Vesolje lahko tako »skuhamo« kar iz vrenja delcev in antidelcev, ki jih temna energija delno potisne narazen in z več sinhronimi podobnimi dogodki (nekateri omenjajo tudi resonanco – veliki pok), se rodi vesolje (idej o nastanku vesolja je seveda na pretek ...). Kot smo že omenili - s tem ugibanjem o možnem začetku vesolja seveda nismo rešili osnovnih vprašanj - ne vprašanja razloga same pojavnosti kvantnega »vrenja« (fluktuacij) vakuuma in ne izvora kozmološke konstante; tudi ne – ali je opisan recept nastanka vesolja vsaj blizu resnice. A brez novih idej, ki dopolnjujejo ali zanikajo stare, ni napredka v zgodovini znanosti. Tako je bilo tudi z vsemi ostalimi razkritimi resnicami (recimo o gibanju planetov, dinamiki vesolja, nukleosintezi in izjemni energiji zvezd - nastanku težjih elementov ...) skozi vsa tisočletja človeškega truda, da končno le spoznamo (spoznavamo) logiko stvarstva, vesolja, da spoznamo, zakaj smo in od kod prihajamo in slutimo bodoči razvoj dogodkov ... Čaka se tudi na dodatno potrditev velikega poka – inflacije vesolja, ki bi morala za sabo pustiti gravitacijske valove in detekcija le teh bi nem zelo olajšala dodatne sklepe o začetkih vesolja. Ti valovi bi lahko zasukali ravnino polarizacije mikrovalovnega ozadja; detekcijo tega zasuka pa je predlagal dr. Uroš Seljak (vodja Centra za kozmološko fiziko na Berkeleyju). Torej iščemo zasuk polarizacije mikrovalov ozadja – prasevanja, ki bi bil posledica gravitacijskih valov hitre širitve (inflacije) vesolja (nekaj, žal lažnih, signalov smo že ujeli 2014/2015 – ujeli smo zasuk polarizacije mikrovalov zaradi magnetnega polja galaksije, a to »tavanje« je del poti do resnice). Kdaj so kolateralni rezultati vsaj toliko pomembni kot iskani cilj.
Inflacija vesolja - eksponentno širitev prostora je leta 1980 predlagal Alan H. Guth in
kmalu dobil podpornike. Inflacija vesolja bi naj poskrbela (glej graf zgodovine vesolja),
da je vesolje na veliki skali, v vseh smereh, povsod podobno (izotropno), po delcih,
temperaturi, gostoti, po fizikalnih zakonih. Inflacija pa je pomembna tudi za nastanek
osnovnih delcev (je hkrati pot do rojstva delcev – začetek ločevanja sil, močne
od elektrošibke ...).
Ko se inflacija konča, se temperatura vrne na predinflacijsko temperaturo (lahko,
da zaradi delovanj sil med delci). To se imenuje ponovno ogrevanje ali termizacija,
ker velika potencialna energija inflatonskega polja razpade v delce in torej napolni
vesolje z osnovnimi delci (fotoni, kvarki, gluoni, elektroni ...).
Torej vključno z
elektromagnetnim sevanjem. Še pojasnilo - nosilec inflatonskega polja bi naj bil delec inflaton (torej še en potencialni bozon).
Takrat se tudi začne faza vesolja v kateri prevladuje
sevanje in ta faza traja vsaj 380000let. Kmalu po inflaciji se z združevanjem
treh kvarkov (kvarke lepi močna jedrska sila preko nosilcev sile gluonov) začnejo
rojevati tudi protoni, nevtroni (to je v trenutku, ko je temperatura padla na
10 12 K,
vesolje pa je bilo staro zgolj okrog 10-4 s in ta proces traja vsaj nekaj sekund).
Vesolje se ves čas širi, temperatura posledično pada - in ko temperatura pade na
3000 K, se pojavijo tudi prvi atomi (pozitivna jedra obdana z elektronskim oblakom),
to so gradniki življenja ..., vesolje je takrat staro okrog že omenjenih 380000 let
(od takrat je mikrovalovno sevanje ozadja tudi prosto, prej je prihajalo do sipanj
svetlobe na nukleonih, zadnje meritve kažejo, da je to obdobje trajalo od starosti
372.000 do 487.000 let.). Ker narava inflacije še ni do konca znana,
je ta postopek še vedno slabo razumljen - naj bi potekal preko t. i.
»parametrične resonance«.
Preprosta razlaga prevlade materije nad antimaterijo. Da bi ostalo nekaj
malega več materije od antimaterije, bi se naj zgodilo ob koncu obdobja
GUT (velika teorija poenotenja sil - Grand Unified Theory – kjer se poenoti
elektromagnetno, šibko in močno silo – gravitacija tukaj ne paše zraven,
lahko pa, da so vse štiri sile bile poenotene, torej skupaj z gravitacijo,
pred Planckovim časom
10-43 s
v prvotni sili velikega poka) – ko pa se močna
jedrska sila loči od GUT sile – vir inflacije vesolja in konec prevlade kvantnih
fluktuacij vakuuma, prevlada materija nad antimaterijo – za to bi naj bil odgovoren
Higgsov bozon (polje), ki je dal delcem maso (zlom simetrije v prid delcev je kot
zlom geometrijske simetrije med prehodom vode v kristalno urejeni led – molekule
vode so pred kristalno strukturo, v tekoči obliki, simetrično pokrivale vse smeri,
po kristalizaciji pa so se uredile). Teorije velikega poenotenja predpostavljala,
da so simetrijske skupine ali grupe SU(3), SU(2) in U(1) (modeli se nanašajo na
Liejeve algebre in ne na Liejeve skupine), ki opisujejo posamezne interakcije,
pravzaprav podskupine neke večje simetrijske skupine. Pri velikih energijah (pred GUT)
- mnogo večjih od tistih, dosegljivih s pospeševalniki (pred inflacijo vesolja –
pred hitrim napihovanjem) - se simetrija poenotene skupine ohranja, pri nizkih pa
se reducira na SU(5) ⊃ SU(3)×SU(2)×U(1), v procesu poimenovanem spontani zlom
simetrije (prehod iz tekoče vode v led - simbolično). Spajanje močnih in
elektrošibkih interakcij se zgodi pri veliki energiji združevanja (poenotenja
– nekje od 1025 eV do 1016 GeV, glej graf), znani tudi kot GUT energijski nivo:
ΛGUT ≈ 1016 GeV.

Grafa prikazujeta relativno sestavo gostote energije vesolja - materije nasproti ostalim
oblikam energije vesolja v sedanjem času (zgoraj) in v času ločevanja svetlobe od materije,
ko je vesolje postalo prozorno (spodaj), to je 380000 let po velikem poku (to so rezultati
merjenj misije WMAP in drugih).
Izraz "atomi" pomeni "normalno snov": atomi, molekule ...
A »prozorno« vesolje je bilo še kar nekaj 100 milijonov let še precej temno, ker na začetku
še ni bilo zvezd, »ki bi nam dale luč ...« A tudi, ko so nastale prve zvezde, je bila gostota
materije še zmeraj velika. Prve in to zelo masivne zvezde so nastale po približno 200 milijonih
let (zaradi masivnosti so hitro porabljale vodik, helij in so kmalu eksplodirale, takrat
nastane tudi prvi kisik in nekateri ostali težji elementi). A vesolje je bilo še zmeraj
gosto in komaj po 400 do 500 milijonov let, se je vesolje zaradi širjenja dovolj
razredčilo, da lahko danes brez težav zaznavamo spektralni odtis takratne materije.
Sestava vesolja se torej spreminja skozi čas: temna snov in atomi postajajo manj gosti,
ker se vesolje širi, podobno kot pri običajnem plinu. Procent gostote materije pade iz
12 % na 4.6 %, procent temne snovi pa iz 63 % na danes 23 %, temna energija pa iz
zanemarljivih vednosti na začetku vesolja do danes naraste kar na 72 %. Fotoni in
nevtrini pa tudi izgubljajo energijo zaradi širjenja vesolja.
Tako se gostota energije
fotonov manjša precej hitreje od same gostote energije snovi, čeprav so fotoni oblikovali
kar velik delež vesolja pred približno 13,8 milijardami let (pa je danes njihov delež
zanemarljiv. Tako kažejo meritve – zato energijskega deleža fotonov in nevtrinov ni
več na zgornji sliki z naslovom DANES). Zdi pa se, da se gostota temne energije sploh
ne zmanjšuje, tako da danes z do 72% celo očitno prevladuje v dinamiki vesolja
(ga pospešuje), čeprav je bil njen prispevek pred 13,8 milijarde let praktično zanemarljiv
(a nikakor ne ničen) v celotnem deležu energij (zato je tudi ni na sliki, ki prikazuje
začetek vesolja). Narave temne energije in temne snovi še zmeraj ne poznamo – jo pa zaznamo
iz pospešenega širjenja vesolja, temno snov pa preko Keplerja v galaksijah, jatah galaksij.
So pa različni kandidati za temno energijo - recimo preko že omenjenih kvantnih fluktuacij
v prostoru-času in kozmološke konstante, ki se skriva v gostoti vakuuma – velikokrat se tudi
sklicujemo na Casimirjev efekt, pokazalo se je, da je lahko Casimirjeva sila pri pojavu v
snoveh z določenimi dielektričnostmi in permeabilnostmi tudi odbojna (recimo fermioni -
gradniki navadne snovi, povzročajo odbojno silo). Fizik Hendrik Casimir je leta 1948
napovedal, da se dve bližnji vzporedni kovinski plošči brez naboja privlačita. Pojav
je (lahko) posledica vakuumskih fluktuacij v prostoru, to je virtualnih parov
delcev-antidelcev. Vrzel med ploščama omejuje dovoljene valovne dolžine za te
virtualne delce (kot stoječe valovaje na struni – ne pozabimo, kvantni delci se
obnašajo tudi kot valovanje) in tako jih je v prostoru med ploščama manj kot
zunaj. Med ploščama je tako nižja energijska gostota, kar povzroči privlak.
Kot smo že omenili je Casimirjeva sila lahko pri pojavu v snoveh z določenimi
dielektričnostmi in permeabilnostmi tudi odbojna, recimo fermioni - gradniki
navadne snovi (elektroni, protoni, nevtroni, kvarki), povzročajo odbojno silo.
Mnogi torej kar tukaj iščejo temno energijo (zaenkrat se zdi to dokaj optimistična
smer iskanja – celo merljiva). A Casimirjev pojav je mogoče razložiti tudi z
Van-der-Waalsovo silo (šibka privlačna sila med dvema molekulama, ki nastane
zaradi interakcije električnih dipolov). Da so določeni fenomeni še precej
nedorečeni, si poglejmo kako vakuum vidi pospešen opazovalec (naj bi). W. G.
Unruh je teoretično pokazal, da je pojem vakuuma odvisen od poti opazovalca
skozi prostor-čas. Z vidika pospeševalnega opazovalca bo vakuum nepospešenega
opazovalca videti kot stanje, ki vsebuje veliko delcev v toplotnem ravnovesju -
topel plin. Lahko pa, da zgolj kvantne fluktuacije, tako kot recimo fotoni odrivajo
električne naboje (ali kaki še neodkriti delci trenutno zapakirani v kozmološki konstanti),
vesolje pospešeno širijo, potiskajo narazen. Ali je torej vesolje v svojem bistvu kot
neke vrste zaporedje valov – kozmičnih valovnih cunamijev, ki si sledijo drug za drugim
in tudi nam je dano, da surfamo na enem izmed njih …? Zgolj ideja za nove raziskave,
razmišljanja – tudi protislovja, stranpoti.
Vse te omenjene dileme o vakuumu, fluktuacijah, iskanju temne energije, »paradoksih«
pospešenega gibanja, Casimirjev pojav ..., kažejo na porodne težave kvantne in kozmološke
razlage začetkov sveta, razlage geneze. A to so hkrati veliki izzivi za vse teoretike
in praktike - torej nas čaka še veliko dela, zagotovo tudi vse bodoče generacije,
kar pa je v resnici zelo dobra (optimistična) novica za mlade (in tudi manj mlade)
iskalce resnice!

Modelska shematska slika razvoja vesolja skozi čas, nastanek delcev, osnovnih sil,
preko energije delcev pri dani temperaturi.
Zgornja »preprosta« shema razvoja vesolja je tudi ena izmed iztočnic za oceno trenutka,
ko se je del prvotne energije vesolja pretvoril v maso – v atome, ki so danes temeljni
gradniki življenja. Kvarki so se v času 1/1000 s po velikem poku začeli združevati v
nukleone (protone, nevtrone).
In tukaj se pojavi znameniti Higgsov bozon kot nosilec
Higgsovega polja (recimo, da hipoteza velja). In zakaj so ga vpeljali?
Zelo, zelo
preprosto razmišljanje gre nekako takole – čas obrnimo nazaj in ... no pa začnimo in
to kar na primeru vode.
Kaj se zgodi, ko recimo segrevamo led – dovajamo energijo? Molekule se začnejo premikati z večjo hitrostjo, kar povzroči, da se kristali ledu pretvorijo v tekočo vodo. Če se temperatura še poveča, tekoča voda postane plin. Ne pozabite, ko se temperatura viša, se molekule premikajo vedno hitreje, kajne? Molekule se kmalu razgradijo v atome, v ione - v plazmo, ko elektroni niso več vezani na atome, temperatura še naprej strmo narašča in jedra atomov se razgradijo v osnovne delce (protone, nevtrone). Nato se nukleoni razgradijo na njihove komponente (kvarki, gluoni, leptoni – elektroni, mioni ...). V času smo se zdaj že vrnili praktično v prve tisočinke sekunde po rojstvu vesolja – 13,8 milijard let nazaj. Zdaj si lahko že predstavljajte, da se podatomski delci premikajo že z ogromno hitrostjo (čas inflacije vesolja – ko se je baje prostor-čas širil hitreje od svetlobe?! – vse se hipoma zgosti). Kaos, kajne? In noben od delcev naj ne bi več sodeloval drug z drugim. Lahko si predstavljate, da pri teh pogojih, pri najvišji temperaturi, ki sploh lahko obstaja, osnovni gradniki nimajo več mase (podobno kot fotoni - glejte graf razvoja vesolja), ker so razčlenjeni na ... »no ... nič«! To je prvotno vesolje (ko bi naj bile vse sile združene v enotno silo GUT - Grand Unified Theory – glejte graf razvoja vesolja), kot si ga predstavljamo takoj po »eksploziji«. Toda, ko se je vesolje hladilo, so se »najpomembnejši« delci (kvarki in leptoni) začeli vzajemno čutiti in oblikovali materijo. Toda KAKO, če niso imeli mase? Znanstveniki so dolgo razmišljali o tem in leta 1964 so Peter Higgs, Francois Englert, Robert Brout, Gerald Guralnik, C. R. Hagan in Tom Kibble razvili hipotezo, da obstaja Higgsovo polje sile, ki delce upočasnjuje (skupaj s temperaturo ohlajanja) in tako so, prej delci brez mase, zdaj prejeli maso na račun zmanjšane hitrosti (po Einsteinu to seveda drži ΔE/c2). Tako so nastali recimo protoni in nevtroni, kmalu tudi atomi ...
Prispodobo lahko iščemo recimo v puščavah, kjer z mrežami v nočnih in jutranjih urah lovijo vodo iz zraka, ki se je ob ohlajanju kondenzirala na nitke mreže. Higgsovo polje in nosilec bozon je torej simbolično mreža, ki kondenzira vodne hlape v kapljice vode (kot Higgsovo polje na začetku vesolja kvarke v protone, nevtrone in v atome), ostale atome zraka pa pusti na miru. Kot recimo Higgsovo polje ne reagira s fotoni, ki so brez mase (čeprav obstajajo logične domneve, da bi naj tudi svetloba čutila Higgsov bozon).
Higgsov bozon poznamo tudi pod imenom "Božji delec"!
Nekateri zavračajo to ime, spet
drugi predlagajo prav nasprotno poimenovanje ("Totally Secular Particle" ali kar »Masson«).
Ime "Božji delec" mu je dodelila istoimenska knjiga 'Božji delec: če je vesolje odgovor,
kaj je vprašanje? (The God Particle: If the Universe is the Answer, What is the Question?)',
ameriškega fizika Leona Ledermana, ki pa je dejansko želel, da ga imenujemo »Preklet delec«
(Goddamn particle – zaradi težavnosti odkrivanja), a si je urednik izprosil ime "Božji delec".
Na Boga so se sklicevali tako Newton, Faraday, Maxwell, Einstein ... tako da tako poimenovanje
zagotovo dodatno poudari zagato, kako težko je doumeti ter opisati dogajanje v naravi in samo
sosledje dogodkov v vesolju.
Higgsov bozon zelo hitro razpade - v času 1 zeptosekunde v druge delce – in kdo je Higgsovemu
bozonu dal »maso - energijo« (otroško vprašanje ali tudi ne in v tem kontekstu poimenovanje »Božji delec«
simbolično nekaterim veliko pomeni, drugim pač ne)? A bistveno je, da se ga da detektirati in
razumeti!?
Higgsov bozon je torej nosilec polja (kot smo že omenili, fiziki so vsakemu polju pripisali delce,
ker si drugače ne znajo (znamo) predstavljati delovanja med delci – se spomnimo na podajanje žoge ...).
Higgsov bozon v zgodnjem vesolju pripravi kvarke do sodelovanja, jih upočasni (na manjšo hitrost
od svetlobne) in s tem gre del energije v maso (materijo). Morebiti ni odveč primerjava, da je
Higgsov bozon nekaj takega v svetu osnovnih delcev, kot je pri ljudeh želja po sodelovanju
(to željo sicer težko definiramo, a deluje) - da torej delujemo kot skupnost, kajti drugače
iz nas ne bi bilo praktično nič. Smo ljudje, ker sodelujemo (prenašamo in dopolnjujemo kulturne
pridobitve iz roda v rod – govor, pisano besedo, izročilo, hrepenenje po presežnem, znanje,
umetnost, miselne in ročne spretnosti ..., no danes tudi nemo gledanje v ekrane,
pa še nekatere manj krepostne vrline imamo, recimo napuh ...). Torej ne begamo
v prazno, ampak se ustavimo (ustavi nas »Higgsov« bozon sodelovanja), premislimo
in skupaj delamo naprej. Higgsov bozon je imel torej podobno vlogo na začetku vesolja
in to pri tvorbi materije. Higgsov bozon je v resnici zelo težko slikovito razložiti,
sploh če nam šola v programu ne ponudi opisa koncepta polj v naravi – zato je nekdanji
angleški minister za znanost William Waldegrave leta 1993 celo podelil nagrado profesorju
Davidu Millerju iz UCL za najboljšo laično razlago Higgsovega bozona. Profesor David Miller
pravi takole. "Higgsovo polje" ima to lastnost - da maso lahko razumemo kot merilo upora
proti gibanju (za manjšo hitrost od svetlobne). "Higgsovo polje" je prof. prikazal kot sobo
fizikov, ki med seboj živahno klepetajo. Soba je torej polna ljudi, v prostor pa vstopi nov
znanstvenik in vznemirja - z vsakim korakom privablja nove občudovalce in vsi močno sodelujejo,
debatirajo z njimi - podpisuje avtograme ... Množica se še kar zbira okrog znanega znanstvenika,
obkrožen z novimi oboževalci, se zato zmeraj težje premika po sobi - v tej analogiji pridobi maso
zaradi "polja" oboževalcev, pri čemer vsak oboževalec deluje kot en sam Higgsov bozon. A v sobo
vstopi še en znanstvenik – tako se pojavita dve množici okoli različnih znanstvenikov, ena velika
in ena majhna. Če torej v sobo vstopi manj priljubljen (uspešen ali manj retorično spreten)
znanstvenik, se zbere okrog njega le majhna množica, nihče ne prosi za pozornost.
Lažje se premika po sobi - po analogiji je njegova interakcija z bozoni manjša,
zato ima manjšo maso. Z uporabo dveh različnih metod odkrivanja so fiziki v CERN-u
(pospeševalnik protonov, to je hadronov: LHC - Large Hadron Collider) zaznali maso,
ki bi naj bila v območju Higgsovega bozona. Julija 2012 sta skupini sodelavcev
na detektorjih CMS in ATLAS neodvisno sporočili, da sta potrdili odkritje prej neznanega
bozona z maso med 125–127 GeV/c2, katerega lastnosti se s standardno deviacijo
5 sigma »ujemajo« s Higgsovom bozonom. Zato je večina raziskovalcev iz tega področja
prepričanih, da je Higgsov bozon odkrit!
Večkrat se omenja Planckov čas tp.
V grobem nakažimo, kaj se skriva za tem pojmom. Fizikalni
opis sveta ima določene omejitve glede najkrajših razdalj, časov, ki jih lahko še pomerimo
ali smiselno izrazimo in recimo glede maksimalnih temperatur, ki so še smiselne v svetu, ki
ga poznamo ali količin, ki jih lahko zgolj sestavimo iz osnovnih konstant.
Podobno kot Planckov čas tp,
bomo izrazili še Planckovo maso – ki pa ima mejni pomen v mikrogravitaciji
- in še Planckov naboj. To so torej tako imenovane Planckove enote – ki nas pripeljejo do
nekaterih limit, a v njih ne smemo videti kaj veliko več kot uporabne domiselne enote –
in omejitve pri meritvah.
Začeli bomo (skoraj samoumevno) s svetlobo c = 299792458 m/s, s Planckovo
konstanto h = 6,62607015·10-34 Js in gravitacijsko konstanto
G = 6.67430 10-11 Nm2/kg2 ± 0.00015 10-11 Nm2/kg2
(podatek iz feb. 2025, ta vrednost se z meritvami nekoliko spreminja !).
Vemo, da je pošiljanje informacij omejeno s
hitrostjo svetlobe, elektromagnetnega valovanja v vakuumu, to je: c = 3 108 m/s). Potem so
tukaj omejitve na samem nivoju sveta atomov (subatomskih delcev) in seveda že omenjenih
naravnih konstant (svetloba hitrost c, gravitacijska konstanta G (ali tudi κ), reducirana
Planckova konst. ℏ = h/(2π = 105457168·10-34 Js),
Boltzmannova konstanta kB = 1.380649×10-23 J/K,
Coulombova konstanta
1/(4πεo),
kjer je εo permitivnost, tudi influenčna ali dielektrična konstanta in znaša
εo = 8.8541878188×10-12 s*A/(mV), velja še povezava εo = 1/(c2μo),
kjer je μo permeabilnost vakuuma ali tudi indukcíjska konstanta.
Tako bi naj veljalo, da je tudi za »najmanjšo« smiselno razdaljo (lp) in »najkrajši«
čas (tp) njun kvocient še zmeraj enak hitrosti svetlobe:
c = lp/tp
Iz energije fotona (Ef = hν, kjer naj bo frekvenca podana s Planckovim časom tp in deljena z 2π: ν = 1/(2πtp) – zaradi ujemanja z ostalimi konstantami in enačbami - zakoni) in znamenite Einsteinove enačbe za ekvivalent energija in mase (E = mc2), pridemo do Planckove mase mp:
hν = mpc2 => h/(2πtp) = mp(lp/tp)2
Končna povezava med mp, lp in tp je torej:
mp = ℏtp/l2p
Sedaj se zapodimo v svet gravitacije in zapišimo še centripetalno silo ob Planckovi
masi na Planckovi razdalji ob maksimalni hitrosti (svetlobni) zaradi mikrogravitacije,
od koder bomo ocenili Planckov čas (seveda – gre za ocene). Velja:
c2 = Gmp/lp.
V dano enačbo vstavimo
mp = ℏtp/l2p in
za razdaljo lp = ctp.
Tako dobimo: c2 = Gℏtp/l3p
= Gℏtp/(ctp)3p.
Iz zadnje enačbe po krajšanju izrazimo Planckov čas:
tp = (Gℏ/c5)1/2 = 5,39124·10-44 s ≈ 10-43 s
Kot vidimo, smo čas izrazili z osnovnimi fizikalnimi konstantami (G, ℏ, c). Zagotovo velja, da je ta čas najmanjši, ki ga lahko še smiselno izrazimo z dimenzijami sveta, ki ga dokaj dobro opisuje trenutni model vesolja. Tako je to tudi začetni čas v standardnem modelu vesolja (veliki pok, inflacija, širitev vesolja, tvorba atomov, zvezd, galaksij, življenja ...), po katerem se zdi, in tudi upamo (in delno že zmoremo) opisati dinamiko prostor-časa, samega vidnega vesolja. Pri tem nam zelo pomagajo pospeševalniki delcev, ki dajejo verodostojnost standardnemu modelu vesolja že pri starosti t = 10-10 s in temperaturi T = 1015 K (to je vsekakor »grozovit« uspeh trkalnika LHC – CERN in seveda tudi ostalih pospeševalnikov delcev). Pred Planckovim časom (10-43 s) pa še ne poznamo fizike, ki bi smiselno zaobjela samo rojstvo vesolja – ali opisala začetno obliko energije, gravitacijo in samo dinamiko začetka. Pred tem bi naj veljala kvantna gravitacija (valovni paketi, ki jih recimo opisuje teorija strun – podobno kot to počne »klasična« kvantna mehanika elektromagnetnega valovanja v povezavi z opisom osnovnih delcev iz sveta atomov).
Sedaj lahko izračunamo še ostale Planckove količine – imenovane tudi Planckove enote. Planckova masa je tako:
mp = ℏtp/l2p = ℏtp/(ctp)2 = (ℏc/G)1/2 = 2,176470×10-8 kg.
Planckova masa je tudi domnevna majhna mejna črna luknja, katere Schwarzschildov polmer je enak Planckovi dolžini ( rs = lp ≈ 2Gmp/c2 ). Tako smo se približali pojmu kvantne gravitacije.
Če Planckove enote limitirajo na skrajne vrednosti maksimalne temperature in minimalne smiselne vrednosti časa in dolžine - pa Planckova masa nima tege pomena (ekvivalent energije mpc2 ustreza recimo kemični energiji 57,2 litrov bencina pri kurilni vrednosti 34,2 MJ/l). Ima pa smisel pri določitvi enote za mikrogravitacijo sestavljeno iz osnovnih konstant.
Planckova dolžina pa ima po definiciji vrednost:
lp = ctp = 1.616229×10-35 m.
Planckova dolžina bi naj imela posebni pomen v kvantni gravitaciji. Na razdaljah, ki imajo velikost Planckove dolžine, bi naj bila zgradba prostor-časa drugačna od običajnega 4D sveta (kvantna gravitacija bi naj preprečevala singularnost – neskončno gostoto in neskončno majhno vesolje). Planckova dolžina je približno 1020 krat manjša (10-15m/10-35m) kot je velikost protona in jo imenujejo tudi kvant dolžine, ker naj bi imela velikost valovnega paketa (velikost strune v teoriji strun - sodobne teorije vključujejo tudi večrazsežne objekte, ki so znane kot brane).
Nič ni narobe, če omenimo modele (recimo v tem primeru teorijo strun), ki se trudijo razložiti zgodnje vesolje pred Planckovim časom. Čeprav eksperimentalnih potrditev za teorijo strun ni – a pričakujemo posredne potrditve (kot še zmeraj iščemo inflacijski gravitacijski val takoj po velikem poku in to posredno preko polarizacije mikrovalov – predlagal dr. Uroš Seljak – vsekakor zelo, zelo vroča tema zadnjih 20 let). Tudi za brane (strune) iščejo posredno potrditev preko naključnih gravitacijskih valov. Severnoameriški nanohertzni observatorij za gravitacijske valove (NANOGrav: North American Nanohertz Observatory for Gravitational Waves) je pred letom poročal o dokaj močnih dokazih o obstoju spektrov "naključno povezanih" gravitacijskih valov, ki vplivajo na frekvenco valov pulzarjev (zamik časa). Analiza temelji na 12,5-letnem naboru meritev. Nedavne rezultate NANOGrav se interpretirajo v smislu stohastičnega gravitacijskega ozadja iz metastabilnih kozmičnih strun (počakajmo na nove meritve in analize).
Planckovo temperaturo pa dobimo iz kinetične teorije plinov, kjer velja znana povezava:
mv2 ∝ kBT.
Za Planckovo temperaturo tako poenostavimo izraz iz klasične termodinamike (hitrost v nadomestimo s hitrostjo svetlobe c) in dobimo vrednost:
Tp = mpc2/kB = (ℏc5/Gk2B)1/2 = 1,416808×1032 K.
Ta vrednost se tako zmeraj pojavi pri oceni temperature vesolja, ko je od velikega poka minil Planckov čas (Planckova doba).
Poglejmo še Planckovo energijo:
Ep = mpc2 = (ℏc5/G)1/2 = ℏ/tp = 1,9561 × 109 J = 1,2209× 1019 GeV.
Tudi ta vrednost energije se pojavlja pri modelu začetnega razvoja vesolja (seveda ne
pomeni energije vesolja, je zdaleč, zdaleč premajhna … – ampak nam recimo (med drugim)
kaže energijo Planckove mase skozi čas glede na dinamiko temperature vesolja v znani
poenostavljeni termodinamični povezavi:
E ∝ mpv2 = kBT).
K kozmološkim
grafom se pa namesto Planckove energije lahko doda energija svetlobe, z valovno dolžino
vrha Planckovega sevanja črnega telesa pri dani temperaturi (Wienov zakon:
λmaks=b/T),
ko velja E = hc/λ = hcT/b. A vrednosti energij sta si pričakovano zelo blizu.
Torej - vse tri količine (čas, temperatura in energija: t, T in E) se v kozmologiji
na začetku vesolja (po velikem poku) večinoma izražajo v Planckovih enotah –
v vrednostih, ki jih lahko še smiselno izrazimo iz osnovnih konstant s katerimi
danes opisujemo energijo, sile in s tem dinamiko vesolja.
Z naraščanjem časa pa
se pričakovano zaradi raztezanja vesolja temperatura manjša – posledično pa tudi
gostota energije.
Omenimo še Planckov naboj (pomagajmo si Planckovo silo in Coulombovim zakonom: Fp = mpc/tp = c4/G = epep/(4πεol2p) ) od koder sledi:
ep = qp = (4πεoℏc)1/2 = 1,8755459 × 10-18 As
Je 11,706 krat večji od naboja elektrona eo.
Reissner-Nördstromova rešitev metrike naboja masivne črne luknje pri dimenzijah Planckove dolžine gre proti Planckovemu naboju. A to so zgolj špekulacije ... Planckov naboj ima torej osnovni smisel kot konsistentna enota za naboj v naboru Planckovih enot. Planckove enote torej niso neke čarobne količine, kot se to kdaj prehitro sklepa. Vsekakor pa dolžina, temperatura in čas v Planckovem zapisu enot predstavljajo meje, preko katerih še nismo uspeli pomeriti naravnih fenomenov in najti ekvivalentnega fizikalnega opisa (no - teoriji strun ali superstrun se zdita v tem kontekstu zaenkrat dokaj konsistentni).

V resnici se imajo kvarki, nukleoni in atomi radi – ta preprosta prispodoba je
marsikateremu otroku približala svet atomov in molekul.
Zgodovinsko zgodba osnovnih gradnikov sveta teče nekako takole (naj bi po Planckovem času 10-43 s). Vesolje se po času 0,001 s že kar ohladi. Kvarki so se po trije začeli združevati v protone in nevtrone, ko je temperatura vesolja padla pod 2 1012 K (zaradi širjenja) in takrat je bilo vesolje staro le okrog 0,001 s. Energija delcev je bila takrat okrog 180 MeV. Še prej pa je vesolje sestavljala plazma neodvisnih kvarkov in gluonov (kvarki nimajo celega naboja, zelo radi se družijo in se jih praktično ne da videti ločenih – le posredno, preko sproščene energije - še prej pa Higgsovo polje da maso kvarkom, elektronom in ostalim osnovnim masnim delcem, kot smo že omenili). Gluoni pa so torej nosilci močne jedrske sile in povezujejo kvarke v nukleone (protone, nevtrone, v atomska jedra pa povezujejo mezoni, to so pioni, ki so tudi sestavljeni iz kvarkov ...) – to tvorjenje nukleonov se je zgodilo torej »že« po času 0,001 s.
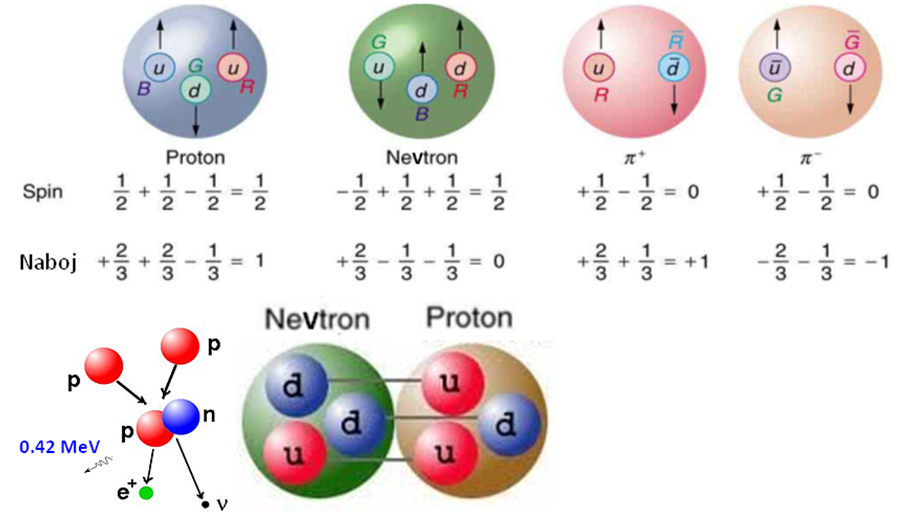
Zgoraj so predstavljeni proton, nevtron ter mezona kot nosilca (recimo) močne sile med
protoni in nevtroni (piona π+ in π-,
obstaja še pion π0 - sestavljeni so iz dveh kvarkov).
Levo zgoraj je torej - shematski model tvorbe protona, nevtrona in pionov (mezonov) iz
kvarkov, ki jih povezujejo (»lepijo«) gluoni. Slika, ki sledi pa je shematski prikaz vezave
(nukleosinteze) dveh nukleonov v devterij, to je izotop vodika s protonom in nevtronom -
gluoni torej posredno (preko mezonov – to je pionov) vežejo tudi protone in nevtrone v
masivnejša jedra. Za zdaj poznamo šest kvarkov, sledi opis u in d kvarkov, ki tvorita
protone in nevtrone.
Ime kvarka sim. naboj (e)
Gor (Up) u +2/3
Dol (Down) d -1/3
Spin (v kvantni fiziki) je v grobem analogija z vrtilno količino (rotacijo okrog lastne
težiščne osi) velikih teles. Zgornja slika naj bo vzpodbuda, da si vzamete v roke kako
knjigo o fiziki osnovnih delcev (nekaj malega o osnovnih delcih bomo še povedali …).
Kako pa so ugotovili sestavo atoma in kako recimo protona? Tako, kot smo že omenili,
da so trkali atome z hitrimi delci (recimo, da so folijo iz zlata trkali, obstreljevali
z alfa delci – ioniziranim helijem) in opazovali, kako se delci odbijajo od atomskega
jedra, večina jih je šla čez folijo (tako so sklepali na velikost jedra - presenetilo
jih je, da ima atomsko jedro napram atomu le cca 1/10000 premera). Sestavo jedra so
določili tudi preko gibanja nukleonov ali ioniziranih atomov, itn., recimo v magnetnem polju,
skozi podhlajeno paro, ki jo hitri delci ionizirajo in kondenzirajo – in tako vidimo sledi,
polmeri krožnih poti pa so odvisni od mase in naboja jedra, za majhne hitrosti velja Lorentzov
izraz za centripetalno silo v magnetnem polju B:
Fc = mv2/r = evB). Magnetno polje
tudi takoj razjasni ali je recimo nastali delec pri trkih v pospeševalnikih nevtralen ali mu
je lasten električni naboj (nabitemu delec, ki se giblje pravokotno na magnetno polje,
se tirnica ukrivi, smer je odvisna od predznaka naboja). Fotoni seveda nimajo mase in ne
naboja – le oni lahko potujejo s hitrostjo 3x108 m/s.
Pri sestavi nukleonov (recimo protonov) pa so težave (kvarki se namreč radi družijo in
se jih praktično ne da videti ločenih). A preko določitve neke mejne količine energije,
pri kateri se v pospeševalnikih lahko tvorijo pari delec, antidelec (elektron-pozitron,
mion-antimion, kvark-antikvark), se zdi model materialnega sveta sestavljenega iz kvarkov
kar pravilen. Recimo CERN - trkalnik protonov LHC - lahko pospeši vsak proton do energije
Ek = 7 TeV = 7 1012 eV,
med trkom dveh nasprotno gibajočih protonov pa se sprosti kar 2x več energije.
Tukaj je še PETRA v raziskovalnem centru DESY blizu Hamburga – kjer so, v zgodnjih 80. letih
20. stoletja, prvič eksperimentalno zaznali tudi gluone. Še definicija enote za energijo eV.
Elektronvolt (oznaka eV) je količina energije, ki jo pridobi ali izgubi posamezen nevezan
elektron v vakuumu pri preletu elektrostatične potencialne razlike (napetosti) enega volta.
To je za makroskopske sisteme zelo majhna količina energije, a za svet atomskih delcev zelo
priročna, velja:
1 eV ≈ 1,602176634 · 10-19 J,
oziroma 1 J ≈ 0,624150907· 1018 eV.
To je torej zelo uporabna enota za računanje energij (ali dela) v svetu atomov. Še povezava
z maso eV/c2 = 1,782662 · 10-36 kg, to je izračun preko energije
E = mc2.
Masa protona je tako 0.938 GeV/c2 .
Podajmo še eno od hipotez o bodočnosti materije in
s tem tudi vesolja (poleg recimo toplotne smrti vesolja). Ena od posledic teorije
velikega poenotenja nekaterih sil GUT (Grand Unified Theory, kjer se poenoti elektromagnetno,
šibko in močno silo – gravitacija tukaj ne paše zraven, če pa sprejmemo zgolj Einsteinovo
ukrivljenost prostor-časa kot posledico energije, mase, se zadeva zelo poenostavi in se zdi,
da ko iščemo vzrok za gravitacijo, v bistvu iščemo zgolj očala na nosu – a gravitonu kot nosilcu
gravitacije se še ni odrekla nobena teorija) je tudi napoved, da proton razpade z
razpolovno dobo ~ 1032 let. Protoni, sestavljeni iz treh kvarkov, se recimo lahko razkrojijo
z izmenjavo izredno masivnih delcev, imenovanih X in Y bozona, z življenjskim časom, ki je za
20 redov daljši od starosti vesolja. Proton (barion) razpade v pozitron (lepton) in nevtralni
pion (mezon):
p => e+ + πo
(in naprej πo => 2γ,
iščemo torej gama žarke ali pione). Razpad bi
(vsaj za nekaj časa) pomenil konec materije v današnji obliki pojavnosti, in če proton res
razpade, bo imelo to ogromne kozmološke posledice (neke vrste kontra masni defekt, pobiranje
energije iz prostora, vesolja in morebitno krčenje vesolja ali pa kaj tretjega). Eksperimenti,
meritve (recimo v rudnikih), kjer so iskali razpad protonov, so zaenkrat bile neuspešne
(KGF Indija, Super Kamiokande na Japonskem, Park City v Utahu – ZDA ...). Zanimivo je, da
zmeraj govorimo o masnem defektu in sproščanju energije (elektromagnetnega valovanja katerega energija
je blizu
E = Δmc2)
pri nukleosintezi težjih atomov v zvezdah (do železa). O nasprotnem efektu,
črpanju energije iz okolice za razpad atomov lažjih od železa (razen kot prehodnih pojavov
pri fuzijskih reakcijah v zvezdah ali seveda v trkalnikih CERN ...), pa se redko razmišlja
(razen kot neznanka o stanju osnovnih delcev v črnih luknjah). Hipoteza o razpadu protona je
tukaj še dodatna velika enigma življenja – tudi vezana na hipoteze o materiji in antimateriji,
ter porušitvi simetrije med obema v prid materiji (da danes lahko rečemo, da torej smo).
Lahko se tudi sklicujemo na dejstvo, da je (teoretični) razpad protonov izjemno redek
dogodek z razpolovno dobo neverjetnih ~ 1032 let – a če torej obstaja razpad protonov,
kaj potem?
A vrnimo se k atomom – k protonom in nevtronom, elektronom. Trenutno torej (še) nič ne kaže, da protoni razpadejo!
Polmer atomskega jedra se približno izračuna po enačbi: R=roA1/3
Kjer je A atomsko masno število (A je vsota števil protonov Z in nevtronov N), ro = 1.25 fm = 1.25 × 10-15 m, ro ima natančnost okrog 0.2 fm (odvisno od jedra). Premer jedra železa (A = 56) je tako približno velik 10 fm = 1x10-14 m. Uran (A = 235) pa se približa premeru 15 fm. O stabilnosti atomskega jedra odloča število protonov in nevtronov. Razen primarnega vodika, so vsa ostala jedra mešanica protonov in nevtronov – porazdelitev (geometrija) in število le teh v jedru odloča o stabilnosti atoma – o porazdelitvi privlačnih in odbojnih sil. Mnogih elementov je zato manj v naravi, ker so manj stabilni - glede na prisotnost večinskih atomov – recimo fluora je veliko manj kot sosedov (v periodnem sistemu) kisika in neona – v zvezdah nastane, a težko obstane v procesu fuzije - fluor je kar velika enigma vesolja.
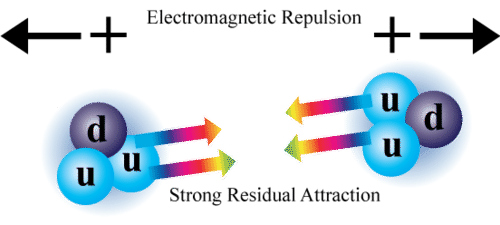
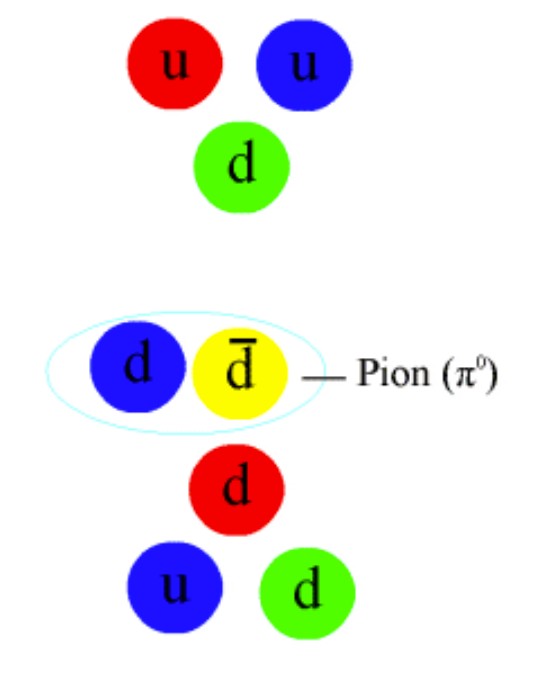
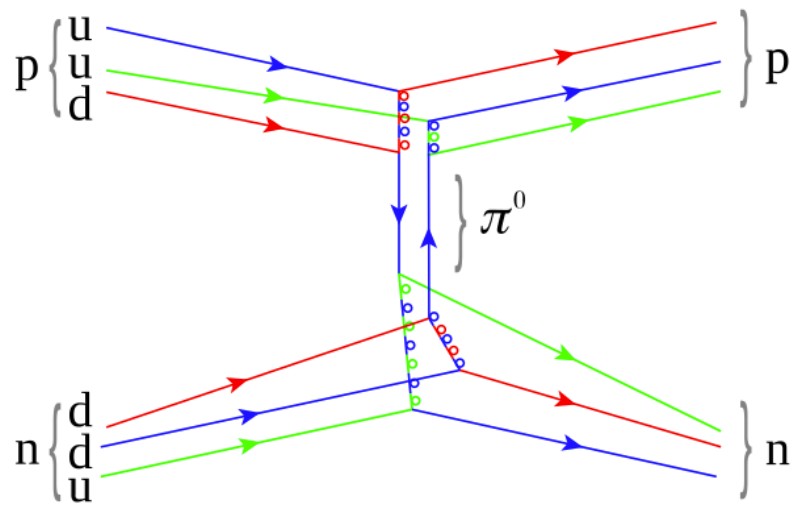
Boj med električno odbojno silo in privlačno močno jedrsko silo, ki jo nosijo
pioni (sestavljeni iz dveh kvarkov) znotraj atomskega jedra (slika levo).
Slika na sredi - prikaz (shema) izmenjave piona (ali ostanka močne sile)
in desno Feynmanov diagram enake interakcije (ravne črte so kvarki, večbarvne
zanke pa so gluoni - nosilci sile). Barvni naboj ima podoben namen kot električni
naboj pri drugih delcih. Barva kvarkov in gluonov v resnici nima nobene povezave
s pojmom dojemanja barve. Izraz barve je bil privzet samo zato, ker se nanaša na
tri oblike pojavljanja, podobno kot pri treh primarnih barvah (rdeča, zelena in modra).
Barvni naboj je v kvantni kromodinamiki (oznaka QCD) značilnost kvarkov in gluonov
(zanje je značilna močna interakcija).
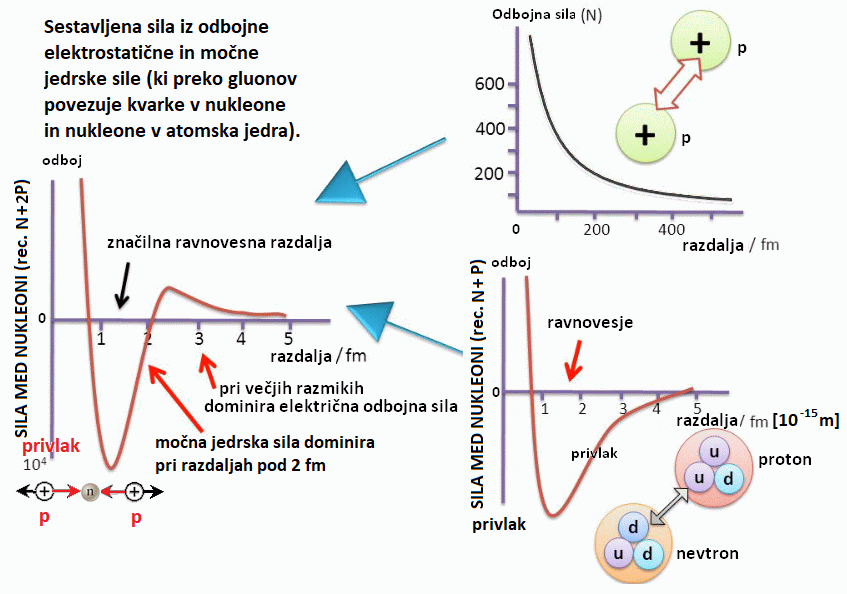
Zgornja slika kaže shematski pregled sil (klasični približek) v jedru in v bližini
atomskega jedra (proton in nevtron sestavljajo po trije kvarki, ki jih skupaj druži
močna jedrska sila).
V elementih masivnejših od vodika, oz. njegovih izotopih,
imamo v atomskem jedru prisotne, zaradi večjega števila nukleonov, odbojne sile
med protoni (Coulombov zakon,
F = e1e2/(4πεor2) = k/r2,
slika desno zgoraj). Da se atomsko jedro ne razleti pa poskrbijo močne jedrske
sile (kratkega dosega, slika desno spodaj za silo
F = e-ar(ka/r + k/r2)
med samimi protoni in nevtroni. Tako rešitev (potencial močne jedrske sile
in Coulombove sile, slika levo – posledično je definirana tudi prirejena
kromodinamična energija) je leta 1935 predlagal Japonec Hideki Yukawa
(sila e-ar(ka/r + k/r2)
je odvod potenciala V = -ke-ar/r).
Levi graf je vsota obeh sil – močna jedrska sila je pomnožena z -1
(odbojna sila je pozitivna, privlačna je negativna, v vsakem primeru
zvezda nekaj energije izgubi pri premagovanju odbojne sile, veliko
več pa je dobi iz dela privlačne močne jedrske sile – Sonce bo danes
proizvedeno fuzijsko energijo izsevalo komaj po nekaj 100000 letih).
Na razdalji večji od dveh fm med nukleonoma prevlada Coulombova
odbojna sila (ali tudi potencial, če je komu to bližje), pod 2 fm
pa močna jedrska sila, ki druži protone in nevtrone v atomsko jedro.
Levi graf je, kot smo že omenili, sestavljen iz obeh sil (odbojne
električne in močne privlačne) in kaže dokaj realno sliko sil v jedru
in ob jedru sestavljenega atoma (klasična slika). Enota femtometer ima
vrednost 1 fm=10-15 m.
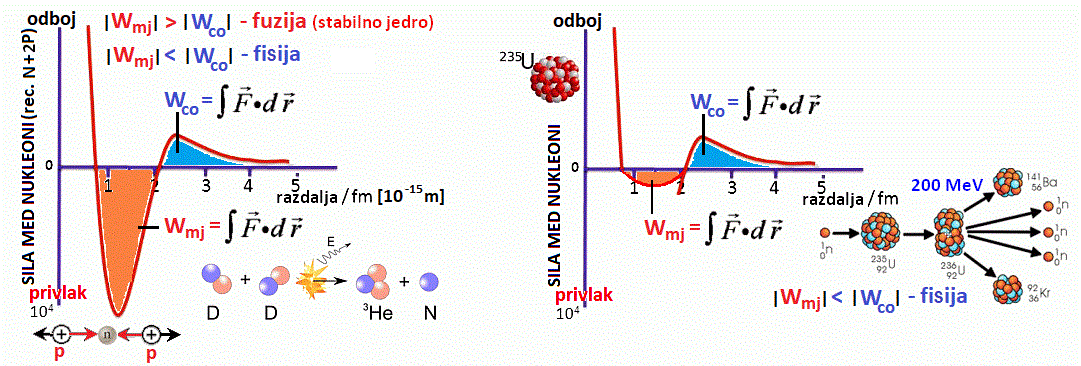
Grafa prikazujeta dva primera sil med nukleonom (protonom) in jedrom (skici nista v merilu,
to je zgolj groba shema za razumevanje bilance fuzije!). Desni graf kaže sile na nukleon v
masivnem atomskem jedru (recimo v uranu in ob razpadu le tega, med fisijo) in izven njega.
Levi graf pa kaže podobno odvisnost – le da med nastajanjem (fuzijo) lahkega atoma
(lažjega od železa). Na levem grafu je tako prikazana sila med dvema protonoma glede
na razdaljo, kar ustreza recimo helijevemu jedru
32He
(odbojna sila izven jedra in po
absolutni vrednosti večja prevladujoča močna sila v jedru). Modra barva v grobem predstavlja
delo, da premagamo odbojno silo med protoni, oranžna pa delo močne jedrske sile (kratkega dosega),
ki bližajoči proton pri razdalji okrog
10-15 m
posrka v novo atomsko jedro. Delo močne privlačne
sile je do železa večje od dela odbojne sile (kar pomeni več sproščene energije, kot je bilo
vložene), pri fuziji težjih elementov od železa naprej pa je delo močne sile manjše, zato težji
elementi od Fe nastajajo pri energetsko ekstremnih dogodkih eksplozij supernov in trkov zvezd ...
To je klasični pogled na zlivanje jeder, ki je le ocena dogajanj. V resnici so zadaj kvantno
mehanski efekti – tudi tuneliranje nukleonov čez potencial odbojne sile jedra. Tuneliranje pomeni,
da lahko gre delec skozi potencialno prepreko, čeprav je njegova kinetična energija nekoliko
manjša od potencialne energije prepreke - kar v klasičnem opisu ni mogoče (s sankami se tako
ne moremo, po spustu iz manjšega hriba, povzpeti na vrh višjega sosednjega hriba ...,
s kvantnimi sankami pa je to kdaj mogoče) – valovna narava kvantnih delcev (in valovna
funkcija gibanja to lastnost opiše) to verjetnost dopušča - to je hkrati zelo pomemben
pojav pri fuziji (nastanku težjih atomov) v zvezdah. V atomskem jedru je potrebno upoštevati
tudi kvantno stanje nukleonov (recimo Paulijevo izključitveno načelo, ki pravi, da gradniki
atoma ne morejo imeti hkrati enakih vseh štirih kvantnih števil
n, l, ml, ms (lega, azimutno ali orbitalno
kvantno število, magnetno kvantno število, spin). Ker ima helij 2 protona in 2 nevtrona je
lahko vsak od njih v najnižjem kvantnem (energijskem) stanju in zato najmočneje veže elektrona
ter ima tako največjo ionizacijsko energijo (rabimo največ dela, da mu slečemo elektronsko
frizuro). Zakoni kvantne mehanike seveda tudi diktirajo polnjenje elektronskih orbital (nivojev)
atomov.
Odbojna sila med protonoma
(F = ee/(4πεor2),
e = 1,6021766208×10-19 As,
εo = 8,854187817×10-12 As/Vm )
na razdalji
10-15 m je kar okrog neverjetnih 160 N.
In močna jedrska sila mora kompenzirati ta izjemen odboj. Če izračunamo klasično
električno potencialno energijo
( Up = ee/(4πεor) )
med dvema protonoma v jedru na
razdalji okrog r = 1,2 10-15 m, dobimo precej veliko vrednost:
Up = ee/(4πεor) = 1,2 MeV.
Ocenimo še delo privlačne močne jedrske sile - kar iz slike. Velja ocena, da je za
pot
Δr = 10-15 m, pri sili
104 N/2 (sila je prebrana iz slike, pri napisu privlak), ocena dela
W = FΔr = 10-15 m*104 N/2 = 5 10-12 J
= 30 10-12 1018 eV = 30 106 eV = 30 MeV
(to je zgolj ocena). Če bi računali delo odbojne sile, bi dobili le okrog 1 MeV
(velikost potenciala). To so samo ocene, ki pa kažejo na bistvo, da je delo
močne jedrske sile veliko večje od dela odbojne sile med protoni – velikostni
red sproščene energije pa je pravilen (same številke pa NE). Sproščena energija
močne jedrske sile nam torej omogoča tvorbo težkih elementov (večinoma v zvezdah),
hkrati pa naredi vesolje svetlo – zvezde svetijo, oddajajo elektromagnetno valovanje
in s tem (lahko) omogočajo tudi življenje.
Velja torej, da je masa jedra (recimo helija) manjša kot seštevek posameznih mas (protonov),
ker je del mase pretvorjen
preko močne jedrske sile
v vezavno energijo atomskega jedra - ki je sedaj po zlitju
neto nižja energija, kot pred zlitjem.
Vezavna energija atomskega jedra
Ponazoritev izrazov polempirične masne formule v kapljičnem modelu atomskega jedra.
Atomsko jedro se po tem modelu obnaša kot molekule v kapljici tekočine. A tokrat
je "tekočina" sestavljena iz nukleonov (protonov in nevtronov), ki jih skupaj drži močna jedrska sila.
Model tekočinske kaplje je prvi predlagal George Gamow, nadalje pa sta ga razvila Niels Bohr in John Archibald Wheeler.
Jedro obravnava kot kapljico nestisljive tekočine z zelo visoko gostoto, ki jo skupaj drži jedrska sila
(učinek močne sile) in torej obstaja dokaj velika podobnost s strukturo sferične tekočinske kapljice.
Model tekočinske kapljice torej upošteva sferično obliko večine jeder in
daje grobo napoved vezavne energije. Katere energije moramo upoštevati:
* Volumenska energija - vsota vseh nukleonov enake velikosti je zapakirana skupaj v najmanjši volumen in
vsak notranji
nukleon je vezan na določeno število drugih nukleonov, je v stiku z njim preko močne jedske sile.
Torej je ta del jedrske energije sorazmeren z volumnom.
* Površinska energija popravi prejšnjo predpostavko, da vsak nukleon interagira z
enakim številom drugih nukleonov. Ta izraz je negativen in sorazmeren s površino, zato je približno
enakovreden površinski napetosti tekočine.
* Coulombova energija, potencialna energija vsakega para protonov. Ker je to odbojna sila,
se vezavna energija zmanjša.
* Energija asimetrije (imenovana tudi Paulijeva energija), ki upošteva Paulijevo izključitveno načelo.
Neenako število nevtronov in protonov pomeni zapolnjevanje višjih energijskih ravni za eno vrsto delcev,
medtem ko nižje ravni energije za drugo vrsto pustijo prazne.
* Energija združevanja parov, ki pojasnjuje težnjo po nastanku protonskih in nevtronskih parov.
Sodo število delcev je zaradi spinske sklopitve bolj stabilno kot liho število.
Izredno pomembno vlogo pri tvorbi atomov (nukleosintezi) pa igrajo nevtroni. Jedro zgolj iz protonov namreč takoj
razpade, v kombinaciji z nevtroni, pa je razdalja med protoni ravno toliko večja, da izrazito prevlada močna
privlačna jedrska sila nad odbojno Coulombovo silo. Modeli atomskih jeder so zato kar zapleteni matematičnofizikalni
opisi. Kombinacija protonov in nevtronov ter njihova geometrija, porazdelitev – določajo stabilnost in vezavno energijo
atoma. Kdaj pomeni le en nevtron več v jedru porušeno ravnotežje samega atoma, ki tako razpade (prevladajo odbojne sile).
Zgolj shematičen prikaz geometrije atomskega jedra iz protonov in nevtronov – v kvantnem opisu lahko zgolj govorimo o
verjetnosti lege določenega nukleona v samem jedru, ki se s časom spreminja.
Masa atomskega jedra je podana z vsoto mas posameznih nukleonov v jedru, a zmanjšana za vezavno energijo (!!!) deljeno
s kvadratom hitrosti svetlobe (EB/c2). Velja, masa atomskega jedra je:
m = Zmp + Nmn - EB/c2
Z – je število protonov, N – je število nevtronov, A – je atomsko masno število (A=Z+N), mp - je masa protona
in mn – je masa nevtrona. Masa protona je mp = 1,672621898×10-27 kg,
masa nevtrona pa je nekaj večja in sicer mn = 1.67492749804(95)×10-27 kg =
939.56542052 MeV/c2,
masa elektrona pa
9,10938356×10-31 kg.
Posebej poudarimo, da je velika večina mase zbrana v jedru atoma, elektroni imajo namreč zelo majhno
maso v primerjavi s protoni, oz. nevtroni (proton je 1836 masivnejši glede na elektron). A jedro je
veliko le nekaj krat 10-15 m - samo velikost atomov pa (nekoliko protislovno) določa oblak lahkih
elektronov okrog jedra. Premer atoma je tako velikostnega reda 10-10 m. Razmerje med velikostjo
atoma in jedra je kar od 104 do neverjetnih 105.
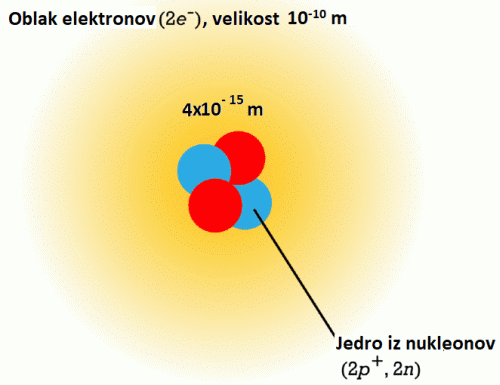
Shematični model atoma helija (42He).
Vezavna energija atomskega jedra je podana z Weizsäckerjevo semiempirično masno enačbo:
EB = avolA - asurfA2/3 -
acombZ(Z-1)*A-1/3 - asym(A-2Z)2*A-1
+
(((-1)Z + (-1)A-Z)/2)apZ(Z-1)*A-1/2
Prvi člen (15,56 MeV*A) je notranja energija jedra, drugi člen (17,23 MeV *A2/3)
opisuje energijo površinske lupine jedra.
Tretji člen
(0.7 MeV*Z(Z-1)*A-1/3) opisuje energijo zaradi elektrostatskega Coulombovega odboja protonov v jedru, četrti
člen
(23,6 MeV*(A-2Z)2*A-1) pa energijo, ki upošteva, da imajo lahka jedra približno enako število protonov in nevtronov
(če ne, pa izvrednoti energijo zaradi razlike protonov in nevtronov).
Zadnji člen (11,2 MeV* A-1/2 )
je paritvena energija, ki opisuje, da so najmočneje vezana jedra s sodim številom protonov in sodim številom nevtronov,
najmanj pa taka z lihim številom protonov in lihim številom nevtronov. Konstante členov se s časom, preko meritev,
nekoliko popravljajo. Večje je jedro (število A), večjo vezavno energijo ima.
Še komentar.
Formula je precej neuporabna za zelo lahka jedra z majhnim številom nukleonov; za večja jedra je dober približek.
Toda tudi tukaj ne more razložiti na primer posebno velikih veznih energij
v območjih okoli magičnih števil. Samo model lupine ponuja razlago za to.
Magično število je število nukleonov (protona in nevtrona) v atomskem jedru,
ko je to atomsko jedro zelo stabilno:
2, 8, 20, 28, 50, 82 in 126.
Dvojno magična in še bolj stabilna so jedra z magičnim številom protonov in
nevtronov, na primer:
helij
2He4, kisik 8O16, dva izotopa kalcija 20Ca40
in 20Ca48,
dva izotopa
niklja 28Ni48 in 28Ni78, svinec 82Pb208.
Lupinski model atomskega jedra - osnove

Model lupine v jedrski fiziki temelji na kvantnomehanskih zakonitostih, predvsem na
kvantizaciji vrtilne količine in Paulijevem principu, in tako na primer
uspešno pojasnjuje že omenjene magične številke v
sestavi atomskih jeder.
Model je bil razvit leta 1949 po neodvisnem delu več fizikov, predvsem Eugene
Paul Wigner, Maria Goeppert Mayer in J. Hans D. Jensen, ki sta si za svoje prispevke leta 1963
delila Nobelovo nagrado za fiziko.
Model jedrske lupine je delno podoben modelu atomske lupine, ki opisuje razporeditev elektronov v atomu,
saj napolnjena lupina povzroči boljšo stabilnost. Pri dodajanju nukleonov (protonov ali nevtronov)
v jedro obstajajo določene točke, kjer je vezavna energija naslednjega nukleona bistveno
manjša od zadnjega. Ta ugotovitev, da obstajajo posebna magična kvantna števila
nukleonov (2, 8, 20, 28, 50, 82, 126), ki so tesneje vezana kot naslednje višje število,
je izvor lupinskega modela.
Lupine za protone in nevtrone so neodvisne druga od druge. Zato lahko obstajajo tako "magična jedra",
v katerih je ena ali druga vrsta nukleona pri magičnem številu,
kot tudi "dvojno magična kvantna jedra", kjer sta obe vrsti nukleonov številsko "magični".
A tudi lupinski model atomskega jedra ima težave!
Da bi dobili te številke, model jedrske lupine izhaja iz povprečnega potenciala z obliko nekje med kvadratno
jamo in harmoničnim oscilatorjem. Temu potencialu je dodan termin vrtilne orbite. Kljub temu skupna motnja
ne sovpada z eksperimentom, zato je treba dodati empirično sklopitev vrtilne orbite z vsaj dvema ali tremi
različnimi vrednostmi njene sklopitvene konstante, odvisno od preučevanih jeder.
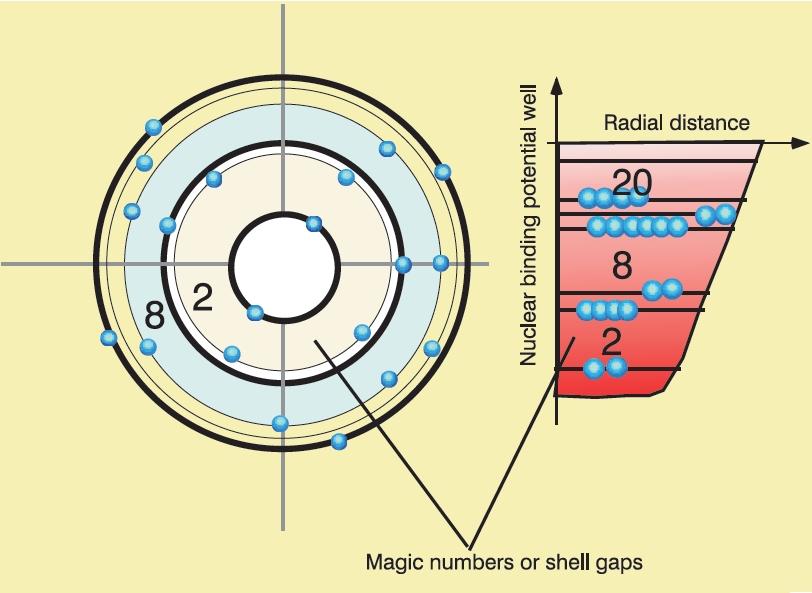
Skupaj s spin-orbitalno interakcijo in za ustrezne vrednosti obeh učinkov, pride do naslednje kvalitativne slike:
na vseh ravneh imajo najvišja stanja j svoje energije premaknjene navzdol,
zlasti pri visokih n (kjer je najvišji j visok ). Število n je nivo in kvantno število j = |l +/- s| je število
celotnega kotnega momenta (s je spin, l je azimutno kvantno število ali kotni moment).
1. lupina: 2 stanji (n = 0, j = 1/2).
2. lupina: 6 stanj (n = 1, j = 1/2 ali 3/2).
3. lupina: 12 stanj (n = 2, j = 1/2, 3/2 ali 5/2).
4. lupina: 8 stanj (n = 3, j = 7/2).
5. lupina: 22 stanj (n = 3, j = 1/2, 3/2 ali 5/2; n = 4, j = 9/2).
6. lupina: 32 stanj (n = 4, j = 1/2, 3/2, 5/2 ali 7/2; n = 5, j = 11/2).
7. lupina: 44 stanj (n = 5, j = 1/2, 3/2, 5/2, 7/2 ali 9/2; n = 6, j = 13/2).
8. lupina: 58 stanj (n = 6, j = 1/2, 3/2, 5/2, 7/2, 9/2 ali 11/2; n = 7, j = 15/2).
Čarobne (magične) številke so torej:
2
8=2+6
20=2+6+12
28=2+6+12+8
50=2+6+12+8+22
82=2+6+12+8+22+32
126=2+6+12+8+22+32+44
184=2+6+12+8+22+32+44+58
Več na to temo najdete v strokovni literaturi.
Vrnimo se k vezavni energiji nukleonov v atomskem jedru.
Še veliko bolj pa je zanimiva vezavna energija deljena z A (s številom nukleonov – vsoto protonov in nevtronov).
Absolutna vezavna energija na nukleon
(EB/A)
je največja v jedru železa 5626Fe. Naslednji graf je tako zelo poučen,
saj kaže porazdelitev atomskih elementov po vezavni energiji na nukleon. Vezavna energija na nukleon »pada« nekje
do -8,8 MeV pri železu, niklju, nakar pa začne naraščati. Elementi z atomskim masnim številom okrog 56 ali 60
so zato zelo stabilni – protoni in nevtroni so v teh jedrih najmočneje vezani.
Ta ugotovitev ima zelo
zanimive posledice za razlago narave nastanka atomov do železa in spet drugačno razlago za tvorbo velike
družine težjih elementov od železa.
Kot bomo videli, se pri zlivanju lažjih v masivnejša jedra (do železa),
sprosti veliko več energije, kot je je potrebno, da se premaga odbojne sile med protoni bodočega jedra.
Ti elementi nastajajo v zvezdah, sproščena energija fuzije pa omogoča zvezdam, da sevajo milijarde
let dolgo enormne količine energije. Vsi masivnejši elementi od železa pa rabijo več energije za
premagovanje odbojne sile, kot se je nato sprosti v vezavni energiji jedra (pri velikih
jedrih pričakovano pada vpliv močne jedrske sile, saj ima le ta kratek doseg in posledično
se veča vpliv odbojnih sil). Masivnejši elementi so torej neto porabniki energije in zato nastajajo
večinoma med eksplozijami supernov in med trkih zvezd, tudi pri trkih nevtronskih zvezd – recimo zlato.
Zlivanje v težje elemente od železa, bi zvezdo ohladilo in s tem ustavilo nuklearne reakcije
(sintezo masivnejših elementov) ... Pri razlagi razlik med fuzijo in fisijo si bomo pomagali
z grafi sil med nukleoni v jedru in z vloženim delom pri združevanju nukleonov (premagovanju
Coulombove sile, bariere) ter sproščeno energijo zaradi dela močnih privlačnih sil v samem jedru
med nukleosintezo (negativni del grafa sile glede na razdaljo).
Pri nekoliko zapleteni nukleosintezi vodika (protonov) v helij (4) velja naslednja shema in bilanca energije - mase.

Shematični prikaz najpomembnejšega P-P I niza zlivanja vodika v helij v Sončevem jedru.
Večina energije Sonca izhaja iz p–p (proton–proton) verige zlivanj vodika v helij:
4p => 4He + 2e+ + 2νe
Od tega je kar 83.3 % energije iz P-P I niza, ki sprosti 26.732 MeV energije (0.7 % mase
protonov
Δm = ΔE/c2
gre v energijo). Fuzija se seveda dogaja
v Sončevem jedru, znotraj območja - 0.25xRSonca - pri temperaturah okrog
14 milijonov Kelvinov in pri gostoti jedra kar
162.2 kg/dm3
(v povprečju se v jedru sprosti
L/(4πRje2)
~ nekaj 10 Watov/m3,
v centru pa že blizu 300 W/m3, relativno malo - a je polmer
Rje jedra Sonca, kjer poteka fuzija, zelo velik -
okrog 28 polmerov Zemlje). Seveda – zvezdo drži skupaj lastna gravitacija,
ta stiska večinoma ioniziran plin v vročo kroglo – to je v našem primeru
lastna teža Sonca.
Izsev Sonca je
L = 3.828×1026 W, do Zemlje pride
j = L/(4πR2) = 1367 W/m2
(to je energija, ki nam daje življenje). Sonce zaradi fuzije vsako sekundo izgubi
4,26 milijonov ton mase (gre v izsev pri tvorbi težjih atomov). Tudi v vesolju
ni nič zastonj – čeprav se to tako kdaj zdi ... in še dobro, da je tako!
Zadnji grafi torej kažejo, koliko dela zvezde (delo plazme) je bilo potrebno vložiti, da premagamo odbojno silo med protoni (ploščina obarvana modro pod grafom F od r je kar delo - saj je delo (work) definirano kot W = ∫Fdr – skalarni produkt med silo in potjo) in koliko dela je bilo vrnjenega v sistem preko negativne močne jedrske sile, večinoma preko sevanja (oranžno obarvana površina je negativno delo močne jedrske sile)! Iz energijske bilance zvezd razberemo, da je sistem (recimo sredica Sonca) prejema pri tvorbi helija veliko več povrnjene energije, kot je je vložil - notranje energije (kinetične energije delcev, ki se odraža v temperaturi) – ta višek je posledica potencialne energije močne sile. Oranžno obarvana površina (levi graf) je veliko večja od modre površine, ki predstavlja delo pri premagovanju odbojne sile. Kdo bi lahko izjavil, vprašal (in tako vprašanje je umestno), da tukaj nekaj ne »štima« – da smo prejeli več energije, kot smo je vložili. Ja – to bi držalo – če ne bi 'odkrili' in upoštevali močne jedrske sile, torej vezavne jedrske energije, in če tako posledično ne bi del mase jedra šel v sevanje - Δmc2 – (vsako pospešeno gibanje električnih delcev, kar se pri hipni fuziji zgodi, pomeni izsevanje elektromagnetnega valovanja - energije) in to je direktni dokaz, da je masa samo ena izmed oblik energije. In ta pozitivna bilanca oddane energije fuzije (zlivanja) drži zvezdo v termičnem ravnotežju, presežek pa se izseva v vesolje (pravimo, da zvezde svetijo, Sonce obilno tudi na naš planet in s tem omogoča življenje).
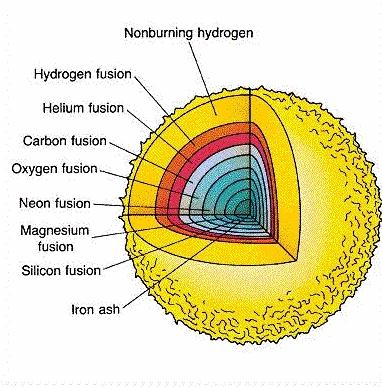
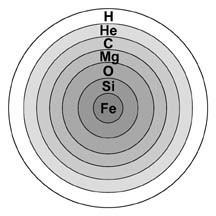
Končna faza porazdelitve lupin masivne zvezde glede na vsebnost atomov
(velja za zvezdo z začetno maso okrog 10 M☉) po koncu nukleosinteze
(fuzije, zlivanja lažjih atomskih jeder v težja, do železa Fe).
Zelo masivna zvezda je tako na koncu fuzije po notranji zgradbi podobna čebuli, kjer je v jedru železo -
iz železovega središča navzven pa imamo naslednje plasti:
silicijevo, dušikovo, kisikovo, ogljikovo, helijevo, v zunanji plasti zvezde pa vodikovo plast
(vmes so tudi lupine magnezija, neona ...).
Kot zanimivost - astronomija povezuje vse vede in tega se
razumniki iz vseh področij tudi zavedajo - povejmo, da se je pred leti naši
astronomski skupini priključila tudi dr. Elza Leskovec ( Biotehniška fakulteta v Ljubljani ),
ki je s selekcijo vzgojila imenitno čebulo Belokranjko. Sploh agronomi, kmetje, so v bistvu
"čarodeji", ki nam pridelujejo hrano iz zvezdnega prahu in hkrati sledijo letnemu gibanju Sonca,
ki odloča o letnih časih, ki so bistveni pri načrtovanju setve, žetve,
obdelave tal. S poznavanjem genetike in s pomočjo selekcije pa žlahtnijo rastline - tudi čebulo, simbol sestave zvezd
- kot naša dr. Elza.
| Gorivo | Glavni produkti | sekundarni produkti | Temperature (milijarde kelvinov) | Trajanje (leta) |
| H | He | N | 0.03 | 1 x 107 |
| He | C, O | Ne | 0.2 | 1 x 106 |
| C | Ne, Mg | Na | 0.8 | 1 x 105 |
| Ne | O, Mg | Al, P | 1.5 | 0.1 |
| O | Si, S | Cl, Ar, K, Ca | 2.0 | 2 |
| Si | Fe | Ti, V, Cr, Mn, Co, Ni | 3.3 | 0.01 |
Ta tabela prikazuje reakcije nukleosinteze (fuzije), ki se pojavljajo v zaporednih stopnjah pri masivnih zvezdah (mase > 8M☉, čas zlivanja je precej manj ko milijardo let, velja znana ocena t = 1010(M☉/M)2.5 let). Tabela povzema glavne reakcije in njihove produkte (vključno z ostalimi elementi, ki nastanejo v sledovih), temperature, pri katerih pride do reakcij in koliko časa je potrebnega, da se porabi razpoložljivo vhodno gorivo, nukleoni. Konvekcija prinese elemente blizu površine zvezde, kjer jih močni zvezdni vetrovi delno razpršijo v vesolje. Zelo masivne zvezde z zajemanjem nevtronov delno proizvajajo tudi elemente težje od železa. Kot vidimo - pri taki klasični zvezdi in njeni nukleosintezi ni prisoten fluor (saj ne v izobilju), kisik pa je. Vir: https://imagine.gsfc.nasa.gov/educators/elements/imagine/05.html

M82: primer galaksije, kjer se zvezde rojevajo s supervetrom in z mešanico težkih elementov.
Eksplozije supernov in močni vetrovi iz masivnih zvezd povzročajo izbruhe nastajanja zvezd
v M82 in izrazit odtok snovi. Dokazi o supervetru iz osrednjih območij galaksije so jasno
vidni na ostrem teleskopskem posnetku. Sestavljena slika poudarja emisijo dolgih vlaken
atomarnega vodikovega plina v rdečkastih odtenkih. Del plina v supervetru, obogaten s
težkimi elementi v masivnih zvezdah, bo sčasoma ušel v medgalaktični prostor. Izraziti
izbruh nastajanja zvezd v M82, sprožen zaradi srečanja z bližnjo veliko galaksijo M81,
bi moral trajati približno 100 milijonov let. Znana tudi kot galaksija Cigara zaradi
podolgovatega vizualnega izgleda, meri M82 okoli 30.000 svetlobnih let. Nahaja se
12 milijonov svetlobnih let od nas blizu severne meje Velikega Medveda. Galaksiji
M82 in M81 sta vidni ob temni noči že z daljnogledom 15X70, s teleskopom pa sta to
idealni tarči za učence – tudi za slikanje. Galaksij kot porodnišnic zvezd, je na nebu
zelo veliko, v naši Galaksiji pa je odlično vidna (že s prostim očesom, z daljnogledom
pa toliko lažje) znamenita porodnišnica v Orionovi meglici M42 - oddaljena je
»zgolj« 1500 svetlobnih let
(v premeru meri okrog 40 svetlobnih let).
Krasna tarča za mlade radovedneže, tako za opazovanja
kot za fotografiranja. Vir: apod.
Prve zvezde v vesolju nastanejo že kmalu po velikem poku, imajo zelo nizko vsebnost kovin (imenujemo jih populacija III). Pojasnimo še, da z izrazom kovina tu mislimo na vse ostale kemijske elemente, težje od vodika in helija. Obstajajo še zvezde populacije II, to je take z nekaj več težkih elementov. Zvezde "nedavnega" nastanka (z relativno visoko vsebnostjo kovin) pa populacija I. Zvezde populacije III so nastale že približno 400 milijonov let po velikem poku (ki bi se naj zgodil pred 13,8 milijarde let). Sonce ima razmeroma veliko kovin, ostalih težjih elementov od vodika, helija in je tako nastalo pred "nedavnim", pred približno 4,6 milijarde let in torej pripada populaciji I. Nastalo je torej v času, ko so masivne zvezde (populacije III in II) z zlivanjem lažjih atomov v težje že eksplodirale kot supernove (ali so nevtronske in druge zvezde trčile) in tako že izvrgle v vesolje elemente do mase železa, med samo eksplozijo ali trki zvezd pa so nastali še težji elementi od železa - tudi za človeka toliko zaželeno zlato.
Železo je izjemno stabilno in onemogoča nadaljnjo fuzijo. Zakaj? Temperatura sredice zvezde iz železa tako lahko doseže 3 milijarde K. Ko železna sredica doseže kritično maso, silovito kolapsira v eksplozijo supernove in mnogi nastali težji atomi so tako še dodatno odvrženi v vesolje. Zakaj se torej pri železu ustavi fuzija v sredici zvezde (železo sestavlja 26 protonov in 30 nevtronov, še bolj pa je stabilen recimo izotop 60Fe)? Ko atomsko jedro narašča (narašča število protonov in nevtronov v jedru) se veča tudi razdalja med nukleoni in s tem odbojna sila med protoni, sploh zunanji deli jedra so manj gosti s protoni – velikokrat to opišemo z vezavno energijo na nukleon (na proton in nevtron, veliko je odvisno tudi od same geometrije jedra, kako je sestavljeno). Pri železu 5626Fe torej tudi velja, da ima največjo absolutno vezavno energijo na nukleon (EB/A, da tako jedro razbijemo, rabimo največ dela). Prav pri železu se tudi zgodi, da je za naslednje elemente potrebno nekaj več energije, da se nov proton poveže, recimo, v masivnejše jedro kobalta, kot se pri tem sprosti energije zaradi fuzije. Po domače - sila, ki na kocu veže nov proton v kobalt je tako nekoliko manjša kot sila s katero potisnemo proton proti jedru. Če pogledamo delo obeh sil, potem velja, da je vloženo delo zvezde večje, od oddanega pri vezavi na jedro in s tem se tudi temperatura zvezde zmanjša in se tako tudi praktično ustavi zlivanje manjših jeder v masivnejaša jedra - atome (ki so masivnejši od železa). Težji elementi od železa lahko nastanejo torej le pri ekstremno visokih energijah (temperaturah, gostotah) – ki se sprostijo pri eksplozijah supernov in trkih zvezd.
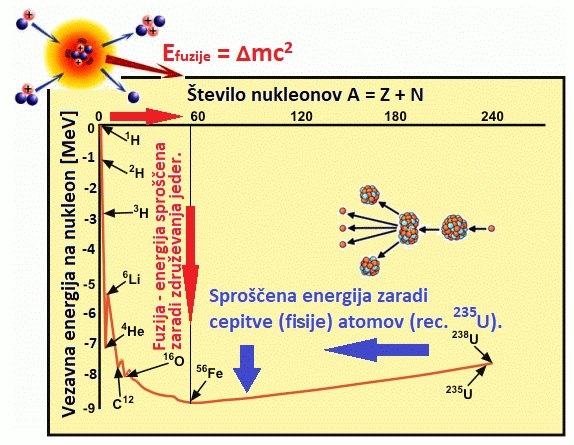
Graf vezavne energije na nukleon (EB/A) glede na maso atomskega jedra. Vezavna
energija na nukleon pada nekje do
EB/A = - 492,3 MeV/56 = -8,8 MeV
pri železu
5626Fe,
nakar pa začne naraščati. Razlog se skriva v ravnovesju med
močno jedrsko silo in odbojno silo med protoni. Pomembno vlogo pa igra
tudi število nevtronov, brez njih ni stabilnega atomskega jedra –
razen vodikovega. Graf je zelo pomemben s stališča razumevanja narave
nastanka elementov in razlage enormnih količin energije, ki jo sproščajo
zvezde. Na njem se skriva tudi del odgovora o verigi dogodkov, ki so privedli
do življenja.
Še beseda o jedrski energiji v umetnosti, v filmu
in o težavah v katere smo zabredli zaradi odkritja cepitve urana 235 leta 1938/39.
Igralec
Cillian Murphy
v filmu Oppenheimer poudari, da ni ravno dober v praksi, v laboratoriju, a je dober teoretik ... in zgodila se je
strašna sprostitev delčka zvezdne energije.
Oglejte si torej film Oppenheimer, čeprav si prizori v filmu sledijo precej zmedeno, nekoliko kaotično - kot se to recimo
dogaja v kvantni mehaniki preko izmenjave virtualnih
fotonov, nedoločenosti lege in gibalne količine, med fluktuacijami vakuuma ...
Ali so to povezavo hoteli tudi prikazati preko
kaotičnega zaporedja prizorov, ne vem? A vseeno ima nekaj človeško-kozmološke duše tale film.
Film poudari izjemno neugoden trenutek velikega odkritja, cepitve masivnih atomov v nuklearni fiziki,
tik pred drugo svetovno vojno.
Takrat so že bili na sledi fuziji, kot viru energije zvezd - več o tem morebiti v naslednjih člankih.
A hkrati so odkrili sprostitev energije
pri cepitvi masivnih atomskih jeder. Oboje je povezano z znamenito enačbo E = Δmc2.
Otto Hahn in
Fritz Strassmann (sodelovala je tudi Lise Meitner)
leta 1938/39 odkrijeta, da se z nevtronskim obstreljevanjem atomskega jedro urana 235 le ta razcepi na dve lažji atomski jedri.
L. Meitner je dala razlago te jedrske reakcije in jo poimenovala jedrska cepitev, fisija. Na tej reakciji temelji
delovanje jedrskih reaktorjev in žal tudi zloglasnih jedrskih bomb.
Pri tipični fisijski reakciji se jedro urana-235, potem ko absorbira nevtron in za trenutek postane jedro izotop
U-236 (velja:
n + 23592U => 23692U ),
razcepi recimo na jedri kriptona in barija in pri tem sprosti še tri nevtrone (tudi ogromno energije).
Ne samo, da lahko dobimo različne izotope barija in kriptona z različnim številom prostih nevtronov,
ampak lahko dobimo tudi različne elemente (recimo La - lantan; Br - brom.)
Srednje velika jedra, kot so Ba, Kr, La in Br, imenujemo fisijski fragmenti, produkti.
Večinoma niso običajni izotopi teh elementov in so posledično zelo radioaktivni.
Proces predstavlja torej tudi sproščanje velike količine energije.
Od kod ta sproščena energija?
Pri fuziji, tvorbi atomov v zvezdah do železa, se energije sprošča (v našem Soncu že skoraj 5 milijard let)
in je končna masa jedra (recimo helija) zato manjša od gradnikov pred zlitjem (masni "defekt").
Pri tvorbi težjih elementov od železa (ti se NE tvorijo v zvezdah) pa je proces ravno obraten.
Energija se mora namreč pri tvorbi zelo masivnih jeder dovajati (recimo iz energije eksplozij supernov
ali energije trkov nevtronskih zvezd) in je tako končna masa (recimo urana 235) večja kot masa začetnih gradnikov
(glejte zgornji graf).
Med tvorbo masivnejših atomov od železa namreč efektivno nekoliko prevlada delo odbojne sile protonov nad
delom privlačne močne jedrske sile med nukleoni - zato so ta jedra lahko precej nestabilna.
Pri velikih jedrih počasi prevlada odbojna sila med protoni nad močno jedrsko vezavno silo, ki deluje le na kratke razdalje.
Na splošno je geometrijska porazdelitev protonov in nevtronov tista, ki določa
stabilnost nekega atoma - vse kombinacije protonov in nevtronov še zdaleč niso stabilne
(precej težko med fuzijo nastane recimo najbolj reaktiven element fluor - 199F).
Velikokrat si pomagamo s kapljičnim modelom
jedra atoma (kjer se upošteva vezavna energija zaradi močne jedrske sile, površinske napetosti,
energija zaradi odbojnih sil med protoni,
energija združevanja parov, energija asimetrije - ki upošteva Paulijevo izključitveno načelo).
Pri razpadu masivnih atomov U-235 + n (recimo v jedrskih reaktorjih) pa gre ravno za obrnjen proces.
23692U => 14456Ba + 8936Kr + 3n
Torej je skupna masa (produktov razpada m_kon) na desni strani enačbe manjša od mase na levi (U-236, m_zac).
Velja torej m_zac > m_kon.
Čeprav je število protonov in nevtronov enako, sta jedri kriptona in barija tesneje vezani kot jedro urana;
njuna vezavna energija je večja (in sta zato lažji).
Sproščena energija je torej kar E = (m_kon - m_zac)c2 in ta nam v kontrolirani obliki prinese ogromno
energije v nuklearnih reaktorjih, a hkrati strašno razdiralno moč med jedrsko eksplozijo - verižno reakcijo.
Tako se torej sprosti tudi delček enormnih energij eksplozij supernov in silovitih trkov zvezd, ki so delno
shranjene v masivnih atomskih jedrih (U-235, U-238, Pu-239) - naš NEK je torej tudi del burnih dogajanj
v preteklosti vesolja (supernove, trki zvezd).
V filmu se prav dilema razdiralne moči jedrske energije pričakovano močno poudarja - in rešitve žal še danes nismo našli,
ker je pač taka trenutna narava človeka ...
(Ali je res zaradi jedrskega orožja manj vojn? Zagotovo je več delitve plena iz nabora manjših držav med velike ...,
tudi v tem trenutku!).
Ko opazujemo vesolje, tudi na prosto oko, z daljnogledom
ali teleskopom, je prav, da razumemo tudi osnove naravnih procesov in pomen
dogajanj tam daleč - recimo v zvezdah - "v naših atomskih mamah."
Ni napak, če si ogledamo tudi serijo Černobil - tudi kontrolirana fisija je potencialno zelo nevarna,
če ni kompetentne civilne kontrole nad
ekipami inženirjev, konstruktorjev in nad politiko, ki daje neumne ukaze ...
Astronomija v šolah bi zagotovo veliko prispevala k ekološki in znanstveni ozaveščenosti bodoče družbe,
tega nam danes še kako manjka (znanja in celostnega razumevanja delovanja narave)
in zato so poteze odločevalcev velikokrat zelo, zelo napačne. Da ne bomo načenjali zgolj
velikih tem - poglejmo samo, kaj damo v usta -
vse kar nam zavijejo v plastiko, hormonski motilci tako vztrajno najedajo našo naravo
in v službe se vozimo z dvema tonama železa, plastike, nafte pod zadnjico ...
Verižna reakcija
Teoretične študije v zgodnjih štiridesetih letih prejšnjega stoletja so pokazale, da cepitev
vključuje postopno spreminjanje oblike prvotnega jedra, nekako takole:
Ko nevtralni nevtron prileti v jedro uran 235, ga vrže iz ravnovesja – jedro se raztegne in tako prevladajo
odbojne sile med protoni nad
močnimi jedrskimi silami kratkega dosega. Tako pride do cepitve urana, upajmo da le še v jedrskih elektrarnah.
Recimo, da imate kos urana, ki je večinoma 235U in vanj vnesete en nevtron. Eno jedro
absorbira nevtron, da proizvede 236U, ki se nato razcepi. Po tej cepitvi ostanejo trije prosti nevtroni.
Vsak od teh nevtronov lahko zadene drugo uranovo jedro in tako čez nekaj časa pride do treh novih cepitev
in devetih prostih nevtronov. Vsak od teh lahko povzroči novo cepitev in nato 27 prostih nevtronov.
Tako pride do zelo hitrega razmnoževalnega učinka, tako da kljub temu, da začnemo z enim nevtronom,
končamo z zelo velikim številom uranovih jeder, ki se cepijo. V delčku sekunde se lahko celoten vzorec
s približno 1027 jedri razcepi. Ta proces razcepa imenujemo verižna reakcija.
Ko nevtron nastane pri cepitvi, ne zadene v trenutku drugega uranovega jedra. Ne pozabite, da je vzorec
urana sestavljen iz atomov in med jedri (ki jih zasedajo elektroni) so velike razdalje (prazni prostori),
skozi katere se nevtroni
lahko premikajo, ne da bi povzročili cepitev. Običajno nevtron potuje 2 ali 3 centimetre, preden zadene jedro. Če
je torej vzorec zelo majhen (recimo 1 cm v premeru), se bo večina nevtronov premaknila skozenj in šla ven ob straneh,
preden bo povzročila novo cepitev. Da bi prišlo do dovolj cepitev, da se torej ohrani učinek množenja verižne reakcije,
mora biti vzorec urana določene minimalne velikosti. Če gre za kroglo, se izkaže, da je najmanjša velikost
približno 20 cm premera. Ta količina urana se imenuje kritična masa.
Sedaj, ko smo na kratko opisali zvezde kot nebesne plavže za izdelavo težkih atomov in na preprost način razložili naravo atomov in vpliv le teh na življenje, pa si poglejmo še enega od junakov življenja – to je kisik O. Pri spajanju atomov v molekule (v bistvu trku) se sprosti veliko energije v obliki povečanja kinetične energije reagentov - in s tem toplote (saj velja kT ∝ mv2) – ker se spremenijo tudi razdalje med elektroni in protoni, bolj pravilno, spremenijo se energijski nivoji elektronskih porazdelitev, tako pride tudi do sproščanja fotonov (elektromagnetnega valovanja – lep primer je nam vsem poznam ogenj). Gorenje torej pomeni hipno kemijsko vezavo kisika, ko se kisik kot kak nepridiprav, tečnež, vagabund zelo rad, zaradi elektronegativnosti, zaletava v sosednje plešoče atome in molekule in pri tem se (kot pri mehanski energiji) električna potencialna (kemijska) energija spreminja v elektromagnetno in kinetično in vmes lahko naredi še nekaj trkov in s tem razbije sosednje molekule ali celo ionizira atome. Zakaj ravno kisik?
Oksidaciji bi morali posvetiti posebno pozornost, saj je bistvena reakcija našega življenja, ga omogoča (poteka v samem telesu živali, ljudi, v okolju pa oksidacijo najbolje prepoznamo preko že omenjenega ognja). Masni delež kisika v sestavi Zemlje je kar 28,2 %, takoj za železom z 35,1 % (praktično vsi težji elementi, od vodika naprej, so nastali v zvezdah, tudi ob trkih zvezd, eksplozijah zvezd). Kaj je torej zadaj, za procesom življenja – kaj je oksidacija? Redoks reakcije so procesi premeščanja zunanjih elektronov iz atoma (molekule, iona) na drugi atom (molekulo, ion). Reakcije s kisikom pa so skoraj vedno redoks reakcije, pri katerih kisik običajno vzame dva elektrona in se tako reducira v oksid nekega drugega atoma. Zato velja kisik kot izredno močan oksidant (od tod tudi ime oksidacija, recimo ogljika C v CO2, vodika v izjemno pomembno vodo H2O - tekočino življenja, železa v okside FeO ali Fe2O3 ali Fe3O4, posredno preko silikatnega preperevanja v apnenec – to je v kalcijev karbonat CaCO3, kisik je vezan v aminokisline - torej v beljakovine življenja ..., seveda veže tudi sam sebe v molekulo O2). Izjema so recimo zlato, nekatere ostale žlahtne kovine in seveda žlahtni plini, ki imajo zunanje orbitale že polne, ki s kisikom ne reagirajo. Pogosto reakcije s kisikom, zaradi visoke energije atomske vezi, ki se sprosti, potekajo tudi z močnim sproščanjem toplote, posredi je lahko tudi ogenj, eksplozije. Še prej pa beseda o periodnem sistemu in osnovnih elektromagnetnih silah, ki oblikujejo ta naš svet.
Kako razumeti obnašanje atomov pri »sobnih« temperaturah (ki nam omogočajo življenje)? Na to vprašanje podajmo nekoliko poenostavljen model – rahlo drugačen, kot smo ga navajeni iz stare šole. Narava kvantnih delcev (recimo elektronov ob atomskem jedru) je približno taka, kot je (lahko) logika naselitve stanovalcev v stolpnico, v stolpnice in logika povezav med stolpnicami zaradi principa nadstropij. Za stanovanjsko stolpnico velja, da vsako nadstropje (v primeru atoma naj bo to orbitala), s svojo potencialno energijo, sprejme le določeno število stanovalcev (kot atom elektronov na posamezni orbitali). In tako kot stanovalci ne morejo živeti z nogami malo v prvem in z glavo malo v drugem nadstropju, tako tudi elektroni ne morejo biti na poljubnih legah okrog atoma – ampak zavzemajo točno določene energijske nivoje (»orbitale«, »nadstropja«) in za prehod iz nižjega na višji nivo sprejmejo energijo (recimo s trki ali direktno preko absorpcije svetlobe), ko se pa vrnejo na nižji nivo pa svetlobo oddajo. In če gledamo na uporabno (že naseljeno) velikost stanovanjskega bloka preko nadstropij, ki jih naselijo stanovalci, se le ta uporabna velikost močno poveča, ko se prvi stanovalec naseli v prvo višje nadstropje (spodnja pa so po pravilu varčevanja z energijo že polna). Prav podobno je pri atomih in elektronih – ko se prve orbitale nekega atoma že do konca napolnijo in se recimo zadnji elektron kot edini naseli v naslednjo orbitalo, se atom zelo poveča in tako naprej. Pri atomu je celo tako, da spodnje (negativne) orbitale že zelo zakrivajo protone jedra zadnjemu (edinemu) elektronu na višji orbitali, ker električna privlačna (odbojna) sila pada obratno sorazmerno z razdaljo 1/r2 (potencialna energija elektrona napram protonu pa je sorazmerna z -1/r, je negativna). Te sile pa zato zadnji (najoddaljenejši) elektron čuti toliko manj, in ker le ta čuti še odbojno silo vseh ostalih negativnih orbital, se zato atom, ki ima na zadnji orbitali le en elektron, zelo poveča napram atomu, ki ima zadnjo orbitalo popolnoma (ali skoraj) napolnjeno (zadnja skupina elektronov, ki zapolnjujejo zadnjo orbitalo – ali jo skoraj zapolnjuje - čuti torej tudi več pozitivnega naboja jedra – kot edinček na zadnji orbitali). Primeri.
Kisik 8O ima 2 elektrona manj (polmer 66*10-12 m), fluor 9F (polmer 64*10-12 m) pa samo enega manj kot žlahtni plin neon Ne. Neon (10Ne, polmer 62 ali 58*10-12 m, podatek je nekoliko odvisen tudi od vira, odvisno od metode izračuna, ocene) z desetimi protoni in desetimi elektroni je zato najmanjši atom v periodi 2 (saj popolnoma zapolni tudi drugo orbitalo – lahko pa tudi rečemo, da verjetnostni oblak elektronov maksimalno prekrije vpliv pozitivnih protonov v jedru). Zakaj pa je potem naslednji element natrij (Na, prvi atom tretje orbitale) z 11-imi protoni postane tako zelo velik (ima polmer kar 186*10-12 m, to je približno 3x več kot je velikost fluora ali kisika)? Odgovor nam spet da sila, ki pada kot 1/r2 in princip polnjenja orbital. Na zadnji orbitali natrija je samo en elektron, ki je posledično šibko vezan in tako enormno poveča sam atom napram predhodnemu sosedu (povejmo še enkrat, da v tem primeru za 3x). Podobna logika velja tudi za ione znotraj molekul. Recimo v molekuli soli NaCl, ko natriju zbeži zadnji elektron na klor, ima pričakovano sedaj Na+ manjši polmer, samo še 95 pm, recimo ion Cl- pa postane večji od nevtralnega Cl (iz 99 pm gre na 167 pm)?
Povedano se lepo razbere iz tabele atomov izraženih z oceno velikosti.
Recimo pri relativno velikem
litiju (čeprav ima samo 3 elektrone in seveda 3 protone) napram relativno majhnemu fluoru (čeprav
ima ta kar 9 protonov in zato 9 elektronov). Sploh pa je zanimiva primerjava fluora pred reakcijo
in po reakciji v litijev fluorid, LiF (slika na spodnjem robu periodnega sistema podanega z
velikostjo atomov). Po reakciji združitve v molekulo se velikost litija zelo zmanjša, ker
je njegov zadnji šibko vezan elektron sedaj prevzel manjši fluor (saj je sila na elektron
sorazmerna s številom protonov in z velikostjo atomov pred reakcijo, zato lahko zapišemo
9ep/r2F > 3ep/r2Li).
Fluor pa se je tozadevno nekoliko povečal, saj ima pri sebi sedaj elektron več glede
na število protonov (»ukradeni« elektron je zato napihnil zadnjo orbitalo fluora).
To so seveda večinoma prispodobe klasične fizike, a so celo merljive in so za razumevanje
narave atomov dovolj – celo ključne (seveda je pravilnejši kvantni opis preko valovnih
funkcij in diskretnih energijskih nivojev atomov in molekul). Pa še naslednja lastnost,
zanimivost, se lahko primerja med atomi in stanovanjskimi stolpiči – to je manjšanje
stroškov (energije). Če je neko nadstropje skoraj polno, bo zaradi zmanjšanja stroškov
stanovalec iz sosednjega bloka, ki je sam v zadnjem nadstropju, raje šel v sosednji blok,
kjer recimo manjka v zadnjem nadstropju zgolj še en stanovalec (tako bo zaradi racionalizacije
stroškov plačeval nižjo mesečno vsoto). Prav enaka logika je pri atomih, ko tvorijo molekule -
elektroni v kombinaciji atomov zavzamejo najnižjo energijo, najmanjše »stroške«. Še o velikosti
atomov – ta namreč odloča o tvorbi molekul (združevanju atomov - manjši atomi in tisti,
ki imajo skoraj polno zadnjo orbitalo, zelo radi vežejo nase večje atome, oziroma
njihove elektrone iz manj polnih zunanjih orbital - zaradi manjše razdalje r,
je sila manjšega atoma na zunanji elektron sosednjega atoma večja od sile tega
matičnega atomskega jedra z večjim polmerom). Molekule pa so spet kot neke nove
tvorbe, ki se spet lahko vežejo v nove strukture, molekulske verige in s tem se kombinacija
novih možnih povezav in tvorb atomov zelo poveča. Ob primerni temperaturi, atomski sestavi
in strukturi okolice, tudi v življenje, v organske velike biomolekule ..., v adenozin
trifosfate (ATP), ki so neke vrste baterije naših celic, pa tudi v DNK vijačnice,
ki so ustave, predpisi o tem, kako neka celica in organizem živi, se razvija.
Vrnimo se k atomom – logika polnjenja orbital atomov z elektroni je naslednja,
prva sprejme 2 elektrona, druga 8 (skupaj 10), ... glejte priloženi periodni
sistem (logika polnjenja je: 2, 10, 18, 36, 54, 86). To je Madelungovo pravilo, ki je bilo najprej določeno
preko vzorca periodnega sistema in meritev, nato delno teoretično potrjeno preko T. Tietzevega približka
porazdelitve elektronov v elektronskem oblaku okrog jedra atomov (raziskave so začeli in so tudi razvijali model atoma mnogi, naštejmo
le nekatere:
J. J. Thomson, Rutherford,
Bohr,
De Broglie, Schrödinger, Heisenberg,
Bose, Einstein, Fermi, Thomas,
preko vzorca Madelung, Tietz, Klečkovski ...). Povejmo pa, da Madelungovo pravilo ne velja strogo,
poznamo 20 izjem, ne velja točno za krom, baker. Še danes ni dokončno rešen kvantni problem polnjenja
orbital z elektroni - se le dokaj dobri teoretični približki.

Madelungovo pravilo.
Vrstni red, v katerem elektroni zasedajo orbitale, je opisan s pravilom n + l
(znano tudi kot Madelungovo pravilo po Erwinu Madelungu ali pravilo Klechkowskega v nekaterih,
večinoma francosko govorečih državah ali Moellerjevo pravilo pravilo v nekaterih večinoma špansko govorečih državah):
Orbitale z manjšo vrednostjo n + l so zapolnjene pred orbitalami z večjo vrednostjo.
n: glavno kvantno število
l: manjše tirno magnetno kvantno število
Če sta vrednosti n + l enaki, se najprej zapolni orbitala z manjšo vrednostjo n.
Primeri iz periodnega
sistema nam bodo, preko prispodobe z bivanjskimi stolpnicami, zelo pomagali
pri razumevanju, zakaj je naš svet takšen kot je. Recimo – že omenjeni litij
s tremi protoni in tremi elektroni, ima torej tretji elektron na drugi orbitali
(prva je že zapolnjena z dvema) in ima zato precej večji premer, kot recimo za
proton manjši sosednji helij z dvema elektronoma, ki sta oba na prvi orbitali
in njun verjetnostni elektronski oblak skoraj idealno pokriva helijeva protona v jedru.
Helij zato ne reagira z drugimi atomi (le pri zelo nizkih temperaturah) in smo ga zato
našli prej na oddaljenem vročem Soncu (v spektru Sonca) kot doma na Zemlji. Helij spada
v družino žlahtnih plinov - žlahtni plini imajo t. i. vse zunanje orbitale zasedene –
prekrivanje pozitivnih protonov v jedru z elektronskim oblakom je optimalno – pravimo
da atom na ven ne kaže presežka naboja, žlahtni plini so torej v 8. skupini (oz. v 18.
skupini razširjenega sistema):
helij [2He], neon [10Ne],
argon [18Ar], kripton [36Kr],
ksenon [54Xe], radon [86Rn],
ununoktij [118Uuo].
Naslednji tak žlahtni nereaktivni element
(plin) za helijem je torej kateri (tisti ki ima polno naslednje nadstropje - orbitalo) –
in to je neon z 10 elektroni in je tako spet po velikosti precej manjši napram sosednjemu
natriju z 11 elektroni. Njegov enajsti elektron je namreč na naslednji orbitali čisto sam
in se zato zelo poveča velikost natrija napram neonu (poglejte primerjavo velikosti na
spodnjem skrčenem periodnem sistemu, oziroma kar na dveh sistemih - prvi ima pripisane
elektrone po orbitalah, drugi pa velikost atomov. Tega zadnjega si sploh logično lažje
zapolnimo in ga ZELO priporočam za uporabo pri pouku. Takoj pred neonom sta fluor z
devetimi elektroni in kisik z osmimi – ki, kot vemo, se zelo rada vežeta v molekule,
sploh s prvo skupino, ki ima zadnji oddaljen elektron slabo vezan na jedro. Podajmo
nekaj najbolj značilnih povezav (molekul) med atomi prve skupine in recimo sedme in
šeste skupine: recimo znamenita molekula H2O (kisiku manjkata dva elektrona
do popolne zasedbe zadnje orbitale, zato veže dva vodika v tekočino življenja
H2O) ali sol NaCl,
potem je tukaj HF - vodikov fluorid (če malo špekuliramo, še dobro, da ni veliko fluora,
sicer bi se fluor vezal na vodik, sedaj pa se kisik z vodikom v vodo), poznamo seveda tudi
vodikov sulfid H2S (strupen, zelo hitro ga zaznamo z vonjem, rec. pri
gnilih jajcih), potem vodikov selenid
H2Se ...
Ti primeri so za razumevanje osnovne
logike periodnega sistema čisto dovolj in so hkrati zelo pomembni za razumevanje sveta,
ki ga živimo.
V resnici je, kot smo že omenili, opis kvantno-mehansko precej bolj zapleten, a za osnove
je orbitalna poenostavitev dovolj dobra – v bistvu je nujna. Če povzamemo - atomi, ki imajo
zadnje orbitale zelo polne ali pa celo popolnoma zasedene, so zato manjši od tistih atomov,
ki imajo malo elektronov na isti orbitali (velja za družine atomov, ki polnijo isto periodo,
vrstice od desne proti levi) in seveda velikost narašča tudi po skupini (koloni) navzdol
glede na število elektronov (in protonov). Na sliki je naraščanje velikosti atomov po
periodah in skupinah prikazano s puščicama. Če poenostavimo, debeli atomi iz (leve)
prve skupine zelo radi oddajo oddaljen elektron iz zadnje orbitale suhcem iz (desne)
šeste in sedme skupine, ki so že skoraj polni in zaradi svoje majhnosti (sila je večja,
če je r manjši, saj velja
Fc ∝ 1/r2)
zelo radi nase vežejo tuje elektrone in
s tem tudi atom(e) v molekule (v ta naš pisan svet). Atomi so torej po logiki obnašanja
res zelo podobni stanovanjskim blokom. Večji sprejmejo več stanovalcev – selitve
(stanovalcev, elektronov) pa sledijo logiki znižanja stroškov, pri atomih pa energije.
A atomi ostanejo združeni v molekulo, dokler jih kak zunanji vpliv ne razbije
(trki zaradi povišanja temperature ali vpadne svetlobe, torej, če jih zadane kaka
molekula ali foton, jih lahko razbije, če ima seveda dovolj energije, pri
elektromagnetnem valovanju dovolj visoko, pravšnjo, frekvenco in s tem energijo).
Žlahtni plini so pa recimo elitni bloki bogatašev, ki so polni in zato ne reagirajo
z okolico. A stanovanjski bloki, ki niso idealno polni, imajo zato veliko selitev in so
tako veliko bolj zanimivi, živahni, povezljivi – tudi v življenje. Tako je tudi med atomi,
na planetu, ki bi imel zgolj žlahtne pline, se življenje (najbrž) ne bi oblikovalo. Človeka
– življenje - lahko tvorijo samo atomi, ki niso žlahtni (idealni) in se zato združujejo
v molekule, v prelepe strukture, tudi v aminokisline, v beljakovine, v celice, v DNK
in torej v življenje. Torej – še dobro, da ta naš svet ni narejen zgolj iz žlahtnih
plinov, elementov. Tega se zavedajmo, če pa nam kdo slučajno očita, da nismo žlahtni
(»idealni«) – pa lahko odgovorimo, »hvala bogu!« A žlahtni helij je zaradi svoje
samosvojosti (kemijskega »egoizma«, ker se noče vezati) odigral recimo ključno
vlogo pri raziskovanju prasevanja našega vesolja. Torej so žlahtni plini tudi zelo
uporabni, recimo za letenje (vzgon recimo za balone, saj je lažji od kisika in
dušika), varjenje, v potapljaških jeklenkah, v polprevodniški industriji ...
(He torej povsod izpodrine preveč oksidativni kisik, tudi dušik iz krvi).
Helij se tudi zelo težko utekočini – pri zelo nizkih temperaturah, zakaj –
ker se ne veže rad, vsako izrazito termično gibanje helija ga odcepi od sosedov -
izpari. In ta lastnost je lahko tudi zelo, zelo uporabna. Tekoči helij se zato
uporablja tudi za doseganje zelo nizkih temperatur (»blizu« absolutne ničle),
na primer za hlajenje superprevodnih magnetov v pospeševalnikih, hlajenje MRI naprav ...
Zakaj je temu tako – ali se to vidi iz periodnega sistema? Ja – kot smo že omenili,
helij je prvi atom, ki ima prvo orbitalo polno (z dvema elektronoma) in se zato
nikakor ne veže rad (težko tvori tekočo fazo), ima zato tudi najnižje vrelišče izmed
vseh elementov in sicer pri -268,96°C, zamrzne pa le pod zelo visokim pritiskom
2.5 MPa pri 0.95 K (-272.20 °C). Dr. Petrač je tako predlagal metodo za hlajenje
infrardečih detektorjev s tekočim helijem (izparevanje tekočega helija niža
temperaturo senzorju) in je tako omogočil detekcijo prasevanja, ki prihaja
iz vseh smeri vesolja. Temperatura mikrovalovnega ozadja je okrog 2.7 K, oz.
-270.45 °C. Po Wienovem zakonu
T = b/λ
velja, da daljša valovna dolžina »maksimalnega«
izseva (Planckov zakon) pomeni nižjo temperaturo telesa, ki seva kot črno telo -
v našem primeru je to kar vesolje. Pri sevanju ostanka prapoka govorimo torej
o valovnih dolžinah okrog milimetra, in če hočemo meriti te temperature, oz.
valovne dolžine, moramo senzor (termometer) ohladiti pod 2.72548 ± 0.00057 K
(v čem je problem - po domače, termometer, ki ima višjo temperaturo, območje
meritve, od temperature telesa, ki mu merimo temperaturo, ne bo pravilno meril
– temu pravimo tudi problem šuma in prav tukaj je priskočil na pomoč žlahtni plin
helij in naš dr. Dušan Petrač – NASA, JPL). Helij III (3He), to je izotop z
enim protonom, ima vrelišče še nižje, pri 3.19 K. Zadnja stopnja hlajenja senzorjev,
recimo na zgolj 0,3 K ali manj, se doseže z uporabo sorpcijskega hladilnika 3He
(sproščanje, izhlapevanje helija). Tukaj omenimo še pomembno dejstvo in sicer,
absolutne ničle nikoli ne moremo doseči (takrat bi bila entropija 0, popolno
mirovanje ni mogoče – to je tretji zakon termodinamike ali Nernstov zakon, pri
kvantnem opisu sveta bomo to dejstvo tudi razumeli), lahko pa se temperaturni
ničli zelo približamo (to je recimu nujno tudi pri kvantnih računalnikih).
Ko merimo mikrovalovno ozadje, ki izvira iz časa, ko je vesolje postalo
prozorno in je bilo staro približno 379.000 let ter je imelo temperaturo približno
3000 K in se je do danes ohladilo na zgolj 2,7 k, se moramo torej spustiti pod
to trenutno vrednost in prav to nam omogoča (iz periodnega sistema) prvi žlahtni
plin helij. Odstopanje od te temperature (2.72548 ± 0.00057 K) pa nam veliko
pove o nehomogenostih v mladem vesolju in začetnemu razlogu zgoščevanja snovi
v zvezde in galaksije ... Omenimo še eno izjemno lastnost helija, ki nam lahko
zelo pomaga obvarovati naš planet pred nadaljnjo ekološko degradacijo. Dosedanji
(na dolgi rok napačni) pristop kurjenja fosilnih goriv je končno primoral mnoge
države, da so začele iskati različne tehnologije fuzijskih reaktorjev (ZDA, J.
Koreja, Avstralija, Nemčija, Kitajska, najbolj počasna je naša EU z ITERjem ...).
Pri fuziji lahko nastopa tudi helij, kot vhodni element, zmeraj pa tudi kot produkt.
Fuzija izotopa helija 3 in izotopa vodika 2 (devterija) vrne kot produkt le ionizirana
heliji 4 in vodik – obe atomski jedri je tako že sami po sebi možno direktno
izkoristiti kot električni tok – in pri tej reakciji ni nevarnih hitrih nevtronov,
ki pri ostalih reakcijah vzamejo s sabo veliko sproščene energije in povzročajo
s trki še nevarno sevanje ...
Pri fuziji: 3He + D => 4He + H
(18,3 MeV sproščene
energije), torej ni izgub energije na nevarnih hitrih nevtronih in fuzija se začne
pri zelo nizki temperaturi. Problem je, da na Zemlji helija-3 ni ravno veliko,
veliko pa ga je na Luni, v njenih tleh – tam ga odlaga Sončev veter (na Zemlji
to preprečuje ozračje). Na Luni bi ga lahko pridobivali s segrevanjem zgornjih
plasti na 600 °C.
| perioda\skupina | I. | II. | III. | IV. | V. | VI. | VII. | VIII. |
| 1. | H (1) | He (2) | ||||||
| 2. | Li (2, 1) |
Be (2, 2) |
B (2, 3) |
C (2, 4) |
N (2, 5) |
O (2, 6) |
F (2, 7) |
Ne (2, 8) |
| 3. | Na (2, 8, 1) |
Mg (2, 8, 2) |
Al (2, 8, 3) |
Si (2, 8, 4) |
P (2, 8, 5) |
S (2, 8, 6) |
Cl (2, 8, 7) |
Ar (2, 8, 8) |
| 4. | K (2, 8, 8, 1) |
Ca (2, 8, 8, 2) |
Ga (2, 8, 18, 3) |
Ge (2, 8, 18, 4) |
As (2, 8, 18, 5) |
Se (2, 8, 18, 6) |
Br (2, 8, 18, 7) |
Kr (2, 8, 18, 8) |
| 5. | Rb (2, 8, 18, 8, 1) |
Sr (2, 8, 18, 8, 2) |
In (2, 8, 18, 18, 3) |
Sn (2, 8, 18, 18, 4) |
Sb (2, 8, 18, 18, 5) |
Te (2, 8, 18, 18, 6) |
I (2, 8, 18, 18, 7) |
Xe (2, 8, 18, 18, 8) |
| 6. | Cs (2, 8, 18, 18, 8, 1) |
Ba (2, 8, 18, 18, 8, 2) |
Tl (2, 8, 18, 32, 18, 3) |
Pb (2, 8, 18, 32, 18, 4) |
Bi (2, 8, 18, 32, 18, 5) |
Po (2, 8, 18, 32, 18, 6) |
At (2, 8, 18, 32, 18, 7) |
Rn (2, 8, 18, 32, 18, 8) |
| 7. | Fr (2, 8, 18, 32, 18, 8, 1) |
Ra (2, 8, 18, 32, 18, 8, 2) |
Okrnjena (skrčena) matrika klasičnega periodnega sistema iz 18 na 8 skupin – kjer so atomi porazdeljeni po periodi in po skupini, zasedenosti zunanje orbitale. Zraven atomov so v oklepaju podane porazdelitve elektronov po orbitalah. Če bi dodali še grafično ponazoritev velikosti atomov, bi taka kombinacija bila veliko bolj razumljiva, učljiva s stališča razumevanja struktur in čudes našega sveta in vesolja. Zgornji periodni sistem je nekoliko okrnjen, ker ni prikazanih prehodnih kovin od 3 do 12 skupine (manjka torej 10 skupin), to so recimo titan, vanadij, železo, volfram, platina, nikelj, baker ... (ti pri nastajanju vezi uporabljajo predzadnjo elektronsko lupino in tudi zunanjo, kar je posebna lastnost, te kovine so trdne in žilave, imajo visoka vrelišča in tališča in so dobri prevodniki toplote in elektrike, pogosto so del zlitin). A nas ta del za našo razumevanje vezi tokrat ne zanima. Manjkajo tudi lantanoidi in aktinoidi – redke zemlje (zaradi katerih, vzrok so tudi mobilni telefoni, bomo počasi popolnoma preluknjali naš planet ..., tudi električni avtomobili na današnji tehnološki zasnovi, vetrnice in posledično številni generatorji elektrike ... so lako velika ekološka past).
Kisik – atom z glavno vlogo v filmu »Življenje«
Res, da je za življenje zelo pomemben ogljik (ogljikovodki, aminokisline,
beljakovine, sladkorji,
nukleinske kisline, ...), seveda so nepogrešljivi tudi dušik, vodik in ostali elementi ...
A kot bomo videli, kisik je edini oksidant na Zemlji v dovolj velikem številu,
ki omogoča zares energijsko uspešno oksidacijo hrane, rec. glukoze - kar
je omogočilo razvoj velikih živali, seveda tudi človeka, z zelo
učinkovitimi možgani ... Še boljši oksidant od kisika je fluor, a pri njem nastopijo težave
in zato ni del življenjskega cikla.
Fluora je na Zemlji malo in je pričakovano ves vezan (sila 1/r2), kisika
pa je ogromno in zato je plin kisik glavni igralec na našem planetu (povsod še veže in
spreminja okolico). Ključni dogodek za pojav prostega kisika pa je pojav fotosinteze pri
rastlinah, še prej pri cianobakterijah, kjer se sprošča v obliki molekul O2
in s tem je kisik dokončno trasiral pot razvoja same Zemlje, njene atmosfere,
burnega podnebja našega planeta in posledično pot razvoja velikih živali
(o tem smo delno pisali že v Spikah 2021 – o veliki konjunkciji). Sam kisik
je bil takoj po ohladitvi planeta, pred približno 4 milijardami let, ves vezan
v molekule, v spojine – počasi so ga začele sproščati šele prve cianobakterije
(prva fotosinteza, energija se črpa iz energije sončevih žarkov), a je spet
prihajalo do oksidacije, tokrat železa, mineralov, a po dolgotrajni in uspešni
oksidaciji planeta se je kisik LE začel nabirati v atmosferi, kjer pa je spet
povzročil razdejanje, razbitje toplogrednega metana CH4 v ozračju – podrobnosti
sledijo pozneje. In res, kisik in fluor imata tudi največjo elektronegativnost
(to je lastnost kako rad se nek atom veže z drugim atomom, preko njegovih zunanjih
elektronov – glavno vlogo torej igra elektromagnetna sila med (+) in (-) delci
(F ∝ 1/r2
in ta sila je tudi sila, ki omogoča vezavo atomov v organske molekule,
v življenje, v pretvorbo energije preko celičnega dihanja). Kisik ima po Paulingovi
lestvici (ki teče od 0,7 do 4 in je delno povezana z elektronsko afiniteto) elektronegativnost
kar 3,5. Največjo elektronegativnost (4) ima pa pričakovano sosednji fluor, ki je v naravi
zato zmeraj vezan v spojine (je zelo agresiven), nekoliko manjšo pa klor z elektronegativnostjo
3 (je tudi močan oksidant). Vrednosti elektronegativnosti so odvisne tudi od definicij (poznamo
še Allenovo, Tantardini-Oganovo, Mullikenovo ... elektronegativnost).
Periodni sistem elementov, ki prikazuje vrednosti relativne elektronegativnosti atomov.
Vir: https://theory.labster.com/electronegativity-vdw/
Nasprotna lastnost
je elektropozitivnost, ki je merilo sposobnosti oddajanja elektronov (to so recimo atomi
prve skupine, kot smo se naučili v uvodu). Elektronegativni in elektropozitivni atomi se
imajo torej radi in tvorijo molekule.
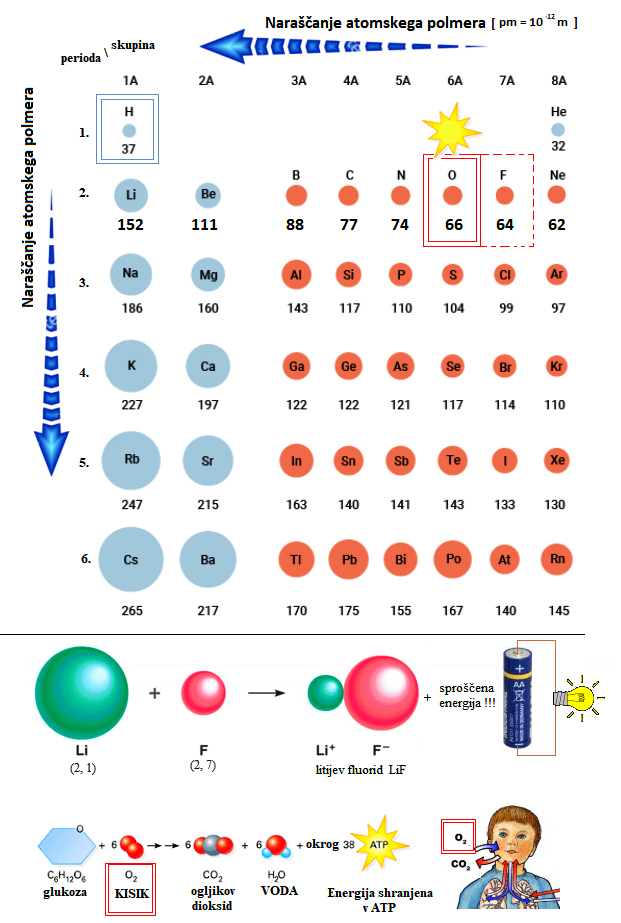
SLIKA: Polmeri atomov po periodi (vrstici) od alkalijskih kovin proti
žlahtnim plinom padajo, v posamezni skupini (koloni) navzdol pa rastejo
(to je na nek način »H-R« diagram kemijskih elementov - in še - teoretično
bi naj na dolgi rok tudi vsi atomi razpadli ...). Seveda, prikazana velikost
je le pričakovana verjetnostna porazdelitev dosega elektronskega oblaka atomov
– a je pedagoško izjemno poučna. Če bi nam periodni sistem predstavili s podobo
velikosti atomov, »dimenzijski« pristop, bi ga najbrž celo večina bolje razumela,
si ga zapomnila ... (čeprav so nekateri zadržani do take predstavitve atomov,
se vendar zmeraj bolj uveljavlja – sploh v tujini, kjer iščejo razumevanje in
ne znanstvenega purizma).
In opisano nadgrajeno slike sveta atomov nam lahko ponudi predmet astronomija
in kot bomo tudi videli, iz te matrike velikosti atomov (lege in velikosti kisika O)
in iz dejstva, da je na Zemlji v masnem deležu kisik zastopan kar z
28,2 %, sta to ključa podatka, zakaj je kisik glavni igralec (Sonce pa je režiser)
v filmu (poimenujmo ga kar »Geneza ali Stvarjenje, po hebrejsko Bereshit - V začetku« -
upam da ne bo kdo slabe volje zaradi uporabi te prispodobe). »Film« opisuje dramo
nastanka današnjih oblik življenja, nastanka velikih živali na Zemlji (pri seveda
vseh ostalih izpolnjenih pogojih, ki smo jih opisali v Spikah 11, 12/2020 in 1/2021
in delno 3/2021, v bistvu v skoraj celotnem ciklu člankov o Veliki konjunkciji 2020).
Pot do »Adama in Eve« je bila precej, precej negotova in zelo, zelo dolga in bodočnost
je na nek način dobesedno zapisana v zvezdah ..., vse kar se bo dogajalo z našim planetom,
z življenjem? Kdaj si morebiti preveč domišljamo, da držimo vse vajeti v rokah?!
A vseeno bodimo zbrani, odgovorni in modri – na mnoge atribute preživetja
imamo še zmeraj velik vpliv.
Ko že govorimo elektronegativnosti in periodnem sistemu, se na tem mestu spomnimo
na nekaj, kar ima vsak vsaj v telefonu, če že ne v kakem slušnem aparatu ...
To je baterija - ekološko zelo sporna, a zmeraj več je baterij med nami, tudi v avtomobilih,
brez njih več ne znamo živeti.
Poglejmo delovanje baterije preko povezave z elektronegativnostjo atomov in molekul.
Elektronegativnost je, kot smo že omenili, lastnost atomov, ki nam pove, kako močno privlačijo elektrone v kemijskih vezavah.
Elektronegativnost določa, katera snov bo "žrtvovala" svoje elektrone in katera jih bo "pobrala".
To ustvarja električni potencial (napetost), ki poganja električni tok skozi porabnika (žarnica, mobilni telefon,
električni motor avtomobila, kamera, teleskop ...).
Atomi z višjo elektronegativnostjo bolj privlačijo elektrone.
Atomi z višjo elektronegativnostjo (npr. kisik, fluor) bodo bolj privlačili elektrone v kemijski vezi.
Atomi z nižjo elektronegativnostjo (npr. natrij, cink) pa bodo elektrone lažje oddali.
Kako to deluje v bateriji?
Baterija temelji na tem, da različni materiali z različnimi elektronegativnostmi povzročijo,
da se elektroni premikajo od ene elektrode na drugo, kar ustvari električni tok.
Kemične reakcije v bateriji (recimo za alkalno cink-manganovo baterijo Zn/MnO2):
Anoda (negativna elektroda):
Cink (Zn) je material, ki se uporablja na anodi.
Cink ima nizko elektronegativnost, kar pomeni, da zlahka oddaja elektrone (oksidacija).
Na anodi cink izgubi elektrone, ki gredo skozi zunanje električne naprave, kot so žice, žarnice, telefoni ...,
in se premikajo proti katodi.
Reakcija:
Zn → Zn2+ + 2e-
Katoda (pozitivna elektroda):
Na katodi je manganov dioksid (MnO2), ki ima visoko elektronegativnost. Mangan bo sprejel elektrone, ki jih odda cink,
in se veže z ioni iz elektrolita (npr. OH-).
Ta sprejem elektrona je redukcija, kjer elektroni preidejo z negativne na pozitivno polje.
Reakcija:
MnO2 + 2e- + H2O → MnOOH + OH-
Kako to povzroči gibanje elektronov?
Cink (anoda) zlahka odda elektrone, ker je elektronegativnost cinka manjša kot pri manganovem dioksidu na katodi.
Elektroni se premaknejo skozi zunanjost baterije (naprave, kot je rec svetilka) in dosežejo katodo.
Ko elektroni pridejo do katode, manganov dioksid (MnO2) sprejme te elektrone zaradi svoje visoke elektronegativnosti.
Elektrolit:
Elektrolit je potrebna snov (kot je kalijev hidroksid ali cinkov klorid), ki omogoča gibanje ionov med elektrodama.
Ioni v elektrolitu zagotavljajo električno nevtralnost in omogočajo, da se reakcije na elektrodah lahko nadaljujejo.
Povzetek
Anoda (cink) zlahka oddaja elektrone zaradi nizke elektronegativnosti.
Pozitivna katoda (MnO2) sprejema elektrone, ker je elektronegativnost manganovega dioksida visoka.
Elektroni tečejo od negativne anode do pozitivne katode, kar povzroči električni tok.
Ioni v elektrolitu pomagajo uravnotežiti naboj med elektrodama, da baterija deluje.
Na kratko: Baterija uporablja razlike v elektronegativnosti različnih materialov
(kot je recimo cink in manganov dioksid), da povzroči premikanje elektronov in s tem električni tok!
Prve baterije so temeljile na bakru in cinku, in jih lahko štejemo za začetke elektro-kemije.
Cink (Zn) deluje kot anoda (negativni pol), baker (Cu) – deluje kot katoda (pozitivni pol).
Elektrolit je lahko slana raztopina ali vlažen filter papir s kislo raztopino (npr. solna raztopina, kis, raztopina žveplene kisline itn.),
kar sestavimo v plasteh: Cu | elektrolit | Zn.
Danes so zaradi lahkosti in zmogljivosti najbolj popularne
litij-ionske polnilne baterija, kjer se ioni litija (Li+) premikajo med dvema elektrodama (anodo in katodo) skozi elektrolit.
Negativna anoda (shrani litijeve ione med polnjenjem) je večinoma grafit (ogljik),
pozitivna katoda pa kovinski oksidi (npr. LiCoO2, LiFePO4, LiMn2O4
- sprejema litijeve ione med praznjenje in v katodi se Li+ in e- ponovno združita.
Elektrolit je
litijeva sol v organskem topilu (npr. LiPF6).

Molekula vode je izjemno topilo in toplogredni plin. Zelo didaktična prispodoba
vode – desno (vodika sta pozitivna učka – kisik pa ima negativna usta).
Tetraedrska struktura vode. V molekuli vode zveznici vodik - kisik tvorita kot 104,5 °.
Atoma vodika sta blizu dveh vogalov tetraedra, glede na kisik. Na drugih dveh vogalih sta
samotna para valenčnih elektronov, ki ne sodelujeta pri povezovanju. V popolnem tetraedru
bi atomi tvorili kot 109,5 °, vendar je odboj med osamljenimi pari elektronov večji kot
odboj med vodikovima jedroma. Dolžina vezi O-H je približno 0,096 nm.
Kisiku smo pripisali izjemno vlogo, a večkrat slišimo, da je bistvo življenja voda – H2O. Oboje drži – tudi vodo tvori kisik. Voda ima še vrsto ostalih izjemnih lastnosti (omenimo dve, je toplogredni plin in odlično topilo, oboje pa je za življenje pomembno) - ima obliko črke V – dve anteni vodika štrlita s kisika v oglišču (in tako lahko voda učinkovito absorbira dolge toplogredne valove). Zakaj je dobro topilo? Ker ima oglišče, kjer je kisik, neto negativen naboj (dva elektrona sta namreč skočila na kisik iz vodika), vrhova (rogova) črke V, kjer čepita vodika pa imata nekoliko pozitiven naboj, saj je vsak svoj elektron posodil kisiku. S tem izrazitim kazanjem naboja, voda raztrga skoraj vse molekule, ki so v bližini – recimo sol, NaCl. Kisikova stran V molekule vode pograbi natrij (Na je v molekuli soli rahlo pozitiven, ker je svoj zunanji elektron posodil kloru), vodik iz vode pa zagrabi klor (ki je v molekuli soli rahlo negativen zaradi elektrona, ki mu ga je podaril natrij) in tako voda molekulo soli razbije. Še bi lahko naštevali – z vodo se tudi umivamo, ker dobro topi umazanijo. V naših celicah voda dovaja hrano, odvaža odpadke, združuje ostale molekule v nove snovi pomembne za delovanje celic, skozi ožilja tvori cirkulacijo za oskrbovanje celotnega telesa in odvoz odpadkov oksidacije, itn – je neke vrste tekoči trak življenja, kar 70 % našega telesa sestavlja voda. In ni čudno, da se je življenje najprej razvilo v morjih, in ko so živali imele (razvile) dovolj stabilno kožo, so počasi pricapljale na kopno.
Skrivnost fluora
No – življenje bi, kot smo že omenili, težko nastalo na osnovi fluora – če bi ga bilo
na kakem planetu veliko, saj je zelo agresiven (zelo elektronegativen) in je kisik
tako še kako primeren igralec v igri čudeža življenja (ali bi se fluor lahko izločal
pri fotosintezi – ne! – v bistvu zavira fotosintezo, če se pojavi v rastlinah,
jih poškoduje; seveda, kje lahko nastane tudi nekoliko drugače kemično sestavljen
planet, a najbrž ne radikalno drugačen kamniti planet, kot so recimo Zemlja, Mars,
Venera ...) – saj je niša nastanka življenja, to je dolgoživeče zvezde, bogate z
raznovrstnimi atomi, železom, ogljikom, kisikom ... in večjim številom planetov,
zelo ozka. Fluor je v resnici velika uganka – v vesolju je zelo redek, saj ni produkt
običajnih jedrskih procesov fuzije v zvezdah, hitro se zlije v druga jedra ..., nastane
le pri določenih pogojih fuzije. Zato je kar nekaj predlogov, kako sploh nastane fluor
( recimo preko supernove tipa II - bombardiranje neonskih atomov z nevtrini namreč
lahko povzroči pretvorbo v fluor; tudi zgodnji »sončev« veter Wolf-Rayetovih masivnih zvezd bi lahko
odpihnil fluor od vseh vodikovih in helijevih atomov; ali pa morebiti fluor nastaja v
konvekcijskih tokovih, ki izhajajo iz fuzije orjaških zvezd ( v HR diagramu je to področje
AFG – asymptotic giant branch ). Če smemo špekulirati še naprej, je v resnici to umanjkanje
fluora, za življenje kot ga poznamo na Zemlji, velika sreča. Če bi bilo na Zemlji toliko
fluora kot vodika, kot smo že omenili, bi se le ta takoj ves vezal v vodikov fluorid.
To je še en dokaz, ker tudi drugje v vesolju ni veliko fluora, da je najbrž tudi zelo
razvito življenje kje drugje v vesolju zasnovano na prav podobnih mehanizmih kot na
Zemlji (voda, dihanje kisika, tukaj so še seveda ostali izjemno pomembni elementi
ogljik, dušik, fosfor, železo, kalcij, natrij ...).
Vsaka drugačna kombinacija se
zdi zelo neobetavna, oksidacija preko kisika da optimalno energijo celicam (o tem
v nadaljevanju), fluora je malo (tudi drugje v vesolju) in je tudi preagresiven za
kaj podobnega kot je življenje – a pustimo se presenetiti. Seveda, k življenju
nikakor ne štejemo »naprednih« računalniških sistemov, »avtonomih« robotov. Danes
vemo, da možgani porabijo, od vse v presnovi dobljene energije, kar 20–25 % le te
za lastno delovanje. To je približno od 13 do 20 W moči (možgani dojenčkov pa porabijo
celo do 50% vse pridobljene energije). Pri zavestnem reševanju nalog, razmišljanju, se
poraba energije seveda tudi poveča za kak procent. Torej tudi za razmišljanje rabimo
zelo veliko energije. Že iz teh podatkov je dokaj logično, zakaj anaerobna bitja težko
postanejo to, kar zmorejo bitja na kisik. Anaerobno dihanje še zdaleč ne zadošča za
delovanje možganov, kaj šele za delovanje celotnega telesa (pri anaerobnem dihanju se
namreč sprosti le približno 5 % energije, ki jo proizvede kisik v naših celicah – no,
lahko bi se vprašali, kaj pa če se lahko razvijejo visokorazviti možgani, ki rabijo
veliko manj energije ..., odprto vprašanje, ki pa ne rešuje problema fizičnega
udejstvovanja takega bitja ...).
. 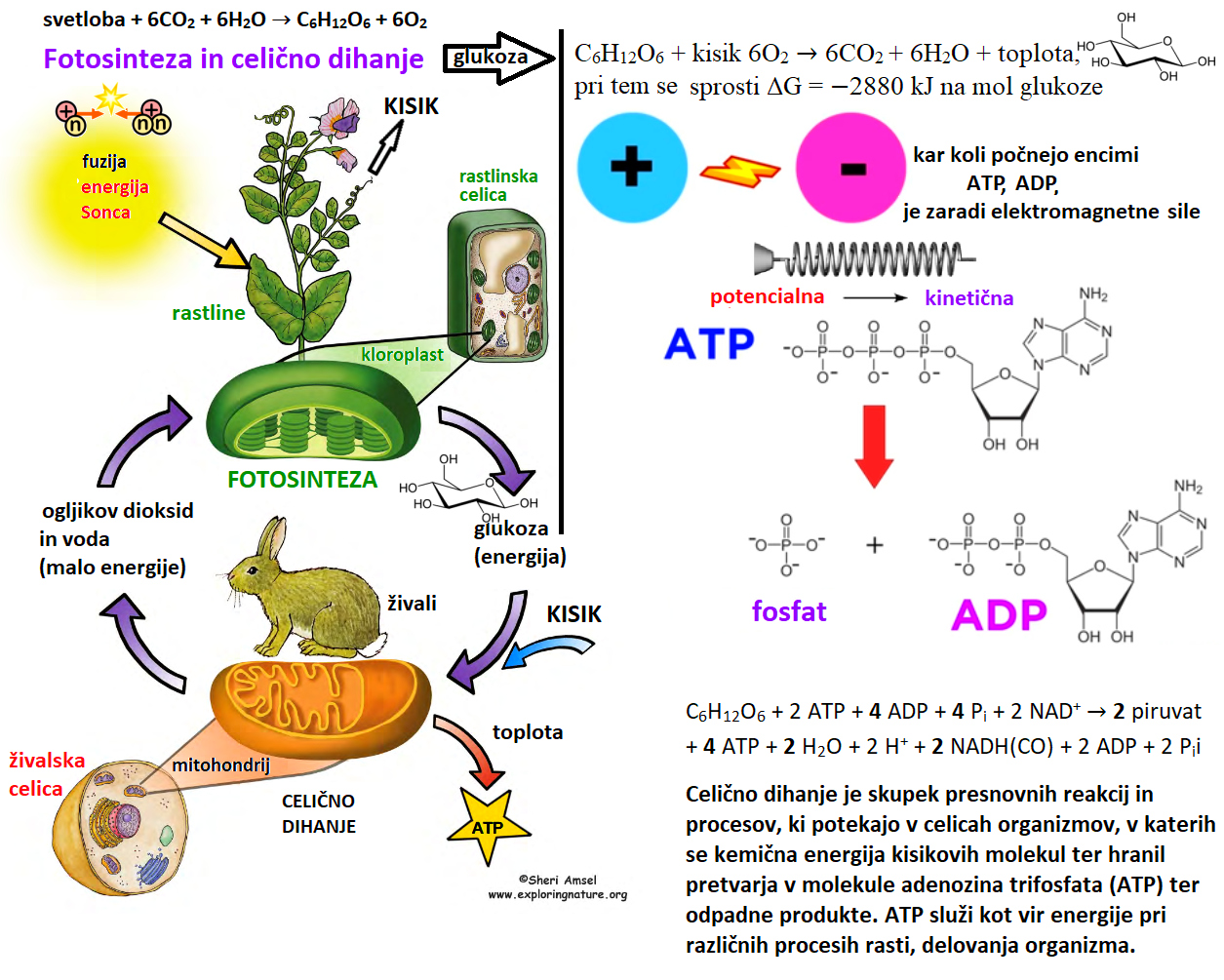
Ponovimo še prehranski krog - poenostavljeno velja: nepogrešljivo Sonce da energijo,
svetloba v rastlinah razbije molekule vode in začne se proces => voda kot donor elektronov
12H2O + ogljikov dioksid 6CO2 = ogljikov hidrat, npr. glukoza
C6H12O6 + kisik 6O2 + voda 6H2O.
Ko živali ali ljudje pojemo tako rastlino pa je proces obraten – sedaj pa poteka oksidacija
hrane, glukoze -
C6H12O6
se pretvori v ogljikov dioksid in redukcija kisika v vodo. Povedano
je formula prehranjevanja in rasti. Slika zgoraj hkrati kaže krog celičnega dihanja rastlin
in živali. Sonce nam pošlje dovolj svetlobe pravšnje energije
(E = hν = hc/λ),
valovnih dolžin, da le ta sproži rastlinsko fotosintezo, produkt katere
je prost kisik O2 (brez fotosinteze ga v zraku ne bi bilo v obliki
O2),
ki omogoča oksidacijo glukoze v živalskih celicah (pri tem se sprosti
veliko energije – prispodoba z ognjem je prav na mestu) in s tem tvorbo
ATP molekul z dovolj akumulirane energije za rast in življenje kompleksnih
živali (mitohondrij je celični organel evkariontskih celic, ki služijo
kot vir celične energije – v njem se tvori ATP – mitohondriji naj bi
nekoč bili prosto živeče bakterije, ki jih je preprosto pojedla celica
naših prednikov – eni govorijo o simbiozi obeh celic zaradi izmenjave
vodika in ogljikovega dioksida). Noben drug prost plin ali element še
zdaleč ne da toliko energije celicam kot ravno kisik – recimo anaerobna
bitja se zato težko razvijejo v kompleksna bitja (čeprav anaerobna bitja
živijo na Zemlji veliko dlje kot bitja na kisik, pa se zaradi oksidacije
glukoze z ostalimi elementi sprosti premalo energije, le okrog 5% te kjer
nastopa kisik, da bi lahko tako nastala kompleksna anaerobna bitja, kot
so recimo vretenčarji, ki dihajo kisik in imajo večinoma zelo razvite možgane).
Vretenčarji so tako dobili priložnost komaj pred približno 600 milijoni let v vodi,
anaerobne oblike pa se trudijo že milijarde let ... – a so vseeno zelo
pomembne oblike življenja, so vsaj posredno naši predniki (brez njih nas
zagotovo ne bi bilo).
A še pred prostim kisikom v atmosferi (na začetku, kot smo že omenili,
je bil zaradi svoje izjemne elektronegativnosti ves vezan), pred več kot
tremi milijardami let, so tudi obstajale neke vrste živali, organizmi,
ki pa so uporabljale namesto kisika za oksidacijo druge molekule, anaerobni
organizmi, npr. molekularni dušik (N2), oz.
nitrat NO3 (produkt je N2),
potem
PO43-.
HPO3-,
Fe3+,
SO42-,
ClO4-,
ClO3-,
tudi CO2 ...
A ta bitja niso dosegla (ne dosegajo) velikosti in kompleksnosti vretenčarjev
(nobena molekula, noben element od teh, tudi dušik ne, čeprav je sosed kisika
v periodnem sistemu, ni tako močno oksidativen kot kisik (no fluor je še precej hujši
oksidant, a ga je malo in je »na srečo« že vezan v molekule) in hkrati kisik, recimo
med oksidacijo glukoze, ne naredi toliko škode v (današnjih) celicah, da bi ogrozil
življenje – seveda v zmernih koncentracijah, zato je uporaba respiratorjev za
dovajanje dodatnega kisika v naša pljuča lahko tudi zelo nevarna, lahko
»zažgemo pljuča« ...). Seveda je kisik ob začetku svoje dominacije, pred
približno 2,4 milijarde let, verjetno povzročil izumrtje večine anaerobnih
organizmov, a je hkrati omogočil celicam, novonastalim bitjem, vretenčarjem,
veliko boljši izkoristek hranil, saj je oksidacija glukoze preko kisika 15 do
20x bolj energijsko učinkovita od ostalih oksidantov. Energije, ki se sprosti
pri anaerobnih procesih je le okrog 5 % tiste, pri kateri sodeluje kisik pri
aerobnih procesih. Dihanje in posledična oksidacija glukoze v celicah je prenos
energije v ATP, adenozin trifosfat – to je molekula
C10H16N5O13P3.
Pri oksidaciji glukoze se torej sprosti veliko energije prav v obliki ATP,
velja:
C6H12O6
+ kisik 6O2 => 6CO2 + 6H2O +
toplota,
pri tem se sprosti kar
ΔG = -2880 kJ na mol glukoze C6H12O6.
Pridobljena energija pa je torej na voljo v obliki adenozin trifosfata (ATP),
za življenjske procese, ki seveda porabijo to energijo; pri anaerobnih procesih
pa se sprosti le okrog 150 kJ, to je približno 5 % od tega, kar proizvede kisik.
Zadnji podatek je tudi odgovor – zakaj življenje, kjer oksidant ni kisik,
ni uspelo razviti velikih živali (čeprav je trajalo veliko dlje časa kot življenje
na kisik. »Pa razkrijmo še največjo zaroto našega življenja - kisik je najsmrtonosnejši plin,
ker 100% ljudi, ki ga diha, tudi umre.«
In še zanimivost.
Naše mišice so sposobne tudi anaerobnega dihanja. Ko so mišične celice izpostavljene intenzivnim naporom,
se začne proces mlečne fermentacije,
ki povzroči kopičenje tega izdelka (mlečne kisline) v mišicah in ustvarja utrujenost.
Tudi globoke oceanske vode spadajo med življenjska okolja, kjer je kisika ni
(so anaerobne oziroma anoksične) ali ga je malo (so hipoksične).
Določanje tipov anaerobov je mogoče z gojitvijo v tekoči kulturi, saj je za vsako skupino značilen točno določen položaj
v epruveti:
Anaerobne in aerobne mikrobe lahko razvrščamo po njihovi razporeditvi v prilagojenem tekočem gojišču.
(1) Obvezne (obligatne) aerobne bakterije se v velikih količinah zberejo na zgornji strani epruvete,
da lahko na tak način pridobijo kar največ kisika, ki ga na drugih mestih gojišča ni ali se nahaja v manjši koncentraciji.
(2) Obvezne (obligatne) anaerobne bakterije se vedejo obratno, saj se vrha epruvete zaradi toksičnosti kisika
izogibajo, največ pa se jih zbere na spodnjem delu, kjer je koncentracija kisika najmanjša.
(3) Fakultativne anaerobne bakterije ravnajo podobno kot obvezne aerobne bakterije (največ jih je na vrhu epruvete),
četudi so prve zmožne preživeti tudi v okolju brez kisika. Tovrstni mikrobi so raje v s kisikom bogatem okolju, ker
so reakcije aerobnega tipa presnove energijsko bolj ugodne in ekonomične. Kljub temu se delež fakultativnih anaerobov
nahaja tudi v drugih delih epruvete, kjer je kisika manj ali ga sploh ni.
(4) Mikroaerofilne vrste so aerobi, ki se v največji količini nahajajo na zgornji polovici epruvete,
a ne na samem vrhu, ker jim zadostujejo že majhne koncentracije kisika (izpostavljenost previsokim koncentracijam
kisika je lahko za tovrstne bakterije celo strupena).
(5) Porazdelitev aerotolerantnih bakterij je raznolika, saj na njo prisotnost kisika nima vpliva
(njihova presnova je v osnovi anaerobna, a jim prisotnost kisika ne škodi). Zatorej so tovrstne bakterije
najpogosteje enakomerno porazdeljene po epruveti.
SLIKA: Kako pa je z definicijo velikosti atomov? V kemiji, fiziki ni
čisto dobro definirana velikost atomov. Obstaja teoretična velikost
elektronskega oblaka atoma in seveda tudi različne meritve, metode
(in pričakovano smo teoretični model velikosti atomov »našraufali«
do te mere, da meritve in izračuni še kar sovpadajo). Nekaj definicij,
recimo – da je polmer polovica minimalne razdalje med jedroma dveh atomov
istega elementa, ki nista vezana v isti molekuli, potem je tukaj razdalja
med atomskimi jedri v molekuli – recimo za kovalentno vez, ionsko vez ...
Zato so tudi podatki o velikosti atomov precej različni, odvisno od metode.
Graf prikazuje izmerjen (preko kovalentnih vezi v molekulah), izračunan in
Van der Waalsov polmer atomov. Van der Waalsov polmer se določi z merjenji
medatomskega prostora med pari vezanih atomov v kristalih.
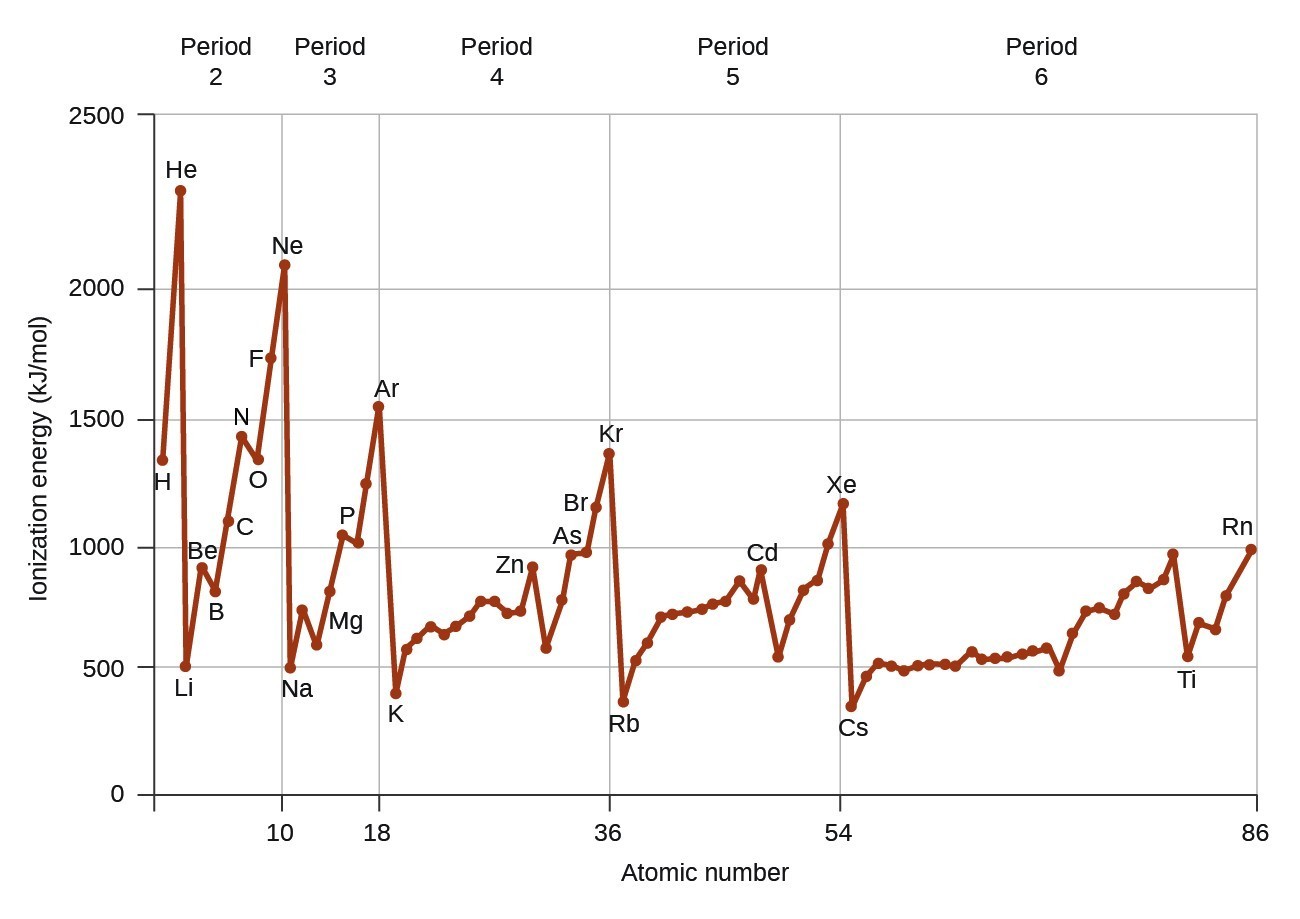
https://courses.lumenlearning.com/chemistryformajors/chapter/periodic-variations-in-element-properties-2/ NX_Chem_06_05_Firstiongr (1).jpg
Graf ionizacijskih energij za različne atome. Pri večjih atomih iste periode
(kjer je na zadnji orbitali recimo le en elektron in je r velik) je ta energija
pričakovano manjša (Li, Na, K ...), saj velja
F ∝ epee/r2,
zato so ti
atomi tudi bolj elektropozitivni. Pričakovano pa imajo največje ionizacijske energije
žlahtni plini – pri njih je težko odstraniti elektrone od jedra. Velike oksidacijske
energije imajo pričakovano tudi odlični oksidanti: fluor, kisik, klor ... Zmeraj
znova izstopa kot pomemben igralec kisik, ki ga je na Zemlji, Marsu in recimo na
Veneri na pretek, na zadnjih dveh planetih v atmosferah večinoma vezanega v molekule
CO2 (ne pozabimo, da atomi C in O
tudi obilno nastajajo v zvezdni nukleosintezi, takoj za helijem !!!).
Kisik in radikalne podnebne spremembe ter izjemno dolga in zavita pot do kompleksnih
organizmov – »zakaj smo torej (simbolično) nastali šele pred 30 sekundami«
(toplogredni plini so nas že nekoč rešili)
In ta tečnež med atomi, posebnež kisik, je po milijardah let neutrudnega oksidiranja
našega planeta (sproščal se je preko fotosinteze v cianobakterijah), le to oksidacijo
uspešno končal in pred slabo milijardo let je končno dosegel znatno rast v atmosferi.
Kisik je tako komaj pred kratkim (komaj v zadnjih 10 % obstoja Zemlje, Sončevega sistema)
omogočil današnje oblike življenja, tudi človeka, ogenj, polete v vesolje, toplo gredo
posredno preko CO2 molekul iz vulkanov, ko je bila Zemlja še popolnoma v
ledu in je življenje pred dobrima dvema milijardama let (huronska poledenitev)
vegetiralo zgolj še v globinah, na srečo še tekočih, oceanov (poleg anomalije
gostote vode pri 4 °C, ko je voda najgostejša, je spodaj v oceanu naše mini
prednike vsaj minimalno grela še toplota matere Zemlje, vroče jedro). Bodimo
pošteni – kisik je najprej, preko fotosinteze (cianobakterij) sproščen v
ozračje tudi zakuhal poledenitev – razbil je molekule izrazito toplogrednega
metana
CH4
in s tem povzročil huronsko poledenitev za 400 milijonov let.
Velja reakcija
CH4 + 2 O2 => CO2 + 2 H2O.
Povejmo še pomembno dejstvo, da je CO2 manj toplogreden plin
kot metan CH4 (in od tod tudi ohladitev). Zakaj sta to toplogredna
plina – za CO2 je značilno prečno nihanje
↑↓ molekule
O=C=O (nihanje ogljika med kisikoma) je recimo tisto, ki ulovi toplotne
valove in jih delno spet seva nazaj proti tlom.
Vrnimo se nazaj v huronsko globalno poledenitev. Si predstavljate, da bi pred
dvema milijardama let mimo Zemlje letela vesoljska ladja radovednih Nezemljanov,
kaj bi videli? V led objet planet, belo snežno kroglo, kjer se tu in tam iz ledu,
snega, kadi kak vulkan. Videli bi nas, kot recimo danes mi vidimo Jupitrovo
luno Ganimed ali Neptunovo luno Triton, Saturnov Enkelad (in bi razmišljali ali
je spodaj pod ledom tekoča voda in preproste oblike življenja ...). In kako zanimiva
je danes (ko sta minili že dve milijardi let od huronske poledenitve) naša Zemlja (?) - danes
je polna različnih oblik življenja, barv, geografskih raznolikosti - le Nezemljanov (še) ni,
da bi se zemljani, zemljanke lahko pohvalile, kako zelo lep planet (še) imamo ...
Strokovnjaki (NOAA) ocenjujejo, da 50-80% proizvodnje kisika na Zemlji prihaja iz
oceanov. Večina te proizvodnje je iz planktona - plavajočih rastlin, alg in nekaterih
bakterij, ki ga lahko fotosintetizirajo. Posebna vrsta, prochlorococcus (cianobakterija
odkrita leta 1986), je najmanjši fotosintetski organizem na Zemlji. Toda ta majhna
bakterija proizvede do 20 % kisika v celotni biosferi. To je višji odstotek, kot
skupaj vsi tropski deževni gozdovi na kopnem. Kot je človek bistveno odvisen od
mikroorganizmov, je v resnici tudi cel živi planet odvisen od drobcenih bitij – in
to so precej nova »šokantna« spoznanja, ki se jih generacije izpred 50 let sploh nismo
učile. Paziti moramo torej, ne samo na gozdove, ampak seveda tudi na oceane, na vse vodne
površine. Pomembno pa je tudi vedeti, da čeprav ocean proizvaja vsaj 50% kisika na Zemlji,
približno enako količino porabi morsko življenje (ponudba in povpraševanje
veljata torej tudi
pri razširjenosti življenja, v krogu nastajanja in minevanja – a ne pozabimo, vse to poganja
Sonce). A še posebej problematično je, če alge odcvetijo in proces razgradnje porabi kisik
hitreje, kot ga je mogoče obnoviti. To lahko ustvari območja z izredno nizko koncentracijo
kisika ali hipoksijo in posledično lokalna izumrtja.
Določeni viri navajajo,
da alge proizvedejo celo 70 % kisika na planetu Zemlja, in da na našem planetu živi čez 30 000 vrst alg.
Alge so sluzaste in se tako med oseko ne posušijo. So začetni del prehrambne verige morij.
Da so oceani glavni viri kisika (fotosinteza zaradi cianobatkterij,
imenujemo jih tudi modrozelene bakterije - alge, tudi vseh ostalih vrst alg)
je seveda logično - živali na kisik (vretenčarji, ribe -
naši predniki) so nastali v vodi, še preden je na kopnem bilo prisotno rastlinstvo.
Nadaljujmo to zgodbo oksidacije s kroženjem ogljika in kisika med zemeljsko skorjo, organizmi, hidrosfero in atmosfero, kjer je spet pomemben igralec kisik. Rastline vežejo ogljikov dioksid, ta postaja sestavina organske snovi, ki jo porabljajo živali in mikroorganizmi – njihovi ostanki se delno tudi nalagajo v plasteh Zemlje – v sedimente. Apnenec je tako sedimentna kamnina, ki jo sestavlja pretežno kalcijev karbonat (CaCO3), nastal je z odlaganjem apnenčastih hiš (školjk, polžev, koral ...) in okostij izumrlih morskih živali in do neke mere rastlin. Alpe (apnenec), kras ... so tako v veliki meri posledica življenja – kroženja ogljika in kisika, ki ga omogoča čudežno življenje – torej tudi naš junak kisik. To samo kaže, kaka mogočna sila je življenje, spremenilo je sestavo tal, celine in ozračje – izjemno pomemben režiser pa je (že 100 x omenjeni - namerno) naš junak kisik in seveda Sonce, ki je vse to omogočilo, omogoča (relativno skromna zvezda – a ravno ta skromnost ji omogoča dolgo življenje t = 1010(M☉/M)2.5 let, ki ustvarja čudeže na Zemlji in širše v vesolju).
Pred 2,4 milijarde let
Ata, kako bomo živeli na tem planetu, to je vendar ledena krogla?
Danes
Ata, super si izbral ta modri planet, tukaj bomo živeli. Pred 2,4 milijardami let pa si
se zmotil, bili smo malo prezgodnji!
Še malo znanstvene fantastike - kako pa lahko ta oče in sin tako dolgo živita – najbrž
sta z letečim krožnikom na polno pospeševala in zavirala, potovala sem ter tja po vesolju
(in tako upočasnila čas lastnega staranja), dokler Zemlja ni dozorela za njuno poselitev ...
Za ozadje še malo biologije. Evkarionti so praktično vse rastline in živali, medtem ko so prokarionti bakterije in arheje. Širše sprejeta kronologija velike oksigenacije kaže, da so prosti kisik najprej proizvajali prokariontski organizmi (cianobakterije, oz. v slovenščini imenovane modrozelene cepljivke, postopoma so omogočile razvoj aerobnih organizmov, ki potrebujejo kisik za dihanje in rast), šele kasneje se pojavijo evkarionti, sposobni fotosinteze, ki kisik proizvajajo kot stranski produkt. Ti organizmi (cianobakterije) so živeli že veliko pred veliko oksigenacijo, verjetno že pred 3,5 milijardami let. Nastali kisik proizveden preko cianobakterij je bil pred milijardami let, na začetku nastanka preprostega življenja - prokarionti - hitro odstranjen iz prvotne atmosfere po reakciji z minerali, z železom ... Raztopljeno železo v oceanih dokazuje ponore O2 (pretvorba v Fe3O4). Prosti kisik, proizveden v tem času, je kemično zajelo raztopljeno železo. Cel proces pretvori železo Fe in Fe2+ v magnetit ( Fe2+ Fe23+ O42-), ki je v vodi netopen in se je potopil na dno plitvega morja (morja so tako postala bistra), kjer so se zato na dnu ustvarile trakaste formacije železa, kakršne najdemo recimo v Minnesoti in Pilbari, Zahodni Avstraliji. Potrebno je bilo 50 milijonov let ali nekaj več, da so se ponori kisika izčrpali. Danes je povprečen čas, ko molekula O2 preživi v zraku, preden jo geološki ponori porabijo, približno 2 milijona let (dolga doba – kar je ugodno za življenje). Ko se je po domače oksidiralo vse kar se je dalo, se je lahko začel kisik hitro kopičiti. Prosti kisik je "strupen" za anaerobne organizme (ki ne potrebujejo kisika za rast), ki so bili do takrat večinska oblika življenja. Cianobakterije so bile torej tudi odgovorne za najobširnejše izumrtje v zgodovini Zemlje. Dviganje koncentracije kisika v atmosferi je povzročilo izumrtje večine takratnega življenja. Prvi del oksigenacije se je zgodil pred približno 2,3 ali 2,4 milijarde let, ko se kisik ni več porabljal za oksidacijo mineralov, železa ... - bilo je že vse oksidirano.
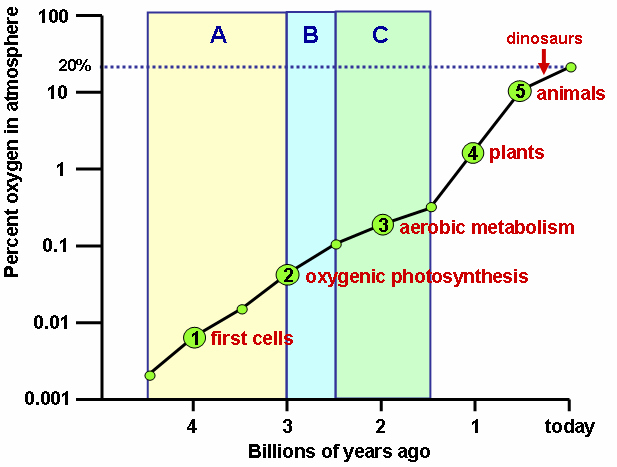
Nazoren graf prikazuje razvoj atmosfere glede na koncentracijo kisika in razvoj
življenja na Zemlji skozi milijarde let. Najpomembnejših je zadnjih 600 milijonov let,
ko je kisik narastel čez 10 % in je omogočil razvoj vretenčarjev - velikih živali,
tudi primatov - ljudi. Seveda so pomembne tudi ostale faze, tudi razvoj rastlin,
ki so pospešile oksigenacijo - relativno hiter prirast kisika O2.
Vir: https://www.wikiwand.com/en/Talk:Great_Oxidation_Event
V silurju
(pred 443.8 ± 1.5 – 419.2 ± 3.2 milijoni let)
se pojavijo prve kopenske rastline, ribe oklepnice, ščipalci,
stonoge ter veliko morskih alg. Začetek silurja zaznamuje veliko
izumrtje 60 % morskih vrst. V silurju je koncentracija kisika prvič
dosegla vrednosti okoli 14 odstotkov. Glavni vzroki takratnih bioloških
kriz so bile pretežno tektonske dejavnosti (premik plošč) v povezavi
z izjemno intenzivnim vulkanizmom.
V tej časovni skali stabilnosti izseva Sonca moramo torej iskati
možnost razvoja visoko razvitih bitij na Zemlji. Ali
se pri drugih zvezdnih sistemih (z eksoplaneti), kjer
pričakujemo življenje - podobno kot na Zemlji -
odvija podoben scenarij, časovno, kemijsko, biološko, podnebno?
Prostorninski deleži plinov zraka so danes naslednji:
78,084 % dušika
(N2), 20,947 % kisika
(O2 – prinašalec energije celicam preko dihanja, oksidacije),
0,934 % argona (Ar) in 0,033 %
ogljikovega dioksida (CO2 toplogredni plin, prispevek 9–26%).
Zrak večinoma vsebuje še
Ne, He,
Kr, SO2, CH4 (toplogredni plin, prispevek 4–9%), H2, N2O
(toplogredni plin, prispevek do 7%), Xe, O3
(toplogredni plin, prispevek 3–7%), NO2,
I2 , CO, NH3 ter vodnih hlapov (H2O –
izrazit toplogredni plin,
izjemen prispevek, kar 36–72% k energijski bilanci).
Zrak lahko vsebuje torej od 0 do 7 % vodne pare –
ki določa vodni krog in s tem življenje na kopnem.

Ponazoritev Zemlje v obdobju huronske poledenitve. Precej hladno ...
Sprememba sestave ozračja je posledično s sabo prinesla tudi podnebne spremembe. Novo nastali prosti kisik je reagiral z metanom CH4 (močan toplogredni plin), nastal je ogljikov dioksid (šibkejši toplogredni plin) in voda. Koncentracija metana v atmosferi se je močno zmanjšala (zato se je Zemlja začela ohlajati), kar je sprožilo huronsko poledenitev (pred 2.4 do 2.1 milijarde let) in verjetno najdaljše obdobje celotne poledenitve planeta v zgodovini. Poledenitev je trajala od 300 do 400 milijonov let. IN - kako se je ta ledena doba končala - sledi zanimiv scenarij. Med huronsko ledeno dobo naj bi bila Zemlja prvič popolnoma prekrita z ledom, kar je praktično ustavilo fotosintezo. Zelo se je povečala odbojnost (albedo) Zemlje. Ker ni bilo fotosinteze, ni bilo ponorov CO2 in ta toplogredni plin se je dodatno kopičil iz vulkanskih izbruhov in zelo, zelo počasi se je začela atmosfera le segrevati in led se je tako začel tajati. Zanimivo - CO2 nas je že rešil pred ledeno smrtjo - a nas bo tudi pokopal v vročini tople grede ...? Geološki dokazi za opisano kronologijo so - ledeniške strukture po vseh kontinentih v tistem obdobju (zdrobljeni kamni, tiliti - kamnina, ki jo sestavljajo nahajališča na območju ledeniškega roba, stranska, končna ali talna morena - v tem smislu so tiliti geološko stara, že strjena balvanska glina (sedimente je odkril Arthur Philemon Coleman leta 1907 pri jezeru Huron v Severni Ameriki). Še povezava imena Huron z junaki naše mladosti, takrat smo iz filmov, med drugim, spoznali tudi Indijance skupnosti Huronov – bilo je vznemirljivo ...
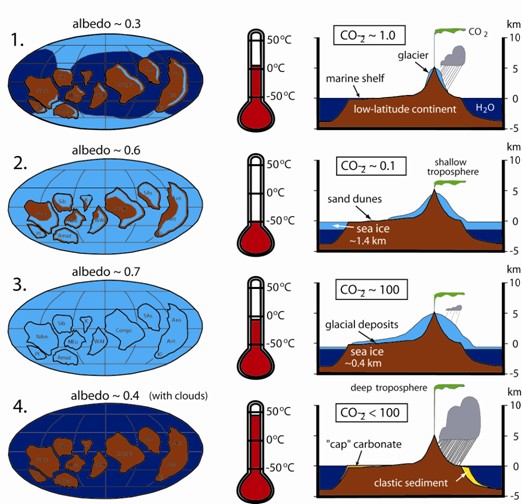

Razlaga poledenitve - cianobakterije so razvile kisikovo fotosintezo, pojavi
se molekularni kisik
O2, ki oksidira močno toplogredni metan
CH4 v ogljikov dioksid in vodo
( CH4 + 2 O2 ==> CO2 + 2 H2O );
CO2
je manj toplogreden plin (zemlja se zato ohlaja) in zato se pojavi ledena doba ...
In kako se konča ledena doba - vulkani kopičijo CO2 v zraku, ni ponorov,
ker ni fotosinteze, temperatura se zato počasi viša in po 400 milijonih let konča
ledeno dobo ... Zgoraj je slika karbonatne plasti nad ledeniškimi sedimenti v Namibiji
(v ledeniških plasteh pa ni videti določenih izrazitih karbonatnih usedlin - ker se
je ogljikov cikel ustavil). Še kratka definicija ogljikovega cikla. Kroženje ogljika
je premeščanje ogljika med zemeljsko skorjo, organizmi, hidrosfero in atmosfero.
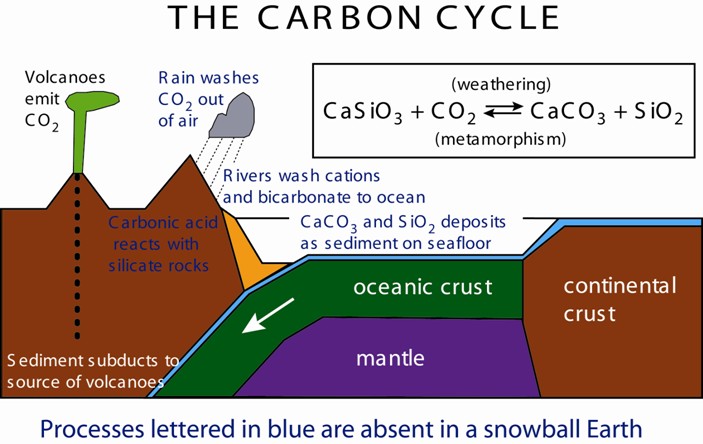
Dolgoročni geokemični krog (cikel) ogljika - nalaganje karbonatnih plasti je torej
umanjkalo med Zemljo ujeto v led - ko je bila Zemlja podobna snežni kepi (nebesni Eskim).
To se opazi v plasteh tal, v sedimentih, nanosih ledenikov po vseh celinah. Silikatno
preperevanje:
CaSiO3 + H2O + 2CO2 ==>
Ca (HCO3)2 + SiO2
SiO2 (kremenčev pesek) in CaCO3 (kalcijev karbonat)
prideta pod zemeljsko skorjo s subdukcijo (podrivanje tektonskih plošč).
Tam jih toplota stopi in reagirajo na silikat in CO2, ki preko
vulkanov nato pridejo do zemeljske površine. Ta cikel se imenuje karbonatno-silikatni cikel.
Več
CO2
je vezanega kot izpuščenega, tako da se vsebnost CO2 v ozračju
zmanjša. Kalcit se obori iz nasičene raztopine kalcijevega hidrogenkarbonata s povečanjem
vrednosti pH, ki sprošča CO2.
Če apnenec pride v kontakt z drugo kislino, na primer žvepleno kislino, ki lahko nastane
iz vodikovega sulfida in žveplovega dioksida, ki ga vulkani sproščajo z oksidacijo in
reakcijo z vodo, se CO2 sprosti v ozračje:
CaCO3 + H2SO4 ==> CaSO4 + H2O + CO2
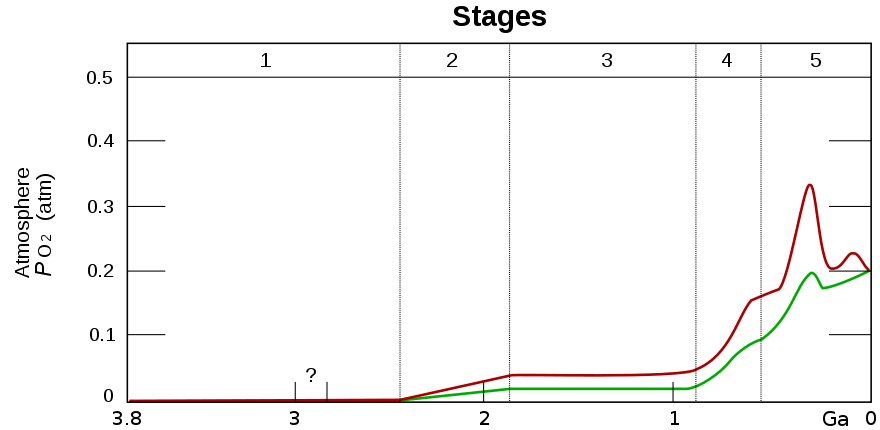
Nalaganje kisika O2 v zemeljski atmosferi (v procentih). Rdeča
in zelena črta predstavljata skrajni meji ocen, čas pa se meri v milijardah
let nazaj (Ga).
1. stopnja (3,85–2,45 Ga): V ozračju praktično ni O2. Oceani so
bili večinoma brez kisika (anoksični), z izjemo O2 v plitvih oceanih.
Faza
2 (2,45–1,85 Ga): proizvedeni O2 se je zvišal do vrednosti
0,02 do 0,04 atm., vendar se absorbira v oceanih, v kamninah na morskem
dnu (proizvajajo ga arheje in bakterije - cianobakterije) - pred približno
2,4 milijarde let verjetno povzročila izumrtje večine anaerobnih organizmov,
celično dihanje, ki uporablja kisik pa je omogočilo aerobnim organizmom,
da proizvedejo mnogo več ATP (adenozin trifosfat je koencim - služi kot vi
r energije pri različnih procesih v celicah) kot anaerobni organizmi, kar
je pripomoglo k njihovi kasnejši prevladi v Zemljini biosferi.
Faza 3 (1,85–0,85 Ga): O2 se začne izločati iz vode, oceanov,
vendar ga absorbirajo kopenske površine. Ni bistvene spremembe ravni kisika
v atmosferi, a nastane že ozonska plast.
4. in 5. faza (0,85 Ga - danes):
nasitijo se še preostali ponori O2;
plin se kopiči v ozračju. Pred približno 300 milijoni let je vsebnost kisika
v ozračju dosegla svoj višek 35 vol %, kar je morda pripomoglo k razvoju
ogromnih žuželk in dvoživk (najdeni fosili). V peti fazi se razvijejo
veliki vretenčarji (velike živali na kisik), rastline in živali so
poselile kopno – na koncu se pojavijo primati in čisto na koncu
človek.
Vir: wiki
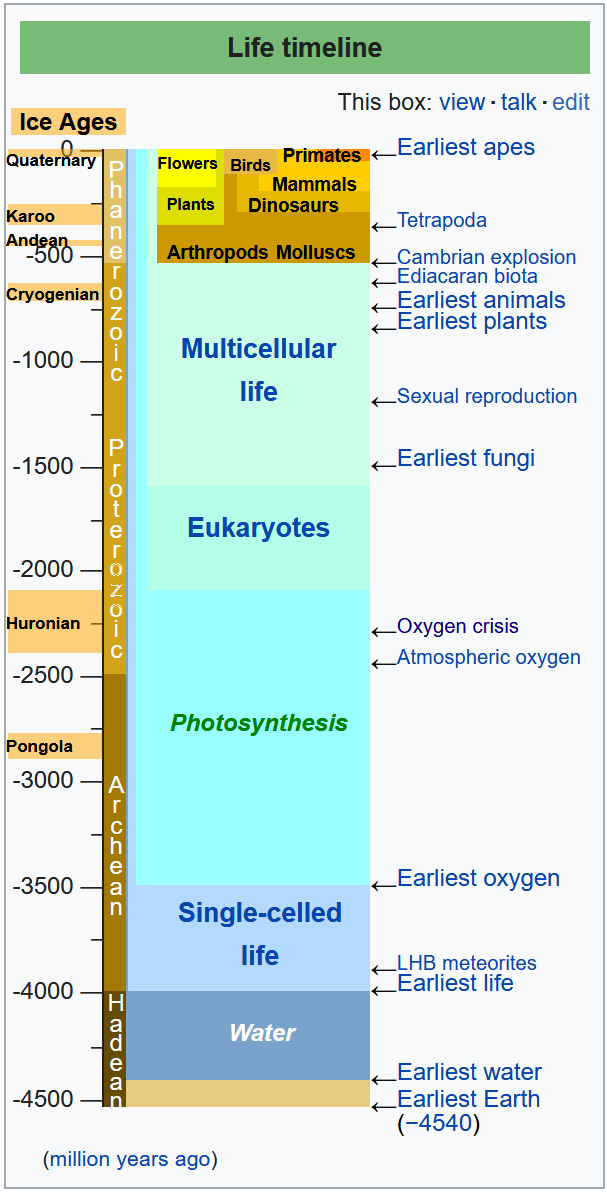
Časovnica razvoja življenja v milijonih let.
Vir: wiki
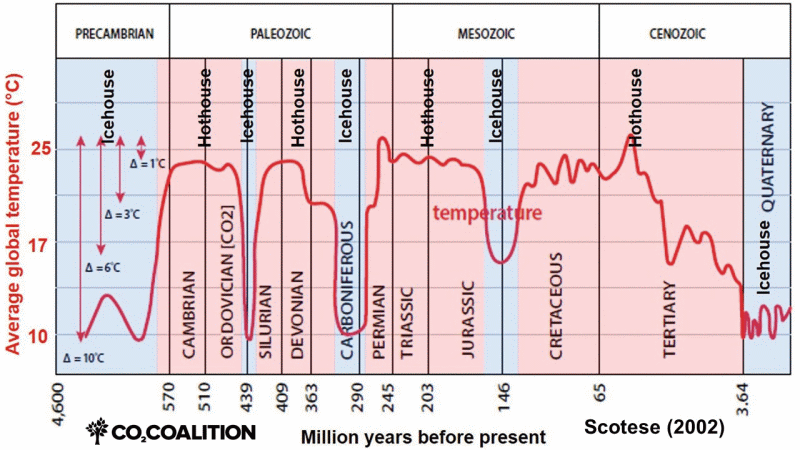
Danes je povprečna temperatura zraka na višini 2 m (v meteorološki hišici) dobrih 14 st. C (velja za celotno Zemljo).
Vir: https://www.acs.org/climatescience/energybalance/earthtemperature.html
V preteklosti pa so poprečne temperature našega planeta dosegale tudi vrednostni 25 st. C ..., glej zgornji graf.
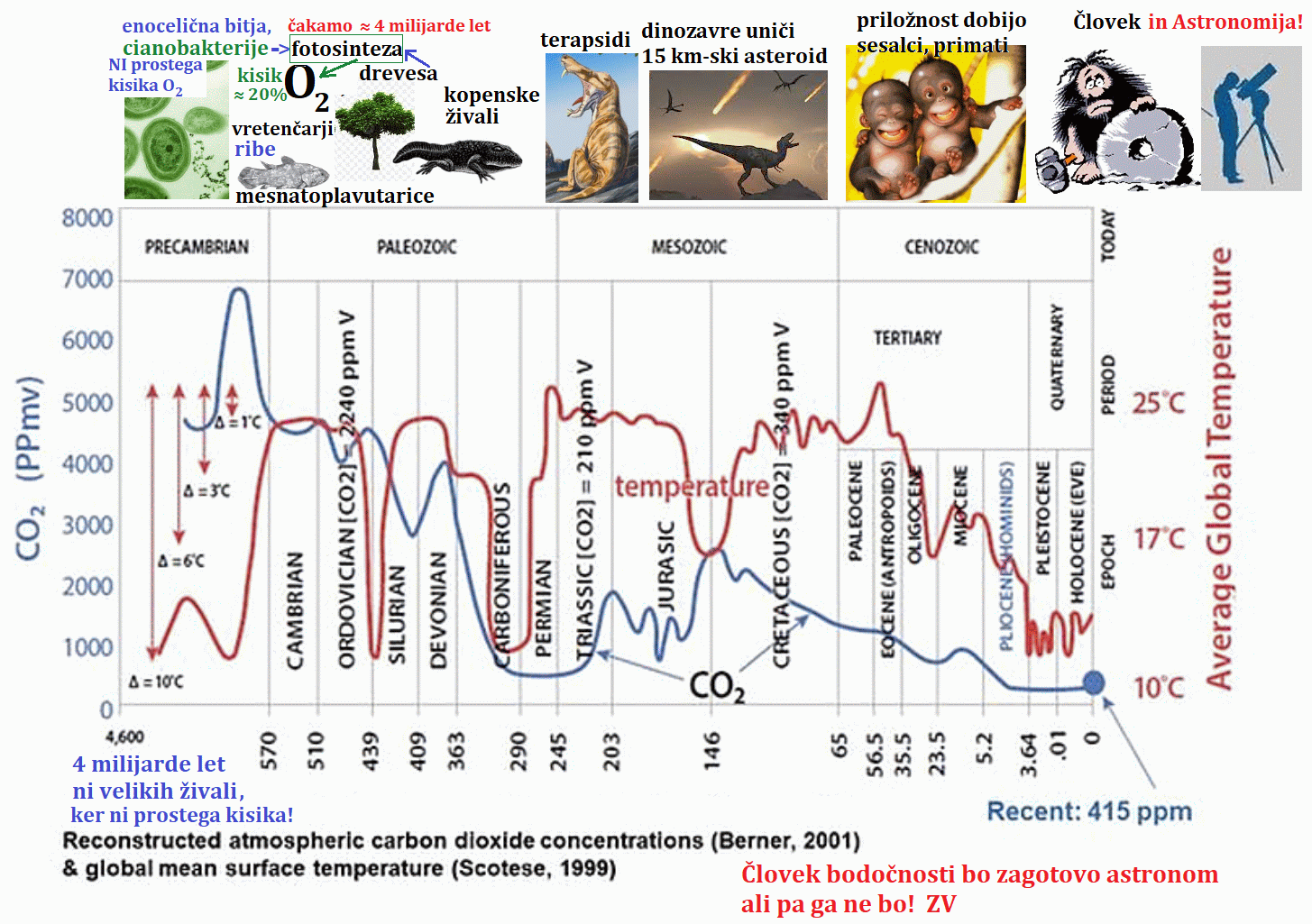
Človek bodočnosti bo zagotovo astronom
ali pa ga ne bo! Z. Vičar
(The man of the future will surely be an astronomer or he will not be! Z. Vičar)
Zavedajmo se, da kar 4 milijarde let na Zemlji ni bilo velikih živali, le enocelična (anaerobna) bitja.
Ko se je torej v zraku nabralo, zaradi fotosinteze, dovolj kisika, je kisik postal
tisti oksidant (aerobno dihanje), ki je s svojim izjemnim energijskim prispevkom (recimo pri oksidaciji glukoze),
omogočil razvoj
večceličnih bitij, na koncu tudi ljudi. Velja razmerje: 0.5 Mlet/4.5 Mlet = 1/9 ≈ 0.1,
torej le komaj 10 % življenja, razvoja Zemlje (tudi Sončevega sistema),
nam le ta omogoča večcelična bitja - to je zadnje pol milijarde let. Prej pa je naš planet zelo, zelo počasi
biološko-kemično dozoreval (kar 4 milijarde let),
da so lahko nastala tudi visoko inteligentna ustvarjalna bitja.
Kaj podobnega, glede razvoja življenja, pričakujemo tudi na ostalih eksoplanetih, ki so v naselitveni coni
centralne zvezde. In seveda, centralna zvezda mora biti najbrž podobna Soncu,
da lahko oddaja dokaj konstantni izsev okrog 10 milijard let - sicer se življenje na x-planetu
nima časa razviti, saj kompleksno ne, ki bi znalo komunicirati z nami ...
Mi smo morali čakati skoraj 5 milijard let, da smo sploh lahko nastali.
Če Zemljo primerjamo s skrbno nosečo bodočo mamico, potem je
to tako, kot če bi naša mama zanosila pri starosti nekaj let,
nas potem nosila kar okrog 80 let in bi se rodili, ko je mama recimo
že stara čez 80 let ... Tako se je tudi Zemlja pripravljala večino dosedanjega življenja,
da smo komaj pred kratkim lahko sploh nastali ljudje.
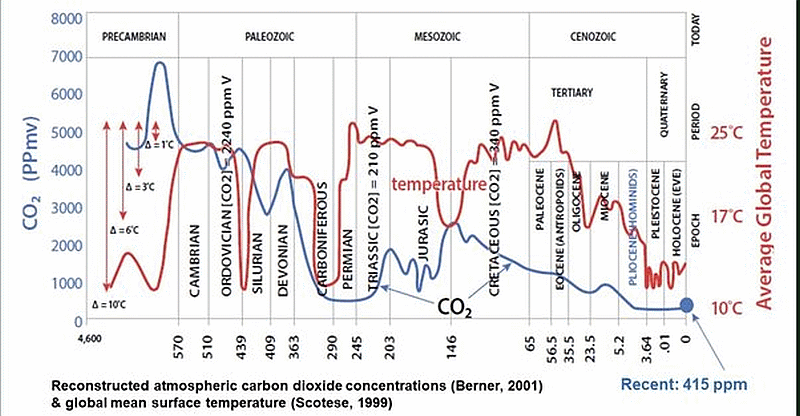
Nihanja temperatur in ogljikovega dioksida skozi zgodovino razvoja Zemlje,
variabilnost njene atmosfere,
so vezana tudi na razvoj življenja - skozi približno 4,6 milijarde let naše zgodovine.
Časovna skala je zelo nelinearna - zato previdno z interpretacijo!
Huronska poledenitev (led, sneg je prekrival velik del planeta, a ne celotnega)
je na grafu drugi minimum temperature z leve
- rdeča črta. Včasih so bile koncentracije CO2
precej višje - tudi 10x in več od današnjih. A atmosfera je bila takrat tudi
drugačna, najprej je bilo v atmosferi kar veliko metana,
molekul kisika O2 pa je bilo zelo malo - takoj se je vezal v druge molekule
(počasi pa so kisik začele izločati cianobakterije preko fotosinteze) ...
Vsi ti podatki (ocene) vplivajo na burne debate o korelaciji med koncentracijo
toplogrednega plina CO2 in temperaturo planeta, saj ta povezava ni zmeraj enoznačna.
Zagotovo pa že kar trajno kemijsko onesnaževanje zraka, vode, prsti povzroča
človeku in živalim hude težave, tudi huda hormonska odstopanja od
prvotnih razmerij, dodatne težave z demenco ..., a ta problematika je žal zasenčena z
debato o globalnem segrevanju ... (zakaj je temu tako?). Globalno segrevanje ni
nepomembno, a so ostali vplivi potrošniške družbe na okolje,
na življenje, na človeka kar naenkrat žal podcenjeni ...
Viri:
https://www.quora.com/Could-humans-raise-the-concentration-of-carbon-dioxide-in-Earth-s-atmosphere-enough-to-cause-global-warming-out-of-control-runaway-global-warming
https://www.quora.com/Do-we-have-to-extract-carbon-from-the-atmosphere-to-stop-human-driven-climate-change-or-is-it-enough-to-cut-emissions
Robert Arbuckle Berner (25. november 1935 – 10. januar 2015) je bil ameriški znanstvenik,
znan po svojih prispevkih k modeliranju ogljikovega cikla. Od leta 1965 do 2007 je poučeval geologijo
in geofiziko na univerzi Yale, kjer je bil nazadnje do svoje smrti zaslužni profesor. Njegovo delo
na sedimentnih kamninah je privedlo do soavtorstva modela BLAG, to je gibanja atmosferskega ogljikovega
dioksida skozi čas,
ki upošteva geokemične in biološke prispevke k ogljikovemu ciklu - vir wiki.
Christopher R. Scotese (rojen 4. maja 1953) je ameriški geolog in paleogeograf.
Doktoriral je na Univerzi v Chicagu leta 1985.
Je ustvarjalec Paleomap projekta (climate history),
katerega namen je raziskati Zemljo v zadnjih milijardah let in je zaslužen za napoved Pangea Ultima, možne prihodnje
konfiguracije superkontinenta ...
Nnjegov glavni fokus je zajet v knjigi z naslovom: "Zgodovina Zemlje, razvoj zemeljskega sistema".
Je soavtor več kot 100 znanstvenih publikacij, njegove karte in animacije so bile uporabljene
v številnih geoloških učbenikih, znanstvenih raziskavah in so na ogled v muzejih po vsem svetu.
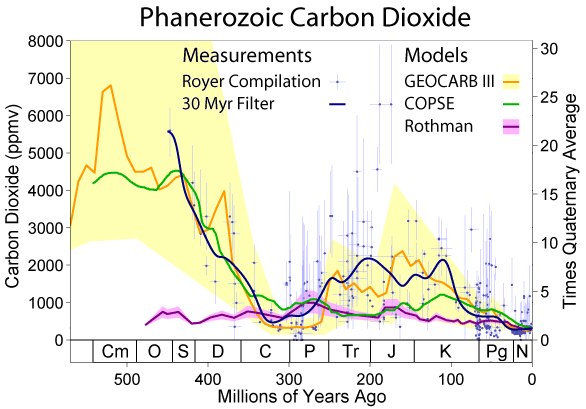
Vsebnost CO2 v fanerozoiku po modelih GEOCARB in COPSE.
Pričakovano se modeli razlikujejo.
VIR:
https://de.wikipedia.org/wiki/Robert_A._Berner
Fanerozoik predstavlja obdobje vidnega življenja na Zemlji, ime namreč nakazuje na »vidno življenje«.
Pričenja se pred približno 545 milijoni let v času pojava prvih živali z lupino,
ki so pomenile začetek Kambrijske
eksplozije, nenadnega razcveta številih oblik kompleksnega življenja (tukaj so veliki vretenčarji, ribe, pozneje tudi ljudje ...).
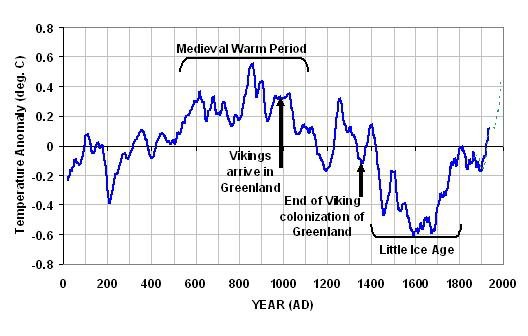
Ste se kdaj vprašali, zakaj se Grenlandija imenuje "ZELENA" dežela?
To je zato, ker je bila v srednjeveškem toplem obdobju ... bujno pokrita z zelenimi rastlinami, drevesi,
gozdovi in zelenimi obdelovalnimi površinami ... ko so jo Vikingi našli ... in jo poimenovali.
In potem jo je mala ledena doba pahnila v deželo, pokrito z LEDOM, kjer je še danes ….
vendar se danes segreva in zdi se, da se vrača nazaj k temu, kar je nekoč bila … resnično zelena dežela ….
Nekateri pravijo, da so bila topla obdobja v zgodovini vedno povezana z razcveti civilizacij
(sumerske pred 6000 leti, egipčanske pred 5200 leti, minojske pred 4000 leti, rimske pred
2300 leti), vmesna obdobja hude ohladitve pa je zaznamovalo pomanjkanje hrane, vojne,
kužne bolezni ...
Vsekakor pa tako preprosto sklepanje ni celostno in enolično - bomo pozneje pokazali, zakaj
je lahko zavajajoče - upoštevati je namreč potrebno vse glavne značilnosti nekega podnebja in
podnebnih sprememb (zgolj nasprotje toplo, hladno je premalo).
Po koncu ledene dobe pred 11600 leti se je ozračje hitro in močno ogrelo, morje se je dvignilo za več kot 120 m
(to je tudi najbrž povod za spise, kjer se omenja vesoljni potop).
Vir grafa: https://www.quora.com/What-caused-climate-change-in-the-middle-ages
Podoben graf so objavili tudi v poročilu IPCC(1), pozneje pa ne več.
Groba shema globalne cirkulacije atmosfere. Oznaki C in A predstavljata ciklone (padavine,
nizek tlak – zrak se dviga, razpenja in vlaga kondenzira) in anticiklone (lepo vreme, visok
tlak – zrak odteka in se spušča, posledično se stiska, segreva in zato suši). Celoten
vremenski vzorec poganja seveda energija Sonca – na vrh atmosfere pade gostota energijskega
toka blizu 1400 W/m2. Od tega energijskega toka se globalno od Zemlje odbije okrog 30 %.
Območja v neposredni bližini ekvatorja prejmejo največ sončnega sevanja in so najtoplejša.
A glede poenostavljenih sklepov v stilu toplo dobro, hladno slabo,
moramo biti previdni. Ne premrzlo in ne pretoplo vreme ne koristi življenju na kopnem.
Ko se nekje na jugu preveč segreje - se ljudje selijo proti severu in obratno (tudi Vikingi so to počeli).
Ni toliko problem segrevanje, ampak sprememba vremenskih vzorcev in s tem padavinskega režima.
Z nihanjem temperatur se namreč spreminja tudi velikost vremenske Hadleyeve celice in se tako po
geografski širini premika
tudi področje suhega vremena in padavinskega pasu - slika zgoraj.
Velikost in intenziteto spreminjata tudi Ferrelova in polarna celica globalne
cirkulacije atmosfere.
Tukaj je še problem vpliva temperature
na cirkulacijo oceanov in obratno. Ko so propadle zelo razvite civilizacije pred približno 3000 leti v
Sredozemlju, je bil razlog tudi v spremembi klime, premalo padavin.
V tisti čas sodijo Trojanske vojne (zapisi so - recimo Homerjeva Iliada,
potem Odiseja, tudi njo pripisujejo Homerju, pa opisuje vračanje enega največjih grških junakov trojanske vojne, Odiseja,
domov na Itako),
propadli so tudi
Hetiti, ki so bili starodavno anatolsko ljudstvo, ki je ustanovilo svoj imperij
s središčem Hatuša (danes vas Bogazköy v Turčiji) v severnem delu osrednje Anatolije okoli
leta 1600 pred Kr. Takrat je propadlo še vrsto ostalih manjših držav, kultur -
recimo mikenska civilizacija ali mikenska Grčija.
Egipt pa je preživel tudi zaradi dejstva,
ker je imel zaloge vode in s tem žita (namakanje polj) ... v reki Nil.
Takrat se govori, piše o napadih ljudstev z morja - zapisi iz časa Ramzesa III.
Ljudstva z morja so bili najbrž konfederacija pomorskih ljudstev, ki so v srednji in pozni bronasti dobi
(1200–900 pr. Kr.), najbrž zaradi lakote, ki jih je prinesla suša,
napadala Egipt in druge sredozemske regije.
Njihov izvor je nezanesljiv. Domneva se, da so izvirali iz Male Azije,
egejskih in sredozemskih otokov in južne Evrope.
Zagotovo podnebje in prisotnost vode odločilno vplivata na naselitev
določenih območij Zemlje. A podnebne spremembe vzorce naselitvenih habitatov na Zemlji
skozi čas spreminjajo. Na podnebne spremembe moramo torej biti zelo pozorni - a z zdravo pametjo.
Je pa problem, če se podnebne spremembe opisuje neobjektivno, ko se recimo upošteva zgolj metode, ki nekomu
ideološko v nekem trenutku odgovarjajo. Primer - recimo kdaj temperature ocenjujejo zgolj z letnicami prirasta
dreves - v čem je lahko problem te metode? Problem je, ker na prirast drevesne mase zelo vplivajo tudi padavine
in ne zgolj temperatura.
To so zgodbe, špekulacije, ki mečejo slabo luč tako na pregrete apologete usodnih podnebnih sprememb,
kot na njihove
vročekrvne nasprotnike.
Podnebne spremembe so problem, nanje vpliva celotno življenje, posebej človek. A zdi se, da so
bolj usodni sami ekološki problemi -
onesnaženje tal, zraka, vode, prehrambne verige s kemičnimi koncentrati - a ta krucilani problem se
zakrije pod krinko kričanja le o podnebnih spremembah.
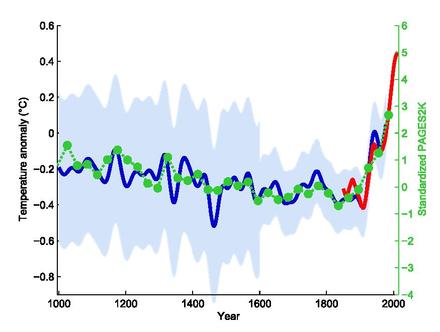
Graf podnebne "hokejske palice" (Hockey stick) na severni polobli – zglajena krivulja;
krivulja je prikazana v modri
barvi, njeno območje negotovosti pa je podano v svetlo modri barvi, prekrito z zelenimi pikami,
ki prikazuje 30-letno globalno povprečje rekonstrukcije iz leta 2013.
Rdeča krivulja prikazuje
izmerjeno globalno povprečno temperaturo po podatkih HadCRUT4 od 1850 do 2013.
Vir: https://en.wikipedia.org/wiki/Hockey_stick_graph_(global_temperature)
Kot vidimo je raztros (območje negotovosti ) možnih vrednosti temperatur skozi čas (svetlo modro polje) zelo velik -
različne metode ocene temperatur namreč dajejo nekoliko različne rezultate ...
Ta graf se močno razlikuje od zgornjega, ker je spodnji graf večinoma narejen
preko debeline drevesnih letnic (branik),
na rast katerih pa vplivajo močno (izraziteje) tudi padavine ... Povzetek ene od študij je spodaj.
Na debelino letnic torej ne vpliva zgolj temperatura
(drevesa je moč najti daleč na sever in visoko v gorah, kjer je veliko padavin).
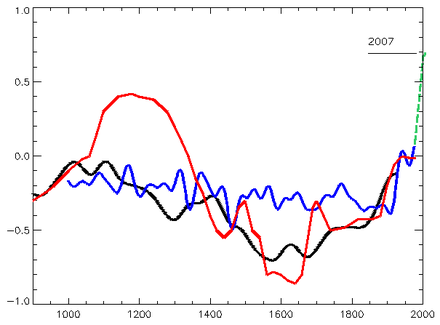
Rdeča črta: shematski diagram IPCC 1990 Slika 7.1(c) (temelji na Lamb 1965) natančno
sledi temperaturam v osrednji Angliji (dobljena z
uporabo zgodovinskih, botaničnih in arheoloških dokazov); zelena črtkana črta prikazuje temperature v osrednji
Angliji do leta 2007. Modra črta je Mann, Bradley & Hughes 1998 40-letno povprečje iz IPCC TAR 2001
"hokejska palica",
črna črta je Moberg et al. 2005 nizkofrekvenčni signal.
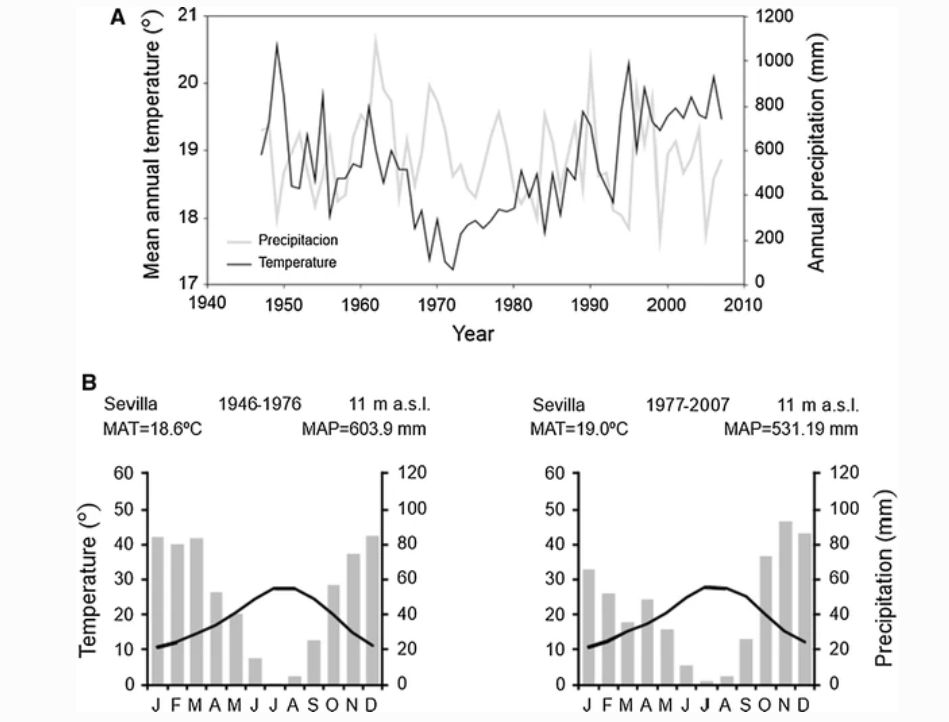
A - srednja letna temperatura (1946–2007) in skupna letna količina padavin (1946–2007) v
bližini študijskega območja; podatki iz meteorološke postaje Sevilla in
B - klimatski diagrami
za meteorološko postajo v Sevilli (37°23'10'' S, 5°59'33'' Z, 11 m n. m. ) za obdobji 1946–1976
in 1977–2007, ki prikazujejo medletna porazdelitev povprečnih mesečnih temperatur (črta)
in mesečne skupne količine padavin (stolpci); MAT povprečna letna temperatura (°C)
in povprečna letna količina padavin [mm]
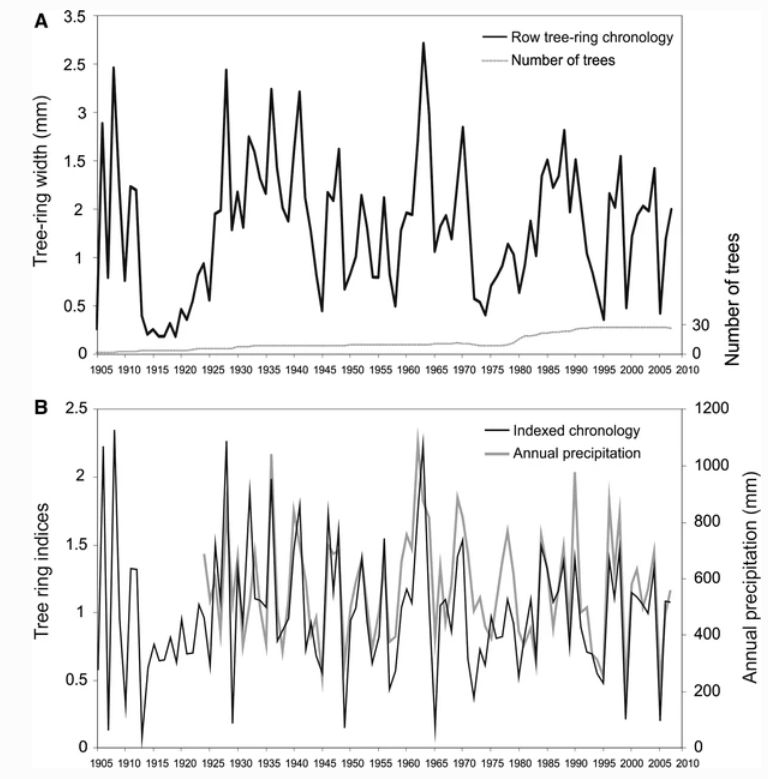
Vrstna kronologija P s številom izmerjenih dreves (a)
in indeksirana kronologija
z letnimi podatki o padavinah iz vremenske postaje Sevilla (b)
Rast dreves (v tem primeru
Pyrus bourgaeana, iberska hruška)
je bila močno in pozitivno povezana (korelirana) z letnimi padavinami, vsotami od septembra
prejšnjega leta do avgusta tekočega leta (
R^2 = 0,66). Rast dreves ni bila korelirana s skupno
količino padavin prejšnjega leta (regresija ostankov: R^2 = 0,01).
Korelacijski koeficienti so pokazali, da so za rast dreves še posebej pomembne padavine od novembra
prejšnjega leta do januarja tekočega leta. Skoraj enako je bilo ugotovljeno z uporabo
koeficientov odzivne funkcije; padavine prejšnjega oktobra, prejšnjega novembra ter januarja in
februarja tekočega leta so pozitivno vplivale na rast. Pozitivno so na rast vplivale
tudi padavine od februarja do junija letošnjega leta, med temi meseci pa so bile najpomembnejše junijske.
Srednja mesečna temperatura je manj vplivala na rast dreves kot padavine.
Obstaja pozitivna korelacija med rastjo dreves in temperaturo prejšnjega oktobra.
Tudi visoka zimska temperatura (prejšnji december in tekoči januar) je pozitivno vplivala na rast,
vendar je bilo to razmerje pomembno le za trenutno januarsko temperaturo. Visoka temperatura od
aprila do junija tekočega leta je negativno vplivala na nastanek drevesnih obročev, vendar je bilo
to razmerje pomembno le za maj. Koeficienti odzivne funkcije med mesečnimi temperaturami
in rastjo niso bili pomembni v nobenem mesecu, čeprav so kazali podobne trende
kot pri korelacijskih funkcijah.
Rast P. bourgaeana (iberske hruške) je vsekakor določena s podnebnimi razmerami
v celotnem proučevanem obdobju.
Razmerje med podnebjem in rastjo je bilo bolj izrazito v poznem dvajsetem
in zgodnjem enaindvajsetem stoletju, ko je podnebje postalo bolj sušno. Očitno močnejša povezava med padavinami
in rastjo dreves je bila ob koncu dvajsetega stoletja, ko se je povečalo tudi število manjkajočih obročev.
Vendar pa negativni vpliv podnebnih sprememb ni bil tako močan, kot bi pričakovali.
Podatki še kažejo, da se je pozitivna povezava med jesensko in zimsko temperaturo ter rastjo dreves okrepila
ob koncu dvajsetega stoletja,
kar sovpada s trendom naraščanja temperature v tem obdobju. Zdi se, da je zimsko segrevanje sprožilo pozitiven
odziv na rast. Vsekakor pa brez padavin ni rasti.
VIR: https://link.springer.com/article/10.1007/s00468-016-1472-8

Omenimo še podatek, da pri kurjenju fosilnih goriv (oz. ogljikovodikov)
tvorimo cca 3x toliko kg ogljikovega dioksida, kot smo uporabili kg goriva.
Ogljikovodiki so dolge alifatske verige molekul CH2
in v povprečju se pri eksplozijah v motorjih z notranjem izgorevanjem
med oksidacijo (eksplozijami v cilindrih) tvorita
ogljikov dioksid CO2 in voda H2O. Zgorevanje je v grobem videti takole:
CH2 + (3/2)O2 ==> CO2 + H2O + toplota
Molekulska masa CH2 = 14 in CO2 kar 44.
Razmerje med emisijo CO2 in gorivom verigo CH2 molekul
je torej kar:
44/14 ≈ 3
In to ne glede na gorivo.
Polietilen z verigo n*CH2
ima kurilno vrednost 46,3 MJ/kg in večina znanih goriv (bencin, nafta, butan, kerozin, tudi živalska ali
rastlinska maščoba) ima kurilno vrednost med 40 MJ/kg in kurilno vrednost 50 MJ/kg.
Malenkost višjo kurilno vrednost imajo lažji plini ...
Razen vodika, je to največ, kar lahko dobimo energije iz kemijskih vezi fosilnih goriv,
a proizvedemo žal 3x več ogljikovega dioksida CO2.
Ko torej pokurimo recimo 10 kg goriva na 100 km v eni uri, spustimo v zrak
cca 30 kg ogljikovega dioksida CO2.
Pri zgorevanju se torej ogljik v gorivu veže z dvema atomoma kisika iz zraka (CO2).
Ker ima kisik veliko maso (16 in molekula O2 torej 32), nastane več kilogramov CO2 kot je mase samega goriva.
A v zrak gre neto veliko manj mase, saj je molekularni kisik O2 bil že prej v zraku.
Torej gre v zrak cca 1/3 ogljika (torej cca 1 kg) in nekaj vodika v obliki vodne pare H2O (v resnici pa je na novo nastale
vodne pare cca 18/14 = 1,3 kg ). To so približni izračuni - verodostojnejši izračuni za izgorevanje recimo oktana (dober približek za bencin)
( 2C8H18 + 25O2 ==> 16CO2 + 18H2O )
pa vrne izpust 3,09 kg ogljikovega dioksida (CO2) in izpust
1,42 kg vodne pare (H2O) na kg goriva (torej so naše ocene
bile dokaj korektne).
Moramo pa vedeti, da je vodna para še veliko močnejši toplogredni plin od
ogljikovega dioksida, a voda se prej preko vodnega kroga izloči iz zraka - v zimskem času so značilne
industrijske padavine (sneg) recimo v okolici termoelektrarn.
Zaradi navedenih razlogov (zraven je še kemijska degradacija zemlje, vode, zraka)
je potrebno najdi rešitve v nuklearni energiji (fisija že deluje, potrebno jo je optimizirati,
fuzija pa se žal le počasi prebija), seveda so nam na razpolago tudi naravni viri, Sonce, veter, termalni vrelci ...
ki nam lahko precej pomagajo.
A ne tako, da zaradi njih uničimo še zadnje neokrnjene predele Zemlje.
A vsak večji poseg na površini Zemlje ali v sami atmosferi nam spremeni albedo (odbojnost Sončevih žarkov) in
vetrovno sliko nekega območja - kar spet vpliva na vreme (in tudi sama izdelava vetrnic in sončevih panelov
je večinoma ekološko precej obremenjujoča).
Sledi nekaj tematike o podnebnih spremembah preko umetniških slik in tudi zapisov iz kronik,
tudi iz slovenskega prostora - izjemno.
_-_Google_Art_Project.jpg)
‘Hunters in the snow’ (Lovci v snegu), Pieter Bruegel starejši, februar 1565,
pokrajina v času ostre zime (Nizozemska ali bližnji kraji, danes ne poznajo tako hudih zim).

Franz Josef Fellner - led na Dravi leta 1766 - Ptuj. Slika - Ptujski grad, Pokrajinski muzej Ptuj Ormož.
Danes takih skrajnih zimskih prizorov na Dravskem polju (tudi če ne bi bilo dravskih elektrarn),
ni več moč doživeti, opaziti ...

Od leta 1875 do 1878 so sočasne večletne suše v Aziji, Braziliji in Afriki,
imenovane Velika suša, povzročile ekstremno skromne pridelke, pomanjkanje hrane,
kar je povzročilo tako imenovano globalno lakoto, ki je imela za posledico do
50 milijonov smrtnih žrtev in dolgotrajne družbene posledice.
Tihi ocen je predhodno zajelo dolgo obdobje
nizkih temperatur (1870 - 1876), kar je vplivalo na energijsko
bilanco globalne cirkulacije morskih tokov (le ti generirajo
smeri vetrov in s tem vreme, padavine). To dogajanje je oslabilo
zimski monsun v Indiji – ki je tako prejela manj padavin.
1877 pa se je zgodil preobrat, druga skrajnost, začne se vroče
obdobje nad Tihim oceanom (pojavijo se izraziti topli morski
tokovi proti Južni Ameriki - temperature morske površine so ostale
visoke kar 16 mesecev), kar pomeni začetek izrazitega El Nina,
ki prepreči kar dva monsuna v Aziji (topel oceanski tok, ki se
pojavi ob zahodnih obalah Južne Amerike, prinaša s sabo mokro
in deževno vreme ter poplave na sicer suhih območjih Južne Amerike,
a hkrati sušno obdobje na zahodnem delu Pacifika, v Aziji, Indoneziji ...).
V Pokrajini Šansi (Kitajska) od 1877 do 1878 ni padla niti kaplja dežja.
V Aziji je to bila najbolj obsežna suša v zadnjih 800 letih. Leta 1877
pa se je v severnem Atlantiku pojavila še dolgotrajna vroča anomalija
(topla voda), na območju Indijskega ocena pa je nastal t. i.
temperaturni dipol (ob obalah Somalije se je namreč ocen nadpovprečno segrel,
vode ob zahodnih obalah Avstralije pa so se izrazito ohladile). Nedavne
raziskave so pokazale, da se anomalije v temperaturah oceanske površinske
vode (od 2 do 8 °C višje temperature) pojavljajo v nepravilnih časovnih
presledkih 3 do 5 let (a v letih od 1875 do 1878 pa je prišlo celo do
sočasnih neljubih dogodkov, temperaturnih anomalij v vseh treh velikih
oceanih).
Izjemno bogati arhivi in kronike slovenskih pokrajin od leta 800 naprej
Iz starih kronik za deželo Štajersko (iz “Dogodivšine štajerske zemle - 1845”, zapiše
Anton Krempl [1790 - 1844, izjemno delo, prva prava zgodovina v slovenščini, hkrati vir
informacij za klimatologe, a ...] iz Male Nedelje v Slovenskih goricah in Krones Lapajnetove
“Pripovesti iz zgodovine Štajerske”).
- leta 820 je bilo nerodovitno, umirajo od lakote,
- leta 872 so roji kobilic zakrili Sonce in uničevali vse zelene rastline,
lakota,
- leta 993 je na božič nek sij tako razsvetlil nebo, da je bilo svetlo
kot podnevi (komet, meteorit, polarni sij, ...), sledila je huda zima,
- leta 1186 je meseca februarja cvetelo sadno drevje, v maju so bila zrela
vsa žita, trgatev je bila konec avgusta (smo blizu temu),
- v letih 1187 in 1188 je bila huda zima, ki je trajala vse do binkošti,
zato je vse zelo pozno dozorelo, trgatev je bila ob božiču,
- leta 1194 je bilo slabo leto, polno raznih nadlog: povodnji, kužnih bolezni,
kug, ki so uničile cele vasi (posledice - danes imamo recimo vas Puščava,
Slovenska vas, Nemška vas, itn); ponoči je bilo moč videti "krvave" zvezde
repatice (meteorski roj?); pojavljali so se požari in nadležna mrčes,
- leto 1248 je bilo zelo mokro,
- leta 1255 je po hudi zimi bila strašna suša, da njive, sadovnjaki
in vinogradi niso nič obrodili,
- leta 1270 je bila najprej ostra zima, potem pa je prišla strašna suša,
ki je vse pokončala; nastala je takšna lakota, da so cele kupe mrličev,
ki so od lakote umrli, metali v skupne jame,
leta 1289 so se letni časi čisto zmešali ...
- leta 1312 so žito za naše dežele vozili iz Sicilije,
- leta 1570 je bila strašna lakota, otroci so po livadah lazili in travo
jedli,
- "po 1600 hude zime“,
- leta 1767 je bil 4, maja hud mraz, 6. maja pa je močno snežilo,
sneg je do vznožja pokrival Ivančičo še nekaj dni,
- LETA 1788 JE BILO IZVRSTNO VINO, KI JIH JE VELIKO V GROB
SPRAVILO,
- 24. maja 1866 je bil hud mraz, ki je po vinogradnih in na poljih
naredil veliko škode (sem preveril v našem met. arhivu).
Lahko bi šli še v antične čase, konec rimskega imperije so tudi zaznamovale izjemno nizke temperature,
začetek srednjega veka pa vulkanski prah, ki je preprečeval Soncu proces rastlinske fotosinteze na Zemlji in s tem rast
...
Ohladitev pred 1500 leti zaradi
izbruhov vulkanov je bila usodna za mnoge
prebivalce Evrope - posledica izbruhov prahu, plinov je bilo dvoletno mračenje neba v
letih 535–536, srednji vek se je tako začel z lakoto in smrtjo, ki ji do danes ni para ...
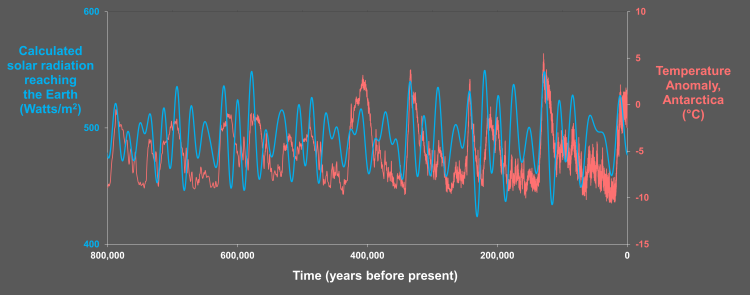
Cikli temperatur in gostote Sončevega obsevanja,
narisani skupaj z rekonstrukcijami površinske temperature Antarktike
iz meritev ledenih jeder:
Milankovitch Orbital Data Viewer, Colorado State University.
EPICA Dome C Ice Core 800KYr Deuterium Data and Temperature Estimates.
IGBP PAGES/World Data Center for Paleoclimatology, Data Contribution Series # 2007-091.
NOAA/NCDC Paleoclimatology Program, Boulder CO, USA.
Figure by Ingrid Zabel for PRI's Earth@Home project (CC BY-NC-SA 4.0 license).
Vir: https://earthathome.org/quick-faqs/are-orbital-changes-causing-global-warming/
Razlogi za podnebne spremembe so tudi v nabesni mehaniki - poglejmo tri pomembne cikle,
ki so tudi narisani na zgornjem grafu.
Ekscentričnost, ki jo povzročajo gravitacijske sile drugih planetov v našem
sončnem sistemu, spremeni obliko orbite v 100 000 - letnem ciklu iz krožne v bolj eliptično obliko
(od od skoraj ciklične z ekscentričnostjo 0.0034, do precej eliptične
z ekscentričnostjo 0.058).
Nagnjenost Zemlje je sprememba kota zemeljske osi, ki se giblje od 22° do 24,5°
od normale (od pravokotnice) na ekliptiko in se spreminja v 41 000 - letnem ciklu.
Precesija, nekateri jo imenujejo tudi "nihanje" Zemljine osi,
vpliva na spremembo višine Sonca (žarkov) na Zemljini površini, na geometrijski položaj Zemlje v orbiti,
na katerem severna
in južna polobla doživljata poletje in zimo
(ni vseeno ali je recimo poletje v prisončju ali odsončju,
saj je nad ekvatorjem več kopnega). Precesija se odvija v približno 26 000 - letnem ciklu.

Zdi se, da se sprememba gostote svetlobnega toka pričakovano precej dobro odraža
v nihanju temperatur s faznimi zamiki - kot to velja tudi čez dan temperatura
ni najvišja ob kulminaciji Sonca (12 h), ampak okrog 2 uri pozneje.
Problem napovedi podnebnih sprememb je prezapleten v smeri, da bi lahko bili zelo uspešni (tudi potresov
ne znamo napovedovati). Zakaj? Ker na podnebje vplivajo tudi vulkanski izbruhi, trki z asteroidi in kometi,
meteorski roji,
aktivnost Sonca, položaj Sonca v orbiti okrog središča Rimske ceste, premnogi sekundarni vplivi
iz vesolja, tudi eksplozije nov in supernov ter sama nedoločenost nebesne mehanike Sončevega sistema ...
Pa še vseh bioloških odzivov narave ne poznamo - kamor spada tudi človek.
Zagotovo je življenje skozi kar milijarde let dolgo obdobje močno preobrazilo planet, podnebje (fotosinteza
da prost kisik in tako lahko nastanejo velike živali, tudi ljudje), da je postal primeren tudi
za visoko razvite primate. In zagotovo tako bizoni, kot druge živali, tudi ljudje, vplivamo na
podnebje (vplivamo na rabo tal, vode, odbojnost planeta, na ravnotežje v okolju
s kurjenjem fosilnih goriv, z razvojem kemije in posledično obremenjevanjem
okolja z nenaravnimi koncentracijami kemikalij, plinov ...).
A moramo torej v bodoče bolj paziti,
da zrak ostane čist, enako voda, prst - a tukaj smo že kar precej porušili ravnovesje,
hormonski motilci so že spremenili značaj živali in ljudi ... in to je kar zelo zaskrbljujoče.
Problem so tudi povratne zanke - ko recimo
pride do taljenja ledu, se zmanjša albedo (odbojnost Zemlje)
in se tako Zemlja še hitreje segreva.
A tudi sama ekstremistična zelena politika je lahko še bolj nevarna od samih podnebnih sprememb.
Ko je človek lačen, je lahko zelo drugačen - agresiven in določeni indici kažejo na to,
da se namerno ideološko politično ruši prehranska veriga za 8 milijard ljudi - lakota, to je veliko hujši destruktivni
pojav kot
ekološka bomba, trenutne podnebne spremembe ... Če je recimo danes kje suša ali je preveč padavin in zato primanjkuje hrane,
le to lahko dokaj hitro pripeljemo iz drugega konca sveta. A če bomo uničili temelje globalnega kmetijstva
in živinoreje, potem nam ni pomoči (globalna lakota je primerljiva le s katastrofo, ki nastane
pri padcu velikega asteroida na Zemljo).
Civilizacije so se začele z razvojem poljedelstva in živinoreje pred 10000 leti in
če to ukinemo, si odrežemo korenine človeškega obstoja.

Ena izmed bolj ironičnih podob (glej zgornjo sliko) in hkrati zelo povednih eksistencialnih ugank,
predstav o tem, kako zelo ranljivo je v resnici življenje na Zemlji (tudi zaradi
človeške neumnosti - zaradi napačne rabe virov, ekstremnega potrošništva in tudi vojaške agresivnosti).
A tudi v teh protislovjih se kaže del rešitve ..., recimo obramba pred trki kometov in asteroidov.
Ko se išče življenje na eksoplanetih, se velikokrat stavi na spektralne črte kisika oz.
molekule
O2,
ki bi naj bil, kot prost plin v
atmosferi, posledica fotosinteze – torej procesov življenja. Ali
bi lahko s to metodo zaznali življenje v zgodnejših obdobjih zgodovine
Zemlje? Odgovor je, najbrž ne – vsaj ne preko kisika. V prvi polovici
zgodovine planeta v zraku tako rekoč ni bilo kisika. Ve se tudi, da je imel
naš planet v prvi polovici obstoja v atmosferi še vedno štiri dolgoročno
nezdružljive pline: ogljikov dioksid, metan, dušik in vodo (pri iskanju
življenja na eksoplanetih bo najbrž potrebno staviti tudi na dinamiko
koncentracij plinov – kot na Zemlji, tudi na sezonsko nihanja).
Tudi večji del druge polovice življenja naše Zemlje so bile ravni
kisika res nizke. To pa zato, ker je približno milijardo let trajalo,
da je življenje začelo proizvajati kisik v večjih količinah, potem ko so
se pojavili prvi živi organizmi (veliko kisika se je oksidiralo, recimo
v mineralih, oksidacija železa ...). A minilo je še mnogo milijonov -
kar kakšna milijarda let, da je Zemlja pridobila preko fotosinteze
spodobno kisikovo atmosfero, ki je omogočila razvoj vretenčarjev.
"Bi torej lahko zaznali življenje v zgodnejših obdobjih zgodovine Zemlje?"
To je sedaj naše vprašanje!? Tudi Spika je maja 2021 objavila novico (ko je
ta prispevek že bil praktično končan), da so preko računalniških modelov,
simulacij, poustvarili planete z različnim začetnim deležem kemijskih elementov
in ugotovili - da se pri zelo vodnatih planetih ali pri planetih z malo vode
in tudi pri planetih z veliko več CO2, kjer se lahko pojavi efekt
izrazite tople grede, ko visoke temperature onemogočajo oksidacijo – lahko
veliko prostega kisika nahaja v atmosferi, ki pa seveda ni posledica bioloških
procesov. Iskalo se bo torej še ostale prstne odtise življenja – recimo metana
CH4 v kombinaciji s CO2.
Veliko metana je na dolgi rok težko razložiti brez življenja,
če je prisoten tudi CO2 – ki metan sčasoma razgradi.
Ko imamo CO2 in večje deleže CH4 na nekem
eksopotepuhu, bi to naj bil dokaj verodostojen dokaz prisotnosti
življenja, ki stalno izloča metan. A so še druge metode. Recimo,
Zemljin ogljikov dioksid se skozi vse leto dviguje in spušča,
ko rastline na severni polobli jeseni odmrejo in spomladi spet
zrastejo (na južni polobli je manj kopnega). Letna raven
CO2 pade za približno 6 ali 7 ppm (približno 50 Gt)
od maja do septembra, med rastno sezono severne poloble
in nato naraste za približno 8 ali 9 ppm. Severna polobla
pričakovano prevladuje nad letnim ciklusom CO2,
ker ima veliko večjo površino in rastlinsko biomaso kot
južna polobla. Koncentracije dosežejo vrh maja, ko se začne
spomladansko ozelenjevanje severne poloble in se zmanjša na
minimum oktobra, ob koncu rastne sezone (razlika v prirastu
in padcu je posledica človeškega sežiganja geološkega fosilnega
ogljika, po ocenah sprostimo v atmosfero več kot 30 gigaton
CO2 na leto).
Podoben sezonski cikel bi se lahko dogajal tudi drugje.
Poleg prisotnosti kisika, imamo pri roki še kar nekaj
metod za detekcijo, oceno prisotnosti življenja na eksoplanetih
– torej v kombinaciji plinov in v morebitnih sezonskih
nihanjih koncentracij ter tudi v spremembi odbojnosti zaradi
vegetacije (pojavile se bodo tudi nove metode). A tudi pri
nihanjih
CO2
je lahko kar velik problem – ta plin namreč
zelo niha tudi na Marsu, a ne zaradi prisotnosti
življenja, ampak zaradi sezonske tvorbe polarnih
kap, kjer se temperature gibljejo med
-113 ° C in -153 ° C, kar je dovolj,
da CO2 kondenzira (v suh led, 1 do 2 m debel).
Letna spremenljivost atmosferskega tlaka
≈ 25%, povprečna
vrednost tlaka na Marsu pa je le 610 Pa (Mars je manjši
od Zemlje, premore le 0.107 mase Zemlje, s težnim pospeškom
3.72076 m/s2,
nima magnetnega polja, zato Sončev veter še
dodatno odnaša atmosfero).
Glede na računalniško modeliranje starodavnega podnebja na planetih, so znanstveniki z NASA-inega Goddardovega inštituta za vesoljske študije (GISS - NASA’s Goddard Institute for Space Studies) v New Yorku ugotovili, da je Venera morda nekoč imela plitvi ocean s tekočo vodo in za življenje primerne (bivalne) temperature na površini, v prvih dveh milijardah let svoje zgodnje zgodovine. Zdi se, da je bilo torej dovolj vode za razvoj življenja, ob primernih temperaturah. Takrat je Sonce tudi sevalo do 30 % manj energije, a še zmeraj je Venera prejela 40 % več energije kot Zemlja danes. So pa določene simulacije, da so zaradi počasne rotacije Venere (dan na Veneri traja 117 zemeljskih dni) lahko bile v tropskih krajih obilne padavine (tudi obilno izhlapevanje zaradi izrazitega dvomesečnega segrevanja določenega dela Venere), torej razmere, ki bi na nek način lahko ohranjale temperaturo na vrednostih ugodnih za razvoj življenja. Vendar je, kot smo že omenili, Venera bližje soncu kot Zemlja in prejema veliko več sončeve svetlobe, energije. Posledično je Venerin zgodnji ocean izhlapel, molekule vodne pare so bile razbite, zaradi ultravijoličnega sevanja in vodik je ušel v vesolje. Ko na površini ni bilo več vode, se je ogljikov dioksid kopičil v ozračju, kar je povzročilo tako imenovani toplogredni učinek, ki je ustvaril sedanje razmere - visoke temperature blizu 500 °C. Venera torej nima več oceana, nima kemičnega preperevanja in subdukcije (podrivanje tektonskih plošč) karbonatov v svoj plašč (nima ogljikovega cikla - kroženje ogljika pomeni premeščanje ogljika med skorjo planeta, organizmi, hidrosfero in atmosfero) in ves CO2 ostaja kot toplogredni plin v atmosferi. Venera in Mars sta tako blizu, a hkrati tako daleč od življenja – vsaj glede visoko razvitih oblik življenja. Saj v naših časih je tako, kako pa bo v prihodnosti, pa se pustimo presenetiti ... Tudi Zemlja je potrebovala okrog 3 milijarde let, da je bila sposobna preko cianobakterij in rastlin s fotosintezo proizvesti dovolj kisika za gromozanski evolucijski preskok. Preskok v razvoj velikih živali na izjemno reaktiven (energijski) kisik. Končno so se lahko razvili vretenčarji z velikimi možgani - primati pa smo vzniknili komaj pred zdajci.
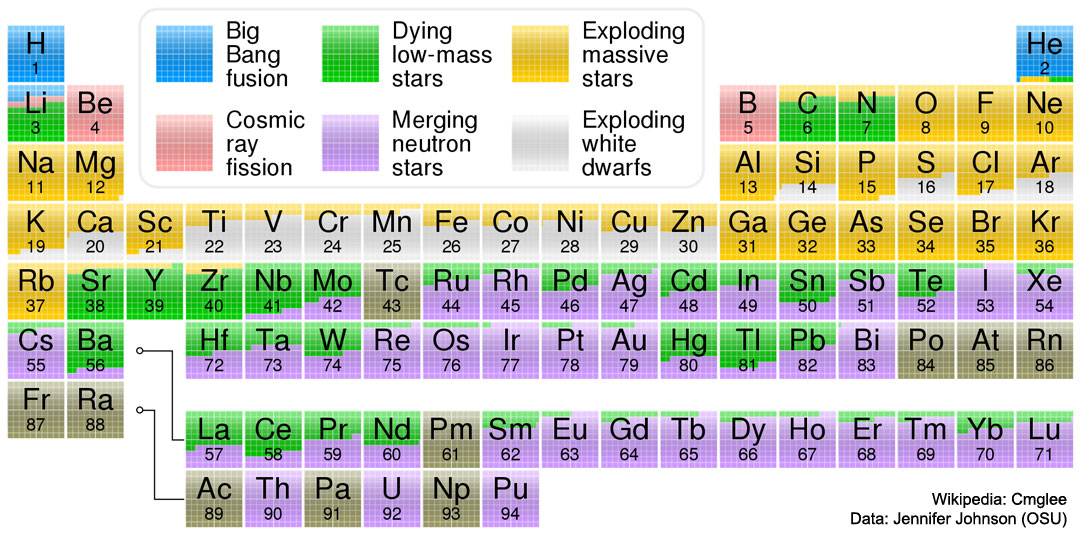
Izvor kemičnih elementov
Avtorstvo:
pravice:
Wikipedia:
Cmglee;
podatki:
Jennifer Johnson
(OSU)
Pojasnilo: Vodik v tvojem telesu, ki je del vsake molekule vode, je nastal ob velikem poku. V vesolju ni drugih znatnih virov vodika. Ogljik v tvojem telesu je nastal z jedrskim zlivanjem v notranjosti zvezd, enako tudi kisik. Veliko železa v tvojem telesu so naredile supernove, to je eksplozije zvezd, ki se zgodile že davno in daleč proč. Zlato v tvojem nakitu verjetno izvira iz trkov nevtronskih zvezd, ki jih je bilo morda za trenutek videti kot izbruhe gama žarkov ali zaznati tedaj nastale gravitacijske valove. Elementov kot so fosfor ali baker je v naših telesih le malo, vseeno pa so nujni za obstoj vseh znanih oblik življenja. Zgornja periodična tabela ima barvne oznake, ki označujejo, kako ljudje mislimo, da z jedrskim zlivanjem nastajajo vsi znani elementi. Jedrskega nastanka nekaterih elementov, na primer bakra, zares ne poznamo dobro, zato je to tema opazovanj in računskega raziskovanja.
Vir: APODKratka ponovitev dozorevanja atmosfere naše Zemlje, razvoja življenja - smo živ planet, kjer je minevanje samo novo rojevanje večinoma še bolj kompleksnega življenja in ta čudež bo trajal še vsaj "nekaj" časa!
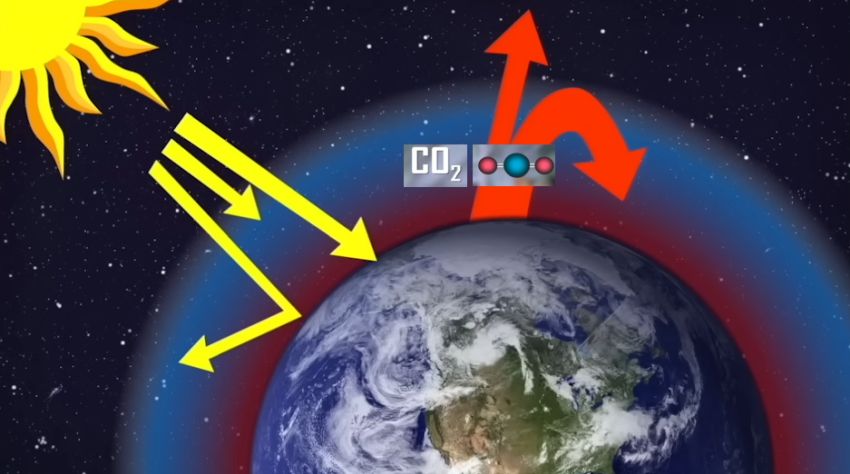
Na zgornji sliki je zgolj simbolično podan ogljikov dioksid kot toplogredni plin,
ki absorbira del dolgovalovnega sevanja Zemlje in ga izseva nekaj nazaj proti
površini Zemlje. Zelo pomembna toplogredna plina sta tudi še metan in vodna para - slike spodaj.
Spodnje slike kažejo temperaturo na površju Zemlje brez toplogrednih plinov (Zemlja bi bila
ujeta v led, minus -18 °C pri izsevnosti 1) in s toplogrednimi plini
(povprečna temperatura plus +15, oz. +16 °C,
kar omogoča tekočo vodo in nastanek
življenja).
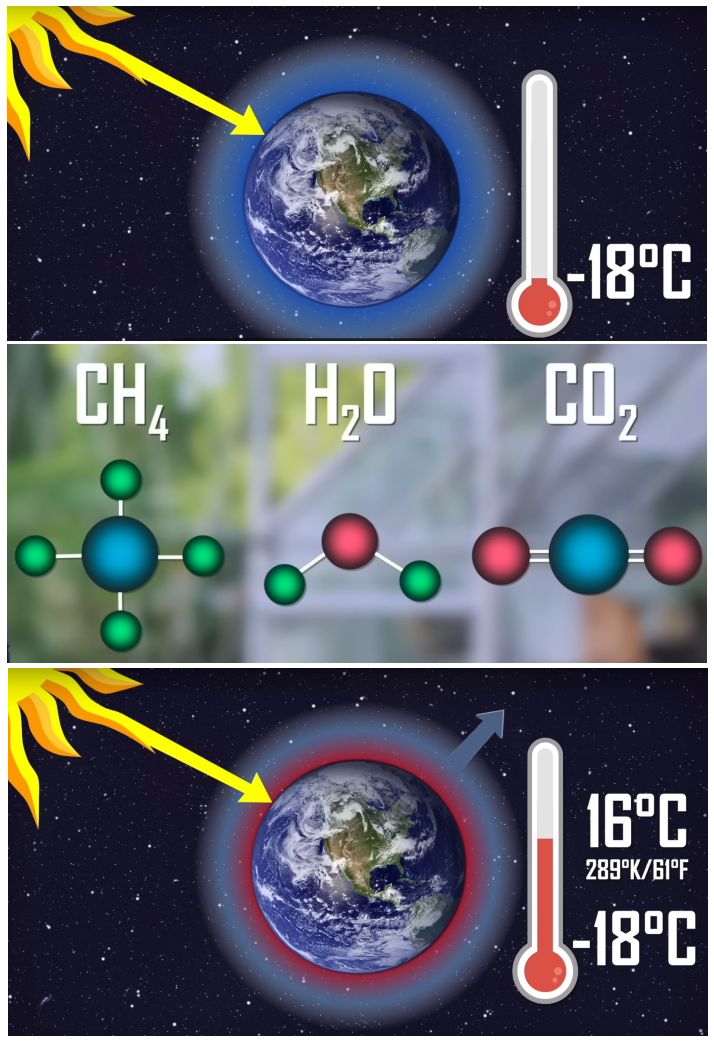

Zgornje slikice zelo lepo kažejo velik pomen toplogrednih plinov
za temperature nad 0 °C, da je tako na Zemlji lahko prisotna tekoča voda, ki je omogočila razvoj
čudežnega življenja.
Toplogredni plini, molekule plinov, vsrkajo del izsevanih toplotnih valov, ki jih sevajo površina Zemlje
in delno zračne mase in jih tako naknadno delno sevajo nazaj proti tlom (od tod višja temperatura prizemne plasti),
del valovanja pa seveda izsevajo v vesolje (drugače bi se skuhali ...).
Seveda pa so previsoke koncentracije toplogrednih plinov lahko velik
problem zaradi trenutnega globalnega
segrevanja - a trenutno je še veliko večji eksistencialni problem samo onesnaženje zraka, vode in samih tal
(recimo hormonski motilci, ki spreminjajo identiteto človeka, živali in rastlin).
Morebiti pa nas kdaj toplogredni plini rešijo pred ledeno dobo, če seveda preživimo kot vrsta.
Sledi kviz življenja!
A veste, kateri toplogredni plin je omogočil pred milijardami let razvoj prvih enoceličnih bitij,
tudi cianobakterij? To je bil toplogredni plin metan, ki je držal temperaturo nad 0 ° C!
A veste kdo je razbil molekule metana (pred približno 2.4 do 2.1 milijarde let)
in tako povzročil dolgo globalno
huronsko poledenitev Zemlje (brez metana je temperatura padla pod 0 ° C, saj se je emisivnost, izsevnost povečala,
posledično nastali ogljikov dioksid je manj toplogreden in ga je bilo zato premalo, da bi preprečil ohlajanje Zemlje).
To je bil kisik, ki so ga preko fotosinteze sproščale cianobakterije.
V času huronske globalne ledene dobe, se je razvoj življenja ustavil, nekaj življenja
je ostalo le v oceanih pod ledom.
Ali veste, kdo je to globalno ledeno dobo počasi končal (ledena doba je namreč ustavila fotosintezo ...)?
To je bil današnji glavni grešni kozel, toplogredni plin CO2,
ki so ga počasi v ozračje Zemlje bruhali vulkani - res poučno.
In vse ostalo je zgodba zadnjih poznih 500 milijonov let (ko je kisik v zraku končno lahko narastel daleč čez 10 %),
ko so nastala mogočna
mnogocelična bitja, tudi človek, ki končno lahko dihajo veliko bolj energijsko učinkovit kisik (
recimo za presnovo, oksidacijo glukoze). Kisik je seveda proizvod fotosinteze s strani
cianobakterij, alg, velikih rastlin.
Na začetku nastanka Zemlje pa je bil ves kisik kje? Prostega v zraku ni bilo. Zaradi izjemne reaktivnosti pa je bil ves
vezan v vodo, v CO2, v metan, v minerale, pozneje
v organske molekule, v železo ... (kot smo že omenili, v zraku prostega kisika O2 praktično ni bilo).
Zemlja je torej morala najprej dolgo zoreti in dozoreti - v kar skoraj štiri milijarde let dolgi
dobi, da so tako komaj pred "kratkim" sploh lahko nastale visoko razvite oblike življenja,
najprej v vodi, pozneje tudi na kopnem – to so recimo
primati, človek z izjemnimi možgani ...
Fiziko računanja ravnovesnih temperatur zaradi toplotnega sevanja
nam je podaril izjemen Slovenec, fizik Jožef Štefan že v 19. stoletju.
Izračuni so v članku:

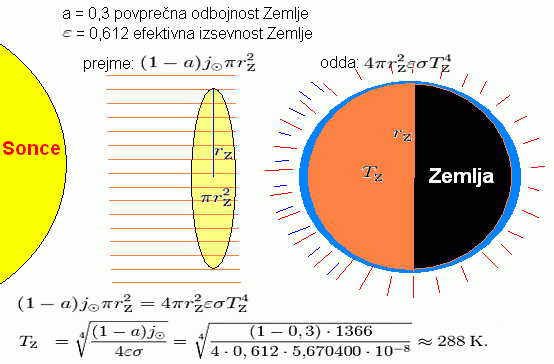
»Slovenija pod skupnim nebom« v 2020
Velika konjunkcija 2020 (XI)
Potepuhi in življenje (II)
(Vičar Zorko, revija Spika 12 [2020], strani 506 - 508)
Za življenje, kot ga poznamo na Zemlji, so zagotovo nujni naslednji kemijski elementi
v zanimivi besedni sestavljenki CHNOPS.
To so: ogljik (C - Carbon), vodik (H - Hydrogen), dušik (N - Nitrogen), kisik (O - Oxygen),
fosfor (P - Phosphorus),
žveplo (S - Sulfur).
Seveda so tukaj še ostali pomembni kemijski elementi, recimo brez železa nam živeti ni
(slabokrvnost žal doleti
mnoge ljudi), saj v
krvi veže in prenaša kisik do celic, kjer se zgodi oksidacija glukoze - naša energija življenja ...
Tukaj so še izjemno pomemben
kalcij (Ca - Calcium), že omenjeno železo (Fe - Iron), kalij (K - Potassium), magnezij (Mg - Magnesium),
jod (I - Iodine),
natrij (Na - Sodium), baker (Cu - Copper) in še mnogi ostali.
Omenjene elemente pa lahko povežete v besedne sestavljanke CaFe FeKI CuNaMg.
Med organskimi molekulami so zagotovo pomembne:
- aminokisline
(za beljakovine; aminokislina je molekula,
ki vsebuje tako aminsko (–NH2) kot karboksilno (–COOH) funkcionalno skupino;
v biokemiji se ta krajši in splošnejši termin pogosto uporablja za α-aminokisline
– aminokisline, pri katerih sta aminska in karboksilna skupina vezani na isti ogljikov atom. ),
- lipidi
(masti, olja, steroidi ... - lipidi predstavljajo velike biomolekule iz sestavljanke atomov C, H, O,
ki vežejo nase recimo še fosfor P, dušik N ...,
med
glavne funkcije lipidov spadajo shranjevanje energije, celično ter tkivno
signaliziranje in gradnja celičnih membran, kjer se zadržuje tudi voda
- pomembno je torej, da lipidi niso topljivi v polarni vodi, so
pa topljivi v nepolarnih organskih topilih, rec. heksan
CH3(CH2)4CH3),
- nukleotidi
(so osnovni gradniki nukleinskih kislin DNK in RNK,
sestavljeni so iz sladkorja (pentoze C5H10O5- ogljikovi hidrati),
dušikove baze in fosfatne skupine ...,
kjer se torej nahajajo omenjeni kemijski elementi, združeni
preko električnih sil med atomi pri danem tlaku in temperaturi, v primernem okolju.
Kjer voda in zrak igrata posebno pomembno vlogo. Zunanji dejavniki so gravitacija (ki veže
kamnine, prst, ostale molekule in elemente v planet) in seveda
Sonce kot praktično naš edini stabilni vir energije v daljšem obdobju. Sonce torej
igra glavno vlogo v čudežu ŽIVLJENJA.
10 najpogostejših elementov v galaksiji Rimska cesta Razvrstitev Element Masni delež (ppm) 1 vodik 739.000 2 Helij 240.000 3 Kisik 10.400 4 ogljik 4.600 5 Neon 1.340 6 Železo 1.090 7 Dušik 960 8 Silicij 650 9 magnezij 580 10 Žveplo 440Fosfor se v vesolju pojavlja v majhnih količinah okrog 50 ppm. Pojavlja se tam, kjer je raznolikost elementov podobna kot v našem Osončju (zvezde zadnje generacije iz ostankov supernov). Fosfor je torej zelo dober indikator za zvezde podobne Soncu - kjer bi lahko nastalo še kakšno življenje na eksoplanetu v naseltveni (zlatolaskini) coni.
Koncept zgornje podobe prikazuje sedem skalnatih eksoplanetov v sistemu Trappist-1,
ki se nahajajo 40 svetlobnih let od Zemlje, ki so slikovito upodobljeni
v agregatni podobi vode, glede na oddaljenost od centralne zvezde.
Tam kjer je tekoča voda (to je naselitveni, zlatolaskin, pas),
je velika možnost za nastanek življenja, bližje zvezdi je prevroče in voda izhlapi,
dlje navzven od naselitvenega pasu, pa je voda, če je na planetu, zamrznjena.
Res pedagoško zelo nazorna ilustracija.
No, naša kamnita Zemlja je glede na Sonce tam, kjer je tekoča voda.
Vir: https://webbtelescope.org/contents/media/images/2020/13/4623-Image?news=true
Kako so posejani kemijski elementi življenja po vesolju?
Težjih elementov od vodika in helija je najmanj v zelo starih prvotnih zvezdah,
ki se nahajajo v kroglastih kopicah in eliptičnih galakasijah.
V omenjenih strukturah je torej manj kandidatov za razvoj življenja.
Bolj dinamične razmere in s tem primerne za rojevanje mladih zvezd iz težjih elementov
(torej zvezde zvisoko kovinskostjo), ki so že nastali
med eksplozijami supernov starejših masivnih zvezd,
so v diskih spiralnih galaksij, kjer je tudi Sonce, Zemlja ... in človečki.
V središčih galaksij so mlade kovinske zvezde pogoste, a je tam zaradi visoke gostote zvezd
in s tem tudi intenzivnega sevanja, malo verjetno, da se bo razvilo življenje.
Na robu galaksij pa je dinamika preskromna in je spet manj mladih kovinskih zvezd.
A vseeno se kar okrog 20 % vseh zvezd nahaja v tistem delu diska galakij,
ki je naseltveno (habitatno) ugodno (mlade zvezde z visoko kovinskostjo in ne preveč sevanja
iz okolice, ker zvezde niso pregosto porazdeljene).
Če je zvezda hladna, je naselitveno področje ozko - planet se mora nahajati
na točno določeni orbiti.
Če pa je zvezda zelo vroča, je naselitveno območje nekoliko širše,
a masivne zvezde živijo manja časa (t
= 1010(M☉/M)2,5 let ) in se tako življenje težko razvije
do stopnje primatov (mi smo nastali komaj pred kakim milijonom let,
Zemlja pa je stara približno 4540 milijonov let (če zaokrožimo, 1/4000 časa bivanja Zemlje smo potrebovali,
da smo nastali ..., tik pred zdajci)).
Iz povedanega sledi, da so najprimernejše zvezde s planetnim sistemom za razvoj življenja
ravno srednje masivne zvezde spektralnega tipa G, kot je tudi naše Sonce, ki vztrajajo na glavni veji
HR diagrama okrog 10 milijard let (stabilno svetijo, zlivajo lahka jedra v težja).
Seveda iščemo življenje tudi pred domačim pragom (Venera, Mars)
in tudi na (v) Jupitrovi Luni Evropa (imena Jupitrovim lunam je dal Simon Marius).
Evropa ima pod ledenim površjem vodo, ki bi morebiti lahko gostila preprosto življenje.
Še bolj primerna kandidatka pa se zdi Saturnova luna Enkelad, ki na južni polobli
iz gejzirjev bruha vodno paro in ledene delce stotine km daleč. Pojav je prva
posnela sonda Casssini. Tam so detektirali tudi fosfor,
ortofosfat (PO43-), ki je za življenje zelo pomemben.
V vsaki galaksiji je vsaj nekaj milijard zvezd (v naši
Rimski cesti kar 200 do 400 milijard zvezd).
V vidnem vesolju je okrog 100 milijard galaksij kar da oceno
okrog 100*109*109 zvezd = 1021 zvezd v vesolju.
Ocenjuje se, da je okog 10 % vseh zvezd podobnih Soncu.
Zemlja je stara okrog 4,5 109 let, vesolje pa 13,8 109 let.
Večina galaksij je starih 12 109 let - skoraj 3x toliko kot je Sonce.
Torej, zdi se, da je kar veliko možnosti, da so še kje
podobni pogoji za razvoj življenja kot na Zemlji.
Sklepati je tudi možno, da so se kje razvile tudi naprednejše oblike življenja,
z višjo inteligenco, tehnologijo ...
Problem komunikacije med morebitnimi nezemljani - med civilizacijami Rimske ceste - je
oddaljenost, pričakovana nesinhronost pojavljanja življenja in najbrž
precej kratka doba razvitih oblik civilizacij (problem podnebja
na posameznih planetih ni zanemarljiv - Zemlja je rabila milijarde let,
da je omogočila razvoj človeka, ker atmosfera prej tega enostavno ni dovoljevala
zaradi premalo kisika, problem so bile različne sestave atmosfere
(zmeraj so prisotne povratne zanke vpliva življenja na sestavo atmosfere, tal in obraten
vpliv - torej spremenjene atmosfere na razvoj življenja - izjemno velik skok se je zgodil
pred približno pol milijarde let s pojavom večjega deleža kisika v ozračju zaradi
fotosinteze); potem so lahko problem pri nastanku ali obstanku življenja tudi
izrazite ledene dobe, tektonski premiki - potresi, vulkani, hladna in vroča obdobja, udari
asteroidov in kometov, umanjkanje magnetnega polja ...
Za življenje, kot ga poznamo na Zemlji, je osnovna sestavina izjemno topilo, to je voda H2O,
molekula, kjer kisik naše veže dva vodika (ali obratno).
Največja uganka je, kako je voda prišla na Zemljo. Ko je Zemlje bila mlada in vroča,
se zdi, da se voda ni mogla zadržati na planetu in pozneje tudi ne tvoriti.
Danes se veliko govori, da so vodo s sabo na Zemljo prinesli kometi med trki. Danes
so kandidati tudi temni kometi, ki nimajo prašnega repa in kome, so nek hibrid med asteroidom in kometom in se jih zato zelo težko opazi.
Ko se približajo Soncu, prihaja do sublimacije (prehod iz trdne v plinsko fazo) lahkohlapnih snovi.
Ta plinski potisk pa tako rahlo spreminja tirnico kometa - kot skromen naravni raketni pogon.
Tako se kometom, tudi temnim, spreminja orbita mimo Keplerjevih zakonov - in če jih je nekoč
dovolj trčilo z Zemljo (tudi z ostalimi planeti), so lahko s sabo prinesli tudi vodo, CO2 ...
Kometi in asteroidi so najbrž ostanki planetezimalov, majhnih teles, ki so na začetku
gravitacijsko gradila planete, lune. Tisti planetezimali iz protoplanetarnega diska,
ki se niso združili v večja telesa, so po formiranju planetov doživeli njihove gravitacijske plimske sile
(kot se recimo Luna zaradi plimskih sil počasi oddaljuje od Zemlje, cca 4 cm/leto). Te sile so asteroide
zbrale med Marsom in Jupitrom v asteroidni pas. Ostale bolj ledene
so potisnile v Kuiperjev pas za Neptunom
in še v bolj oddaljen Oortov oblak ledenih
teles - kometov, ki vsebujejo veliko ledu. Zaenkrat so to le teoretični odgovori,
ki pa čakajo na vzorce morebitne sonde, ki bi pristala na enem izmed temnih kometov. To bi se naj
zgodilo leta 2031 s pomočjo misije Hayabusa2, ki se bo srečala s temnim kometom 1998 KY26.
Takrat bodo vzorci, recimo razmerje izotopov v ledu, pokazalo, a ti modeli držijo.
Prvi tak temni komet so opazili 2017 - Oumuamua (k nam naj bi prišel iz medzvezdnega
prostora, kazal je tako lastnosti asteroida, kot kometa) - a leta 2025 jih poiznamo že 14.
Odstiranje resnice o vesolju, Zemlji in življenju, je torej v polnem zamahu.
Celica kot osnovna enota življenja - kompleksno povezovanje atomov
ob prisotnosti tekoče vode
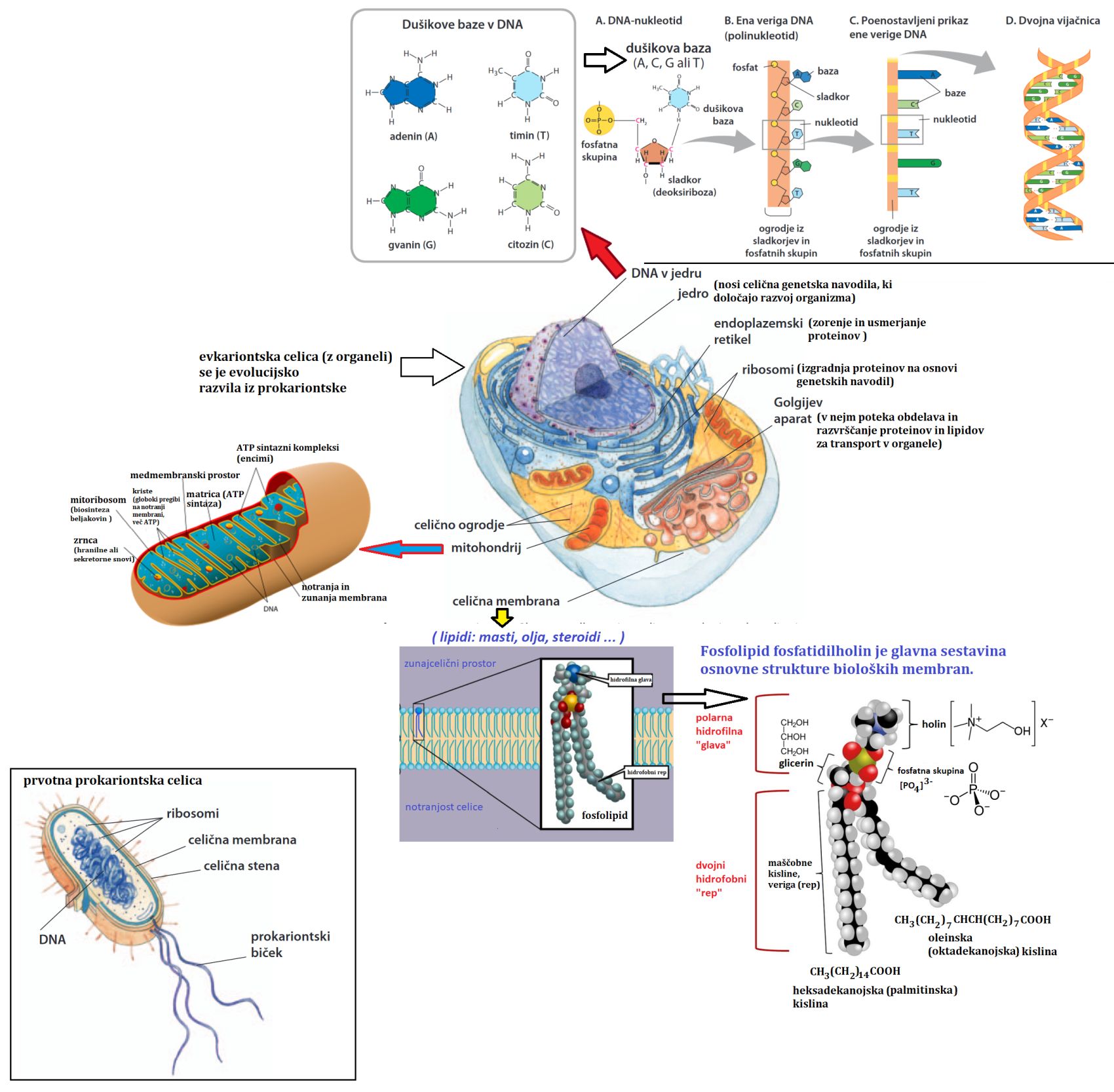
Celica je osnovna gradbena in funkcionalna enota živih organizmov. Glavna gradbena tipa celic
sta prokariontska celica (levo spodaj v okviru) in
evkariontska celica (preostali del slike, kjer so opisane tudi posamezne bistvene
podstrukture celice, recimo, membrana, jedro in mitohondrij).
Kot primer evkariontske celice je prikazana (naša) živalska celica.
Na sliki sta zelo nazorno kemijsko opisana zunanja membrana (obleka) celice
in jedro s kemično sliko dvojne vijačnice velike molekule DNA, ki je
pri vseh organizmih nosilec dedne informacije - pove nam, kakšni smo in kako bomo
živeli.
Če preštejemo število atomov v preseku dveh fosfolipidov, ki se dotikata z maščobnima repkoma in tvorita
membrane celic, je ta številka okrog 40 (sami preštejte na sliki).
Velikost tipičnega atoma je 10-10 m = 0,1 nm.
Če število atomov preseka celične membrane pomnožimo z velikostjo atoma 0,1 nm, dobimo za celično
membrano debelino okrog 4 nm, torej vsekakor pod 10 nm. Tako skromno molekularno debelino
pa lahko zaznamo le pod elektronskimi
mikroskopi. To samo kaže, kako tanke in fine strukture tvorijo osnovne gradnike življenja, to so celice.
Ena glavnih nalog membrane je zaščita dragocene vsebine celice (DNA - organskega računalnika,
kako se naj celica in organizem razvijata, delita ... ) in kako naj celica kontrolirano
komunicira z zunanjostjo
(prejema molekule, atome, torej energijo od zunaj in molekule presnove tudi vrača nazaj v okolje).
Temu tudi učeno rečemo, da membrana vzdržuje membranski potencial.
Namen te slike je dojeti, kateri gradniki - kemijski elementi, molekule - določajo, gradijo
izjemen pojav v vesolju, ki mu pravimo življenje. Izvor katerega iščemo že
stoletja. Kaj je bil sprožilec združevanja atomov v fenomen življenja, ki se
razmnožuje, delno kopira, a hkrati postaja skozi zgodovino vedno bolj kompleksno.
Prvotno imamo enostavne prokariontska celice, kot samostojna enocelična bitja (bakterije in arheje),
nato se razvijejo evkariontske celice, ki se združujejo v rastline in v vse večcelične
živali.
Obstajajo tri vrste evkariontske celice, živalska, rastlinska in celica gob (gliv),
ki se nekoliko razlikujejo v celični zgradbi.
Tipična evkariontska celica je ovalne oblike in rastlinska celica je velika
do 100 μm
(povprečna človeška celica pa 10-20 μm).
S svetlobnim mikroskopom (povečava do 2000×) vidimo celico kot vrečasto tvorbo,
ki je obdana s celično membrano, izpolnjena s citoplazmo in ima celično jedro. Z elektronskim mikroskopom
(povečava do 1.000.000×) lahko opazujemo podrobno zgradbo celičnih organelov (ribosomi, lizosomi,
endoplazemski retikulum, Golgijev aparat, mitohondriji, strukturo celične membrane ...), ki opravljajo različne naloge.
Fosili, ki so jasno povezani s sodobnimi oblikami življenja, so se po ocenah začeli
pojavljati pred približno 1,2 milijarde let v obliki rdečih alg, čeprav nedavna odkritja
kažejo na obstoj fosiliziranih nitastih alg v porečju Vindhya, ki segajo morda pred 1,6
do 1,7 milijarde let.
Evkariontske celice povezujemo s prvimi geološkimi zapisi pojava znatnega deleža
molekularnega kisika med velikim oksidacijskim dogodkom ( Great Oxidation Event (GOE),
pred približno 2,45 – 1,85 milijarde let, glej graf
nalaganje kisika O2 v zemeljski atmosferi (v procentih) skozi razvoj Zemlje ).
Vir slike: kombinacija http://vedez.dzs.si/datoteke/bio-celice-izbrano.pdf, ostali spletni viri
Glavni trik, ki je omogočil življenje, je (samo)oblikovanje
organskih "ogljikovih" molekul, ki jih voda ne topi. To so recimo maščobe, olja
in zato je na sliki posebej poudarjena
celična membrana iz fosfolipida fosfatidilholina, kjer se lepo
prikazani lipidni dvosloji, ko se hidrofobni repi (maščobe, ki ne prepuščajo vode)
poravnajo drug proti
drugemu in tvorijo membrano hidrofilnih glav (ki se vežejo z vodo) na obeh straneh membrane, obrnjenih
proti vodi. Fosfolipidi so tako maščobne ovojnice (membrane) celic s hidrofilno glavo,
ki na tak način tvorijo življenje v simbiozo z vodo,
ki je odlično topilo, a ne topi maščobnega dela lipidnih dvoslojnih membran.
Glede na naboj ima torej fosfolipid hidrofilno glavo (se veže z vodo) in hidrofobna repa (ne prepuščata vode).
Hidrofilna glava je sestavljena iz glicerina in fosfata (na katerega je
vezana organska skupina), takšen hidrofilni del pa je nosilec električnega
naboja, ki privlači dipolne molekule vode. Hidrofobni "repi"
(dve dolgi verigi ogljikovodikov, ena nasičena in druga nenasičena), sestavljeni torej
iz dveh maščobnih kislin pa niso naelektreni in se zato ne raztopijo v vodi.
Zato se fosfati fosfolipidov v vodi vedno obračajo proti vodi, maščobne kisline pa druga proti drugi
(neke vrste samoorganizacija potencialnih bodočih molekul celičnih membran ...).
Na ta način
se ustvari dvojna plast fosfolipidov, ki v konstrukciji membran preprečuje nekontroliran
izhod (vhod) tekoče vsebine.
Seveda celice morajo komunicirati z okolico, tudi druga z drugo, zagotovo preko žilnega sistema s krvjo,
delno z atmosfero v dihalnem sistemu ...,
a to počne kontrolirano.
Membranski transport lahko poteka direktno skozi lipidni dvosloj
(predvsem prenos majhnih nenabitih nepolarnih molekul, kot so O2, CO2, N2 ali benzen),
preko posebnih proteinskih
kanalčkov v membrani (ioni, majhne nenabite polarne molekule, kot so glicerol ali H2O),
preko proteinskih prenašalcev (ioni, velike nenabite polarne molekule, kot so glukoza, fruktoza)
in preko proteinskih črpalk (ioni).
Hitrost prenosa ionov preko kanalčkov je okrog
1 000 000 ionov/s (to je izjemna številka),
so pa izmed vseh transporterjev najmanj selektivni.
Transport je seveda tudi odvisen od gradientne razlike snovi na obeh straneh membrane,
kar tudi imenujemo kemijski gradient. Imamo še aktivne transporte skozi membrano v smeri večje koncentracije
(ker je proces entropijsko neugoden, je stehiometrično sklopljen s hidrolizo ATP).
Poznamo še nemembransko
endocitozo in
eksocitozo - pri obeh so molekule zaprte v membranske vezikle ("mehurčki" z membrano
iz fosfolipidnega dvosloja), ki jih celica uvozi ali izvozi.
Vsaka celica v človekovem telesu vsebuje okoli milijardo molekul ATP (adenozin trifosfat) in energija,
ki jo nosijo s seboj je bistvenega pomena za mnoge reakcije in funkcioniranje vsake celice.
ATP je sestavljen iz adenozina (adenin in riboza), ter treh verižno vezanih fosfatnih ostankov,
povezanih z fosfoanhidridnimi vezmi. In prav v teh vezeh se skriva kemijska energija, ki se sprošča pri hidrolizi.
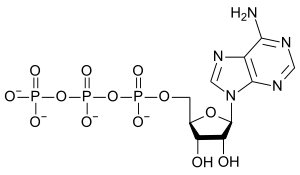
Adenozin trifosfat - ATP, koencim. Vsaka molekula ATP je dnevno obnovljena 1000 do 1500 krat. Sedaj tudi lahko slutimo, zakaj se koencimi tako dobro prodajajo v lekarnah in drugod. Recimo koencim Q10 - pravijo mu tudi ubikinon, ki se primarno nahaja na notranji mitohondrijski membrani, kjer je nujno potreben za produkcijo ATP (ki daje, kot smo že omenili, energijo za vse vitalne celične funkcije). ATP je sestavljen iz adenozina (adeninski obroč, povezan s sladkorjem ribozo) in treh fosfatnih skupin (trifosfat).  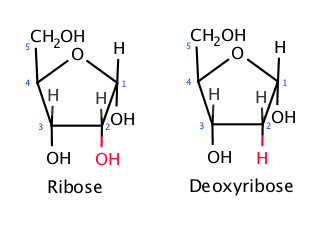
Pri fosfatnih vezeh se energija pridobiva s celičnim procesom fosforilacije. Fosforilacija je proces, pri katerem se dodatni fosfat veže na adenozin monofosfat (AMP) z energijsko bogato vezjo in nastane adenozin difosfat (ADP). Proces se ponovi, ko se še en fosfat veže na drugega v ADP in nastane še tretja energijsko bogata fosfatna vez (dobimo ATP). Proces fosforilacije poteka v mitohondrijih, energija, vložena v vezi, pa je energija, pridobljena s celičnim dihanjem. |
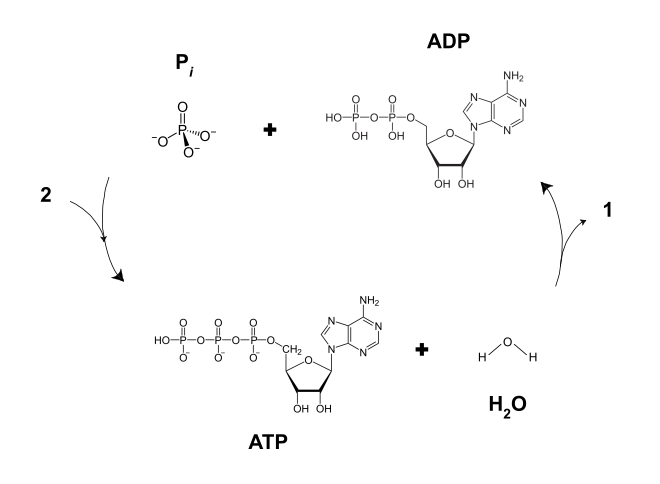
Cikli sinteze in razgradnje ATP; fazi 2 in 1 predstavljata vnos (obnovo) in izhod energije. |
 |
 |
 |
 |
 |


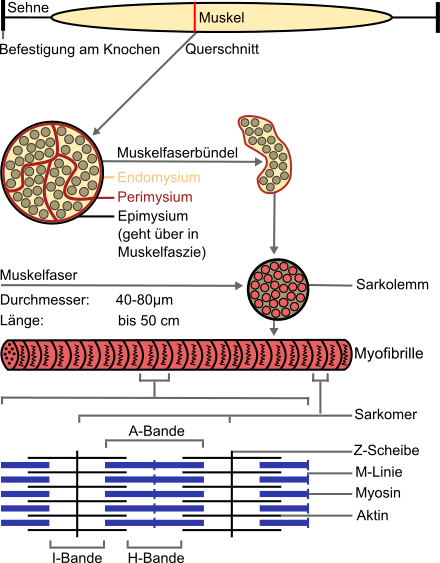
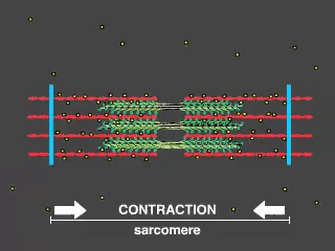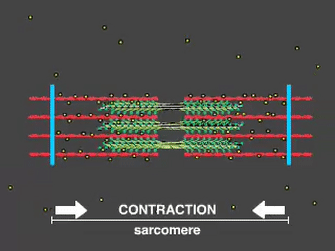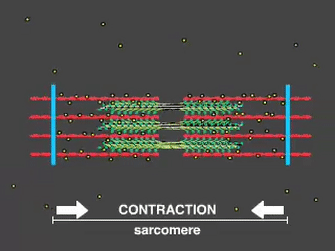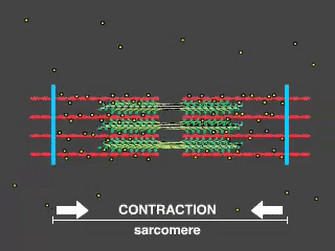


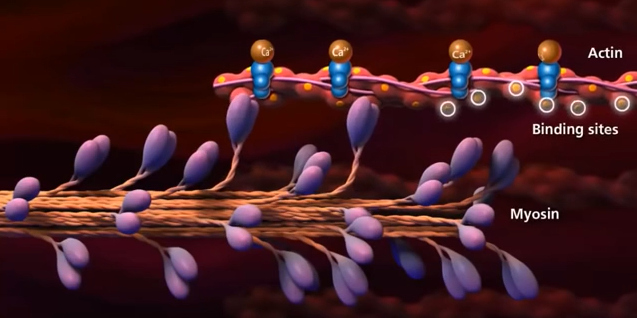
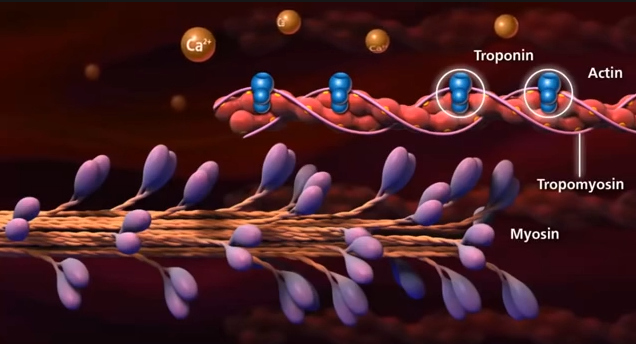
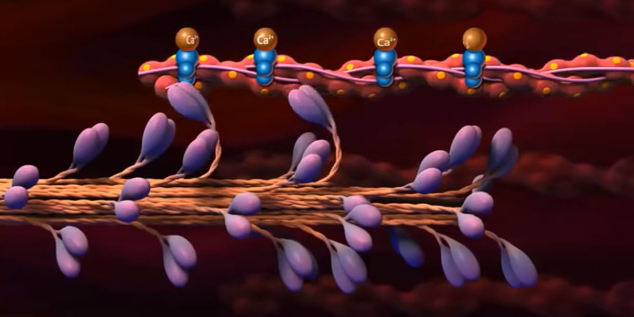
L_M_BV_32 := TBD.T_ENTIER_32S ((1.0/C_M_LSB_BV) * G_M_INFO_DERIVE(T_ALG.E_BV));
if L_M_BV_32 > 32767 then
P_M_DERIVE(T_ALG.E_BV) := 16#7FFF#;
elsif L_M_BV_32 < -32768 then
P_M_DERIVE(T_ALG.E_BV) := 16#8000#;
else
P_M_DERIVE(T_ALG.E_BV) := UC_16S_EN_16NS(TDB.T_ENTIER_16S(L_M_BV_32));
end if;
P_M_DERIVE(T_ALG.E_BH) :=
UC_16S_EN_16NS (TDB.T_ENTIER_16S ((1.0/C_M_LSB_BH) * G_M_INFO_DERIVE(T_ALG.E_BH)));
Vir:
https://itsfoss.com/a-floating-point-error-that-caused-a-damage-worth-half-a-billion/
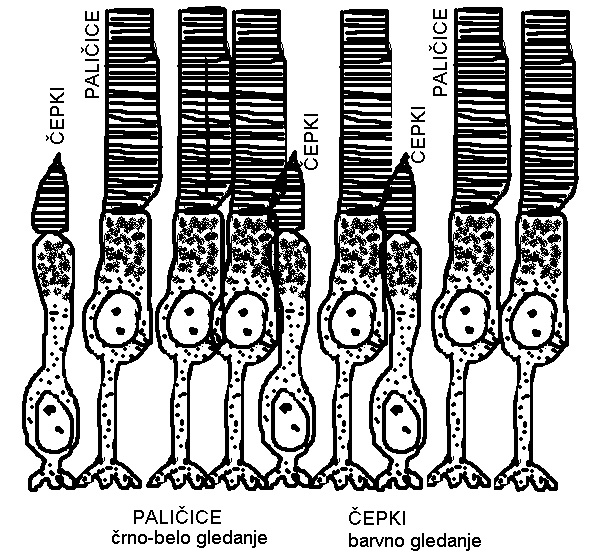
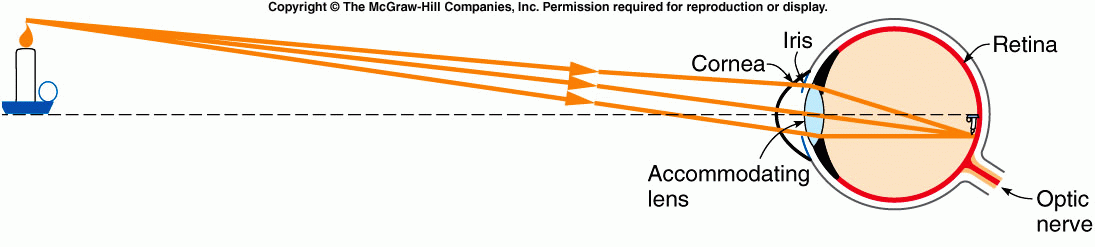




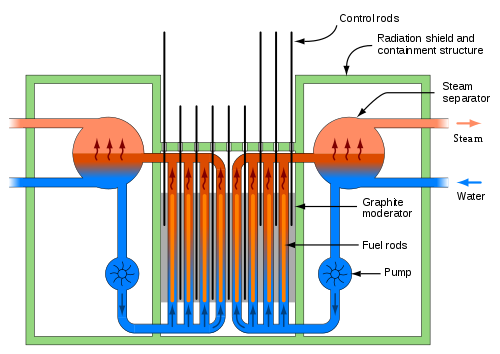





Molekula vode je izjemno topilo in toplogredni plin. Zelo didaktična prispodoba
vode – desno (vodika sta pozitivna učka – kisik pa ima negativna usta).

Tetraedrska struktura vode. V molekuli vode zveznici vodik - kisik tvorita kot 104,5 °.
Atoma vodika sta blizu dveh vogalov tetraedra, glede na kisik. Na drugih dveh vogalih sta
samotna para valenčnih elektronov, ki ne sodelujeta pri povezovanju. V popolnem tetraedru
bi atomi tvorili kot 109,5 °, vendar je odboj med osamljenimi pari elektronov večji kot
odboj med vodikovima jedroma. Dolžina vezi O-H je približno 0,096 nm.
Kisiku smo že večkrat pripisali izjemno vlogo, a večkrat slišimo, da je bistvo življenja voda –
H2O. Oboje drži – tudi vodo tvori kisik. A voda ima še vrsto ostalih izjemnih
lastnosti (omenimo dve, je toplogredni plin in odlično topilo, oboje pa je za življenje
pomembno) - ima tudi izjemno zanimivo obliko črke V. Dve anteni vodika štrlita s kisika v oglišču (in tako lahko
voda učinkovito absorbira dolge toplogredne valove). Zakaj je dobro topilo? Ker ima oglišče,
kjer je kisik, neto negativen naboj (dva elektrona sta namreč skočila na kisik iz vodika),
vrhova (rogova) črke V, kjer čepita vodika pa imata nekoliko pozitiven naboj, saj je vsak
svoj elektron posodil kisiku. S tem izrazitim kazanjem naboja, voda raztrga skoraj vse
molekule, ki so v bližini – recimo sol, NaCl. Kisikova stran V molekule vode pograbi
natrij (Na je v molekuli soli rahlo pozitiven, ker je svoj zunanji elektron posodil
kloru), vodik iz vode pa zagrabi klor (ki je v molekuli soli rahlo negativen zaradi
elektrona, ki mu ga je podaril natrij) in tako voda molekulo soli razbije. Še bi lahko
naštevali – z vodo se tudi umivamo, ker dobro topi umazanijo. V naših celicah voda dovaja
hrano, odvaža odpadke, združuje ostale molekule v nove snovi pomembne za delovanje celic,
skozi ožilja tvori cirkulacijo za oskrbovanje celotnega telesa in odvoz odpadkov oksidacije,
itn – je neke vrste tekoči trak življenja. Kar 70 % našega telesa sestavlja voda.
In ni čudno, da se je življenje najprej razvilo v morjih, in ko so živali imele
(razvile) dovolj stabilno kožo, so počasi pricapljale na kopno, kjer pa nas je dodatno začel ščititi pred sevanjem Sonca
še novonastali ozon O3 - trikisik.
Če je voda dobro topilo, zakaj je potem sploh nastalo življenje?
Tisto, kar pa je poseben trik življenja, so organske "ogljikove" snovi,
ki jih voda ne topi, to so recimo maščobe, olja.
Še enkrat torej ponovimo osnovne gradnike življenja na Zemlji.
Med organskimi molekulami so zagotovo pomembne:
- aminokisline
(za beljakovine; aminokislina je molekula,
ki vsebuje tako aminsko (–NH2) kot karboksilno (–COOH) funkcionalno skupino;
v biokemiji se ta krajši in splošnejši termin pogosto uporablja za α-aminokisline
– aminokisline, pri katerih sta aminska in karboksilna skupina vezani na isti ogljikov atom. ),
- lipidi
(masti, olja, steroidi ... - lipidi predstavljajo velike biomolekule iz sestavljanke atomov C, H, O,
ki vežejo nase recimo še fosfor P, dušik N ...,
med
glavne funkcije lipidov spadajo shranjevanje energije, celično ter tkivno
signaliziranje in gradnja celičnih membran, kjer se zadržuje tudi voda
- pomembno je torej, da lipidi niso topljivi v polarni vodi, so
pa topljivi v nepolarnih organskih topilih, rec. heksan
CH3(CH2)4CH3),
- nukleotidi
(so osnovni gradniki nukleinskih kislin DNK in RNK,
sestavljeni so iz sladkorja (pentoze C5H10O5- ogljikovi hidrati),
dušikove baze in fosfatne skupine ...,
Genski inženiring - ko se igramo Boga?
Ali je to prav - pogojno sprejemljivo je le pod zelo strogimi pogoji in cilji - recimo odprava določenih napak, hib ...!
Slika je simbolična - kaže pa bistvo genskega inženiringa -
umetno poseganje v sestavljanje molekulo DNK iz različnih zaporedij nukleotidov!
Nukleotidi so osnovni gradniki nukleinskih kislin DNK in RNK. Nukleotid je sestavljen iz sladkorja
(pentoze), dušikove baze in fosfatne skupine.
V DNK je prisotna 2'-deoksiriboza, v RNK pa riboza.
Na sladkor je preko N-glikozidne vezi vezana dušikova baza. Ta je lahko adenin (v DNK ali RNK), gvanin
(v DNK ali RNK), citozin (v DNK ali RNK), timin (samo v DNK)
in uracil (samo v RNK). Sladkor in dušikova baza skupaj tvorita nukleozid, če pa je na sladkor vezana
še fosfatna skupina, dobimo nukleotid.
Nukleotidi se povezujejo v nukleotidno verigo (nukleinsko kislino) preko fosfodiesterskih vezi,
natančneje: 3'-OH skupina enega nukleotida se poveže s 5'-fosfatno skupino naslednjega nukleotida.
To je torej zapis podobe in vedenja življenja na Zemlji na atomski ravni - zapis bitij, ki zrejo tudi v vesolje.
Kitajci, v sodelovanjem z zahodnimi znanstveniki, so že spremenili
sekvenco človeške DNK - da sta se rodili dvojčici odporni na HIV.
Postopek in spremljanje rezultatov sta se zelo zapletla - ne vemo, kaj se dogaja z zdravnikom He Jiankui-jem
in otročičkoma iz 2018 - genom spremenjen z gensko tehnologijo CRISPR-Cas9.
Gensko inženírstvo je tehnologija, ki omogoča gensko rekombinacijo oziroma umetno sestavlja
molekulo DNK iz različnih zaporedij nukleotidov. Gre za uporabo različnih in številnih tehnik izolacije
genov in genetskih elementov, njihovo in vitro ali in vivo prekonstruiranje in razvrščanje v nova zaporedja
ter njihovo namnoževaje z molekulskim in celičnim kloniranjem.Če se nova hibridna ali rekombinantna
DNK vstavi v gostiteljsko celico, lahko celica ustvari beljakovino, ki je sicer ne bi proizvajala.
Organizmi, ki so ustvarjeni s pomočjo tehnik genetskega inženirstva, so gensko spremenjeni organizmi.
Prvi gensko spremenjeni organizmi so bile bakterije, ustvarjene leta 1973, gensko spremenjeno miš so
ustvarili leta 1974. Leta 1982 so na tržišče uvedli bakterije, ki izdelujejo inzulin, od leta 1994 pa
se na tržišču pojavlja gensko spremenjena hrana. Leta 2003 so začeli prodajati prvi gensko spremenjeni
organizem, ustvarjen za hišnega ljubljenčka, in sicer ribico Glofish.
Tehnike genetskega inženirstva se uporabljajo na številnih področjih, in sicer v raziskavah,
kmetijstvu, industrijski biotehnologiji in medicini.
Priprava rekombinantne DNK
DNK lahko pripravimo na več načinov: s kemično sintezo, s pomočjo restrikcijskih endonukleaz iz daljšega
fragmenta DNK ali z verižno transkripcijo mRNK. Najpogosteje se uporablja rezanje DNK na več fragmentov
s pomočjo endonukleaz.
Metoda CRISPR-Cas9?
CRISPR-Cas9 so prepoznali v bakterijskem »imunskem sistemu«,
ki omogoča bakterijam učinkovito obrambo proti virusni DNK. Princip prepoznave in razreza virusne
DNK so znanstveniki iz bakterij prenesli tudi v druge organizme za namen genskega inženiringa.
Mogoče ga je sprogramirati tako, da na določenem mestu v genomu razreže točno določeno gensko zaporedje.
Če celici hkrati ponudimo še ustrezen nadomestek za uničeno DNK, dobimo gensko spremenjeno celico po svojem okusu.
Delovanje sistema CRISPR je sestavljeno iz dveh delov: majhnega dela RNK in Cas9, encima, ki deluje kot škarje
za rez v DNK, in sicer na mestu, kamor ga usmeri kratka veriga RNK. S tehnologijo vsiljenega gena se modifikacija
po vnosu na tarčno mesto širi naprej pri potomcih z »rezanjem« tarčnega mesta v spolnih celicah. Tako se vsiljeni
gen prenese na skoraj sto odstotkov potomstva.
Sedaj, ko poznamo osnovne gradnike naših celic, ki so prvotno nastale
v tekočini življenja, v vodi, sledi naslednje pomembno vprašanje.
Kdaj torej stopimo na kopno ali se celo vračamo nazaj v morja?
Ko so vodne rastline preko fotosinteze ustvarile dovolj kisika (ki se je prvotno milijarde let
vezal na druge atome, železo, v
kalcijev karbonat CaCO3, v mnoge minerale ...), se je pojavil tudi ozon,
ki ščiti kopenske rastline in živali pred smrtonosnim UV-C sevanjem, delno pred UV-B, prepušča pa UV-A sevanje.
Nekaj milijonov let po tem, ko so kopno naselile prve rastline in so tako poskrbele za dovolj kisika in hrane,
so na kopno prišle tudi prve živali.
To so bili členonožci, predniki pajkov, stonog, rakov ...
Vretenčarji pa so rabili še nekaj več časa in domneva se, da preko omenjenih rib
mesnatoplavutaric.
Enocelične diatomeje predstavljajo največji del mase fitoplanktona.
Glede na nedavne raziskave se zdi, da je absolutno največ ogljikovega
dioksida vezanega v rastlinskem planktonu in ne, kot se je doslej mislilo,
v tropskih gozdovih (proizvajajo do 50 % vsega kisika).
Kar je seveda logično - živali na kisik (vretenčarji, ribe -
naši predniki) so nastali v vodi, še preden je na kopnem bilo prisotno rastlinstvo.
Torej so cianobakterije (te bakterija proizvedejo kar do
20 % kisika v celotni biosferi), alge v morjih ustvarile dovolj kisika za razvvoj
življenja v morjih in pozneje na kopnem. Kar seveda ne pomeni, da gozdovi, rastlinstvo
na kopnem niso pomembni, a potrebno se je zavedati, da so oceani bili in bodo
odločilni izvori kisika na Zemlji. Oceani so najpomembnejši ekosistemi na Zemlji (pazimo nanje).
Zaporedje dogodkov, prvoten in bistven izvor kisika v oceanih, se premalo poudarja v celostni sliki
razvoja in obstoja življenja na Zemlji. To je velika škoda za pravilno
razumevanje razvoja življenja,
atmosfere in kopnega na Zemlji.
Najstarejši znani fosil kopenske rastline je star 420 milijonov let (Cooksonia - velika za mezinec).
A predvideva se, da
so kopno rastline poselile že nekaj 10 milijonov let prej.
Pred približno 450 milijoni let so kopno poselile prve mnogocelične živali,
pajkovci, stonoge, rakci ... Žuželke so nastale iz rakov pred približno 400
milijoni let.
Najzgodnejše delno kopenske štirinožne živali (akantostega - prevod "bodičasta streha" in recimo ihtiostega)
so bile dolge nekje okrog
enega metra in še kaj več. Večinoma sta živeli v vodi - lahko sta lezli tudi po kopnem ...
Pojavili sta se približno pred 370 milijoni let.
Prvi vretenčarji, katerih potomci pa so ostali na kopnem do danes
pa so na kopno prišli približno pred 360 milijoni let.
Takrat je naš prednik naredil prve korake v relativno hitrem razvoju vretenčarjev v skupino sesalcev (poleg ostalih
vrst).
Prvi sesalci (v Kempovem smislu) so se pojavili v poznem triasu (pred približno 225 milijoni let),
40 milijonov let po prvih terapsidih. Iz izrazite žužkojede niše so se razširili od sredine jure in naprej;
jurski castorocauda pa je bil že bližnji sorodnik pravih sesalcev, ki so bili že prilagojeni za plavanje in
tako tudi za lovljenje rib.

Pristerognathus, terapsidi velikosti mačk.

Sesalec castorocauda - obdobje: srednja jura
pred 174,1 do 163,5 milijoni let.
Je najzgodnejša najdena žival s krznom.
Še o rastlinah, ki jih srečujemo v gozdovih, na kamnih, na drevesih in spadajo
med najstarejša kopenska bitja, rastline - to so mahovi, ki so nastali iz zelenih
alg (groba ocena starosti je okrog
470 milijonov let) in so tako nekako logično povezani tudi s povečano vlago.
Ko tako hodimo po mahu, se ga dotikamo,
smo v kontaktu praktično s prvim življenjem na kopnem, izjemno - to si velja zapomniti.
Samo v Sloveniji najdemo več kot 800 vrst mahov ( po ocenah pa obstaja približno 12000 vrst mahov ).
Še zanimivost.
Nedavne raziskave kažejo, da bi starodavni mah lahko pojasnil,
zakaj so nastopile ordovicijske ledene dobe
(ordovicij traja 41,6 milijonov let, od konca kambrijskega obdobja
pred 485,4 milijona let, do začetka silurskega obdobja pred 443,8 milijona let).
Ko so se predniki
današnjega mahu pred 470 milijoni let začeli širiti po kopnem, so absorbirali CO2
iz ozračja in črpali minerale z izločanjem organskih kislin, ki so topile kamnine,
na katerih so rasli. Te kemično spremenjene kamnine so nato reagirale z atmosferskim
CO2 in oblikovale nove karbonatne kamnine v oceanu s preperevanjem kalcijevih in
magnezijevih ionov iz silikatnih kamnin. Preperele kamnine so sprostile tudi
znatne količine fosforja in železa, ki so končali v oceanih, kjer so povzročili
množično cvetenje alg, kar je povzročilo ponikanje organskega ogljika,
posledično pa se je iz ozračja črpalo še več ogljikovega dioksida. Majhni organizmi, ki so se
hranili s temi hranili, so ustvarili velika območja brez kisika, kar je povzročilo množično
izumrtje morskih vrst, medtem ko so ravni CO2 padle po vsem svetu
(in s tem je padla tudi temperatura, saj je CO2 toplogredni plin,
in če ga je manj v atmosferi, temperature
v spodnjih plasteh padejo,
kot da bi si ljudje pozimi slekli plašč na prostem), kar je omogočilo
nastanek ledenih kapic na polih.
Še o lišajih.
Lišajem podobni fosili, sestavljeni iz kokoidnih celic (cianobakterij?) in tankih filamentov
(mucoromycotinan Glomeromycota?), so permineralizirani v morskem fosforitu formacije Doushantuo
na južnem Kitajskem. Ti fosili naj bi bili stari vsaj od 551 do 635 milijonov let.
Prvotni lišaji pa so najverjetneje precej starejši.

Mahovi in lišaji so med prvimi kopenskimi prebivalci.
Preprosta slika, ki posredno in slikovito povezuje razvoj vesolja, življenja na Zemlji,
življenja na kopnem v zadnjih skoraj 500 milijonov let. Na kopno so najprej prišle
rastline, med prvimi so se razvili mahovi (na sliki), nato živali, ki danes preko človeka
(lastne tehnologije - na sliki mobilni telefon)
raziskujejo ta naše začetke na kopnem, v vodi in v vesolju.
Zmeraj znova se tudi sprašujemo, zakaj to počnemo ...?
Več je ocen, koliko lahko trajajo pogoji na Zemlji za visoko razvito življenje (vretenčarji, ljudje).
Ena od ocen omenja dobro milijardo let - torej je pred nami še dobre pol milijarde let, časa,
da preživimo to obdobje in se potem nekako preselimo na lune, planete (Mars) v naši okolici,
oz. še kam dlje - ali bo
zanamcem uspelo, držimo pesti.
Za časa rimskega cesarja Avgusta je bilo na Zemlji okrog 200 milijonov ljudi,
v srednjem veku leta 1000 pa okrog 300 milijonov ljudi. Leta 1800 smo dosegli
milijardo ljudi - danes - po dobrih 200 letih pa že kar 8
milijard ljudi. In koliko nas Zemlja prenese, lahko nahrani, da dolgoročno ohranimo še ostale
ekosisteme?
 |
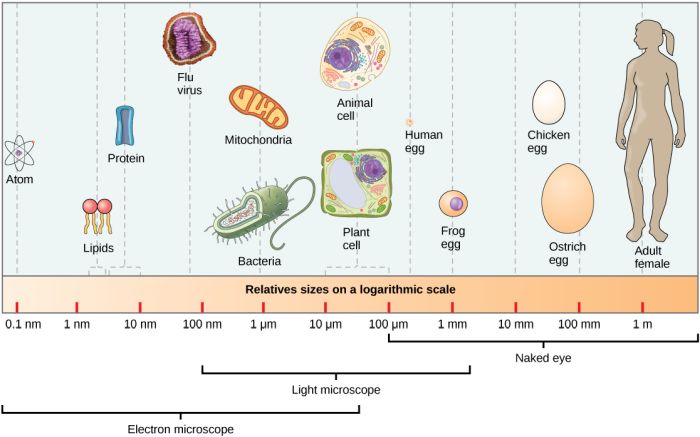
|


Po razlagi osnov življenja, oksidacije (ognja, oksidcije hrane v živih bitij) lahko pride na vrsto seveda življenje v
vesolju (eksoplaneti, metode detekcije, naselitveni pas okrog zvezd,
enačba Franka Draka o verjetnem številu civilizacij v naši Galaksiji),
pomen ekologije. Zakaj trenutno še nismo bili uspešni pri iskanju razvitih
civilizacij v naši galaksiji (ali obstajajo)? Koliko časa pa sploh obstaja
življenje na kisik, koliko časa smo ljudje na Zemlji in koliko časa imamo
tehnologije za komunikacijo na daljavo? Kakšna pa bi naj bila bitja, ki
recimo prebivajo na enem izmed eksoplanetov? Ali bi morala dihati kisik,
kakšna pa so bitja na Zemlji, ki za oksidacijo ne uporabljajo kisika?
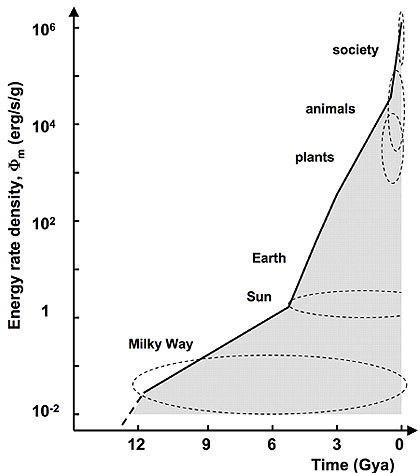
Chaisson je pokazal, da se znotraj vsakega od zapletenih sistemov vesolja (Rimska Cesta,
Sonce, Zemlja, rastline, živali, družba, računalniki ...), njegova metrika kompleksnosti
začne z majhno stopnjo, nato pa se razvija in s časom narašča (čas je podan v milijardah let).
Zato recimo naši možgani na gram mase oddajajo stotisočkrat več energije kot
Sonce na gram svoje mase (govorimo o stacionarnih procesih, to ne velja za trke ali eksplozije, recimo
supernov).
Vir: https://www.informationphilosopher.com/solutions/scientists/chaisson/
Opomba: erg je fizikalna enota za energijo v sistemu cgs (tudi sistem enot centimeter-gram-sekunda), ki je enaka 10-7 J (ali 1 erg =10-7 J = 100 nJ).
Eric Chaisson je
astrofizik in kozmolog, ki predlaga novo metriko
za kompleksnost v različnih kozmoloških in bioloških sistemih. V svoji knjigi iz
leta 2001, Cosmic Evolution: The Rise of Complexity in Nature, Chaisson trdi,
da imajo vsi organizirani sistemi skupne generične pojave, ki označujejo njihov nastanek,
razvoj in evolucijo.
Drugi misleci so se zavzemali za podobnosti in homologije v vseh razvijajočih se sistemih, vendar Chaisson predlaga enotno "metriko kompleksnosti", ki lahko količinsko opredeli glavne spremembe v kozmoloških in bioloških časovnih lestvicah.
Chaissonova metrika kompleksnosti je "gostota stopnje energije", pretok energije na sekundo
in na gram materiala v danem sistemu. Tako Sonce v svoji jedrski
notranjosti ustvari 4 x 1033 ergov/sekundo in ima maso 2 x 1033
gramov, tako da je Chaissonova metrika kompleksnosti za Sonce 2 (erg/s/g).
Naredimo še oceno za možgane. Možgani tehtajo od 1.2 do 1.4 kg in rabijo okrog 20 W moči za delovanje.
Če naredimo zgolj grobo oceno gostote energije na gram, dobimo: 20 W/1000 g = 20 107 erg /1000
= 200 000 (erg/s/g).
Možganska skorja, ki je največji del možganov, pri povprečnem človeku šteje od 15 do 33
milijard nevronov. Vsak se s sinapsami povezuje z več tisoč drugimi nevroni.
Ti nevroni komunicirajo med seboj prek nevritov,
ki prenašajo akcijski potencial do oddaljenega predela možganov ali do tarčne celice.
Res občudovanja vreden organ, ki nam daje skoraj vse komande, ustvarjalnost in smisel življenja ...
Chaisson ne uporablja mase planeta Zemlje v svoji masno normalizirani meritvi stopnje energije iz dveh razlogov. Prvič, toplota, ki jo proizvede Zemlja v notranjosti, je majhen del vpadnega sončnega sevanja. Drugič, sončna energija se odlaga v površinsko plast atmosfere in biosfere, iz katere se ponovno seva v temno nočno nebo, ko se zemlja obrača.
Tok sončne energije, ki pada na Zemljo, je približno 2 x 1024 ergov/sekundo. Chaisson uporablja maso atmosfere in plasti vode v oceanih kot maso ustreznega kompleksnega sistema, pri čemer izpelje gostoto hitrosti energije približno 75 (ergs/sec/gm).
Chaisson nato oceni metrike kompleksnosti za rastline, živali, človeške možgane in produkt naših možganov – družbo kot celoto.
Informacije in kompleksnost
Chaisson ugotavlja, da so dosedaj uporabljali informacije kot merilo zapletenosti.
Pravi, "do katere mere je sistem urejen, je mogoče oceniti s sklicevanjem na informacijsko
teorijo; bolj ko je sistem urejen, večjo informacijsko vsebino
(ali negentropijo / negativno entropijo) ima.
" (Kozmična evolucija, str.127)
Pravi tudi, da je "potreben (čeprav ne nujno zadosten) pogoj za rast informacij zagotovljen
s samo širitvijo vesolja." (str.128)
Če se plin ne bi ohladil, ne bi nastale zvezde, ki so lokalno zmanjšale entropijo
(le v hladnem veoslju gravitacija
lahko združuje velike oblake plina v "majhne" zvezde in planete)
in tako so nastali težji atomi, kamniti planeti,
rastline, živali, razumna bitja, ki lahko naredijo stroje, računalnike ...
Preberi si tudi poglavje o entropiji.
Na začetku, ko so
prvotna atomska jedra razpadla, so šla iz prvotnega ravnotežja, so njihove reakcije še vedno povzročale
povečanje entropije (predvsem z ustvarjanjem novih fotonov in nevtrinov, kot se bo to
kasneje dogajalo v jedrih zvezd), vendar ta povečanja niso zadostovala za ponovno
vzpostavitev ravnovesja. v skladu s tem se je razkorak med dejansko entropijo S
in največjo možno entropijo S, ki bi lahko bil dosežen, če bi bilo ravnovesje
ponovno vzpostavljeno, še povečal, s čimer se je povečala prosta energija, ki
se bo sprostila (se sprošča) veliko kasneje, ko so se zvezde že oblikovale. Tako torej
dobimo vpogled v izvor proste energije; to ni neka nova energija kot taka,
temveč na novo preurejena energija, ki je nato na voljo za uporabo
v teku evolucije zvezd, fuzije, ob tvorbi planetov, življenja na njih ...
Iz analiz se razbere, da se veliki koristniki energije na gram lastne mase
nahajajo v zelo majhnih delih vesoljske snovi (recimo v ljudjeh na Zemlji, ki smo naredili
še bolj kompleksne naprave, računalnike ...).
Smo torej neke vrste prviligiranci znotraj majhnega koščka vesolja
in zato smo tudi sploh lahko tako biološko-fizikalno urejeni,
s kompleksnim telesom in možgani - zmožni izjemnega ustvarjalnega delovanja - kot občestvo, skupnost.

Grafi razvoja vesolja glede na čas, temperaturo in energijo: t (Planckov »prvi«
čas 10-44 s),
T (začetna temperatura 1032 K)
in E = kBT (začetna energija 1019 GeV)
- t, T, E
grafi so izjemno učinkovita in strnjena metoda za učenje osnov
kozmologije in hkrati fizike osnovnih delcev.
Pri tem pogledu na razvoj vesolja je človek le obrobni dogodek (slučaj)
v izjemno bogati zgodovini razvoja prostor-časa: veliki pok, hitra širitev vesolja (inflacija),
osnovni delci, hitro ohlajanje, nastanek vodika in helija, meglic, prevlada gravitacije nad sevanjem,
posledično nastanek zvezd, galaksij,
težjih atomov pri visokih temperaturah v sredicah zvezd - med fuzijo.
Pojavijo se eksplozije supernov, trki zvezd, izmet težkih elementov v prostor,
posledično nastanek novih zvezd z znatno vsebnostjo
težjih elementov in tudi nastanek kamnitih planetov ..., z določeno verjetnostjo nastanka življenja na njih
(odvisno od razdalje planet - zvezda, od prisotnosti vode, atmosfere ...).
Taka slika kozmološke podobe razvoja vesolja do človeka bi morala viseti v vsaki učilnici.


|
 |

Sprememba sestave ozračja zaradi pojava kisika (vzrok so bile cianobakterije)
je posledično s sabo prinesla tudi podnebne
spremembe. Novo nastali prosti kisik je reagiral z metanom
CH4
(močan toplogredni plin), nastal je ogljikov dioksid (šibkejši toplogredni plin)
in voda. Koncentracija metana v atmosferi se je močno zmanjšala (zato se je
Zemlja začela ohlajati), kar je sprožilo huronsko poledenitev (pred 2.4 do
2.1 milijarde let) in verjetno najdaljše obdobje celotne poledenitve planeta
v zgodovini. Poledenitev je trajala od 300 do 400 milijonov let.
IN - kako se je ta ledena doba končala - sledi zanimiv scenarij. Med huronsko
ledeno dobo naj bi bila Zemlja prvič popolnoma prekrita z ledom, kar je praktično
ustavilo fotosintezo. Zelo se je povečala odbojnost (albedo) Zemlje. Ker ni bilo
fotosinteze, ni bilo ponorov CO2 in ta toplogredni plin se je dodatno
kopičil iz vulkanskih izbruhov in zelo, zelo počasi se je začela atmosfera le
segrevati in led se je tako začel tajati. Zanimivo - CO2 nas je že
rešil pred ledeno smrtjo - a nas lahko tudi pokoplje v vročini tople grede ...?
Ne smemo tudi pozabiti, da so ognjeniki na začetku Zemlje bistveno spremenili geološko sestavo planeta,
saj so na površje (ali potisnili tik pod površje) izbruhali veliko kovin, tudi železa
(včasih smo ga kopali na Pokljuki - praktično na površju - še danes so tam vidne številne kotanjice).

Vretenčarji so dobili priložnost razvoja komaj pred približno 600 milijoni let v vodi (določeni
viri navajajo 525 ali 535 milijonov let) - to je čas, ko se preko fotosinteze
sprosti čez 20 % kisika v zrak, ki se pomeša tudi z vodo (dihanje večine rib preko škrg ali
preko plavalnega mehurja,
ribe pljučarice).
Morfološke inovacije, kot so čeljusti, zobje in vretenca, veljajo za gonilno silo evolucijskega uspeha.
Najprej se razvijejo v morjih - v tem kontekstu se sprašujemo, katera
žival je prišla na kopno in je naš davni prednik.
Razporeditev kosti latimerije (živega fosila - riba iz družine
mesnatoplavutaric ujeta 1938) v prsnih plavutih je enaka
kot pri prednjih okončinah plazilcev
(imajo podobne kosti kot mi v rokah, nadlahtnico, podlahtnico, koželjnico, zapestne
koščice in celo zametke prstov),
zaradi česar so bolj sorodne kopenskim vretenčarjem kot ribam in pojasnjuje izvor prvih kopenskih vretenčarjev.
Za dihanje poleg škrg uporabljajo tudi zračni mehur. Samice skotijo žive mladiče, ki so takoj sposobni
za samostojno življenje. Njihova nosečnost traja 13-15 mesecev.
Ribe mesnatoplavutarice so torej najbrž naši vodni predniki, ki so se počasi prilagodili za življenje na kopnem,
ko se tam pojavi dovolj rastlin - hrane.
Prvi vretenčarji, katerih potomci so ostali na kopnem do danes pa so na kopno prišli približno pred 360 milijoni let.

Pristerognathus, terapsidi velikosti mačk.
Prvi sesalci (v Kempovem smislu) so se pojavili v poznem triasu (pred približno 225 milijoni let),
40 milijonov let po prvih terapsidih.

Kayentatherium, sesalec iz mezozojske dobe, na sliki s parom
Dilophosaurov v ozadju in prazgodovinsko želvo Kayentachelys
v ospredju. Nova študija kaže, da so sesalci, ki so bili
v času dinozavrov večinoma nočna bitja,
postali bolj aktivni podnevi kmalu po
izumrtju dinozavrov. Avtor podobe: Mark Witton
Vir: https://www.nytimes.com/2017/11/06/science/dinosaurs-mammals-daytime.html

Ljudje smo del primatov - prvakov in seveda sesalcev.
Izumrtja vrst v zgodovini planeta so številna ter drastična (okrog 95 % vseh vrst
je že izginilo, ocena gre tudi do 99 %)
in so paradoksalno omogočila spet nov zagon, porast biodiverzitete,
novih vrst življenja, pred kratkim tudi razvoj primatov in človeka (po izumrtju
velikih plazilcev zaradi padca 15 km-skega asteroida pred približno 65,8 milijoni
let, ko preživi le nekaj sesalcev – naših prednikov – rec. Kayentatherium).
Glede na starost vesolja 13,8 milijarde let, če ta čas skrčimo na eno leto,
so sesalci dobili priložnost v zadnjem dnevu leta – človek poljedelec pa se
pojavi komaj 31 Dec, ob 23:59:32 (pred 28-imi sekundami) …. Apokaliptični
dogodki so torej neke vrste stikalo, za nastanek novih vrst in slovo večine
do takrat bivajočih vrst. Tukaj je še ena zanimivost iz časov, ko so
sobivali majhni sesalci (naši predniki) in ogromni dinozavri. Takrat
so majhni sesalci lovili le ponoči, ker bi jih sicer veliki »zmaji«
čez dan polovili (te trditve so dokazane) … Lahko bi še naprej špekulirali
in sicer, da ima od takrat človek tudi velik (iz časa dinozavrov v naše
majhne prednike vgrajen) talent za ponočevanje in raziskovanje zvezdnega
neba … Če drugo ne, je to lahko dober izgovor za pozen jutranji prihod domov
– če vas partner(ka) krega, se torej sklicujte na evolucijo, dinozavre in
vesolje … Tukaj se tudi kaže velika prednost toplokrvnih bitij, ki lahko
same regulirajo telesno temperaturo in tako tudi čas aktivnega življenja
– recimo ponoči. Plazilci bi težko postali astronomi …
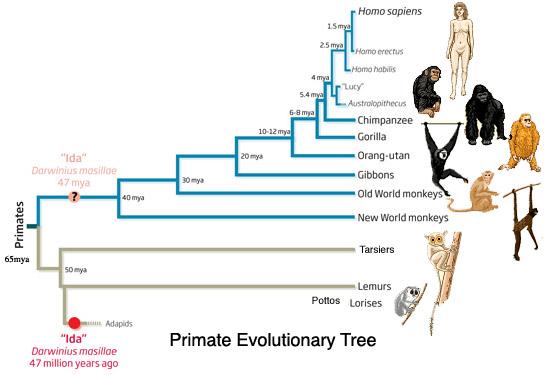 |  |









Enote in pisava skozi čas
V zgodovini je bilo veliko zapletov zaradi nekaterih nepremišljenih reform,
ki so bile kdaj zgolj politično motivirane (francoska revolucija). Hkrati
pa so lahko recimo reforme koledarjev tudi pozitivno vplivale na družbo,
spet drugič so lahko poglabljale razdore (kljub razlikam med kulturami pa
je recimo v praksi skoraj ves svet sprejel gregorijanski koledar, ki bo
dosegel napako enega dneva, glede na višino Sonca, komaj po dobrih 3200 letih od uvedbe).
A iz kulturnih razlogov mnogi vzporedno ohranjajo manj praktične koledarje,
recimo za datiranje starih praznikov, kot del tradicije – in tako z nami živijo
vse stopnje in različice razvoja koledarjev (julijanski, Lunin koledar 12 luninih
faz da 354,37 dni,
planetni koledarji, recimo tudi klimatološki koledar
glede na pojav padavin, zato so ljudje v Stari zavezi
lahko živeli tudi nekaj 100 let ... »Geneza 5: 5,8,27« –
to je ena od hipotez) in to je hkrati živa astronomija zamrznjena iz
preteklih tisočletij. Povedano je lahko hkrati tudi pravi izziv za pouk
astronomije. Med francosko revolucijo (ki se je hitro odločala za giljotino)
je recimo njena skupščina hotela uvesti desetiški sistem tako za čas (nekaj
let je v Franciji vsaj uradno dan trajal 10 ur po 100 minut po 100 sekund,
torej 100 000 sekund), kot za vse ostalo. Uspelo ji je samo pri revolucionarnem koledarju! Urarjem,
ki so ravnokar veliko vložili v izdelovanje kronometrov (natančnih ur) za široko javnost,
je to prekrižalo načrte, vloženo delo, standarde (še danes urarji po celem svetu uporabljajo
za dolžinsko enoto pariško linijo, v Sloveniji smo jo uporabljali še pred 150 leti za
merjenje višine padavin). Neuspeh se je iz podobnih razlogov ponovil konec 19. stoletja
tudi pri merjenju kotov, razdelitev na 400 o ni nikoli zamenjala 360o (6*60 = 360,
šestdesetiški sistem ima namreč svoje prednosti, 60 se deli z 1, 2, 3, 4, 5, 6, 10,
12, 15, 20, 30 in 60 brez ostanka, od katerih so števila 2, 3 in 5 praštevila, kar
je zelo praktično)! Naši predniki so tako zakoličili mnoge standarde – še legenda,
ki pa ima nekaj soli. Baje so Rimljani (poleg pisave, ki so nam jo zapustili) s svojo
gradnjo cest po Evropi in drugod ter preko takratne dolžine osi vozov (medkolesne
razdalje, ki je določila širino kolesnic, seveda tudi počasi vklesanih v kamen),
tako tudi delno definirali večino prečnih medkolesnih razdalj v Evropi vse do danes?
Vsakemu vozniku, ki je recimo v srednjem veku vozil po rimskih cestah in ni upošteval
rimske razdalje med kolesi, so izjemno velike prečne sile kolesnic polomile kolesa voz.
Ta medkolesna razdalja se je tako baje prenesla tudi na vlake ... Obstaja tudi sum,
da je naš veliki matematik Jurij Vega prezgodaj umrl nasilne smrti, ker je zagovarjal
današnji dolžinski metrični sistem.
Še beseda o današnjem poimenovanju mesecev in tudi o določenih protislovjih (recimo, da je december 12. mesec, čeprav decem v latinščini pomeni deset ...). Rimska in slovenska imena mesecev pa generalno kažejo na dejstvo, da je koledar že v antiki upošteval višino Sonca in s tem letne čase. Rimljani so sprva upoštevali lunine mene za osnovo svojemu koledarju. Romulovo leto je štelo deset mesecev, kralj Numa iz 6. stoletja pr. Kr., pa je uvedel 12 mesecev. Rimsko leto se je začelo s 1. marcem, z nastopom pomladi. JANUAR (prosinec) - je dobil ime po rimskem bogu Janusu – bogu začetka in konca (Janus je imel dva obraza za pogled naprej, v bodočnost in za pogled nazaj); slovensko ime prosinec »prosi proso« je dobil ime po prosi, saj je bil januar lačni zimski mesec, poln želja po prosu. FEBRUAR (svečan) - v besedi februar se skriva rimski praznik očiščevanje »febra«. Pred prihodom novega leta se je bilo treba obredno »očistiti«. Rimljani so namreč po starem koledarju začeli leto s 1. marcem. Februar, ki je bil poleg januarja naknadno dodan staremu rimskemu koledarju, je bil zadnji mesec v letu in tako zanj ni ostalo dovolj dni in je postal tako najkrajši mesec v letu. Slovensko ime svečan povezujemo z besedo sveča – pa naj bo narejena iz voska ali iz ledu na strehi, za obe sveči je v mrzlem in temnem zimskem mesecu pravi čas. MAREC (sušec) - stari rimski koledar je, kot že rečeno, začel leto s pomladjo. Prvi mesec v letu je takrat torej bil marec. Bojeviti Rimljani so prvi mesec v letu posvetili bogu vojne Marsu. Slovensko ime za marec je sušec in pomeni čas, ko zemlja pije snežnico, se začne sušiti in se pripravljati na pomladno rast. APRIL (mali traven) – latinska besed »aperire« pomeni odpreti. V aprilu se zemlja »odpira« v novo rast. Tudi slovensko ime - mali traven – govori o mladem, novem, malem zelenju po gozdovih, travnikih in poljih. MAJ (veliki traven) – Maja je bila rimska boginja pomladi in rodovitnosti. Rimljani so jo počastili tudi tako, da so najlepšemu mesecu v letu dali njeno ime. Tudi slovensko ime (veliki traven) tega pomladnega meseca pomeni isto: bujno pomladno rast. JUNIJ (rožnik) - juniju je dala ime Junona, boginja neba, žena Jupitra, najvišjega rimskega boga. Z Jupitrom in Junono so Rimljani zamenjali Zeusa in Hero, ko so grške bogove kopirali in »preselili« na svoje ozemlje. Slovensko ime rožnik označuje mesec, ko polja in travniki dehtijo od tisočerih rož. JULIJ (mali srpan) - v juliju se je rodil rimski vojskovodja Julij Cezar, ki pa se ni ukvarjal le z vojnami. Med drugim je dal prenoviti stari rimski koledar. Novi, julijanski koledar, je imel dvanajst mesecev in je v Evropi veljal več kot 1500 let. Za našega kmeta je visoko poletje čas žetve s srpom, od tod ime meseca v visokem poletju - mali srpan. AVGUST (veliki srpan) - leta 27. pr. Kr. je prvi rimski cesar Octavianus, nečak Julija Cezarja, dobil od rimskega senata vzdevek – Augustus, kart pomeni Vzvišeni. Avgustov stric, Julij Cezar, ki je dal prenoviti stari rimski koledar, je ovekovečil svoje ime v sedmem mesecu koledarja. Tudi Avgust je hotel svoje ime videti v koledarju in še več kot to. Zahteval je, da ima tudi njegov mesec 31 dni, čeprav bi moral imeti 30 dni, ker ima po koledarskem redu vsak drugi mesec 31 dni. Tako so avgustu dodali še en dan in že tako kratkemu februarju še enega odvzeli. V poljedelski deželi, kot je naša, osmi mesec v letu pomeni čas velike žetve s srpom – veliki srpan. SEPTEMBER (kimovec, kimavec) – septem v latinščini pomeni sedem. September je bil sedmi mesec po starem rimskem koledarju. Slovenski kimovec je dobil ime po sadju, ki je v tem jesenskem mesecu zrelo in »kima« na vejah sadnega drevja. OKTOBER (vinotok) - octo v latinščini pomeni osem. Po starem koledarju je bil oktober osmi mesec. Za našega vinogradnika je vinotok mesec, ko »vino teče« v sode v času vesele trgatve. NOVEMBER (listopad) - novem v latinščini pomeni devet in je po starem rimskem koledarju bil november deveti mesec. Po našem koledarju je november enajsti mesec. Ime mu je listopad. To je čas, ko se narava pripravlja na zimsko spanje in listje pada z dreves. DECEMBER (gruden) – decem v latinščini pomeni deset – deseti mesec po starem rimskem koledarju. Naš kmet je v zadnjem mesecu leta opazoval zemljo in videl, da pozimi zaledenela v grude leži po polju – od tod ime gruden. Beseda koledar izhaja iz latinske besede »calare« - klicati. Prvega dne vsakega meseca so namreč Rimljani imenovali »calende«, to je bil v Rimu dan, ko so z glasnimi klici glasniki oznanjali, da je prišel dan, ko so prebivalci mesta morali plačati davke. Leto 46 pr. n. št., ko je bila izvedena Cezarjeva »koledarska« reforma (svetoval mu je Grk Sosigen, astronom in matematik), je dobilo ime »zadnje leto zmede«, saj je to leto štelo 445 dni. Leto zmede je premostilo skoraj vse koledarske napake in razlike, ki so se nabrale v teku stoletij. Novi koledar je v resnici začel normalno delovati leto pozneje, po končani preureditvi, torej leta 45 pr. kr. To je prvo leto brez zmede, ki s presledki (zaradi razpada Rimskega imperija) traja do danes. No - večje napake Sosigen-Cezarjeve reforme smo odstranili z Gregorijanskim koledarjem leta 1582. Sedaj se napaka enega dneva, glede na višino Sonca, zgodi približno vsakih 3200 let, pri julijanskem koledarju pa že na približno 128 let. Od prihoda Sonca iz pomladišča v pomladišče traja 365 povprečnih Sončevih dni in približno 6 ur (v resnici dobrih 11 minut manj, natančneje 11.248 minut manj). Iz teh podatkov se izlušči logika (in tudi relativno majhna napaka) Gregorijanskega koledarja.
Pregovori o vremenu nosijo s sabo veliko več kot le golo ugibanje. Kažejo na
človeško radovednost, željo razumeti vremenske vzorce – razumeti dogajanje
v atmosferi. V njih se skriva vodni krog in energijski zakon. Naštejmo nekatere
pregovore na temo vremena.
Če v prosincu (januarja) ni snega, ga mali traven (maj) da.
Če svečana (februarja)
mačka na soncu leži, v sušcu (marcu) spet rada za peč pribeži.
Če se sušca (marca)
da orati, bo treba v malem travnu (maju) jokati.
Če je majnika lepo, je dobro za
žito in za seno. Če junija sonce pripeka in vmes dežek rosi, obilo zemlja rodi.
Če julija so hladni, mokri dnevi, bodo prazni sodi, prazni hlevi.
Če se avgusta
po gorah kadi, kupi si kožuh za zimske dni.
Če zgodaj selijo se ptiči, bo huda
zima o božiči.
Če vinotoka (oktobra) mraz in burja brije, prosinca (januarja)
in svečana (februarja) sonce sije.
Če listopada (novembra) mokro zemljo sneg pokrije,
bo malo prida za kmetije.
Če ob božiču led visi od veje, se velika noč vsa v cvetju
smeje
(Vir: Dušica Kunaver prof., njen tast Pavel K. je dolga leta vodil astronomijo
na Šentvidu).
Še pregovori vezani na december, najbrž najbolj umirej mesec v letu naši prednikov.
* Na Barbaro (4.12.) mraz, bo trajal ves zimski čas.
* Barbara če po poljih pokrije (s snegom) strnišča,
kuri nam v dolgi zimi peči in ognjišča.
*
Grudna mraz in sneg, žita dosti prek in prek.
*
Kadar v adventu jug hladi, drugo leto dosti sadja rodi.
*
Kakršen adventni mošt, takšen post.
*
O božiču(25.12) se spodobi malo snega in belega kruha.
*
Kolikor ivja se o božič(25.12) na vejah blesti, toliko sadja prihodnje leto zori.
*
Zelen božič(25.12), bela velika noč.
*
Če Štefana (26.12.) burja prinese, vinogradniku pridelek odnese.
*
Dež na Štefanje(26.12.) obeta le malo žita drugo leto.
*
Tepežki dan (28.12.) oblačen, k letu ne boš lačen.
*
Opomba.
4. december – god sv. Barbare
Zgodba o sveti Barbari govori o lepem in pametnem poganskem dekletu, doma iz grške Nikomedije,
ki pa je imelo to nesrečo, da je bil njen oče Dioskur izjemno posesiven. Da bi nadziral njene
socialne stike in vplive nanjo, je sezidal stolp in Barbaro zaprl vanj. Kljub temu je prek
Origenovih spisov in služinčadi prišla v stik s krščansko vero.
Ko očeta ni bilo doma, se je dala krstiti, služabnike pa je prosila, naj na stolpu poleg dveh
že obstoječih okenc naredijo tretje, da jo bodo tako trije snopi svetlobe spominjali na sv.
Trojico. Ko je prišel oče in izvedel, kaj se je zgodilo, je pobesnel. Hčer je izročil sodnikom
(bilo je leto 306, čas krutih Dioklecijanovih preganjanj kristjanov). Sodniki so Barbaro obsodili
na smrt z obglavljenjem, oče, od vedno zagrizen nasprotnik kristjanov, pa se je ponudil,
da bo sodbo izvršil sam. Kar se je tudi zgodilo: oče Dioskur je v imenu države obglavil
lastno hčer Barbaro.
Barbaro so v srednjem veku prišteli k štirinajstim pomočnikom v sili. Najdemo jo v
‘ženski trojici’, kjer se je pridružila sv. Katarini in sv. Marjeti. Upodabljajo jo s stolpom,
ki je simbol vsakega jetništva, vrata, ki se čudežno odpro, pomenijo rešitev iz vsake stiske,
Ime Barbara: razlagajo ga z grško besedo Barbaros oz. latinsko barbarus, ki pomeni: »tuj, negrški;
tujec, negrk, neomikan, neveden, krut, divji, barbar«.
Vremenski pregovori sledijo letnim časom (višini Sonca) in posameznim vremenskim vzorcem znotraj njih.
Vsi poznamo ledene može, polulano Zofko, ohladitve začetek decembra, mesec marec kot sušec ...
A mnogi vremenski vzorci se zaradi podnebnih sprememb spreminjajo - a pregovori o vremenu so
prva tipanja naših prednikov v smeri napovedovanja vremena. Kdaj pregovori niso veliko slabši
od "resne" znanosti ...
Od zadaj pa je zmeraj dogajanje v vesolju !!!
Zanimivo je tudi spodnje branje, kaj vse meteorološko ekstremnega smo doživljali na ozemlju Slovenije
od leta 800 napej (srednji vek - čas, ko se je Evropa spet začela kulturno in politično pobirati in zapisovati
kronike).
Iz starih kronik za deželo Štajersko (iz “Dogodivšine štajerske
zemle - 1845”, zapiše župnik Anton Krempl [1790 - 1844, izjemno delo, prva prava zgodovina v slovenščini, hkrati vir
informacij za klimatologe, a ...] iz Male Nedelje v Slovenskh goricah in
Krones Lapajnetove “Pripovesti iz zgodovine Štajerske”):
- leta 820 je bilo nerodovitno, umirajo od lakote,
- leta 872 so roji kobilic zakrili Sonce in uničevali vse zelene rastline,
lakota,
- leta 993 je na božič nek sij tako razsvetlil nebo, da je bilo svetlo
kot podnevi (komet, meteorit, polarni sij, ...), sledila je huda zima,
- leta 1186 je meseca februarja cvetelo sadno drevje, v maju so bila zrela
vsa žita, trgatev je bila konec avgusta (smo blizu temu),
- v letih 1187 in 1188 je bila huda zima, ki je trajala vse do binkošti,
zato je vse zelo pozno dozorelo, trgatev je bila ob božiču,
- leta 1194 je bilo slabo leto, polno raznih nadlog: povodnji, kužnih bolezni,
kug, ki so uničile cele vasi (posledice - danes imamo recimo vas Puščava,
Slovenska vas, Nemška vas, itn); ponoči je bilo moč videti "krvave" zvezde
repatice (meteorski roj?); pojavljali so se požari in nadležna mrces,
- leto 1248 je bilo zelo mokro,
- leta 1255 je po hudi zimi bila strašna suša, da njive, sadovnjaki
in vinogradi niso nič obrodili,
- leta 1270 je bila najprej ostra zima, potem pa je prišla strašna suša,
ki je vse pokončala; nastala je takšna lakota, da so cele kupe mrličev,
ki so od lakote umrli, metali v skupne jame,
leta 1289 so se letni časi čisto zmešali ...
- leta 1312 so žito za naše dežele vozili iz Sicilije,
- leta 1570 je bila strašna lakota, otroci so po livadah lazili in travo
jedli,
- "po 1600 hude zime“,
- leta 1767 je bil 4, maja hud mraz, 6. maja pa je močno snežilo,
sneg je do vznožja pokrival Ivančičo še nekaj dni,
- LETA 1788 JE BILO IZVRSTNO VINO, KI JIH JE VELIKO V GROB
SPRAVILO,
- 24. maja 1866 je bil hud mraz, ki je po vinogradnih in na poljih
naredil veliko škode (sem preveril v našem met. arhivu).
*** Preberi tudi poglavje -
»zakaj smo torej nastali tako pozno« (toplogredni plini so nas rešili) ...
Že zgolj aktualna civilizacijska protislovje nas pripeljejo do neke nove-stare uganke, kaj je človek – pripeljejo nas recimo do fenomena razvoja jezika, komunikacije, kot prvega orodja našega bivanja, do govora kot enega od temeljev civilizacije, do izjemne a hkrati krhke sposobnosti prenosa (in počasne nadgradnje) znanja na potomce. Seveda nas ta vprašanja pripeljejo tudi do fenomena astronomije, znanosti, do definicije skrivnostnega časa ... Če nam umanjka le en od navedenih atributov, recimo zavedanje časa (ali zgolj definicija časa – o tem, kaj je čas, se še zmeraj »kregamo«), sta znanost, oz. astronomija kot jo poznamo danes nemogoča. Kaj vse je vplivalo na naš tok razvoja in zavesti, recimo od Kaldejcev do naše generacije, so zgolj bolj ali manj posrečena ugibanja (naravne danosti, podnebje, pokrajina, rastline, živali, posledično razvoj poljedelstva, nebesni dogodki, kometi, prihodi, selitve določenih spretnih, zelo premetenih plemen in posameznikov na »prava« mesta ob pravem času, ...).

Feničanska pisava dopolnjena s samoglasniki (stara je več kot 3000 let – za
Feničani tudi Kenaani je ostala pisava in arhitektura ter velik vpliv na
poznejše civilizacije – bili so trgovci v Sredozemlju, uvedli so dolge,
ozke in zato hitre ladje – zelo težko so našli skupni imenovalec z ostalimi
ljudstvi).
A nastanek moderne pisave ni čisto dorečen – prve najdbe segajo
3800 let nazaj blizu Luksorja (Egipt), spet drugi pripisujejo nastanek in
uporabo moderne abecede med semitskimi ljudstvi na Sinajskem polotoku
(rudniki bakra – tam so rudarili sužnji iz Kanaana). A Feničani so
iz praktičnih potreb moderno pisavo prvi posejali po sredozemskem bazenu
– prej njene preprostosti oblastniki niso želeli sprejeti (zakaj bi pa vsi pisali in
brali …, to je vendar nevarno?). Izmenjava blaga, trgovanje, pomeni tudi prenos znanja
in dobrih praks (žal tudi manj dobrih).
Za trenutek se ustavimo pri pisavi – omogoča eleganten prenos in nadgradnjo kompleksnih znanj, razmišljanj, čutenj, književnosti, umetnosti, duhovnosti na generacije, ki prihajajo čez tisočletja in nas same povezuje s predniki tisočletja v zgodovino - izjemno. Ni vsaka izbira znakov abecede in zapisa števil enako uspešna pri razvoju in širjenju znanja, sploh na kar se da veliko populacijo ljudi, recimo preko »obveznega« šolanja. Fonemi so najmanjše glasovne enote s katerimi tvorimo besede in to je tudi logika modernih abeced – zapis fonemov z znaki, črkami (ločimo soglasnike in samoglasnike). Najbolj enostavne in učinkovite abecede so grajene na temelju feničanske soglasniške abecede. V Evropi smo torej sledili feničanski logiki, kjer vsak znak predstavlja en ali več glasov, dodali pa smo še samoglasnike (na koncu je prevladala latinica – a razlika glede na Feničane je zgolj v znakih in nekaterih fonemih). Samoglasnike se izgovarja iz pljuč skozi ustno votlino brez ovir (ustnice in jezik ne nihajo, zgolj glasilke – naredite vajo za a, e, i, o, u), pri soglasnikih (več glasov) pa vibrira ali jezik ali ustnice (izrazito se spreminja tudi oblika ustne votline, glasilke so popolno ali delno zaprte, manj aktivne). Primeri: [p] - je izgovorjen z ustnicami; [t] – se izgovarja s sprednjim delom jezika; [k] – se izgovarja z zadnjim delom jezika; [h] – se izgovarja izrazito v grlu; [f] in [s] - se izgovarjata s potiskanjem zraka skozi ozek kanal (frikativ, pripornik); pri [m] in [n] - zrak teče skozi nos. Smo torej dediči feničanske abecedne kulture – če kaj, je prav feničanska abeceda naredila največjo revolucijo v pisavi (hvala jim). Logografske pisave ali izražanje s podobami, predmeti (piktografija), so rodile sumerski klinopis, egipčanske hieroglife, kitajske, japonske pisave, pismenke ... – a te pisave so precej zahtevnejše za učenje (imele pa so eno veliko prednost – niso bile toliko vezane na jezik). Sam razvoj jezika ni enoznačno pojasnjen – velik pomen je v prilagoditvi človeških možganov, potem glasilk – kontrola nad obraznimi mišicami in ustno votlino. Zanimivo je, da baje kar 60 % govora namenimo obrekovanju drugih – nekateri v tem (za obrekovane v slabem vzgibu) iščejo veliko motivacijo za razvoj govora – ki smo ga potem seveda začeli uporabljati še za plemenite, tudi znanstvene namene (recimo da 40 %, bojimo se da manj). Ker razvoj astronomije temelji predvsem na fizikalnem ozadju in geometriji - matematiki, omenimo še pomen zapisa števil. Najprej beseda o arabskih številkah - v bistvu so indijske (»hindi«), razvite baje okrog leta 500 v Indiji. Arabci so jih le prenesli v Evropo. Nekje v 15. in 16. stoletju, tudi zaradi razvoja tiska, so postale splošno sprejete v večjem delu Evrope (rimska števila so precej nerodna za zapis in računanje). Arabci imajo nekoliko drugačne oznake za števila. To dejstvo omenjamo zato, da vas ne preseneti umanjkanje »arabskih« števil v arabskem svetu, ko boste recimo potovali na Bližnji vzhod – mnoge je to dejstvo že presenetilo. Vsekakor pa je t.i. »arabski« zapis števil bolj praktičen kot recimo zapis rimskih števil. »Arabski« (Hindi) sistem je bil velik korak naprej – tudi zaradi vključitve ničle (0 1 2 3 4 5 6 7 8 9), preprostosti, nazornosti znakov in logične definicije zaporedja, položaja števil pri zapisih konkretnih vrednosti (… stotic, desetic, enic, decimalk …). »Hindi« zapis števil se je zato prijel skoraj po celotnem svetu – saj v znanosti. Tudi sami številski sistemi niso nepomembni, čeprav obstajajo pretvorbe med njimi. Navajeni smo desetiškega številskega sistema (pravijo, da zaradi 10 prstov na rokah, nogah), a v razvoju računalništva sta odigrala veliko vlogo tako dvojiški, kot šestnajstiški sistem. Sumerci pa so recimo uporabljali šestdesetiški sistem – delno smo ga ohranili tudi danes v astronomiji, pri merjenju časa, pri geografskih koordinatah, pri merjenju kotov v geometriji (polni kot 360 °, 1 ° = 60 ', 1 ' = 60 ''). Da pa narava seveda ni odvisna od številskega sistema, ampak se da opisati z vsakim konsistentnim številskim sistemom, nas uči zgodovina matematike (a seveda je večinoma v veliki prednosti kultura, ki uporablja kar se da preprosto abecedo in števila – zaradi pismenosti množic, prenosa vedenja).
Na mestu je tudi vprašanje, od kod človeku želja po štetju in računanju, pismenosti? Postopno zaradi razvoja kompleksnosti civilizacij, zaradi samega preživetja, boljšega sporazumevanja, nujnega sodelovanja med nami – in najbrž najvažnejši razlog, ker je moderni človek te vrline tudi fiziološko, mentalno zmogel ...!!! Zagotovo je naš prednik postopoma uvidel velik pomen govorice, nato tudi črkovnega zapisa besed, stavkov, idej, števil: uvidel je pomen štetja dni v letu (kar koli je takrat leto že pomenilo) za načrtovanje poljedelskih opravil, obdelav površin, njiv, pašnikov, vodnih zajezitev, pri načrtovanju preživetja neke skupnosti (dovolj hrane, živine, semen ob pravem času), pri gradnji bivališč, hiš, templjev – svetišč, observatorijev za višino Sonca, zvezd (koledarjev – pravijo, da so svetišča bila hkrati koledarji), pri izdelavi zdravil, orodij, posod, oblek, orožja, pri načrtovanju vojaških taktik, vozov, rudnikov, peči, ladij – nujno je torej potreboval števila, načrte, navodila in merske enote (dolžinske, volumske, masne, tudi časovne ...) …; vse to je potreboval v danem prostoru in času za izvedbo omenjenih veščin.
Merjenja in osnovne enote pa so bile premalo, človek je iskal tudi površinske in prostorske vzorce, geometrijske like in logiko razmerij med njihovimi sestavnimi deli (minimum informacij za izračun razdalje, obsega, površine, volumna, mase, ...). Ko je meril, je nastala metrika v prostoru (danes smo dodali še komponento časa v povezavi s hitrostjo svetlobe). Kot eden najbolj praktičnih izrazov metrike je, »ne boste verjeli«, znameniti Pitagorov izrek. Danes je Pitagorov izrek nepogrešljiv v vektorski analizi (ko recimo učenci računajo velikosti vektorjev, se večinoma sploh ne zavedajo, da uporabljajo Pitagorov izrek). In v resnici se je nekoliko preoblikovan Pitagorov izrek izkazal tudi kot nepogrešljiv zapis, izraz metrike (merjenja »razdalj«) tako v specialni (velike hitrosti), kot v splošni teoriji relativnosti (močna gravitacija ali pospeški - pa čeprav tam radi govorimo o ukrivljenem prostoru). Pitagorov izrek je torej nepogrešljiv v metriki prostor-časa. Če ga ne bi prenesli iz antike (nastal je v Mezopotamiji), bi ga morali vpeljati »danes«. To samo kaže, kako močna je povezava med prvimi koraki človeka na poti do poljedelstva, načrtovanja, štetja, merjenj, na poti do pisave ..., z današnjim vedenjem, z današnjimi orodji znanosti, z našimi »samoumevnimi« navadami. »Pitagorov« izrek so poznali že vsaj 1500 let pred pitagorejci tudi Babilonci. Pred antičnimi Grki so ga zagotovo uporabljali že Egipčani in Kitajci. To še enkrat potrjuje dejstvo, da je nastal iz praktične potrebe gradbenikov, poljedelcev ... In še nasvet, da se izognemo nadaljevanju protislovij današnjega časa. Če človek (otrok) v odraščanju ne dobi izkušenj preživetja in dela v naravi, občutka prostora in časa skozi delo in igro (ne doživi neke vrste »antike«), bo najbrž imel velike težave pri dojemanju šolskih (učnih) vsebin, pri razumevanju opisa sveta (saj ga ne pozna in kako bi ga potem lahko razumel - kar ne vidiš ne veš da obstaja). In to je eden glavnih problemov moderne dobe – razvitemu svetu tako (protislovno) manjka mojstrov obrti in hkrati inženirjev, naravoslovcev (oboje je povezano), ... in jih uvaža iz okolij, kjer otroci na lastni koži še spoznavajo »metriko« narave in preživetja, tako kot smo to doživljali še mi (saj večina) v otroštvu. Malo smo zašli – a težave izobraževanja se ne začnejo v šoli, ampak že kmalu po rojstvu, če otrok ne odrašča polnega otroštva v naravi, pri igri in delu, z uporabo orodij odraslih, v sodelovanju s sovrstniki in odraslimi pod zvezdnim nebom, pod Soncem. V resnici je danes mnogo mladih, žal in seveda ne po svoji, ampak po naši krivdi, vzgojenih v smeri (v maniri) nekaterih ljudstev deževnega gozda, ki živijo »brez časa«.
Še nekaj podatkov, primerov, kako smo skozi čas zapisovali številke.
Zapis številk tudi
odpira ali pa delno zapira prostor matematičnemu zapisu, verodostojnemu opisu modelov, ki se trudijo
kar se da točno napovedati dinamiko v vesolju, na Zemlji, v bioloških
sistemih. Danes smo si dokaj enotni, da je indijska osnova zapisa števil do 9, skupaj z ničlo,
zelo pospešila razvoj matematike, fizike, biologije, matematike,
inženirstva in seveda razvoj modelov opisovanja stvarstva - vesolja.
Danes smo torej navajeni desetiškega številskega sistema, a zanimiv je tudi šestdesetiški sistem.
Mogoče je, da so ljudje za štetje na prste do števila 12 uporabljali palec in z njim kot kazalom šteli
členke prstov iste roke. Takšen način štetja se še vedno uporablja v mnogih delih Azije in pomaga razložiti
nastanek številskih sistemov z osnovama 12 in 60 in sistemov z osnovami 20, 10 in 5. V tem sistemu štetja se
je običajno štelo s prsti desne roke, število ponovitev pa s prsti leve roke, dokler ni število doseglo vrednosti
5 · 12 = 60.
Po mnenju Otta Neugebauerja je osnova 60 nastala s štetjem trikrat do dvajset. Sistem 3-20 je kasneje prešel
v sistem 6-10 preko simbolov za šestine (na primer 1/6, 2/6, 3/6, 4/6, 5/6), povezanih z desetiškimi števili,
kar je privedlo do slovitega sumerskega sistema deljenja. V normalni rabi so bila števila naključna zbirka enic,
desetic, šestdesetic in stotic. Število 192, ki je v eni izmed sumerskih preglednic
zapisano z 3A2 (A pomeni število 10), se pravi
(3 · 60 + 10 + 2), bi se,
vključeno v besedilo, zapisalo z XIxxxii, se pravi 100 (X) + 60 (I) + 30 (xxx) + 2 (ii).
Še danes velja, kadar številko izgovorimo, recimo dvainštirideset (dva-in-štiri-deset) v bistvu množimo in seštevamo,
v tem primeru 2 in (+) 4*10. A se tega večinoma ne zavedamo.
Določeni narodi so tudi odštevali - recimo rimska štirica IV je 5 - 1 = 4.
Pomembno je tudi zapisovanje besedila številk.
Danes v Evropi pišemo z leve proti desni, Arabci recimo z desne proti levi, lahko se piše od zgoraj navzdol
Japonci lahko uporabljajo vse 4 orientacije,
zapisane od desne proti levi v stolpcih od zgoraj navzdol. Knjige pa berejo od zadaj naprej.
Kaka sporočila pa so lahko tudi zapisana v vrsticah od desne proti levi ...
Če ima recimo nek ekran miselni vzorec za odklepanje - s prstom po ekranu ga tudi zapišemo -
je zelo pomembno, da se ve zaporedje zapisa številk.
Zelo domače so nam recimo rimske številke, a so za matematične operacije precej nerodne.
Klasični rimski zapis števila 1424 je bil prvotno zelo dolg in sicer
MCCCCXXXIIII. Kar se interpretira z današnjim zapisom kot 1000 + (100 + 100 + 100 + 100) +
(10 + 10 + 10) + (1 + 1 + 1 + 1) - torej gre za kumulativo števil.
Kitajci pa to število zapišejo z množilnim principom in sicer: (1 x 1000) + (4 x 100) + (3 x 10) + 4.
Danes uporabljene številke (znaki za števila) tako v večini sveta presegajo jezikovne ovire. To recimo lepo opazimo,
če gremo na japonsko Wikipedijo. Tam lahko zasledimo indijske številke (kot na zahodu) in tudi simbolni jezik v formulah je
latinica.
Včasih je bil v veljavi tudi dvanajstiški sistem - ducat je 12. Je uporaben pri šestdesetiškem sistemu, ki se uporablja za čas.
Tudi mesecev v letu je 12, 12 ur razdeli dan na dva dela ...
Obrnjena izgovorjava dvomestnih števil (od 21 do 99, razen desetic) v slovenščini, nemščini, danščini, nizozemščino,
delno tudi v ostali osrednji Evropi kaže, da pišemo drugače, kot izgovarjamo.
A zadeva ni tako nerazložljiva, v določenih delih sveta se je pisalo z desne proti levi in tako tudi bralo (danes še zmeraj ta princip
uporabljajo Arabci in nekatere sosednje kulture Azije). Enaindvajset torej najbrž izhaja iz stare tradicije sanskrta.
Slovenščini in sanskrtu je sorodno torej že »obrnjeno«
zaporedje enic in desetic, npr. enaintrideset (ekatrimšat),
dvaintrideset (dvatrimšat) itn.; zelo podobnih si je tudi prvih
nekaj številk: ena (eka), dve (dve), tri (trini), štiri (čatvari),
pet (panča) šest (šat); prvi (prathama), drugi (dvitija), tretji (tritija),
četrti (čaturthi); podobno je sklanjanje prvih štirih številk v vseh
treh spolih – »ena« se sklanja le v ednini, »dve« v dvojini,
»tri« in »štiri« le v množini, števila od pet naprej se sklanjajo
enako v vseh treh spolih (le v množini).
Recimo tudi Francozi imajo v jeziku števil še zmeraj določene posebnosti
poimenovanja za 70, 80 in 90.
Številki 70 rečejo soixante-dix, kar je 60 in 10,
80 je quatre-vingts, kar pomeni štiri dvajsetice, zelo posebna pa je številka 90, ki je
quatre-vingts-dix, je torej sestavljena iz štirih dvajsetic in desetice.
Dvajsetice bi naj bile posledica vplivov Galcev ("Obelixov") - v bistvu zelo uporabno.
Med slovenskimi narečji se je dvajsetiška oblika ohranila v rezijanščini, kjer za 60 rečejo trikatdveisi
(to je eno od znamenj, da smo že dolgo živeli na širšem delu Evrope). Za 70 rečejo
trikatdveisi anu deset - podobno za 80 in 90.
Tudi Danci imajo veliko posebnosti, za 60 rečejo tres, kar je okrajšava za tresindetyve,
kar spet pomeni 3 krat 20. Za 50 pa seštejejo 2 krat po 20 in dodajo polovico od 20: halvtreds,
kar lahko prevedemo v pol-tretja dvajsetka.
Podobno je 70 pol-četrta dvajsetka in 90 pol-peta dvajsetka.
Ker Danci izgovarjajo dvomestne številke obrnjeno kot Slovenci, Nemci ..., se tako 54
izgovori kot fireoghalvtreds, torej štiri-in-pol-tretja dvajsetka.
Pri denarju pa uporabljajo "normalno" štetje, kjer je firti 40, femti 50,
seksti 60 evrov ...
Tudi izumrli baltski "slovinski" jezik je uporabljal dvještaza za 40 in
trištazi ali kuop (torej kup) za 60.
Za 30 so pa uporabljali kar izraz pol kupa - pouluopa.
Stara angleščina je za 110 in 120 uporabljala eleventy in twelvety.
Nekoč pa so v Franciji številke po dvajseticah
v rimski obliki označevali množilno s "kvazi potenčnim zapisom" in seštevalno: 160 so recimo
zapisali kot VIIIXX, 8 krat po 20.
Za 170 so zapisali VIIIXX&X, kar pomeni 8 krat po 20 in 10. Številko 199
pa so kje zapisali kot IXXX&X&IX, kar je 9 krat 20 plus 10 in še plus 9.
V starih kronikah so zapisi mesecev v Sloveniji precej zanimivi, danes lahko dvoumni - pazite, kako jih razumete (berete).
So kombinacija številke in končnice (prebrati pa morate besedo za mesec). V starih knjigah lahko torej najdete
zapise mesecev 7-er, 8-er, 9-er, 10-er. To niso meseci 7, 8, 9, 10 - ampak gre za okrajšavo latinske
izgovorjave, ko je leto po takratni definiciji še imelo deset mesecev.
Recimo septem za 7, octo za 8, novem za 9
in decem za 10. Velja torej, da je 7-er september, 8-er je oktober,
9-er je november in 10-er je december. Zelo poučno - Rimljani so nekoč imeli 10 mesecev.
Februar, ki je bil poleg januarja naknadno dodan staremu rimskemu koledarju, je bil takrat zadnji mesec v
letu (Rimljani so po starem koledarju začeli leto s 1. marcem)
in tako za februar ni ostalo dovolj dni in je postal tako najkrajši mesec v letu.
Stara imena mesecev torej izhajajo iz leta z 10 meseci in mi smo jih ohranili (tako recimo naš dvanajsti mesec nosi ime
za deseti mesec decem-ber iz starega Rima) - to je mala zmešnjava, a je v bistvu
jezikovna arheologija (zelo zanimivo). Zagato smo že omenili pri poimenovanju mesecev.
Matej Šekli iz Lj. univerze in inštituta Frana Ramovša in že prej Poljaka Tadeusz Lewaszkiewicz ter Wieslaw
Wydra (univerza Poznan) sta odkrila najverjetneje najstarejše zapisane številke v Slovenščini iz 12. stoletja.
Gre za "kustode", številske oznake snopičev
v knjigi, po katerih knjigovez prepozna zaporedje besedil za ustrezno vezavo v knjigo.
Knjigovez je torej bil najverjetneje Slovenec iz Podjune (morebiti Poljak). A prepis krščanskega besedila misleca Janeza Kasijana
(Ioannus Cassianus , 4. stoletje) z oznako Cod. 250, je iz 12. stoletja in je nastal v Avstriji - opatija Heiligenkreutz -
torej najverjetneje gre slovensko štetje, da je štetje nedvoumno
zagotavljajo pridane rimske številke:
et I no - edno ali eno,
drv II gi - drugi,
TRE III TIGI - tretiji ali tretji,
ces IIII tiri - čtiri ali štiri,
pa V nt - pent ali pet,
scl VI zt - šist ali šest,
zed VII em - sed'm ali sedem,
oz VIII zem - osem,
de VIIII wanϑ - deveth ali devet,
de X zenthetasym; - deseth ali deset.
Potrebno je dodati, da sta prepis dala v ponovno analizo raziskovalca Dunajske akademije znanosti, Franz Lackner in
Alois Haidinger.
Povejmo še, da je uporaba števil, simbolike, v vsakdanjem življenju edina pot, da otroci sami
dojamejo pomen in veliko uporabnost števil, štetja, računanja. Poleg abecede in seveda prej govora, so
števila jedro našega razvoja, prenosa znanja na potomce in seveda na sopotnike skozi naše življenje.
Šola ta praktični del spoznavanja pomena simbolike črk, števil,
geometrijske simbolike nekako ne pokriva prav dobro in zato imajo otroci na začetku velike
težave v motivaciji - kar je velika škoda.
Če torej zaključimo tale babilon zapisov, štetja in izgovorjav števil v različnih časih in kulturah,
nas je torej dosedanji razvoj pripeljal do najbolj praktičnega splošnega desetiškega sistema števil, zapisa in štetja, to so
števila (osnova je iz Indije): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Vse ostalo, seštevanje, odštevanje, množenje, decimalni zapis, ulomki, koreni, potence ... pa je nadgradnja
zelo preproste osnove desetiškega sistema in zapisa števil.
Računalniki seveda lažje računajo in kombinirajo seveda v dvojiškem sistemu 0 in 1 ali kake drugem in na koncu vse pretvorijo
nazaj v desetiškega (tudi v črke in ostale simbole, grafiko, glasbo ... - še čustva simuliramo preko robotov,
a mnogim to pomaga ...).
Vrnimo se v svet fizike, v tisti del, ki je neposredno povezan z našim zaznavanjem sveta, vesolja, simbolov,
sebe in sočloveka - poglobimo se v čudovit svet svetlobe
(»Fiat Lux! Bodi svetloba! - Let there be light«).
Še beseda o svetlobi - vpeljali jo bomo nekoliko alternativno, preko indukcije,
ki je radikalno spremenila tehnološki razvoj človeštva in je
hkrati "mama nove moderne" fizike relativnosti!
Kot uverturo v opis narave svetlobe obudimo izjemno povedno anekdoto o znanosti in ministru. Eminenten raziskovalec, eksperimentator, samouk in genij Michael Faraday, se je nekoč trudil razložiti ministru za finance W. Gladstoneu in drugim politikom, kako pomembno je njegovo novo znanstveno odkritje. Edini komentar Gladstonea je bil: »A navsezadnje, zakaj pa je to sploh uporabno? Zakaj, gospod,« je odgovoril Faraday: "obstaja velika verjetnost, da boste uporabo lahko kmalu obdavčili!" Tega dogodka se je spominjal Faradayev prijatelj – najverjetneje je pogovor tekel o električnem generatorju - indukciji.
In indukcija je direktno povezana s svetlobo - zakaj - sledi kratka ponovitev srednješolske fizike magnetnega in električnega polja ter indukcije. Rezultat je presenetljiv - na sledi mu je bil že naš ljubi eksperimentator Faraday.
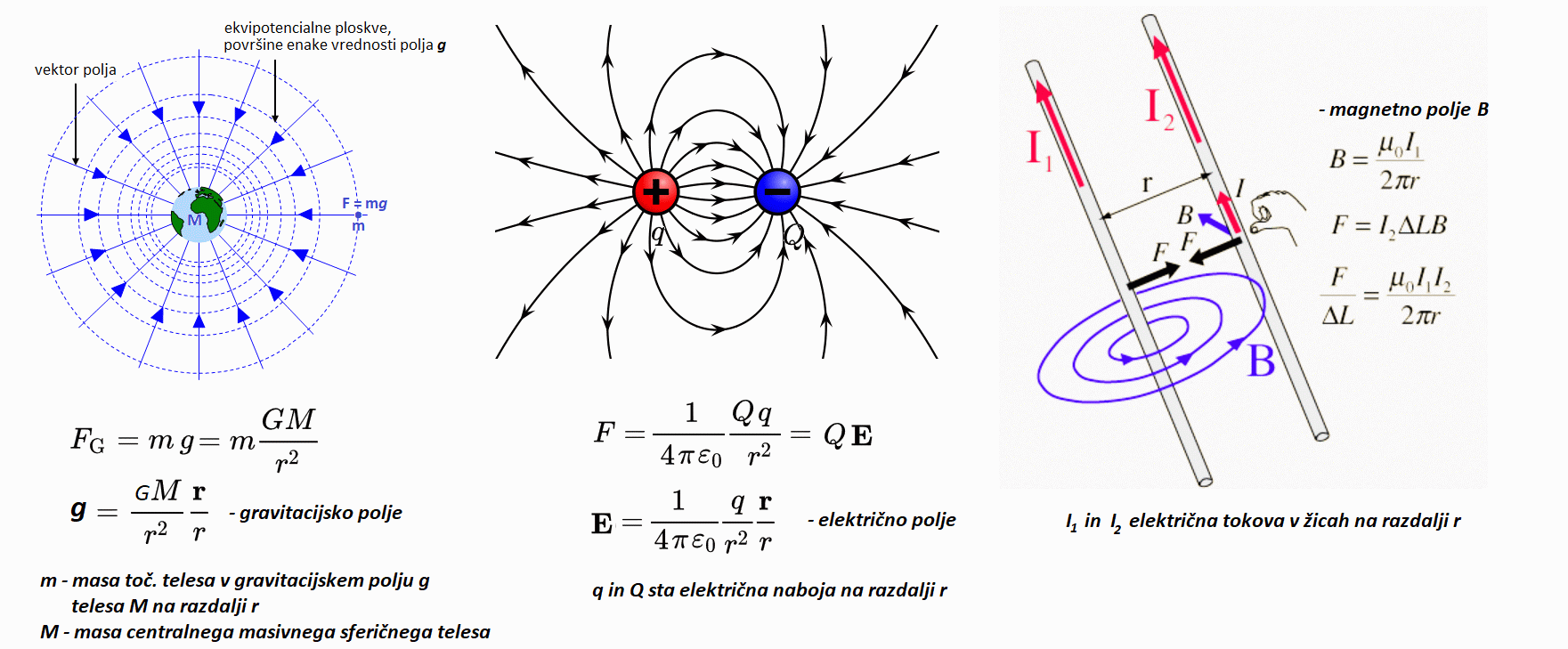
Shema gravitacijskega (g), električnega (E) in magnetnega
(B) polja
za konkretne primere. Polja predstavljajo
vektorji (silnice), ravnine pravokotne na silnice pa ekvipotencialne ploskve
– kjer je potencial enak (ekvipotencialne ploskve so označene zgolj
pri gravitaciji, enako bi jih lahko označili recimo pri električnem polju
– matematično sta geometriji podobni). Magnetne silnice imajo v vsaki
točki prostora smer tangente na smer magnetnega polja. Magnetne silnice
so tudi zmeraj sklenjene v zanko – kar pa ne velja za ostala polja.
Gostota magnetnega polja B tudi ni pravi vektor, ampak psevdovektor
(saj pri zrcaljenju tokovne zanke magnetno polje ni samo zrcalno ampak
tudi obrnjeno). Ko električno polje E (sila na nabit delec je kar
F = qE) požene električne delce po vodniku, nastane električni tok,
ki povzroči nastanek magnetnih silnic pravokotno na vodnik.
Iz povedanega lahko sklepamo, da sta električno E in magnetno
B polje povezana in med sabo pravokotna. To je izjemno pomembna
relacija – kmalu bomo videli zakaj in kako povezavo
ima to dejstvo z relativnostjo. Vzporedna vodnika z enako
usmerjenima električnima tokoma se privlačita –
če sta tokova nasprotna pa odbijata (sila je vektorski
produkt med tokom in magnetnim poljem: F = I(lxB). Več v nadaljevanju.
Električna energija
Električna energija je posledica električnih sil
in posledično električnih polj, energija je
shranjena v njih (za točkasta naboja e1 in e2,
(tudi q1 in
q1),
na razdalji r velja naslednji izraz za privlačno ali odbojno silo
F =e1e2/(4πε0r2) –
to je Coulombov zakon.
Matematično je to enaka odvisnost
kot pri gravitacijski sili,
ε0 je influenčna konstanta ali dielektričnost vakuuma).
Po
definiciji vsak električni delec obdaja električno polje, za točkasto telo
(ali nabito
kroglo) velja, polje
E = e/(4πε0r2)
ali q/(4πε0r2) –
v izrazu 4πr2
prepoznamo površino krogle. V kondenzatorju z nabojem e in površino plošče S
pa je električno polje E = e/(ε0S).
Energija kondenzatorja (glej sliko –
izhajamo iz definicije električnega dela pri prenosu naboja pri dani napetosti
WE
= ∫Ude = d∫Ede), za razdaljo d med ploščama (velja U =
Ed), pa je enaka delu WE = d∫Ede
= (d/(ε0S))∫ede
= de2/(2ε0S)
. Za gostoto energije električnega polja (uE) pa velja
uE = WE/V
= WE/(Sd) = ε0E2/2
- izpeljan izraz
uE = ε0E2/2
bomo rabili
pri izpeljavi hitrosti svetlobe.
Magnetna energija

To je potencialna energija, ki je posledica
magnetnih polj in je shranjena v njih. Magnetno polje na razdalji r
od žice s tokom I je B = μ0I/(2πr), v tuljavi dolžine
l z N navoji pa je B = μ0NI/l, μ0 je indukcijska
konstanta ali permeabilnost vakuuma. Sila med vzporednima žicama s tokoma
I1 in
I2 na dolžini
ΔL pa je
F = Δμ0I1I2/(2πr). Energija
tuljave (glej sliko – spet izhajamo iz definicije električnega dela pri prenosu
naboja, a tokrat pri inducirani napetosti zaradi spremembe
magnetnega pretoka B skozi
N ovojev s površino ovoja S, tako velja WB = ∫(dΦ/dt)de =
∫NS(dB/dt)de = ∫NSIdB ) s presekom S je enaka delu WB =
NS∫IdB = (N2Sμ0/l)∫IdI
= μ0N2SI2/(2l)
= B2Sl/(2μ0). Ker je V = Sl
volumen tuljave, je gostota magnetne energije uB
= WB/V kar
uB = B2/(2μ0)
–
izraz bomo rabili pri izpeljavi hitrosti svetlobe.
Za energiji električnega in magnetnega polja, recimo shranjeni v tuljavi
in kondenzatorju, smo tako zapisali tudi gostoti energij (magnetnega in električnega polja,
sta seveda splošno veljavna zapisa), ker ju bomo rabili pri izpeljavi hitrosti
svetlobe.
Do teh oblik energij smo recimo v šolah še nekako prisopihali –
za kaj več (recimo energije na nivoju atomov) pa smo že opešali.
Premikanje vodnika pravokotno na magnetno polju s hitrostjo v - kaj se zgodi?
Kaj pa se zgodi, če po žici (ki je v magnetnem polju - podkvasti magnet) poženemo električni
tok
(pravokotno na magnetno polje)?
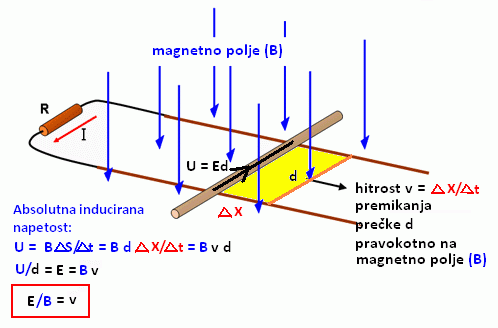
Slika prikazuje preprost eksperiment inducirane napetosti,
pri premikanju s hitrostjo (v) dela žice v sklenjeni električni
zanki pravokotno na magnetne silnice (B). Premikajoča žica dolžine
d v magnetnem polju povzroči, da se v žici začnejo premikati električni
delci - pojavi se električni tok I, ki ga poganja napetost v žici (U = Ed).
Inducirana napetost pa je tudi enaka (negativni) spremembi magnetnega pretoka
(Φ = BS), deljeni s časom spremembe (inducirana napetost zmeraj nasprotuje
spremembi magnetnega pretoka, recimo sila na induciran tok, zavira gibanje
žice, to je Faradayev zakon indukcije:
U = -BΔS/Δt = -BΔS/Δt = -BΔxd/Δt = -vBd).
Razmerje med električnim poljem E in magnetnim poljem B je kar hitrost potovanja
žice: E/B = v (absolutna vrednost). Električno in magnetno polje sta pravokotni,
hitrost pa je pravokotna na ravnino obeh.
To je »preprost« eksperiment,
ki pa je dodobra spremenil ta svet. V teoriji nas je pripeljal do posodobljene
mehanike.
V življenju pa danes večino tehnologij temelji na inducirani napetosti,
električni energiji. Najprej smo preko žabjih krakov prišli do baterije
in ta je omogočila stabilen vir napetosti in s tem eksperimentiranje.
Omenimo še za večino neznanega Williama Sturgeona, ki je leta 1824 kot
samouk (veliko je bral) izumil elektromagnet. Njegov prvi elektromagnet
je bila stara železna podkev (pa naj kdo reče, da podkev ne prinese sreče),
ki jo je ovil s približno 18 ovoji bakrene žice (izolirane žice takrat še
ni bilo). Železo je polakiral, da ga je izoliral od navitja žiče. Ko je z
baterijo pognal tok skozi tuljavo, je železo postalo namagneteno; to je bil
korak v električne generatorje, elektromotorje, transformatorje, v električni
nihajni krog kondenzatorja in tuljave – oddajnike in sprejemnike, v svet
izjemnih novih tehnologij, računalnikov, gospodinjskih pripomočkov ...,
ki so danes temelj moderne družbe – moderne znanstvene metode, tudi astronomije.
Ali nas ta preprost eksperiment z indukcijo pripelje tudi do hitrosti svetlobe?
JA!


Tuljava in kondenzator (levo) in iskrni brezžični
telegraf z uporabo električnega nihajnega kroga na
kondenzator in tuljavo podaljšano v oddajno anteno (desno).
Nekaj podobnega je počel tudi Marconijev telegraf na
Titaniku in na drugih ladjah - to je bil res velik napredek v komunikaciji.
Izkazalo se je, s podobnimi napravami in meritvami,
da je hitrost elektromagnetnega valovanja (svetlobe) v
vakuumu kar:
c = 1/(ε0μ0)1/2 =
1/(8,854187817*10-12As/Vm*4*π*10-7Vs/Am)1/2
c =
(m/s)109/(8,854187817*0,4*π )1/2 = 299792458 m/s
To je maksimalna hitrost potovanja energije - in bistveno določa naravo, energijo
vesolja in s tem čas.
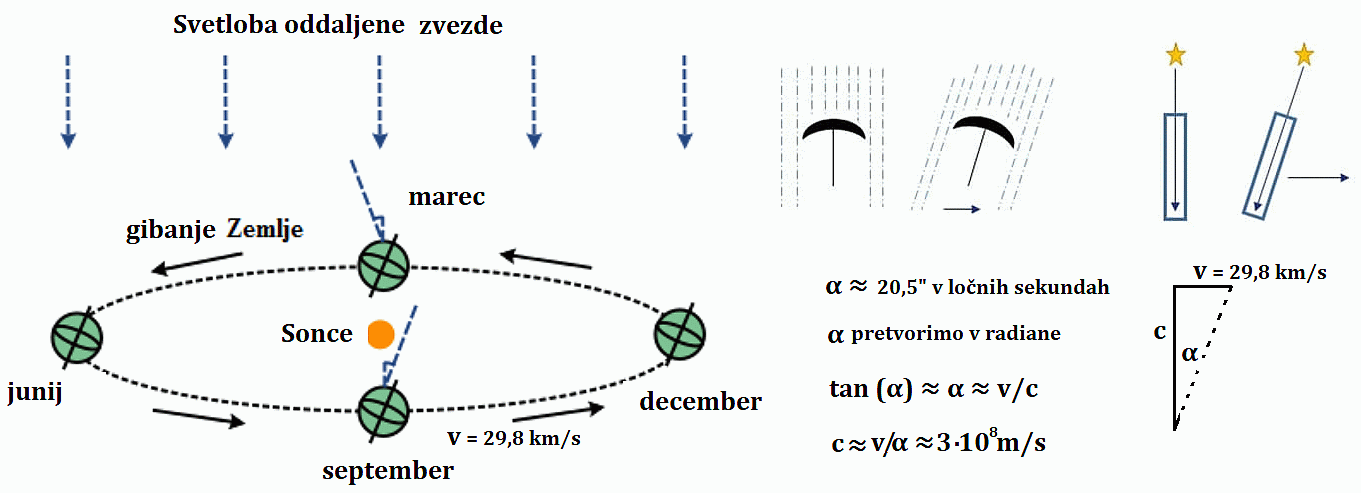




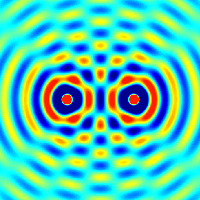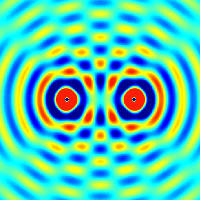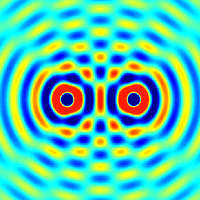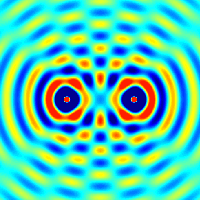
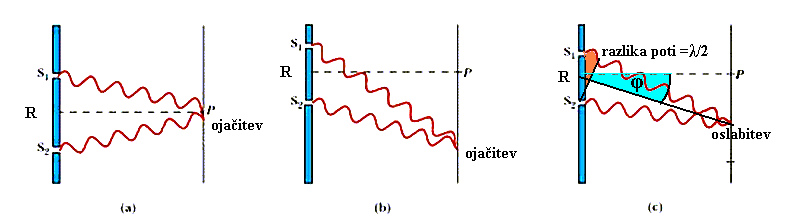
Zgornje slike pozna večina srednješolcev, saj z njihovo pomočjo izpeljejo kriterije za
interferenčne maksimume (razlika poti je enaka večkratniku valovne dolžine λ) in minimume
(razlika poti je enka lihemu večkratniku polovice valovne dolžine,
λ/2) dveh točkastih koherentnih izvorov valovanja na
razdalji R. Povedano zapišimo z enačbama (N je celo število):
R sin(φ) = Nλ
- (koti φmaks pri katerih pride do ojačitev valovanj)
R sin(φ) = (N + 1/2)λ - (koti φmin pri katerih pride do oslabitev valovanj)
Thomas Young je tako sprožil eksperimentalni, kot teoretični preskok v moderno fiziko.
Na osnovi interference sta izvedla iskanje t. i. etra za prenos svetlobe tudi
Michelson in Morley leta 1887. Izdelala sta interferometer z dvema pravokotnima krakoma.
Ideja eksperimenta je bila preprosta: če je svetlobna hitrost konstantna glede na domnevni eter,
skozi katerega se Zemlja giblje, potem bi njeno gibanje lahko določili s primerjavo relativne svetlobne hitrosti
v smeri gibanja Zemlje,
v kateri naj bi veljala za hitrost razlika, oz. vsota svetlobne hitrosti in hitrosti gibanja Zemlje
in s primerjavo svetlobne hitrosti, ki potuje pravokotno
na smer gibanja Zemlje.
Pri čemer se svetlobna hitrost pravokotna na smer gibanja Zemlje naj ne bi spreminjala.
Ker sta po mnenju takratne večine, ti dve hitrosti različni, bi morala oba žarka
prepotovati različen čas do detektorja - ki bi zaznal spremembo interferenčnega vzorca.
Njun rezultat je bil ZAČUDA ničelni, nič se ni zgodilo, nobene spremembe v interferenčni sliki.
Kot bomo videli, je ta ničelni rezultat spravil fizike v veliko zadrego (ni etra,
svetloba v vseh nepospešenih sistemih potuje enako hitro) in čez nekaj 10 let
se je tako rodila nova veja fizike - zelo dolgo zavračana teorija relativnosti.
Preko interference smo tako tudi določili ločljivost optičnih naprav, ki je pričakovano sorazmerna
z vpadno valovno dolžino svetlobe in obratno sorazmerna s premerom objektiva, sorazmernostni
koeficient je 1,22. Na objektivih pride namreč do uklona svetlobe - tudi na zenici očesa -
in ta svetloba interferira in s tem določa mejni kot, ki ga še razločimo na opazovani sliki
(če pade slika objekta v prvi interferenčni minimum, ga še lahko razločimo).
Interferenca svetlobe (elektromagnetnega valovanja) nam pomaga tudi pri raziskavah in študiju medatomskih
razdalj v kristalnih strukturah. Tudi pri razvoju laserjev je interferenca osnovna
predpostavka - razdalja med zrcali v resonatorju laserja ni poljubna (je: L = mλ/(2n), m je celo število,
n je lomni količnik - v resonatorju nastane stoječe valovanje).
S pomočjo interference lahko merimo zelo, zelo majhne premike in je tudi glavna metoda pri detekciji gravitacijskih valov,
kjer je natančnost, ne boste verjeli - vsaj 1000-inka premera protona. Zakaj?
Na podlagi trenutnih modelov astronomskih dogodkov in napovedi splošne teorije relativnosti
se pričakuje, da bodo gravitacijski valovi, ki izvirajo več deset milijonov svetlobnih let od Zemlje,
popačili 4 kilometre (2,5 milje) dolg zrcalni razmik interferometra za približno 10-18 m,
kar je manj kot tisočinka premera naboja protona.
V resnici interferometer lahko zazna spremembo v premiku zrcal (odmaknjenih za 4 km) za manj kot 1/10000
premera protona (to je 10-19 m).
To je enakovredno relativni spremembi razdalje kraka interferometra za približno 1021 del.
To je enako merjenju razdalje med Soncem in zvezdo Proksima Kentavra s točnostjo manjšo kot
je premer preseka človeškega lasu.
Kot smo že omenili, je ločljivost teleskopa odvisna od premera objektiva, večji je premer,
manjši so uklonski koti vpadne svetlobe, več podrobnosti vidimo. In to lastnost smo
uporabili večinoma pri radijski astronomiji, kjer smo na tisoče km oddaljene radijske teleskope
povezali v interferometrično mrežo. Tako se ločljivost enormno poveča - saj je le ta obratno sorazmerna
z razdaljo med teleskopi. To nam je omogočilo snemanje protoplanetarnih diskov pri oddaljenih
mladih zvezdah - kjer se ravno rojevajo mladi planeti ( recimo
protoplanetarni disk HL Tauri - izjemen posnetek ESO sistema radijskih teleskopov
"Atacama Large Millimeter Array" (ALMA) - v disku se vidijo sledi nastajajočih planetov ...
).
Posneli pa smo celo
akrecijske diske na robu, preden padajo v črne luknje v centrih oddaljenih galaksij
(recimo v črno luknjo v centru galaksije M87). Izjemno!
Thomas Young je torej kot začetnik eksperimentalne interference svetlobe sprožil nesluten
razvoj znanosti; tako v smeri razumevanja valovne narave sveta, življenja
kot v smeri izjemne natančnosti merjenj,
beleženje premikov velikostnega reda kvarkov in še manj.
Leta 1845 je Michael Faraday ugotovil, da se ravnina linearno polarizirane
svetlobe (nihanje valov v eni ravnini) vrti, ko svetlobni žarki potujejo vzdolž
smeri magnetnega polja v prisotnosti medija. To je bil prvi dokaz, da
je svetloba povezana z elektromagnetizmom. Faraday je leta 1847 predlagal, da
je svetloba visokofrekvenčna elektromagnetna vibracija, ki se lahko propagira celo v odsotnosti
medija, etra - in imel je še kako prav.

Michael Faraday [májkl feredej], FRS, angleški fizik in kemik, * 22. september 1791, Newington, grofija Surrey,
Anglija, † 25. avgust 1867, Hampton Court pri Londonu, Anglija.
Družina ni imela denarja za šolanje otrok, zato je mladi Michael hodil v šolo
le toliko, da se je naučil brati in pisati.
Leta 1805 je šel za vajenca knjigovezu in prodajalcu knjig Georgeu Riebau. Med prostim časom je v
delavnici bral knjige, mojster, ki je razumel njegovo željo po znanju, pa ga pri tem ni oviral
in mu je celo dovolil obiskovati znanstvena predavanja. Leta 1812 je nek kupec podaril Faradayu
vstopnice za predavanja Humphryja Davyja na Kraljevem inštitutu. Faraday si je med obiskovanjem
predavanj vestno delal zapiske, zvezek pa je na koncu obsegal 386 strani. Micheal je zvezek poslal
Davyju, na katerega so zapiski napravili izreden vtis.
Po tem, ko si je v nekem poskusu Davy poškodoval oči, je zaposlil Faradaya kot tajnika.
Kasneje, ko so na Kraljevem inštitutu odpustili Johna Payna, enega od asistentov, je Sir Humphry
Davy dobil nalogo, da najde njegovo zamenjavo. Ta je 1. marca 1813 na mesto asistenta za kemijo
zaposlil Faradaya.
12. junija 1821 se je poročil s Sarah Barnard.
Ob proučevanju elektrike, magnetizma in kemijskih učinkov električnega toka je Faraday prišel
do mnogih novih spoznanj. Začel je delati kot knjigovez, nato pa je postal pomočnik Humphryja Davyja
na Kraljevem inštitutu v Angliji in ga nazadnje tudi nasledil kot direktor inštituta.
Bil je odličen predavatelj in znanstvenik - čeprav s skromno izobrazbo,
a se je sam izobraževal.
Navduševal se
je nad električnimi pojavi in leta 1821 izumil preprost model elektromotorja. Uporabil je Φrstedovo
odkritje, da električni tok, ki teče po žici, povzroči odklon magnetne igle v bližini žice. Faraday
je tudi poskušal ugotoviti, kako bi s pomočjo magnetizma dobil električni tok.
Svoja odkritja o elektromagnetni indukciji je objavil leta 1831. Istega leta je naredil tudi prvi
transformator in prvi model električnega generatorja. V dveh zakonih o elektrolizi, ki se danes
imenujeta po njem in ki ju je objavil leta 1834, je opisal, kakšne spremembe povzroči električni tok,
ki teče skozi kapljevino. Odkril je tudi kemijsko spojino benzen, diamagnetizem (magnetna lastnost vseh
snovi) in vpliv močnega magnetnega polja na svetlobo. Prvi je poskusil pojasniti delovanje magnetne sile
s pomočjo magnetnega polja, ki nastane okrog magneta. Zasnova polja se je kmalu izkazala kot zelo uporabna
v fiziki, zlasti pri razlagi gravitacijskih in elektromagnetnih pojavov.
Obudimo še izjemno povedno anekdoto o znanosti in ministru.
Eminenten raziskovalec, eksperimentator, samouk in genij Michael Faraday, se je nekoč trudil
razložiti ministru za finance W. Gladstoneu in drugim politikom, kako pomembno je njegovo novo
znanstveno odkritje. Edini komentar Gladstonea je bil: »A navsezadnje, zakaj pa je to sploh
uporabno? Zakaj, gospod,« je odgovoril Faraday: "obstaja velika verjetnost, da boste uporabo
lahko kmalu obdavčili!" Tega dogodka se je spominjal Faradayev prijatelj – najverjetneje je
pogovor tekel o električnem generatorju - indukciji.

James Clerk Maxwell, škotski fizik in matematik, * 13. junij 1831, Edinburgh, Škotska,
† 5. november 1879, Cambridge, Anglija.
Maxwell se je rodil na India Street 14 v znani škotski družini kot edini sin odvetniku Johnu Clerku.
Družina se je zatem preselila na posestvo v Glenlair pri Dumfriesu. Pri 9. letih mu je za rakom umrla
mati, drugače je imel srečno otroštvo.
Že zgodaj je kazal znake nadarjenosti za matematiko. Vpisal se je na Akademijo Edinburgh, kjer so ga klicali
'Dafty'. Tukaj je spoznal Taita.
S 15. leti je leta 1845 poslal Kraljevi družbi v Edinburghu prispevek o načrtovanju ovalnih krivulj
s pomočjo kosa niti. Bil je tako dovršen, da mnogi niso mogli verjeti, da ga je sam sestavil.
Na Univerzi v Cambridgeu je diplomiral kot drugi najboljši v letniku.
Leta 1871 je, čeprav nerad, prevzel mesto profesorja eksperimentalne fizike na Univerzi v
Cambridgeu in postal prvi profesor na tem področju. Kot predavatelj se ni obnesel. Sledilo
mu je lahko le malo študentov, tisti redki pa so veliko pridobili. Ukvarjal se je s teorijo
treh barv (optika), s kinetično teorijo plinov.
Med letoma 1867 do 1873 je odkril zakone elektrodinamike (Maxwellove zakone) in jih zapisal
v znamenitih Maxwellovih elektrodinamičnih enačbah. Teorijo je objavil leta 1873 v Razpravi
o elektriki in magnetizmu (Treatise on Electricity and Magnetism).
Maxwell je s pomočjo izjemnega Faradaya pokazal, da je svetloba elektromagnetno valovanje. Po njem se imenuje dopuščena
merska enota za magnetni pretok Maxwell (M). Znana je Maxwellova porazdelitev števila molekul
ali atomov v razredčenem plinu.
Faradayevi rezultati so
navdihnili Jamesa Clerka Maxwella, da je začel študirati elektromagnetno sevanje, svetlobo. Maxwell
je odkril, da elektromagnetni valovi poljubnih valovnih dolžin potujejo skozi vesolje s
konstantno hitrostjo, ki je enaka svetlobni (c = 299792458 m/s). Iz teh
računov je Maxwell sklepal, da je svetloba oblika elektromagnetnega sevanja: prvič je
ta rezultat navedel leta 1862 v "On Physical Lines of Force". A
Maxwell je, za razliko od Faradaya, napačno trdil, da svetloba potuje po
nekem etru - po analogiji z zvokom, ki rabi recimo zrak za
širjenje v prostor. Leta 1873 je objavil razpravo o elektriki in magnetizmu,
ki je vsebovala matematični opis lastnosti električnih in magnetnih polj, danes znanih
kot Maxwellove enačbe (še zanimivost, knjigovez Faraday je znal le pisati in
brati – za kaj več ga niso poslali v šole - a
so bila njegova predavanja zmeraj polna poslušalcev, Maxwell pa je bil študiran
matematični genij, a je predaval skoraj prazni predavalnici – karizma, katera energija
je že to?). Maxwell je enačbe v prvotni obliki zapisal s kvaternioni
(kjer velja: i2 = j2 = k2 = ijk = -1
in kvaternion je definiran kot q = a + bi + cj
+ dk, pozneje so raje vpeljali vektorski zapis).
Kvaternioni imajo vključeno tudi
skalarno komponento, ki je vektorji nimajo (zanje tudi ne velja zakon komutativnosti,
ko qp ni enako pq, kar je večino stroke odvrnilo od kvaternionov).
Izbira določenih pravil lahko tudi vpliva na globino matematičnega zapisa naravnih procesov
in končne sklepe – in to si velja zapomniti – ali se
res učimo optimalno matematiko(?).
James Clark Maxwell je tako tudi dokazal –
preko teorije elektromagnetizma - da je hitrost svetlobe v vakuumu povezana z
drugima dvema naravnima konstantama, dielektrično konstanto
ε0 = 8,854187817×10-12 As/Vm in indukcijsko
konstanto (permeabilnostjo)
μ0 = 4π10-7 Vs/Am v vakuumu.
Velja preprosta
povezava:
c = 1/(8,854187817*10-12As/Vm*4*π*10-7Vs/Am)1/2 = (m/s)109/(8,854187817*0,4*π)1/2 = 299792458 m/s
Obe konstanti (
ε0,
μ0 ) smo zagotovo spoznali med poukom
fizike pri električnem in magnetnem polju pri računanju sil, napetosti ter indukcije.
Ta povezava je bila in je še zmeraj izjemno pomemben dosežek znanosti.
Zapišimo eno izmed modernih oblik Maxwellovih enačb s skicami in kratko razlago.
Te enačbe so Lorentza pripeljale do relativnostne teorije, ki jo je Einstein
dopolnil in javno zagovarjal. Poudarimo še, da brez relativnega časa,
vezanega na opazovalni sistem, Maxwellove enačbe ne bi bile enake za
vse inercialne sisteme – vsak inercialni sistem (nepospešeni opazovalec)
namreč pomeri enako hitrost elektromagnetnega valovanja:
1/c2 = ε0μ0, in
matematično-fizikalni opis mora to upoštevati. Kot pomoč pri razumevanju
Maxwellovih enačb so nam lahko tudi uvodne slike osnovnih sil in polj,
ter same skice zraven enačb.
εo je
influenčna in µo indukcijska konstanta.
E je električno polje in B je magnetno polje (magnetni pretok je
Φ = BS, q je naboj, A je površina,
s je dolžina, i je tok):
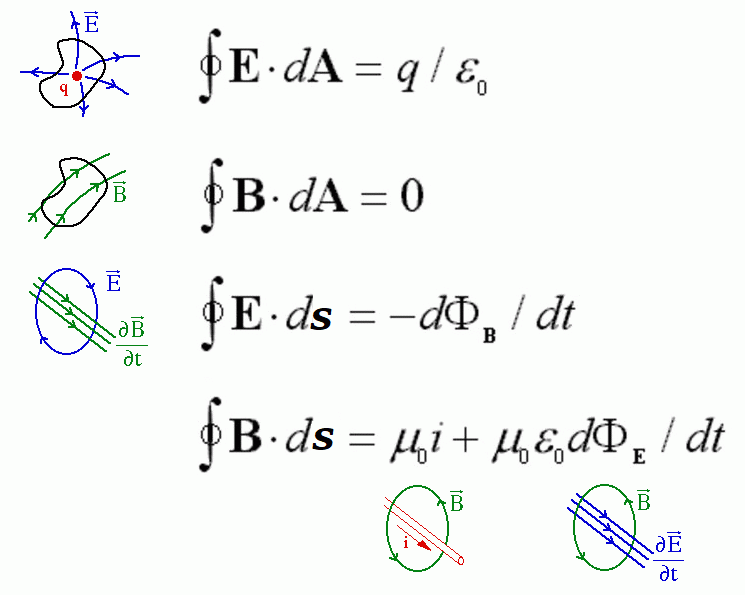 |
Električni (E) pretok skozi zaključeno ploskev (A) je enak objetemu naboju
q ali e (Gaussova zakona o pretoku). Ali: ∇·E = ρ/ε0, kjer je gostota naboja ρ = e/V Magnetni pretok (B) skozi zaključeno ploskev (A) je enak nič – magnetne silnice so namreč zmeraj sklenjene. Ali: ∇·B = 0 V zanki inducirana napetost (U = ∳Eds) je enaka negativni časovni spremembi objetega magnetnega pretoka ( dΦm/dt = d(BS)/dt - Faradayev indukcijski zakon). Ali: ∇xE = - ∂B/∂t Magnetna napetost (∳Bds) vzdolž zaključene zanke je enaka vsoti objetih tokov in premikalnih tokov (Amperov zakon). Ali: ∇xB = μ0j + ε0μ0∂E/∂t j = i/A = i/S je gostota el. toka |

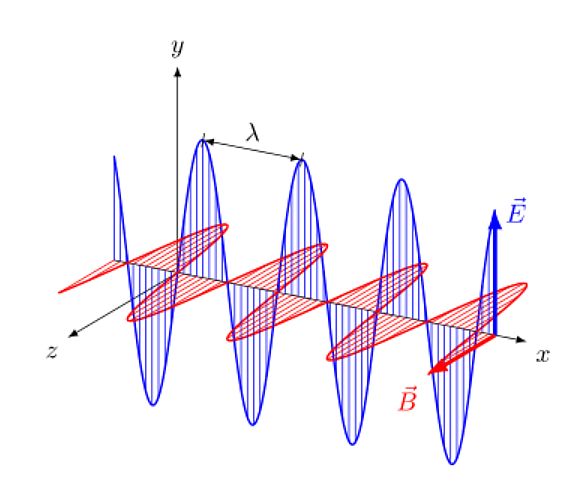
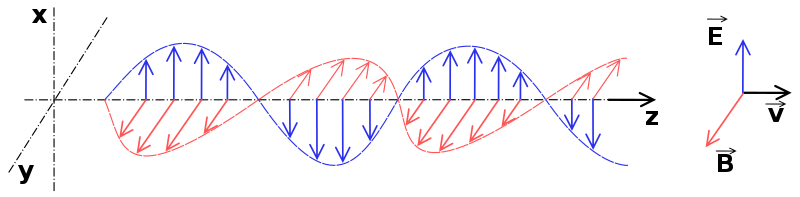


|
|
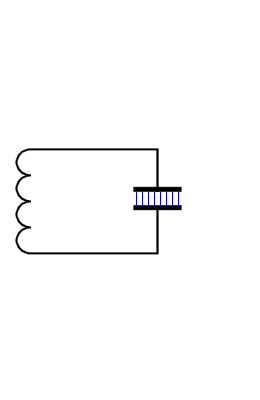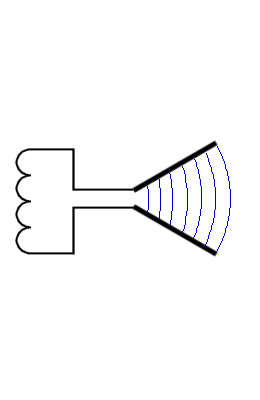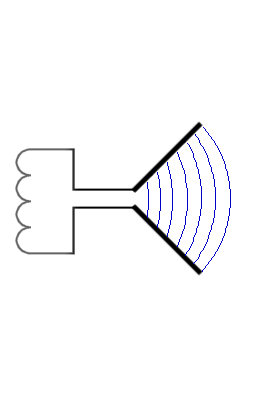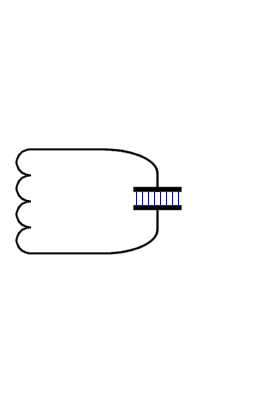
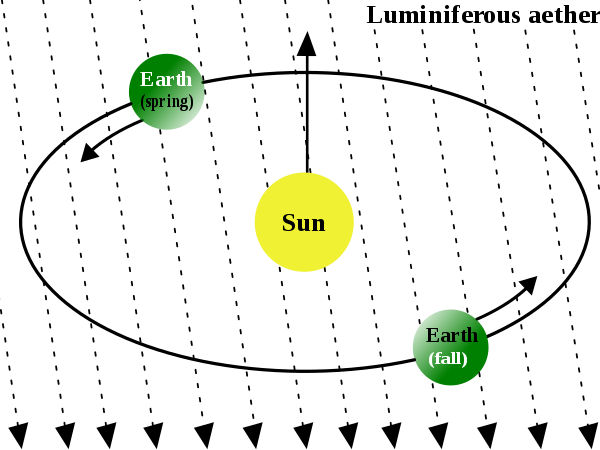
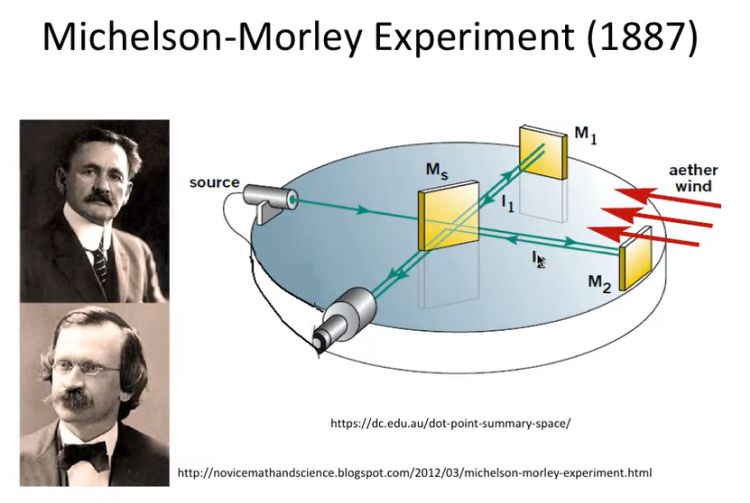
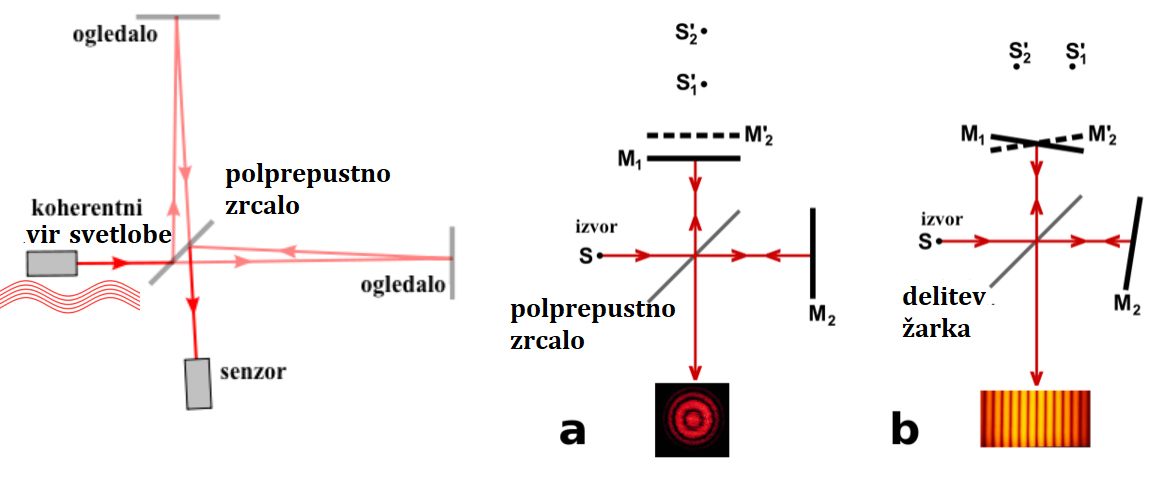
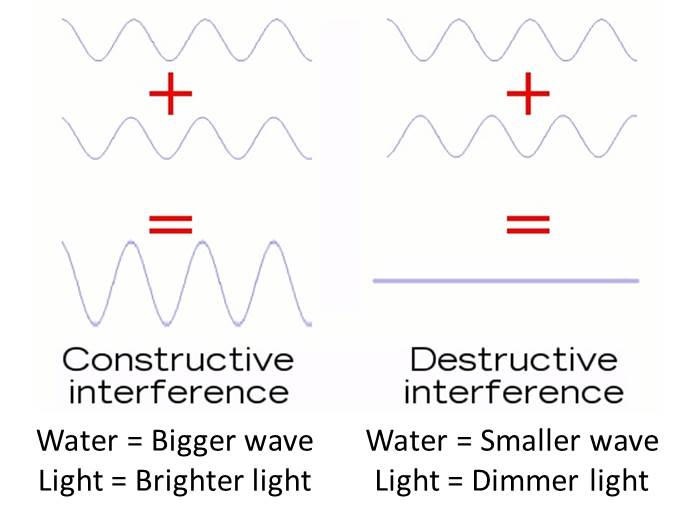

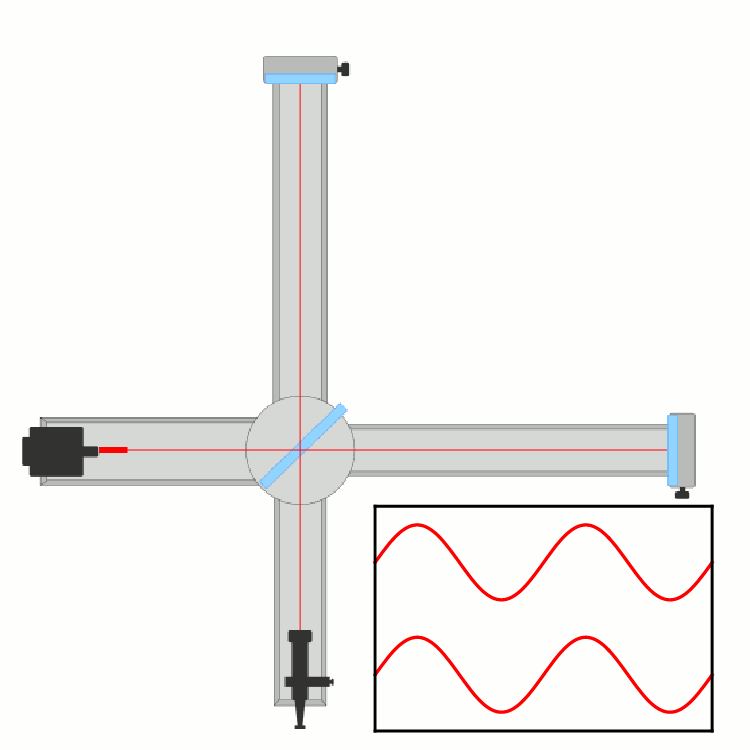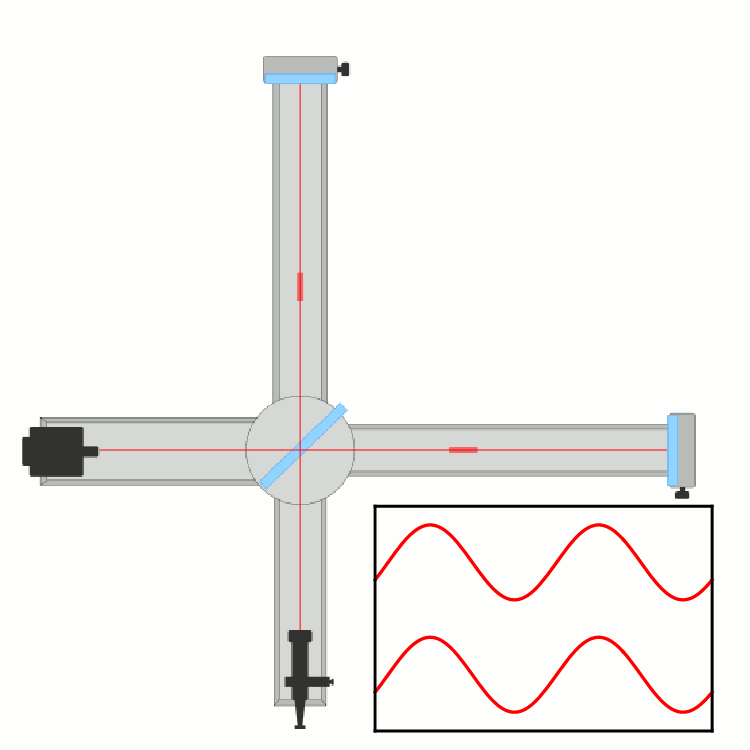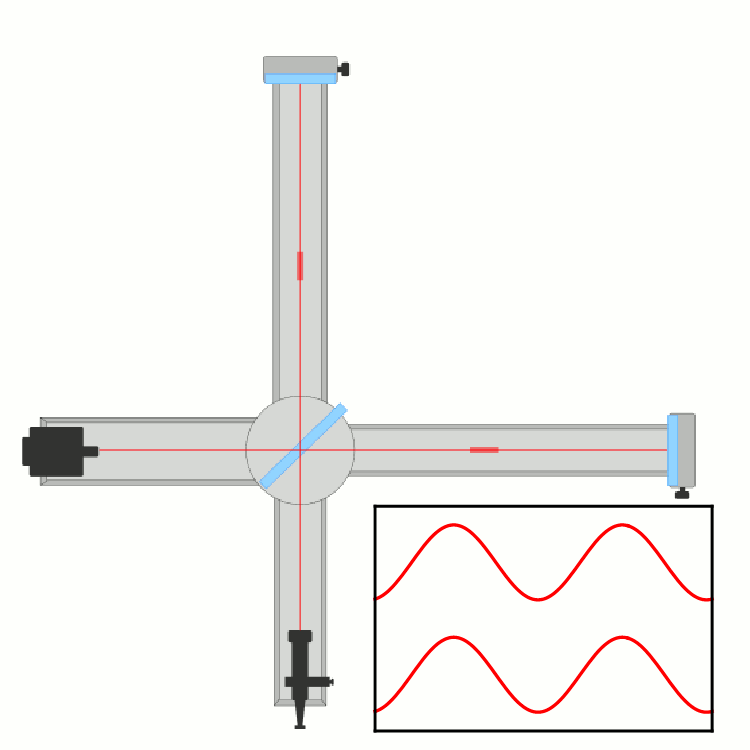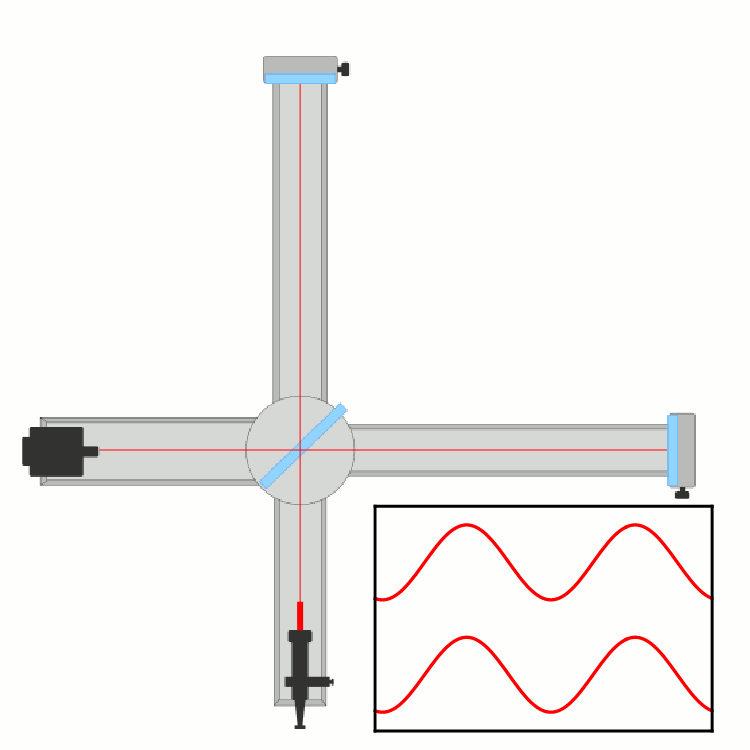 Mirujoč interferometer da interferenčne maksimume odbite koherentne svetlobe, saj žarka fazno sovpadata, med njima ni razlike glede na prepotovani poti (sočasno prispeta do senzorja). |
V smeri gibanja Zemlje bi naj bil čas odboja do prečnega ogledala: tl = L/[c - v] + L/[c + v]. Razlaga je spodaj. |
V pravokotni smeri glede na gibanje Zemlje bi naj bil čas odboja: tt = 2L/(c2 - v2)1/2. Razlaga je spodaj. |
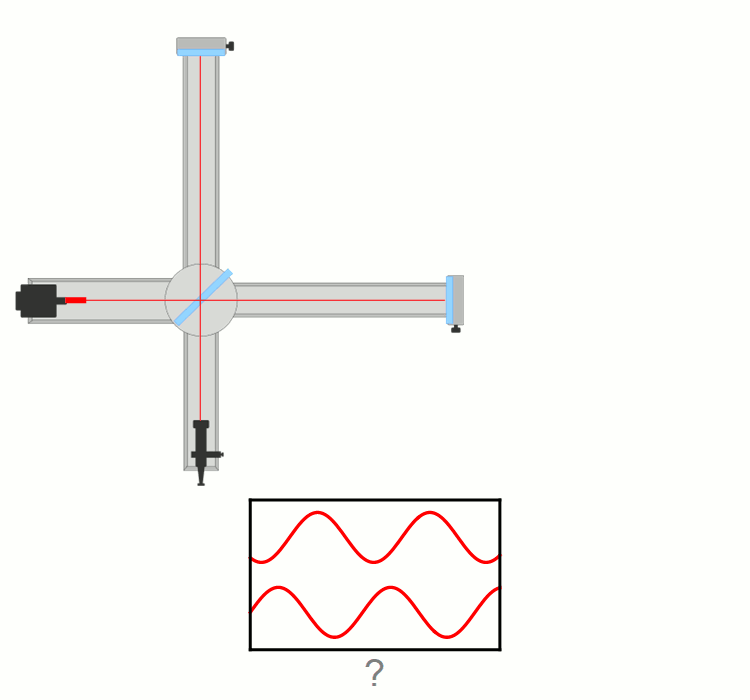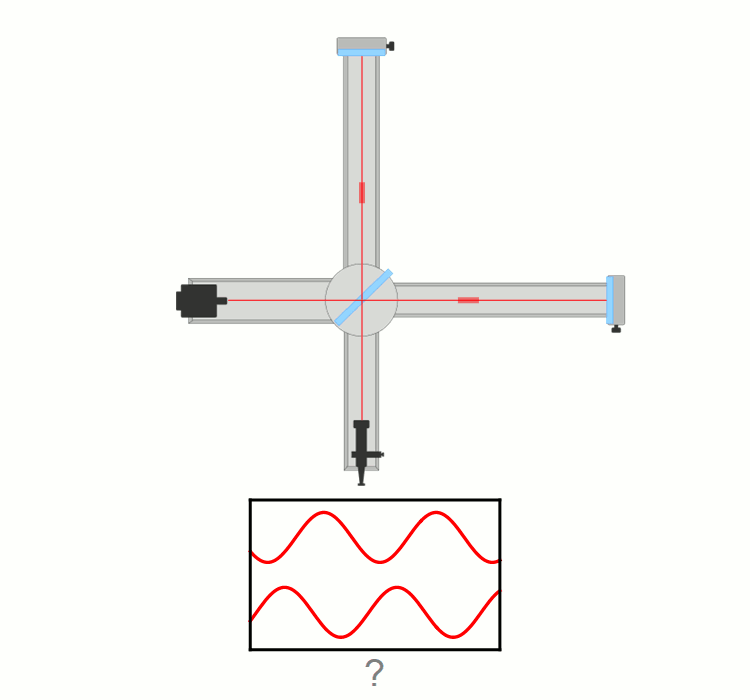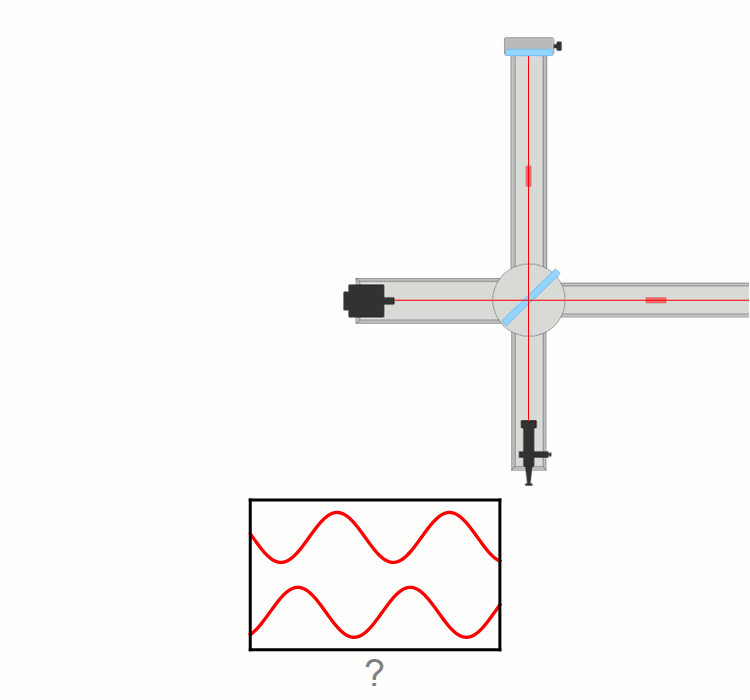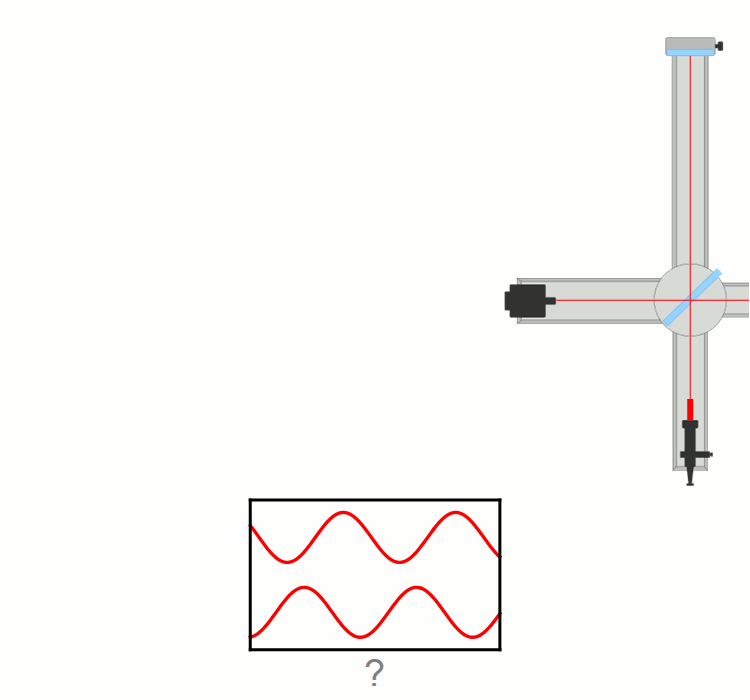
A interferometer med gibanjem ni pokazal razlike v času - v poti svetlobe - zato je na sliki vprašaj (?) TOREJ ni prišlo do spremembe interferenčne slike glede na mirovanje (prva slika levo zgoraj). Zakaj se pričakovanja na sliki niso izpolnila ? |

Poglejmo še, od kod faktor krčenja v smeri gibanja?
Ker niso zaznali spremembe interferenčnega vzorca, cΔt = 0, so sklepali, da s v smeri gibanja
dolžina skrči (označimo z malo črko l). Poglejmo od kod ta že omenjen
faktor krčenja 1/γ = (1 - v2/c2)1/2. Še enkrat
zapišimo časa, a brez približkov:
tl
= (2 l/c)/(1 - v2/c2) = (2 l/c)γ2
tt = (2L/c)/(1 - v2/c2)1/2 = (2L/c)γ
Časa odštejemo in kdaj bo razlika cΔt = 0 ?
Δt = tl - tt = (2l/c)γ2 - (2L/c)γ
= (2/c)γ(lγ - L) = 0
Δt = 0 , ko velja:
(lγ - L) = 0, od koder sledi, da je l :
l = L/γ = L(1 - v2/c2)1/2
Dolžina l v smeri gibanja se torej skrči glede na L (dolžina ob mirovanju) za faktor
1/γ = (1 - v2/c2)1/2
.
Tega dejstva večina laikov in fizikov ni sprejela skoraj 20 let.
Omenili smo še eno "NORO" dejstvo, da
čas ni več enak za gibajočega
in mirujočega opazovalca
- od kod ta sklep?
Če analiziramo sliko poti žarka pravokotno na smer gibanja,
dobimo trikotnik poti in čas odboja (izpeljan prej):
t
= (2L/c)/(1 - v2/c2)1/2 = (2L/c)γ
To je čas (t) za opazovalca "zunaj" interferometra.
Kaj pa bi izmeril opazovalec v interferometru (čas t', ki ni enak času t) -
videl bi navpično pot žarka navzgor in navzdol.
Opazovalec, ki se premika z zrcalom na stropu višine
L, zazna navpično gibanje svetlobe in temu primerno izmeri
čas potovanja svetlobe do stropa po preprosti povezavi
(L/c) -
čas ponovne zaznave svetlobe je kar opravljena
pot
(2L – pot
do stropa in nazaj) deljena s hitrostjo
svetlobe:
t' = 2L/c
Če izenačimo iz obeh enačb vertikalo L = ct'/2 in še L = ct/(2γ), dobimo:
ct/(2γ) = ct'/2
Tako je povezava med urama v interferometru (čas t') in zunaj (čas t):
t = γt' = t'/(1 - v2/c2)1/2
Evidentno je, čeprav se je na začetku to zdela zgolj matematika, da je čas
odvisen od sistema - hitrosti! "Opazovalec" v interferometru izmeri krajši čas
t' = t/γ = t(1 - v2/c2)1/2.
Ali se to sklada s krčenjem dolžini v smeri gibanja - preverimo? Velja t'/t = 1/γ.
in v gibajočem sistemu velja 2ct' = 2L. Za x smer velja (izpeljali zgoraj) 2ct = 2lγ2
Od koder sledi (2L = 2ct' pomnožimo in delimo s t):
2ct't/t = (2ct)(t'/t) = 2lγ2/γ = 2L
Torej velja:
lγ = L
Zunanji opazovalec vidi torej skrajšano dolžino l, ko velja:
l = L/γ = L(1 - v2/c2)1/2
Najdaljša je torej tista dolžina predmeta, ki jo izmeri opazovalec,
ki potuje skupaj s predmetom (v našem primeru v interferometru).
Tako smo pokazali, da ni neskladja med različnima časoma (t in t') in dolžinama
(l in L),
le odvisnost je obratna in jo določa Lorentzov člen gama γ
= 1/(1 - v2/c2)1/2.
In to je dokazal zelo brihten Michelson–Morleyjev eksperiment iz leta 1887,
ki je hotel odgovoriti na staro trditev mnogih, da
(ali) svetloba potrebuje snov za gibanje (t. i. "eter") - kot recimo zvok rabi plin, zrak.
Dobili smo odgovor, da svetloba ne potrebuje etra in da lahko potuje tudi v vakuumu!!!!
In hkratna kolateralna korist je bila izjemna - TO JE relativnostna teorija!
Ki pa je recimo, kot lahko preberemo, Nobelovec Albert Abraham Michelson nikoli ni sprejel,
čeprav je eksperimentalno eden od utemeljiteljev, praoče posebne teorije relativnosti.
Večkrat se zgodi, da oče ne prizna sina,
ki je nato izjemno uspešen!
Prvo serijo meritev je Michelson naredil v Potsdamu leta 1881
z denarjem podpornikov in s svojim lastnim. A je bankrotiral in doživel še živčni zlom,
etra pa ni in ni izmeril, ker ga ni. To samo kaže, kako je znanost draga, rezultati pa, tudi če so pravilni,
ne zagotavljajo nujno tudi preživetja. Ko znanost le sprejme rezultate, ker so pravilni, je usoda
znanstvenikov lahko že zaključena v revščini in razočaranju, brez prijateljev in družine ..., lahko so že
pokojni. A problem Michelsona in Morleyja je bil, da nikoli nista v celoti sprejela
ničelnega rezultata svojih izjemnih meritev (posledica je izjemna teorija relativnosti)
- kdaj se ljudje torej ne znamo veseliti svojega uspeha ali
pa ga sploh ne prepoznamo, celo ne razumemo (a smo vseeno bistveno prispevali k razumevanje narave).
Michelson niti Morley torej nista nikoli prenehala verjeti v eter.
Arthur Conan Doyle je nekoč zapisal, da imajo »nekateri ljudje, ki nimajo genija,
izjemno moč, da ga spodbujajo«. Morley to zamisel odlično potrjuje. Za življenja
ni bil slaven; javnost zanj ni bila pozorna. Pa vendar so njegova napačna sklepanja vodila
druge do izjemnih idej.
Kaj pa danes - so vse naše domneve pravilne?
Temna snov, temna energija ... ali je možno, da bomo te koncepte nekoč,
tako kot eter, ki bi naj prenašal svetlobo,
morali zavreči? Zagotovo sta temna snov in temna energija plod merilnih rezultatov.
Problem pa je, da trenutno še ne vemo, kaj ju sestavlja, ne poznamo točno njune narave,
razen posledic delovanja ... V tem je razlika z etrom, ki so ga preko
koncepta mehaničnega valovanja teoretično predvidevali tudi za elektromagnetno valovanje, a nikoli izmerili.
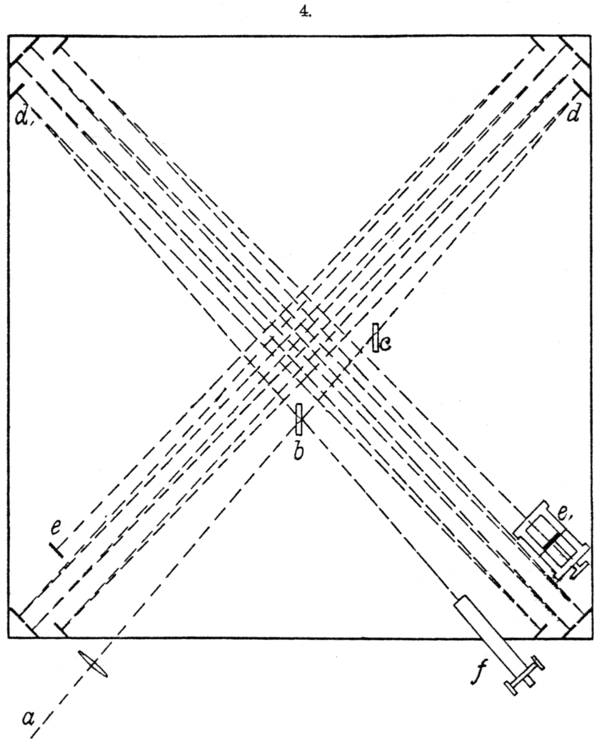

Ta slika (levo) ponazarja odbojno pot svetlobe
uporabljeno v Michelson–Morleyjevem interferometru,
ki je omogočil
dolžino poti kar 11 m. Vir svetlobe je bila oljenka. b je razdelivec žarka
(polprepustno zrcalo).
c je kompenzacijska plošča, tako da tako odbiti kot oddani žarek
potujeta skozi enako količino stekla (pomembno, ker so bili poskusi
izvedeni z belo svetlobo, ki ima izjemno kratko koherenčno dolžino,
kar zahteva natančno ujemanje dolžin optične poti, da so robovi vidni.
Enobarvna natrijeva svetloba je bila uporabljena le za začetno poravnavo zrcal - poti.
- d, d' in e so zrcala. e' je ogledalo s fino nastavitvijo. f je "teleskop".
Slika desno. Michelson-Morleyjeva postavitev interferometra
na kamnito ploščo,
ki plava v koritu živega srebra - da bi zmanjšali vibracije, lažja rotacija.
Postavljen je bil v Clevelandu.
Tudi pri detekciji gravitacijskih valov so uporabili podoben interferometer (LIGO - jih je več)
s čim daljšo potjo (4 km dolgi roki) - s
tem se poveča občutljivost, kot kažejo naši računi.
Interferometri so izjemno koristni senzorji, merilne naprave
majhnih premikov - so tudi resnični začetniki relativistične
mehanike.

Če se malo pohecamo, "Michelson-Morleyjev interferometer" (IDEJA), je dala "pozitiven" rezultat komaj
pri detekciji gravitacijskih valov (tokrat smo res zaznali spremembo interferenčnega vzorca - projekt LIGO,
pri njem je sodeloval tudi naš prof. astronomije dr. Andrej Čadež).
A tokrat se dolžina krakov spremeni zaradi gravitacijskega vala, spremembe dimenzij samega
prostor-časa ...
Tako se je krog sklenil.
Michelson-Morleyjev interferometer (princip) je utemeljil relativnost (s katero pa se Michelson in Morley nikoli nista sprijaznila ...!)
in hkrati potrdil
enega zadnjih nerešenih problemov napovedi splošne relativnosti -
neposredno je zaznal gravitacijske valove. RES FASCINANTNO!
Izjemen observatorij LIGO (Livingston - Louisiana) smo po nekem srečnem naključju ali pa tudi ne, obiskali 11. aprila 2024
po srečno uspešnem
opazovanju Sončevega mrka 8. aprila 2024 v ZDA - Texas.
LIGO je kratica za: Laser Interferometer Gravitational-Wave Observatory.
Tukaj se še enkrat kaže izjemna genialnost (skromno šolanega) Faradaya,
ki je (glede na naravo svetlobe, ki je
elektromagnetno valovanje)
trdil, da svetloba ne rabi etra za prenos, kot ga tudi ne potrebuje indukcija ...
Faradaya tudi prvi eksperimentalno (preko zasuka polarizacije svetlobe ob potovanju vzdolž magnetnega polja)
poveže svetlobo z električnim in magnetnim poljem.
Kdaj je torej dobro, da obstajajo dvomljivci - ne, ker bi imeli (vedno) prav,
ampak ker njihova zavrnitev lahko rodi nove dokaze, nove resnice -
v tem primeru relativnost preko interferometra za iskanje t. i. "etra".
Pravijo, da se ni pametno prepirati z "norci".
Najbrž res - a kdaj lahko pametni in umirjeni argumenti nasproti "norcem" rodijo nekaj veličastnega.
In o tem izjemnem fenomenu bo tekla beseda (izračuni) v naslednjih nekaj poglavjih - o fiziki
velikih hitrosti, energij!

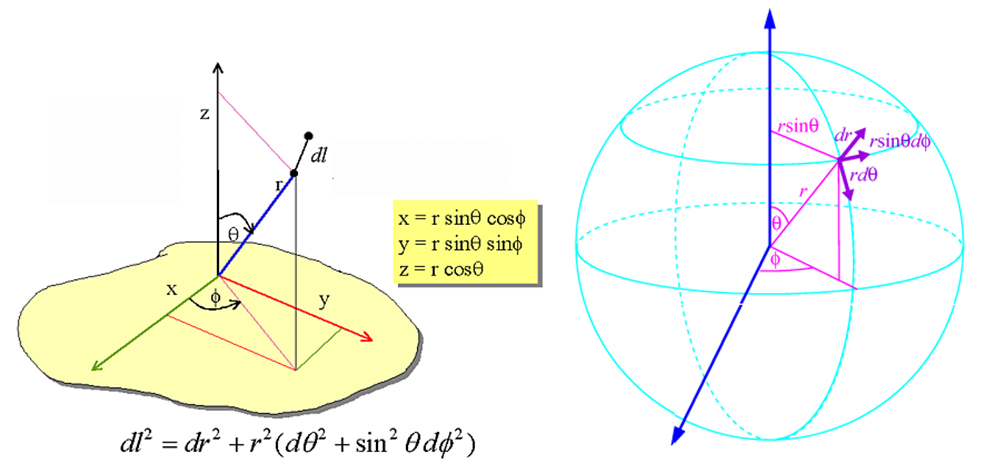 | 
|
Zgoraj sta podana dva sklopa slik in nekaj končnih enačb zapisa metrike (izračuna razdalj 'ds') in energij pri visokih hitrostih
in potem še v gravitaciji sferičnih teles. Te izraze hočemo razumeti, pot do tja je zelo poučna, a
začnimo to poglavje tako kot smo končali prejšnjega. Prehojene poti nam ne bo žal.


Levo - Albert Abraham Michelson, nemško-ameriški fizik, * 19. december 1852,
Strelno, Posen, Prusija (sedaj Strzelno,
Poljska), † 9. maj 1931, Pasadena, Kalifornija, ZDA.
Desno - Edward Williams Morley, ameriški fizik in kemik, * 29. januar 1838, Newark,
New Jersey, ZDA, † 24. februar, 1923, West Hartford, Connecticut, ZDA.
Michelson in Morley sta (skupaj s sodelavci) dobesedno tlakovala (interferirala)
pot v fiziko velikih hitrosti, pospeškov in energij.
Nadvse nepričakovan ničelni rezultat njunih interferometričnih
meritev med iskanjem t. i. etra (ki ga ni) za prenos svetlobe je šokiral prav vse,
ki so se zavedali (ni jih bilo veliko),
da po tem eksperimentu ne bo nič več tako
kot je bilo pred njima (velja tako za fiziko, astronomijo, kemijo, biologijo,
filozofijo, pogled na stvarstvo ...).
Tudi sama se na začetku nista čisto zavedala, kaj sta naredila.
Ne samo, da sta dokazala da "eter" (x-snov) ni potreben za prenos elektromagnetnega
valovanja. Dokazala sta še, da je svetlobna hitrost v vakuumu konstanta v vseh nepospešenih sistemih -
je tudi maksimalna
možna hitrost prenosa energije na daljavo.
Pokazala sta še, da sta čas in dolžina odvisna od opazovalnega sistema,
hitrosti, pospeškov (gravitacije, ukrivljenosti prostor-časa), energij.
Posredno sta stopila še na pot rešitve stare uganke, od kod zvezdam toliko energije,
da lahko svetijo z izjemnimi izsevi milijarde let dolgo. Zvezde so tako preko
fuzije proizvedle
(še proizvajajo)
kemijske elemente za nastanek življenja ...
Vse poti moderne fizike torej vodijo do Michelson - Morleyjevega eksperimenta.
EKSPERIMENT ŠTEJE!
Dolžina krivulje - ponovitev - in v tem poglavju se skriva bistvo metrike (dolžina krivulje, poti)
Določanje dolžine loka krivulje (recimo za kartezični koordinati x in y) je v bistvu seštevanje
majhnih koščkov krivulje, ki se izračunajo kar po Pitagorovem izreku
kot hipotenuze katet Δx in Δy (glejte sliko), velja:
Δs2 = Δx2 + Δy2
V limiti in v postopku inetgracije (seštevanja koščokov) veljajo naslednji zapisi:
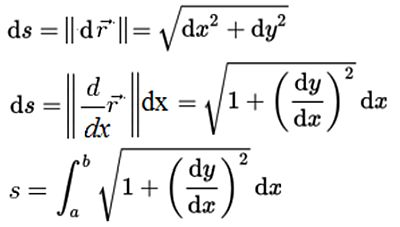 |
 |
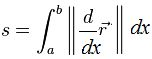
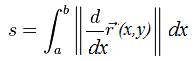
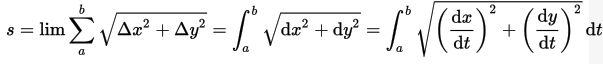
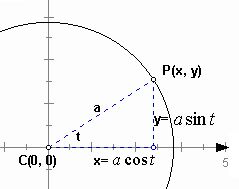
Δt = γΔt'
Upoštevajmo povedano in naredimo eksperiment z dvema opazovalcema, prvi naj miruje, drugi pa naj potuje (avto, vlak, raketa ...) in izseva svetlobo, ki se mu odbije nazaj od zrcalnega stropa. Predstavljajmo si torej prvega opazovalca v vozilu s hitrostjo (v), ki meri čas (Δt') med izsevom svetlobe in njeno ponovno detekcijo (zaznano po odboju od zrcala na stropu vozila na višini Lo) in drugega opazovalca, ki miruje, a hkrati opazuje gibajoči se sistem (prvega opazovalca z lučko) in meri čas (Δt) med dogodkoma, izsev svetlobe in vrnitev po odboju. Če je hitrost (v) vozila majhna v primerjavi s hitrostjo svetlobe (c), sta čas Δt in Δt' enaka, če pa je hitrost vozila primerljiva s svetlobno, pa sledi veliko presenečenje – izpeljali bomo Lorentzov člen (faktor) γ = 1/(1 – v2/c2)1/2, ki povezuje čas t in t'. Na koncu velja transformacija med časoma: Δt = Δt'/(1 – v2/c2)1/2. Pokažimo, od kod ta dokaj nepričakovana povezava.

Opazovalec, ki se premika v vozilu z zrcalom na stropu višine
Lo, zazna navpično gibanje svetlobe in temu primerno izmeri
čas potovanja svetlobe do stropa po preprosti povezavi
(Lo/c) -
čas ponovne zaznave svetlobe je kar opravljena
pot
(2Lo – pot
do stropa in nazaj) deljena s hitrostjo
svetlobe:
Δt' = 2Lo/c
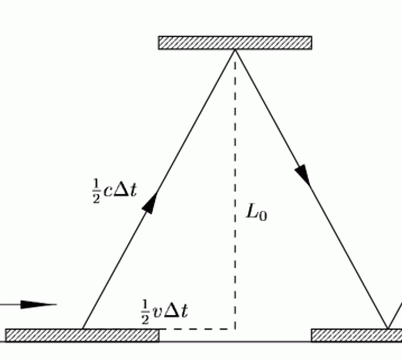
Opazovalec, ki miruje in gleda od zunaj izsev in detekcijo odbite
svetlobe, pa opazi, da žarek potuje poševno (saj se je vozilo premaknilo
za razdaljo vΔt). Ker je v vakuumu hitrost svetlobe neodvisna od tega,
kako hitro potuje vir, ki je svetlobo oddal (načelo invariantnosti svetlobe),
velja da je pot D do stropa dolga kar cΔt/2 (hitrost svetlobe krat polovični čas),
enako velja za pot po odboju. Iz slike razberemo geometrijo dogodka, kjer opazimo
pravokotni trikotnik s hipotenuzo D = cΔt/2 in katetama Lo in vΔt/2. Iz Pitagorovega
izreka izpeljemo povezavo med časom Δt, hitrostjo svetlobe (c) in hitrostjo vozila
(v), namesto Lo pa vstavimo čas iz Δt' = 2Lo/c, od koder sledi
Lo = Δt'c/2,
tako velja:
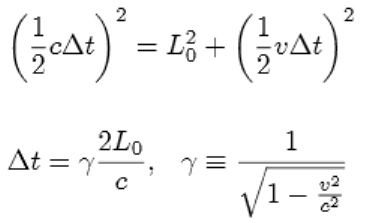
Sledi končni rezultat za povezavo med časoma Δt in Δt'.
Δt = γΔt'
Tako smo izpeljali povezavo med časoma v dveh sistemih, ki se relativno
gibljeta. Ta zamik časa opazimo izrazito le pri hitrostih (v), ki
so primerljive s svetlobno hitrostjo (c), a še zmeraj manjše. Zadnji
izraz torej podaja izjemno pomembno povezavo med časoma v dveh
sistemih. Velikokrat čas t' označujemo s simbolom
tau τ
in ga
imenujemo lastni čas (proper time) –
čas v sistemu, v katerem se dogodek zgodi.
Nekateri fiziki formalno oporekajo tej izpeljavi - oporekajo predpostavkam o merjenju časa.
Zakaj?
Uporaba Pitagorovega izreka pomeni, da predpostavimo enotno definicijo časa v sistemu opazovalca — kar
že predpostavlja Einsteinovo sinhronizacijo ur (implicitno je torej vključena relativnost sočasnosti).
Uporablja se posebna ura — svetlobna ura, postavljena navpično.
Kritiki (npr. Rindler, Landau) pravijo: ni dokazano, da se vse ure upočasnijo enako, rezultat bi torej naj veljal
le za navpično svetlobno uro (svetlobna ura se obravnava le v eni smeri - pravokotno na gibanje).
Toda eksperimentalno in teoretično se da dokazati, da je to splošno res (tudi z drugimi vrstami ur).
Popolna strogost zahteva torej še dokaz, da ta formula velja za čas v vsaki smeri,
kar se v celoti pokaže šele z Lorentzovimi transformacijami (so zapisane in izpeljane pozneje).
Strogo formalistično - matematično - ji nekateri oporekajo,
češ, da vrne
pravilen rezultat, a da to ni samostojna izpeljava.
A recimo Einstein, French, Resnick pravijo, da je ta pot odlična za razlago bistva posebne teorije relativnosti,
je pedagoška in intuitivna.
Velja tudi, da je ta geometrija (uporaba Pitagorovega izreka za pot svetlobe) direktno posledica
postavitve Michelson - Morleyjevega eksperimenta, samega koncepta interferometra (kar smo
omenili že v uvodu v fiziko velikih hitrosti).
Skrčenje dolžin (kontrakcija)
Dolžina gibajoče palice L' se za mirujočega zunanjega opazovalca skrči na L, velja:
L = L'/γ
Izvedimo vajo merjenja dolžine palice, ki potuje in z njo tudi eden od opazovalcev, kakšno dolžino torej izmerita zunanji opazovalec (L) in opazovalec, ki potuje s palico (L')?
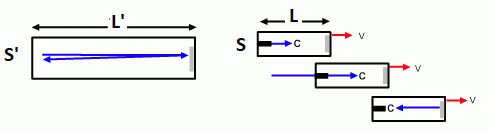
Metoda merjenja dolžine palice (razdalj) naj spet temelji na oddanem, nato odbitem in
(spet) prejetem žarku svetlobe (velja: L' = ct'/2, če palica in opazovalec drug glede
na drugega mirujeta). Kako pa tako merjenje (dolžino) vidi nekdo, glede na katerega se
palica giblje?
Naj torej sistem S' potuje s hitrostjo v. V njem je tudi palica dolžine L' z zrcalom na
koncu. Prvi opazovalec, torej v sistemu S', pošlje iz začetka palice žarek proti zrcalu
na drugem koncu palice dolžine L' = ct'/2 in počaka, da se odbiti žarek vrne v izhodišče. Kako
pa vidi dogodke drugi opazovalec v sistemu S, ki »miruje« glede na prvega opazovalec v
sistemu S'. Tudi drugi opazovalec bo izmeril čas vrnitve žarka, označimo ga s t (brez
črtice). Iz tega časa bo določil dolžino palice L (brez črtice). Seveda pa zunanji opazovalec
tudi opazi, da se palica premika, in da bo zato oddani žarek dohitel zrcalo nekoliko pozneje,
saj je relativna hitrost žarka pri lovljenju zrcala enaka c-v, pri odboju pa je hitrost c+v
(glejte sliko). Čas t do povratka žarka je torej
t = L/(c-v) + L/(c+v) = L2c/(c2 – v2).
Ker pa smo že v prvem koraku izpeljali povezavo med časoma v gibajočem in mirujočem sistemu,
jo tudi uporabimo, velja
t = γ·t' = γ·2·L'/c,
iz česar sledi, ker velja (če ponovimo: t = γ·t' in t = L2c/(c2 – v2) in t'= 2·L'/c):
γ·2·L'/c = L·2·c/(c2 – v2),
- oziroma
γ·L' = L·c2/(c2 – v2)
= L/(1 – v2/c2) = L·γ2.
Iz zadnjega izraza izhaja, da je izmerjena dolžina palice L
(za opazovalca, ki miruje glede na gibajočo palico) krajša od dolžine
L', ki je izmerjena v sistemu v katerem palica miruje (v našem primeru
se palica giblje skupaj s prvim opazovalcem in zato zanj miruje). Končni
rezultat za izmerjeno dolžino premikajoče palice je:
L = L'/γ = L'(1 – v2/c2)1/2
Čeprav je zgornja razlaga krčenja dolžin fizikalno pravilna in skladna z rezultati posebne teorije relativnosti,
ji nekateri fiziki-teoretiki
oporekajo kot »izpeljavi« v strogem pomenu besede. Zakaj?
Ni popolnoma samostojna izpeljava saj
uporabimo že znan rezultat — časovno dilatacijo — ki pa sama izvira iz Lorentzovih transformacij (zapisane spodaj).
Torej je ta »preprosta izpeljava« v resnici posledična, ne neodvisna.
A v resnici je ta izpeljava pedagoško zelo ustrezna, odlična za razumevanje, fizikalno pravilna -
če jo prej jasno razložimo, utemeljimo, da torej temelji na postulatih posebne teorije relativnosti.
Postulata posebne teorije relativnosti pa sta:
- vsi zakoni fizike so enaki v vseh inercialnih sistemih (sistemih, ki se med seboj gibljejo enakomerno in premo),
- hitrost svetlobe v vakuumu je enaka za vse opazovalce, ne glede na gibanje vira svetlobe ali opazovalca.
Iz teh dveh preprostih načel sledi vse:
časovna dilatacija, krčenje dolžin, relativnost sočasnosti in Lorentzove transformacije.
Kot pedagoška razlaga (npr. v srednješolskih ali začetnih univerzitetnih učbenikih) je torej naša prehojena pote povsem legitimna.
Če povzamemo.
Zakaj se prostor, dolžina krči pri opazovalcu, ki opazuje gibajoč sistem?
Če se čas raztegne, podaljša
(vsi procesi se zdijo počasnejši), potem mora biti tudi dolžina v smeri gibanja krajša,
da se ohrani enaka svetlobna hitrost c. To pokaže tudi naša izpeljava.
Tukaj se postavlja nekaj dilem, recimo ali ne bi razdalj merili še na
kak drug način, s kako drugo metodo? A pri gibajočem telesu (ali mirujočem)
nam na koncu ostane edina relevantna metoda preko svetlobe. Tudi, ko po domače
(z navadnim metrom) merimo neko dolžino, je zadaj »le« svetloba, ki od objekta
in metra prihaja v naši očesi.
Sedaj naenkrat opazimo, da stara trirazsežna metrika (x,y,z) klasičnega trirazsežnega prostora (3D) ne velja – merjenje dolžin je odvisno od hitrosti merjenega telesa. Zakaj? Ker smo pri velikih hitrostih spoznali, da se dolžina nekega telesa glede na različni opazovalni sistem ne ohranja, tudi čas ni več absoluten. Staro merjenje, stara metrika je torej odpovedala (mi si želimo sisteme, kjer se vsaj metrika, dolžina, ohranja). Ali je mogoče nekako dograditi naš opis sveta z novo metriko na način, da se bodo »razdalje« v novi metriki (bolje metrike) vseeno ohranjale (iščemo "novo" metriko, ki bo invariantna, enako kot svetloba, neodvisna od koordinatnega sistema)? Trirazsežni prostor nam te želje, seveda pri višjih hitrostih primerljivih s hitrostjo svetlobe (c), ne omogoča. Kako bi torej utemeljili novo metriko? Spet se spomnimo na uvodni primer z opazovalcema in odbojem svetlobe - prvi naj miruje, drugi pa potuje in izseva svetlobo, ki se mu odbije nazaj od zrcalnega stropa. Opisujeta torej isti dogodek in izmerita različna časa in različna kraja dogodka – razdaljo med njima (mi bi radi ohranili vsaj novo »dolžino«). Zapišimo še enkrat Pitagorov izrek - geometrijo dogodka.

(cΔt/2)2 = L2o + (vΔt/2)2
= (cΔt'/2)2 + (vΔt/2)2
Po preoblikovanju enačbe, ko na eni strani ohranimo videnje dogodka v gibajočem sistemu,
na drugi strani pa videnje zunanjega opazovalca, dobimo:
- (cΔt')2 = - (cΔt)2 + (vΔt)2
Ker je
vΔt = Δx, velja:
-c2Δt'2 = -c2Δt2 + Δx2
Zadnji zapis
[ ds'2 = ds = -c2Δt'2 = -c2Δt2 + Δx2 ]
je vreden vse pozornosti – je sicer preinterpretiran zgolj
na dogodek izsevanja in detekcije žarka (v časih
Δt in Δt',
za razdaljo
med dogodkoma na x in x' osi, saj sta začetna in končna koordinata y in y'
enaki, enako z in z', zato velja
Δy = 0 in Δz = 0).
A iz zgornjega zapisa
lahko sklepamo na splošno veljavno povezavo. Na desni imamo klasični člen
trirazsežnega prostora – to je X komponenta krajevnega vektorja
R = (X, Y, Z)
in člen
(cΔt).
Na levi pa samo člen
(cΔt'), ker je za opazovalca
v vozilu člen
Δx'2 enak 0 (žarek se namreč za opazovalca v vozilu po odboju vrne v isto
točko x'1 = x'2).
Ali je to torej zveza, nova metrika, ki jo iščemo?
JA – to je zapis nove metrike, vključuje tako različne
koordinate, kot različen čas in
je torej ta metrika invarianta ds = ds' - se ohranja v vseh opazovalnih sistemih.
Sedaj torej poznamo načelo invariantnosti svetlobe in invariantnost nove metrike preko zapisa četverca prostor-časa.
Enako velja tudi za električni naboj - je invarianta.
V bistvu smo tako vpeljali četrto dimenzijo, produkt med svetlobno hitrostjo in časom
(ct). Prvi korak k novemu zapisu naj bo, da tridimenzionalnemu vektorju (x,y,z)
dodamo še četrto časovno komponento ct (tako razširitev imenujemo prostor Minkowskega).
Nov zapis je vektor četverec
Xμ = (ct, x, y, z) = (x0, x1, x2, x3)
za opis prostor-časa. Po Einsteinovi interpretaciji
je
»dogodek presečišče lege in časa
in je edina dejansko merljiva
fizikalna količina. Skalarni produkt v diferencialni obliki, velikost
(ds2= dxμ·dxμ)
ali kar metrika ds2, se sedaj v splošnem
zapiše kot diferencial (Pitagorov izrek za majhne premike):
ds2 = -c2dt2 + dx2 + dy2 + dz2
Razlika med starim in novim izračunom poti ds je ta, da je člen cdt pri množenju s samim seboj negativen (kot zapis kompleksnega števila, za imaginarno enoto i, ko velja i2 = -1). Zakaj tako - smo že pokazali na primeru podaljšanja časa.
Pa preverimo (za vsak slučaj), če ta nova metrika deluje na skrčenju dolžin!
Izvedimo še drugo vajo merjenja dolžine potujoče palice, z njo potuje tudi opazovalec.
Kašno dolžino torej izmerita zunanji opazovalec in tisti, ki potuje s palico? Morali
bi dobiti enak rezultat, kot med prvo vajo za skrčenje dolžin. Mirujoči opazovalec
bo meril čas
Δt
med obema bliskoma (na začetku in koncu palice,
ki se zgodita ob mimohodu krajišč palice skozi mirujoče izhodišče sistema S)
in sklepal, da za dolžino velja L = vΔt! Predstavljajmo si, da se levi koordinatni
sistem S' bliža sistemu S. Ko se palica L' dotakne sistema S, se sproži na konici prvi blisk.
Enako se zgodi, ko začetek palice L' (levi konec) sovpade s sistemom S. Drugi blisk se torej
sproži po času
Δt = L/v
na začetku palice L' (levi konec) –
ko točki A' in A sovpadata.
Za sistem S' velja, da se prvi blisk sproži ob času t1' = 0 in s koordinato x1' = L',
za sistem S velja, da je x1 = 0, t1 = 0 (izhodišče sistema S). Po času
t2 = L/v (za mirujočega opazovalca) se sproži drugi blisk na levem delu palice,
ko sovpada z izhodiščem sistema S, zato je tudi dogodek drugega bliska v izhodišču,
v točki x2 = 0. V sistemu S' pa je potekel
čas t2' = L'/v in pri koordinati
x2' = 0. Vstavimo podatke med dogodkoma obeh bliskov v novo metriko
Δs'2 = Δs2.
–c2Δt'2 + Δx'2 = – c2Δt2 + Δx2
- to je univerzalna povezava za gibanje (metriko) na premici, jo bomo še kdaj uporabili
Ker velja: Δt' = t2' – t1' = L'/v, Δx' = x2' - x1' = -L', Δx = 0 in Δt = t2 – t1 = L/v,
se metrika dogodka izseva obeh bliskov zapiše kot:
–c2 (L'/v)2 + L'2 = –c2(L/v)2 + 0
L'2((c/v)2 – 1 ) = L2(c/v)2
L'2(c/v)2 (1 – (v/c)2) = L2(c/v)2
Metrika štirirazsežnega prostor-časa (4D) torej deluje – dolžini sta v obeh štirirazsežnih koordinatah enaki (levi in desni del enačbe). Iz zadnjega računa pa brez težav izrazimo že znano povezavo za 3D metriko, kjer dolžini nista enaki in velja že izpeljana transformacija dolžin:
L' = L/(1 – v2/c2)1/2 = Lγ
L = L'(1 – v2/c2)1/2 = L'/γ
To so poučne vaje za spoznavanje metrike štirirazsežnega prostor-časa, ki imajo za posledico pravilnejšo sliko mehanike, tudi opisa energij. Kot bomo videli – iz zapisanega in povedanega izhajajo zares daljnosežne posledice, spremembe pri pogledu na svet, tudi na vesolje kot celoto.
Če še enkrat analiziramo prvi primer izseva svetlobe proti zrcalnemu stropu višine y = Lo
v vozilu in kako dogodek vidi nekdo, ki stoji ob cesti,
spet velja ohranitev metrike v obeh sistemih.
Za recimo gospo v vozilu velja
Δs' = (c Δt', Δy'),
za gospoda ob cesti pa
Δs = (c Δt, Δy).
Kjer so spremembe v smeri y za oba enaka
Δy'= Δy = 0
(svetloba se odbije v izhodišče),
za
Δx' = 0
(ker se v avtomobilu žarek ni premaknil v x smeri), za x smer pa velja
Δx = vΔt
(avto se je premaknil za
vΔt – za opazovalca ob cesti).
Ali je res
Δs'2 = Δs2 ?
Seveda je, a preverimo preko vektorja četverca!
-c2Δt'2 + 0 = -c2Δt2 +
(vΔt)2 = - c2(1- v2/c2)Δt2
= - c2(1/γ)2Δt2 = -c2Δt'2
Nova 4D metrika torej da v vseh sistemih enako dolžino, stara pač ne!
Tudi fizikalni zakoni se v novi mehaniki sedaj korektneje zapišejo –
recimo gibalna količina, energija (a o tem pozneje)!
Še nekaj stavkov o znamenitem paradoksu enakomerno gibajočih se opazovalcev.
Zdi se, da lahko drug drugemu očitata, da pri sosedu teče čas počasneje ...
V tem seveda ni nobenega paradoksa – oba namreč upoštevata Lorentzova pravila.
Pri pospešenih sistemih (t. i. paradoks dvojčkov) pa primerjava ur dejansko
pokaže različna časa (na spletu lahko najdemo kar nekaj izračunov na to temo,
recimo na strani:
https://de.wikipedia.org/wiki/Zwillingsparadoxon#Beschleunigte_Bewegungen).
Recimo, da en opazovalec lovi drugega (prvi najprej ustavi raketo in nato
pospeši do drugega opazovalca, ki cel čas potuje enakomerno), in ko se srečata,
prvi opazovalec pokaže uro, ki dejansko kaže krajši čas (zaradi pospešenega gibanja)
od kolegove ure (je torej nekoliko mlajši od drugega kolega, ki cel čas potuje enakomerno).
Ta del posebne teorije relativnosti in še mnoge ostale uganke iz čudežnega sveta vesoljskih
pojavov, so rodile razmislek o času v gravitaciji – in Einsteina pripeljale do splošne
teorije relativnosti.
V splošni
teoriji relativnosti igra glavno vlogo gravitacija (pravilneje ukrivljen prostor-čas,
ki ga krivi masa in ostale oblike energij), torej so v igri opisa realnosti glavni
odločevalci pospešeni sistemi, kjer pričakujemo
dejansko vpliv "gravitacije" na čas - na hitrost ur in seveda na merjenje razdalj (na metriko ds).
Več v naslednjih poglavjih.
Ker se v Lorentzovem členu nahaja kvadrat hitrosti, ki je tudi v izrazu za kinetično energijo,
se je na tem mestu smiselno vprašati o bolj posplošeni količini, ki vpliva
na čas, dolžine v posameznih opazovalnih sistemih. Tukaj se nam tako energija ponuja, kot bolj
univerzalna, bolj ustrezna fizikalna količina za razumevanje časa in prostora.
Posplošimo torej Lorentzov člen s prehodom na energijo delca (označeno kot E'), ustreznejša je posplošitev kar na potencial Φ.
Velja torej zapisati člen v2 s klasično energijo.
Za kinetično energijo (označimo jo s črtico ') velja E' = mv2/2, od koder sledi člen za kvadrat hitrosti:
v2 = 2E'/m
A smemo kaj podobnega sklepati tudi pri gravitaciji, kjer je potencial masivnega sferičnega homogenega
telesa M kar enak Φ = -GM/r - izkazalo se bo, da ja.
Za velikost potencialne energije velja E' = |GMm/r|, oziroma člen 2E'/m se zapiše kot:
-2E'/m = -2GM/r = 2Φ
Tako za Lorentzov člen dobimo naslednji splošen izraz povezan s klasično energijo:
1/(1 – v2/c2)1/2 = 1/(1 – 2E'/(mc2))1/2
Pri potencialni energiji (potencialu Φ) pa torej po analogiji velja:
1/(1 – 2E'/(mc2))1/2 = 1/(1 – 2GM/(rc2))1/2
= 1/(1 + 2Φ/c2)1/2
Kot bomo videli v nadaljevanju, je taka posplošitev zelo koristna in korektneje razloži
določene pojave, ki so vezani na realen prostor-čas, tudi v gravitaciji velikih teles.
Tak poenostavljen pristop mnogi zavračajo, a ima določene konceptualne prednosti.
Lorentzove transformacije, zapis metrike in nekaj vaj
Galilejeve transformacije ( x' = v - vt , y' = y , z' = z
, t' = t ) pri velikih hitrostih ne
veljajo. Galilejeve transformacije namreč napačno privzamejo, da čas teče povsod z enako
dinamiko, to pomeni, da je za enakomerno gibajočega opazovalca koordinata x' različna
za lasten premik vt glede na x in preprosto trdi, oz. izračuna
x' koordinato kot: x' = x – vt (slika zgoraj). Kar pa
seveda dokaj dobro velja le za hitrosti (v) gibanja sistema S', ki
so precej manjše od svetlobne hitrosti (recimo v/c < 0,0001).
Poglejmo torej, kako
se zapišejo transformacije med nepospešenimi sistemi za hitrosti primerljive s hitrostjo svetlobe
(recimo v/c > 0,0001) – to so Lorentzove transformacije:
γ = 1/(1 –
v2/c2)1/2
---------------------
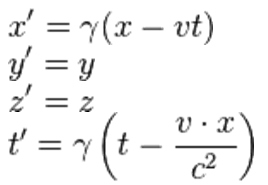
Razložimo zgornje povezave – oba opazovalca merita
lego x, oz. x' in časa t in t'.
Opazovalec, ki miruje, vidi
dolžino x' nekoliko krajšo (in sicer x'/γ, skrčenje dolžin), zato velja
x =
vt + x'/γ - od koder dobimo povezavo za koordinato x'
= γ(x – vt).
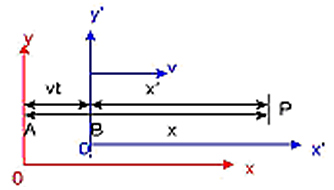
Opazovalec v gibajočem sistemu pa vidi, da se
je njegov sistem premaknil za vt', in če zraven prišteje še x'
(za katero velja iz prejšnjega razmisleka povezava x' = γ(x – vt)
), vidi razdaljo x nekoliko krajšo (in sicer x/γ), zanj torej velja
x/γ
= vt' + x' = vt' + γ(x – vt)
Iz prve
enačbe torej dobimo:
x' = γ (x – vt).
Iz druge enačbe izrazimo čas
t' = x/(γv) – x'/v, če za x' vstavimo γ(x – vt),
tako dobimo t' = x/(γv) - xγ/v + γt = (x/v)(1/γ - γ)
+ γt [ in še upoštevamo,
da je 1 - γ2
= -γ2v2/c2 ], končni izraz
za čas t' je torej:
t' = γ(t – vx/c2)
Preverimo še resničnost zgornjih povezav. Če je
x = vt, kar velja za naš primer z avtom in odbitim žarkom,
dobimo za čas t' = γ (t – v2t/c2) = γt(1 –
v2/c2) = γt/γ2 = t/γ = t(1 – v2/c2)1/2, kar smo torej
že pokazali.
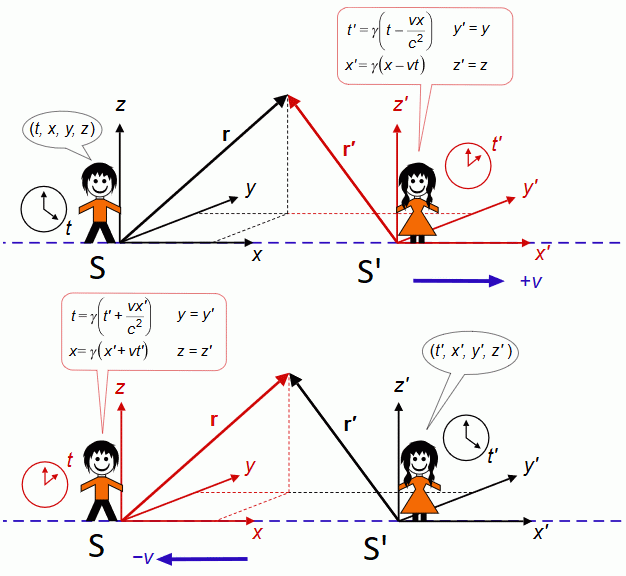
Slika kaže Lorentzove transformacije (relativno gibanje opazovalcev v smeri
x koordinate), kjer oba nepospešena opazovalca pravilno trdita, da v sosednjem opazovalnem
sistemu teče čas drugače, a pri obeh se ohranja hitrost svetlobe. Slika
(meritve) dogajanja je za oba simetrična v četvercu metrike prostor-čas.
V literaturi lahko
najdete več poti do Lorentzovih transformacij – mi smo uporabili najbolj preprosto
in večini najbolj razumljivo. Lorentzove transformacije pa lahko izpeljete tudi matematično bolj
formalistično, recimo za primer, ko sta na začetku t = t' =
0 koordinati (x in x') poravnane (y=y', z=z') in velja za
oba opazovalca, da se v obeh žarek svetlobe širi z enako hitrostjo
c, ko torej velja:
-c2t2 + x2 = -c2t'2 + x'2
Poskusite z linearno
transformacijo, kjer se bo ohranjala metrika v obeh nepospešenih sistemih:
x' = Ax + Bct
ct' = Cx + Dct
Z nekaj znanja hiperboličnih funkcij ali na kak drug način se boste
dokopali do Lorentzovih transformacij ( x' = γ(x – vt) in t'
= γ (t – vx/c2) ) po nekoliko zahtevnejši poti. Lorentzov
člen γ = 1/(1 – v2/c2)1/2 je seveda enak kot pri naši
preprosti izpeljavi.
Naredimo torej še ta napor in razrešimo ti enačbi s štirimi spremenljivkami, neznankami
in se neoporečno dokopljimo do Lorentzovih transformacij.
Naj točkasto svetilo odda svetlobo, ki se širi v obliki svetlobne sfere (krogle), kateri se veča radij kot R = c*t.
Imamo dva opazovalca v sistemih S' in S.
Ob mirovanju obeh sistemov oba vidita svetlobno sfero - ki jo oddaja točkasto svetilo. Kaj pa, če se
svetilo enakomerno premo giblje skupaj s sistemom Š'? Opazovalec v sistemu S' bo še zmeraj videl
širjenje, rast svetlobne sfere - torej pričakovano dogajanje (kot recimo na vlaku, ki se enakomerno premo giblje, vidimo
fizikalne zakone enako, kot nekdo v trdnem laboratoriju - v nepospešenem vlaku lahko recimo igramo
namizni tenis, kot v dvorani - enako velja za širjenje svetlobe)! Kako pa vidi širjenje svetlobe
opazovalec, ki miruje glede na sistem S' in svetilo (upoštevati pa
moramo osnovno načelo relativnosti - in sicer, da v vseh nepospešenih sistemih svetloba potuje enako hitro)?
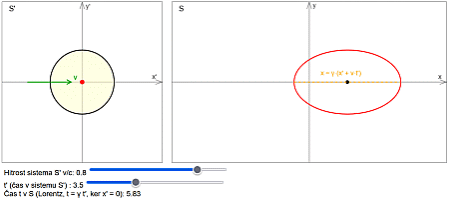
Za uvod si lahko ogledate tudi JavaScript animacijo - Interaktivna Lorentzova elipsa (rast svetlobne sfere - transformacija v elipso),
poučno.
Velja postulat za vse nepospešene sisteme o metriki Δs2 = Δs'2 in to rešitev tudi iščemo:
-c2(t2 - t1)2 + (x2 - x1)2
+ (y2 - y1)2
+ (z2 - z1)2
=
-c2(t'2 - t'1)2 + (x'2 - x'1)2
+ (y'2 - y'1)2
+ (z'2 - z'1)2
Kjer (t, x, y, z) so prostorsko-časovne koordinate, ki se uporabljajo za določanje dogodkov v enem okvirju
(koordinatnem sistemu S), in (t ', x ', y ', z ') so koordinate v drugem okvirju (koordinatnem sistemu S').
Želimo linearno zvezo med koordinatama (x,ct)in (x',ct'),
ker inercialno gibanje (enakomerno, premo) mora ostati linearno.
Vpeljemo ct, da imata obe spremenljivki iste enote (dolžino).
Konstantnost svetlobne hitrosti v obeh sistemih.
Simetrijo (relativnost — ni privilegiranega sistema).
Invariantnost svetlobnega intervala.
Najbolj splošna linearna oblika Lorentzove transformacije je torej:
x' = Ax + Bct
ct' = Cx + Dct
Prav iz nje lahko z nekaj računanja izpeljemo pravilno obliko Lorentzovih transformacij.
To je torej izhodišče, ki ne predpostavi ničesar razen linearnosti.
Vpeljemo še ct, da imata obe spremenljivki iste enote (dolžino).
Torej velja:
|x' | |A B||x | | | = | || | |ct'| |C D||ct|To matriko bomo zdaj omejili z Einsteinovimi postulati.
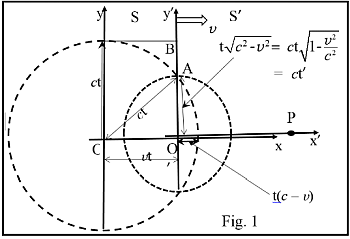

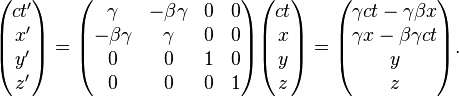
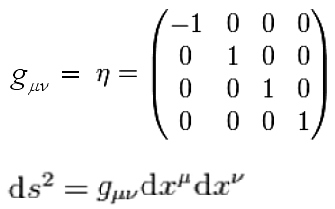
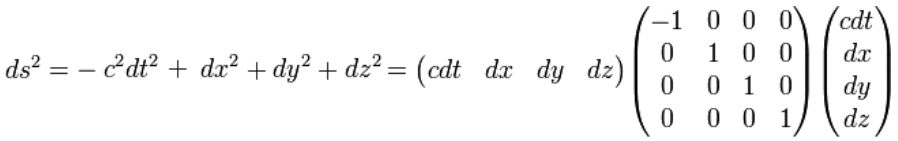
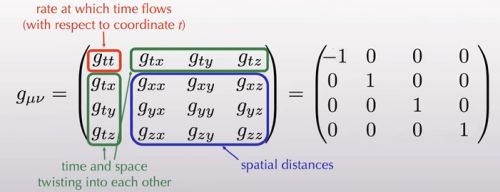
-(cm)2 = -(mcγ)2 + (mγv)2
-(cm)2 = -mγ(mγc2) + (mγv)2
Iz četverca gibalne količine moramo tako pri izračunih pri visokih hitrostih, energijah, silah računati
s krajevnim delom gibalne količine:
p = mγv
V splošnem velja pravilo, da je sila odvod gibalne količine po času:
F = dp/dt = d(mγv)/dt = m(v*dγ/dt + γ*dv/dt)
Več sledi.
Najprej izrazimo diferencial Lorentzevega člena γ.
γ = 1/(1 – v2/c2)1/2
dγ/dv = vdv/(c2(1 – v2/c2)3/2 ) = (vγ3/c2)
Velja tudi ( pospešek je a = dv/dt ) ter:
dγ/dt = (dγ/dv)(dv/dt) = (vγ3/c2)*a
Kako pa je s silo, oziroma s pospeškom za pospeševanje delca z maso 'm' v 'x' smeri?
V splošnem velja, da
zunanja sila ali rezultanta sil na nek opazovani sitem v določenem času (dt) spremeni
gibalno količino ( dp=d(mγv) ). Povedano zapišimo za masni delec z maso 'm' in
upoštevajmo relativistični člen (γv):
Fx = dp/dt = md(γv)/dt
d(γv)/dt = (v2γ3/c2)dv/dt + γdv/dt
= (v2γ3/c2)a + γa
d(γv)/dt = aγ3 (v2/c2 + 1/γ2)
= aγ3 (v2/c2 + 1 - v2/c2) = aγ3
Tako velja:
Fx = dp/dt = md(γv)/dt = maxγ3
ax = Fx/(γ3m)
Torej zgornja enačba velja, ko je hitrost usmerjena v smeri x in je u = ux = v = vx, kjer je
v = vx hitrost med koordinatnima sistemoma, u pa je hitrost telesa, na katerega deluje sila v x smeri.
Kako je z enakomernim kroženjem delca (naj bo r polmer kroženja, v = rω pa hitrost, m pa masa delca)?
Ker se pri enakomernem kroženju hitrost (v) ne spreminja, velja dv/dt = 0 in dγ/dt = 0, velja torej da je odvod velikosti
obeh količin enak 0:
d(γv)/dt = (v2γ2/c2)dv/dt + γdv/dt = 0
 |
 |
E = mc2
Poglejmo vektor prostor-čas (četverec) zapisan za gibanje v smeri x:
(ct', 0) ⇔ Xμ = (ct, x).
Kjer vektoraja X'μ in Xμ po smeri nista enaka, po velikosti (dolžini) pa sta enaka, to je bistvo metrike ds,
torej velja |(ct', 0)| = |(ct, x)|,
zato simbolni zapis z znakom ⇔, ki povezuje vektorja četverca X'μ in Xμ:
(ct', 0) ⇔ Xμ = (ct, x).
Ostale smeri (y, z) v tem primeru niso relevantne, zato smo jih izpustili.
Še enkrat ponovimo vajo z vpeljavo gibalne količine (p) pri visokih energijah, hitrostih.
V sistemu S' naj telo z maso m miruje, za diferencial premika dx v sitemu S velja:
(cdt', 0) ⇔ dXμ = (cdt, dx)
- namesto dt' zapišemo že izpeljano povezavo dt' = dt/γ in delimo z dt (v resnici levo
in desno stran odvajamo po času t, hitrost v = dx/dt), tako dobimo četverec hitrosti,
(cdt/γ, 0) ⇔ dXμ = (cdt, dx) - levi in desni del enačbe pomnožimo z γ
in odvajamo po času dt
(c, 0) ⇔ (cγ, γdx/dt)
(c, 0) ⇔ (cγ, γv)
- če enačbo pomnožimo z maso m, dobimo po definiciji četverec gibalne količine
Pμ ali kar P,
|P| = |(cm, 0)| ⇔ (mcγ, mγv) = (mcγ, p)
Poiščimo velikost četverca ( to je skalarni produkt |p| = |(cm, 0)| ⇔ |(mcγ, mγv)| ).
-(cm)2 = -(mcγ)2 + (mγv)2
-(cm)2 = -mγ(mγc2) + (mγv)2
Iz četverca gibalne količine moramo tako pri izračunih pri visokih hitrostih, energijah, silah računati
s krajevnim delom gibalne količine:
p = mγv
A sedaj si podrobneje oglejmo spodnji četverc velikosti gibalne količine in člen mγc2.
-(cm)2 = -mγ(mγc2) + (mγv)2
Kaj se skriva v členu mγc2 ?
Če privzamemo, da je pri majhnih hitrostih (v) izraz
1/(1 – v2/c2)1/2 ≈
1 + v2/(2c2),
potem velja za
mc2γ = mc2/(1 – v2/c2)1/2
≈
mc2(1 + v2/(2c2))
= mc2 + mv2/2.
Za majhne hitrosti torej velja, da je zraven kinetične energije
(Ek = mv2/2) prištet
še člen mc2. Izraz E ≈ mc2 + mv2/2 =
Eo + Ek imenujemo polna energija delca, zatorej je tudi izraz
E = mc2γ
polna energija delca z maso m z veliko hitrostjo.
Izraz
Eo = mc2
pa imenujemo mirovna energija
telesa z maso m (toliko zaloge energije se nahaja v njem
– v atomih, elektronih, v kvarkih, gluonih, vezavnih silah …).
Ali je tak sklep upravičen? Poglejmo sestavo protona.
Kot smo že omenili, je v resnici večina energije protona v vezavni
energiji gluonov brez mase – vežejo pa zelo lahke kvarke - tako da
je
mc2 dejansko zaloga energije neke mase, poljubnega delca.
Do enakega izraza (Ek = E - mc2) pridemo, če izračunamo
kinetično energijo preko diferencialnega računa:
dEk = vdp = vd(mγv) => Ek
= mc2γ - mc2 =
mc2(1/(1 – v2/c2)1/2 - 1);
a to v tem kontekstu ni potrebno ( vsak pa lahko ta račun,
če se še spomni matematike iz srednje šole, izvede sam,
za pomoč
dv = dγ/(vγ3/c2) ). Ta vaja je tudi sicer izvedena nekoliko nižje
v poglavju (Kako do kinetične energije Ek preko definicije ∫vdp ?).
Dotaknimo se še morebitnega vpliva gravitacije na prostor-čas.
Kot smo že omenili, se pri pospešenem gibanju zgodi, da ure dejansko kažejo krajši čas
in velja tudi načelo ekvivalentnosti, da ne moremo ločiti pospešenega sistema od vpliva gravitacije
(več o tem pozneje).
Torej lahko pričakujemo, da bodo ure v gravitaciji tudi tekle počasneje, kot nekje daleč vstran od vpliva teže.
In kaj bi pri skromni gravitaciji lahko pričakovali? Poglejmo primerjavo. V posebni teoriji relativnosti preidemo v klasično mehaniko pri
majhnih hitrostih glede na svetlobno in tako
velja prehod v klasično kinetično energijo (mv2/2) -
prepišimo enačbo za energijo od prej:
mc2/(1 – v2/c2)1/2
≈
mc2(1 + v2/(2c2))
= mc2 + mv2/2
Pri skromni gravitaciji (recimo na Zemlji, kjer naj delec miruje) bi
upravičeno pričakovali prehod iz relativistične v klasično mehaniko - torej v klasično
potencialno energijo (Ep = -GMm/r = Φm, kjer je potencial zapisan kot Φ = -GM/r).
Zgolj šibka gravitacija na delec torej da
rezultat:
mc2 - GMm/r = mc2 + Φm = mc2(1 + Φ/c2).
Z metodo primerjave z izrazom [ mc2(1 + v2/(2c2)) ] lahko sklepamo,
da bo na čas in metriko,
ter seveda na energijo (zaradi gravitacije)
vplival člen 2Φ/c2. Tako dobimo enak izraz, kot smo ga že vpeljali nekaj odstavkov prej, pri razmišljanju
zgolj o Lorentzovem členu in energiji.
Zakaj dvojka, izraz (2Φ)?
Ker, ko za skromno gravitacijo, to je za male vrednosti, člen
2Φ/c2 damo iz korena (razvoj v vrsto), se dvojka okrajša in
dobimo vrednost Φ/c2 = - GM/(rc2).
Če torej, kot pri kinetični energiji, izraz (1 + Φ/c2)
pomnožimo z mirovno energijo mc2,
potem dobimo, poleg mirovne energije, še potencialno energijo delca
[ mc2(1 + Φ/c2) =
mc2 - GMm/r ]. Klasična potencialna energija je torej:
Ep = -GMm/r.
To je izjemno zanimiv in celo pravilen razmislek. Ta člen
2Φ/c2, ki vpliva na čas, metriko in energijo v gravitaciji,
potrjujejo tudi meritve in seveda Einsteinove enačbe splošne teorije relativnosti.
Več o tem in z dodatnimi razmisleki, argumenti, v naslednjih poglavjih.
Vrnimo se k posebni relativnosti.
O polni energiji v posebni teoriji relativnosti več pozneje,
a preoblikujmo sedaj naš skalarni produkt
vektorja gibalne količine v še bolj enostaven izraz preko polne energije
E = mc2γ,
(ne)časovni del izraza za gibalno količino (mγv) pa zapišimo
kar z oznako p, ko torej velja p = mγv.
-(cm)2 = -m2c2γ2c2/c2
+ (mγv)2
-(cm)2 = -E2/c2 + (p)2
-(c2m)2 = -E2 + (cp)2
Na koncu dobimo zelo poučen rezultat, ki povezuje polno energijo E delca, mirovno energijo c2m in gibalno količino p:
E2 = (c2m)2 + (cp)2
Povezavo bomo še uporabili, tudi izraz za polno energijo E = mc2γ. Povezava energije in gibalne količine E2 = (c2m)2 + (cp)2 je zanimiva v navezavi s fotonom z energijo E = hν (h je Planckova konstanta, ν pa frekvenca valovanja – očeta te enačbe sta Max Planck in Einstein preko fotoefekta), torej za svetlobo, za katero vemo, da nima mase (m = 0) in je člen (c2m)2 = 0. Iz česar sledi E2 = 0 + (cp)2 ali E = cp, gibalna količina p fotona je torej kar:
p = E/c = hν/c = h/λ
Sedaj tudi lažje razumemo, kako delujejo fotonska (svetlobna) jadra (svetloba je lahko tudi
dodaten pogon za lahke vesoljske sonde). Ko se foton odbije od ogledala (jadra), ga s sunkom
sile, ki je enak spremembi gibalne količine, tudi odrine – pa čeprav nima mase. Tudi
elektromagnetno silo, recimo znotraj atoma, prenašajo fotoni – delci polja. Še večji
vpliv je imela ta povezava (p = h/λ) na zapis (nekoč nezaslišane) valovne funkcije
gibajočih kvantnih delcev. Louis de Broglie je na začudenje večine sklepal, da
za kvantne masne delce (recimo elektrone) velja dvojna narava, tudi valovna in
bi naj zveza za gibalno količino fotona (p = h/λ) veljala tudi za masne delce,
recimo elektrone v atomu. Izpeljal je valovno dolžino λ za gibalno količino
p = γmv kvantnega delca.
Iz analogije sledi:
λ = h/(γmv) = h(1 – v2/c2)1/2/(mv).
Če je hitrost elektrona zelo blizu svetlobne, velja da je energija
γmc2 >> mc2 in zatorej iz izraza
E2 = (c2m)2 + (cp)2
lahko sklepamo na približek E2 ≈ (cp)2 ,
od koder sledi
E ≈ cp = hν =2πνh/(2π) = ℏ*ω.
Kjer je ℏ = h/(2π)
reducirana Planckova konstanta. Končni izraz za kotno frekvenco je
ω = E/ℏ - ta enačba je del Schrödingerjeve valovne funkcije.
Heisenberg pa je tako že vedel (slutil), da pri določanju lege
kvantnih delcev (recimo, ko preverjamo resničnost naših izračunov),
recimo da pogledamo nek elektron s svetlobo in iz odboja določimo lego – s
tem tudi bistveno zmotimo njegovo pozicijo in gibanje - gibalno količino.
Tako je prišel do načela nedoločenosti (ΔpΔx ≥ h/(4π),
s tem je postavil
meje spoznanjem fizike). Načelo nedoločenosti se danes šteje tudi za eno
od idej začetka vesolja.
Povejmo še, da je Newton »trmaril«, da je za opis sveta dovolj izrek o
ohranitvi gibalne količine. Relativno kmalu pa se je izkazalo, da je
potrebno vpeljati še kinetično energijo zaradi gibanja in tudi ostale
oblike energij. A v zapisu nove Einsteinove mehanike se zdi, kot da je
Newton na nek način imel prav – velikost četverca gibalne količine je
direktno povezana z energijo (a nova mehanika ima nekoliko drugačne postulate).
Če lahko Newtonu pripišemo kakšno misel za nazaj, zagotovo velja, da je slutil,
da se v gibalni količini razkriva tudi energija, a takrat še pojem, definicija
energije, ni bila dovolj razvita – ukrotili smo jo komaj v 20. Stoletju,
saj zdi se tako.
Kako do kinetične energije Ek preko definicije ∫vdp ?
Ker je gibalna količina enaka p = mγv, in ker je kinetična energija enaka vsoti prispevkov
vdp velja ∫dEk = ∫vdp, bomo najprej izrazili diferencial Lorentzovega člena γ.
γ = 1/(1 – v2/c2)1/2
dγ = vdv/(c2(1 – v2/c2)3/2 ) = (vγ3/c2)dv
dv = dγ/(vγ3/c2)
Gibalna količina je: p = mγv.
Zapišimo diferencial (»delček«) dEk kinetične energije.
dEk = vdp = vd(mγv) = mv(γdv + vdγ)
= mv(γdγ/(vγ3/c2) + vdγ) = m(c2/γ2 + v2)dγ
Ker velja c2/γ2 + v2
= c2(1 - v2/c2) + v2 = c2,
se izraz dEk zelo poenostavi.
dEk = m(c2/γ2 + v2)dγ = mc2dγ
∫dEk = m∫c2dγ
Ek| = mc2γ|
Integrirajmo od kinetične energije Ek = 0 do Ek in od hitrosti v = 0 do v.
Ek = mc2(γ- 1/(1 – 0/c2)1/2) = mc2(γ - 1)
Končni rezultat za kinetično energijo Ek je torej (po Albertu Einsteinu):
Ek = mc2(γ - 1) = mc2γ - mc2
= mc2/(1 – v2/c2)1/2 - mc2
Lastna (tudi mirovna) energija delca je definirana kot: Eo = mc2.
Polna energija delca je definirana kot:
E = Ek + Eo = mc2γ
Enačbo zgoraj lahko zapišemo še kot E = Ek + Eo = mc2(γ - 1) + mc2 = mc2γ.
Ta povezava zgoraj za polno energijo hitrega delca v ravnem prostoru je zelo pomembna.
V polju gravitacije, kar bomo opisali v osnovah splošne teorije relativnost,
pa pričakujemo še potencialni del (a že zdaj zapišimo enačbo polne energije
E = Ek + Eo + Ep = (1 – 2GM/(c2r))1/2mc2γ ,
pot do nje
izvedemo v naslednjih poglavjih, glejte -
energija hitrega delca v močnem gravitacijskem polju ).
A sedaj ostajamo še v raven prostoru.
Poglejmo ali kinetična energija pri majhnih hitrostih preide v klasični izraz Ek = mv2/2.
Za dokaz privzamemo, da je pri majhnih hitrostih izraz
1/(1 – v2/c2)1/2 ≈ 1 + v2/(2c2).
Ek = mc2γ - mc2 = mc2/(1 – v2/c2)1/2 - mc2
≈ mc2(1 + v2/(2c2)) - mc2 = mv2/2
In to je zelo eleganten dokaz, da smo pravilno izpeljali povezavo za relativistično kinetično energijo:
Ek = mc2(γ - 1).
Poiščimo še povezavo med energijo E in gibalno količino p.
E = mc2γ = mc2/(1 – v2/c2)1/2
E2 = (mc2)2/(1 – v2/c2)
E2(1 – v2/c2) = (mc2)2
E2 – (mc2)2γ2v2/c2
= E2 – (mγvc)2 = E2 – (pc)2 = (mc2)2
E2 = (mc2)2 + (pc)2
Če smo prav razmišljali, bi morali dobiti (s tem premislekom smo tudi začeli)
enak rezultat tudi iz četverca prostor-časa, ki smo ga že izpeljali za
gibalno količino, kjer je velikost vektorja:
|(cm, 0)| = |(mcγ, mγv)|.
Za vajo poiščimo še enkrat velikost četverca (to je skalarni produkt).
-(cm)2 = -(mcγ)2 + (mγv)2
-(cm)2 = -m2c2γ2c2/c2 + (mγv)2
-(cm)2 = -E2/c2 + (mγv)2
-(c2m)2 = -E2 + (cp)2
Na koncu dobimo pričakovan rezultat, a veliko hitreje in elegantneje
(zato smo poglavje o energiji tudi začeli kar s četvercem gibalne količine):
E2 = (c2m)2 + (cp)2
Rezultati naših računskih vaj kažejo na konzistentnost metrike prostor-časa
in take vaje nas vodijo v poglobljeno razumevanje teorije relativnosti.
Prehojena pot od metrike do enačbe
E2 = (c2m)2 + (cp)2
ima izjemen nauk - in sicer, da se osnovne zakone mehanike
da izjemno elegantno in konzistentno izpeljati zgolj iz metrike – merjenja razdalj (v osnovi iz Pitagorovega izreka,
dopolnjenega s kateto produkta hitrosti svetlobe in časa). Sam dokaz, da se kinetična energija pri majhnih hitrostih
izenači s klasičnim zapisom kinetične energije
(Ek = mc2γ - mc2
= mc2/(1 – v2/c2)1/2 - mc2 ≈ mc2(1 + v2/(2c2)) - mc2 = mv2/2),
daje teoriji relativnosti še dodatno konsistenco.
Energija se v relativnosti pripiše recimo delcu in je torej definirana glede na njegovo mirovno maso in hitrost glede na opazovalca.
V splošni teoriji relativnosti pa se doda še člen, ki upošteva ukrivljenost prostor-časa.
V limiti skromnih hitrosti (glede na svetlobno), pričakujemo seveda
klasični zapis kinetične energije delca
(in v teoriji splošne relativnosti pri skromni gravitaciji še zapis klasične potencialne energije delca).
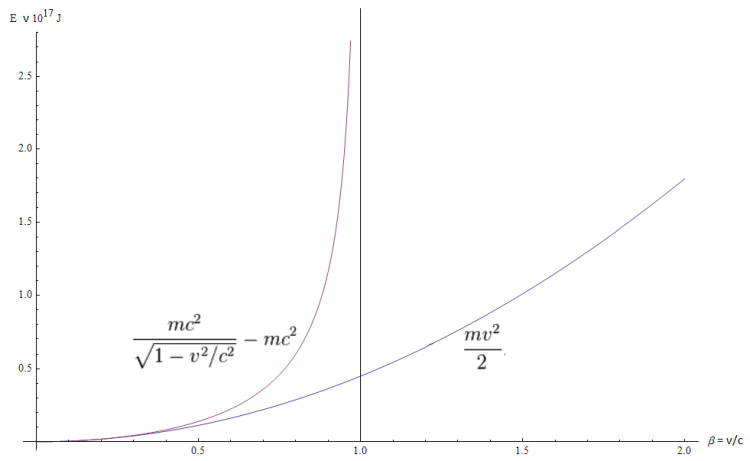
Graf kinetične energije (za m = 1 kg) v klasični (nepravilni) obliki in relativistični pravilni obliki glede na
razmerje β = v/c. Ta graf nazorno kaže, da pri pospeševanju delcev (elektroni, protoni, ...)
blizu svetlobne hitrosti, za povečanje hitrosti le za nekaj procentov, rabimo veliko več energije
kot pri klasičnem opisu in majhnih hitrostih.
To je eden od »problemov« pospeševalnikov.
***
Glej tudi: Lorentzov člen (kalkulator) - The Lorentz Factor Calculator
Primera
A) V pospeševalniku
"Large Electron–Positron Collider (LEP)"
v Cernu so leta 1989 za Lorentzov faktor gama dosegli vrednost že kar γ = 88000
(E = mγc2 = 45 GeV vložene energije deljene z mirovno maso elektrona
m*c2 = 511 keV).
To pomeni, da so elektrone pospešili do izjemnih hitrosti:
v = 0.9999...*c, čisto blizu svetlobne.
Pozneje so šli celo do energij 100 Gev.
B)
Nadgradnja pospeševalnika v Cernu.
V pospeševalniku LHC (Large Hadron Collider - prvi zagon leta 2008, v letu 2012 so potrdili
Higgsovih bozonov) pa vsak proton doseže energijo kar Ek = 7 TeV = 7 1012 eV (seveda se načrtuje
tudi višje energije). Protoni potujejo v nasprotnih smereh in v določenih točkah se curka
iz obeh tunelov križata - trčita (animacija spodaj) - in tako se pri trkih sprosti ogromno energije,
delcev,
katerih potrditev iščemo - prvi cilj je bil seveda tudi Higgsovih bozonov.

Masa protona je precej večja od mase elektrona in je produkt mase in kvadrata svetlobne
hitrosti kar: mc2 = 9,383·10-4 TeV. Vrednost Lorentzovega člena
je, kljub precej večji energiji, zato manjša. Sledi izračun.
γ = Ek/(mc2) = 7 TeV/9,383·10-4 TeV = 7460
Hitrosti protonov pa so še zmeraj zelo visoke v = 0,999999991·c, tako
praktično velja: v ≈ c.
Da ustvarimo tako izjemno centripetalno silo, skrbi 1232 magnetnih dipolov nameščenih v
osmih lokih. Vsak dipol ima magnetno delovanje na dolžini 14,3 m, kar da skupno dolžino:
1232 × 14,3 = 17618 m
Tako bolj natančno določimo t. i. polmer ukrivljenosti ("bending radius"):
Rb =17618m/(2π)
Rb = 2804 m
Zakaj je bolje pospeševati protone, kot elektrone?
Odgovor podajo spodnje enačbe (Larmorjeva formula o sevanju pospešenega električnega naboja).
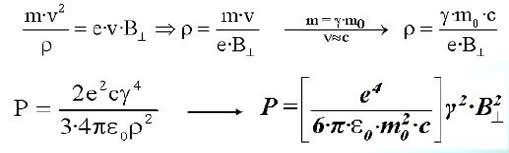
Pri elektronih, ker so lahki, sicer
hitreje dosežemo
visoke hitrosti. A vsako krožno gibanje je hkrati pospešeno gibanje in naboji tako med
kroženjem sevajo - to pa pomeni izgube, ki jih je potrebno nadomestiti.
Zgornja enačba kaže, da je moč sevanja sorazmerna z γ4 in
tako je sevanje elektronov 1013 večje od krožečih protonov.
ρ je polmer kroženja.
Za elektrone so zato bolj primerni linearni pospeševalniki.
http://www.lhc-closer.es/taking_a_closer_look_at_lhc/0.relativity
Klasična mehanika pravi, da je po trku in pred trkom, skupna gibalna količina enaka nič: p = 0 = mv – mv. Nič pa klasični izraz direktno ne pove o energiji, masi ... (po postulatih klasične mehanike kar privzamemo, da se masa ohrani; a to je napačen pristop, masa se spremeni – bomo videli zakaj – sledi eleganten dokaz nove mehanike). Kaj nam torej razkrije nova mehanika relativnosti? Kot prvo - nepričakovana posledica nove metrike – in sicer, da ima tudi mirujoča masa gibalno količino p = mγ(c, 0). Kar se zdi protislovno, noro – spet so fiziki svet obrnili na glavo (ko se bomo navadili na to trditev, se bo to zdelo samoumevno - konsistentno). Kot bomo pokazali na primeru, je tak pristop celovit, univerzalen in sam po sebi pove, kaj se dogaja recimo z maso, s snovjo, z energijo, med trki, tudi posredno pri nukleosintezi (tudi atomi, preko lastnega gibanja in sami nukleoni v atomu, so nosilci gibalne količine).
Zapišimo vsoto četvercev gibalnih količin obeh vozičkov (glej sliko),
gibalna količina se ohranja – neprožen trk, ob predpostavki,
da je rezultanta zunanjih sil enaka nič.
Velja, da je v1 = v, v2 = -v in m1 = m2 = m.
Za Lorentzov člen velja že izpeljani izraz
γ = 1/(1 – v2/c2)1/2.
p = mγ(c, v) + mγ(c, -v) = mγ(2c, 0) = 2mγ(c, 0).
Razčlenimo rezultata!
Člen
M = 2mγ
nekateri imenujejo relativistična masa, v resnici se v
tem členu skriva celotna energija – zaloga energije.
Rezultat končne gibalne količine je torej kar:
P = 2mγc
Uporabimo še izraz za polno energijo (E = mc2γ).
Za mirujoči sistem (γkon = 1) po trku velja, da je polna energija
obeh vozičkov kar
Ek = mkc2γkon
= mkc21 = mkc2.
Pred trkom pa je gibalna količina
p = 2mγc = 2mγc2/c = Ez/c, od koder sledi, da je začetna energija enaka:
Ez = 2mγc2.
Če predvidevamo, da gre vsa energija v notranjo energijo
(združenemu telesu se poviša temperatura T, hitrost molekul vm,
torej se poveča kinetična energija Emk molekul [velja
Emk ∝ kT ∝ mmvm2] - no,
temu ni čisto tako, nekaj energije gre
v deformacijo teles ali raztezanje,
a se vseeno lahko tej predpostavki kar približamo)
in seveda velja, da se skupna energija trka ohranja
znotraj obeh teles (pred in po trku, oznaki sta z in k), za kratek
čas zagotovo velja (Ez = Ek). Torej gre energija
iz ene oblike (kinetične energija velikih teles
pred trkom) v drugo (notranjo kinetično energijo
molekul, atomov... po trku), potem lahko zapišemo:
mkc2 = 2mγc2.
Od koder sledi, da je nova masa mk po trku
(vozička mirujeta) enaka:
mk = 2mγ
To je rezultat, ki direktno dokazuje, da je masa samo ena od oblik energije,
in če bi stehtali tako zlepljeno telo (z zelo, zelo natančno tehtnico),
bi izmerili maso mk in seveda velja, da je mk > 2m. In za koliko
je masa mk večja od začetne mirovne mase pred trkom mz = 2m? Za:
Δm = 2mγ - 2m = 2m(γ - 1).
Zagotovo lahko zatrdimo, da velik del te (kinetične) energije gre v
notranjo energijo, v povišanje temperature:
Δmc2 = 2m(γ - 1)c2 ∝ ΔT,
in s tem v maso mk = 2mγ.
To je zelo poučen rezultat, ki ga klasična mehanika ne predvideva in direktno
kaže na povezavo mase in energije – da je recimo toplejše telo nekoliko masivnejše
(v njem se molekule hitreje gibljejo, nihajo, imajo več energije ... in to se pozna
na masi; enako je s fotoni znotraj Sonca, prispevajo k masi, a ko se izsevajo,
se masa Sonca nekoliko zmanjša - za kar okrog 4,3 milijone ton na sekundo, preko
E = mc2).
Sedaj tudi lažje razumemo, zakaj se masa končnega jedra pri fuziji nekoliko
zmanjša, glede na mase vhodnih nukleonov – ker se pri nukleosintezi sprosti
ogromno energije v obliki sevanja. Gravitacija torej ni posledica direktno
mase, ampak energije (tudi, če bi vso materijo v Soncu spremenili v sevanje
in ga nekako obdržali skupaj, bi še zmeraj fotonsko Sonce z enako silo
teže delovalo na okolico – Einstein pravi, da zvezde ukrivljajo okolico
z energijo zbrano v telesu zvezde). Danes tudi vemo, da se v protonu
(nevtronu) skriva le 1% mase, najbrž v treh kvarkih (če sploh),
vse ostalo pripada vezavni energiji močne jedrske sile brezmasnih
gluonov (a se nam ta fenomen kaže kot materija
preko
mnukleona = E/c2).
Torej sta že Kepler in seveda tudi Newton,
s »svojim« gravitacijskim zakonom
(F = GmM/R2),
v bistvu (ne da bi vedela), govorila o vplivu energije
zvezde (preko
M = E/c2)
na okolico, recimo na delce,
na planet, Luno, ki pa imajo tudi
neko lastno energijo
m = Em/c2,
Einstein ta vpliv imenuje ukrivljenost zaradi energije zvezde.
Če strnemo - zakaj je temu tako, da je celo veliko več mase v obliki
E/c2, kot klasične mase mkv? Recimo v protonu velja za potencialno
maso treh kvarkov mkv, napram celotni vezavni energiji znotraj protona naslednje
razmerje:
Eprotona/c2 >> mkv,
oziroma kar neverjetno razmerje v prid vezavne energije napram mkv:
mkvc2/Eprotona = 0.01.
Ker je torej večino videnega,
kar danes imenujemo masa,
brez klasične mase,
ima pa energijo
(gluonov) brezmasnih delcev močne jedrske sile, ki veže kvarke
v nukleone in to šteje – to mi čutimo in vidimo kot maso.
Polna energija telesa je torej njen kinetični del (Ek ),
zaradi gibanja in zraven še celotna zaloga energije v masi
(mc2),
ki jo v 99 % sestavlja energija nemasnih gluonov, ki vežejo lahke kvarke - zraven
so še elektroni in elektromagnetne vezavne, odbojne energije. Izraz
mc2
je torej še kako upravičen. Zapišimo še enkrat polno energijo E telesa:
mc2γ = Ek + mc2
Na začetku vesolja, ko je še vladala visoka temperatura – kmalu
po inflaciji, hitrem napihovanju vesolja – so najprej nastali
povsem ločeni delci, ki se danes skrivajo v izrazu
mc2.
Vesolje je torej na začetku, zaradi visoke temperature, intenzivnih trkov,
bila vroča »juha« ločenih kvarkov, gluonov in še obilo ostalih delcev.
Iz nakazanih izpeljav, fenomenov pa morebiti tudi nekoliko bolje razumemo
Higgsov koncept, da so delci, ki imajo danes manjšo hitrost od svetlobne
(protoni, elektroni …), na začetku vesolja prelili del energije zaviranja,
zaradi Higgsovega polja (preko bozonov), v maso, preko povezave
m = E/c2 -
ko je temperatura seveda dovolj padla, pod 1028 K. Ko pa je temperatura
vesolja padla »zgolj« na 1012 K, takrat so pa gluoni že začeli lepiti kvarke
v protone in nevtrone, ki jih takrat, že manj intenzivni trki, niso več razbili.
To so torej delci, ki sestavljajo danes ta naš »materialni« svet atomov in molekul,
velikih teles, nas samih.
Da ne govorimo pravljic, pa povejmo, da smo v trkalnikih (recimo CERN - LHC)
dosegli že temperature blizu
1016 K
(mv2, bolje mc2(γ - 1) ∝ kT,
vsak proton v LHC trkalniku trenutno lahko doseže energijo vsaj
Ek = 7 TeV = 7 1012 eV,
kar da neverjetno hitrost protona
v = 0,999999991·c,
izračunajte iz izpeljanih enačb, pri trkih lahko dosežemo celo dvojne vrednosti energij),
tako da zelo dobro poznamo razmere v vesolju vsaj od časa 10-10
s po velikem poku (poznamo
ocene, kdaj se recimo protoni razbijejo v kvarke, gluone, kdaj nastanejo protoni ...).
Oglejte si še enkrat graf razvoja vesolja skozi čas!
Že pred Einsteinom sta Oliver Heaviside in Fritz Hasenöhrl (pa še kdo prej ali sočasno),
dokaj smiselno iskala povezavo med energijo, maso in kvadratom svetlobne hitrosti
(našla sta sorazmernost). A Einstein je leta 1905 (v prekrasnem, čudežnem letu -
annus mirabilis) kot prvi objavil pravilno povezavo med lastno energijo in maso
(E = mc2),
a brez direktnega dokaza. Einstein zapiše enačbo v naslednji obliki
(in z drugačnimi oznakami kot danes, L kot energija, V kot hitrost) – in
sicer pravi, da če telo odda energijo L v obliki sevanja, se njegova masa
zmanjša za L/v2 (s tem je že skoraj razrešil zelo star in težek
problem, od kod zvezdam toliko energije, da nekatere intenzivno svetijo kar
milijarde let). Einstein je enačbo izpeljal naknadno, še istega leta.
Leta 1905 je izpeljal še pravilen izraz za kinetično energijo delcev v članku
"On the electrodynamics of moving bodies" (»O elektrodinamiki gibajočih se teles«):
(ali)
Ek = mc2(1/(1 – v2/c2)1/2 - 1)
V članku "Does the inertia of a body depend upon its energy content?" ("Ali je vztrajnost telesa odvisna
od njegove skupne energije?") pa je podal še dokaz za trditev E = mc2 na primeru, ko telo oddaja
dva svetlobna žarka v nasprotnih smereh. O korektnosti tega dokaza še danes nekateri dvomijo – a
je bilo pozneje izpeljanih in potrjenih še veliko ostalih dokazov o povezavi mase in energije deljene s
kvadratom svetlobne hitrosti. Dognanja omenjenih raziskovalcev, velikih znanstvenikov:
G. F. FitzGerald,
Heaviside, Hasenöhrl, Lorentz, Einstein ... (a danes se morebiti preveč poenostavljeno vse pripisuje Einsteinu),
so izjemno pomembni mejniki v iskanju odgovorov na osnovna vprašanja, kaj in kakšen je ta svet,
kaj je bilo in kaj nas čaka. Ta vprašanja, recimo energija skrita v masi ali ekvivalent mase
glede na energijo, bodo tudi rdeča nit naših naslednjih razmišljanj.
Teorija relativnosti je bila tudi precej
pred časom, saj so pravo naravo fisije in fuzije atomski delcev (Perrin, Eddington, gospa
L. Meitner – cepitev 1939,
Hahn, Bethe – fuzija 1938, Weizsäcker, ...) odkrili nekaj desetletij
pozneje (žal v času priprav na najhujšo vojno). In prav tukaj se je - sicer najprej kot zgolj
teorija na papirju - relativnost pokazala kot še kako realna, pravilna. In sicer pri fisiji -
cepitvi masivnih atomskih jeder, torej pri prehodu dela mase v (tudi rušilno) energijo - in pri
fuziji, v razvozlanem izvoru nastanka težkih elementov do železa
in s tem se je teorija relativnosti izkazala
tudi pri dolgo iskanem viru
enormne energije zvezd. Razlika mas nukleonov (recimo protonov in nevtronov) pred in po zlitju
v masivnejša jedra - pomnožena s kvadratom svetlobne hitrosti - je, zgoščeno povedano, kar naše
življenje = Δmc2. Izjemno!
Torej, če povzamemo, princip fuzije v zvezdah – nukleosinteze (zlivanja) lažjih v težje elemente
(in posledično sprostitve enormne energije zaradi delovanja močne jedrske sile),
je bil razrešen komaj (ali ŽE) v 30-ih letih 20. stoletja. Pokritje mu je dala teorija
relativnosti že vsaj leta 1905 - le mehanizem fuzije je bil
še v povojih. To je bil eden največjih
dosežkov človeštva vseh časov, da torej vemo zakaj sploh smo – odprl nam je tudi pot
v razumevanje dogajanja ob rojstvu vesolja – v genezo.
Pa zaključimo to poglavje z zelo preprostim modelom snovi, ki neprožno trka.
Spodaj je slika, ki poenostavi telo, ki ga sestavljajo atomi in vezi med njimi (
v samem telesu ti atomi, elektroni, nukleoni tudi nihajo, delno potujejo - termično gibanje),
v zelo lahko ogrodje (škatlo), v katerem je masivno nihalo (naj nosi večino mase).
Ko dve taki enaki telesi potujeta druga proti drugi z nasprotno enakima hitrostma
in neprožno trčita, se ustavita in zdi se celo, kot da bi kinetična energija
teles 2*mv2/2 nekam izginila. A če pogledamo dogajanje po
trku - obe nihali zanihata, in če je nihalo zelo masivno napram lahkemu ogrodju,
večino energije preide v nihali (kjer se pretvarja energija iz kinetične v potencialno in nazaj ...).
V resnici se je sedaj večino kinetične energije premega gibanja spremenilo v energijo
nihanja nihal. Temu rečemo v snovi, da se je energija delno pretvorila v notranjo
energijo - termično intenzivnejše gibanje nukleonov, elektronov ...
In to je lep prikaz - kjer lahko slutimo princip dogajanja v snovi med trki in
delno tudi, da je masa povezana z energijo.
Zorkotov mehanični model neprožnega trka in prenos energije po trku v gibanje osnovnih gradnikov snovi,
tudi v povezavi z maso in energijo:
mk = E/c2.
Kot smo že izračunali, velja, da je nova masa mk po trku
(vozička mirujeta) enaka:
mk = 2mγ
In to je vsekakor več kot začetna masa 2m. Sedaj tudi vidimo zakaj, v našem preprostem modelskem
primeru je to na račun nihanja
nihal - v realni snovi pa večinoma na račun termičnega gibanja atomskih jeder, elektronov, lahko tudi
zaradi nihanj kristalnih struktur, če so prisotne ...
Še primer z vzmetjo med vozičkoma.
Zgornjo sliko bi lahko nadomestili recimo s klasično vzmetjo med masivnima vozičkoma, ki se ob trku stisne (skrči za X),
in če ostaneta vozička speta, gre začetna kinetična energija večinoma v prožnostno energijo
Ek = KX2/2.
In spet bi stehtali mk = 2mγ in
razlika mase Δm bi bila v energiji vzmeti deljena s c2:
Δm ∝ KX2/(2c2)
Vse lastnosti telesa, ki so povezane z energijo,
kot je njegova temperatura ali vezavna energija sistemov,
kot so jedra ali molekule, prispevajo k masi tega telesa (lahko jo tudi zmanjšajo - vezavna energija),
tudi elektromagnetno valovanje, fotoni.
V splošni teoriji relativnosti pa vse te lastnosti delujejo še kot vir gravitacije,
kjer se seveda upošteva še vse ostale količine, ki so neposredno povezane z energijo
in gibalno količino, to sta še notranji tlak in napetost.
V matematični formulaciji splošne teorije relativnosti so vse te količine le vidiki bolj splošne
fizikalne količine, imenovane (napetostni) tenzor energije in gibalne količine,
ki določa ukrivljenost prostor-časa.
Skrčenje dolžin in elektromagnetizem
Lorentzovo gibanje električnega naboja.
Zgoraj: naboj miruje v sistemu F, zato ta opazovalec vidi statično električno polje.
Opazovalec v drugem okviru F' se premika s hitrostjo v glede na F in vidi,
da se naboj premika s hitrostjo -v s spremenjenim električnim poljem E zaradi
krčenja dolžine in magnetnim poljem B zaradi gibanja naboja.
Spodaj: podobna naloga, a naboj mirovanju v sistemu F'.
Teorija posebne relativnosti ima pomembno vlogo v sodobni teoriji klasičnega elektromagnetizma.
Podaja formule za to, kako se elektromagnetni elementi, električna in magnetna polja,
spremenijo pod Lorentzovo transformacijo iz enega inercialnega referenčnega sistema v drugega.
Osvetli razmerje med elektriko in magnetizmom ter pokaže, da referenčni okvir določa,
ali opazovanje sledi električnim ali magnetnim zakonom. Rezultira v kompakten in priročen
zapis za zakone elektromagnetizma, in sicer v "očitno kovariantno" tenzorsko obliko.
Maxwellove enačbe, ko so bile prvič navedene v svoji popolni obliki leta 1865,
so se izkazale za združljive s posebno teorijo relativnosti. Še več, navidezna naključja,
v katerih sta dva različna opazovalca opazila enak učinek zaradi različnih fizikalnih pojavov,
se s posebno relativnostjo dokaže, da sploh niso naključna.
Da ne bomo zahajali v podrobnosti (ki smo jih že razložili v uvodu v teorijo relativnosti),
povejmo takoj, da se vektorji magnetnega in električnega
polja skrčijo za opazovalca, ki se giblje glede na sistem v katerem naboj miruje
(kot pri krčenju palice L' = γL , glejte uvod v relativnost).
A potrebno je upoštevati Maxwellove enačbe - ko smo jih zapisali, smo obdelali
tudi primer naboja in opazovalca, ki se giblje glede na naboj.
V teh dveh sistemih, ki se premikata z relativno hitrostjo v, sta E-polje in B-polje povezana z
naslednjimi relacijami - recimo, da je za gibajočega opazovalca F hitrost sistema F' v x smeri (naboj miruje
v sistemu F'), tako velja
v = (vx,0,0) in je zapis
(transformacija med sistemoma) komponent vektorjev magnetnega in električnega polja naslednji.
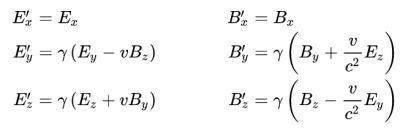
Sledi še splošni vektorski zapis povedanega, to je električnega in magnetnega polja za električni delec, ki ga zazna gibajoči se opazovalec -
za sistem F', kjer naboj miruje, velja:
E' = γ(E + vxB)
B' = γ(B - vxE/c2)
Zgornji povezavi smo že razložili pri Maxwellovih enačbah, sedaj smo le dodali relativistični člen γ.
V bistvu je Lorentz najprej dobil to obliko enačb, da je lahko ohranil
hitrost elektromagnetnega valovanja v vseh sistemih enako.
Tako je preko
negativnih rezultatov Michelsonovih poskusov (Michelson-Morleyjevih), ki so bili
četrt stoletja eden od največjih
nerešenih problemov fizike (enigma) in
neobičajne hipoteze krčenja (kontrakcije) dolžine v smeri gibanja, ki jo je že leta 1892
podal G. F. FitzGerald, prišlo, preko več sugestij, izračunov, tudi Lorentza, Poincaréja,
Einsteina ... do nove teorije, mehanike relativnosti.
Če torej domnevamo, da se dolžina v smeri gibanja skrči za faktor:
1/γ = (1 - v2/c2)1/2
- se izriše povsem nov, pravilnejši, opis sveta.
Če so hitrosti majhne, je γ ≈ 1 in dobimo prvotni klasični zapis
premikanja naboja preko Maxwellovih enačb:
E' ≈ E + vxB
B' ≈ B - vxE/c2
Analogno za gostoto naboja ρ = e/V in gostoto toka J = I/S za vzporedno
(||) in pravokotno smer (⊥)
glede na hitrost, veljajo naslednje enačbe, transformacije:
J||' = γ(J|| - vρ)
ρ' = γ(ρ - vJ||/c2)
J⊥' = J⊥ - za pravokotno smer
Še zelo zanimiva računska vaja
O relativističnem gibanju izstrelkov (balistika, poševni met): o dometu in navpični višini
⤼
⇑
⇒
↑ ⬈ →
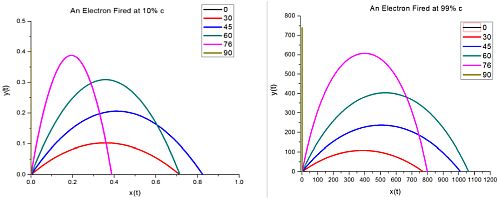
Povzetek
Lastnosti izstrelkov, ki se približujejo svetlobni hitrosti, bomo proučevali matematično ter
v primerjavi z nerelativističnimi projektili. Ugotovili bomo, da je kot,
pod katerim je doseg enak navpičnici
(maksimalni višini) za relativistične izstrelke odvisen od hitrosti in se giblje od 76 °
do 80,3 °. Torej se razlikuje od nerelativističnega
primera, kjer je kot neodvisen od hitrosti in je stalen pri cca 76 °.
Upoštevani bodo različni scenariji z uporabo protonov in
elektronov v navpičnih poljih sile, da bomo tako lažje razumeli naše rezultate.
1. Uvod
Projektili so definirani kot predmeti, ki se premikajo skozi prostor pod
vplivom konstantne sile navzdol (kot npr
sila gravitacije ali homogenega električnega polja).
Primeri takega gibanja vključujejo gibanje žog za baseball, nabojev in vodnih fontan ali elektronov, protonov,
ionov
v električnem homogenem polju.
Kinematika teh normalnih, nerelativističnih projektilov je dobro razumljena
in dokumentirana v skoraj vseh
temeljni učbenik fizike.
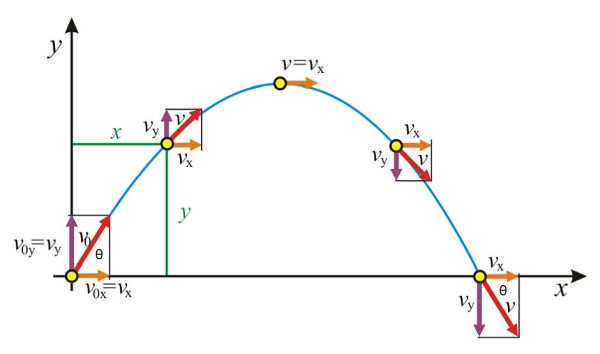 | 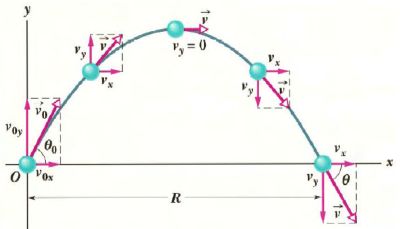
|

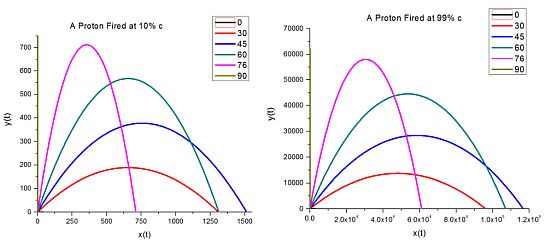
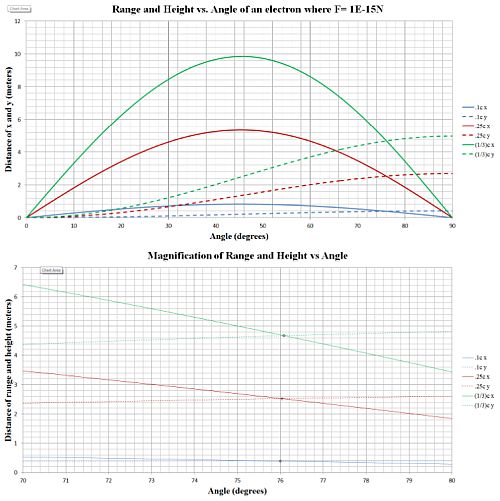
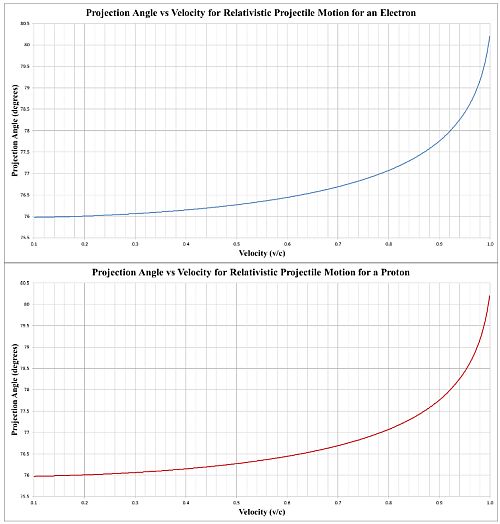
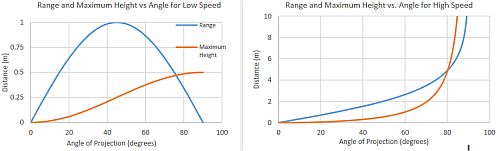




 | 
|

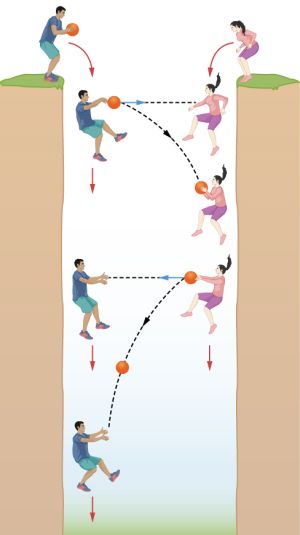
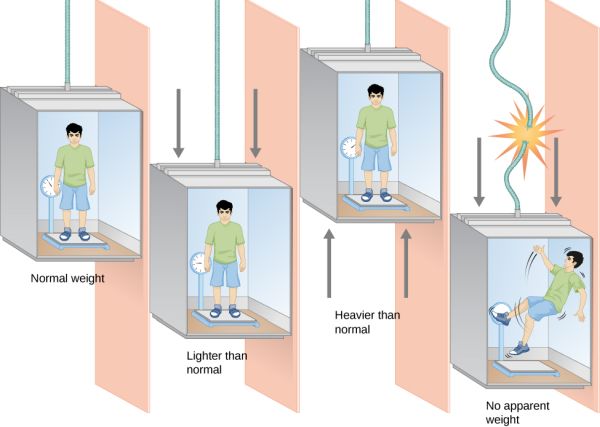
Ker je zgolj pogled na relativnost preko hitrosti za mnoge sporen in v resnici je energijska slika
veliko bolj celostna (sploh, ker energija vpliva na prostor, obnašanje
delcev v prostoru, in ker je masa zgolj ena izmed oblik energije), še enkrat ponovimo,
kaj se skriva v polni energiji delca E = mγc2 ?
Če privzamemo, da je pri majhnih hitrostih (v) izraz
1/(1 – v2/c2)1/2 ≈
1 + v2/(2c2),
potem velja za
mc2γ = mc2/(1 – v2/c2)1/2
≈
mc2(1 + v2/(2c2))
= mc2 + mv2/2.
Za majhne hitrosti torej velja, da je zraven kinetične energije
(Ek = mv2/2) prištet
še člen mc2. Izraz E ≈ mc2 + mv2/2 =
Eo + Ek imenujemo polna energija delca, zatorej je tudi izraz
E = mc2γ
polna energija delca z maso m z veliko hitrostjo.
Izraz
Eo = mc2
pa imenujemo mirovna energija
telesa z maso m (toliko zaloge energije se nahaja v njem
– v atomih, elektronih, v kvarkih, gluonih, vezavnih silah …).
Torej, če pogledamo samo vpliv gravitacije na energijo delca (mase m ali na foton), moramo dobiti pri majhnih
težnostnih pospeških klasični izraz za potencialno energijo (oz. potencial).
Posplošimo torej Lorentzov člen s prehodom na energijo delca, označeno kot E', bolje, pravilneje na potencial Φ.
To smo delno že storili v poglavju o fiziki velikih hitrosti, energij.
Velja torej zapisati člen v2 s klasično energijo.
Za kinetično energijo (označimo jo s črtico ') velja E' = mv2/2, od koder sledi člen za kvadrat hitrosti:
v2 = 2E'/m
Potencial masivnega sferičnega homogenega
telesa M je kar enak Φ = -GM/r.
Za velikost potencialne energije velja E' = |GMm/r|, oziroma člen 2E'/m se zapiše kot:
-2E'/m = -2GM/r = 2Φ
Tako za Lorentzov člen pri skromni gravitaciji dobimo naslednji izraz:
1/(1 – v2/c2)1/2 = 1/(1 – 2E'/(mc2))1/2 ≈
1 + E'/(mc2)
Pri potencialni energiji (potencialu Φ) pa moramo torej dobiti potencial Φ = E'/m = -GM/r
(seveda, G je gravitacijska konstanta, M je centralna sferična
homogena masa, r je razdalja od središča homogene sferične mase), od koder primerjalno sledi, da je izraz,
za majhne vrednosti 2GM/(rc2) << 1 (na površini Zemlje to zagotovo velja),
kar (≈) enak:
1 + E'/(mc2) = 1 + Φ/c2 =
1 - (GM/r)/c2
Torej, če nam je koncept ubežne hitrosti tuj, pa je energijski pogled, sama izvedena primerjava,
konsistentna za člen, ki vpliva
na čas in geometrijo prostora zaradi centralne mase, naslednji - za sfero torej velja, za velike gravitacije:
1/(1 – 2GM/(rc2))1/2
A zgornji razmislek se bo še v nadaljevanju nadgradil. Zakaj?
Ker se ob masivnih telesih svetloba odmakne od prvotne poti in ker
svetloba (elektromagnetno valovanje) nima klasične mase, nanjo torej ne more delovati
sila teže (klasična gravitacija), je smiselno govoriti o ukrivljenosti prostora,
ki ga ukrivlja energija, večinoma masa velikih vesoljskih teles (E = mc2), zvezd, galaksij ...
Ta ukrivitev prostora pa potem vpliva tako na masne delce, kot na svetlobo.
Zato je člen, ki določa razdalje in čas nekega sistema, prostora ... pravilneje opisati s potencialom
(v bistvu z energijo).
Ali znamo izračunati recimo hitrost ur v gravitaciji ali ukrivitev svetlobe, Dopplerjev zamik valovnih dolžin zaradi gravitacije? Vemo, da gravitacija prispeva k spremembi kinetične energije – torej k spremembi hitrosti teles in tukaj bomo poiskali rešitev nove metrike in vpliv gravitacije nanjo!
Kako se bomo lotili problema gravitacije in vpliva le te na metriko prostora, na čas in razdalje
ob zvezdah, planetih, v satelitih ...?
Pomembno je, da izhajamo iz
Michelson–Morleyjevega eksperimenta
in
iz invariante četverca prostor-čas in seveda, da je v limiti
zmeraj veljavna klasična mehanika.
To pomeni klasična kinetična energija
Ek = mv2/2
pri majhnih hitrostih delcev
in klasična potencialna energija
Ep = -GMm/r
za skromne centralne mase ali velike razdalje r od središča
homogene sfere.
Velja tudi, da prostor-čas v limiti majhnih hitrosti in gravitacije
lahko obravnavamo kot klasičen 3D prostor.
Torej, če miselno naredimo pot od majhnih hitrosti v skromni gravitaciji,
ki so nam blizu, velja klasični Pitagorov izrek za izračun razdalj v prostoru
ds2 = dx2 + dy2 + dz2,
- sedaj pa
gremo na hitrosti blizu svetlobne, pri zanemarljivi gravitaciji, ko velja
(iz
Michelson–Morleyjevega eksperimenta, ki je pokazal, da je hitrost elektromagnetnega valovanja, svetlobe,
v vseh
nepospešenih opazovalnih sistemih enaka) Pitagorov izrek v četvercu prostor-čas
ds2 = -c2dt2 + dx2 + dy2 + dz2,
- na koncu pa se premaknimo še v prostor z izrazito gravitacijo, za katerega
še ne poznamo metrike, to je Pitagorovega izreka, a zapišimo splošno
enačbo za razdaljo (gibanje v x smeri, ki naj bo kar radialna smer glede na masivno sfero, ki povzroča gravitacijo)
ds2 = Bdt2 + Adx2 + dy2 + dz2,
Člena A in B moramo še poiskati - to je torej naša naloga. Uporabili bomo 4 metode.
Če zadevo pogledamo obrnjeno in zgolj skozi vektorje četverce, potem pričakujemo, da velja:
četverec za izrazito gravitacijo in veliko hitrost (B1/2t, A1/2x, y, z) =>
prehaja v skromni gravitaciji v vektor četverec ravnega prostora (ct, x, y, z) =>
prehaja v 3D vektor za majhne hitrosti delcev (x, y, z).
Brez zgoraj omenjenih limit, predpostavk, se ne da z nobeno metodo izpeljati metrike (ds) ob sferičnih telesih.
Uporabili bomo 4 poti in vsaka na koncu predvideva ob skromni gravitaciji klasično potencialno energijo delca,
postulate ravnega prostora, če gravitacija limitira proti 0 in ob majhnih hitrostih kar
klasičen Pitagorov izrek za računanje razdalj (to je učeno rečeno, metrike ds).
Splošno razdaljo ds2 = Bdt2 + Adx2 + dy2 + dz2
v gravitaciji si upamo zapisati, ker bomo obravnavali gravitacijo sferičnih homogenih teles (čemur se
planeti in zvezde zelo približajo in kjer je vpliv gravitacije zgolj radialen).
V resnici bomo raje računali s sferičnimi koordinatami, ker se sila gravitacija spreminja z 1/r2,
potencial pa kar obratno sorazmerno z razdaljo od središča (1/r) - recimo nad površino zvezde, planeta, lune.
A gremo po vrsti.
Ponovimo in nadgradimo osnove iz prejšnjih poglavij
Če v izraz za prostor-čas metriko
ds2 = -c2dt2 + dx2 + dy2 + dz2
vstavimo sferični zapis koordinat (kajti zvezde in planeti so v približku dokaj dobre krogle):
x = r sinϑcosφ, y = r sinϑsinφ, z = r cosϑ
dx = dr sinϑcosφ + r dϑ cosϑcosφ - r dφ sinϑsinφ
dy = dr sinϑsinφ + r dϑ cosϑsinφ + r dφ sinϑcosφ
dz = dr cosϑ - r dϑ sinϑ
- dobimo izjemno koristno obliko računanja razdalj ob sferi
(to so pa seveda planeti, zvezde, itn.)
dS2 = -c2dt2 + dx2
+ dy2 + dz2 = -c2dt2 + dr2
+ r2(dϑ2 + sin2ϑ dφ2)
Sledi slika za pomoč
(kjer je ds2 = dl2 = dx2 + dy2 + dz2).
V sferičnih koordinatah pa velja še naslednji zapis vektorja četverca metrike (pomoč so zapisi zgoraj in slike):
ds = ( cdt, dr , rdϑ , r sin ϑ dφ )

V uvodu v fiziko velikih hitrosti smo obravnavali dogodek vertikalnega izseva svetlobe
v stropno zrcalo glede na gibajoč sistem in glede na opazovalca, ki miruje
(recimo ob vlaku) – a na vlaku bi lahko obravnavali tudi premik v smeri
gibanja … Naredimo ta primer v gravitaciji. Ogledali si bomo dogodek ob
poljubni zvezdi, planetu, ko se recimo nek delec premika ob zvezdi, planetu
(gledamo torej spremembo časa dt' in recimo radialni premik dr').
Sedaj imamo v igri tri opazovalce, prvega, ki je zelo daleč vstran
od Zemlje (od teže), drugega recimo na Zemlji in na koncu bomo vpeljali
še tretjega, ki prosto pada.

Načelo ekvivalentnosti v splošni teoriji relativnosti upošteva, da ni
mogoče razločevati učinka težnostnega polja v nepospešenem opazovalnem
sistemu od učinka pospeševanja opazovalnega sistema v prostoru, kjer ni
težnostnega polja. V pospešeni raketi prav tako deluje vzgon (topel zrak
se dviga, zato lahko enostavno kuhamo z ognjem kot na Zemlji), telesa
v pospešeni raketi pospešeno padajo, poševni met izgleda enako kot na
Zemlji ..., če sta pospešek g in a enaka, tudi ure tečejo enako.
Torej, če raketa pospešuje z enako odvisnostjo
(a ∝ 1/r2)
od razdalje kot je odvisen od razdalje od središča nebesnega telesa gravitacijski pospešek
(g ∝ 1/r2),
potem bo v vsaki točki in razdalji fizika v raketi (potek časa, vzgon, pot delcev ...), enaka fiziki
v gravitacijskem polju - recimo Zemlje ...
Pri pospešenih sistemih (t. i. paradoks dvojčkov - glejte posebno teorijo relativnosti)
primerjava ur dejansko pokaže različna časa
(na spletu lahko najdemo kar nekaj izračunov na to temo, recimo na strani:
https://de.wikipedia.org/wiki/Zwillingsparadoxon#Beschleunigte_Bewegungen).
Recimo, da en opazovalec lovi drugega (prvi najprej ustavi raketo in nato pospeši
do drugega opazovalca, ki cel čas potuje enakomerno), in ko se srečata, prvi opazovalec
pokaže uro, ki dejansko kaže krajši čas (zaradi pospešenega gibanja) od kolegove ure
(je torej nekoliko mlajši od drugega kolega, ki cel čas potuje enakomerno).
Ta del posebne teorije relativnosti in še mnoge ostale uganke iz čudežnega
sveta vesoljskih pojavov, so rodile razmislek o času v gravitaciji –
in Einsteina pripeljale do splošne teorije relativnosti. V splošni teoriji relativnosti
igra glavno vlogo gravitacija (pravilneje ukrivljen prostor-čas, ki ga krivi masa in
ostale oblike energij), torej so v igri opisa realnosti glavni odločevalci pospešeni
sistemi, kjer pričakujemo dejansko vpliv "gravitacije" na čas - na hitrost ur
in seveda na merjenje razdalj (na metriko ds). Več sledi.
Zaradi plimskih sil se je
Einsteinu zdelo potrebno izraziti pridržek, da njegovo načelo ekvivalentnosti (enakovrednosti) ne bi izgubilo veljave:
in sicer je reduciral njegovo uporabnost na eno točko. Več o tem pozneje.
Kot smo že pri uvodu v fiziko velikih hitrosti povedali, da paradoksa dvojčkov ni,
razen če en od njiju potuje pospešeno, spremeni smer gibanja (potem mu čas, ura
teče počasneje) – je pri gravitaciji natančno enako (Načelo ekvivalentnosti
v splošni teoriji relativnosti upošteva, da ni mogoče razločevati učinka
težnostnega polja v nepospešenem opazovalnem sistemu od učinka pospeševanja
opazovalnega sistema v prostoru, kjer ni težnostnega polja.).

Ura v pospešenem sistemu, to je recimo kroženje (radialni pospešek je
ar = vt2/r = ω2r), teče počasneje.
Ura v krožečih sistemih dejansko tečejo počasneje, velja:
dτ = dt(1 – vt2/c2)1/2
To so pokazale tudi meritve. Podobno velja za satelite in tudi za ure na Zemlji,
ki zaradi kroženja Zemlje, tečejo nekoliko počasneje,
a v tem primeru je hitrost odvisna od geografske širine φ, velja:
vt = ωrzcos(φ)
A tudi sama teža upočasnjuje čas - ure (živimo namreč v pospešenem sistemu,
recimo planeta Zemlja) – a več o tem v nadaljevanju.
Lenz-Schiffov pristop (Rindler’s counterexample) za pospešene soisteme - so veliki pomisleki, a ima določene prednosti:
https://arxiv.org/pdf/gr-qc/0611104
Sedaj se spomnimo na primer,
da v pospešenem sistemu čas teče počasnje ( dt(1 - v2/c2)1/2, recimo pri kroženju )
in tam se tudi dolžine skrčijo ( dr/(1 – v2/c2)1/2 ), uporabimo ta premislek
v prehodu v pospešene sisteme.
Tako bi lahko drzno za metriko spodaj zapisali naslednji izraz (intuitivno - in izkaže se, da je končni
rezultat pravilen, kjub poenostavitvam - to je t. i.
Lenz-Schiffov pristop (Rindler’s counterexample) za pospešene soisteme).
Če za spremenljivki dt' in dr' v metriki
ds2 = -c2dt'2 + dr'2
+ r2(dϑ2
+ sin2ϑ dφ2)
(recimo za premik dr') vstavimo že znani transformaciji za čas in koordinato
dt' = dt(1 – v2/c2)1/2
in
dr' = dr/(1 – v2/c2)1/2 – za gibanje v radialni smeri (pospešen sistem, recimo gravitacija),
potem dobim naslednjo obliko metrike:
ds2 = -c2dt2(1 - v2/c2)
+ dr2/(1 - v2/c2) + r2(dϑ2 + sin2ϑ dφ2)
Sedaj pa se vprašajmo, kolikšen pa je lahko prispevek teže (gravitacije) k metriki (glej sliko)? Prispevek se skriva v hitrosti v in je posledica gravitacije – velja pa načelo ekvivalentnosti. Gibajoči sistem tik ob Zemlji ima radialno hitrost v = (2GM/r)1/2, to je hitrost v primeru, da je telo padlo iz neskončnosti. Glejte tudi poglavje o poševnem žarku in treh opazovalnih sistemih ter o Einsteinovi najsrečnejši misli v življenju. Prispevek je torej tolikšen, kolikšen je prirast hitrosti zaradi teže (spet načelo ekvivalentnosti). Gledamo torej za kratek trenutek dt' metriko, ki jo čuti oseba recimo na Zemlji in metriko, ki je za čas dt enaka, a jo vidi nek zelo oddaljen (mirujoč) opazovalec. Pričakujemo torej lahko, da se bo metrika na Zemlji poračunala za hitrost, ki je posledica teže – in to je hkrati ubežna hitrost. Kako jo izračunamo (srednja šola)?
Primerjava metrike
( ds2 = -c2dt2(1 - v2/c2)
+ dr2/(1 - v2/c2) + r2(dϑ2 + sin2ϑ dφ2) )
enakomerno se gibajočega sistema S' (s hitrostjo v) in recimo velikega telesa (Zemlje
z maso M in polmerom r), kjer je vpliv na metriko zaradi gravitacije podoben, kot če bi
se sistem S' gibal z ubežno hitrostjo
(v2 = 2GM/r).
Velja za oddaljenega
»mirujočega« opazovalca.
Kot smo že omenili v prejšnjem poglavju (o poševnem žarku), lahko člen Φ = E'/m = -GM/r razumemo tudi kot vpliv gravitacijskega
potenciala (energije) centralne
mase, recimo zvezde, na čas in merjenje dolžin (na prostor - čas), ko velja
(1 + 2Φ/c2)1/2
≈ 1 + Φ/c2 =
1 - (GM/r)/c2 (velja za majhne vrednosti 2GM/(rc2) << 1).
Načelo ekvivalentnosti v splošni teoriji relativnosti upošteva, da ni
mogoče razločevati učinka težnostnega polja v nepospešenem opazovalnem
sistemu od učinka pospeševanja opazovalnega sistema v prostoru, kjer ni
težnostnega polja. V pospešeni raketi prav tako deluje vzgon (topel zrak
se dviga, zato lahko enostavno kuhamo z ognjem kot na Zemlji), telesa
v pospešeni raketi pospešeno padajo, poševni met izgleda enako kot na
Zemlji ..., če sta pospešek g in a enaka, tudi ure tečejo enako.
Torej, če raketa pospešuje z enako odvisnostjo
(a ∝ 1/r2)
od razdalje kot je odvisen od razdalje od središča nebesnega telesa gravitacijski pospešek
(g ∝ 1/r2),
potem bo v vsaki točki in razdalji fizika v raketi (potek časa, vzgon, pot delcev ...), enaka fiziki
v gravitacijskem polju - recimo Zemlje ... Torej se bo tudi hitrost sistema z opazovalcem (ki opazuje
fiziko v prostoru pospešene rakete) spreminjala
enako, kot je odvisna ubežna hitrost od razdalje od nebesnega telesa.
Do zapisanih primerjav smo lahko zadržani, a če ne znamo principa ekvivalentnosti vključiti
v razumevanje metrike (vsaj na fenomenološki ravni), to pomeni, da na nek način zanikamo veljavnost principa
ekvivalence (ki je eden od temeljev splošne relativnosti - z določenimi omejitvami, recimo pri
pri razlagi plimovanja, a pri plimovanju gre za mehaniko velikih teles).
Načelo ekvivalentnosti (EP) se ukvarja s homogenimi gravitacijskimi polji,
ki se jim v realnem prostoru
težko približamo, razen lokalno pri točkastem telesu.
Einstein namreč pravi, da bi lahko ugotovil, kje smo, z majhnim poskusom: spustili bi dva predmeta
in če padeta popolnoma vzporedno,
smo v pospešeni raketi nekje v vesolju daleč od masivnih teles.
Toda, če predmeti padajo v rahlo konvergentnih smereh '\ /' (se približujeta), je to pojav padanja na Zemlji.
Zakaj?
Ker na Zemlji predmeti padajo proti središču mase.
Za ta primer se je Einsteinu zdelo potrebno izraziti pridržek, da njegovo načelo ekvivalentnosti (enakovrednosti) ne bi
izgubilo veljave: reduciral je njegovo uporabnost na eno točko. Seveda na točki ni mogoče izkusiti
"plimskih sil", kot fiziki radi imenujejo sile, zaradi katerih dva predmeta sledita opisani konvergentni smeri
ali pa recimo, da zaradi razsežnosti padajočega predmeta sila teže
na del, ki je bližje središču, recimo Zemlje, delujejo močneje kot
na bolj oddaljen del padajočega telesa (tako bi nas gravitacija raztrgala, še preden bi padli v črno luknjo).
Kako do pravilnega izraza za metriko v gravitaciji (preko primerjave z metriko ravnega prostora)?
Časovni del metrike
Bolje, kot da ugibamo člen v2/c2, ga zapišimo kot X/c2 in
se vprašajmo, kako se izraža neznanka X v gravitaciji?
Recimo v limiti skromne gravitacije, ko moramo iz metrike
za mirujoč delec z maso m dobiti klasično gravitacijsko energijo ob masivnem sferičnem telesu
z maso M in polmerom r. Recimo na Zemlji.
Če torej primerjamo časovni člen četverca ravnega prostora [ γ = 1/(1 – v2/c2)1/2 ]
in iskani člen ob recimo Zemlji (gravitacija upočasni ure, načelo ekvivalentnosti, zato velja
[ dt' = dt(1 - X/c2)1/2 ]), ki oba
opisujeta energijo delca,
- potem bi pričakovali, da enako kot pri ravnem prostoru, ko pri majhni hitrosti delca, energija preide
v klasično kinetično obliko energije
Ek = mv2/2 (kar smo že dokazali in dokaz zapišimo še enkrat):
mc2γ = mc2/(1 – v2/c2)1/2
≈
mc2(1 + v2/(2c2))
= mc2 + mv2/2.
- da tudi pri skromni gravitaciji (recimo, če delec miruje na Zemlji, potem je člen γ = 1) potem dobimo kar
klasično gravitacijsko energijo delca z maso m, ko velja
Ep = -GMm/r.
In kako se potem izraža iskana neznanka X pod korenom. Pri skromni gravitaciji bi torej naj
veljalo:
mc2(1 - X/c2)1/2 ≈ mc2(1 - X/(2c2)) =
mc2 - mX/2 = mc2 - GMm/r
Od koder sledi, da je X = 2GM/r = -2Φ
Na Zemlji bi torej moralo veljati, da čas teče nekoliko počasneje
in ga lahko opišemo kar z enačbo
dt' = dt(1 - X/c2)1/2 = dt( 1 - 2GM/(rc2) )1/2
= dt( 1 + 2Φ/c2)1/2
Krajevni del metrike
Časovni del s klasično potencialno energijo v limiti skromne gravitacije se zdi zelo prepričliv. Kaj pa krajevni del metrike,
gre vendar za iskanje ukrivljenega prostor-časa, na koncu tudi za gravitacijske valove v samem prostor-času.
V radialni smeri dr, v kateri deluje gravitacija, pa bi pričakovali skrčenje dolžin zaradi teže
(gre za pospešen sistem in Einsteinov princip ekvivalence).
Poiščimo torej parameter 'b' v spodnji enačbi.
[ dr' = dr/(1 - b/c2)1/2 ])
Ker gre pri klasični izpeljavi Lorentzevega člena &gammma; za vpliv tako na čas kot na dolžine,
pričakujemo, da bo tudi parameter 'b' enak kot pri upočasnitvi časa v gravitaciji, torej bi naj veljalo b = 2GM/r.
Tako lahko zapišemo za diferencial dr' koordinate v radialni smeri kar izraz:
dr' = dr/(1 - 2GM/(rc2))1/2
Tako za metriko ds ob masivnem sferičnem telesu lahko zapišemo izraz (ki je pravilen):
ds2 = -c2dt2(1 - 2GM/(c2r)) +
dr2/(1 - 2GM/(c2r)) + r2(dϑ2 + sin2ϑ dφ2)
V časovnem delu metrike smo bili pri izpeljavi dokaj suvereni (dt' = dt( 1 - 2GM/(rc2) )1/2),
pri krajevnem delu dr' pa nekoliko manj.
To zgoraj prehojeno pot do metrike ds v prostor-času ob sferičnem masivnem telesu
bi lahko nekako povzeli kot
Lenz-Schiffov pristop (Rindler’s counterexample) - povedali smo že, da so veliki pomisleki ob tem poenostavljenem
sklepanju, a to sklepanje ima določene prednosti, sploh v pripravi resnejšeših izpeljav, razmislekov v splošni relativnosti:
https://arxiv.org/pdf/gr-qc/0611104
A kot bomo videli pri bolj korektnih izpeljavah metrike, recimo že
preko Euler–Lagrangeeve enačbe, je naš dokaj hevristični pristop dal pravilen rezultat.
Enak rezultat dobimo tudi z ubežno hitrostjo - a o tej metodi ubežne hitrosti se mnenja še bolj krešejo. A vendar zadaj tiči
poučen razmislek - to je prehod iz ravnega prostora v gravitacijo. To je zelo pomemben ramislek,
kaj nam torej gravitacija dodatnega prinese v metriko. In rezultat je za sferično telo relativno zelo preprost, v limiti se ujema
s klasično gravitacijo.
Na tej spletni strani pa najdemo tudi še
Schwarzschildovo rešitev iz Einsteinovih enačb polja - to je uveljavljen geometrijski pristop (II)
in
zelo nazorno kombinirano izpeljavo metrike preko
Euler–Lagrangeeve enačbe (III).
A kot bomo videli, sta obe izpeljavi
na koncu vezani na limito, ki da za rešitev kar klasično gravitacijsko potencialno energiji pri
skromni gravitaciji - pri skromni masi centralnega sferičnega telesa ali pri dovolj veliki oddaljenosti od sfere
(raven prostor Mikowskega). In to je hkrati ključ, da so preprostejši razmisleki do Schwarzschildove metrike
še kako utemeljeni. Sploh, če se spomnimo postulata o ohranitvi vsote potencialne in kinetične energije,
iz katere smo tudi izpeljali kvadrat ubežne hitrosti.
Še enkrat se torej dotaknimo razmisleka z ubežno hitrostjo - ki da za metriko enak rezultat - in ki
ima svoj pojavni smisel v prehodu iz ravnega v ukrivljen prostor.
Ubežna hitrost (v) z določene zvezde ali z Zemlje (s polmerom r
in maso M) se izračuna kar iz energijskega zakona, ko se vprašamo s kolikšno kinetično
energijo moramo zalučati nek predmet z Zemlje, z zvezde, da se bo v neskončnosti ustavil
v∞ = 0
(bo ušel gravitaciji – enako je, če bi se vprašali, s kakšno hitrostjo
bo predmet padel na Zemljo, na zvezdo iz neskončnosti). Če ni dela drugih
sil (delo teže je zapakirano v potencialni energiji), se vsota kinetične
[mov2/2]
in potencialne energije [- GmoM/r] telesa ohranja.
Energija telesa je enaka na zvezdi kot v neskončnosti
(kjer vemo, da je vsota obeh in vsake posebej 0, saj velja
mo02/2 = 0 in -GmoM/r∞ = 0).
Kar zapišimo kot
E = mov2/2 - GmoM/r = 0 + 0,
od koder sledi ubežna hitrost.
v2 = 2GM/r
v = (2GM/r)1/2 - to je torej ubežna hitrost z zvezde z maso M in s polmerom r
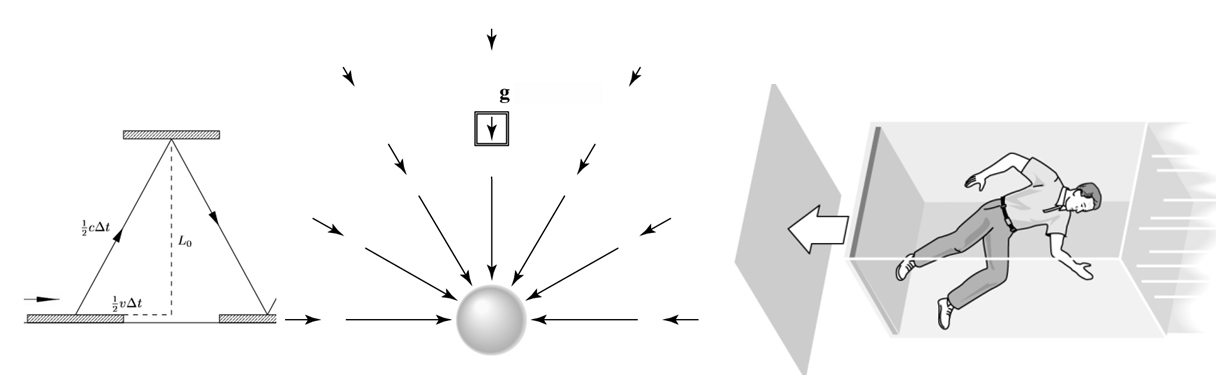
Ker je v2 = 2GM/r tista hitrost, ki vpliva na opažanja opazovalca na
Zemlji, zvezdi in tistega zelo daleč vstran od Zemlje, to hitrost tudi vstavimo
v že izpeljano metriko:
ds2 = -c2dt2(1 - v2/c2)
+ dr2/(1 - v2/c2) + r2(dϑ2 + sin2ϑ dφ2)
In - rezultat je za v2 = 2GM/r zelo, zelo zanimiv (imenuje se tudi Schwarzschildova metrika):
ds2 = -c2dt2(1 - 2GM/(c2r)) + dr2/(1 - 2GM/(c2r)) + r2(dϑ2 + sin2ϑ dφ2)
Kot smo že omenili v prejšnjem poglavju (o poševnem žarku), lahko člen Φ = E'/m = -GM/r razumemo tudi kot vpliv gravitacijskega potenciala (energije) centralne mase, recimo zvezde, na čas in merjenje dolžin (na prostor - čas), ko velja (1 – 2GM/(rc2))1/2 = (1 + 2Φ/c2)1/2 ≈ 1 - (GM/r)/c2 (velja za majhne vrednosti 2GM/(rc2) << 1).
V sferičnih koordinatah pa velja še naslednji zapis vektorja četverca metrike (pomoč so spet zapisi zgoraj in slike):
ds = ( c(1 - 2GM/(c2r))1/2dt, dr/(1 - 2GM/(c2r))1/2 , rdϑ , r sin ϑ dφ )
= ( c(1 - rs/r)1/2dt, dr/(1 - rs/r)1/2 , rdϑ , r sin ϑ dφ )
V resnici se uvede metrični tenzor g.
Iz zapisa lahko uganemo metrični tenzor g. Po diagonali bo imel
vrednosti:
-(1 - 2GM/(c2r), 1//(1 - 2GM/(c2r), r2,
r2 sin2ϑ
- vsi ostali členi bodo 0 (gre za sferično telo).
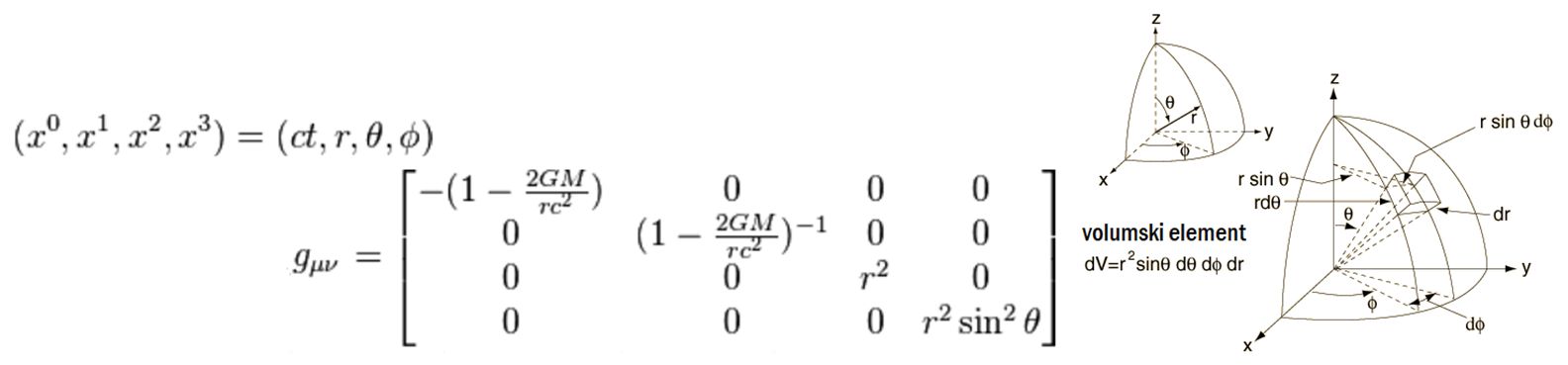
Za sferične koordinate torej velja vektor
dxμ = (dx1, dx2 , dx3 , dx4) = ( cdt, dr, dϑ, dφ )
in naslednji zapis metrike ds2 (4d Pitagorov izrek ob masivni sferi,
ds2 = gμνdxμdxν =
∑μνg(x)μνdxμdxν
):

V bistvu je metrični tenzor gμν sestavljen iz ravnega prostora brez gravitacije ημν
(po diagonali ima člene -1, 1, 1, 1 - vsi ostali so nič)
in ukrivljenosti zaradi gravitacije hμν. Tako velja:
gμν = ημν + hμν
Še vaja - kako računamo razdaljo ds2 z metričnim tenzorjem. Velja ds2:

Računanje razdalj ds2 preko metričnih tenzorjev (gij, oziroma
ηij zgoraj).
Velja:
ds2 = ∑ijg(x)ijdxidxj
Primer računanja, če indeksa i in j štejemo od 1 do 4:
ds2 = g11dx12
+ 2g12dx1dx2 ... + g44dx42
Velja, če so le členi η00, η11, η22 in
η33 različni od nič, potem je vsota produktov kar enaka:
ds2 = -c2dt2 + dx2 + dy2 + dz2
kar je razdalja Minkoswkega v 4D prostor-času in je le v tem primeru enaka kar skalarnemu
produktu vektorja četverca.
Skrajšani zapis je:
ds2 = ηijdxidxj
Schwarzschildovo metriko zapišimo še s substitucijo Schwarzschildovega polmera rs = 2GM/c2 in vpeljimo še kot dΩ2 = dϑ2 + sin2ϑ dφ2 (to je recimo kotni zasuk satelita na orbiti). Tako dobimo krajši, nekoliko bolj pregledni zapis metrike.
ds2 = -c2dt2(1 - rs/r) + dr2/(1 - rs/r) + r2dΩ2
To metriko je izpeljal že Karl Schwarzschild leta 1915 – ko je
Albert Einstein objavil tenzorske enačbe polja splošne teorije
relativnosti (teorija seveda vključuje gravitacijo, bolje energijo
prostora) in Schwarzschildova metrika je hkrati rešitev Einsteinovih
enačb za sferično porazdeljeno maso (za zvezde, planete).
Glejte tudi izpeljavo
Schwarzschildove rešitve iz Einsteinovih enačb polja - na tej strani, ena redkih v slovenščini (2023).
Karl
Schwarzschild ŽAL leta 1916 hudo zboli na fronti.
Izkaže se tudi, da ta naš »preprost« premislek potrjujejo tudi
meritve in potrjuje ga seveda tudi dosledna Schwarzschildova
izpeljva znotraj splošne teorije relativnosti.
Še komentar na člen 2Gm/(c2r).
Imenujemo ga tudi deformacija prostora in je podana
z izrazom
h = 2Gm/(c2r).
Srečali ga bomo tudi pri gravitacijskih
valovih. Ime je po svoje posrečeno izbrano, saj nam brez dimenzijski h pove,
za koliko se spremeni čas ali odmik (neka dolžina) od ravnega prostora
(raven prostore je mišljen kot
območje, kjer ni gravitacije, pospeškov ...).
V členu h = 2Gm/(c2r), je tudi izraz Gm/r, ki je direktno vezan na energijo (bolje potencial telesa), kar
nam spet sugerira, da prostor, njegovo geometrijo, v resnici deformira, bolje določa, energija nekega sistema (recimo zvezde, sistema zvezd, galaksij, ostale oblike
energij zaradi gibanja, sevanja ...).
V enem od poglavij se bomo vprašali ali znamo pomerit člen
h = 2Gm/(c2r)
in tako ujeti gravitacijske valove.
Izhajajmo iz Lorentzevih transformacij za dolžino in pomislimo še na možnost,
da se tudi sam prostor skrči - zelo zanimiva ("prevratniška") misel - in s tem smo na sledi nihanju, valovanju prostora,
še prej pa na poti do ukrivljenega prostor-časa.
Za krčenje dolžine iz relativnosti velja
L = L'/γ = L'(1 – v2/c2)1/2 = L'(1 – 2Gm/(c2r))1/2
= L'(1 – h)1/2
- in nekako tako je razmišljal
leta 1905 tudi Francoz Henri Poincaré, ki je prvi predlagal gravitacijske valove (ondes gravifiques),
ki izvirajo iz pospešene mase in se širijo s svetlobno hitrostjo, v idejo je vključil Lorentzove transformacije.
Sedaj vidimo zakaj.
Na spletu je veliko pdf in html dokumentov,
kjer je Schwarzschildova metrika izpeljana
preko simetričnega metričnega tenzorja, ko so samo členi diagonale različni od 0
(gre za sferična masivna telesa, recimo zvezde ...), to je, preko Riccijevega tenzorja
(ki opisuje, kako se ukrivljenost spreminja od točke do točke), ki je zunaj sfere 0 - ker predpostavimo vakuum
in gledamo zelo lokalno, kjer ukrivljenost ne igra vloge,
kot to recimo počnemo na Zemlji, ko lokalno uporabljamo evklidsko geometrijo, recimo pri mestni urbanistiki, ...,
potem preko Christoffelovih simbolov
(ki opisujejo kako se lokalne koordinatne baze spreminjajo od točke do točke).
Glejte tudi izpeljavo
Schwarzschildove rešitve iz Einsteinovih enačb polja - uveljavljen geometrijski pristop (II), na tej strani,
eden redkih v slovenščini na spletu (2023).
Še dva linka na izpeljavo Schwarzschildove metrike:
https://en.wikipedia.org/wiki/Derivation_of_the_Schwarzschild_solution
https://www.etsu.edu/cas/math/documents/theses/simpson-thesis.pdf
Spodnja citata, ki sta izjemno zgovorna (in potrjujeta naša razmišljanja
o povezovalnosti astronomije, o njenem velikem pomenu),
sem našel in dodal 28. aprila 2023 (nekaj let [osem] po zapisu te strani,
bolje vsebine) iz vira:
https://www.cantorsparadise.com/karl-schwarzschilds-letter-to-albert-einstein-6661734dd3e
Pismo Karla Schwarzschilda Albertu Einsteinu:
"Le vizija celote, kot je vizija svetnika, norca ali
mistika, nam bo omogočila razvozlati prava načela, ki sestavljajo vesolje."
»Matematika, fizika, kemija, astronomija korakajo v eni fronti. Kdor zaostaja
bo sledil. Kdor hiti naprej, pomaga drugim.”
O P O M B A !
Naša izpeljava Schwarzschildove metrike je za mnoge preenostavna (a kar nekaj literature
gre po naši poti), je pa fenomenološko razumljiva in
matematika tako ne zakrije razumevanja fizike, izjemnih pojavov - poglejmo zakaj (na primerih)!?
Gravitacijski rdeči premik in Schwarzschildova metrika
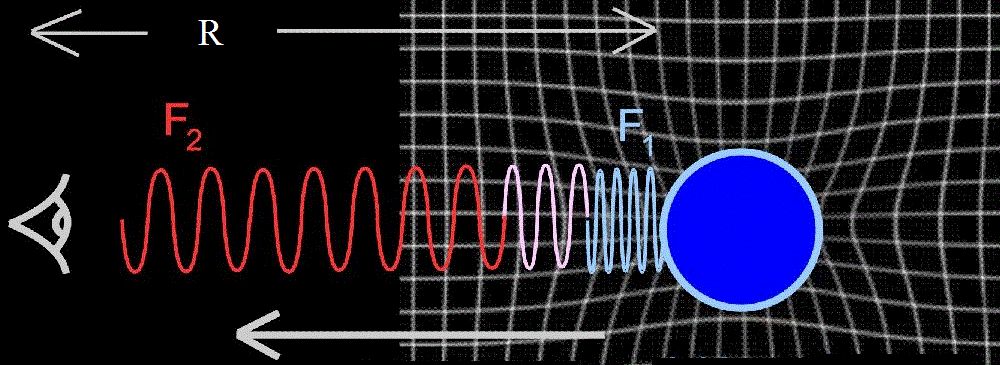
Frekvenca blizu masivnega telesa je simbolično označena z F1, daleč vstran pa z F2.
Foton (delec svetlobe), ki se oddaljuje od (recimo) zvezde, izgublja energijo (Ef = hν = hc/λ)
in se mu zato valovna dolžina veča – tozadevno se ta pojav imenuje gravitacijski rdeči premik
(rdeča svetloba ima namreč v vidnem delu elektromagnetnega valovanja najdaljšo valovno dolžino).
Kot smo že omenili, je naša izpeljava Schwarzschildove metrike za mnoge preenostavna,
je pa pojavno in konceptualno razumljiva in zadeva bistvo učinka gravitacije na mehaniko, na
čas - elektromagnetno valovanje
(zato ima tudi zagovornike) in v bistvu daje dodatno potrditev
splošni teoriji relativnosti. Zakaj?
Če se boste
pogledali izpeljavo preko tenzorskih enačb splošne relativnosti, so na koncu sklepi
praktično enaki. Ko rešujejo sistem enačb, pogledajo učinek gravitacije ob zvezdi in daleč od nje,
ko gravitacija pada proti 0 - v limiti lahkih centarlnih teles pa mora biti veljavna tudi Newtonova gravitacija,
mehanika - kot sta recimo pojma energije, ubežne hitrosti in nujne posredne povezave na
posebno teorijo relativnosti.
Glejte torej tudi
izpeljavo
Schwarzschildove rešitve iz Einsteinovih enačb polja - uveljavljen geometrijski pristop (II) - na tej strani,
sploh ena redkih v slovenščini na spletu (2023 - na koncu izpeljave nikakor ne gre brez limite za klasični gravitacijski zakon
in metrike Minkowskega za raven prostor pri skromni gravitaciji - prehod na posebno teorijo
relativnosti).
Mnogi viri tako danes recimo
več ne skrivajo razlage, da gre pri gravitacijskem rdečem, modrem premiku
( λ1/λ2
= (1 - rs/R1)1/2/(1 - rs/R2)1/2 )
spektralnih črt elektromagnetnega valovanja (rec. svetlobe)
za analogijo Dopplerja in ubežne hitrosti ali korektneje, kar gravitacijskega
potenciala ve2 = 2GM/Re = 2Φ =
c2rs/Re, od koder sledi, da je razmerje obeh hitrosti kar:
ve2/c2 = rs/Re .
Kar pa direktno izhaja iz Schwarzschildove metrike.
Radialna in tangentna komponenta Schwarzschildove metrike sta nič, saj vir svetlobe miruje
na zvezdi in je dr nič, zanima pa nas samo vpliv gravitacije na dolžino valovne dolžine,
ki deluje centralno (radialno).
Tako ostane samo
časovni člen metrike ds2 = (cdτ)2
= -c2dt2(1 - 2GM/(c2r)) = -c2dt2(1 - rs/r),
in ker velja za valovno dolžino povezava λ = cτ
(kjer je lastni čas τ kar 1/ν), in ker računamo z razmerji, se
hitrost c in čas t pokrajšata,
tako dobimo ključno povezavo, razmerje med valovnima dolžinama na razdaljah R1 in R2:
λ1/λ2 = τ1/τ2
= (1 - rs/R1)1/2/(1 - rs/R2)1/2
...
),
od koder recimo sledi rdeči premik v neskončnosti:
1 + z = λ∞/λe
= 1/(1 - (2GM/Re)/c2)1/2 .
Še enkrat poudarimo, da je čas dτ tisti,
ki ga meri opazovalec na masivnem telesu (recimo na zvezdi, kjer meri valovno dolžino),
čas dt pa izmeri hipotetični opazovalec, ki ni podvržen gravitacijskemu polju, daleč stran od zvezde.
Newtonova limita pa je:
z = Δλ/λ ≈ rs/(2R)
= GM/(Rc2) = gR/c2, polmer objekta R
je veliko večji od Schwarzschildovega polmera rs,
velja recimo za Zemljo in meritve valovnih dolžin (frekvence) svetlobe to potrjujejo ...
Povedano daje naši poti do Schwarzschildove metrike (principa merjenja razdalje
ob masivnih sferičnih telesih, zvezdah ...) veliko mero verodostojnosti -
pomembno je razumevanje fenomena in ne zgolj računska spretnost.
Slika spodaj - zvezda manjša energijo sevanemu fotonu in s tem se veča
valovna dolžina (gravitacijski rdeči premik).

1 + z = 1/( 1 - (2GM/rc2) )1/2
kjer je
* G - gravitacijska konstanta,
* M - masa objekta, zvezde, ki ustvarja gravitacijsko polje,
* r - polmer zvezde,
* rop - razdalja, koordinate opazovalca
(ki so analogne klasični razdalji
od središča predmeta,
vendar pa so dejansko Schwarzschildove koordinate),
enačba velja,
ko je 1/rop ≈ 0 (ali rop >> r)
* c - hitrost svetlobe,
* z = Dl/l -
rdeči premik.
Še en razmislek o besedni zvezi teorija relativnost. Danes zagotovo
vemo, da to ni zgolj teorija, ampak je kar »zakon relativnosti«.
Kot imamo Newtonove zakone, ki pa so s stališča današnjega vedenja
bolj približna teorija (približek za majhne hitrosti, katere so nam
ljudem seveda blizu). Torej bi bilo bolje zadevo obrniti in reči,
da poznamo »Newtonovo teorijo« in »zakone relativnosti«.
Dve vaji:
Iz podatkov o Soncu izračunajmo rdeči premik za žarek valovne
dolžine 500 nm, ki zapusti Sonce
in ga zaznamo na Zemlji. Podatki o Soncu so:
R = 6.955·108 m (polmer Sonca)
M = 1.989·1030 kg (masa Sonca)
r = 1.4960·1011 m (razdalja Zemlja - Sonce)
G = 6.6742·10-11 Nm2/kg2
Enačbo za rdeči premik poenostavimo, saj so členi 2GM/(c2r)
zelo majhni in
zato uporabimo naslednje izraze (binomski izrek): 1/(1-x) ≈ 1 + x in
(1 - x)1/2 ≈ 1 - x/2.
Z + 1 = (1 - 2GM/(c2r))1/2/(1 - 2GM/(c2R))1/2
Z = GM/(c2R) - GM/(c2r) = (GM/c2)(1/R – 1/r) = 2.12·10-6
Δλ = z·λ = 2.12·10-6·500·10-9 m = 1.06·10-12 m
= 0.00106 nanometrov (nm)
To je relativno skromen rdeči premik, razlika med urami v enem
letu pa bi znesla že okrog minute
(zgolj zaradi gravitacije).
Za povprečno nevtronsko zvezdo pa je rdeči premik
(podaljšanje valovne dolžine)
že kar opazen. Podatki za klasično nevtronsko zvezdo so:
Rn = 104 m
Mn = 3·1030 kg
r = 1.4960·1011 m (zgolj hipotetična razdalja
Zemlja – nevtronska zvezda na razdalji Sonca)
Sedaj je potrebno uporabiti korektno enačbo:
Z + 1 = (1 - 2GMn/(c2r))1/2/(1 - 2GMn/(c2Rn))1/2
z = 0.343
Δλ = z·λ = 1.71 10-7 m = 171 nm
Taki rdeči premiki se dejansko izmerijo.
Zakasnitev v času v enem letu pa bi bila na nevtronski zvezdi
že nekaj mesecev.

Karl Schwarzschild (1873–1916) – oče relativističnih enačb za metriko (merjenje razdalj
in časa) ob zvezdah in planetih (v ukrivljenem prostor-času). Dolgo se je zdelo, da je
to le teorija za njemu podobne »čudake« in so nanj in enačbe pozabili dokler nismo
začeli potovati v vesolje in ...
Schwarzschildovo metriko zapišimo še enkrat s substitucijo rs = 2GM/c2 in
dt' = dτ:
-c2dτ2 = -c2dt2(1 - rs/r)
+ dr2/(1 - rs/r)
+ r2(dϑ2 + sin2ϑ dφ2)
Levi del enačbe (-c2dτ2) je sedaj opazovalec,
ki prosto pada s pospeškom
g = GM/r2 in
torej ne čuti gravitacije in to je hkrati Einsteinova najsrečnejša misel
v življenju. A. Einstein je skozi okno svoje pisarne na Patentnem uradu
v Bernu opazoval krovca na sosednji strehi (leto 1906). Pomislil je, kaj
bi se zgodilo, če bi možak padel v globino. "Če človek prosto pada, ne
čuti teže. Postal sem razburjen. Ta preprosta misel je name naredila globok vtis.
Približala me je teoriji gravitacije." Kasneje je Einstein svoj miselni poskus
s krovcem označil kot najsrečnejšo misel svojega življenja. Nič težnosti,
nič gibanja (v njegovem sistemu – kot v liftu, ki prosto pada). Tudi moderni
"krovec", astronavt, prosto pada in zato zanj ni težnosti, poleg tega pa
lahko povsem utemeljeno trdi, da miruje. Drugi opazovalci lahko vidijo
dogajanje drugače, toda to na astronavtova opažanja in meritve ne vpliva.
Dejansko naše ure kažejo čas τ - to lastni čas, ki je posledica gravitacije,
delno rotacije Zemlje, enako sateliti, a drugačnega (tečejo hitreje), ker je
tam gravitacija manjša, a orbitalna hitrost večinoma večja,
a njen prispevek na čas je manjši od gravitacije (recimo GPS sateliti).


Ura v pospešenem sistemu, to je kroženje, teče počasneje ali v večji gravitaciji.
Še enkrat ponovimo - kot smo že pri uvodu v fiziko velikih hitrosti povedali,
da paradoksa dvojčkov ni,
razen če en od njiju potuje pospešeno (potem mu čas, ura teče počasneje) –
in pri gravitaciji je
natančno enako (Načelo ekvivalentnosti v splošni teoriji relativnosti upošteva,
da ni mogoče
razločevati učinka težnostnega polja v nepospešenem opazovalnem sistemu od učinka
pospeševanja
opazovalnega sistema v prostoru, kjer ni težnostnega polja.). Ure na Zemlji bodo
tako tekle
s hitrostjo
dτ = dt(1 - 2GM/(c2r) – vt2/c2)1/2,
ki jo določa Schwarzschildova metrika, vt je tangentna hitrost vrtenja zemlje
( odvisna je od geografske širine
vt = ωrzcos(φ) )
– več o tem v nadaljevanju.
Izpeljana Schwarzschildova metrika, enačba, je tako tudi eksaktno rešila problem sinhronizacije
ur v GPS navigacijskem polju satelitov, ki frčijo okrog Zemlje. S to enačbo se tudi korektno
poračuna uklon žarka ob zvezdah (izračun objavimo kdaj drugič ..., Spika si to zasluži).
Ta uklon so nekoč merili ob mrkih (ob masivnem Soncu), danes pa ga enostavneje merijo kar
preko odklona radijskih signalov iz kvazarjev z radijskimi teleskopi. Iz zapisane metrike
se na eleganten način izpelje polmer črne luknje – Schwarzschildov polmer - ko velja, da
je člen 1 - 2GM/(c2r) = 0. Od koder sledi, da ta pogoj velja za posebne čudaške
zvezde s polmerom r = rs =2GM/c2 (črne luknje). V tem primeru se lastni čas dt'
(oznaka je večinoma dτ) v črni luknji ustavi, saj velja
dτ2 = dt2(1 - 2GM/(c2r)) = 0,
člen dr2/(1 - 2GM/(c2r))
pa gre proti neskončnost – singularnost, kolaps v črno luknjo, gostota gre navidezno
celo proti neskončnosti (a kot bomo videli, se da teoretično narediti celo črno luknjo
zgolj gostote, ne bi verjeli, zraka), ukrivljenost-gravitacija se enormno veča, ko prav
nobeno telo, delec, signal ne morejo zapustiti nastale črne luknje, torej tudi svetloba
ne (a Hawking izpelje možnost zelo počasnega razpada črne luknje, ko na robu nastaneta
delec - antidelec in preko načela nedoločenosti, en od njih zapusti dogodkovni horizont
črne luknje – pride do sevanj, črna luknja velikosti 10 Sončevih mas bi naj razpadala
1067 let,
velja τ ≈ 1067(M/M☉)3 v letih).
Enako idejo za polmer črne luknje je že leta
1783 podal John Michell - izpelje se iz energijskega zakona, bolje
potenciala - ko se je vprašal, kolikšen mora biti mejni polmer neke zvezde,
da tudi svetloba ne more uit z zvezde:
c2/2 – GM/r = 0, od koder
sledi r =2GM/c2.

Centralna črna luknja M87 v polarizirani svetlobi (masa črne luknje je kar šest
milijard Sončevih mas). Slika prikazuje pričakovano notranjo smer vrtenja
(polarizacijo) radijskih valov. Polarizacijo ustvarja močno magnetno polje,
ki obdaja supermasivno črno luknjo v središču eliptične galaksije M87.
Radijske valove je zaznal teleskop Event Horizon (EHT), ki združuje podatke
iz radijskih teleskopov po celem svetu. Polarizacijska struktura, predstavljena
z računalniško generiranimi tokovnicami, je nanešena na znamenito EHT sliko črne
luknje, prvič objavljeno leta 2019. Predhodne analize kažejo, da deli polja, kot
je bilo pričakovano, krožijo okoli črne luknje skupaj z akrecijsko snovjo. Vendar
se druga komponenta na videz odmakne proč od črne luknje. Ta komponenta bi lahko
razložila, kako se snov upira padcu v črno luknjo in se namesto tega izstreli v
curek galaksije M87.
Da je taka slika sploh lahko nastala, niso bili potrebni zgolj zmogljivi radijski
teleskopi (recimo sistem ALMA) razpršeni širom Zemlje, na koncu pa zbrani v velik
interferometrični teleskop (v grobem velik kot Zemlja), ampak so morali strokovnjaki
različnih strok najprej počakati na dovolj zmogljive računalnike, ki so zbrali na
stotisoče gigabajtov podatkov, okrog petabajt (milijon gigabajtov) podatkov na
posamezni observatorij. Opazovanja so opravili leta 2017. Goro podatkov so
pretočili v računalniški grozd. Analize se je lotilo 200 strokovnjakov, ki
so delo opravljali vse do leta 2019. Odstraniti so morali vse domnevne šume,
skupaj sestaviti opazovanja (signale) različnih teleskopov, ki dajejo po
definiciji različne izide (za vajo, če boste primerjali fotografijo, recimo planeta,
s 100-milimetrskim teleskopom in 300-milimetrskim, boste videli razliko, v čem je
problem). Najprej so ustvariti "zemljevid" radijske slike ozadja in potem preostanek
posameznih slik zlepiti (preko »kunštnih« računalniških interpolacij) – v celoto
akrecijskega diska ob črni luknji (same črne luknje se seveda po definiciji ne da videti).
Galaksija M87 je približno 57 milijonov svetlobnih let oddaljena - leži v Devici.
Glede na izjemno relativno svetlost (ima magnitudo 8,6, a je tudi skoraj
5x masivnejša od naše Galaksije), se jo da dokaj enostavno opazovati s
šolskimi teleskopi. Vir: apod.
Tudi v središču naše Galaksije je črna luknja mase okrog
4,154 milijonov Sonc (v smeri ozvezdja Strelec - oznaka je Strelec A).
Izmerjene orbite šestih zvezd okoli kandidatke
za supermasivno črno luknjo Strelec A* v središču Rimske ceste.
GPS navigacijski sistem satelitov in Schwarzschildova metrika
GPS uporablja sistem trilateracije - to je
določanje lege točke na podlagi njene razdalje od vsaj treh znanih točk
(pri GPS se uporablja 4 satelite - bomo videli, zakaj).
Triangulacija pa meri kote (na osnovi znane baze – recimo razdalje med opazovalcema).
GPS (ZDA, kratica izhaja iz zveze "Global Positioning System") uporablja 24 satelitov, nekaj dodatnih je seveda v rezervi.
Krožijo pa
20180 km nad površino Zemlje. Njihova natančnost je
od 30 do 500 cm. Svoje satelite v sistemu Galileo ima tudi Evropa. Ta navigacijski sistem že deluje
od 24. januarja 2023, na koncu bi naj imel
24 aktivnih satelitov in 6 v rezervi (natančnost ima kar 20 cm, višina satelitov je 23222 km).
Tukaj je še ruski GLONASS, 24 satelitov (višina satelitov 19130 km), natančnost od 2.8 do 7.38 m.
Kitajci imajo sistem BeiDou s 24 sateliti na višini 21500 km - natančnost 3.6 m (globalno, javno),
2.6 m (azijsko-pacifiška regija, javno), 10 cm (šifrirano). Prihaja tudi kitajski sistem Compass na višini 21150 km.
Med omenjenimi navigacijski sistemi so določene tehnične razlike pri oddanih valovih, modulaciji, itn,
a osnovni princip je povsod enak.
A posvetimo se GPS-u, ki je oče vseh ostalih navigacijskih satelitskih sistemov.

Za vajo izvrednotimo metriki in izrazimo časa dt' satelitov in čas ur na površini
Zemlje. Kaj dobimo (kot dΩ2 = dϑ2
+ sin2ϑ dφ2 je kotni zasuk satelita po tirnici,
izpostavimo dt in c ter okrajšajmo hitrost svetlobe c) :
-c2dt'2 = -c2dt2(1 - 2GM/(c2r))
+ dr2/(1 - 2GM/(c2r)) + r2dΩ2
dt'2 = dt2( (1 - 2GM/(c2r)
- (dr2/dt2/c2)/(1 - 2GM/(c2r))
- (r2/c2)dΩ2/dt2)
dt'2 = dt2( (1 - 2GM/(c2r)
- (vr2/c2)/(1 - 2GM/(c2r))
– vt2/c2)
Kot pomoč pri opisu smo vpeljali dve znani hitrosti vr
in vt.
vr = dr/dt – radialna hitrost (pojavi se pri gibanju po elipsi)
vt = rdΩ/dt = rω -
je tangentna (obodna) hitrost, recimo kroženja satelita
Za satelit, ki kroži velja: vt = rdΩ/dt = rω
tangentna hitrost, radialna hitrost pa je pri kroženju nič,
vr = dr/dt = 0. Pri kroženju velja torej poenostavljena enačba -
lasten čas dt' se velikokrat zapiše
kar z oznako dτ:
dτ = dt(1 - 2GM/(c2r) – vt2/c2)1/2
dt = dτ/(1 - 2GM/(c2r) – vt2/c2)1/2
Ta enačba se torej uporablja tudi za sinhronizacijo ur GPS satelitov
in GPS sprejemnikov (izračun je bil narejen v uvodu v to serijo člankov) –
poleg vseh ostalih popravkov, beri prvi članek. Če izpustimo vpliv gravitacije,
kaj dobimo? Dobimo enačbo
dτ = dt(1 – v2/c2)1/2 = dt/γ -
ki je hkrati znana enačba iz začetka poglavja o transformaciji časa, mirujoč,
gibajoč opazovalec (tako smo tudi testirali naše matematične povezave - ko ni
teže, samodejno velja posebna relativnost).
Izračunajmo torej, za koliko km (ja prav ste prebrali, gre za kilometre)
se poveča napaka sistema GPS, če ne upoštevamo,
da čas teče drugače v satelitu kot teče recimo na Zemlji (kjer recimo mi z mobilnim
telefonom določamo svoj položaj).
Izračune časov
satelitov in sprejemnikov se torej izvede preko znane (smo ravno izpeljali iz Schwarzschildove metrike)
relativistične enačbe za čas τ
v gravitacijskem polju (kjer je [t] referenčni čas brez gravitacije in ostalih pospeškov
zaradi premikanja po orbiti (čas t merijo torej ure daleč vstran od gravitacijskega lijaka).
τz naj bo čas, ki ga kažejo ure sprejemnikov na Zemlji in
τGPS čas, ki ga merijo sateliti z lastnimi urami),
izpeljava splošne transformacije časa je nakazana v točki 30 in se glasi:
t = τ/(1 - 2•G•M/(c2•R) – v2/c2)1/2
Izračunamo torej naš čas τZ
na Zemlji (v gravitacijskem lijaku), R = Rz = 6378 km je razdalja od centra do površine Zemlje
(v = vtz je hitrost vrtenja na Zemlji zaradi dnevne rotacije, siderski čas je = 86164 s - je
za okrog 4 minute krajši od našega dneva, obrata Zemlje glede na Sonce, ki je 24 ur,
hitrost opazovalca na ekvatorju zaradi rotacije je približno vtz
= 2πRz/86164s = 465.09 m/s) in τGPS
čas na orbiti GPS satelitov (višje v gravitacijskem lijaku Zemlje), ki so od središča Zemlje oddaljeni za
R = RGPS = Rz + 20180 km. Za hitrost satelitov velja
v = vts = (G•M/RGPS)1/2 = 3.88 km/s.
Masa Zemlje je M = 5.974 1024 kg,
G = 6.67384 10-11 Nm2/kg2
.
Obe enačbi (časa) delimo, t se okrajša.
τGPS/τz =
(1 - 2GM/(c2RGPS) –
vts2/c2)1/2/(1 - 2GM/(c2Rz) – vtz2/c2)1/2
= 1.000000000447367
Za τz bomo privzeli kar en dan, to je τz = 86400 s.
Razlika med časoma je torej za en dan:
Δτ = τGPS - τz =
τz(τGPS/τz – 1) = 86400 s (1.000000000447367 – 1) = 3.86525*10-5 s
V enem dnevu pa se vseeno kumulativno nabere napake za okrog:
c*Δτ = 11595.7 m = 11.6 km.
Zato ure satelitov zaradi relativističnih učinkov (različna gravitacija, kroženje) pridobijo približno
38.640 nanosekund na dan ali 38,6 µs na dan.
Da bi nadomestili ta prirastek, je treba frekvence ur GPS satelitov upočasniti za ta prispevek
(že izračunali prej τGPS/τz):
τGPS/τz – 1 = 4,472×10-10
Ta vrednost se odšteje od 1 in pomnoži s predhodno nastavljeno frekvenco (takt) ure 10,23 MHz:
(1 – 4,472×10-10) × 10,23 = 10,22999999543
To pomeni, da moramo upočasniti satelitske GPS ure iz 10,23 MHz (radijski signal valovne dolžine
λ = 29.3 m)
na 10,22999999543 MHz, da izničimo oba učinka dilatacije časa.
Pri GPS je potrebno upoštevati tudi Dopplerjev efekt, gibljejo se tako sateliti, kot opazovalci,
ki merijo svoj položaj na Zemlji.
Viri napak GPS lege
vir napaka (m)
Prihod signala C/A ±3 (namerna napaka GPS informacije - varnost)
Prihod signala P(Y) ±0,3 (detekcija signala P(Y) z boljšim dekoderjem)
Ionosferski učinki ±5 (ionizirana plast atmosfere)
Napake efemerid ±2,5 (Spremenljivost tlaka sončnega sevanja posredno vpliva na natančnost GPS,
na lego satelita - njegove efemeride o legi, TTFF je "time to first fix")
Napake satelitske ure ±2
Večpotno popačenje ±1 (odbijajo od okoliškega terena)
Troposferski učinki ±0,5
3 σRC/A ±6,7 (3 x standardni odklon napake ocenjenega položaja sprejemnika)
3 σRP(Y) ±6,0 (boljši dekoder)
Ionosferska zakasnitev mikrovalovnega signala je odvisna od njegove frekvence.
Izhaja iz ionizirane atmosfere (določa jo vsebnost elektronov). Ta pojav je znan kot
disperzija in se lahko izračuna iz meritev zakasnitev za dva ali več frekvenčnih pasov L1 in L2,
kar omogoča oceno zakasnitev pri drugih frekvencah (ta napaka se dokaj uspešno sproti korigira, povpreči).
V troposferi pa igra veliko vlogo sprememba vlage (težje korigirati) in tudi tlaka
(se lažje korigira preko plinske enačbe).
Da bi zboljšali ločljivost na cenejših sprejemnikih, je bil satelitom Block IIR-M dodan nov civilni kodni
signal na L2, imenovan L2C, ki je bil prvič izstreljen leta 2005. Omogoča neposredno primerjavo signalov
L1 in L2 z uporabo kodiranega signala namesto nosilnega vala.
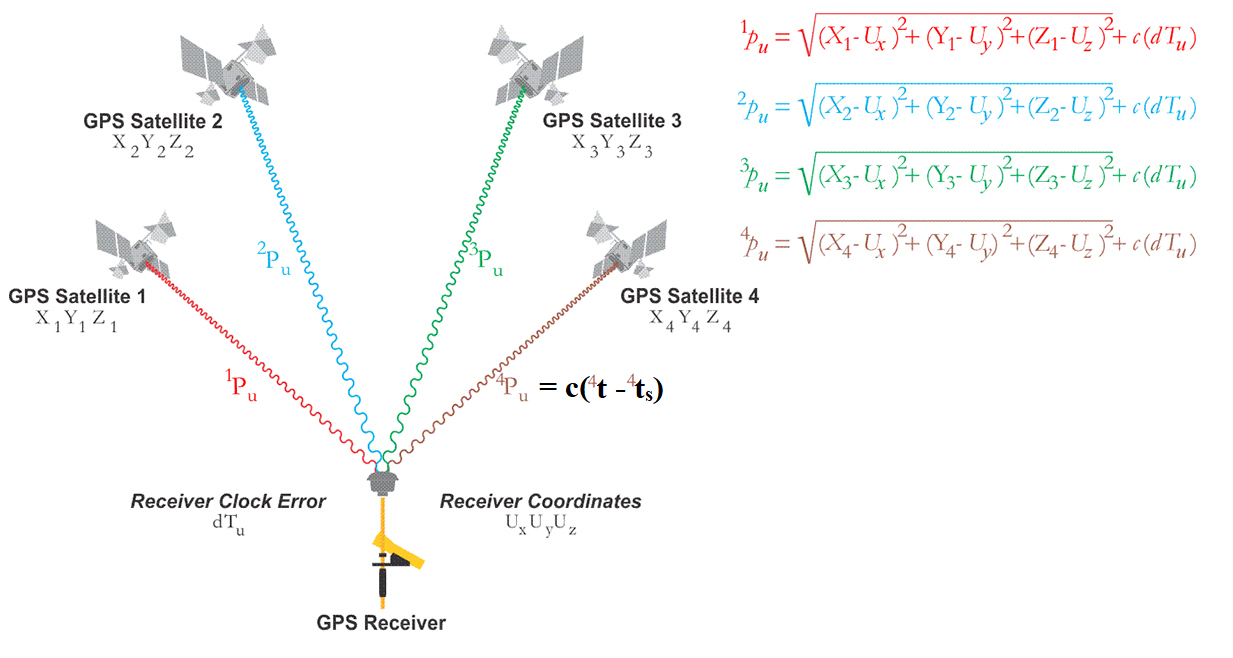
Ta vrsta pozicioniranja točke je znana kot absolutno pozicioniranje, pozicioniranje ene točke ali navigacijska rešitev. Zanj je značilen en sam sprejemnik, ki meri svoj doseg do najmanj štirih satelitov hkrati. Avtonomno določanje položaja GPS ni naknadno obdelano in resnično ni komunikacije s postajo, ki je na znani točki. Z drugimi besedami, avtonomno pozicioniranje ni diferencialno (relativno); sprejemnik deluje neodvisno. Kot vedno so potrebni štirje sateliti, kot je navedeno tukaj. Sprejemnik je na neznanem položaju in mora sam odpraviti napako ure sprejemnika. Rešiti mora x, y, z in čas. Navigacijska rešitev je v nekem smislu izpolnitev prvotne ideje za GPS. Zanaša se na kodirano meritev psevdorazdalje in se lahko uporablja za tako rekoč takojšnje določanje položaja. Pri tej metodi so položaji satelitov na voljo iz podatkov njihovih oddajnih efemerid (preko signala, ki ga oddajajo sateliti). Odmik satelitske ure in ionosferski popravek sta na voljo tudi v navigacijskih sporočilih vseh štirih satelitov. Kot veste, ti popravki iz tega sporočila niso idealni. Tudi če vsi podatki v navigacijskem sporočilu ne vsebujejo napak, in napake zagotovo so, ostajajo štiri neznanke: položaj sprejemnika v treh kartezičnih koordinatah, ux, uy in uz, ter napaka ure sprejemnika dTu. Trije psevdorazponi zagotavljajo dovolj podatkov za rešitev za ux, uy in uz. In četrti psevdorazpon zagotavlja informacije za rešitev zamika ure sprejemnika. Zmožnost merjenja dT, napake ure sprejemnika, je eden od razlogov, da je zmerna stabilnost tehnologije ure s kvarčnimi kristali popolnoma primerna kot oscilator ure sprejemnika. Tukaj je edinstvena rešitev, saj število neznank ni večje od števila opazovanj. Sprejemnik spremlja najmanj 4 satelite hkrati; zato je mogoče te štiri enačbe rešiti hkrati za vsako obdobje opazovanja. Epoha v GPS je zelo kratko obdobje opazovalnega časa (tj. 1 sekunda ali morda manj) in je na splošno le majhen del daljše meritve. Vendar pa je teoretično dovolj informacij v kateri koli posamezni dobi za rešitev teh enačb. To je razlog, zakaj je mogoče s to metodo določiti pot sprejemnika v premikajočem se vozilu. S 4 razpoložljivimi sateliti sta ločljivost položaja in hitrosti sprejemnika na voljo s hkratno rešitvijo teh štirih enačb, recimo v vašem mobilnem telefonu.
Za namen iskanja stabilnejših koordinat v vesolju, so vzpostavili tudi sistem ICRF - The International Celestial Reference Frame (referenčne točke v oddaljenem vesolju, ki so kar se da pri miru).

Umetniška upodobitev akrecijskega diska v ULAS J1120+0641,
v zelo oddaljenem kvazarju, ki ga v centru poganja supermasivna črna luknja z maso,
ki je dve milijardi krat večja od Sončeve. Ima rdeči premik z = 7 in je tako oddaljen
12.9 milijard sv. let - to je čas potovanja svetlobe.
Ker pa se vesolje širi, je sedaj resnična razdalja kvazarja do nas kar 28.85 milijard sv. let.
Kvazarji so torej zelo mlade galaksije (vidimo jih take, kot so nastale kmalu po začetku
širjenja vesolja). V mladi galaksiji se kmalu tvori velikanska črna luknja, ki srka bližnjo snov.
Njena masa naraste do nekaj milijard Sonc. V disku padajoče snovi
(glejte tudi tekst o akreciji)
se le ta zelo segreje, na milijone Kelvinov, pri čemer oddaja veliko elektromagnetnega valovanja,
tako v rentgenskem, vidnem in radijskem delu spektra.
A problem lege teles (koordinat) v vesolju je precej zapleten, saj se tudi bližnje zvezde premikajo.
Tako so astronomi za natančno določanje lege GPS satelitov in ostalih objektov v vesolju,
izbrali vire (nebesne svetilnike), ki se v okviru natančnosti naših meritev
najmanj premikajo po nebu in so zato najbolj oddaljeni (so iz začetkov vesolja) in dovolj svetli, da jih še
lahko zaznamo.
In ti viri so zelo oddaljene in svetle galaksije (milijarde svetlobnih let) - ki se imenujejo kvazarji
(quasar - "Quasi-stellar object"). To so izjemno aktivna galaktična jedra iz začetkov vesolja.
Zaradi širjenja vesolja je spekter elektromagnetnega valovanja teh galaksij premaknjen v rdeči del
(to pomeni podaljšanje valovnih dolžin tako radijskih valov, vidne svetlobe in ostalega spektra ...).
Tako se je vzpostavil Mednarodni nebesni referenčni sistem
(ICRS - The International Celestial Reference Frame,
oz. International Celestial Reference System - ICRS), ki pomaga pri določanju lege nebesnih teles in tudi pri sistemih
GPS, Galileo, GLONASS.
Meritve lege kvazarjev temeljijo na
sistemu zelo oddaljenih radijskih teleskopov - torej na interferometriji z zelo dolgo osnovno
linijo - bazi - in na referenčnem sistemu, ki ga določajo optično izmerjeni
položaji zunajgalaktičnih virov satelitskega sistema Gaia.
Položaji večine virov (kvazarjev) so tako znani na 1 ločno milisekundo natančno ali celo bolje -
radijski interferometri so namreč izjemno natančni.
ICRF oddaljeni objekti (zgoraj), večinoma kvazarji, 608 referenčnih točk iz 1995, ki nam pomagajo pri orientaciji v vesolju.
Z njimi tudi vodimo sonde na druge planete, asteroide, nam pomagajo pri slikanju, recimo drobnih asteroidov.
Hkrati pa z njimi določimo točne lege GPS satelitov in tako izboljšamo navigacijo.
Vir slike: https://hpiers.obspm.fr/icrs-pc/icrf/icrf.html
Spodaj - nadgradnja iz 2018, enaka porazdelitev (le rektascenzijska os se začne na sredi), a sedaj kar
4536 radijskih virov (modrih) vključenih v ICRF3 (S/X), Hammer-Aitoff-projekcija na nebesno sfero;
303 glavni referenčni radijski viri so prikazani z oranžnimi krogci [Charlot et al., 2020].
Vir slike: https://ggos.org/item/celestial-reference-frame/
ICRF3 je tretja večja nadgradnja ICRF, ki jo je IAU sprejela avgusta 2018, da bi začela veljati
1. januarja 2019. Modeliranje vključuje učinek galaktocentričnega pospeška sončnega sistema,
ki je nova funkcija poleg ICRF2 meritev (2009) in ICRF1 (1998).
ICRF3 vključuje tudi meritve v treh frekvenčnih pasovih,
kar zagotavlja tri neodvisne in nekoliko drugačne izvedbe ICRS: dvofrekvenčne meritve pri
8,4 GHz (X pas) in 2,3 GHz (S pas) za 4536 virov; meritve 824 virov pri 24 GHz (pas K)
in dvofrekvenčne meritve pri 32 GHz (pas Ka) in 8,4 GHz (pas X) za 678 virov. Od tega so 303 viri,
enakomerno porazdeljeni na nebu, identificirani kot "določujoči viri", ki določajo osi okvirja, koordinatnega sistema.
ICRF3 je prav tako povečal število virov (kvazarjev) na južnem nebu.
Problem uporabe GPS sistemov je tudi, da lahko sprejem satelitskih signalov preprečijo GPS motilniki
(t. i. jammer - v večini držav so prepovedani),
ki se za malo denarja dobijo na spletu. Tako imajo mnogi sistemi, tudi vojaški, še ostale sisteme (tudi manj natančne)
za določanje geografskega položaja.
Problem daljšanja dneva in navigacija
Graf, ki prikazuje razliko med UT1 (opazovani sončni čas) in UTC (Coordinated Universal Time - linearni
čas, ki ga merijo atomske ure). Navpični skoki ustrezajo prestopnim sekundam.
Velik problem pri GPS navigaciji so tudi prestopne sekunde, ki se občasno dodajajo dolžini dneva, ki
se večinoma daljša zaradi zaviranja rotacije Zemlje, ki je posledica plimske sile Lune na Zemljo, delno tudi
Sonca - a je ta manjša.
V literaturi najdemo različne podatke o zaviranju vrtenja Zemlje zaradi plime: 1,5 ms na sto let, 2 in 2,3 ms
(tisočinke sekunde) na sto let.
Glejte članek - Ali se upočasnjuje vrtenje Zemlje okrog lastne osi
in ali se Luna oddaljuje od Zemlje?
(Spika, marec 2000).
Tukaj so še spremembe vztrajnostnega momenta Zemlje ob potresih, vulkanih, ob podnebnih
spremembah (kopičenje in taljenje ledu na polih), premeščanje vode - tukaj so plimovanja,
cunamiji, obsežnejši vremenski pojavi ... Dan se ne nujno samo daljša, lahko se občasno tudi krajša.
Dolžina dneva se danes tako najnatančneje meri preko že omenjenih
zelo oddaljenih kvazarjev - ICRF objekti.
Vsaka vrinjena prestopna sekunda moti GPS sistem in tudi sicer serverje v svetovni mreži.
Danes razmišljajo o "smear" (razmazu) samodejnih zamikih ur - to je več manjših zamikih časa pod sekundo,
ki tako ne bi zmedli sistemov
navigacije in serverjev.
Odstopanje dolžine dneva od dneva na podlagi SI (86400 sekund) zaradi spremembe hitrosti vrtenja Zemlje.
1962 do 2021: Odklon dolžin dneva (-1,1...+4,4 ms) in kumulativni premik (-7...+27 s) glede na leto 1972.
V okrog 5000 letih (groba ocena) bi se brez korekcij tako polnoč premknila za približno eno uro.
Mionometrični sistem za določanje položaja (muPS - Muometric positioning system), tudi pod zemljo,
pod vodo
Izjemno - kozmični žarki kot navigatorji!
Satelitsko navigacijo pogosto uporabljajo kritično pomembne vladne organizacije za navigacijo
ladij in letal, vendar je mogoče signale zlahka motiti in ponarediti. Tukaj je še problem
uničenja satelitov s strani konkurence - sploh v vojnem stanju.
Leta 2020 je Hiroyuki K.M. Tanaka ustvaril povsem nov pristop, mimo GPS,
ki sedaj locira položaj sprejemnika preko mionov - sekundarnih kozmičnih žarkov.
Mionometrične tehnike vključujejo mionometrični sistem za določanje položaja (muPS),
mionometrični brezžični navigacijski sistem (MuWNS - muometric wireless navigation system) ali muPS brezžični navigacijski sistem (muWNS),
kozmični časovni sinhronizator (CTS) in kozmični časovni kalibrator (CTC).
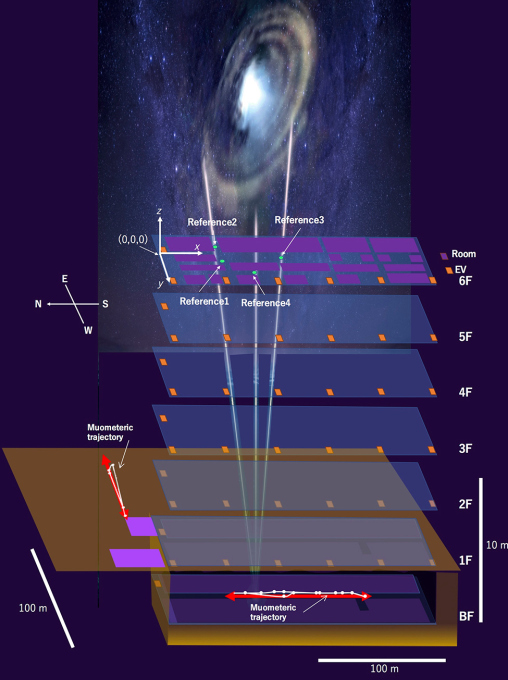
Navigacija v notranjosti kleti, z detektorji na mione. Rdeča črta na tej sliki predstavlja pot,
ki jo je prehodil »navigator«, bela črta s pikami pa prikazuje pot,
ki jo je zabeležil detektorji MuWNS. Na vrhu zgradbe so štirje referenčni sprejemniki -
2023 Hiroyuki K.M. Tanaka.
Pozicioniranje in navigacija
Muometrične tehnike določanja položaja in navigacije temeljijo na času
preleta mionov - relativističnih kozmičnih žarkov med referenčnimi
detektorji in detektorjem sprejemnika, ki se običajno nahaja v zaprtih
prostorih, pod zemljo ali pod vodo. Namesto sprejema signala GPS zaznavajo mione kozmičnih žarkov.
Trije ali bolje več referenčnih detektorjev, ki so nameščeni na znanih položajih
in z znanimi časovnimi referencami.
Tako kot pri GPS morajo biti ure med referenčnimi sprejemniki in sprejemnikom na locirani lokaciji
dobro sinhronizirane. Za razliko od GPS ta tehnologija omogoča tudi navigacijo na arktičnih območjih,
kjer je dostop satelitov omejen zaradi orbitalnih omejitev GPS satelitov.
Prvotni prototip je zahteval ožičenje med sprejemnikom in vsakim referenčnim detektorjem
za natančno časovno sinhronizacijo. Vendar je ta konfiguracija omejila obseg uporabnosti
sistema. Prizadevanja za iskanje načina za navigacijo brez žic,
ki izhajajo iz uspeha omenjenega začetnega sistema, so žice zamenjala z natančno uro.
Pričakuje se, da se bo muWNS uporabljal za reševalne ekipe, na primer za vodenje robotov
pod vodo in pod zemljo s postavitvijo v predorih, v zgradbi ali rudnikih.
Mionometrični sistem za določanje položaja (muPS - Muometric positioning system), ki uporablja vektorje smeri mionov
(kozmičnih žarkov) za brezžično navigacijo v zaprtih prostorih s centimetrsko natančnostjo.
VIR: https://www.nature.com/articles/s41598-023-41910-y
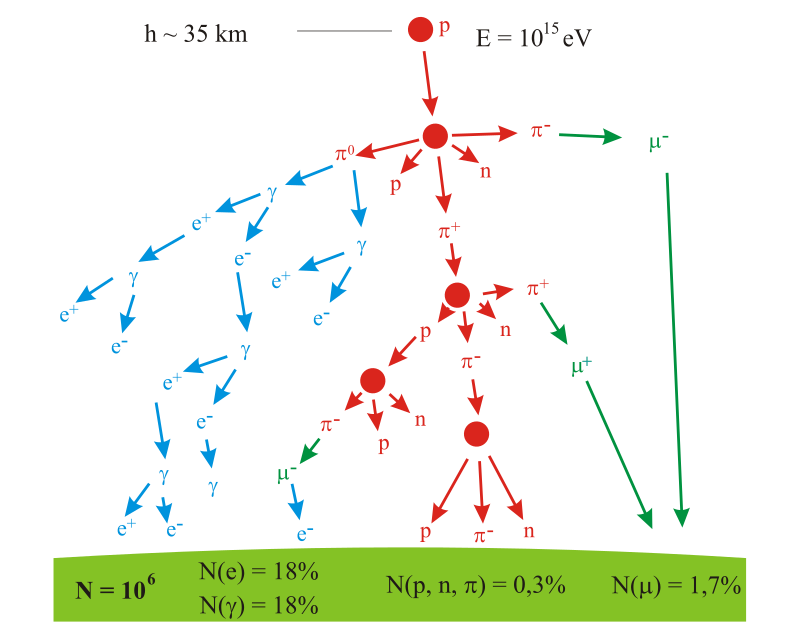
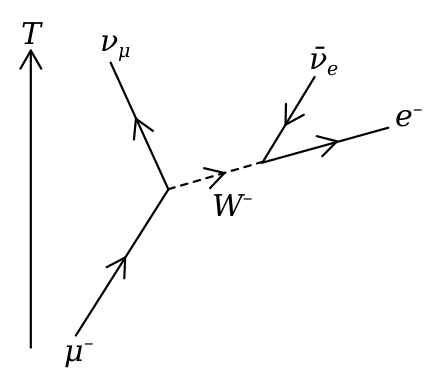
Primarni kozmični delci trčijo z molekulami atmosfere
(slika levo, trk s protonom p, na višini 35 km) in ustvarjajo roje osnovnih in sestavljenih
delcev, antidelcev, kot v pospeševalnikih (protoni – p,
nevtroni - n,
mioni - μ,
pioni - π,
elektroni – e,
nevtrini - ν,
delta barion – Δ,
fotoni - γ ...).
Mnoge
zelo hitre delce (recimo elektrone) lahko ujamemo v vodi preko Čerenkovega učinka
(v dielektriku, rec. v vodi, je lahko nabit delec, elektron, recimo hitrejši od
fazne hitrosti svetlobe, nekateri pri tem radi potegnejo analogijo z Machovim
stožcem pri preboju hitrosti zvoka) – v vodi se pojavi sevanje, kjer delci
oddajajo vidno modro svetlobo. Življenjska doba zelo hitrih mionov (μ),
ki nastanejo zaradi trčenja kozmičnih delcev z molekulami v zgornji atmosferi, je
tudi daljša od življenjske dobe počasi premikajočih se mionov (razpolovni čas mionov
ustvarjenih in razpadajočih v laboratoriju je 2,2 µs). To je hkrati potrditev teorije
relativnosti – dilatacije (podaljšanja) časa - zaradi velike hitrosti in pospešenega
gibanja mionov (μ). Če bi se razpad zgodil v 2,2 µs, bi polovica mionov prepotovala
samo okrog 456 metrov poti in ne bi dosegli površine Zemlje – zaradi efekta podaljšanja
časa, pa veliko mionov prispe do tal, tudi globoko pod površino. Razpad negativnega
miona ima naslednje produkte - nosilec razpadne šibke sile je W- bozon (glejte sliko):
µ- → e- + νe + νµ
Veliko osnovnih delcev smo tako odkrili v vesolju (preko kozmičnih delcev, sevanj). Kot
zanimivost,
celo sam atom helija smo prej odkrili na Soncu (v spektru) kot na Zemlji.

Številni sekundarni kozmični delci dosežejo površino Zemlje.
Vasko minuto okrog 10000 mionov na kvadratni meter - ali na
kvadratni centimeter naše kože prodre vsaj en mion na minuto.
A na srečo mioni skoraj neovirano potujejo skozi naša telesa
in prodrejo tudi globoko v tla, pod vodo.
Še zanimivost
Naključne časovne dogodke, ki jih sprožijo kozmični žarki,
uporabljeni v tej shemi za sinhronizacijo kozmičnega časa,
je mogoče uporabiti za generiranje naključnih števil za varen prenos podatkov - za kriptiranje.
Pošiljatelj in prejemnik uporabljata iste mione za ustvarjanje resnično naključnih kriptografskih
ključev iz časovnega odtisa mionov. Na podlagi natančnega časovnega zamika med pošiljateljem
in prejemnikom, izračunanega iz razdalje med detektorjema, in ker
prejemnik pozna zasebni ključ, ne da bi ga bilo treba neposredno izmenjati med pošiljateljem in prejemnikom, je tak prenos zelo varen.
Aplikacije potencialno segajo od varnega shranjevanja v oblaku,
komunikacij, do ustvarjanja virtualne valute ...
Tudi v arheologiji so na tak način že odkrili (zdi se) neznane prostore v Keopsovi piramidi.
Taka metoda se lahko uporablja tudi za geološke raziskave, recimo pri ognjenikih premik magme
in s tem doseči napredek pri morebitni napovedi izbruhov.
Tudi pri iskanju razbitin letal, ladij
bi se na tak način lažje našlo. Tudi reševanje iz porušenih zgradb bi lahko bilo s to tehniko
lažje in varnejše.
Kombinirana uporaba GPS in mionov preko MuWNS sistema nam lahko poveča
gotovost pozicioniranja - sploh če GPS odpove zaradi nagajanja konkurenčnih držav ali morebitnih
poškodb satelitov zaradi možnosti, da del satelitov poškoduje močan
izbruh Sončeve koronarne mase. V tem primeru so mioni manj ranljivi.
A problem podmornic je še zmeraj, da pri večjih premikih ne poznajo referenčnih sprejemnikov in da ni enostavne
povratne informacije, voda ustavi elektromagnetno valovanje ...
Aktualni problem so torej zagotovo podmornice, ki potopljene ne morejo določati
svojega položaja s sateliti. Zato se morajo zanašati na žiroskope in akcelerometre
(sešteta navigacija), ki pa imajo omejeno natančnost. Kot priznava vojska,
se napak v enem samem dnevu nabere za kakšen kilometer. To pa je nesprejemljivo.
Kvantni kompas deluje zelo poučno in je
približno tisočkrat natančnejši od obstoječih načinov navigacije. Uporabljajo
odkritje, ki je leta 1997 prineslo Nobelovo nagrado. Z laserji je atome mogoče
ohladiti na vsega nekaj milijonink kelvina, tako da se sesedejo v osnovno stanje,
v katerem so silno občutljivi na Zemljino elektromagnetno in gravitacijsko polje.
Potem te atome v vakuumu sledimo z drugim laserjem, kar da zelo dobro informacijo
o gibanju. Na ta način je navigacija še vedno sešteta, a bistveno natančnejša.
Kot zadnjo vajo z urami v naši okolici ocenimo še, za koliko teče čas na Luni (z manjšo gravitacijo)
hitreje kot na Zemlji (z večjo gravitacijo)?
Izračunajmo zamik časa zgolj zaradi različnih gravitacij.
Izračunamo torej še enkrat naš čas τZ
na Zemlji (v gravitacijskem lijaku), R = Rz = 6378 km je razdalja od centra do površine Zemlje
in
čas na Luni (v gravitacijskem lijaku Lune), ki je od središča Zemlje oddaljena
RZL = 384400 km (obhod Lune okrog Zemlje traja 27.321661*24*3600 s = 2360591.51 s).
Masa Zemlje je M = 5.974 1024 kg, masa Lune je ML = 7.342 1022 kg, polmer lune je
RL = 1737.1 km. Gravitacijska konstanta je G = 6.67384 10-11 Nm2/kg2.
Obe enačbi (časa) delimo, t se okrajša.
τL/τz =
(1 - 2GM/(c2RGPS) )1/2/(1 - 2GML/(c2RL) )1/2
= 1.00000000066323
Za τz bomo privzeli kar en dan, to je τz = 86400 s.
Razlika med časoma je torej za en dan:
Δτ = τL - τz =
τz(τL/τz – 1) = 86400 s (1.00000000066323 – 1) = 5.73*10-5 s
= 57.3 mikrosekunde.
Ta razlika v časih na dan na Luni in na Zemlji je torej okrog 57.3 mikrosekunde na dan (zgolj zaradi gravitacije), kar je
precej več, kot je razlika v GPS orbitah, ki znaša 38.6525 mikrosekunde na dan (gravitacija Zemlje na orbitah GPS satelitov
je še zmeraj veliko močnejša, kot gravitacija na Luni ...). Če bi upoštevali še gravitacijo Zemlje na razdalji Lune in samo
hitrost Lune, itn - rezultat ne bi bil bistveno drugačen.
Resnične meritve kažejo razliko 58,7 mikrosekunde na dan (odvisno je tudi, kje smo
na ovalni Luni) - torej je naša ocena iz Schwarzschildove metrike bila zelo solidna.
Torej, če recimo delamo določene meritve lokacij na Luni in jih pošiljamo na Zemljo (ali pristajamo na Luni), je nujno potrebno
upoštevati to razliko v hitrosti delovanja atomskih ur.
Tako bodo ZDA (tudi Evropska vesoljska agencija) za Luno najbrž definirale poseben čas,
ki bo za cca 57.3 mikrosekunde na dan pred Zemeljskim dnevom.
V 50 letih delovanja ur na Luni, se nabere za eno sekundo prehitevanja časa na Zemlji.
Smiselno bi bilo torej, da bi tudi ostala nebesna telesa,
rec. Luna ali Mars, imela svoj lastni časovni srčni utrip - frekvenco (čas).
Vrnimo se k fiziki visokih energij
Ne da bi na veliko razglašali, smo v bistvu vpeljali nekaj postulatov posebne
in splošne teorije relativnosti. Einstein objavi svojo interpretacijo posebne
relativnosti leta 1905, Hendrik Lorentz pa večino enačb, transformacij, zapiše
že veliko prej, preko Maxwellovih enačb, ko ohrani hitrost svetlobe konstantno
za različne nepospešene opazovalne sisteme in seveda privzame, da povsod veljajo
enaki fizikalni zakoni - kovarijantnost. Na koncu pa smo podali še rešitev metrike
splošne teorije relativnosti, ki (po klasični sliki) upošteva gravitacijo (Einstein
objavi enačbe polja 1915, kjer utemeljeno, namesto gravitacije, predlaga ukrivljen
prostor-čas). Karl Schwarzschild pa še istega leta (1915) najde rešitev Einsteinovih
enačb za metriko (merjenje razdalj in časa) ob zvezdah in planetih (rešitev smo
na preprost način izpeljali tudi mi). Za vesolje kot celoto pa to stori Alexander
Friedmann. Leta 1922 poda možnost, da se vesolje širi, temu se pridruži najprej
Lemaître in kmalu tudi še Hubble z meritvami. Einstein se dolgo z njimi ni strinjal,
se je upiral tej zamisli - a jo je na koncu le sprejel. Sprejel je nova dejstva,
meritve, novo realnost razširjajočega se vesolja - a res čisto na koncu, no - med
zadnjimi ...
Pri relativnosti smo se večinoma osredotočili na astronomske dejavnike. A bežno smo
omenili tudi znameniti paradoks enakomerno gibajočih se opazovalcev – recimo, da lahk
o drug drugemu očitata, da pri sosedu teče čas počasneje ... Še enkrat povejmo, da
v tem seveda ni nobenega paradoksa – oba namreč upoštevata Lorentzova pravila. A pri
pospešenih sistemih (t. i. paradoks dvojčkov) pa primerjava ur dejansko pokaže različna
časa (na spletu lahko najdemo kar nekaj izračunov na to temo, recimo na strani:
https://de.wikipedia.org/wiki/Zwillingsparadoxon#Beschleunigte_Bewegungen).
Recimo,
da en opazovalec lovi drugega (prvi najprej ustavi raketo in nato pospeši do drugega
opazovalca, ki cel čas potuje enakomerno), in ko se srečata, prvi opazovalec pokaže
uro, ki dejansko kaže krajši čas (zaradi pospešenega gibanja) od kolegove ure (je
torej nekoliko mlajši od drugega kolega, ki cel čas potuje enakomerno). Kot smo videli,
se enako dogaja tudi pri satelitih, kjer gre za vpliv gravitacije (pospeševanja)! Načelo
ekvivalentnosti v splošni teoriji relativnosti namreč upošteva dejstvo, da ni mogoče
razločevati učinka težnostnega polja v nepospešenem opazovalnem sistemu od učinka
pospeševanja opazovalnega sistema v prostoru, kjer ni težnostnega polja. Velja tudi,
da sta težnostna in vztrajnostna masa enaki. Veliki matematik David Hilbert je v času
tekme za prvenstvo matematičnega zapisa splošne teorije relativnosti tudi izjavil,
da
je fizika pretežka za fizike. V mislih je imel kdaj skromno matematično znanje fizikov,
zato jim je tudi sam zelo pomagal – s tenzorskimi enačbami gravitacijskega polja (objavil
je tekst "The Foundations of Physics", kjer poda aksiomatsko izpeljavo enačb polja).
Fizikalno teoretično je oče splošne relativnosti Albert Einstein (veliko nastavkov pa so nakazali že nekateri misleci pred njim), matematično pa David Hilbert. Oba skupaj (Hilbert - Einstein) sta zloglasna »MA-FI-JA«!
Dvojčki in GPS izračun
Da ne bomo zgolj teoretično razglabljali, se še enkrat vrnimo k izračunu GPS sistema, ki nam je
vrnil rezultat, da ure v GPS satelitih prehitevajo tiste na Zemlji približno za
3.86525*10-5 s, oz. za 38.7 μs na dan.
Še enkrat se posvetimo dvojčkom in staranju. Vidimo, da bo dvojčku na Zemlji tekel
čas celo počasneje (se bo majčkeno počasneje staral),
ker živi v močnejši gravitaciji, kot recimo dvojček v orbiti GPS satelita
(čeprav ta tudi potuje okrog Zemlje s hitrostjo
v = vts = (G•M/RGPS)1/2 = 3.88 km/s, a mu čas zaradi
padca gravitacije teče veliko hitreje, saj za kroženje na tirnici R velja
lastni čas
τ = t(1 - 2•G•M/(c2•R) – G•M/(c2•R) )1/2
).
Za koliko več pa se postara dvojček v satelitu v enem letu?
Razlika (kot smo že izračunali) je v enem letu
le 3.86525*10-5 s * 365 =
0.0141 s = 14 s/1000. V enem letu torej zelo malo. V času 1s/0.0141 = 70.9 ≈
71 letih pa bo razlika v starosti še zmeraj zanemarljiva, zgolj
ena sekunda.
A problem je drugje ... Če se v življenju na Zemlji postaramo za eno sekundo manj kot
recimo ljudje v satelitih orbite GPS, pa imajo ljudje v breztežnosti lahko veliko večje težave
kot je le ena sekunda več ko umrejo ...
Breztežnost v krožečih satelitih je posledica izenačitve gravitacijske in
sistemske centrifugalne sile (sta si nasprotno enaki).
A breztežnost ima za človeka po daljšem času hude posledice. Ni hidrostatičnega tlaka,
Sunita W. nam je na Šentvidu povedala, da imajo v ISS postaji vsi napihnjene glave, ker ni teže,
tudi kosti se več ne regenerirajo - osteoporoza ...,
na začetku se pojavlja huda slabost ... V breztežnosti tudi težko lulamo, se težko umivamo,
težko spimo,
težave imamo pri orientaciji, hranjenju ... No - najde se tudi kaj prijetnega, raziskave,
čudoviti pogledi na Zemljo, vragolije v breztežnosti ...
Vprašanje varnosti ljudi v vesolju je sprožilo kar nekaj raziskav,
recimo preiskavo fizičnih učinkov dolgotrajne izpostavljenosti
breztežnosti.
Junija 1991 je Space Shuttle (Spacelab Life Sciences - 1) v devetih dneh
izvedel 18 poskusov na dveh moških in dveh ženskah.
V okolju brez gravitacije so ugotovili, da se odziv belih krvnih celic in mišične mase zmanjša.
Poleg tega se je
v prvih 24 urah, preživetih v breztežnem okolju, volumen krvi zmanjšal za 10 %. Dolga breztežnostna obdobja
lahko povzročijo otekanje možganov in težave z vidom. Po vrnitvi na Zemljo učinki dolgotrajnega breztežnostnega
stanja še naprej vplivajo na človeško telo, saj se tekočine zbirajo nazaj v spodnjih delih telesa,
srčni utrip se poveča, pride do padca krvnega tlaka in se tako zmanjšana toleranca telesa za
obremenitve.
Človeka je torej bistveno oblikovala sila teže Zemlje
- Zemlja seveda leži na ravno primerni (idealni) razdalji od Sonca, temperature namreč omogočajo
tekočo vodo in ...
Naša evolucija je potekala pod vplivom teže in smo hkrati njeni otroci.
Teža tudi drži ob Zemlji atmosfero v kateri je tudi naš plin nastanka in preživetja,
to je kisik (molekula O2).
Atmosfera nas tudi (poleg magnetnega polja) ščiti pred ionizirajočim sevanjem iz vesolja, Sončevim vetrom,
je del vodnega kroga
...
Gravitacija nam je dala torej obliko telesa, konstrukcijo, torej okostje, vretenca ...
Občasno radi izjavimo, da je teža življenja prehuda (v prenesenem in dobesednem pomenu).
A "lahkotnost" bivanja v breztežnosti je še
na dolgi rok veliko hujši problem kot sama teža na Zemlji.
Zato se astronavti tudi zelo radi vrnejo nazaj na Zemljo kjer
vlada dobesedno pravi raj (glede na utesnjenost in pogoje bivanja in ostale fiziološke težave v ISS).
Astronavti torej direktno na lastni koži in pod njo čutijo, da
kako izjemno eksistencialno vrednost, udobje, stabilnost (če hočete srečo)
nam nudi ta naš modri planet. Čeprav je naš planet od daleč videti zgolj kot modra pikica – pa
ga v resnici moramo obravnavati (kot smo to videli iz dosedanjih razmišljanj in sosledja dogodkov)
skupaj z Luno, ostalimi planeti in s Soncem (zvezda populacije I, skromna a dovolj bogata s kovinami)
kot celoto, ki nam omogoča življenje in je hkrati del verige »neverjetnih« dogodkov od velikega poka
do danes in naprej.
Dolga potovanja po vesolju so tako lahko kar velik problem za fiziologijo
človeka, živali. Poleg breztežnosti, je tukaj še problem sevanja in še veliko ostalih
"malenkosti" ...
Predlaga se torej umetna gravitacija (večinoma) preko rotacije dovolj velikega bivalnega kolesa
(predlagal že naš pionir poletov v vesolje inženir Herman Potočnik v knjigi, ki izide
konec leta 1928 [z letnico 1929] v Berlinu,
Problem vožnje po Vesolju - Raketni motor ali Das Problem der Befahrung des Weltraums – Der Raketenmotor,
v slovenščino jo prevede Peter Srakar . komaj leta 1986 ).
Vendar trenutno ni nobene praktične uporabe umetne gravitacije v vesolju za ljudi
zaradi različnih pomislekov. Problem je glede velikosti in cene vesoljskega plovila,
ki je potrebno za generiranje
uporabne centripetalne sile, primerljive z jakostjo gravitacijskega polja
na Zemlji (g).
Znanstveniki so zaskrbljeni zaradi vpliva takšnega sistema na notranje uho astronavtov.
Zdi se, da bo uporaba centripetalne sile za ustvarjanje umetne gravitacije povzročila motnje
v notranjem ušesu, kar bo povzročilo slabost in dezorientacijo.
Škodljivi učinki se lahko tako izkažejo za nevzdržne za potnike.
Ker je sistemska centrifugalna sila sorazmerna kvadratu kotne hitrosti in polmera (Fcf =
mω2r ≈ mg), pa se z večanjem polmera bivalnega kolesa
in s povečanjem rotacijskega časa lahko zmanjšajo
učinki rotacije in dodatne sistemske Coriolisove sile (kaj recimo povzroča
Coriolisova sila - če se astronavt v vrtečem se okolju z umetno
gravitacijo premakne proti osi vrtenja ali stran od nje, bo začutil silo, ki ga potiska v ali
proti smeri vrtenja - ta sila recimo povzroča ciklone in anticiklone na Zemlji, vrtinčenje morij ...).
Na splošno velja, da pri 2 obratih na minuto ali manj ne bo prišlo do nobenih škodljivih
učinkov Coriolisove sile.
Za simulacijo gravitacije, podobne Zemljini gravitaciji 1 g, mora biti v tem primeru
polmer kolesa vsaj 224 m,
kar predstavlja zelo veliko vesoljsko postajo.
Da bi zmanjšali njegovo maso, bi lahko bil sestavljen zgolj iz dveh elementov, povezanih s kablom.
Nekateri pa predvidevajo, da bi zadostoval že pospešek 0.1*g.
Pokazalo pa se je celo, da se ljudje prilagajajo hitrostim celo do 23 vrtljajev na minuto.
Zlasti pri nameravanem šestmesečnem potovanju na Mars, se zdi
izpostavljenost umetni neprekinjeni ali vsaj občasni gravitaciji,
zelo smiselna, da se prepreči ekstremno
izčrpavanje astronavtov med samim potovanjem.


Levo slika Potočnikove vizionarske knjige. Desna slika pa je podoba umetnika na TEMPO3 v orbiti -
to je predlagana misija, ki zavrti dve polovici vesoljskega plovila, ki sta povezani s kablom, da bi tako
preko rotacije ustvarili umetno gravitacije na misiji s posadko na Mars. Ena od podob je tudi spodaj
med približevanjem Marsu.

Med približevanjem Marsu - sonda z umetno gravitacijo - ali se bodo Potočnikove sanje uresničile?.
Gravitacija na Marsu je precej šibka in znaša gM =
3.72076 m/s2 = 0.3794 g in bi najbrž zadoščala za lajšanje težav v našem telesu v novem okolju.
Pa še zaključimo to poglavje z dvojčki, ko bi se en od njiju rad počasi staral.
Pri počasnem staranju se zdi, da bi nam torej zelo pomagala močnejša gravitacija, recimo 2g.
A problem velike teže je spet prevelika obremenitev telesa. Pojavijo se velike tlačne razlike,
obremenitve srca, pri 2g čuti človek s 70 kg kar težo kot pri 140 kg na Zemlji.
Tako da je idealno za dvojčka in vse nas, da kar ostanemo na modrem planetu - ga varujemo.
Seveda pa si skoraj vsak od nas želi vsaj 1x v življenju poleteti v vesolje in
v breztežnost vsaj za nekaj ur. Kdo ve - lahko da nam kmalu uspe.
Prakticiranje (razvijanje) poletov v vesolje je tudi pomembno, ko bo potrebno za zmeraj zapustiti
naš trenutni dom Zemljo, ko se bo Sonce razširilo do tirnice našega planeta. Do takrat je še ZELO daleč,
tudi ne vemo kaj bo z življenjem, s človekom na Zemlji v naslednjih tisočletjih, milijonih let.
A zagotovo delno sami odločamo o lastni o usodi - smo vsaj malo svoje sreče kovači.
Energija delca zaradi visoke hitrosti in gravitacije
Vrnimo se k Schwarzschildovi metriki in jo še rahlo preoblikujemo, da iz nje izluščimo energije.
Enačbo delimo z lastnim časom dτ, že prej smo vpeljali kot zasuka
dΩ2 = dϑ2 + sin2ϑ dφ2:
c2 = c2(1 - rs/r)(dt/dτ)2
– (dr/dτ)2/(1 - rs/r) - r2(dΩ/dτ)2
- enačbo pomnožimo z izrazom (1 - rs/r) in dobimo izraz,
(1 - rs/r)c2
= c2(1 - rs/r)2(dt/dτ)2
– (dr/dτ)2 - (1 - rs/r)r2(dΩ/dτ)2
Levi člen (1 - rs/r)c2, če ga pomnožimo z maso delca, predstavlja neke vrste mirovno energijo delca v potencialu gravitacije masivnega objekta (rec. zvezde).
Tako kot v četvercu brez teže, se tudi v tej enačbi skriva energija.
Če zgolj osvežimo spomin in še enkrat izračunamo velikost četverca
gibalne količine brez gravitacije in naredimo še primerjavo s četvercem
z gravitacijo za zelo oddaljenega opazovalca, ki ne čuti gravitacije,
potem velja (upoštevajmo pa že znano Einsteinovo enačbo za polno energijo
delca E = γmc2):
(cdτ, 0) ⇔ dXμ = (cdt, dx) = (cdt, vdt) = (cγdτ, vγdτ)
= dτ(cγ, vγ)
(c, 0) ⇔ vμ = (cγ, vγ) = (cE/(mc2), vγ)
– četverec brez gravitacije ( γ = E/(mc2) )
(c, 0) ⇔ (c(1 - rs/r)1/2(dt/dτ), ...) – prvi člen metrike z gravitacijo, od zgoraj
[- še zapis celotnega četverca za gravitacijo
(cdτ, 0, 0, 0)
⇔ dXμ = ( c(1 - rs/r)1/2dt, dr/(1 - rs/r)1/2 , rdϑ , r sin ϑ dφ )
]
Primerjava nam da za prvi člen obeh četvercev naslednji izraz (kjer privzamemo, da je dt/dτ = γ, gre za gibanje delca):
E/(mc2) = (1 - rs/r)1/2(dt/dτ)
= (1 - rs/r)1/2γ
Tako dobimo energijo delca še v gravitacijskem polju za oddaljenega opazovalca:
E = (1 – rs/r)1/2γmc2
Spet bi lahko izpeljali, pa to naredite sami, povezavo:
E2 = (c2m)2 + (cp)2
Kjer je E polna energija delca,
mirovna energija delca je c2m in kvadrat gibalne količine delca pa je torej kar
p2
= m2( (dr/dτ)2/(1 - rs/r) + r2(dΩ/dτ)2 ) .
Za energijo delca velja enako kot pri posebni relativnosti, le da nastopi
še dodaten člen, to je gravitacijska (potencialna) energija. Na koncu, glede na povedano,
lahko izraz za polno energijo E tako še razčlenimo:
E = Eo + Ekin + Epot = (1 – rs/r)1/2γmc2
To energijo smo že omeili pri opisu fizike visokih hitrosti v ravnem prostoru (če ste preleteli
poglavje -
razkrinkajmo enačbo E = mc2 ), kot nadgradnjo ravnega prostora - sedaj jo samo utemeljujemo.
Kjer je seveda:
E = (1 – rs/r)1/2γmc2
- celotna energija, izpeljali zgoraj
Eo = mc2 - mirovna energija
Ekin = (γ - 1)mc2
= ((1 – v2/c2)-1/2 - 1)mc2
- kinetična energija (za male hitrosti je mv2/2)
Epot = E - Eo - Ekin
= (1 – rs/r)1/2γmc2 - mc2 - (γ - 1)mc2
= ((1 – rs/r)1/2 - 1)γmc2
Potencialna energija delca z maso 'm' ob sferičnem masivnem (homogenem) telesu je torej:
Epot = ((1 – rs/r)1/2 - 1)γmc2
- levo je torej zapis potencialne
energije
Lorentzov člen je
γ = (1 – v2/c2)-1/2.
V splošnem velja, da je kvadrat hitrosti v2 po Pitagoru vsota kvadratov radialne
in tangentne hitrosti
v2 = vr2 + vt2.
Pri šibki gravitaciji in majhni hitrosti delca moramo dobiti klasičen izraz
za energijo - in to tudi zares velja. Pri majhni hitrosti je kinetična energija (že izpeljali)
Ekin =
((1 – v2/c2)-1/2 - 1)mc2
≈ ((1 – v2/(2c2)) - 1)mc2
= mv2/2.
Pri šibki gravitaciji in pri skromnih hitrostih pa velja,
da je γ ≈ 1
(oziroma (1 - v2/c2)-1/2 ≈
1 + v2/(2c2) ),
in ko je gravitacija šibka, je člen rs/r = 2GM/(rc2) zelo majhen [ in velja
(1 – 2GM/(rc2) )1/2
≈ 1 – GM/(rc2) ], tako dobimo povezavo
((1 – rs/r)1/2 - 1)*(1 - v2/c2)-1/2
≈ (1 – GM/(rc2) -1)*(1 + v2/(2c2) )
=
-GM/(rc2) - (v2/(2c4) )GM/r
od koder sledita dve poenostavitvi za potencialno energijo pri skromni gravitaciji in hitrosti
Epot = ((1 – rs/r)1/2 - 1)γmc2 ≈
[-GM/(rc2) - (v2/(2c4) )GM/r]mc2
= -GmM/r - (mv2/(2c2) )GM/r ≈ - GMm/r.
Kjer nam člen
-(mv2/(2c2) )GM/r = -(Ek/c2)GM/r
predstavlja
potencialno energijo "mase" zaradi kinetične energije ( Ek/c2 ) - tega praktično nikoli ne upoštevamo pri vsakdanjih računih,
če bi pa ga v določenih primerih -
pa bi recimo prišli do ocene in razumevanja, zakaj prihaja do precesije perihelija planetov,
izrazito recimo pri Merkurju, glej tudi
oceno dodatne sile iz relativistične mase.
Še enkrat zapišimo potencialno energijo, a tokrat s poudarkom na členu
γm = c2γm/c2 = Er/c2 = mr,
ki nam predstavlja "relativistično maso" in
potencialna energija se ne računa zgolj na mirovno maso, ampak v bistvu na člen γm = mr.
Er nam predstavlja relativistično energijo delca zaradi gibanja - izpeljali v specialni teoriji.
Povejmo še, da so mnogi alergični na zapis pojma relativistična masa - in imajo po svoje tudi prav -
a tukaj ga (jo) omenjamo zato, ker nam kaže na bistvo splošne relativnosti, ki se primarno ukvarja z energijami.
In gravitacija tukaj ni zgolj sila na nek masni delec, ampak sila na energijo Er delca deljeno
s c2, to je na (Er/c2) ali kar na "zloglasno relativistično" maso mr.
Lahko torej pozabite na pojem relativistične mase, a nikakor ne spreglejte, da se v potencialni energiji
upošteva člen Er/c2 = γm. In ta razmislek je eden bolj prepričljivih, ko iščemo razlog za
zasuk perihelija planetov zaradi relativističnih efektov. Planetu s precej eliptično tirnico, ki potuje
okrog skupnega težišča s Soncem, se namreč hitrost na orbiti precej spreminja. Sploh v periheliju (prisončju) se mu
zelo poveča in se produkt γm precej poveča in s tem se zelo spremeni potencialna energija
(sama sila, če gledamo klasično).
To je v klasični sliki tudi razlog, da se znamenita smer
Laplace–Runge–Lenzovega vektorja glavne osi elipse ne ohranja (pride do precesije).
Glejte tudi - izpeljava Keplerjevih zakonov (II),
uporaba Laplace–Runge–Lenz vektorja. Ali - glej tudi
oceno dodatne sile iz relativistične mase.
Zapišimo torej potencialno energijo še z relativistično energijo delca zaradi gibanja
Er = γmc2 = mrc2:
Epot = ((1 – rs/r)1/2 - 1)γmc2 =
((1 – rs/r)1/2 - 1)mrc2 =
((1 – rs/r)1/2 - 1)Er
Schwarzschildova metrika v drugi obliki
(
(1 - rs/r)c2
= c2(1 - rs/r)2(dt/dτ)2
– (dr/dτ)2 - (1 - rs/r)r2(dΩ/dτ)2
), recimo za opazovalca na matični zvezdi (glej sliko, kjer je simbolično
opazovalec na zvezdi K. Schwarzschild), je po
obliki navidezno enaka kot za oddaljenega opazovalca (opazujemo gibajoč
delec – nanj vpliva tako efekt hitrosti, kot gravitacije)
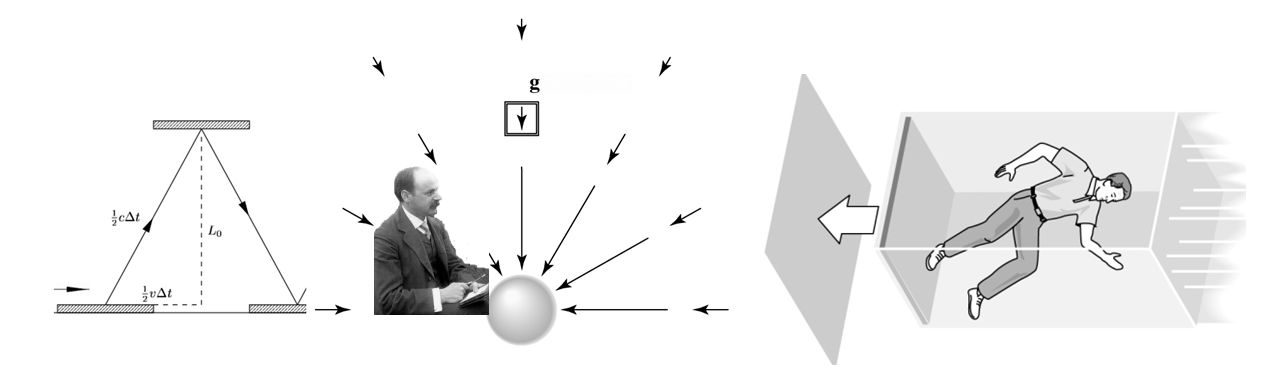
(1 - rs/r)c2
= c2(1 - rs/r)2(dt/dτ)2 –
(dr/dτ)2 - (1 - rs/r)r2(dΩ/dτ)2
- a sedaj za gibajoč delec velja E/(mc2)
= (1 – rs/r)dt/dτ
(ali tudi E2/(m2c2)
= c2(1 - rs/r)2(dt/dτ)2),
saj je čas dt v tem primeru enak
dt = γdτ/(1 – rs/r)1/2 .
Zakaj? - ker na izračun lokalnega lastnega časa
dτ,
poleg gibanja
dt/γ
- enako kot pri posebni relativnosti
- sedaj dodatno vpliva
še gravitacija s členom
(1 – rs/r)1/2,
kar smo zapisali že na začetku poglavja
o gravitaciji in metriki;
sedaj torej velja
dτ = dt(1 – rs/r)1/2/γ ali dt/dτ
= γ/(1 – rs/r)1/2 ), tako da še zmeraj velja znana povezava
E/(mc2) = (1 – rs/r)1/2γ.
To dejstvo zapišemo, upoštevamo, še v nekoliko preoblikovani Schwarzschildovi metriki:
(1 - rs/r)c2 = E2/(m2c2)
– (dr/dτ)2 -
(1 - rs/r)r2(dΩ/dτ)2
Iz zadnje enačbe se lahko, z nekaj matematične telovadbe,
izpelje vrsto pojavov (uklon žarka ob zvezdi, zasuk perihelija,
gravitacijski premik frekvence svetlobe, zamik ur – torej časa).
Za konec zgodbe o velikih hitrostih in pospeških, podajmo še kratek šolski opis vpliva »nove« (no, več kot 100 let stare) mehanike na opis vesolja (tudi na modrovanje, kako se je vse skupaj sploh začelo: začetek prostor-časa).
Slika - nazoren prikaz in opis členov Einsteinovih enačb polja – sliko se da razumeti
in posplošiti na celotno vesolje (čeprav nekoliko kozmološko nedosledno – saj vesolje
nima središča ..., pa vendar!).
V bistvu je metrični tenzor gμν sestavljen iz ravnega prostora brez gravitacije ημν
(po diagonali ima člene -1, 1, 1, 1 - vsi ostali so nič)
in ukrivljenosti zaradi gravitacije, energije, to je člen, tenzor hμν. Tako velja:
gμν = ημν + hμν
Kljub zahtevnosti tenzorskih enačb, pa lahko nekaj
povemo o njih za mejni primer – kaj nam torej povedo enačbe za prazen prostor?
V praznem prostoru, ki je torej raven, je Riccijev tenzor
Rµν = 0,
enako velja za
Riccijev skalar
R,
metrični tenzor
gµν
pa ima v tem primeru v prvem
členu vrednost
goo = -1 (napetostni tenzor pa ima v prvem členu vrednost
T00 = -ρvacc2 = -Λc4/(8πG) )
in ostaneta nam zgolj enačbi (prva člena tenzorja - znak minus pred -ρvacc2 predstavlja 'odbojno'
energijo):
Zadnja enačba
ρvac = Λc2/(8πG)
predstavlja tako imenovano gostoto vakuuma (naj se sliši še tako čudno,
a v vakuumu se stalno dogajajo fluktuacije, pari delec-antidelec, ...).
To je hkrati matematični zapis (poleg Heisenbergovega načela nedoločenosti
[ ΔEΔt ≥ h/(4π) - ki nam posredno sporoča, da si je moč
energijo iz ničesar sposoditi,
če se le ta dovolj hitro 'povrne'] (izraz ΔEΔt ≥ h/(4π) kdaj imenujemo tudi
Mandelshtam-Tammova enačba)), v katerem se skriva druga možna razlaga začetka
vesolja.
Strnjen scenarij začetka vesolja je lahko: fluktuacije v vakuumu, pari
delec-antidelec, porušitev simetrije v prid delcev, pospešeno širjenje
prostor-časa ... – in sedaj že lahko rečemo, da smo ... Vesolje bi simbolno
lahko primerjali tudi z zloglasno italijansko pizzo - osnovni sestavni
deli so neki ostanki od ostankov sira, zelišč, starih salam (ni nujno),
moke, paradajza, kvasa ... (neugledni koščki nič od nič), a ko to zložimo
skupaj in dobro toplotno obdelamo se pizza razširi, vzhaja (inflacija)
– pa dobimo jed, ki je osvojila (skoraj) cel svet ..., kot vesolje.
Ali so začimbe Higgsovo polje ...? To so le (zgolj okusne) prispodobe ...
Še zgodba o kozmološki konstanti
Λ
(danes ta člen merijo sateliti
preko detekcije variabilnosti mikrovalovnega sevanja ozadja, meri
pa se ga tudi preko sija supernov tipa Ia – beležimo razdaljo in hitrost).
Člen s kozmološko konstanto je izvirno vpeljal Einstein leta 1917, da bi omogočil takšno rešitev enačb polja (po kmečki logiki, da je vesolje na veliki skali mirno – zvezdno nebo se na prvi pogled res zdi zmeraj enako ...), ki bi podprla model statičnega, nerazširjajočega se Vesolja. Ta poskus uvedbe konstante se je pokazal za neuspešnega. Statično Vesolje je bilo že po teoriji nestabilno in 1927 je Georges Lemaître objavil članek ("A homogeneous Universe of constant mass and growing radius accounting for the radial velocity of extragalactic nebulae" - "Homogeno vesolje konstantne mase in naraščajočega polmera izračunanega iz radialne hitrosti izvengalaktičnih meglic"). Enako je Hubble, po desetletju opazovanj, leta 1929 odkril oddaljevanje galaksij, kar je kazalo na širjenje Vesolja. Einstein je na koncu člen Λ opustil in imenoval vpeljavo kozmološke konstante »za svojo največjo zablodo v življenju«. Dolgo časa so menili, da je vrednost kozmološke konstante enaka 0. Novejša (izboljšana) astronomska opazovanja pa so odkrila, preko sija supernov tipa Ia in satelitov (fluktuacije v mikrovalovnem ozadju), da rezultate lahko pojasni le od 0 različna kozmološka konstanta Λ , saj se vesolje celo pospešeno širi.

Grafit Einsteinovih tenzorskih enačb polja na stari lokomotivi. Izjemno zgovorno sliko
sem prvič videl na prvem kongresu (in žal edinem) Slovenija in vesolje: včeraj, danes
in jutri – oktober 2009 – predstavil jo je prof. Andrej Čadež. Redko katera slika bolj zgosti
razvoj življenja, človeka, njegovega tehničnega in mentalnega razvoja – izjemnega napora, rudarjenj,
razvoj kultur, znanosti …, kot ta slika – ki v trenutku časa povzame razvoj vesolja, osnovnih sil,
nastanek težjih elementov, kovin in življenja v prostor-času ... na opuščeni lokomotivi v puščavi.
Rešitve teh enačb opisujejo določeno geometrijo prostora-časa. Schwarzschildova rešitev na primer opisuje geometrijo okoli sferične, nerotacijske mase, kot je zvezda ali črna luknja, medtem ko Kerrova rešitev opisuje rotirajočo črno luknjo. Spet druge rešitve lahko opisujejo gravitacijsko valovanje. V primeru rešitve, ki jo podajajo Friedmann–Lemaître–Robertson–Walker, dobimo metriko za razširjajoče se vesolje. Najenostavnejša rešitev je neukrivljen prostor-čas Minkowskega, prostor-čas, ki ga opisuje posebna relativnostna teorija. V tem tekstu se ukvarjamo skoraj z vsemi navedenimi rešitvami. Posebej dobro pa obdelamo posebno relativnostno teorijo, iz splošne teorije relativnosti pa Schwarzschildovo rešitev - metriko (in tako tudi obdelamo gravitacijski rdeči premik, ukrivitev žarka ob masivni zvezdi, precesijo perihelija planetov, GPS sistem … ) in dokaj podrobno obdelamo tudi Friedmann–Lemaître–Robertson–Walkerjevo metriko (element) za celotno vesolje. Nakažemo pa tudi izpeljavo Einsteinovih enačb polja.
Zakaj po učbenikih, ekranih, gledamo lijake ukrivljenega prostor-časa?
Ko gledamo razne podobe gravitacijskih lijakov (kot je ta zadnji z mrežo krogov in krivulj -1/R),
na sredi pa je postavljena krogla - zvezda, planet ... - je to prispodoba
ukrivljenosti prostor-časa, ki jo povzroča prav to centralno telo.
Zakaj taka podoba? Če narišemo potencial neke zvezde, se le ta zapiše
zelo preprosto
Φ = - GM/R
in prostorski graf tega potenciala
po vseh kotih nam da podobo lijaka.
Krogi na lijaku nam povedo področje z enakim potencialom
na razdalji R (ali potencialno energijo nekega malega telesa
m, to je seveda nam vsem poznana enačba
Ep = Φm = -GMm/R).
Tak potencial recimo čuti satelit, ki kroži okrog Zemlje.
Ta prispodoba je zaživela, ko je Einstein obrnil fiziko na
glavo in sicer z zelo utemeljeno izjavo, da se vesolje, galaksije,
zvezde, planeti obnašajo tako kot se - ne zaradi teže, ampak zaradi
ukrivljenosti prostor-časa, ki ga pa krivi energija zbrana v masah,
delcih, sevanjih, napetostih. Danes poznamo še temno snov in temno
energijo. Gravitacijski zakon po Newtonu velja samo za masne objekte,
a ker se tudi svetloba ukrivi na poti skozi vesolje (svetloba pa nima mase),
je koncept ukrivljenosti prostor-časa (gravitacijskih lijakov) še kako utemeljen.
Tudi čas teče v gravitacijskem lijaku počasneje kot čas ur (daleč) izven njega.
Nekateri pravijo, da je komaj Einstein razložil silo gravitacije preko ukrivljenosti
prostor-časa ("gravitacijskih lijakov") zaradi masivnih objektov vesolju in ostalih energij.
A tudi koncept gravitona, kot nosilca gravitacijske sile, še živi.
Seveda je tudi Newton imel težavo, kako razložiti silo na daljavo med recimo Zemljo in Luno.
Einstein pa pravi, da je Luna v gravitacijskem lijaku Zemlje, ki pa je v gravitacijskem lijaku Sonca, ki pa je
v gravitacijskem lijaku Galaksije, ki pa je v gravitacijskem lijaku lokalne jate galaksij, ...
Stephen Hawking je predlagal, da obstaja možnost počasnega izginotja, razpada (izhlapevanja) črnih lukenj - in to preko para delec-antidelec (na "robu" črne luknje), saj se tudi v popolnem vakuumu dogajajo kvantne fluktuacije, zraven je še potrebno upoštevati Heisenbergov princip nedoločenosti. Črna luknja tako na robu pritegne antimaterijo (antidelce - primer je recimo pozitron napram elektronu) in se s tem njena masa zmanjša, delec materije pa zavirajoče odfrči v vesolje, lahko ga pa črna luknja posrka ali potuje okrog črne luknje. V vseh primerih je to pospešeno gibanje električnega delca in posledično tak delec seva (izven lupine Schwarzschildovega polmera) - valovna dolžina je primerljiva velikosti črne luknje. To sevanje je na nek način podobno sevanju črnega telesa (po našem rojaku Jožefu Stefanu). Elektromagnetno sevanje je enako - kot da ga oddaja črno telo - a s temperaturo, ki je obratno sorazmerna z maso črne luknje. Tako se izkaže, da je tudi entropija črne luknje končna.

Stephen William Hawking, angleški fizik, astrofizik, matematik in kozmolog,
* 8. januar 1942, Oxford, Anglija,
Združeno kraljestvo, † 14. marec 2018, Cambridge.
Znan je po teoriji o sevanju črnih lukenj (zaenkrat še nepotrjeni),
poljudnih knjigah, največja uspešnica je "Kratka zgodovina časa"
(tu so še: Črne luknje in otroška vesolja, Vesolje v orehovi lupini ...)
in težavah, boju proti hudi bolezni ( bolezen gibalnih nevronov, imenovano
amiotrofična lateralna skleroza, ki ga je praktično povsem ohromila).
Leta 1994 so kultni Pink Floyd za skladbo Keep Talking z albuma Division
Bell uporabili odlomke njegovega sintetiziranega glasu. Slišati pa ga
je mogoče še v skladbi Talkin' Hawking z albuma The Endless River, ki je
izšel natanko dve desetletji pozneje, torej leta 2014. Odlomek njegovega govora
v pesmi Keep Talking ("Ne odnehaj govoriti") je naslednji: " Milijone let
smo ljudje živeli tako kot druge živali. Potem pa se je zgodilo nekaj,
kar je s povodca spustilo moč naše domišljije. Naučili smo se govoriti."
Bi bil kdo bolj primeren, da izreče take besede kot prav Hawking na vozičku
s sintetiziranim glasom ...
Bil je velik popularizator znanosti - mediji pa so ga imeli radi tudi zaradi
nezavidljivega položaja - a velikokrat so ga citirali tudi zaradi svetovnega nazora.
Veliko laikov je z vsemi štirimi prijelo njegovo zagovarjanje vzporednih vesolj -
čeprav je ta teorija za mnoge neznanstvena (protislovna znanstveni metodi - poeziji
ali poljudni filozofiji, religiji, tudi matematiki pa seveda ni tuja ..., če bomo
kdaj fizično odkrili »več vesolj« - le to namreč v empirični znanosti šteje - bo
to seveda eno razčlenjeno vesolje – v današnjem pojmu vesolja se namreč skriva vse;
današnja teorija več vesolj je po definiciji bližje religiji – veri – kot znanosti –
kar pa seveda ni nič narobe). Einsteinova teorija relativnosti se nikoli ni oddaljila
od empiričnega, merljivega, od razlage pojavnega sveta (zato danes tudi brez nje ne
moremo razvijati modernih tehnologij). Razložil je vir energije zvezd, nastanek težkih
atomov, vpliv gravitacije (pospešenega gibanja), energije na čas - prostor, razložil je
mehaniko vesolja, potrdil je kvantizacijo svetlobe, nasprotoval je verjetnosti kot bistvu
kvantne mehanike (bil je znanstveno in filozofsko avtonomen – trmast, kar je Einsteinu
zelo koristilo, a trma ne koristi vsem ...) ...
Vrnimo se k Hawkingu - vsekakor pa je njegovo soočenje z hudo boleznijo in hkrati znanstveno
udejstvovanje, postalo sinonim za neko posebno življenjsko energijo - upanje za vse, ki se
tako ali drugače znajdejo v primežu neozdravljivih bolezni. Pokazal je, da bistvo človeka
ni v njegovi podobi ampak intelektu - kar pa se žal redko odraža v potrošniških vrednotah ...
A ljudem ne moremo in ne smemo vzeti njihove (naše) narave – zagotovo je del naše narave
tudi potrošništvo – lahko pa potrošništvo blažimo (zakaj je narava ustvarila tako močno
željo človeka po imeti kar koli, tudi položaj? ...). In tega so se zavedali tudi naši predniki
– ko so pronicljivo trdili, da sit ne razume lačnega (to v prenesenem pomenu velja za vse
vidike našega bivanja – tudi za »zdravega« človeka napram hendikepiranemu sočloveku).
Kar se tiče Hawkingove temperature, se oceni z naslednjimi koraki, uporabili bomo: Wienov in Stefanov zakon, Schwarzschildov polmer črne luknje, kvantne fluktuacije na robu črne luknje, Heisenbergov princip nedoločenosti, sevanje električnega delca zaradi pospešenega gibanja.
Maksimum sevanja črnega telesa je iz Wienovega zakona pri valovni dolžini:
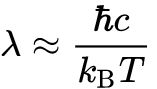
Pri črnih luknjah uporabimo kot enoto dolžine Schwarzschildov polmer -
ta določa dogodkovni horizont. Znotraj dogodkovnega horizonta ne vidimo,
kajti noben signal ne more zapustiti izjemno močne gravitacije črne luknje
(tudi svetloba ne). Zunaj dogodkovnega horizonta pa signal lahko potuje
v vesolje - v okolico. Kako določimo polmer dogodkovnega horizonta -
Schwarzschildov polmer? Po energijskem zakonu velja za delec ob zvezdi
s skupno energijo nič, torej za drugo kozmično hitrost, da je vsota kinetične
in potencialne energije enaka 0. Delec ima na začetku ravno toliko kinetične energije,
kot negativne potencialne energije in se zato v neskončnosti ustavi - velja torej:
mv2/2 - GmM/r = 0
(od tod dobimo za radij izraz r = 2GM/v2, za foton pa predpostavimo enako
relacijo, le da upoštevamo hitrost svetlobe 'c'):
rs =2GM/c2
Nekaj časa se je zdelo, da se masa črni luknji lahko samo veča, saj s svojo
izjemno gravitacijo vase potegne, posrka vse delce iz okolice, ki se črni
luknji dovolj približajo in imajo negativno energijo. Tudi če krožijo okrog
črne luknje, se zaradi gravitacijskega sevanja počasi približajo Schwarzschildovemu
polmeru in jih tako črna luknja posrka vase. A Hawking je razmišljal korak naprej,
poglejmo kako! Razmišljal je podobno kot Jožef Stefan in sicer, da tudi črna luknja
(protislovno) seva elektromagnetno valovanje. A kateri mehanizem bi to lahko omogočil
- odgovor je našel v kvantnih fluktuacijah na robu črne luknje.
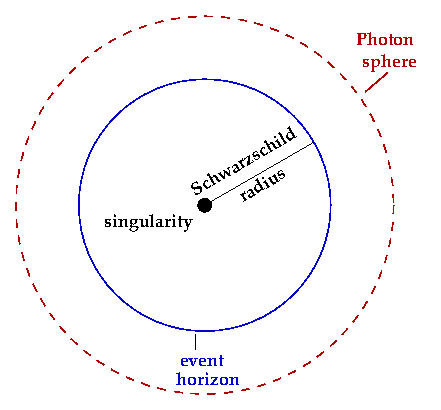
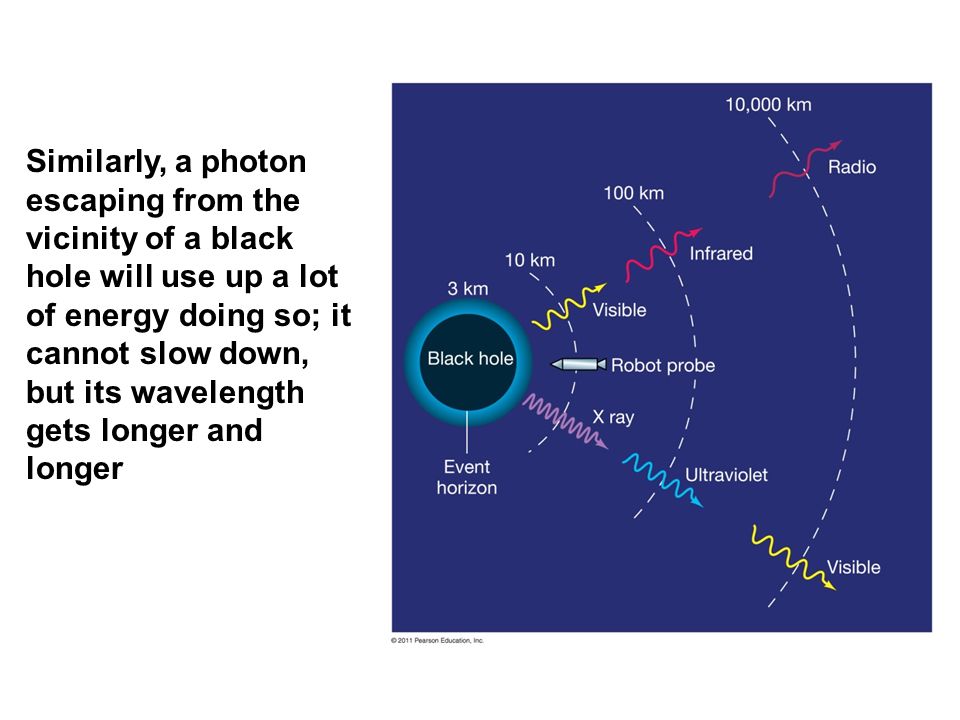
Tudi na "robu" črne luknje se dogajajo (naj bi se) kvantne fluktuacije
(delec - materija in antidelec - antimaterija), zraven je potrebno upoštevati
še Heisenbergov princip nedoločenosti lege (možnost lege delca izven
Schwarzschildovega polmera). Črna luknja tako blizu roba pritegne antimaterijo
(antidelce - primer je recimo pozitron napram elektronu) in se s tem njena masa
zmanjša, delec materije pa zavirajoče odfrči v vesolje, lahko ga posrka črna
luknja ali potuje okrog črne luknje.
V vseh primerih je to pospešeno gibanje
električnega delca in posledično tak delec seva
(izven lupine Schwarzschildovega
polmera). Valovna dolžina je torej, glede na naravo pospešenega gibanja, glede
na polmer kroženja, primerljiva velikosti črne luknje. Zadnji razmislek upoštevamo
tako, da izenačimo valovno dolžino in oceno velikosti Schwarzschildovega radija
(še enkrat povejmo, da gre zgolj za ocene):
λ ≈ rs ≈ 2GM/c2
Ocenjen Schwarzschildov polmer je kar:
rs ≈ 2GM/c2
Iz zgornje ocenjene temperature velja:
kBT ≈ ℏc/rs
Za temperaturo (v Kelvinih ) v masah Sonca
M☉
velja (iz enačbe kBT ≈ ℏc/rs):
T ≈ ℏc3/(kBGM) ≈ 10-6M☉/M
- temperatura sevanja je torej obratno sorazmerna z maso črne luknje.
Za površino (A - 'area') sevanja privzamemo kar znano formulo za sfero:
A ≈ 4πrs2
------------------------------------------------------
Sevalno moč (izsev) lahko ocenimo kar iz Stefan-Boltzmannovega zakona (tako hkrati
dodatno spoznavamo pomen Stefanovega raziskovalnega dela), v enačbo vstavimo zgoraj
izpeljane in ocenjene spremenljivke:
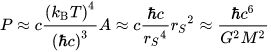
V enotah MKS dobimo naslednji rezultat za izsev črne luknje glede na njeno maso M:
P ≈ 1038 W/M2
Sistem enot MKS je metrični sistem merskih enot, ki vsebuje kot osnovne enote meter
(oznaka m) za dolžino, kilogram (oznaka kg) za maso in sekundo (oznaka s) za čas.
Življenjska doba črne luknje
τ
se izrazi z upoštevanjem enačbe za produkt izseva in
življenjskega časa, ki je enak Einsteinovemu izrazu za energijo
(τP ≈ Mc2),
iz povedanega sledi:
τ ≈ G2M3)/(ℏc4)
τ ≈ 10-20(M)3 sekund
ali
τ ≈ 1064(M/M☉)3 LET
Življenjska doba črne luknje je torej precej večja, kot je "trenutno" staro vesolje. Za črno luknjo za maso desetih sončevih mas (M = 10M☉) je ocena časa obstoja (razpada) kar 1067 let. Kaj se zgodi na koncu procesa elektromagnetnega "izparevanja" črne luknje preko parov delec-antidelec - je več špekulacij. Hawking je drzno predlagal celo rojstvo novega vesolja, a ... počakajmo. Zdi se, da ni nič večnega, a kaj je večnost?
Opomba
Morebiti pogrešate natančnejše izračune. Recimo izsev lahko zapišemo v diferencialni
obliki, a po integriranju se spremeni nekoliko le konstanta - ker gre za oceno -
so naši izračuni pri teh velikostnih redih čisto korektni.
Korektne enačbe:
P = c2dM/dτ
= hc6dτ/(2πG2M2) = konst/M2
c2M2dM = konst*dτ
∫c2M2dM = ∫konst*dτ
Tudi po integriranju se velikostni red ne spremeni ...
Drži pa tudi, da dolgo časa črna luknja črpa energijo iz okolice, tudi
iz mikrovalovnega sevanja ozadja – tako da na začetku dobi več energije
iz okolice, kot je odda s Hawkingovim mehanizmom sevanja. Temperatura črne
luknje je (kot smo že izpeljali) zelo majhna in je obratno sorazmerna z maso
(eksakten rezultat za temperaturo črne luknje je
T = ℏc3/(8πGkBM)
= 6 10-8 (M☉/M) ) K.
Za črno luknjo mase Sonca je temperatura komaj
6 10-8 K,
to je precej manj od sevanja mikrovalovnega ozadja
To = 2,725 K.
Ko je v današnjem vesolju masa črne luknje pod
M = 6 10-8 K M☉/2,725 K
≈
2 10-8 M☉
(to je nekje masa Lune), bi naj začela izgubljati maso s sevanjem.
Za razliko od večine predmetov, se temperatura črne luknje poveča,
ko zgublja maso. Stopnja povečanja temperature je eksponentna,
najverjetnejša končna točka pa je raztapljanje črne luknje v
silovitem izbruhu gama žarkov. Za črno luknjo s težo
1011 kg
je
čas izhlapevanja 2,6 × 109 let (to je pod starostjo vesolja).
Zato nekateri astronomi iščejo znake eksplozije morebitnih prvotnih črnih lukenj.
Še o gostoti črne luknje – teoretično zelo poučno. Schwarzschilda gostota
se izračuna preko standarne povezave
ρ = M/V = 3M/(4πR3),
če privzamemo,
da je polmer črne luknje kar dogodkovni horizont
R = Rs = 2GM/c2, potem za gostoto črne luknje
dobimo zanimiv izraz:
ρ = 3M/(4πR3) = 3c6/(32G3πM2)
∝ 1/M2
Kaj pomeni ta rezultat, da je gostota črne luknje
obrano sorazmerna z maso na kvadrat?
Če bi izdelali črno luknjo iz približno 4 milijard Sonc,
bi imela gostoto zraka
(1,3 kg/m3)
in take luknje
sploh ne bi bilo potrebno stiskati – dovolj bi bila le sama gravitacija.
A vesolje ima na kubni meter le kak atom – in to pojasnjuje, zakaj takih
črnih lukenj po vesolju ne srečamo kar tako. Problem je tudi, da ne vemo,
kaj se dogaja s snovjo znotraj črne luknje.
Še gostota črne luknje izražena s Schwarzschildovim radijem:
ρ = 3c2/(8GπRs2)
Črna luknja tudi rotira in ima naboj.
.gif)
Pri črnih luknjah je potrebno upoštevati še rotacijo, tudi naboj, vztrajnostni moment J,
ko se dogodkovno obzorje še zmeraj izraža preko Schwarzschildovega polmera, a nekoliko bolj zapleteno,
s Kerrovo metriko (ko je črna luknja - dogodkovni horizont zaradi rotacije nekoliko sploščen).
Velja:
α = J/(Mc)
rH = (rs + (rs2 - 4α2)1/2)/2
rE = (rs + (rs2 - 4α2cos2θ)1/2)/2
https://en.wikipedia.org/wiki/Ergosphere
https://it.wikipedia.org/wiki/Metrica_di_Kerr
https://en.wikipedia.org/wiki/Kerr_metric
SCENARIJI DINAMIKE VESOLJA,
KRATEK RAZMISLEK
O BODOČNOSTI - kozmologija
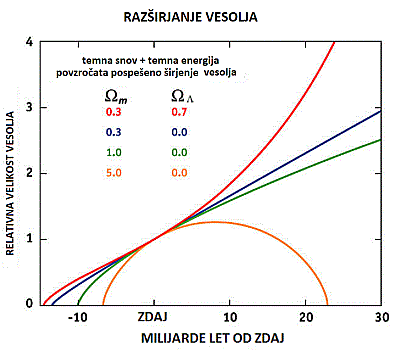
Dinamika vesolja – krivulje velikosti vesolja v odvisnosti od časa glede na različne scenarije.
Oranžna krivulja predstavlja »zaprto vesolje« (se širi, ustavi in začne krčiti, gostota
je večje od kritične
[Ω = ρ/ρc velja Ω > 1] ).
Zelena krivulja pomeni, da se bo vesolje
v neskončnost nehalo širiti (»ravno vesolje«, gostota je enka kritični
[ Ω = 1]).
Modra krivulja pomeni, da se bo vesolje večno širilo (»odprto vesolje«,
gostota je manjša od kritične [ Ω < 1]). Pojem kritične gostote bomo srečali
v nadaljevanju in tudi kaj pomeni presenetljiva rdeča krivulja (vesolje
celo pospešeno beži narazen), ki je, preko opazovanja oddaljenosti supernov tipa Ia,
postala aktualna leta 1998 in eksperimentatorji so bili zanjo leta 2011 tudi nagrajeni
z Nobelovo nagrado za fiziko.
Do podobnih krivulj (glejte graf) lahko pridemo že s klasičnim razmislekom za mehanično
energijo preprostega sistema s centralno sferično maso M. Res - da z nekoliko nedoslednimi
sklepi - glejte kar sliko, kjer smo razlagali Einsteinov tenzor ukrivljenosti prostor-časa
na preprostem modelu sferične mase, kjer postavimo v ukrivljen prostor, v »lijak«,
majhno točkasto telo in prav dinamika tega telesa nas tokrat zanima. A vesolje seveda
nima take narave, središča, roba ... pa vendar. Zapišimo torej energijo delca m ob sferični
masi M (vsoto kinetične
mv2/2
in potencialne
-GMm/R
energije – dodajmo še pogoj,
da delec z maso m trenutno beži vstran od centralne mase M, podobo kot se trenutno tudi naše
vesolje širi). Enačbo za Energijo E pozna (in razume?) vsak srednješolec:
mv2/2 - G M m/R = E
Kakšni so scenariji, če se trenutno vesolje širi (prispodoba - kamen vržemo navzgor)?
Če je energija pozitivna E > 0 (odprto vesolje, potem je kinetična energija večja od potencialne, mv2/2 > GMm/R, to pomeni večno širjenje vesolja, kamen ne bo padel na Zemljo), če je E negativna E < 0 (zaprto vesolje, mv2/2 < GMm/R, to pomeni širjenje in nato krčenje vesolja, kamen se ustavi in nato pade na tla), in če je E = 0 (ravno vesolje, mv2/2 = GMm/R, kamen se bo v neskončnosti ustavil).
A po letu 1998 (preko meritev hitrosti in sija supernov tipa Ia) se kaže scenarij odprtega vesolja (E > 0) in celo pospešenega širjenja – rdeča krivulja.
Ali lahko izrazimo še kaj bolj univerzalnega za vesolje kot celoto – in to kar iz našega preprostega zapisa energijskega zakona – recimo kako količino »brez mase M, brez polmera R, brez hitrosti v ...«?
V ta namen se spomnimo, da o težnosti (gravitaciji) na neki zvezdi, planetu, odločajo - kot razberemo iz enačbe za pospešek g = GM/R2 - pričakovano masa telesa M in polmer R. A o masi odločata gostota in volumen: M = ρV. Recimo – potepuh Saturn (Rs = 58232 km) je le malo manjši od Jupitra (RJ = 69911 km, gJ = 24,79 m/s2, vJ-ubežna = 59,5 km/s, ρJ = 1,326 kg/dm3 ), a Saturn ima precej manjši gravitacijski pospešek (gS = 10,44 m/s2, podoben Zemljinemu) in tozadevno precej manjšo ubežno hitrost vS-ubežna = (GMS/RS)1/2 = 35,5 km/s, kot njemu podoben Jupiter. Zakaj je temu tako? Ker ima Saturn precej manjšo gostoto od Jupitrove. Povprečna gostota Saturna je le ρS = 0.687 kg/dm3 (je celo manjša od vode) in je skoraj 2x manjša od Jupitrove. Gostota torej bistveno odloča o dinamiki nekega sistema, recimo o ubežni hitrosti. Poiščimo torej gostoto vesolja.
Enačbo za energijo
( E = mv2/2 - GMm/R )
preoblikujemo v spremenljivke, ki smo jih pomerili za vesolje kot celotno – v t. i.
v Friedmannovo obliko. Radi bi se torej znebili polmerov, mas in dobili gostoto vesolja
– ali je to možno? Kaj pa poznamo na skali vesolja – ne veliko, recimo Hubble-Lemaîtrov zakon.
Pa dajmo, iz malega (skromnega) raste veliko. V srednješolsko enačbo vstavimo torej maso
izraženo z gostoto in volumnom, hitrost pa nadomestimo s Hubble-Lemaîtrovim zakonom.
V = HR - Hubble-Lemaîtrov zakon, H je Hubble-Lemaîtrova konstanta, V je hitrost galaksije,
R pa je oddaljenost (recimo oddaljenost galaksije).
M = ρV = ρ4πR3/3
Še beseda o Friedmannovi enačbi
Prvotna oblika je:
H2 = 8πGρ/3 - k c2/R2
Dopolnjena pa se nanaša na pospešeno širjenje vesolja in zato vsebuje kozmološki člen Λ :
H2 = 8πGρ/3 - k c2/R2 + Λ c2/3
Kako pridemo do te enačbe?
Kar iz energijske enačbe:
mv2/2 - GMm/R = E, oziroma mv2/2 = GMm/R + E
Za hitrost v privzamemo Hubble-Lemaîtrov zakon v = HR, enačbo delimo z m in pomnožimo z 2:
(HR)2 = G2M/R + 2E/m
Velikokrat zapišemo člen 2E/m enačbe kot 2E/m = konst c2 = -Kc2, K – je
povezan z
ukrivljenostjo. Namesto M pa zapišemo (M = ρV = ρ4πR3/3), gostoto pa kdaj izrazimo recimo s trenutno
gostoto ρo in danim polomerom Ro, velja ρ = ρoR3o/R3.
Enačbo delimo še z R2.
Po preoblikovanju dobimo Friedmannovo enačbo:
H2 = 8πGρ/3 - Kc2/R2
Ker velja, da je H = (dR/dt)/R, zapišimo še naslednjo obliko:
H2 = (dR/dt)2/R2 = 8πGρ/3 - Kc2/R2
Če uvedemo faktor umeritve a (scale factor) a = R/Ro (a se s časom spreminja,
Ro je trenutni vidni horizont vesolja),
potem dobimo še eno obliko klasične anačbe (izpeljana leta 1922,
Friedmann žal zelo mlad umre leta 1925, na Krimu se je na poročnem potovanju okužil
s tifusom):
H2 = (da/dt)2/a2 = 8πGρ/3 - Kc2/a2
Izrazimo čas kot funkcijo velikosti R, tako sledi diferencial:
dt = dR/(8πGρR2/3 - Kc2)1/2 =
(1/(cK1/2))dR/(8πGρR2/(3Kc2) - 1)1/2
∫dt = (1/(cK1/2))∫dR/(8πGρR2/(3Kc2) - 1)1/2
∝ ∫dR/(kon·R2 - 1)1/2
To je enačba, integral, katerega rešitve (možne dinamike vesolja) bomo spoznali nekoliko pozneje.
Friedmann je bil med prvimi, ki je ponudil zelo korektne rešitve za dinamiko
in model(e) vesolja - Einstein se na začetku ni strinjal z njim, ker je Friedmann dovoljeval
dinamično vesolje ...
Reklama tudi v znanosti skrajša pot k uspehu in priznanju - Friedmann in Lemaitre žel nista zelo reklamirala svojih
pravilnih rešitev dinamike vesolja.
Enake "težave" je imel z Ensteinom tudi Lemaitre - pozneje so se duhovi pomirili,
saj so končni odgovor dale meritve (najprej Dopplerjev premik spektralnih črt svetlobe
zaradi premikanja, oddaljevanja galaksij, pozneje detekcija mikrovalovnega sevanja ozadja in to iz vseh smeri
vesolja ...
), torej živimo v dinamičnem vesolju in ne statičnem
(statično vesolje so med drugimi zagovarjali Newton, Einstein, F. Hoyle ...).
IN še citat: "Newton's Hypothesis - The universe is infinite, static and uniform." -
https://slideplayer.com/slide/4325597/
A že Newtonova mehanika (gravitacijski zakon) nam sugerira, da je vesolje prej
dinamično kot statično ... A bistvo je kdaj očem nevidno, skrito - pravi Mali princ ...
Navidezna statičnost medsebojne lege zvezd, galaksij, meglic, kopic je
varljiva na skali človeškega življenja ...
Dopolnjeno zgoraj že zapisano enačbo s kozmološkim členom (+ Λ c2/3 ) bomo spoznali
pri temni energiji, ki pospešeno širi vesolje.
SLEDIJO ZELO POUČNI IZRAČUNI, IZRAZI, SCENARIJI O NAŠEM VESOLJU
E = m v2/2 - G M m/R = mH2R2/2 – 4πGρR2m/3
Enačbo pomnožimo z 2/(mR2), da izrazimo Hubble-Lemaîtrovo konstanto brez
vsakih drugih produktov.
2E/(m R2) = H2 – 8πGρ/3
Pa smo uspeli – v enačbi ni mase vesolja, tudi ne polmera, ne hitrosti. Sedaj pa
lahko spet ponovimo, preko enačbe s Hubble-Lemaîtrovo konstanto in gostoto, enake scenarije
glede bodočnosti vesolja kot prej preko energije (energija je spet lahko 0 ali
E > 0 ali E < 0), recimo,
če H2 – 8πGρ/3 > 0 potem se bo vesolje večno širilo,
od koder sledi enačba, povezava,
H2 > 8πGρ/3
In - kaj nam razkriva zadnji zelo eleganten pogoj?
Da o bodočnosti vesolja odloča gostota ρ !!!
Za konstantno (bolje ravno vesolje) vesolje bi veljalo
H2 – 8πGρ/3 = 0 in mejna (kritična) gostota je kar:
ρc = 3H2/(8πG),
- izračunajmo to mejno gostoto, tudi v številu protonov
na kubični meter (bo tudi simbolno lažje za razumeti).
Masa protona je mprotona = 1.67 10-27 kg,
Hubble-Lemaîtrova konstanta naj bo H=73 km/s/Mpc,
lahko bi vzeli tudi nekoliko manjšo vrednost za H ...,
a meritve konstante H in obdelave še trajajo,
»problem« sta dve metodi,
dva rezultata - preko mikrovalovnega ozadja in supernov tipa Ia.
Rezultat je:
ρc = 3H2/(8πG) = 10-29g cm-3 = 10-26 kg m-3 = 6 protonov/m3
Kritična gostota vesolja je torej še zmeraj zelo, zelo majhna
(10-26 kg/m3) –
in tako ekstremnega
vakuuma (kot je ocena kritične gostote vesolja) sploh ne znamo ustvariti
v laboratorijih, zgolj
6 protonov na kubični meter ... Če vstavimo za kritično gostoto vesolja
Hubble-Lemaîtrovo konstanto z vrednostjo
67,36 km/s/Mpc (ocena iz mikrovalov ozadja),
dobimo 5.1 protonov na m3.
V resnici je v vesolju še manj protonov - na nekaj
m3
komaj en – vse ostalo pripada temni snovi in
večina temni energiji (lokalno pa po gostoti seveda izstopajo gravitacijsko
združeni plini in prah v zvezde,
planete, tudi v življenje, v človečke …).
Kaj pa pravijo trenutne meritve gostote?
Še prej pa definirajmo
brezdimenzionalno relativno gostoto Ω, kot razmerje med pomerjenimi
gostotami in kritično gostoto
(tako bomo dobili kar deleže posameznih glavnih igralcev našega vesolja).
Ω = ρ/ρc = 8πGρ/(3H2) - parameter gostote (omega) ali relativna gostota glede na kritično
Trenutne vrednosti meritev relativnih gostot (in delno ocen) so:
Ωm = ρm/ρc = 0.042 (rel. gostota vidne snovi = 0.25 protona/m3, iz te snovi smo recimo ljudje, zvezde, planeti)
Ωt = ρt/ρc = 0.24 (rel. gostota temne snovi, lahko rečemo, da drži galaksije skupaj)(?)
Ωs = ρs/ρc = 4.6 x 10-5 (rel. gostota sevanja, »masa« izhaja iz energije kozmičnega mikrovalovnega sevanja ozadja [cosmic microwave background (CMB)] – masa_prasevanja = E/c2)
ΩΛ = ρΛ/ρc = 0,72
- blizu ostanka, razlika do 1, ΩΛ ≈ 1- Ωm - Ωt - Ωs (to je rel. gostota temne energije, ki pospešeno širi vesolje - tako vsaj kažejo trenutne meritve dinamike oddaljevanja galaksij, preko supernov tipa Ia)Kot smo že zapisali, so se razmerja gostot skozi zgodovino vesolja spreminjala. Po Einsteinovi teoriji velike mase, kot so galaksije, črne luknje, ostale oblike energije, ukrivljajo prostor-čas. Toda meritve kažejo, da je vesolje na velikih (kozmoloških) razdaljah ravno. Kar pomeni, da je gostota vesolja uravnotežena med večnim širjenjem in ponovnim krčenjem (zdi se torej, da je kinetična energija enaka potencialni Ek + Ep = 0 ali kot smo že zapisali prej, velja: H2 – 8πGρ/3 = 0 - beri uvod v poglavju "SCENARIJI DINAMIKE VESOLJA"). Tako so danes ocene, kljub pospešenemu širjenju vesolja, da je ukrivljenost vesolja blizu ničle, da potencialna energija zaradi same gostote vesolja torej ne prevladuje nad kinematiko (dinamiko) vesolja (obe energiji sta v ravnovesju ali blizu). Torej tudi ne bi smelo biti težav z globalnim časom, merjenjem razdalj ...
Trenutno bi naj torej vesolje sestavljalo okrog 4,2 % atomov in ostalih masnih delcev, 24 % temne snovi in kar 72 % temne energije in zanemarljiv prispevk, delež, ostalih virov energije (sevanje mikrovalovnega ozadja, ukrivljenost ...). Če privzamemo za Hubble-Lemaîtrovo konstanto vrednost 67,36 km/s/Mpc, se delež temne energije spusti na okrog 68 %.
Še beseda o pospešenem širjenju vesolja – še pred desetletji so to bile zgolj domneve »čudakov«. 1998 Perlmutter, Schmidt in Riess - dve skupini - eno je vodil Perlmutter, v drugi sta delovala Riess in Schmidt, sta tekmovali v kartiranju vesolja, odkrili sta, da se vesolje pospešeno širi. To sta dokazali z opazovanjem svetlobe oddaljenih supernov tipa Ia, ki so šibkejše od pričakovanj (izračunov iz Dopplerjevega rdečega premika). Projekt se je imenoval - »The Supernova Cosmology Project«. Gre za okoli 50 supernov, ki so svetile zelo šibko. Zamisel, da se vesolje širi pospešeno, je elegantna rešitev problema svetlosti supernov, a je po drugi strani zelo radikalna ideja. Šele ko sta obe skupini prišli do enakih sklepov, je teorija dobila potrditev v znanstveni srenji.
Sedaj velja dopolnjena
Friedmannova enačba
(smo jo že spoznali) - opis vesolja s kozmološkim
členom (Λc2/3), ki vesolje pospešuje:
H2 = 8πGρ/3 - k c2/R2 + Λ c2/3
Oznaka H je Hubblova (oz. Hubble-Lemaître-ova) konstanta, Λc2/3 izhaja pa iz Einsteinovih
(tudi Hilbertovih) enačb polja. Ocena gostote vakuuma (temne energije,
ki baje pospešeno širi vesolje) za
Λ ≈ 1.1056 10-52 m-2 je:
ρvak = Λc2/(8πG) = 5,9 10-27 kg/m3,
to je 3,5 protonov na m3, to je okrog 70 % (pričakovana
vrednost glede na kritično gostoto 6 protonov na m3,
gostota podana v protonih je zgolj simbolična, zaradi lažje predstave).
Razlika do 6 protonov na m3 (ena izmed ocen kritične gostote)
pa večinoma pripada energiji temne snovi (okrog 25 %), le okrog štirje procenti
pa delcem, ki sestavljajo atome, nas same, vidno vesolje.
Kljub neupoštevanju postulatov splošne teorije relativnost (tenzorskih enačb) - oziroma ohlapni uporabi, je naš rezultat za kritično gostoto vesolja pravilen!!! Hubble-Lemaîtrovo konstanto se danes meri z velikim zagonom, piše se ogromno člankov. Trenutno se pojavljata dve vrednosti (Spika 5, 2021), H = 74,03 km/s/Mpc (preko hitrosti oddaljevanja galaksij z Dopplerjem, kjer se meri razdalje s pomočjo Kefeid in supernov tipa Ia) in iz nehomogenosti mikrovalovnega sevanja ozadja, odtis prapoka, ki zaenkrat da vrednost H = 67,36 km/s/Mpc. Obeta se še tretja pot merjenja Hubble-Lemaîtrove konstante in sicer s pomočjo gravitacijskih valov pri zlitju zvezd. Preko izračunane moči samega zlitja in zaznane moči na Zemlji, se bo določila razdalja do trka in ob hkratnem merjenju spektra elektromagnetnega valovanja (Dopplerja), se bo določila hitrosti oddaljevanja. Meritve razdalj so res velik problem kozmologije, hkrati pa nam vsaka nova metoda razkrije še več resnic o vesolju in nas samih.
Tako smo preleteli potencialne scenarije življenj (dinamik) našega vesolja, ne da bi se preveč trudili z matematiko ..., vse skupaj smo zapakirali zgolj v kritično gostoto in se vprašali, kakšna je dejanska gostota materije, temne energije, temne snovi in to troje (v grobem) odloča o bodočnosti vesolja in tudi življenja. Materija in temna snov nas vlečeta skupaj, temna energija pa nam pospešeno širi vesolje (simbolično poteka »boj med združevalnimi in razdiralnimi silami«, a ne tega boja vzeti zares, je le prispodoba ...). Mikrovalovno sevanje ozadja se zdi, da danes več ne igra pomembne energijske vloge v dinamiki vesolja, a včasih jo je. Seveda pa se v »ostarelem« sevanju skrivajo prstni odtisi začetka vesolja, zato ga tudi toliko pomerjamo, opazujemo – je enciklopedija zgodovine vidnega vesolja ...
Vesolje bi se ob takem scenariju v neskončnosti nehalo širiti – ravno vesolje. Spet se vprašamo, kako bi se gibalo točkasto telo m, ki se s hitrostjo v odmika od centralne mase M, na razdalji R od centra (predpostavimo, da zunanji predeli vesolja pri homogenem vesolju ne vplivajo na našo lokalno dinamiko našega vidnega obzorja R – sile se odštejejo, to je neke vrste »Faradayeva gravitacijska kletka – zgolj znotraj osamljene votline, ki jo obdaja homogena snov«). V tem primeru velja (ravno vesolje), da je vsota kinetične in potencialne energije nič.
mv2/2 - GMm/R = 0 sledi mv2/2 = GMm/R
v2 = 2GM/R
Ali znamo izraziti funkcijo, kako se vesolje (vidno obzorje) širi s časom, iščemo torej R(t), ki g še vidimo iz neke točke vesolja, recimo iz Zemlje - R(t) je torej razdalja do roba obzorja dogodkov. Tokrat bo matematika na naši strani in to zgolj srednješolska. Izrazimo torej hitrost v.
v = (2GM/R)1/2 - ker je radialna hitrost,
v = dR/dt, odvod radija po času, velja
dR/dt = (2GM/R)1/2
∫R1/2 dR = ∫(2GM )1/2 dt
(meje integracije so »skoraj« od 0 do R in od 0 do t)
- po integraciji dobimo
(2/3)R3/2 = (2GM )1/2 t
- ker je hitrost po Hubble-Lemaîtrovem zakonu
v = HR , velja
v2 = 2GM/R ,
oziroma za trenutni polmer Ro velja:
H2 = 2GM/Ro3, to enačbo uporabimo v rešenem integralu
(2/3)R3/2 = (2GM )1/2 t
= (2GMRo3/ Ro3 )1/2 t
= (H2Ro3)1/2 t = H Ro3/2t
=> t = (2/3)R3/2/(HRo3/2)
t = (2/(3H))(R/ Ro)3/2 = to(R/Ro)3/2
=> to = 2/(3H)
Časovna funkcija dimenzije vesolja je torej:
t = to(R/Ro)3/2
- vpeljali smo trenutno starost vesolja to = 2/(3H), ki je kar obratno sorazmerna
s H, sorazmernostni koeficient je 2/3.
Velikost R ravnega vesolja (nam še vidnega vesolja) pa se spreminja sorazmerno s »časom na 2/3«, velja R = Ro(t/to)2/3:
R = Ro(t/to)2/3
Povejmo še, da je v prvem obdobju (ravnega) vesolja
(prvih 47000 let po inflaciji) – ko je prevladovalo
sevanje nad masnimi delci – veljala drugačna odvisnost
za R in sicer: R ∝ t1/2. Pred prevlado materije
nad sevanjem torej velja, da je hitrost sorazmerna korenu iz
R in povedano zapišimo še v matematični obliki
v = dR/dt ∝ R1/2,
zato je dR/R1/2 ∝ dt,
od koder po integriranju sledi
R ∝ t1/2.
Izpeljano spodaj -
o širjenju zgodnjega vesolja.
Velikokrat se zgornja enačba zapiše zgolj preko faktorja širitve (scale factor a(t), vidnost
vidnega horizonta s = a(t)R = a(t)r ).
Oznake so različne, se spreminjajo glede na vir.
Tako velikokrat najdemo zapis:
a = ao(t/to)2/3
Ocenimo še starosti »ravnega« vesolja, za
H = 73.2 ± 0.3 km/s/Mpc (vrednost pred letom 2011)!
Uporabimo izpeljano enačbo. Enota km/s/Mpc =1/(9.78877*1011) let.
t(zdaj) = (2/3)*(1/H(zdaj)) = (2/3)* 13372632796 let = 8.9 milijard let
Ta rezultat velja danes kot neveljaven (zadnje meritve namreč kažejo,
da se bo vesolje »večno« pospešeno širilo), splošna ocena starosti
vesolja je približno kar obratna vrednost Hubble-Lemaîtrove konstante
tH = (1/H),
kar znaša 13.4 milijard let (to je blizu trenutno veljavnim ocenam zaokroženim med
13.7 in dobrih 13.8 milijard let).
V splošnem velja
t_vesolja = F*(1/H).
F je korekcijski faktor starosti vesolja.
Za zaprto vesolje je F enak izračunanemu razmerju 2/3, če pa upoštevamo kozmološko
konstanto, je ta faktor blizu 1 (2013 je bil F=0.956). F se določa numerično. Kot
bomo videli, se ocene za H gibljejo nad 70 km/s/Mpc in pod to vrednost, recimo
misija Planck 2013 (H=67.80 ± 0.77 km/s/Mpc), kar da za starost vesolja:
t_vesolja = F*(1/H) = 13.8 milijard let.
Še ena vzpodbudna primerjava iz meritev in modelov zvezd – trenutni (2013) modeli razvoja zvezd ocenjujejo starost najstarejše znane zvezde na 14.46 ± 0,8 milijarde let (to je zvezda HD 140283 - leži v smeri Tehtnice, pričakovano vsebuje zelo malo težkih elementov).
Bolj sofisticirana od izpeljane enačbe t = (2/(3H))(R/Ro)3/2 je naslednja enačba:
t(z) = (2/3)*(1/(H(zdaj) Ωo1/2(1 + z)3/2))
– bomo izpeljali, v bistvu smo jo že
Rdeči premik »z« (preko Dopplerja) se v splošnem,
tudi za visoke hitrosti, izrazi kot relativistični izraz:
z = Δλ/λ = ((1+v/c)/(1 -v/c))1/2 - 1
v/c = ((z + 1)2 - 1)/((z + 1)2 + 1)
Komentar
Pri velikih hitrostih moramo namreč upoštevati Lorentzov zamik
časa τ = t/γ = t(1 – (v/c)2)1/2.
Sprejemnik elektromagnetnega valovanja zazna valovno dolžino
λr = cτ
(kjer je lasti čas τ = 1/ν).
Za izvor valovanja pri oddaljevanju velja
λs + vt = ct, oziroma
λs = ct(1 – v/c) = cτγ(1 – v/c) =
cτ(1 – v/c)/(1 – (v/c)2)1/2 =
λr(1 – v/c)/(1 – (v/c)2)1/2 =
λr((1-v/c)/(1 +v/c))1/2,
za valovno dolžino
λr,
ki jo sprejme sprejemnik torej upoštevamo izraz:
λr = λs((1+v/c)/(1 -v/c))1/2
Rdeči premik z je torej preko upoštevanja razlike (λr - λs) =
(λs((1+v/c)/(1 -v/c))1/2 - λs)
= λs(((1+v/c)/(1 -v/c))1/2 - 1) kar:
z = Δλ/λ = (λr - λs)/λs = ((1 + v/c)/(1 - v/c))1/2 - 1
Hubblova razdalja poti svetlobe (pogled nazaj v času) se izrazi ( preko že izpeljane povezave v/c = ((z + 1)2 - 1)/((z + 1)2 + 1) ) kot:
d = v/H = (c/H)*((z+1)2-1)/((z+1)2+1),
- a to ni velikost vidnega vesolja, ki se recimo oceni z že izpeljano
enačbo R = Ro(t/to)2/3,
ki pomeni horizont še vidnega vesolja.
Včasih se uporablja tudi zapis z malim r, velja:
r = ro(t/to)2/3 (odvisno od avtorjev zapisov).
IN MED NJIMA (med d in R) JE VELIKA RAZLIKA – ker je eno pot svetlobe v statičnem vesolju, drugo pa širjenje prostora (zaradi inflacije prostora in ker se prostor, vesolje danes še zmeraj širi, je tako pridelana okrog 3x-na razlika v prid R, torej širjenju prostora, vidnemu horizontu - bomo izpeljali).
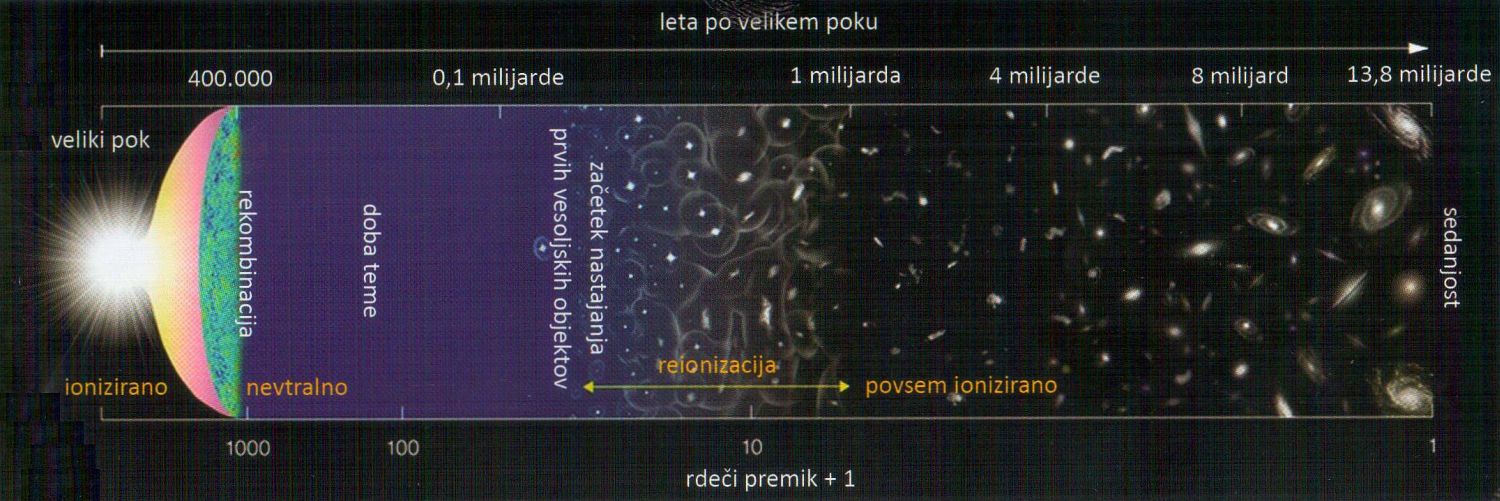
Ko so nastale prve zvezde in galaksije so se v vesolju prižgale luči
(zvezde oddajajo svetlobo) - takrat se je zgodila ponovna ionizacija (reonizacije)
vodika, helija in svetloba se je potem lahko skoraj neovirano širila po vesolju.
Vesolje postane 10 % prosojno za svetlobo 475 milijonov let po velikem poku in
v obdobju 250 milijonov let je vesolje postalo skoraj povsem ionizirano in tako
prozorno za vidno svetlobo.
Iz tega obdobja vidimo tudi prve galaksije (z = 11, JW zazna že z = 12)
- prej je bil prostor za vidno svetlobo neviden (doba teme) -
saj so atomi svetlobi preprečevali neovirano potovanje - komaj nastajajoče zvezde (razlog
je gravitacija, ki združuje vodik in helij in temna snov, ki tvorbo zvezde pospeši)
so ustvarile dovolj velik izsev, energije, da so počasi ionizirale atome.
Po nastanku atomov in pred nastankom zvezd, je prevladovaka infrardeča svetloba,
ki jo je zadrževala atomska megla vodika in helija.
Le mikrovalovno sevanje je vidno takoj po nastanku nevtralnih atomov (380 000 let po velikem poku,
temperatura vesolja je bila takrat 3000 K),
je ušlo v prostor mimo atomov.
Slika tudi prikazuje, kako se je spreminjal rdeči premik (z) skozi čas za trenutne opazovalce - ljudi.
Zadnji tak velik uspeh in hkrati napor je izstrelitev (25. dec. 2021) novega izjemnega vesoljskega
teleskopa James Webb v Lagrangevo točko L2 (6,5 m premera - sestavljen je iz 18 zrcal, šesterokotnikov
velikosti 1,32 metra, v raketo so zrcala zložili na principu origamija). Za razliko od Hubbla,
ki vesolje opazuje v bližnjem ultravijoličnem, vidnem in bližnje infrardečem delu
(0,1–1,0 μm)
spektra, pa JWST opazuje v območju s krajšimi valovnimi dolžinami, od dolgovalovne
vidne svetlobe (rdeče) do srednje infrardečega sevanja (0,6–28,3 μm) - to je svetloba
v obdobju teme vesolja (čas med 380 000 let do okrog 400 milijonov let po velikem poku,
ko temperatura pade iz 3000 K na okrog 60 K, od valovnih dolžin sevanja 970 nm do okrog 50 μm).
Tako lahko zazna objekte z visokim Dopplerjevim rdečim premikom z ≈ 20, ki
so za Hubbla prestari, prešibki, oz. preveč oddaljeni. Relativni Dopplerjev
premik (z = Δλ/λ ) valovnih dolžin svetlobe zaradi premikanja s hitrostjo
v, je v splošnem 1 + z = ( (1 + v/c)/(1 - v/c) )1/2,
c je hitrost svetlobe. Hubble teoretično vidi Dopplerjev premik
z ≈ 11,1, to je približno
400 milijonov let po velikem poku, J. Webb teleskop pa vidi v same zgodnje začetke vesolja,
zagotovo več kot 13,5 milijarde let nazaj, teoretično celo približno 180 milijonov
let po velikem poku, za z ≈ 20. Torej teoretično je z = 20
dovolj, da vidimo prve galaksije (≈ 270 milijonov let) in zgodnje zvezde
(≈ 100 do 180 milijonov let
po velikem poku)
Prvi Webbovi posnetki so glede ločljivosti in števila zaznanih šibkih objektov,
zvezdic, naravnost fascinantni (kot da bi človeštvu operirali sivo mreno – toliko
več šibkih objektov razločno zaznamo). Skratka – ne bo nam dolgčas.
Vir slike: Spika 9/2016 - stran 357.
VAJA ZA OGREVANJE (razlika med d in R, pozneje bomo uporabili tudi oznako s)
Če recimo privzamemo vrednost za 1/H = 13.4 milijard let (od prej) in poračunamo razdaljo d preko
Hubble-Lemaîtrovega zakona
d = v/H = (c/H)*((z+1)2-1)/((z+1)2+1)
za zelo oddaljeno galaksijo
GN-z11, ki ima (leta 2022) največji redeči premik z = 11.09, dobimo za razdaljo d vrednost:
d = v/H = (c/H)*((z+1)2-1)/((z+1)2+1) =
c*13.4 109 let*((11.09+1)2-1)/((11.09+1)2+1) = 12.377 109 sv. let.
To je blizu roba vesolja, a to ni vidni horizont R oz. s.
Kot bomo izračunali, je današnji vidni horizont (od koder še dobivamo svetlobo) že zelo daleč - približno
R = Ro(t/to)2/3 = 46,6 109 sv. let.
To je približno 3ctstarost_vesolja - bomo izpeljali.
Kozmična razdalja Rd galaksije
GN-z11 pa je že okrog Rd = 32 109 sv. let in ne 12.377 109 sv. let.
Premislek in izračuni sledijo.
Drugo enačbo
(R = Ro(t/to)2/3.)
utemeljuje tudi enormno povečanje valovne dolžine
mikrovalovnega ozadja od starosti 380 000 let
(ko se tvorijo atomi) do danes (13,8 109 let).
Veljajo torej naslednje izjemno poučne povezave:
1 + z = λdanes/λoddana
= Rdanes/Rzačetni = Tzačetna/Tdanes
= 3000 K/2,72548 K ≈ 1100.
Prasevanje ali mikrovalovno sevanje ozadja, se da vsaj približno ponazoriti z analogijo zvoka. Zelo popularen je primer koncerta, ko recimo velikanska množica na velikem travniku (recimo Woodstock) konča s ploskanjem po nekem dobrem »štiklcu« - kaj se zgodi z zvokom? V določenem območju poslušalci nehajo ploskati, a še slišijo oddaljeno ploskanje? Zakaj? Kljub temu, da so tudi na drugem (x) koncu travnika nehali ploskati, se to ploskanje (hitrost zvoka je približno 330m/s) z zakasnitvijo t = x/330m/s širi do x metrov oddaljene skupine poslušalcev (velja tudi obratno). Seveda s časom, oddaljenostjo, jakost zvoka pada, enako je s prasevanjem. A vsaka analogija ima svoje meje – je zgolj pomoč za lažjo predstavo!
Ali znamo kaj konkretnejšega povedati o termiki vesolja, kako se temperatura vesolja spreminja s časom?
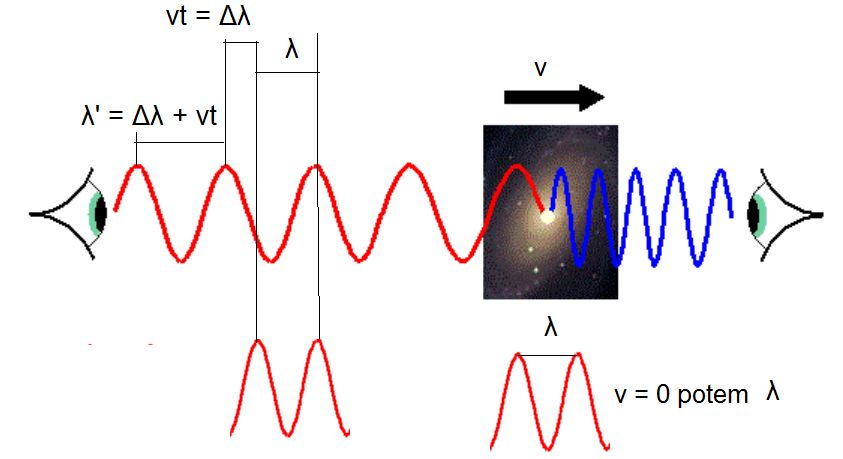
Še prej pa Hubble-Lemaîtrov zakon ( V = HR ) preoblikujemo, oziroma zapišemo rdeči premik
(z = v/c = Δλ/λ,
povezava izhaja iz Dopplerjevega pojava, za majhne hitrosti)
spektralnih črt s Hubble-Lemaîtrovim / Hubblovim zakonom (delimo ga s hitrostjo svetlobe in kaj dobimo?):
z = v/c = Δλ/λ = HR/C
Poglejmo še povezavo med valovno dolžino
λ' = Δλ + λ,
ki se zaradi širjenja vesolja daljša
(mikrovalovno sevanje ozadja) in t. i. polmerom vesolja
R – količini sta sorazmerni. Iz zveze Δλ/λ = HR/C sledi,
da je Δλ, oz. da je valovna dolžina kar sorazmerna z dimenzijo vesolja R:
λ' ∝ R.
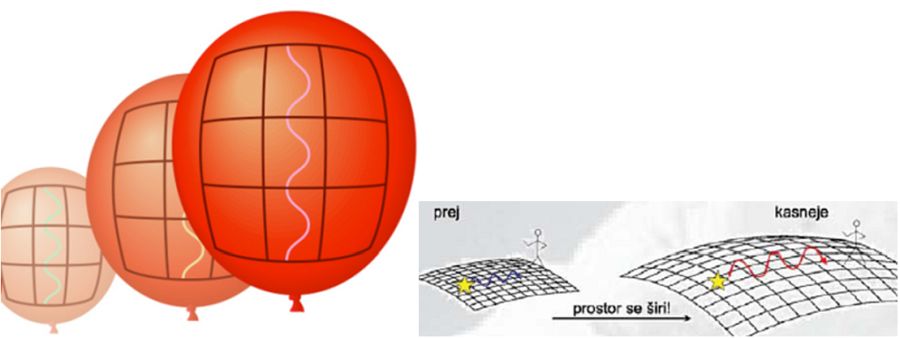
Rdeči premik (Dopplerjev pojav) lahko razumemo tudi kot širjenje prostora.
Svetloba z oddaljene galaksije potrebuje veliko časa, da doseže opazovalca.
Med tem potovanjem se je vesolje širilo – in skupaj z njim se je valovna
dolžina raztegnila – premaknila proti rdeči. Lahko si pomagamo s prispodobo
napihajočega balona s poslikanim vzorcem valovanja. Spet velja
λ' ∝ R.
|
Recimo, da je na desni krogla iz N fotonov z energijo
(Nhν),
ki se širi – t. i.
prasevanje (kozmično ozadje). Kako se s časom spreminja temperatura takega vesolja?
Najprej nakažimo razlago, zakaj velja za gostoto energije fotonov (w), v razširjajočem vesolju, izraz: w ∝ 1/R4 in za gostoto energijskega toka fotonov j: j = cw. |

|
w ∝ 1/R4
In še beseda o gostoti energijskega toka fotonov j = (E/t)/S, S je površina skozi katero potujejo fotoni (glej sliko):
j = E/(tS) = Ec/(ctS) = Ec/(xS) = Ec/V = cw
Če uporabimo Stefanov zakon (j = σ*T4, gostota energijskega toka elektromagnetnega valovanja črnega telesa 'j' je sorazmerna s Stefanovo konstanto σ in absolutno temperaturo T na četrto potenco), in če privzamemo enačbo širjenja vesolja iz prejšnjega poglavja (R = R0(t/t0)2/3) s kritično gostoto, in če privzamemo (smo tudi izpeljali), da gostota sevanja w pada z 1/R4, in da je gostota energijskega toka enaka j=cw, potem velja:
j = wc ∝ 1/R4 ∝ T4 => T = RoTo/R => T=To(to/t)2/3
Torej iz Stefanovega zakona izhaja znamenita enačba za časovno odvisnost temperature vesolja:
T=To(to/t)2/3
Naredimo vajo, kako daleč nazaj v času bi recimo lahko opazovali nevtralni vodik, ki oddaja 21 cm valovno dolžino.
V temni srednji vek zgodnjega vesolja - zakaj?
Nevtralni atomi nastanejo po okrog 380 000 letih od rojstva vesolja,
ko temperatura pada na okrog 3000 K. A vesolje je še zmeraj precej temno.
Ko temperatura pade na okrog 300 K, je rdeči premik okrog z = 100, saj velja:
z = Tzačetna/Tdanes
= 300 K/2,72548 K ≈ 100.
Takrat je nevtralni vodik že seval
značilno emisijsko črto λoddana_H = 21 cm (sprememba spina elektrona).
Koliko pa je do danes narasla valovna dolžina zaradi širjenja vesolja, velja enostavna povezava:
1 + z = λdanes_H/λoddana_H = Tdanes/T .
Iz
zadnje enačbe sledi ocena λdanes_H ≈ 100*21 cm ≈ 20 m.
To so pa valovne dolžine, ki bi jih recimo ŠE lahko beležili
z velikimi radijskimi teleskopi. A kje?
Teh valovnih dolžin ne moremo sprejemati na Zemlji, ker jih ionosfera absorbira.
A na delu Lune, ki je obrnjen vstran od Zemlje (tam ni motenj
iz Zemlje, ta del Lune tudi kar pol meseca kaže vstran od Sonca in je potem na
senčnem delu Luni zelo hladno - kar je tudi ugodno za same senzorje, da so ohlajeni, manj šuma).
Vemo tudi, da Luna praktično nima atmosfere - Sončev veter je praktično vse pline odpihnil.
Tako bi lahko gledali vesolje v starosti rdečega premika z = 100,
ko je bilo staro okrog 12 milijonov let. Zadnji izračun je iz izpeljane povezave:
T=To(to/t)2/3,
oziroma starost
t = to(To/T)3/2 = to(To/( Tdanes(z +1)) )3/2
= 380000*POWER((3000/300);3/2) let ≈ 12000000 let
ali temperatura (testni račun)
T = 2.725 *POWER((13.8*1000000000*365*24*3600/(12*1000000*365.25*24*3600));2/3) K ≈ 300 K.
Tako bi (bomo) opazovali temni srednji vek zgodnjega vesolja - nizkofrekvenčna radijska astronomija.
Lahko bi torej preučevali strukturo zgodnjega vesolja.
Številke se razlikujejo glede na privzeti model - a ne bistveno.
Ali pridemo do enačbe
t(z) = (2/3)*(1/(H(zdaj) Ωo1/2(1 + z)3/2))
iz naše preproste izpeljave o širjenju vidnega
vesolja
dR/dt = (2GM/R)1/2,
ko je Ωo = ρ/ρc = 1 in še M = ρV
= ΩoρcV = McΩo.
Po izračunu
dR/dt = (2GMcΩo/R)1/2 smo dobili izraz.
(2/3)R3/2 = (2GMcΩo)1/2 t
= (2GMcΩoRo3/ Ro3)1/2 t
= (H2Ro3Ωo)1/2 t
= HΩo1/2Ro3/2t
t = (2/(3HΩo1/2))(R/Ro)3/2
Že prej smo pokazali povezavo med rdečim premikom in valovno
dolžino 1 + z = λdanes/λoddana ≈ 1100 in
še λdanes/λoddana ≈ Ro/R = 1 + z.
Torej je R/Ro = 1/(1 + z) in sledi končni rezultat:
t(z) = (2/(3HΩo1/2))(1/(1 + z)3/2)
– (starost vesolja glede na rdeči premik z) ne velja za mlado vesolje
Pogled nazaj v času tLB (lookback time - kako daleč nazaj vidimo) je:
tLB = to –t(z) = 2/(3HΩo1/2)
- (2/(3HΩo1/2))(1/(1 + z)3/2)
= (2/(3HΩo1/2))(1 - 1/(1 + z)3/2)
Primer, ko recimo opazujemo galaksijo z rdečim premikom z, to pomeni, da jo vidimo tako, kot je bila v preteklosti, ko je svetloba šele začela svojo pot proti nam. Lookback time nam pove, koliko let nazaj v času gledamo, ko opazujemo objekt z določenim z. Ne gre za razdaljo danes, ampak časovni zamik.
Upoštevajmo še kozmološko konstanto Λ.
Če pa računamo še s temno snovjo in kozmološko konstanto Λ potem je Lookback time
funkcija nekoliko bolj zapletena. Zapišimo najprej splošno enačbo.
Kot smo že omenili, je
faktor umeritve a (scale factor) a = R/Ro (a se s časom spreminja,
Ro je trenutni vidni horizont vesolja),
potem dobimo še eno obliko zapisa Hubblove (Hubble–Lemaîtrove) konstante:
H = (da/dt)/a
Ker velja danes a(to) = 1 in ker velja povezava 1 + z = λdanes/λoddana,
je ta odvisnost
direktno povezana s širitvijo vesolja, ki se odraža v podaljšanju valovne dolžine
zaradi same širitve. Tako lahko zapišemo
1 + z = λdanes/λoddana = a(to)/a(t) = 1/a(t)
To nas vodi do pomembne enačbe, ki povezuje rdeči premik in širitev vesolja (z in a):
1 + z = 1/a
- po odvajanju po času dobimo izraz:
dz = -(da/dt)/a2 = -(1 + z)H(z)dt.
Kar preoblikujemo v obliko (upoštevamo, da je 1 + z = 1/a in H = (da/dt)/a):
dt = - dz/((1 + z)H(z))
Zapišemo še pogled nazaj v času tLB (lookback time - kako daleč nazaj vidimo), tako dobimo:
tLB(z) = to - t(z) = t(z)to∫dt
Končni integral s spremenljivko z' ima tako splošno obliko spodaj in se večinoma rešuje numerično:
tLB(z) = oz∫ dz'/ ( (1 + z')H(z') )
Še enkrat zapišimo Friedmannovo enačbo in iz nje izpeljimo splošno obliko za Hubble–Lemaître-ovo konstanto:
H2 = (da/dt)2/a2 = 8πGρm/3 - Kc2/a2
Dopolnjena pa se nanaša na pospešeno širjenje vesolja in zato vsebuje kozmološki člen Λ :
H2 = 8πGρm/3 - k c2/a2 + Λ c2/3,
To dopolnjeno Friedmannovo enačbo še nekoliko preoblikujmo, poenostavimo.
Upoštevajmo, da je gostota vesolja odvisna od volumna, torej kvocienta 1/R3 ∝ 1/a3
in ker velja a = 1/(1 + z), lahko gostoto zapišemo
kot
ρm = ρmo(1 + z)3
.
Potem zapišimo še kritično gostoto vesolja preko že izpeljane povezave
Ho2 = 8πGρkrit/3,
kjer je
Ho = 70 km/s/Mpc ≈ 2.27×10-18s-1.
Vse relativne relativne gostote Ωi = ρi/ρkrit
pa se torej zapišejo kot razmerja s kritično gostoto (mislimo na gostoto barionske in temne
snovi, gostoto temne energije, gostoto sevanja in ukrivljenosti).
V zgornji enačbi je oznaka k parameter ukrivljenosti vesolja (±1, 0) in tako lahko vpeljemo še
gostoto ukrivljenosti ρk preko povezave
-kc2/a2 = Ho2Ωk(1+z)2,
kjer je
Ωk = -kc2/(a2Ho2(1+z)2)
= -kc2/Ho2
= ρk/ρkrit.
Ker velja
Ho2 = 8πGρkrit/3
in
H2 = 8πGρm/3 - k c2/a2 + Λ c2/3,
od koder sledijo naslednje oblike Friedmannove enačbe, upoštevamo še
da je ρm = ρmo(1 + z)3 in še 1/a = (1 + z):
H2 = 8πGρm/3 - k c2/a2 + Λ c2/3
= Ho2( 8πGρm/(3Ho2) - k c2/(a2 Ho2) + Λ c2/(3 Ho2) )
= Ho2( (1 + z)3ρmo/ρkrit
+ (1 +z)2ρk/ρkrit + ρΛ/ρkrit )
Ker je 1/a = (1 + z), dobimo
s primerjavo zgornjih oblik enačbe naslednje člene,
za
ΩΛ = ρΛ/ρkrit
= Λc2/(3Ho2) = Λc2/(8πGρkrit)
in
ρΛ = Λc2/(8πG) - gostote vakuuma ali temne energije,
za Ωk = ρk/ρkrit = -kc2/(aoHo2) = -kc2/Ho2, ker je ao privzet za ao = 1.
Kot smo že omenili,
vse relativne gostote Ωi se zapišejo kot razmerja s kritično gostoto,
zapišimo jih:
Ωm = ρmo/ρkrit - relativna gostota snovi danes (normalna + temna snov)
ΩΛ = ρΛ/ρkrit -
relativna gostota temne energije (kozmološka konstanta), ki je neodvisna od rdečega premika,
Ωk = ρk/ρkrit - predstavlja prispevek ukrivljenosti,
če je parameter ukrivljenosti k = 0, potem je vesolje ravno (plosko), tako se zdi danes.
Ωr = ρr/ρkrit - gostota radiacije, sevanja (fotoni, nevtrini)
- trenutno zelo skromen prispevek
Kako se išče gostotni parameter Ωk, ki opisuje ukrivljenost vesolja?
Sestavljena je kot razlika med 1 (kritično gostoto) in vsoto vseh drugih gostotnih parametrov.
Torej kar z raliko do 1.
Ωk = 1 - Ωm - ΩΛ - Ωr
Gostota energije sevanja (npr. fotonov) pada s širjenjem vesolja hitreje kot gostota snovi, in sicer kot:
ρr(z) = ρro(1+z)4
Zakaj (1+z)4?
Zgoščevanje (razredčenje): kot pri snovi, se volumen širi s faktorjem a3, kjer je
a = 1/(1 + z). To pomeni, da se gostota energije zaradi širitve prostora zmanjša kot:
∝ 1/a3 = (1+z)3
Rdeči premik fotonov (redshift energije):
energija posameznega fotona se zaradi širjenja vesolja zmanjša zaradi rdečega premika.
Energija fotona E ∝ ν ∝ 1/a, torej z vsakim povečanjem a
(zmanjšanjem z) foton izgubi energijo.
To pomeni dodatno zmanjšanje gostote energije kot:
∝ 1/a = (1+z)
Skupaj:
ρr(z) ∝ 1/a3×1/a = 1/1/a4 = (1+z)4
Razlog za potenco 4 pri gostoti sevanja Ωr(1+z)4 leži v dejstvu, da sevanje s širjenjem vesolja pada s (prostornino)×(energija fotona, ki pade).
Tako se celotna Friedmannova enačba z vsemi gostotami in preko Hubble–Lemaîtrove konstante zapiše kot:
H2 = (da/dt)2/a2 =
Ho2[ Ωr(1+z)4 - Ωm(1+z)3
+ Ωk(1+z)2 + ΩΛ ]
Za ravno vesolje (ukrivljenost je k = 0, to pomeni, da je Ωk = 0, uporabimo Friedmannovo enačbo, kjer zanemarimo tudi sevanje Ωr ≈ 0) tako za lookback time (pogled nazaj v zgodovino) tLB(z) = oz∫ dz'/ ( (1 + z')H(z') ) in za H2 = Ho2[ Ωm(1+z)3 + ΩΛ ] velja naslednji izraz:
tLB(z) = (1 / H0) · oz∫ dz'/[ (1 + z') · (Ωm(1 + z')3 + ΩΛ)1/2 ]
Zgornji integral časa pogleda za nazaj tLB(z) lahko testirate v JavaScript aplikaciji - num_integral_lbtim8.html (Simpsonova metoda)
Primeri za realne vrednosti
(ΛCDM, ravno vesolje, velja Ωm + ΩΛ = 1):
Z realnimi parametri (Planck 2018):
* Ωm ≈ 0.315
* ΩΛ ≈ 0.685
* Ho ≈ 67.4 km/s/Mpc
V standardni kozmologiji velja:
Ωm = celotna gostota materije v vesolju (vidna + temna).
Ωm = Ωb + Ωcdm
Kdaj poimenujejo
ΩΛ kar
Omegavac - gostota vakuuma.
Kjer sta:
Ωb = gostota barionske snovi (običajna snov: atomi, zvezde, plin …),
Ωcdm = gostota hladne temne snovi (cold dark matter)
Tipične vrednosti (Planck 2018):
Parameter / približna vrednost
Ωb ~0.049
Ωcdm ~0.266
Ωm = Ωb + Ωcdm ~0.315
ΩΛ ~0.685
To pomeni, da:
~5 % vesolja sestavlja barionska snov,
~27 % temna snov,
~68 % temna energija.
Numerični izračun lookback time za ravno vesolje
(Ωm + ΩΛ = 0.315 + 0.685 = 1):
z / Lookback time (Gyr ali milijarde let)
0.5 / ~5.0
1.0 / ~7.8
2.0 / ~10.3
3.0 / ~11.5
5.0 / ~12.6
10.0 / ~13.2
Opomba: starost vesolja je približno 13.8 milijard let, zato t_LB ne more biti večji od tega.
Za izračune lahko
uporabite kozmološki kalkulator (JavaScript), vstavite rdeči premik 'z' in izberite ravno ali odprto vesolje,
spreminjate lahko tudi gostoto:
https://www.astro.ucla.edu/%7Ewright/CosmoCalc.html
(ali kalkulator lokalno).
Poičimo enačbo ohranitve energije (ali kontinuitetno enačbo) v kozmologiji.
Pove nam, kako se energijska gostota
ρ v vesolju spreminja s časom zaradi širjenja.
Izhaja iz prvega zakona termodinamike in splošne teorije relativnosti.
V razširjajočem se vesolju velja prvi zakon termodinamike:
dE = -PdV
E = ρc2V - je energija (snovi) vesolja,
P - je tlak
V ∝ a3 - je prostornina vesolja (a je faktor širjenja).
Izračunajmo odvod:
d(ρc2V)/dt = - PdV/dt
Ker
V ∝ a3, potem:
dV/dt = 3a2da/dt = 3V(da/dt)/a = 3HV
Zapišimo zdaj celotno enačbo:
d(ρc2V)/dt = Vc2dρ/dt + c2dρdV/dt = - PdV/dt
Vstavimo dV/dt = 3HV:
Vc2dρ/dt + c2dρ3HV = - P3HV
Deli obe strani z
V in
c2, tako dobimo enačbo ohranitve energije (ali kontinuitetno enačbo) v kozmologiji:
dρ/dt + 3H(ρ + P/c2) = 0
Pove nam, kako se gostota
ρ v vesolju spreminja s časom zaradi širjenja.
Tlak vpliva na hitrost tega padanja.
Snov prah, nima posebne komponete tlaka (P = 0, ρ ∝ 1/a3),
sevanje ima komponento tlaka P = ρc2/3 in ρ ∝ 1/a4 (potenco 4 že izpeljali,
je posledica širjenja vesolja)
in za temno energijo (w = -1) velja P = -ρc2 in ρ je konstanten.
V splošni teoriji relativnosti (GR)
je zakon ohranitve energije zapisan kot:
∇μTμν = 0
Za homogeno in izotropno vesolje (FLRW-metrika) in idealen tekočinski stresno-energijski tenzor
Tμν, ta enačba vodi ravno do enakega izraza:
dρ/dt + 3H(ρ + P/c2) = 0
Kako energijska gostota
(ρc2) v vesolju pada, ko se vesolje širi?
Poglejmo, zakaj velja naslednja povezava:
ρ(a) ∝ a-3(1+w)
za poljubno enačbo stanja P = wρc2
kjer je
w konstanta (lahko je 0 za snov,
1/3
za sevanje,
-1 za temno energijo itd.).
Najprej vstavimo tlak P = wρc2 v
kontinuitetno enačbo za kozmologijo:
dρ/dt + 3H(ρ + P/c2) = 0
Tako dobimo:
dρ/dt + 3H(ρ + wρc2/c2) = 0
dρ/dt + 3Hρ(1 + w) = 0
Ker je Hubble–Lemaîtrova konstanta H = (da/dt)/a, dobimo,
dρ/dt + 3ρ(1 + w)(da/dt)/a = 0
Ker velja dρ/dt = (dρ/da)(da/dt), zgornjo enačbo poenostavimo.
(dρ/da)(da/dt) + 3ρ(1 + w)(da/dt)/a = 0
Obe strani delimo z da/dt in dobimo:
dρ/da + 3ρ(1 + w)/a = 0
Integriramo obe strani:
∫dρ/ρ = -∫3(1 + w)da/a
Rešitev je:
ln ρ = - 3(1 + w)ln a + C
ρ(a) = C'a-3(1 + w)
- ker a = 1/(1+z), velja:
ρ(z) ∝ (1 + z)3(1 + w)
Tako se celotna Friedmannova enačba z vsemi gostotami za k = 0 (ravno vesolje)
in preko Hubble–Lemaîtrove konstante zapiše kot:
H2 = (da/dt)2/a2 =
Ho2[ Ωm(1+z)3
+ ΩΛ(1+z)3(1 + w) ]
Če temna energija nima konstantne enačbe stanja w ampak je odvisna od faktorja a, potem za gostoto velja :
ρ(a) = ρΛo e-3∫(1 + w(a))da/a
Za rešitev je treba w(a) parametrizirati, na primer w(a) = wo + wa(1-a).
Po integraciji dobiš:
ρ(a) ∝ a-3(1 + wo + wa) × e-3 wa(1 - a)
Tako se celotna Friedmannova enačba z vsemi gostotami večinoma zapiše brez rdečega premika z, uporabi se raje
a - to je faktor širjenja:
H(z)2 = (da/dt)2/a2 =
Ho2[ Ωm(a-3
+ ΩΛa-3(1 + wo + wa) × e-3 wa(1 - a) ]
Računske vaje z razlago:
Po času t = 380 000 let po velikem poku, se je snov začela razvijati
neodvisno od sevanja – (pra)sevanje se ni več sipalo na plazmi,
nastanejo atomi (vesolje je postalo prozorno) – temperatura je padla na
T = 3000 K, plazma preide v plin (jedra iz nukleonov ujamejo elektrone
in postanejo nevtralnimi atomi, energija sevanja pa je premajhna,
da bi jih ionizirala), o dinamiki med delci več ne odločajo električne
sile, ampak začne svojo pot oblikovanja vesolja gravitacija, ki tako
dokončno prevlada. Še pojasnitev – za ionizacijo vodika (da izbijemo
elektron vstran od protona), rabimo 13,6 eV energije - izraženo v temperaturi
je to
T = E/kB = 13,6 eV/8,61733 10-5 eV/K ≈ 1.6 106 K
– a pri temperaturi 3000 K energija trkov in fotonov pade pod 0,3 eV, kar
je meja za stabilnost atomov (elektronski oblak je varno združen z jedrom
atoma – fotoni prasevanja pa sedaj lahko potujejo po svoje, lahko se sipajo,
a atomov več ne ionizirajo). Iz enačbe za temperaturo vesolja v odvisnosti
od časa
( T=To(to/t)2/3 ),
izračunajmo trenutno temperaturo
vesolja (mikrovalovnega sevanja ozadja ali tudi prasevanja).
Za čas to torej privzemimo starost vesolja to = 13.8 milijard let,
za temperaturo T pa 3000 K, za čas t = 380 000 let
(takrat je temperatura vesolja padla na 3000 K in nastopi doba atomov). Velja:
T=To(to/t)2/3
PRVI POMEMBEN IN PRIČAKOVAN REZULTAT ZA DANAŠNJO TEMPERATURO VESOLJE (To) JE TOREJ:
Iz te enačbe dobimo za trenutno temperaturo vesolja To =
T(t/to)2/3
= 2,7 K, kar se kar ujema z meritvami.
Za: t = 380 000 let, to = 13,8*109 let, T = 3000 K.
Če pa se vprašamo zgolj po oceni, kolikšna je bila temperatura
T mladega vesolja komaj t = 100 sekund po velikem poku, ko
se je že tvoril helij v razmerju z vodikom
H/He = 75 %/25 %
(prva kratka fuzija),
pa nam zgornja približna enačba
vrne kar pravilen velikostni red (1010 K).
Enačba T=To(to/t)2/3 – pa
zagotovo več ne velja za vesolje mlajše od sekunde,
tudi za ocene ne.
DRUGI POMEMBEN IN PRIČAKOVAN REZULTAT ZA TEMPERATURO VESOLJA PRI STAROSTI 100 s PA JE:
T =To(to/t)2/3 = 2,725 K*(13,8*109*365*24*3600/100)2/3 = 72636844432 K = 7 1010 K
TRETJI POMEMBEN IN (NEKOLIKO) NEPRIČAKOVAN REZULTAT PA JE GLEDE STAROSTI IN VELIKOSTI VESOLJA:
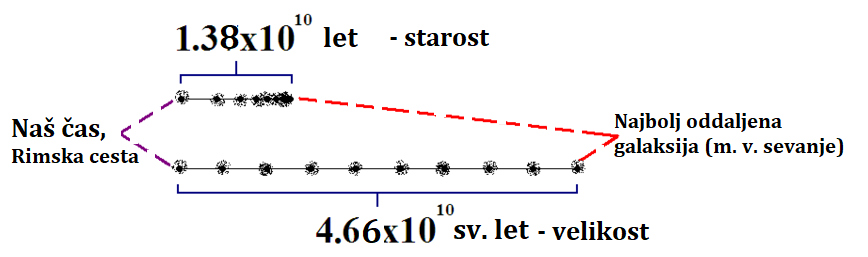
Slika, ki pojasnjuje razliko v podatkih o starosti vesolja
(1,38 × 1010 let)
v primerjavi z oceno dejanskega polmera za nas vidnega vesolja
(4,66 × 1010 svetlobnih let),
glede na mikrovalovno sevanje ozadja, ki nam pove,
kako se prostor širi (zato tudi taka razlika med
starostjo in velikostjo v sv. letih – zdi se protislovno,
a gre za samo širjenje prostora).
V najbolj oddaljenih
galaksijah (teleskop Hubble – ki zaznava globoko preteklost)
so opazili večjo gostoto snovi na kubični centimeter vesolja.
Lahko bi dejali, da Hubble slika »starost vesolja«, ki je po ocenah
glede širitve vesolja, veliko večje kot zmnožek starosti in svetlobne
hitrosti.

Ko so nastale prve zvezde in galaksije so se v vesolju prižgale luči
(zvezde oddajajo svetlobo) - takrat se je zgodila ponovna ionizacija (reonizacije)
vodika, helija in svetloba se je potem lahko skoraj neovirano širila po vesolju.
Vesolje postane 10 % prosojno za svetlobo 475 milijonov let po velikem poku in
v obdobju 250 milijonov let je vesolje postalo skoraj povsem ionizirano in tako
prozorno za vidno svetlobo.
Iz tega obdobja vidimo tudi prve galaksije (z = 11, JW zazna že z = 12)
- prej je bil prostor za vidno svetlobo neviden (doba teme) -
saj so atomi svetlobi preprečevali neovirano potovanje - komaj nastajajoče zvezde (razlog
je gravitacija, ki združuje vodik in helij in temna snov, ki tvorbo zvezde pospeši)
so ustvarile dovolj velik izsev, energije, da so počasi ionizirale atome.
Po nastanku atomov in pred nastankom zvezd, je prevladovaka infrardeča svetloba,
ki jo je zadrževala atomska megla vodika in helija.
Le mikrovalovno sevanje je vidno takoj po nastanku nevtralnih atomov (380 000 let po velikem poku,
temperatura vesolja je bila takrat 3000 K),
je ušlo v prostor mimo atomov.
Slika tudi prikazuje, kako se je spreminjal rdeči premik (z) skozi čas za trenutne opazovalce - ljudi.
Zadnji tak velik uspeh in hkrati napor je izstrelitev (25. dec. 2021) novega izjemnega vesoljskega
teleskopa James Webb v Lagrangevo točko L2 (6,5 m premera - sestavljen je iz 18 zrcal, šesterokotnikov
velikosti 1,32 metra, v raketo so zrcala zložili na principu origamija). Za razliko od Hubbla,
ki vesolje opazuje v bližnjem ultravijoličnem, vidnem in bližnje infrardečem delu
(0,1–1,0 μm)
spektra, pa JWST opazuje v območju s krajšimi valovnimi dolžinami, od dolgovalovne
vidne svetlobe (rdeče) do srednje infrardečega sevanja (0,6–28,3 μm) - to je svetloba
v obdobju teme vesolja (čas med 380 000 let do okrog 400 milijonov let po velikem poku,
ko temperatura pade iz 3000 K na okrog 60 K, od valovnih dolžin sevanja 970 nm do okrog 50 μm).
Tako lahko zazna objekte z visokim Dopplerjevim rdečim premikom z ≈ 20, ki
so za Hubbla prestari, prešibki, oz. preveč oddaljeni. Relativni Dopplerjev
premik (z = Δλ/λ ) valovnih dolžin svetlobe zaradi premikanja s hitrostjo
v, je v splošnem 1 + z = ( (1 + v/c)/(1 - v/c) )1/2,
c je hitrost svetlobe. Hubble teoretično vidi Dopplerjev premik
z ≈ 11,1, to je približno
400 milijonov let po velikem poku, J. Webb teleskop pa vidi v same zgodnje začetke vesolja,
zagotovo več kot 13,5 milijarde let nazaj, teoretično celo približno 180 milijonov
let po velikem poku, za z ≈ 20. Torej teoretično je z = 20
dovolj, da vidimo prve galaksije (≈ 270 milijonov let) in zgodnje zvezde
(≈ 100 do 180 milijonov let
po velikem poku)
Prvi Webbovi posnetki so glede ločljivosti in števila zaznanih šibkih objektov,
zvezdic, naravnost fascinantni (kot da bi človeštvu operirali sivo mreno – toliko
več šibkih objektov razločno zaznamo). Skratka – ne bo nam dolgčas.
Vir slike: Spika 9/2016 - stran 357.
Graf razdalje (v giga – ali milijardah - svetlobnih letih) v primerjavi
z rdečim premikom po modelu Lambda-CDM. dH (v črni barvi – v grobem velja
naša izpeljava dH = R = Ro(t/to)2/3,
kjer Ro in to veljata za
starost vesolja 380 000 let, ocena za takratni polmer vesolja
Ro ≈ 42,7 milijonov sv. let)
je razdalja premikanja vidnega vesolja od
Zemlje do lokacije s Hubblovim rdečim premikom z, medtem ko je ctLB
(LB pomeni »lookback«, graf v pikčasto rdeči barvi) hitrost svetlobe,
pomnožena s časom pogleda nazaj (lookback) na Hubblov rdeči premik z.
Razdalja je podoba vesolja med zdaj in oddaljeno lokacijo, ki trenutno
limitira velikost opazljivega vesolja na približno dH = 47 milijard svetlobnih
letih (od tam še dobivamo informacije o mladem vesolju, a nikakor ne današnjega
stanja snovi na tej razdalji). Čas nazaj (lookback) pa je razdalja
(ki jo je prepotoval foton od trenutka, ko je bil oddan) deljena
s svetlobno hitrostjo, pri čemer največja časovna "razdalja"
13,8 milijard
svetlobnih let ustreza starosti vesolja.
Zakaj ta razlika (?) - ker se je na začetku prostor preko inflacije razširil hitreje od svetlobe
in ker se še danes zmeraj širi in to pospešeno.
Velja pa, za recimo starost 380 000 let in ta trenutek vesolja,
že izpeljana izjemno pomembna povezava:
1 + z = λdanes/λoddana
= Rdanes/Rzačetni = Tzačetna/Tdanes
= 3000 K/2,72548 K ≈ 1100.
Zgolj ocene za ta dva grafa
(ctLB = ct in dH = Ro(t/to)2/3)
dobimo, če za čas vstavimo že izpeljano enačbo v odvisnosti od rdečega
premika (velja le za vesolje po starosti 380 000 let, ko sevanje ni več dominantno):
t = (2/(3HΩo1/2))(1 - 1/(1 + z)2/3)
Še o širjenju zgodnjega vesolja, ko je prevladovalo zgolj sevanje.
V prvih 47000 letih po inflaciji je prevladovalo sevanje - to je ocena (do takrat se ne tvorijo
nevtralni atomi, imamo samo ione in ločene elektrone - plazmo).
Kot smo že povedali, o bodočnosti vesolja odloča gostota!
Za konstantno (bolje ravno vesolje) vesolje smo pokazali, da velja:
H2 – 8πGρ/3 = 0
in mejna (kritična) gostota je kar:
ρc = 3H2/(8πG),
Izraz za Hubble-Lemaîtrovo konstanto lahko zapišemo tudi kot:
H = (dR/dt)/R
Od koder sledi enačba za zgodnje vesolje, kjer je gostota zgolj sevalna (ρrad):
((dR/dt)/R)2 - 8πGρrad/3 = 0
OPOMBA
R naj bo umeritveni faktor (scale factor) brez dimenzije, ker ne poznamo dejanskih dimenzij širjenja vesolja
in naj danes znaša R = 1 pri temperaturi vesolja To = 2,7 K.
Včasih R (scale factor) označijo tudi z a ...
Notranja energija U fotonskega plina (po Stefanu) je odvisna od volumna V in temperature T:
E = U = aVT4
Kjer a je: a = 4σ/c
Za gostoto energije torej velja:
w = E/V = aT4
Če pa privzamemo enačbo E = mc2 = ρVc2, dobimo enačbo za gostoto sevanja:
ρrad = E/(Vc2) = aT4/c2
Če v našo enačbo dinamike vesolja vstavimo ρrad = aT4/c2,
dobimo izraz:
(dR/dt)/R = (8πGaT4/(3c2))1/2
Če uporabimo že razloženo enačbo
Rdanes/Rzačetni = Tzačetna/Tdanes, velja:
RT = konstanta
Torej lahko zapišemo izraz (dR/dt)/R s temperaturo T:
(dR/dt)/R = -(dT/dt)/T = -(1/T)(dT/dt)
in
-(1/T)(dT/dt) = T2(8πGa/(3c2))1/2
Tako dobimo integral temperature T od neskončno do neke iskane temperature in čas od začetka t=0, do neke
poljubne vrednosti, kot:
∫dT/T3 = -(8πGa/(3c2))1/2∫dt
Kar da rezultat za temperaturo v odvisnosti od časa v začetnem sevalnem vesolju kot:
T = (3c2/(32πGa))1/4t-1/2,
- kjer je:
(3c2/(32πGa))1/4 = 1,52 1010Ks1/2
Za R (scale factor, danes je R = 1 pri To = 2,7 K) pa dobimo, ko privzamemo
RT = konstanta = 1*To, iz zadnje enačbe:
R = (32πGaTo4/(3c2))1/4t1/2
- kjer je:
(32πGaTTo4/(3c2))1/4 = 1,8 10-10s-1/2
ZAPOMNIMO SI TOREJ
V obdobju prevlade sevanja se je torej velikost vesolja spreminjala sorazmerno s koremom časa:
R ∝ t1/2; v času prevlade atomov (snovi) pa se dinamika vesolja bolje
opiše z izrazom:
R ∝ t2/3.
Koliko je bilo staro vesolje, ko se je začel tvoriti helij (?) - ocena.
Ko se je začel tvoriti helij je bila temperatura okrog T = 109 K. Takrat je
je bilo vesolje staro:
t ≈ (1,52 1010Ks1/2)2/T2 = 230 s
Takrat po 230 s (pri. 4 min) je bil faktor širjenja vesolja (a ali R) le:
a = R = (1,8 10-10s-1/2)t1/2 = 2.7 10-9
in rdeči premik z = 1/R - 1 = 3,7 108.
Zadnja enačba pride iz že razložene povezave 1 + z = Rdanes/Rzačetni = 1/R,
če je danes R = 1.
Ocena velikosti vesolja takoj po inflaciji (po času 10-32 s od velikega poka).
Velja faktor rasti (a(t) je sedaj R ...):
a(t) ≈ (2(Ω(r,0))1/2 Hot)1/2,
- za polmer vesolja takrat velja enačba,
r(t)=a(t)ro (ro je polmer danes)
r(10-32s) = a(10-32s)ro
= 2×10-26×4,66 × 1010 svetlobnih let = 9 m.
Sila in delec inflacije
Mnogi fiziki kot gonilo začetne inflatorne rasti vesolja korektno (glede na teorijo prenosa sil preko polj
in nosilcev polj) predlagajo novo
temeljno silo z lastnim poljem, posredovano z delcem, imenovanim inflaton (torej še en potencialni bozon).
Spet drugi predlagajo več polj z več delci. Čas bo pokazal, kdo ima prav, če sploh.
Pojasnilo
ΛCDM (lambda in hladna temna snov - model) ali Lambda-CDM model,
je parametrizacija kozmološkega modela velikega poka, v katerem
vesolje vsebuje tri glavne komponente: prvič, kozmološko konstanto,
označeno z lambda (grško Λ), povezano s temno energijo, ki pospešeno
širi vesolje; drugič, domnevna hladna temna snov (skrajšano CDM);
in tretjič, navadna snov iz masnih delcev. Pogosto ga imenujemo
standardni kozmološki model velikega poka. Je najpreprostejši model,
ki razmeroma dobro pojasnjuje trenutne razmere v vesolju in preteklo
dogajanje, ki ga zaznamo preko meritev oddaljenih galaksij, zvezd, supernov,
preko valovnih dolžin oddane svetlobe in Dopplerjevega pojava. Mi smo ta
model opisali s srednješolko matematiko in se v veliki meri približali
jedru razlage preko interpretacije meritev (Doppler in širjenje vesolja,
fenomen nastanka osnovnih delcev in atomov, zvezd, planetov, galaksij in preko
temperature vesolja, ki se odraža v mikrovalovnem sevanju ozadja - s pomočjo
gravitacije smo še ocenili časovno odvisnost razdalje trenutno še vidnega vesolja
– od koder seveda dobivamo zgolj še signale iz preteklosti - 13,8 milijard let
starega vesolja, sama enačba vidnega horizonta pa nam je pomagala še pri časovni
odvisnosti temperature vesolja).
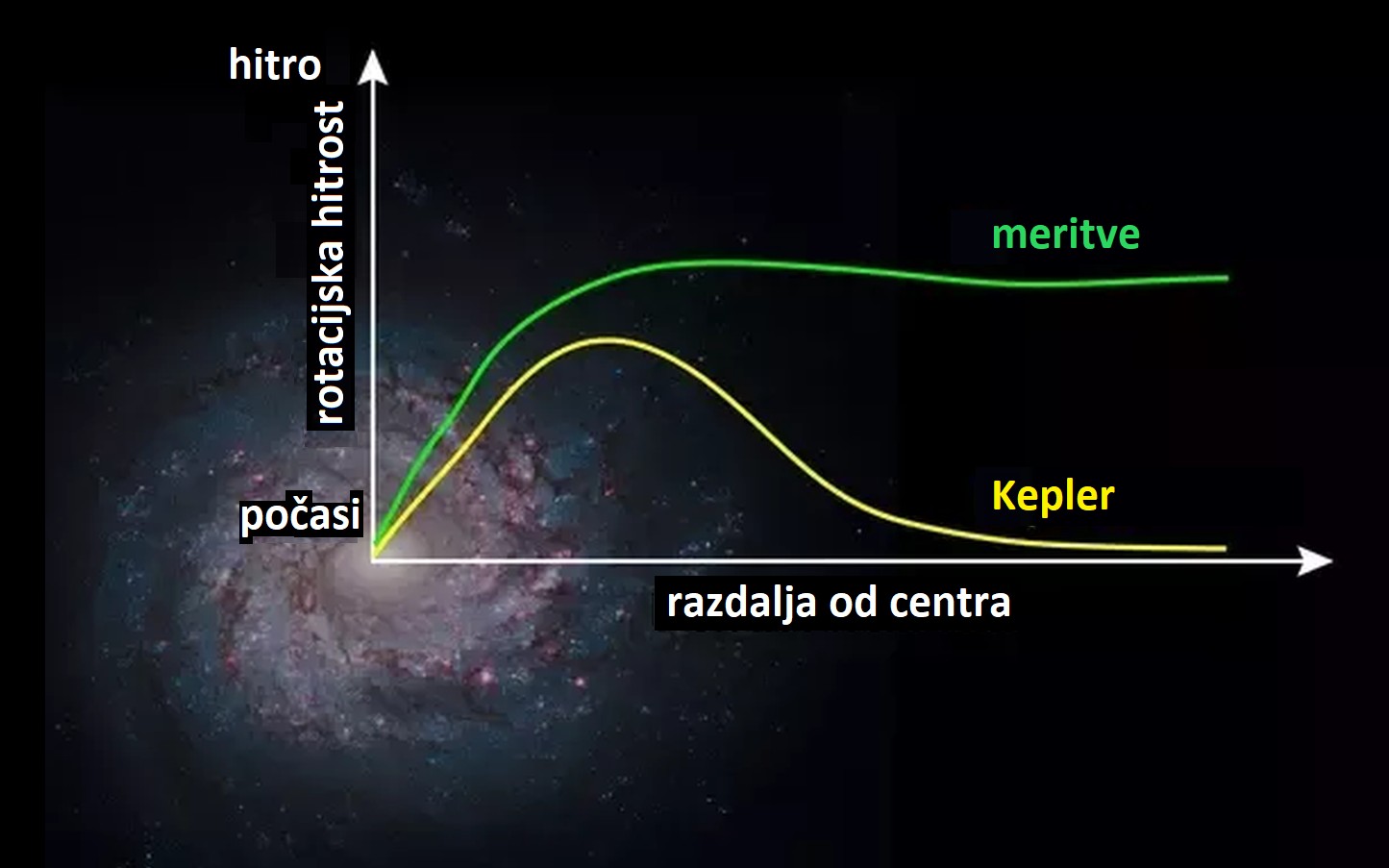

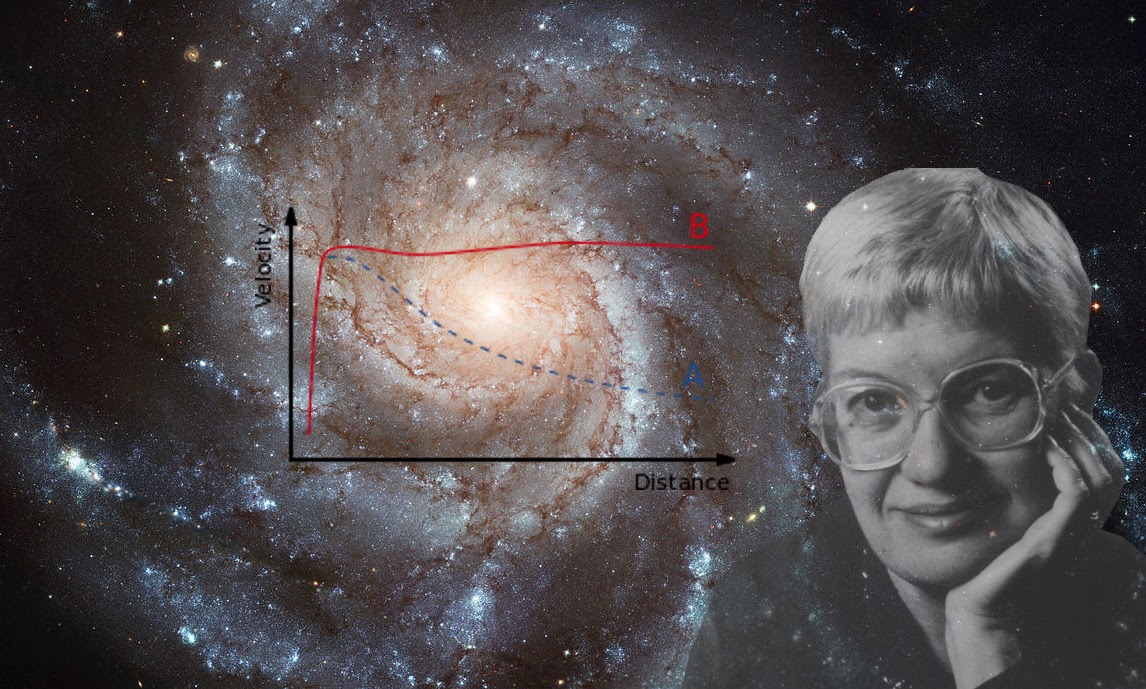
Temna snov (nismo je veliko omenjali – pomerila
sta jo Vera rubin in Kent Ford), je odgovorna za tvorbo galaksij in jo zaznamo
preko preoblikovanega tretjega Keplerjevega zakona
(v = (GM/r)1/2)
-
ko hitrost z razdaljo od centra galaksij večinoma ne pada (kot bi pričakovali
po gostoti vidne snovi), ampak dolgo ostaja skoraj konstantna, zaradi prisotnosti
temne snovi. Povejmo, da je temno snov prvi v kozmologijo vpeljal James Peebles
(prejme polovico Nobelove nagrade za fiziko leta 2019) – v članku 1982 je temno snov
vključil v nastanek večjih struktur – zvezd, galaksij ... Leta 1984 je Peebles, da
bi razložil fenomen inflacije mladega vesolja in struktur, spet obudil Einsteinovo
kozmološko konstanto.
Ko je vesolje bilo staro 380000 let (vrednosti se nekoliko razlikujejo, recimo
379000 let, itn),
so se pojavili prvi atomi (rekombinacija) in mikrovalovno sevanja ozadja
je začelo tedaj skoraj neovirano pot skozi prostor in čas. Vidno vesolje
je bilo takrat veliko približno 42 milijonov svetlobnih let (vrednost izhaja
iz današnje ocene oddaljenosti horizonta, od skoraj začetka vesolja starosti
380 000 let (groba ocena):
Robzorje_dabes = 3ct = 3*13,8 109) sv. let = 41,4 milijard svetlobnih let).
Novejše ocene dajo Robzorje_dabes = 46,6 109) sv. let.
Vesolje se namreč širi pospešeno.
Za temno snov še iščemo kandidate.
Nekateri predlagajo
aksione (axion, oznaka A0 - predvideva ga teorija Peccei-Quinn, ki pravi,
da se fizikalni zakoni ne spremenijo, če se zamenja osnovni delec z njegovim antidelcem ...)
Aksion bi naj imel spin enak 0, tudi njegov naboj bi naj bil 0.
Maso naj bi imel od 10-6 do 1 eV/c2.
Razpadel naj bi na dva fotona ali pa se v njih preobrazil v prisotnosti močnega magnetnega polja.
Njegov interakcijski presek za močne in šibke interakcije bi naj bil zelo nizek.
Zaradi tega z običajno snovjo izredno malo sodeluje.
Aksion je torej verjetno tudi sestavni del temne snovi v vesolju.
Večje število aksionov bi naj nastalo med velikim pokom - na grafih sestave začetnega vesolja
predstavlja temna snov nad 60 % energije. Danes pa okrog 23 %, temna energija pa danes
zavzema čez 70 % energije (na začetku vesolja pa je bila temna energija zanemarljiva).
Tukaj so še
"sterilni" nevtrini (ali inertni nevtrini
- "sterile or inert neutrino"), ki so hipotetični delci
(nevtralni leptoni – nevtrini), za katere se domneva, da medsebojno delujejo
le preko gravitacije in ne preko katere koli druge temeljne interakcije standardnega modela.
Izraz sterilni nevtrino se uporablja za razlikovanje od znanih, običajnih aktivnih nevtrinov
v standardnem modelu, ki nosijo izospinski naboj ±1/2 in sodelujejo v šibki interakciji.
Sterilni nevtrino z maso okrog keV je torej tudi kandidat za temno snov.
Številni sterilni nevtrini na začetku vesolja
ne motijo trenutne teorije nukleosinteze velikega poka.
Ekipe na pospeševalnikih se trudijo, da bi jih detektirali, a večjih premikov
zaenkrat ni - določeni rezultati pa še dopuščajo nekaj verjetnosti za obstoj inertnega nevtrina.
Omenimo še masivne delce WIMP-e: Weakly interacting massive particles (WIMPs) s šibko interakcijo.
Generalno je to nov hipotetični osnovni diskretni delec,
ki medsebojno deluje prek gravitacije in katere koli druge
sile (ali sil), ki morda ni del samega standardnega modela,
ki je tako šibek ali šibkejši od šibkega jedrske sile, ampak ima dovolj moči za učinek temne snovi. Pričakuje se, da so bili številni kandidati za WIMP proizvedeni termično v zgodnjem vesolju,
podobno kot delci standardnega modela v skladu s kozmologijo velikega poka
in potencialno sestavljajo hladno temno snov.
Vendar pa so nedavni ničelni rezultati poskusov neposrednega zaznavanja skupaj
z neuspehom dokaza o supersimetriji v poskusu velikega hadronskega trkalnika
(LHC) postavili dvom o najpreprostejši hipotezi WIMP.
Alfred Amruth z Univerze v Hongkongu je s sodelavci s podrobnim računalniškim
modeliranjem ugotavljali, kako bi bile slike popačene, če bi bila temna snov
sestavljena iz WIMP-ov ali iz aksionov. Model z aksioni je dal zelo verodostojno sliko
gravitacijskega lečenja HS 0810+2554 (nastane več slik iste galaksije iz ozadja po
modelu temne snovi iz aksionov, ki imajo bolj valovne lastnosti,
se torej ujema z dejanskimi slikami -
iz WIMP-ov pa model ni tako dober) - vir: SPIKA 5, 2023.
To je prva na pol eksperimentalna lastovka, ki
kaže, da bi čez čas le detektirali delce temne snovi - morebiti aksione.

Primer
gravitacijskega lečenju objekta HS 0810+2554, ko nastane več slik iste galaksije iz ozadja.
Vir:
https://i.redd.it/astronomers-reveal-hs-0810-2554-the-farthest-known-hidden-v0-qad2oe3q68va1.jpg?s=faefd29f68c26a26a19da9c120fbd5aa1b81ec14
Kot lahko preberemo pri nekaterih avtorjih, nekateri vidijo potencialno temno snov kot množico zelo majhnih
črnih lukenj, ki bi lahko nastale takoj po velikem poku, v prvi sekundi.
Te bi naj bile tako majhne, da bi lahko njihovo delovanje na snov (recimo majčkeni tuneli v starih kamninah)
videli komaj pod mikroskopom. Naredimo grobo oceno.
Črne luknje bi naj tudi
izhlapevale - glejte poglavje
Hawkingovo sevanja črne luknje.
Tam najdemo tudi izpeljavo časa izhlapevanja τ, oznaka M☉ pomeni maso Sonca,
enačba za čas izhlapevanja črne luknje je:
τ ≈ 10-20(M)3 sekund
≈ 1064(M/M☉)3 LET.
Ko je v današnjem vesolju masa črne luknje pod
M = 6 10-8 K M☉/2,725 K
≈
2 10-8 M☉
(to je nekje masa Lune, 7,3477×1022 kg, kar je
0,0123 Zemljine), bi naj začela izgubljati maso s sevanjem.
Za razliko od večine predmetov, se temperatura črne luknje poveča,
ko zgublja maso. Stopnja povečanja temperature je eksponentna,
najverjetnejša končna točka pa je raztapljanje črne luknje v
silovitem izbruhu gama žarkov. Za črno luknjo z maso
1011 kg
je
čas izhlapevanja 2,6 × 109 let (to je pod starostjo vesolja).
Zato nekateri astronomi iščejo znake eksplozij morebitnih prvotnih črnih lukenj.
A manjše črne luknje bi v resnici potem že morale izhlapeti. Kaj pa črne luknje,
ki bi naj še živele, koliko so velike in masivne, ali bi jih lahko videli pod mikroskopom, vsaj njihove sledi
v trdni snovi?
Sledi črnih lukenj, ki bi jih lahko videli z optičnim mikroskopom, so velike cca
1 mikrometer (ocena je r ∝ 2GM/c2) pa bi naj imele
maso cca 1019 kg in te bi torej še lahko živele
in puščale sledi, recimo v kamninah.
A zaenkrat še nismo odkrili nobene črne luknje, ki ne bi bila posledica
gravitacijskega krčenja mas vsaj 1.4 x Sončeva masa in več. Tako, da so mikro
črne luknje zgolj teoretičana možnost in nič več.
Črne luknje v resnici tudi počasi rastejo, saj je vesolje skoraj prazno ...
Recimo,
še črna luknja naše Rimske ceste, ki ima maso cca 4 milijone Sončevih mas in je stara okoli
12 milijard let, ima povprečno stopnjo rasti zgolj 0,0003 Sončeve mase/leto.
Kljub temu, da se snov proti središču galaksij
kar gosti.
Masivnejše galaksije, ki imajo seveda območja z gostejšim jedrom, pa lahko imajo
povprečno stopnjo rasti tudi med 0,1 in 1,0 Sončeve mase/leto.
A zgolj teoretične mikro črne luknje (iz začetka vesolja, takoj po velikem poku)
torej naj ne bi zelo hitro rasle in odsotnost
teh teoretičnih lukenj v realnem vesolju to tudi dokazuje - vsaj zaenkrat se tako zdi.
Še nekaj besed o ravnem vesolju. Kot smo že zapisali, so se razmerja gostot skozi zgodovino vesolja spreminjala. Po Einsteinovi teoriji velike mase, kot so galaksije, črne luknje, ostale oblike energije, ukrivljajo prostor-čas. Toda meritve kažejo, da je vesolje na velikih (kozmoloških) razdaljah ravno. Kar pomeni, da je gostota vesolja uravnotežena med večnim širjenjem in ponovnim krčenjem (zdi se torej, da je kinetična energija enaka potencialni Ek + Ep = 0 ali kot smo že zapisali prej, velja: H2 – 8πGρ/3 = 0 - beri uvod v poglavju "SCENARIJI DINAMIKE VESOLJA"). Tako so danes ocene, kljub pospešenemu širjenju vesolja, da je ukrivljenost vesolja blizu ničle, da potencialna energija zaradi same gostote vesolja torej ne prevladuje nad kinematiko (dinamiko) vesolja (obe energiji sta v ravnovesju ali blizu, velja torej k = 0). Torej tudi ne bi smelo biti težav z globalnim časom, merjenjem razdalj ...
Če torej pogledamo metriko pri k = 0 (ravno vesolje, gostota je enaka kritični), je ta metrika zelo podobna
Schwarzschildovi. V Robertson-Walkerjevi metriki pa odloča o merjenju razdalj
v vesolju člen a(t), ki nam pove, kako se dinamika vesolja spreminja s časom.
a(t) je umeritveni faktor (scale factor). Člen 1/(1-kr2) pa nam
pomaga pri dinamiki, geometriji vesolja, če je le to zaprto ali odprto (ima podobno vlogo
kot računanje razdalj na poljubni krivulji, ravnini, v prostoru). Glej spodnji premislek o razdalji
na sferi, ukrivljenosti in nato o razdalji in ukrivljenosti v prostoru vesolja.
Izhajajmo iz geometrije na krogli, sferi (slika zgoraj).
Za izračun razdalje dl uporabimo Pitagorov izrek.
Dolžina dl med točkama P1 in P2 na
sferi je torej:
dl2 = (Rdϑ)2 + (rdφ)2
r = Rsinϑ in dr = Rcosϑdϑ
in
Rdϑ = dr/coxϑ = Rdr/(R2 - r2)1/2
= dr/(1 - (r/R)2)1/2
- dl sedaj zapišemo z razmerjem r/R:
dl2 = dr2/(1 - (r/R)2) + (rdφ)2
Ker je Gaussova ukrivljenost sfere K = 1/R2,
lahko zapišemo razdaljo dl na sferi kot:
dl2 = dr2/(1 - Kr2) + (rdφ)2
O merjenju razdalj na sferi odloča torej ukrivljenost K = 1/R2.
ALI je v prostoru (v vesolju) podobno? Tako so razmišljali že Robertson, Walker, Friedmann, Lemaitre!
V ukrivljenem prostoru (vesolju) tako povzamemo analogijo - glej Schwarzschildovo metriko ob sferi:
dl2 = dr2/(1-Kr2)
+ r2(dϑ2 + sin2ϑ dφ2)
Zadnji korak k metriki prostor-časa vključuje seveda še čas.
Z razdaljo razumemo lastno (proper) razdaljo med dvema prostorsko-časovnima dogodkoma,
ki se zgodita sočasno glede na opazovalca.
V vesolju, ki se širi, mora biti položaj dveh točk zabeležen hkrati,
če naj bi imela njuna medsebojna razdalja kakršen koli pomen. V izotropnem,
homogenem vesolju, ni razloga, da bi čas v povprečju tekel različno hitro
za različne lokacije (razen izjemoma lokalno, izrazita gravitacija ob nevtronskih zvezdah,
ob črnih luknjah); tako mora biti na veliki skali upoštevan zgolj časovni del cdt.
Metriko
potem zapišemo kot:
ds2 = (cdt)2 - dr2/(1-Kr2)
- r2dϑ2 - r2sin2ϑ dφ2
Sedaj še poudarimo, da se vesolje s časom različno hitro širi, kar recimo zapišemo kot:
R(t) = a(t)·r
Ker širjenje vesolja vpliva na vse njegove geometrijske lastnosti, vključno z njegovo ukrivljenostjo,
je koristno definirati tudi časovno odvisno
ukrivljenost glede na faktor umeritve ( a(t) - scale factor) in časovno neodvisno konstanto k:
k = K/a(t)2
Povedano zapišemo v končno metriko vesolja v standardni obliki
med bližnjima dogodkoma (Robertson-Walkerjev element ali tudi Friedmannov in Lemaitrov element):
ds2 = (cdt)2 - a(t)2 (dr2/(1-kr2)
+ r2(dϑ2 + sin2ϑ dφ2) )

Tri možne geometrije vesolja.
V sferičnem zaprtem vesolju (zgoraj levo, k = 1 oz. Ωo > 1) seštevek treh kotov trikotnika znaša
več kot 180 stopinj.
V sedlastem odprtem vesolju (na sredini, k = -1 oz. Ωo < 1) seštevek treh kotov trikotnika znaša
manj kot 180 stopinj. V ravnem vesolju (zgoraj desno, k = 0 oz. Ωo = 0)
seštevek treh kotov trikotnika znaša 180 stopinj.
To je seveda zgolj matematična
prispodoba geometrije vesolja, ki vpliva na dinamiko, o kateri pa odločajo
masni delci in temna snov z gravitacijo in seveda ne dolgo nazaj odkrita
temna energija, ki pospešuje vesolje - zmeraj hitreje se širi. Seveda imajo določeno
vlogo tudi sevanje, fotoni in ostali kvantni delci.
a(t) je faktor umeritve (scale factor), ko velja razdalja do horizonta s(t) = a(t)·r, oziroma s(t) = a(t)ct
za ravno vesolje k = 0.
Za žarek svetlobe velja ds=0 ("sedimo" na žarku in čas ne teče, ds = cdτ = 0)
in naj bo kot dΩ = 0 , to je
potovanje fotona v radialni smeri (najkrajša pot, ničelna, nulta geodetka),
potem velja za opazovalca na Zemlji (izhajamo seveda iz že zapisane metrike vesolja
ds2 = (cdt)2 - a(t)2 (dr2/(1-kr2)
+ r2dΩ2)
):
cdt/a(t) = ± dr/(1-kr2)1/2
Kjer predznak ± pomeni oddana svetloba (+) in minus (-) prejeta svetloba.
∫dt/a(t) = (1/c)∫dr/(1-kr2)1/2
Naslednji premislek velja za lastno razdaljo (proper distance)
ds (razdalja iz sistema, kjer sta dogodka sočasna, ko je torej dt = 0 in cdt = 0,
govorimo o kozmološki razdalji).
Razdalja s(t) do horizonta je potem:
s(t) = a(t) ∫dr/(1-kr2)1/2
Če kombiniramo obe enačbi (integrala) potem velja (za ravno vesolje k = 0)
za razdaljo do vidnega horizonta naslednji pomemben izraz (integrira se od časa 0 do t):
s(t) = a(t) ∫cdt/a(t)
Ker smo izpeljali, da je a ∝ t2/3 (za vesolje, ko je prevladala snov
nad sevanjem),
potem velja (konstante se okrajšajo, integriramo od časa 0 do t, do starosti vesolja):
s(t) = a(t) ∫cdt/a(t) = t2/3 ∫cdt/(t2/3)
= t2/3 3 ct1/3
= 3ct.
To je groba ocena vidnosti horizonta, ki da
za ct = 13,8 109 sv. let za razdaljo do horizonta:
s(t) = 3ct = 41,4 109 sv. let.
Bolj točne novejše ocene dajo nekoliko večjo vrednost in sicer
okrog 46,6 109 sv. let - naše vesolje se namreč širi pospešeno (ni ravno).
Zagotovo torej lahko povemo, da je vesolje veliko vsaj toliko kot je daleč vidni horizont
(torej vsaj tri razdalje produkta starosti vesolja in hitrosti svetlobe: ct),
a večina domneva, da je vesolje veliko večje! Koliko pa?
(odgovora še ni, ali ga bomo kdaj imeli?)
Foton, ki je bil oddan v času
t = 0, je prečkal področja v prejšnjih obdobjih, ko je vesolje
bilo še veliko manjše (zato je razdalja do horizonta večja od ct).
Kot da bi hodil po raztegujočem se žvečilnem gumiju ali napihujočem se balonu
(glejte uvodni graf tega poglavja).
Trenutno ima največji redeči premik (z = 11.09) galaksija GN-z11. Odkrita je bila leta 2015
v ozvezdju Velikega medveda.
Ocena za resnično razdaljo do te galaksije je 32 milijard svetlobnih let.
Nastala je, ko je bilo vesolje staro 400 milijonov let (po velikem poku), torej pred
(13,8 - 0,4) milijard let = 13,4 milijard let.
James Webb v Lagrangevo točko L2 bo teoretično meril
objekte z zelo visokim Dopplerjevim rdečim premikom z ≈ 20.
JWST opazuje v območju s krajšimi valovnimi dolžinami, od dolgovalovne vidne svetlobe
(rdeče) do srednje infrardečega sevanja (0,6–28,3 μm).
Za zgodnje vesolje, ko prevladuje sevanje, smo izpeljali za faktor širjenja
a ∝ t1/2.
Iz te povezave dobimo pa rezultat za oddaljenost še vidnega horizonta (zgodnje vesolje):
s(t) = 2ct
Preverite sami.
Poglejmo še rešitve integrala za razdalje v vesolju,
za kozmično razdaljo, horizont (proper distance)
ds = cdτ (razdalja iz sistema, kjer sta dogodka sočasna, ko je torej dt = 0 in cdt = 0,
govorimo torej o kozmološki razdalji - do vidnega horizonta).
Kot smo že zapisali, je razdalja s(t) do horizonta potem:
s(t) = a(t) ∫dr/(1-kr2)1/2
Rešitve te enačbe so (povsod se integrira od krajevnega vektorja 0 do r):
s(t) = a(t)·k-1/2 sin-1(rk1/2) za k > 0 s(t) = a(t)·r za k = 0 s(t) = a(t)·|k|-1/2 sinh-1(r|k|1/2) za k < 0In te rešitve metrike so tudi rešitve že prej izpeljane Friedmannove enačbe za dinamiko vesolja iz energijskega zakona (se spomnite). To pomeni, da so razmisleki o metriki ds2 skladni z energijskim zakonom. To je seveda pričakovano, a dobro je to dokazati z računom.
rhor = sin(c∫dt/a(t)) za k = 1 (zaprto vesolje) rhor = c∫dt/a(t) za k = 0 (ravno vesolje) rhor = sinh(c∫dt/a(t)) za k = -1 (odprto vesolje)Iz zgornjih enačb tako dobimo čase za pot svetlobe od krajevnega vektorje rhor za tri različne scenarije vesolja. Za k = 0 (ravno vesolje) smo že našli rešitev za vidnost horizonta s(t) = a(t)·rhor:

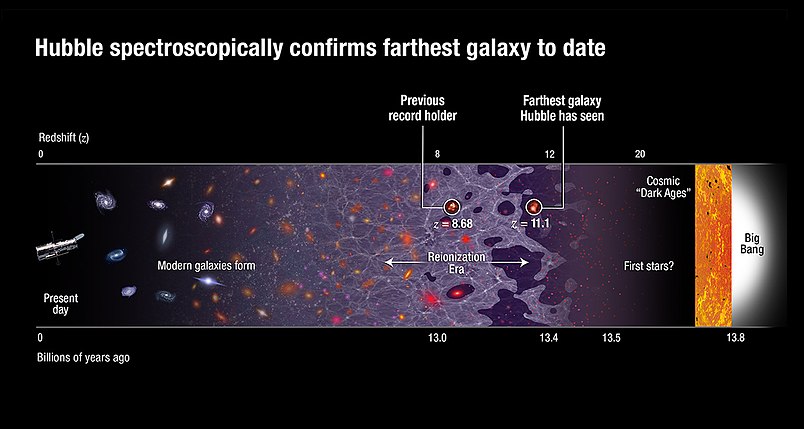
Spekter prasevanja izmerjen z inštrumentom FIRAS na satelitu COBE
je najbolj točno izmerjen spekter absolutno črnega telesa v naravi.
Podatkovne točke in napake v grafu zakriva teoretična krivulja po
Planckovem zakonu. Spekter za črno telo pri temperaturi
T2 = 2,72548 K. Vrh spektra je v mikrovalovnem delu s frekvenco 160,4 GHz,
kar odgovarja valovni dolžini 1,870 mm. Če pa upoštevamo gostoto na enoto
valovne dolžine, bo po Wienovem zakonu vrh pri valovni dolžini 1,062 mm,
kar odgovarja frekvenci 282,2 GHz. Pri starosti vesolja 380 000 let in
temperaturi 3000 K pa je bil vrh Planckovega sevanja pri valovni dolžini
λoddana = λdanes/(z +1) = 1,062 mm/(1089 + 1)
= 0,000974312 mm = 974,3 nm ≈ 970 nm (bližnja infrardeča svetloba)
– v spektru je bilo takrat še tudi veliko vidne svetlobe.
Meritve prasevanja z različnimi inštrumenti (slika levo):
Holmdelska rogasta antena (1965), COBE (1992) in WMAP (2003).
Primerjava rezultatov prasevanja na 10 ° delu neba (slika desno)
s satelitov COBE, WMAP in Planck, 21. marec 2013. Odkrita so bila tudi
zelo majhna nihanja (odstopanja od povprečja – zato vzorci v sevanju
ozadja) temperature (1/100 000), ki kažejo na začetke današnje strukture
vesolja. Tako majhna nihanja so tudi dokaz kozmološkega načela -
ki pravi, da je vesolje enako v vseh smereh. Ta nihanja so znana kot
"valovanje na robu vesolja". Temperaturna nihanja se razlaga kot
razlike v gostoti snovi v tistem obdobju, kar je le delno vzrok
današnji strukturi vesolja. Danes vemo, da so te fluktuacije
najbrž premajhne in za tvorbo galaksij - pri katerih je imela
najbrž odločilno vlogo temna snov.
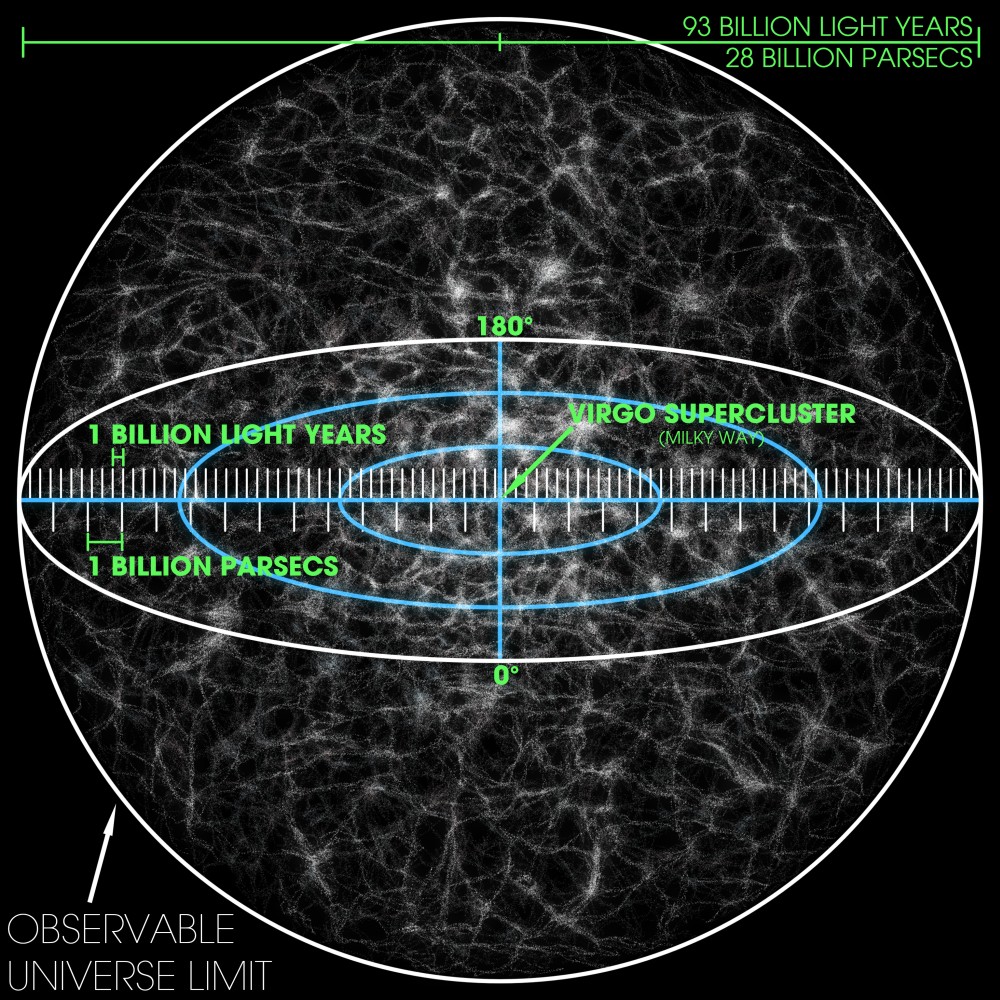
Vizualizacija celotnega vidnega vesolja. Merilo je takšno, da drobna zrna
predstavljajo zbirke velikega števila galaktičnih superjat. Superjata Device
- dom Rimske ceste - je označen na sredini, vendar je premajhen, da bi ga
lahko videli. Polmer vidnega vesolja je 46,6 milijard svetlobnih let (torej
premer okrog 93 109 sv. l. ali 28 milijard parsekov). Rob je torej vidna preteklost
iz časov začetka vesolja, približno 13,8 milijard let nazaj. A v tem času se je
vesolje napihnilo z rdečim premikom
z + 1 = λdanes/λnekoč_oddana =
1,062 mm/0,000974312 mm = Tnekoč/Tdanes
= Rdanes/Rnekoč = 46,6 109 sv. l./ 42 106 sv. l. ≈ 1100.
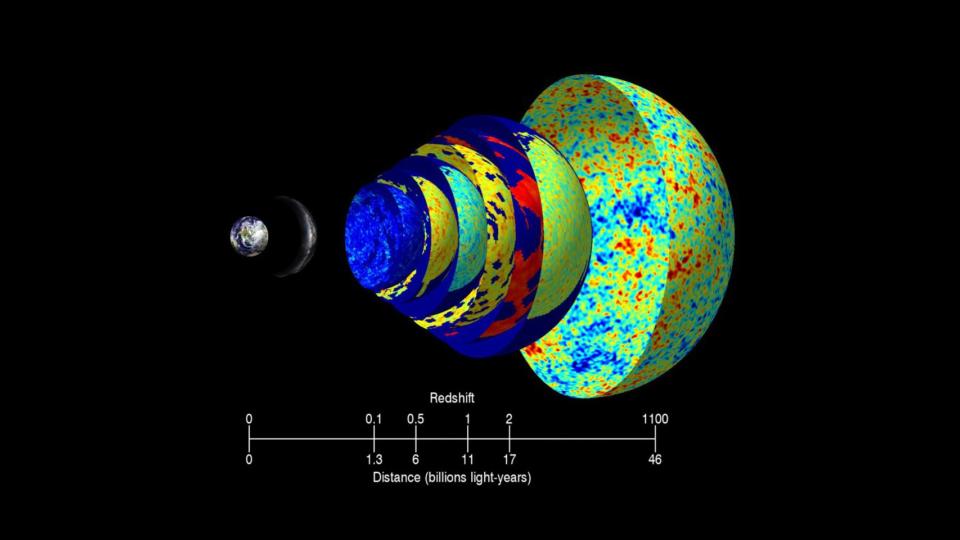
V katerem koli obdobju naše kozmične zgodovine bo vsak opazovalec izkusil enakomerno "kopel"
vsesmernega (izotropnega) sevanja, ki izvira iz velikega poka. Danes je z našega zornega kota temperatura
vesolja le 2,725 K
nad absolutno ničlo in ga zato opazimo kot kozmično mikrovalovno ozadje z najvišjo vrednostjo
mikrovalovnih frekvenc. Na velikih kozmičnih razdaljah, ko pogledamo nazaj v preteklost, je bila
ta temperatura višja, odvisno od rdečega premika opazovanega, oddaljenega objekta. Ko mine vsako novo leto,
se CMB (cosmic microwave background -
kozmično mikrovalovno sevanje ozadja)
dodatno ohladi za približno 0,2 nanokelvina in bo v nekaj milijardah let postalo posledično toliko daljše, da
bo imelo radijske frekvence namesto mikrovalovnih.
velja Wienov zakon, ki povezuje temperaturo
in valovno dolžino maksimalnega izseva:
λ = b/T,
kjer je konstanta
b = 2897768,5 nm•K.
Velja pa, za recimo starost 380 000 let in ta trenutek vesolja,
že izpeljana izjemno pomembna povezava:
1 + z = λdanes/λoddana
= Rdanes/Rzačetni = Tzačetna/Tdanes
= 3000 K/2,72548 K ≈ 1100.
Na x-osi je podana razdalja do vidnega horizonta
dH = R = Ro(t/to)2/3 > 3ct.
Ta razdalja je torej večja od produkta starosti vesolja in svetlobne hitrosti,
saj se vesolje širi - celo pospešeno. Vidni horizont je direktno povezan
z rdečim premikom 'z' - predprejšnja enačba to dokazuje.
Danes je (še) vidni
horizont od nas oddaljen skoraj dH = 47 milijard svetlobnih letih.
Tako smo preko preprostih (večinoma srednješolskih matematičnih in fizikalnih orodij) sklepanj o širjenju delcev vstran od centralne sferične mase – z upoštevanjem gravitacije preko energijskega zakona (ohranitve vsote kinetične in potencialne energije delca) – prišli do zelo uporabnih ocen o dinamiki vesolja skozi čas, velikosti našega vidnega horizonta vesolja. A tudi do kronološke temperaturne odvisnosti vesolja, ki je odločala o nastanku prvih nukleonov (po 0,0001 sekunde), potem atomskih jeder (po nekaj minutah), sledijo nevtralni atomi (po okrog 380 000 letih), nato zvezd (gravitacija prevzame vajeti v roke dokaj zgodaj, kar že okrog 100 milijonov let po velikem poku se pojavijo prve zvezde), planetov, galaksij (prve se pojavijo že po okrog 400 milijonih let po velikem poku) in na Zemlji zagotovo tudi življenje pred okrog 4 milijardami let (za katerega pričakujemo, da se je razvilo še kje v naši Galaksiji, tudi v ostalih, morebiti celo veliko prej). A moderni človek se pojavi komaj pred kakimi 200 000 leti, načrtno generirane elektromagnetne signale pa znamo v vesolje pošiljati komaj dobrih 100 let. Da je vesolje veliko milijarde svetlobnih let (da vesolje torej ni zgolj naša Galaksija - Rimska cesta premera 100 000 sv. l.) pa smo se prepričali (naučili) pred komaj slabimi 100 leti (preko sija utripajočih zvezd kefeid smo najprej ugotovili, da je nam sosednja galaksija M31 daleč vsaj milijon sv. l. – danes vemo, da je oddaljena okrog 2,5 milijona sv. l.). Nebesno mehaniko pa nam je razkril Kepler pred 400 leti. Velik problem naših modelov je merjenje razdalj v vesolju …!!!
Tako smo zaokrožili nekaj temeljnih poglavij o raziskovanju vesolja in
modeliranju njegove narave (od kvantnih fluktuacij, prvotne svetlobe,
osnovnih delcev, do nastanka atomov, molekul, zvezd - fuzije, planetov,
galaksij, mikrovalovnega sevanja ozadja, življenja), od začetkov do danes
– do življenja (ki raziskuje vesolje in s tem tudi samega sebe).
O velikem poku (izbruhu vesolja) sklepamo preko dinamike vesolja,
galaksije se druga od druge oddaljujejo, tukaj je še mikrovalovno
»prasevanje« (torej je bilo nekoč vesolje veliko manjše, bolj vroče …).
Veliki pok (prapok) se torej zdi smiseln začetek vesolja.
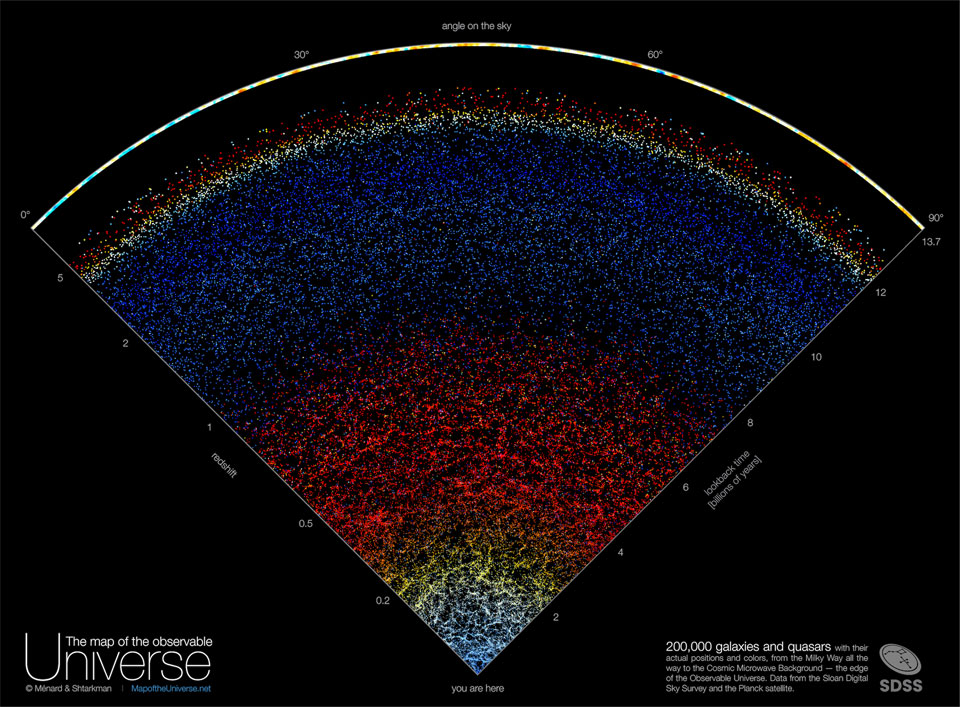
Karta opazljivega vesolja
Avtorstvo slike & avtorske pravice:
B. Ménard &
N. Shtarkman;
podatki:
SDSS,
Planck,
JHU,
Sloan,
NASA,
ESA
Pojasnilo:
Kaj če bi lahko videli do roba
opazljivega vesolja?
Videli bi galaksije, galaksije, galaksije in potem, no,
kvazarje, ki so zelo svetla središča zelo oddaljenih
galaksij.
Da bi razširili razumevanje največjih lestvic, ki jih človeštvo lahko vidi, je bila sestavljena
karta galaksij in kvazarjev, ki jih je odkril
Sloanov digitalni pregled
neba od leta 2000 do 2020 – skoraj do
roba
opazljivega vesolja.
Na sliki je predstavljen en izsek iz te raziskave, ki zajema okoli
200.000 galaksij in
kvazarjev, s pogledom vse do 12 milijard let
nazaj s
kozmološkim rdečim premikom 5.
Uporabite
kozmološki kalkulator za testiranje.
Skoraj vsaka pika v bližnjem spodnjem delu
ilustracije predstavlja
galaksijo, pri čemer rdečina kaže naraščajoči
rdeči premik in razdaljo.
Podobno skoraj vsaka pika na zgornjem delu predstavlja oddaljeni
kvazar, pri čemer so modro osenčene pike bližje kot rdeče.
Med številnimi odkritji, je jasno razvidno,
da je gravitacija med galaksijami povzročila lokalne
kondenzacije bližnjega vesolja, ki je postalo vse
bolj nitasto v primerjavi z
oddaljenim vesoljem (pogled nazaj).

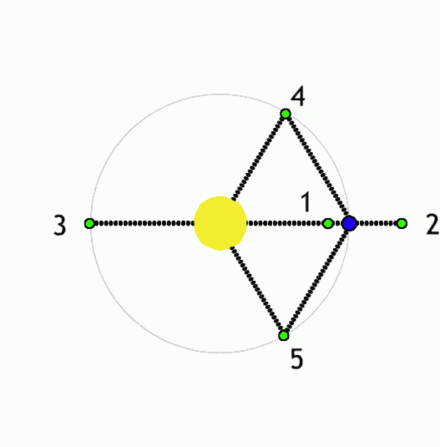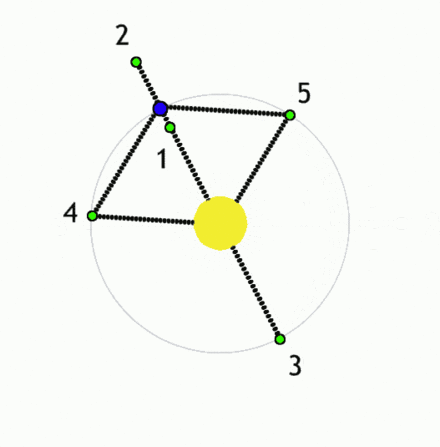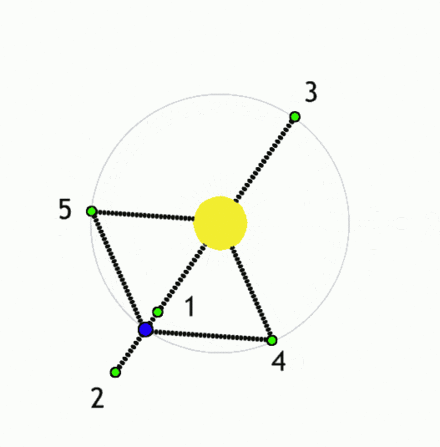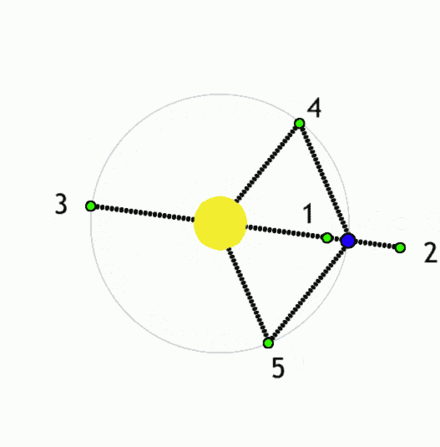
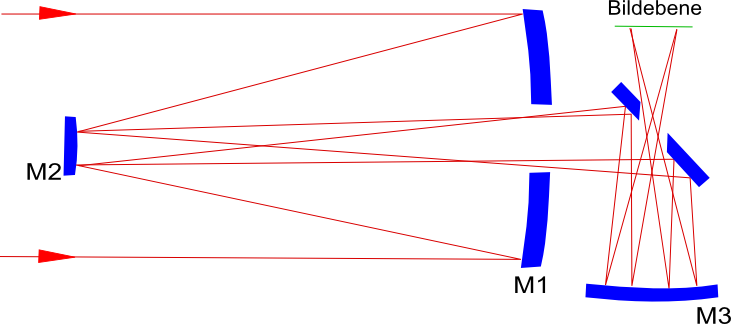
O tem nam bosta zagotovo več povedali že omenjeni misiji Evklid in "Rimska cesta" - torej
raziskovanja globalnega vesolja ter ostali podobni projekti.
A poglejmo na možne končne scenarije stvarstva z vedenjem, ki ga imamo v tem trenutku v rokavu, v znanstveni
zavesti naših generacij.
Enkrat smo si že zastavili podobno vprašanje - ali je torej vesolje v svojem
bistvu kot neke vrste zaporedje valov – kozmičnih valovnih cunamijev,
ki si sledijo drug za drugim in tudi nam je dano, da surfamo na enem izmed njih …?
Problem trenutne razlage bodočega razvoja vesolja je, da ne vemo, kako se vesolje
pospešuje (ali odbojna sila skrita v temni energiji narašča in kako, ali bo začela
popuščati?). Od kod energija, ki pospešuje vesolje (pojem neskončne energije nam
je tuj) ali se bo vesolje torej kdaj nehalo pospešeno širiti (pospešeno se širi že
okrog 5 milijard let). Če bi se (odrivalni) pospešek izrazito povečeval, bi naj
prišlo do velikega raztrga – vse bi razpadlo, galaksije, zvezde, tudi atomska
jedra, odboj bi lahko bil silovitejši od močnih jedrskih sil … Če pa pogledamo
preslikavo zgolj trenutnega stanja (pospeška) v bodočnost, se zdi, da se bo prostor
čez okrog 1000 milijard let širil hitreje od svetlobe (kot med začetno inflacijo
– to ni fizično gibanje zvezd, ampak širjenje prostora, zato se ne krši pravilo
meje svetlobne hitrosti). Kaj bi to pomenilo? Da, razen lokalne jate galaksij,
ki gravitacijsko čepi skupaj (M31, M33, M32, M110, NGC 6822, NGC 185, IC 1613, NGC 147 …)
ali čez čas zgolj še združeni naša Galaksija in M31, ne bi videli nobenih ostalih jat galaksij
– ker nas njihova svetloba ne bi več dosegla. Naše kozmološko obzorje bi
se torej skrčilo iz več kot trenutnih 13 milijard svetlobnih let (kar zazna
teleskop Hubble) - oziroma iz 46,6 milijard svetlobnih let, zgolj na nekaj
milijonov svetlobnih let znotraj naše jate galaksij. Tudi danes ne vidimo celotnega
vesolja - najbolj oddaljeni objekti, katerih svetlobo lahko teoretično zaznamo danes,
so bili v času, ko so oddajali to svetlobo (pri starosti vesolja 380 000 let), na
razdalji le 42 milijonov svetlobnih let od Zemlje. Danes nas od teh objektov (kot
smo že omenili) teoretično loči 46,6 milijard svetlobnih let (razlog je širjenje
vesolja – prostora - in posledično zelo velik rdeči premik sevanja ozadja, okrog
λdanes/λnekoč_oddana = (z +1) ≈ 1100
– skoraj od začetkov vesolja, bolje od tvorbe atomov, ko je vesolje bilo staro
okrog 380000 let pa do danes). Ker pa bodo objekti in dogodki v tem primeru
že zdavnaj prestopili obzorje dogodkov, ni (ne bo) mogoče vedeti, kaj se »danes«
dogaja z njimi na tej razdalji. Zanamci torej tako več ne bi razumeli naše trenutne
kozmologije, v kateri govorimo o oddaljevanju galaksij, jat galaksij – tega preprosto
ne bi več mogli preveriti, izmeriti (morali bi nam torej verjeti na besedo in korektnosti
naših opazovanj ter meritev – a mi verjamemo spisom naših prednikov – no ja, kakor nam paše …).
Je pa tukaj še vrsto ostalih vprašanj - recimo o razpadu nukleonov, protonov (protonu ocenjujemo
razpolovno dobo kar na 6.6×1033 let).
Trenutno se zdi, da bodo kmalu (no čez nekaj 1000 milijard
let) ugasnile tudi najmanjše zvezde (z desetino mase Sonca) s počasno fuzijo, ki torej svetijo
(rdeče) veliko dlje kot Sonce. Takrat morebitni zanamci ne bodo več videli zvezdnega neba,
ker bodo ostali le temni ogorki (»še dobro, da smo rojeni v tem času vesolja …, ko še
velja pesem o Orionu«), ker bodo vse zvezde ugasnile … in bodo tudi zelo redko posejane
po še bolj praznem vesolju … A do takrat je še kar dovolj časa, da si recimo s »kozmičnimi
buldožerji« naredimo nov planet, novo Sonce s fuzijo – ki trajnostno proizvaja energijo …
Vse povedano pa je v resnici še zelo, zelo daleč od morebitnega razpada
protonov 1033 let ali še dlje od trajanja Hawkingovega sevanja
črnih lukenj, 1064 ali več let ... Baje se bo nekaj dogajalo (bivalo)
celo do 10^10^68 let = 101068 let.
No, še prej pa nas čaka »drobna« obveznost,
ohranitev življenja na Zemlji in čez kako milijardo let v
njeni bližini (morebiti na Marsu, Titanu ali kje drugje) … in seveda,
še vključitev astronomije v šolo (no, najbrž bomo lažje ohranili
življenje na Zemlji …).
»Boltzmannovi možgani« so ideja za samozavedajočo entiteto, strukturo, ki
nastane zaradi izjemno redkih naključnih nihanj v stanju termodinamičnega
ravnovesja. Na primer, v homogeni newtonski juhi je mogoče teoretično čisto po slučaju
vse atome ločiti in spet medsebojno povezati tako, da tvorijo funkcionalne človeške
možgane (čeprav bi to v povprečju trajalo veliko dlje od trenutne življenjske
dobe vesolja). Ta ideja je dobila ime po avstrijskem fiziku (Stefanovem učencu)
Ludwigu Boltzmannu (1844-1906), ki je leta 1896 objavil teorijo, ki pravi,
da je vesolje sicer v malo verjetnem stanju neravnovesja, a le, če se takšna stanja
(neravnovesja) pojavijo naključno, se lahko pojavijo možgani, ki se zavedajo vesolja.
Pomanjkljivost hipoteze o "Boltzmannovem vesolju" je najbrž v dejstvu, da so najpogostejša
toplotna nihanja v vesolju na splošno zelo blizu ravnovesja in tudi zelo številčna - zato
bi po katerem koli razumnem merilu človeške možgane v Boltzmannovem vesolju, z množico
sosednjih zvezd, po številu daleč presegli "Boltzmannovi možgani", ki pa lahko obstajajo
sami zase v skoraj praznem vesolju (seveda tudi razpadejo - entropija). Boltzmannovi
možgani so dobili nov pomen okoli leta 2002, ko so nekateri kozmologi postali
»zaskrbljeni«, da v mnogih novih teorijah vesolj(a) človeške možgane v sedanjem vesolju
po številu, v prihodnjih vesoljih, močno presegajo Boltzmannovi možgani, ki imajo
popolnoma enaka dojemanja kot naši možgani. To vodi do absurdnega zaključka, da smo
potem verjetno tudi mi Boltzmannovi možgani. Takšen argument reductio ad absurdum
se včasih uporablja kot protiargument nekaterim teorijam vesolja. Argumenti za obstoj
Boltzmannovih možganov, ki se nanašajo na novejše teorije multiverzuma, so del
nerešenega problema merjenj v kozmologiji (merljivi multiverzum je potem spet eno
vesolje …).
Bodočnost vesolje je v vsakem primeru zavita v veliko skrivnost – a vseeno se splača
navesti nekaj teoretičnih projekcij, ki presegajo trenutno oceno starosti vesolja
(1010 let)
vsaj za neverjetnih 1055 let
ali več. Ta pogled nam na nek način
približa današnji trenutek vesolja – da veliki pok v resnici ni tako zelo
oddaljen od nas, in da nam grafi, ki kažejo razvoj vesolja skozi čas, preko temperature,
energije sevanja, inflacije, nastanka delcev, nukleonov, atomov, zvezd, planetov, galaksij
– vse do življenja na Zemlji – postanejo ZELO DOMAČI (se z njimi vsaj delno poistovetimo).
Veliko je ugibanj o obstoju razuma, zavesti v vesolju – recimo Boltzmannovi možgani -
ali so to zgolj človeški možgani (ali je še zraven kaka žival na Zemlji, ki ji mi tega
ne pripisujemo ... ali kje drugje v vesolju). Veliko je torej želja, konceptov, kako
ohraniti minimalno možnost zavesti – zavedanja, vedenja, razuma v globoki bodočnosti,
sploh če bo ta šla v smeri ničelne temperature. Končni odgovor je zmeraj v upanju,
da dokler bo še kaj temperaturnih razlik v vesolju, bo tudi možen pretok energij
(toplote) in s tem biološka stikala, ali v možganih ali umetni inteligenci, še lahko
delujejo ... Zadaj je problem povečanja entropije – približevanje absolutni ničli,
tukaj je še napoved razpada protonov ... Zaradi bivanjske zagate in tudi gole radovednosti,
tako nastaja tudi vedno več (miselnih) modelov vesolja. Nekateri si tako nikakor ne želijo
začetka vesolja (jim je tuj koncept velikega poka iz kulturnih ali ideoloških razlogov -
časi se torej od srednjega veka niso kaj veliko spremenili) in zato navijajo za pulzirajoče
vesolje ali tudi ciklično vesolje (da se z vsakim ciklom vesolje razširi bolj kot skrči in s
tem se entropija ne kopiči – ampak celo nekoliko zmanjša, tako se pet nabere »kakovostna«
energija razlik v prostoru – vroče zvezde, dovolj hladni planeti, torej temperaturne
razlike in prenos energije s sevanjem in spet se nekje (na x-planetu) vzpostavijo pogoji
za življenje, civilizacije, spet nov študij sebe - nastalega bitja (bitij) in seveda
vesolja (a pojma začetka vesolja se v bistvu ne da odpraviti – tudi ne s cikli – lahko
pa se delamo, da je pojem cikla dovolj – ali res?). Teoriji cikličnega vesolja danes pomaga
preživeti tudi temna pospeševalna energija (vesolje, ki ne eksplodira samo enkrat, ampak sčasoma
večkrat – tudi če vse razpade in ni več časa, le svetloba …, se ravno zato lahko spet začne
naslednji cikel kvantnih fluktuacij velikega poka …). V teh teorijah cikličnega vesolja nastopajo
eminentna imena, kot so - Einstein, Tolman, Steinhardt, Turok, Penrose, Hawking … in seveda
posredno tudi vsi ostali radovedni posamezniki (naj jih bo čim več, a o tem odločajo tudi šole …),
ki črpajo nova spoznanja in ideje iz sveta omenjenih nadobudnih raziskovalcev, Nobelovcev,
tudi univerz, inštitutov, ostalih raziskovalnih in izobraževalnih ustanov. A vse na koncu
povedano (ciklična vesolja, itn), je zgolj področje domnev, ugibanj, lahko tudi bivanjskih
frustracij – to je sicer (v določeni meri) luštno početje –
»A« vseeno je najprej potrebno
razumeti dosedanje rezultate astronomskih meritev, opazovanj in na njih temelječe
koncepte – nebesna mehanika, standardni kozmološki model vesolja (veliki pok,
inflacija, osnovni delci, ločitev osnovnih sil, nastanek nukleonov, atomov, temna snov,
temna energije, mikrovalovno sevanje ozadja, nastanek zvezd, težkih elementov, planetov,
galaksij, življenja). Že to kar poznamo in se skoraj vsak dan dopolnjuje, je izjemno
vznemirljivo, čudežno – hkrati pa toliko bolj pomembno za obstoj življenja, preživetje
človeka, za iskanje rešitev. Iskanje smisla ni nikoli dokončana pot – je vir življenja.
Zagotovo pa drži misel, je renica (omenja jo tudi Exupéry),
da se svetloba nekaterih v jasnih nočeh iskri, ko jih že davno ni več.
Enako velja za iskrive ljudi ...
Nekaj astronomskih vaj, meritev smo že omenili. Razdelimo jih v štiri kategorije, lahka vaja bo označena z eno zvezdico *, manj zahtevna z dvema **, zahtevna s tremi ***, zelo zahtevna s štirimi ****. Predlogi vaj, sledijo si približno po težavnosti (število vaj približno ustreza številu ur namenjenih praktičnim vajam):
* Opazovanja neba, učenje ozvezdij, zvezd, asterizmov, določanje magnitud, merjenje razdalj in višin na nebu s prsti na roki, iskanje Severnice, smeri neba, kulminacij, poudarek na živalskem krogu, Rimski cesti, na asterizmih (pomladni in poletni trikotnik, zimski šestkotnik, jesenski Pegazov kvadrat – za lažje učenje) …
* Določanje mejnega sija neba, poudarek na svetlobnem onesnaženju, težavah živali in ljudi.
* Uporaba zavednih kart iz atlasov, vrtljive zvezdne karte (Spika ponuja zelo kvalitetne in nazorne karte).
* Risanje analeme preko sence vrha palice (na terasi šole, ob šoli, na šolskem vrtu …), traja eno leto, najbolje ob 12. h po soncu – s tem zaznamo tudi spremembo višine Sonca po letnih časih, mesecih, razliko med Sončevim časom in srednjim, linearnim časom naših ur.
* Risanje Luninih faz skozi cel mesec, lege na nebu, od mlade Lune do Lune stare 18 dni, spremljanje zahodov Lune (vsaj za nekaj dni mlade Lune, beleži se čase), kulminacije Lune poleti in pozimi; učenci naj premislijo, ali lahko vsako večer ob jasnem vremenu, recimo ob 21. h, opazujemo Luno (NE in zakaj ne?).
* Uporaba daljnogledov za iskanje nekaterih objektov globokega neba, dvojnih zvezd, Jupitrovih lun, opazovanje Lune, kometov …
* Uporaba Dobsonovega teleskopa za ročno iskanje nebesnih objektov in seveda opazovanja, tudi risanja objektov …
* Uporaba goto teleskopa, kako ga sestavimo, umeritev …, seveda opazovanja, fotografiranje teles globokega neba, planetov, dvojnih zvezd, kometov, meritve, preizkušanja različnih okularjev, mejne magnitude, ločljivosti, maksimalne še smiselne povečave, uporaba filtrov ...
* Spremljanje in risanje poti Venere kot večernice med zvezdami.
* Spremljanje in risanje Marsa med zvezdami, tudi Jupitra in Saturna (lahko tudi Merkurja), sledi razlaga retrogradnega gibanja – in pomen opazovanj za razvoj moderne znanosti, fizike, astronomije, kemije, biologije, geologije, matematike, humanizma ...
* Slikanje vrtenja neba – fotoaparat se postavi na fotografsko stojalo in osvetljuje, recimo del neba proti Severnici, vsaj 15 minut, tako dobimo sledi navideznega vrtenja zvezd, tudi barve zvezd se lahko deloma razloči.
* Slikanje meteorskih rojev, lahko ocenimo smer in radiant roja (točko neba, od koder navidezno letijo utrinki), tudi magnitudo utrinka …
* Opazovanje in risanje Sonca ali s pomočjo projekcije (bolj varna metoda) ali preko opazovanj s teleskopom, na objektivu teleskopa pa je seveda v tem primeru obvezno nameščena prav za to namenjena solarna folija (filter), to počnemo več dni zapored, preko peg se določi čas rotacije Sonca (Sonce ni togo telo, zato rotira različno hitro, glede na solarno širino); če je minimum aktivnosti, brez peg, si pomagamo s starejšimi slikami; obvezno preko štetja peg in skupin določimo ( izračunamo: R = k(10g + s) ) tudi Wolfovo število.
* Opazovanje in risanje Sonca skozi H-alfa teleskop, določanje velikosti izbruhov, morebiti hitrosti izbruhov, če pride do izmeta koronarne mase.
* v razredu pokažemo uporabo kakega programa za prikazovanje zvezdnega neba, recimo Stellariuma, tukaj je še Sky Charts / Cartes du Ciel …, mladi morajo pod zvezdno nebo, a tudi taka orodja so zlata vredna (objekte lahko centriramo, zoomiramo in spreminjamo datume, lahko gremo v zgodovino in poiščemo premike pomladišča, jesenišča, osi vrtenja Zemlje – nekoč sta bili in bosta spet »severnici« Vega in Deneb, tukaj so potepuhi - planeti skozi čas na zvezdnem ozadju, mrki skozi čas, objekti globokega neba, ozvezdja, koordinatne mreže, konjunkcije, okultacije, kometi, brez težav narišemo analemo, spremenimo opazovališče – koordinate, dodamo svoje obzorje, okolico, v program, zremo v nebo naših davnih prednikov in tako lažje razumemo tudi njihove rituale - kakor na nebu tako na Zemlji …).
* Pregled uporabnih astronomskih vsebin na spletu, tudi spletnih kalkulatorjev s področja astronomije, efemerid.
* Spremljanje aktualnih dogodkov na nebu in spremljanje človeških misij v Osončju in že tudi zunaj njega.
** Opazovanje in risanje spektra Sonca, recimo preko projekcije uklona reže z uklonsko mrežico, določimo glavne absorpcijske črte.
** Slikanje Lune, določi se premere nekaterih kraterjev, globine kraterjev, višina gora, pišče naš krater Vega (Jurij), premislimo, zakaj se pa ne vidi še krater Stefan (Jožef), poimensko določimo večje kraterje, morja, gorske verige in približno pristanek Apolla 11 leta 1969, 20. julij …
** Slikanje Sonca s teleskopom, na objektivu teleskopa pa je seveda v tem primeru obvezno nameščena prav za to namenjena solarna folija (filter), to počnemo več dni zapored, preko peg se določi čas rotacije Sonca (Sonce ni togo telo, zato rotira različno hitro, glede na solarno širino); če je minimum aktivnosti, brez peg, si pomagamo s starejšimi slikami.
** Slikanje in opazovanje Sonca skozi H-alfa teleskop, določanje velikosti izbruhov, morebiti hitrosti izbruhov, če pride do izmeta koronarne mase.
** Slikanje neba s teleobjektivom, recimo od 50 do 200 mm (čas ekspozicije okrog 30 s in več), aparat naj bo na stojalu z vodenjem (če nimate takega stojala, bo za silo tudi šlo, krajši objektivi in časi); sledi analiziranje slik, katera ozvezdja vidimo, svetlejše zvezde (morebiti barve, dvojne zvezde), katere objekte globokega neba smo ujeli – zagotovo vam ne uide M31, M33, M42, M43, Plejade (Gostosevci), Deževnice, M44, M13, M22, M8, M20 in še veliko ostalih čudovitih objektov.
** Detekcija kozmičnih delcev. Meglično komoro lahko naredite tudi sami. Gre za
difuzijsko meglično komoro na izopropanol, hlajeno bodisi s tekočim dušikom ali
suhim ledom. Na Gimnaziji Šentvid nam jo je uspelo narediti (dokaj enostavno in
nazorno se opazi sledi kozmičnih delcev) – posnetek je tudi na:
https://www.youtube.com/watch?v=knTzEOuhKwI
** Izdelava najenostavnejšega spektrografa na uklonsko mrežico - "slitless spectrograph". Rabimo uklonsko mrežico s 100 režami na mm – ima jo vsaka šola v fizikalnem kabinetu (vstavimo jo v odprtino fokuserja), seveda teleskop in digitalni fotoaparat z možnostjo namestitve na teleskop, pc za obdelavo slik. Posnamemo absorpcijske spektre svetlejših zvezd različnih spektralnih tipov (določimo osnovne črte različnih tipov zvezd – narišemo grafe jakosti spektra in jih primerjamo med seboj) in obvezno posnamemo še emisijski spekter katere od planetarnih meglic. Zelo primerna je planetarna meglica M57 v Liri - dve najizrazitejši barvi meglice sta rdeča (zaradi vodika) in modra (zaradi kisika).
*** Slikanje supernov, nov – teleskop goto, vsaj 200 mm premera objektiva (ccd kamera
ali DSLR fotoaparat), na leto se najde v oddaljenih galaksijah nekaj 100 supernov
(določi se magnituda, tip, oceni oddaljenost). Kdaj se lahko opazuje supernovo
tudi neposredno skozi teleskop, kot recimo SN 2014J.

*** Slikanje planetov s spletno kamero, teleskop 150 mm ali več, Barlowa leča okrog 5x (ali okularna projekcija), program za zlaganje in obdelavo slik (iz slik se lahko razbere prenekatere podrobnosti, iz zaporedja slik se oceni tudi čas rotacije, premik lun, velikosti površinskih podrobnosti, seveda odvisno od planeta, tudi filtrov …).
**** Slikanje svetlobne krivulje zvezde z eksoplanetom (detekcija prehoda).
**** Določanje površinske temperature zvezd preko slikanja kopic skozi B in V filtra, modelsko risanje H-R diagrama kopice, določanje starosti kopice ...
**** Uporaba radijskega teleskopa in lovljenje signala iz Rimske ceste, a večina šol takega teleskopa nima, a se lahko recimo uporabi signal vodikove črte (21,106 cm) šentviških meritev in iz Dopplerja oceni relativne hitrosti rokavov Rimske ceste.
Že ena bi veliko prispevala k verodostojnosti predmeta.
Povedano velja tudi za astronomske krožke in astronomijo kot izbirni predmet v OŠ. Obisk »Astronomsko geofizikalnega observatorija Golovec« bi moral biti skoraj da obvezen del učnega programa. V Sloveniji praktično nikjer ni postavljene javne astronomske zbirke. Pobuda za tako zbirko je bila poslana v »Tehniški muzej Slovenije« (Bistra), kjer so obljubili, da bodo enkrat v bodočnosti svoje zbirke dopolnili tudi z astronomsko in tudi z zbirko slovenskih znanstvenikov in izumiteljev (naših vzornikov – ali so res to naši vzorniki?). Držimo jih za besedo (minila so že leta). Ker je torej trenutno stanje v Sloveniji glede astronomskih zbirk zelo skromno (izjema je delno astronavtika, ki jo pokriva KSEVT - »Kulturno središče evropskih vesoljskih tehnologij« - Vitanje) - priporočam, poleg obiska Golovca in KSEVT-a, še obisk hiše eksperimentov EXPI v Kočuhi na avstrijskem Koroškem. Vodi jo fizik, koroški Slovenec dr. Samo Kupper. V EXPI imajo izjemno iskrno komoro za detekcijo kozmičnih delcev (bolje produktov kozmičnih žarkov - v veliki meri so to mioni, ki nastanejo, ko primarni kozmični žarki trčijo z molekulami naše atmosfere). Tudi sicer je v hiši eksperimentov EXPI astronomija zelo solidno zastopana. S takim obiskom damo tudi nekaj podpore naši manjšini v Avstriji (tudi planetarij v Celovcu ima del programa v slovenščini). Vsekakor je lepa izkušnja tudi obisk enega od obeh napihljivih planetarijev v Sloveniji (AD Nova – Jesenice in Krško - www.planetarium.si). Slovenija spada – to moramo povedati - med najbolj nerazvite države Evrope, saj smo edina država brez profesionalnega planetarija. V Sloveniji priporočamo še obisk Prirodoslovnega muzeja Slovenije v Ljubljani (imajo meteorita Jesenice izpod Mežakle in tudi meteorit Novo mesto, za razumevanja razvoja življenja na Zemlji pa je njihova zbirka fosilov zelo primerna – astronomija, vesolje in čudež življenja, sta dve plati iste medalje). Vsekakor se splača ustaviti tudi na domačiji matematika Jurija Vege. Zelo lepo vas sprejmejo v jedrskem reaktorju v Podgorici (imajo ličen muzej in odlične predstavitve v živo), podobno velja za jedrsko elektrarno Krško, ki smo jo večinoma kombinirali z ogledom Bogenšperka (Valvasor je bil član Angleške kraljeve družbe, dopisoval si je z znamenitim astronomom Halleyem).
So pa izjemno atraktivni tudi obiski večjih evropskih mest s staro tehnično in naravoslovno tradicijo, kjer so čudoviti tehnični muzeji, ki večinoma vključujejo tudi astronomske zbirke, astronavtiko, planetarije, Foucaultova nihala, kje se da tudi opazovati - vsaj Sonce. Je pa zmeraj prisoten problem časa in stroškov. A ekskurzije so vsekakor odlična naložba v znanje in svetovljanstvo vseh nas. Šentviški astronomi smo obiskali naslednje prestolnice znanja: Padova, Dunaj, München, Praga, Celovec, Frankfurt, London (Greenwich, Kraljeva družba, tehnični muzej), Gradec ..., nobena prestolnica nas ni razočarala. München ima enega od največjih tehničnih muzejev na svetu – in ni daleč. Na bližnjem Dunaju je naš eminenten arhitekt Maks Fabiani zgradil izjemno zvezdarno Uranio (Avstro-Ogrska Greenwich), lahko jo obiščete. Dunaj ima tudi zelo kvaliteten planetarij, prirodoslovni muzej z meteoritom iz Avč, zelo priporočam obisk stare univerze na Dunaju (tam vas pod arkadami »pričakajo« Jožef Stefan, njegov učenec Boltzmann, Franc Miklošič in ogromno ostalih eminentnih znanstvenikov, pa še dobro kavo imajo ...). Na Dunaju se sedaj lahko obišče tudi grob Hermana Potočnika – Slovenci smo res močno zaznamovali Dunaj (Plečnik, Fabiani, Miklošič, škof Jurij Slatkonja z dunajskimi dečki, Jožef Stefan, Andrej Perlah, Bernard Pergerl ...). Tudi Keplerjeva in delno Einsteinova, Plečnikova, Brahejeva Praga ima ogromno astronomskih vsebin (poleg znamenite srednjeveške astronomske ure Praški orloj, je tukaj imeniten planetarij, tehnični muzej, Keplerjev muzejček in zelo poučen stari observatorij nad mestom – veliko vam pokažejo – in Prage noben ne zapusti žejen ali slabe volje ...). O Londonu, mesto nultega mereidiana, pa ni potrebno izgubljati besed – je nekoliko daleč – a mesto Hooka, Newtona, Halleya, Christophera Wrena ... nas lahko kar za nekaj dni priveže na sedanjost in hkrati na zgodovino astronomije in fizike, sveta.
Literatura za učence
Potrebno je zbrati astronomske vsebine, gradivo, literaturo za učence, kot dopolnilno
(prostovoljno) zanimivo branje, html, pdf dokumenti, knjige (France Avsec, Marijan Prosen:
Astronomija. DZS: Ljubljana, 1971, ponatisi ...).
Recimo, da je dovolj naštevanj in vprašanj. Potrudimo se torej, da se astronomija še bolj približa vsakemu od nas – šola je naš drugi dom.
- ...
Metoda – »čez 15 let!«
Ko razmišljamo o vsebini in metodah izbirnega predmeta astronomija (in zagotovo velja
za vse ostale predmete), je smiselno vprašanje - kaj pričakujemo od povprečnega
učenca, da bo znal, razumel, ohranil v spominu, recimo po 15-ih letih, od naših
astronomskih prizadevanj iz šole (iz razreda, kontrolk, mature, iz opazovanj, taborov)?
Kaj bi si želeli, da bi vaši (naši) učenci poučnega pokazali, povedali o astronomiji
svojim znancem, otrokom ali pozneje celo vnukom (ker so se tega naučili v šoli)?
Za katere vsebine nam je danes žal, da nam jih niso predstavili v procesu šolanja
(čeprav smo takrat videli mnoge učitelje kot tečneže)?
Vprašajmo se tudi, kak smisel ima za naše življenje množica neutrjene snovi iz srednje
šole, ki se je čez leta sploh več ne spomnimo ali pa je že v šoli ne razumemo,
je ne znamo umestiti v noben kontekst. In ravno to se dogaja s predmeti, ki imajo
skromno število ur, učni program pa je prenatrpan, zahteven. Fizika, kemija, biologija ...
so že taki zahtevni predmeti, kjer praktično ni časa za še kako prepotrebno utrjevanje
učnih vsebin. In odnos mladih do teh predmetov je precej odklonilen (pustimo izjeme).
Astronomija je lahko tako v podobni ali še nekoliko hujši zagati (a ni nujno). Lahko
pa je prav astronomija, kot samostojen predmet, krasna nadgradnja fizike, biologije, kemije.
Astronomija lahko v celoto poveže vse omenjene predmete (tudi ostale), jim da (nov)
smisel, ki ga mladi, ko begajo iz ure v uro, iz predmeta v predmet, v tej ihti ne
zaznajo (ne vidijo smisla v množici nepovezanih predmetov). Recimo - astronomija nam
lahko pojasni, od kod kemijski elementi, od kod enormne količine izsevane energije zvezd,
Sonca, zakaj je nastalo življenje ravno na Zemlji, do kdaj bo življenje na Zemlji še imelo
pogoje za obstoj, zakaj ima Zemlja ravno tako (»idealno«) kemijsko sestavo, zakaj
je kamniti planet, astronomija nam razloži od kod letni časi in klimatski pasovi, pojasni
nam pomen časa in koledarja, matematiki pa da možnost, da se izkaže pri opisu vesolja,
recimo pri opisu poti, gibanja planetov, astronomija nam lahko krasno dopolni fiziko pri
klasični mehaniki, utrdi izjemen pomen narave povsod prisotne svetlobe, spektrov,
Dopplerja (Hubble-Lemaîtrov zakon je na nek način uvod v kozmologijo), Stefanov zakon nam
nepričakovano razkrije skrivnosti življenja zvezd, planetov, astronomija nam poda
razloge za podnebne spremembe in hkrati organsko pokaže na pomen ekologije. Štiri
osnovne sile narave in njihovi nosilci (ki bi morale dobiti domovinsko pravico v
šolskem prostoru preko astronomije) nam utemeljijo:
obstoj atomskega jedra, svet atomov (elektro-magnetna sila), gradnike življenja,
molekul in gravitacijo, ki povezuje pline v zvezde, planete, v galaksije ...
Astronomija nam torej podaja določene primarne odgovore, ki jih brez nje ni moč
utemeljiti zgolj preko klasične šolske in študijske predmetne sheme – in tega načrtovalci
izobraževanja žal še niso dojeli. Še zmeraj vztrajamo pri shemi pouka »iz leta 1600 ...«
ali pa smo celo korak nazaj (V renesansi so poučevali sedem umetnosti: gramatika, retorika,
dialektika, geometrija, aritmetika, glasba, astronomija. Izbor v kontekstu časa sploh ni
bil slab!). Nazaj v času, pred renesanso, pred Kuzanskim, Kopernikom, Keplerjem, Galilejem ..., saj
otrokom ne omogočamo pogleda v zvezdno nebo in razlage videnega ...
Določeni predmeti pa imajo samoumevno šolsko pravico izvajanja 9 ali celo
več let, kot da bodo vsi naši otroci nekoč Mozarti, Michelangeli ali Hilberti.
A na koncu večina ne zna risati (in mislijo, da Leonardo da Vinci igra za Barcelono in
Kepler za Clipperse), ne poznajo not, ne vedo, kaj je logaritem in ne znajo izraziti polmera
iz enačbe
v2/r = GM/r2 …
Ni vse črno, a veliko zamujamo, ker so
šolska vrata zaprta za nova vedenja, spoznanja – brez vsake potrebe. Če še enkrat
ponovimo - v renesansi so poučevali sedem umetnosti: gramatika, retorika, dialektika,
geometrija, aritmetika, glasba, astronomija. Izbor v kontekstu časa sploh ni bil slab!
Ali se v našem šolstvu sploh da kaj spremeniti – na bolje? Seveda se DA – tudi z uvedbo astronomije v šole (da se spet vsaj malo približamo renesansi) in z več raznolikosti šolskih programov – zagotovo z uvedbo naravoslovne gimnazije, progam skoraj v celoti že poznamo iz prve polovice devetdesetih let 20. stoletja.
Ko se v mraku začnejo prižigati zvezde, je to eden najlepših in najbolj pričujočih dogodkov naših dni.
Sledi kratek povzetek oseb in teorij, ki so z opazovanji, predvsem pa na začetku z bolj ali manj posrečeno intuicijo, prispevali k današnjemu modelu vesolja – ki nikakor ni dokončen. Po vrsti si sledijo: ('anonimni' Kaldejci - Grki - »Pitagora«), Aristarh, Ptolemaj, srednjeveški učenjaki Oresme, Kuzanski, renesančni astronomi - Kopernik, Brahe, Lippershey, Kepler, Galilei, Huygens, Hooke, Römer, Halley, Newton, Leibniz, Michell, Coulomb, Volta, Fraunhofer, Niépce, Sturgeon, Bessel, Doppler, Maxwell, Boltzmann, Stefan, Clausius, Edison, Lorentz, gospa Henrietta Swan Leavitt, Rutherford, Bohr, Einstein, Schwarzschild, de Sitter, Friedmann, De Broglie, Schrödinger, Heisenberg, Lemaître, Hubble, Gamov, Hoyle, Penzias, gospa Vera (Cooper) Rubin, Alan H. Guth, »Perlmutter, Schmidt in Riess«. Higgs, »Weiss, Barish in Thorne«. Sledijo slike v enakem vrstnem redu in nato kratek povzetek njihovih dognanj.
Hooke - ni sli / Michell–ni sli

Sledijo letnice, imena in spoznanja – kratek opis (za nekatere osebe boste zagotovo
prvič slišali, nekateri dosežki se zdijo čisto tehnične narave, a brez njih ni moderne
znanstvene metode, ni astronomskih meritev, ni modelov tega sveta ...):
• 3000 do 500 pr. Kr. (okoli) : najstarejši zapis danes t. i. »Pitagorovega« izreka
( a2 + b2 = c2 );
zagotovo so ga poznali že Babilonci
vsaj 1500 let pred Pitagoro (živel je v 6. stol. pr. Kr.). V tem pomembnem
izreku se skriva zgoščen prikaz človeškega razvoja zadnjih 100000 let, ko
smo izoblikovali govor (izjemen korak). Pred približno 8000 leti pa se je
zgodil prehod v moderno družbo - del človeškega rodu se je namreč začel
ukvarjati s poljedelstvom, ki je zahtevalo kompleksno načrtovanje opravil
obdelave zemlje, prostora, časa, koledarja, štetje, merjenje površin, meja,
načrtovanje bivališč, svetišč; šli smo na pot pisave, novega vedenja, zavedanja,
samorefleksije. Ustvarili smo nova komunikacijska orodja (govor, novo organizacijo
družbe z vpeljavo merjenja prostora in časa, pisavo, matematiko, astronomijo,
filozofijo, poezijo, ...) in korenine teh začetkov so danes nezavedno vgravirane
v ritem našega vsakdana, v temelje modernih civilizacij – tudi in predvsem v
kozmološke modele. Od takrat smo prevzeli osnove geometrije (recimo krog razdeljen
na 360 delov, »Pitagorov« izrek ...), osnove koledarja (leto dolgo okrog 365 dni),
teden dolg 7 dni – vsak dan je bil posvečen enemu od nebesnih teles, ki se premikajo
med zvezdami (5 planetov ter Sonce in Luna), periodo sarosa za napovedovanje mrkov (18 let,
11 ali 10 dni, 8 ur) ... To je bil tudi čas začetka rudarjenja, pridobivanja kovin, posledično
novih orodij in vedenj o snovi, naravi, začetki kemije – in tudi to so materialni in duhovni
temelji moderne družbe (danes že skoraj samoumevni).
Prve začetke geometrije lahko najdemo v Mezopotamiji, Egiptu (Rhindov papirus) in v dolini
Inda okoli leta 3000 pr. Kr. Ta geometrija je bila predvsem praktično usmerjena.
Preučevala je probleme povezane z zemljemerstvom. Tudi sama beseda
geometrija izvira iz
grških besed [ge] (starejša oblika: [gaja]) = zemlja +
[metria] = merjenje
(direkten prevod je torej: geometrija = zemljemerstvo). Beseda geometrija
(zemljemerstvo) torej razkriva, da je začetek poljedelstva hkrati katalizator
razvoja matematike – poljedelstvo je dalo zagon razvoju matematike, seveda tudi
astronomiji, fiziki, biologiji, kemiji, filozofiji, teologiji, medicini,
ostalim vedam.
V tem kontekstu
moramo poseči prav na začetek stvarstva, kot so ga nekoč dojeli naši predniki
– in tako ne moremo mimo
omembe zametkov preproste kozmologije iz svetih spisov – posebno iz Stare zaveze
(povezava na začetek vesolja, na modelski veliki pok iz citata »Fiat Lux!
Bodi svetloba! - Let there be light« - Prva Mojzesova knjiga/Geneza) –
v kontekstu časa seveda.
V Družini (27. okt. 2024, rubrika LOGOS) je ga. N. Gačnik na primer omenila Izakove (Isaac, Sveto pismo) misli:
"Čas se giblje tam, kjer je delovanje teles; kjer ni časa, ni teles; kjer ni teles, tam ni ničesar,
kar bi bilo višje ali nižje od enotne hipostaze, saj je v vsaki hipostazi
enakovrednost, kot je ..." Zadnji citat zelo spominja na moderne definicije prostor-časa in začetka vesolja.
Iz že omenjenega citata »Fiat Lux!
Bodi svetloba! - Let there be light« sledi, da sploh ni čudno, da
je širitev vesolja, »veliki pok« iz drobne vroče točke (t. i. prvobitnega
atoma) prvi vpeljal – ne boste verjeli kdo (saj se žal v šolah
in medijih o tem ne govori) - matematik, fizik in župnik hkrati,
Belgijec Georges Lemaître leta 1927 (preko lastnih rešitev Einsteinovih enačb polja splošne
relativnosti). Danes to krivico popravljajo in na spletu že lahko najdemo Hubble–Lemaîtrov
zakon v = HD (ki pravi, da je širjenje vesolja, hitrost oddaljevanje
galaksij »v«, kar sorazmerna oddaljenosti galaksij D, sorazmernostna konstanta H pa se
posledično imenuje Hubble-Lemaîtrova konstanta). Pred desetletji se je govorilo le o Hubblovem
zakonu in Hubblovi konstanti.
Med vsemi članicami Mednarodne astronomske zveze je bilo
leta 2018 na Dunaju opravljeno glasovanje in sprejeta je bila resolucija o
preimenovanje Hubblovega zakona v Hubble–Lemaîtrov zakon.
Protislovno Hubble-Lemaîtrova konstanta še danes ni
dokončno določena (obstajata dve vrednosti) in je poleg iskanja temne snovi in
temne energije, v samem središču astronomskih raziskovanj, v srcu skrivnostne kozmologije. Kozmologija
je veda o nastanku in razvoju, kronologiji vesolja, o izvoru vsega -
ki združuje tako opazovalno astronomijo na veliki skali in fiziko osnovnih delcev
na drugi strani naše realnosti (atomi molekule). Toliko za uvod v kronologijo raziskovanja
vesolja.
Sledijo letnice in imena oseb, ki so, po trenutnih znanih virih, veliko
prispevale v zakladnico znanja, resnice o fizki sveta, vesolja, življenja, človeka.
• 310 pr. Kr. - okoli 230 pr. Kr. : Aristarh predlaga geocentrični in tudi heliocentrični sistem - vesolje. Tukaj podajmo nekaj izjemnih antičnih metod merjenja razdalj – brez razdalj ni kozmoloških modelov. Aristotel je pred približno 2350 leti utemeljeno trdil, da je Zemlja okrogla, ker ima ob Luninih mrkih Zemljina senca na površini Lune okrogel obris. Eratosten je pred 2260 leti s pomočjo razdalje med Aleksandrijo in Sieno (Asuanom) in vpadnih kotov Sončevih žarkov določil polmer Zemlje (računanje polmera iz loka in kota). Nekoliko pozneje in natančneje ter z boljšo metodo sta razmerje Zemlja-Luna določila še v antični Grčiji Aristarh in kasneje Hiparh.
• 190 Hiparh pr. Kr. Niceja – okoli 120 pr. Kr. Rodos: Grk Hiparh je bil izjemno natančen opazovalec, analitik in poznavalec kaldejske astronomije. Bil je hkrati astronom, geograf in matematik. Izvedel je zelo natančne meritve položajev zvezd in njihovih navideznih magnitud, ki jih je radelil na lestvici od 1 do 6 (kar še danes dokaj dobro velja). Naredil je prvi veliki katalog z 850 zvezdami, v katere je poleg njihovih položajev zapisal tudi navidezne magnitude. Meril je dolžino tropskega leta in sinodskega meseca. S primerjavo s podatki iz prejšnjih katalogov je odkril precesijo enakonočij in neenakomerno gibanje Lune. Zdi se, da je prav Hiparh izumil astrolab in amilarno sfero, ki jo je uporabljal med izdelavo zvezdnega kataloga. Prvi je določil lege krajev na Zemlji s pomočjo geografskih (geografskih) zemljepisnih širin in dolžin (vzporednike in poldnevnike je vpeljal že Eratosten), Hiparh je tudi začetnik trigonometrije. Tudi Klavdij Ptolemaj je Hiparhove rezultate vključil v svoja dela. Hiparh je s pomočjo trajanja Luninega mrka določil, da v Zemljino senco (med Luninim mrkom) lahko postavimo približno 8/3 Lun. Tako so v antiki že dokaj točno ocenili razdaljo Zemlja – Luna in sicer na 62 polmerov Zemlje. Ker so poznali velikost Zemlje, so tako lahko izračunali tudi velikost Lune. Aristarh pa je preko trikotnika Luna (prvi krajec Lune), Zemlja, Sonce ocenil razdaljo »Zemlja – Sonce« na 19 razdalj »Zemlja – Luna« (prava vrednost je sicer 397x več). V bistvu je bila to za tiste čase, glede na okorne metode merjenja kotov, drzna in dolgoročno še zmeraj izredno pomembna ocena (nakazovala je, da je Sonce veliko večje od Zemlje, in kako je to mogoče, da bi veliko Sonce krožilo okrog majhne Zemlje ... – danes vemo, da je skupno težišče praktično skoraj v središču Sonca in tako je videti, kot da Zemlja potuje okrog Sonca, v resnici pa obe telesi potujeta okrog skupnega težišča – kar se premalo poudarja).
• 168 : Ptolemaj privzame geocentrično sliko vesolja. Slika deluje matematično solidno, a je daleč od dejanske dinamike. Takratni argument za Zemljo v središču je - s prostimi očmi nezaznavna paralaksa zvezd – o argumentu nezaznavne paralakse piše že Aristotel. Ptolemaj je zbral grška spoznanja v 13 knjigah Velikega matematičnega sistema astronomije, bolj znan kot latinski Almagest (izhaja iz grške besede megiste - "največji"), v skladu z naslovom arabskega prevoda, v katerem je njegov nauk ohranjen (v 15. Stoletju so s padcem Bizanca prišla tudi grška besedila Almagesta v Italijo). Tako posredno poznamo mnoge antične avtorje, za katerimi bi se sicer zgubile vse sledi. V Almagestu, kot smo že poudarili, Ptolemaj razlaga starodavno znanost o prostoru, vesolju znotraj, na prvi pogled samoumevnega, geocentrizma – kar je veljalo kot resnica do renesanse – do Kuzanskega, Kopernika, Keplerja.
• 1320 – 1382 : Oresme dopušča tudi heliocentrični sistem - bolj smiselno se mu zdi, da okrog masivnejšega Sonca potujejo manjši planeti, a sprejema tudi, takrat splošno uveljavljeno, geocentrično sliko vesolja.
• 1401 – 1464 : Nikolaj Kuzanski je v »Učeni nevednosti« zatrjeval, da se Zemlja vrti okoli svoje osi in kroži okoli Sonca, da v vesolju ni nobenega zgoraj ali spodaj, da je svetovje brezmejno, da so zvezde druga sonca in vežejo nase druge naseljene svetove.
• 1514 : Kopernik še enkrat (po Aristarhu v antiki in srednjem veku - Orseme, Kuzanski, ...) predlaga heliocentrično sliko vesolja.
• 1588 : Tycho Brahe nastopi proti heliocentričnemu modelu, ker pri opazovanjih zvezd ne opazimo paralakse (ravna podobno kot Aristotel); predlaga sliko, da Sonce kroži okrog Zemlje, planeti pa okrog Sonca (enako sliko je podal že Grk Apolonij). Njegove meritve lege Marsa so odločilnega pomena pri nastanku Keplerjevih zakonov nebesne mehanike.
• 1608: optik Hans Lippershey predstavi v nizozemskem parlamentu prvi uporabni daljnogled (teleskop), je še nekaj drugih teorij o izumu daljnogleda (daljnogled predstavlja prelomni korak v opazovalni astronomiji).
• 1609 : Johannes Kepler – izpelje zakone gibanja planetov: so ključni za potrditev
Kopernikovega heliocentričnega modela (seveda tudi potrditev razmišljanja Kuzanskega
in Oresma) - planeti se premikajo po elipsah in ne krogih (leta 1618 zapiše z besedami
tretji zakon:
T2/a3 = konst,
ki je že vseboval pot do gravitacijskega zakona).
• 1610 : Galilej s teleskopom odkrije lune, ki krožijo okoli Jupitra: hud udarec za Ptolemajev geocentrični model.
• 1659 : Huygens, izpelje izjemno pomemben izraz za centripetalno silo:
Fr = m*v2/r.
• Hooke (1635 - 1703) : sklepa, da je gravitacijska sila odvisna od 1/r2.
• 1675: Römer izmeri (oceni) hitrost svetlobe s pomočjo zakasnitve okultacije Jupitrove lune (končna hitrost svetlobe je izjemnega pomena pri opisu vesolja in pri omejitvah, ki ga to dejstvo prinaša s sabo).
• 1684: Halley komunicira z Newtonom in mu predlaga določene pomembne rešitve pri matematičnem opisu gibanja nebesnih teles.
• 1687 : Newton objavi »Philosophiae Naturalis Principia mathematic« (rec. Matematične metode v naravoslovju)
(zapis gravitacijskega zakona
Fg = Gm1m2/r2
[ m1•---->--------r-------<-----• m2 ] ).
• 1676–1689: Gottfried Wilhelm Leibniz govori o ohranitvi žive sile
(conservation of 'vis viva'), omenjal je količino, ki ima dimenzijo energije in
iz katere izhaja današnji koncept energije, njenega ohranjanja; definiral jo je
kot produkt mase in kvadrata hitrosti določenega telesa (danes je tak produkt
povezan z definicijo kinetične energije 'mv2/2'), hkrati pa je bil na
sledi potencialni energiji 'mgh', bolje (-GMm/r). Pozneje ga je v tej ideji zelo
podpirala matematičarka in fizičarka gospa Émilie du Châtelet (1706 - 1749). Prvi
pa preimenuje omenjene Leibnizove pojme v energijo Thomas Young leta 1807. Zagotovo
je pri vpeljavi energije veliko vlogo igral opis poenostavljenega sistema v katerem
trčita dve telesi. Pri tem ohranitev gibalne količine, ki jo je kot zadosten opis
narave zagovarjal Newton, ni dala zadovoljivih odgovorov – pri prožnem trku se brez
vpeljave (kinetične) energije ni dalo izračunati končnih hitrosti, pri neprožnem trku
pa se ni dalo razložiti končnih posledic gibanja (deformacije, segrevanja teles, ...).
Pojem energije, toplote in dela je - poleg sile in ohranitvenih zakonov energije,
gibalne količine, vrtilne količine ... – eden od temeljnih kamnov opisa narave in
s tem vesolja. V astronomiji je, med drugimi, zelo pomembna kinetična
(Ek = mv2/2) in potencialna energija (Ep = -GMm/r),
recimo za sistem Sonce – planet velja:
E = Ek + Ep = mv2/2 - GMm/r .
Leta 1676 je Leibniz razvil infinitezimalni račun, neodvisno od Newtona;
velja da je odvod funkcije f(x) strmina tangente (df(x)/dx = f(x)')
na dano funkcijo v dani točki x:
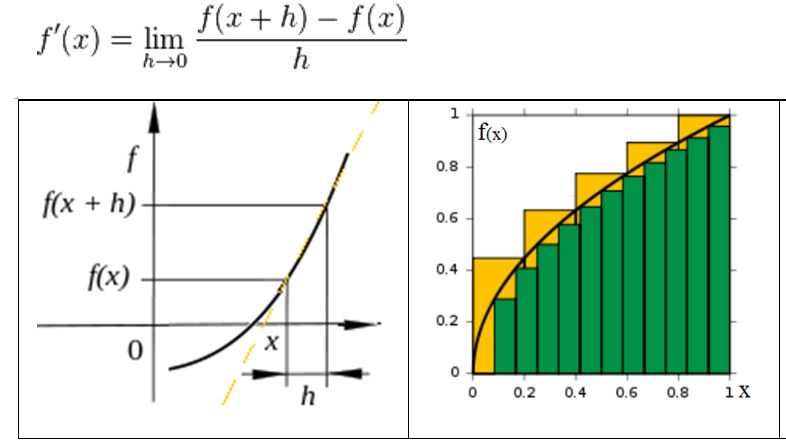
Recimo da poznamo funkcijo
F(x) = xq + 1/(q + 1), odvod je: F(x)'= f(x) =dF(x)/dx
= d(xq + 1/(q + 1))/dx = xq,
integral pa je (geometrijsko tudi ploščina pod funkcijo) nasprotna funkcija odvodu.
Iz prejšnjega primera velja, da je integral za funkcijo f(x) = xq enak
F(x) = xq + 1/(q + 1).
Integral kot vsoto ( sumo z znakom
∫
) majhnih ploščin f(x)dx zapišemo kot (
F(x) = ∫x1/2dx = x3/2/(3/2) + k. = 2x3/2/3 + k.):
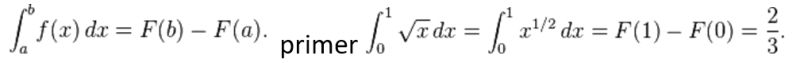
Že prej navedeni Leibnizevi, Newtonovi in Huygensovi fizikalni in
matematični pojmi so osnovna orodja pri matematičnem opisu sveta in
vesolja. Seveda pa brez razumevanja dogajanj v vesolju matematični opis
ne velja prav nič.
• 1783: duhovnik in geolog John Michell se sprašuje ali gravitacija vpliva na svetlobo, ali imajo nekatere zvezde tako veliko maso, da svetloba ne more pobegniti z njih (imenuje jih temne zvezde, pravilno izpelje celo njihov polmer iz predpostavke, da je ubežna hitrost iz zvezde enaka hitrosti svetlobe r = 2GM/c2). To je osnova za teorijo črnih lukenj in Einsteinove izračune več kot 120 let pozneje. Do enakega zaključka je nekaj let pozneje prišel matematik Pierre Simon de Laplace.
• 1783: Charles Augustin de Coulomb je leta 1783 s svojo torzijsko tehtnico
prvi raziskoval in objavil izraz za silo med dvema točkastima električnima nabojema.
Absolutna vrednost sile je premo sorazmerna produktu obeh nabojev in obratno sorazmerna
s kvadratom razdalje med njima. Sila je privlačna, če sta naboja različno predznačena
(eden pozitivno in drugi negativno), in odbojna, če sta enako predznačena:
Fe = e1e2/(4ε0πr2)
ali
Fe = q1q2/(4ε0πr2).
Ta zakon
je pomemben za razlago atomske slike sveta in
seveda tudi vesolja, matematično je enak gravitacijskemu zakonu.
• 1800: Alessandro Volta je na osnovi Galvanijevih raziskav sestavil dve ploščici
iz bakra in cinka, vmes pa je dal klobučevino prej namočeno v žvepleno kislino.
Takšne elemente je povezal in sestavil prvo električno baterijo (Voltov člen,
kemijske reakcije so
[ cink: Zn => Zn2+ + 2e-; žveplena kislina:
2H+ + 2e- › H2 ]).
S tem je ustvaril nov vir elektrike, ki je precej razširil
eksperimentalne in uporabne možnosti, kar je bil praktični uvod v elektrifikacijo
sveta – v naš svet svetlobe, motorjev, strojev, ekranov, računalnikov, telekomunikacij,
izjemne informatike, računalniških modelov, obdelave podatkov, ta orodja so nepovratno
zaznamovala vse znanosti, tudi astronomijo ...
• 1814: Joseph von Fraunhofer je med preskušanjem svojih izjemnih prizem in raziskovanjem
Sončevega spektra, odkril - po njem imenovane – številne temne absorpcijske črte v
Sončevi svetlobi. To odkritje je čez desetletja postala osnovna metoda raziskovanja
vesolja (iz črt se da določiti atomska zgradba in temperatura oddaljenih zvezd, galaksij,
iz Dopplerjevega premika črt pa hitrosti zvezd
[ v/c = Δλ/λ ],
galaksij, plinov,
poznamo tudi gravitacijski premik črt ...). Spektralne črte so tudi omogočile spoznanje,
da se vesolje širi in to spet s pomočjo Dopplerjevega (rdečega) premika galaksij in
tozadevnega Hubble-Lemaîtrovega zakona ( v = HR ). Preko premika spektralnih črt smo detektirali
tudi temno snov, ki je je celo veliko več kot vidne snovi. Danes vemo, tudi preko Bohrove
slike atoma, da vsak atom seva ali absorbira zgolj njemu lastne valovne dolžine
svetlobe – atome torej ločimo po spektrih, ki jih seveda določajo energijska stanja,
ki so vezana na število protonov v jedru. Še zanimivost - leta 1801 se je podrla
optična delavnica, v kateri je kot 14-letni deček stanoval in delal tudi Fraunhofer -
in bil je edini preživeli.

• 1822: Nicéphore Niépce izumi metodo foto jedkanice in tako nastane prva obstojna fotografija (a ekspozicija je trajala kar nekaj ur). 1839 je Jacques Daguerre našel kemijsko osnovo za permanentni fotografski pozitiv – za nekoliko krajše ekspozicijske čase. Slovenec Janez Avguštin Puhar pa je leta 1842 izumil fotografijo na steklo, z zelo kratkim časom ekspozicije - 15 sekund – take slike se dajo tudi reproducirati. Fotografija je v znanosti postala nepogrešljivo orodje objektivnega zaznavanja in obdelave podatkov – tudi v astronomiji. Danes je klasični kemijski fotopostopek zamenjala digitalna fotografija, tozadevno pa so se možnosti uporabe zelo povečale, tudi sama računalniška obdelava posnetkov je zelo napredovala. Tako lahko recimo preko elektromagnetnih valov sprejemamo slike iz sond na robu Sončevega sistema.
• 1824: William Sturgeon je kot samouk (veliko je bral) izumil elektromagnet. Njegov prvi elektromagnet je bila stara železna podkev (pa naj kdo reče, da podkev ne prinese sreče), ki jo je ovil s približno 18 ovoji bakrene žice (izolirane žice takrat še ni bilo). Železo je polakiral, da ga je izoliral od navitja žice. Ko je pognal tok skozi tuljavo, je železo postalo namagneteno; to je bil korak v električne generatorje, elektromotorje, transformatorje, v električni nihajni krog kondenzatorja in tuljave – oddajnike in sprejemnike, v svet izjemnih novih tehnologij, ki so danes temelj moderne družbe – moderne znanstvene metode, tudi astronomije.
• 1831: Michael Faraday uspe s pomočjo indukcije (premikanjem prevodnika v magnetnem polju) ustvariti prvo inducirano napetost in s tem električni tok (prej so uporabljali le nerodne baterije). Faradayev indukcijski zakon pravi, da je v zanki inducirana napetost enaka negativni časovni spremembi objetega magnetnega pretoka Ta medsebojna povezanost kaže, da sta električno in magnetno polje povezani, kar je kmalu razkrilo, da je svetloba v bistvu elektromagnetno valovanje – kar matematično opiše Maxwell. Faradayeve meritve zasuka polarizacije svetlobe v magnetnem polju so dodatno potrdile, da je svetloba povezana z električnim in magnetnim poljem (pravilno je tudi sklepal, da za prenos elektromagnetnega valovanja ni potrebno nobenega medija, etra). Michael Faraday se je nekoč trudil razložiti ministru za finance W. Gladstoneu in drugim politikom, kako pomembno je njegovo novo znanstveno odkritje - indukcija. Edini komentar Gladstonea je bil: »A navsezadnje, zakaj pa je to sploh uporabno? Zakaj, gospod,« je odgovoril Faraday: "obstaja velika verjetnost, da boste uporabo lahko kmalu obdavčili!"
• 1838: Bessel izmeri paralakso zvezde 61 Laboda, tako tudi dokaže, da zvezda leži daleč onstran solarnega sistema, in da Zemlja potuje »okrog« Sonca (pade eden zadnjih dvomov, ki so še držali geocentrizem pri životarjenju).
• 1842: zdravnik Julius Robert von Mayer objavi vrednost mehanskega ekvivalenta toplote; določil jo je v poskusu, v katerem je konj gnal stroj za mešanje papirne pulpe v kotlu – primerjal je opravljeno delo z dvigom temperature; Mayer je pravilno postavil in razumel tezo o ohranitvi energije (recimo mehanične in notranje energije, ki se lahko pod določenimi pogoji transformirata ena v drugo) še pred, iz učbenikov bolj znamenitima gospodoma, Joulom in Helmholtzom.
• 1842: Doppler razloži fizikalni pojav pri valovanju, ko zaradi gibanja vira valovanja,
opazovalca ali obeh nastane razlika v valovni dolžini in frekvenci zvoka ali svetlobe
(ta pojav je v astronomiji eno od glavnih orodij pri opisu dinamike zvezd, galaksij,
vesolja):
v/c = Δλ/λ.
• 1862: James Clerk Maxwell zapiše osnovne zakone elektrodinamike,
ki povezujejo električno in magnetno polje v elektromagnetno polje
ter opisujejo njegove časovne spremembe in širjenje v prostoru.
Svetloba (elektromagnetno valovanje) nam prinaša osnovne informacije
iz vesolja, za svoj prenos ne rabi nobenega medija (sklepal že Faraday),
njena hitrost je c=3*108 m/s in je maksimalna možna hitrost v vesolju –
iz tega izhajajo tudi Lorentzove transformacije in teorija relativnosti
in vsi kozmološki modeli morajo te lastnosti svetlobe upoštevati. Hitrost
svetlobe se izraža z osnovnima konstantama
c = 1/(εoµo)1/2 = 299792458 m/s,
kjer sta εo in µo
influenčna in idukcijska konstanta.
Maxwellove enačbe za električno polje
E in magnetno polje B (magnetni pretok je
Φ = BS, q je naboj, A je površina,
s je dolžina, i je tok):
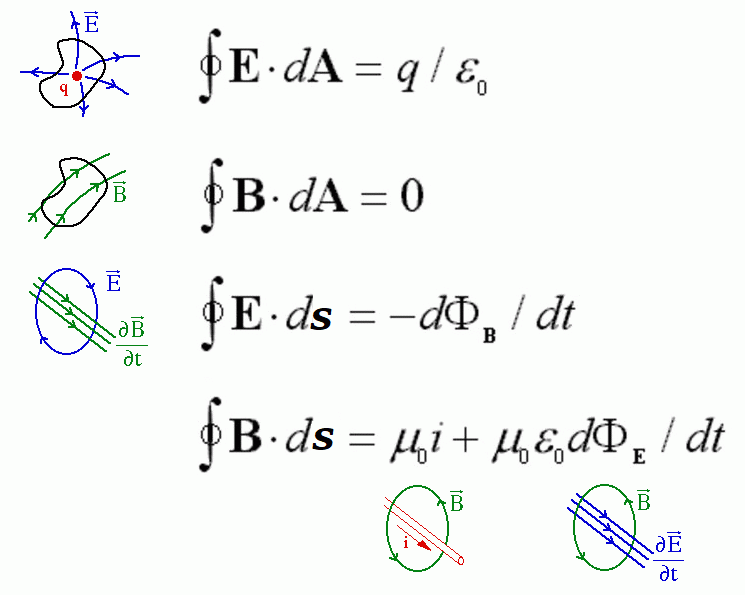 |
Električni (E) pretok skozi zaključeno ploskev (A) je enak objetemu naboju
q (Gaussova zakona o pretoku).
Magnetni pretok (B) skozi zaključeno ploskev (A) je enak nič – magnetne silnice so namreč zmeraj sklenjene. V zanki inducirana napetost (U = ∳Eds) je enaka negativni časovni spremembi objetega magnetnega pretoka ( dΦm/dt = d(BS)/dt - Faradayev indukcijski zakon). Magnetna napetost (∳Bds) vzdolž zaključene zanke je enaka vsoti objetih tokov in premikalnih tokov (Amperov zakon). |
• 1877: Ludwig Edward Boltzmann izpelje, iz statistike gibanja plina,
enačbo, ki povezuje entropijo S in stopnjo neurejenosti sistema:
S = kB ln (p)
kjer je P število možnih mikroskopski stanj, oziramo verjetnost stanj.
Entropija se v zaprtem realnem sistemu s časom lahko samo veča (narašča,
je pozitivna količina) – zmožnost za delo pa je s tem manjša. Enačba je
konceptualno veljavna za večino nepovratnih (ireverzibilnih) dogodkov.
Razloži nam tudi, zakaj se staramo in zakaj se ne moremo pomladiti,
bolje rečeno – ostati zdravi … A življenje, narava je ponudila boljšo
rešitev – to so otroci, ki so (po logiki genetike) boljši od predhodnih
generacij. Saj tako so tudi nastale izjemne življenjske oblike, tudi človek.
Znameniti kvantni fizik Erwin Schrödinger zato uvede »čudež« t. i. negativne entropije.
Zakaj? Princip življenja je namreč ravno nasproten procesom v mehaničnem, neživem svetu,
kjer se entropija (nered) samo povečuje (poznana je zgodba o toplotni smrti vesolja –
izenačenje temperatur) – a pri življenju se začuda lokalno in začasno entropija manjša
in posledično veča red. Zakaj? Vsako bitje je namreč »maksimalno« urejeno, povečuje red
– recimo, ko se delijo celice, ko odrašča … Boltzmann je razvil tudi kinetično teorijo
plinov, kjer je kinetična energija plinskega delca sorazmerna absolutni temperaturi,
izpeljal je tudi porazdelitve gibanja molekul plina.
• 1879: Jožef Stefan pride preko absolutne temperature do zakona o sevanju črnega telesa ( j = σ*T4 ), zakon je ključ do moderne astrofizike, prasevanja, razlage življenja vesolja - kozmologije, energijske bilance Zemlje, dogajanj v njeni atmosferi (vremena), ... Z njim računamo tudi temperaturo vesolja, razdalje do zvezd, naselitvene cone okrog zvezd (iščemo planete primerne za življenje), je eden od ključev do prapoka. itn.
• 1865: Rudolf Clausius vpelje entropijo kot količnik med izmenjano toploto in temperaturo: ( δS= δQ/T ), ki se pri reverzibilnih (ponovljivih) spremembah ohranja, pri ireverzibilnih (nepovratnih) spremembah pa se veča (tako se zdi, da se v vesolju entropija veča). Ena izmed razlag entropije trdi, da ker se s časom entropija veča, se veča tudi nered in s tem zmanjšuje zmožnost opravljanja dela - okrog interpretacije entropije se med znanstveniki krešejo vroče razprave. Nekateri entropiji v vesolju pravijo tudi toplotna smrt vesolja (idejo poda William Thomson že v letih 1851 - 1862) – torej se vesolje kot sistem v neskončnosti bliža temperaturi 0 Kelvinov. Če dodamo še opcijo, da bodo vsi delci razpadli, je slika končnega vesolja še bolj skrivnostna. Drugi scenarij, drugo ugibanje pa predvideva, da maksimalna možna entropija vesolja narašča hitreje od toplotne smrti - temu pojavu rečemo tudi »entropijska vrzel« in naj bi se pojavila že ob samem začetku nastanka vesolja. Malo zapleteno – a ti pojmi še čakajo popolnejših fizikalno-matematičnih modelov na podlagi novih meritev, spoznanj.
• 1880: Thomas Alva Edison dobi patent za žarnico (polnjeno z ogljikovo nitjo), uporabi višji vakuum in še učinkovito žarilno nitko (polnilo iz ogljika z visoko upornostjo), kar je njegovo žarnico naredilo trajno in zato uporabno. Nekateri viri celo navajajo 22 kronoloških soavtorjev, že leta 1802 Humphry Davy (kmalu po izumu baterije) spusti električni tok skozi tanek listič platine, ki je zasvetil. Tehnologija žarnic (vakuuma v steklenih bučkah) je močno vplivala na razvoj elektronk, diod, tranzistorjev, pozneje televizijskih katodnih cevi, pospeševalnikov osnovnih delcev (Edison je spoznal, da med žarilno nitko in ločeno ploščico v bučki lahko teče električni tok, a le v eno smer – tako je odkril diodo, a njena uporabnost je bila nekaj časa neznana). John Ambrose Flaming pa je leta 1904 prišel do zamisli, da bi lahko Edisonov pojav uporabil za izdelavo radijskega sprejemnika na elektronko - diodo. Dve leti zatem je ameriški izumitelj Lee de Forest elektronki dodal še krmilno mrežico s čimer je dioda postala trioda (ojačevalnik). Danes sta večino elektronk izpodrinila polprevodniška dioda in tranzistor. Vse to so gradniki računalnikov in seveda množice detektorjev, brez katerih si danes ni več moč zamisliti znanstvenega eksperimentalnega udejstvovanja.
• 1892: Hendrik Lorentz objavi transformacije (nazadnje 1904, pri izpeljavi transformacij
je sodelovalo več sodobnikov). Z njimi je dokazal, da so Maxwellove enačbe invariantne,
nespremenjene pri transformacijah. Hitrost svetlobe (c) oziroma hitrost elektromagnetnega
valovanja v praznem prostoru, je v vseh inercialnih (nepospešenih) opazovalnih sistemih
konstantna. Lorentzove transformacije povezujejo meritve v prostoru in času dveh ali
večih opazovalcev, ki se gibljejo z različnimi hitrostmi. Transformacije pridejo do
izraza, če je hitrost gibajočega opazovalnega sistema znatna glede na hitrost svetlobe.
Opazovalci izmerijo različne razdalje, pretečeni čas in lahko tudi drugačen vrstni
red dogodkov. Odločilen je Lorentzov člen (faktor):
γ = 1/(1 – v2/c2)1/2.
Posledica povedanega je, da je recimo dolžina (L') palice najdaljša
v tistem sistemu, v katerem miruje ( L' = Lγ ), dolžina gibajoče palice L'
se za zunanjega mirujočega opazovalca skrči na
L = L'/γ .
Čas (Δt),
ki ga izmeri mirujoč opazovalec, je daljši od časa
(Δt'),
ki ga izmeri opazovalec, ki se giblje z dogodkom (recimo
odboj svetlobe v vozilu), velja:
Δt = Δt'γ .
Iz omenjenih predpostavk tudi sledi znamenita enačba
( E=mc2 ). Tako je bila odprta pot do Einsteinovih enačb
splošne teorije relativnosti, kjer je upoštevana tudi gravitacija - vesolje.
Povejmo ŠE, da je temelje relativnosti postavil že
Michelson-Morleyjev poskus leta 1887,
ki je zavrnil trditve nekaterih, da bi se naj Zemlja gibala
relativno glede na "eter", ker "etra" enostavno ni.
Svetloba torej potuje tudi v vakuumu in ne potrebuje nobene snovi
za prenos, kot recimo naš vsakdanji zvok potrebuje zrak, torej snov za prenos.
To je bil začetek poti v teorijo relativnosti.
Poskus je bil torej namenjen določitvi relativne hitrosti gibanja Zemlje glede na eter,
hipotetični medij, skozi katerega naj bi se širili svetlobni valovi. Občutljivi
Michelsonov interferometer je med poskusom posredno primerjal dolžine poti svetlobe,
ki se je gibala v dveh med seboj pravokotnih smereh: v smeri gibanja Zemlje okoli Sonca
in pravokotno na to smer. Ideja eksperimenta je bila preprosta: če je svetlobna hitrost
konstantna glede na domnevni eter,
skozi katerega se Zemlja giblje, potem bi njeno gibanje
lahko določili s primerjavo relativne svetlobne hitrosti v smeri gibanja Zemlje, v kateri naj bi veljala
za hitrost razlika, oz. vsota svetlobne hitrosti in hitrosti gibanja Zemlje,
saj bi naj svetlobo prenašal neznan "eter"
(torej razlika hitrosti [c - v] v smeri gibanja Zemlje, ker se (na sliki)
desno zrcalo odmika od smeri svetlobe - in
vsota hitrosti [c+v] po odboju od desnega zrcala, ko svetloba potuje proti smeri
gibanja Zemlje in
se diagonalno polprepustno zrcalo približuje odbitemu žarku - glejte
tudi animacijo). Čas povratka žarka v smeri gibanja bi naj bil
torej:
tl = L/[c - v] + L/[c + v].
Pri čemer se svetlobna hitrost
pravokotna na smer gibanja Zemlje naj ne bi spreminjala.
Iz geometrije slike (Pitagorov izrek - slika spodaj: (ctt/2)2 - (vtt/2)2 = L2) tako razberemo za čas povratka
pravokotnega žarka:
tt = 2L/(c2 - v2)1/2.
Vrednost v/c je zelo, zelo majhna, saj je hitrost Zemlje okrog Sonca "zgolj" v = 30 km/s, torej
zelo majhna napram svetlobni hitrosti c = 3 108 m/s.
Zagotovo bi lahko upoštevali še ostale hitrosti, recimo samega Sonca, Galaksije ...
A vsekakor bi lahko pričakovali vsaj razmerje v/c = 10 -4 ali kaj večje.
Če povedano upoštevamo je čas tl ( ko približno velja
1/(1 - v2/c2)
≈ 1 + v2/c2 ... za v/c = 10 -4):
tl = L/[c - v] + L/[c + v]
= (2L/c)/(1 - v2/c2) ≈ (2L/c)(1 + v2/c2)
in tt (
ko približno velja 1/(1 - v2/c2)1/2
≈ 1 + (v2/c2)/2 ... za v/c = 10 -4 ):
tt = 2L/(c2 - v2)1/2 ≈
(2L/c)(1 + (v2/c2)/2)
.
Razlika obeh časov je (pri L = 11 m) približno:
Δt = tl - tt =
(2L/c)(1 + v2/c2) - (2L/c)(1 + v2/c2/2) =
(L/c)(v/c)2.
Razlika v poteh (valovni dolžini) pa je torej Δλ = cΔt = L(v/c)2 =
1,1 10 -7 m = 110 nm. In pri svetlobi valovne dolžine λ = 500 nm bi to zneslo
zamik skoraj četrtine valovne dolžine (blizu λ/4) obeh žarkov. Torej bi se valovanji
morali precej oslabiti - spremeniti interferenčni vzorec - spodnja slikica.

Razlika obeh časov (poti žarkov) bi torej morala povzročiti spremembe v interferenčni
sliki združenih žarkov - slika zgoraj.
IN - KAJ SE JE ZGODILO - glejte sliko spodaj?

IN vendar - ni bilo opažene nobene razlike (interferenčna slika se ni spremenila,
kakor koli sta obračala interferometer), od tod tudi ime -
ničelni rezultat. Odsotnost pričakovanega rezultata je počasi odpravila
stoletja staro teorijo o obstoju
etra in prispevala k spoznanju, da je svetlobna hitrost univerzalna konstanta -
hitrost svetlobe torej ni odvisna
od hitrosti samega opazovalca. Čeprav
ni zanesljivo potrjeno, da je Albert Einstein pri oblikovanju relativnostne teorije
leta 1905 izhajal iz tega rezultata, je eksperiment vsekakor omogočil sprejetje nove fizike
in novih konceptov prostora in časa v primerjavi s klasično Newtonovo fiziko.

Pričakovana fazna razlika med svetlobo, ki potuje vzdolžno
in pravokotno glede na kraka Michelson-Morleyevega
interferometra -
A TA NI BILA ZAZNANA v interferenčni sliki odbitih žarkov.
Negativen rezultat Michelsonovih poskusov je bil četrt stoletja eden od največjih
nerešenih problemov fizike (enigma).
Neobičajno hipotezo krčenja (kontrakcije) dolžine v smeri gibanja pa je že leta 1892
podal G. F. FitzGerald.
Razlike torej ni, če domnevamo, da se dolžina v smeri gibanja skrči za faktor:
1/γ = (1 - v2/c2)1/2
Kot bomo videli - tudi čas ni več enak za gibajočega
in mirujočega opazovalca.
Dolžina pravokotna na smer gibanja pa ostane nespremenjena.
Očitno je, da je ta hipoteza
nasprotna vsem starim fizikalnim predpostavkam,
kjer so spremembe oblike, dolžine povezane z delovanjem sil in ne z gibanjem.
Hipotezo krčenja je takoj sprejel H. A. Lorentz, najbrž neodvisno od G. F. FitzGeralda
(Michelson-Morleyjev poskus je preko Maxwellovih enačb Lorentza pripeljal
do relativnostne teorije - poznane so znamenite Lorentzove transformacije,
ki jih je Einstein pozneje intenzivno javno zagovarjal in teoretično
dodelal v teoriji relativnosti).
Albert Einstein je ob tem poskusu zapisal: »Če nas poskus Michelson–Morley
ne bi spravil v resno zadrego, nihče ne bi imel teorije relativnosti kot
(napol) odrešitve.«
Poglejmo še, od kod faktor krčenja v smeri gibanja?
Ker niso zaznali spremembe interferenčnega vzorca, cΔt = 0, so sklepali, da s v smeri gibanja
dolžina skrči (označimo z malo črko l). Poglejmo od kod ta že omenjen
faktor krčenja 1/γ = (1 - v2/c2)1/2. Še enkrat
zapišimo časa, a brez približkov:
tl
= (2 l/c)/(1 - v2/c2) = (2 l/c)γ2
tt = (2L/c)/(1 - v2/c2)1/2 = (2L/c)γ
Časa odštejemo in kdaj bo razlika cΔt = 0 ?
Δt = tl - tt = (2l/c)γ2 - (2L/c)γ
= (2/c)γ(lγ - L) = 0
Δt = 0 , ko velja:
(lγ - L) = 0, od koder sledi, da je l :
l = L/γ = L(1 - v2/c2)1/2
Dolžina l v smeri gibanja se torej skrči glede na L (dolžina ob mirovanju) za faktor
1/γ = (1 - v2/c2)1/2
.
Tega dejstva večina laikov in fizikov ni sprejela skoraj 20 let.
Omenili smo še eno "NORO" dejstvo, da
čas ni več enak za gibajočega
in mirujočega opazovalca
- od kod ta sklep?
Če analiziramo sliko poti žarka pravokotno na smer gibanja,
dobimo trikotnik poti in čas odboja (izpeljan prej):
t
= (2L/c)/(1 - v2/c2)1/2 = (2L/c)γ
To je čas (t) za opazovalca "zunaj" interferometra.
Kaj pa bi izmeril opazovalec v interferometru (čas t', ki ni enak času t) -
videl bi navpično pot žarka navzgor in navzdol.

Opazovalec, ki se premika z zrcalom na stropu višine
L, zazna navpično gibanje svetlobe in temu primerno izmeri
čas potovanja svetlobe do stropa po preprosti povezavi
(L/c) -
čas ponovne zaznave svetlobe je kar opravljena
pot
(2L – pot
do stropa in nazaj) deljena s hitrostjo
svetlobe:
t' = 2L/c
Če izenačimo iz obeh enačb vertikalo L = ct'/2 in še L = ct/(2γ), dobimo:
ct/(2γ) = ct'/2
Tako je povezava med urama v interferometru (čas t') in zunaj (čas t):
t = γt' = t'/(1 - v2/c2)1/2
Evidentno je, čeprav se je na začetku to zdela zgolj matematika, da je čas
odvisen od sistema - hitrosti! "Opazovalec" v interferometru izmeri krajši čas
t' = t/γ = t(1 - v2/c2)1/2.
Ali se to sklada s krčenjem dolžini v smeri gibanja - preverimo? Velja t'/t = 1/γ.
in v gibajočem sistemu velja 2ct' = 2L. Za x smer velja (izpeljali zgoraj) 2ct = 2lγ2
Od koder sledi (2L = 2ct' pomnožimo in delimo s t):
2ct't/t = (2ct)(t'/t) = 2lγ2/γ = 2L
Torej velja:
lγ = L
Zunanji opazovalec vidi torej skrajšano dolžino l, ko velja:
l = L/γ = L(1 - v2/c2)1/2
Najdaljša je torej tista dolžina predmeta, ki jo izmeri opazovalec,
ki potuje skupaj s predmetom (v našem primeru v interferometru).
Tako smo pokazali, da ni neskladja med različnima časoma (t in t') in dolžinama
(l in L),
le odvisnost je obratna in jo določa Lorentzov člen gama γ
= 1/(1 - v2/c2)1/2.
In to je dokazal zelo brihten Michelson–Morleyjev eksperiment iz leta 1887,
ki je hotel odgovoriti na staro trditev mnogih, da
(ali) svetloba potrebuje snov za gibanje (t. i. "eter") - kot recimo zvok rabi plin, zrak.
Dobili smo odgovor, da svetloba ne potrebuje etra in da lahko potuje tudi v vakuumu!!!!
In hkratna kolateralna korist je bila izjemna - TO JE relativnostna teorija!
Ki pa je recimo, kot lahko preberemo, Nobelovec Albert Abraham Michelson nikoli ni sprejel,
čeprav je eksperimentalno eden od utemeljiteljev, praoče posebne teorije relativnosti.
Večkrat se zgodi, da oče ne prizna sina,
ki je nato izjemno uspešen!
• 1900 : Max Planck leta odkrije spektralno gostoto energijskega toka
elektromagnetnega valovanja pri vseh valovnih dolžinah idealnega
črnega telesa pri absolutni temperaturi T (po njem imenovan Planckov zakon):
dj/dλ = πBλ =
(2πhc2/λ5)(ehc/(λkBT) - 1)-1

Planck je predpostavil kvantizacijo pet let preden je Einstein pri razlagi
fotoelektričnega pojava predvidel obstoj svetlobnih kvantov, fotonov.
Izraz za fotone je leta 1926 skoval Lewis. Planckova enačba predvideva,
da bo črno telo sevalo energijo pri vseh frekvencah, uporabna pa je le,
če se pri meritvah upošteva dovolj veliko število fotonov. Sevalno polje
črnega telesa se lahko predstavlja kot fotonski plin, v katerem bo ta
gostota energijskega toka ena od termodinamskih spremenljivk plina.
Vzor mu je bila Boltzmannova verjetnostna porazdelitev (tudi Maxwell-Boltzmannova),
ki je osnova kinetične teorije plinov, kjer se recimo natančno opiše porazdelitev
kinetične energije delcev plina (od tam tudi eksponent). Ta zakon nam zelo pomaga pri
študiju sevanja zvezd – določanje spektralnih tipov in površinske temperature zvezd.
• 1908 : gospa Henrietta Swan Leavitt odkrije povezavo med izsevom in frekvenco utripanja zvezd kefeid, odpre se pot za merjenje razdalj do galaksij (Hubblovega, oz. Hubble-Lemaîtrovega zakona o širjenju vesolja).
• 1909: so pod Rutherfordovim vodstvom na Manchesterski univerzi z obstreljevanjem zlatih lističev odkrili, da je atom sestavljen iz majhnega pozitivno nabitega jedra in velikega negativno nabitega elektronskega oblaka, ki obdaja jedro (iskanje lastnosti in zgradbe atomov je neločljivo povezano z razvojem vesolja, nas samih).
• 1913: Niels Bohr poda zanimiv koncept atoma – pri vodiku izpelje emisijski in
absorpcijski diskretni spekter svetlobe, ki ga je empirično določil že Rydberg s
formulo:
1/λ = R(1/n12 – 1/n22),
n1 in n2 sta kvantni (naravni)
števili(a) (1, 2, 3, ...).

Predpostavil
je diskretne stacionarne valovne orbite elektrona z različnimi
energijami, z danimi kvantnimi naravnimi števili. Atom izseva
foton pri prehodu iz višje energijske orbite na nižjo, pri absorpciji
fotona pa elektron skoči na višjo orbito. Orbite so točno določene in
se razlikujejo za različne atome, molekule. Valovne dolžine izsevanih
fotonov so tako hkrati njihovi prstni odtisi, kar predstavlja izjemno
orodje v rokah astronomije, saj lahko tako, le iz valovnih dolžin svetlobe,
določi kemijske elemente zvezd, plinov, ki so oddaljeni milijone in
milijarde svetlobnih let. To je bila vmesna slika med klasično podobo
atoma, ki bi moral biti, zaradi pospešenega gibanja elektronov –
tozadevnega sevanja - nestabilen in kvantno sliko atomov Heisenberga in
Schrödingerja. Heisenbergovo načelo nedoločenosti govori, da ne moremo
hkrati določiti lege in hitrosti kvantnega delca, recimo elektrona.
Govorimo lahko torej le o verjetnosti, da na določeni oddaljenosti od
jedra najdemo elektron. Iz Rutherfordovega eksperimenta izhaja, da je
atom sestavljen iz majhnega (10-15 m), a masivnega pozitivno nabitega
jedra in velikega (10-10 m) negativno nabitega lahkega elektronskega oblaka.
Iz tega dejstva izhaja veliko dilem. Če je masa atoma zgoščena v majhnem jedru
atoma iz večih nevtronov in protonov, ki se med sabo odbijajo, odrivajo –
zakaj tak atom takoj ne razpade? Odgovor je - ne razpade, ker ga skupaj drži
močna jedrska sila, ki je znotraj razdalje nekaj 10-15 m močnejša od
elektrostatične odbojne sile. To je torej razlog, da imamo poleg vodika
še težje elemente – da lahko obstajamo živa bitja v taki obliki ...
Seveda pa atomi tudi razpadejo. Ker ima močna jedrska sila omejen doseg,
je tudi velikost atomskega jedra navzgor omejena, zadnje stabilno jedro ima
izotop svinca z 208 gradniki (82 protonov in 126 nevtronov). Razpolovni čas
razpada urana-238 je še zmeraj 4.47 milijarde let (starost Zemlje), izotopa
U-235 pa 704 milijonov let. Ununoktij (294 - Uuo je sestavljen iz 118 protonov in 176 nevtronov)
pa ima razpolovni čas zgolj 0,89 ms. Za radioaktivni razpad je odgovorna šibka jedrska sila –
in zdi se, da vsi atomi razpadejo, razpade tudi recimo sam proton, kateremu
ocenjuje razpolovno dobo kar na
6.6×1033 let. Kako bo torej končalo naše vesolje
– bo vse razpadlo? A še prej se pojavi vprašanje, kje in kako so nastali težji
elementi od vodika?


Bohrov (vmesni) model vodikovega atoma – danes atom opišemo z valovnimi funkcijami.
Spodnja slika - atomsko jedro je (simbolično) zeleno, elektron je modre barve.
izsevani foton rdeč. Elektronske orbite predstavljajo črtkani krogi; polmer
orbite se veča z n2,
kjer je n glavno kvantno število.
Iz prikazanega prehoda 3 => 2 nastane foton valovne dolžine 656 nm.
To je črta H-alfa, ki je izjemno pomembna v astronomskih
meritvah, pri opazovanjih, ...
• 1915: Einsteinova splošna teorija relativnosti opiše vesolje kot celoto,
energija - materija ukrivlja prostor-čas:
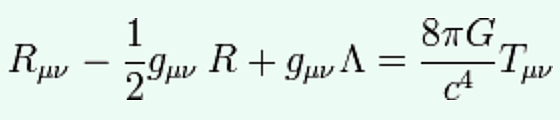

Einstein tudi potrdi, dokaže, foton preko razlage fotoefekta.
Odvisnost največje mogoče kinetične energije izbitih fotoelektronov
iz kovine Ek od frekvence (ν) vpadle svetlobe, podaja Einsteinova
enačba iz leta 1905:
Ek = mv2/2 = h(ν - νo) = hν - Wi;
Wi je izstopno delo, h je Planckova konstanta, energija fotona je
Ef = hν
(energijske delce svetlobe, fotone, vpelje že leta 1900 Max Planck
pri razlagi spektra sevanja črnega telesa – velik dosežek – iz
integrala Planckovega spektra dobimo Stefanov zakon). Predvsem
razlaga fotoefekta je Einsteinu prinesla Nobelovo nagrado za fiziko
(njegove teorije relativnosti dolga leta niso razumeli).
Zgodovinsko ozadje odkritja fotoefekta.
Philipp Eduard Anton von Lenard je
kot fizik največ prispeval k študiju katodnih žarkov, ki ga je začel leta 1888 (razvil je posebno Lenardovo okensko cev - v bistvu
rentgen).
V povezavi s svojimi in drugimi prejšnjimi poskusi absorpcije žarkov v kovinah je prišel do splošnega spoznanja,
da so elektroni sestavni deli atoma. To je Lenardu omogočilo pravilno trditev, da so atomi večinoma
sestavljeni iz praznega prostora. Predlagal je, da je vsak atom sestavljen iz praznega prostora
in električno nevtralnih korpuskul, imenovanih "dinamide", od katerih je vsak sestavljen
iz elektrona in enakega pozitivnega naboja.
Kot rezultat svojih raziskav Crookesove cevi je pokazal, da so žarki, ki nastanejo
pri obsevanju kovin v vakuumu z ultravijolično svetlobo, v mnogih pogledih podobni
katodnim žarkom. Njegova najpomembnejša ugotovitev je bila, da je energija žarkov
v fotoelektričnem učinku neodvisna od jakosti svetlobe (ampak le od frekvence).
Ta zadnja opažanja je Albert Einstein razložil kot kvantni učinek.
Ta teorija je predvidevala, da bo graf energije katodnega žarka v odvisnosti od frekvence ravna
črta z naklonom, ki je enak Planckovi konstanti, h. Nekaj let pozneje se je izkazalo, da je tako.
Fotoelektrična kvantna teorija je bilo delo, ki je dobilo veljavo in so ga splošno citirali šele, ko je Einstein prejel
Nobelovo nagrado za fiziko leta 1921.
Lenard ni oporekal Einsteinovi razlagi
fotoelektričnega učinka - sam je k temu tudi veliko prispeval.
Je pa postal zelo nejevoljen nad zaslugami Wilhelma Röntgena,
ki je leta 1901 prejel prvo Nobelovo nagrado za fiziko, za odkritje rentgenskih žarkov.
Lenard je zapisal, da je on,
ne Roentgen, "mati rentgenskih žarkov", saj je izumil aparat za njihovo proizvodnjo.
Lenard je Roentgenovo vlogo primerjal z vlogo "babice", ki le pomaga pri porodu.
Lenard je leta 1905 prejel Nobelovo nagrado za fiziko kot priznanje za svoje delo.
Lenard je bil dober fizik, a madžarsko-nemški nacionalist, kar mu ne gre v prid ...
Ni imel dobrega mnenja o "angleški fiziki", za katero je menil, da je svoje ideje ukradla Nemčiji.
Tudi ni zaupal Einsteinovi teoriji relativnosti - to je bila zanj "judovska fizika".
Lenardova knjiga, Great Men in Science, A History of Scientific Progress,
ki je bila prvič objavljena v angleščini leta 1933, je trdila,
da so bili vsi ti možje »arijski znanstveniki«
(knjiga sicer kaže, da je dobro poznal fiziko, a je bil rasno in kulturno pristranski).
Danes so te delitve presežene. Je pa res - kot pravijo:
"Medalja in krogla vedno zadeneta napačne prsi."
To je sicer pretiran pregovor za znanstveno rabo - a napačne ocene in zgrešene nagrade
ne prispevajo k strpnosti med ljudmi.
• 1915 : Schwarzschild poda rešitev Einsteinove enačbe za sfero in sicer za kvadrat
razdalje med dogodkoma ob krogli mase M - Schwarzschildova metrika torej je:
ds2 = -c2dt2 (1 - 2GM/(c2R))
+ dR2/(1 - 2GM/(c2R))
+ R2dϑ2 + R2sin2ϑ dφ2
S tem se je odprla pot k razumevanju in izjemno natačnim izračunom vpliva gravitacije
na dogodke (uklon svetlobe, precesija perihelija, korekcija časa pri satelitski navigaciji,
gravitacijsko lečenje, gravitacijski Dopplerjev premik ...).
• 1917 : de Sitter reši Einsteinove enačbe gravitacijskega polja v katerih je napetostni tenzor 0, kjer je gostota mase nič in, ki je nakazovala eksponentno razširjanje Vesolja, »z dinamiko brez snovi«; to je bil presenetljiv rezultat in po Hubblovih meritvah ga je sprejel tudi Einstein sam; kozmologi podobne sklepe uporabijo spet čez 70 let, ob teoriji inflacije – hitrega širjenja vesolja.
• 1917 (1922) : Friedmann zapiše enačbo širitve vesolja z maso
(ena izmed izpeljank enačbe je:
H2 = 8 π G ρ /3 - k c2 / R2.
• 1924: De Broglie pokaže na dvojno naravo gibanja kvantnih delcev
z maso (recimo elektronov), ki jih lahko obravnavamo tudi kot valovanje,
pravilno zapiše tudi njihovo valovno dolžino kot kvocient Planckove konstante
in gibalne količine:
λ = h/(mv).
Temu so se nekateri na začetku posmehovali,
a so resni eksperimentatorji kmalu potrdili pravilnost njegovega razmišljanja
– elektronski mikroskopi pa s pridom izkoriščajo to izjemno lastnost dvojne
narave delcev. Brez elektronskega mikroskopa si ne moremo predstavljati
raziskav celic, genskega zapisa, ...


De Brogliju se je ideja porodila zaradi kvantizacije energijskih nivojev atomov
(slika levo – ta model je danes večinoma presežen, je pa zgodovinsko zelo pomemben).
Desna slika pa prikazuje interferenčno sliko elektronov na dveh režah. De Broglie
je vplival na Einsteina in Schrödinger pod tem vplivom zapiše diferencialno enačbo
za valove povezane z delci in rodi se valovna funkcija lege delca v času in prostoru.
• 1925 - 1926: Erwin Schrödinger zapiše in objavi diferencialno enačbo za opis
dinamike kvantnih delcev:
iℏ∂Ψ/∂t = HΨ
Rešitev te enačbe je Schrödingerjeva valovna funkcija
Ψn(r,t) =
e– iEnt/ℏΨn(r)
. Povejmo še, da rešitve za krajevni del funkcije
Ψn(r) večinoma ni enostavno najti.
Produkt valovne funkcije ΨΨ nam da verjetnostno gostoto za lokacijo delca
(velja pa seveda, da je verjetnost 1, če integriramo po celotnem prostoru
∫ΨΨd3r = 1,
torej je delec zagotovo del našega sistema, ne vemo pa točno kje je –
govorimo o verjetnosti). V enačbi je
En je lastna
(diskretna) vrednost energijskega stanja.
To - kar je naredil Einstein preko tenzorskih enačb polja za opis vesolja, je
Schrödinger naredil za opis gibanja v svetu osnovnih delcev preko diferencialne
enačbe (upošteval je delčno in valovno naravo kvantov) in njene ustrezne rešitve -
valovne funkcije. Einstein in seveda večina sodobnikov, se je zanimala tako za
svet velikih teles, za vesolje, kot za svet osnovnih delcev (kvantni svet), za
gradnike, ki nas sestavljajo. In oba svetova sta povezana – sta eno. Omenjeno
povezanost sveta velikih teles in kvantnih delcev posebej dojamemo pri raziskovanju
rojstva vesolja – ko se rodijo tudi osnovni delci, sile, tudi nosilci, delci sil –
ki na nek način tudi pospešujejo vesolje ... In matematiki opisa obeh svetov se
dokaj prepleta.
• 1927: W. Heisenberg zapiše osnovni postulat kvantne mehanike - načelo nedoločenosti, ki v svetu atomskih delcev (kvantne mehanike) izraža lastnost, da je recimo nemogoče hkrati natančno pomeriti (določiti) lego delca in njegovo hitrost (gibalno količino: Δx Δp ≥ h/(4π)b ) ali energijo delca v danem časovnem intervalu, kar se zapiše kot ΔE Δt ≥ h/(4π) (zadnji izraz - bolje Mandelshtam-Tammova enačba - ima za mnoge izjemen pomeni, saj lahko sklepamo, da se je vesolje začelo s kvantno fluktuacijo, ko se je za delček časa Δt pojavil paket energije ΔE z delci in antidelci, nakar se je simetrija med delci in antidelci podrla in nastalo je vesolje, kjer prevladuje materija nad antimaterijo, tako smo nastali tudi ljudje ...). Primer za časovno-energijske negotovost ΔE Δt ≥ h/(4π) se najde v spektroskopiji, kjer imajo vzbujena stanja atomov končno življenjsko dobo. Po načelu časovno-energijske negotovosti atomi nimajo točno določene energije ΔE in vsakič, ko se foton izseva, se energija, ki se sprosti, nekoliko razlikuje (spremeni se recimo širina spektralne črte). Ali je enačba upravičena pri razlagi začetka vesolja – »ko še ni bilo časa (ali pač med kvantnimi fluktuacijami)« - pa je drugo vprašanje. A ideje o začetkih vesolja štejejo – tudi če so negotove. Sploh pa je problem razlaga – zakaj je narava (fizika) taka kot je?
• 1927 : Georges Lemaître (belgijski duhovnik in fizik) objavi svojo novo idejo, da se vesolje širi (prvi izpelje Hubblov zakon in poda prvo opazovalno oceno Hubble-Lemaîtrove konstante - tako jo po novem imenujemo).
• 1929 : Hubble dokaže, da so določene meglice (galaksije) daleč
izven naše galaksije, in da se oddaljujejo od nas s hitrostjo,
ki linearno narašča z oddaljenostjo
d ( v = Hd ).
H je Hubble-Lemaîtrova konstanta.
Trenutno se pojavljata dve vrednosti (Spika 5, 2021), H = 74,03 km/s/Mpc (preko
hitrosti oddaljevanja galaksij z Dopplerjem, kjer se meri razdalje s pomočjo Kefeid
in supernov tipa Ia) in iz nehomogenosti mikrovalovnega sevanja ozadja, odtis prapoka,
ki zaenkrat da vrednost H = 67,36 km/s/Mpc. Obeta se še tretja pot merjenja Hubblove (Hubble-Lemaîtrove)
konstante in sicer s pomočjo gravitacijskih valov pri zlitju zvezd. Preko izračunane
moči samega zlitja in zaznane moči na Zemlji, se bo določila razdalja do trka in
ob hkratnem merjenju spektra elektromagnetnega valovanja (Dopplerja), se bo
določila hitrosti oddaljevanja. Meritve razdalj so res velik problem kozmologije,
hkrati pa nam vsaka nova metoda razkrije še več resnic o vesolju in nas samih.
• 1932 : Zwicky, preko opazovanja dinamike jate galaksij v Berenikinih kodrih, pride na sled temni masi.
• 1938 : Hans Bethe zapiše cikel termonuklearnih pretvorb (Bethejev cikel) – fuzija v Soncu kot glavni vir energije za milijarde let stabilnega izseva. Leta 1935 je Bethe razdelal Bethe-Weizsäckerjev cikel nastajanja energije v zvezdah. A zgodovina odkritja je bila dolga. Konec 19. stoletja se je na veliko iskalo vir energije v zvezdah (je tudi najvažnejše vprašanje našega obstoja – brez nje ni težkih elementov, ni planetov, ni energije za nastanek življenja). Einstein in že nekateri drugi pred njim, so videli povezavo med maso in energijo – prvi jo pravilno zapiše Einstein 1905 (pravi, da je oddana energija zvezde sorazmerna z izgubo mase m = E/c2). A mehanizma pretvorbe nikakor še dobro desetletje niso prepoznali (a z razvojem atomske fizike in eksperimentiranja so počasi napredovali). Leta 1920 je Arthur Eddington predlagal, da bi bila fuzija vodik-helij lahko glavni vir zvezdne energije. Kvantno tuneliranje je odkril Friedrich Hund leta 1929 (omogoča fuzijo), kmalu zatem pa sta Robert Atkinson in Fritz Houtermans z izmerjenimi masami lahkih elementov pokazala, da se lahko z zlitjem majhnih jeder sprosti velika količina energije. Na podlagi zgodnjih eksperimentov z umetno jedrsko pretvorbo Patricka Blacketta, je laboratorijsko fuzijo izotopov vodika izvedel Mark Oliphant leta 1932. V preostalem desetletju je teorijo glavnega cikla jedrske fuzije v zvezdah razvil Hans Bethe. Raziskave fuzije za vojaške namene so se začele v zgodnjih štiridesetih letih prejšnjega stoletja v okviru projekta Manhattan. Samoobstojna jedrska fuzija je bila prvič izvedena 1. novembra 1952 v preskusu z vodikovo (termonuklearno) bombo pod kodiranim imenom »Ivy Mike« (na Enewetak atolu v Maršalovem otočju). Danes mnogi znanstveniki stavijo na kontrolirano fuzijo v jedrski reaktorjih in s tem pridobivanje bolj čiste energije – recimo tokamak (ITER – fuzija v toroidni komori z magnetnimi tuljavami) – nujno je potrebno prekiniti z umazanim in destruktivnim kurjenjem fosilnih goriv.
• 1948 : Gamov uvede začetno singularnost.
• 1948 : Hoyle skuje nekoliko norčavo zvezo 'veliki pok' – 'Big Bang' (ker je sam zagovarjal stacionarno vesolje - vzhodni blok [ideologija večnosti materije] ga je zato imel za kralja, a izkazalo se je, da je "nag").
• 1964 : Penzias in Wilson odkrijeta mikrovalovno ozadje - prasevanje vesolja iz časov velikega poka (tako so zavrnili Hoylov statični model vesolja).
• 1975 : gospa Vera (Cooper) Rubin pomeri hitrosti na robu galaksij in tako pride do t. i. "ravnih krivulj vrtenja« (hitrosti niso padale po Keplerju v = (GM/r)1/2 ), to je, po Zwickeju, eden najneposrednejših in najbolj čvrstih dokazov o t. i. temni snovi (rezultate objavi skupaj s sodelavcem Fordom).
• 1980 : Alan H. Guth predlaga zamisel o inflaciji vesolja - faza eksponentnega (bliskovitega) razširjanja (tako bi tudi lažje razložili enakost vesolja v vseh smereh) - posledica hitrega širjenja morajo biti tudi gravitacijski valovi, ki bi lahko zasukali ravnino polarizacije mikrovalovnega ozadja; za detekcijo teh valov je Seljak predlagal prav iskanje zasuka polarizacije mikrovalov ozadja - prasevanja.
• 1998 : Perlmutter, Schmidt in Riess - dve skupini - eno je vodil Perlmutter,
v drugi sta delovala Riess in Schmidt, sta tekmovali v kartiranju vesolja,
odkrili sta, da se vesolje pospešeno širi. To sta dokazali z opazovanjem
svetlobe oddaljenih supernov tipa Ia, ki so šibkejše od pričakovanj (izračunov
iz Dopplerjevega rdečega premika). Projekt se je imenoval - »The Supernova
Cosmology Project«. Gre za okoli 50 supernov, ki so svetile zelo šibko.
Zamisel, da se vesolje širi pospešeno, je elegantna rešitev problema svetlosti
supernov, a je po drugi strani zelo radikalna ideja. Šele ko sta obe skupini
prišli do enakih sklepov, je teorija dobila potrditev v znanstveni srenji.
Sedaj velja dopolnjena Friedmannova enačba - opis vesolja s kozmološkim členom
(Λc2/3),
ki vesolje pospešuje:
H2 = 8 π G ρ /3 - k c2 / R2) + Λ c2/3
Oznaka H je Hubble-Lemaîtrova konstanta. Ocena gostote vakuuma (temne energije)
za Λ ≈ 1.1056 10-52 m-2 je:
ρvak = Λc2/(8πG)
= 5,9 10-27 kg/m3,
to je 3,5 protonov na m3, to je okrog 70 %
(pričakovana vrednost glede na kritično gostoto 6 protonov
na m3, gostota podana v protonih je zgolj simbolična,
zaradi lažje predstave). Razlika do 6 protonov na m3
(ena izmed ocen kritične gostote) pa večinoma pripada energiji
temne snovi (okrog 25 %), le okrog štirje procenti pa delcem,
ki sestavljajo atome, nas same, vidno vesolje.
• 2013 : Peter Ware Higgs prejme Nobelovo nagrado - leta 1964 je, neodvisno od dveh belgijskih raziskovalcev, napovedal obstoj Higgsovih bozonov, ki naj bi bili nosilci skalarnega Higgsovega polja in naj bi dajali osnovnim delcem maso. Higgsovih bozonov je osnovne delce na začetku vročega vesolja (ko se zdi, da so imeli vsi hitrost svetlobe) upočasnil in jim s tem nekaj energije zaviranja prelil v maso m =E/c2 (to so delci, ki danes sestavljajo zvezde, planete in tudi človeka). 4. julija 2012 sta znanstveni skupini detektorjev CMS in ATLAS (CERN - LHC) neodvisno sporočili, da sta potrdili formalno odkritje prej neznanega bozona z maso med 125–127 GeV/c2, katerega vedenje se s standardno deviacijo 5 sigma »ujema« s Higgsovim bozonom (s t. i. »Božjim delcem«).
• 2017 : Nobelovo nagrado za fiziko so prejeli trije znanstveniki iz ZDA za prvo neposredno potrditev obstoja gravitacijskih valov, in sicer Rainer Weiss, Barry Barish in Kip Thorne. Z detektorjem LIGO (Laser Interferometer Gravitional-Wave Observatory) jim je 2016 uspelo dokazati obstoj teh valov iz Velikega Magellanovega oblaka. Izmerjeni gravitacijski valovi se ujemajo s pričakovanimi iz dveh črnih lukenj, ki se spajata po spirali v novo črno luknjo, ki za trenutek zaniha prostor in se nato umiri. Pojav, ki ga je napovedal Einstein je zgodovinsko odkritje in temeljni kamen človeškega razumevanja gravitacije in temeljev fizike. Gravitacijski valovi so torej še en vir valovanja za merjenje dogodkov, energij in razdalj v vesolju – za oceno dinamike vesolja, dopolnitev kozmološkega modela, Hubble-Lemaîtrove »konstante« H.
Konec zgodovine astronomije - seveda zgolj za nekaj časa, saj se ta trenutek (2021/2022) piše že novo nadaljevanje napete zgodbe človeškega raziskovanja vesolja; recimo z izstrelitvijo vesoljskega teleskopa "James Webb Space Telescope".
Ta pregled je narejen s poudarkom na modelih vesolja in na nastanku
življenja – zato je izpuščenih več pomembnih dognanj iz področja
fizike zvezd in ostalih vej astronomije, fizike, naravoslovja.
Je pa tako, da medalja in krogla redko zadeneta pravega –
veliko znanstvenikov žal ni omenjenih ...
Pregled (zgodovine astronomije) smo začeli z »iznajdbo« govora,
ki ga lahko obravnavamo kot prvi odločilen korak v učlovečenje,
k napredku komunikacije – v novo kvaliteto in smisel življenja.
Nato smo poudarili tudi izjemen pomen uvedbe pisave, likovne
govorice, kot naslednji korak v globlje samozavedanje človeka,
pot k razvoju humane družbe, ekonomije, znanosti, kulture,
pravičnosti. Zaključimo pa ta pregled z nadvse zanimivo
lastnostjo človeka, da dokaj radi dvomimo v novosti,
inovacije (seveda kdaj upravičeno). Tako se je že v
antiki Grk Sokrat delno bal uporabe pisave, spisov, takrat
dokaj nove iznajdbe za večino Grkov (zanj je bila komunikacija
iz oči v oči edini način za prenos znanja na drugo osebo).
Zdelo se mu je, da se nam bo zaradi pisave poslabšal spomin
(včasih so tudi rekli, da zaradi pisave lahko že vsak 'bedak' bere ...).
Pisava je seveda preživela in s tem moderni človek, pospešila je napredek
človeštva (kot inflacija vesolje, pospešeno napredovanje človeštva se spet
pojavi z iznajdbo tiska, danes svetovnega spleta) – spomin človeštva se
je tako ohranil in preživel kot celota prav v pisavi. Zgolj ustno izročilo
se lahko hitro prekine (bolezni, vojne) in ima seveda omejeno kapaciteto v širini
in globini reševanja problemov – v nadgradnji. Pisava in branje sta dobila tudi
univerzalen presežni pomen pri razlagi, razumevanju sveta. Tako slikovito pravimo,
da recimo beremo zgodovino Zemlje iz geoloških plasti (ko so geologi že dolgo vedeli,
da se starost Zemlje in vesolja meri v milijardah let, so astronomi sanjali komaj
o kakšnem milijonu), naravo vesolja beremo recimo tudi iz Dopplerjevega zamika
spektralnih črt svetlobe z oddaljenih svetov, oddaljenost supernov tipa Ia pa
spet beremo iz njihovega spektra in krivulj upadanja sija ... še in še bi lahko
naštevali. Zapisana razmišljanja naših prednikov, merjenja, ohranjene skice,
slike, kipi, poezija, svetišča, domovanja … so tisto, kar nam zmeraj znova pomaga,
tudi po 1000-letni pozabi, napredovati v razumevanja narave, vesolja, naše zgodovine,
kulture. O tem priča recimo miselni preskok v renesansi, ko so nam pri tem preskoku
pomagale tudi antične knjige padlega Bizanca in arabski prepisi knjig starega veka.
Glinena plošča Plimpton 322 nam je razkrila, da so »Pitagorov« izrek poznali že Babilonci
pred skoraj 4000 leti. Zgolj ena ohranjena slika zadnje Valvasorjeve hčerke na sv.
Bolfenku (Kogu) nam je pred leti razkrila, da Valvasorjevi potomci še zmeraj prebivajo med
nami - po Evropi (nadvse zanimive, poučne usode). Pred nedavnim so nam pisni viri tudi
razkrili, da Lukrecij Kar, sodobnik Julija Cezarja, v izredno obsežni pesnitvi O naravi
sveta, originalno »De rerum natura«, že veliko pred Galilejem ovrže Aristotelove teorije
o tem, da težja telesa v praznem prostoru padajo hitreje kot lažja. Sporočilno moč pisnih,
ostalih materialnih, virov nam tudi kaže občasna velika želja posameznih samodržcev po
njihovem uničevanju (sežiganje knjig, uničevanje podob in pisave na kamnih, glini, lesu ...).
Eden najstarejših papirusov je preživel 4500 let (kraj Wadi el-Jarfu), spominski diski
in usb ključki pa le nekaj let ... Tudi digitalne kopije naših zapisov, izračunov,
programov, arhivov podatkov, lahko v trenutku uniči že zgolj kratek, a močan
elektromagnetni sunek – a tiskane astronomije (recimo Spike) pač ne more.
Ves razvoj znanosti je seveda vezan na zgodovinksi kontekst in na skrivnostno človeško naravo.
s katero moramo živeti in jo obrniti (če se le da) v prid resnici. A proti toku podivjane
množice se ne da
boriti, umaknite se, da preživite (kot se umaknete pred plazom ...).
Pravijo pa, da se v vsakem od nas skrivata oba principa, divjak in razmišljujoči, ustvarjalni človek.
V povedanem kontekstu tako sledi še nekaj misli na tematiko obnašanja ljudi.
** "Veliko lažje je pretentati ljudi, kakor prepričati jih, da so bili pretentani."
Mark Twain
Danes so lažne novice celo večinske, v stilu "primite tatu", žal ...
** "Ljudje znorimo v čredah,
spametuje pa se le vsak posebej."
Charles Mackay
** "Težki časi ustvarjajo močne može,
močni možje ustvarjajo dobre čase,
dobri časi rodijo šibke može,
šibki možje ustvarjajo težke čase."
G. Michel Hopf
** Med kritičnimi zgodovinarji priljubljen epigram pravi:
"Bog je vsemogočen, a celo On ne more spreminjati preteklosti.
Za to je ustvaril zgodovinarje."
John Stachel, 1983
(rojen leta 1928 - fizik in filozof znanosti)
** Larry Niven (priznan pisatelj znanstvene fantastike) pravi takole:
"Dinozavri so izumrli, ker niso imeli vesoljskega programa. In
če bomo mi izumrli, ker ne bomo imeli vesoljskega programa,
si to zaslužimo."
Ali ga imamo (ustrezen program), ga gradimo v pravi smeri – velja za vse znanosti,
za vse programe, naš odnos do same Zemlje, življenja ... Odgovore moramo
iskati vsi, tudi vsak pri sebi in ...
Vičar Zorko
April 2015 – dopolnil feb. - maj 2021 in naprej, Lj.
DODATKI
Za konec (in začetek dodatkov) pa posladek – izračun kota ukrivitve žarka ob zvezdi
To je izračun, ki je dokončno spremenil pogled na prostor in čas in »zavrgel« Newtonovo fiziko (o meritvah odklona žarka smo pisali v januarski Spiki 2018, s tem prispevkom tudi izpolnjujemo obljubo o objavi izračuna, ki je spremenil ta naš svet).

Korekten opis gibanja v orbiti zvezde preko zapisa vrtilne količine in energije delca ter Schwarzschildove metrike. Schwarzschildovo metriko preoblikujmo z uporabo vrtilne količine (L) in energije (E) za delec z maso (m) v orbiti masivnega telesa – recimo v orbiti Sonca ( rs = 2GM/c2 je Schwarzschildov radij). Tako se bomo v enačbi tudi znebili časa! Sledimo torej spodnjim točkam z oznako »O« (odklon).
O1)
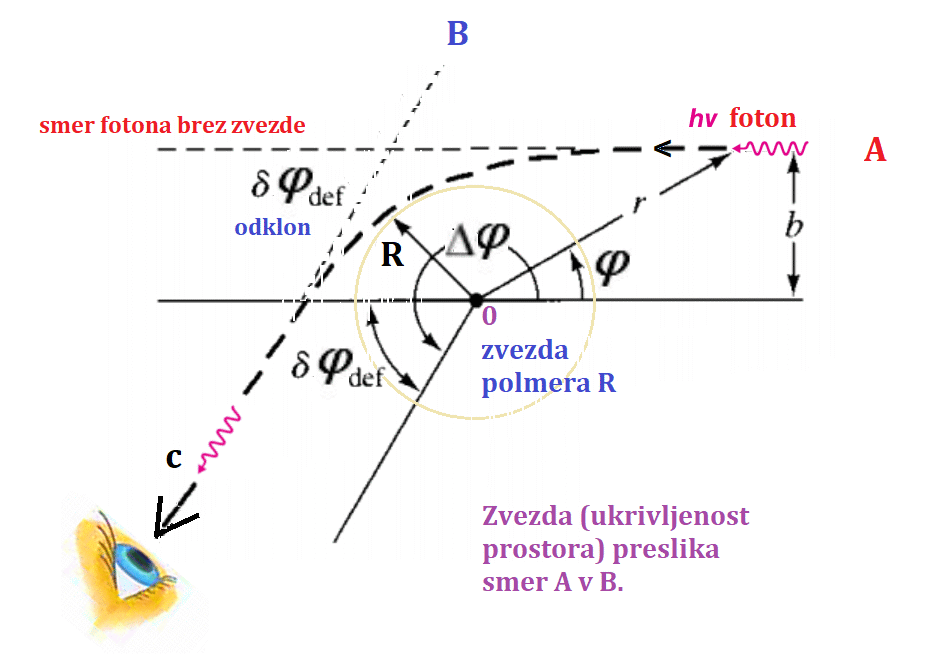
Iščemo zasuk smeri žarka, ki je večji od 180 °, oziroma razliko Δφ - 180 °, ki je na sliki
označena s kotom δφdef
(The angle of deflection of light that passing close to the Sun).
Žarek (matematično) prihaja z neskončnosti in potuje v neskončnost v nasprotni smeri,
če ni gravitacije (φ teče od 0 ° do 180 °, glejte sliko), če je masa (rec. zvezde)
velika in posledično gravitacija
(bolje ukrivljenost), potem je kot
Δφ > 180 °.
Že znana Schwarzschildova metrika se torej zapiše kot (O1):
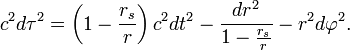
V tej enačbi je Ω nadomeščen kar s φ.
Če zgolj osvežimo spomin in še enkrat izračunamo velikost četverca gibalne
količine brez gravitacije in z gravitacijo.
Schwarzschildovo metriko zapišimo še s substitucijo
rs = 2GM/c2 in dt' = dτ:
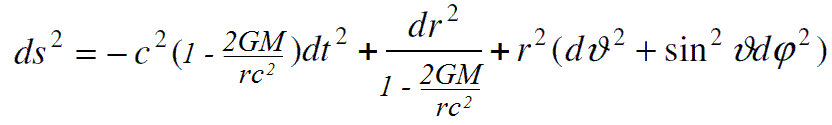
-c2dτ2 = -c2dt2(1 - rs/r)
+ dr2/(1 - rs/r) + r2(dϑ2 + sin2ϑ dφ2)
Enačbo delimo z lastnim časom dτ, že prej smo vpeljali kot zasuka
dΩ2 = dϑ2 + sin2ϑ dφ2:
c2 = c2(1 - rs/r)(dt/dτ)2
– (dr/dτ)2/(1 - rs/r) - r2(dΩ/dτ)2
- enačbo pomnožimo z izrazom (1 - rs/r) in dobimo izraz,
(1 - rs/r)c2
= c2(1 - rs/r)2(dt/dτ)2
– (dr/dτ)2 - (1 - rs/r)r2(dΩ/dτ)2
Levi člen (1 - rs/r)c2, če ga pomnožimo z maso delca, predstavlja neke vrste mirovno energijo delca v potencialu gravitacije masivnega objekta (rec. zvezde).
Tako kot v četvercu brez teže, se tudi v tej enačbi skriva energija.
Če zgolj osvežimo spomin in še enkrat zapišemo velikost četverca
gibalne količine brez gravitacije in naredimo še primerjavo s četvercem
z gravitacijo za zelo oddaljenega opazovalca, ki ne čuti gravitacije,
potem velja (upoštevajmo pa že znano Einsteinovo enačbo za polno energijo
delca E = γmc2):
(cdτ, 0) ⇔ dXμ = (cdt, dx) = (cdt, vdt) = (cγdτ, vγdτ)
= dτ(cγ, vγ)
(c, 0) ⇔ vμ = (cγ, vγ) = (cE/(mc2), vγ)
– četverec brez gravitacije ( γ = E/(mc2) )
(c, 0) ⇔ (c(1 - rs/r)1/2(dt/dτ), ...) – prvi člen metrike z gravitacijo, od zgoraj
[- še zapis celotnega četverca za gravitacijo
(cdτ, 0, 0, 0)
⇔ dXμ = ( c(1 - rs/r)1/2dt, dr/(1 - rs/r)1/2 , rdϑ , r sin ϑ dφ )
]
Primerjava nam da za prvi člen obeh četvercev naslednji izraz:
E/(mc2) = (1 - rs/r)1/2(dt/dτ)
= (1 - rs/r)1/2γ
Tako dobimo energijo delca še v gravitacijskem polju za oddaljenega opazovalca:
E = (1 – rs/r)1/2γmc2
Za energijo delca velja enako kot pri posebni relativnosti, le da nastopi
še gravitacijska (potencialna) energija, na koncu lahko izraz še razčlenimo:
E = Eo + Ekin + Epot,
kjer je:
E = (1 – rs/r)1/2γmc2
- celotna energija, izpeljali zgoraj
Eo = mc2 - mirovna energija
Ekin = (γ - 1)mc2
= ((1 – v2/c2)-1/2 - 1)mc2
- kinetična energija (za male hitrosti je mv2/2)
Epot = ((1 – rs/r)1/2 - 1)γmc2 - potencialna
energija (za male hitrosti in gravitacijo velja –GmM/r)
Lorentzov člen je γ = (1 – v2/c2)-1/2. V splošnem velja, da je v2 po Pitagoru vsota kvadratov radialne in tangentne hitrosti v2 = vr2 + vt2.
Pri šibki gravitaciji in majhni hitrosti delca moramo dobiti klasičen izraz za energijo - in to tudi zares velja. Pri majhni hitrosti je Ekin = ((1 – v2/c2)-1/2 - 1)mc2 ≈ ((1 – v2/(2c2)) - 1)mc2 = mv2/2. Pri majhni gravitaciji in hitrosti velja, da je γ ≈ 1, in ko je gravitacija šibka, velja (1 – rs/r)1/2 = (1 – 2GM/(rc2))1/2 ≈ 1 - GM/(rc2), od koder sledi Epot = ((1 – rs/r)1/2 - 1)γmc2 ≈ (1 - GM/(rc2) – 1)mc2 = - GMm/r.
Schwarzschildova metrika v drugi obliki
(
(1 - rs/r)c2
= c2(1 - rs/r)2(dt/dτ)2
– (dr/dτ)2 - (1 - rs/r)r2(dΩ/dτ)2
), recimo za opazovalca na matični zvezdi (glej sliko, kjer je simbolično
opazovalec na zvezdi K. Schwarzschild), je po
obliki navidezno enaka kot za oddaljenega opazovalca (opazujemo gibajoč
delec – nanj vpliva tako efekt hitrosti, kot gravitacije)

(1 - rs/r)c2
= c2(1 - rs/r)2(dt/dτ)2 –
(dr/dτ)2 - (1 - rs/r)r2(dΩ/dτ)2
- a sedaj za gibajoč delec velja E/(mc2)
= (1 – rs/r)dt/dτ
(ali tudi E2/(m2c2)
= c2(1 - rs/r)2(dt/dτ)2),
saj je čas dt v tem primeru enak
dt = γdτ/(1 – rs/r)1/2 .
Zakaj? - ker na izračun lokalnega lastnega časa
dτ,
poleg gibanja
dt/γ
- enako kot pri posebni relativnosti,
- sedaj dodatno vpliva
še gravitacija s členom
(1 – rs/r)1/2,
kar smo zapisali že na začetku poglavja
o gravitaciji in metriki;
sedaj torej velja
dτ = dt(1 – rs/r)1/2/γ ali dt/dτ
= γ/(1 – rs/r)1/2 ), tako da še zmeraj velja znana povezava
E/(mc2) = (1 – rs/r)1/2γ.
To dejstvo zapišemo, upoštevamo, še v nekoliko preoblikovani Schwarzschildovi metriki:
(1 - rs/r)c2 = E2/(m2c2)
– (dr/dτ)2 -
(1 - rs/r)r2(dΩ/dτ)2
Iz zadnje enačbe se lahko, z nekaj matematične telovadbe, izpelje vrsto pojavov
(uklon žarka ob zvezdi – to ravno počnemo, zasuk perihelija, gravitacijski premik
frekvence svetlobe, zamik časa, ur – to bomo tudi še poračunali ...).
O2)
Vrtilna količina je L = mr2dφ/dτ, od koder sledi enačba (O2):
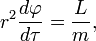
Še glede vrtilne količine L in enačbe L = mr2dφ/dτ.
Klasična vrtilna količina za točkasto telo (m) pri kroženju s hitrostjo
(v = rdφ/dt)
in gibalno količino (p = mv) na polmeru (r) je
kar: L = mvr = rp
Relativistična vrtilna količina je torej po analogiji z gibalno količino
(p = mγv) enaka izrazu (dΩ smo nadomestili z dφ):
L = rp = rmγv = rmγrdφ/dt = mr2γdφ/dt = mr2dφ/dτ
(saj pri kroženju velja γ/dt = 1/dτ)
Pri pospeševalnikih delcev se tudi računa z relativistično mehaniko
(relativistično maso,
v resnici z energijo E/c2).
Še namig za kroženje.
Izjemno pomembna je tudi povezava med kotnima hitrostima v obeh sistemih
(ω velja za oddaljenega nepospešenega opazovalca), pri kroženju.
dφ/dτ = ω’ = γdφ/dt = γω
Kotna hitrost ω’ je posledica sistemske sile zaradi kroženja. Čutimo jo
recimo v avtomobilu v vožnji skozi ovinek – takrat govorimo o (sistemski)
centrifugalni sili, ki deluje na potnike. Centrifugalna sila je posledica
centripetalne sile s katero podlaga deluje na kolesa avtomobila, da lahko
sploh zvozimo ovinek (v primeru ledu je to pri večji hitrosti misija nemogoče,
sploh če ovinek ni nagnjen). Razdelajmo še kotne hitrosti in nekaj presenetljivih
posledic.
Velja tudi: 2π/dτo
= (γ2π)/to = (2π + δ)/to
γ2π = (2π + δ) od koder sledi:
δ = γ2π - 2π ali δ = 2π( γ-1)
Iz zadnje matematične telovadbe se zdi, kot da oddaljeni opazovalec
vidi, da recimo krožeče telo naredi zasuk δ več v času, ko naredi
krožeči sistem zasuk 360° (oz. 2π).
Da to ni zgolj matematični trik, se vidi pri precesijah perihelijev
planetov (glavnih osi elips - apsid).
O3)
V splošni relativnosti je princip polne energije E v četvercu, oziroma
metriki, po analogiji s splošno teorijo, enak kot v posebni teoriji.
Tako dobimo enačbo (O3):
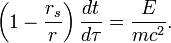
Še preprost dokaz – za vajo ne škodi. Če je gravitacijsko polje nič
ali neizrazito
(rs/r = 2GM/(rc2) ≈ 0) -
kot je recimo na Zemlji - za večino pojavov preide energija hitrih delcev
v šibki gravitaciji v obliko energije, kot jo predvideva specialna teorija
relativnosti. Velja:
(1 - rs/r)dt/dτ ≈ dt/dτ
= E/(mc2) = 1/(1 – v2/c2)1/2 = γ
ali
E/c2 = (1 – rs/r)mdt/dτ = (1 – 0)mγ = mγ -
izraz že poznamo, sklepanje je bilo torej pravilno
Sedaj pa v Schwarzschildovi metriki, po deljenju z
dτ2,
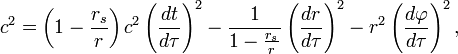
nadomestimo zapisane izraze z enačbama O2 in O3.
O4)
Časovno odvisnost pa je mogoče odpraviti z uporabo vrtilne
količine L, saj velja
dτ/dφ = mr2/L.
Tako dobimo enačbo (O4):
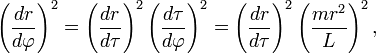
O5)
Tako iz metrike dobimo prehodno enačbo delca (O5), ki še vedno vsebuje čas
(dr/dτ)2:
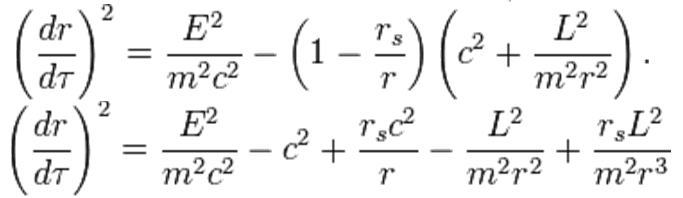
O6)
Kar pa pripelje do končne enačbe orbite delca, saj izraz
(dr/dτ)2 = (dr/dφ)2(L/(mr2))2
iz enačbe (O4) vstavimo v enačbo (O5). Osnovi za nadaljnjo iskanje
enačbe orbite delca sta dve obliki zapisa preoblikovane metrike z
vpeljavo parametrov
a = L/(mc) in b = cL/E. Tako pridemo do enačbe (O6):
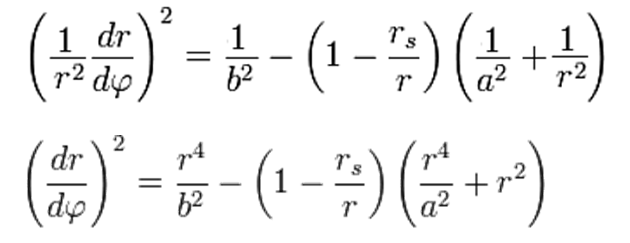
Enačbo smo, kot smo že omenili, poenostavili z uvedbo dveh konstant a in b (glede na začetne pogoje):
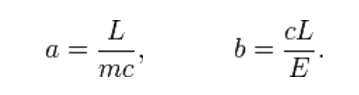
O7)
Za zasuk (φ) orbite delca na potovanju v bližini masivnega objekta tako
dobimo integral, enačbo (O7):
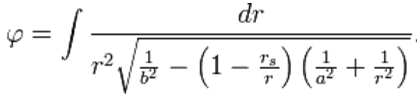
Člen
1/a2 = (mc)2/L2
ima za foton, ki je brez mase,
vrednost 0 (mc = 0). Enako enačbo za kot
φ
je mogoče izpeljati tudi iz Lagrangeove mehanike
ali Hamilton – Jacobijeve enačbe. Sledi še modificirana formula za uklon svetlobe.

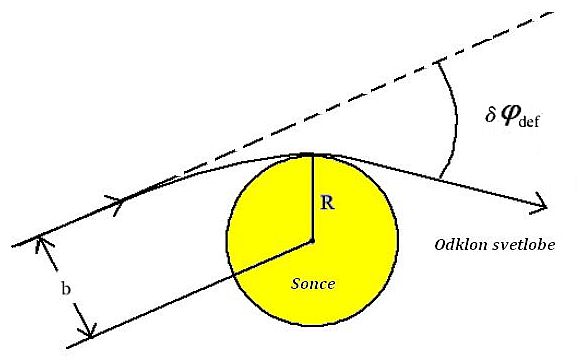
Slika levo - meritve odklona lege zvezd ob Sončevem mrku v
bližini Sonca (pod vplivom gravitacije), ki jih je opravil
Eddington leta 1919, so prepričale (skoraj) cel svet, da
so sprejeli splošno relativnost. Slika desno – skica
za pomoč pri razumevanju izračuna orbite svetlobe ob Soncu
(odklon je seveda zdaleč pretiran).
O7 b)
Kot smo že povedali, ima člen
1/a2 = (mc)2/L2 za foton,
ki je brez mase, vrednost 0 (mc = 0),
zato velja modificirana enačba odklona (O7 b):
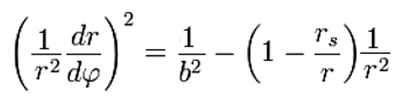
Odklon svetlobe Δφ oz. δφ pa se v splošnem pri sferičnem
telesu (zvezdi) seveda izračuna z integralom po celotni poti potovanja fotonov.
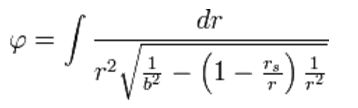
Razmerje
rs/r
je prevladujoči člen za kotni odklon
δφ
kvanta brez mase (fotona), ki prihaja iz neskončnosti
in potuje proti neskončnosti. Po integralu, ki je nekoliko zahtevnejši
(uvedemo novi spremenljivki u = R/r [polmer Sonca deljen z razdaljo do žarka],
za diferencial du velja zveza
du = - Rdr/r2 in še kotno odvisnost
u = cos α, od koder izhaja du = - sin
α dα). Poiščimo
še parameter b, v temenu poti fotona (glejte sliko orbite -
pri r = R je hkrati ekstrem orbite in zato velja, da je odvod
razdalje po kotu v temenu enak nič: dr/dφ = 0), kjer je izraz za
b (oziroma 1/b2) enolično določen in ga izrazimo kar iz enačbe
(O7 b) , ki ima torej v tej točki vrednost nič:
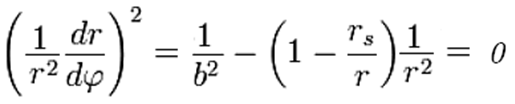
1/b2 = (1 - rs/R)/R2 = (1 - 2GM/(c2R))/R2,
ker je v temenu dr/dφ = 0
Pri Soncu je člen b za svetlobo praktično enak polmeru Sonca R.
A pustimo člen b v polnem zapisu, saj enačba velja splošno, tudi
za masivne zvezde.
Na koncu, po poenostavitvi integrala za zvezde podobne Soncu,
pridemo do končne rešitve za odklon žarka tik ob površini Sonca
(klasična fizika nam je dala napačen rezultat – revija Spika 1
[2018], članek Zgodovina in mrki). Iščemo torej izraz:
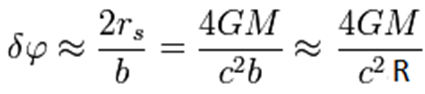
Sledi izvrednotenje integrala ( rezultat δφ = 4GM/(c2R) ), ki ga žal ne bomo našli v tabelaričnih seznamih rešenih integralov. Bo pa potek reševanja zelo poučen. Morebiti pa bo kak srednješolec, študent (tudi bivši) ob tem postopku za nazaj našel smisel matematične “telovadbe” z integrali (recimo iz četrtega letnika, ki se je takrat mnogim zdela odveč) – da torej le obstajajo področja, kjer integrali lahko, recimo ključno, prispevajo v zakladnico človeškega znanja (če že o tem ni bil prej prepričan). Recimo pri razumevanju, potrditvi pravilnejše fizikalne slike narave, sveta, vesolja. Ta izpeljava je (bo) strogo korektna. Na koncu pa bomo, poleg matematičnih pravil, vključili še fizikalni čut in sicer z razrešitvijo integrala za parameter (bolje spremenljivko) majhne vrednosti (GM/(c2R) = 2,1*10-6, ta vrednost velja za Sonce) in bomo tako prišli do elegantne končne rešitve.
Tokrat (zaradi postopka integriranja – po domače, seštevanja malih koščkov) zapišimo enačbo za odklon žarka ob zvezdi v razširjeni obliki, s Schwarzschildovim radijem v osnovnem zapisu rs = 2GM/c2. Integrirali bomo od temena poti žarka (ko oklepa smer “središče zvezde – teme“ kot α1 = 0 °), do α2 = π/2 (90°), ko je žarek že zelo daleč vstran od zvezde (matematično rečeno v neskončnosti). Vrednost se pomnoži z dve, ker gre za simetričen pojav (pot žarka iz neskončnosti do zvezde – do temena ob zvezdi – in naprej do neskončnosti; lahko pa sta meji tudi kar [-π/2, π/2], ko seveda množenje z dve odpade). Uporabili bomo še trigonometrično povezavo, za tan(x/2) = sin(x)/(1 + cos(x)), odvod tan(x/2) pa je kar d(tan(x/2))/dx = 1/(1 + cos(x)). Integral je torej ∫dx/(1 + cos(x)) = tan(x/2) + c. No pa začnimo z že preoblikovano metriko!

Smer π pomeni prvotno smer, če ni gravitacije zvezde
(če je prostor raven),
PRISPEVEK:
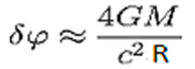
pa predstavlja odmik žarka od prvotne smeri zaradi ukrivljenosti prostora ob zvezdi, recimo Soncu.

Za Sonce velja odmik žarka od prvotne smeri 1.75 '' (tik ob Soncu):
δφ = 4GM/(c2R) = 1.75 '' (loč. sekunde).
Med Sončevim mrkom, 29. maja leta 1919, je Einsteinovo napoved (1.75 loč. sekunde)
izmeril Eddington (približno).
Čeprav je ta formula le približna (za zvezde podobne Soncu pa čisto korektna), je jasno, da je za večino meritev pojava gravitacijskega lečenja odločilno razmerje rs/r. Za svetlobo, ki potuje mimo površine Sonca, je kotni zasuk žarka okoli 1.75 ločnih sekund. In to vrednost so večkrat izmerili – recimo med popolnimi Sončevimi mrki v vidni svetlobi in z radijskimi teleskopi. Izračun so najprej napačno zastavili (s klasično Keplerjevo mehaniko in tako pridelali napako polovične vrednosti) Einstein leta 1911 in že drugi pred njim (recimo Soldner), a je Einstein enačbo, preko splošne teorije relativnosti, korigiral leta 1915.
Še opravičilo vsem tistim bralcem Spike, ki jih ta tematika (matematika) ne zanima – a v postopku in rezultatu se skriva izjemno uspešen trud mnogih generacij, da bi razumeli naravo vesolja in nas same.
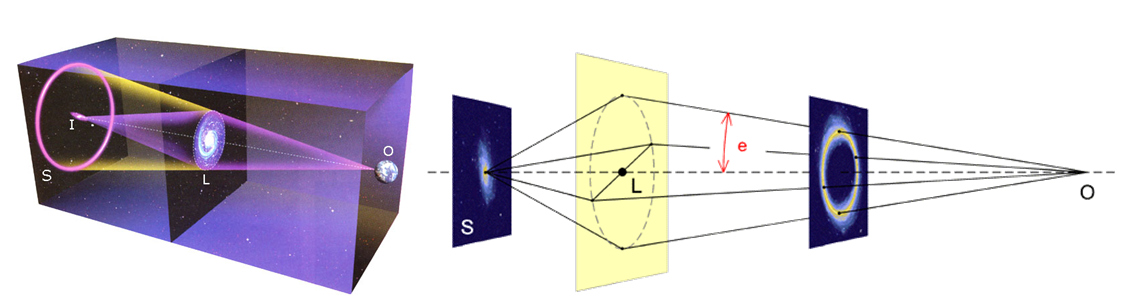
Gravitacijsko lečenje je zgolj posplošitev odklona žarka ob zvezdi na
poljubne izrazite gravitacijske vire (masivne objekte), večinoma na galaksije …
Slika prikazuje
"teleskop s Soncem kot gravitacijsko lečo".
Roji majhnih vesoljskih plovil, ki jih poganjajo sončna jadra, bi poleteli do mesta - fokusa,
kjer gravitacija našega Sonca popači in poveča svetlobo bližnjega zvezdnega sistema,
kar bi nam omogočalo, da zajamemo ostro sliko eksoplaneta, podobnega Zemlji.
Koncept je znan kot "the Solar Gravity Lens telescope".
Vir:
https://www.planetary.org/space-images/solar-gravity-lens-telescope
Obstajajo tudi ideje, da bi Sonce uporabili kot najbližjo dokaj zmogljivo
gravitacijsko lečo. Problem je, ker je ukrivitev žarka tik ob Soncu le okrog φ =
1.75 ločnih sekund (1.75 °/3600). Izračunajmo gorišče take gravitacijske leče,
glejte skico - žal je gorišče Sonca zelo daleč
(polmer Sonca Ro je velik okrog četrtine stopinje 0.26 ° krat razdalje Zemlja-Sonce;
razdalja Zemlja-Sonce je astronomska enota, krajše AE = 150 milijonov km):
fSon = RSon/φ
= 0.26 ° * AE/φ
= 0.26 AE * 3600/1.7 = 550 AE.
Ločljivost bi s tem povečali teoretično na 10-10" (
za ločljivost velja približek: θ ≈ 140/Dv_mm [''], oziroma
pravilneje je kot ločljivosti enak: θ = 1,22*λ/D, v tem primeru je D premer Sonca, sami izračunajte ...),
kar pomeni, da bi
lahko na bližnjih eksoplanetih zaznali morebitne celine, oceane ...
Koliko ločnih sekund pa meri recimo eksoplanet na razdalji 10 sv. let,
recimo, da je velikosti Zemlje? Premer Sonca je 109 premerov Zemlje.
Na razdalji AE je Zemlja velika
okrog 30*60"/109 = 17 ". Eno sv. leto je približno 6,324 104 AE.
Če delimo 17 " z 10 sv. leti, dobimo vrednost φekso = 17"/(10*6.324 104 )
= 2,7 10-5 ". Kar je teoretično 100 000 krat večji kot od ločljivosti solarnega teleskopa - kar daje veliko upanje
in smisel gravitacijskemu solarnemu teleskopu.
A problem takega gravitacijskega teleskopa na Sonce je zelo oddaljeno gorišče, kar 550 astronomskih enot
(razdalj Zemlja - Sonce). Eden od Voyagerjev (izstreljen 1977) je oddaljen trenutno 160 AE, kar je še zelo daleč
do 550 AE. Torej je problem današnja precej neučinkovita pogonska tehnika.
Danes upamo, da bomo čez nekaj let lahko dosegli hitrosti okrog
120 km/s (22 AE/leto) - kar bi potovanje detektorjev svetlobe v gorišče Sonca skrajšalo na okrog 20 let.

Primer rekonstrukcije Zemlje z uporabo svetlobnega obroča okoli Sonca, ki ga projicira sončna gravitacijska leča.
Algoritem, ki omogoča to rekonstrukcijo, je mogoče uporabiti za eksoplanete za vrhunsko slikanje.
Vir: https://www.space.com/sun-gravity-could-help-observe-exoplanets-in-detail
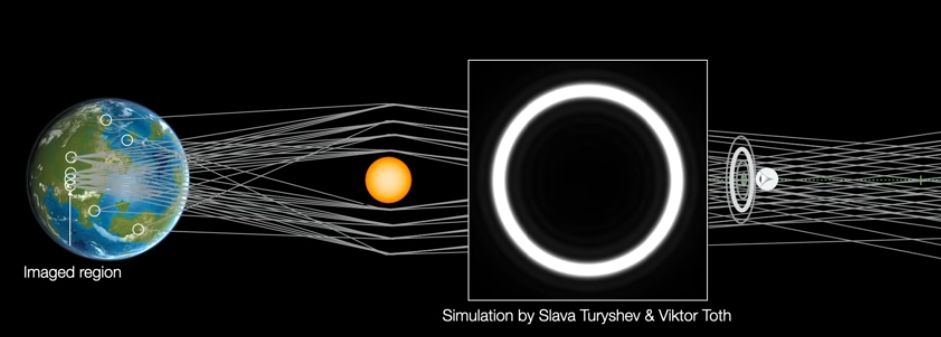

Princip snemanja eksoplaneta preko Sonca (ukrivitev svetlobe) - senzorji, ki lovijo
svetlobne obroče (uklone), slikaj iz različnih pozicij in tako sestavijo sliko eksoplaneta - konvolucija.
Lahko počakamo, da se tudi eksoplanet, matična zvezda premakne. Uporabili bi senčnike za zastiranje Sonca
in tudi oddaljene zvezde ...
https://www.google.com/search?q=the+Solar+Gravity+Lens+telescope&btnG=najdi#fpstate=ive&vld=cid:82b00b1c,vid:NQFqDKRAROI
Kotna velikost Sonca na tej razdalji je okrog:
φ550AE =
30*60''*1AE/550AE = 3.3 ''.
To je velikostni red pod katerim se nam razkriva recimo planet Uran - s prostim očesom
tega (Urana) seveda ne zaznamo - razen pod posebnimi pogoji le medlo piko na nočnem nebu.
Gostota svetlobnega toka Sonca pa je na tej razdalji 550 AE:
J550AE = 1400 W/m2*(1AE/550AE)2 = 0.0046 W/m2.
To svetlobo bo potrebno zasenčiti. Magnituda Sonca na tej razdalji 550 AE je okrog minus -13,2.
Torej je
Sonce na tej razdalji še zmeraj svetlejše od polne Lune opazovane z Zemlje, ko ima magnitudo -12.74.
Magnituda Sonca na razdalji AE (na Zemlji) pa je seveda kar minus -26.91.
"Solar gravity lens" (SGL)
omogoča ojačanje svetlosti do faktorja ≈ 1011 (pri 1 µm).
Leta 2020 je Nasin fizik Slava Turyshev predstavil svojo zamisel o neposrednem slikanju z več
slikovnimi senzorji in spektroskopiji eksoplaneta z misijo v gorišče Sončeve gravitacijske leče.
Tak gravitacijski objektiv
bi lahko rekonstruiral sliko eksoplaneta s površinsko ločljivostjo ≈ 25 km v 6 mesecih integracijskega
časa, kar je dovolj, da se vidijo površinske značilnosti in znaki naseljenosti - ali celo civilizacije.
Njegov predlog
je bil izbran za fazo III NIAC 2020 (NASA Inštitut za napredne koncepte). Turyshev predlaga uporabo
sončnih jader realne velikosti (≈ 16 lopatic 103 m2), da bi dosegli potrebno
visoko hitrost
v periheliju (≈ 150 km/s), ki bi v 17 letih dosegla 547 AE.
https://en.wikipedia.org/wiki/Solar_gravitational_lens
Princip uporabe lahkega solarnega jadra v bližini Sonca - kjer sta fotonska gostota in s tem tudi
tlak (Sončev veter) na jadro največja.
Newtonska (rdeča) v primerjavi z Einsteinovo orbito (modra) enega planeta,
ki potuje okoli sferične zvezde (in precesira zaradi relativističnih efektov).
Večji del precesije (zasuka) glavne osi eliptične tirnice Merkurja povzročajo motnje ostalih planetov (532"/stoletje) Sončevega sistema. Enak efekt se opazi tudi pri ostalih planetih, a najizraziteje, kot smo že omenili, pri Merkurju, ki ima izrazito ekscentrično orbito in je Soncu najbližji planet. Vpliv kvadropolnega momenta Sonca v gravitacijskem potencialu prispeva le okrog 0.025" na stoletje. A še večji prispevek od nesferičnega Sonca (več kot 40" na stoletje) prispeva nek drug (relativistični) efekt – in o tem bo tekla beseda.
Le Verrier je leta 1847 odkril da se prisončje eliptičnega tira Merkurja precesijsko suče v večji meri, kot je predvidel Newtonov splošni gravitacijski zakon. Pojav je korektno teoretično pojasnila šele Einsteinova splošna teorija relativnosti v letu 1916. Paul Gerber pa je že leta 1898 izpeljal enako odvisnost – a z nekoliko drugačnimi predpostavkami.
Dopolnjena kvaziklasična razlaga pravi, da se perihelij suče, ker sta prečno in radialno gibanje povezani, in ker je hitrost spremembe gravitacijskega polja končna – enaka hitrosti svetlobe (nekako tako je razlagal Gerber). Merkurjev zasuk perihelija je sicer samo 43"/stoletje, kar se dobro skladala z Einsteinovim izračunom (in Gerberjevim). Je pa gibanje planetov precej zapleteno, zadaj je tudi efekt vrtenja Sonca, ki je zato sploščeno in moramo upoštevati še dodatni člen masnega kvadropolnega momenta v gravitacijskem potencialu (prispevek je zelo majhen, smo že omenili - okrog 0.025"/stoletje). Mi bomo izvedli krajši izračun in nakazali izračun zasuka s Schwarzschildovo metriko in privzeli, da je Sonce idealna krogla.
Zasuk glavne osi orbite Merkurja (precesija perihelija) je bil prvi preizkusni kamen nove slike sveta, ki se imenuje splošna teorija relativnosti – in nadgradnja Newtonove mehanike je uspešno prestala prvi test in zaenkrat tudi vse ostale (ukrivitev svetlobe pod vplivom gravitacije - gravitacijsko lečenje - gravitacijski rdeči premik svetlobe, elektromagnetnega valovanja - brez nove slike sveta tudi GPS sateliti ne bi delovali kot se šika, itn).
Pred Gerberjevim in Einsteinovim izračunom (razlago) so večinoma trdili, da je teh 43'' zasuka
perihelija na 100 let posledica vpliva še neodkritega planeta (Le Verrier je leta 1845 je trdil,
da je med Merkurjem in Soncem še neodkrit planet - imenoval ga je Vulkan), itn.
Nakažimo
pot – kjer bo zanimiv predvsem energijski zapis Schwarzschildove metrike metrike. Še enkrat zapišimo
enačbo delca – to smo že naredili pri iskanju odmika fotona ob
zvezdi od prvotne poti.
Obravnavajmo primer, ko je M >> m ( oz. m/M ≈ 0, ko je recimo masa m planeta veliko manjša od mase zvezde M) in velja μ = mM/(m + M) = m/(1 + m/M) ≈ m
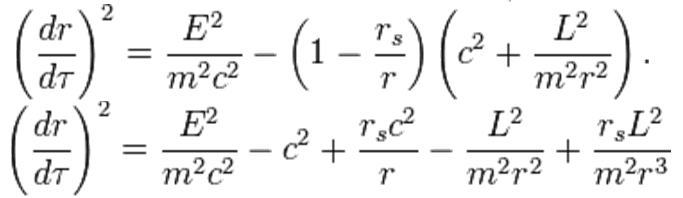
Izraz še preoblikujemo z uporabo splošne oblike
Schwarzschildovega radija (rs = 2GM/c2) kot:
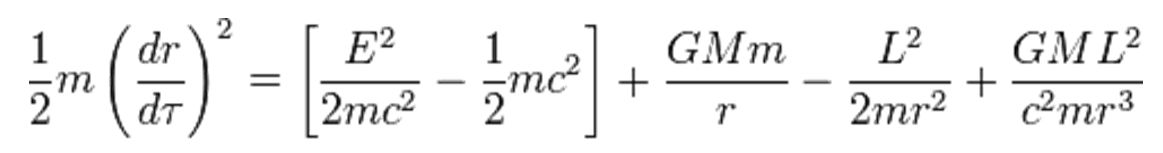
Kaj opazimo pri tej enačbi –
v bistvu energijo delca. Člene bomo dodatno pojasnili.
Potencialna energija delca V(r) je enaka:
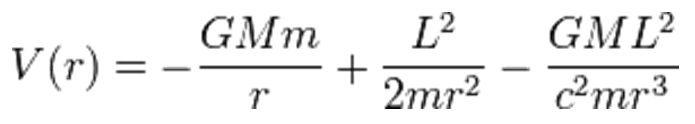
Podajmo še splošen zapis energije z reducirano maso μ = mM/(m + M):
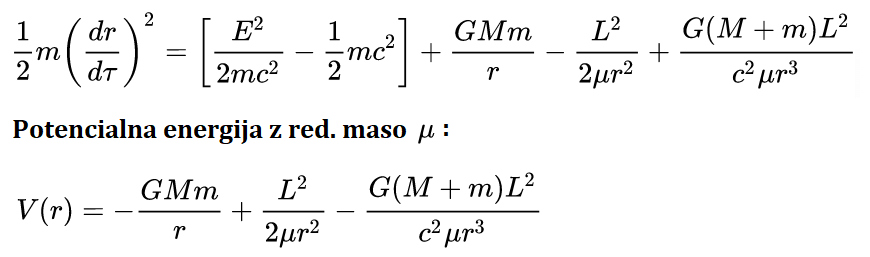
A izpeljavo bomo naredili za primer, ko je μ = mM/(m + M) = m/(1 + m/M) ≈ m.
Oglejmo si torej člene potenciala
(
V(r) = (-GMm/r + L2/(2mr2) - GML2/(c2mr3)
).
Prvi člen je klasični ( -GMm/r ) – privlačnost gravitacije da Newtonovo
potencialno energijo - drugi člen
( L2/(2mr2) )
ustreza potencialu (energiji) kroženja (recimo »spinu«),
tretji
izraz ( - GML2/(c2mr3) )
je energija kot »posledica« splošne relativnosti (že sama masa se spreminja zaradi gibanja). Iz
enačbe je razvidno, da je ta energija obratno sorazmerna (inverzna) kubu razdalje
in ravno ta povzroča precesijo eliptične orbite za kot
δφ
na obrat
(smo že izpeljali).
Potencial V(r) zapišimo še z novima (starima) spremenljivkama:
a
= L/(mc) in rs = 2GM/c2.
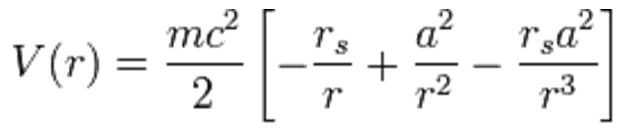
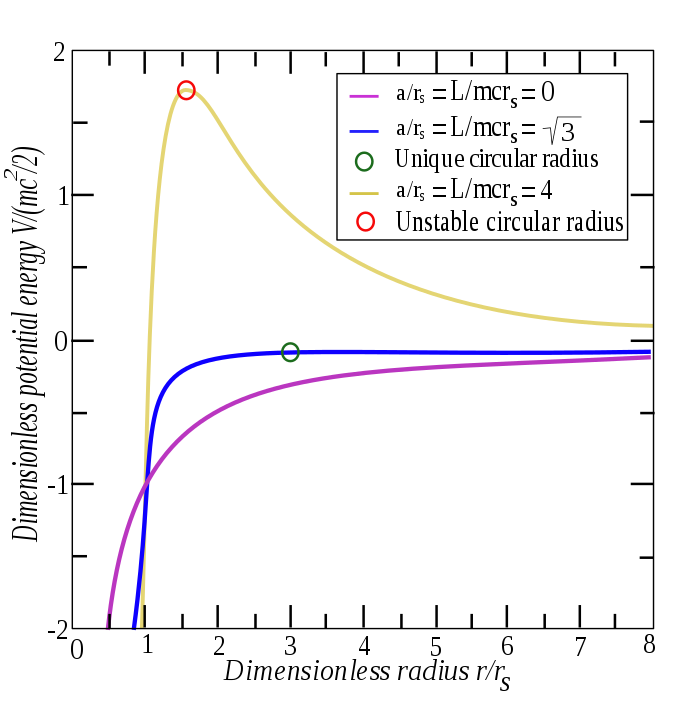
Grafi
efektivnega potenciala V v enotah
r/rs Schwarzschildovega radija
(rs = 2GM/c2)
glede na vrednosti
a/rs = L/(mcrs),
za: a/rs = 0, a/rs = 31/2, a/rs = 4.
Krožna orbita je mogoča, če je dejanska sila na delec enaka nič (gravitacijska je enaka sistemski, kot v satelitih to čutijo astronavti).
Še vmesni premislek o relativistični masi in potencialu!
- orbito, oziroma animacijo precesije lahko sprogramirate, zelo priporočam ...
FG = GMmγ/r2
Ker je hitrost
Merkurja napram svetlobni relativno skromna, in ker je oddaljenost od Sonca znatna
(tudi Sonce ni ravno po masi gigant, posledica je manj intenzivna fuzija
– kar je dobro za nas, za relativno mirno bivanje vseh živih
bitij na našem planetu), velja
γ = dt/dτ ≈ 1 + 3GM/(2c2r)
= 1 + 3v2/(2c2) –
izpeljali že v prejšnjem poglavju, upoštevali smo
tudi zelo blago eliptično orbito, kjer približno velja za orbitalno hitrost
(v2
= GM/r).
Ker je hitrost v = rdϑ/dt, in ker je specifična
relativna vrtilna količina na maso kar
l = rγv = γr2dϑ/dt, velja:
kjer je konstanta
∈ pri dani orbiti enaka: ∈ = (GM)2/(lc)2.
Tako se končni izraz
za gravitacijsko silo zapiše kot:
Vrnimo se k korektni Schwarzschildovi metriki
in enačbi za silo ter izpeljavi kota zasuka precesije apside elipse "planet - zvezda":
Obstajata dve
rešitvi kvadratne enačbe (rsr2 – 2a2r + 3rsa2 = 0)
- dva
ekstrema, kjer je to ravnotežje mogoče, označeni sta kot rinner in router.
To sta:
Če seštejemo router + rinner, dobimo uporaben izraz:
Rešitvi kvadratne enačbe pripeljeta do sklepa, da je
router vedno večji od 3rs, rinner pa leži
med rs3/2 in
3rs, orbita je nestabilna (to se vidi na grafu potenciala – rumena
krivulja z izrazitim maksimumom). Krožne orbite manjše od rs3/2 niso mogoče.
Za delce brez mase gre člen a v neskončnost ( a =
L/(mc) – foton nima mase), kar pomeni, da je krožna orbita za
fotone pri:
rinner = 3rs/2 = 3GM/c2.
Krogla s takim radijem je znana pod
imenom fotonska sfera (smo jo že omenili v uvodu v splošno relativnost).
Razdalja router pa je torej namenjena masnim delcem.
Hitrost orbitalne precesije se lahko
izračuna z uporabo potencialne energije V (že za kroženje velja dV/dr = Fc
= mω2r, od koder sledi
ωr2 = (1/m)dF/dr = d(ω2r)/dr - torej iščemo rešitve v tej smeri).
Majhen radialni odmik od krožne orbite router (apsida elipse)
se bo konstantno zamikal s kotno frekvenco, ki jo lahko zapišemo kot
drugi odvod potenciala. Zakaj je temu tako?
Sledi
izpeljava zasuka perihelije, tokrat iz Schwarzschildove metrike.
ωr2 = (1/m)(d2V/dr2) = (c2/2)
[ -2rs/r3 + 6a2/r4 - 12rsa2/r5 ]
V končnem izrazu za kot zasuka (kot smo že omenili) je velika polos elipse zapisana z veliko črko
A, da ne bi bilo zamenjave z malo črko a, ki je že
bila prej uporabljena kot spremenljivka (a = L/(mc), oziroma univerzalneje
a = L/(μc) ). Če strnemo -
A je velika polos elipse in e ekscentričnost elipse.
Opomba!
ZGODOVINSKA ZAGATA GLEDE PRECESIJE APSIDE
Še zanimivost - gospod Paul Gerber je že leta 1898 izpeljal enako enačbo:
δφ = 6πGM/(c2a(1 - e2)) = 6πGM/(c2A(1 - e2)) ,
- privzel je, da je hitrost gravitacijske
sprememba praktično skoraj enaka svetlobni. A njegovo izpeljavo mnogi štejejo kot nedosledno.
Njegovi kritiki pravijo, da je Gerber neskladen s splošno teorijo relativnosti
– tudi z lastnimi predpostavkami, in da je zato napačno privzel, da
Sonce miruje. A vseeno je bil njegov napor kamenček v mozaiku do
končne rešitve problema gravitacije in časa – splošne teorije relativnosti. Napovedal je
odklon žarka ob Soncu, a za faktor 3/2 preveč. No zmotil se
je manj kot nekateri pred in po njem.
Različica danes izpodrinjenih teorij je
bila torej tudi Gerberjeva, ki jo razvil med letoma 1898 in 1902.
Predpostavil je končno hitrost gravitacije
cg
in za gravitacijski potencial dobil
zvezo:
Po binomskem izreku do drugega reda sledi:
Po Gerberju je zveza
med hitrostjo gravitacije cg in zasukom Merkurjevega prisončja Ψ:
kjer je:
,
in tukaj je ∈
izsrednost tira,
a velika polos,
τ obhodna doba.
Gerberjeva enačba da za zasuk Merkurjevega prisončja:
Ernst Gehrcke je leta 1916 omenil, da je matematično enaka Einsteinovi zvezi
iz splošne teorije relativnosti, ki jo je Einstein izpeljal leta 1915.
kjer je e izsrednost (ekscentričnost) tira, a glavna polos,
T obhodna doba, c hitrost gravitacije (enaka svetlobni), κ gravitacijska
konstanta (mi jo označujemo z G), m☉ Sončeva masa.
Einstein je leta 1920 zapisal: » ... even
if I had been aware of it, I would not have had
any reason to mention it. (...ich hätte aber auch keinen Anlaß gehabt,
sie zu erwähnen, wenn ich von ihr Kenntnis gehabt hätte.)«.
Einstein torej
trdi, da ni bil seznanjen z Gerberjevo izpeljavo, a tudi če bi
bil, ni imel nobenega razloga, da bi ga (Gerberja) omenil.
Zagotovo pa je
Gerber prvi na svetu rezultatsko pravilno povezal gravitacijo in osnovne naravne konstante
v oceni precesije Merkurjevega perihelija – in to je bila kvečjemu pomoč
vsem njegovim naslednikom in ne obratno (tudi če teoretično danes njegova pot
ni več verodostojna). Če bi bili enako strogi do vseh ostalih znanstvenikov
kot smo do Gerberja, bi morali zamolčati tako Keplerja kot Newtona ...,
no Hooku se je to delno tudi zgodilo (Hooke poda pravilno odvisnost
gravitacije od razdalje 1/R2 ).
Potrebno se je spomniti še na gospoda, ki
je prvi pravilno napovedal polmer črne luknje (takrat črne zvezde) - to
je bil John Michell leta 1783 (predpostavka je bila, da svetlobo sestavljajo
delci – danes vemo, da se svetloba obnaša kot valovanje in hkrati
ima lastnosti delcev, ki jim pravimo kvanti (fotoni), so brez mase z
energijo
E = hν
– Planckova konstanta krat frekvenca). Uporabil je enačbo
za ubežno hitrost (c2/2 – GM/r = 0). Danes temu polmeru pravimo
Schwarzschildov polmer dogodkovnega obzorja črne luknje (rs = 2GM/c2).
Fenomen singularnosti (ko gre
gostota proti neskončnosti, svetloba pa ne more uidet s telesa pod polmerom
rs = 2GM/c2) lahko opazujemo pri telesih, ki so velikosti tega radija
oz. skrivajo svojo maso (bolje energijo) pod tem radijem. V vesolju
seveda večinoma najdemo telesa, ki so pri dani masi precej večja od
rs (podajmo mejna polmera za Zemljo in Sonce):
Zemlja: rs = 8.8 mm
A ti dve
telesi sami zase ne moreta kolapsirati v črno luknjo, ker imata premajhno
maso! Precej zanimivo pa je obnašanje svetlobe na teh območjih (malo pravljic).
Vprašanje je, kam potuje svetloba (če v črni luknji sploh še obstaja
energija v obliki elektromagnetnega valovanja? Če ne, potem tam velja druga metrika
in s tem fizika ...). Vemo, da se svetloba premika tako, da
je po naravi sami metrika ds2 = 0 – fotoni so simbolično »brezčasni delci«.
Če zanemarimo spin
(rotacijo okrog Sonca), se v tem primeru sila zapiše v naslednji obliki:
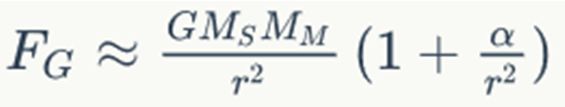
Primer take rešitve je na:
*problem_dveh_teles_zv.html
Še nekaj zelo koristne improvizacije - potem se vrnemo nazaj na izpeljani potencial.
Do te enačbe lahko pridemo tudi
preko (nekoliko sporne) Lagrangeeve formulacije s klasično mehaniko, ko privzamemo relativistično maso
Merkurja (podobno kot pri pospeševalnikih mγ).
v2/c2 = ((rdϑ/dt)/c)2 ≈ l2/(rc)2,
za majhen člen γ.
Če uvedemo novo
spremenljivko (krožno orbito pri konstantni specifični relativni vrtilni količini) ro = l2/(GM),
velja naslednja povezava:
γ ≈ 1 + 3GM/(2c2r) ≈ 1 +
3v2/(2c2) = 1 + 3l2/(2(rc)2)
= 1 + 3∈(ro/r)2/2,
FG = GMmγ/r2
= GMm(1 +3∈(ro/r)2/2)/r2 = GMm(1/r2
+3∈ro2/(2r4))
Če poiščemo še potencial:
V(r) = ∫FGdr = -GMm(1/r + ∈ro2/(2r3)),
dobimo praktično
enako formulacijo kot pri Schwarzschildovi metriki brez spina. Tukaj smo kombinirali klasično
in relativistično formulo (z veliko poenostavitvami), kar je narobe, kakšna polovička je
tako odveč ... V primeru ekvivalentnega upoštevanja relativistične mase centralnega telesa pa
bi celo uganili pravilno enačbo
(FG = GMm(1/r2 +3∈ro2/r4)).
A namen je
bil le, predstaviti še en vidik razumevanja precesije perihelija planetov. Velikokrat preberemo,
da prihaja do precesije perihelija planetov (apside elipse) zaradi spreminjanja energije planeta
(na orbiti elipse se planetu stalno spreminja hitrost in delno tudi potencialna
energija in s tem celotna energija planeta, posledično relativnostna masa »mγ«), kar
vpliva na orbito planeta, ki se suče v cvet (odgovor ima nekaj
soli – saj je gravitacija odvisna od mase, ki pa je funkcija
spreminjajoče se energije). Če narišete animirani graf poti planeta pri korigirani
gravitacijski
sili ( FG = GMm(1 + 3∈(ro/r)2/2)/r2 )
v koraku dovolj kratkega
časovnega intervala, boste po vsakem obhodu planeta animirali precesijo perihelija
(apside elipse).
Primer take rešitve (animacije precesije) je na:
*problem_dveh_teles_zv.html
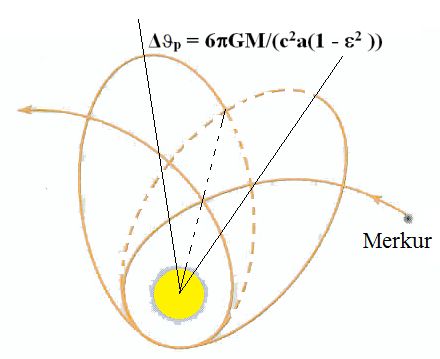
Zasuk kota precesije je pretiran.
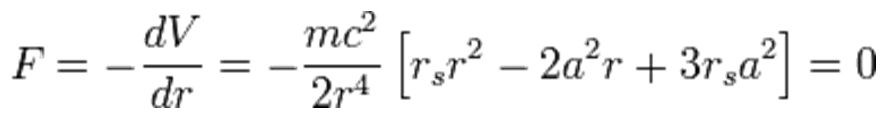 .
.
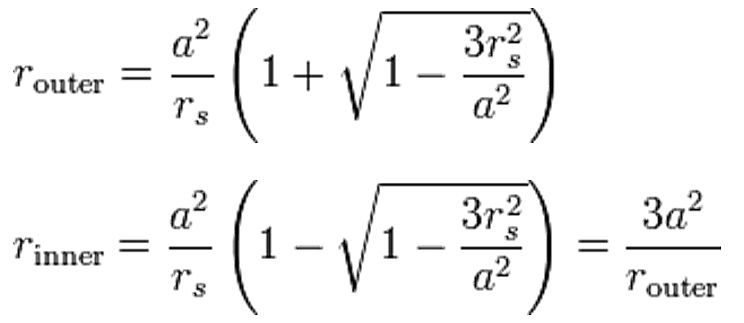
router + rinner = 2a2/rs
in
router - rinner = (2a2/rs)(1 - 3rs2/a2)1/2
- če je a veliko večji od rs (klasična mehanika), potem velja:
router ≈ 2a2/rs oziroma 2a2 ≈ routerrs
in
rinner ≈ 3rs/2
Preden se lotimo precesije perihelija, oziroma glavne osi elipse,
ponovimo še Keplerjev zakon, ki pravi, da bo planet imel
kotno hitrost ωφ (recimo za polmer router):
GMm/r2 = μωφ2r
- μ je reducirana masa: μ = Mm/(M + m) = m/(1 + m/M), če je M >> m
velja μ ≈ m, saj je m/M ≈ 0, tako tudi približno velja;
ωφ2
= GM/router3
= rsc2/(2router3)
Če zapišemo celotni potencial za krožeče telo
(gravitacijski in kinetični V = -GMm/r - mω2r2/2
je že prvi odvod nič,
ker velja dV/dr = GMm/r2 - mω2r = 0, ker je Fc = Fg = mω2r = GMm/r2. Pri dopolnjenem potencialu, ki ga razkrije splošna relativnost pa
se poleg omenjenih dveh potencialov, pojavi še tretji člen
- GML2/(c2mr3) in po prvem in drugem odvodu potenciala
V(r) = -GMm/r + L2/(2mr2) - GML2/(c2mr3)
nikakor ne dobimo ničle, ampak kotno hitrost ωr,
ki je nekoliko manjša od Keplerjeve kotne hitrosti (ωφ2
= GM/r3 ), saj je čas obrata nekoliko večji zaradi precesije. Razlika kotnih hitrosti, pomnožena s časom, pa
ustreza kotu δφ dodatnega zasuka zaradi precesije apside elipse.
Bodimo še bolj precizni.
Gibanje po skoraj krožni tirnici
Načeloma je krožna orbita možna orbita katere koli privlačne centralne sile.
Vse sile pa ne povzročijo stabilnih krožnih orbit.
Za samo kroženje v gravitaciji velja centralna sila:
F = -mω2r = -m2ω2r4/(mr3)
= -L2/(mr3) =
-GmM/r2
Sledi izpeljava gibanja za ostale krivulje, ki so splošne (elipsa, parabola, hiperbola).
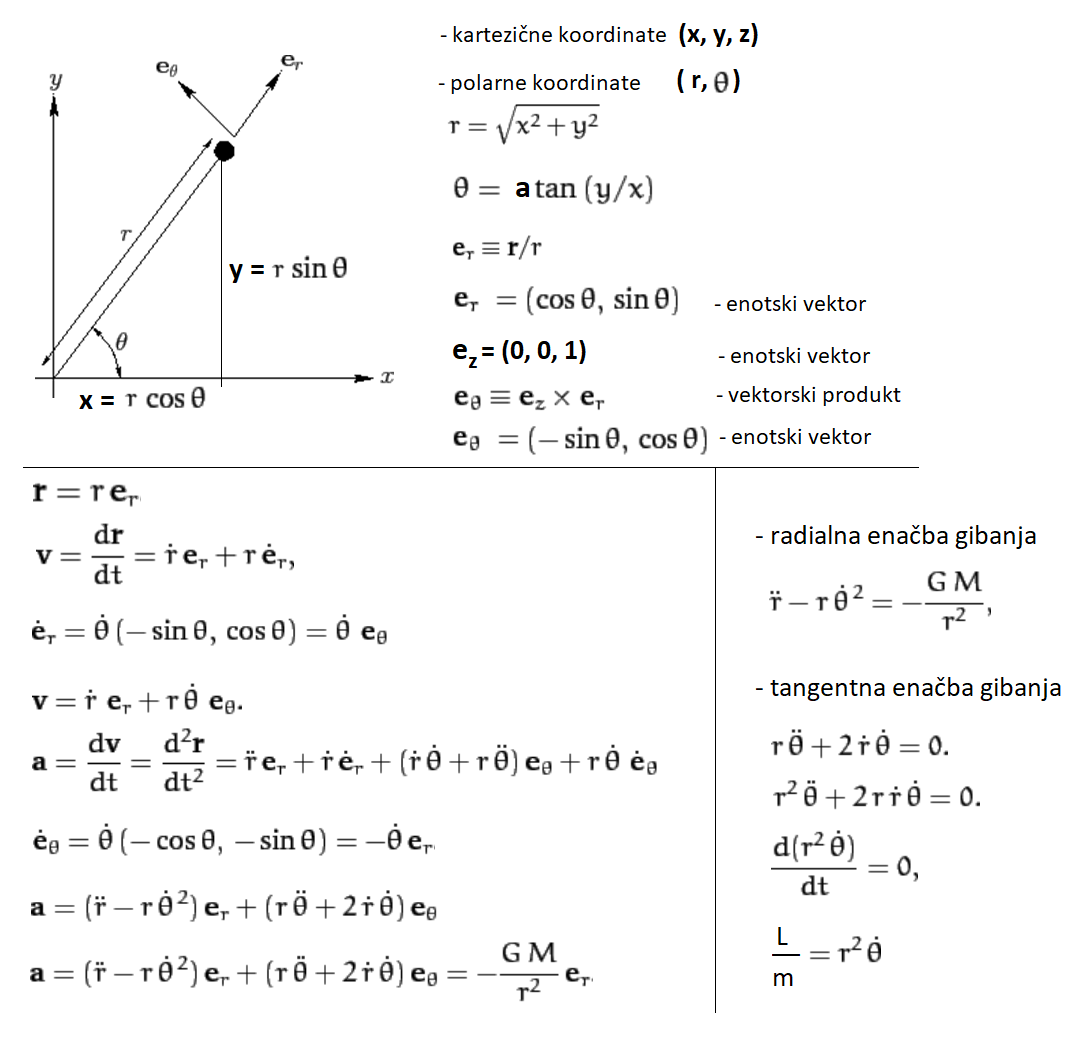
Zgornja slika kaže, kako lahko gibanje v ravnini, pod vplivom centralne sile, vektorsko razdelimo
na radialno komponento in tangentno. Račun ima določene prednosti, če za ta namen
vpeljemo polarne koordinate (r, θ)
namesto kartezičnih (x, y). Iz zgornjih računov se tudi razbere, da se veliko elegantneje računa,
če za vektorski zapis vpeljemo velikost vektorja pomnoženo z enotskim vektorjem, ki ima smer
vektorja, njegova velikost pa je 1 (recimo zgoraj, enotski vektor za razdaljo r je er
= (cos θ, sin θ), ko velja za velikost
|er| = (cos θ)2 + (sin θ)2 = 1).
Enotski vektor za kot θ pa je lahko kar vektorski produkt enotskega vektorja ez = (0. 0, 1),
ki je pravokoten na ravnino
gibanja in enotskega vektorja er. Oba sta pravokotna in tako dobimo eθ =
ez x er = (0. 0, 1) x (cos θ, sin θ = (-sin θ, cos θ).
Lahko pa enotski vektor eθ preberete tudi kar iz slike, to je kar projekcija
eθ na koordinati x in y in dobite enak rezultat eθ = (-sin θ, cos θ).
Tako smo opremljeni za izračuna hitrosti in pospeška točkastega telesa v ravnini (x, y) ali (r, θ),
na katerega deluje centralna sila (recimo gravitacijska = -GMer/r2,
znak minus je zato, ker privlačna sila kaže proti centru).
Ča na sistem "centralna masa - točkasto telo", ne deluje
nobena zunanja sila (navor), nam zgornji vektorski izračuni pokažejo elegantno pot do hitrosti in pospeška
v radialni smeri, za katero poznamo silo in v tangentni smeri.
Kepler je že pred dobrimi 400 leti
pokazal, da se v tem primeru ohranja vrtilna količina ( L = mr2ω ),
kar je poimenoval, ohranitev ploščinske hitrosti
planeta (to je drugi Keplerjev zakon), glej levo sliko zgoraj
(dA kot del ploščine lahko izračunamo kot ploščino trikotnika
rdl/2 = rrdθ/2 = r2dθ/2), velja dA/dt =
(r2/2)dθ/dt = r2ω/2 = L/(2m)
(takrat namreč še pojma vrtilne količine in kdaj se ohranja [če je vsota vseh zunanjih navorov enaka nič],
še niso poznali, navor namreč povzroča pospešeno rotacijo ...).
Za zadnjo trditev glejte zgornjo
tangentno enačbo gibanja: rd2θ/dt2 + 2(dr/dt)(dθ/dt) =
r2d2θ/dt2 + 2r(dr/dt)(dθ/dt) = 0,
od koder sledi
d[(r2(dθ/dt)]/dt = 0.
Kar pomeni, da je r2(dθ/dt) = r2ω = konstanta =
L/m. Tako smo pričakovano dokazali, da se pri centralni sili vrtilna količina
za točkasto telo L = mr2ω
ohranja, kar opisuje II. Keplerjev zakon.
Glej tudi poglavje
izpeljave Keplerjevih zakonov in uporaba Laplace–Runge–Lenz vektorja.
Če je kdo pozabil, odvod sin je cos, odvod cos je -sin,
če odvajamo kot še po času, oznaka s piko na vrhu, potem velja, recimo
d(cos θ)/dt = -(dθ/dt)sin θ.
Odvajali smo torej cos in potem še ta odvod pomnožili z odvodom kota (dθ/dt) ...
Vektor odvajamo tako, da vsak člen vektorja odvajamo posebej. Podajmo
za vajo primer odvoda
enotskega vektorja er po času (d/dt):
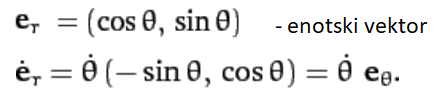
Za gibanje (recimo po elipsi) velja za centralno gravitacijsko silo v splošnem, da povzroča radialni in tangentni
pospešek (glej izpeljavo zgoraj - za radialno smer pomnoženo z maso telesa, dobimo znano enačbo, centripetalna sila zaradi
rotacije in delež zaradi spremembe radija):
F = - GmM/r2 = md2r/dt2 - mrω2
= md2r/dt2 - L2/(mr3)
- in še enaka enačba v skrajšani obliki, kjer se odvod po času kar označi s piko:
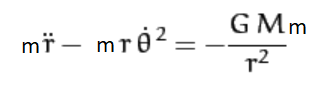
L = ωmr2 je vrtilna količina, ki se ohranja (točkasto telo).
Razmislimo sedaj še o stabilnosti krožnih orbit v splošnem centralnem polju sil.
Za krožno orbito velja, da je md2r/dt2 = 0 in zgornja enačba se skrči na
F(ro) = -L2/(mro3)
- kjer je ro polmer orbite.
Poglejmo še posledice majhnih odstopanjih x od krožnice. Naj bo torej x majhen odmik od orbite ro:
x = r - ro
r = ro + x
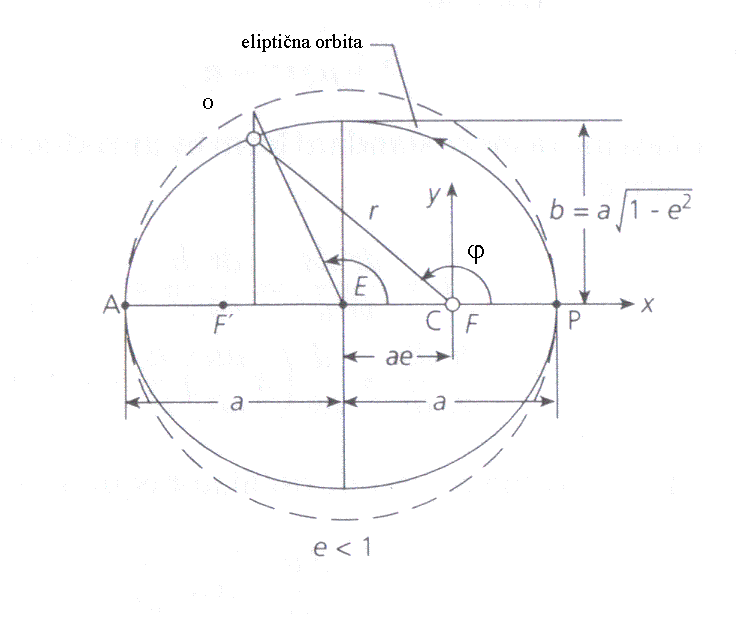
Velja F' = dF/dr in dr = dx in md2(ro + x )/dt2
= md2x/dt2 in
F(ro + x) = F(ro) + F'(ro)x (srednja šola, kjer smo izpeljali F'(ro) = ( F(ro + x) - F(ro) )/x ).
Enačbo za silo F(r) v točki r torej lahko zapišemo v naslednji obliki:
F(ro + x )
= md2x/dt2 - L2/(m(ro + x )3)
[ analogija iz prejšnje enačbe 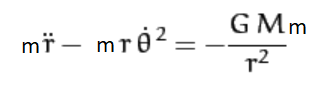 ]
]
Če člena, ki vključujeta ro + x razvijemo v potenčno vrsto preko x/ro, in ohranimo vse
člene do prvega reda, tako dobimo:
F(ro) + F'(ro)x
= md2x/dt2 - L2/(m ro3) [1 - 3x/ro ]
= md2x/dt2 + F(ro)[1 - 3x/ro ]
kjer torej
znak ' označuje odvod. Z uporabo enačbe ( F(ro) = -L2/(mro3) ),
se zgornja enačba reducira na:
md2x/dt2 + [-3F(ro)/ro - F'(ro)]x = 0
ali
md2x/dt2 + kx = 0 - enačba je enaka kot pri harmoničnem nihanju vzmeti:
ω = (k/m)1/2.
Če je člen v oglatih oklepajih pozitiven, potem dobimo preprosto harmonično enačbo (sinusno nihanje odmika x,
srednja šola, poglavje iz nihanja, velja ω = 2π/T =
([-3F(ro)/ro - F'(ro)]/m)1/2,
za katero že vemo, da je orbita stabilna na majhne motnje.
Če pa je člen v oglatih oklepajih negativen in recimo sila pada kot 1/r4 ali celo hitreje,
je orbita nestabilna - lahko precesira (tole bomo tudi računsko dokazali).
Apsidalna točka v orbiti pomeni radialno razdaljo, kjer doseže r največjo ali najmanjšo vrednost.
Tako sta perihelij in afelij apsidalni (apsidni) točki planetarnih orbit.
Kot za katerega se zasuka radij (krajevni) vektor med dvema zaporednima apsidalnim točkama,
se imenuje apsidalni (apsidni) kot.
Tako je apsidalni (apsidni) kot za eliptične orbite v inverznem kvadratnem polju sile
(1/r2) seveda π.
Za primer stabilnih (skoraj krožnih) orbit smo videli, da r sinusno niha
okoli svoje srednje vrednosti ro. Dejansko je iz enačbe
( md2x/dt2 + [-3F(ro)/xo - F'(ro)]x = 0 ) razvidno,
da je perioda T nihanja kar (snov iz srednje šole, nihanje - pokazali že zgoraj) :
T = 2π/[-3f(ro)/ro - f'(ro)]1/2 = 2π/([-f(ro)/ro]1/2[3 + rof'(ro)/f(ro)]1/2)
Kjer je f = F/m sila na enoto mase.
Apsidalni (apsidni) kot je količina, za katero se θ poveča med največjo in najmanjšo vrednostjo r.
Čas, potreben za dosego tega, je seveda T/2. dθ/dt = L/(mr2), kjer je L konstanta gibanja
(vrtilna količina se ohranja), r pa je skoraj konstanten (če je x majhen). Tako je
kotna hitrost
dθ/dt = ω =2π/T
približno konstantna. Pravzaprav velja - le za kroženje:
ω ≈ L/(mro2) = [-F(ro)/(mro)]1/2 = [-f(ro)/ro]1/2
Apsidalni kot ψ je torej:
ψ = Tω/2
Za čas T vstavimo izpeljano enačbo: T = 2π/([-f(ro)/ro]1/2[3 + rof'(ro)/f(ro)]1/2)
Tako dobimo za ψ izraz:
ψ =
(2π/(2[-f(ro)/ro]1/2[3 + rof'(ro)/f(ro)]1/2)*[-f(ro)/ro]1/2
= π/[3 + rof'(ro)/f(ro)]1/2
Za primer privlačnih potenčnih centralnih sil v odvisnosti f(r) = -crn,
kjer je c > 0, postane apsidalni kot kar:
ψ = π/(3 + n)1/2
Analiza rezultata
Iz enačbe razberemo, da mora biti apsidalni kot ψ kar delež polnega kota 2π, če so orbite
zaprte vase. Za dve (majhni) celoštevilski vrednosti n
za potenčno odvisnost sile, je imenovalec celo število.
Kot smo videli, je za inverzni kvadrat sile (za n=-2, to je recimo gravitacija)
apsidalni kot ψ kar π. Za linearni zakon sile (za n=1, recimo Hookov zakon F = -kr)
je apsidalni kot ψ pa kar π/2. Vendar pa je za kvadratne (za n=2) ali kubične (za n=3)
sile apsidalni kot ψ iracionalen del 2π, kar pomeni, da se ne-krožne orbite pri
takšni sili polja, nikoli ne zaprejo sama vase. Recimo apsida elipse se s časom premika.

Apsida - daljša vodoravna os na sliki -
za inverzni kvadrat sile
(za n=-2, to je recimo gravitacija F = -GMm/r2 = -GMmr-2 )
je apsidalni kot ψ kar π. Kot bomo videli pri drugačnih centralnih
silah z višjo potenco odvisnosti (recimo
F = -GMm/r2 - α/r4
- kar je v našem primeru posledica relativističnega prispevka
k energiji planeta blizu Sonca), se kot apside π s časom spreminja - "kvazi elipsa" rotira,
precesira.
Dobimo orbitalni cvet obhodov okrog centralne mase, bolje težišča.
Odločilen je torej člen rof'(ro)/f(ro), oziroma f'(ro), torej df/dr = (1/m)d2V/dr2.
Kaj nam torej ta drugi odvod potenciala (V) pove?
Če pogledamo enačbo: ψ = π/[3 + rf'/f]1/2
= π/(31/2[1 + rf'/(3f)]1/2),
iz opazovanj in izračunov lahko sklepamo, da je člen rf'/(3f) zelo majhen in uporabimo
razvoj v vrsto,
od koder sledi, da je člen πrf'/f ∝ ψ.
V tem primeru bomo lahko tudi računali brez poenostavitev glede prehoda
iz krožnice v elipso ali kako drugo obliko orbite.
Poiščimo torej prvi odvod sile, oziroma drugi
odvod potenciala deljen z maso:
df/dr = (1/m)d2V/dr2.
Povedano izvedimo - pot do kotne hitrosti precesije apside elipse
ωr2 = (1/m)(d2V/dr2)r = router
Izvedimo torej dvojni odvod ( (1/m)(d2V/dr2) )
potenciala
V(r) = -GMm/r + L2/(2mr2) - GML2/(c2mr3)
= (mc2/2) [ -rs/r + a2/r2 - rsa2/r3 ]
.
Rezultat je znan - a vaja ni odveč:
ωr2
= (c2rs/(2r4))[ -2r + 6a2/rs - 12a2/r ]
- uporabimo že izpeljani povezavi
router + rinner = 2a2/rs
in rinner = 3a2/router in kaj dobimo, ko vstavimo
v enačbo točko router?
ωr2 =
(c2rs/(2router4))
[ -2router + 6a2/rs - 12a2/router ]
= (c2rs/(2router4))
[ -2router + 3(router + rinner ) - 4rinner ]
ωr2 =
= (c2rs/(2router4)) [router - rinner]
Izraz ωr2 še poenostavimo.
ωr2 = (c2rs/(2router4))
[router - rinner] =
(c2rs/(2router4))(2a2/rs)(1 - 3rs2/a2)1/2
Upoštevamo še, da je 2a2 ≈ routerrs, in da je
ωφ2
= GM/router3
= rsc2/(2router3), tako dobimo
ωr2
= ( rsc2/(2router3) )(1 - 3rs2/a2)1/2
=
ωφ2(1 - 3rs2/a2)1/2
Po korenjenju velja:
ωr
= ωφ(1 - 3rs2/a2)1/4
Če ta izraz razvijemo v Taylorjevo vrsto (izraz
3rs2/a2 je namreč zelo majhen) dobimo:
ωr
≈ ωφ(1 - 3rs2/(4a2) )
- tako velja,
ωφ - ωr
= ωφ3rs2/(4a2)
= (2π/T)3rs2/(4a2)
Kot zasuka perihelija na čas obhoda T je
δφ = (ωφ - ωr)T - rezultat še razdelajmo:
***
δφ = (ωφ - ωr)T =
(2π)3rs2/(4a2)
Iskani zasuk δφ pri precesiji
zapišimo še z vrtilno količino a = L/(mc) in z maso M centralnega telesa
rs = 2GM/c2, tako dobimo:
δφ = (2π)3rs2/(4a2)
= 3πm2c2rs2/(2L2)
= ( 3πm2c2/(2L2) ) (4G2M2/c4)
= 6πG2M2m2/(c2L2)
Iz nebesne mehanike poznamo izraz za vrtilno količino L pri eliptičnem gibanju glede na veliko polos,
ekscentričnost in masi (Glej članek
Komet C/2002 C1 Ikeya-Zhang in elementi tira, točko 5):
L2 = Gm2MA(1 - e2)
Kjer je A velika polos elipse, e pa ekscentričnost.
Če ta izraz vstavimo v enačbo za kot precesije, dobimo končni iskani izraz:
δφ = 6πGM/(c2A(1 - e2))
V primeru, da sta masi m in M primerljivi, velja dopolnjen izraz za kot precesije na obrat
(izraz dobimo, če zasuk izpeljujemo z reducirano maso):
δφ = 6πG(M + m)/(c2A(1 - e2))
To je eden večjih uspehov splošne teorije relativnosti. V našem računu smo zanemarili
maso Merkurja. Masa Sonca M = 1,989 1030 kg, ekscentričnost Merkurja je e = 0.205630,
velika polos Merkurjeve orbite a = 57.909 109 m, hitrost svetlobe c = 299792458*108 m/s,
G = 6.6726*10-11 m3s-2kg-1,
obhodni čas Merkurja okrog Sonca je tm = 87.9691 dni.
V 100 letih se Merkur zasuka okrog Sonca približno 415 krat.
Vrednost zasuka perihelija v sto letih je 43'' (43 ločnih sekund):
δφp100
= 100let*360*3600''*6πGM/((c2A(1 - e2 ))tm2π) = 43''
Za Zemljo je zasuk perihelija 3.84'', za Venero pa 8.62", ta dva relativistična prispevka lahko
izračunate sami.
ŠE POMOČ za razumevanje zgornjega univerzalnega zapisa zasuka apside
( δφ = 6πG(M + m)/(c2A(1 - e2)) )!
Zapis energije je seveda podoben, le da z reducirano maso
μ = mM/(m + M)
(kar je korektno, ker velja
splošno za vsa razmerja velikosti teles m in M) in
upoštevamo še dopolnjen izraz za vrtilno količino L z reducirano maso μ, velja
[ L2 = Gμ2(M + m)A(1 - e2) -
glejte izpeljavo Keplerjevih zakonov]
ter za konstanto a še [ a = L/(μc) ].
Energija v splošni obliki se zapiše:
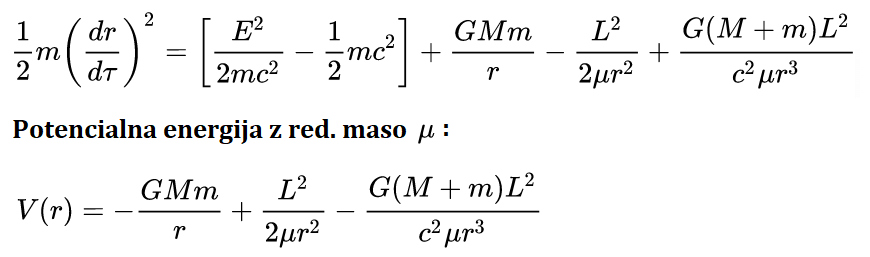
V izraz (ki smo ga že izpeljali zgoraj, pod oznako ***)
δφ
= (2π)3rs2/(4a2)
vstavite torej a = L/(μc) in
L2 = Gμ2(M + m)A(1 - e2),
tako dobimo končno (že prej zapisano) univerzalno rešitev za zasuk apside zaradi precesije:
δφ = 6πG(M + m)/(c2A(1 - e2)) .
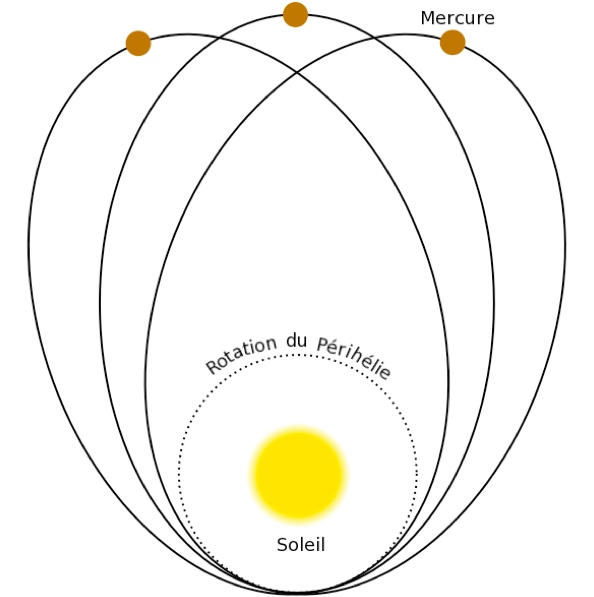
Povejmo še enkrat, da poleg učinkov splošne relativnosti,
dodatno znatno precesijo perihelija Merkurja povzročajo
tudi motnje ostalih teles, planetov, Jupitra ..., nekaj še rahlo nesferično Sonce itn.
V resnici predstavitveno najbolj prepričljiva podoba precesije osi elipse dvojnega sistema
nebesnih teles
izhaja iz Laplace–Runge–Lenz vektorja
(D = vxL - GMμlr), ki v klasični sliki (fiziki) ohranja smer glavne osi elipse.
Ko pa upoštevamo splošno relativnost pa vidimo, da v resnici
Laplace–Runge–Lenz vektor
D ne ohranja smeri.
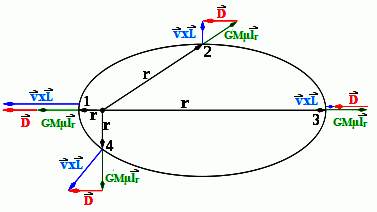
Slika: D = vxL - GMμlr je Laplace–Runge–Lenz vektor (LRL), ki
ohranja smer in velikost glavne osi elipse (apside) - kar pa zaradi relativističnih
efektov le delno drži. V večini literature je vektor LRL podan s
črko A, povezava z D pa je preko enačbe
A = mD = mvxL - GmMμlr = pxL - GmMμlr.
Pri našem zapisu vektorja
D gre v bistvu za normiranje vektorja A z maso objekta m,
ki mu določamo orbito.
Relativistična slika mehanike pa TOREJ razkrije
dodatni potencial, ki povzroča precesijo in je
kar sorazmeren z -1/r3
(res elegantno izpeljali zgoraj iz Schwarzschildove metrike).
Izkaže pa se, da v tem primeru vektor D seveda ni konstanten.
Zakaj?
Če D = vxL - GMμlr
odvajamo po času [ dD/dt = d(vxL - GMμlr)/dt ], je drugi člen
dD/dt ∝
-Glrd(Mμ)/dt
zagotovo različen od klasične mehanike, saj se
masi m1 in m2 rahlo spreminjata glede na Lorentzov člen γ = (1 - v2/c2)-1/2
zaradi neenakomerno pospešenega
gibanja po elipsi (glejte sliko spodaj). Člen vxL pa je kvečjemu manjši od klasične mehanike,
saj pri povečanju sile hitrost počasneje narašča, kot to parvi klasična mehanika. To je sicer premislek iz posebne
teorije relativnosti, ko privzamemo zgolj spremembo mase zaradi spremembe energije (E/c2), a
konceptualno gre razmišljanje v pravo smer.
Laplace–Runge–Lenz vektor D s časom torej spreminja smer
in to je eden najbolj direktnih
nazornih prikazov precesije perihelija.
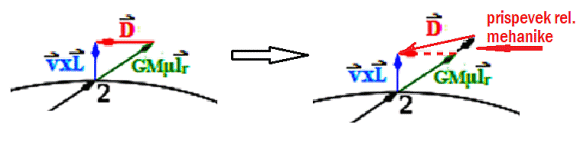
Izpeljava Laplace–Runge–Lenz vektorja D je na (že omenjeni) strani -
Oblike orbit zaradi centralne sile sorazmerne z 1/r2 .
V resnici se zasuk perihelija poda še z bolj natančnimi izračuni, kjer se recimo upošteva
še relativistični prispevek radialne hitrosti ...
Preinterpretirana Newtonova mehanika trdi, da če se gravitacijski vpliv širi s končno hitrostjo,
planeti čutijo privlačnost do prejšnje lege Sonca in ne do trenutne razdalje do Sonca.
To spoznanje je povzročalo v preteklosti (19. stoletje) velike težave in mnogi so trdili,
da če je temu tako,
bi moral biti Sončev sistem nestabilen. Po svoje (v grobem) so imeli celo prav, saj danes vemo,
da so pri pospešenih gibanjih teles pojavljajo gravitacijski valovi (a so za Sončev sistem
izjemno šibki). Danes vemo, da je tudi čas vezan na gravitacijo. Einstein je rešil dilemo tako,
da je vpeljal gravitacijsko ukrivljen prostor-čas po katerem potujejo telesa in svetloba.
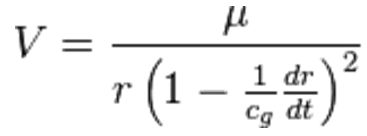
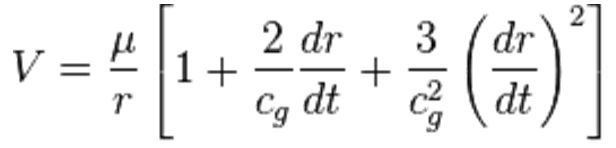
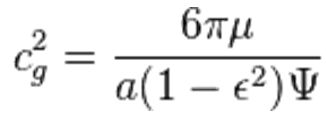
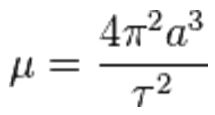
S podatki za Merkur je izračunal hitrost gravitacije 305500 km/s,
kar je skoraj enako svetlobni.
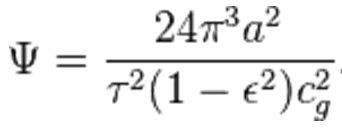
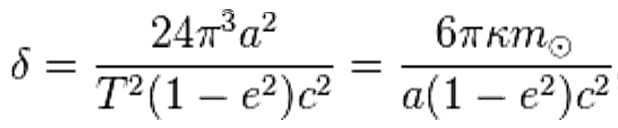
Kar koli si mislimo o izjavah velikih mož in žena ..., iz šolskih dni vsi vemo,
da je izpeljava končne vrednosti veliko lažja, če že poznamo rezultat ...
Zagotovo pa je Einstein živel v času, ko so se s problemi energije, s problemi ocene
hitrosti gravitacije, precesijo planetov, ukrivitvijo žarkov
v bližini zvezd ..., ukvarjali številni znanstveniki po svetu.
Bilo je veliko rivalstva - kar pa je (kot skoraj zmeraj)
pripeljalo do napredka v znanosti,
v razumevanju sveta.
Sonce: rs = 2,96 km
|
ds2 = -c2dt2(1 - 2GM/(c2r)) + dr2/(1 - 2GM/(c2r)) + r2(dϑ2 + sin2ϑ dφ2) |
ds2 = 0 = -c2dt2(1 - 2GM/(c2r)) + dr2/(1 - 2GM/(c2r))
cdt(1 - 2GM/(c2r))1/2 = dr/(1 - 2GM/(c2r))1/2
Vidimo, da se fotoni, ki
se nahajajo na Schwarzschildovem radiju ne morejo gibati v radialni smeri. Nenavadnost
radija rs pa je tudi v tem, da se s prehodom na
območje
r < rs,
zamenjata vlogi koordinat dr in cdt.
Namreč
ob prehodu pod rs, se v metriki zgodi to, da (matematično) metrična elementa pred
njunima kvadratoma spremenita predznak (gibanje nazaj v času). To pa ob primerjanju
z metriko Minkowskega (ds2 = -c2dt2 + dr2) pomeni, da dr prevzame
vlogo časa in cdt vlogo kraja
(velja cdt(1 - 2GM/(c2r)) < 0, za r < rs v ČRNI LUKNJI,
pri r = rs po definiciji velja 2GM/(c2rs) = 1).
Seveda pa moramo ostati realisti - eno je
matematika, a drugo realnost ...
Hitrost svetlobe dr/dt blizu zvezde, kot jo zazna od zvezde zelo oddaljeni opazovalec
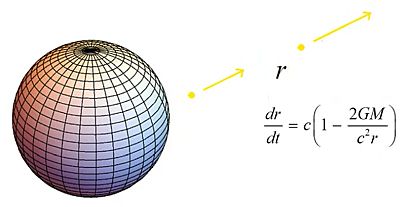
Iz zgoraj izpeljane enačbe za ds = 0 (koordinatni sistem sledi fotonu, nulti radialni geodetki)
cdt(1 - 2GM/(c2r))1/2 = dr/(1 - 2GM/(c2r))1/2
izpeljimo hitrost dr/dt svetlobe, kot jo zazna oddaljeni opazovalec, ki praktično ne čuti gravitacije.
Kaj dobimo:
dr/dt = c(1 - 2GM/(c2r))
Bližje, ko je sevalec svetlobe Schwarzschildovi razdalji
rs = 2GM/c2 od središča mase (recimo črne luknje), manjšo hitrost svetlobe
zazna oddaljeni opazovalec (dr/dt < c). To kaže tudi spodnji graf. Pri Schwarzschildovi razdalji rs = 2GM/c2
fotoni ne morejo več zapustiti gravitacije črne luknje - od tod tudi ime nenavadne masivne zvezde, to je "črna luknja".
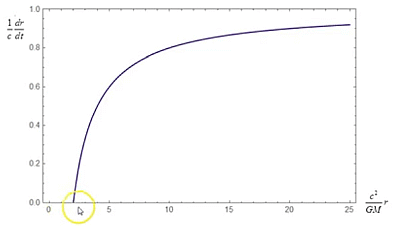
Graf hitrosti svetlobe ob
masivni zvezdi [ dr/dt = c(1 - 2GM/(c2r)) ], kot jo zazna oddaljeni opazovalec;
oziroma graf (1/c)(dr/dt) od x = c2r/(GM). Torej enačba grafa je: (1/c)(dr/dt) = (1 - 2/x).
Velja torej (dr/dt < c).
Lahko še izvedemo integral:
∫dr/(1 - 2GM/(c2r)) = c∫dt
in tako dobimo funkcijo r od t, je logaritemska:
ct = r + (2GM/c2) ln(rc2 - 2GM) + konst.
Lokalno merjenje hitrosti svetlobe (recimo v padajočem sistemu zaradi gravitacije)
Kako pa je lokalno z merjenjem hitrosti svetlobe?
Lokalno bomo zmeraj izmerili c = 3 108 m/s. Zakaj?
Lokalno velja za čas v gravitaciji dτ = dt(1 - 2GM/(c2r))1/2 - že izpeljali.
Za premik v radialni smeri pa velja ds = dr/(1 - 2GM/(c2r))1/2 - že izpeljali
(merjenje razdalje sočasno in je dt = 0).
Za nulto geodetko pa tudi velja:
0 = -c2dt2(1 - 2GM/(c2r)) + dr2/(1 - 2GM/(c2r)),
tako je dr/dt = c(1 - 2GM/(c2r)) - že izpeljali (prejšnje poglavje).
Tako velja v lokalnem koordinatnem sistemu za hitrost svetlobe kar odvod metrike dS
po lokalnem lastnem času dS/dτ, in rezultat je:
dS/dτ = dr/(1 - 2GM/(c2r))1/2/dt(1 - 2GM/(c2r))1/2 = (dr/dt)/(1 - 2GM/(c2r)).
Za dr/dt vstavimo izraz dr/dt = c(1 - 2GM/(c2r)) in tako dobimo rezultat, da je lokalno
merjena hitrost svetlobe zmeraj c (recimo za opazovalca zgoraj, v njegovem referenčnem okvirju, koordinatnem
sistemu, ki prosto pada pod vplivom gravitacije, je na geodetki):
dS/dτ = (dr/dt)/(1 - 2GM/(c2r)) = c(1 - 2GM/(c2r))/(1 - 2GM/(c2r)) = c
( 1 - 2GM/(rc2) )c2dt2 = r2 sin2ϑ dφ2
Kjer za ϑ privzamemo vrednost π/2, velja sin( π/2) = 1.
(dφ/dt)2 = c2/r2 - 2GM/r3
Izraz korenimo, da dobimo kotno hitrost dφ/dt =
( c2/r2 - 2GM/r3 )1/2.
Ker gre za enakomerno kroženje, je drugi odvod kotne hitrosti
nič, velja torej:
d2φ/dt2 = 0
Če torej odvajamo izraz [ dφ/dt = ( c2/r2 - 2GM/r3 )1/2 ] še enkrat po času, dobimo na desni strani enačbe, znotraj daljšega izraza, tudi člen [ -2/r3 + 6GM/(r4c2) ], ki mora po definiciji odvoda konstante biti enak nič. Tako pridemo do že znanega rezultata za polmer fotonske sfere ob črni luknji:
rf = 3GM/c2
Črne luknje ovenčane z Nobelovo nagrado za fiziko.

Podoba, ki jo vidi opazovalec, ki gleda proti črni luknji tik nad ravnino akrecijskega diska (disk
je sestavljen iz vročega materiala, ki ga iz okolice srka izjemna močna gravitacije, teža črne luknje).
Kot da bi prepognili palačinko. Glej spodnjo sliko.
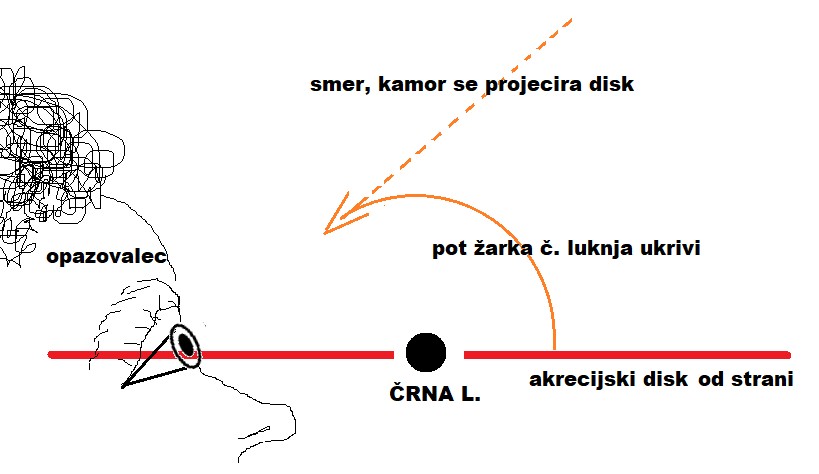
Shematični prikaz popačitve slike akrecijskega diska od strani, za opazovalca blizu
ravnine diska. Črna luknja zaradi izjemno močne gravitacije (bolje ukrivitve prostor-časa)
ukrivi žarek - in zato se navidezno za opazovalca
na nasprotni strani črne luknje disk dvigne, upogne navzgor
(fotonska sfera ima polmer rf = 3GM/c2). Tudi blizu Sonca se žarki
ukrivijo, a za zelo majhen kot.
Črne luknje ovenčane z Nobelovo nagrado za fiziko.
Mnogi pravijo, da je relativnostna mehanika nekaj najlepšega, kar je lahko človek
ustvaril ali doumel. Morebiti bo na koncu tudi kdo od bralcev enakega
mnenja. Zagotovo pa so njeni rezultati v temeljih spremenili dojemanje narave, vesolja,
človeka.




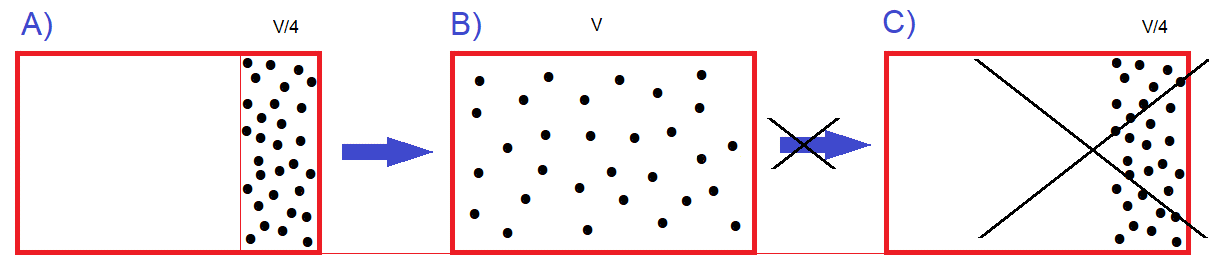
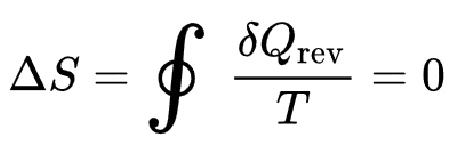
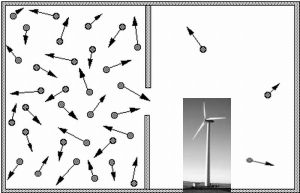
N P = (1/2)N 1 0.5 2 0.25 3 0.125 4 0.0625 5 0.03125 10 0.00098 100 7.9×10–31 1000 9.3×10–302 6×1023 ~ 0Kot lahko razberemo iz tabele, je verjetnost za eno molekulo sicer pričakovano 50 %, a za več molekul hkrati je celotna verjetnost kar produkt verjetnosti za posamezno molekulo in ta je že za 10 molekul komaj p = (1/2)10 ×100 % = 0.098 %.

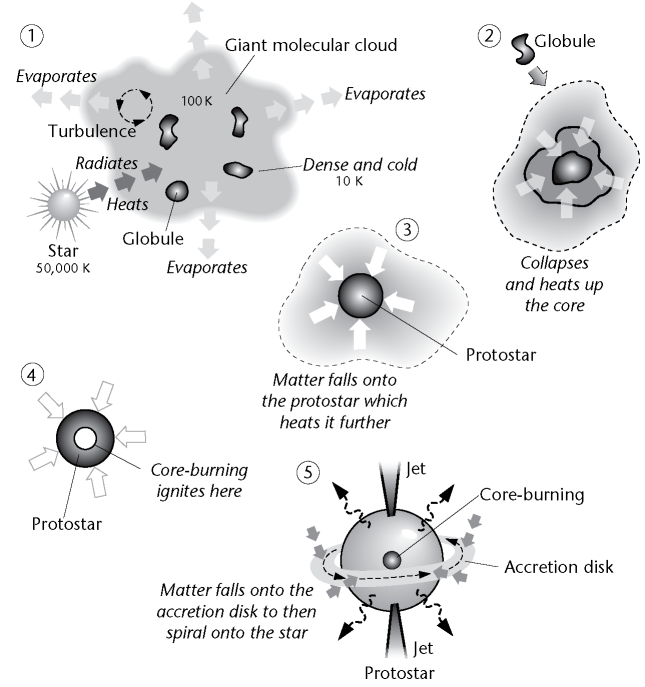
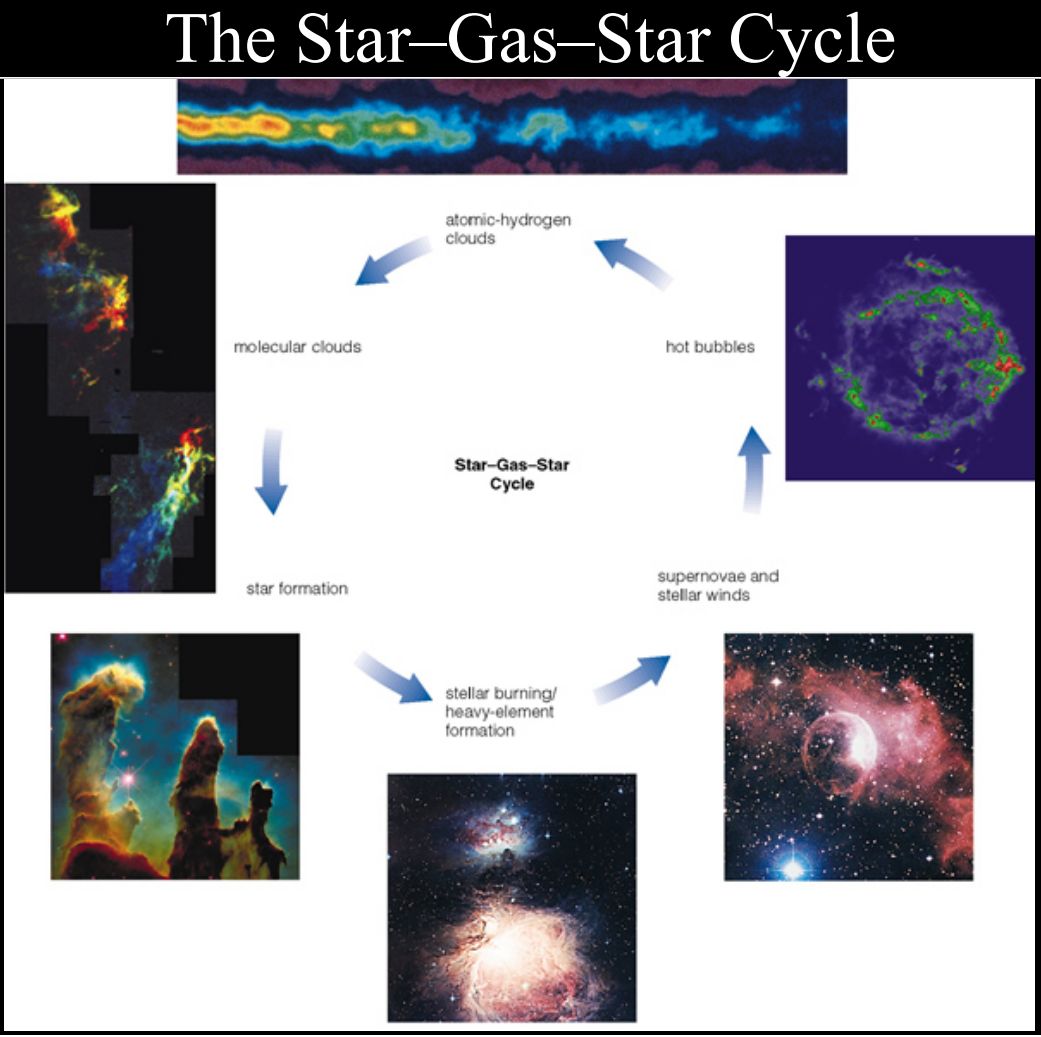

|
 |
 |



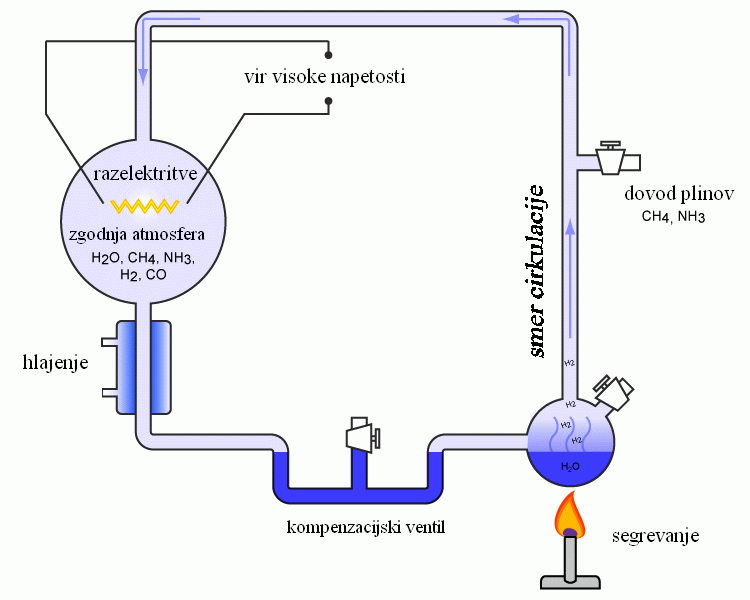

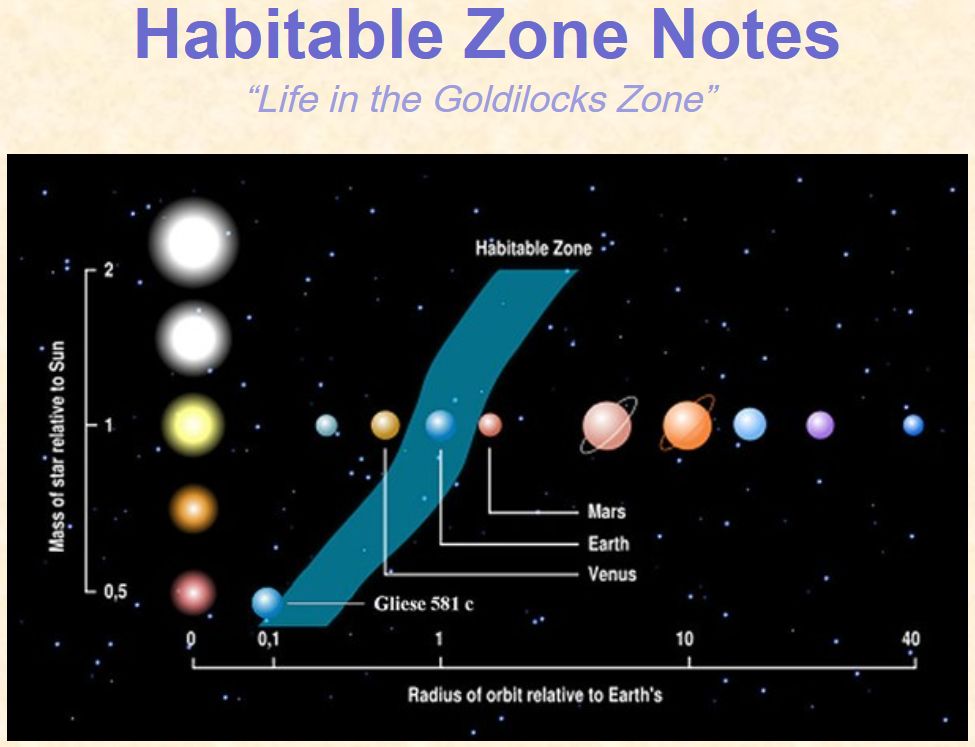
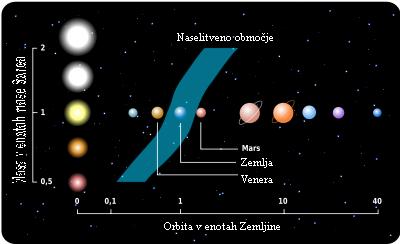

j = L/(4*p*R2) = s*T4
Lson/(4*p*Rae2) = Lzve/(4*p*Rnp2)
- iz zgornje zveze sledi: Rnp = Rae(Lzve/Lson)1/2
Primer, zvezda s 25% izseva Sonca bo imela srednji del naselitvenega področja
na razdalji okrog 0.50 ae od jedra, zvezda z dvakratnim izsevom Sonca pa
na razdalji 1.4 ae.
Dr Frank Drake (rojen 1930. ZDA, astronom, poda enačbo civilizacij,
ustanovitelj projekta SETI -
Search for Extraterrestrial Inteligence).
Dr Frank Drake, 1960/61 - Univerza v Kaliforniji, oceni število
vesoljskih civilizacij,
ki eksistirajo vzporedno z našo civilizacijo v naši galaksiji in bi morebiti
z njimi lahko komunicirali:
N = R* x f_p x n_e x f_l x f_i x f_c x L
* R* = 10/leto (10 zvezd se formira na leto v naši galaksiji)
* f_p = 0.5 (polovica novih zvezd formira planete)
* n_e = 2 (2 planeta na zvezdo sta primerna za razvoj življenja)
* f_l = 1 (100% vsi planeti razvijejo življenje - se razvije)
* f_i = 0.01 (1% jih razvije inteligentno življenje)
* f_c = 0.01 (1% od teh razvije zmožnost komunikacije)
* L = 10,000 let (trajale bodo 10 000 let)
Drake dobi vrednost:
N = 10 × 0.5 × 2 × 1 × 0.01 × 0.01 × 10,000 = 10.0
Torej skupaj bi naj bilo 10 civilizacij v naši galaksiji, ki
bi se morebiti lahko sporazumevale.
Problem so razdalje - 100 000 sv. let je premer naše galaksije,
gostota inteligentnih bitij pa je tako majhna, da je zelo mala verjetnost,
da se v obdobju razcveta zaznamo (hitrost elektromagnetnih valov je namreč
"samo" 300 000 km/s)
Nastale so različne ocene,
več informacij najdemo na:
N = R* x f_p x n_e x f_l x f_i x f_c x L
* R* = 6/leto (10 zvezd se formira na leto v naši galaksiji)
* f_p = 0.5 (polovica novih zvezd formira planete)
* n_e = 2 (2 planeta na zvezdo sta primerna za razvoj življenja)
* f_l = 0.1 do 0.33 (10 do 33% planetov razvije življenje)
* f_i = 1*10-7 (0.00001% jih razvije inteligentno življenje)
* f_c = 0.01 (1% od teh razvije zmožnost komunikacije)
* L = 420 let (trajale bodo 420 let), ali od leta 1938, to je 2007-1938 = 69 let
R* = 6/leto, f_p = 0.5, n_e = 2, f_l = 0.33, f_i = 1×10-7 , f_c = 0.01, in L = 69 let
N = 6 × 0.5 × 2 × 0.33 × 1×10-7 × 0.01 × 69 = 1.3 ×10-7 = 0.0000001
Ocena o številu planetov v celotnem Vesolju, podobnih Zemlji,
je približno N = 5 * 1015 (se spreminja glede
na nove meritve).
Ocena razdalje med njimi:




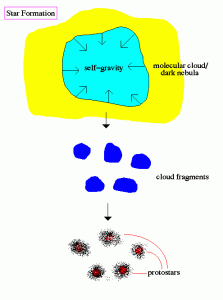
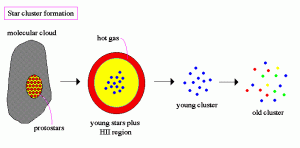

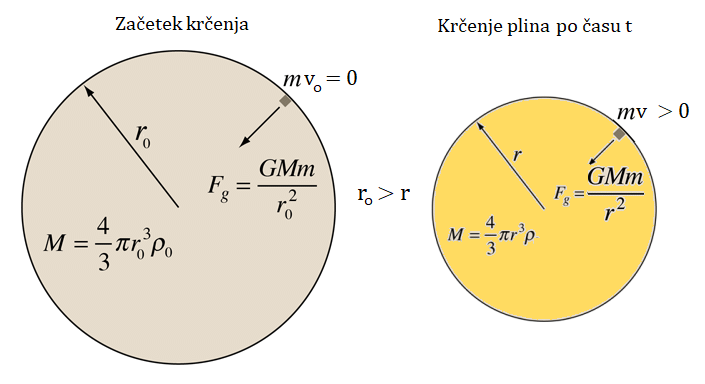



 | 
|



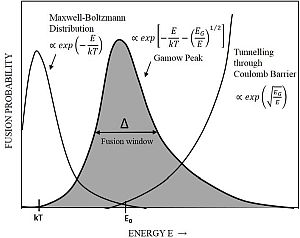
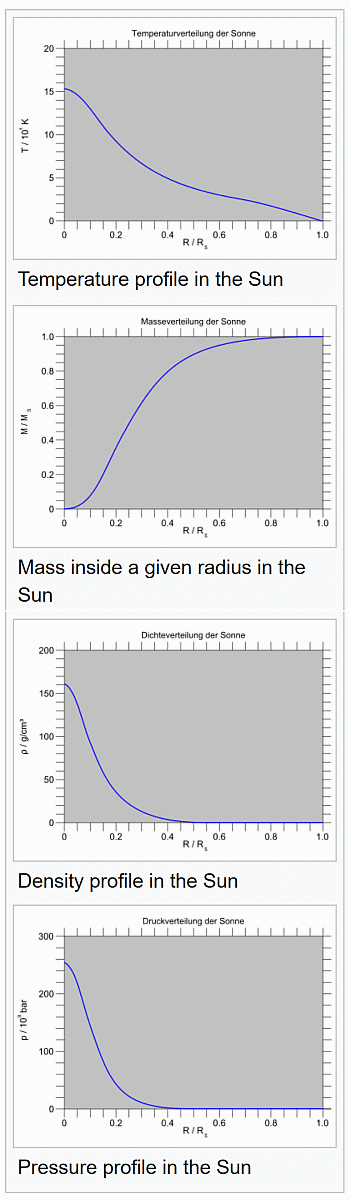
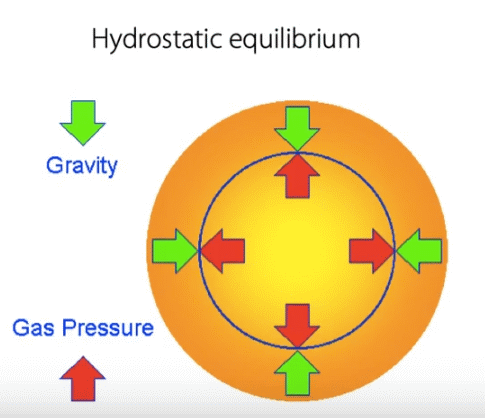 |
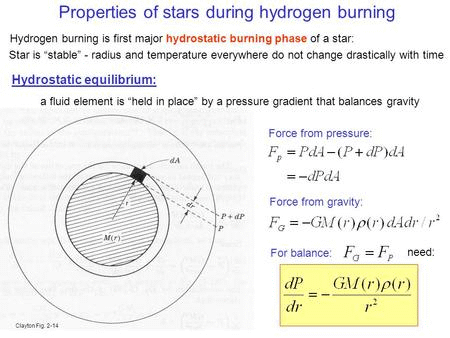 |
proces v zvezdi reakcija minimalna T fuzija vodika H -> He 10 106K fuzija helija He -> C, O 100 106K fuzija ogljika C -> O, Ne, Mg, Na 500 106K fuzija neona Ne -> O, Mg 1200 106KOcenimo še najmanjšo maso, da še ravno nastane zvezda.

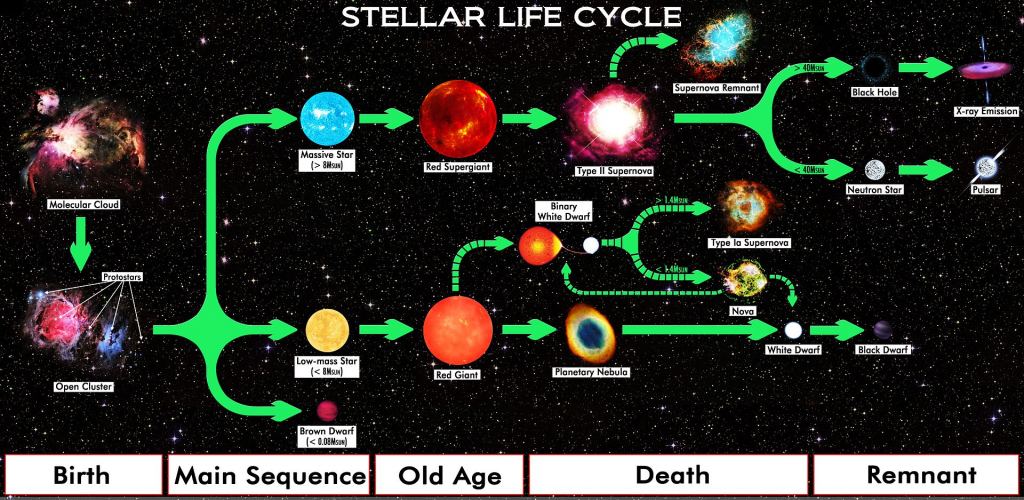
Zdaj se je med astrofiziki ustalilo mnenje,
da lahko pride do eksplozije supernove tipa Ia vsaj po dveh različnih poteh,
v obeh primerih v dvozvezdju. Obe možnosti sta pokazani na sliki.
Pri prvi, ki ji pravijo enkrat degeneriran model, sta v dvozvezdju
normalna zvezda in bela pritlikavka (degenerirana zvezda). Bela pritlikavka
krade svoji sosedi snov, ki se nabira na njej.
Ko skupna masa preseže
Chandrasekharjevo limito, se bela pritlikavka sesede
in eksplodira kot supernova.
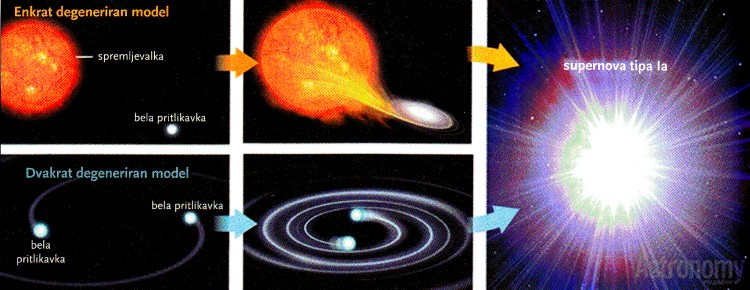
Pri drugi možnosti, ki ji pravijo dvakrat degeneriran model,
pa dvozvezdje sestavljata dve beli pritlikavki (dve degenerirani zvezdi), ki se med obkrožanjem
po spiralni poti približujeta druga drugi in na koncu trčita, se zlijeta in eksplodirata kot
supernova, če je skupna masa obeh belih pritlikavk večja od Chandrasekharjeve limite.
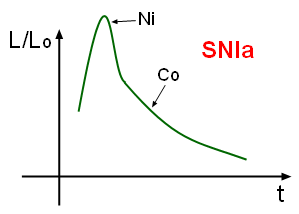





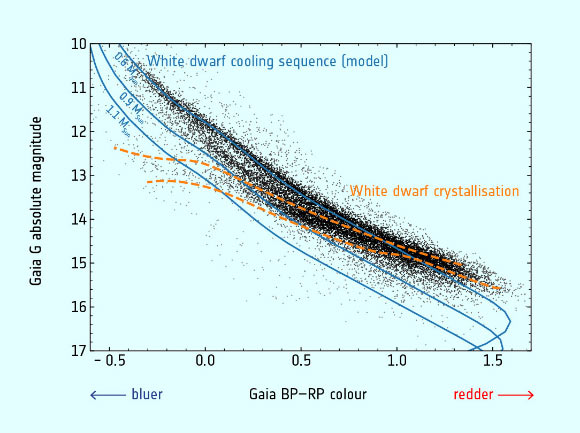
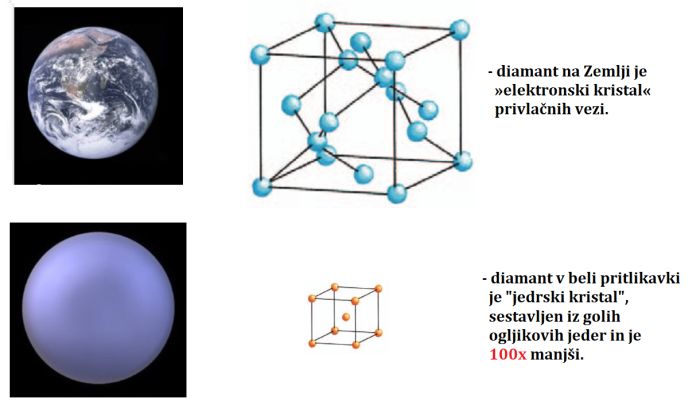
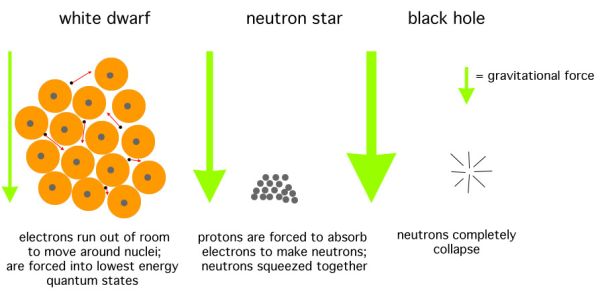
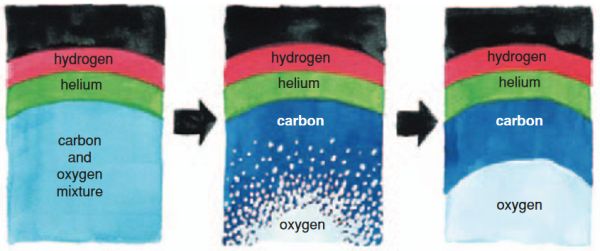

Pojasnilo: Eta Carinae bo morda eksplodirala. Toda nihče ne ve, kdaj - morda bo naslednje leto, lahko pa čez milijon let. Masa Eta Carinae - je približno 100-krat večja od našega Sonca - zaradi česar je odličen kandidat za popolno supernovo. Zgodovinski zapisi kažejo, da je pred približno 170 leti Eta Carinae doživela nenavaden izbruh, zaradi katerega je postala ena od najsvetlejših zvezd na južnem nebu. Eta Carinae, v Meglici Keyhole, je edina zvezdica, za katero trenutno velja, da oddaja naravno LASERSKO svetlobo. Ta izjemna slika razkriva podrobnosti v tej nenavadni meglici, ki obdaja to "prevarantsko" zvezdo. Uklonske konice, ki jih povzroča teleskop, so vidne kot svetle večbarvne črte, ki izhajajo iz središča Eta Carinae. Dva različna režnja meglice Homunkulus zajemata vroče osrednje območje, medtem ko je nekaj nenavadnih radialnih prog vidnih tudi v rdeči barvi, ki segajo proti desnemu delu slike. Režnja sta napolnjena s pasovi plina in prahu, ki absorbirata modro in ultravijolično svetlobo, ki se izseva blizu središča. Proge pa ostajajo nepojasnjene.
VIR: APOD
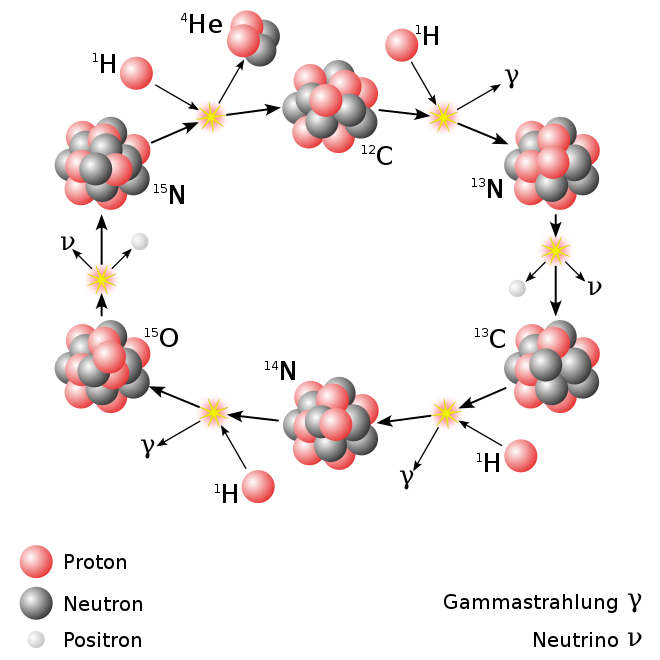
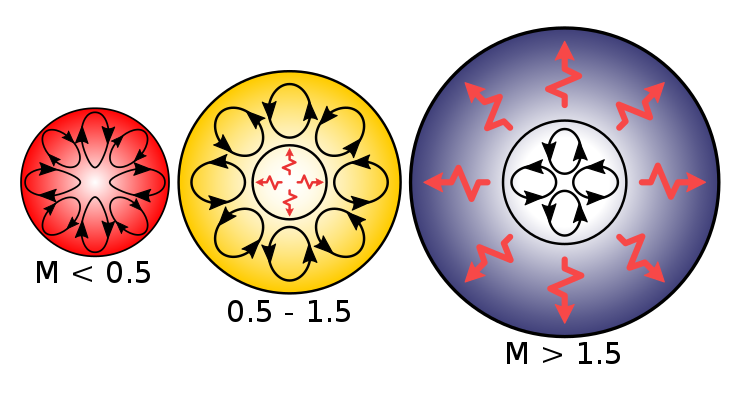
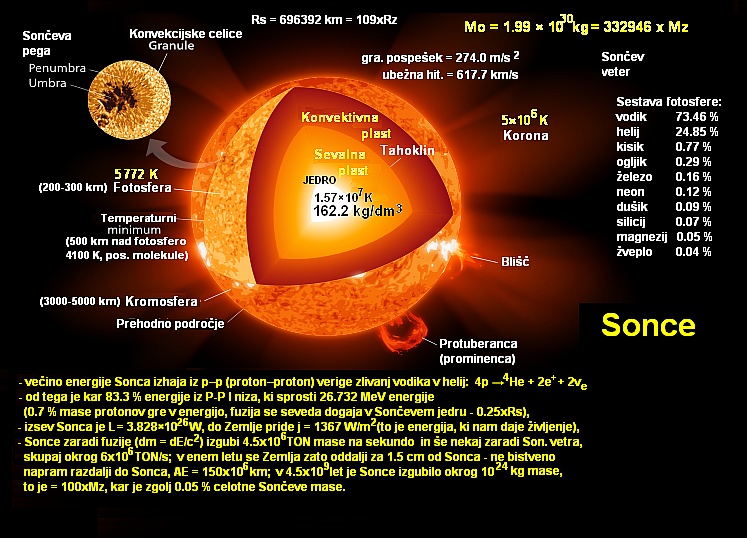

Če poznamo maso Sonca in masni delež, ki se pretvori v energijo na reakcijo,
ter izsev L (velja Lt = E),
lahko
izračunamo čas trajanja fuzije v sredici Sonca.
Če Sonce oddaja 3.827×1026 J energije na sekundo,
koliko fuzijskih reakcij se zgodi vsako sekundo?
3.827x1026 Joulov/sekundo / 4.2 x 10-12/reakcijo
= 9.1 x 1037 reakcij/sekundo.
Vsaka reakcija spoji 4 atome vodika:
(9.1 x 1037 reakcij/sekundo) x (6.693 x 10-27 kg/reakcijo)
= 6.091 x 1011 kg/s
Koliko časa tf bo torej Sonce porabilo, da se izvrši vsa fuzija?
Vzeli bomo zgornjo mejo za celotno maso Sonca Mo = 1.9885 x 1030 kg in
na koncu bomo rezultat popravili.
tf = 1.9885 x 1030 kg / ( 6.091 x 1011 kg/s 3.213 x 1018 sekund)
= 102 109 let!
V resnici celotno Sonce ni vodik in do fuzije prihaja samo v gostem jedru.
Približno 70 % Sonca je na voljo za fuzijo, zaradi česar je ta številka manjša, čas trajanja
fuzije,
manjši od 100 milijard let. Približno polovico protonov je Sonce do sedaj
že porabilo in v tem času je posledično na Zemlji nastalo življenje
(Zemlja prejme na vrhu atmosfere okrog 1400 J energije na kvadratni meter na sekundo,
seveda je potrebno upoštevati še vpadni kot in odbojnost atmosfere, same površine Zemlje).
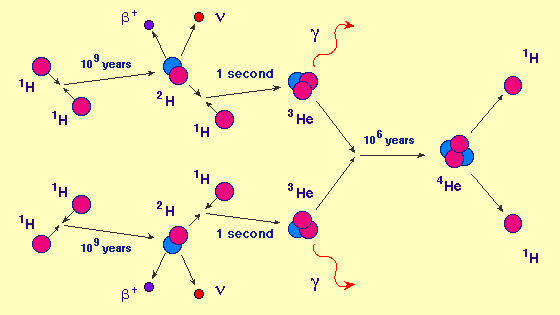
Še časovvni koraki, ki so potrebni, da se v p–p (proton–proton) verigi zlivanja vodika rodi helij.
Povprečni čas, ki je potreben, da jedro opravi vsak korak tega zaporedja v tipični
notranjosti Soncu podobni zvezdi, je prikazan na zgornji sliki. Tako na primer vodikovo jedro čaka v povprečju kar
1 milijardo let, preden pride v interakcijo z drugim vodikovim jedrom, da se začne zaporedje! Ker vsi
drugi koraki zahtevajo veliko manj časa kot ta, je ta začetni korak tisti, ki nadzoruje hitrost reakcije.
Ta neverjetno dolga stopnja kljub temu pojasnjuje izsev normalnih zvezd, saj je v jedru zvezde toliko
vodikovih atomov, da so v katerem koli trenutku mnogi podvrženi reakcijam verige P-P.
Vir: https://www.pas.rochester.edu/~blackman/ast104/ppchain.html
V masivnejših zvezdah od Sonca so tudi temperature v jedru višje in tam poteka tudi
zlivanje helija in ostalih večjih atomskih jeder v še masivnejše atome - tja do železa.

Naše Sonce ima (k sreči) premajhno maso za črno luknjo ali nevtronsko
zvezdo in bo končalo kot bela pritlikavka velikosti Zemlje.
Pri prehodu v belo pritlikavko se pojavi helijev blišč. Zakaj? Med sesedanjem zvezde,
po porabi vodika zlitega v helij temperatura in tlak v sredici padeta -
in tako se hipno sprosti ogromno gravitacijske in posledično še enkrat fuzijske
energije, temperatura naraste (v jedru Sonca se bo začel, čez približno 5 milijard in pol, tako
helij zlivati v ogljik in kisik, ki bosta v jedru izpodrinila helij in gravitacija bo spet prevladala)
- v zunanjih plasteh pa se posledično začasno vname (fuzija) še vodik v helij
in tako se pojavi helijev blišč, ki zunanje plasti zvezde (v primeru Sonca)
razširi vsaj tja do tirnice Marsa. Na sredi pa bo ostala bela pritlikavka (majčkeno Sonce) v glavnem iz
ogljika in kisika, ki bo svetila še nekaj milijard let. Sčasoma
pa bo naše, nekoč svetlo Sonce, postalo le temna mrzla krogla v vesolju
(ali bomo to belo pritlikavko in pozneje mrzlo zvezdico človečki še opazovali ...,
našo zibelko, naš stari, nekoč topli, dom?).
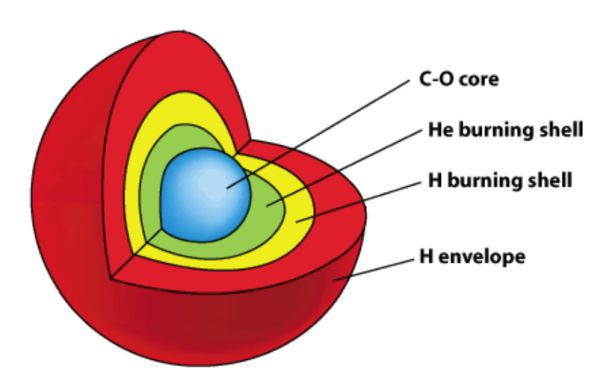
Faza Soncu podobne zvezde po helijevem blišču. Zaradi fuzije helija v ogljik zvezdo napihne.
Zvezda se nekoliko površinsko ohladi in gre v HR diagramu v vejo rdečih velikank - Red Giant Branch (RGB).
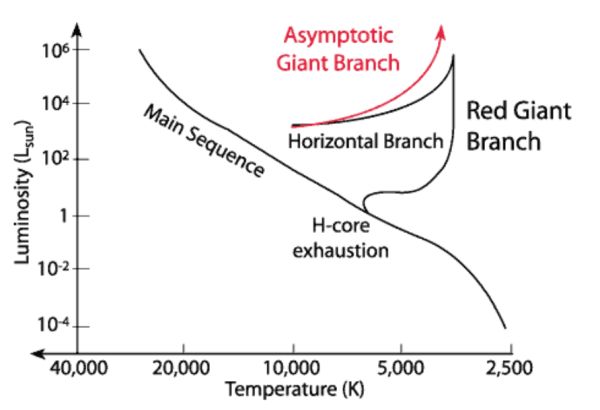
Po helijevem blisku postane jedro ponovno aktivno. Zdaj jedro pretvarja helij v ogljik, kisik s pomočjo trojnega procesa alfa.
Zvezda se skrči in njena površinska temperatura se poveča. Tako se premakne v levo na HR diagramu.
Ime horizontalna veja je podano zaradi prisotnosti zvezd z enakim sijem (svetlostjo, ki je na osi y) čez horizontalno
vejo zvezd različnih spektralnih tipov (temperatura površine je na osi x).
V zvezdi je jedro, kjer gori helij v ogljik, kisik, čemur sledi ovoj ali lupina, kjer gori vodik.
To je razlog, zakaj hladne in masivne zvezde AGB kažejo močne ogljikove črte v svojem spektru.
Z dodatnim napihovanjem (posledično ohlajanjem zunanje plasti)
gre zvezda še v asimptotično vejo orjakinj - Asymptotic Giant Branch (AGB).
Njen polmer lahko naraste do 1 AU
(astronomske enote) - do tirnice Zemlje.
Do takrat, do napihovanja Sonca čez nekaj milijard let (helijev blišč - v resnici že čez nekaj 100 milijonov let),
bo moralo življenje na Zemlji
(zunanje plasti vročega Sonca bodo namreč Zemljo posrkale) narediti
vesoljsko Noetovo barko, raketo, da se naš čudež življenja odseli na takrat
življenju bolj prijazno telo ... Bo to našim zanamcem uspelo? Držimo
pesti ...!?
Problemi med potovanjem na druga telesa Rimske ceste in potem med samim življenjem,
bivanjem kje drugje v vesolju, bodo zelo veliki.
Tudi še ne vemo, kako bo vplivalo potovanje, novo okolje na rast zarodkov, razvoj otrok.
Prisotni bodo
tako izjemni fiziološki pritiski na telo v drugačni težnosti, okolju, kot mentalno
soočenje z drugačnimi pogoji bivanja, komunikacije med ljudmi, delom narave, ki bo
potovala z nami ...
V resnici so tako projekti in tekmovanje med velikimi kulturami tega sveta (ZDA, Evropa, Kitajska, Indija, Rusija, Japonska,
J. Koreja ...),
kdo se bo prej naselil na Luni, Marsu,
prava priprava na oddaljeno bodočnost.
Tudi v luči nekoliko krute kozmične selekcije prilagajanja naših zanamcev na bivanje
v pogojih, ki jih določajo nova vesoljska telesa - lahko tudi umetne tvorbe, kolonije vesoljskih vozil.
Zakaj se že malo mudi?
Kako živi Sonce?
Sonce postopoma postaja bolj vroče v svojem jedru, pričakovano bolj vroče na površini,
posledično večje v polmeru in izseva več energije,
dokler je na glavni veji HR diagrama.
Od začetka svojega življenja na glavni veji HR diagrama, se je polmer povečal za 15 %
in površinska temperatura se je povečala od 5620 K (5350 °C) na 5777 K (5504 °C), kar je povzročilo
48-odstotno povečanje izseva - od 0,677 do današnjega Sončevega izseva 1,0.
To se dogaja,
ker imajo atomi helija v jedru višjo povprečno molekulsko maso kot atomi vodika, ki so bili zliti, kar ima za
posledico manjši toplotni tlak. Jedro se torej krči, kar omogoča, da se zunanje plasti Sonca približajo središču
in sproščajo gravitacijsko potencialno energijo. Po virialnem izreku gre polovica te sproščene gravitacijske
energije v segrevanje, kar vodi do postopnega povečanja hitrosti fuzije in s tem povečanja izseva.
Ta proces se pospeši, ko se jedro postopoma zgosti. Trenutno se njegov izsev poveča za približno
1 % vsakih 100 milijonov let. Od tega trenutka bo trajalo vsaj 1 milijardo let, da tekoča voda z
Zemlje izpari zaradi takšnega povečanja. Po tem bo Zemlja prenehala podpirati kompleksno,
večcelično življenje in zadnji preostali večcelični organizmi na planetu bodo utrpeli dokončno,
popolno množično izumrtje.
Sonce je zvezda glavne veje HR diagrama tipa G,
ki predstavlja približno 99,86 % mase Osončja.
Sonce ima absolutno magnitudo +4,83, kar je po ocenah svetlejše od približno 85 % vseh zvezd v Rimski cesti,
od katerih je večina rdečih pritlikavk.
Sonce je zvezda populacije I ali zvezda bogata s težkimi elementi
(v astronomiji se izraz težki elementi ali kovine, nekako širše nanaša na vse kemične elemente, razen vodika in helija,
ki sta produkt začetka vesolja).
Nastanek Sonca so morda sprožili udarni valovi ene ali več bližnjih supernov.
To nakazuje velika številčnost težkih elementov v Osončju, kot sta zlato in uran,
v primerjavi z številčnostjo teh elementov v tako imenovani populaciji II,
zvezdah revnih s težkimi elementi.
Težke elemente bi najverjetneje lahko proizvedli z endotermnimi jedrskimi reakcijami med eksplozijo supernove
ali s transmutacijo z absorpcijo nevtronov v masivni zvezdi druge generacije.
Poleg HR diagrama, nam starost zvezd omogoča tudi radioaktivni razpad masivnih atomov.
Oboje se kar dobro ujema.
Starost posameznih zvezd v Rimski cesti je mogoče oceniti z merjenjem številčnosti dolgoživih radioaktivnih elementov,
kot sta
torij-232 (razpolovna doba 14 milijard let)
in uran-238 (razpolovna doba 4,5 milijard let
- išče se črte enkratno ioniziranega urana
pri valovni dolžini 389,59 nm),
nato pa rezultate primerja z ocenami njihove prvotne številčnosti. Ta metoda je
imenovana
nukleokozmokronologija. Te vrednosti prinašajo približno 14,0 ± 2,4 milijarde let
za zvezdo CS 31082-001 in 13,8 ± 4 milijarde let za zvezdo BD+17° 3248. Tukaj je še metoda določevanja starosti
preko temperature - sevanja. Ko se oblikuje bela pritlikavka,
se začne ohlajati s sevanjem in površinska temperatura vztrajno pada. Z merjenjem temperatur
najhladnejših od teh belih pritlikavk in njihovo primerjavo z njihovo pričakovano začetno temperaturo,
je mogoče narediti oceno starosti. S to tehniko je bila starost kroglaste kopice M4 ocenjena na 12,7 ± 0,7 milijarde let.
Kroglaste kopice so med najstarejšimi objekti v galaksiji Rimska cesta, ki tako postavlja spodnjo mejo starosti galaksije.
Ocene starosti najstarejše od teh skupin dajejo najboljšo oceno 12,6 milijarde let in 95-odstotno zgornjo mejo zaupanja
do 16 milijard let.
Vse te ocene so v zelo solidnem sozvočju z standardnim kozmološkim modelom Lambda-CDM.
Sončev dvojček je zvezda, ki se v večini bistvenih značilnosti (spektralni razred, temperatura površja,
vrtilna hitrost, masa, spremenljivost in kovinskost) ujema s Soncem in njegovimi vrednostmi.
Če je zvezda podobna Soncu fotometrično, je Sončev analog(on). Sončevi analogoni so običajno zvezde iz
glavnega niza ali podorjakinje s podobnim barvnim indeksom B-V kot ga ima Sonce ( B-V = 0,65 ).
Te zvezde so torej fotometrično podobne Soncu in imajo naslednje lastnosti:
- temperatura znotraj 500 K od Sončeve (5278 do 6278 K),
- metalnost 50–200 % (± 0,3 dex) Sončeve, kar pomeni, da bi zvezdin protoplanetarni disk imel podobne količine prahu,
iz katerega bi lahko nastali planeti,
- brez bližnjega spremljevalca (z orbitalno dobo deset dni ali manj), ker takšen spremljevalec spodbuja zvezdno aktivnost,
kar recimo ni dobro za razvoj življenja ...
Navedimo tri zvezde
sončnega tipa znotraj 20 svetlobnih let, ki skoraj izpolnjujejo merila za Sončne analoge (barva B-V med 0,48 in 0,80.
Zgledi zvezd istega spektralnega razreda so: Alfa Kentavra A (α Cen A, tip G2V in temperatura površine 5790 K, razdalja 4.37 sv. l.),
82 Eridana (tip G8V in temperatura površine 5338 K, razdalja 19.8 sv. l.)
in Tau Kita (τ Cet, tipa G8V in temperatura površine 5344 K, razdalja 11.9 sv. l.).
Misija CoRoT ( Convection, Rotation and Planetary Transits mission) in zvezda Sol 1.
Izstrelitev misije CoRoT je bila 27. decembra 2006. Upravlja jo Centre national d'études spatiales (CNES)
ob sodelovanju znanstvenih programov Evropske vesoljske agencije (ESA), ESA Oddelek za podporo raziskavam
in znanosti (ESA-RSSD), Avstrija, Belgija, Brazilija, Nemčija in Španija.
Misija je 2013 odkrila zvezdo
CoRoT-1 (Sol 1). To je zvezda glavne veje HR diagrama - rumena, podobna Soncu, stara 6,7 milijarde let.
Zvezda se nahaja približno
2630 svetlobnih let v ozvezdju Samoroga (Monoceros).
Navidezna magnituda te zvezde je 13,6, kar pomeni, da ni vidna s prostim očesom; vendar ga je mogoče videti
skozi srednje velik amaterski teleskop v jasni, temni noči. Prvi eksoplanet, odkrit med misijo CoRoT,
kroži okoli te zvezde; velja za "vroč Jupiter" in je približno tako masiven kot sam planet Jupiter.
8,2 m veliko zrcalo japonskega teleskopa Subaru in izjemna natančnost njegovega spektrografa z visoko
disperzijo, sta omogočila izvedbo te podrobne študije spektrov tako šibke zvezde.
Masa (količina snovi) in kemična sestava zvezde sta glavni značilnosti, ki določata njen razvoj.
Preučevanje zvezd z enako maso in sestavo kot Sonce, tako imenovani »sončni dvojčki«, nam lahko dajo
več informacij o našem lastnem Soncu; sončni dvojčki različnih starosti ponujajo posnetke razvoja
Sonca v različnih fazah
CoRoT-1 je zvezda tipa G, kar pomeni, da je svetloba, ki jo oddaja, podobna svetlobi Sonca.
Sol 1 ima skoraj enako temperaturo in maso kot Sonce, tudi perioda rotacije 29 dni je podobna Sončevi.
Zakaj je pomembna taka zvezda? Ker je nekoliko starejša od Sonca in kot smo že omenili - iz nje lahko sklepamo na razvojno pot
samega našega Sonca - koliko časa bomo lahko še živeli na Zemlji.
Sol 1 ima teko nekoliko drugačno kemijsko sestavo, saj ima dve milijardi let več
fuzije in zato recimo manj litija kot Sonce.
Ko planet pade na zvezdo - potrjeni dogodki!
Da zgodba o požiranju planetov s strani centralnih zvezd ni samo matematična fizika,
priča primer zvezde ZTF SLRN -2020, ki je v približno enem tednu močneje zasvetila in nato
prešla na prejšnjo raven sija. Snov, ki je povečala sij, je bila molekularna - spet je
glavno vlogo odigrala spektroskopija.
Torej je pogoltnila planet - saj so le planeti zapleteno molekularno
sestavljeni. Povečanje sija je prvi opazil
Zwicky Transient Facility (ZTF) - to je program, ki ga samodejno izvajajo na
Caltechovem observatoriju Mt. Palomar v Kaliforniji, ZDA. Ta program neprestano
opazuje - primerja - objekte, ki se spreminjajo po siju ali legi od slike do slike
na zvezdnem nebu.
Ko se planet velikosti Jupitra približuje zvezdi (ali napihujoča zvezda planetu), ta najprej odtrga
od zvezde plin, ki se zato ohladi in se tako najprej majčkeno poveča infrardečo sevanje
(to so zares našli v arhivskih
meritvah - ta IR sij je trajal približno eno leto). Po tem dogodku, pa je zvezda močneje zasvetila, saj
je pojedla cel planet. Morda bodo čez cca 5 milijard let astronomi na kakem bližnjem eksoplanetu
opazovali tako kratkotrajno povečanje sija umirajočega Sonca, ko bo leto pojedlo naš ljubi planet
(našega potepuha).
Razmere za življenje na Zemlji pa bodo že tako postale nemogoče že nekaj 100 milijonov let prej.


Hipoteza, da bo Sonce na neki točki pogoltnilo Zemljo, ni nova. Ta ideja pa se vsak dan krepi zaradi
zadnjih vesoljskih opazovanj, v katerih se je pokazalo, kako je bodoča bela pritlikavka požrla planet.
To se je zgodilo približno 15 000 svetlobnih let stran od nas, a v naši galaksiji - Rimski cesti. Tam so astronomi
zahvaljujoč instrumentu Zwicky Transient Facility (ZTF) posneli, kako je zvezda ZTF SLRN-2020c z
lastnostmi, podobnimi Soncu, pogoltnila planet velikosti Jupitra.
"Potrditev, da Soncu podobne zvezde požirajo notranje planete, nam daje manjkajočo povezavo
v našem razumevanju usode sončnih sistemov, vključno z našim," je dejal Kishalay De,
podoktorski sodelavec na MIT in vodilni avtor odkritja.
Ali zmoremo napovedati, kako bi lahko bil povezan izsev L zvezde z maso M preko povezave polmera in mase?
Tlak fotonov Pf v jedru zvezde smo že zapisali preko sevanja črnega telesa
in gostote energije fotonov u = 4σT4/c, od tega je relevantna 1/3
fotonov - kot pri idealnem plinu -
tako smo dobili zelo zanimiv rezultat:
Pf = u/3 = (4/3)σT4/c
Ker veljata povezavi:
P ∝ ρT
T ∝ M/R
Zapišimo nekaj sorazmernosti.
Pf ∝ j ∝ L/R2 ∝ T4 ∝ (M/R)4
Tako približnoi velja (ker je R ∝ Mh):
L ∝ M4/R2 ∝ M(4 - 2h) ∝ Ma
Dobili smo dokaj pričakovan rezultata - podoben Eddingtonovem (izpeljali že prej).
Iz sorazmernosti torej sklepamo, da je tudi izsev zvezde L odvisen od določene potence (a) mase zvezde:
L ∝ Ma.
In res - za Sonce ta odvisnost velja kar s četro potenco:
L/Lo = (M/Mo)4
(za razpon mas: 0.43 Mo < M < 2 Mo )
Povezava med maso in izsevom je torej v splošnem odvisna od same mase zvezde - a se spreminja glede
velikosti zvezd (različen je tudi prenos energije iz jedra na površino zvezde, glede na maso).
Splošna enačba L/Lo = (M/Mo)a in običajna vrednost a = 3.5,
velja samo približno za zvezde glavne veje HR diagrama
z maso
2Mo < M < 55Mo in seveda ne velja za rdeče velikanke ali bele pritlikavke.
Ko se zvezda približa Eddingtonovemu izsevu, je a = 1.
Eddingtonov izsev, imenovan tudi Eddingtonova meja, je največji izsev,
ki ga telo (kot je zvezda) lahko doseže, ko obstaja ravnotežje med silo sevanja,
ki deluje navzven in gravitacijsko silo, ki deluje navznoter. Lo je izsev Sonca, Mo pa masa Sonca.
(***)
Če povzamemo, so razmerja (med L/Lo in M/Mo) za zvezde z različnimi razponi mas v
dobrem približku naslednja:
L/Lo ≈ 0.23(M/Mo)2.3 ( M < 0.43 Mo )
L/Lo = (M/Mo)4 ( 0.43 Mo < M < 2 Mo )
L/Lo ≈ 1.4(M/Mo)3.5 ( 2 Mo < M < 55 Mo )
L/Lo ≈ 32000(M/Mo) ( M > 55 Mo )
Nekaj splošnih podatkov o barvah zvezd, posledično tipih, o povezavi izseva L in mase M
Večina teles seva kot nečrno telo, sevajo neodvisno od smeri (tako imenovani Lambertov sevalec),
katerega emisijska sposobnost ε ( T ) ima enako vrednost za vse frekvence
(tako imenovano sivo telo). V tem primeru je moč oddanega sevanja ali izsev L za sferično telo kar
enak:
L = jS = jA = εσ4πR2T4
Emisivnost ε ( T ) je utežena povprečna emisivnost za vse valovne dolžine, utežna
funkcija pa je porazdelitev energije črnega telesa. ε ( T )
se spreminja med približno 0,012 in 0,98,
odvisno od snovi. Če je emisijska sposobnost odvisna od valovne dolžine,
se porazdelitev sevanja ne spremeni le zaradi spremembe Planckove porazdelitve.
Zaradi morebitne temperaturne odvisnosti, skupna moč sevanja ni več strogo
sorazmerna s četrto potenco absolutne temperature.
Za sevalec, v katerem emisija ni neodvisna od smeri ali frekvence, pa
je potrebno integrale izračunati posamezno, da se tako določi skupna sferna
emisija ε(T) na podlagi ustreznih zakonov.
A večina teles le malo odstopa od idealnega Lambertovega sevalca,
torej se emisijska sposobnost le malo spreminja v frekvenčnem območju,
v katerem telo oddaja opazen del svoje sevalne moči;
v teh primerih pa potem lahko uporabimo Stefan-Boltzmannov zakon vsaj približno.
Za zvezde in planete to kar dobro velja.
Na emisivnost Zemlje močno vpliva tudi sestava atmosfere - recimo
koncentracije toplogrednih plinov.

Vroče zvezde so svetlejše in bolj modre, kot hladne, ki so bolj rdeče.
Vmes so oranžne, rumene in bele.
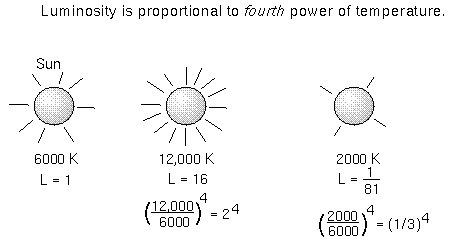

Tipi zvezd (O, B, A, F, G, K, M) in njihove površinske temperature ter pripadajoče barve.
Rdeče zvezde so hladne (s temperaturami okrog 3000 K), vroče pa modre (s temperaturami nad 30 000 K),
vmes pa so vse ostale barve in pripadajoče površinske temperature zvezd.
Kako si pa recimo zapomnite 7 osnovnih tipov zvezd po temperaturah
in barvah (O, B, A, F, G, K, M) - recimo kar preko začetnic besed
prikupne fraze v angleščini:
"Oh, Be A Fine Girl, Kiss Me"
Rumeno Sonce spada v G tip - je torej "Girl" - s površinsko temperaturo
okrog 5769 K. Temperaturo površine Sonca je že leta 1879 pravilno izračunal naš rojak fizik Jožef Stefan
- kot prvi na svetu iz lastnega zakona o toplotnem sevanju teles.
Povezava med maso in izsevom je odvisna od same mase zvezde.
Enačba L/Lo = (M/Mo)a in običajna vrednost a = 3.5,
velja samo približno za zvezde glavne veje HR diagrama
z maso
2Mo < M < 55Mo in ne velja za rdeče velikanke ali bele pritlikavke.
Ko se zvezda približa Eddingtonovemu izsevu, je a = 1.
Eddingtonov izsev, imenovan tudi Eddingtonova meja, je največji izsev,
ki ga telo (kot je zvezda) lahko doseže, ko obstaja ravnotežje med silo sevanja,
ki deluje navzven in gravitacijsko silo, ki deluje navznoter. Lo je izsev Sonca, Mo pa masa Sonca.
(***)
Če povzamemo, so razmerja (med L/Lo in M/Mo) za zvezde z različnimi razponi mas v
dobrem približku naslednja:
L/Lo ≈ 0.23(M/Mo)2.3 ( M < 0.43 Mo )
L/Lo = (M/Mo)4 ( 0.43 Mo < M < 2 Mo )
L/Lo ≈ 1.4(M/Mo)3.5 ( 2 Mo < M < 55 Mo )
L/Lo ≈ 32000(M/Mo) ( M > 55 Mo )
Ali se za zvezde na glavni veji HR diagrama da povezati maso M in polmer R?
Za zvezde glavne veje HR diagrama je značilno določeno razmerje med maso in polmerom.
Vendar pa je
razmerje kaže pomemben prelom okoli mase Sonca Mo, velja torej približna povezava:
R ∝ Mh,
kjer
je h ≈ 0.57 za M > Mo in h ≈ 0.8 za M < Mo. To
delitev določa meja konvektivne ovojnice. Konvekcija
teži k povečanju pretoka energije iz zvezde, kar povzroča, da se
zvezda rahlo skrči. Kot rezultat, zvezde s konvektivnimi
ovojnicami ležijo pod razmerjem masa-polmer za nekonvekcijske
zvezde. To krčenje poviša tudi osrednjo temperaturo
(preko virialnega teorema) in tudi premakne zvezdo nad nominalno
razmerje med maso in izsevom. Za zvezde glavne meje HR diagrama te negotovosti
vplivajo na izračunane radijev zvezd
(in efektivne temperature), vendar le malo.
Seznam eksoplanetov se hitro povečuje in se tako povečuje tudi raznolikost mas,
orbitalnih razdalj in vrst zvezd.
Dolg seznam nas motivira, da razmislimo, kateri od teh svetov
bi lahko podpiral življenje in kakšno življenje bi tam lahko obstajalo.
Edini (trenutni) pristop k odgovoru na ta vprašanja temelji na opazovanju
življenja na Zemlji. V primerjavi z astronomskimi cilji je življenje na Zemlji
enostavno raziskati in naše znanje o njem je obsežno – vendar ni popolno.
Najpomembnejše področje, na katerem nam manjka znanje o življenju na Zemlji,
je njegov izvor.
Nimamo enotne teorije o izvoru življenja, niti ne poznamo časa ali lokacije izvora.
Kar vemo o življenju na Zemlji, je tisto, iz česar je sestavljeno,
in poznamo tudi njegove ekološke zahteve in omejitve.
Tako ni presenetljivo, da se večina razprav o življenju na
eksoplanetih osredotoča na zahteve za obstoj življenja, a ne tudi na njegov izvor.
Zahteve za življenje na Zemlji, njena elementarna sestava in okoljske omejitve
omogočajo tudi oceno bivalnosti eksoplanetov (potenciala za obstoj življenja).
Temperatura je ključna tako zaradi
svojega vpliva na tekočo fazo vode kot tudi zato, ker jo je mogoče neposredno oceniti iz orbitalnih
in podnebnih modelov eksoplanetarnih sistemov. Življenje lahko uspeva in se razmnožuje pri temperaturah
od –15 °C do 122 °C.
Študije o življenju v skrajnih puščavavskih razmerah kažejo, da je na suhem področju lahko
že majhna količina dežja, megle, snega in celo atmosferske vlage,
zadostna za fotosintetično dejavnost,
ki ustvari majhno, a zaznavno mikrobno skupnost. Življenje lahko uporablja svetlobo na ravneh,
ki so manjše od 10-5 sončnega toka na Zemlji. Številni mikroorganizmi lahko prenašajo UV
ali ostalo ionizirajoče sevanje v zelo visokih ravneh
in je malo verjetno, da bi to sevanje omejevalo življenje
na eksoplanetu. Biološko dostopen dušik lahko omeji bivalno sposobnost.
Raven O2 nad nekaj odstotki
na eksoplanetu bi bila skladna s prisotnostjo večceličnih organizmov, visoke ravni O2 na Zemlji podobnih
svetovih pa kažejo na kisikovo fotosintezo. Drugi dejavniki, kot sta recimo pH in slanost,
se verjetno drugje spreminjajo, a najbrž
ne omejujejo življenja na celotnem eksoplanetu ali njegovi luni.
Seveda je tudi zelo pomembno, da je masa planeta, velikost ravno pravšnja - dovolj velika,
da zadrži atmosfero, in da je planet kamnit. Vse našteto izjemno optimalno
izpolnjuje seveda naša Zemlja, ki jo dodatno varuje še lastno magnetno polje (upočasnjuje hitre
nabite delce s Sonca in vesolja).
Zvezde sijejo tudi za vse nas!
Brez vode si težko predstavljamo življenje.
Sledi slikovita primerjava volumna vode zbranega v krogli glede na planet Zemljo.

Kolikšen del planeta Zemlja je iz vode? Pravzaprav zelo malo. Čeprav pokrivajo oceani
okoli 70 procentov Zemljine površine so ti oceani plitvi v primerjavi z Zemljinim
polmerom. Zgornja ilustracija prikazuje kaj bi se zgodilo, če bi vso vodo na ali
blizu Zemljine površine združili v kroglo. Polmer te krogle bi bil le okoli
700 kilometrov, manj kot polovico polmera Zemljine Lune in le malo večji od
Saturnove lune Rea, ki je podobno kot mnoge lune v zunanjem Osončju večinoma
iz vodnega ledu. Kako se je ta voda pojavila na Zemlji in ali je morda znaten
delež vode ujet daleč pod Zemljinim površjem ostaja predmet raziskav.

Dopolnjena primerjava iz 2025 - APOD.
Največja modra krogla
prikazuje količino, če bi vse vode na ali v bližini površja Zemlje združili v sfero (enako kot zgoraj).
Naslednja najmanjša krogla prikazuje vse tekoče sveže vode Zemlje,
medtem ko najmanjša krogla prikazuje količino vseh zemljinih sladkovodno jezer in rek.
Preprosta predstavitev H-R diagrama.
Največ možnosti za nastanek življenja je na planetu ob lahki
zvezdi (saj v njej fuzija teče počasi - 10 milijard let in več)
na glavni veji HR-diagrama. Blizu rumene zvezdice - blizu Sonca.
To je tudi področje, kjer na eksoplanetih (najprej v naši Galaksiji) lahko upamo na detekcijo
še kakšnega življenja v vesolju.
Mikro črne luknje - zaenkrat zgolj hipoteza
Mikro črne luknje, imenovane tudi mini črne luknje ali kvantno mehanske črne luknje, so hipotetično majhne (<1 Mo)
črne luknje, pri katerih igrajo kvantno mehanski učinki pomembno vlogo.
Koncept, da lahko obstajajo črne luknje, ki so manjše od minimalne zvezdne mase, je leta 1971 predstavil Stephen Hawking.
Možno je, da so bile takšne črne luknje ustvarjene v okolju visoke gostote zgodnjega vesolja (ali velikega poka)
ali morda s kasnejšimi faznimi prehodi (imenovanimi prvobitne črne luknje). Astrofiziki bi jih lahko opazovali skozi
delce, ki naj bi jih oddalo Hawkingovo sevanje. Lahko bi bile rešitev uganke o izvoru temne snovi.
Proizvodnja črne luknje zahteva koncentracijo mase ali energije znotraj ustreznega Schwarzschildovega polmera.
Vesolje naj bi bilo kmalu po velikem poku
dovolj gosto, da se je lahko kateri koli del prostora prilegal svojemu Schwarzschildovemu radiju.
Kljub temu se vesolje takrat zaradi enakomerne porazdelitve mase in hitre rasti ni moglo sesesti v singularnost.
To pa ne izključuje popolnoma možnosti, da so črne luknje različnih velikosti nastale lokalno. Tako oblikovana
črna luknja se imenuje primordialna črna luknja in je najbolj splošno sprejeta hipoteza o možnem nastanku mikro
črnih lukenj. Računalniške simulacije kažejo, da je verjetnost nastanka prvotne črne luknje obratno sorazmerna
z njeno maso. Tako je najverjetnejši rezultat simulacije nastanek mikro črne luknje.
Nekatere hipoteze, ki vključujejo dodatne vesoljske dimenzije, predvidevajo, da bi mikro črne luknje lahko nastale
pri nizkih energijah okrog TeV, ki so na voljo v pospeševalnikih delcev, kot je recimo veliki hadronski trkalnik
(Roger Penrose).
Takrat so se pojavili številni pomisleki glede scenarijev konca sveta (bilo je kar nekaj razprav o varnost trkov delcev v velikem
hadronskem trkalniku LHC - CERN). Vendar pa bi takšne kvantne črne luknje takoj izhlapele, bodisi v celoti, bodisi bi pustile
le zelo šibko medsebojno delujoč ostanek.
Poleg teoretičnih argumentov, so tukaj eksperimentalni zadržki, saj kozmični žarki, ki zadenejo Zemljo,
ne povzročijo nobene škode, čeprav dosežejo energije v območju stotin TeV.
Planckova masa je tudi domnevna majhna mejna črna luknja,
katere Schwarzschildov polmer je enak Planckovi dolžini.
Tako smo se približali pojmu kvantne gravitacije.
Planckova masa je definirana kot (glej -
Planckove enote ):
mp =
ℏtp/l2p
=
ℏtp/(ctp)2
= (ℏc/G)1/2 = 2,176470×10-8 kg.
Domneve o končni usodi črne luknje vključujejo popolno izhlapevanje in na koncu
ostanka črne luknje v velikosti Planckove mase. Takšne črne luknje Planckove mase bi bili
lahko dejansko stabilni objekti, če jim kvantizirane vrzeli med njihovimi dovoljenimi
energijskimi nivoji preprečujejo oddajanje Hawkingovih delcev ali gravitacijsko absorbiranje
energije kot to počne klasična črna luknja, ki lahko raste.
V takem primeru pa bi bili to masivni delci s šibkim medsebojnim
delovanjem; ti pa bi potem lahko pojasnili temno snov.
A zaenkrat še ni nobenih potrditev v smeri opisane kvantne gravitacije - to je zgolj ena od hipotez.
Kaj se zgodi, če v Sonce postavimo mini črno luknjo?
Umetnikov vtis postavitve majhne črne luknje v središče Sonca preko miselnega eksperimenta.
Vir: Wikimedia/Creative Commons.
Vir slike:
https://phys.org/news/2023-12-black-hole-sun-1.html
Po hipotetičnem scenariju bi lahko na novo nastajajoče zvezde zajele majhne, ??prvotne črne luknje.
Mednarodna ekipa, ki jo vodijo raziskovalci na Inštitutu Maxa Plancka za astrofiziko, je
zdaj modelirala razvoj teh tako imenovanih "Hawkingovih zvezd" in ugotovila, da imajo lahko
presenetljivo dolgo življenjsko dobo, ki je v mnogih pogledih podobna običajnim zvezdam.
Delo je objavljeno v
The Astrophysical Journal: https://iopscience.iop.org/article/10.3847/1538-4357/ad04de.
Asteroseizmologija bi lahko pomagala identificirati takšne zvezde, kar bi nato lahko potrdilo
obstoj prvobitnih črnih lukenj in njihovo vlogo kot komponente temne snovi.
Naredimo znanstveno vajo: če predpostavimo, da je veliko število zelo majhnih črnih lukenj
nastalo tik po velikem poku (tako imenovane primordialne črne luknje), bi jih lahko nekatere
ujeli med nastajanjem novih zvezd. Kako bi to vplivalo na zvezdo v času njenega življenja?
"Znanstveniki včasih postavljajo nora vprašanja, da bi izvedeli več," pravi Selma de Mink,
direktorica oddelka za zvezde na Inštitutu Max Planck za astrofiziko (MPA). "Sploh ne vemo,
ali takšne prvobitne črne luknje obstajajo, vendar lahko vseeno izvedemo zanimiv miselni eksperiment."
Primordialne črne luknje bi se oblikovale v zelo zgodnjem vesolju s širokim razponom mas,
od nekaterih tako majhnih kot asteroid do več tisoč sončnih mas. Lahko bi bili pomemben
sestavni del temne snovi, pa tudi semena za supermasivne črne luknje v središču današnjih galaksij.
Z zelo majhno verjetnostjo bi lahko novonastajajoča zvezda zajela črno luknjo z maso asteroida
ali majhne lune, ki bi nato tvorila središče zvezde. Takšna zvezda se imenuje "Hawkingova zvezda",
poimenovana po Stephenu Hawkingu, ki je to idejo prvi predlagal v članku v sedemdesetih letih prejšnjega stoletja.
Črna luknja v središču takšne Hawkingove zvezde bi rasla le počasi, saj je vdor plina, ki napaja
črno luknjo, oviran zaradi odtekajoče svetlobe navzven, ki zunanjim plastem, ne dovoli,
da bi padle proti centru zvezde. Mednarodna skupina znanstvenikov je zdaj modelirala
razvoj takšne zvezde z različnimi začetnimi masami za črno luknjo in z različnimi modeli akrecij
za zvezdno središče. Njihov osupljiv rezultat: ko je masa črne luknje majhna, se zvezda v bistvu
ne razlikuje od običajne zvezde.
"Zvezde, ki imajo v svojem središču črno luknjo, lahko živijo presenetljivo dolgo," pravi Earl
Patrick Bellinger, postdoc MPA in zdaj docent na univerzi Yale, ki je vodil študijo.
"Naše Sonce bi v središču lahko imelo celo črno luknjo
mase planeta Merkurja, ne da bi to opazili."
Glavna razlika med takšno Hawkingovo zvezdo in običajno zvezdo bi bila v bližini jedra, ki bi postalo
konvektivno zaradi akrecije na črno luknjo. Ne bi spremenila lastnosti zvezde na njeni površini in bi
se izognila sedanjim zmožnostim zaznavanja. Vendar pa bi jo bilo mogoče zaznati z relativno novim področjem
asteroseizmologije, kjer astronomi uporabljajo akustična nihanja za raziskovanje notranjosti zvezd.
Tudi v njeni kasnejši evoluciji, v fazi rdeče orjakinje, lahko črna luknja vodi do značilnih sledi.
S prihajajočimi projekti, kot je PLATO, bi lahko takšne objekte odkrili. Vendar pa so potrebne nadaljnje
simulacije, da bi ugotovili posledice postavitve črne luknje v zvezde različnih mas in sestave - količine kovin.
Če so prvobitne črne luknje res nastale kmalu po velikem poku, bi lahko bilo iskanje Hawkingovih
zvezd eden od načinov za njihovo iskanje.
"Čeprav se Sonce uporablja kot vaja, obstajajo dobri razlogi za domnevo, da bi bile Hawkingove
zvezde običajne v kroglastih kopicah in ultra šibkih pritlikavih galaksijah," poudarja profesor
Matt Caplan na državni univerzi Illinois, soavtor študije.
What happens if you put a black hole into the Sun?
- https://www.mpa-garching.mpg.de/1092647/news20231219
"To pomeni, da bi lahko bile Hawkingove zvezde orodje za preizkušanje obstoja prvobitnih črnih
lukenj in njihove možne vloge v sestavi temne snovi."
Beseda o unikatnem paru Luna - Zemlja,
- zgolj nekaj hipotez
Izhajajmo iz zanimivih dejstev, recimo o gostoti Zemlje in Lune, nagnjenosti rotacijske osi Zemlje in še kemijska primerjave ...
Luna ima razmeroma majhno železno jedro, zaradi česar ima Luna nižjo gostoto kot
Zemlja. Računalniški modeli velikanskega trka telesa v velikosti Marsa z Zemljo kažejo,
da bi del železnega jedra telesa, ki je trčilo z Zemljo verjetno prodrl v sredico Zemlje in se
z njim zlil. To bi pustilo Luno, ki je nastala iz izmetov preostalega materiala,
ki niso bili zliti s proto-Zemljo, z veliko manj železa kot to
velja za druga planetarna telesa.
Luna je v primerjavi z
Zemljo osiromašena s hlapnimi elementi (s plini). Zaradi uparjanja pri sorazmerno nižjih temperaturah bi
se lahko izgubili v visokoenergijskem dogodku, pri čemer jih manjša gravitacija Lune
ne bi mogla ponovno ujeti, medtem ko jih Zemlja je ujela.
Tudi v drugih zvezdnih sistemih obstajajo dokazi o podobnih trkih (to je velik dosežek
večjih teleskopov in spektroskopije - ki loči spektre molekul in atomov), ki
so za sabo pustili diske s snovjo, recimo za tvorbo lun.
Velikanski trki so tudi skladni z vodilno teorijo o nastanku Osončja.
Razmerja stabilnih izotopov lunarne in zemeljske kamnine so dokaj enaki, kar lahko nakazuje skupen izvor.
Pričakovali bi, da je rotacijska os (spin) Zemlje, pravokoten na orbito okrog Sonca (vrtilna količina
se namreč v taki ogromni gmoti iz katere je nastal Sončev sistem namreč na širši skali ohranja - če seveda ni drugih motenj).
Ker je Zemljina os nagnjena za 23.439 ° (ta kot nekoliko niha - za 2 °)
glede na pravokotnico na ekliptike - torej na ravnino potovanja Zemlje okrog
skupnega težišča s Soncem - je za pričakovati, da je tak odmik (23.4 °) posledica trka, recimo z manjšim
proto-planetom Tejo (velikosti Marsa). Domneva se sliši dokaj logična.
Teja je dobila ime po Teji, ki je bila v grški mitologiji mati Selene, boginje Lune,
kar je vzporednica s hipotetičnim trkom med Tejo in zgodnjo Zemljo,
za katerega se domneva, da je povzročil nastanek Lune.
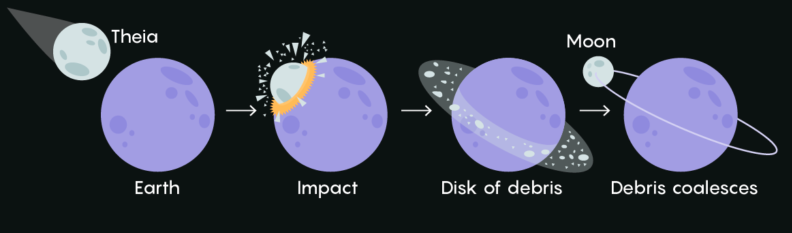
Poenostavljena predstavitev hipoteze o velikem trku protoplaneta Teje z mlado Zemljo.
Argumenti so vsaj trije: med trkom Teja, ki pozneje (iz ostankov) postane Luna,
izgubi večji del železa, ki ga posrka Zemljino jedro - težnost,
zato je Luna precej manj gosta oz Zemlje;
os rotacije Zemlje je nagnjena za 23.439 ° prav zaradi trka s Tejo;
Razmerja
stabilnih izotopov lunarne in zemeljske kamnine so dokaj enaki, kar lahko nakazuje skupen izvor.
En od modelov pravi, da je
Luna bila po nastanku od Zemlje oddaljena le približno desetino današnje razdalje
in je popolnoma zapolnila večerno nebo.
Ne glede na hitrost Zemljine rotacije in njen naklon osi, je po trku njen dan trajal le pet ur.
Zaradi Luninega vpliva (plimovanje) se je skozi zgodovino vrtenje Zemlje upočasnilo, tako da danes
dan traja "le še" 24 ur. Zaradi zmanjšanja učinka Coriolisove sile je to najbrž zelo ugodno.
Obstoječe podnebje je posledica tudi zelo stabilnega naklona Zemljine osi pri 23 stopinjah - za kar tudi skrbi Luna.
Nestabilen naklon bi namreč prinesel kaotične in izjemno hitre podnebne spremembe.

Vzhod Zemlje 1: popravljena zgodovinska slika
Avtorstvo slike:
NASA,
Apollo 8 Crew,
Bill Anders;
obdelava in
licenca:
Jim Weigang
Pojasnilo:
"O, moj Bog! Poglej ta prizor! Prihaja Zemlja. Kako lepo je!"
Kmalu po
teh izgovorjenih besedah,
24. dec. 1968 je bila iz
Lunine orbite posneta
ena najbolj znamenitih,
kadarkoli posnetih slik.
Danes znana kot
"vzhod Zemlje",
prikazuje ikonično sliko Zemlje, ki vzhaja
nad robom Lune, kot jo je
posnela posadka
Apolla 8.
Vendar je bila dobro znana slika
vzhoda Zemlje v resnici
drugi posnetek
vzhajajoče Zemlje nad lunarnim robom -- bila je le prva v barvah.
Vendar, z moderno digitalno tehnologijo je bil pravi prvi posnetek vzhoda Zemlje (prvotno črno-bel)
zdaj dopolnjen, da ima ločljivost in barvo
prvih
treh
posnetkov.
Glej!
prikazana slika je povečan posnetek slike, o kateri je
govoril astronavt Apolla 8
Bill Anders.
Zdaj jo lahko vsi vidimo, zahvaljujoč moderni tehnologiji in
človeški iznajdljivosti.
(Zgodovinska opomba:
drugačno zgodovinsko črno-belo sliko zahoda Zemlje za Luninim robom je posnel robotizirani
Lunar Orbiter 1, dve leti prej.)
Vira: apod
Poenostavljena predstavitev hipoteze o velikem trku.
Astronomi menijo, da se je trk med Zemljo in Tejo zgodil približno
4,4 do 4,45 milijarde let nazaj; približno 0,1 milijarde let po tem, ko
se je začel oblikovati Sončev sistem. V astronomskem smislu je bil udar
zmerne hitrosti. Menijo, da je Teja udarila v Zemljo pod poševnim kotom,
ko je bila Zemlja že skoraj v celoti oblikovana. Računalniške simulacije tega scenarija
"poznega trka" kažejo, da je začetna hitrost udarnega telesa v "neskončnosti" (dovolj
daleč, da gravitacijska privlačnost ni dejavnik) pod 4 kilometre na sekundo (2,5
mi/s), ki narašča, ko se približuje Zemlji na več kot 9,3 km/s
(5,8 mi/s) ob udarcu, in da je kot udarca bil okrog 45°. Vendar pa številčnost
izotopov kisika v Luninih kamninah kaže na "izrazito mešanje" gradnikov Teje in Zemlje,
kar pa tudi kaže na strm udarni kot.
Tejino železno jedro bi se naj preko težnosti potopilo
v jedro mlade Zemlje in večina Tejinega plašča bi se naj prirasla na
Zemljin plašč. Vendar pa bi naj bil znaten del materiala plašča iz Teje
in Zemlje izvržen v orbito okoli Zemlje (če bi bil izvržen z
hitrostmi med orbitalno hitrostjo in ubežno hitrostjo) ali v posamezne orbite okoli
Sonca (če bi bil izvržen pri večjih hitrostih).
Modeliranje je privzelo, da
se je material v orbiti okoli Zemlje kopičil in oblikoval Luno
v treh zaporednih fazah;
najprej akrecija iz izvrženega materiala - teles, ki so bila prvotno
prisotna zunaj Rocheve meje Zemlje (Rocheva meja
določa bližnjo razdaljo od planeta, ki zaradi plimovanja, težnostnega gnetenja, več ne omogoča
tvorjenja lun - značilno Saturnovi obročki ležijo znotraj Rocheve meje),
kar je omejilo material notranjega diska znotraj
Rocheve meje. Notranji disk se je počasi in viskozno razširil nazaj do
zemeljske Rocheve meje in
potiskal snov vzdolž zunanjih ostankov trka prek resonančnih interakcij (ko se recimo objekta na različnih
orbitah najbolj približata, se poznajo znatni učinki gravitacije). Po
nekaj desetih letih se je disk razširil čez Rochevo mejo in začel
prinašati nov material, ki je nadaljeval rast Lune, dokler notranji disk po
več sto letih ni izgubil mase. Preostali material v stabilnih Keplerjevih orbitah je
tako verjetno zadel sistem Zemlja-Luna kdaj pozneje (saj je tudi Keplerjeva orbita sistema
Zemlja-Luna okoli Sonca ostajala stabilna). Ocene, ki temeljijo na računalniških simulacijah takšnega
dogodka kažejo, da bi kakih dvajset odstotkov prvotne mase Teje končalo kot
krožni obroč razbitin okoli Zemlje, približno polovica te snovi pa se je
združila v Luno.
Zemlja bi zaradi takšnega trka pridobila precejšnje količine vrtilne
količine in mase. Ne glede na hitrost in nagib Zemljine rotacije pred
trkom, bi po trku naj dan trajal le približno pet ur, Zemljin ekvator in
Lunina orbita pa bi naj postala koplanarna (dve premici, lahko ravninski krivulji, sta
v tridimenzionalnem prostoru komplanarni, če obstaja ravnina,
ki vključuje obe - v tem primeru Zemljin ekvator in Lunino orbito).
Ves material iz obroča ni bil takoj
pometen na Luno: odebeljena skorja Lunine (ki je z Zemlje ne vidimo) kaže na možnost, da se je pojavila še
"druga luna" s premerom približno 1000 km (620 milj) v Lagrangeovi
točki L1 sistema Luna - Zemlja. Manjša luna je morda ostala v orbiti več deset milijonov
let. Ko pa sta se ti dve luni oddaljili od Zemlje, so učinki sončnega
plimovanja (in sprmememba orbit) povzročili nestabilnost prvotne Lagrangeove orbite,
kar je morebiti povzročilo trčenje pri počasnih hitrostih,
ki je manjšo luno "razpršilo" na tisti del Lune, kar je danes oddaljena stran
Lune in je tako dodalo material njeni skorji. Lunarna magma se tako ne more prebiti
skozi debelo skorjo oddaljene strani, posledično je tam manj luninih magmatskih morij, medtem ko
ima bližnja stran Lune tanko skorjo in ima zato na površini velika magmatska "morja", vidna z Zemlje
(s prostim očesom).
 |  |
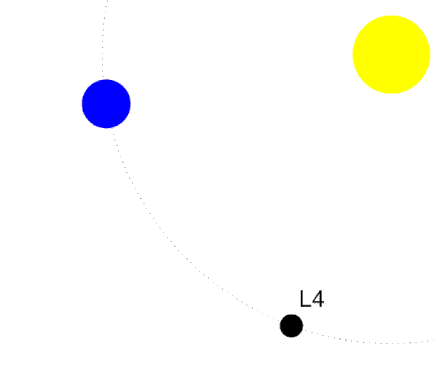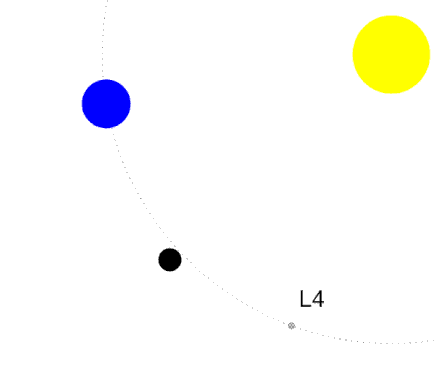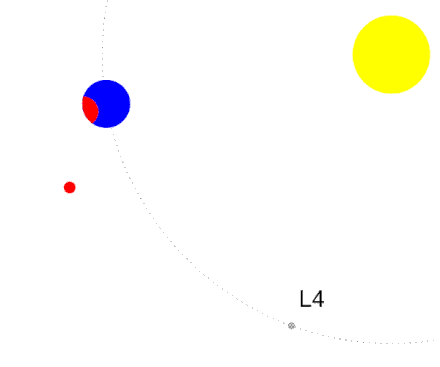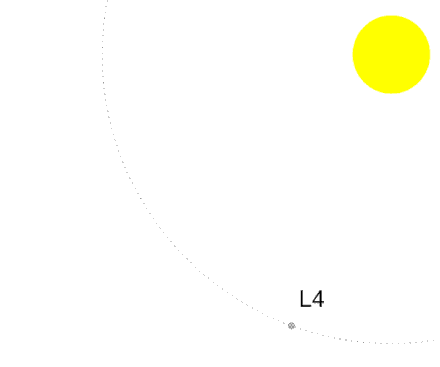
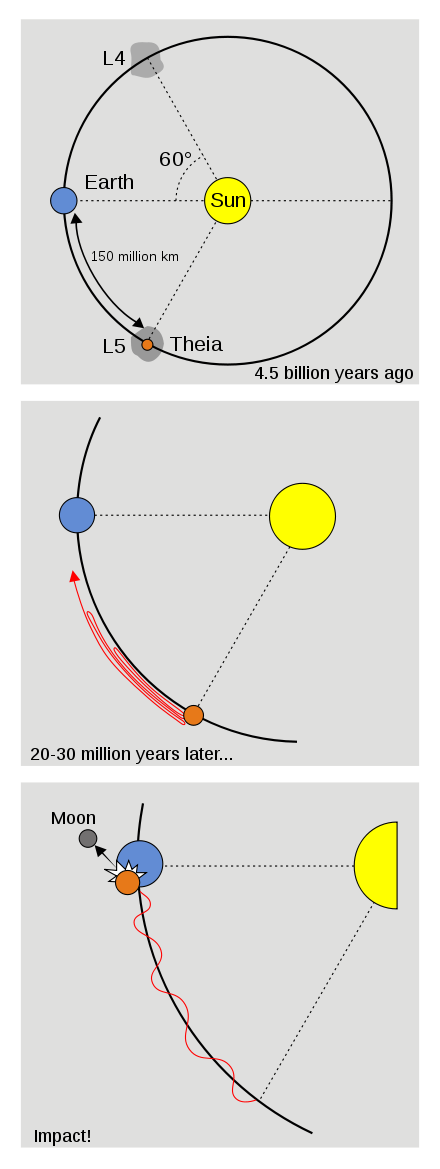
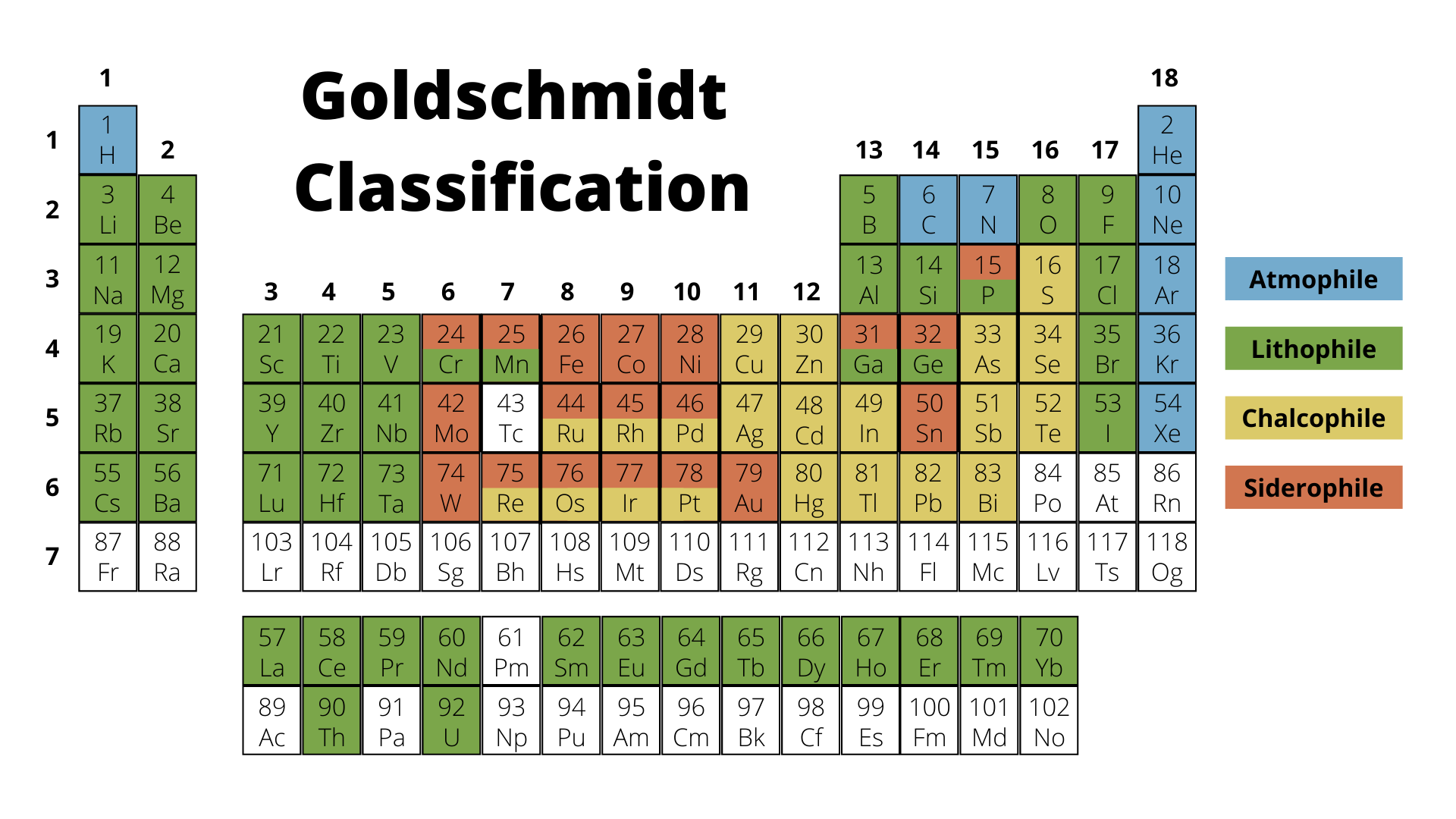


Pojasnilo: Fomalhaut je svetla zvezda, 25 svetlobnih let oddaljena od planeta Zemlja v smeri ozvezdja Južna riba (Piscis Austrinus). Astronomi so Fomalhautovo prekomerno infrardečo sevanje prvič opazili v osemdesetih letih prejšnjega stoletja. Vesoljski in zemeljski teleskopi so od takrat identificirali vir infrardečega sevanja kot disk prašnih ostankov, ki obkrožajo vročo mlado zvezdo, povezano s trenutnim nastajanjem planetarnega sistema. Toda ta ostra infrardeča slika iz kamere MIRI vesoljskega teleskopa James Webb, razkriva podrobnosti Fomalhautovega diska razbitin, ki jih še nikoli nismo videli, vključno z velikim oblakom prahu v zunanjem obroču, ki je možen dokaz za trčenje teles, ter notranjim diskom prahu in presledkom, ki je verjetno oblikovan in ga vzdržujejo vgrajeni nevidni planeti. Merilo slike v a.e. ali astronomskih enotah (povprečna razdalja Zemlja-Sonce), je prikazano spodaj levo. Fomalhautov zunanji okolizvezdni prašni obroč leži na približno dvakratni razdalji od Kuiperjevega pasu našega Osončja, sestavljenega iz majhnih ledenih teles in ostankov onkraj orbite Neptuna.
Zvezda Fomalhaut se krasno vidi v jeseni na južnem nebu (je skrivnostna samotna svetla kraljica tega dela južnega neba). Mnogi zvezdo Fomalhaut uporabljajo tudi za izhodišče pri iskanju prekrasne planetarna meglica Vijačnica (Helix) ali NGC 7293 v ozvezdju Vodnarja. Helix je najsvetlejša planetarna meglica na našem nebu (s sijem 6,3 magnitude in je tudi zelo velika, navidezno skoraj kot Luna, dobro vidna že z daljnogledom 15x70 ali še lepše z 20x80). Oglejte si torej izjemno zvezdo Fomalhaut, kjer se ravno rojevajo planeti in še planetarno meglico Helix - to je krasen sprehod po jesenskem večernem nebu. Tudi Sonce bo končalo življenjsko pot kot planetarna meglica, oziroma bela pritlikavka. Tako imamo pred sabo dve skrajni fazi razvoja zvezd (rojevanje planetov ob Fomalhautu in "smrt" zvezde sredi planetarne meglice Helix) - mi pa lepo opazujem z Zemlje, ki potuje okrog izjemno stabilne zvezde, našega Sonca, ki je ravno nekje na sredi svoje življenjske poti.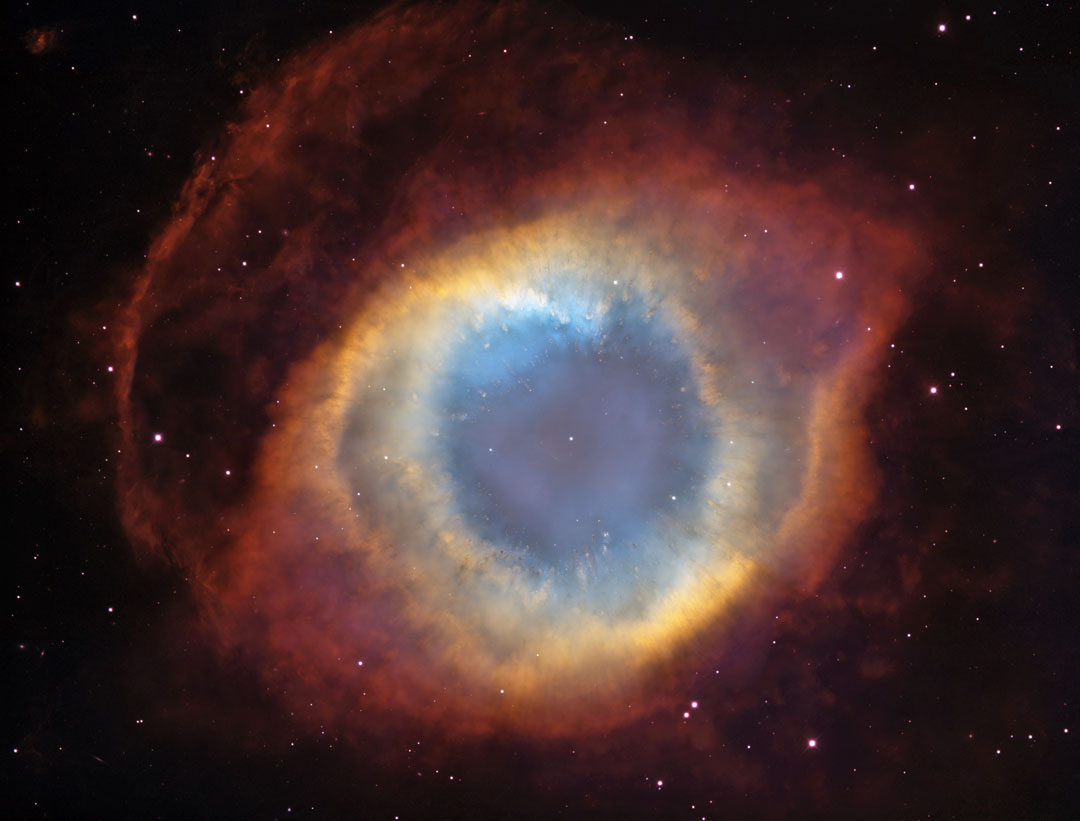


Preden gremo na Lagrangeevo mehaniko, še nekaj besed
o računanju razdalj preko metričnega tenzorja g.
Velikokrat se računanje metrike ds2 zapiše z generaliziranim skalarnim produktom
(xTMx) preko metričnega tenzorja M oz. g
( ds2 = gμνdxμdxν. ), za raven prostor velja
(posebna teorija relativnosti):
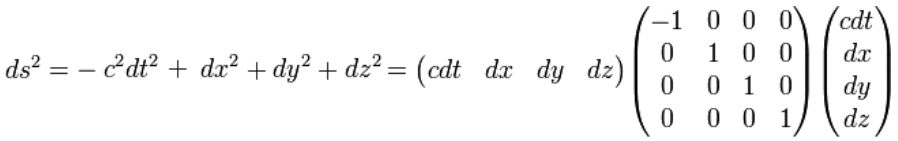
Za sferično telo
(splošna teorija relativnosti - upošteva se gravitacija) velja že znana metrika
- računanje razdalj ds2 smo že izpljeli v poglavju
"Fizika velikih hitrosti in pospeškov ...":
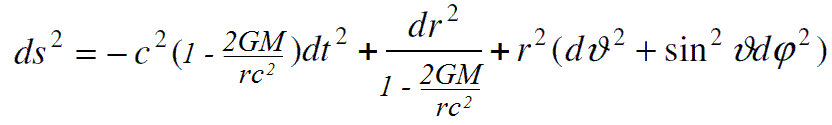
Iz zapisa lahko uganemo metrični tenzor g. Po diagonali bo imel
vrednosti:
-(1 - 2GM/(c2r), 1//(1 - 2GM/(c2r), r2,
r2 sin2ϑ
- vsi ostali členi bodo 0 (gre za sferično telo).
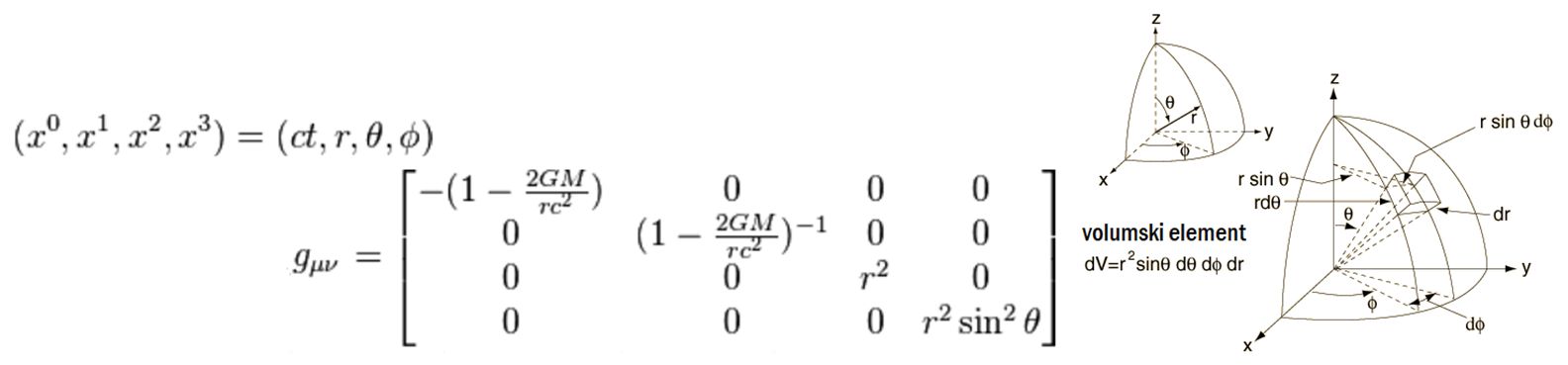
Za sferične koordinate torej velja vektor
dxμ = (dx1, dx2 , dx3 , dx4) = ( cdt, dr, dϑ, dφ )
in naslednji zapis metrike ds2 (4d Pitagorov izrek ob masivni sferi,
ds2 = gμνdxμdxν =
∑μνg(x)μνdxμdxν
):

Še primer deformacije prostora dveh bližnjih (tesno povezanih) masivnih zvezd,
ki krožita okrog skupnega težišča in tako oddajata znatne gravitacijske valove,
ki ga opišemo s tenzorjem, kjer se rotacija dogaja v ravnini (x, y), pravokotni na
smer širjenja valovanja. Če usmerimo os z v smer širjenja
valovanja, ima metrični tenzor v (sicer) ravnem prostoru
obliko:
|-1 0 0 0 |
| 0 1+h+ hx 0 |
gμν = | 0 hx 1-h+ 0 |
| 0 0 0 1 |
pri čemer se odmik 'h' harmonično spreminja
h+ = A+ cos(kz - ωt) in hx = Ax cos(kz - ωt)
|-1 0 0 0 ||cdt|
| 0 1+h+ hx 0 ||dx |
ds2 = gμνdxμdxν = (cdt,dx,dy,dz)| 0 hx 1-h+ 0 ||dy | = -(cdt)2 + (1+h+)dx2 + (1-h+)dy2 + 2hxdxdy + dz2
| 0 0 0 1 ||dz |

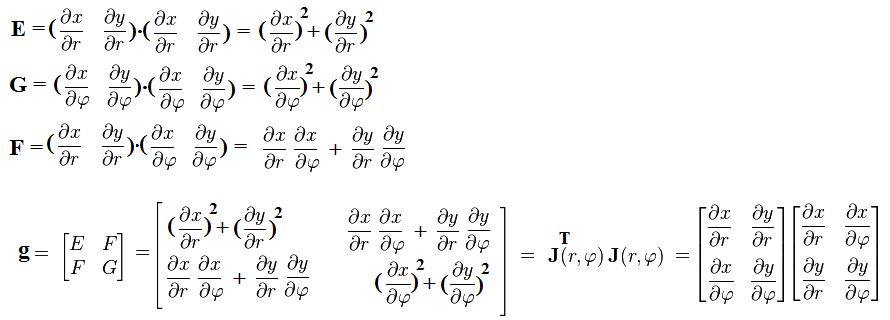


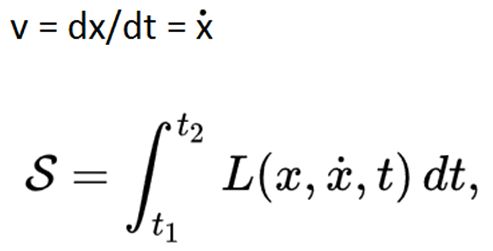
V resnici bi morali za sistem več spremenljivk uporabljati nekoliko baročno oznako ℒ in ne L, a o tem več pozneje.
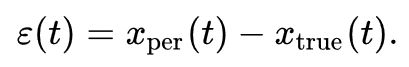
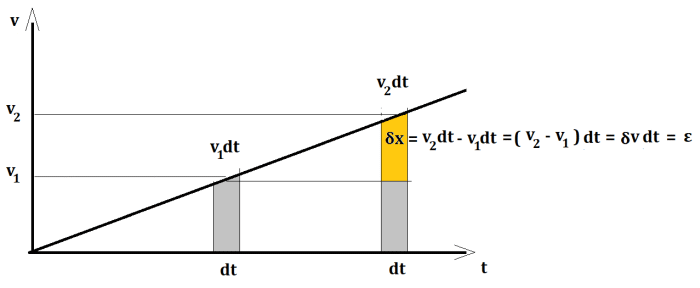
Lahko si predstavljamo dve telesi, ki padata ena za drugo (a nista bili spuščeni hkrati),
a ju slikamo ob istem času in še enkrat po zamiku časa dt. Narišimo še graf hitrosti od časa, ploščina pod grafom je kar pot x.
Pričakovano opazimo, da je telo, ki je začelo prej padati v intervalu časa dt naredilo veloko večjo pot in
razlika poti naj bo
δx = v2dt-v1dt = (v2- v1)dt = δvdt = ε.
In ta razlika poti δx med telesoma v
času dt je označena z oranžno barvo.
Razliko akcije δS pogledamo v času t za majhen premik (perturbacijo ε).
Hitrost v je, kot smo že omenili, odvod x-sa po času in naj bo označen s piko v = x˙ = dx/dt.
In po zgornji definiciji
za perturbacijo poti x v času dt velja
δx = dtδv
in naj bo ta produkt kar označen z
ε = δvdt = δx in časovni odvod ε je kar ε˙ = δv.
Kot razberemo iz grafa, je dx = δx + v1dt, ker pa gledamo prirastek δx in tako privzamemo v1 = 0, potem velja dx = δx = ε.
Na sliki je razlika t2 - t1 (kjer imamo označeni hitrosti v1 in v2) precej večja od dt (a to je samo zaradi
nazornosti), a tukaj išemo ekstrem, recimo najkrajše poti - in zato privzamemo, da je dt = δt, tako je tudi
δv = dv = ε˙.
Tako velja:
(∂L/∂x)δx = (∂L/∂x)ε
in
(∂L/∂v)δv = (∂L/∂x˙)ε˙
Zapišimo variacijo δS :
δS = ∫( (∂L/∂x)ε + (∂L/∂x˙)ε˙ )dt
Pri integriranju bomo uporabili
tudi metodo per partes ∫wdz = wz - ∫zdw
in bomo drugi del integrala ∫(∂L/∂x˙)ε˙dt zapisali kot razliko.
Velja: w = (∂L/∂x˙) in dz = ε˙dt in z = ε
∫(∂L/∂x˙)ε˙dt = ε(∂L/∂x˙) - ∫ε(d[(∂L/∂x˙)]/dt) dt
= - ∫ε(d[(∂L/∂x˙)]/dt) dt
Ker gre ε proti 0, velja
ε(∂L/∂x˙) t1|t2 = 0.
Spodaj je povedano zapisano še strnjeno.
Tako velja - iščemo ekstrem za akcijo S:
0 =
δS = ∫( ε(∂L/∂x) - εd[(∂L/∂x˙)]/dt ) dt
Še povzetek
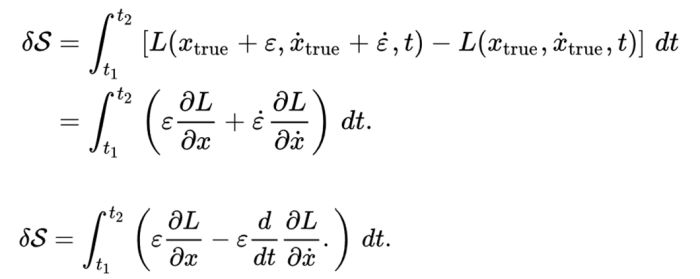
Iz variacije - pogoja δS = 0, ohranitve skupne energije, sledi Euler–Lagrangeeva enačba parcialnih odvodov:
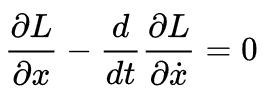
Primeri za gibanje po eni osi. Za majhne vertikalne premike ob površini Zemlje velja:
L = Ek – Ep = m(dx/dt)2/2 – mgx
Po odvajanju dobimo naslednji uporaben rezultat.
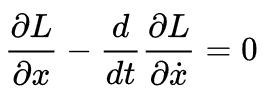
-mg – m(d2x/dt2) = 0
Tako dobimo znano enačbo za gibanje v gravitaciji.
g + d2x/dt2 = 0
Še splošen primer točkastega telesa z maso m v gravitacijskem polju velikega homogenega sferičnega telesa M
(ko velja, Ek = mv2/2 = m(d2x/dt2)/2 in Ep = - GMm/x ).
L = Ek – Ep = m(d2x/dt2)/2 - ( -GMm/x) = m(d2x/dt2)/2 + GMm/x
Velja: ∂L/∂x = -GMm/x2 in d/dt(∂L/∂v) = md2x/dt2
Spet pridemo do znane rešitve za gibanje točkastega telesa v gravitacijskem polju masivnega homogenega sferičnega telesa:
-GMm/x2 - md2x/dt2 = 0
MG/x2 + g = 0
Pri večjih hitrosti brez gravitacije pa velja za Lagrangeevo funkcijo kar relativistični izraz za sistem v katerem masa m miruje: Ek – Ep = 0 - mc2 = -mc2. Ep se tukaj šteje kot zaloga energije mirovne mase po Einsteinovi enačbi E = mc2. Čas v takem sistemu je kar lasten čas dτ = dt/γ = dt(1 – v2/c2)1/2.
S = ∫-mc2 dτ = -mc2 ∫dt/γ = -mc2 ∫(1 – v2/c2)1/2dt = ∫Ldt
Za sistem, za zunanjega opazovalca, ki glede na gibajoče telo miruje - pa torej velja naslednja Lagrangeeva funkcija L (v je relativna hitrost telesa z maso m):
L = -mc2(1 – v2/c2)1/2
Ker velja: ds2 = -c2dτ2 = -c2dt2 + dx2 + dy2 + dz2 in ds = dτc, pravilneje ds = c(-dτ2)1/2
- se akcija zapiše z metriko,
S = ∫-mc2 dτ = -mc∫ds
V polju masivnih teles pa se akcija izraža z metričnim tenzorjem gμν, časom in volumnom, kar bomo spoznali v naslednjem poglavju.
Ali se torej tudi enačbe splošne relativnosti da izpeljati iz principa akcije? Izkaže se,
da je to tudi najbolj razumljiva in elegantna pot. Einsteinove enačbe polja se torej izpelje
iz Einstein–Hilbertove akcije S (zato smo tudi ponovili pomen Euler–Lagrangeeve enačbe in
izpeljali relativistično akcijo
S = -mc∫ds).
Akcija se torej izpelje iz časovnega
integrala Lagrangeeve funkcije, gostote
(S = ∫ℒdt ali kar iz metrike
S = -mc∫ds,
v polju velikih teles in ostalih energij pa kot
S = ∫ℒd4x).
V resnici se integrira preko determinante metričnega tenzorja, oziroma po volumnu
(-g)1/2d4x.
S tem je integral neodvisen od koordinat,
saj je koren metričnega tenzorja enakovreden Jacobijevi determinanti – z njo
lahko računamo (se spomnimo iz matematike) recimo volumne (a tokrat v prostor-času).
V splošni teoriji relativnosti se Lagrangeeva gostota ℒ zapiše kot
ℒHE = R/(2κ),
torej z Riccijevim skalarjem (ta opiše ukrivljenost prostora, kar si je teoretično
zamislil Einstein – njegova najsrečnejša misel) in s funkcijo
ℒM,
ki predstavlja prisotnost
mase, v resnici gostoto energije (recimo sorazmerno z ρc2 ter gostoto vseh ostalih
energij).
Za Lagrangeevo gostoto torej velja naslednja povezava:
ℒ =
ℒHE +
ℒM = R/(2κ) +
ℒM
V akciji je g determinanta metričnega tenzorja
( g = det(gμν) ),
konstanta se žapiše kot
κ = 8πG/c4.
Riccijev skalar
je za sfero (recimo za zvezdo), kot smo že omenili, kar dvojna Gaussova ukrivljenost
R = 2/r2. Povedano
strnimo v SPLOŠNO enačbo Einstein–Hilbertove akcije S.
A ker govorimo o večrazsežnem prostor-času, ki ga določa masa in ostale oblike energije, bomo za opis
geometrije prostor-časa uporabili geometrijo mnogoterosti (topološki prostor),
ki jo najbolje opiše Riemannova geometrija (Riemannov tenzor ukrivljenosti). Tako bomo iz odvoda
Hilbert-Einsteinove akcije S, preko Riemannove geometrije, poiskali ustrezne tenzorske zapise za člene variacije δS = 0
in s tem tudi poiskali tenzorske Einsteinove enačbe polja.
Povejmo še, da so enačbe polja koncipirane tako, ta pri skromni gravitaciji ob sferi (recimo ob Zemlji)
preide prvi člen enačb v klasični zakon gravitacije, Riemannov ali
Riccijev tenzor ukrivljenosti (prvi člen R00) se v tem primeru zapiše kar
kot drugi odvod gravitacijskega potenciala, deljen s c2:
R00 ≈
∇2Φ = 4πGρ/c2
No - pa začnimo.
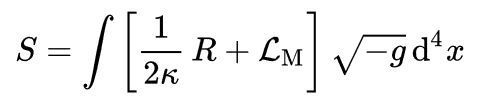
To akcijo bomo še podrobneje razdelali, sedaj pa preletimo, kako iz nje izpeljemo enačbe polja. Akcijo (enačbo) je prvič predlagal David Hilbert leta 1915. Še glede integrala, oziroma diferenciala d4x, ta je recimo kar d4x = dτdx'dy'dz' ali d4x = dx0dx1dx2dx3. Iz splošnega pogoja za variacijo δS = 0 (ohranitev energije) se izpelje Einsteinove enačbe polja (izpeljava zahteva kar nekaj napora …). Osnovni koraki so nakazani v nadaljevanju (gledamo majhno spremembo metrike δgμν, torej lege v prostor-času).
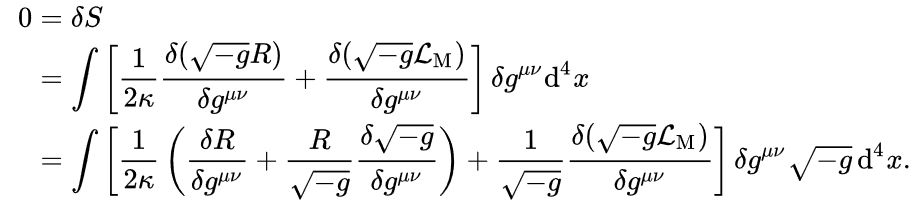
Sledi enačba gibanja (po analogiji s klasično mehaniko, enačba v oglatem oklepaju je enaka 0, saj za variacijo velja δS = 0, ohranitev energije):
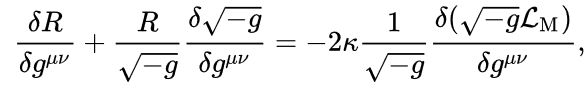
Sledijo členi enačbe gibanja (izvrednoteni napetostmi tenzor Tμν, Riccijev tenzor Rμν, metrični tenzor gμν):
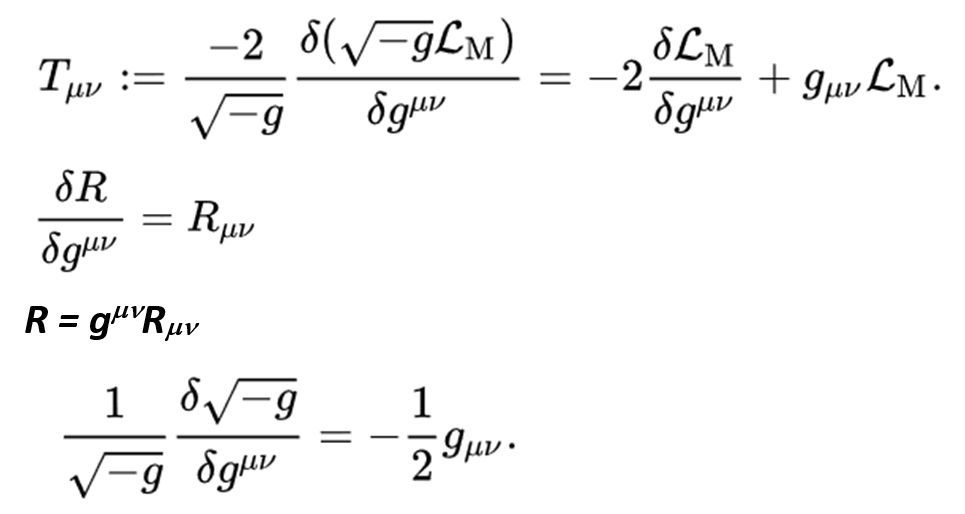
R = gμνRμν
Ko zložimo zgornje dele (Einstein–Hilbertove akcije S z uporabo Riemannove tenzorske geometrije) v celoto, se torej znamenita tenzorska enačba polja glasi (dodan je tudi kozmološki člen gμνΛ, ki bi naj pospešeno širil vesolje):
Rμν - Rgμν/2 + gμνΛ = 8πGTμν/c4
Spodaj je podana je tudi prostorska geometrijska slika s kratko razlago členov enačbe.

Slika - nazoren prikaz in opis členov Einsteinovih enačb polja – sliko se da razumeti
in posplošiti na celotno vesolje (čeprav nekoliko kozmološko nedosledno – saj vesolje
nima središča ..., pa vendar!).
V bistvu je metrični tenzor gμν sestavljen iz ravnega prostora brez gravitacije ημν
(po diagonali ima člene -1, 1, 1, 1 - vsi ostali so nič)
in ukrivljenosti zaradi gravitacije, energije, to je člen, tenzor hμν. Tako velja:
gμν = ημν + hμν
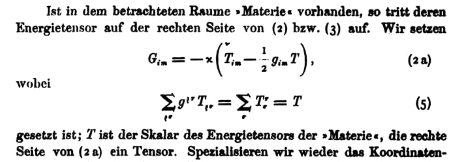
V tej drugi obliki je Einstein objavil enačbo v svojem članku
"The Field Equations of Gravitation", iz 25. novembra 1915 v Königlish Preussiche Akademie der Wissenschaften.
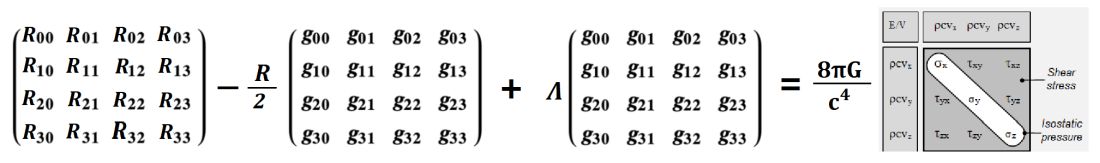
Zapis Einsteinovih enačb polja s tenzorji v matrični obliki - ta je didaktično najbolj
razumljiv.
Podrobneje analizirajmo tenzorje in ostale člene zgornje Einsteinove enačbe.
Za izračun variacije (δ) Riccijeve ukrivljenosti začnemo z izračunom variacije
Riemannovega tenzorja,
nato Riccijevega tenzorja.
Poudarimo, da je
Riemannov tenzor drugega reda
lokalno definiran le s Christoffelovimi simboli Γ. To so parcialni odvodi metričnega tenzorja; na površini sfere je recimo
metrični tenzor kar gij = [ r2 0, 0 (r*sinθ)2 ], bomo povedali, zakaj.
Christoffelovi simboli Γ so tudi del znamenite geodetske enačbe, ki opiše najkrajšo pot (geodetko)
med dvema sosednjima točkama
poljubne površine
d2xα/dτ2
= - Γαβγ(dxβ/dτ)(dxγ/dτ )
.
Poudarimo še, da na vsaki točki geodetske črte (geodetke) njena glavna normala sovpada z normalo na površino.
Zapišimo torej Riemannov tenzor drugega reda:
Rlikj
= ∂kΓlij
- ∂jΓlik +
Γlkλ Γλij
- Γljλ Γλik .
V Riemannovi geometriji je Riemann-Christoffelov tenzor ukrivljenosti najpogostejši način
za izražanje ukrivljenosti Riemannovih mnogoterosti ali splošneje mnogoterosti z afino povezavo,
z ali brez torzije.
Razmislite o dveh geodetskih črtah ukrivljenega prostora, vzporednih v bližini točke P. Ni nujno,
da bo vzporednost ohranjena tudi na drugih točkah prostora. Riemannov tenzor ukrivljenosti izraža razvoj
teh geodezij (linij, črt geodezik) glede na drugo.
Bolj kot je prostor ukrivljen, hitreje se bodo geodetske linije približevale
ali oddaljevale.
 | 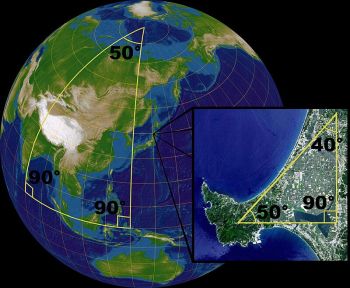
|
 |
 |
 |
Končna znamenita tenzorska enačba polja se torej glasi - še preko indeksov μν (zgoraj kj):
V enačbo polja je dodan še kozmološki člen Λ,
ki po zadnjih ugotovitvah predstavlja energijo, ki nasprotuje gravitaciji
(ima globalno gledano nasprotno ukrivljenost), akcija se v tem primeru s
kozmološkim členom Λ zapiše kot:
S = ∫[(R-2Λ)/(2κ) + ℒM](-g)1/2d4x
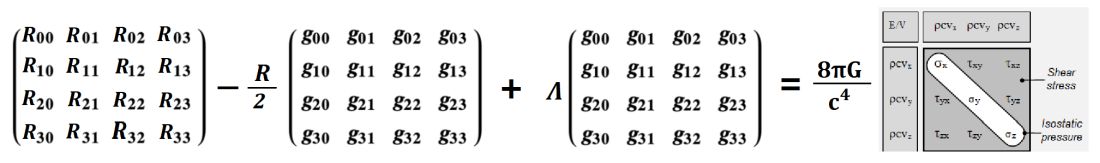
Zapis Einsteinovih enačb polja s tenzorji v matrični obliki - ta je didaktično najbolj
razumljiv.
Enačbe Einsteinovega polja
(
Rμν - Rgμν/2 + gμνΛ = 8πGTμν/c4
)
so bolj zapletene, kot se zdi.
Glede na dano porazdelitev snovi in energije v obliki tenzorja
napetosti-energije (Tμν), se zgornji Einsteinov zapis razume kot enačbe metričnega tenzorja gμν,
saj sta Riccijev tenzor in skalarna ukrivljenost odvisna od metrike na zapleten nelinearen način.
Ko so enačbe v celoti zapisane, predstavljajo sistem desetih sklopljenih,
nelinearnih, hiperbolično-eliptičnih
parcialnih diferencialnih enačb. Ni 16 enačb ampak 10 - ker je tenzor simetričen.
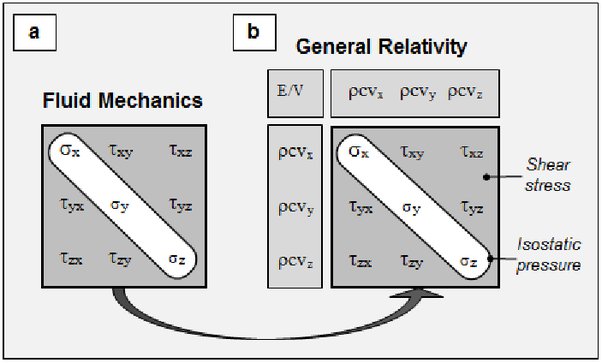

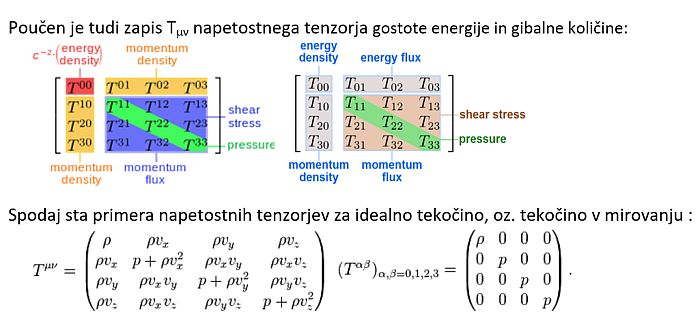
Še opis napetostnega tenzorja - ki napenja (krivi) prostor-čas zaradi mase in ostalih
oblik energije v vesolju.
Vir: https://www.quora.com/What-exactly-is-the-stress-energy-momentum-tensor-in-Einsteins-field-equations
Za vajo izpeljimo Riccijevo ukrivljenost R za masivno sferično telo z maso M in s polmerom rz.
Še prej pa povežimo klasično mehaniko z zapisom splošne relativnosti.
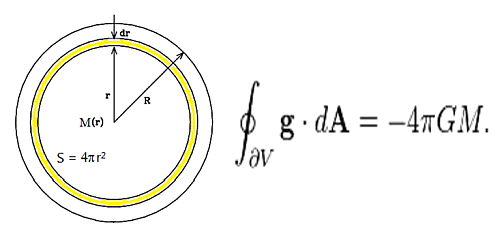
Gaussov gravitacijski zakon zakon obravnava težo preko gravitacijskega polja,
kot posledico mase in sam integral pospeška po celotni zaključni površini
'A' je sorazmeren zaobjeti masi:
4πr2GM/r2 ∝ M
Ker velja, da je sila na telo z maso m ob sferičnem telesu kar sorazmerna odvodu,
gradientu gravitacijskega potenciala Φ, to zapišemo kot:
F = md2r/dt2 = mdΦ/dr = GMm/r2.
Gradient je tukaj mišljen zgolj
v radialni smeri, saj se pri sferičnem
homogenem telesu gravitacija ne spreminja po poti loka okrog telesa. Odvod (gradient) potenciala je po
definiciji kar pospešek g = -dΦ/dr = -GM/r2.
V prostoru, v vesolju, nas recimo zanima, kako se na neki
ukrivljeni ploskvi spreminja pospešek, oziroma sila na neko telo. Ploskovni prispevek lupine k pospešku
na razdalji r od centra sferičnega telesa lahko zapišemo preko diferenciala dM mase lupine, ki jo izrazimo
z gostoto in diferencialom volumna (glej sliko: dM = ρdV = ρSdr = ρ4πr2dr,
kjer je S=4πr2
kar površina lupine - krogle na razdalji r); velja
dg = -GdM/r2 = -Gρ4πr2dr/r2 = -Gρ4πdr.
Iz česar sledi,
da je odvod (gradient) pospeška kar dg/dr = -Gρ4π, oziroma drugi odvod potenciala φ po r
je
d2Φ/dr2 = 4πGρ.
Namesto d/dr bi morali pisati parcialne odvode
∂/∂x+∂/∂y ... (uporabimo standardni
simbol za gradient ∇ = ∂/∂r), oz. drugi odvod s simbolom
∂2/∂r2, kar zapišimo z znakom
∇2 (to je Laplaceov operator).
Tako smo prišli do Poissonove enačbe
∇2Φ = 4πGρ
(dejansko smo čez palec uporabili tudi Gaussov zakon). Sedaj smo pa že delno izpolnili
naš zastavljeni cilj – na desni strani enačbe je ostala zgolj gostota telesa pomnožena
s konstantama 4π in G, na levi pa dvojni gradient potenciala, ki določa dinamiko teles v prostoru.
Če pogledamo enote in če enačbo delimo s c2, dobimo enoto ukrivlenosti (R = 1/r2 [1/m2]).
Tudi same enačbe relativnosti so tako nastavljene, da pri skromni gravitaciji prvi člen Riccijevega tenzorja ukrivljenosti
R00 preide v klasični Newtonov zakon, v drugi odvod potenciala
(
∇2Φ = 4πGρ ) deljen s c2:
R00 ≈ 4πGρ/c2
Če strnemo,
izhajamo iz Newtonove gravitacije, ki jo lahko zapišemo kot teorijo skalarnega polja Φ,
ki predstavlja gravitacijski potencial v Joulih na kilogram gravitacijskega polja in velja:
g = -∇Φ, to je Gaussov zakon za gravitacijo
∇ 2 Φ ( x , t ) = 4 π G ρ ( x , t )
kjer je ρ masna gostota. Orbita prosto padajočega delca izpolnjuje pogoj
d2x(t)/dt2 = g = - ∇ Φ (x(t), t).
Ali znamo torej iz prehoda na klasično mehaniko pri skromni gravitaciji, izluščiti ukrivljenost
prostor-časa zaradi prisotnosti sferične mase?.
To ukrivljenost namest z R tokrat označimo s T.
Uporabimo kar Riccijev člen R00 za sferično telo s polmerom rz in
maso M ter gostoto ρ.
Za prvi člen metričnega tenzorja
g00 = -(1 - 2Gm/(c2rz) )
bomo privzeli kar vrednost -1. Torej je prostor skoraj raven in bi pričakovali, da je Riccijev tenzor v limiti kar
klasični približek 4πGρ/c2, to še zapišimo:
R00 ≈ 4πGρ/c2
Za velikost prvega člena napetostnega tenzorja T00,
za gostoto energije E/V, velja kar dober približek za povprečno zvezdo ali še bolje
planet:
T00 = E/V = ρc2
Za prve člene Einsteinove enačbe torej velja:
R00 - g00T/2 = T008πGρ/c4
Izrazimo R00 in po definiciji privzamemo za šibko gravitacijsko polje
g00 ≈ -1 (približek ravnemu prostoru):
R00 = T008πGρ/c4 + g00T/2 =
8πGρ/c2 - T/2
Ker mora v klasični limiti veljati R00 ≈ 4πGρ/c2,
dobimo naslednjo povezava za ukrivljenost T:
R00 =
8πGρ/c2 - T/2 = 4πGρ/c2
Izrazimo še iskano ukrivljenost T:
T = 2 ( 8πGρ/c2 - 4πGρ/c2 ) = 8πGρ/c2
Ukrivljenost T ali R prostora zaradi sferne mase je torej kar:
R = T = 8πGρ/c2
To je zelo pomemben rezultat - kajti v vesolju imamo večinoma opravka z zvezdami, planeti ...
Če se vrnemo na splošno obliko z znatno gravitacijo, je potem prvi člen Riccijevega tenorja ukrivljenosti kar enak
R00 = T008πG/c4 + g00T/2
ALI
R00 = 8πGρ/c2 -(1 - 2Gm/(c2rz) )8πGρ/(2c2) =
(8πGρ/c2) (1 - (1 - 2Gm/(c2rz) )/2 )
Če se zelo oddaljimo od zvezde, je člen 2Gm/(c2rz) ≈ 0 in potem dobimo klasičen
člen za gravitacijo.
R00 ≈ (8πGρ/c2) (1 - 1/2 ) = 4πGρ/c2
Za skromno gravitacijo, kot smo že izpeljali, velja tudi znan izraz:
∇2Φ=4πGρ.
Zelo poučna vaja, da se navadimo na Einsteinov tenzorski zapis splošne teorije relativnosti.
Posvetimo še nekaj odstavkov razumevanju izjemno pomembne enačbe Einstein–Hilbertove akcije S
in dejstvu, da Riemannov ali Riccijev tenzor ukrivljenosti (prvi člen R00)
preide pri skromni sferični masi v klasični gravitacijski zakon ali celo v raven prostor:
R00 ≈
∇2Φ = 4πGρ/c2
V skromni gravitaciji in pri majhnih hitrostih se akcija S = ∫[R/(2κ) + ℒM](-g)1/2d4x skrči na znan rezultat s kinetično energijo (mc2 predstavlja mirovno potencialno energijo delca – zalogo energije):
∫(-mc2 + mv2/2)
Čez palec dokažimo zadnje trditve še iz Einstein–Hilbertove akcije, torej da le ta pri majhni gravitaciji preide v akcijo posebne teorije relativnosti.
S = ∫-mc2dτ = -mc2 ∫dt/γ = -mc2 ∫(1 – v2/c2)1/2dt:
Kot dokaz - izhajamo torej iz splošne Einstein–Hilbertove akcije S, za ℒM privzamemo gostoto energije ℒM = ρc2.
S = ∫[R/(2κ) + ℒM](-g)1/2d4x = ∫[R/(2κ) + ρc2](-g)1/2d4x
Za sfero (recimo Zemljo) velja za ukrivljenost R = 2/r2, a to je ukrivljenost geometrijskega telesa, a pri časovno-prostorski ukrivljenosti pa je najpomebnejša masa. Tako je pri majhni masi sfere Riccijev skalar R (ukrivljenost) praktično nič (R ≈ 2/∞ ≈ 0) , konstanta κ = 8πGc-4 v tem primeru ne igra vloge, saj je R/(2κ) praktično nič. Metrični tenzor za raven prostor (brez gravitacije), pa je kar g = det(gμν) = -1 (rešitev korena je zmeraj lahko +, -). Čez palec še privzamemo ∫ρdV' = m, torej zgolj opazovano maso točkastega telesa (čeprav je ta člen v resnici rezerviran za velika nebesna telesa, pa pri tej oceni nismo zagrešili nobene usodne konceptualne napake), tako nam ostane samo že od prej znana enačba (seveda uporabimo znano povezavo med maso, gostoto in volumnom m = ∫ρdV):
S = ∫[R/(2κ) + ρc2](-g)1/2d4x = ∫[0 + ρc2](1)1/2dτdx'dy'dz' = -∫ρc2dτdV = -∫ρc2dτdV' = -∫mc2dτ
Tako smo dokazali prehod splošne akcije (iz gravitacije) na raven prostor.
S = ∫-mc2 dτ = -mc2 ∫(1 – v2/c2)1/2dt = -mc∫ds
Pri majhnih hitrostih v pa velja (1 – v2/c2)1/2 ≈ 1 - v2/(2c2), tako pridemo do že omenjene klasične nerelativistične akcije.
S = ∫-mc2 dτ = -mc2∫(1 - v2/(2c2))dt = ∫(mv2/2 - mc2)dt = ∫(Ek – Ep)dt
Kjer je člen mc2 kar potencialna energija maksimalne zaloge energije skrite v masi.
A kot bomo videli, ima tudi sama gravitacija Zemlje v določenih primerih pomemben vpliv na relativistične efekte. Recimo pri sinhronizaciji ur med sateliti in Zemljo, pri GPS sistemih. Večinoma pa pri vsakdanjem življenju ne upoštevamo relativističnih vplivov gravitacije Zemlje na tek ur - na čas, itn. Če bi živeli na nevtronski zvezdi, pa bi relativistične vplive gravitacije (gravitacijskega lijaka) čutili na vsakem koraku – tudi pri uklonu svetlobe.
Še beseda o konstanti κ = 8πGc-4 .
Izbrana je tako, da računamo ukrivljenost prostora zaradi gravitacije,
različnih energij – na koncu, pri majhnih masah teles (recimo Zemlje) in
hitrostih, pa pridemo do klasičnih zakonov mehanike (ko privzamemo, da velja
Newtonov gravitacijski zakon, in da čas teče povsod enako ...).
https://www.imperial.ac.uk/media/imperial-college/research-centres-and-groups/theoretical-physics/msc/dissertations/2013/LI_INCOMPACT3D2014.pdf
Podrobneje si oglejmo še, na primeru sfere, naravo členov Einstein–Hilbertove akcije
S = ∫[R/(2κ) + ℒM](-g)1/2d4x,
– »sedaj bomo bika pa za roge prijeli«
Nekoliko baročna oznaka ℒ (Lagrangeeva gostota, prej smo govorili kar o funkciji L) se uporablja pri večih neodvisnih spremenljivkah, recimo v splošni relativnosti so to spremenljivke prostor-časa:
x, y, z, t.
Akcija v splošni teoriji relativnosti je torej integral Lagrangeeve gostote ℒ po celotnem prostor-času:
S = ∫ℒ d3xdt.
V resnici se integrira preko determinante metričnega tenzorja, oziroma volumnu
(-g)1/2d4x.
S tem je integral neodvisen od koordinat,
saj je koren metričnega tenzorja enakovreden Jacobijevi determinanti – z njo
lahko računamo (se spomnimo iz matematike) recimo volumne (a tokrat v prostor-času).
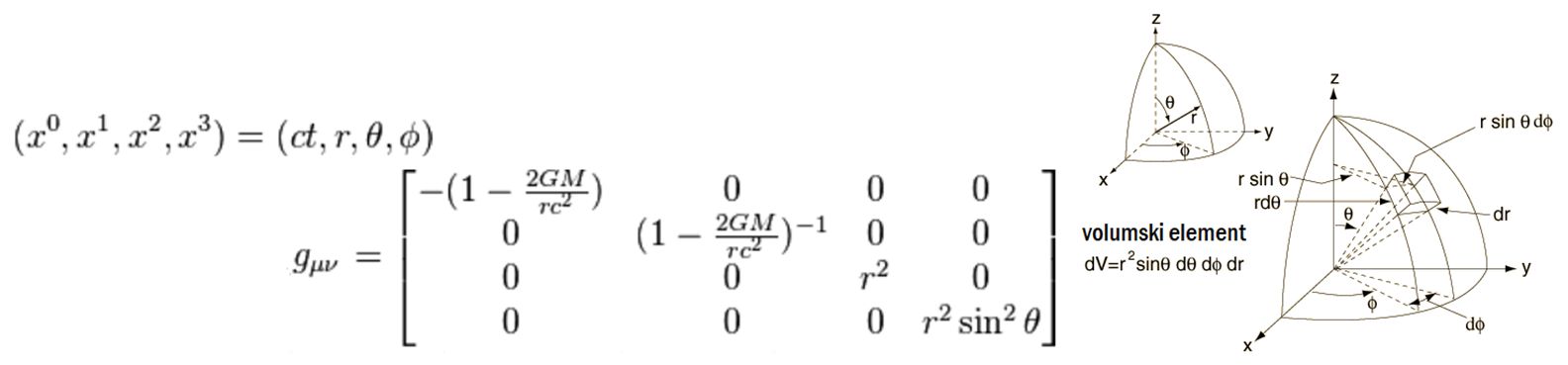
Vaja - determinanta metričnega tenzorja gμν za sferično telo je kar (zmnožek členov diagonale, ostali produkti so 0) g = det(gμν) = –r4sin2 ϑ, koren pa (-g)1/2 = r2sinϑ. Člen (-g)1/2d4x = cdt(r2sinϑdϑdφdr) = cdtdV, pa je kar volumski element sfere pomnožen s časovnim delom vektorja prostor-čas. Toliko o prostoru v 4d razsežnem prostor-času.
Da se bomo globlje vživeli v prvi del akcije ℒM = R/(2κ), se še enkrat dotaknimo hevrističnega rezultata - razmišljanja o kroženju svetlobe okrog masivnega objekta preko (klasične – za svetlobo neustrezne, a gre za ocene) enačbe za centripetalni pospešek:
v2/r = GM/r2
Hitrost v zamenjamo s hitrostjo svetlobe c in za M vstavimo znano povezavo M = ρV = ρ(4πr3/3).
Tako pridemo do izraza za skalarno Gaussovo ukrivljenost (R) sfere polmera r v splošni teoriji relativnosti.
R = 2/r2 ≈ Gρ8π/(3c2) ∝ 8πGρc2/c4
Pravilna vrednost je:
R = 2/rg2 = 8πGρc2/c4 = 8πGT00/c4
Za normalno zvezdo je dober približek ukrivljenosti povezan z gostoto in tlakom, a hidrostatični tlak ima precej manjši vpliv od mase,
zato velja:
2/rg2 = 8πG(ρc2+3p)/c4 ≈ 8πGρc2/c4 = 8πGρ/c2
Povprečno ukrivljenost bi tako lahko ocenili kar z izrazom
8πGρ/c2.
Če not vstavimo povprečno gostoto ρ = M/(4πRson3/3), se tako lahko povprečen skalar
Riccijeve ukrivljenosti (blizu površine Sonca) zapiše kot:
2/rg2 = 6GM/(Rson3c2 )
Zapišimo enačbo za ukrivljenost z novo spremenljivko κ = 8πG/c4:
R = κρc2
Po analogiji Lagrangeeve funkcije za kinetično in potencialno energijo:
L = Ek – Ep = m(dx/dt)2/2 - ( -GMm/x) = m(dx/dt)2/2 + GMm/x
- se vprašajmo, kako bi pojem ukrivljenosti vpeljali v splošni opis prostor-časa, ki je napolnjen z masivnimi objekti (recimo z zvezdami) in ostalimi oblikami energij. V nemotenem vezanem sistemu (recimo satelit - Zemlja) tudi velja, da je potencialna energija enaka dvakratni vrednosti kinetične energije (E = mv2/2 – GmM/r, ker je pri kroženju izpolnjen pogoj mv2/r = GmM/r2, velja Ep = -2Ek, v splošnem pa velja ta povezava za vse vezane sisteme, tudi vesolje kot tako – imenuje se virialni teorem, Lagrangeeva funkcija pa je po definiciji L = Ek - Ep). Povedano uporabimo pri iskanju akcije v prostor-času.
Izhajamo torej zgolj iz posebnega primera dinamike ob sfernem (okroglem) masivnem telesu – recimo ob zvezdi! Po domače izpeljani izraz za ukrivljenost R = κρc2 nas posredno spominja na kinetično energijo (ρc2 = R/κ) in po tej analogiji velja za energijo (pravilneje rečeno za gostoto energije ρc2 = R/κ ∝ E_dinamična/V) zaradi gibanja kar zveza E_dinamična/V = ℒHE = R/(2κ). Gibanje je torej določeno z ukrivljenostjo prostor-časa (za sfero je to kar R = 2/r2). Pri potencialni energiji pa je seveda spet bistven prispevek mase teles, katere gostota energije se v preprostih primerih zapiše kar kot E_pot/V ∝ ρc2 ∝ ℒM, oziroma splošno kar kot Lagrangeeva gostota ℒM (naj vas ne moti, da pri t. i. gostoti potencialne energiji ne nastopa gravitacijska konstanta – ta je del konstante κ, je le posledica normiranja in predvsem dejstva, da iščemo ukrivljenost prostor-časa, pri kateri v vesolju igra glavno vlogo masa [vsaj lokalno], na globalnem nivoju pa tudi ostale oblike energij). Ker govorimo o gostoti energij, moramo pri akciji S integrirati tako po času, kot po prostorskih koordinatah. Integral pa mora upoštevati metrični tenzor (koren njegove determinante), kar smo že omenili in pojasnili v tem poglavju: (-g)1/2d4x. Z determinanto se znebimo odvisnosti od koordinat. Oboje (ukrivljenost ℒHE = R/(2κ), po starem v povezavi z dinamično energijo in maso ℒM ∝ ρc2, po starem v povezavi s potencialno energijo) strnemo v enačbo Einstein–Hilbertove akcije:
S = ∫[R/(2κ) + ℒM](-g)1/2d4x
Tako smo torej prišli do Einstein–Hilbertove akcije (
S = ∫[R/(2κ) + ℒM](-g)1/2d4x )
preko primerjave s klasično akcijo v gravitaciji
( S = ∫Ldt = ∫(mv2/2 + GmM/r)dt ).
To je najbolj elegantna in najbolj razumljiva pot do enačb polja vesolja,
Hilbert-Einsteinova pot (a zadaj sta še zmeraj stari dobri Lagrange in ohranitev energije ter
Gaussova ukrivljenost).
A ker govorimo o večrazsežnem prostor-času, ki ga določa masa in ostale oblike energije, bomo (smo) za opis
geometrije prostor-časa uporabili geometrijo mnogoterosti (topološki prostor),
ki jo najbolje opiše Riemannova geometrija (Riemannov tenzor ukrivljenosti). Tako bomo (smo) iz odvoda
Hilbert-Einsteinove akcije S, preko Riemannove geometrije, poiskali ustrezne tenzorske zapise za člene variacije δS = 0
in s tem tudi poiskali tenzorske Einsteinove enačbe polja.
Več matematičnih podrobnosti, izračunov, vaj iz splošne teorije relativnosti si lahko ogledate na sledečih straneh:
https://math.stackexchange.com/questions/1394372/ricci-tensor-of-2-sphere-s2
https://physics.stackexchange.com/questions/62907/ricci-tensor-for-a-3-sphere-without-math-packets
http://einsteinrelativelyeasy.com/index.php/general-relativity/70-the-riemann-curvature-tensor-for-the-surface-of-a-sphere
http://einsteinrelativelyeasy.com/index.php/general-relativity/100-the-einstein-hilbert-action
https://arxiv.org/pdf/gr-qc/0401099.pdf
http://pi.math.cornell.edu/files/Research/SeniorTheses/rudeliusThesis.pdf
How Hilbert has found the Einstein Equations before Einstein and forgeries of Hilbert’s page proofs
https://arxiv.org/pdf/physics/0610154.pdf
Iz posebnega primera smo prišli na splošno enačbo – in ta primerjalna pot je tudi pot do splošnega
zapisa akcije v prostor-času in iz nje izhaja izpeljava znamenitih Einsteinovih (tudi Hilbertovih)
tenzorskih enačb polja.
Taka primerjava (Lagrangeeve funkcije za kinetično in potencialno energijo, ter energij – oz.
ukrivljenosti prostor-časa) se zdi nekoliko banalna – a s stališča odstiranja tančice skrivnosti
iz enačb splošne teorije relativnosti – didaktično še kako nujna! Ko je Hilbert zapisal to akcijo
leta 1915 – je delno deloval tudi intuitivno in primerjalno – po analogiji – in hkrati je bil
v dialogu z Einsteinom (gravitacija) in tudi z Miem (elektromagnetizem).
Še beseda o časovni dinamiki, pravi drami iskanja enačb polja.
Do leta 1907 je Einstein postavil
temelje teorije gravitacije, nato pa se je skoraj osem let ves obupan boril s težavo, kako
teorijo oblikovati v končno matematično obliko. Do začetka poletja leta 1915 se je matematik
David Hilbert (rojen v Prusiji 1862 v kraju Wehlau blizu takrat znamenitega Königsberga –
poslovi se leta 1943 v Göttingenu) osredotočil na splošno relativnost in povabil Einsteina
v Göttingen, da izvede teden predavanj o tej temi. Med predavanji je Einstein izvedel, da je Hilbert
deloval tudi na enačbah polja in si je sam tako še bolj prizadeval za končno obliko enačb. V novembru
1915 je Einstein objavil več dokumentov, ki so dosegli vrhunec v "Field Equations of Gravitation"
(Enačbe gravitacijskega polja). Skoraj istočasno je David Hilbert objavil "The Foundations of Physics",
aksiomatsko izpeljavo enačb polja. Hilbert je v celoti priznal Einsteina kot izvirnika teorije in noben
javni spor o avtorstvu enačb ni nikoli nastal med tema dvema velikanoma znanosti (se pa iz njunih pisem
razbere, da je med njima bilo kar nekaj napetosti – kdo je komu pomagal do enačb polja …). Prav je torej,
da osvetlimo še velik Hilbertov prispevek k matematičnemu zapisu – izpeljavi enačb polja. Na Hilberta
je imel velik vpliv tudi že omenjen rojak Gustav Mie – ki se je ukvarjal s teorijo relativnosti
v povezavi z elektromagnetizmom. Danes je nekako sprejeto večinsko mnenje, da je Hilbert prvi
pravilno formuliral enačbe polja, a splošna teorija relativnosti je teoretično Einsteinov dosežek,
medtem ko je Hilbert razvil enotno teorijo gravitacije in elektromagnetizma (vpliv Gustava
Mie-ja in Einsteinovega razmišljanja o gravitaciji). Hilbert je tudi izjavil, da je fizika pretežka
za fizike – v mislih je imel kdaj njihovo skromno matematično znanje, zato jim je tudi sam pomagal.
Sodelovanje z Miem in Einsteinom ter z ostalimi sodobniki, to dokazuje. Hilbert je bil po naravi novodobni
matematični Kepler – garač, inteligenten, preprost in povezovalen – tudi kdaj za ceno lastne slave, ki
pa mu je tako ni manjkalo. Nacionalsocialistom pa je v obraz povedal (ministru za izobraževanje Bernhardu
Rustu 1934) – da so z izgonom judovskih in ostalih svetovnonazorsko drugačnih matematikov iz Göttingena
praktično uničili inštitut za matematiko. Takrat so iz Göttingena, večinoma v ZDA, odšli, bili izgnani:
Edmund Landau, Richard Courant, Max Born, Felix Bernstein, Emmy Noether, Otto Blumenthal, Hermann Weyl …
Še zgovorna zanimivost. Prve rešitve lastnih enačb polja pa ne podata Einstein ali Hilbert, ampak Karl Schwarzschild (najde metriko za sferično telo, tudi mi smo jo po bližnjici, žal leta 1916 hudo zboli na fronti – Schwarzschild je bil v kontaktu tudi s Hilbertom), kar samo kaže na dejstvo, da oče teorije tudi ni zmeraj oče otroka rešitve. Zgodba nakazuje na univerzalno resnico, da brez sodelovanja ni napredovanja – a kot pravijo - »medalja in krogla nikoli ne zadeneta pravega«. V tem primeru povedano še kako kar dobesedno drži.
Po analizi logike Einsteinovih tenzorskih enačb polja se vrnimo zgolj k naši novi korektni metriki (eni od rešitev Einsteinovi enačb polja) – k merjenjem dolžin v prostor-času ob sferičnih telesih. Pot do metrike preko sistema Einsteinovih enačb je seveda precej zahtevnejša, a rezultat je enak (kot smo ga izpeljali v poglavju "Fizika velikih hitrosti in pospeškov ...") in nam tukaj gre predvsem za razumevanje samega fenomena – to je opis prostora in časa ob masivnih sferičnih telesih. Schwarzschildova metrika, ki je rešitev Einsteinovega sistema enačb, je torej:
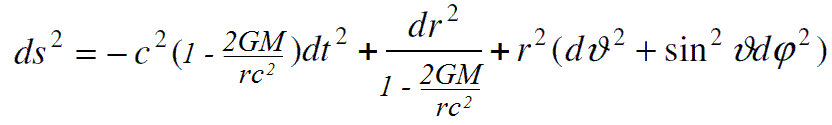

Karl Schwarzschild, oče metrike vesolja!
dS2 = -c2dτ2 = -c2dt2(1 - 2GM/(c2r)) + dr2/(1 - 2GM/(c2r)) + r2dΩ2
Sedaj že z gotovostjo lahko trdimo, da je prispevek gravitacije k metriki zares tak,
kot smo sklepali pri našem miselnem eksperimentu in pri primerjavi gravitacije ter kroženja.
Torej - če ima neko telo lastno dinamiko, gibanje – pa sama gravitacija k temu prispeva
še dodatno metriko časa in prostora s členi, ki smo jih ravnokar izpeljali.
In ta Schwarzschildova rešitev Einsteinovih enačb polja je za astronomijo
dejansko najbolj relevantna (vsaj na nivoju planetov, zvezd in galaksij).
Izpeljava Newtonovega gravitacijskega zakona iz Einsteinovih enačb polja
Newtonovo gravitacijo lahko zapišemo kot teorijo skalarnega polja Φ,
ki je gravitacijski potencial v Joulih na kilogram gravitacijskega polja
g = -∇Φ, glej Gaussov zakon za gravitacijo
∇ 2 Φ ( x , t ) = 4 π G ρ ( x , t )
kjer je ρ masna gostota. Orbita prosto padajočega delca izpolnjuje pogoj
d2x(t)/dt2 = g = - ∇ Φ (x(t), t).
V tenzorskem zapisu postanejo ti pogoji naslednji
Φ, i i = 4 π G ρ
d2xi/dt2 = - Φ, i.
V splošni teoriji relativnosti so te enačbe nadomeščene
z enačbami Einsteinovega polja v obliki obrnjene poti (tukaj je oznaka za ukrivljenost T in ne R - to zamenjavo pogosto srečamo pri izračunih)
R μν = K ( T μν - T g μν/2 )
za iskano konstanto K in geodetsko enačbo velja
d 2 xα / d τ 2
= - Γαβγ (d xβ /d τ)
(d xγ /d τ ).
Da bi videli, kako se slednji zakon reducira na prvega, predpostavimo,
da je hitrost testnega delca približno nič
d xβ/d τ ≈ ( d t/d τ , 0 , 0 , 0 )
in s tem
d( d t/d τ )/dt ≈ 0
in da so metrika in njene izpeljanke približno statične in da so kvadrati
odstopanj od metrike Minkowskega zanemarljivi. Uporaba teh poenostavljenih
predpostavk za prostorske komponente geodetske enačbe vrne
d 2 xi/d t 2 ≈ - Γi00
kjer sta dva faktorja časa dt/dτ razdeljena. To se bo pod danim pogojem
reduciralo na newtonsko rešitev
Φ, i ≈ Γi00
= (1/2) gi α
(gα 0, 0 + g0 α, 0 - g00, α ).
Naše predpostavke zahtevajo, da je α = i in časovni (0) odvod enak nič. Povedano se
torej poenostavi na izraz
2 Φ, i ≈ gij ( - g00,j ) ≈ - g00 , i
ki se zadovolji s pogojem
g00 ≈ - c 2 - 2 Φ .
Če se ozremo na Einsteinove enačbe, potrebujemo samo časovno-časovno komponento
R00 = K ( T00 - Tg00/2 )
nizka hitrost in predpostavke statičnega polja vrnejo izraz
Tμν ≈ diag(T00 , 0, 0, 0) ≈
diag(ρc4, 0, 0, 0).
torej
T = gα β Tα β ≈ g00 T00
≈ - ρ c 4/c2 = - ρc2
in s tem
K ( T00 - Tg00/2 ) ≈
K ( ρ c 4 - (1/2)( - ρ c 2 ) ( - c 2 ) )
= K ρ c 4 / 2.
Iz definicije Riccijevega tenzorja
R00 = Γρ00 , ρ
- Γρ ρ 0 , 0 +
Γρρλ Γλ00
- Γρ 0 λ Γλρ 0 .
Zaradi naših poenostavljenih predpostavk kvadrati Γ izginejo skupaj s časovnimi odvodi
R00 ≈ Γ i00 , i .
Kombinacija zgornjih enačb vrne naslednje povezave
Φ, i i ≈ Γi00, i ≈
R00 = K ( T00 - Tg00/2)
≈ K ρ c4/2
ki se reducira na podano Newtonovo enačbo polja
Kρc4/2 = 4πGρ
kar velja, če je konstanta K enaka
K = 8πG/c4 .
Izpeljava Schwarzschildove rešitve iz Einsteinovih enačb polja (II)
Rab - Rgab/2 = 8πGTab/c4
Schwarzschildova rešitev opisuje prostor-čas pod vplivom masivnega, nerotacijskega,
sferično simetričnega homogenega telesa. Za uvod torej kar zapišimo Schwarzschildovo metriko ds, ki nam pove,
kako računamo razdalje ob sferičnem masivnem telesu:
ds2 =
- c2dt2(1 - 2Gm/(c2r) )
+ dr2/(1 - 2Gm/(c2r) ) + r2(dθ2 + sin2θ dΦ2)
Nekateri menijo, da je ta rešitev ena najpreprostejših in najbolj
uporabnih rešitev enačb Einsteinovega polja. Izpeljimo jo!
Predpostavke in oznake
Pri opisu (koordinatnega) prostora s koordinatami (r, θ, Φ, t),
označenimi z indeksi od 1 do 4, začnemo z metriko v njeni najbolj splošni
obliki, formi (to je 10 neodvisnih komponent, od katerih je vsaka zvezna
funkcija 4 spremenljivk) - še opomba -
večinoma smo navajeni zapisa časovne komponente na prvem mestu, a vse je stvar dogovora.
Predpostavlja se,
da je rešitev sferično simetrična, statična in vakuumska.
Za namene te izpeljave so potrebne predpostavke lahko
navedene na naslednji način, spodaj (za dodatne definicije glejte
ustrezne povezave):
A) Sferično simetričen prostor-čas je tisti, ki je nespremenljiv glede na rotacije in zrcalne slike.
B) Statični prostor-čas je tisti, v katerem so vse metrične komponente neodvisne od časovne koordinate t
(tako da je odvod metričnega tenzorja po času ∂gμν/∂t = 0
in geometrija prostor-časa se ne spremeni pri časovnem obratu t → - t (ta obrat je zaenkrat zgolj matematična možnost in ne fizikalna).
C)
Vakuumska rešitev je tista, ki izpolnjuje enačbo Tab = 0, torej velja Rab - Rgab/2 = 0.
Iz ničelnega napetostnega tenzorja Tab
velja, da je tudi Riccijeva skalarna ukrivljenost R = 0.
Iz Einsteinovih
enačb polja (z ničelno kozmološko konstanto) potem torej velja, da je torej Riccijev tenzor Rab = 0,
(seveda vse njegove komponente). In te bomo tudi računali pri iskanju
Schwarzschildove rešitve.
Zakaj smemo privzeti, da sta T in R nič? Ker vemo, da se lokalno pri Riemannovem tenzorju metrika obnaša
kot v ravnem prostoru, kar smo že poudarili pri opisu Riemannovega tenzorja ukrivljenosti (dokaz je računanje z ravninsko geometrijo na površini Zemlje, ki
je dovoljena v lokalnem prostoru - načrtovanje dimenzij hiš, ulic, površin parcel preko evklidske geometrije ...).
D) Tukaj bo uporabljen metrični predpis (+,+,+,-), lahko bi bil tudi obrnjen.
Diagonalizacija metrike
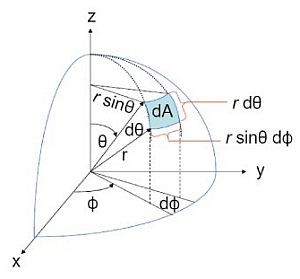
Prva poenostavitev, ki jo je koristno narediti, je diagonalizacija metrike.
Pod koordinatno transformacijo, to je recimo pri obratu časa
(r, θ, Φ, t) → (r, θ, Φ, -t),
morajo vse metrične komponente ostati enake. Metrične komponente gμν
( μ ≠ 4)
se pod to transformacijo spremenijo kot:
g'μ4 =
(∂xα/∂x'μ)(∂xβ/∂x'4) gαβ
= - gμ4 ( μ ≠ 4)
Ker pa pričakujemo g'μ4 = gμ4
(metrične komponente ostanejo enake), to pomeni, da nediagonalne komponente povezane s časom ostanejo 0:
gμ4 = 0 ( μ ≠ 4)
Podobno transformacije koordinat
(r, θ, Φ, t) → (r, θ, -Φ, t)
in
(r, θ, Φ, t) → (r, -θ, Φ, t)
dajejo naslednje povezave - spet so nediagonalne komponente 0:
gμ3= 0 ( μ ≠ 3)
gμ2 = 0 ( μ ≠ 2)
Če vse to združimo in tako dobimo splošni predpis za sferični tenzor za nediagonalne člene, ki so 0:
gμν = 0 ( μ ≠ ν )
in zato mora biti metrika ds2 zapisana le z diagonalnimi členi:
ds2 = g11d r2 + g22dθ2 + g33dΦ2 + g44dt2
kjer so štiri metrične komponente neodvisne od časovne koordinate t (po statični predpostavki).
Poenostavitev komponent
Na vsaki hiperpovršini pri "konstantnem" t (sočasnost), konstantnem kotu θ in konstantnem kotu Φ (tj. pri vsaki radialni liniji - mirovanje ob krogli
v poljubni radialni oddaljenosti od površine, oz. od težišča)
naj bi bil g11 odvisen zgolj od r (zaradi sferične simetrije). Zato je g11 funkcija ene spremenljivke:
g11 = A ( r )
Podoben argument, uporabljen za g44, kaže, da je:
g44 = B ( r )
Na hiperpovršinah pri konstantnem t in konstantnem r se zahteva, da je to metrika na 2D-sferi
(recimo krožeči satelit na orbiti r, kjer ure tečejo enakomerno in se dolžina poti, loka, dl zapiše
kot):
dl2 = r02( dθ2 + sin2 θ dΦ2 )
Če izberete eno od teh hiperpovršin (na primer tisto s polmerom r0 ), metrične komponente,
omejene na to hiperpovršino (ki jo označimo z g22
in g33
)
bi morala biti nespremenjena pri rotacijah čez θ in Φ (spet zaradi sferične simetrije).
Primerjava oblik metrike na tej hiperpovršini daje:
g22(dθ2 + (g33/g22)dΦ2 )
= r02( dθ2 + sin2 θ dΦ2 )
kar seveda pomeni:
g22 = r02
in g33 = r02 sin2 θ
To pa seveda mora veljati za vsako hiperpovršino; torej lahko zapišemo,
g22 = r2
in g33 = r2 sin2 θ
Drug intuitiven način, da vidimo, da morata biti g22 in g33
enaka kot za ravni prostor-čas, je raztezanje ali stiskanje elastičnega materiala
na sferično simetričen način (radialno) ne bo spremenilo kotne razdalje med dvema točkama.
Tako lahko metriko postavimo v obliki:
ds2 =A(r)dr2 + r2dθ2 + r2sin2 θ dΦ2
+ B(r)dt2
Kontravariantni tenzor gij dobimo z izračunom inverzne matrike elementov gij.
V našem primeru so komponente kontravariantnega metričnega tenzorja po diagonali
naslednje:
grr = 1/A, gθθ = 1/r2,
gΦΦ = 1/(r sin θ)2, gtt = 1/B
s členoma A in B, za katera še ne poznamo funkcijske odvisnosti od r.
Upoštevajte, da če bi bila A ali B na neki točki enaka nič, bi bila metrika na tej točki singularna (bi recimo limitirala
oddaljenost proti neskončnosti ali bi imeli opravka z neskončno gostoto, gravitacijo, kar pa ni mogoče).
Izračun Christoffelovih simbolov
Riccijev tenzor, kot smo to že pokazali pri Riemannovi geometriji,
se zapiše s Christoffelovmi simboli Γ:
Γlkj = (glm/2)(
∂gmk/∂xj
+
∂gmj/∂xk
-
∂gkj/∂xm
)
=
(glm/2)(
gmk, j
+
gmj, k
-
gkj, m
)
Z uporabo zgornje metrike izračunajmo, zapišimo Christoffelove simbole,
kjer so indeksi ( 1 , 2 , 3 , 4 ) =
(r, θ, Φ, t). Znak ' označuje totalni odvod funkcije
(skupni odvod po vseh spremenljivkah).
Γlkj = (glm/2)(
∂gmk/∂xj
+
∂gmj/∂xk
-
∂gkj/∂xm
)
Za vajo izračunajmo recimo Christoffelove člene za Γrrr = A'/(2A)
in ΓrΦ Φ = - r sin2 θ/A.
Zapišimo še kontravariantne člene (vsi ostali nediagonalni
členi metričnega tenzorja so nič - kar zelo olajša
računanje):
grr = 1/A, gθθ = 1/r2,
gΦΦ = 1/(r sin θ)2, gtt = 1/B
Γrrr = (grr/2)(
∂grr/∂xr
+
∂grr/∂xr
-
∂grr/∂xr
)
Γrrr =
(1/(2A))(∂A/∂r + ∂A/∂r - ∂A/∂r) = (1/(2A))∂A/∂r = A'/(2A)
ΓrΦΦ
= (grr/2)(
∂grΦ/∂xΦ
+
∂grΦ/∂xΦ
-
∂gΦΦ/∂xr
)
ΓrΦΦ
= (1/(2A))( ∂(grΦ = 0)/∂Φ + ∂(grΦ = 0)/∂Φ - ∂(r2 sin2 θ)/∂r)
=
(1/(2A))(0 + 0 - 2r sin2 θ) = - r sin2 θ/A
ΓrΦ Φ = - r sin2 θ/A
ΓΦΦ θ = (gΦΦ/2)(
∂gΦΦ/∂xθ
+
∂gΦθ/∂xΦ
-
∂gΦθ/∂xΦ
)
ΓΦΦ θ = (1/(2r2sin2 θ))(
∂(r2sin2 θ)/∂θ = 2r2 cos θ sin θ)
+
(∂gΦθ = 0)/∂Φ
-
(∂gΦθ = 0)/∂Φ
)
ΓΦΦ θ = cos θ/sin θ = cot θ
Za vajo izračunajte še ostle Christoffelove izraze - rabimo jih za izračun
Riccijevega tenzorja ukrivljenosti - iščemo namreč metriko ob sferičnem telesu.
Zapišimo torej samo od nič različne Christoffelove člene, izračune.
Γtt r = Γtr t = B'/(2B) ,
Γrr r = A'/(2A) ,
Γrt t = -B'/(2A) ,
ΓΦ Φ θ = ΓΦθ Φ = cos θ/sin θ = cot θ ,
Γrθθ = - r/A , ΓrΦ Φ = - r sin2 θ/A ,
Γθ θ r =
Γθ r θ = ΓΦr Φ = ΓΦ r Φ = 1/r ,
ΓθΦΦ = - sin θ cos θ .
Ostali Christoffelovi členi so 0.
Sledi še tenzorski matrični zapis zgornjih izračunov, za indekse ob Γ velja ( 1 , 2 , 3 , 4 ) = (r, θ, Φ, t).

Uporaba enačb polja za iskanje členov A(r) in B(r)
Za določitev A in B se uporabijo enačbe vakuumskega polja, Ricijev tenzor ukrivljenosti Rαβ, za katerega v tem primeru velja (utemeljili na začetku izpeljave):
Rαβ = 0
Zato, ker velja, da je v tem primeru Riccijev tenzor enak 0, ga zapišimo
s Christoffelovmi simboli in uporabimo za določitev členov A in B:
Rij = Rkikj
= ∂lΓlji
- ∂jΓlli +
Γllλ Γλji
- Γljλ Γλli = 0
kjer je parcialni odvod označen z indeksom, spremenljivko, ki se uporablja za odvajanje.
Riccijeva tenzorska ukrivljenost Rab je v danih koordinatah diagonalna:
Rtt = - B'( A'/A - B'/B + 4/r)/(4A) - (B'/A)'/2 = 0 ,
Rrr = - ( B'/B )'/2 - ( B'/B )2/4 + A'( B'/B + 4/r )/(4A) = 0 ,
Rθθ = 1 - (r/A)' - r( A'/A + B'/B )/(2A) = 0 ,
RΦΦ = sin2 (θ) Rθθ = 0
A' pomeni odvod metričnega člena A' = dA/dr in B' = dB/dr. Pri reševanju enačb kmalu dobimo
povezavo:
A(r)B(r) = konst.
A postopek še nekoliko razdelajmo.
Samo tri enačbe polja so neodvisne (četrta enačba je samo sin2 θ krat tretja enačba Rθθ)
in po poenostavitvi dobimo tri enačbe:
4 A ' B2 - 2 r B ” A B + r A ' B ' B + r B '2 A = 0
- 2 r B ” A B + r A ' B ' B + r B '2 A - 4 B ' A B = 0
r A ' B + 2 A2 B - 2 A B - r B ' A = 0
Če odštejemo prvo in drugo enačbo, dobimo odvoda A' in B' pomnožena s funkcijo B ali A. V
bistvu vsoto omenjenih produktov, ki je nič, od koder sledi:
A'B + AB' = 0 ⇒ A ( r ) B ( r ) = K
kjer je oznaka K različna od nič realna konstanta. Če vstavimo AB = K
ter A'B = -AB' v tretjo enačbo, dobimo naslednji izraz:
rA' = A(1 - A)
Nekoliko razdelajmo to diferencialno enačbo, oziroma izvedimo integral.
rdA/dr = A(1 - A)
∫dA/(A(1 - A)) = ∫dr/r
∫dr/r = ∫(1- A + A)dA/(A(1 - A)) = ∫dA/A + ∫dA/(1 - A)
ln(r) + C1 = ln(A) - ln(1 - A) + C2
Kjer je konstanta ln(S) = C1 - C2
in velja: ln(r) + ln(S) = ln(A) - ln(1 - A)
ln(Sr) = ln(A/(1 - A))
Sr = A/(1 - A)
zveza ima splošno rešitev:
f(r) = A = 1/( 1 + 1/(Sr) )
A dodali smo še
neko neničelno realno konstanto S, zaradi konsistence končne
metrike ob masivnem sfernem telesu (recimo klasičnega gravitacijskega zakona in
prehoda na raven prostor pri skromni gravitaciji) in tudi zaradi enot (ta konstanta S nič ne vpliva
na integral, je pa fizikalno nujna). Zato se metrika za statično, sferično simetrično vakuumsko rešitev zdaj zapiše v naslednji obliki:
ds2 =
+ dr2/(1 + 1/(Sr)) + r2(dθ2 + sin2θ dΦ2)
+ Kdt2(1 + 1/(Sr))
Tako dobimo člena A(r) in B(r), kjer pa moramo še poiskati konstanti S in K:
g11 = A = 1/(1 + 1/(Sr))
g44 = B = K(1 + 1/(Sr))
Pri iskanju rešitev za K in S upoštevajmo še, da je prostor-čas, ki ga predstavlja zgornja metrika,
asimptotično raven, tj. ko je r → ∞,
se metrika približa metriki Minkowskega, prostorsko-časovna mnogoterost pa je podobna prostoru Minkowskega.
Uporaba približka šibkega gravitacijskega polja za iskanje K in S
Člen (ga bomo še poiskali) g44 = B = -c2 + 2GM/r se ob predpostavki,
da se gibanje zgodi daleč stran od črne luknje (r se približa pozitivni neskončnosti),
preobrazi
v metriko Minkowskega. Kako torej pridemo do te predpostavke?
Geodezijske črte metrike
(dobljene, ko je ds ekstrem: 0 = δ∫(ds/dt)dt) se morajo v neki meji
(npr. proti "neskončni" svetlobni hitrosti) ujemati z rešitvami Newtonovega gibanja
(npr. dobljene z Lagrangeevimi enačbami v klasični mehaniki).
Metrika mora biti v limiti omejena tudi na raven prostor Minkowskega [ct, x, y, z],
ko masa, ki jo predstavlja masivno telo M, izgine iz enačb. Tako lahko zapišemo znan pogoj ekstrem:
0 = δ∫(ds/dt)dt = δ∫(Ek + Epg)dt
(kjer je Ek kinetična energija in Epg
potencialna energija zaradi gravitacije).
Konstanti K in S sta v celoti določeni z nekaj različicami povedanega pristopa.
Primerjava metrik ravnega prostora in ukrivljenega prostora ob masivni sferi.
Zapis kvadrata hitrosti preko Schwarzschildovo metrike se glasi:
c2 = c2(1 - rs/r)(dt/dτ)2
– (dr/dτ)2/(1 - rs/r) - r2(dΩ/dτ)2
Tako kot v četvercu brez teže, se tudi v iskani metriki ob masivni sferi skriva energija.
Če zgolj še enkrat osvežimo spomin in zapišemo velikost četverca
gibalne količine brez gravitacije in naredimo še primerjavo s četvercem
z gravitacijo za zelo oddaljenega opazovalca, ki ne čuti gravitacije,
potem velja (upoštevajmo pa že znano Einsteinovo enačbo za polno energijo
delca E = γmc2):
(cdτ, 0) ⇔ dXμ = (cdt, dx) = (cdt, vdt) = (cγdτ, vγdτ)
= dτ(cγ, vγ)
(c, 0) ⇔ vμ = (cγ, vγ) = (cE/(mc2), vγ)
– četverec brez gravitacije ( γ = E/(mc2) )
(c, 0) ⇔ (c(1 - rs/r)1/2(dt/dτ), ...) – prvi člen metrike z gravitacijo, od zgoraj
[- še zapis celotnega četverca za gravitacijo
(cdτ, 0, 0, 0)
⇔ dXμ = ( c(1 - rs/r)1/2dt, dr/(1 - rs/r)1/2 , rdϑ , r sin ϑ dφ )
]
Primerjava nam da za prvi člen obeh četvercev naslednji izraz:
E/(mc2) = (1 + 1/(Sr))1/2(dt/dτ)
Tako dobimo energijo delca še v gravitacijskem polju za oddaljenega opazovalca.
Kot smo torej recimo pri posebni relativnosti dobili klasično kinetično energijo za majhne hitrosti napram svetlobni, ko velja:
E = mc2γ = mc2/(1 – v2/c2)1/2
≈
mc2(1 + v2/(2c2))
= mc2 + mv2/2.
Ker je tokrat časovni del metrike B povezan s členom Kdt2(1 + 1/(Sr)), in ker moramo pri šibki gravitaciji
(recimo, da telo miruje na Zemlji dt/dτ = γ = 1) dobiti klasično potencialno energijo
Ep = -Gmmd/r,
in ker je, po primerjavi s posebno relativnostjo
Ep ∝ mdc2(1 + 1/(Sr))1/2,
bomo za majhno vrednost 1/(Sr) dobili
Ep ∝ mdc2(1 + 1/(2Sr)) ∝ mdc2(1 - Gm/(rc2) )
= mdc2 - Gmdm/r .
Iz aproksimacije šibkega polja za metriko torej pridemo do rezultata (za časovni del metrike velja, da mora biti pred njim negativen predznak):
g44 = K (1 + 1/(Sr)) = - c2 + 2Gm/r = - c2(1 - 2Gm/(c2r) )
kjer je G gravitacijska konstanta, m (ali M) masa gravitacijskega vira in c svetlobna hitrost. Izkaže se, da
primerjava z zgornjo enačbo vrne rešitev za iskana koeficienta K in S:
K = - c2 in 1/S = - 2Gm/c2
Zato na koncu velja!
Za radialno komponento r velja
A(r) = 1/(1 - 2Gm/(c2r) )
in časovni del B(r) = -c2(1 - 2Gm/(c2r) ) .
Tako lahko Schwarzschildovo metriko ds končno zapišemo v obliki:
ds2 =
dr2/(1 - 2Gm/(c2r) ) + r2(dθ2 + sin2θ dΦ2)
- c2dt2(1 - 2Gm/(c2r) )
- ali zapis metrike v bolj pričakovanem zaporedju, s časovnim energijskim členom na levi:
ds2 =
- c2dt2(1 - 2Gm/(c2r) )
+ dr2/(1 - 2Gm/(c2r) ) + r2(dθ2 + sin2θ dΦ2)
Upoštevajmo še, da velja:
2Gm/c2 = rs
- to je definicija Schwarzschildovega polmera (dogodkovnega horizonta
črne luknje) za telo z maso m,
zato lahko Schwarzschildovo metriko ds zapišemo še v alternativni obliki:
ds2 =
- c2dt2(1 - rs/r )
+ dr2/(1 -rs/r ) + r2(dθ2 + sin2θ dΦ2)
kar kaže, ta metrika postane singularna, ko se približujemo obzorju dogodkov (to je r → rs).
Metrična singularnost ni fizična (čeprav obstaja resnična
fizična singularnost pri r = 0, kar lahko pokažemo z uporabo ustrezne koordinatne transformacije
(npr. Kruskal–Szekeresov koordinatni sistem).
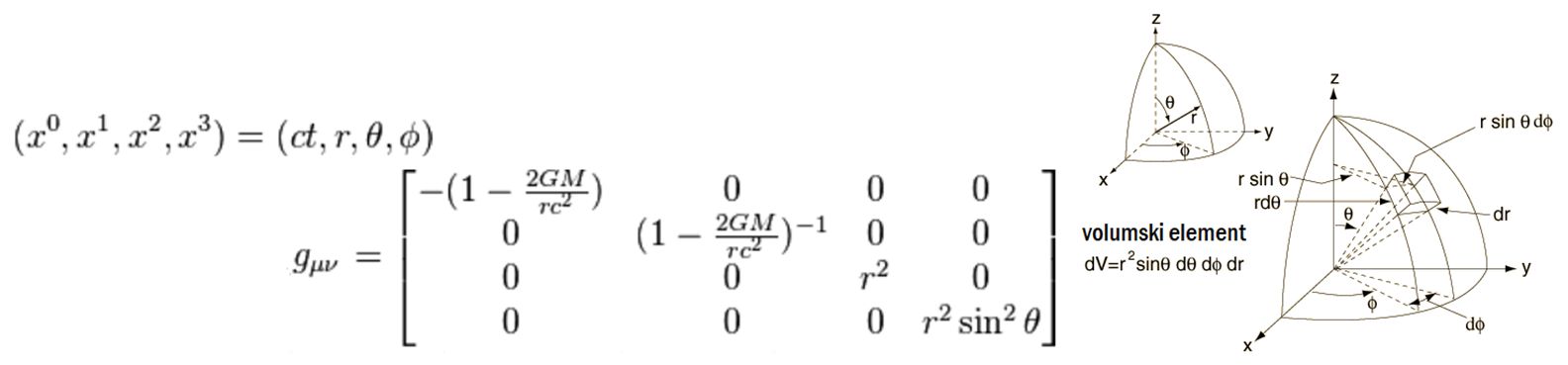

Še zapis metričnega tenzorja gμν homogene sfere (recimo zvezde) z maso M
in izračun metrike
ds2 = gijdxidxj
= ∑ijg(x)ijdxidxj
ds2 =
- c2dt2(1 - 2Gm/(c2r) )
+ dr2/(1 - 2Gm/(c2r) ) + r2(dθ2 + sin2θ dΦ2)
preko metričnega tenzorja gij in vektorja diferenciala koordinat, recimo (cdt,
dr, dθ, dΦ). Indeksi za opis koordinat in členov tenzorjev
so tukaj stvar dogovora - ali so i, j ali μ, ν ...
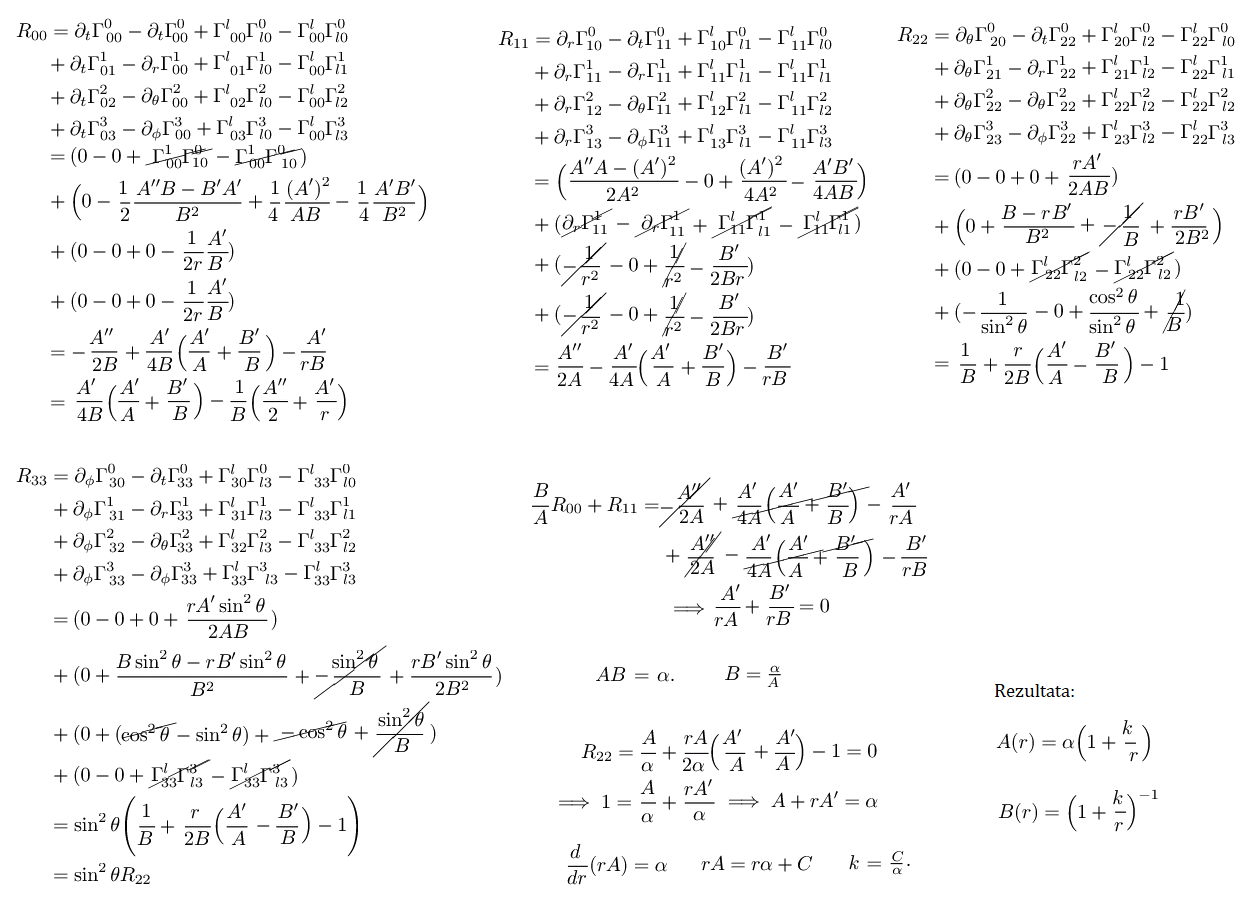
Še enaka izpeljava (zgoraj), le da sta člena A in B obrnjena (indeksi pa tečejo
od 0 do 3) in metrika ima klasični
vrstni red:
ds2 = A(r)dt2 + B(r)dr2 + r2dθ2 + r2sin2 θ dΦ2
VIR:
https://www.researchgate.net/publication/330765008_Schwarzschild_Solution
Poudarek je na Riccijevem tenzorju. Če i ≠ j, potem so ti členi tenzorja Rij = 0.
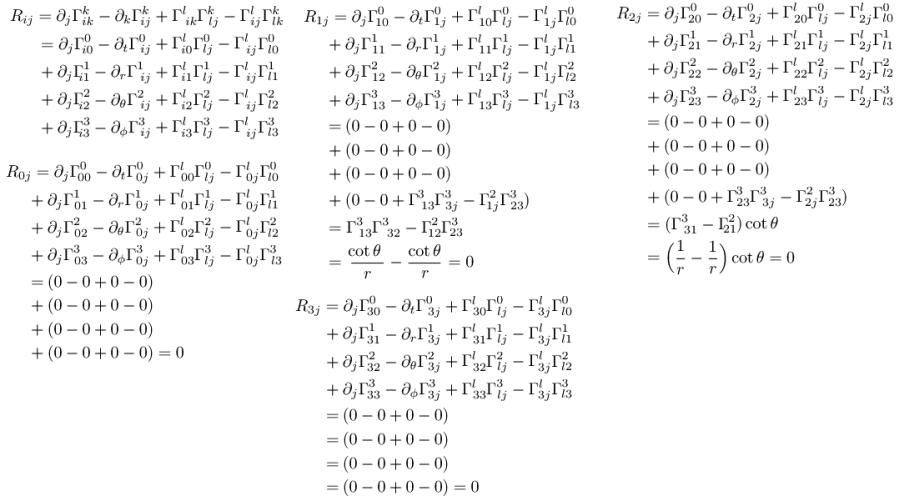
Še izračun nediagonalnih členov Riccijevega tenzorja ob masivni sferi, ko velja
Rij = 0, če i ≠ j. Indeksi tečejo
od 0 do 3 - primer zgoraj.
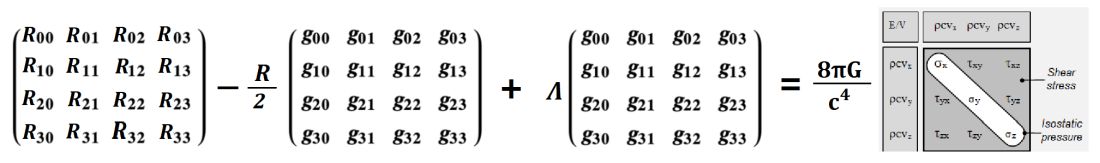
Zapis Einsteinovih enačb polja s tenzorji v matrični obliki - ta zapis je didaktično najbolj
razumljiv. Tako si tudi lažje predstavljamo, kako se v tenzorski matrični obliki zapišejo
členi Rij Riccijevega tenzorja (ukrivljenosti).
Alternativna izpeljava metrike ob sferi z delno uporabo klasične fizike v posebnih primerih preko Euler–Lagrangeeve enačbe
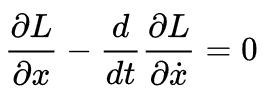

Schwarzschildovo metriko je mogoče izpeljati tudi z uporabo znane fizike za krožno orbito
in začasno stacionarno točkovno maso.
V Lagrangejevi funkciji nastopata dve ohranitveni količini, vrtilna količina (L) in energija (E).
Tako bomo tudi preverili ali so bila naša uvodna razmišljanja o energiji pravilna (v splošni relativnosti).
Spet začnimo z neznano metriko ob sferi s koeficientoma A in B, ki ju skušamo poiskati preko zakonov gibanja:
ds2 = A(r)dr2 + r2dθ2 + r2sin2 θ dΦ2
+ B(r)dt2
Za člen r2dθ2 + r2sin2 θ dΦ2
bomo privzeli
konstanten θ, recimo 90 °, tako, da nam ostane v bistvu člen r2dΦ2.
ds2/dτ2 =
-c2
=
A(r)dr2/dτ2 + r2dΦ2/dτ2
+ B(r)dt2/dτ2
- zapis še skrajšajmo, kjer r˙ pomeni časovni odvod r˙ = dr/dτ in Φ˙ = dΦ/dτ ter t˙ = dt/dτ
-c2 = ds2/dτ2 = s˙2 =
A(r)r˙2 + r2Φ˙2
+ B(r)t˙2
Sedaj uporabimo Euler–Lagrangeovo enačbo za integral dolžine loka od τ1 do τ2
J = ∫(-ds2/dτ2)1/2dτ .
Ker je po definiciji ds/dτ
konstanten, lahko integrand zamenjamo kar s kvadratom invariante
(ds/dτ)2,
- ker je enačba E–L popolnoma enaka, če se integrand pomnoži s katero koli konstanto.
Iz variacije - pogoja δS = 0, ohranitve skupne energije, v tem primeru računamo
najkrajšo pot ds v gravitaciji masivnega telesa, sledijo
Euler–Lagrangeeve enačbe parcialnih odvodov:
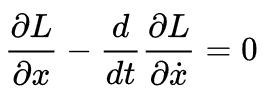
Odvajajmo (ds/dτ)2 po vseh spremenljivkah r, Φ, t in
kot razberemo iz Euler–Lagrangeeve enačbe parcialnih odvodov, še po
r˙, Φ˙, t˙ in seveda še po τ po zgornjem pravilu
( velja A' = dA/dr, B' = dB/dr, r˙ = dr/dτ, Φ˙ = dΦ/dτ, t˙= dt/dτ in recimo
dA/dτ = (dA/dr)(dr/dτ) = A'r˙, enako velja za člen B ).
-c2 = (ds/dτ)2 = A(r)r˙2 + r2Φ˙2
+ B(r)t˙2
-------------------------------------------------------------
**1** Najprej odvajajmo po r in r˙ ter τ:
∂[(ds/dτ)2]/∂r = A'(r)r˙2 + 2rΦ˙2 + B'(r)t˙2
∂[(ds/dτ)2]/∂r˙ = 2A(r)r˙ + 0 + 0
IN
d(∂[(ds/dτ)2]/∂r˙)/dτ = 2(dA(r)/dr)(dr/dτ)r˙ + 2A(r)r¨ =
2A'(r)r˙2 + 2A(r)r¨
Iz poudarjenih odvodov, ki jo po pravilu izenačimo, dobimo enačbo L1 spodaj.
-------------------------------------------------------------
**2** Odvajajmo še po Φ in Φ˙ ter τ:
∂[(ds/dτ)2]/∂Φ = 0 + 0 + 0
∂[(ds/dτ)2]/∂Φ˙ = 0 + r22Φ˙ + 0
IN
d(∂[(ds/dτ)2]/∂Φ˙)/dτ = 4rr˙Φ˙ + 2r2Φ¨
Iz poudarjenih odvodov, ki jo po pravilu izenačimo, dobimo enačbo L2 spodaj in enačbo krajšamo še z 2.
-------------------------------------------------------------
**3** Odvajajmo še po t in t˙=dt/dτ ter τ:
∂[(ds/dτ)2]/∂t = 0 + 0 + 0
∂[(ds/dτ)2]/∂t˙ = 0 + 0 + 2B(r)t˙
IN
d(∂[(ds/dτ)2]/∂t˙)/dτ = 2(dB(r)/dr)(dr/dτ)t˙ + 2B(r)t¨ = 2B'(r)r˙t˙ + 2B(r)t¨
Iz poudarjenih odvodov, ki jo po pravilu izenačimo, dobimo enačbo L3 spodaj in enačbo krajšamo še z 2.
Če torej uporabimo enačbo E–L za J (odvodi zgoraj)
s spremenjenim integrandom, dobimo naslednje izraze (spomnimo se: r˙ pomeni časovni odvod dr/dτ, A' pa odvod po radiju dA/dr in
t˙ je odvod dt/dτ):
L1) A'(r)r˙2 + 2rΦ˙2 + B'(r)t˙2 = 2A'(r)r˙2 + 2A(r)r¨
L2) 0 = 2rr˙Φ˙ + r2Φ¨
L3) 0 = B'(r)r˙t˙ + B(r)t¨
kjer (˙) pika označuje odvod glede na lastni čas τ.
Enačba L2 je 2rr˙Φ˙ + r2Φ¨ = 0 in jo v bistvu
lahko zapišemo v še skrajšani obliki odvoda produkta d(r2Φ˙)/dτ = 0.
Kar pa je zelo pomenljiva oblika, zakaj?
Ker velja
r2Φ˙ = konst. = L/m
- to je torej kar dokaz o ohranitvi vrtilne količine,
ki jo podaja drugi Keplerjev zakon, ki se glasi:
Zveznica med Soncem in planetom opiše v enakih časovnih intervalih enake ploščine.
Ohranja se torej ploščinska hitrost (to je ohranitev vrtilne količina na maso).
Kepler je bil najmanj 200 let pred časom - izpeljal je namreč ohranitev vrtilne količine, a te pojme in zakonitosti
so teoretično utemeljili veliko pozneje.
A za nas je bolj pomembna enačba L1, saj iščemo člena A in B. Razdelajmo jo.
V krožni orbiti je r˙ = r¨ = 0, zato je prva enačba E–L zgoraj enakovredna
2rΦ˙2 + B'(r )t˙2 = 0 ⇔ B'(r) = -2rΦ˙2/t˙2 = -2r(dΦ/dt)2
Lastni čas τ zgoraj se okrajša, zakaj (?)
- velja Φ˙ = dΦ/dτ in t˙ = dt/dτ, od koder sledi
Φ˙/t˙ = (dΦ/dτ)/(dt/dτ) = dΦ/dt.
Tretji Keplerjev zakon gibanja planetov nam bo, zaradi člena (dΦ/dt)2,
tako pomagal pri iskanju končne rešitve členov A in B in s
tem Schwarzschildove metrike ds pri masivnih sferičnih telesih.
Zapišimo torej tretji
Keplerjev zakon:
T2/r3 = 4π2/(G(M + m)).
V krožni orbiti je perioda T enaka 2π/(dΦ/dt), tako po poenostavitvi dobimo pomemben izraz:
(dΦ/dt)2 = GM/r3
Ker je 'točkovna' masa telesa m zanemarljiva v primerjavi z maso osrednjega telesa M.
Torej je
B'(r) = dB/dr = -2GM/r2
in integracija te povezave vrne ∫dB = ∫-2GMdr/r2 rezultat:
B(r) = 2GM/r + C ,
kjer je C neznana konstanta integracije. C je mogoče določiti, če privzamemo, da je centralna masa
M = 0 in je B(r) = 2GM/r + C = C,
v tem primeru je prostor-čas raven, velja torej že znana metrika Minkowskega
ds2 = -c2dτ2 = -c2dt2 + dx2
+ dy2 + dz2 = -c2dt2 + dr2
+ r2(dϑ2 + sin2ϑ dφ2)
----------- spodnji člen B(r)dt2 je večinoma na prvem mestu metrike ds ----------
ds2 = A(r)dr2 + r2dθ2 + r2sin2 θ dΦ2
+ B(r)dt2
- in tako preko primerjave velja B(r) = -c2 = 0 + C. Torej je C = - c2,
na koncu pa dobimo iskani izraz B(r):
B(r) = 2GM/r - c2 = c2(2GM/(c2r) - 1 ) = c2(rs/r - 1)
= -c2(1 - rs/r) .
Ko telo začasno miruje, velja r˙ = 0
in Φ˙ = 0.
Prvotna metrična enačba (
-c2 = (ds/dτ)2 = A(r)r˙2 + r2Φ˙2
+ B(r)t˙2 ) postane kar preprosta enakost:
t˙2 = - c2/B(r)
in prva enačba E–L (glejte L1) zgoraj dobi obliko
A(r) = B'(r)t˙2/(2r¨) = -c2B'(r)/(2r¨B(r)).
Ko telo za trenutek miruje, je r˙˙ gravitacijski pospešek
r˙˙ = -MG/r2.
Torej na koncu dobimo še člen A(r):
A(r) = (-2GM/r2)( - c2/(2MG/r - c2) ) ( - r2/(2MG) )
= 1/(1 - 2MG/(rc2) ) = 1/(1 - rs/r) .
Tako lahko Schwarzschildovo metriko ds spet zapišemo v že znani obliki:
ds2 =
dr2/(1 - 2GM/(c2r) ) + r2(dθ2 + sin2θ dΦ2)
- c2dt2(1 - 2GM/(c2r) )
- ali zapis metrike v bolj pričakovanem zaporedju, s časovnim energijskim členom na levi:
ds2 =
- c2dt2(1 - 2GM/(c2r) )
+ dr2/(1 - 2GM/(c2r) ) + r2(dθ2 + sin2θ dΦ2)
Kje pa se skriva energija sistema (recimo delca v ukrivljenem prostor-času) E?
Energija se v relativnosti pripiše recimo delcu in je definirana glede na njegovo mirovno maso, hitrost glede na opazovalca
in glede na ukrivljenost prostor-časa. V limiti skromne gravitacije in hitrosti (glede na svetlobno), pričakujemo seveda
klasični zapis kinetične in potencialne energije.
Energija se nahaja v tistem členu, ki se s časom (t) ne spreminja, velja za zaprt sistem (brez zunanjih sil)
- in so hkrati njeni podčleni odvisni od razdalje (r). Za primerjavo se spomnimo še na klasično ohranitev
vsote potencialne in kinetične energije delca.
Razčlenimo torej še enačbo L3,
velja 0 = B'(r)r˙t˙ + B(r)t¨ .
Kar lahko zapišemo tudi kot
d(Bt˙)/dt = 0
Od koder sledi, da je produkt
Bt˙= Bdt/dτ = konst.
Kaj nam pomeni ta člen? Ohranitev vrtilne količine smo že spoznali v enačbi L2,
v enačbi L3 pa je zapisana ohranitev energije sistema delec m ob masivnem okroglem telesu (rec. zvezdi) z maso M.
Ta konstanta je energija E/(mc2) za opazovalca na zvezdi. Ker je
B = -c2( 1 - 2GM/(c2r) ) in je torej
d(Bt˙)/dt = -c2d[( 1 - 2GM/(c2r) )t˙]/dt = 0 , velja:
konstanta =
( 1 - 2GM/(c2r) )t˙ = (1 - 2GM/(c2r) )dt/dτ = E/(mc2) - energija delca
m za opazovalca na (ob) zvezdi z maso M
Zgornji izraz je zelo pomemben.
Za oddaljenega opazovalca, kot smo že omenili v prejšnjih poglavjih, pa je energija kar:
E/(mc2) = (1 - 2GM/(c2r) )1/2dt/dτ
- oziroma, kot smo že zapisali v prejšnjih poglavjih
E = mc2(1 - 2GM/(c2r) )1/2γ = mc2(1 – rs/r)1/2γ
Tako smo lepo fenomenološko po zahtevnosti zaokrožili pomen Schwarzschildove metrike ds preko štirih različnih poti do nje
(
[1] preko klasične potencialne energije pri majhni gravitaciji
Ep = -GMm/r,
[2] ubežne hitrosti
v2 = 2GM/r,
[3] izpeljava preko
Einsteinovih enačb polja,
[4] izpeljava s pomočjo
Euler–Lagrangeevih enačb za najkrajšo pot
)
in pokazali na konsistentnost
njenih členov v povezavi z energijo, vrtilno količino in časom.
Delec torej zmeraj uboga (njegova pot, to je ds - metrika) zunanje sile, energije ali bolj korektno, ukrivljenost prostor-časa in
oboje je povezano v celoto - izhaja eno iz drugega (sile, energije določajo pot, ukrivljenost prostor-časa;
in pot ter čas pa nam spet povesta vse o energijah - silah, lokalnih časih, ukrivljenosti prostora).
Prehojena pot je zaobjemala srednješolski nivo in se je postopoma prelevila tudi na višji nivo - a najvažnejše je seveda razumevanje
pojavov (zato smo uporabili delno tudi preproste razlage). Zelo poučno in pomembno za človeški razvoj, bodočnost je
recimo razumevanje trajektorij fotonov ob masivnih telesih (gravitacijsko lečenje),
potem gravitacijski rdeči premik, uporabo
Schwarzschildove metrike v navigacijskem sistemu satelitov GPS, razumevanje gravitacijskih valov ...

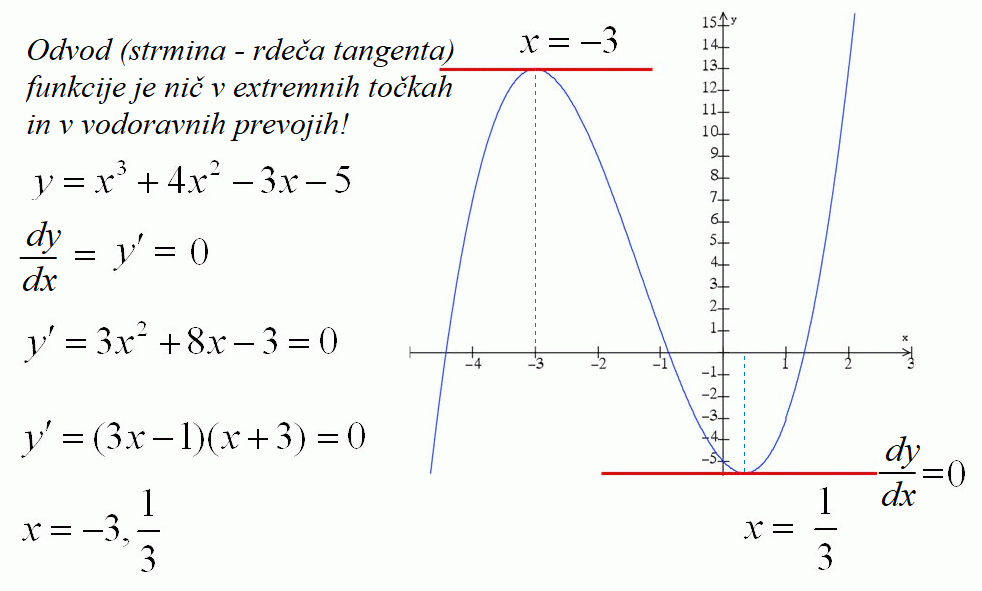
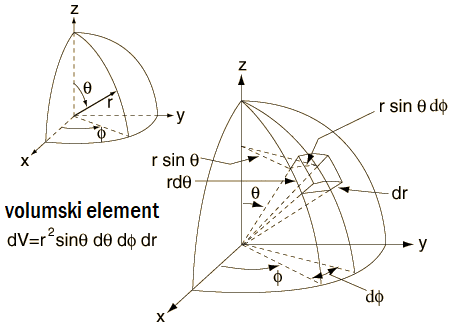
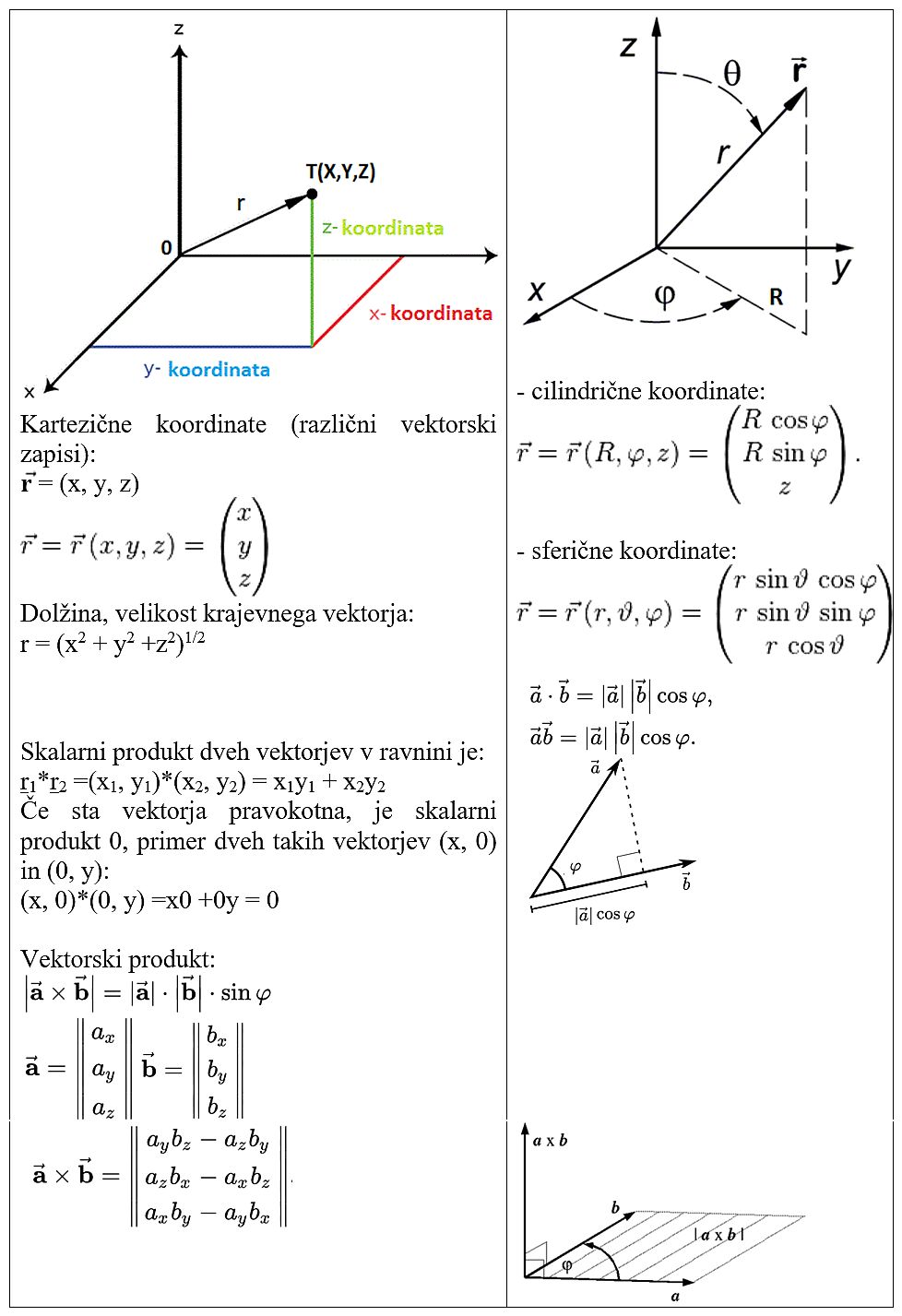
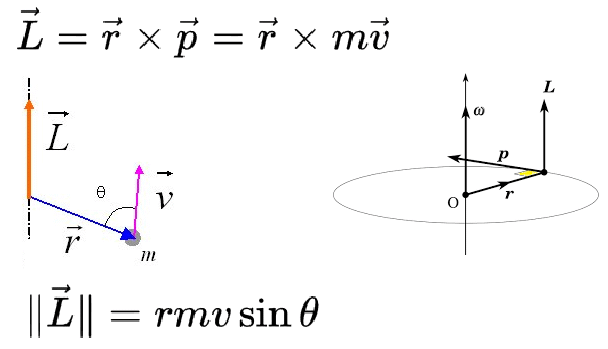

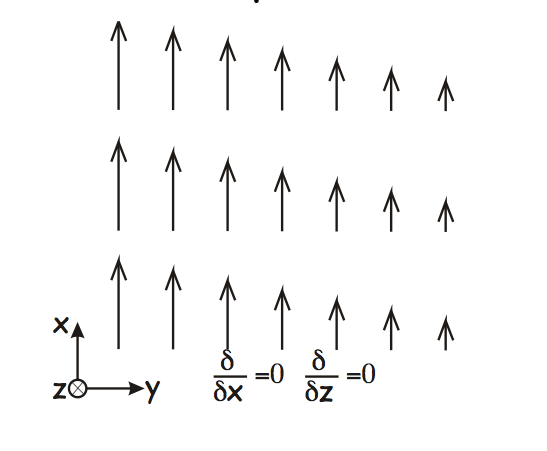



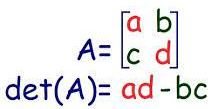
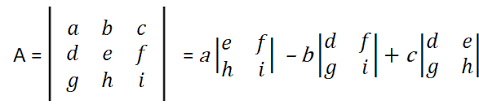
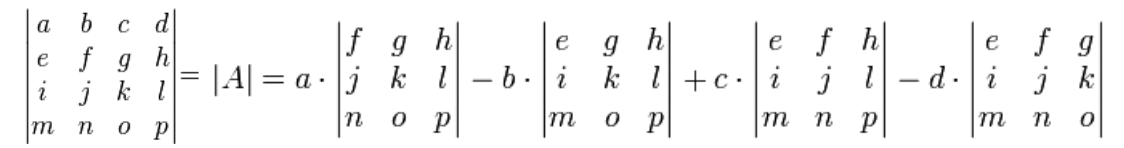


gij = | 1 0 |
| 0 r2|
gij = | 1 0 |
| 0 1/r2|





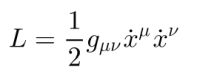
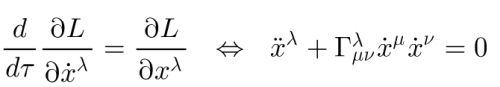
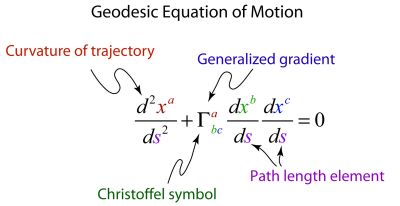




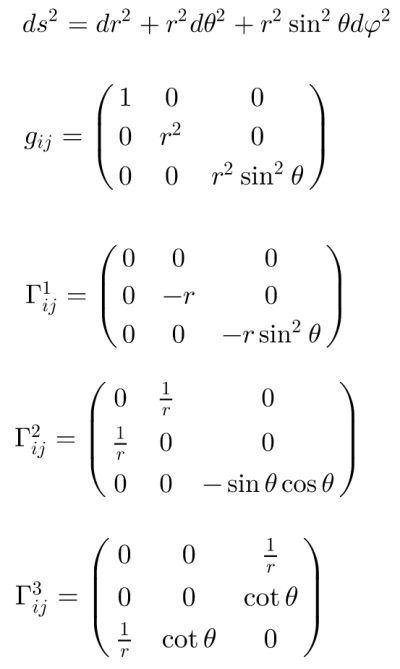
Še kratek skok v znanstveno fantastiko, ki to ni - je neke vrsta kritika naših navad,
večinoma upravičena, kdaj pa tudi protislovna - ker kdaj človeka obravnava preveč resno, kritično,
protislovno, smo le del vesolja!
Štoparski vodnik po galaksiji ("The Hitchhiker's Guide to the Galaxy", Douglas Adams - BBC Radio 4 between 1978 and 1980 ...)
- še zmeraj zelo brana satirična znanstvenofantastična knjiga
Povzetek
Artur Dent je v začetku knjige v šoku, saj je spoznal, da bo ostal brez hiše,
zaradi izgradnjo nove avtoceste, obvoznice. Vendar se izkaže,
da je Zemlja še bolj "nepomembna" – uničena bo s strani Vogonov
zaradi izgradnje kozmološke avtoceste,
ki bo omogočila hitre potniške poti skozi galaksijo
(Vogoni so rasa neprijetnih in birokratskih tujcev).
Pred tem pa Artur še izve, da Ford Prefect, njegov prijatelj (ki je pravzaprav
vesoljski raziskovalec, raziskuje za
"The Hitchhiker's Guide to the Galaxy") izhaja drugega planeta,
torej ni človek, ampak vesoljski tujec - nezemljan.
Ford ga reši pred uničenjem in skupaj se odpravita v vesolje.
Artur in Ford sta pobegnila na vesoljsko ladjo "Heart of Gold",
kjer srečata nenavadne like, vključno z Zaphodom Beeblebroxom
(Beeblebrox je Fordov ekscentrični polbrat),
galaktičnim predsednikom (ki je odločen, da bo vesolje obvladoval po svoji volji),
Trilliano (Tricia McMillan), še eno človeško bitje, žensko, ki je preživelo uničenje Zemlje,
in Marvina, depresivnega robota z visokim IQ, ki trpi zaradi popolne apatije in nihilizma.
Arthur še izve, da je bila Zemlja pravzaprav velikanski superračunalnik,
ki bi naj ugotovil, kakšno je v resnici bilo prvotno vprašanje.
Ustvaril (Zemljo kot računalnik) ga je še en superračunalnik,
Deep Thought - z odgovori katerega pa niso bili zadovoljni.
Zemljo (ki je bila v resnici računalnik za iskanje
prvotnega vprašanja) so uničili Vogoni tik preden so bili njeni izračuni končani.
Med absurdnimi prigodami iščejo
odgovore na “temeljna vprašanja življenja, vesolja in sploh vsega".
Na ta vprašanja odgovori računalnik Deep Thought, ki po milijonih letih izračunavanja
poda odgovor: 42. Težava je v tem, da nihče ne ve, kakšno je dejansko vprašanje.
Glavni liki in poudarki so:
Hitchhiker’s Guide to the Galaxy -> galaktični vodič (elektronska knjiga - zelo vizionarski pristop avtorja)
Heart of Gold -> vesoljska ladja
Infinite Improbability Drive -> pogon ladje
Don’t Panic -> glavno geslo vodiča
Arthur Dent -> glavni lik (Zemljan)
Ford Prefect -> avtor prispevkov za vodič
Zaphod Beeblebrox -> predsednik Galaksije
Marvin -> depresivni robot
Glavne misli Štoparskega vodnika po Galaksiji:
The universe is absurd, life has no predefined meaning, and the only
sensible response is curiosity, humor, and not panicking.
Prevod v slovenščino:
Vesolje je absurdno, življenje nima vnaprej danega smisla,
edini razumni odzivi pa so: radovednost, humor in to, da ne paničarimo.
1.
- znanost brez smiselnih vprašanj je prazna
- ljudje pogosto iščejo odgovore, ne da bi razumeli vprašanje
2. Ne jemlji vesolja preveč resno
Vesolje je absurdno
Logika pogosto odpove
Humor je edini razumen odziv na kaos
3. Nič panike!
DON’T PANIC
Glavno življenjsko vodilo
Panika nikoli ne pomaga,
saj panika v kaotičnem svetu samo poslabša stvari.
Brisača je najpomembnejši predmet v vesolju
(Douglas Adams se šali, da je brisača najbolj uporaben predmet, ki ga ima lahko medgalaktični štopar.
V knjigi lahko brisačo uporabiš za:
ogrevanje na mrzlih planetih
zaščito pred soncem ali plini
jadranje po pesku
signaliziranje v sili
kot orožje (če je mokra)
kot oblačilo ali odejo
kot psihološko oporo)
4. Majhnost človeka
Človeštvo ni središče vesolja
Zemlja je nepomembna (in uničena brez ceremonije)
Ego je kozmično smešen
5. Tehnologija ni enako modrost
Superračunalniki obstajajo
Ampak ne razumejo življenja
Inteligenca brez razumevanja je nevarna
6. Smisel življenja ni enostaven
Če je odgovor preprost, je vprašanje napačno
Smisel ni v rešitvi, ampak v iskanju
7. Humor kot filozofija
Satira je način razmišljanja
Smeh razkriva resnico
Nesmisel je pogosto najbolj iskren opis sveta
8. Svobodna volja in naključje
Veliko dogodkov je naključnih
Vesolje nima “načrta”
A kljub temu obstaja pomen, ki ga ustvarimo sami
9. Kritika birokracije
Vogoni, obrazci, postopki (npr. Vogoni, ki recitirajo poezijo in so izjemno birokratski).
Sistem brez smisla je bolj nevaren kot zlo
10. Človečnost
Prijaznost, čaj, prijateljstvo
Majhne stvari imajo največjo težo
Še povedna misel
Življenje je nerazumljivo, vesolje absurdno — zato se smej, razmišljaj in ne pozabi brisače.
-----------------------------
Zakaj številka 42?
42 je odgovor na ultimativno vprašanje o življenju, vesolju in sploh vsem.
Izračuna ga superračunalnik Deep Thought po 7,5 milijona let.
Težava:
nihče ne ve, kakšno je vprašanje
Simbolni pomen
Iskanje odgovorov brez razumevanja vprašanja
Kritika slepe vere v:
znanost
tehnologijo
“velike resnice”
Adams pokaže, da:
številka sama po sebi ne pomeni nič
pomen nastane šele v kontekstu
* 42 je simbol nesmisla absolutnih odgovorov.
Zakaj ravno 42?
Adams je sam rekel, da ga je izbral naključno
prav zato deluje:
vesolje ni dolžno biti smiselno
pomen ni v številu, ampak v interpretaciji
Riba Babel (Babel fish)
Kaj je to?
Majhna rumena riba
Če jo daš v uho, razumeš vse jezike v vesolju
Simbolni pomen
A. Jezik ni enako razumevanje
Čeprav vsi govorijo isti jezik:
se še vedno ne razumejo
konflikti ostajajo
Težava ni v jeziku, ampak v nerazumevanju, egih in interesih.
B. Satira na religije
V knjigi obstaja “dokaz”:
Babel fish je tako popolna
da dokazuje obstoj Boga
Bog pa zaradi tega izgine (paradoks)
Kritika logičnih dokazov v metafiziki.
C. Tehnologija kot lažna rešitev
Tehnologija odpravi ovire
ne pa nesporazumov
Skupno sporočilo obeh simbolov
Simbol Sporočilo
42 Odgovori brez vprašanj so prazni
Babel fish Razumevanje ni isto kot prevajanje
Povzetek!
Vesolje nam lahko da odgovore in jezike, govor, a smisel in razumevanje moramo ustvariti sami.
------
Pripomba na zadnjo tezo - je v določeni meri v protislovju s trditvijo, da je vesolje absurdno ...,
ljudje smo le del vesolja in imamo vse atribute, ki so imanentni vesolju
(smisel in razumevanje je torej del vesolja).


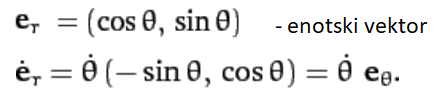
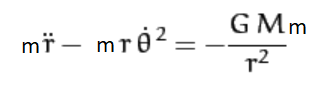

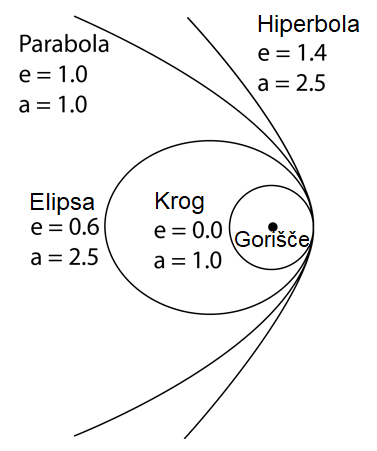
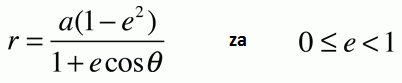
| stožnica | enačba | ekscentričnost (e) | "semi-latus rectum" (l) (kdaj tudi p) | goriščni parameter (p) (kdaj tudi k) | krog | x2 + y2 = a2 | 0 | a | ∞ | elipsa | x2/a2 + y2/b2 = 1 | (1 - b2/a2)1/2 | b2/a = a(1 - e2) | b2/(a2 - b2)1/2 = l/e | parabola | y2 = 4ax | 1 | 2a | 2a | hiperbola | x2/a2 - y2/b2 = 1 | (1 + b2/a2)1/2 | b2/a | b2/(a2 + b2)1/2 |
 |
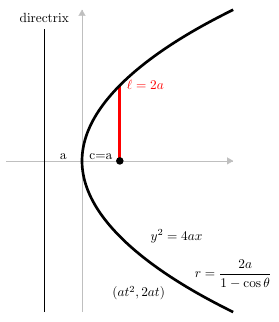 |
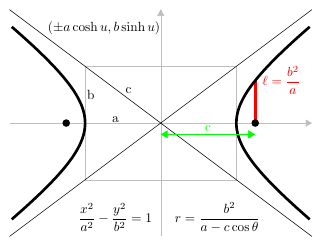 |
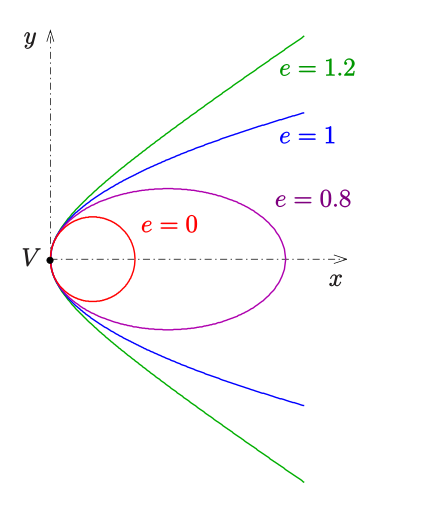
|
Prereze stožnic z osjo x kot simetrijsko osjo, z enim ogliščem v izhodišču (0, 0)
in enakim "semi-latus rectum-um" p, je mogoče predstaviti z enačbo v naslednji obliki:
y2 = 2px + (e2 - 1)x2 , e ≥ 0 , z ekscentričnostjo e. Za e = 0 je stožnica krog, za 0 < e < 1 elipsa, za e = 1 parabolo z enačbo y2 = 2 p x , za e > 1 hiperbola (glejte sliko). |


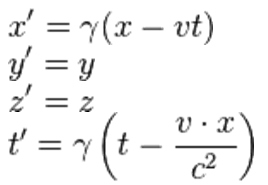

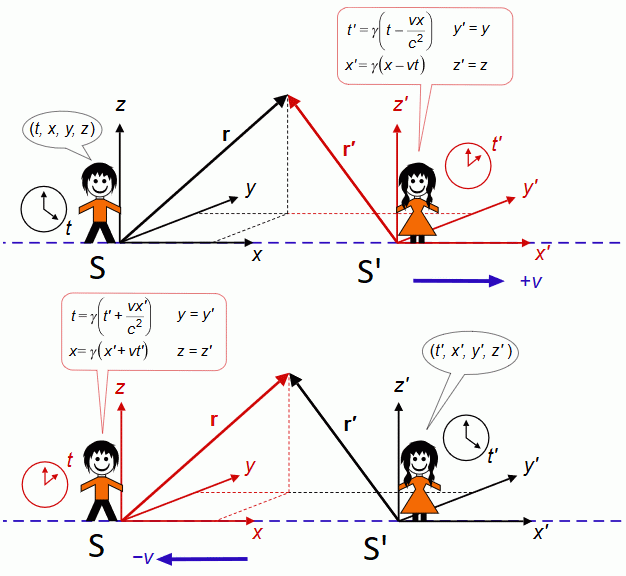

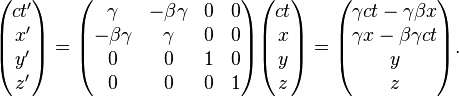
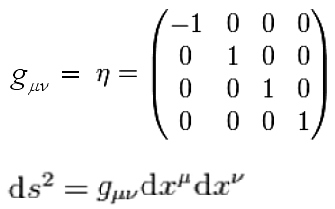
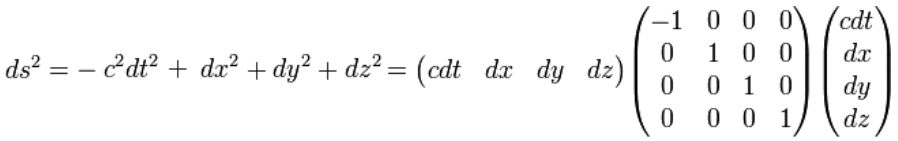

Metrični tenzor gμν ob masivnem homogenem sferičnem telesu.
Po diagonali ima
vrednosti:
-(1 - 2GM/(c2r), 1//(1 - 2GM/(c2r), r2,
r2 sin2ϑ
- vsi ostali členi bodo 0 (gre za sferično telo).
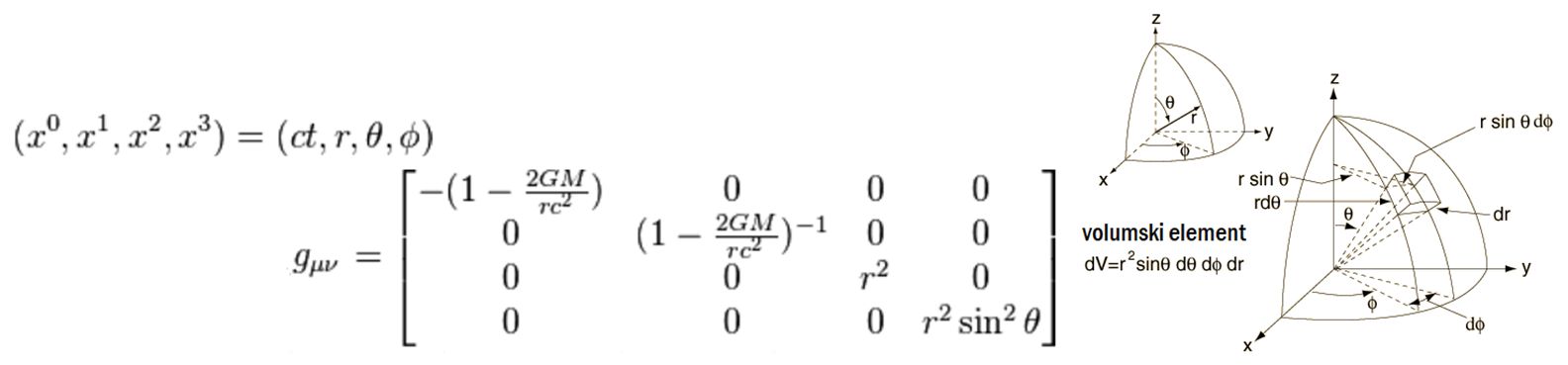
Za sferične koordinate torej velja vektor
dxμ = (dx1, dx2 , dx3 , dx4) = ( cdt, dr, dϑ, dφ )
in naslednji zapis metrike ds2 (4d Pitagorov izrek ob masivni sferi,
ds2 = gμνdxμdxν =
∑μνg(x)μνdxμdxν
):

V bistvu je metrični tenzor gμν sestavljen iz ravnega prostora brez gravitacije ημν
(po diagonali ima člene -1, 1, 1, 1 - vsi ostali so nič)
in ukrivljenosti zaradi gravitacije hμν. Tako velja:
gμν = ημν + hμν
Metrika dS v sferičnih koordinatah se torej zapiše v naslednji obliki:
ds2 = ds'2 = dSτ2 = -(cdτ)2
= -c2dt2 (1 - 2GM/(c2R))
+ dR2/(1 - 2GM/(c2R))
+ R2dϑ2 + R2sin2ϑ dφ2
Še primer deformacije prostora dveh bližnjih (tesno povezanih) masivnih zvezd,
ki krožita okrog skupnega težišča in tako oddajata znatne gravitacijske valove,
ki ga opišemo s tenzorjem, kjer se rotacija dogaja v ravnini (x, y), pravokotni na
smer širjenja valovanja. Če usmerimo os z v smer širjenja
valovanja, ima metrični tenzor v (sicer) ravnem prostoru
obliko:
|-1 0 0 0 |
| 0 1+h+ hx 0 |
gμν = | 0 hx 1-h+ 0 |
| 0 0 0 1 |
pri čemer se odmik 'h' harmonično spreminja
h+ = A+ cos(kz - ωt) in hx = Ax cos(kz - ωt)
|-1 0 0 0 ||cdt|
| 0 1+h+ hx 0 ||dx |
ds2 = gμνdxμdxν = (cdt,dx,dy,dz)| 0 hx 1-h+ 0 ||dy | = -(cdt)2 + (1+h+)dx2 + (1-h+)dy2 + 2hxdxdy + dz2
| 0 0 0 1 ||dz |



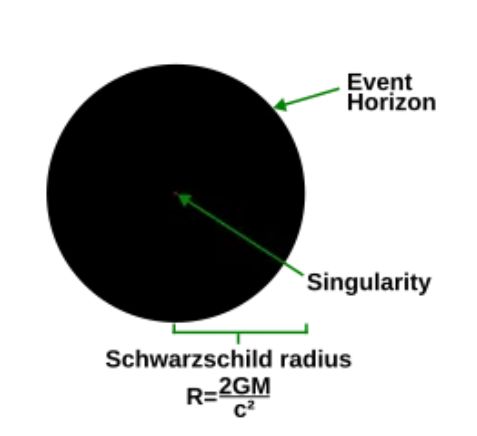


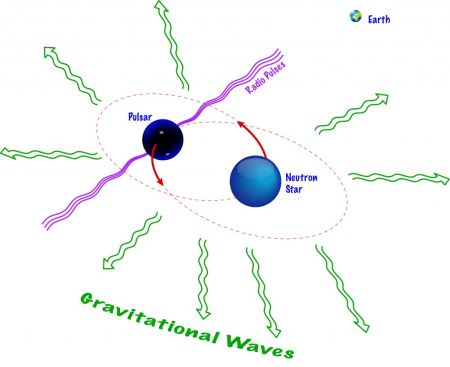
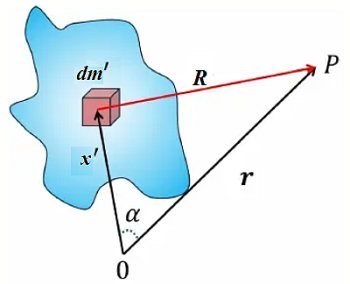
| cos(2ωt) + 1/3 sin(2ωt) 0 |
Iij = | sin(2ωt) 1/3 - cos(2ωt) 0 |
| 0 0 -2/3 |
Za matriko zgoraj glejte stran 14 na naslovu: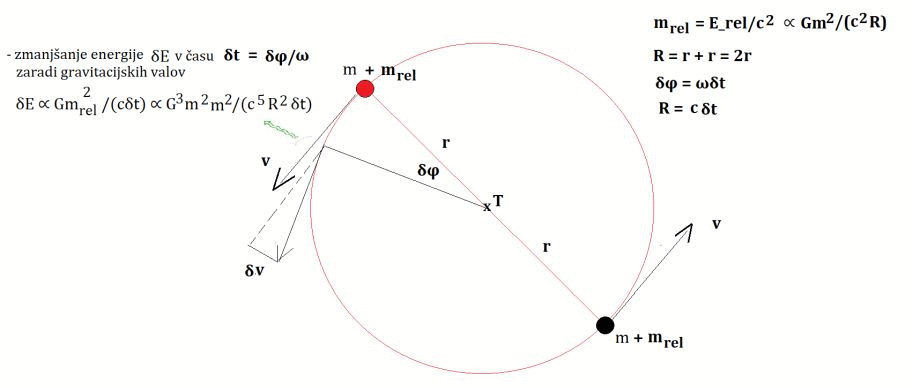

LIGO je kratica za: Laser Interferometer Gravitational-Wave Observatory.
VIR: https://www.quora.com/How-fast-do-gravity-waves-travel
Detektor LIGO gravitacijskega polja meri spremembo
gravitacijskega polja preko deformacije telesa v dveh
prečnih smereh. Če ne vemo, v kateri smeri je izvir polja,
jo lahko določimo tako, da poiščemo smer, v kateri je
razteg telesa največji. V primerjavi z dipolno anteno, pri
kateri je velikost sile na enega od nabojev kar eE, je
občutljivost gravitacijskega detektorja veliko manjša; v
električnem primeru je sorazmerna z R–2, v gravitacijskem
pa z R–3, če je R razdalja med telesom in izvirom polja.
Vidimo, da poleg šibkosti gravitacijske sile v primerjavi z
elektromagnetno, dodatno težavo pri detekciji gravitacijskega
valovanja predstavlja relativno slabša občutljivost
detektorja.
Tudi pri tako dolgih krakih (4 km) so na začetku najmočnejši gravitacijski valovi spremenili razdaljo med koncema
krakov le za največ približno 10-18 m (to je ocena velikosti kvarka, daleč pod polmerom protona).
Kolaboracija LIGO pa je tako uspela
meriti tenzorski odmik
od ravnega prostora h z natančnostjo večjo od h ~ 5 · 10-22
(saj velja δL = h*L = 4000 m * 5 · 10-22 ~ 10-18 m).
Kjer h meri odmik tenzorja od ravnega prostora, recimo h = 2GM/(c2r)
- to je znan izraz za sferično telo, rec. zvezde (srečali pri izpeljavi Schwarzschildove metrike).
Deformacijo prostora opišemo s tenzorjem v ravnini, pravokotni na
smer širjenja valovanja. Če usmerimo os z v smer širjenja
valovanja, ima metrični tenzor v (sicer) ravnem prostoru
obliko
|-1 0 0 0 |
| 0 1+h+ hx 0 |
gμν = | 0 hx 1-h+ 0 |
| 0 0 0 1 |
pri čemer se odmik 'h' harmonično spreminja
h+ = A+ cos(kz - ωt) in hx = Ax cos(kz - ωt)

|-1 0 0 0 ||cdt|
| 0 1+h+ hx 0 ||dx |
ds2 = gμνdxμdxν = (cdt,dx,dy,dz)| 0 hx 1-h+ 0 ||dy | = -(cdt)2 + (1+h+)dx2 + (1-h+)dy2 + 2hxdxdy + dz2
| 0 0 0 1 ||dz |


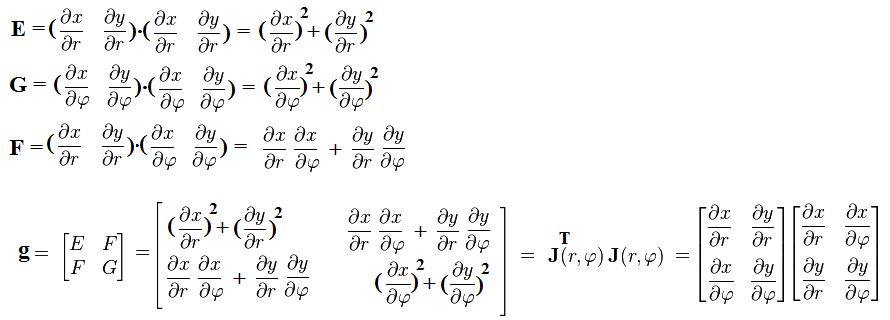


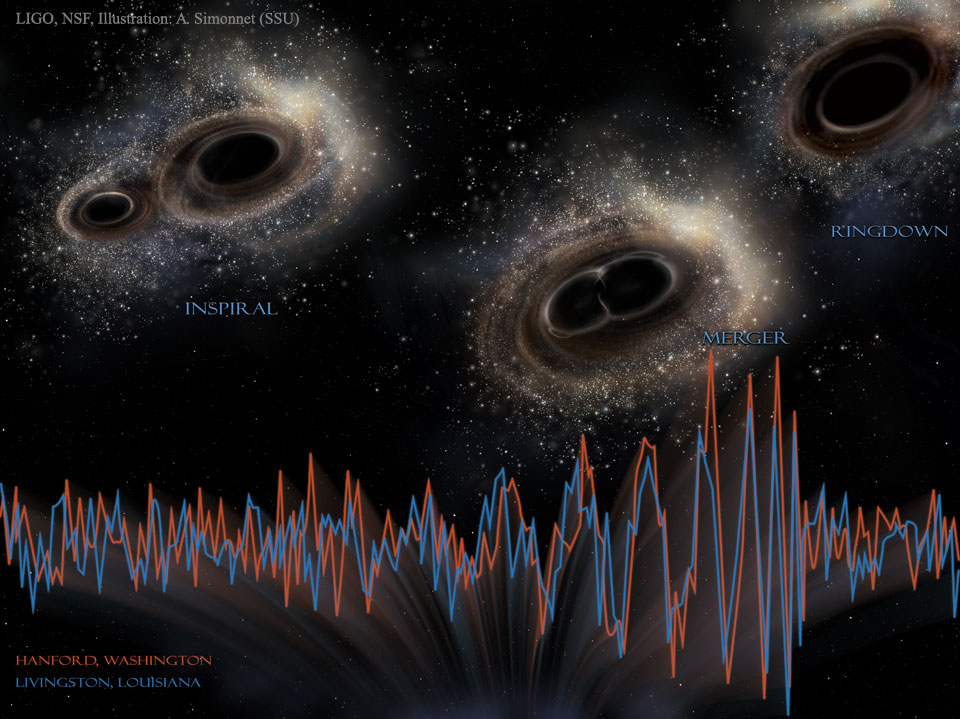
Pojasnilo: Gravitacijsko sevanje je bilo odkrito neposredno. Do zdaj prva detekcija je bila narejena hkrati z obema napravama projekta Laser Interferometer Gravitational-Wave Observatory (LIGO) v Washingtonu in Louisiani, prejšnjega septembra. Po številnih preverjanjih realnosti ima danes objavljeno odkritje zanesljivost 5-sigma. Izmerjeni gravitacijski valovi se ujemajo s pričakovanimi iz dveh črnih lukenj, ki se v oddaljeni galaksiji spajata po nepovratni spirali v novo črno luknjo, ki za trenutek zaniha in se umiri. Pojav, ki ga je napovedal Einstein je zgodovinsko odkritje in temeljni kamen človeškega razumevanja gravitacije in temeljev fizike. Obenem je tudi do zdaj najbolj neposredna detekcija črnih lukenj. Gornja ilustracija prikazuje dve spajajoči črni luknji, z močjo signala dveh detektorjev v času 0,3 sekunde, ki je naložen čez spodnji del slike. Pričakovana bodoča odkritja z naprednim LIGO in drugimi detektorji gravitacijskih valov ne bodo le potrdila spektakularno naravo teh meritev, ampak človeštvu obetajo nov načine pogleda in raziskovanja našega vesolja.
VIR: http://apod.fmf.uni-lj.si/ap160211.html


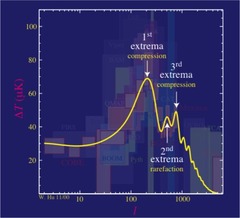
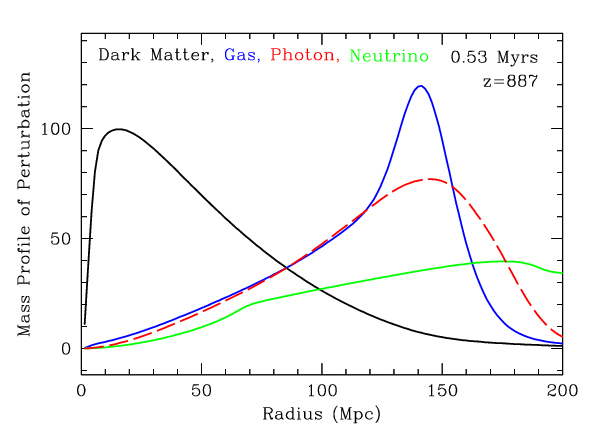

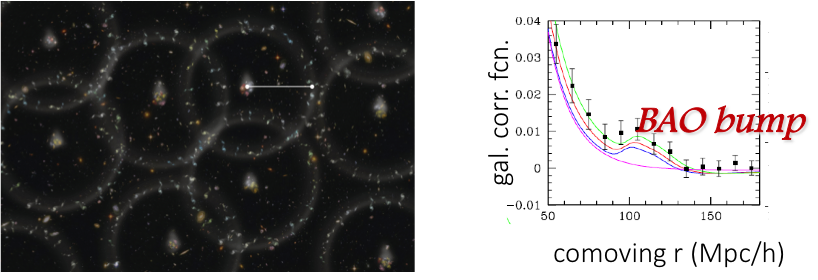
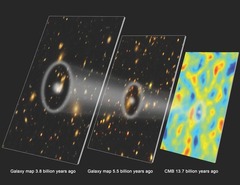



Zorko Vičar
Korona pomlad 2021 (delno objavljeno sep. 2022, spletne objave že leta 2015)