.gif)



.gif) |
 |
 |
 |
Katere izračune in ocene o Sončevih mrkih lahko podamo mladim v srednji šoli?
Med mrkom 21. avg. 2017, se je nabralo kar nekaj gradiva za primerjavo z ostalimi mrki. Mrki pa so lahko tudi primerno izhodišče za predstavitev zgodovinskega procesa iskanja lege Zemlje v vesolju in hkrati iskanja odgovorov, kateri fizikalni opis sveta je primernejši. A o tem v prihodnji v prihodnji številki Spike.
Tokrat bomo ocenili širino sence mrka, temperaturo med mrkom, hitrost in trajanje mrka, smer gibanja sence, koliko časa bomo iz Zemlje še lahko opazovali ta prelep pojav (Luna se namreč vsako leto oddalji od Zemlje za okrog 4 cm). Te ocene nam bodo odstrle ozadje dinamike mrka, Lune, Zemlje, nekatere manj znane pojave, ki so del izjemnega fenomena, ki je (in še) dobesedno spreminjal znanost, zgodovino, pogled na svet – tudi odnose med ljudmi.
Energijska bilanca med mrkom
K energijski bilanci na globalni ravni delno prispevajo ura mrka, letni čas, nadmorska višina, podnebni pas – geografska lega poti, bistveno stanje ozračja in tla ter seveda dolžina mrka. Med mrkom Luna počasi zakriva Sonce. Nekje na polovici zakritja (odvisno od začetne temperature tal in stanja atmosfere) izsev tal na površini črte mrka postne večji od prispele sončne energije. Temperaturi tal in posledično ozračja zato začneta padati. Hitrost padanja temperature je odvisna od toplotne kapacitete tal (suha tla se hitreje hladijo – recimo puščava), nadmorske višine in v največji meri od vlage v zraku. Vodna para je izrazit toplogredni plin, saj odlično absorbira dolgovalovno sevanje iz tal in ga delno spet seva nazaj proti tlom (zato so oblačne noči toplejše kot jasne – velja za noči brez vetra).
Primerjalna tabela mrkov glede na temperaturo, relativno vlago in gostoto vodne pare. Gostota vodne pare je izračunana iz lastnih meritev temperature in relativne vlage. Meritve so seveda potekale v senci.
Tem.[°C] R. Vla.[%] Gos. H20 pare[g/m3] Sončev mrk ------- --------- ------------------- --------------------------- 26 26 6 2017-08-21 S. MRK maks. tem. ***** 20 35.5 6 2017-08-21 S. MRK min. tem. ***** 25 52 12 1999-08-11 S. MRK maks. tem. 21 65 12 1999-08-11 S. MRK min. tem. 18.5 62 10 2006-03-29 S. MRK maks. tem. 16.5 71 10 2006-03-29 S. MRK min. tem.
Zgornja tabela kaže, da je zdaleč najmanj zračne vlage bilo prav med mrkom 21. 8. 2017 v kraju Casper, ZDA - nadmorska višina 1600 m (nizka vlaga je značilna za visoke lege, recimo za Kredarico). Gostota vodne pare (zaokrožena na gram/m3) je bila leta 2017 le 6 g/m3, na Madžarskem 1999 pa kar 12 g/m3 (2x več). Kot smo že omenili, je vodna para izjemno dober absorber dolgih valov, ki jih seva površina Zemlje (je najvažnejši toplogredni plin v atmosferi, ki nam omogoča življenje - toplogredni plini torej niso zmeraj škodljivi, le preveč jih ne sme biti). Če je pare manj, se torej površina Zemlje in zrak hitreje ohlajata. Na kratko povzeto - med Sončevim mrkom v okolici kraja Casper, 1600 m nad morjem, so nizka vlaga, visoka nadmorska lega in suha tla botrovali k nekoliko nepričakovani dinamiki poteka temperature – glede na prejšnje mrke. Temperatura zraka je med letošnjim mrkom padla kar za 6 °C ali celo več glede na ostale vire. Direktno primerljiva sta samo poletna mrka 1999 in 2017, mrk 2006 je bil namreč opazovan spomladi ob morju – drug letni čas in drugačni pogoji. Pri vseh mrkih je razvidno, da se absolutna količina vlage v zraku med mrkom praktično ni spreminjala (gostoti vodne pare sta glede na minimalno in maksimalno temperaturo pri vseh Sončevih mrkih ohranjali enako vrednost) - torej se zračna masa, glede razmerij med plini, na kraju meritev v povprečju ni zamenjala (razen občasnega mešanje zraka zaradi zmernega vetra, kar se opazi na grafih v nihanju temperature in relativne vlage).
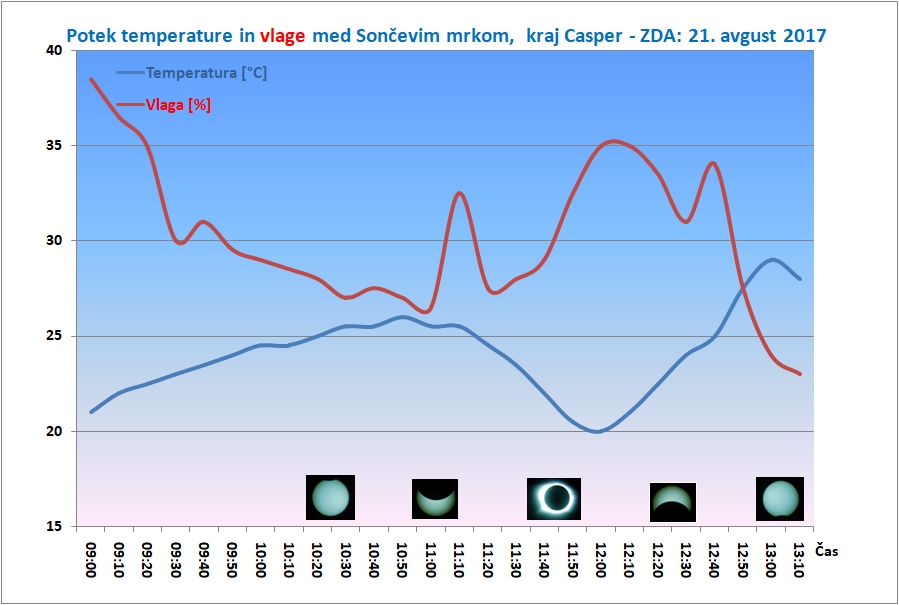
Slika: Potek temperature in vlage med Sončevim mrkom - Casper, ZDA: 21. 8. 2017. Graf je podoben tistima iz Madžarske in Turčije, a z nekaj pomembnimi razlikami. Temperatura je ob tem mrku padla kar za 6 °C,
oziroma celo za 9 °C, če bi upoštevali temperaturo po polni fazi mrka. Ob upoštevanju ocenjenega dnevnega hoda temperature brez mraka pa je padec okrog 8 °C. Temperatura ob mrku na Madžarskem je padla zgolj za slabe 4 °C (1999)
in samo za 2 °C v Turčiji (2006). Tudi absolutna in relativna vlaga sta bili letos precej nižji. Očitno je izsevanje učinkovitejše na višjih nadmorskih višinah (1600 m višine, manj vlage, manj in redkejše ozračje).
Zanimivo je tudi, da so letos (sploh prvič) znanstveniki v laboratoriju NOAA (National Oceanic and Atmospheric Administration) v Boulderju (Colorado) dodali pot mrka v računalniški prognostični model imenovan »High-Resolution Rapid Refresh« ali »HRRR«. V centralni do 115 km široki liniji mrka je model napovedal zmanjšanje temperature med 2,8 in 6,7 °C. Meritve, ki sem jih izvedel v Casperju, potrjujejo njihovo uspešno prognozo. Lep uspeh fizikov modelarjev.
Ocena padca efektivne dnevne temperature Zemlje
Naredimo še poučno oceno, za koliko lahko zaradi mrka pade efektivna temperatura celotne Zemlje v enem dnevu. Rezultat bo nekoliko nepričakovan. Pri tem si bomo pomagali z rojakom Jožefom Stefanom, oziroma z njegovim zakonom o sevanju črnega telesa (j = σ*T4). Stefan je prvi na svetu pravilno izračunal površinsko temperaturo Sonca, za nas najpomembnejše zvezde, ki nam pošilja svetlobo življenja.

Slika: Jožef Stefan (* 24. marec 1835, Sveti Peter pri Žrelcu,
sedaj predel Celovca, † 7. januar 1893, Dunaj). Z meritvijo toplotne
prevodnosti plinov je Stefan spoznal, da je le absolutna temperatura
lahko merilo za kinetično energijo delcev (mv2/2 = 3kT/2 ).
Bil je tudi prvi, ki je sprevidel, da brez absolutne temperature ni moč
razumeti toplotnega sevanja teles, kar je rezultiralo v njegov zakon o
sevanju črnega telesa
(j = σ*T4). Brez njegovega zakona o sevanju ni moderne
astronomije. Svoje razumevanje kinetične teorije atomskih delcev v povezavi
s temperaturo, je prenesel tudi na svojega imenitnega učenca L. Boltzmanna,
ki je uspešno nadaljeval Stefanovo delo. Med počitnicami je mladi Stefan učil
mamo pisati in brati - res izjemna gesta sina mlinarja in mlinarce, v mladosti
je bil tudi poet – a je njegovo poezijo neutemeljeno raztrgal F. Levstik ...
Tabela časovnega poteka mrka 21. Avg. 2017 od Pacifika čez ZDA do Atlantika. Začetek delnega mrka 15:46:48 UT Začetek popolnega mrka 16:48:32 UT Najdaljše trajanje mrka 18:26:40 UT Konec popolnega mrka 20:01:35 UT Konec delnega mrka 21:04:19 UT

Ker je Luna, glede na razdaljo do Sonca, praktično pri Zemlji, in ker tudi polsenca Lune večinoma med mrkom v celoti pade na površino Zemlje (vsaj med letošnjim), bomo od celotne dnevne energije, ki jo Zemlja prejme od Sonca v 24 urah, odšteli energijo, ki jo je nekaj ur zastirala Luna. Za letošnji mrk dolg tm = 4,3 ure (v čas je vključeno tudi polovično trajanje delnega mrka) je ta blokirana energija EL enaka produktu površine preseka
Lune (S = π*RL2), gostote energijskega toka iz Sonca (j) in časa mrka (tm):
EL = π*RL2*j*tm. Če privzamemo, da od gostote energijskega toka Sonca 1400 W/m2, doseže Zemljo nekje j=1000 W/m2, ostalo so v glavnem odboji, dobimo za blokirano energijo s strani Lune vrednost: EL = 1,47*1020 J. Energija, ki jo prejme Zemlja iz Sonca v td = 24 urah pa je:
EZ = π*RZ2*j*td = 111*1020 J. Te ‘ukradene’
Energije torej niti ni tako malo - ampak kar dober procent (1,3 %). Po Stefanovem zakonu (j = σ*T4) zapišimo še razmerje obeh energij in povprečnih
temperatur na četrto potenco. Velja:
(T/To)4 = 0.987. T je povprečna dnevna temperatura na dan mrka, To = 288 K pa za dan brez mrka (še pojasnilo, povprečna temperatura Zemlje To je za skoraj 10 °C višja od teoretične za črno telo in to predvsem zaradi toplogrednih plinov - vodne pare, ogljikovega dioksida in metana). Na dan mrka je tako ocena povprečne temperature Zemlje T = To*(0.987)1/4 = 287,1 K. To pomeni (288 K - 287,1 K) okrog 0,9 K nižja temperatura – kar pa sploh ni tako malo! Vemo pa, da na polni črti mrka temperatura pade kar za nekaj stopinj Celzija, lahko tudi blizu 10 °C (podobno vrednost smo tudi pomerili). Pa vendar – najverjetneje je učinek delnega zasenčenja Zemlje s strani Lune, razen na črti mrka, precej manjši od običajnih temperaturnih nihanj (oblačnost, vremenske fronte) in je v bistvu neopažen. Sploh pa so mrki zelo redki.
Je pa ta premislek, o energiji in temperaturi na dan mrka, bil zanimiv z vidika,
kako lahko že, na prvi pogled relativno zanemarljiv dejavnik (mrk), vpliva na
temperaturo Zemlje. Podobno je s toplogrednimi plini – a človeka ne bo neposredno
ugonobilo globalno segrevanje, ampak (najverjetneje) posledično dolgotrajno
onesnaževanje planeta (recimo hormonski motilci). Smo to, kar jemo – in kaj jemo,
dihamo, pijemo!?
Zakaj mrk, senca, potuje približno od zahoda proti vzhodu in s kakšno hitrostjo, koliko časa traja popolna faza mrka?
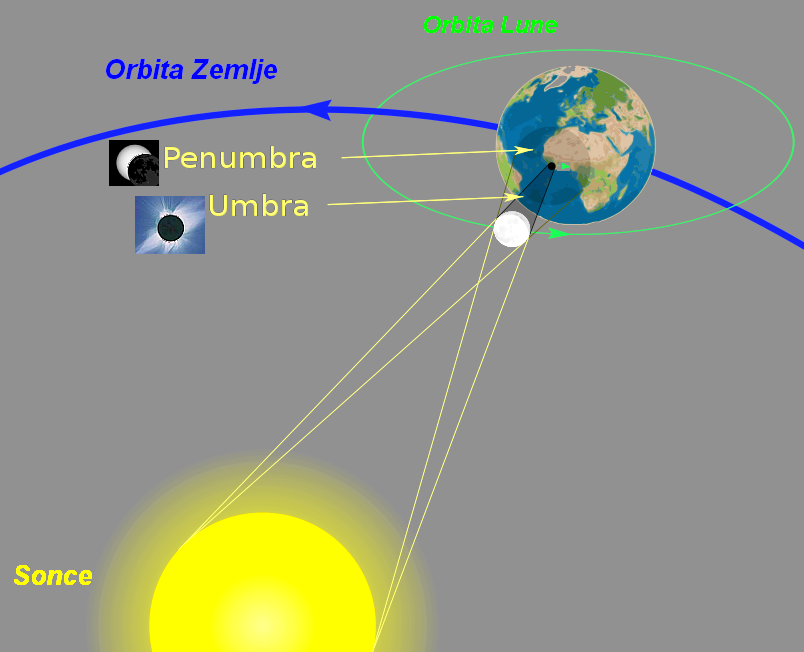
Slika: Shematični prikaz nastanka Sončevega mrka in smeri gibanj Lune,
površine Zemlje, kot pomoč pri oceni hitrosti potovanja sence mrka.
V enaki smeri kot se vrti naš planet - od zahoda proti vzhodu - potuje tudi Luna okrog Zemlje (približno s tako hitrostjo potuje tudi senca Lune na Zemlji). Hitrost mrka bo zato blizu razlike obeh hitrosti. Hitrost določenega kraja na površini Zemlje je odvisna od ge. širine Φ. v = 2πRzCOS(Φ)/to - v resnici se tudi polmer Rz nekoliko spreminja z ge. širino ... Na ekvatorju je ta hitrost ve = 2πRz/to = 465,1 m/s. Čas obrata Zemlje glede na zvezde je to = 23 h 56 min 4,10 s. V naših geografskih širinah hitrost pade na vrednost ve*cos(46°) = 323 m/s. Luna pa potuje okrog Zemlje s povprečno hitrostjo vl = 2πRzl/tol = 1023 m/s = 1 km/s (tol = 27,321661 dni - obhod Lune okrog Zemlje glede na oddaljene zvezde). Realno hitrost lahko določimo tudi preko Keplerjevega zakona, oz. gravitacijskega zakona, gibanje po elipsi. Hitrost Lunine sence je torej precej večja od rotacijske hitrosti krajev na Zemlji, a obe kažeta v isto smer. Ocena relativne hitrosti mrka (sence) je zato hitrost Lune (s katero približno potuje tudi senca mrka), minus hitrost kraja na Zemlji. Na zmernih geografskih širinah je to približno 700 m/s (ocena velja za S once ob 12. h, ko prečka krajevni meridian, v resnici je potrebno vektorsko seštevanje hitrosti na sferi, kjer se upošteva tudi nagib Zemlje, itn – a tokrat gre zgolj za ocene). Poglejmo, kako hitro je mrk prečkal ZDA. Za razdaljo 4017 km je senca mrka rabila 90,7 minut. Povprečna hitrost sence je bila torej vm = 4,017 km/90,7 min = 738,14 m/s = 2,657 km/h. In to je kar blizu naši oceni hitrosti mrka. Z zelo hitrimi nadzvočnimi letali lahko torej sledimo mrku. Ocena časa trajanja mrka je tako tm = 2y/vm = 109000 m/738 m/s = 147,7 s = 2 min 28 s. To je kar dobra ocena časa - za korektno širino mrka v Casperju (2y = 109 km). Sedaj tudi vemo, zakaj je recimo mrk 2006 v Turčiji trajal kar 4 minute. Kot bomo izračunali v naslednjem poglavju, je bila tam širina Lunine sence kar okrog 180 km.
Ocena širine Lunine sence (umbre) na Zemlji ob popolnem Sončevem mrku
Ocena širine poti Lunine sence popolnega mrka bo izhajala iz zelo preprostih
predpostavk – iz razmerij stranic podobnih trikotnikov. Rezultat bo pa
prav zadovoljiv.
Ob mrku vsekakor poznamo polmer
Zemlje (RZ), Lune (RL), Sonca (RS), poiščemo še razdaljo med središčema
Sonca in Zemlje (XS) ter Lune in Zemlje (XL).
Tir potovanja Lune okrog Zemlje je eliptičen, enako Zemlje okrog
Sonca (dokazal že J. Kepler).
Razdalji Zemlja - Sonce, Luna poiščemo recimo na naslovu:
http://www.stargazing.net/kepler/jsmoon.html
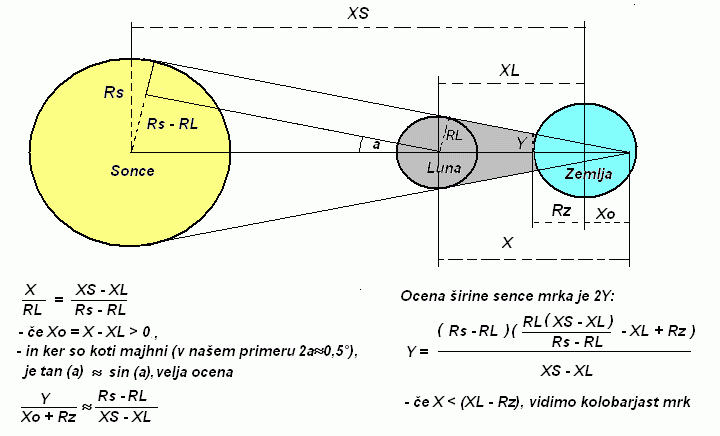
Slika: Prikaz geometrije popolnega Sončevega mrka v primeru, ko pada senca
Lune centralno proti središču Zemlje.
Iz podobnih pravokotnih trikotnikov, in ker so koti majhni, dobimo iz razmerij
stranic dokaj preprost rezultat, oceno, za polmer Lunine sence (Y),
oz. širino (2Y). Razmerja velikosti teles in razdalj na sliki niso realna -
so podana zgolj za ponazoritev geometrije mrka in izpeljavo širine
Lunine sence.
Obravnavali bomo preprost primer, ko senca Lune pada centralno proti središču Zemlje. Poiskali bomo kar
dolžino daljice na tangenti, kjer center mrka prebada Zemljo. Dolžino daljice omejuje stožec Lunine
sence - glejte
sliko - in naj bo to kar ocena širine mrka (2Y). Definirajmo še dve spremenljivki, razliki razdalj
in polmerov
(pomagajte si sliko):
XLS = XS – XL
RSL = RS – RL
Iz podobnih pravokotnih trikotnikov, in ker so koti majhni, dobimo iz razmerij stranic dokaj preprost rezultat za oceno polmera Lunine sence (Y):
Y = RSL(RL*XSL/RSL - XL + Rz)/XSL
Iz enačb razberemo še pogoj, kdaj je mrk kolobarjast [če je višina X < (XL - Xz), potem vrh stožca Lunine sence več ne doseže površine Zemlje].
Za vajo podajmo dva rezultata - za letošnji mrk in za mrk 29. 3. 2006. V enačbo bomo vstavili naslednje vrednosti: RZ = 6378 km, RS = 695700 km, RL = 1737 km.
* Razdalja, 21. 8. 2017 ob 18:27 po UT (20170821.1827), Zemlja - Sonce je bila XS = 151318246,2 km, Zemlja - Luna pa XL = 371199.6. Rezultat za 2Y = 120 km (maksimalna širina je bila nekje okrog 115 km, v Casperju pa 109 km).
* Razdalja, 29. 3. 2006 ob 10:57 po UT, Zemlja - Sonce je bila XS = 149358514,1 km, Zemlja - Luna pa XL = 360038,1 km. Rezultat za 2Y = 180 km (širina pa je bila v Turčiji okrog 184 km).
Seveda so napake posledica necentralnosti Lunine stožčaste sence
in velikih poenostavitev pri izpeljavi (razdalja Zemlja-Luna-Sonce
se spreminja iz trenutka v trenutek, tukaj so še oblike teles,
projekcija na sfero, itn). Za vajo v srednji šoli pa je to lahko
prav poučen geometrijski primer ocene širine Lunine sence na površini
Zemlje ob popolnem Sončevem mrku.
Kot smo že omenili, se iz razmerij razbere tudi pogoj, kdaj je mrk kolobarjast.
Ker pa se razdalje med telesi stalno spreminjajo, lahko nastanejo tudi
hibridni mrki - nekje na črti je kolobarjast, drugje pa popoln mrk.
Še ocena velikosti polsence mrka (penumbre)
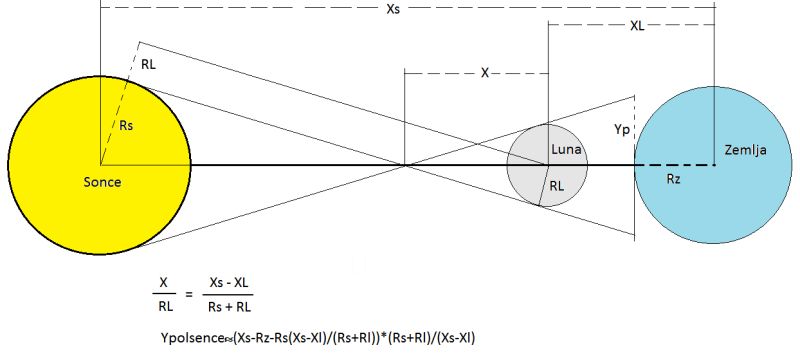
Slika: Geometrija za oceno velikosti polsence med Sončevim mrkom.
Razmerja velikosti
teles in razdalj na sliki niso realna – so podana zgolj za ponazoritev
geometrije mrka.
Pri izpeljavi enačbe polsence si spet pomagajmo s skico. Definirajmo še
dodatno spremenljivko: RRSL = RS + RL
Enačba za oceno polmera polsence Lune na tangenti Zemlje ob centralnem mrku
je:
Yp = (Xs-Rz-Rs*XLS/RRSL)*RRSL/XLS
Mogoči so še ostali enakovredni zapisi.
Iz podatkov za mrka iz 21. 8. 2017 in 29. 3. 2006 – je za mrk 2017ocena širine polsence v ZDA 2Yp = 6785 km in za mrk 2006 v Turčiji 2Yp = 6846 km.
Polsenca je torej približno 2x večja od premera Lune, kar je približno enako polmeru Zemlje. Ta okoliščina (ogromna polsenca in s tem vidnost delnega mrka daleč vstran od centralne črte) je pomagala astronomom v Babilonu in okolici, da so lahko z dolgoletnimi opazovanji mrkov, določili periodo ponovitve mrka. Medsebojni položaji Zemlje, Lune in Sonca se ponovijo po 18 letih in 11 dneh [ali 10 dneh - odvisno od št. prestopnih let] ter 8 urah. Danes to periodo imenujemo saros – to, nekoliko napačno poimenovanje, je predlagal E. Halley. Sumersko/babilonska beseda »sar« ("saru") je Kaldejcem pomenila nekaj "v vesolju", najverjetneje pa kar mersko enoto in je imela številsko vrednost 60*60 = 3600. Koledar, delitev leta na mesece, tedna na 7 dni po nebesnih telesih, številska osnova 60 za delitev ur na 60 minut, minut na 60 sekund, krog razdeljen na 360 delov, geometrija – »Pitagorov« izrek, zagotovo še danes berljiva pisava ... – vse to je izjemna živa dediščina vrlih Sumercev izpred okrog 6000 let – Kmetov in hkrati Astronomov z veliko začetnico. Letošnji mrk pripada 145. sarosu, enako kot tisti iz leta 1999, ki je bil viden iz sv Slovenije. Zaradi osmih ur razlike se mrk istega sarosa po 18-ih letih in 11-ih dnevih zgodi približno 120 ° zahodneje. 12. Septembra leta 2053 se bo mrk 145. sarosa spet vrnil v bližino Evrope – kjer bo viden kot delni. Črta popolnega mrka pa se bo vila čez severno Afriko. Če smo malo predrzni, lahko rečemo, da torej že v eni generaciji (naši), preko spremljanja mrkov, pridemo na sled periodi sarosa ...
Ali se bo obdobje popolnih Sončevih mrkov končalo in kdaj?


Slika: Ko vrh stožca Lunine sence ne bo več dosegel površine Zemlje, ne bo več popolnih Sončevih mrkov,
ampak le še delni kolobarjasti.
Kot se razbere iz podatkov, so popolni mrki na meji, da se sploh zgodijo. In v oddaljeni bodočnosti bo za ljubitelje mrkov samo še slabše - zakaj?

Slika: Plimska valova preko navora gravitacijske sile Luno oddaljujeta,
Luna pa hkrati zavira rotacijo Zemlje. Zaviranje Zemlje so nam razkrili
prav mrki!
Luna se namreč oddaljuje od Zemlje in sicer za okrog dl = 4 cm na leto (zadnje ocene so 3,8 cm). Glavni razlog za oddaljevanje Lune od Zemlje je navor plimovanja oceanov na samo Luno, glejte sliko. Plimski val je namreč, zaradi rotacije Zemlje in viskoznosti vode, premaknjen iz smeri Zemlja - Luna (posledično se tudi rotacija Zemlje upočasnjuje in dan daljša – za okrog 2,3 ms na sto let - skupna vrtilna količina obeh teles pa se seveda ohranja) - glejte članek: Ali se upočasnjuje vrtenje Zemlje okrog lastne osi in ali se Luna oddaljuje od Zemlje? (Spika, marec 2000).
Iz povedanega tudi sledi, da se Lunina navidezna velikost napram Soncu manjša (manjša se njen zorni kot), in da nekoč ne bo več popolnih Sončevih mrkov. Najdaljši mrk je takrat, ko je Luna na svoji orbiti okrog Zemlje blizu perigeja (prizemlja), Zemlja pa hkrati blizu afelija (odsončja). Recimo 16. 7. 2186 bo v Guyani mrk trajal kar 7 min in 4 s (na Atlantiku pa celo 25 s dlje – to bo najdaljši mrk med letoma 4000 pr. Kr. in 6000, pripada sarosu 139, kot »naš« mrk 2006). Trenutek najširše sence nastopi le 50 minut po izhodu Lune iz perigeja. Naredimo nekaj preprostih izračunov – ocen prav na tem dolgem mrku.
Razdalja, 16. 7. 2186 ob 18:00 po UT, Zemlja - Sonce bo XS = 152051275.8 km, Zemlja - Luna pa XL = 356849.1 km. Rezultat za 2y = 267 km (bolj natančni izračuni dajo enako vrednos - 267 km). Če za ta mrk izračunamo razdaljo vrha stožca sence do površine Zemlje (Xo+Rz), dobimo razdaljo 29223.4 km (2,3 Zemljina premera). Ko se bo Luna za toliko oddaljila, bodo tudi najdaljši Sončevi mrki postali zgolj še kolobarjasti. Vrh stožca Lunine sence bo namreč nastal nad površino Zemlje. In v kolikem času se bo Luna oddaljila za toliko km od Zemlje? Razdaljo (Xo+Rz) bomo delili kar z letnim odmikom 4 cm:
t = 29223.4*100000 cm/4 cm/leto = 731 milijonov let.
In koliko je vreden ta rezultat, ta ocena? V tem času se bo tudi orbita Zemlje in Lune nekoliko spremenila - a gre za oceno. Če se Luna oddalji za 2,3 Zemljina premera, se s tem zmanjša tudi privlačna sila med Zemljo in Luno - a le za 7 %, kar daje dodatno verodostojnost naši oceni. Seveda tudi Luna ni ravno idealna krogla. Na spletu sem našel različne ocene za čas konca popolnih Sončevih mrkov: okoli 500 milijonov let, 650 milijonov let, manj kot milijarda let. To pomeni, da je naša ocena zadovoljiva in dostopna srednješolcu - kot vaja iz geometrije, navora, vrtilne količine, astronomije nasploh, itn.
Da so ocene nekoliko krajše (600 milijonov let) gre pripisati tudi napovedim, da se bo Sonce nekoliko napihnilo - povečalo. Tak proces pa seveda dodatno skrajša dolžino mrkov in s tem se tudi skrajša čas do prenehanja popolnih Sončevih mrkov.
Sonce namreč v sredici kontinuirano zliva ("kuri") vodik v helij (to je naš
vir energije, življenja - fuzija poteka pri izjemno visoki temperaturi 15,7
milijonov K in gostoti kar 162.2 kg/dm3) in
zato se sredica nekoliko krči, kar pa povzroča dodatno
segrevanje - višanje temperature in tlaka. Posledično se
zato zunanji plašč Sonca rahlo napihuje. V zadnjih 4 milijardah
let bi se naj Sonce povečalo za okrog 20 %. Z upoštevanjem širitve
Sonca pa se naša ocena približa vrednosti 500 milijonov let do
konca popolnih Sončevih mrkov. A za zdaj še kake očitne rasti
Sonca nismo zaznali, saj je morebitno povečanje premera zdaleč
premajhno na letni ali nekaj desetletni časovni skali. S trenutnimi
merilnimi metodami povečanja Sonca, za nekaj milijardink ločne minute,
še ne znamo pomeriti (tudi ne spremembe izseva). Lahko pa, da bo prav
čas konca mrkov, glede na izračune, dokazal, da se Sonce v resnici napihuje
("no - malo še moramo počakati").
Nadaljevanje sledi.
Šentvid, nov. 2017
Zorko Vičar