ASTRONOMY

Ladijski kronometer
- povej mi koliko je ura  in povem ti, kje si
in povem ti, kje si

Zakaj je dobro poznati lego poljubne točke na Zemlji?
Oglejmo si nekaj primerov.
Merjenje paralakse med prehodom Venere
Edmond Halley je leta 1716 predlagal, da bi prehod Venere uporabili za natančnejšo določitev razdalje Zemlja-Sonce Rz.

Slika zgoraj pojasni bistvo Halleyevega predloga.
Halley je predlagal naj se meri paralaksa Venere
med prehodom čez Sonce, hkrati pa upošteva takratna ocena paralakse Sonca in tako
izračuna razdalja r od Zemlje do Venere med prehodom. Iz tretjega Keplerjevega zakona se nato
izračuna razdaljo Zemlja-Sonce Rz, to je astronomsko enoto AE. Meritve so uspele šele po Halleyevi smrti.
Odprave so poslali na različne konce sveta. S sabo so morale imeti natančne ure, kar je bil takrat
problem, ki so ga rešili šele izboljšani ladijski kronometri. Takrat so večinoma določali gegografsko dolžino
preko lege Lune, kar pa je bila precej nezanesljiva metoda.
Podrobnosti si lahko preberete na:
http://www.dsellers.demon.co.uk/venus/ven_ch8.htm.
Glej spodaj Halleyevo skico prehoda 1761, ki ga ni doživel.
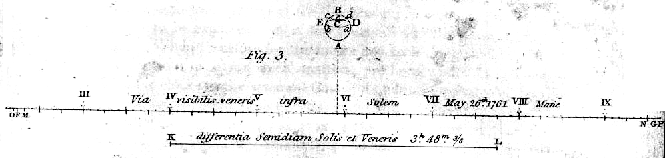
V letih 1761 in 1769, so opazovali
prehode Venere čez Sonce in merili relativno pralakso na Soncu. Meritve je res natančno obdelal šele Johann Franz Encke (1791-1865)
v
prvi polovici 19. stoletja. To je bila za tiste čase kar dobra metoda za določitev astronomske enote,
ki pa je dala za nekaj procentov večje vrednosti od današnjih meritev, ki seveda ne temeljijo več na paralaksi pri
prehodih Venere. Predvsem preseneča velik časovni zamik med meritvami in obdelavo, ja včasih ni bilo
računalnikov in računalniških paketov za računanje efemerid, ni bilo
Postgres, Oracle, MySql, ... podatkovnih baz. Takrat se je vse računalo peš z logaritemskimi tablicami, vse na papirju,
z možgani kot procesorjem, gosjim peresom kot printerjem in "harddiskom".
Zato je bil Jurij Vega takrat s svojimi logaritmi "bestseller" - a še živi pomen tega genija v našem zgodovinskem
spominu
(naredimo kaj, da bo v bodoče še bolj cenjen)?.


Ladijski kronometer


 in povem ti, kje si
in povem ti, kje si 




