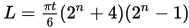Origami - osnove
Beseda origami izhaja iz japonske besede orikami.
Ori pomeni prelaganje,
kami pa papir.
Sprememba kami v gami je posledica
posebnosti v japonskem oblikoglasju, ki se imenuje
rendaku.
In - ne boste verjeli, origami je izjemno uporaben v arhitekturi (pročelja,
žaluzije, senčniki, akustični elementi, ...),
medicini (rec. žilne opornice, ...) pa še kje ...
in seveda tudi v astronomiji - oz. satelitski tehnologiji.
V laboratoriju Lawrencea Livermora so se lotili izdelave teleskopa iz
Fresnelovih leč
(The Eyeglass Space
Telescope), tudi do
premera 100 m (velikost nogometnega igrišča)
za geosinhrono (geostacionarno) orbito 42000 km
vstran od središča Zemlje.
V vesolje se ga da poslati po zaslugi origamistov, ki jim je uspelo
zložiti dele Fresnelovih leč v pregibe na končno dimenzijo nekaj metrov,
da se objektiv tako lahko
spravi v raketo.
Fresnelove leče so tanke in zato lahke, primerne
za origami komponente - vse to je njihova prednost.
Vir: https://str.llnl.gov/str/March03/Hyde.html
Eden večjih uspehov origami principa je uspešna izdelava
vesoljskega teleskopa "The James Webb Space Telescope",
premera 6.5 m, ki ga sestavlja 18 šesterokotnih zrcalnih segmentov iz pozlačenega berilija.
Da so lahko poslali teleskop z raketo v vesolje, so morali
zrcala in velikanski večplastni toplodni ščit po origami principu
zložiti v paket, ki je šel v
raketo Ariane 5.
JWST potuje okoli Sonca blizu druge Lagrangeove točke ( L2 ) sistema Sonce-Zemlja,
ki je 1500000 km dlje od Sonca kot Zemljina orbita
in približno štirikrat dlje od Lunine orbite. In tam daleč se je origami mehanika po načrtu samodejno (preko računalniških
ukazov)
razprla - razprl se je toplotni ščit in zrcala so se sestavila v teleskop, kamere so se postavile
v nosila blizu gorišča. Projekt je uspel.
Teleskop je dobil ime po Jamesu E. Webbu, ki je od 1961 do 1968 vodil
agencijo NASA in je imel osrednjo vlogo v programu Apollo.
Edina alternativa origami principu je tehnologija, ki bo v vesolju izdelovala komponente.
Eden od projektov je samodejna vesoljska ladja Archinavt, ki bo izdelovala preko 3D tiskalnike komponente
za satelite, velike teleskope ... in jih hkrati zlagala v celoto. Surovine bodo najprej prihajale z Zemlje,
pozneje pa morebiti z Lune, asteroidov ...
A origami bo še zmeraj dopolnilni princip bodočih tehnologij.



Eyeglass teleskop iz origami Fresnelovih komponent.
Določenih matematičnih ugank iz antike tudi Evklidovi
aksiomi, oziroma postulati, niso rešili.
Recimo
kako razdeliti kot na tri enake dele ali
kako dvakrat povečati kocko (faktor za množenje stranice je
x = 21/3).
Kot bomo videli, se da ti dve uganki rešiti na osnovi razdelitve
kvadrata na tri enake dele. Primeri sledijo.
Uganke iz antične zgodovine
-----------------------------------
Vedež iz apolonovega svetišča na otoku Delosu
je prerokoval ljudstvu v Atenah, da se bo rešilo kuge,
če bodo njegov oltar v obliki kocke povečali tako, da bo njegova
prostornina dvakrat večja od prvotne.
Najbrž so delski problem zaupali Platonu, ki ga je predložil
geometrom v svoji Akademiji. Dejansko so se s podvojitvijo
kocke ukvarjali številni grški matematiki (Menhmus, Arhitras, Evdoks,
Eratosten, Papus, Diokles, Hipokrat)
- in tudi prišli do rešitve. Vendar pa noben od njih ni rešil naloge
z evklidskim orodjem, ker to ni mogoče.
Jedro problema je namreč v konstrukciji števila 21/3, ki ni mogoča
z evklidskim orodjem. Trden dokaz, da to ni mogoče,
so matematiki našli šele v 19. stoletju.
Origami (pregibanje s papirjem) pa omogoča konstruirati
naravna števila, racionalna števila, njihove kvadratne korene
in števila oblike a + a1/2 in tudi števila oblike
21/3.
Znana je tudi zgodba matematično neukega grškega
pesnika. Pisal je o kralju Minosu, ki ni bil zadovoljen z grobnico
svojega sina
Glavka.
Zahteval je dvakrat večjo grobnico in napačno sklepal,
da je to mogoče doseči s podvojitvijo vseh njenih dimenzij.
To napako so nato reševali matematiki ... (zgodbi povzeti po ŽIT 2017/02)
Kaj pravi Evklid.
Evklidovo delo se začenja z naslednjimi petimi postulati, aksiomi
(zapisano v sodobnem matematičnem jeziku):
a) Skozi poljubni dve točki poteka točno ena premica.
b) Premica je neomejena - lahko jo podaljšamo v neskončnost.
c) Za katerokoli daljico obstaja krožnica, ki ima to daljico
za polmer in eno od krajišč za središče.
d) Vsi pravi koti so med sabo skladni.
f) Če poljubni premici sekamo s tretjo premico (prečnico) in je
vsota notranjih kotov na eni strani prečnice manjša od dveh pravih kotov,
potem se dani premici sekata na tej strani prečnice.

Peti postulat: če je alfa + beta < 180°, se premici h in k sekata v točki S.
Peti postulat je nekoliko nerodno formuliran. Poznejši matematiki
so ga nadomestili z aksiomom o vzporednici, ki je razumljivejši,
po matematičnem pomenu pa je enakovreden:
Skozi poljubno točko T, ki ne leži na premici p, poteka točno
ena vzporednica k premici p.
Po Evklidu nastopi origami
-------------------------------
Prepogibanje papirja - origami - pa je
komaj pred nekaj desetletji
razrešilo določene stare antične matematične uganke (brez uporabe kalkulatorjev
in rač. grafike, ...).
Huzita–Hatori-Justinovi aksiomi origami geometrije pa
so podani pod primeri.
Poglejmo si torej rešitvi dveh ugank preko kvadrata razdeljenega
na tri enake dele:
* Kako razdeliti kvadrat na tri enake dele?
'a' je stranica kvadrata,
iščemo a/3.

Kvadratni papir s stranico 'a' prepognemo po diagonali,
nato čež polovico, nakar še iz polovice proti
vogalu.
Presečišče zadnjega prepogiba in diagonale da a/3.
Spodnji rešitvi sta nadaljevanje razdelitve kvadrata na tri enake dele.
* Kako razdeliti kot na tri enake dele?
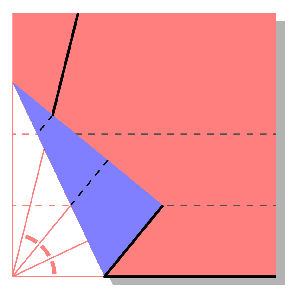




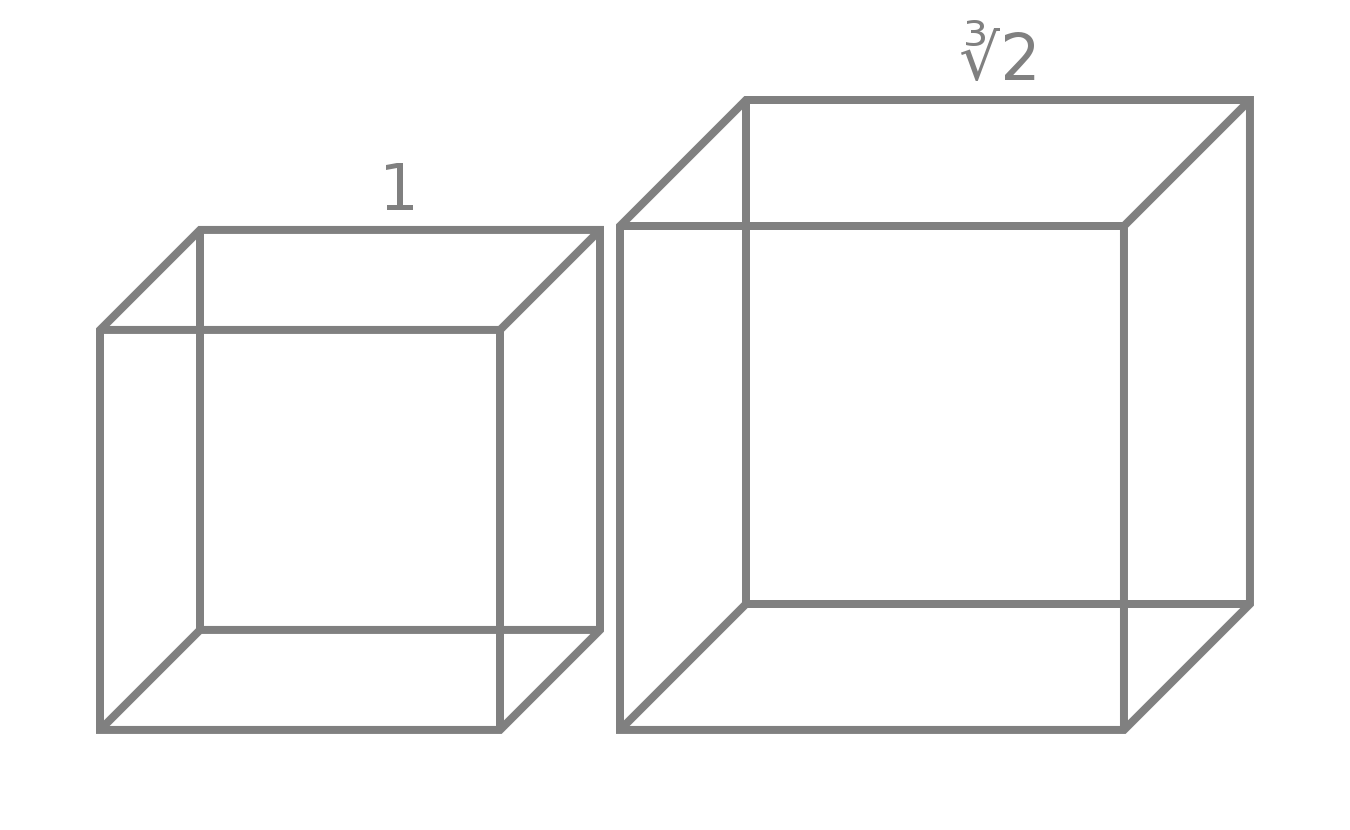
* Kako dvakrat povečati kocko (faktor za množenje stranice je
x = 21/3 ?
V = 2Vo sledi (xa)3 = 2a3
x = 21/3 (za rešitev je dovolj zgolj en sam dodaten pregib,
rešitev je našel Peter Messer)

 |
Sledi dokaz (glej levo sliko in oznake):
CB = 1
AC = x
AB = x + 1 (stranica kvadrata)
CI = (x + 1)/3
BF = 2(x + 1)/3
CF = 2(x + 1)/3 - 1 = (2x - 1)/3
d = BJ
CJ = x + 1 - d
d2 + 1 = (x + 1 - d)2 (Pitagorov izrek)
d = (x2 + 2x)/(2x + 2)
- sledijo razmerja stranic podobnih pravokotnih trikotnikov CFI, CBJ, saj je
kot gama enak kotu alfa,
CI = (x + 1)/3
d/(x + 1 - d) = ((2x - 1)/3)/((x + 1)/3) = (2x - 1)/(x + 1)
(x2 + 2x)/(x2 + 2x + 2) = (2x - 1)/(x + 1)
x3 + 3x2 + 2x = 2x3 + 3x2 + 2x - 2
x3 = 2 oziroma x = 21/3(in to je elegantna rešitev zgolj s prepogibanjem papirja).
|
Viri:
http://www.origami-resource-center.com/divide-paper-into-thirds-3.html
http://www.origami-resource-center.com/divide-paper-into-nths.html
https://www.sciencenews.org/article/trisecting-angle-origami
http://matheducators.stackexchange.com/questions/9784/impossibility-of-trisecting-the-angle-doubling-the-cube-and-alike-what-are-rea
http://www.cutoutfoldup.com/409-double-a-cube.php
https://plus.maths.org/content/power-origami-1
https://plus.maths.org/content/power-origami
The genius of origami (Genialnost origamija)
Huzita–Hatori-Justinovi
aksiomi origami geometrije
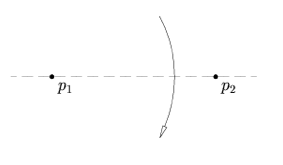
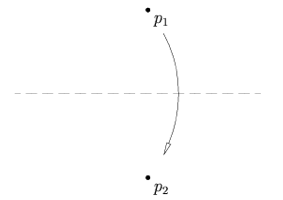
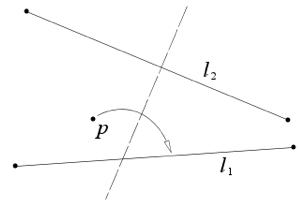
O1) Skozi dve različni točki p1 in p2 lahko naredimo samo en pregib.
O2) Obstaja en sam pregib, s katerim dano točko p1 prenesemo na dano točko p2 in p1 ni enaka p2.
O3) Obstajata dva pregiba, s katerima dano premico l1 prenesemo na dano premico l2, če se premici sekata in en sam, če sta premici vzporedni.
O4) Samo na en sam način lahko naredimo pravokoten pregib, skozi dano točko p1 na dano premico l1.
O5) Obstaja samo en pregib skozi dano točko p2, prek katerega se točka p1 prezrcali na dano premico l1.
O6) Če sta dani različni premici l1 in l2, ki se sekata in različni točki p1 in p2, obstaja natančno en pregib, prek katerega se točka p1 prezcali na premico l1 in se točka p2 prezcali na premico l2.
O7) Če so dane točka p ter premici l1 in l2, obstaja pregib, ki točko p preslika na premico l1 in je pregib pravokoten na premico l2.
Sedmi aksiom je leta 2001 dodal Koširo Hatori.
Prvih šest pa je objavil Humiaki Huzita,
Jacques Justin pa jih je vseh 7 (baje) odkril že leta 1986, a jih ni objavil.
Imen je več in tudi letnic odkritij.
Nič novega v zgodovini - vsaka velika država si prilašča vsa velika
odkritja - resnico pa pozna le On.
Saj poznate naslednjo modrost.
Med kritičnimi zgodovinarji priljubljen epigram pravi:
"Bog je vsemogočen, a celo On ne more spreminjati preteklosti.
Za to je ustvaril zgodovinarje." John Stachel, 1983
(rojen 29. mar. 1928 - fizik in filozof znanosti)
Slike k aksiomom so spodaj (angleški in slovenski tekst).
Just as Euclid devised axioms for planar geometry, the modern mathematicians Humiaki
Huzita and Koshiro Hatori devised a complete set of axioms to describe
origami geometry — the Huzita–Hatori axioms (click here
to skip the axioms and see the rest of the article):
Axiom 1: Given two points 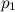 and and 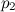 , there is a unique fold that passes through both of them. , there is a unique fold that passes through both of them.
[Skozi dve različni točki p1 in p2 lahko naredimo samo en pregib.]
|
|
Axiom 2: Given two points 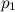 and and 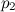 , there is a unique fold that places , there is a unique fold that places 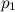 onto onto 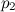 . .
[Obstaja en sam pregib, s katerim dano točko p1
prenesemo na dano točko p2 in p1 ni enaka p2.]
|
|
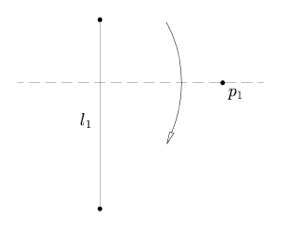
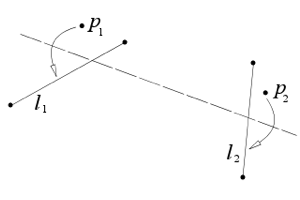
Axiom 3: Given two lines 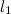 and and 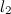 , there is a fold that places , there is a fold that places 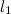 onto onto 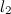 . .
[Obstajata dva pregiba, s katerima dano premico
l1 prenesemo na dano premico l2, če se premici sekata in
en sam, če sta premici vzporedni.]
|
|
Axiom 4: Given a point 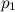 and a line and a line 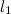 , there is a unique fold perpendicular to , there is a unique fold perpendicular to 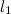 that passes through point that passes through point 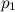 . .
[Samo na en sam način lahko naredimo pravokoten pregib,
skozi dano točko p1 na dano premico l1.]
|
|
Axiom 5: Given two points 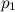 and and 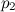 and a line and a line 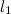 , there is a fold that places , there is a fold that places 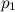 onto onto 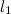 and passes through and passes through 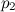 . .
[Obstaja samo en pregib skozi dano točko p2, prek katerega se točka p1
prezrcali na dano premico l1.
]
|
|
Axiom 6: Given two points 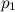 and and 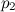 and two lines and two lines 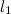 and and 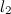 , there is a fold that places , there is a fold that places 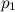 onto onto 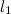 and and 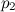 onto onto 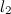 . .
[Če sta dani različni premici l1 in l2, ki se sekata in različni
točki p1 in p2, obstaja natančno en pregib, prek katerega se točka p1
prezcali na premico l1 in se točka p2 prezcali na premico l2.]
|
|
Axiom 7: Given one point 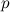 and two lines and two lines 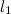 and and 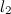 , there is a fold that places , there is a fold that places 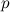 onto onto 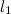 and is perpendicular to and is perpendicular to 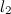 . .
[Če so dane točka p ter premici l1 in l2, obstaja pregib,
ki točko p preslika na premico l1 in je pregib pravokoten
na premico l2.]
|
|
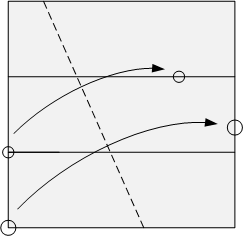
Kazuo Haga pokaže kako računamo ulomke s pomočjo pregibanja papirja.

Sledi izpeljava, glejte zgornjo sliko, za podobna trikotnika velja:
d/x = (1-x)/z, velja d = x(1-x)/z, oziroma 1-d = (z - x(1-x))/z
z2/(z2 + (1-x)2) = x2/(1-d)2
- v kvadrat zapisanega razmerje vstavim 1-d = (z - x(1-x))/z
z2/(z2 + (1-x)2) = z2x2/(z - x(1-x))2
z2 - 2zx(1-x) + x2(1-x)2
= x2z2 + x2(1-x)2
z2 - 2zx(1-x)
= x2z2
(1 - x2)z2 = 2zx(1-x)
(1 - x)(1 + x)z = 2x(1-x)
Rezultat po krajšanju je:
Z = 2x/(1+x)
w = z/2 = x/(1+x)
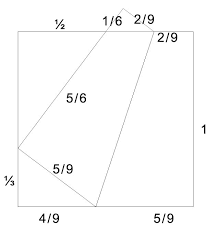
Sledijo primeri še nekaterih ulomkov - sami izpeljite povezave glede na sliko spodaj
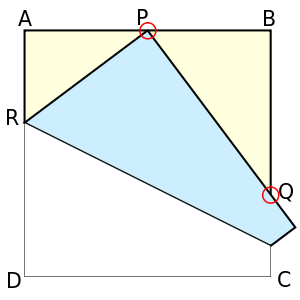 AP = x
BQ = 2x/(1+x)
QC = (1-x)/(1+x)
AR = (1-x2)/2
PQ = (1+x2)/(1+x)
-------------------------------
AP BQ QC AR PQ
1/2 2/3 1/3 3/8 5/6
1/3 1/2 1/2 4/9 5/6
2/3 4/5 1/5 5/18 13/15
1/5 1/3 2/3 12/25 13/15
AP = x
BQ = 2x/(1+x)
QC = (1-x)/(1+x)
AR = (1-x2)/2
PQ = (1+x2)/(1+x)
-------------------------------
AP BQ QC AR PQ
1/2 2/3 1/3 3/8 5/6
1/3 1/2 1/2 4/9 5/6
2/3 4/5 1/5 5/18 13/15
1/5 1/3 2/3 12/25 13/15
Primeri origamijev - en kos papirja in taka umetnina!


Vir: https://en.wikipedia.org/wiki/Origami
Zgodovina origamija (zvijanje papirja)
Najbolj pogosto origami povezujemo
z izumom papirja na Kitajskem okrog 2. stoletju pr. Kr.
Pravi razcvet je doživel na Japonskem, kjer se obravnava kot del nacionalne umetnosti.
Poleg Japonske, so to spretnost posvojili tudi v drugih delih sveta,
recimo v Španiji, kjer je znan pod imenom "papiroflexia".
Že v 8. stoletju je origami postal sestavni del različnih slovesnostih
na Japonskem.
Samuraji so izmenjevali darila z okraski "tuti" - to so umetelno
prepognjeni trakovi papirja.
Med obredi šintoističnih porok,
so uporabljali origami metulje, ki simbolizirajo mladoporočenca.

Primer origami ptice iz 1797 - Japonska.
https://es.wikipedia.org/wiki/Origami

Z vsako gubo se določena količina papirja
izgubi za dodatno zgibanje. Funkcija minimalne potrebne dolžine
papirja 'L' pri pregibanju
papirja (poljubnega materiala) pri debelini 't' in 'n' pregibih je:
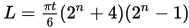
Papir je seveda lahko daljši.
Funkcijo je izpeljal Gallivan leta 2001.
Člen t2n je hkrati mnogokratnik osnovne debeline 't' pri
pri 'n' pregibih papirja (če pregibamo 1x, je debelina plasti podvojena t*2, če ta papir
še prepognemo n=2, podvojimo, je nova debelina t4 = t22, če ponovimo vajo
in je pregibov n=3, je skupna debelina osmih plasti kar t8 = t23; splošna
formula skupne debeline 'd' zloženih plasti pri n pregibih je torej: d = t2n).
Pokazal je tudi, da se list papirja lahko prepolovi na polovico 12-krat,
v nasprotju s
splošnim prepričanjem, da se papir vseh velikosti lahko zloži največ osemkrat.
Zaključek
Kot otroci pa smo praktično vsi
iz papirja s pregibanjem izdelovali letala, rakete, okraske, ladjice,
kape, zmaje,
"plonk - listke v obliki harmonike", tako da nam origami ni tuj,
ne da bi pri tem kaj veliko razmišljali o matematiki.
Danes se mnogi jezijo, da je vse, kar je ostalo v šolskih
programov od tehnične in rokodelske dediščine, zgolj še papir,
origami (zlaganje papirja, delanje papirnatih ladjic ...).
Če je temu tako, je to pot nazaj.
Če pa otroci še papirnate ladjice ne znajo več narediti - pa je to konec
praktične pedagogike.
Torej origami vsekakor ja, naj pride v šolske programe,
a zraven njega so nujno potrebne vsaj še naslednje spretnosti:
modelarstvo (letala, rakete, ladje, avtomobilči, ...),
delo z lesom, delo z glino, delo s kovinami,
osnove elektrotehnike (tudi spajkanje), vrtnarjenje, sadjarstvo, gozdarstvo,
fotografija, delo z živalmi, ...

Zgodnji model teleskopa James Webb v polnem
obsegu na ogled v NASA Goddard Space Flight Center.
Vse to se je po principu origamija zložilo v paket,
ki je z raketo Ariane 5 leta 2021 uspešno poletel do
Lagrangove točke L2 sistema Sonce-Zemlja, približno 1,5 milijona km vstran od Zemlje.

Vesoljski teleskop Jamesa Webba v celoti sestavljen in v origami zloženem položaju v čisti sobi v Kourouji,
tik preden je bil nameščen v nosilno raketo Ariane 5; tehnik desno na dnu fotografije je za merilo.

Primerjava velikosti zrcal vesoljskih teleskopov Spitzer, Hubble in James Webb.
Brez origami principa bi James Webb moral po koščkih preko veliko misij potovati v vesolje, recimo ...
Nekaj vaj:
http://operationmigration.org/Origami.pdf
https://courses.csail.mit.edu/6.849/fall10/lectures/L23_images.pdf
http://www.origami-fun.com/printable-origami.html
http://tabor-2013.famnit.upr.si/predavanja/tabor2012_Kuzma.pdf
Povzel: ZORKO Vičar
E-POŠTA, RFC-822: Zorko.Vicar@guest.arnes.si
Nazaj na aktualno stran.
Nazaj na domačo stran.


























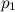 and
and 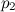 , there is a unique fold that passes through both of them.
, there is a unique fold that passes through both of them.
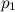 and
and 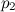 , there is a unique fold that places
, there is a unique fold that places 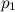 onto
onto 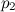 .
.
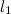 and
and 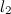 , there is a fold that places
, there is a fold that places 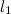 onto
onto 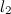 .
.
 and a line
and a line  , there is a unique fold perpendicular to
, there is a unique fold perpendicular to 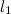 that passes through point
that passes through point 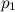 .
.
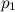 and
and 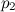 and a line
and a line 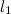 , there is a fold that places
, there is a fold that places 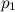 onto
onto 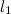 and passes through
and passes through 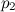 .
.
 and
and  and two lines
and two lines 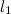 and
and 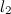 , there is a fold that places
, there is a fold that places 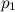 onto
onto 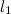 and
and 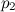 onto
onto 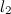 .
.
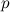 and two lines
and two lines 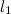 and
and 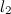 , there is a fold that places
, there is a fold that places 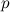 onto
onto 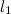 and is perpendicular to
and is perpendicular to  .
.

AP = x BQ = 2x/(1+x) QC = (1-x)/(1+x) AR = (1-x2)/2 PQ = (1+x2)/(1+x) ------------------------------- AP BQ QC AR PQ 1/2 2/3 1/3 3/8 5/6 1/3 1/2 1/2 4/9 5/6 2/3 4/5 1/5 5/18 13/15 1/5 1/3 2/3 12/25 13/15