|
Računanje povratnih dob - Gumbel (Return Period Calculator - Recurrence interval).
V levi stolpec vnesi (recimo) letne maksimalne X izmerke [brez enot]
- v naraščajočem zaporedju [ni nujno, saj jih skripta sama sortira].
POZOR - na koncu stolpiča ne sme biti praznih vrstic!!!
Za korekcije relativnega ranga (desna kolona) večinoma privzamemo
vrednost a = 0, razpon za a je od 0 do 0.5. Za vajo pa najprej poženi
skripto na že vnešenem nizu pretokov. Načeloma velja ta metoda
računanja povratnih dob za večino časovnih nizov (padavine, temperature, veter, ...).
Ker mnogi zadevo poenostavijo in fitajo na podatke kar logaritemsko funkcijo
Y = a*LN(T) + b, je v R E Z U L T A T I H, poleg Gumbelovih povratnih dob,
podana še kolona povratnih dob dobljenih zgolj iz
logaritemske odvisnosti, LN(T). Ko je statistična pomembnost
R^2 > 0.9, so rezultati zaupanja vredni (glejte spodaj izpise rez. po izračunu).
Rezultati so dokaj zanesljivi za povratne dobe, ki največ
5 krat presegajo dolžino niza podatkov.
Pa veliko veselja.
|
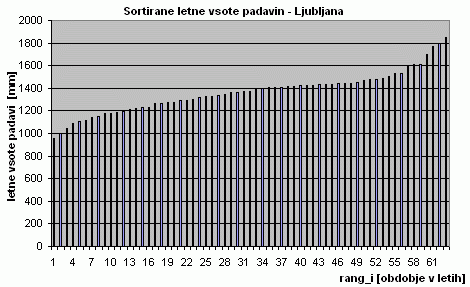
Izračuni veljajo v primerih, ko so po velikosti sortirane
meritve, rec. letnih ekstremov, porazdeljene približno tako, kot jih kaže
zgornji graf. To je Gumbelova porazdelitev:
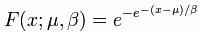
|