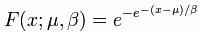 Zbirna funkcija verjetnosti ali porazdelitvena kumulativna funkcija,
tudi CDF (cumulative distribution function).
Zbirna funkcija verjetnosti ali porazdelitvena kumulativna funkcija,
tudi CDF (cumulative distribution function).
 |  |
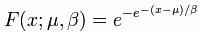 dobimo:
-ln(ln(1/F)) = X*beta - mikro*beta
-ln(ln(1/F)) lahko zapišemo kot -ln(ln(T/(T-1))), kar pa je pri velikih T jih
kar približno enako ln(T), velja torej:
-ln(ln(T/(T-1))) .= ln(T)
(###1)
A smo to povezavo že kje srečali (meritve so sorazmerne z ln(T))?
Ja, na začetku debate o povratnih dobah, ko smo ugibali enačbo za računanje
porazdelitev in porazdelitev dušili (fitali) z ln(T).
Torej je bilo naše ugibanje kar pravšnje.
A ne se zmeraj zanašati na intuicijo.
Ker metoda dopušča neomejeno naraščanje ekstremov z daljšanjem povratne dobe,
so rezultati zanesljivi za povratne dobe, ki največ 5 krat presegajo dolžino
niza podatkov. Rezultati za povratne dobe, ki več kot 10 krat presegajo dolžino
niza, so zelo nezanesljivi.
--------------------------------------------------------------------------
C) Logaritemska metoda
Mnogi ne komplicirajo kaj preveč in kar fitajo logaritemsko odvisnost na
graf meritev glede na, iz izmerkov poračunane, povratne dobe T
(naš prvi primer!!!).
In imajo po svoje prav, saj so vrednosti (recimo vetra, padavin, ...) za
za 100-letne ali celo 1000-letne dogodke zelo negotove.
TO SO LE OCENE!
Ni pa napak poznati še ozadja!!!
Poenostavljena metoda je torej.
Y = a*LN(T) + b
Kako pa dobimo a in b parametra.
Izvedemo linearno regresijo na grafu
Y - meritve
X - LN(T)
Ta metoda je znotraj intervala meritev celo bolj realna, nekoliko
pa podivja izven intervala (za daljše povratne dobe T) in je morebiti
celo boljša za ocne rizičnih simulacij, recimo pri načrtovanju nasipov,
elektrarn, različnih zgradb.
Logaritemska metoda je, poleg Gumbelove, izvedena tudi v spletnem kalkulatorju
za računanje povratnih dob:
http://www2.arnes.si/~gljsentvid10/povratne_dobe_gumbel.html
---------------------------------------------------------------------------------
Še nekaj teorije in vaj
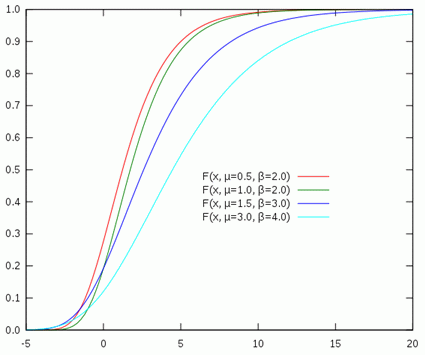
Če torej narišemo graf meritev od F, dobimo neke vrste
porazdelitev za F, katera se (večinoma) dobro prilega Weibullova, Gumbelova ali
Frechetova CDF funkcija (CDF je kratica za cumulative distribution function).
Splošno velja poenoten zapis za vse tri:
F(x) = exp{-[1 + eta*(x - mu)/sigma]^(-1/eta)}
Spodaj je primer grafa za daljši niz maksimalnega vetra za xy lokacijo.
dobimo:
-ln(ln(1/F)) = X*beta - mikro*beta
-ln(ln(1/F)) lahko zapišemo kot -ln(ln(T/(T-1))), kar pa je pri velikih T jih
kar približno enako ln(T), velja torej:
-ln(ln(T/(T-1))) .= ln(T)
(###1)
A smo to povezavo že kje srečali (meritve so sorazmerne z ln(T))?
Ja, na začetku debate o povratnih dobah, ko smo ugibali enačbo za računanje
porazdelitev in porazdelitev dušili (fitali) z ln(T).
Torej je bilo naše ugibanje kar pravšnje.
A ne se zmeraj zanašati na intuicijo.
Ker metoda dopušča neomejeno naraščanje ekstremov z daljšanjem povratne dobe,
so rezultati zanesljivi za povratne dobe, ki največ 5 krat presegajo dolžino
niza podatkov. Rezultati za povratne dobe, ki več kot 10 krat presegajo dolžino
niza, so zelo nezanesljivi.
--------------------------------------------------------------------------
C) Logaritemska metoda
Mnogi ne komplicirajo kaj preveč in kar fitajo logaritemsko odvisnost na
graf meritev glede na, iz izmerkov poračunane, povratne dobe T
(naš prvi primer!!!).
In imajo po svoje prav, saj so vrednosti (recimo vetra, padavin, ...) za
za 100-letne ali celo 1000-letne dogodke zelo negotove.
TO SO LE OCENE!
Ni pa napak poznati še ozadja!!!
Poenostavljena metoda je torej.
Y = a*LN(T) + b
Kako pa dobimo a in b parametra.
Izvedemo linearno regresijo na grafu
Y - meritve
X - LN(T)
Ta metoda je znotraj intervala meritev celo bolj realna, nekoliko
pa podivja izven intervala (za daljše povratne dobe T) in je morebiti
celo boljša za ocne rizičnih simulacij, recimo pri načrtovanju nasipov,
elektrarn, različnih zgradb.
Logaritemska metoda je, poleg Gumbelove, izvedena tudi v spletnem kalkulatorju
za računanje povratnih dob:
http://www2.arnes.si/~gljsentvid10/povratne_dobe_gumbel.html
---------------------------------------------------------------------------------
Še nekaj teorije in vaj
Če torej narišemo graf meritev od F, dobimo neke vrste
porazdelitev za F, katera se (večinoma) dobro prilega Weibullova, Gumbelova ali
Frechetova CDF funkcija (CDF je kratica za cumulative distribution function).
Splošno velja poenoten zapis za vse tri:
F(x) = exp{-[1 + eta*(x - mu)/sigma]^(-1/eta)}
Spodaj je primer grafa za daljši niz maksimalnega vetra za xy lokacijo.
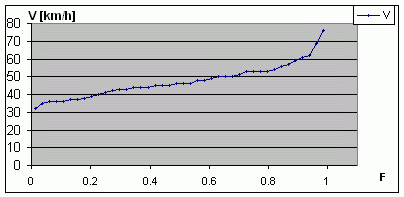 Še nekaj podatkov iz:
http://mds.marshall.edu/cgi/viewcontent.cgi?article=1232&context=etd
http://docsdrive.com/pdfs/medwelljournals/erj/2008/7-14.pdf
stran 5
http://www.vsni.co.uk/products/genstat/htmlhelp/stats/GEVProcedure.htm
F(x) = exp{-[1 + eta*(x - mu)/sigma]^(-1/eta)}, za {x: 1 + eta*(x - mu)/sigma > 0}.
- če eta = 0, je porazdelitev Gumbelova,
- če eta > 0, je Frechetova,
- če eta < 0, je Weibullova.
--------------------------------------------------------------------
kjer -neskončno < x < neskončno; -neskončno < mu < neskončno; sigma > 0
Za eta = 0, je CDF nedifiniran, ko eta limitira
proti nič, dobimo standardno Gumbelovo CDF.
Članek o povratnih dobah najdete tudi v SMD Razpravah iz leta 1987,
spodaj je povezava na razprave_87_29_1_13-32.pdf (SMD: Letnik 29, št. 1):
http://www.meteo-drustvo.si/data/Arhiv_razprave_papers/razprave/po_stevilkah/87/29_1/razprave_87_29_1_13-32.pdf
Še nekaj podatkov iz:
http://mds.marshall.edu/cgi/viewcontent.cgi?article=1232&context=etd
http://docsdrive.com/pdfs/medwelljournals/erj/2008/7-14.pdf
stran 5
http://www.vsni.co.uk/products/genstat/htmlhelp/stats/GEVProcedure.htm
F(x) = exp{-[1 + eta*(x - mu)/sigma]^(-1/eta)}, za {x: 1 + eta*(x - mu)/sigma > 0}.
- če eta = 0, je porazdelitev Gumbelova,
- če eta > 0, je Frechetova,
- če eta < 0, je Weibullova.
--------------------------------------------------------------------
kjer -neskončno < x < neskončno; -neskončno < mu < neskončno; sigma > 0
Za eta = 0, je CDF nedifiniran, ko eta limitira
proti nič, dobimo standardno Gumbelovo CDF.
Članek o povratnih dobah najdete tudi v SMD Razpravah iz leta 1987,
spodaj je povezava na razprave_87_29_1_13-32.pdf (SMD: Letnik 29, št. 1):
http://www.meteo-drustvo.si/data/Arhiv_razprave_papers/razprave/po_stevilkah/87/29_1/razprave_87_29_1_13-32.pdf
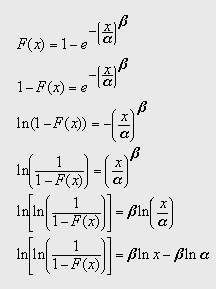 Če zgornjo enačbo primerajmo z enačbo premice Y = mX + b
in narišemo regresijsko premico, dobimo iz grafa, kjer je:
Y-os ( ln(ln(1/(1-F))) )
X-os ( ln (meritev) )
s primerjavo s premico Y = mX + b
- naslednje povezave za alfa in beta
beta = m (to je strmina premice)
-beta*ln(alfa) = b
alfa = exp(-b/beta)
Če je (statistična pomembnost) R^2 premice blizu 1, je Weibullova porazdelitev gotovo
primerna za uporabo - oziroma se porazdelitev meritev
obravnava (analizira) z upoštevanjem Weibullove porazdelitve.
Opomba:
F se v tuji literaturi imenuje tudi "Median Rank"
(ali "numerous plotting position formula").
Smo že omenili, a še ena ponovitev ne škodi.
--------------------------------------------
Zakaj je dobro poznati alfa in beta spremenljivki?
V Excelu je namreč funkcija WEIBULL(x,alpha,beta,cumulative),
kjer sta alfa in beta zamenjana glede na ta tekst (glede na večino literature).
Primer
Recimo, da imamo iz neke vrste meritev izračunana alfa in beta.
Beta (or Shape Parameter) = 4.252482204
Alpha (or Characteristic Life) = 693380.3117
SPET PRIMER:
-------------
Design A Rank Median Ranks 1/(1-Median Rank) ln(ln(1/(1-Median Rank))) ln(Design A Cycles)
Cycles (i-0.3)/(10+0.4)
meritve_x rang_i F 1/(1-F) ln(ln(1/(1-F))) ln(meritve_x)
------- -- ----------- ----------- ------------- -----------
384558 1 0.067307692 1.072164948 -2.663843085 12.8598499
483331 2 0.163461538 1.195402299 -1.72326315 13.088457
508077 3 0.259615385 1.350649351 -1.202023115 13.13838829
515201 4 0.355769231 1.552238806 -0.821666515 13.15231239
615432 5 0.451923077 1.824561404 -0.508595394 13.33007974
666686 6 0.548076923 2.212765957 -0.230365445 13.41007445
726044 7 0.644230769 2.810810811 0.032924962 13.4953659
755223 8 0.740384615 3.851851852 0.299032932 13.53476835
807863 9 0.836538462 6.117647059 0.593977217 13.60214777
848953 10 0.932692308 14.85714286 0.992688929 13.6517591
Če zgornjo enačbo primerajmo z enačbo premice Y = mX + b
in narišemo regresijsko premico, dobimo iz grafa, kjer je:
Y-os ( ln(ln(1/(1-F))) )
X-os ( ln (meritev) )
s primerjavo s premico Y = mX + b
- naslednje povezave za alfa in beta
beta = m (to je strmina premice)
-beta*ln(alfa) = b
alfa = exp(-b/beta)
Če je (statistična pomembnost) R^2 premice blizu 1, je Weibullova porazdelitev gotovo
primerna za uporabo - oziroma se porazdelitev meritev
obravnava (analizira) z upoštevanjem Weibullove porazdelitve.
Opomba:
F se v tuji literaturi imenuje tudi "Median Rank"
(ali "numerous plotting position formula").
Smo že omenili, a še ena ponovitev ne škodi.
--------------------------------------------
Zakaj je dobro poznati alfa in beta spremenljivki?
V Excelu je namreč funkcija WEIBULL(x,alpha,beta,cumulative),
kjer sta alfa in beta zamenjana glede na ta tekst (glede na večino literature).
Primer
Recimo, da imamo iz neke vrste meritev izračunana alfa in beta.
Beta (or Shape Parameter) = 4.252482204
Alpha (or Characteristic Life) = 693380.3117
SPET PRIMER:
-------------
Design A Rank Median Ranks 1/(1-Median Rank) ln(ln(1/(1-Median Rank))) ln(Design A Cycles)
Cycles (i-0.3)/(10+0.4)
meritve_x rang_i F 1/(1-F) ln(ln(1/(1-F))) ln(meritve_x)
------- -- ----------- ----------- ------------- -----------
384558 1 0.067307692 1.072164948 -2.663843085 12.8598499
483331 2 0.163461538 1.195402299 -1.72326315 13.088457
508077 3 0.259615385 1.350649351 -1.202023115 13.13838829
515201 4 0.355769231 1.552238806 -0.821666515 13.15231239
615432 5 0.451923077 1.824561404 -0.508595394 13.33007974
666686 6 0.548076923 2.212765957 -0.230365445 13.41007445
726044 7 0.644230769 2.810810811 0.032924962 13.4953659
755223 8 0.740384615 3.851851852 0.299032932 13.53476835
807863 9 0.836538462 6.117647059 0.593977217 13.60214777
848953 10 0.932692308 14.85714286 0.992688929 13.6517591
X-OS Y-OS ln(meritve_x) ln(ln(1/(1-F))) ------------- --------------- 12.8598499 -3 13.088457 -2 13.13838829 -1 13.15231239 -1 13.33007974 -1 13.41007445 0 13.4953659 0 13.53476835 0 13.60214777 1 13.6517591 1 |
|

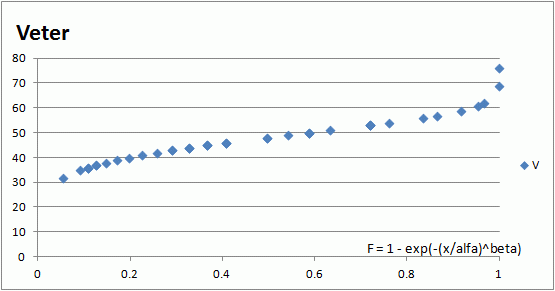 F = 1 - exp(-(x/alfa)^beta), x v F funkciji je v tem primeru veter (spodnji stolpič).
V excelu tole zgleda takole:
=1 - EXP(-POWER((A261/51.0094096339147);6.24901767872693))
Y = 6.249017678726931*X -24.571200742387272 ( R^2 = 0.9052109724371714 )
* alfa = 51.00940963391477
* beta = 6.249017678726931
Alfa in beta veljata za spodnje meritve vetra.
--------------------------------------------------------------------
VETER[km/h] po letih (maks.), F se v tem primeru računa kot (i - 0.44) / (n + 1 - 2*0.44).
32
35
36
36
36
37
37
38
39
40
41
42
43
43
44
44
44
45
45
45
46
46
46
48
48
49
50
50
50
51
53
53
53
53
54
56
57
59
61
62
69
76
*** Uporabi javascript kalkulatot za računanje povratnih dob - Gumbelova porazdelitev.
F = 1 - exp(-(x/alfa)^beta), x v F funkciji je v tem primeru veter (spodnji stolpič).
V excelu tole zgleda takole:
=1 - EXP(-POWER((A261/51.0094096339147);6.24901767872693))
Y = 6.249017678726931*X -24.571200742387272 ( R^2 = 0.9052109724371714 )
* alfa = 51.00940963391477
* beta = 6.249017678726931
Alfa in beta veljata za spodnje meritve vetra.
--------------------------------------------------------------------
VETER[km/h] po letih (maks.), F se v tem primeru računa kot (i - 0.44) / (n + 1 - 2*0.44).
32
35
36
36
36
37
37
38
39
40
41
42
43
43
44
44
44
45
45
45
46
46
46
48
48
49
50
50
50
51
53
53
53
53
54
56
57
59
61
62
69
76
*** Uporabi javascript kalkulatot za računanje povratnih dob - Gumbelova porazdelitev.

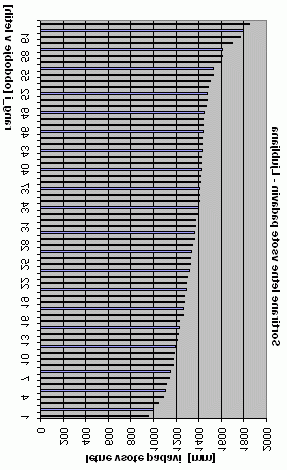
rang_i pretoki[m^3/s] rang_i absolutna_max_tem - LJ rang_i VETER[km/h] rang_i let_padavine_v_mm 1 57406 1 29.6 1 32 1 953.9 2 75806 2 30.8 2 35 2 998.1 3 81806 3 31 3 36 3 1041.4 4 95106 4 31.2 4 36 4 1091 5 99706 5 31.3 5 36 5 1107.1 6 112006 6 31.4 6 37 6 1118.6 7 112006 7 31.8 7 37 7 1140.8 8 114006 8 32 8 38 8 1149.2 9 123006 9 32 9 39 9 1176.5 10 147006 10 32 10 40 10 1178.3 11 32.2 11 41 11 1181.9 12 32.2 12 42 12 1195.9 13 32.2 13 43 13 1211.1 14 32.5 14 43 14 1217.2 15 32.5 15 44 15 1229.9 16 32.6 16 44 16 1233.8 17 32.7 17 44 17 1265 18 32.7 18 45 18 1265.4 19 32.8 19 45 19 1270.2 20 32.8 20 45 20 1273.9 21 32.9 21 46 21 1287.8 22 32.9 22 46 22 1292.4 23 33.1 23 46 23 1301 24 33.1 24 48 24 1315.6 25 33.1 25 48 25 1327.7 26 33.2 26 49 26 1331.3 27 33.2 27 50 27 1336.9 28 33.2 28 50 28 1342.9 29 33.3 29 50 29 1359.2 30 33.3 30 51 30 1363.1 31 33.4 31 53 31 1371.5 32 33.5 32 53 32 1373.7 33 33.5 33 53 33 1395.1 34 33.5 34 53 34 1402.3 35 33.6 35 54 35 1403.3 36 33.7 36 56 36 1405.5 37 33.7 37 57 37 1406.7 38 33.8 38 59 38 1412 39 33.9 39 61 39 1418.4 40 34 40 62 40 1422.8 41 34.1 41 69 41 1423.7 42 34.2 42 76 42 1424.6 43 34.2 43 1432.5 44 34.3 44 1435.1 45 34.7 45 1438 46 34.7 46 1441.6 47 34.9 47 1442.9 48 34.9 48 1446.4 49 34.9 49 1454.7 50 35 50 1469.1 51 35.2 51 1474.7 52 35.3 52 1476.9 53 35.6 53 1490.2 54 35.9 54 1500.7 55 35.9 55 1527.8 56 36 56 1535 57 36.5 57 1605.5 58 36.5 58 1606.9 59 37 59 1610.6 60 37.1 60 1696.1 61 37.1 61 1771.6 62 37.3 62 1797.9 63 37.6 63 1847.5 ----------------------------- a=0.44 www.hurricaneengineering.lsu.edu/.../03Lect4DesignWind.ppt http://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=9&ved=0CHgQFjAI&url=http%3A%2F%2Fwww.hurricaneengineering.lsu.edu%2FCourseMat%2F03Lect4DesignWind.ppt&ei=oGgMUNPJB8eA4gSszMTDCg&usg=AFQjCNEWasI8cTDKjjCt6LVwKJkEF-XlfQ Gust speed (hitrost vetra) v mph 40.97 45.4 46.46 47.97 47.97 48.57 48.57 49.97 50.68 51.74 51.74 52.8 52.8 53.85 53.85 53.96 54.91 62.3 67.58 76.03 a=0.44 T[leta] Veter 1.1 44 2 51.7 5 58.8 10 63.5 25 69.4 50 73.8 100 78.2 250 83.9 500 88.2 1000 92.6 2500 98.3Kako podnebno je raznolika Slovenija lepo kaže zgornji graf, ko maksimalne letne vsote padavin v Veržeju (SV) nikoli ne presežejo minimalnih letnih vsot v kraju SOČA (SZ). leto SOČA_padavine_v_mm SORTIRANE_padavine_v_mm VERŽEJ-padavine_v_mm SORTIRAN_Verzej 1948 2122 1216.5 1949 2256.9 1664.9 1950 2678.6 1748 1951 3418.5 1774.1 980.2 569.6 1952 3016.9 1903.2 862 577.7 1953 1216.5 1927 720.4 603.8 1954 2861.9 1961.3 814.3 642.5 1955 2108.9 1990.5 869.5 655.8 1956 2131.7 2014.1 848.9 661.2 1957 2288.9 2027.8 774.4 684 1958 2676.2 2047.2 852.7 706.7 1959 2526.5 2072.2 876.5 707.6 1960 3476.4 2080.8 892.3 709.2 1961 2367.6 2100.2 835.9 714.4 1962 2313.6 2108.9 1022.2 714.9 1963 2771 2119.7 869.1 714.9 1964 2238.3 2122 908.7 720.4 1965 3196.8 2131.7 1037.8 727.5 1966 2080.8 2137.5 1180.7 739.2 1967 2332.2 2149.2 792.7 767.6 1968 2845 2195.8 661.2 770.9 1969 2386.4 2229.8 912.8 774.4 1970 2294.1 2233.8 847.9 775.5 1971 2014.1 2238.3 569.6 792.7 1972 2273.7 2240.6 1064.3 800 1973 2027.8 2256.9 808 800.6 1974 2137.5 2273.7 851.6 808 1975 2363.3 2286.2 767.6 814.3 1976 2119.7 2288.9 714.9 835.9 1977 2375.9 2294.1 714.9 839.2 1978 2497 2313.6 707.6 845.9 1979 2935.4 2332.2 949 847.9 1980 2399.1 2363.3 893.4 848.9 1981 1748 2367.6 739.2 851.6 1982 2686.3 2375.9 920 852.7 1983 1961.3 2386.4 603.8 854.5 1984 2229.8 2399.1 800 855.8 1985 2586.6 2497 912.1 862 1986 1774.1 2526.5 854.5 869.1 1987 2751.4 2541 995.1 869.5 1988 2047.2 2546.8 727.5 876.5 1989 1990.5 2586.6 775.5 892.3 1990 2842.7 2676.2 845.9 893.4 1991 2707.7 2678.6 855.8 899.7 1992 2896.5 2686.3 714.4 908.7 1993 2240.6 2707.7 684 912.1 1994 2072.2 2737.2 948 912.8 1995 1903.2 2751.4 917.2 917.2 1996 2737.2 2771 934.7 920 1997 2286.2 2842.7 706.7 934.7 1998 2546.8 2845 943.2 940.4 1999 2233.8 2861.9 1006.9 941 2000 3758.5 2863.7 655.8 943.2 2001 2863.7 2868.8 709.2 948 2002 2541 2896.5 770.9 949 2003 2149.2 2935.4 577.7 950.9 2004 3047.5 3016.9 839.2 980.2 2005 1664.9 3047.5 941 995.1 2006 2100.2 3129.1 940.4 1003.5 2007 2195.8 3196.8 899.7 1006.9 2008 3239.8 3239.8 800.6 1022.2 2009 2868.8 3418.5 1003.5 1037.8 2010 3129.1 3476.4 950.9 1064.3 2011 1927 3758.5 642.5 1180.7 ------------------------------------------------------
Kako so lahko kratki nizi meritev zavajujoči - kaže primer poplav v Železnikih - datum: 2007-09-18. Če odstranimo ta datum, dobimo za dnevne padavine (okrog) 200 mm povratno dobo 10000 let (do ledene dobe). S podatkom iz leta 2007 pa "samo" dobrih 1000 let. leto Železniki_max_padavine_v_mm SORTIRANE_Železniki_max_padavine_v_mm 1945 103.2 56.5 1946 64.5 58.2 1947 96.7 60.8 1948 114.5 63.5 1949 86.5 64.5 1950 56.5 65.3 1951 99 65.7 1952 78 66.4 1953 94 66.5 1954 63.5 66.5 1955 66.5 68 1956 75.9 69.5 1957 66.5 69.6 1958 90.5 69.8 1959 76.5 72.5 1960 85.8 72.6 1961 103 74.3 1962 77.5 74.4 1963 105 74.8 1964 99.5 74.9 1965 102.7 75.1 1966 81 75.9 1967 69.8 75.9 1968 77.7 76.3 1969 92.5 76.5 1970 92.1 76.5 1971 75.9 76.5 1972 65.7 76.8 1973 76.3 76.9 1974 69.5 77.2 1975 96.2 77.5 1976 74.8 77.5 1977 74.3 77.7 1978 76.8 78 1979 86.5 78 1980 90.7 78.6 1981 60.8 81 1982 78.6 84.5 1983 74.9 85.1 1984 75.1 85.8 1985 85.1 86.5 1986 88 86.5 1987 96.3 88 1988 93.7 90.5 1989 115.8 90.7 1990 101.2 91.2 1991 77.5 92.1 1992 118.3 92.1 1993 78 92.5 1994 74.4 93.7 1995 106.5 94 1996 77.2 96.2 1997 84.5 96.3 1998 92.1 96.7 1999 76.9 99 2000 112.4 99.5 2001 76.5 101.2 2002 58.2 102.7 2003 65.3 103 2004 72.5 103.2 2005 69.6 105 2006 76.5 106.5 2007 197.2 112.4 2008 66.4 114.5 2009 91.2 115.8 2010 118.1 118.1 2011 68 118.3 2012 72.6 197.2 . http://ponce.sdsu.edu/textbookhydrologyp548.html http://ponce.sdsu.edu/onlinegumbeltable.html http://ponce.sdsu.edu/onlinegumbel.php