








1 ) UVOD
Akrecija (lat. "accretio" - "zraščanje"; accretion, rast, zrast; prirastek nebesnega objekta zaradi trkov, padanja snovi iz okolice) je v astronomiji dobila veljavo po letu 1968, ko sta Prendergast in Burbridge zaznala rentgensko sevanje. Kmalu so nastali modeli, s katerimi so poskušali pojasniti izvor sevanja. Med najbolj uspešnimi je model akrecije v dvojnem sistemu. Sam izvor sevanja je v povezavi s fenomenom kompaktnih objektov - to so bele pritlikavke, nevtronske zvezde in črne luknje.
Za lažje razumevanje pojava si oglejmo preprost primer vpada delcev na kompaktni objekt. Delci, ki imajo daleč vstran od kompaktne zvezde hitrost v∞ in gostoto n∞ =N/V, naj padajo na zvezdo le z ene strani (slika 1).
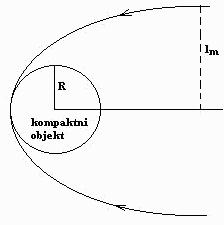
Slika 1. Vpad delcev na kompaktni objekt.
Blizu površine imajo delci parabolično hitrost:
vp=(2GM/R)1/2,
naj bo v∞<<vp.
Maksimalna vrtilna količina ujetih delcev je:
Γ
m=mvp R.
Zanima nas parameter trčenja lm, ki ustreza
tangentnemu vpadu na površino zvezde. Vsi delci, ki se
gibljejo proti zvezdi in katerih vrtilna količina je
manjša od Γ
m , bodo prej ali slej padli na površino.
Iz zakona o ohranitvi vrtilne količine za vsak padajoč
delec dobimo:
lmv∞m=Rvpm.
Sipalni presek kompaktnega objekta za tok delcev s
hitrostjo v∞
pa je:
σ
k=π
l2=π
(vp/v∞
)2R2.
Končno lahko zapišemo masni tok dM/dt= M'
(1)
M'=mn∞
v∞
σ
k=π
ρ
∞
2GR/v∞
=π
rg2cρ
∞
(c/v∞
)(R/rg)
Pri čemer je r g=2GM/c2 Schwarztschildov radij.
Za zelo goste kompaktne objekte (nevtronske zvezde, črne luknje) naša izpeljava ni korektna. Rezultat korektnega računa se ujema z zgornjim, če postavimo R/rg=4 v limiti, ko gre polmer kompaktnega objekta R proti rg.
Izračunajmo še moč, ki se sprošča na površini kompaktnega objekta,
ko pade nanj masni tok M'. Vzamemo lahko, da vsak delec, ki pade na
površino zvezde, izgubi vso kinetično energijo, ki se pretvori
v toploto, oziroma sevanje. Sproščena energija na enoto mase
je E/m=v2p/2
(ker je v∞
<<vp ).
Sproščena moč je enaka izsevu:
L=(E/m)M'=rgGMρ∞
c2/v∞.
Po zadnji formuli bi mogli sklepati, da lahko dosežemo z
akrecijo poljubno velike izseve, kar pa ni čisto res.
Izpeljani rezultat velja namreč samo dokler smemo obravnavati
posamezne delce (atome) kot neodvisne od sosedov, to pomeni,
dokler je prosta pot v plinu
primerljiva s premerom zvezde. Pri večjih gostotah je potrebno
upoštevati tlak, kar naredi račun zapleten. Vendar pa je Eddington
našel preprost argument, ki daje zgornjo mejo za izsev pri akreciji na
kompaktni objekt. Računal je takole. V bližini kompaktnega objekta
je plin gost in ioniziran.
Na elektron v takem plinu deluje sevalna sila navzven zaradi
sevanja kompaktnega objekta (učinek
na proton je bistveno manjši zaradi njegove veliko večje mase pri
enakem naboju). Zaradi močnih elektrostatičnih sil med elektroni in
vodikovimi jedri pa deluje sila tako na elektrone kot na protone.
Če bi bila sevalna sila na elektron in proton večja od gravitacijske
privlačne sile, bi se akrecija
ustavila. Gravitacijska privlačna sila je Fg=GMm/r2.
Sevalna sila, ki deluje v nasprotni smeri, pa ima
velikost
Fs=jσ
r/c=Lσr/(4π
r2c) - obe sili imata enako odvisnost od r. Največji možni
izsev je določen
z minimalno prevlado gravitacijske nad sevalno silo, torej:
GMm/r2 ≥ Lσr/(4πr2c).
Od tod sledi Eddingtonova limita za maksimalni izsev:
(2)
Lkrit=4πMmGc/σ
r=3*104LoM/Mo=1,3*1031WM/Mo
2) ZAPRT SISTEM DVEH ZVEZD

Sestavljata ga normalna zvezda in kompaktna zvezda. Zaprt dvojni sistem je tak, da sta si zvezdi tako blizu, da je manjša zvezda v atmosferi večje. Razdalja med centroma obeh mas je manjša ali enaka premeru normalne zvezde (a' ≈ 2RN). To je tesni dvojni sistem. Take dvojne sisteme najdemo v Cyg x-1 in Cen x-3. Značilne mase so od 1 do 20 M o in razdalje med centri so od 106 do 107 km. Obhodni časi t pa so od 1 do 5 dni.
Za analizo toka plina iz normalne na kompaktno zvezdo uporabimo koordinatni sistem, ki se vrti skupaj z binarnim sistemom, to je s Keplerjevo kotno hitrostjo ω =(G(MN+Mk)/a3)1/2. Napišimo Navier-Stokesovo enačbo:
(3) dv/dt + grad(Φ gc) + 2(ω xv)=-(1/ρ )grad(p) + (2η /ρ )div(def (v))
Pri čemer je v relativna hitrost plina glede na rotirajoči sistem, η koeficient viskoznosti in def(v) tenzor deformacijske hitrosti plina.
(4) Φ gc = Φ c + Φ g = -G( MN/|r-rN| + MK/|r-rK|) - (ω xr)2/2
-rN in rK sta razdalji obeh centrov mas od težišča sistema. Za kvalitativno sklepanje o naravi toka plina iz normalne na kompaktno zvezdo si podrobneje oglejmo potencial (4).
3) POTEK POTENCIALA
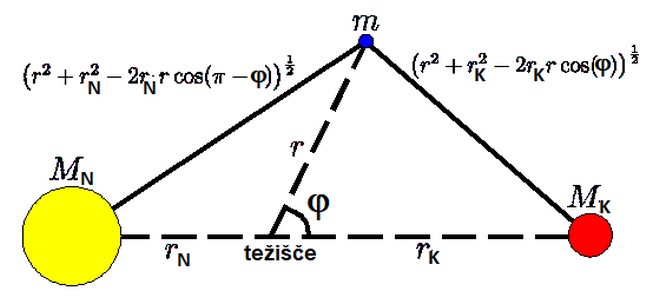
Velja:
cos(π - φ) = -cos(φ)
Velikost razlike vektorjev je:
|r-rN| = (r2 + rN2 - 2rrNcos(π - φ))1/2
= (r2 + rN2 + 2rrNcos(φ))1/2
|r-rK| =
(r2 + rK2 - 2rrKcos(φ))1/2
Potencial (4) lahko zapišemo tudi v naslednji obliki:
Φgc = -G( MN/(r2 + rN2 + 2rrNcos(φ ) )1/2 + MK/(r2 + rK2 - 2rrKcos(φ ) )1/2 ) - ω 2r2/2
Poiščimo lokalne stacionarne točke, z znanima pogojema, parcialna odvoda morata biti 0.
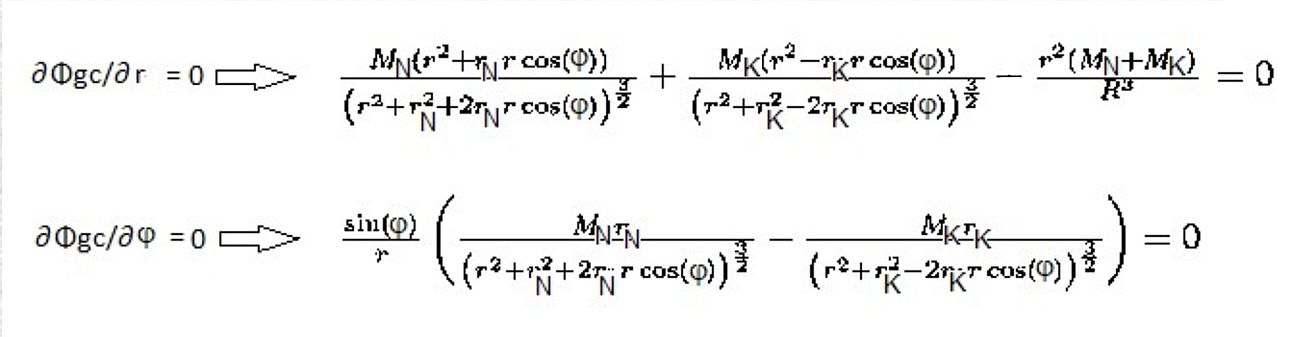
Rešitve zahtevajo numerično reševanje (velja: R = rN + rK,
za ω smo vstavili Keplerjevo vrednost
ω2 = G(MN+MK)/(rN + rK)3 ).
Odvod ∂
Φgc/∂
r=0, je po odvajanju pomnožen z r - tako se lažje najde rešitve. Seveda smo povsod okrajšali
gravitacijsko konstanto G.
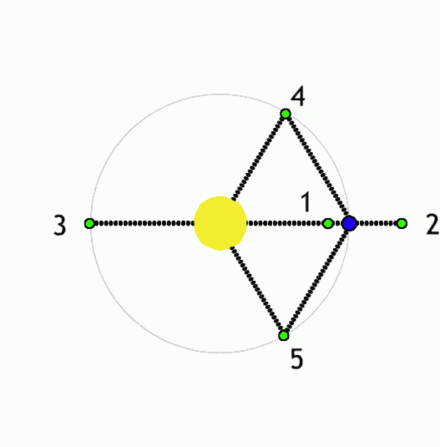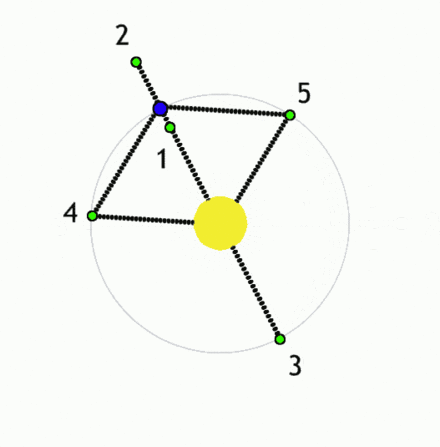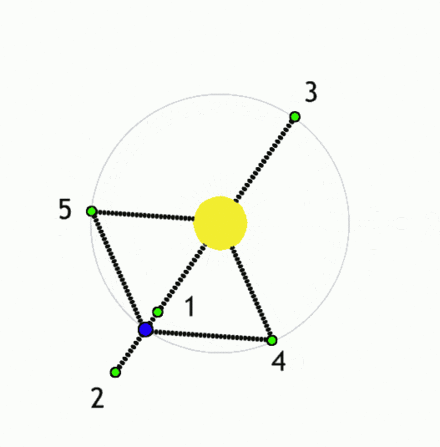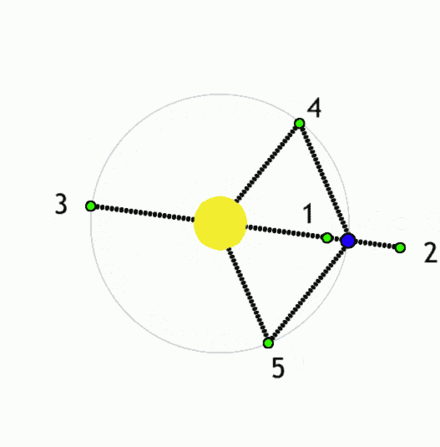
Manjša telesa (zelena) v Lagrangeovih točkah ležijo v območju ravnovesja sil (recimo dveh zvezd).
V kateri koli drugi točki gravitacijske sile prevladajo in telesa se začnejo premikati
proti enemu od obeh masivnih teles, recimo proti zvezdama (lahko tudi izven sistema za točko L2).
Vir: WIKI
Po domače si lahko Lagrangeeve točke predstavljamo kot sile na majhno telo med kroženjem v bližini dveh velikih teles, kjer so - sila zaradi rotacije in obe gravitacijski sili - v ravnovesju (primer vrteče se gramofonske plošče, če nanjo položimo majhno železno kroglico, bo sredobežna sila rotacije kroglico zabrisala s plošče, če pa je v osi vrtenja plošče recimo magnet, bo le ta na določeni razdalji r od središča zadržal kroglico na plošči, kjer se obe sili izničita; privlačna in njej nasprotna sistemska sredobežna sila zaradi rotacije – tej točki lahko rečemo stacionarna ali Lagrangeeva točka – ni pa to zelo stabilna lega).
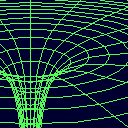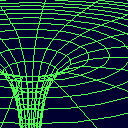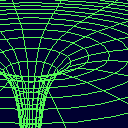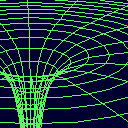
Na sliki 2 je prikazan potek potenciala Φgc za razmerje mas MN/MK=10. Slika je narisana v enotah G(MN + MK)/a.
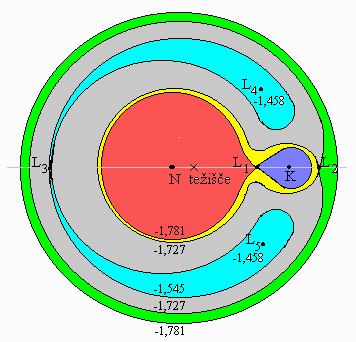
Slika 2a. Sklenjene krivulje potenciala Φgc
so preseki ekvipotencialnih ploskev.
Na sliki je prikazan potek potenciala Φgc
za razmerje mas MN/MK=10.
Slika je narisana v enotah
G(MN + MK)/a.
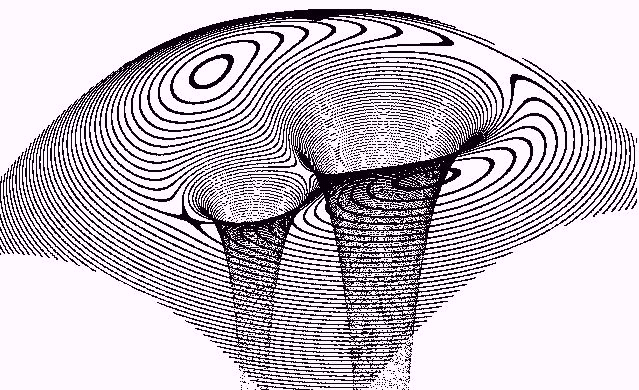
Slika 2b.
Izjemno nazorna 3D predstavitev potenciala dvojnega sistema,
narisal Miha Juras na Mladinskem astronomskem taboru MART 1994
(Ivančna Gorica, 8.-17. julij 1994, mentor Zorko Vičar).
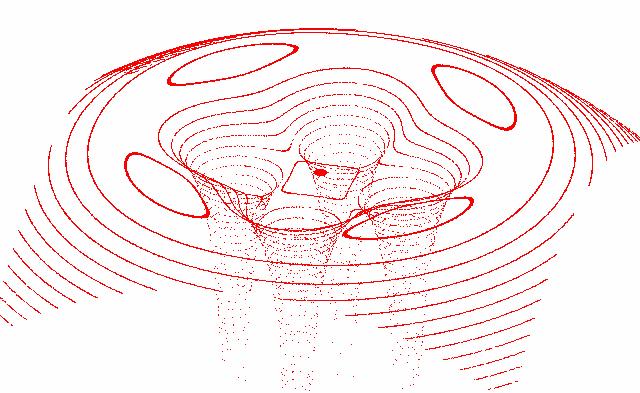
Slika 2c.
Izjemno nazorna 3D predstavitev potenciala sistema štirih zvezd,
narisal Miha Juras na Mladinskem astronomskem taboru MART 1994
(Ivančna Gorica, 8.-17. Julij, mentor Zorko Vičar).
Slika 2d. Še ena zanimiva predstavitev potenciala dvojnega sistema.
Poiščimo lokalne stacionarne točke,
z znanim pogojem
∇
Φgc = 0,
( ∂
Φgc/∂
r=0 in ∂
Φgc/∂
φ
=0 ).
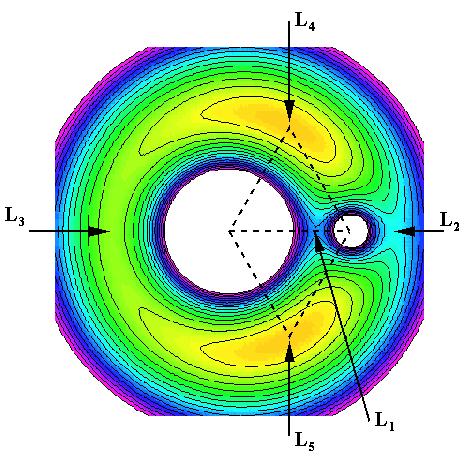
Te točke se imenujejo tudi Lagrangeve točke in so na sliki
označene z L. Točki L4 in L5 sta
ekstrema, L1, L2 in L3 pa so sedelne točke.
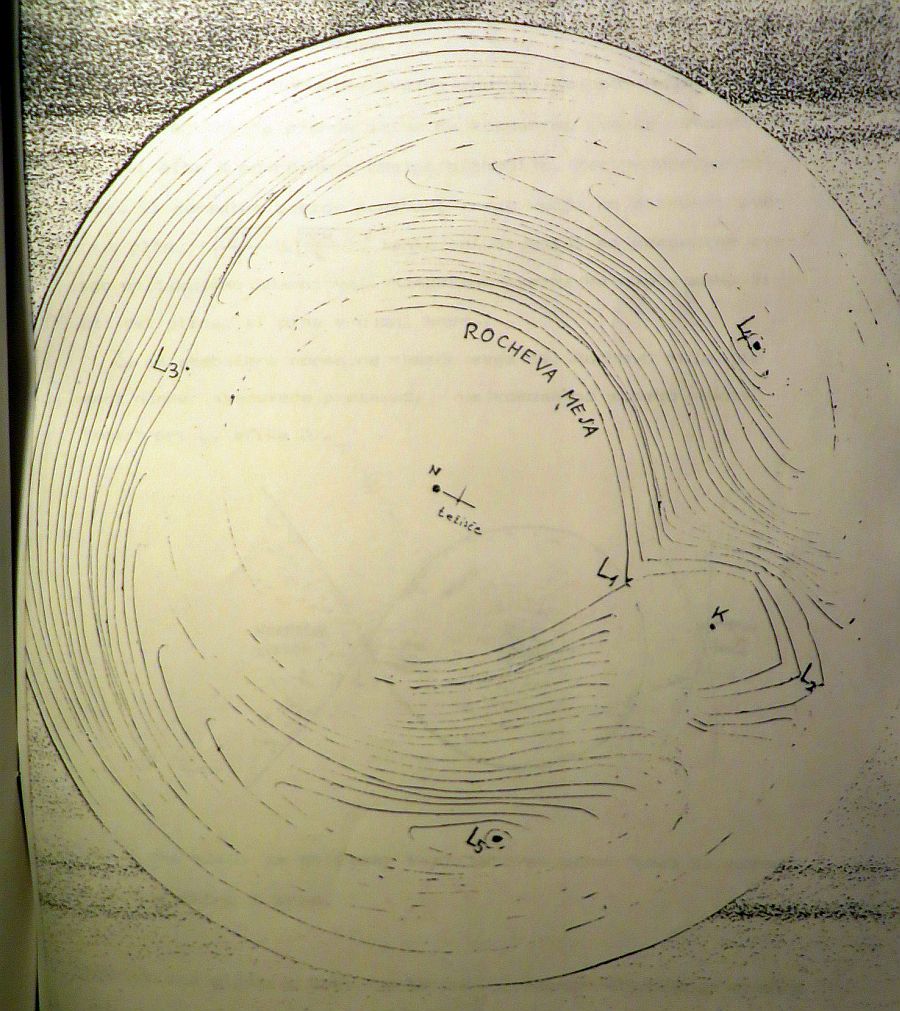
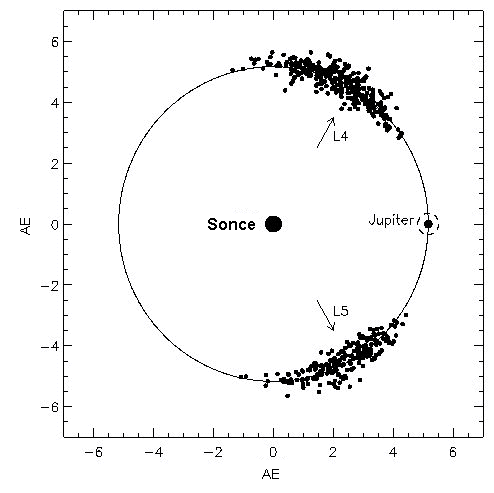
Prva potencialna krivulja od znotraj navzven označuje Rochevo mejo. Znotraj meja, a zunaj zvezdinega površja, prevladuje potencial normalne zvezde. Zunaj meje sta Lagrangevi točki L4 in L5, ki sta stabilni za delce kljub dejstvu, da sta ekstrema. Vzrok tej stabilnosti je Coriolisova sila. V sistemu Zemlja, Luna so v L4 in L5 astronomi opazili zgoščena oblaka. Prav tako vsebuje sistem Sonce-Jupiter v L4 in L5 asteroide imenovane Trojanci (odkril jih je Wolf leta 1906).
4) TOK PLINA IZ NORMALNE NA KOMPAKTNO ZVEZDO
Posebno važna je Rocheva meja, ki določa največjo možno ekspanzijo zvezdine atmosfere. Iz slike 2 je razvidno, da pri L1 potencial lokalno doseže vrh - Rochevo mejo in nato začne padati v smeri kompaktne zvezde.
Če je površina normalne zvezde znotraj Rocheve meje, potem je
edini mehanizem za prenos plina
na kompaktno zvezdo zvezdni veter, ki piha s površine z ubežno
hitrostjo. Ker je ubežna hitrost iz
normalne zvezde po navadi mnogo večja od hitrosti zvoka v plinu
( (χP/ρ
)1/2<<(2GM/R)1/2), lahko
pri akreciji na kompaktno zvezdo pričakujemo udarni val.
Kompaktna zvezda bo ujela samo
tisti del plina, ki piha v njeni smeri.
Če pa atmosfera normalne zvezde sega čez Rochevo mejo, se mora njena atmosfera pretakati na kompaktno sosedo skozi "šobo" pri L1 (slika 3).
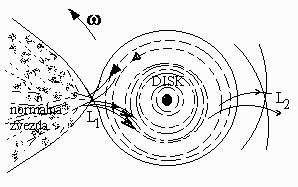


Kvalitativno sliko o toku razberemo iz Navier-Stokesove enačbe 3. Plin teče skozi šobo L1 na kompaktno zvezdo. Po prehodu skozi šobo se mu poveča hitrost na račun potencialne energije. Coriolisova sila ga odkloni v desno, gravitacijska sila kompaktne zvezde pa v levo. Pritekajoči plin zaradi viskoznosti reagira s plinom, ki je že okrog kompaktne zvezde in tvori tako imenovani akrecijski disk. Večji del plina ostane v disku, ostali del pa pridobi vrtilno količino zaradi viskoznih sil in ga vrže ven iz diska nazaj na kompaktno zvezdo ali skozi L2 iz sistema.
Če deluje pretvarjanje kinetične in potencialne energije v sevanje predvsem v plasteh diska, ki so blizu kompaktne zvezde, lahko opišemo dogajanje v disku, ne da bi natanko poznali kvantitativen potek selitve plina iz normalne na kompaktno zvezdo.
5) DISK IN OHRANITVENI ZAKONI
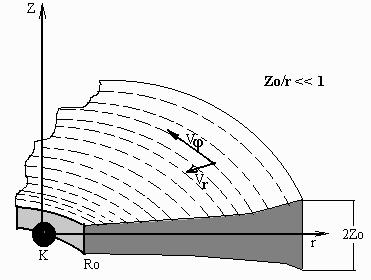
Slika 4. Shematični prikaz diska okrog kompaktne zvezde.
Zaradi viskoznega trenja znotraj diska, ki je posledica naraščanja
obhodne hitrosti plina s padajočim polmerom, se sprošča toplota, ki jo
disk odda v obliki sevanja. Obravnavali bomo primer, ko je izsev
(svetlobna moč) dosti manjši od kritičnega (2), zato je tudi
majhna hitrost akrecije (M'). Privzamemo,
da lahko gibanje plina na razdalji r od kompaktne zvezde
obravnavamo kot Keplerjevo. Torej je
vrtilna količina na enoto mase pri radiju r:
Γ=(GMK/r3)1/2r2=(GMKr)1/2.
Potem, ko se plin spusti
od r1 do r2, je moral na enoto mase oddati vrtilno količino: Δ
Γ
=(GMK)1/2(r21/2-r11/2). Pri toku
akrecije M', mora odtekati tok vrtilne količine: Γ
'=M'(GMKr)1/2. Zaradi majhne viskoznosti so
radialne hitrosti (vr) veliko manjše od obhodnih hitrosti
(vφ
). Velja |vr|<<|vφ|.
Tenzor deformacijske
hitrosti se zato zapiše v naslednji obliki:
|∂vx/∂x 1/2(∂vx/∂y + ∂vy/∂x) 0|
(def(v))=|1/2(∂vx/∂y + ∂vy/∂x) ∂vy/∂y 0|
|0 0 0|
V kartezičnih koordinatah.
|0 σφr 0|
(def(v))=|σφr 0 0|
|0 0 0|
V cilindričnih koordinatah.
Pri čemer je σφr=(∂vφ/∂r - vφ/r)/2
Komponenta tenzorja viskozne napetosti tφr je:
(5)
tφ
r = -2η
σ
φ
r=3ηω/2
Stacionarno stanje določajo štirje osnovni zakoni: ohranitev mase, vrtilne količine, energije, gibalne količine.
a) Ohranitev mase
Masni tok je enak na vseh oddaljenostih od kompaktnega objekta, zato lahko zapišemo -2πr∑vr =M', pri čemer je ∑=2zρ gostota na enoto površine.
b) Vrtilna količina
Če opazujemo disk med r in Ro, potem priteka v ta del vrtilna količina M'(MKGr)1/2, pri Ro pa odteka M'(MKGRo)1/2 . Torej je tok vrtilne količine, ki ga poganja viskoznost:
(6) Δ Γ '= M'(MKG)1/2( (r)1/2-(Ro)1/2 )
Po zakonu o vrtilni količini poganja ta tok navor: 2π r2zotrr, od koder sledi zveza:
2zotr= (M'(MKG)1/2/(2π r2))( (r)1/2 -(Ro)1/2 ) ≈ M'(MKGr)1/2/r2 za r >> Ro
c) Energijski zakon
Moč proizvedena na enoto volumna zaradi viskoznosti je:
ε
=∑
iktik(def(v))ik=2η
Tr(def(v))2=4η
(σ
φ
r)2
.
Ta moč je po energijskem zakonu enaka izsevu.
Gostota skupnega izsevanega toka (j) je enaka proizvedeni moči
na enoto ploščine:
(7) 2j=2zoε =-2σ φ r2zotφ r=(3M'MKG/(4π r2r))( (1 -(Ro/r)1/2 )
Od tod sledi, da je sproščena moč med r1 in r2:
(8) P=r1∫r22zoε2π rdr= =(3/2)M'MKG( ( 1 -2(Ro/r1)1/2/3)/r1 - ( 1 -2(Ro/r2)1/2/3)/r2 ) ≈ (3/2)M'MKG(1/r1-1/r2) za r2>r1>>Ro
Rezultat nas nekoliko zmede. Zakaj faktor 3/2 in ne 1/2 kot bi
pričakovali? Skušajmo pojasniti izvor sproščene energije med r1 in r2.
Sproščena gravitacijska potencialna energija je:
M'M K G(1/r1-1/r2), toda samo polovica te energije
lahko gre v toploto, a ostalo gre v obhodno kinetično energijo
(virialni teorem 2<T>=-Ep).
Torej je
ΔE'top= (1/2)M'MKG(1/r1-1/r2).
Pomembno je vzeti v račun, da viskozne sile razen vrtilne
količine prenašajo še energijo. Prenešena energija čez radij r je:
E'=ω (2π r2zotj rr) =M'MKG( (1 -(Ro/r)1/2)/r.
Oddana energija med r1 in r2 je: Δ E'= (1/2)M'MKG(1/r1-1/r2). Vsota obeh nam da rezultat 8. Izračunajmo zdaj celotno izsevano moč PL:
Pc=Ro∫∞ 2j2π rdr=M'MKG/(2Ro)
To je rezultat, ki smo ga pričakovali. Torej je vzrok navideznega paradoksa transport energije. To pomeni, da energija, proizvedena zaradi viskoznosti med r-(r-dr) ni nujno izsevana na tem intervalu (dr), ampak je prenešena proti robu diska in tam izsevana.
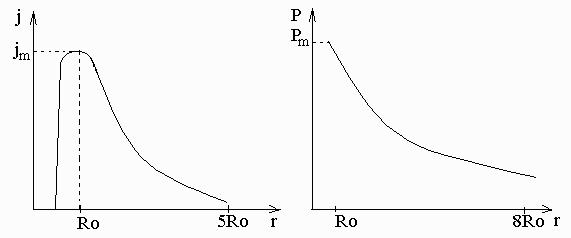
j=3M'MKG( (1 -(Ro/r)1/2 )/(8πr3) P=3M'MKG( (1 -2(Ro/r)1/2/3 )/(2r) rmaks=1,36 Ro rmaks=Ro j(rmaks)=3*66M'MKG/(8πRo77) P(rmaks)=M'MKG/(2Ro)Slika 5. Diagrama kažeta spreminjanje moči in energijskega toka v odvisnosti od radija.
d) Vertikalno ravnovesje sil
Pomagajmo si s sliko 6.
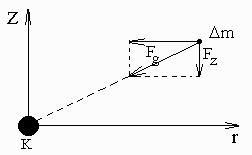
Slika 6. Slika prikazuje silo gravitacije Fg in njeno komponento Fz,
katera deluje na maso Δm
v smeri pravokotno na ekvatorialno ravnino.
Da masa Δm ne pade v ekvatorialno ravnino, mora silo Fz uravnovesiti vertikalna sila tlaka. Iz povedanega sledi, da je debelina diska določena z ravnovesjem med silo tlaka na enoto mase ((1/ρ )∂ P/∂ z) in silo Fz/Δ m. Izračunajmo še vrednost sile Fz pri radiju r:
Fz/Δ m=∂ (MKG/(r2+z2)1/2) /∂ z ≈ GMKz/r3 za z/r<<1.
Ko sta sili v ravnovesju, velja:
(9)
-(1/ρ
)∂
P/∂
z= GMKz/r3
Zapišimo izraz 9 v integralni obliki in po integraciji dobimo
približno vrednost za debelino diska.
-(r3/(ρ GMK))P∫ 0dP=0∫ Zozdz sledi Zo≈ (Pr3/(ρ GMK))1/2
Upoštevajmo še, da je hitrost zvoka v plinu Cz=(P/ρ)1/2 in kotna hitrost ω=(GMK/r3)1/2 . Tako se polovična debelina diska preprosto izrazi kot Zo≈Cz/ω. Ta račun je približen, ker ne poznamo podrobnosti o disku.
5) SPEKTER DISKA
Predpostavimo, da disk seva kot črno telo, po zakonu našega znamenitega rojaka
Jožefa Stefana velja:
(10)
j=σT4.
T=(3 107K)*(M'/(10-3Mo/leto ))1/4*(M/Mo)-1/2*(Mrg/(rMo))3/4*(1-(Ro/r)1/2 )1/4
Največ svetlobe je emitirano pri (Mr g)/( rMo)=10 za črne luknje in nevtronske zvezde ter (Mrg)/(rMo)=10-4 za bele pritlikavke. Energijo fotona zapišemo s pomočjo valovne dolžine hνm = hc/λm . Lambda maksimalni, kjer je gostota izsevanega toka največja, pa izračunamo iz Wienovega zakona: hc/λm = hcT/Kw=(2,44 10-4eV)(T/K). Za T vstavimo izraz 10 in dobimo naslednje vrednosti za energijo izsevanega fotona:
hνm =
(1KeV)(M'/(10-9Mo/leto))1/4(M/Mo)-1/2
za nevtronske zvezde in črne luknje
hνm =
(0,01KeV)(M'/(10-9Mo/leto))1/4(M/Mo)-1/2
za bele pritlikavke
Iz zgornjih izrazov razberemo, da so izsevane energije v mejah od 1 do 10 KeV, torej je to rentgensko sevanje.
Kljub dejstvu, da smo naredili veliko poenostavitev, se naš rezultat dobro ujema z izmerjenimi vrednostmi.
Izmerjene vrednosti izsevanih energij za nekatere nebesne objekte: Cyg x-1 2-6 KeV Ic 443 2-10 KeV MSH 15-52A 2-10 KeV Puppis A 0,2-3 KeV Seminar iz fizike: Zorko Vičar FNT Ljubljana, 1985 Seminar sem zagovarjal še pri profesorju dr. Ivanu Kuščerju (* 17. junij 1918, Dunaj, † 2000, Ljubljana), ki je bil zelo strog, a nad tem seminarjem je bil po predstavitvi zelo navdušen. Kar odleglo mi je ... Zakaj tak strah? Eden od študentov (kolegov) je namreč bil na seminarju ostro zavrnjen s strani Kuščerja in tudi mentorja (kar je bilo precej nenavadno ...) in ta dogodek nas je vse ornk prestrašil ... Spodaj (na dnu strani) je še nekaj zelo zanimivih anekdot iz časa študija.To je bil prvi seminar (prva temeljitejša obdelava) iz področja dvojnih zvezdnih sistemov v Sloveniji. Nato se je to področje hitro razvijalo, tudi študentje astronomije so iz tega seminarja dobivali naloge - kar je bila potrditev kvalitete same vsebine seminarja. Moj mentor je bil iskrivi profesor astronomije in fizike dr. Andrej Čadež.
LITERATURA
I.D.Novikov and K.S. Thorne: Black hole astrophysics, Gordon and
Breanch science publishers, London 1972
G.D. Chagelishvili and I.G.Lominadze:Disk accretion onto black
holes and magnetic fields, International
centre for theoretical physics, Trieste, 1985
Andrej Čadež: Fizika zvezd, Društvo matematikov,
fizikov in astronomov SRS, Ljubljana 1979
Še nekaj takratnega mojega gradiva - poučno (muzejska vrednost naše generacije).

Zapiski nastanka seminarja, zapis potenciala in pogojev za iskanje Lagrangevih točk.

Zapis programa v basicu za izris ekvipotencialnih ploskev dvojnega sistema (razmerje mas 1/10).

Izris ekvipotencialnih ploskev preko basic programa v računalniku Sinclair ZX Spectrum.
Rabil sem še kasetofon za snemanje programov in televizor za prikaz ter iglični printer.

Primer folije za predstavitev, ki smo jo položili na
grafoskop - pisanje vsebine, risanje slik
s flomastri na folijo.

Primer strani iz oddanega seminarja pred zagovorom - kombinacija
printa in pisanje formul z roko med tekst. Nato smo dopolnjene strani kopirali
in vezali ter oddali.
Pomen tesnega dvojnega sistem je z leti v astronomiji samo naraščal - takrat (leta 1985) smo bili
osredotočeni bolj na iskanje črnih lukenj, izvorov rentgenskih žarkov ...
Če na kratko ponovimo.
Iščemo stacionarne točke potenciala Φgc z odvajanjem in iskanjem ničel
odvodov -
to so Lagrangeve točke, primerne recimo za nameščanje znanstvenih satelitov (sond, teleskopov ...).
Na področju točk L4 in L5 pa se nabirajo asteroidi -
recimo Trojanci v sistemu Jupiter - Sonce.
IZJEMNO pomembne pa so tudi (recimo točka L1) v tesnih dvojnih sistemih zvezd pri pretakanju snovi
iz velikih "normalnih" zvezd (N)
na kompaktne
zvezde (K) - recimo na bele pritlikavke ..., torej pri nastanku akrecijskih diskov.
Supernova tipa Ia nastane prav v takem dvojnem sistemu in preko standardnega svetilnika
eksplozije take supernove smo ugotovili šokantno dejstvo,
da se vesolje pospešeno širi.
Ko se prvotno bela pritlikavka poveča do Chandrasekharjeve
meje, na okrog
1.4 M☉ (2.765×1030 kg), eksplodira kot supernova
tipa Ia (elektroni in protoni se pod težo gravitacije združijo
v nevtrone:
e- + p › νe + n,
sprosti se veliko nevtrinov in enormne količine energije - in to kar za
izsev skoraj celotne galaksije, za okrog 5 milijard Sonc).
Razumevanje dvojnega sistem nas je torej dobro desetletje po mojem seminarju
pripeljalo do nenadejane rešitve uganke vesolja - in sicer, da se vesolje
v resnici širi pospešeno (za ta dosežek so seveda bile podeljene Nobelove nagrade).
Ko sem delal ta seminar leta 1985, o teh izjemnih možnostih študija dvojnega sistema
noben na univerzi niti ni slutil - supernove tipa Ia v povezavi z dvojnim sistemom normalne
in kompaktne zvezde (bele pritlikavke), torej meritve dinamike vesolja preko mehanizma
dvojni sistem, supernova in seveda nenadejani rezultati ... To so bile meritve. analize, odkritja,
ki so nas "našle" (nekoliko nepripravljene)
okrog leta 2000.
Fantastično !!!
Povejmo še,
da sodobni standardni model za eksplozije supernov tipa Ia temelji na predlogu Whelana
in Ibena že iz leta 1973 in privzame scenarij prenosa mase na degenerirano zvezdo spremljevalko.
Iz povedanega sledi,
da se splača posvetiti še nekaj strani
tehničnim rešitvam, fiziki dvojnega sistema teles v vesolju.
Kot smo že omenili - potencial lahko zapišemo tudi v naslednji obliki:
Φgc = -G( MN/(r2 + rN2 + 2rrNcos(φ ) )1/2 + MK/(r2 + rK2 - 2rrKcos(φ ) )1/2 ) - ω 2r2/2
Poiščimo lokalne stacionarne točke, z znanima pogojema, parcialna odvoda morata biti 0.
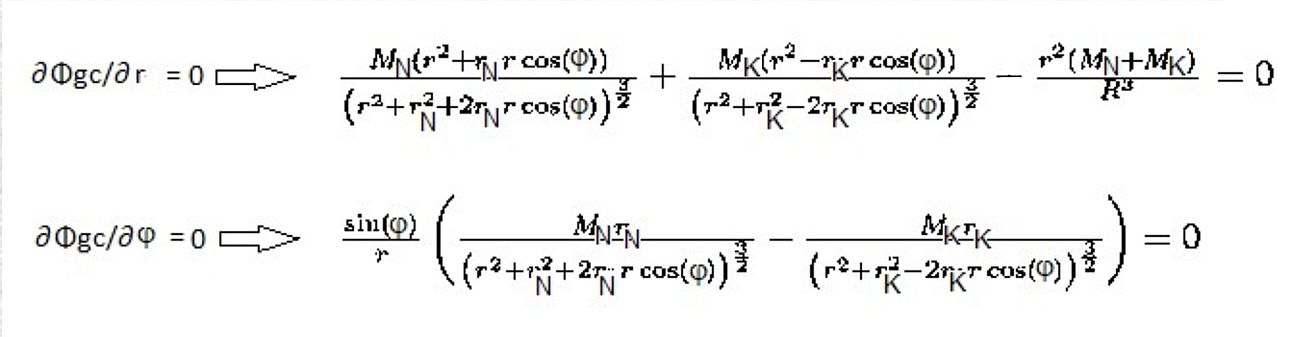
Rešitve zahtevajo numerično reševanje (velja: R = rN + rK,
za ω smo vstavili Keplerjevo vrednost
ω2 = G(MN+MK)/(rN + rK)3 ).
Odvod ∂
Φgc/∂r = 0, je po odvajanju pomnožen z r - tako se lažje najde rešitve. Seveda smo povsod okrajšali
gravitacijsko konstanto G.
∂Φgc/∂r
=
MN(r2 + rNrcos(φ) )/( r2 + rN2 + 2rrNcos(φ) )3/2
- MK(r2 - rKrcos(φ) )/( r2 + rK2 - 2rrKcos(φ) )3/2
- r2(MN + MK)/R3
= 0
Pri iskanju nul najprej gledamo števce (pomnožili smo jih še z r) na zveznici
obeh teles v odvodu potenciala po r, ti števci so:
MN( r2 + rrNcos(φ) )
MK( r2 - rrKcos(φ) )
r2(MN + MK)
Zakaj so pomembni števci v ulomku odvoda potenciala po r?
Ker je odvod potenciala enak sili na telo (imamo torej opravka z vektorskimi količinami),
so torej tudi pomembni
predznaki pri posamznih členih (vsota treh sil na majhno telo mora biti nič v
sisemu dveh velikih nebesnih teles - to so stacionarne točke, ki jih iščemo).
Vemo, da ni vseeno, kako usmerimo sile na zveznici obeh teles,
če je stacionarna točka med telesoma ali izven njiju.
Enačbo, ki ostane po odvodu ∂Φgc/∂r = 0, bomo maksimalno preoblikovali,
za končno iskanje ničel z iteracijo.
Vpeljali bomo spremenljivko x = r/rN in tudi izpostavili MK in računali z
razmerji MN/MK.
Upoštevali bomo tudi, da je rK/rN = MN/MK
(iz definicije težišča) in tudi še, da je R = rN + rK = rN(1 + rK/rN) = rN (1 + MN/MK) .
Za cos(φ) na zveznici obeh teles velja cos (0) = 1 (glej sliko).

Po preoblikovanju enačbe ∂Φgc/∂r = 0, za pogoj cos(0) = 1, ostane dokaj preprosta olika:
(MM/MK)/((x+1)*(x+1)) + 1/((x-rK/rM)*(x-rK/rM)) - x/((1 + MN/MK)*(1 + MN/MK))
= 0
Zgornja enačba je primerna takoj za iteracijo, če pa jo zapišemo še z razmejem
u = MN/MK =
rK/rN in uporabimo potenco 2, potem je enačba še krajša:
u/(x+1)2 + 1/(x-u)2 - x/(1 + u)2 = 0
Enačbo lahko preoblikujemo, delimo z x:
u/(x(x+1)2) + 1/(x(x-u)2) - 1/(1 + u)2 = 0
In seveda brez težav opazimo, da je enačba kubna (sicer v ulomku) in torej lahko
pričakujemo TRI rešitve.
Za MN/MK = 10 velja:
(10)/((x+1)*(x+1)) + 1/((x-10)*(x-10)) - x/((1 + 10)*(1 + 10)) = 0
Da ta enačba ni čisto ustrezna za vse primere, poglejmo
predznake za imenovalce.
L1)
Iščemo nulo za r med težisčem in kompaktnim (majhnim) telesom rK > r > 0, na zveznici φ = 0.
Srednji števec MK( r2 - rrK) bo zato negaiven
(saj v tem primeru velja rrK > r2). Tako dobimo izraz.
(MM/MK)/((x+1)*(x+1)) - 1/((x-rK/rN)*(x-rK/rN)) - x/((1 + MN/MK)*(1 + MN/MK))
= 0
Preprosta shema sistema dveh teles mase MN > MK, za medsebojno razdaljo velja R = rM +rK, slika spodaj:
MN težišče Mk
O--rM---x-----------------rK-------------------o
Sile na majhno telo *, ki je med telesoma MN in MK, Fc je sistemska centrifugalna sila (pomembne so smeri, predznaki):
MN tež. FMN FMK Fc Mk
O x <---- * --> --> o
L1
L2)
Iščemo nulo za r večje od razdaje do kompaktnega majhnega telesa r > rK, na zveznici φ = 0,
v tem primeru se predzanki števcev ne spmenijo.
(MM/MK)/((x+1)*(x+1)) + 1/((x-rK/rN)*(x-rK/rN)) - x/((1 + MN/MK)*(1 + MN/MK))
= 0
Sile na majhno telo *, ki je desno od majhnega MK telesa, Fc je sistemska centrifugalna sila (pomembne so smeri, predznaki):
MN tež. Mk FMN FMK Fc
O x o <-- * <---- ------>
L2
L3)
Iščemo nulo za negativne razdalje r, -r < -rN, na zveznici φ = 0,
v tem primeru pa je r pri trejem členu pokrajšane enačbe negativen in velja enčba -x = -(-r/RN) > 0, zatorej zapišimo:
(MM/MK)/((x+1)*(x+1)) + 1/((x-rK/rN)*(x-rK/rN)) + x/((1 + MN/MK)*(1 + MN/MK))
= 0
Sile na majhno telo *, ki je levo od velikega MN telesa, Fc je sistemska centrifugalna sila (pomembne so smeri, predznaki):
FMN FMK Fc MN tež. Mk
---> * --> <----- O x o
L3
Tako torej z iteracijo (recimo z bisekcijo) poiščemo tri ničle odvoda,
tri Lagrangeve točke L1, L2, L3 (sedelne očke).
A obstajata še dva maksimuma izven smeri zveznice obeh teles.
L4 in L5)
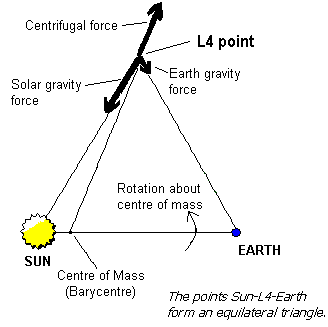
Slika za pomoč pri razumevanju iskanja eksteremov potenciala L4 in L5 izven zveznice obeh teles.
V L4 in L5 je tudi vsota sil na majhno telo enaka nič -
za pomoč pri razumevanju tega fenomena so narisani trije vektorji sil.
Še drugi pogoj za ekstreme je odvod po kotu: ∂Φgc/∂φ = 0.
--------------------------------------
Odvod poenciala dveh teles po kotu ∂Φgc/∂φ = 0 pa nam da
še dva lokalna maksimuma - Lagrangevi točki L4 in L5.
∂Φgc/∂φ
=
(sin(φ)/r)( rNMN/( r2 + rN2 + 2rrNcos(φ) )3/2 - rKMK/( r2 + rK2 - 2rrKcos(φ) )3/2 )
= 0
Ker je rKMK = rNMN
(iz definicije težišča), dobimo iz enačbe ∂Φgc/∂φ = 0 (zgoraj)
naslednji izraz:
r2 + rK2 - 2rrKcos(φ) =
r2 + rN2 + 2rrNcos(φ)
Že ta rezultat (enakost) nam pove, da bo trikotnik od središč obeh
objektov do Lagrangevih točk L4 in L5 enakokrak.
Kot bomo videli proti koncu te obravnave - je ta trikotnik v resnici celo enakostraničen.
Izluščimo cos(φ), odštejemo r2, tako dobimo
rK2 - 2rrKcos(φ) =
rN2 + 2rrNcos(φ), ozioma
cos(φ)2r(rN + rK) = rK2 - rN2
= (rK + rN)(rK - rN), pokajšamo (rK + rN).
Za cos(φ) tako dobimo izraz:
cos(φ) = ( rK
- rN )/(2r)
V enačbo ∂Φgc/∂r = 0 vsatvimo v imenovalec recimo zgornjo enakost:
r2 + rN2 + 2rrNcos(φ).
Tako dobimo
(rMK + rMN - ( rNMN
- rKMK)cos(φ) )/(r2 + rN2 + 2rrNcos(φ))3/2 - r(MK + MN)/(rK + rN)3 = 0
- člen ( rNMN
- rKMK ) = 0 (po defniciji težišča).
Pokrajšajmo še r in tako dobimo:
(MK + MN )/(r2 + rN2 + 2rrNcos(φ))3/2 = (MK + MN)/(rK + rN)3
Od koder dobimo po krajšanju, korenjenju ... :
r2 + rN2 + 2rrNcos(φ) =
(rK + rN)2
Za cos(φ) vstavimo za L4 že izpeljan izraz: cos(φ) = ( rK
- rN )/(2r).
Tako dobimo r2 + rN2 + rN( rK - rN ) = (rK + rN)2,
oziroma:
r2 = rK2 + rKrN + rN2
= rK2(1 + rN/rK + (rN/rK)2).
Končna izraza za razdaljo r in kot φ od težišča do ekstremnih točk potenciala (L4 in L5,
kjer je sila na majhno telo v rotirajočem dvojnem sistemu nič - izven zvznice obeh teles)
sta torej:
r4,5 = rK(1 + rN/rK + (rN/rK)2 )1/2
cos(φ) = ( rK - rN )/(2r)
= ( 1 - rN/rK )/(2(1 + rN/rK + (rN/rK)2 )1/2 )
Še izračun kota φ, recimo v JavaScriptu.
φ =
Math.acos( ( 1 - rN/rK )/(2*Math.sqrt(1 + rN/rK + (rN/rK)2 )) ) * (180/Math.PI)
Še zanimivost - razdalja od središča normalne velike mase MN,
do Lagrangeve točke L4,5 je kar:
rN_L4 = rN + rM = R
Dokaz - glej sliko za r2N, vanj za L4 vstavimo r2 =
rK2 + rKrN + rN2
in za cos(φ) = ( rK - rN )/(2r), tako dobimo :
r2N_L4 = r2 + rN2 + 2rrNcos(φ)
= rK2 + rKrN + rN2
+ rN2 + rN(rK - rN)
r2N_L4
= rK2 + rN2 + 2rKrN
= (rK + rN)2
Tako velja po korenjenju - konec dokaza za razdaljo rN_L4 od centra velikega telesa do Lagrangeve
točke L4 ali L5 je R:
rN_L4 = rK + rN = R
***
Testiraj zgornjo teorijo z JS
kalkulatorjem za računanje Lagrangevih točk in reduciranega potenciala.
Poglejmo za sistem deset in ena Sončeva masa na razdalji 11 astronomskih enot
( MN = 10 M☉ in MK = 1 M☉, na razdalji R = 11 AU)
Lagrangeve točke in potenciale.
rN = R*MK/(MN + MK) in rK = R*MM/(MN + MK)
R = rN + rK = 11 AU
AU ≈ 150 106 km
Lagrangeve točke in potenciali so:
Lagrangeva točka L na razdalji r od težišča sistema:
L1 je na r = 6.892638458 AU
L2 je na r = 13.81691199 AU
L3 je na r = -11.416192062 AU
Kot φ = 64.71500395 °, med r za L 4 in 5 ter zveznico obeh teles
L4 je na r = 10.535653752 AU
L5 je na r = 10.535653752 AU
Lagrangeva točka L na razdalji d od centra velikega telesa:
L1 je na d = 7.892638458 AU
L2 je na d = 14.81691199 AU
L3 je na d = -10.416192062 AU
Kot φ = 60 °, med r za L 4 in 5 ter zveznico obeh teles
L4 je na d = 11 AU
L5 je na d = 11 AU
POTENCIALI Φ v enoti (MN + MK)/(rN + rK), brez konstante G:
Potencial v L1 = -1.785135831552786
Potencial v L2 = -1.7257684907025737
Potencial v L3 = -1.5452887932215131
Potencial v L4 = -1.4586776859504131
Potencial v L5 = -1.4586776859504131
---------------------------------------------------------------------------------------
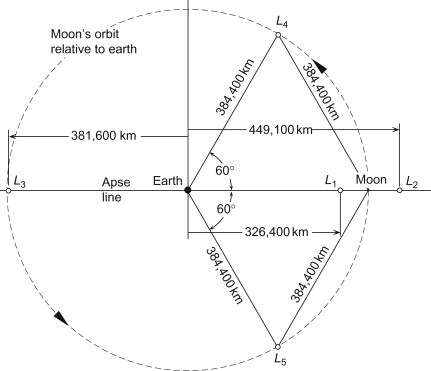
Lagrangeve točke sistema Zemlja-Luna.
Podatki:
R = 384400 km - razdalja Zemlja-Luna
Masa_Lune = 7.34767309 1022 kg = 73476730000000000000000 kg
Masa_Zem = 5.97219 1024 kg = 5972190000000000000000000 kg
Lagrangeva točka L na razdalji d od centra Zemlje:
L1 je na d = 326376 km
L2 je na d = 448921 km
L3 je na d = -381675 km
Kot φ = 60 °, med r za L 4 in 5 ter zveznico obeh teles
L4 je na d = 384400 km
L4 je na d = 384400 km
Lagrangeva točka L na razdalji r od težišča sistema (težišče sistema je odmaknjeno samo za 4671.85 km
od središča Zemlje):
L1 je na r = 321704 km
L2 je na r = 444249 km
L3 je na r = -386347 km
Kot φ = 60.6067 °, med r za L 4 in 5 ter zveznico obeh teles
L4 je na r = 382085 km
L5 je na r = 382085 km
Vir slike: https://www.sciencedirect.com/topics/engineering/lagrange-point
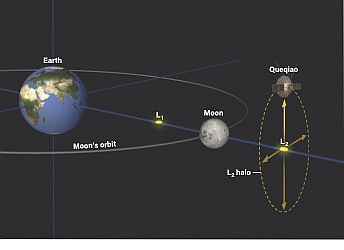
Lagrangeva točka L2 v sistemu Zemlja-Luna je primerna
za komunikacijski satelit, ki lahko cel čas nemoteno komunicira
z Zemljo. Ta komunikacija pride zelo prav pri poletih na Luno.
Lagrangeve točke Zemlja-Sonce so zelo pomembne.
L2 in JWST
L2 = 1.010048271688083 AU,
torej je od Zemlje oddaljena = (1.0100512750134183 -1)*150000000 km = 1507691
km ≈ 1,5 106 km.
Uporabite zgornji kalkulator in preverite podatek za lego L2 glede na Zemljo ...!!!
Vesoljski teleskop James Web se nahaja v Lagrangevi točki L2 - razlogov je
več razlogov. Prvi razlog je,
da je L2 najbolj oddaljena lokacija od Sonca, Zemlje in Lune, ki je še vedno dovolj
blizu Zemlje za enostavno komunikacijo. L2 je skoraj 4x razdalja Zemlja - Luna (384400 km).
Sonce oddaja velike količine sevalne energije, ki bi lahko zakrila tisto, kar lahko
vidi zelo občutljiv teleskop. Zato ima JWST tako velik (4-slojni) sončni ščit. Kljub
temu JWST deluje na Sončno energijo. L2 je tudi v liniji z Zemljo, vendar točka ni tako blizu,
da bi Zemlja blokirala Sončno svetlobo.
Tudi sonda SOHO (Solar and Heliospheric Observatory) recimo kroži skupaj s sistemom
Zemlja-Sonce v Lagrangeevi točki L1 in ima tako cel čas odprt pogled za slikanje Sonca.

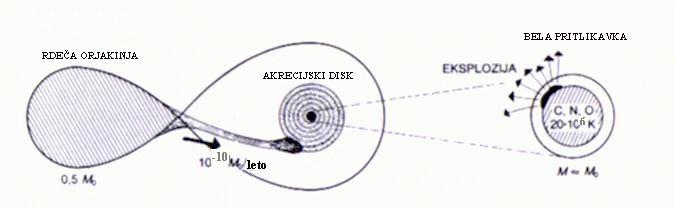
Do eksplozije supernove tipa Ia lahko pride zato,
ker se snov z normalne zvezde prek
Lagrangeve točke L1 (leži na zožitvi toka plazme) pretaka na bližnjo
belo pritlikavko.
Ko tej masa naraste prek Chandrasekharjeve
meje, na okrog
1.4 M☉, se bela pritlikavka pod
lastno težo sesede v nevtronsko zvezdo - eksplozija supernove tipa Ia
(vir: ESA/ATG medialab/C. Carreau).


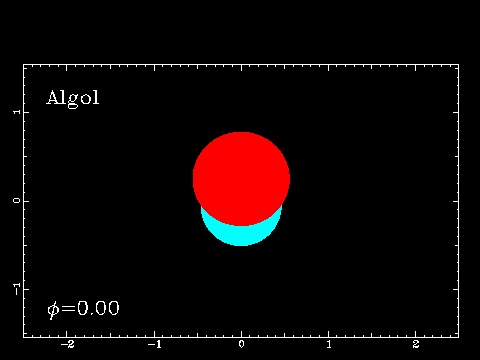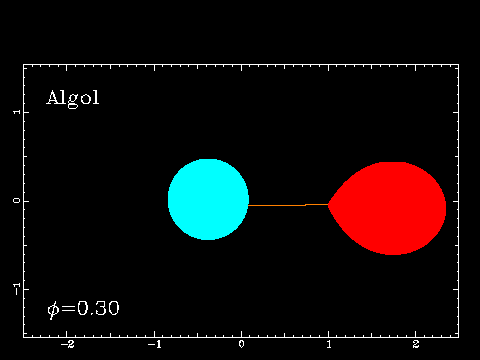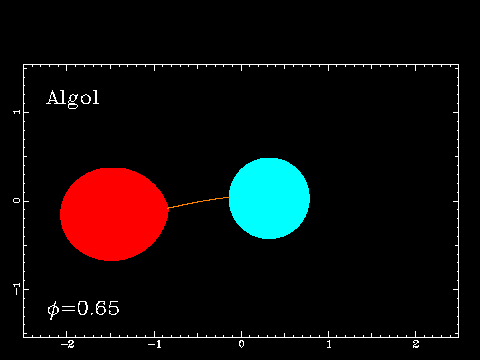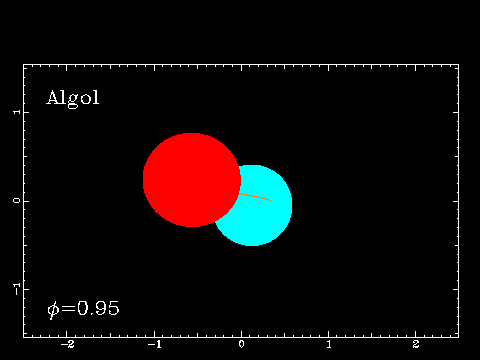








Pripravil Zorko Vičar
Nazaj na domačo stran.