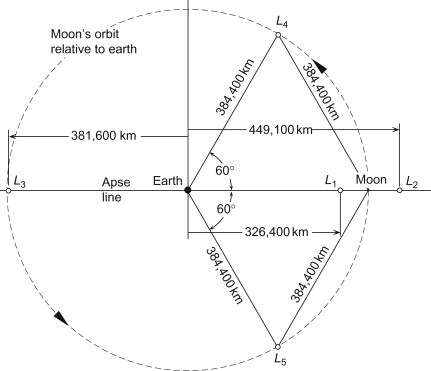
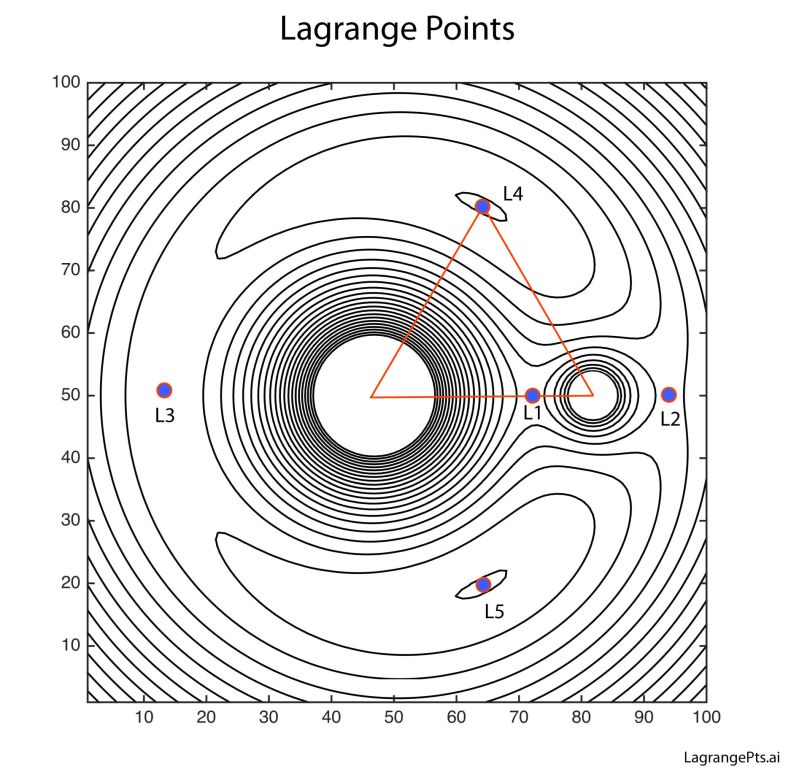
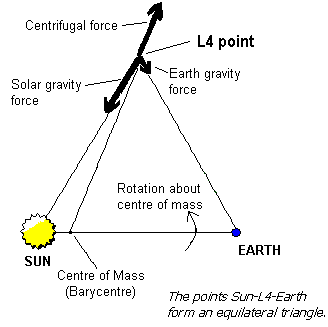
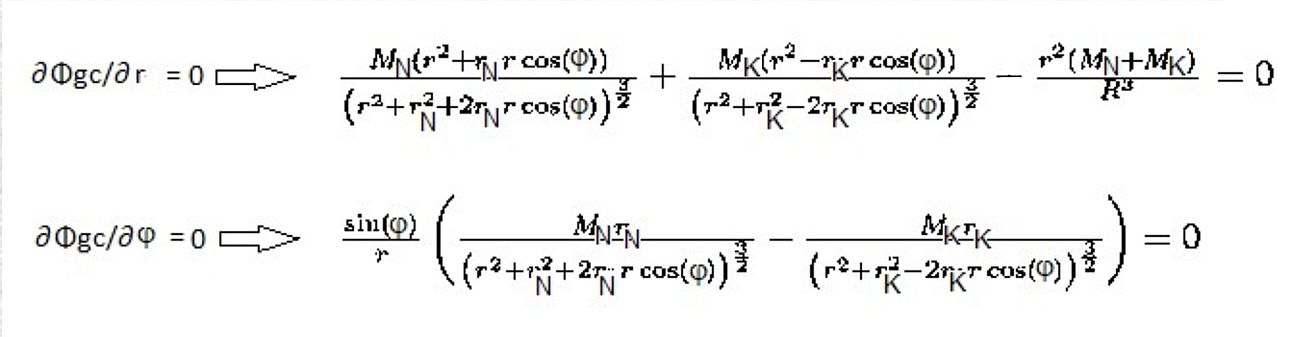Računanje Lagrangevih točk - JavaScript calculator
(LaGrange Points - JS Calculator)
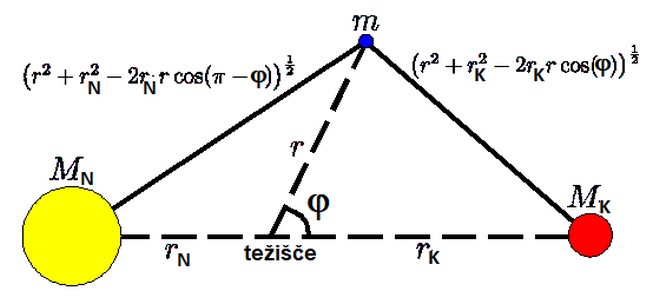
Gravitacijski in centrifugalni potencial Φgc:Φgc = Φg + Φc = -G( MN/|r-rN| + MK/|r-rK|) - (ω xr)2/2
Φgc = -G( MN/(r2 + rN2 + 2rrNcos(φ ) )1/2 + MK/(r2 + rK2 - 2rrKcos(φ ) )1/2 ) - ω 2r2/2
 |
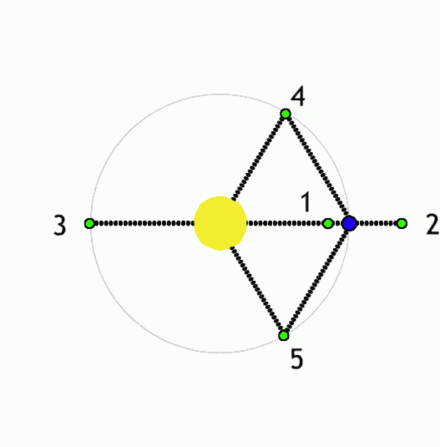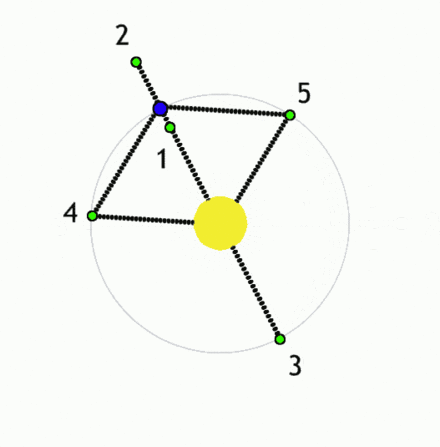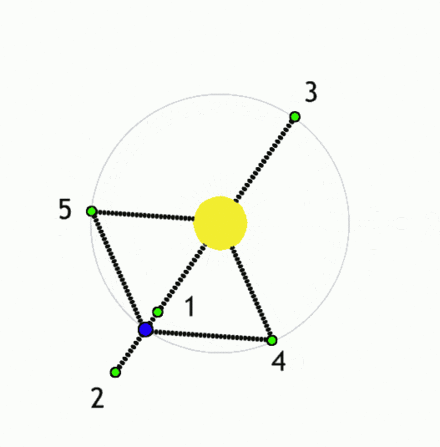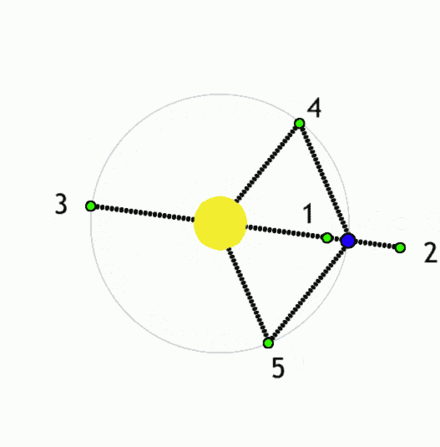
|