Prehodi Merkurja in Venere čez Sonce,
ocene trajanja in ponovitev
7. maja letos (dopoldan med 7:12 - 12:28) smo imeli enkratno priložnost opazovati prehod prvega kamna od Sonca (planeta Merkurja) čez Sonce. Prehod se je dogajal v skoraj idealnem vremenu in je zaradi dobre vidljivosti vse navdušil. Sončeve pege so "mirovale", Merkur, viden kot črna okrogla ploščica, pa se je počasi plazil čez Sonce. Naši mediji so spet zamudili lepo priložnost, da bi ljudem pokazali kaj pametnega in lepega.

Zgoraj, prehod Merkurja čez Sonce 7.5.2003, posnel Astronomski krožek Gimnazije Šentvid - Ljubljana. Podatki: 1/500 sekunde, film Konica 200 ISO; teleskop MEADE LX200 10", f/6,3. Spodaj slika pri f/10, pol ure prej.

Že naslednje leto (8. 6. 2004) bo viden prehod Venere, zadnji prehod Venere se je zgodil davnega leta 1882, čez tri leta bo spet prehod Merkurja, približno 14 prehodov na 100 let, torej bomo (bodo) spet kmalu lahko ponovili vajo. Keplerjeva zadnja usluga astronomiji je bila, ko je leta 1629 izračunal čase prehodov notranjih planetov, Merkurja in Venere, čez Sončevo oblo. Podatki so bili zbrani v znanih tablicah "tabulea rudolfinae". Teh prehodov prej niso nikoli opazili, ampak po Keplerjevih računih so se zanesljivo dogajali. Leta 1631 so takšen prehod Merkurja opazovali trije astronomi, med njim tudi Gassendi in tudi jezuit Johann Baptist Cysat (podatek o J.B. Cysatu je izbrskal prof. Marjan Prosen). Kepler je bil tedaj že leto dni mrtev, a njegova nebesna mehanika je preživela.
Ob takih dogodkih se zmeraj pojavi dilema, koliko in kaj otrokom povedti
o pojavu. Ponavadi smo astronomi veseli že, če večina mladih vsaj v živo
spremlja izjemne nebesne pojave, a včasih se morebiti splača razmisliti o
koraku naprej. Predvsem imam v mislih razumevanje dogodka ali morebiti
oceno trajanja, velikosti, razdalj, ponovitev. V primeru prehoda Merkurja
ali Venere prav nekako štrlita vprašanji o oceni časa trajanja prehoda (zakaj
prehod ponavadi traja kar nekaj ur) in ocena datumske ponovitve dogodka.
Prva miselna vaja, ki seveda temelji na izkušnjah večine otrok je, da je
prehod notranjih planetov čez Sonce načeloma enak kot pojav prehitevanja
pri dveh avtomobilih. V tem primeru zvedavi otrok v počasnejšem vozilu
(Zemlja) opazuje, kako se hitrejši avto (Merkur, Venera) premika glede na
okolico, recimo glede na Kamniške Alpe (Sonce). Druga ocena, to je čas
ponovljivosti dogodka, pa nekoliko bolj upošteva realnost, gre namreč za
periodična gibanja (po elipsah). Lep primer za tako periodično gibanje
teles, so urni kazalci. Urni in minutni kazalec sta recimo vsakih 12 ur
prekrita na isti poziciji. Pri planetih sta sicer prostorska geometrija in
dinamika precej bolj zapleteni, a logika je enaka. Takoj je potrebno
poudariti, da ravnini (orbiti) gibanja Zemlje (ekliptike) in recimo Merkurja
ne sovpadata, sekata se pod določenim kotom (ta kot znaša za Merkur 7 o,
za Venero pa 3,39 o). Ker torej planet potuje okrog Sonca po orbiti, ki je
nagnjena na ravnino ekliptike, seka ekliptiko v dveh točkah, imenovanih
vozla. Točka, kjer planet prečka ekliptiko na svoji poti proti severu, se
imenuje dvižni vozel, ko gre proti jugu pa padni vozel. Gibanje po tirnicah
- elipsah ni enakomerno, Zemlja precesira, ..., še bi lahko naštevali
posebnosti nebesne dinamike. Recimo, zaradi zamika-precesije
Merkurjevega perihelija, presečišče obeh ravnin počasi rotira (zamik za
574" na 100 let, se dogaja zaradi vpliva ostalih planetov in zaradi efektov,
ki jih opiše splošna Einsteinova teorija relativnosti, ki prispeva k zamiku
43" na 100 let). A skoraj vse to bomo na tem nivoju poenostavili, "pozabili
- zanemarili". Do prehoda, prekrivanja Sonca in notranjih planetov pride le,
če se Zemlja in notranji planet, recimo Merkur, nahajata na presečišču obeh
planetnih ravnin, v bližini vozlov (Zemlja, Merkur in Sonce ležijo na ali
blizu presečiščne premice). Če bi bili Sonce in planeti točkasta telesa, bi do
prehoda lahko prišlo le takrat, ko bi bili tako Sonce kot planet in Zemlja
natančno na premici vozlov. Ker pa imajo telesa svojo navidezno velikost,
zorni kot Sonca je kar okrog 0,5 stopinje, pride do prehodov tudi takrat, ko
so telesa zadosti blizu vozlov, blizu presečiščne premice.
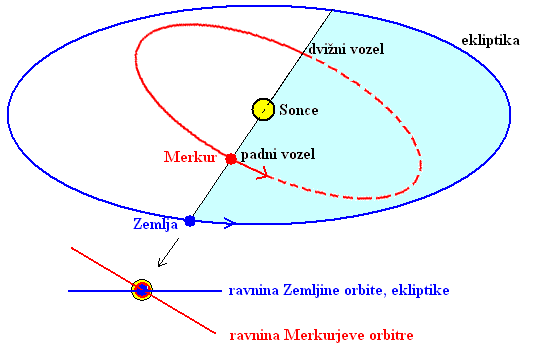
Shematska slika orbit Zemlje in Merkurja ob navideznem prehodu
Merkurja čez Sonce za letošnji prehod.
1) Ocena časa trajanja prehoda
Oceno bomo vezali na poenostavitve, ki bodo rezultirale v tri
podobne trikotnike (glej spodnji skici): oba planeta bomo
obravnavali kot točkasta v isti ravnini, Sonce bomo spremenili v
premico S dolžine premera Sonca (1390000 km), krivo gibanje bomo
poenostavili v premo (v tem primeru to ni hud greh, saj gre za kratke
poti, loke, ki so dolžinsko zelo blizu tetivam), zunanji opazovalec naj
bo v točki 0, ki se nahaja na sečišču povezovalnih premic, ki ju
tvorita Zemlja (Z) in Merkur (M) ob prvem (1) in zadnjem (2)
navideznem dotiku Merkurja s Soncem. Kot med premicama bo
vsekakor manjši od kotne velikosti Sonca (0.5 o), kar pomeni, da si
lahko privoščimo zelo poenostavljen, recimo pravokotni trikotnik.
Začetek dogodka naj bo trenutek, ko Merkur dohiti Zemljo,
povezovalna premica se naj takrat pravokotno dotika roba Sonca
(točke A). Opazovalec na Zemlji sedaj vidi kako ga Merkur prehiteva
in hkrati navidezno potuje če Sonce (S). V času t bo Merkur prišel do
drugega roba B. To je ocena časa, ki ga iščemo. Razdalja RM od
točke A do Merkurja naj bo povprečna razdalja od Sonca do
Merkurja (RM = 58*106 km), RZ razdalja od točke A do Zemlje naj
bo povprečna razdalja od Sonca do Zemlje (RZ = ae = 150*106 km),
R je razdalja od sečišča povezovalnih premic (točka 0) do točke A.
VM*t in VZ*t sta poti, ki ju opravita planeta Zemlja in Merkur v času
prehoda t. Iščemo seveda prav oceno (t) časa prehoda. Za hitrost
Zemlje bomo uporabili zaokroženo vrednost VZ = 30 km/s, za hitrost
Merkurja pa VM = 48 km/s.
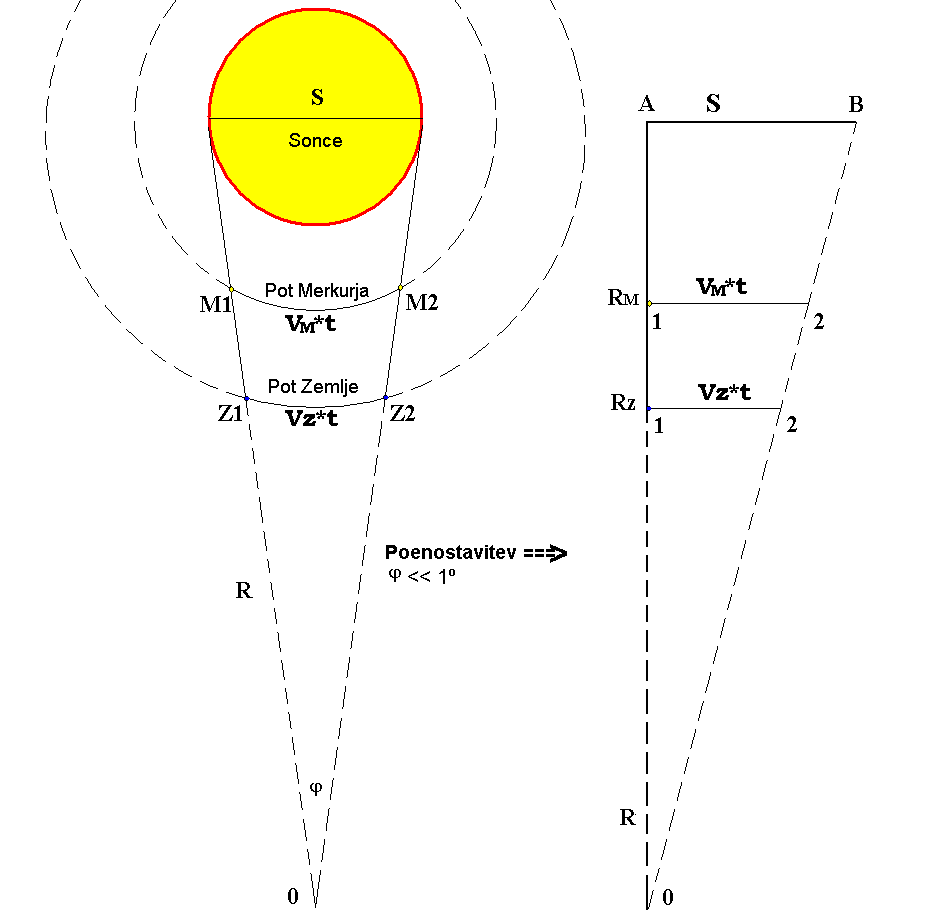
Skica poenostavitve krivega gibanja v premo. Prehod Merkurja čez Sonce
smo poenostavili v dirko dveh avtomobilov.
Sedaj zgolj geometrijske naloge, igre podobnih trikotnikov, se lahko lotimo na dva načina. Napišimo razmerja, ki veljajo med tremi podobnimi trikotniki.
S/R = VM*t/(R-RM) = VZ*t/(R-RZ) ===> (VM/VZ)*(R-RZ) = (R-RM)
Prva pot. Če bi radi čim manj mislili, iz zgornjih povezav izluščimo R (podatke o hitrostih in razdaljah preberemo iz priročnikov ali iz tega prispevka), nato recimo iz povezave
S/R = VM*t/(R-RM) izrazimo in izračunamo čas prehoda (t).
Druga pot je mogoče bolj astronomska.
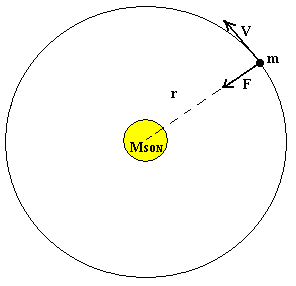
Slika za pomoč pri razumevanju odnosa med centralno maso - Soncem,
razdaljo r in hitrostjo v krožečega telesa (recimo planeta). To je seveda
poenostavitev, saj so orbite planetov elipse in ne krogi, a za naš nivo to ni
greh.
Iz Newtonovega gravitacijskega zakona
(F = m*a = m*v2/r =G*m*MSON/r2) izrazimo hitrost v telesa,
ki kroži okrog centralne mase, Sonca (G je gravitacijska konstanta, r je
razdalja telesa od središča Sonca ):
v = (G*MSON/r)1/2 = konst/r1/2.
Hitrost krožečega telesa je torej obratnosorazmerna s korenom razdalje od Sonca. Večja je razdalja, manjša je hitrost. Če upoštevamo enačbo za hitrost v(r), dobimo za razmerje med hitrostima kar koren obratnega razmerja med razdaljama.
VM/VZ = (RZ/RM)1/2 = X
Za par Zemlja - Merkur je X =1,6. Če pametno izpostavljamo, dobimo po parih vrsticah telovadbe naslednji izraz za čas prehoda Merkurja:
t=(S/VZ)*(X2-1)/(X3-1)
Za Merkur je ocenjen čas t = 6,4 ure. To je zelo dobra ocena, saj velja za prehod čez središče Sonca, v kolikor planet seka Sonce bližje robu, se čas skrajša (7. maja je prehod trajal okrog 5 ur in 16 minut). Pomebno se je zavedati, da je to le rešitev za linerano gibanje, ki pa se kot primerjava lahko uporabi zgolj za razumevanje in oceno časa prehoda notranjih planetov čez Sonce. Korektna rešitev seveda temelji na dinamiki, elementih tira in nebesni trigonometriji. Kot bomo videli, je Merkur zaradi sploščene orbite kar zapleten, pri njem se dogaja 2x več prehodov v dvižnem vozlu kot v padnem. Pri Veneri je ocena trajanja prehoda slabih 8 ur.
Da si oddahnemo od geometrije in razmerij, si privoščimo malo stranpoti in
se ustavimo pri enačbi za hitrost (v=(G*M/r)1/2), sploh, ker smo
nakazali od kod njen izvor. Ta enačba je pomembna iz večih razlogov, med
drugim nas direktno pripelje do "tehtanja", do skrivnosti temne-manjkajoče
snovi (velike zagate današnje astronomije). Ko so namreč astronomi preko
Dopplerjevega premika merili hitrosti materije na robu galaksij (prve
meritve so bile narejen že pred 70 leti, 1933 astronom Fritz Zwicky opozori na problem gibanja galaksij v jatah),
so ugotovili, da tam večinoma
Newtonova povezava za hitrost nekako "ne drži", če seveda upoštevamo
vidni del mase (Mgal_vidna je vsota mas praha, plina in vsota mas vseh
zvezd ...). Hitrosti so namreč večje kot jih daje povezava
v=(G*Mgal_vidna/r)1/2. Zakaj hitrosti od središča galaksije navzven v
določenih delih diska sploh ne padajo? Možnih je več odgovorov, recimo
če fizikalni zakoni, ki smo jih ljudje do sedaj izluščili, veljajo povsod po
vesolju, in če so meritve pravilne, potem iz enačbe sledi samo en odgovor
in sicer, da masa galaksije v disku (v grobem) narašča sorazmerno z
razdaljo r (v enačbi se tako r-a pokrajšata, M(r)/r ). Če to enormno maso
izračunamo iz meritev robne hitrosti
(Mgalaksije_celotna=rgalaksije*v2izmerjena/G) in primerjamo z maso, ki
jo določimo vizualno, se izkaže, da je vidna masa samo 10% nevidne,
temne mase. Temno snov-maso pripisujejo različnim oblikam: množici
temnih pritlikavk, planetov, raznim kvantnim delcem, Einsteinovi
kozmološki "konstanti" ... Temna snov je med drugim tudi izjemno
pomebna zaradi scenarija po katerem bo živelo vesolje. Tako kot nas Sonce
s svojo maso veže v svoj sitem dinamike, tako tudi vesolje z lastno maso
določa dinamiko širjenja, ustavljanja, morebitnega krčenja "našega" sveta.
Stari Newtonov gravitacijski zakon je torej lahko prima popestren z razlago
velike dileme o izvoru in merjenju-tehtanju temne snovi.
|
|
Vrnimo se nazaj k prehodom.
2) Ocena datumske ponovitve dogodka
Kot smo že omenili, se tukaj kaže poslužiti plesa urnih kazalcev, saj poznate pesmico: "Dolgi Luka, kratki Miha, čudna dva možica, noč in dan po eni nogi v krogu se vrtita (lovita) ...". Najprej rešimo problem, kdaj se bosta planeta (kazalca spet srečala). Po analogiji dohitevanja počasnejšega avta, kjer je čas srečanja od trenutka, ko sta premikajoča avtomobila na radalji x, enak t = x/(Vhiter-Vpočasen), je tudi pri kroženju zgodba zelo podobna. V tem primeru je bolje uporabiti kotno hitrost (za enakomerno kroženje velja, da je kotna hitrost w kar polni kot 2*p (360o) deljen z obhodnim časom To, (w = 2*p/To ). Kotna hitrost urnega kazalca je (wu= 2*p/Tu = 2*p/12h, minutnega pa wm = 2*p/Tm = 2*p/1h. Recimo, da začnemo opazovati, ko sta kazalca poravnana skupaj (zagotovo vemo, da sta ob 12:00), potem lahko rečemo, da je razdalja med njima cel obseg, izraženo v kotu je to 2*p.
T (čas) ponovnega srečanja se torej izrazi na naslednji način:
T = kotna_razdalja/(wm - wu) = 2*p/ (wm - wu) = 1/(1/Tm - 1/Tu).
Iz povedanega sledi poučna zveza, ki povezuje obhodna časa (Tm, Tu) obeh kazalcev in čas T, ki preteče med dvema zaporednima srečanjima:
1/T = 1/Tm -1/Tu
T = Tm*Tu/(Tu-Tm) = 12/11 h
Preverite, če opazujemo prvo srečanje obeh kazalcev po 12. uri, je to približno 5 min in 27 s čez 13. uro.
Do ponovnega srečanja na poziciji 12 bo prišlo po enem obratu urnega kazalca in 11 časovnih intervalih srečanja obeh kazalcev (11*T = 11*12/11 = 12 ur). Pomebna ugotovitev, za srečanje na isti poziciji mora torej miniti celo število intervalov srečanj in celo število obhodov počasnejšega telesa (11*T = 1*Tu).
Pri planetih prav tako poznamo obhodne čase gibanja okrog Sonca glede na zvezde, imenujemo jih tudi siderski obhodni časi. Za planeta velja kar enaka zveza za čas T med dvema srečanjima, sinodsko periodo, kot smo jo izpeljali pri urnih kazalcih. To je v primeru, ki nas zanima, čas T med dvema spodnjima konjunkcijama (poravnava, notranji planet je med Zemljo in Soncem, takrat lahko pride do prehoda), recimo za Venero in Zemljo velja:
1/T = 1/TV- 1/TZ

Zgoraj, podoba Venere.
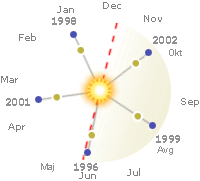
Lega spodnjih konjunkcij Venere med leti 1996 in 2004 tvori 5-erokrak vzorec poravnav.
Planeta potujeta v nasprotni smeri urinih kazalcev.
Poravnava planetov se zgodi vsakih 1.6 let in
se premakne za 3/5 kroga glede na prejšnjo poravnavo. Vzorec se približno ponovi
vsakih 8 let. Zakaj tako in zakaj ni zmeraj prehodov, bomo spoznali v nadaljevanju.
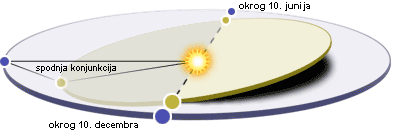
Zgornji sliki gibanja Venere in Zemlje, za pomoč pri razumevanju prehodov, sta povzeti
po: http://www.chocky.demon.co.uk/oas/venus.html.
Ker pa ravnine planetov ne sovpadajo (se sekajo pod kotom), ne bo med vsako spodnjo poravnavo - konjunkcijo prišlo do prehoda čez Sonce (ne bo prekrivanj - "mrkov"). Potrebujemo torej še dodatni pogoj.
Recimo da poznamo, enega izmed datumov prehoda, čez koliko časa se bo ta dogodek spet ponovil (enak problem kot pri uri, ko iščemo čas ujemanja na isti poziciji)? Do takrat bo moralo preteči Nk celo število spodnjih konjunkcij (sinodskih časov T), preteči pa bo moralo tudi Nl celo število siderskih let (ali 1/2 siderskih let, če iščemo prehode na nasprotnem vozlu, saj se prehodi lahko pojavljajo na obeh vozlih). Za ponovitve prehodov pri istem vozlu torej velja pogoj:
Nk*T = Nl*TZ
Ko sta izpolnjena oba pogoja, se bo spet zgodila poravnava Sonca, Zemlje in enega izmed notranjih planetov na (blizu) premici sečišč obeh ravnin, na vozliščni premici.
Ocene datumov Venerinih prehodov
Siderska perioda Venere je TV=224.701 dni in Zemlje TZ=365.256 dni. Sinodska perioda T, v tem primeru je čas med dvema spodnjima konjunkcijama, glede na Sonce:
1/T = 1/TV- 1/TZ ==> T = TVTZ/(TZ-TV) = 583.92 dni
Nl/Nk = T/Tz = 1.59866
Tej številki se zelo približamo že po osmih letih (Nl/Nk = 8/5 = 1,6). Sedaj mogoče tudi že razumemo zgornji 8-letni 5-erokraki vzorec poravnav in zasuk za 3/5 kroga (3/5 = 0,6 = 1,6-1), glede na prejšnjo spodnjo konjunkcijo, poravnavo Venere in Zemlje glede na Sonce.
Po 8 letih Venera zaostaja za začetno točko (prejšnjim morebitnim prehodom) samo 2.5 dni:
5 x 583,92 dni = 2 919.6 dni 8 x 365,25636 dni = 2 922.05 dni
Ujemanje je veliko boljše po 243 letih, ko je število sinodskih period Venere 152 (Nl/Nk = 243/152 = 1.59868):
152 x 583,92 dni = 88 755.8 dni 243 x 365,25636 dni = 88 757.3 dni
Znotraj cikla 243 let se zgodijo štirje prehodi. Po začetnem prehodu se po osmih letih zgodi naslednji prehod, saj je zamik samo 2,5 dni, naslednji zamiki so preveliki, po 16 letih je zamik že 5 dni in ni prehoda. Ker je možen prehod tudi na nasprotni strani Sonca, na drugem vozlu - sečišču obeh ravnin, se le ta v koledarskem letu prehoda datumsko zgodi pol leta pozneje glede na prejšnji prehod (pri Veneri se menjavata meseca junij - december) in sicer čez 121,5 let, kar je 76 sinodskih period Venere. Glej spodnji račun.
76 x 583,92 dni = 44 377, 92 dni 121,5 x 365,25636 dni = 44 378, 65 dniČez 8 let se zgodba spet ponovi in čez 105,5 let se ujame že napovedani cikel 243 let. Glej spodnje tabele.
8 let + 121,5 let + 8 let + 105,5 let = 243 let 5 + 76 + 5 + 66 = 152 sinodskih period
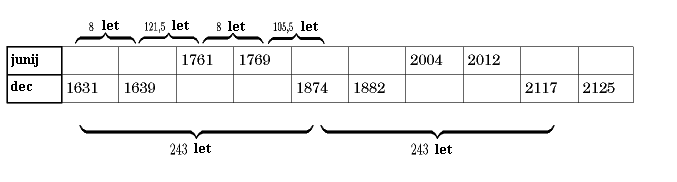
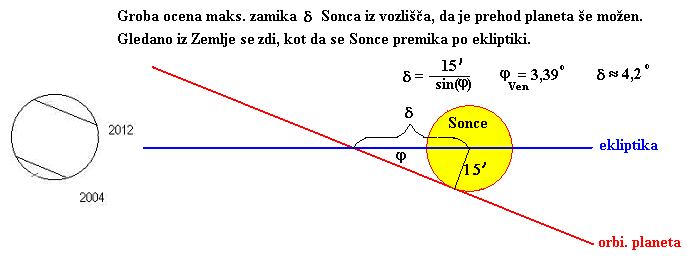
Levo, skica prehodov, ki sta nam časovno najbližja. Prehod Venere bo 8.
junija 2004 potekal od 5h07m UT do 11h33m UT in 5. junija 2012 od
22h03m UT do 6. junija 4h56m UT. Da dobiš poletni čas, prištej 2 uri.
Desno, ocena maksimalnega odmika Sonca iz vozlišča, da je prehod planeta še možen,
to je Zamik gledano iz Zemlje. Sonce obravnavamo iz Zemlje,
kjer se zdi, da potuje po ekliptiki. Če ta zamik upoštevamo še na drugi
strani vozlišča (nad in pod ekliptiko) in podatke o oddaljenosti Venere in
Zemlje, dobimo oceno, da se dvoje zaporednih prekrivanje lahko zgodi
tudi, če Venera za nekaj več kot 2 dni zaostaja za lego prejšnjega prehoda.
Prehoda se zgodita na nasprotnih straneh vozlišča, zato je eden nad drugi pa
pod ekliptiko. Ta ocena je groba saj ne upošteva gibanja po elipsiah,
precesije itn. Vsekakor pa velja, da notranji planet sme biti odmaknjen od
ekliptike za manj kot 15' (to je ločni polmer Sonca gledano iz Zemlje), da
pride do prehoda.
Nekako se zdi, kot da je potrebno ugibati čase med prehodi, vendar se z malo programiranja, recimo v VisualBasicu (Excel), še boljše na mreži v JavaScriptu ali Javi, da iz povedanih povezav programsko oceniti nekatere periode med prehodi. Nekaj takega sem grobo in nahitro spacal na: http://www2.arnes.si/~gljsentvid10/izracun_prehodov1.html
To je lahko prima dodatna vaja za učenje programiranja, kjer ponavadi ponavljajo iste stare vzorce (iskanje razni x-števil ...), ali za kakšen astronomski tabor.
Ocene datumov Merkurjevih prehodov
Izkaže se, da so za zadnje obdobje Merkurjevih prehodov pomembni datumi na začetku maja in novembra. Če se takrat Merkur nahaja med Zemljo in Soncem, bo možen prehod. Prehodi Merkurja čez Sonce so bolj pogosti kot prehodi Venere. V letih 1601 - 2300 lahko naštejemo kar 94 Merkurjevih prehodov, slabih 14 na 100 let.
Dogodke lahko razdelimo v dve skupini.
vseh prehodov = 94 = 100.0%
Maj (padni vozel) = 31 = 33.0%
November (dvižni vozel) = 63 = 67.0%
Zakaj taka porazdelitev?
Merkurjeva orbita je precej ekscentrična (e = 0.2056). Razdalja od Sonca se zelo spreminja, od 46 do 70 milijonov kilometrov. Zaradi relativne bližine Sonca in precejšnje ekscentričnosti, se pojavljajo velike razlike v hitrostih. V periheliju (prisončju) znaša hitrost 59.0 km/s v afeliju (odsončju) pa samo 38.9 km/s. Ravnina orbite Merkurja oklepa z Zemljino orbito (ekliptiko) dokaj velik kot, 7 o. Vse to ima kar velik vpliv na prehode. Velikost (zorni kot) Merkurja pri prehodu maja 1902 je bila 12", to je 1/158 Sonca, novembra leta 1937 pa 10". Velikost Merkurja se lahko relativno zmanjša tudi do 1/194 Sonca. Poglejmo grobe izračune.
Siderska perioda Merkurja je TM = 87.969 dni. Sinodska perioda je 115.877 dni, glej spodnji izračun.
T = TMTZ/(TZ-TM) = 115.877 dni
Nl/Nk = T/Tz = 0.31725
Ocenimo nekaj ciklov ponovitev prehodov. Tej številki (razmerju T/Tz=0.31725) se zelo približamo že po 3.5 letih (3.5/0.31725 " 11 sinodskih period Merkurja), Nl/Nk = 3,5/11 = 0,318. Ti prehodi, z razliko v legah kar okrog 4 dni, so posledica že prej omenjenih posebnosti Merkurjeve orbite, določenih vzorcev (harmonikov) med periodami gibanja Zemlje in Merkurja.
Ujemanje je veliko boljše po 33 siderskih letih, ko je število sinodskih period Merkurja 104 (Nl/Nk = 33/104 =0.31731), še boljše pa po 46 letih (46/145=0.31724):
46 x 115,877 dni = 16802.2 dni 145 x 365,25636 dni = 16801.8 dniRazlika v orbiti je manj kot pol dneva.


Znotraj cikla 46 let se ponavadi zgodi 6 prehodov, v bodoče se bodo dogajali prehodi z naslednjimi zamiki: 3.5, 9.5, 3.5, 13, 7, 9.5 let (skupaj 46 let). Možne so seveda tudi drugačne kombinacije, recimo (3.5, 13, 13, 3.5, 3.5, 9.5 - za obdobje maj 1707 do maj 1753). Zaradi lažjega sortiranja se prehodi razvrščajo, recimo v majske in novemberske serije, v vseh serijah je cikel dolg 46 let, glej zgornji sliki. Serije so oštevilčene glede na zaporedno kronologijo začetnega prehoda v seriji. Majski seriji št. 9 pripada tudi letošnji prehod, tako lahko rečemo, da je to začetek novega 46 letnega cikla. Majski cikli so se (ali se bodo) začeli v letih 1957, 2003, 2049, 2095, 2141, 2187 ... Vsi majski prehodi so posebni, ker se zgodijo približno mesec dni po Merkurjevem afeliju, zelo blizu minimalne hitrosti (najbližje Zemlji). Med dvema majskima 46-letnima cikloma se lega prehoda (črta prehoda) Merkurja glede na Sonce vzporedno premakne za približno 200'', glej sliko. To so kotne razdalje med "vzporednimi" črtami.
Novemberski prehodi se zgodijo samo nekaj dni pred Merkurjevim perihelijem (najdlje od Zemlje glede na spodnjo konjunkcijo), ko je hitrost blizu maksimalne. Zaradi manjše razdalje od Sonca in večje od Zemlje, se lega prehoda med dvema 46-letnima cikloma Merkurja glede na Sonce "vzporedno" premakne približno za 100". Premik je približno 2x manjši kot v afeliju. Večja je razdalja od opazovalca manjša je paralaksa. To pa je tudi glavni razlogov, zakaj imamo več novemberskih prehodov, to je pri dvižnem vozlu. Če afelijev vzorec poševnih črt premaknemo v perihelij, se bo vzorec zgostil približno na gostoto perihelijevega vzorca.
Problem je enak kot pri Sočevih mrkih s SAROS-i (to so cikli, ko se mrki ponavljajo). Pri Sončevih mrkih je več centralnih mrkov kolobarjastih kot popolnih. Razlog je v dejstvu, da so centralni mrki bolj pogosti v apogeju, ko je Luna najdlje od Zemlje. Bolj je Luna oddaljena od Zemlje, večji absolutni del orbite je v polju prekrivanja s Soncem. Seveda je pomembna tudi oddaljenost Zemlje od Sonca. Dogajanje je na nek način podobno ciljanju v tarčo s puško, ki jo imamo med streljanjem naslonjeno na os, podstavek (podstavek predstavlja lego notranjega planeta). Če je podstavek bližje tarči (bolj na koncu cevi), bomo kljub manjši rotaciji ali kljub premiku puške, glede na tarčo (recimo zaradi nemirne roke), še zmeraj lažje zadeli tarčo, kot če je podstavek bližje strelcu. Glej spodnjo skico. Mrki, prehodi notranjih planetov čez Sonce so večinoma prav to, odnosi med tarčo, izstrelkom in opazovalcem, s to razliko, da pri nebesni mehaniki ponavadi vemo v naprej, koliko bo uspešnih dogodkov, zadetkov in kako
uspešni bodo. Če strnemo, mrki in prehodi so bolj pogosti, v primerih, ko je recimo Merkur v periheliju,
bližje Soncu in dlje od Zemlje in pri Sončevem
mrku, ko je Luna v apogeju, ko je dlje od Zemlje. Na tak način se da tudi
razumeti, zakaj je pri Merkurjevem dvižnem vozlu kar 67 % prehodov, pri
padnem pa samo 33 %.
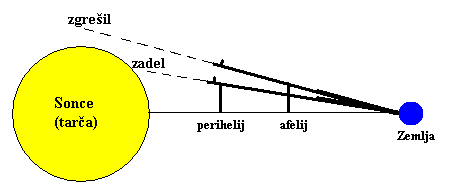
Slika zgoraj. Mrki, prehodi notranjih planetov čez Sonce, so v veliki meri
odvisni od oddaljenosti Lune ali notranjih planetov od Sonca, oziroma od
Zemlje. Na sliki je ta odvisnost pokazana z odnosom med izstrelkom,
opazovalcem in tarčo. Če je podstavek bližje tarči (bolj na koncu cevi),
bomo kljub manjši rotaciji ali kljub premiku puške, glede na tarčo (recimo
zaradi nemirne roke), še zmeraj lažje zadeli tarčo, kot če je podstavek bližje
strelcu.
Časi dotikov (UT)
-----------------------------------------------------------------------------------------------
Greenwich Siderial Min. odd. od
Datum I II Sredina III IV Sonca RA De Time(GST) Serija
h:m h:m h:m h:m h:m " h ° h
2003 May 07 05:13 05:17 07:52 10:27 10:32 708.3 2.926 16.73 14.983 9
2006 Nov 08 19:12 19:14 21:41 00:08 00:10 422.9 14.925 -16.73 3.196 8
2016 May 09 11:12 11:15 14:57 18:39 18:42 318.5 3.130 17.58 15.190 7
2019 Nov 11 12:35 12:37 15:20 18:02 18:04 75.9 15.098 -17.45 3.366 6
2032 Nov 13 06:41 06:43 08:54 11:05 11:07 572.1 15.274 -18.14 3.535 4
2039 Nov 07 07:18 07:21 08:46 10:12 10:15 822.3 14.822 -16.27 3.095 10
2049 May 07 11:03 11:07 14:24 17:41 17:44 511.8 3.000 17.04 15.058 9
2052 Nov 08 23:53 23:55 02:29 05:04 05:06 318.7 14.996 -17.02 3.265 8
2062 May 10 18:16 18:20 21:37 00:53 00:57 520.5 3.206 17.88 15.265 7
2065 Nov 11 17:24 17:26 20:06 22:46 22:48 180.7 15.170 -17.73 3.435 6
2078 Nov 14 11:42 11:44 13:41 15:37 15:39 674.3 15.345 -18.41 3.605 4
2085 Nov 07 11:42 11:45 13:34 15:24 15:26 718.5 14.893 -16.58 3.165 10
2095 May 08 17:20 17:24 21:05 00:47 00:50 309.8 3.075 17.35 15.133 9
Tabela Merkurjevih prehodov za nas in naše vnuke (tabela iz:
http://sunearth.gsfc.nasa.gov/eclipse/transit/catalog/MercuryCatalog.html).
Merjenje paralakse med prehodom Venere
Edmond Halley je leta 1716 predlagal, da bi prehod Venere uporabili za natančnejšo določitev razdalje Zemlja-Sonce Rz.

Slika zgoraj pojasni bistvo Halleyevega predloga. Med prehodom Venere čez Sonce,
se naj meri paralaksa Venere, hkrati pa upošteva takratna ocena paralakse Sonca in tako
izračuna razdalja r od Zemlje do Venere med prehodom. Iz tretjega Keplerjevega zakona se nato
izračuna razdaljo Zemlja-Sonce Rz, to je astronomsko enoto AE. Meritve so uspele šele po Halleyevi smrti.
Odprave so poslali na različne konce sveta. S sabo so morale imeti natančne ure, kar je bil takrat
problem, ki so ga rešili šele izboljšani ladijski kronometri.
Podrobnosti si lahko preberete na:
http://www.dsellers.demon.co.uk/venus/ven_ch8.htm.
Glej spodaj Halleyevo skico za prehod 1761, ki ga ni doživel.
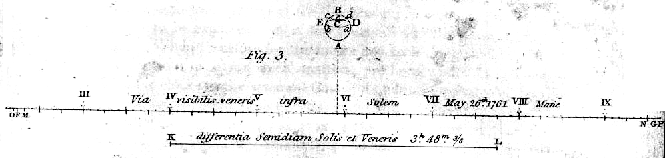
Prehode Venere čez Sonce so opazovali in merili relativno pralakso na Soncu v letih 1761 in 1769, obdelal jih je J. F. Encke (1791-1865) v
prvi polovici 19. stoletja. To je bila za tiste čase kar dobra metoda za določitev astronomske enote,
ki pa je dala za nekaj procentov večje vrednosti od današnjih meritev, ki seveda več ne temeljio na
prehodih Venere. Predvsem preseneča, velik časovni zamik med meritvami in obdelavo, ja včasih ni bilo
računalnikov in računalniških paketov za računanje efemerid, ni bilo
Postgres, Oracle, MySql, ... podatkovnih baz. Takrat se je vse računalo peš z logaritemskimi tablicami, vse na papirju,
z možgani kot procesorjem, gosjim peresom kot printerjem in harddiskom.
Zato je bil Jurij Vega takrat s svojimi logaritmi "bestseler" - a še živi pomen tega genija v našem zgodovinskem
spominu
(naredimo kaj, da bo v bodoče bolj cenjen)?.


Ladijski kronometer