Slovenija pod skupnim nebom Velika konjunkcija 2020 (IX) Od Keplerja do Newtona POBUDA JE NADALJEVANE TISTE IZ 2019

Pot do sile gravitacije temelji na gibanjih planetov in je hkrati odprla avtocesto do moderne kozmologije.

Če se vrnemo nazaj v čas Keplerja, takrat so, ker še ni bilo oprijemljivih podatkov o tem, kako daleč je Sonce, vse računali zgolj z razmerji (računanje z razmerji je še danes za učence velik problem) – enoti sta bili 'leto' (čas obhoda Zemlje okrog Sonca) in recimo razdalja 'Zemlja – Sonce' (astronomska enota, ki je, kot rečeno, takrat še niso poznali, bile so le ocene). A zgolj z izjemnimi meritvami in še bolj genialno obdelavo podatkov, na principu paralakse, je Kepler prišel do osnovnih zakonitosti nebesne mehanike in je s tem naredil odločilen korak do gravitacijskega zakona. Če smo odkriti, ga je že zapisal, a v posebni obliki. Pojem sile je bil takrat še zelo v povojih, sploh če vemo, da je Huygens »komaj« leta 1659 izpeljal izjemno pomemben izraz za centripetalno silo pri kroženju:

Fc = m*v2/r

Centripetalna sila pri enakomernem kroženju:
F_c = m*v²/r = = mω²r = mr4π²/t_o², 't_o' je obhodni čas telesa z maso m na polmeru r od središča kroženja. Ta Huygensova enačba se izpelje v srednji šoli.

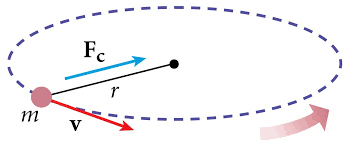
Ta Huygensova formulacija centripetalne sile je skladna s poznejšo Newtonovo definicijo sile (2. zakon) in je pomenila izjemno pomemben korak pri študiju orbit v astronomiji. Je hkrati omogočila prehod iz tretjega Keplerjevega zakona (o gibanju planetov), na »inverzni kvadratni« zakon gravitacije (F_g ∝ 1/r²).
Že Kepler pravi: "Moč (danes sila), ki premika planete prebiva v telesu Sonca ..." in Kepler je bil tudi že na sledi inverznemu kvadratnemu zakonu gravitacije. In, kaj je bilo potrebno še storiti?

Če privzamemo kroženje, velja izraz za centripetalno silo:
F_c = mv²/r = mω²r = mr4π²/t_o².
Ta sila je v resnici posledica gravitacije (Kepler je govoril o neke vrsti magnetni sili, Newton pa o gravitaciji, ki pa jo zaradi nedoslednosti Einstein preseže z ukrivljenostjo prostor-časa), in ker po Keplerju velja, da je:

to2 ∝ r3

- dobimo izraz, iz katerega izhaja, da je gravitacijska sila sorazmerna z obratno vrednostjo razdalje na kvadrat:
F_g = mr4π²/t_o² ∝ mr/r³. Iz zadnjega zapisa torej sledi, da je F_g ∝ m/r².
Še komentar zadnjega drznega sklepa! Tukaj smo malo pogoljufali - saj je razdalja planeta do težišča, centra kroženja, nekoliko manjša od razdalje (r) planet - Sonce. A razlika je za planet zelo majhna in to je bila tudi neke vrste zgodovinska srečna okoliščine, saj je na koncu pripeljala do pravilnega sklepanja glede sile teže. Poglejmo naslednji korak, ki temelji na prvem.
Ker velja zakon o vzajemnem učinku, vzajemnosti sil, velja, da tudi planet deluje na Sonce z nasprotno enako silo (F_pS), ki pa je sorazmerna z maso Sonca M in spet obratno sorazmerna s kvadratom razdalje: F_pS ∝ M/r². Tudi Sonce se premika, a okrog skupnega težišča, ki pa je čisto blizu središča velikega in masivnega Sonca, glede na planet. Iz obeh odvisnosti, zapisov lahko torej razmišljamo v smeri, da je gravitacija sorazmerna produktu obeh mas mM in obratno sorazmerna s kvadratom razdalje, sorazmernostni koeficient je gravitacijska konstanta (danes jo tako imenujemo), oznaka G in jo je bilo potrebno izmeriti. Meritve so to možnost zapisa gravitacijske sile tudi potrdile v laboratorijih. Pri predavanjih mehanike, merjenje gravitacijske sile, med dvema paroma krogel s Cavendishevo tehtnico, pokažejo prav na vseh resnih univerzah po svetu. Povedano še zapišimo:

Fgravitacije = GmM/r2

Gravitacijsko konstanto G smo morali seveda izmeriti: G = 6.673×10^-11 N•(m/kg)². Poudarimo še, da je eden večjih problemov moderne kozmologije merilna (ne)gotovost gravitacijske konstante.

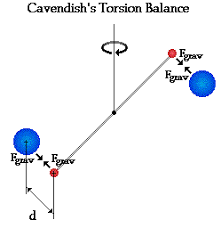
Cavendisheve tehtnica (1797 in 1798) za določitev gravitacijske konstanto G.

Še o metodičnem dvomu - tudi glede veljavnosti gravitacijskega zakona – pomembnost dvoma v znanosti smo omenili že v marčevski Spiki 2020. Novice iz Spike nekako sledijo aktualnosti naših razmišljanj – da so temelji celotne nebesne mehanike postavljeni na Keplerjevem 400 let starem matematičnem opisu gibanja nebesnih potepuhov – planetov. V marčevski Spiki smo tudi omenili (prav prevratno) vpeljavo temne snovi in temne energije – ki seveda spet izhaja iz geometrije gibanja planetov. V omenjeni št. Spike lahko tako preberemo še novico (dvom v veljavo gravitacijskega zakona) o spreminjajoči se Newtonovi dinamiki - Modified Newtonian dynamics (MOND). Ta teorija, poenostavljeno povedano, pomeni, da se gravitacijska konstanta spreminja v času in prostoru – in da vrednost, ki izhaja iz Keplerja (Newtona) velja samo lokalno. Tako MOND privrženci poskušajo razložiti vesolje brez temne energije in temne snovi. Pravijo, da jim je to že delno uspelo z računalniško simulacijo izdelave galaksije brez temne snovi – več najdete v že omenjenih novicah. A zagovorniki šolsko sprejetega standardnega modela vesolja so še zmeraj v prednosti – sploh pri razlagi nehomogenosti mladega vesolja, ki se težko doseže brez temne snovi, ta namreč ne sodeluje s sevanjem, ki je tako ne more razredčiti. Večini fizikov se tudi zdi manj verjetno, da bi osnovni zakoni fizike bili odvisni od lokacije v prostor-času, kar trdi MOND teorija. Kot zanimivost, mama temne snovi Vera Florence Cooper Rubin (1928 – 2016), omenili smo jo v Spiki 3 (2020), je tudi dopuščala možnost veljavnosti teorije MOND – temna snov je v resnici ni »privlačila«.

Kdo so torej zadnji očetje te izjemne enačbe F_gravitacije = GmM/r² (?)

Začel je Brahe z izjemnimi meritvami lege Marsa (v desetletju po letu 1580; 1582 – 1587), a zagotovo ima odločilno vlogo Kepler (1618) z geometrijsko utemeljeno trditvijo, da je kvadrat orbitalne periode planeta sorazmeren kubu velike polosi elipse orbite planeta). Že leta 1645 je duhovnik in astronom Ismael Bullialdus razmišljal, da če bi že kaka sila obstajala (a v bistvu jo je zavračal), bi morala biti obratnosorazmerna s kvadratom razdalje. Za njim si sledita Huygens, ki je leta 1659 zapisal izjemno pomembno enačbo za centripetalno silo (F_c = m*v²/r) in Robert Hooke, ki je tudi že sklepal iz Keplerja, da je sila (zaradi mase) med homogenimi kroglastimi telesi obratno sorazmerna s kvadratom razdalje in je o tem leta 1679 pisal Newtonu (enak rezultat sta recimo poznala še Christopher Wren in Edmond Halley). Ko je leta 1687 Isaac Newton objavil svojo znamenito naravoslovno biblijo »Philosophiae Naturalis Principia mathematic«, je v njej tudi zapisal gravitacijski zakon v današnji obliki:

F_g = Gm₁m₂/r²

Newton je silo med telesi, ki je posledica mase, poimenoval z latinsko besedo za težo 'gravitas' - gravitacija (in ima enak izvor, to je v masi, kot gravitacija, teža na Zemlji, ki je posledica mase Zemlje). Globoka zamera zaradi avtorstva gravitacijskega zakona in drugih rivalstev, je med Hookom in Newtonom trajala do Hookove smrti in še po njej. Newton je namreč celo uničil edina obstoječa Hookova portreta (o tem smo že pisali, Spika 12/2010).

Nekateri sodobniki so sicer kritizirali Keplerjeve sklepe in izračune (recimo že omenjeni teolog in astronom Ismael Bullialdus), a v resnici noben od njih ni presegel njegove izvirne metode obdelave podatkov – tako da lahko Keplerja, brez zadržkov, štejemo za najpomembnejši člen v verigi do zapisa in uporabe nebesne mehanike. Za vajo dokažimo izpopolnejno enačbo tretjega Keplerjevega zakona [T²/a³ = 4π²/(G(M+m))] za kroženje. Predpostavimo krožno orbito, recimo dveh zvezd na razdalji a = r = r₁ + r₂ (opazovani sistem sta torej samo ti dve zvezdi, brez zunanjih vplivov). Kjer je r₁ razdalja od težišča sistema do zvezde z maso m₁, r₂ pa razdalja od težišča do zvezde z maso m₂. Telesi krožita okrog skupnega težišča.
Razdalja med centroma mas je (glej sliko):
r = r₁ + r₂
Težišče je od centra m₁ oddaljeno za r₁ (osnovnošolska snov):
r₁ = rm₂/(m₁ + m₂)
Gravitacijska sila je F_g = F₂₁ = F₁₂:
F_g = Gm₁m₂/r²
Centripetalna sila na m₁ je:
F_c = m₁ω²r₁ = m₁*4π²*r₁/t_o²

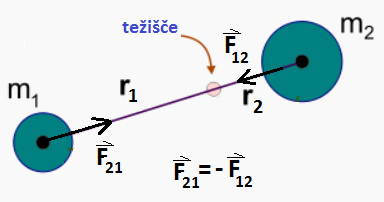
Medsebojno delovanje med dvema masama.

Gibanja okrog skupnega težišča omogoča sila gravitacije, zato zapišimo enakost centripetalne sile in gravitacije:
F_g = F_c.
Gm₁m₂/r² = m₁*4π²*r₁/t_o²
Okrajšamo m₁, namesto r₁ vstavimo r₁ = rm₂/(m₁ + m₂). Tako dobimo izraz:
Gm₂/r² = r*m₂*4π²/(t_o²(m₁ + m₂))
Okrajšamo maso m₂. Razdaljo 'r' in obhodni čas 't_o' izrazimo na levi strani enačbe, gravitacijsko konstanto prenesemo na desno in rezultat je na dlani:

t_o²/r³ = 4π²/(G(m₁ + m₂))

Enak rezultat dobimo preprosteje in hitreje, če kar obe enačbi za centripetalni pospešek teles seštejemo in upoštevamo (r = r₁ + r₂):
Gm₂/r² = 4π²r₁/t_o²
Gm₁/r² = 4π²r₂/t_o²
Za elipso pa namesto polmera podamo veliko polos elipse a:

to2/a3 = 4π2/(G(m1 + m2))

Ta preprosta izpeljava za kroženje je za razumevanje osnov nebesne mehanike čisto zadostna. Izračun za elipso presega namen te serije člankov. Izjemno pomemben dokaz (ki ga ne bomo izvedli) je tudi, da centralna sila sorazmerna z 1/r² (oz. obratno sorazmerna kvadratu razdalje), povzroča gibanje po stožnicah (krog, elipsa, parabola, hiperbola), in da se ploščinska hitrost planetov ohranja (- oglej si članek o elementih tira ali odlomke iz knjige Isaac Newton in njegovo delo , ki pa se ji pozna, da je nastala že pred desetletji, ko še mnogi viri niso bili obdelani). Iz sile F ∝ 1/r² torej izhajajo vsi trije Keplerjevi zakoni nebesne mehanike (prvi dokazal Newton!) – in prav ti zakoni so tudi omogočili zapis splošnega gravitacijskega zakona (izjemna vzajemnost in hkrati potrjena neprecenljiva vrednost Keplerjevega dela).

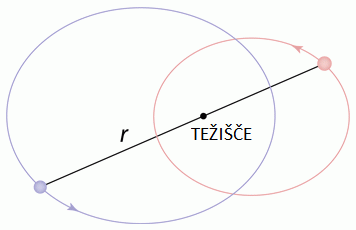
Dokaj realistična podoba gibanja dvozvezdja! Težišče leži med zvezdama, zunaj obeh zvezd.

Kepler in odkrivanje eksoplanetov (mi bi rekli eksopotepuhov)

Keplerjeva mehanika je primerna tudi za detekcijo »Nikolajevih« eksoplanetov! A ne v smislu spremljanja planeta, ampak spremembo hitrosti zvezde zaradi gibanja okrog težiščne točke sistema »zvezda – planet«. Pa ocenimo, kolikšne so te hitrosti. Izhajajmo iz 3. Keplerjevega zakona (obhoni čas bomo označili s T). Masa zvezde naj bo M, planeta pa m, razdalja med njima r = r_z + r_p, kjer sta r_z in r_p razdalji zvezde in planeta do njunega težišča. Za točko težišča tudi velja (načelo gugalnice), da je produkt Mr_z = mr_p.
T²/r³ = 4π²/(G(M + m))
Velja torej: r_p = Mr_z/m in r = r_z + r_p = r_z + Mr_z/m = r_z(m + M)/m. Sedaj preoblikujemo 3. Keplerjev zakon, tako da nadomestimo razdaljo r z ekvivalentnim izrazom r_z(m + M)/m.
T²/(r_z(m + M)/m)³ = 4π²/(G(M + m))
Izrazimo še razdaljo centra zvezde do težišča, r_z.
r_z = (GT²m³/(4π²(M + m)²))^1/3
In vstavimo r_z v izraz za hitrost zvezde (v_z = 2πr_z/T).

v_z = 2πr_z/T = 2πG^1/3T^2/3m/(T((M + m)2π)^2/3) = m(2πG/T)^1/3/(M + m)^2/3

Če privzamemo, da je M >> m, velja 1/( M + m) ≈ 1/M, velja za hitrost zvezde kar izraz:

v_z = m(2πG/T)^1/3/M^2/3

Hitrosti merimo z Dopplerjevim pojavom (sprememba valovne dolžine svetlobe z zvezde zaradi premikanja, rotacije zvezde: v_z = cΔλ/λ, c je hitrost svetlobe) in želimo si seveda, da bi bile hitrosti čim večje, zaradi občutljivosti same metode (problem so namreč »motnje« zaradi visokih površinskih hitrosti plazme na površini zvezde, nekaj 100 m/s, tukaj je še gravitacijski premik valovnih dolžin, samo premikanje Zemlje, itn – vse to je potrebno odšteti od signala). Enačba za hitrost nam pove, da si želimo masivne planete (a Zemlja je majhen planet), ker je hitrost sorazmerna z maso m planeta in - želimo si še relativno skromno maso M zvezde, ker je izraz M^2/3 v imenovalcu in nam tako majhna masa zvezde da tudi večjo hitrost. Kljub že omenjenim izrazitim motnjam pri merjenju Dopplerjevega premika spektralnih črt, se iz signala nekako le da izluščiti periodične spremembe valovnih dolžin. Pomembno je tudi, kako je ravnina kroženja orientirana glede na Zemljo – idealno je, če Zemlja leži v ravnini kroženja eksoplaneta (takrat, gledano iz Zemlje, eksoplanet prečka matično zvezdo točno čez sredino).

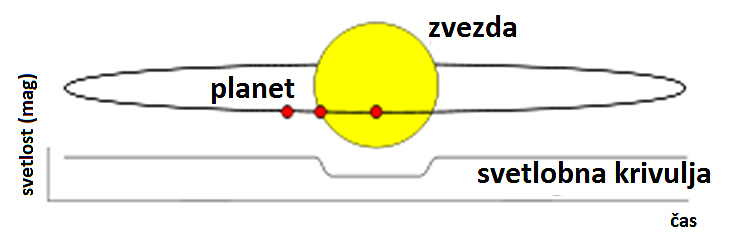
Levo: Keplrjeva metoda radialnih hitrosti in Dopplerjev premik spektra zvezde, zaradi eksoplaneta. Desno: Svetlobna krivulja eksoplaneta, ki pri pogledu z Zemlje prečka matično zvezdo
(https://en.wikipedia.org/wiki/Methods_of_detecting_exoplanets#Transit_photometry)

Če vstavimo v enačbo podatke za Jupiter in Sonce (T = 11.862 leta, m = 1.9×10²⁷ kg, M = 2×10³⁰ kg ), je hitrost premikanja Sonca komaj v_z = 12,4 m/s, polmer r_z kroženja zvezde pa je zgolj velikosti polmera Sonca, ki znaša zaokroženo 55 premerov Zemlje. Za primer planeta podobnega Zemlji, je ta hitrost zvezde (Sonca) le še 0.09 m/s – novejši spektroskopi zmorejo meriti tudi take majhne hitrosti.

Že leta 1995 sta Didier Queloz in Michel Mayor v reviji Nature objavila odkritje planeta ob zvezdi 51 Pegaza - z maso vsaj polovice Jupitrove. In leta 2020 sta prejela polovico Nobelove nagrade. Zagotovo je simbolično del pripada tudi našemu vrlemu Keplerju in vsem ostalim raziskovalcem, ki so recimo razvili imenitne spektroskope, teleskope, rakete, satelite, programe, računalnike, oddajnike, sprejemnike, ccd kamere … Ni slučajno, da je prva večja in zelo uspešna misija za odkrivanje eksoplanetov dobila ime prav po Keplerju.

Po metodi merjenja hitrosti premikanja zvezde iz 3. Keplerjevega zakona (metoda radialnih hitrosti), ki jo povzročajo planeti, je odkritih okrog 19 % vseh planetov. Leta 1999 so začeli uporabljati fotometrijsko metodo beleženja prehodov planetov čez ploskvico zvezde (če je ravnina tira eksoplaneta poravnana s smerjo proti Zemlji, se za nekaj časa, ko je planet med nami in matično zvezdo, svetlost zvezde rahlo zmanjša). Po tej metodi se izmeri okrog 76 % eksoplanetov. Ostalim metodam pripada okrog 5 % odkritih planetov (merjenje polmerov kroženja zvezd, meritve motenj pri pulzarjih, mikrolečenje …). Odkritih je že čez 4000 eksoplanetov (pomlad 2020). Od tega je trenutno nekaj nad 10 takih planetov (ocene se nekoliko razlikujejo), kjer bi potencialno lahko obstajalo življenje (temperature, ki omogočajo tekočo vodo, pogoj je seveda tudi atmosfera in podnebna stabilnost …). Če je planet za nekaj časa med nami in matično zvezdo, se da analizirati tudi kemično sestavo atmosfere. Veliko se obeta pri analizah atmosfere eksoplanetov tudi od ELT teleskopa Evropskega južnega observatorija v Čilu leta 2024. Imel bo premer zrcala 39 m, kar presega svetlobno zbiralno kapaciteto vseh dosedanjih teleskopov. Fotometrijska metoda nam omogoča meritev velikosti planeta, če nam uspe pomeriti še radialno hitrost, lahko iz Keplerja izračunamo še maso zvezde in planeta. Slovenci smo 2019 dobili zvezdo WASP-38 z magnitudo 9,4 in njen planet WASP-38 b v ozvezdju Herkula - s fotometrijsko metodo sta dve skupini tudi v Sloveniji potrdili periodo prehoda planeta WASP-38 b (Spiki 2019, št. 10 in 11 – to samo kaže, kako sta oprema in znanje posameznikov v zadnjih 20 letih tudi pri nas napredovala - tudi sama oprema se je pocenila).

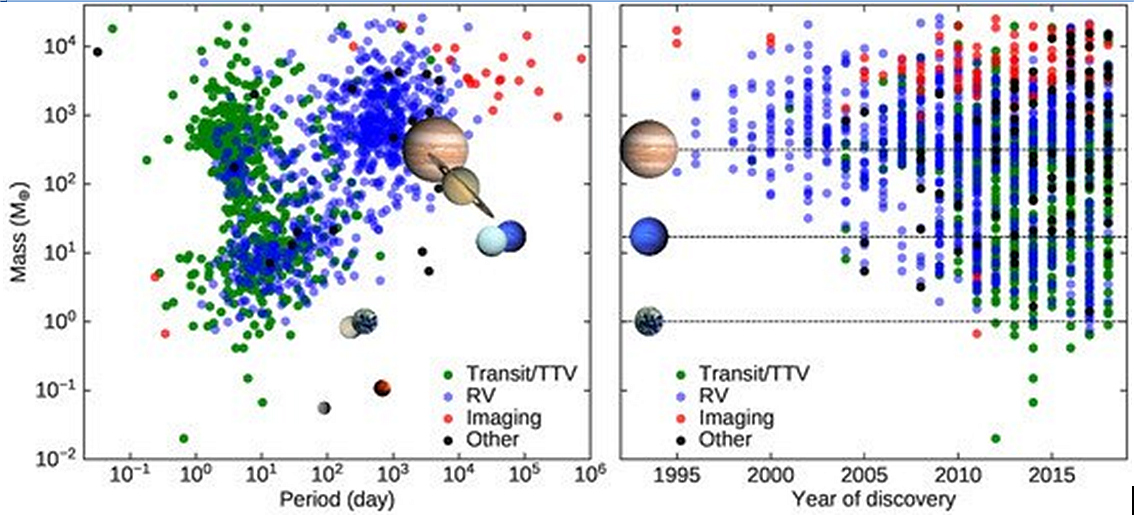
Levo: Populacijska analiza odvisnosti mase (enota je Zemljina masa) in obhodnega časa do sedaj odkritih zunaj sončnih planetov. Modre točke so eksoplaneti dobljeni preko metode radialnih hitrosti (RV, 3. Keplerjev zakon), zelene pa so detekcije prehodov planetov preko zvezdne ploskvice (Transit/TTV, fotometrija). Ostale barve predstavljajo ostale metode. Zemlja in Venera sta narisani pri (blizu) vrednosti (365 dni, masa 1). Desno: Število eksoplanetov odkritih skozi leta glede na velikosti in metode.

Naše razburljivo raziskovanje neba so poleg Sonca, Lune in zvezdnega neba, pred tisoče leti pritegnili tudi planeti, ki so bistveno prispevali k matematičnemu opisu sveta. In danes nas podobne ali celo enake metode vodijo k razburljivemu iskanju eksoplanetov – ali je še kje tam daleč življenje … A kritični in izkušeni analitiki pravijo (tudi tukaj našteta dejstva), da če je še kje razvito življenje, je to zelo daleč in vprašanje je, koliko je še (že) bitij v vesolju, ki bi v tem trenutku (recimo v časovnem oknu nekaj 100 let) bila sploh tehnološko sposobna komunicirati z nami ali mi z njimi.

A če bomo kot vrsta preživeli, če bomo ohranili potepinko Zemljo, se ta verjetnost za komunikacijo z bitji tam daleč v vesolju veča! Komaj pred nekaj sto leti smo prepluli naš planet, pred nekaj desetletji pristali na Luni, danes pa že lahko sanjamo o potovanju na Mars in komunikaciji z drugimi bitji tam daleč med zvezdami. Ko tako pogledamo na svet, nas čaka lepa prihodnost.

Zorko Vičar
Korona pomlad 2020