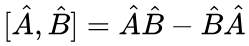Leto 2025 je Mednarodno leto kvantne znanosti in tehnologije (IYQ),
- vesolje na veliki skali je neločljivo povezano s svetom drobnih skrivnostnih kvantnih delcev, gradnikov narave, nas samih

*
S čim se ukvarja kvantna mehanika in zakaj je letos Mednarodno leto kvantne mehanike?
*
Slovenija opazuje Sončev spekter -
predlog slo. šolam ob
Mednarodnem letu kvantne znanosti in tehnologije (IYQ) 2025.
Abeceda vesolja je sestavljena kar iz spektra svetlobe - 2025
(revija Spika 11/2025)
*
A osnove kvantne mehanike (spektroskopija) so stare vsaj 200 let
*
Kvantna mehanika - konec determinističnih sanj, a prav nedoločenost porodi sanje o možnem začetku vesolja
*
Kvantna mehanika je vgrajena tudi v računalniške procesorje - kako bi danes živeli in raziskovali
brez računalnikov, svetovnega spleta, brez baz podatkov, brez izjemne programske opreme, umetne inteligence?
*
Ali smo v resni najprej E/c2 - in šele potem le drobno zrnce materije (in tukaj je še antimaterija)
*
Brez laserja mi živeti ni - pot do kozmičnih meritev.
*
Kvantni delci so zelo nadarjeni atleti za skoke čez ovire - tuneliranje in energija Sonca.
*
Dve muhi na en mah (energija in atomi)
- eden od vrhuncev človeškega umovanja je bil uspešen model zvezdne nukleosinteze - fuzije lažjih atomov v težje.
*
Kako je mlada Dama razrešila skrivnost kemijske sestave večine zvezd in samega vesolja.
*
Higgsov bozon - "Božji delec": če je vesolje odgovor, kaj je vprašanje?
*
Vse se je začelo z barvami - ali je življenje rezultat kockanja (»Bog je morda prebrisan, vendar ni zloben.«)
S čim se ukvarja kvantna mehanika?
Kvantna mehanika je veja fizike, ki proučuje naravo materije, sil in energije na zelo majhni skali
– na ravni atomov in subatomskih delcev, kot so recimo
- osnovni masni delci in sestavljeni masni delci narave :
osnovni masni delci so leptoni (elektroni, mioni, tau lepton, nevtrini),
potem kvarki;
sledijo sestavljeni masni delci, kot so recimo kratkoživi mezoni
(pioni, rho mezoni, omega mezoni, kaoni ... - sestavljeni iz kvarka in antikvarka),
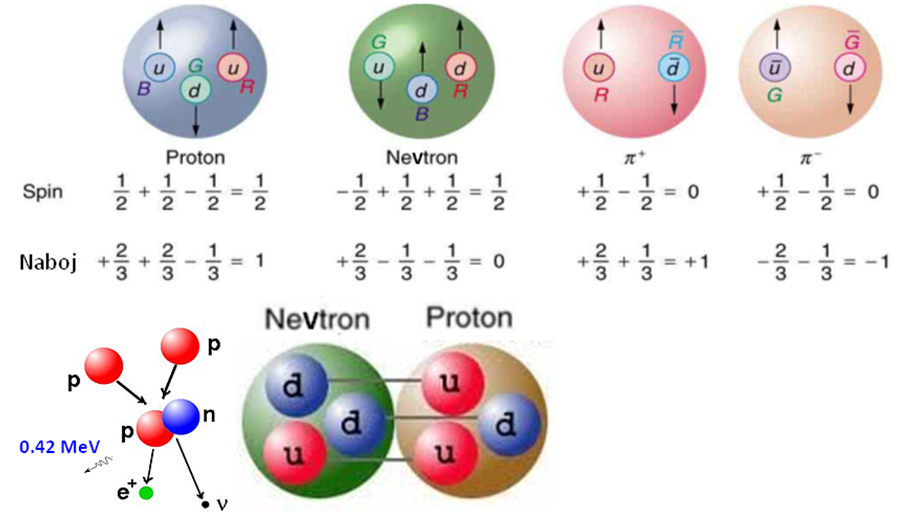
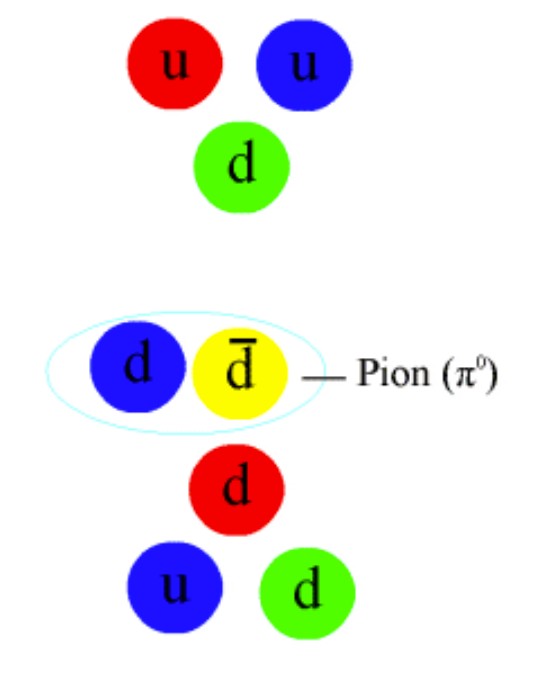
protoni (sestavljeni iz treh kvarkov u, u, d), nevtroni
(sestavljeni iz treh kvarkov u, d, d),
atomi (sestavljeni iz protonov, nevtronov, elektronov), molekule (sestavljene iz več atomov) ...
- in tukaj so še osnovi nosilci sil, to so elementarni bozoni, družijo že naštete osnovne
delce narave v naš pojavni svet, nekateri so brez mase, nekateri pa imajo maso,
naštejmo jih:
fotoni (brez mase, nosilci elektromagnetne sile, virtualni fotoni vežejo recimo negativne elektrone na pozitivna
atomska jedra), gluoni (brez mase - nosilci močne jedrske sile, pravimo tudi, da posredujejo barvno silo,
lepijo kvarke v protone, nevtrone, mezone ...),
Z (ima maso - bozon prenosa šibke sile),
W± bozona (imata maso, prenašata šibko silo),
Higgsov bozon (ima veliko maso, daje vsem ostalim delcem maso), hipotetičen graviton
(nosilec gravitacijske sile - izrazita je med velikimi telesi vesolja in na kozmični
ravni).
Povejmo še, da protone in nevtrone vežejo v atomska jedra
sestavljeni delci mezoni (pioni, rho mezoni, omega mezoni)
- mezoni so torej nosilci močne sile na ravni hadronov (protonov, nevtronov).
Še enkrat poudarimo, da so mezoni torej sestavljeni bozoni.
Poenostavljen shematski grafični prikaz osnovnih kvantnih delcev narave in nekaterih nosilcev sil med njimi -
to je le grob modelski
prikaz, ki je opisan na začetku, v uvodu.
Zgoraj je torej strnjen slikovni opis naše realnosti, opis osnovnih gradnikov vesolja in sil med njimi - to je torej področje, ki ga modelsko
obravnava kvantna mehanika - fizika.
--------------------------
Kratek opis slik:
- slika levo zgoraj prikazuje zelo strnjen pregled osnovnih delcev narave, vesolja,
to so nedeljivi delci in hkrati je na sliki še
povzetek kvantnih interakcij med subatomskimi delci (gluoni recimo vežejo kvarke v protone in nevtrone ...),
vse navedeno je opisano v
standardnem modelu delcev,
- sledi shema sestave protona in nevtrona iz treh kvarkov, shema pionov (sestavljeni iz kvarka in antikvarka),
ki vežejo nukleone v jedra, recimo nevtron in proton v devterij (pri zlivanju dveh nukleonov se sproti veliko energije,
to je fuzija, ki daje zvezdam energijo za dolgoživi izsev),
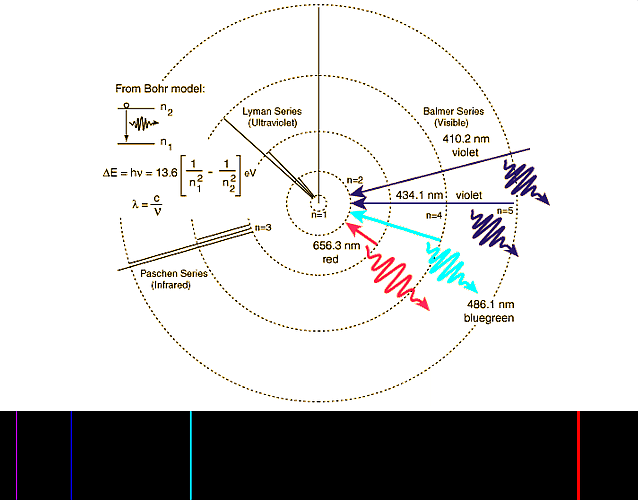
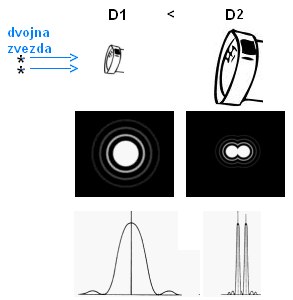
- slika desno zgoraj pa prikazuje preprost Bohrov model atoma (danes že presežen); v tem modelu so tirnice elektrona
lahko le diskretne, točno določene, ne poljubne; razliko v principih klasično <=> kvantno prikazuje
mucek na klancu in na stopnicah;
Bohrov model je konceptualno odlično
razložil valovne dolžine svetlobe (točno določene energijske pakete svetlobe), ki jih vodik lahko oddaja ali absorbira (prejme);
podobno velja za vse ostale atome,
le da imajo drugačno porazdelitev valovnih dolžin (energijskih paketov prejete ali oddane svetlobe), vsak kemijski element
ima tako svoje svetlobne prstne odtise - to je temelj
spektroskopije, ki je še zmeraj temeljna
metoda opazovanj sestave in dogodkov v vesolju,
--------------------------------------------------
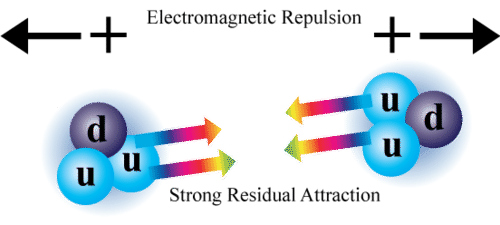
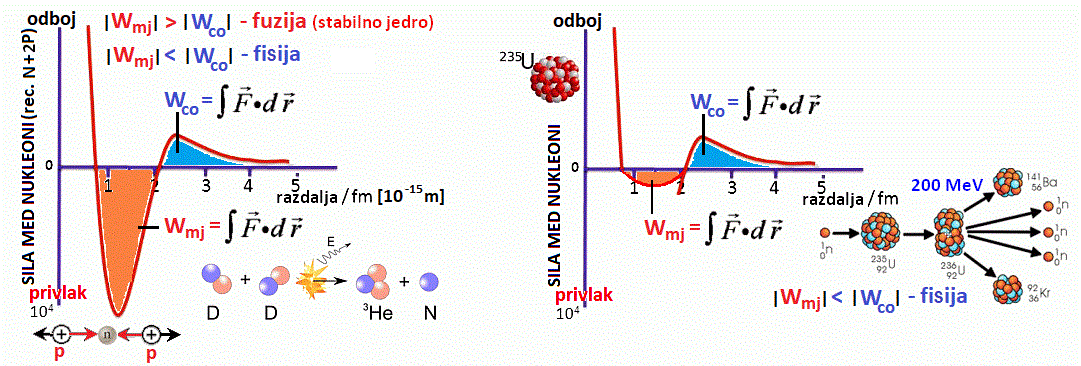
- slika levo spodaj, 'boj' med električno odbojno silo in privlačno močno jedrsko silo,
ki jo nosijo pioni (sestavljeni iz dveh kvarkov) znotraj atomskega jedra,
- sledi slika (shema), ki prikazuje izmenjavo piona (ali delca, ostanka polja močne jedrske sile)
med protonom in nevtronom (jedro devterija),
tako so preko izmenjave pionov nukleoni (protoni in nevtroni) vezani v atomska jedra, naše gradnike,
- slika zraven prikazuje razliko med fuzijo (zlivanjem lahkih jeder v masivnejša),
ki odda energijo, masni defekt (ΔE = Δmc2, odtod zvezdam enormna sevalna energija)
in cepitvijo - fisijo urana; ko imamo namreč opravka z atomskimi jedri masivnejšimi od železa
(nastanejo pri supernovah in trkih zvezd, proces nastanka takih masivni jeder je namreč porabnik energije, to pa
zaradi prevlade odbojnih sil
nad močnimi jedrskimi silami)
lahko pride tudi do razpada teh zelo masivnih atomskih jeder (cepitev),
recimo pri uranu in pri tem se sprosti ogromno energije (to lastnost uporabljajo recimo
jedrske elektrarne ...),
- sledi slika (shema), ki kaže, kako so s sipanjem elektronov na (v) protonih, ugotovili, da je le ta sestavljen iz treh kvarkov,
da kvarke vežejo v protone nosilci močne jedrske sile gluoni, da
Z in
W± bozoni prenašajo šibko jedrsko silo,
recimo pretvorba nevtrona v proton,
ko nastaneta delca β- (elektron) ter
(νe) antinevtrino (ta pretvorba se imenuje tudi razpad
beta),
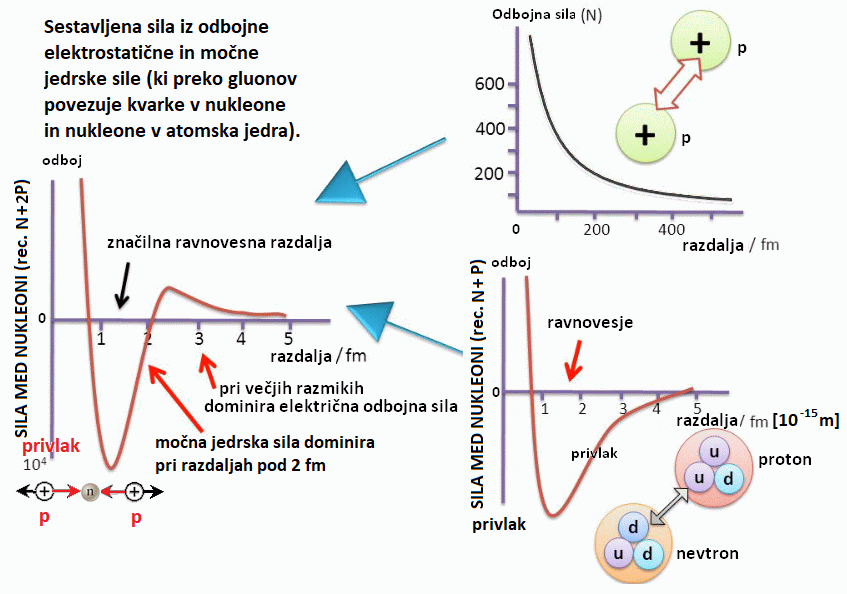
- desna slika spodaj (grafična shema znotraj klasične mehanike) prikazuje odbojno silo med nukleoni
in kako na krajših razdalja prevlada močna jedrska sila nad odbojnimi (recimo zaradi trkov protonov visokih energij v zvezdah)
in tako pride do zlivanja nukleonov
in sproščanja veliko energije, to je masni defekt ΔE = Δmc2 (masa nukleonov pred trkom je nekoliko večja kot
po združitvi v novo atomsko jedro), velja za nastanek atomskih jeder mase do železa; masivnejša
jedra (zlato, uran ...) pa so pri nastanku neto porabnik energije in tako v zvezdah ne morejo nastajat, ker bi zvezde tako ugasnile ...,
nastanejo pa lahko
pri eksplozijah supernov in trkih zvezd; proces fuzije v zvezdah zaradi stiskanja gravitacije
je generator ene od osnovnih oblik energije našega vesolja, zvezd, samega življenja ...,
hkrati pa pri fuziji nastajajo težji atomi, naši gradniki (O, C, N, F, Fe, S ...).
Povejmo še, da
Prvi po masnem deležu je v vesolju seveda element vodik - okrog 74 %, helija pa je cca 24% - nekje vmes do 100 % pa
je še nekaj malega težjih elementov (cca 2% - od teh dveh odstotkov je kar polovico kisika in slaba polovica ogljika),
ki so v veliki meri nastali v vročih sredicah zvezd, kjer poteka fuzija - zlivanje lažjih jeder v težja, do železa.
S stališča življenja se zdi izjemno ugodno, da je poleg vodika (cca 75 %), takoj po velikem poku nastalo le še
cca 25 % helija ..., gre za masne deleže.
Po velikem poku namreč ni bilo časa, vesolje se je namreč hitro širilo in tako ohlajalo,
da bi nastali še ostali masivnejši elementi od vodika (75 %) in helija 25 %
(no - nastane zgolj še nekaj litija, zanemarljivo število ostalih težjih elementov kot so berilij, bor … ).
Zakaj je tak razvoj dogodkov ugoden za nastanek življenja,
sledi v nadaljevanju te napete zgodbe?!
Več torej sledi v nadaljevanju - ta uvod je namenjen le ogrevanju, temu da postanemo radovedni ..., recimo.
Govorimo torej o temeljni kvantni teoriji v sodobni fiziki, ki opisuje, kako delci obstajajo
(tudi antidelci z nasprotnim nabojem in enako maso),
kako se premikajo in medsebojno delujejo, katerih pravil se morajo držati.
Povejmo še, da je sama
osnova, srčika razvitega življenja - to je vsem poznana fotosinteza - seveda tudi kvantni pojav "par excellence",
ki ga poganjajo kvanti svetlobe s Sonca.
Še zanimivost, med kvantnimi delci so tudi taki zelo številčni, a "strpni" delci, to so nevtrini, ki pa se sploh ne zmenijo za nas
(kdaj bi si kaj takega želeli tudi v službi ali med sosedi ...).
Vsako sekundo namreč gre skozi naše telo na milijarde nevtrinov (iz Sonca in iz ostalih delov vesolja),
a praktično noben ne reagira z našo materijo. Ogromno nevtrinov se sprosti recimo ob eksplozijah supernov.

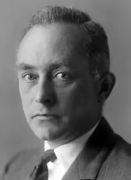




Od leve proti desni - očetje moderne kvantne mehanike:
Werner Heisenberg (1901 – 1976, nemški fizik, dosledna kvantna teorija na matričnih operacijah 1925,
načelo nedoločenosti),
Max Born (1882 – 1970, nemško-britanski teoretični fizik, vpeljal je verjetnost kot osnovno lastnost kvantnega sveta),
Erwin Schrödinger (1887 - 1961, avstrijski fizik, vpelje valovno funkcijo za opis kvantnega sistema),
Paul Dirac (1902 - 1984, britanski fizik in matematik, razvije relativistično kvantno mehaniko, napoved antimaterije),
Wolfgang Ernst Pauli (1900 - 1958, avstrijski fizik, razloži izključitveno načelo - primer, dva fermiona, npr. elektrona,
ne moreta imeti vseh kvantnih števil enakih v istem atomu),
Louis-Victor Pierre Raymond de Broglie (1892 - 1987, francoski plemič in fizik, postavil je temelje valovno-delčnemu dualizmu, na začetku je bil zavrnjen,
a Albert Einstein je prebral njegovo disertacijo in se izrazil nekako takole:
»To je izjemno delo – zdi se mi zelo globoko in pomembno.«).
A temelje kvantne mehanike so zgradile že generacije pred njimi.
Združeni narodi so razglasili leto 2025 za Mednarodno leto kvantne znanosti in tehnologije
(ang. International year of Quantum Science and Technology, IYQ2025).
Iniciativo je dalo Ameriško društvo fizikov (APS),
pobudo pa je podprlo tudi Društvo matematikov, fizikov in astronomov Slovenije (DMFA).
To posebno leto obeležuje 100-letnico razvoja kvantne mehanike in je posvečeno dejavnostim,
ki bodo povečale ozaveščenost javnosti o pomenu kvantne znanosti in njenih aplikacij.
* Več informacij o dogodkih v okviru IYQ2025 najdete na krovni spletni strani https: https://quantum2025.org/
* Dogodki v Sloveniji pa so opisani tudi na spletni straneh Slovenske skupnosti kvantnih znanosti
in tehnologij: https://qutes.si/en/iyq2025-en/
* Evropsko fizikalno društvo je 1. aprila 2025 proglasilo Göttingen za mesto s pomembno zgodovinsko
vlogo za fiziko.
V Göttingenu se je pred 100 leti pisala zgodovina kvantne znanosti. Ob tej priliki je Evropsko
fizikalno društvo sprejelo skupno izjavo o prihodnosti kvantne znanosti v Evropi:
https://www.dmfa.si/Raziskovanje/Dokumenti/20250329%20Europe%20and%20the%20Future%20of%20Quantum%20Science.pdf
Leto 1925 je bilo torej ključno za kvantno mehaniko, kot jo poznamo danes.
Julija 1925 je Werner Heisenberg v revijo Zeitschrift für Physik oddal članek z naslovom
»On quantum-theoretical reinterpretation of kinematic and mechanical relationships /
O kvantno-teoretični reinterpretaciji kinematičnih in mehanskih odnosov«,
s čimer se je rodila moderna kvantna mehanika. Naslednje leto je Erwin Schrödinger,
ki je gradil na de Brogliejevi dualnosti valov in delcev ( λ = h/(mv) ),
razvil valovno mehaniko (valovno enačbo),
kmalu pa je Max Born predstavil verjetnostno interpretacijo valovne funkcije.
Teorijo je še dodatno obogatil izključitveni princip Wolfganga Paulija in
Heisenbergov princip nedoločenosti, kar je na koncu privedlo do razvoja
relativistične kvantne mehanike s strani Paula Diraca. Köbenhavnska interpretacija je
ustvarila verjetnostni okvir za razumevanje teorije. V preteklem stoletju
je kvantna mehanika utrla pot napredku v kvantni teoriji polja, računalništvu
in sodobnih tehnologijah, ki jih najdemo praktično povsod, seveda tudi v medicini, astronomiji,
v znanosti kot taki in vsekakor v vsakdanjem življenju ...
Ta kompleksen
proces, ki je privedel do razvoja kvantne mehanike in
potencialno vodi do novih prebojev sredi zahtevnih konceptualnih interpretacij,
kot jih recimo vidimo na področju umetne inteligence, kvantnih računalnikov
ali v kvantni prepletenosti - teleportaciji
(to so recimo tudi inovativne metode za varno komunikacijo, šifriranje).
Ti dosežki so torej tlakovali pot dvema kvantnima revolucijama,
ki še zmeraj preoblikujeta naše razumevanje fizičnega in posredno duhovnega sveta.
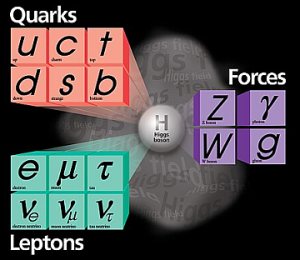
Predstavitev osnovnih kvantnih delcev vesolja,
opisanih v
standardnem modelu.
V ozadju se nahaja masivni in dokaj skrivnostni Higgsov bozon, ki vsem delcem,
razen fotonom (oznaka γ) in gluonom (oznaka g), daje maso (no, odgovor še ni čisto enoznačen za antinevtrine).
Torej, kot smo omenili, model še ni dokončno enoznačen - recimo antinevtrino ima maso, a
najbrž ima Majoranino maso, ki pa NE izvira neposredno iz Higgsovega mehanizma (ampak dodamo zelo težke desne nevtrine
in dobimo mešanico masnih členov, rezultat so zelo lahki levi nevtrini).
Če pa nevtrini dobijo Diracovo maso, jo da Higgs - ta zadnja trditev je nekoliko manj verjetna.
Prva kvantna revolucija, je torej temeljila na valovni naravi kvantnih delcev in na
obstoju energijskih "paketov", imenovanih kvanti, se je začela sredi 20. stoletja. Ta
revolucija ni le poglobila našega razumevanja temeljnega delovanja
vesolja – kar je doseglo vrhunec z razvojem standardnega modela fizike delcev – ampak
je privedla tudi do naprav in tehnologij, ki so zdaj temeljne za naše vsakdanje življenje.
Primeri
vključujejo računalnike in potrošniško elektroniko (kot so mobilni telefoni), ki temeljijo na
polprevodnikih, LED diode, laserje, sodobno medicinsko slikanje in zdravljenje, pozicioniranje in
navigacijo (GPS, Galileo itd.), novo definicijo kilograma, fotovoltaiko,
tehnologije in pristope, ki podpirajo podnebne raziskave, in številne druge.
Druga kvantna revolucija, kjer lahko skoraj v celoti nadzorujemo kvantno obnašanje
osnovnih sestavin, kot so atomi ali fotoni, se je začela nekje na začetku 21.
stoletja. Ta revolucija spreminja način razmišljanja o informacijah, računalništvu,
merjenju in snovi; vodi, kot smo že omenili, na primer do inovativnih metod za varno
komunikacijo, do kvantnega zaznavanja in novih kvantnih materialov.
Edini preživeli, sirota utemelji spektroskopijo.
A same znanstvene osnove kvantne mehanike so veliko starejše - relevantne meritve segajo že v leto 1814,
ko je Joseph von Fraunhofer odkril po njem imenovane absorpcijske (nekoliko temnejše)
črte v Sončevi svetlobi.

Joseph von Fraunhofer (1787 – 1826) - izjemen nemški optik in priučeni fizik.
Leta 1801 se je v Münchnu podrla optična delavnica, v kateri je 14-letni Fraunhofer (sirota) delal in stanoval, bil je edini preživeli.
Knez Maksimilijan IV. je bil osebno prisoten pri njegovi senzacionalni rešitvi in je od navdušenja
Josephu Fraunhoferju podaril 18 dukatov (zlatnikov).
S tem denarjem je Fraunhofer kupil stroj za rezanje stekla in si tudi odkupil preostale mesece vajeništva - izjemno.
Fraunhofer je dodelal prizme in ostalo
optiko do te mere natančno, da je z lastnim spektroskopom naštel kar 574 temnejših črt v
spektru Sonca, današnje naprave pa fizikom omogočajo preučevanje vsaj 10 000 absorpcijskih črt (v resnici na milijone).
Njegov epitaf se glasi: "Aproximavit sidera" - 'Približal je zvezde.'
Omenimo še, da je prva opažanja Sončevega spektra, oziroma spektra bele svetlobe v kozarcu vode (refrakcija svetlobe),
zabeležil že Anglež Roger Bacon (ok. 1214 – ok. 1294).
Newton pa je cca 400 let pozneje opravil podobne eksperimente, le da z bolj uporabno stekleno prizmo.
S prizmo je belo svetlobo razstavil
v barvni spekter in ta spekter je spet sestavil nazaj v belo svetlobo - a najbrž zaradi skromne optike ni opazil
absorpcijskih črt v Sončevi svetlobi.
Fraunhofer je še naprej raziskoval in sicer tudi nekatere ostale zvezde.
Ugotovil je, da se temne
črte pojavljajo tudi
v spektrih več ostalih svetlih zvezd, vendar v nekoliko drugačnih poudarkih posameznih črt.
Izključil je možnost, da so črte nastale, ko je svetloba potovala
skozi Zemljino atmosfero. Če bi bilo tako, se ne bi pojavljale
v različnih spektrih zvezd drugačne širine črt, različne intenzitete na enakem delu spektra.
Ugotovil je, da črte izvirajo iz narave zvezd
in Sonca in nosijo informacije o viru svetlobe, ne glede na to,
kako daleč je ta vir. Ugotovil je, da se spektri Sirija in drugih
zvezd prve magnitude razlikujejo od Sonca in tudi med sabo, s čimer
je utemeljil zvezdno spektroskopijo.
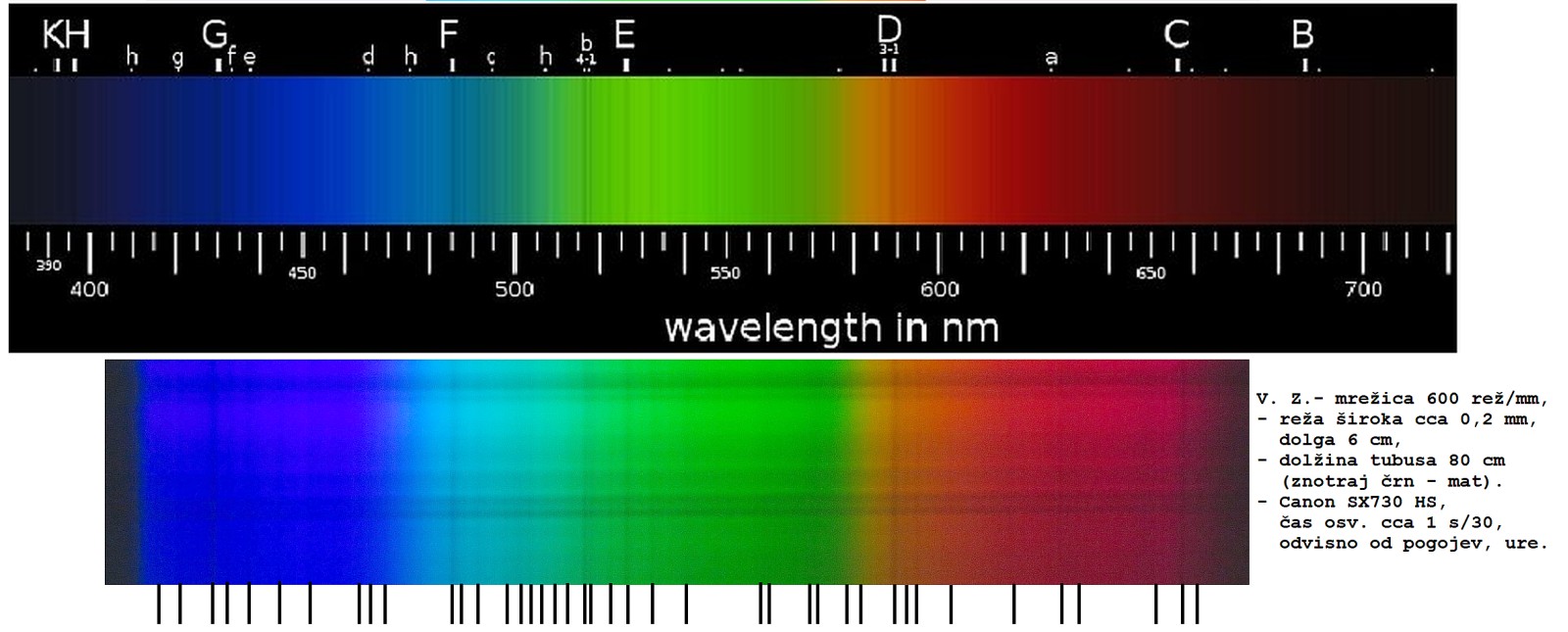
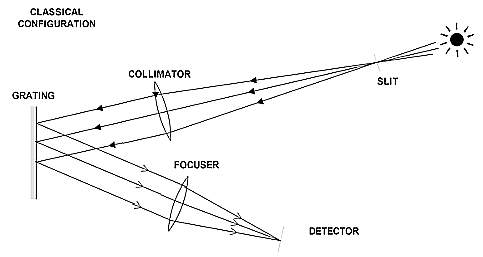
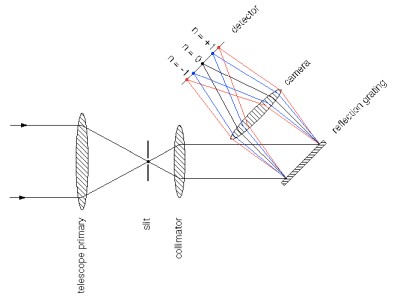
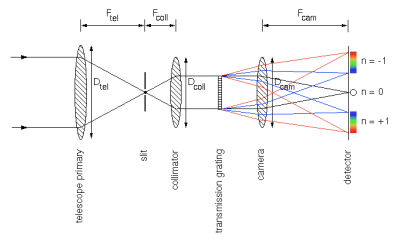
Zgoraj so rezultati
preprostega spektroskopa iz
80 cm dolgega tulca z režo široko cca 0.2 mm.
Na drugo strani tulca se prilepi uklonsko mrežico, raze mrežice morajo biti seveda
vzporedne z
režo (testiramo z rotacijo uklonske mrežice).
Tulec (z režo naprej) se med slikanjem lahko usmeri
proti Soncu, še bolj varno pa je, sploh med opazovanjem, da kar proti beli steni osvetljeni
s Sončevo svetlobo. Spekter se slika skozi mrežico ( v tem primeru 600 rež na mm -
občutljivost ISO100, časi okrog 1/50 s, zoom objektiv za ta namen pride zelo prav).
Zgoraj na sliki je umerjen spekter Fraunhoferjevih absorpcijskih spektralnih črt z uradnimi oznakami, pod njim pa naš spekter
posnet s preprostim spektroskopom z režo in uklonsko mrežico - opazi se čez 40 absorpcijskih črt - označene so zobčki na spodnjem robu.
Prav izdelavo tega preprostega spektroskopa in opazovanja Sončevega spektra (lahko tudi slikanje)
predlagamo slovenskim šolam ob
Mednarodnem letu kvantne znanosti in tehnologije (IYQ) 2025.

William Hyde Wollaston (1766 - 1828) - angleški kemik in fizik.
Povejmo še, da je 7 temnih črt opazil v spektru Sončeve svetlobe že kemik
William Hyde Wollaston leta 1802. A Fraunhofer je dodelal prizme in ostalo
optiko do te mere, da jih je naštel kar 574, današnji fiziki pa približno 10.000 absorpcijskih črt
v spektru Sonca. Fraunhofer je leta 1821 tudi prvi uporabil optično mrežico za uklon svetlobe,
preučeval je tudi spektre ostalih zvezd.
Bunsen in Kirchhoff sta leta 1859 s spektrografom na prizmo odkrila,
da so temne absorpcijske črte iz Sončevega spektra povsem enake izmerjenim emisijskim črtam,
ki jih v laboratorijih
na Zemlji oddajajo posamezni kemični elementi ( Na, K, Ca, Fe, Mg, seveda H ...).


Robert Wilhelm Eberhard Bunsen (1811 – 1899) - nemški kemik in fizik (levo).
Gustav Robert Kirchhoff (1824 - 1887) - nemški fizik (desno).
S spektroskopom na prizmo sta odkrila, da so temne absorpcijske črte
iz Sončevega spektra povsem enake izmerjenim emisijskim črtam,
ki jih v laboratorijih na Zemlji oddajajo posamezni kemični elementi.
To je bil začetek neslutene kvantne odiseje - raziskovanja sestave
in narave oddaljenega vesolja.
Robert Wilhelm Bunsen je tudi prvi pravilno pojasnil
Fraunhoferjeve absorpcijske črte - kot svetlobne prstne odtise posameznih atomov, tudi molekul.
Kaj pa ostale zvezde, meglice, galaksije ...?

Sir William Huggins (1824 – 1910) - angleški učenjak in ljubiteljski astronom, raziskal spektre približno 40 zvezd (to je že delno počel Fraunhofer) in tudi
meglic.
Leta 1862 je William Huggins uporabil 200 mm refraktor s spektroskopom in raziskal spektre približno 40 zvezd (to je že delno počel Fraunhofer)
in v njih našel znane spektralne vzorce mnogih znanih kemičnih elementov.
Raziskal je tudi spektre planetarnih meglic, recimo planetarne meglice »Mačje oko« (NGC 6543) v Zmaju.
Pokazal je tudi, da imajo nekatere meglice, recimo znamenita Orionova meglica M42, emisijski spekter in morajo zaradi tega biti plinaste.
Meglica M31 v Andromedi pa kaže absorpcijski spekter, ki je značilen za zvezde - danes vemo, da jo to galaksija.
Tako je med prvimi razlikoval meglice od galaksij - a takrat še ta razlika ni bila samoumevna.
Spektroskopija (kvantna mehanika) nam je torej na široko približala kemijsko sestavo na tisoče,
milijone in milijarde svetlobnih
let oddaljenih
nebeških objektov. Zvezde, eksoplaneti, meglice, galaksije so torej iz enakih atomov kot Zemlja, naše Osončje. Izjemno!
Niels Henrik David Bohr (1885 - 1962) - danski fizik,
izdela prvi uporaben model vodikovega atoma,
ki uspešno razloži emisijske valovne dolžine preko diskretnih
energijskih nivojev elektrona ob protonu (s krožnimi tirnicami,
ki pa so danes teoretično presežene, a zgodovinsko gledano je bil Bohrov model izjemen uspeh).
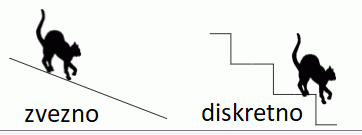
Razliko med klasično in kvantno mehaniko nam lepo ponazori mucek na klancu (leva slika mucka, zvezno, klasično) in na stopnicah
(desna slika mucka, diskretno, kvantno), ki predstavlja princip diskretnih energijskih nivojev (slika je seveda zgolj simbolična).
Prvi spodoben model, kako nastanejo unikatne emisijske in absorpcijske črte atomov, je torej leta
1913 podal Niels Bohr z znamenitim modelom vodikovega atoma - uvede kvantizirane (diskretne)
tirnice za elektrone.
Čeprav Fraunhofer sam ni razvijal kvantne teorije, pa je njegovo izjemno eksperimentalno
delo bilo osnova, je bistveno
prispevalo k razumevanju, da ima svetloba diskretno (kvantno) naravo pri atomskem (molekularnem)
oddajanju svetlobe ali absorpciji le te v atomih (molekulah) in da so tudi energijska
stanja atomov, molekul, elektronov diskretna (kvantizirana). Prehod iz višjih,
točno določenih energijskih nivojev,
recimo v vodiku, na
nižje energijske nivoje, ki so tudi enolično določeni glede na atom, pomeni izsev svetlobe;
prehod iz nižjih na višje energijske nivoje,
pa pomeni absorpcijo okoliške svetlobe ali recimo pridobljeno energijo zaradi trkov med atomi.
Izraz "točno določeni energijski nivoji" moramo razumeti v okviru verjetnosti,
ki jo vrne valovna funkcija - ti nivoji lahko kar precej nihajo
zaradi zunanjih vplivov (trki v plinih - tlak, gostota in temperatura plina,
magnetno in električno polje ...).
To - energijsko diskretno - naravo sveta atomov je
bilo na začetku s strani fizikov
zelo težko sprejeti (pri mehaniki velikih teles, recimo Sonce in tirnice planetov, kometov, asteroidov ... namreč ni opaziti
takih omejitev),
a prav te lastnosti kvantnih delcev nam omogočajo neslutene raziskave tako na Zemlji, kot seveda v vesolju.
Zgolj iz oddanih ali absorbiranih spektralnih valovnih dolžin tako lahko
ugotovimo atomsko sestavo zvezd in galaksij, ki so oddaljene na tisoče, milijone in celo
milijarde svetlobnih let, tudi za eksoplanete velja podobno.
Ugotovimo lahko celo hitrosti oddaljenih teles (preko Dopplerjevega pojava, premika črt - valovnih dolžin),
tlak, temperature in celo magnetna polja (Zeemanov pojav) in električna polja.
Vse trenutne teorije o širjenju vesolja, temni snovi, temni energiji ... so izmerjene
preko spektrov atomov nebesnih teles z upoštevanjem Dopplerjevega pojava (premika spektralnih črt elektromagnetnega
valovanja). V vsakdanjem jeziku elektromagnetno
valovanje pogosto imenujemo kar svetloba, na začetku smo
seveda bili omejeni le na vidni del spektra z valovnimi dolžinami od cca 380 do 750 nm, danes pa lahko detektiramo tudi krajše
gama, rentgenske, UV valove in daljše infrardeče, mikrovalove ter radijske valove.
Raziskovalci tako v svojo korist uporabljajo praktično
cel spekter elektromagnetnega valovanja. To je res velik preskok, sploh če se spomnimo,
da je veliki M. Faraday komaj leta 1845 povezal svetlobo z elektromagnetnim valovanjem -
zabeležil je zasuk polarizacijske ravnine svetlobe v magnetnem polju.
Beseda kvant izhaja iz latinskega izraza quantum, kar pomeni "koliko" ali "koliko določene količine",
recimo koliko energije lahko pripišemo kvantnemu delcu ali kvantnemu sistemu, atomu, molekuli.
Kvanti delci svetlobe se recimo imenujejo fotoni in njihova energija je povezana s frekvenco ν
(oziroma valovno dolžino λ svetlobe), saj velja
Efotona =
hν = hc/λ.
Kjer je c hitrost svetlobe, h pa Planckova konstanta in znaša
h ≈ 6.626070×10-34 J·s = 4.135667696...×10-15 eV·Hz-1 .
Še opomba - mednarodni kvantni dan [World Quantum Day] od leta 2022 obeležujemo 14. aprila,
to je sklicevanje na zaokrožene prve številke Planckove konstante 4,14...×10-15 eV·Hz-1.
Philipp Eduard Anton von Lenard je med leti 1899 in 1902 eksperimentalno
utemeljil enačbo za energijo fotonov: Efotona =
hν.
Preučeval fotoelektrični pojav, izbijanje elektronov iz kovine ob osvetlitvi z ultravijolično svetlobo. Ugotovil je, da energija izbitih elektronov ni naraščala z intenziteto svetlobe, temveč je bila odvisna od valovne dolžine oziroma frekvence svetlobe.
Same teoretične osnove pa je podal M. Planck pri zapisu enačbe spektra toplotnega sevanja teles.
Poudarimo torej, da se je kvantna mehanika začela z astronomijo, z zvezdami,
z zaznavanjem absorpcijskih spektralnih črt
Sonca. To so Fraunhoferjeve absorpcijske črte posameznih elementov, ki sestavljajo atmosfero naše
najpomembnejše Zvezde - to je Sonca. Med popolnim Sončevim mrkom, pa smo preko emisijskih
črt Sončeve atmosfere zaznali tudi drugi po številčnosti in masnem deležu najbolj pogost element v vesolju,
to je helij in to komaj leta
1868 (prej ga zaradi žlahtnosti sploh nismo poznali, saj se He zelo, zelo nerad veže v kake molekule
in se zaradi lahkosti zelo hitro dvigne v zgornje plasti atmosfere, lahko pa celo zapusti Zemljo -
pri sobni temperaturi so nekateri njegovi atomi že zelo blizu ubežne hitrosti z Zemlje, ki je cca 11,2 km/s,
oziroma jo lahko pri višjih toplejših plasteh ozračja celo presežejo).
Prvi po masnem deležu je v vesolju seveda element vodik - okrog 74 %,
helija pa je cca 24% - nekje vmes do 100 % pa je še nekaj malega
težjih elementov (cca 2%, od tega kar polovico kisika in slaba polovica ogljika), ki so v veliki meri nastali v vročih sredicah zvezd,
kjer poteka fuzija - zlivanje lažjih
jeder v težja, do železa. Ta proces nastanka masivnejši atomov (fuzija) od vodika je hkrati
tudi razlaga,
zakaj lahko zvezde svetijo tudi milijarde let. Recimo štirje nukleoni
v heliju so pred zlitjem nekoliko masivnejši kot po zlitju v helij, ker je vezavna energija
atomskega jedra izrazito negativna
- temu pravimo tudi masni defekt Δm in ta del
mase se pretvori v sevalno energijo elektromagnetnega valovanja po znani enačbi E = Δmc2.
Ostali težji elementi od železa pa nastanejo ob eksplozijah supernov in trkih
kompaktnih zvezd (tudi zlato). Obsežna atomska jedra masivnejša od železa namreč (zaradi prevlade
odbojnih sil protonov na močnimi jedrskimi silami) potrebujejo več energije za nastanek,
kot je sprostijo pri fuziji.
Železo (Fe) je tako cca 0,11% celotne mase običajne snovi v vesolju.
Po številu delcev (atomov) je vodika približno 92 % od vseh atomov,
helija približno 7 % in
ostalih elementov pa približno 1 % od vseh atomov v vesolju.
Poglejmo še zanimivosst samega Sonca.
Številčni delež železa (Fe) v Soncu je približno 3×10-5.
To pomeni, da so na vsakih 100.000 atomov v Soncu,
približno le trije atomi železa. Masni delež želza v Soncu pa je cca 0.16 %.
A železo ima izrazite spektralne absorpcijske črte - zakaj? Odgovor sledi.
Te Fe črte so dolgo zavajale astronome, glede sestave Sonca.
A sama kvantna mehanika je tudi ogromno "vrnila vesolju", seveda tudi celotnemu človeštvu. Zakaj?
Razvoj kvantne mehanike in izjemnih polprevodniških kvantnih tehnologij
je namreč omogočil razvoj številnih senzorjev (recimo CCD, CMOS),
naprav (računalnikov, kamer), ki so nam omogočile varno komunikacijo in prenos podatkov
med poleti v vesolje in hkrati hranjenje in obdelavo izjemne količine meritev mnogoterih fenomenov
v vesolju, ki jih
človek nikoli ne bi zmogel ročno zapisati, kaj šele na roke obdelati.
Tudi sam polet proti Luni 21. dec. 1968 in na Luno 20. jul. 1969
brez natančnih sprotnih računalniških preračunov
tirnice ne bi bil mogoč - takrat sta skromna procesorska moč in hitrost
te preračune komaj dohajali.
Zadnji taki uspehi so recimo vezani na detekcijo gravitacijskih valov (LIGO 2015 - potreben je bil razvoj
izjemno natančnih senzorjev preko razvoja kvantnih tehnologij - laserji so tudi del uspešnega razvoja kvantne mehanike
in brez njih ne bi bilo LIGO detektorja)
in vezani so tudi seveda na prva radijska slikanja sevanja akrecijskih diskov ob črnih luknjah.
Prva slika okolice črne luknje v jedru galaksije M87 je bila objavljena 2019 - uporabljen je bil
Event Horizon Telescope (EHT), to je sistem radijskih teleskopov dimenzijsko
porazdeljenih skoraj po vsej Zemlji,
ki so preko interferometrije zbrali kar 9 PB (petabajtov ≈ 1000 TB = 1015 bajtov)
podatkov in potreben je bil
fizičen transport podatkov (tovornjaki), to je diskov po ZDA in po Nemčiji (svetovni splet je bil prešibek
za prenos takega števila podatkov). Brez zmogljivih diskov in računalnikov te
meritve in obdelave ne bi bile mogoče. Celoten proces obdelave, sinteze podatkov
in priprave prve slike je trajal približno 2 leti. V naši mladosti kaj takega ni bilo mogoče
- le kvantne tehnologije so omogočile razvoj tako zmogljivih diskov, računalnikov in to komaj nekje po letu
2010.
Še dve zanimivosti iz sveta elektronike, kjer se danes s pridom uporablja
kvantne lastnosti polprevodnikov (kristali silicija, germanija, GeAs)
za stikala (tranzistorje, kjer so osnova energijski
pasovi, dopiranje - z dodajanjem nečistoč, tuneliranje ...), ki so temelj vseh procesov
računalniške logike. Tranzístor je polprevodniški elektronski element s
tremi priključki, ki ga uporabljamo za ojačevanje, preklapljanje - logična vata
(procesorji - CPU, pomnilniki),
uravnavanje napetosti, modulacijo signalov in v številne druge namene.
Je eden ključnih gradnikov sodobne elektronike in uporabljen v
praktično vsaki elektronski napravi.
Tako
- tiskano vezje (PCB – Printed Circuit Board - razvije Avstrijec Paul Eisler med poletjem 1936
v Londonu - tiskana vezja so še zmeraj osnova za povezavo elektronskih komponent, tudi v računalnikih),
- kot tudi čip (integrated circuit (IC), tudi "microchip" ali kar "chip"
razvije Jack Kilby, mlad uslužbenec v podjetju Texas Instruments leta 1958)
sta bila razvita poleti, ko izumitelja nista šla na dopust –
kar je zelo poučna ironija: medtem ko drugi počivajo, nekdo spreminja svet -
v tem primeru z razvojem majhnih in izjemno zmogljivih procesorjev, računalnikov.
Jack Kilby je v laboratorijski zvezek zapisal naslednje besede:
"The following circuit elements were fabricated on a single piece of germanium."
V svoji patentni prijavi pa pravi:
"a body of semiconductor material … wherein all the components of the electronic circuit are completely integrated."
Robert Noyce (Fairchild Semiconductor)
pa je leto za tem 1959 razvil monolitno integracijo z uporabo silicija (bolj praktično)
in še danes je ta tehnologija del vseh naših pametnih naprav (s tem smo si razbremenili možgane,
morebiti celo preveč).
Nasin program Apollo je bil največji posamezni porabnik integriranih vezij (čipov)
med letoma 1961 in 1965.
Tukaj se tudi skriva kar velik (nujni) del uspešne zgodbe programa Apollo - poleg vseh ostalih
izjemnih tehnologij in vedenj v verigi človeškega razvoja.
Po opisu, kaj vse je kvantna mehanika vrnila človeku in "vesolju", se
vrnimo nazaj k razvoju kvantne mehanike. Matematiki in fiziki so kmalu po
prvih uspešnih opazovanjih emisijskih spektralnih črt atomov, molekul,
začeli iskati enačbo, s katero bi lahko recimo napovedali emisijske (absorpcijske) črte vodika,
pozneje pa tudi ustrezno fizikalno izpeljavo, razlago.
A naloga je bila zelo zahtevna, saj klasična mehanika kaj takega ni
napovedovala - v njeni logiki ni bilo prostora za diskretne energije kakega sistema.
Tako je bil potreben čas - cca 50 let - da so fiziki uspeli narediti tudi
preskok v svojih glavah, v razmišljanju.


Johann Jakob Balmer (1825 - 1898) - švicarski matematik in fizik (levo).
Johannes Robert Rydberg (1854 - 1919) - švedski fizik (desno).
Odkrijeta matematične zakonitosti v vodikovem spektru, napovesta valovne dolžine - to je upanje tudi za fiziko.
Leta
1885 je Johann Balmer zapisal matematično formulo za spekter
vodika, kar je kazalo na določene zakonitosti v atomski strukturi.
Ta Balmerjeva empirična enačba je:
λ=b·n2/(n2 - 22) - za n=3,4,5, …
Velja, da je empirična konstanta b ≈ 364.56 nm in n je celo število večje od 2.
Kasneje se je izkazalo, da je Balmerjeva formula poseben primer Rydbergove formule, ki jo je leta 1888 zasnoval Johannes Rydberg:
Rydbergova
enačba se glasi:
1/λ = RH(1/22 - 1/n2) - za n > 2
kjer je
RH ≈ 1.097×107m-1 (Rydbergova konstanta za vodik) in n je celo število večje od 2.
Splošna Rydbergova
enačba za vodik, ki velja za poljubne prehode med energijskimi nivoji n, se glasi:
1/λ = RH(1/n12 - 1/n22) - za n2 > n1
Johannes Rydberg tako poda tudi matematično napoved črt za nekatere ostale elemente
(recimo za 1x ioniziran He+, kjer ima jedro 2 protona, a le 1 elektron, za Z = 2,
torej se vezavna energija poveča, spektralne črte so tako bližje UV spektru, velja:
1/λ = RHZ2(1/22 - 1/n2) ).
Balmerjevo enačbo oziroma
Rydbergova predvidevanja, da bodo vodilne spektralne linije,
ki se dobijo iz posplošene Rydbergove formule,
pomagale pri teoretskem razumevanju
atomske strukture, je s pridom uporabil leta 1913 Niels Bohr in izpeljal prvi uspešen model vodikovega atoma, ki je pravilno napovedoval spektralne barve (valovne dolžine) vodika.
Tako je seveda izpeljal tudi Rydbergovo konstanto, ki je sestavljena iz osnovnih
konstant, mase elektrona, osnovnega naboja, Planckove konstante, hitrosti svetlobe,
dielektrične konstante:
RH = mee4/(8ch3εo2).
Masa jedra atoma ni neskončno majhna v primerjavi z maso elektrona.
Spekter, ki se ga dobi po običajni Rydbergovi formuli, je tako v resnici treba popraviti z reducirano maso, ki zamenja maso elektrona.

Max Karl Ernst Ludwig Planck (1858 - 1947) - izjemen nemški fizik, kvantiziral elektromagnetno valovanje
po vzoru Boltzmannove kinetične teorije plinov in statistične definicije entropije.
Da ne pozabimo še enega izmed očetov kvantne mehanike, moramo na tem mestu
omeniti še Maxa Plancka ( 1858 – 1947 ), ki po dolgih premislekih
uspešno zapiše porazdelitev gostote toplotnega izseva po valovnih dolžinah za idealno črno telo glede na temperaturo
(danes po njem poimenovan Planckov zakon). Že prej je bil zapisan
Rayleigh-Jeansov zakon za energijsko gostoto sevanja glede na valovno dolžino λ
pri temperaturi T - a je bil zelo pomanjkljiv. Poglejmo zakaj? Ta zakon
se glasi u(λ,T) = 8πkT/λ4. Je sicer dokaj soliden
za dolge valovne dolžine,
a pri kratkih UV sevanjih (valovna dolžina je namreč v imenovalcu)
se popolnoma spridi - to je bil še klasičen pristop brez kvantnih
energijskih paketov.
Temu pravimo tudi
pojav UV katastrofe. Klasična fizika se je torej pokazala kot zelo neučinkovita v svetu
majhnih teles, molekul, atomov, v svetu valovnih pojavov. In kako naprej?
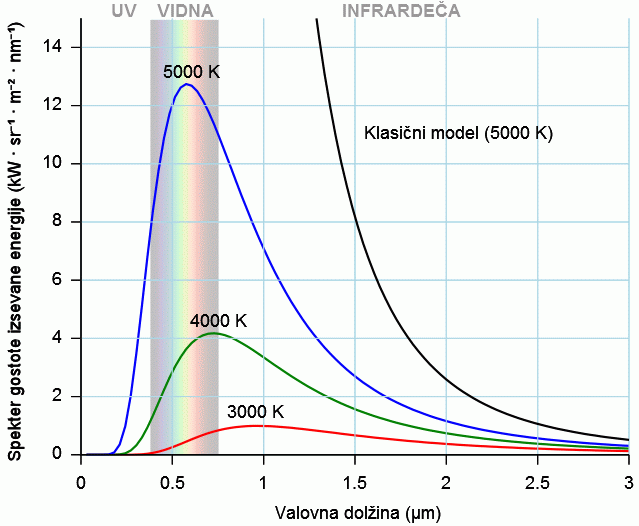
Ko je Planck oblikoval svoj zakon o porazdelitvi gostote toplotnega izseva po valovnih dolžinah - za črno telo:
dj/dλ = (2πhc2/λ5)(ehc/(λkT) - 1)-1
- je uporabil Boltzmannovo zvezo za entropijo, neurejenost [ S = k ln(p) = k ln Ω ].
Entropija S je sorazmerna naravnemu logaritmu števila mikrostanj ( p ali
Ω sta oznaki za število mikrostanj, k je Boltzmannova konstanta) - to je bila revolucionarna izpeljava
in je temelj sodobne statistične mehanike.
Planck je tudi pomenljivo zapisal:
"Acting on an act of desperation, I adopted Boltzmann's interpretation of entropy
(Iz obupa sem sprejel Boltzmannovo interpretacijo entropije.)."


Slovenski fizik, dr. Jožef Stefan (* 24. marec 1835, Sveti Peter pri Žrelcu, sedaj predel Celovca,
† 7. januar 1893, Dunaj) - levo. Odkrije znameniti zakon (Stefanov) o toplotnem sevanju teles:
j = P/S = L/S = σ × T4 - tako leta
1879 tudi prvi na svetu pravilno izračuna površinsko temperaturo (5776 K) našega Sonca,
zvezde, ki nam daje vse, to je življenje ... Globok priklon Jožefu Stefanu. Njegov zakon je edini,
ki se imenuje po kakem Slovencu.
Ludwig Edward Boltzmann - desno, izjemen avstrijski fizik in filozof,
* 20. februar 1844, Dunaj, † 5. september 1906, Devin). Bil je Stefanov učenec na univerzi na Dunaju. Znan je po vpeljavi termodinamične teorije toplote
- kinetične teorije plinov (Maxwell-Boltzmannova porazdelitev molekul po energiji, hitrosti),
po teoretični izpeljavi Stefanovega zakona in po statistični interpretaciji entropije
(kot mere za neurejenost). S takim modelom je močno zaznamoval
tudi Planckov opis spektra toplotnega sevanja.
Boltzmannovo porazdelitev po vzbujenih atomskih stanjih je Dami Ceciliji Heleni Payne tudi omogočila
razrešiti dilemo katerih atomov je največ v zvezdah, v vesolju (H, He). Te izjemne zgodbe se dotaknemo pozneje.
Čeprav Planck ni uporabil Boltzmannove kinetične teorije plinov kot take,
je pa uporabil statistično idejo entropije, ki je bila ključna za prehod v kvantno fiziko.
Povejmo še, da je bil Ludwig Boltzmann na Dunajski univerzi učenec našega genija Jožefa Štefana, ki je prvi
pravilno prišel do enačbe za gostoto toplotnega sevanja teles j glede na absolutno temperaturo T
(privzetek absolutne temperature je bil odločilen).
Za idealno črno telo velja torej Štefanov zakon:
j = σT4
Štefan je iz lastnega zakona tudi prvi pravilno izračunal površinsko temperaturo Sonca.
Štefan je imel tudi odločilen vpliv na Boltzmanna, ki je
tako še statistično dokazal Štefanov zakon. Povejmo še, da Štefanov zakon tudi neposredno
izhaja iz Planckovega zakona - to je iz integrala porazdelitve gostote toplotnega izseva
po valovnih dolžinah (ali frekvencah) za idealno črno telo glede na temperaturo. Ludwig Boltzmann je imel zaradi
statistične kinetične teorije plinov velike težave med kolegi in je, tudi zaradi teh pritiskov, zelo tragično končal
svoje življenje v sosednjem Devinu (blizu Trsta) leta 1906.
Potrebno je še enkrat poudariti, da je m. Plancku
bila vzor Boltzmannova verjetnostna porazdelitev (tudi Maxwell-Boltzmannova),
ki je osnova kinetične teorije plinov, kjer se recimo statistično opiše porazdelitev kinetične energije
delcev plina (od tam tudi eksponent).
Še glede razlike med dvema porazdelitvama.
Maxwell-Boltzmannova porazdelitev opisuje velikost hitrosti delcev,
ki je vedno pozitivna in ima značilno asimetrično obliko.
Gaussova porazdelitev pa opisuje posamezne vektorske smerne komponente hitrosti (npr. v x-smeri),
ki so simetrično razporejene okoli nič
(kaotično gibanje v vse smeri). Pomembna je recimo pri oceni Dopplerjevega pojava pri razširitvi
absorpcijskih črt zvezd.
Maxwell-Boltzmannova porazdelitvena funkcija f(v) za verjetnost,
da ima delec v plinu hitrost v, je torej:
f(v) = (4πv2)(m/(2πkT))3/2e-mv2/(2kT)
Kjer je v celotna hitrost v prostoru, ko velja:
v2 = vx2 + vy2 + vz2
Ta zakon nam tudi zelo pomaga pri študiju sevanja zvezd – določanje spektralnih tipov in površinske temperature zvezd.
In kaj je naredil Planck glede na dano porazdelitev - kvantiziral je energije fotonov (uvedel je fotonski plin),
namesto kinetične energije delcev plina mv2/2, je zapisal
energijo fotonov Ef. Intuitivno je privzel, da je energija fotona sorazmerna frekvenci svetlobe, tako velja:
Ef =
hν = hc/λ.
To je bil izjemno luciden sklep, ki je bil dokončno potrjen komaj čez nekaj let (1905) - praktično pa sočasno
z izpeljavo s strani Lenarda (baje neodvisni poti).
Max Planck je predstavil svojo revolucionarno enačbo za spekter sevanja črnega telesa na srečanju
Nemškega fizikalnega društva (Deutsche Physikalische Gesellschaft) v Berlinu 14. decembra 1900.
Ravno v tem času pa so tudi potekali eksperimenti, ki so potrdili Planckove intuitivne sklepe.
Philipp Eduard Anton von Lenard (1862 - 1947) je ravno
med leti 1899 in 1902 eksperimentalno preučeval fotoelektrični pojav,
torej izbijanje elektronov iz kovine ob osvetlitvi z ultravijolično svetlobo. Ugotovil je, da
energija izbitih elektronov ni naraščala z intenziteto svetlobe,
temveč je bila odvisna od valovne dolžine oziroma frekvence svetlobe.
Pri določeni spodnji mejni frekvenci svetlobe ni prišlo do fotoefekta, ne glede na to, kako močna je bila svetloba.
Lenard je za ta namen razvil posebno 'Lenardovo' okensko cev,
v bistvu rentgen (tudi Lenard je prejel Nobelovo nagrado - je pravi oče rentgenske cevi). Lenardove ugotovitve
je pozneje (1905) potrdil tudi Einstein s teorijo fotonov, ki jih je v bistvu že uvedel Planck, Lenard pa
pomeril. Einstein v bistvu poveže Planckovo porazdelitev sevanja črnega telesa (s "Planckovimi fotoni")
z Lenardovimi ključnimi eksperimentalnimi ugotovitvami.


Ernest Rutherford (1871 - 1937), levo
- novozelandski fizik. Zlato folijo obstreljuje z alfa delci (pozitivno jedro atoma helija - ioniziran helij,
nastanejo večinoma pri radioaktivnem razpadu). Alfa delci večinoma nemoteno prehajajo
skozi zlato folijo - iz poučnih rezultatov eksperimenta sledi realnejši model atoma. Zakaj?
Pri eksperimentu se je le zelo skromen del delcev odklonil, delno tudi odbil,
kar je pokazalo na zelo majhen koncentriran naboj - masivno atomsko jedro je torej pozitivno in zelo majhno (cca d = 1 fm = 10-15 m ),
negativni lahki elektroni pa morajo biti tako zelo oddaljeni
(cca D = 100000 fm = 10-10 m ).
Hideki Yukawa (1907 – 1981), desno - japonski fizik.
Yukawa je leta 1949 kot prvi Japonec prejel Nobelovo nagrado za fiziko
»za napoved obstoja mezonov
- na podlagi teoretičnega dela o jedrskih silah in nosilcih sil, mezonih
(mezoni so posredniki močne jedrske sile ki veže nukleone,
protone in nevtrone, v atomska jedra).«
Leta 1911 Ernest Rutherford poda model atoma z zelo majhnim jedrom
in oddaljenim elektronskim oblakom, kar je še dodatna priprava za
kvantno razlago zgradbe atoma. Komaj leta 1935 je
japonski fizik Hideki Yukawa kot prvi teoretično predlagal obstoj močne jedrske, ki drži skupaj protone in nevtrone v atomskem jedru
(protoni se namreč odbijajo - zato jih mora v jedru nekaj držati skupaj, to je močna jedrska sila, ki deluje na kratke razdalje, seveda je
nujno sodelovanje še nevtronov).
Leta 1924 Louis de Broglie predlaga valovno naravo delcev,
- uvede "noro" idejo kvantnih valov za masne delce, kjer je valovna dolžina λ obratno
sorazmerna gibalni količini p = mv, sorazmernostni koeficient je Planckova konstanta h, zato velja:
λ = h/(mv).
De Brogliju se je ideja porodila zaradi očitne kvantizacije energijskih nivojev atomov (tako tudi nastanejo spektralne črte
posameznih atomov). Obseg tirnice elektrona ob jedru mora vsebovati celo število valovnih dolžin de Broglijevega valovanja
(danes je pojem tirnic, orbit presežen, a v kemiji iz pedagoških razlogov še živi).
De Broglie je s to "noro", a pravilno, hipotezo vplival tako na Einsteina kot na Schrödingerja in seveda
na razvoj elektronskih mikroskopov.
V tem smislu (po naštetih mejnikih) se zdi - da bi morali 100 let kvantne mehanike praznovati že leta 2000 ali 2005, morebiti 2013 (100
let Bohrovega modela vodikovega atoma) ali 2024.
Konec determinizma, a hkrati se odprejo sanje o začetku vesolja.
A leta 1925 in pozneje, so se zgodili čisto novi teoretični premiki, tudi eksperimentalni podatki,
ki so privedli do povsem nepričakovane interpretacije našega sveta.
Heisenberg je leta 1925 razvil matrično mehaniko, prvi dosledni kvantnomehanski formalizem.
To, da so njegovi izračuni matrični (Heisenberg je imel komaj 23 let), mu razkrije Max Born.
Njegov cilj je bil razviti teorijo, ki temelji samo na opazljivih količinah,
kot so spektralne črte, frekvence, ne pa na "neopazljivih" konceptih, kot so recimo Bohrove vprašljive tirnice elektronov.
Uvedel je nemoteče opazovanje in delal z matematičnimi količinami kot so matrike (npr. matrika za položaj, hitrost delca itd.),
ki ne komutirajo, kar vodi do Heisenbergovega načela nedoločenosti. Kaj to pomeni?
Če najprej izmerimo lego x in nato gibalno količino p, dobimo drugačen rezultat, kot če merimo v obratnem vrstnem redu,
a razlika je zmeraj
ih/(2π),
torej ni nič - kar pa neposredno vodi do Heisenbergovega načela nedoločenosti - leto 1927:
Δp·Δx ≥ h/(4π)
Kako razumeti to izjemno pomembno načelo nedoločenosti?
Če želimo natančno vedeti, kje se elektron nahaja (precizno pozicijo lege X), moramo "pogledati" elektron
z zelo natančnim orodjem, kar pomeni, da moramo uporabljati svetlobo kratkih valovnih dolžin (ali delce z zelo
kratkimi valovnimi dolžinami λk). A kratkovalovna svetloba (energija fotona je E = hν = hc/λ)
bo zelo motila elektron in ga bo zagotovo premaknila (mu spremenila hitrost),
zato
ne bomo uspeli točno poznati njegove hitrosti (oz. gibalne količine p = mv).
Če pa želimo natančno izmeriti hitrost (gibalno količino p) elektrona, moramo uporabiti svetlobo dolgih valovnih dolžin
λd, ki ne vplivajo zelo na elektron. Toda, s tem, da uporabljamo dolge valove, ne bomo mogli
točno določiti pozicije (X) elektrona (ločljivost take metode iskanja lege je namreč odvisna od valovne dolžine λ).

Kanonično komutativno pravilo za spremembo položaja q in gibalne količine (momenta) p - dveh spremenljivk delca,
1927. pq - qp = h /(2 πi). Heisenbergovo načelo nedoločenosti, negotovostni, 1927.
V matrični mehaniki je matematična formulacija kvantne mehanike,
vsak par ne-komutativnih sebi-adjungiranih operaterjev, ki predstavljajo opazljive spremenljivke,
podvržen podobnim mejam negotovosti.
Poglejmo preprost primer komutiranja operatorjev položaja
x in gibalne količine
p.
Če je komutator dveh operatorjev neničeln, pomeni, da teh količin ni mogoče hkrati natančno
izmeriti (npr. položaj in gibalna količina).
Komutatorji so povezani z dinamiko sistemov
( prek Heisenbergove enačbe gibanja, kjer je ℏ = h/(2π) reducirana Planckova konstanta):
dA/dt = [A,H]/(iℏ) + ∂A/∂t
Oziroma v doslednejšem zapisu:
dAH(t)/dt = [AH(t),HH(t)]/(iℏ) + (∂AS/∂t)H
Členi v enčbi so:
AH(t) - opazovana količina (operator) v Heisenbergovi sliki,
HH(t) - Hamiltonian v Heisenbergovi sliki (pogosto enak kot v Schrödingerjevi, če je časovno neodvisen)
(∂AS/∂t)H - eksplicitna časovna odvisnost operatorja v Schrödingerjevi sliki,
prenesenega v Heisenbergovo sliko (z uporabo istega U(t)).
--------------------------------------
Kjer je: U(t) = e-iHt/ℏ in inverz: U†(t) = eiHt/ℏ
Pretvorba med obema slikama ( Heisenbergovo 'H' in Schrödingerjevo 'S' )
je torej:
AH(t) = U†(t)AS(t)U(t)
Primer: Operator položaja x
- za prost delec (brez potenciala) je Hamiltonianom: H = p2/(2m)
Operator položaja v Schrödingerjevi sliki je xs. Potem je operator v Heisenbergovi sliki:
xH(t) = U†(t)xS(t)U(t)
S pomočjo komutatorjev lahko pokažemo, da se operator razvije kot:
xH(t) = xs(t) + pS/m
Kjer je pS = -iℏ∂/∂x operator za gibalno količino (moment) v Schrödingerjevi sliki,
ki deluje na valovno funkcijo Ψ(x,t).
Kjer spet velja: pH(t) = U†(t)pS(t)U(t)
(ker je klsaično hitrost enaka v = p/m in torej xH(t) = xs(t) + pS/m
ustreza klasični enačbi gibanja za prost delec, kjer je lega: x = xo + v*t )
Povejmo še razliko med valovnima funkcijama Schrödingerjeve in Heisenbergove slike opisa sveta kvantne mehanike:
ΨS(x,t) - valovna funkcija v Schrödingerjevi sliki se razvija s časom (t).
ΨH(x) - valovna funkcija v Heisenbergovi sliki je fiksna v času.
Velja še ΨS(x,t) = <x|Ψ(t)> - več sledi.
Zato tudi velja:
|ΨH(x)> = |ΨS(0)>
Operatorje bomo torej tukaj pisali v poševnem fontu (Italic), recimo
x in
px, komutator dveh operatorjev pa bo [x, px]. Večinoma
pa jih pišejo s strešico ^, recimo:
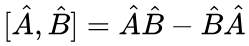
V prostorsko-časovni predstavitvi valovne funkcije, recimo elektrona, velja zapis:
Ψ(x,t) =
Aei(px/ℏ – Et/ℏ) = Ae– iEt/ℏΨ(x)
Zgolj v prostorski predstavitvi (kjer delce opišemo kot funkcije x lege
Ψ(x), sta, kot je zapisano v poglavju
o valovni funkciji, operatorja definirana na naslednji način.
Operator položaja:
x Ψ(x) = x·Ψ(x)
Operator gibalne količine:
pxΨ = -iℏ∂Ψ(x)/∂x
Glejte poglavje :
Delčna in valovna narava osnovnih kvantnih delcev.
To sta osnovna operatorja kvantne mehanike v pozicijski (krajevni) predstavitvi.
Izračunajmo komutator [x, px]Ψ(x).
Po definiciji komutatorja velja:
[x, px]Ψ(x) = x(pxΨ(x)) - px(xΨ(x))
Na koncu uporabimo splošno matematično pravilo.
V kvantni mehaniki obstaja splošna neenakost, ki pravi:
ΔA·ΔB ≥ |<[A,B]>|/2
Ta zgornja formula izhaja iz matematike kvantne mehanike, natančneje iz Schwarzove neenakosti
(tudi Cauchy–Schwarzova neenakost).
Valovno funkcijo Ψ(x) v dokazu pišemo kar kot Ψ.
x(pxΨ) = x(-iℏ∂Ψ/∂x) = -ixℏ∂Ψ/∂x
px(xΨ) = -iℏ∂(xΨ)/∂x = -iℏ(1*Ψ + x∂Ψ/∂x)
Tako velja, ker je ∂x/∂x = 1:
[x, px]Ψ
= -ixℏ∂Ψ/∂x - ( -iℏ(1*Ψ + x∂Ψ/∂x) ) = iℏΨ
Valovno funkcijo Ψ na obeh straneh okrajšamo in tako dobimo izraz za komutator dveh operatorjev
x in px.
[x, px] = iℏ
Ker velja:
ΔA·ΔB ≥ |<[A,B]>|/2, oziroma Δx·Δp ≥ |<[x,p]>|/2
Je končni rezultat kar Heisenbergovo načelo nedoločenosti:
Δx·Δp ≥ ℏ/2 ali Δx·Δp ≥ h/(4π)
Ta zapis v sebi skriva globoko resnico - recimo, da ni vseeno katero količino pomerimo prej (x ali p,
lego ali gibalno količino, obakrat vplivamo na obe količini, kako, sledi v nadaljevanju, a vseeno obstaja spodnja
limita h/(4π), ki smo jo ravno izračunali).
Velja pa tudi, da je komutator na py, torej za pravokotno smer pričakovano enak 0 (saj velja ∂x/∂y = 0):
[x, py]Ψ(x)
= -ixℏ∂Ψ(x)/∂y - ( -iℏ(0*Ψ(x) + x∂Ψ(x)/∂y) )
= (-ixℏ∂/∂y + xiℏ∂/∂y) Ψ(x)
= 0
Za vajo in razumevanje Heisenbergove enačbe gibanja ( dA/dt = [A,H]/(iℏ) + ∂A/∂t )
si oglejmo še
Hamiltonian in sicer energijo sistema glede na položaj x
in gibalno količino p, brez potenciala, torej se kvantni delec (recimo elektron) giblje prosto:
H = p2/(2m)
Heisenbergova enačba za
x,
če se sam operator A ne spreminja s časom velja
∂A/∂t = 0,,
je potem:
dx/dt = [x,H]/(iℏ)
Not vstavimo člen za energijo preko operatorja H = p2/(2m)
dx/dt = [x,H]/(iℏ) = [x,p2/(2m)]/(iℏ) = [x,p2]/(iℏ2m)
Velja tudi:
[x,p2/(2m)] = [x,p2]/(2m)
Izračunamo komutator [x, p2]:
[x, p2] = p[x, p] + [x, p]p =
piℏ + iℏp = 2iℏp
Tako dobimo:
[x,H] = [x, p2/(2m)] = 2iℏp/(2m) = iℏp/m
Končni rezultat je:
dx/dt = [x,H]/(iℏ) = (1/(iℏ))iℏp/m = p/m
To je pa enačba za hitrost v klasični mehaniki glede na gibalno količino v = p/m.
Še Heisenbergova enačba za operator gibalne količine, rabimo torej [p,H].
dp/dt = [p, H]/(iℏ) = [p, p2/(2m)]/(iℏ) = [p, p2]/(iℏ2m)
Spet smo torej privzeli Hamiltonian
H = p2/(2m).
Komutator je:
[p, p2] = 0 => [p, H] = 0 => dp/dt = 0
To pomeni: gibalna količina se ne spreminja s časom ( dp/dt = 0 )
– kar je logično za prost delec brez sile (torej brez potenciala).
To sta bili preprosti vaji za razumevanje Heisenbergove enačbe gibanja, kjer je komutator ključen:
dA/dt = [A,H]/(iℏ) + ∂A/∂t
Heisenbergov princip nedoločenosti se da res slikovito in enostavno prikazati "eksperimentalno - računsko"
na primeru delca (delcev), ki gre skozi ozko režo (tej širino lahko spreminjamo, s tem
pa tudi nedoločenost lege in gibalne količine). Vajo lahko izvedemo v razredu.
Ta vaja je zelo dober pedagoški primer,
kako se negotovost v položaju in gibanju preračunljivo povežeta (Δp·Δx ≥ h/(4π)).

Pri ozki spodnji reži širine w1 pridobimo informacijo o legi valovanja (nedoločenost Δx1 ≈ w1),
a izgubimo na komponenti gibalne količine v x smeri (nedoločenost Δp1x).
Pri širši zgornji reži širine w2 je uklon manjši, a je večja nedoločenost lege fotona, elektrona (Δx2 ≈ w2).
Velja, če:
w2 > w1
potem
Δp1x > Δp2x in Δx2 > Δx1.
Produkt obeh nedoločenosti ΔpΔx pa je kar velikostnega reda Planckove konstante h
- kot je že predvideval W. Heisenberg. Pa to še
dokažimo.
Skozi režo širine
w pošljemo delce (elektrone, fotone ...).
Delce lahko lociramo na širino reže.
Negotovost v legi je torej kar
Δx ≈ w.
Ko gre delec skozi režo, zaradi uklona spremeni svojo smer (poznan pojav tudi iz klasične fizike)
— to pomeni, da ni več natančno določen v smeri gibanja, kar vrne fizikalno negotovost v gibalni količini smeri x,
kar zapišemo kot
Δpx
(prečno na gibanje).
Uklonski vzorec za režo širine
w
in valovno dolžino
λ
ima prvi minimum pri kotu:
α ≈ λ/w
Pojasnilo, zgornja enačba velja samo za uklon na eni reži
(Znotraj reže širine
w
si lahko predstavljamo nešteto točk, ki sevajo valove (Huygensovo načelo).
Ko gledamo, pod katerim kotom
α se valovi iz različnih delov reže med seboj izničijo, velja pogoj, da mora
njihova razlika v poti doseči celotno valovno dolžino - to je drugače kot
pri dveh režah - pri dveh režah pa velja pogoj polovice valovne dolžine).
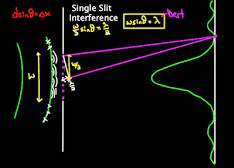
Uklon na eni reži širine w - podobno velja za uklone na objektivih ...
Če poznamo gibalno količino delca:
p = h/λ
potem je prečna komponenta (v smeri
x, zaradi uklona):
Δpx ≈ p·α = (h/λ)·(λ/w) = h/w
Obe oceni vstavimo v Heisenbergovo enačbo
Δx·Δpx ≈ w·h/w = h
Torej:
Δx·Δpx ≈ h ≥ h/(4π)
Kar pa ustreza Heisenbergovemu načelu nedoločenosti!
Kaj pomeni ta rezultat?
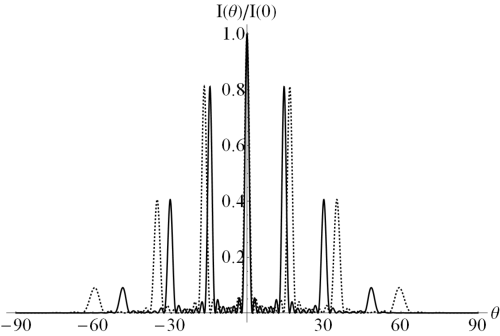
Ožja reža pomeni večjo negotovost v prečni komponenti gibalne količine (kar vrne širši vzorec na zaslonu - slika spodaj).
Torej ni mogoče narediti reže, ki bi ti dala natančno lego in natančno smer hkrati,
saj velja Δx·Δpx ≈ h.
Povedano se lepo razbere iz spodnjih slik.

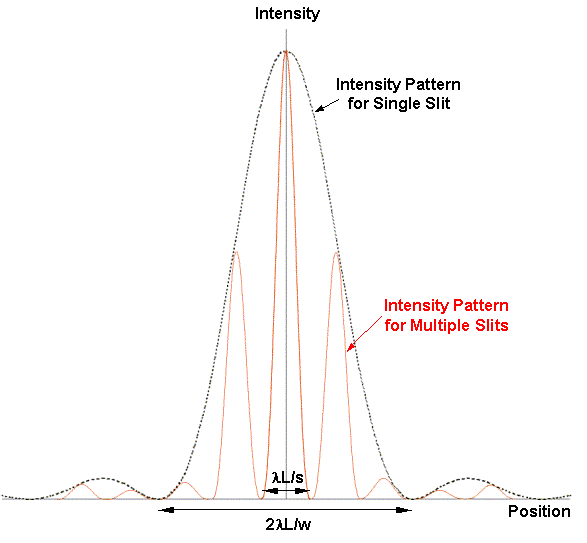
Iz zgornje slike razberemo, da lahko uklonske vzorce ustvari ena sama reža ali dve in več rež ('slits').
Za dve ozki reži na razdalji d sedaj velja, da je Δx ≈ d. Račun se ponovi.
A v tem primeru se zazna še ena zanimivost.
Če merimo, skozi katero režo gre delec (npr. detektor ob vsaki reži),
sicer pridobimo informacijo o položaju delca, ki je sedaj
Δx ≈ d, kar je razdalja med režama (majhna negotovost).
A s tem neizogibno zmotimo njegovo gibalno količino, to pomeni, da se valovna narava izgubi
in interferenčni vzorec izgine.
Obstaja luštna šala na tematiko principa nedoločenosti
gibalne količine in lege. Takole "se je zgodilo".
Bohr s "pametnim" mobilcem telefonira Heisenbergu, ki ravno drvi z avtom
v službo. Bohr ga poheca, da je na sledi njegovemu telefonu in mu tako pove njegovo natančno prekoračitev hitrosti.
A Heisenberg se odzove kot pravi fizik: "U, sedaj ko si mi povedal, kako hitro se peljem, pa ne vem kje sem, čisto sem zgubljen!"

|
|
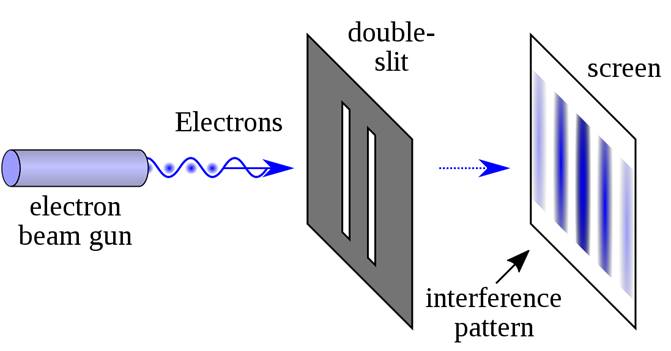
De Brogliju se je ideja o valovni naravi delcev porodila zaradi kvantizacije energijskih nivojev atomov
(slika levo – ta model je danes večinoma presežen, je pa zgodovinsko zelo pomemben).
Desna slika pa prikazuje interferenčno sliko elektronov na dveh režah. De Broglie
je vplival na Einsteina in Schrödinger pod tem vplivom zapiše diferencialno enačbo
za valove povezane z delci in rodi se valovna funkcija lege delca v času in prostoru.
Fiziki se pogosto pošalijo glede
principa nedoločenosti, izrazitih motenj, ki jih povzročijo merjenja v kvantni mehaniki na merjen delec,
recimo pri interferenčnem poskusu, ko recimo elektrone,
ki jih uporabimo v interferenčnem poskusu na režah, radi primerjajo
"z mulci, ki se drugače obnašajo, če jih gledamo, kot če jih ne gledamo".
Omenimo še, da je W. Heisenberg napisal imenitno knjigo "Del in celota" - pogovori v območju atomske fizike
(prevedla in izdala jo je Mohorjeva družba iz Celja, 1977, COBISS.SI-ID - 7722753 ) in to knjigo smo v osemdesetih
letih 20. stoletja brali takrat skoraj vsi študentje fizike in tudi mnogi ostali ...
Načelo nedoločenosti ima tudi obliko zapisa z energijo ΔE = (Δp/Δt)·Δx = F·Δx
in s časom Δt, saj velja:
Δp·Δx = [(Δp/Δt)·Δx]·Δt = ΔE·Δt ≥ h/(4π)
Načelo nedoločenosti nam posredno sporoča, da si je moč energijo iz ničesar sposoditi, če se le ta dovolj hitro 'povrne' - tako si
tudi razlagamo kvantne fluktuacije delcev in antidelcev v "vakuumu" (v "praznem prostoru").
Za kratek čas v vakuumu recimo nastanejo protoni in antiprotoni, a se tudi kmalu izničijo (anihilirajo) in spremenijo
v dva fotona, v tem primeru dva gama žarka (ohranita se energija in gibalna količina sistema).
Več o posledicah tega dejstva pozneje.
Heisenbergovo načelo nedoločenosti in "nepričakovano" spoznanje, da praznega prostora ni, saj so zmeraj možne kvantne
fluktuacije delcev in antidelcev ... in njihova anihilacija v fotone, je pripeljalo do intrigantnega
razmišljana, da bi na tak način morebiti lahko kaj povedali o začetkih - nastanku vesolja. Scenarij našega začetka, začetka vesolja, je recimo
naslednji proces.
Na začetku vesolja, v Planckovem času (≈ 10-43 sekund po Velikem poku),
je bilo vse zgoščeno v izjemno majhen volumen. Po kvantnem načelu velja:
ΔE·Δt ≥ h/(4π)
Kjer:
* ΔE = nedoločenost v energiji,
* Δt = časovna nedoločenost (npr. trajanje fluktuacije).
Ta različica načela pomeni, da se za zelo kratke čase lahko pojavijo fluktuacije energije
– torej delci in antidelci, ki "iz nič" obstajajo za hip, nato izginejo. V ekstremnih pogojih zgodnjega
vesolja so te fluktuacije postale trajni del vesolja in sprožile njegovo širitev.
V modelih kvantne kozmologije, kot je inflacijska teorija, se verjame,
da je vesolje lahko nastalo iz kvantne fluktuacije vakuuma – stanja,
kjer ni "ničesar", a zaradi kvantne nedoločenosti obstaja "nekaj".
Ko kvantna fluktuacija povzroči nastanek energijskega paketa delcev in antidelcev
( ΔE ≥ h/(4πΔt) ), več podobnih sinhronih dogodkov, se iz tega morebiti rodi samo vesolje.
Pri zlomu simetrije
v prid delcev, recimo, da je 10 milijard protonov našlo antiprotone ter se izničilo in spremenilo
v žarke gama [to sevanje še danes zaznamo v obliki mikrovalov ozadja, vesolje se širi], en sam pa
je ostal brez para in naprej (pri neki drugi množici dogodkov) velja enako - za naslednjih 10 milijard protonov torej spet velja, da
en proton ostane brez para ..., iz teh ostankov od ostankov pa smo torej tudi nastali ljudje, današnje vesolje ...
Konceptualni problem je lahko nedoločenost časa, od kod bi se čas vzel, če ni prostora ...
Če odmislimo težave modela, se lahko vseeno vprašamo -
a smo torej ljudje, vesolje kvantna fluktuacija, ki še nekoč mora vrniti sposojeno energijo – lahko da,
saj nobena oblika energije ni večna, saj večina meritev
tako kaže (energija se sicer ohranja, a spreminja pojavne oblike).
Oziroma - nič ni večnega, razen zakonov narave, ki pa jih še ne poznamo ravno dovolj temeljito in ne vseh.
Vsa ta spoznanja
-
Heisenbergov princip nedoločenosti, de Brogliejeva dualnost valov in delcev ( λ = h/(mv) ),
Schrödingerjeva valovna funkcija (navdih da de Broglie),
Max Born in verjetnostna
interpretacija valovne funkcije, Diracova relativistična kvantna mehanika,
Paulijev izključitveni princip ... popolnoma spremenijo okvir razumevanja
pojavnega sveta, ki ga živimo. Einstein recimo nikoli ni sprejel verjetnostnega principa kvantne mehanike.
Kvantna mehanika je polna nepričakovanih pojavov. Omenili smo že recimo
kvantno prepletenost - ko se dva nekoč prepletena delca čutita tudi na daljavo (kvantna teleportacija stanja, recimo spina,
polarizacije). Vsekakor pa je vse močno presenetilo kvanto tuneliranje,
pri katerem delec (npr. elektron) preide skozi energijsko oviro, ki je po klasični fiziki ne bi mogel prečkati, ker nima dovolj energije.
Predstavljajmo si, da imamo žogo in hrib.
Če žoga nima dovolj energije, ne more preskočiti hriba – ostane na eni strani.
Po klasični fiziki bi to pomenilo, da žoga nikoli ne more priti na drugo stran, razen če ji dodamo več energije.
Še beseda o valovanju - večinoma si valove predstavljamo kot recimo kosinusno ali sinusno krivuljo (prehodi med dolinami in
vrhovi, recimo klasični zapis valovanja iz srednje šole v x smeri je A·cos(2πx/λ - ωt);
kjer je A amplituda - višina valov, x lega na premici, λ valovna dolžina,
ω krožna frekvenca valovanja, t pa čas opazovanja). V kvantni mehaniki pa uporabimo Eulerjevo formulo, ki se glasi:
Ψ(x,t) =
A·ei(2πx/λ - ωt),
kjer velja ei(2πx/λ - ωt) = cos(2πx/λ - ωt) + i·sin(2πx/λ - ωt).
S ponovitvijo srednješolke snovi o valovanju smo
tako gibajočemu prostemu elektronu
(brez zunanjih sil, potencialov, z gibalno količino mv) že pripisali pravilno harmonično valovno funkcijo
Ψ(x,t) po Eulerjevi
notaciji. Tako nekako je razmišljal tudi Schrödinger zaradi
de Brogliejeve dualnosti valov in delcev (pripisana valovna dolžina je kar
λ = h/(mv)
- nerelativistični zapis).
Ko se pa recimo elektron ali kak drug kvantni delec sreča z zunanjimi silami (recimo elektron
ob atomskem jedru - v potencialu), se opis gibanja (valovanja) precej spremeni,
kar pa že presega namen tega članka.
Eulerjeva formula je zelo priročen način, da se povežeta eksponentna funkcija in
trigonometrične funkcije (sinus in kosinus),
ki opisujejo valovno naravo sistema. Brez kompleksnih števil bi bil
matematični opis teh pojavov precej bolj zapleten, še posebej pri merjenjih in obravnavi
superpozicij
(kvantni sistem obstaja v več stanjih hkrati - kombinacija različnih možnosti - ko pa pomerimo recimo
elektron, bo ta vstopil v eno izmed možnih stanj)
in interferenc
(interferenca se lahko zgodi samo, če imamo superpozicijo različnih možnosti - recimo interferenca
gibajočih elektronov ali svetlobe na režah).
Podajmo primer interference na dveh režah, ki ga že poznamo iz klasične fizike.
Interferenca nastane, ko imamo več poti (ali stanj), skozi katere lahko sistem preide
in te poti valovanj interferirajo med seboj. Rezultat je, da se verjetnostni vzorec, ki ga opazimo na koncu,
lahko poveča (konstruktivna interferenca) ali zmanjša (destruktivna interferenca), odvisno od faznega zamika med potmi.
Poglejmo, kako to izgleda pri eksperimentu na dveh režah, kjer imamo dve poti, skozi kateri lahko delci (recimo elektroni)
potujejo.
Za ta preprost primer bomo uporabili kompleksna števila, Schrödingerjev zapis, torej Eulerjevo
notacijo in pokazali, kako interferirata dve poti elektronov (privzeli bomo poenostavitev in izraz
(2πx/λ - ωt) zapisali kar kot kot φ - ja, v resnici je to kot).
Recimo, da imamo dve poti: P1 in P2. Valovni funkciji za obe poti bosta zapisani v kompleksni obliki
(kot smo že omenili, kot dve enaki sinusni valovanji z različnimi amplitudami A in B):
Ψ1 = A eiφ1 in Ψ2 = B eiφ2
Pri teh dveh valovanjih poznamo
A in B amplitudi za poti P1 in P2,
φ1 in φ2 pa sta fazi teh poti (višina in zamik valov v dani točki).
Skupna valovna funkcija je superpozicija,
ko se poti P1 in P2 združijo in se valovni funkciji prekrivata, je:
Ψ = Ψ1 + Ψ2 =
A eiφ1 + B eiφ2
- opisuje valovno funkcijo sistema — torej, potencialno stanje, dokler ga ne izmeriš.
Ko izračunamo verjetnost, dobimo interferenco, ki je enaka kvadratu skupne valovne funkcije, tako dobimo:
|Ψ|2 =
|A eiφ1 + B eiφ2|2
Ta izračun lahko izrazimo v naslednji poenostavitvi:
|Ψ|2 = A2 + B2 + 2AB cos(φ1 - φ2)
Konstruktivna interferenca nastane, če je fazni razmik φ1 - φ2 = 0 (ali večkratnik 2π,
ko je razlika poti valovanj 0 ali λ, oziroma mλ, m je celo število ),
amplitudi se seštejeta, kar poveča verjetnost, da bomo opazili določen izid.
|Ψ|2 = A2 + B2 + 2AB
Destruktivna interferenca nastane, če je fazni razmik
φ1 - φ2 = π (ali neparni večkratnik π,
ko je razlika poti valovanj λ/2 ali (2n + 1)λ/2, n je celo število )
potem se amplitudi odštejeta, kar zmanjša verjetnost za opazovanje določenega izida.
|Ψ|2 = A2 + B2 - 2AB
Najprej podajmo klasično sliko valovanja.
Če sta amplitudi A in B enaki, potem pri konstruktivni interferenci dobimo
vrednost za |Ψ|2 = A2 + A2 + 2AA = 4A2,
kar pomeni, da je amplituda skupnega valovanja |Ψ| = 2A.
Pri destruktivni interferenci pa dobimo (če A = B)
vrednost za |Ψ|2 = A2 + A2 - 2AA = 0,
kar pomeni, da je amplituda skupnega valovanja |Ψ| = 0 - valovanji se v tej točki odštejeta.
Ta dva rezultata sta poznana iz klasične fizike.
Kako pa je z interpretacijo v kvantni mehaniki?
Pri elektronih pa to pomeni, da v teh točkah, smereh, kjer velja |Ψ|2 = 0, skoraj zagotovo ne bomo zaznali elektronov.
Pri maksimalni vrednosti |Ψ|2 pa, da jih bomo najverjetneje zaznali.
V kvantni mehaniki kvadrat valovne funkcije (v tem primeru superpozicije dveh stanj)
|Ψ|2 ni gostota delcev (ali amplituda), ampak verjetnost (pravilneje verjetnostna gostota) za delec, recimo elektron.
V resnici je potrebno valovne funkcije (in njihove koeficiente A, B) normirati,
če hočemo, da superpozicija predstavlja veljavno kvantno stanje, saj velja za verjetnost, kje se nahaja delec,
za vse kote ali smeri dx, razdalje, da je le ta:
verjetnost = ∫|Ψ|2dx = 1.
Lahko še podamo analogijo
z glasbo.
Vemo, da z ušesi ne vidimo oblike zvočnega vala.
Kar slišimo, je rezultat interference, jakosti, frekvenc, itn, zvočnega valovanja.
Podobno v kvantni mehaniki ne “vidimo”
valovne funkcije Ψ(x,t), ampak zaznavamo učinke,
ki izvirajo iz nje (npr. interferenca |Ψ|2, verjetnost, energijske vrednosti).
Kvantni delci so zelo nadarjeni atleti za skoke čez ovire - tuneliranje in energija Sonca.
V kvantni fiziki pa delci torej niso le delci – obnašajo se tudi kot valovi.
Ti valovi lahko "uhajajo" malo čez ovire.
In če je ovira dovolj tanka ali kratka, obstaja možnost, da delec "pretunelira" – kar pomeni,
da se kar naenkrat znajde na drugi strani ovire, čeprav je po klasični mehaniki to nemogoče.
Kvantni delci so zelo nadarjeni atleti za skoke čez ovire - kot recimo Tina Šutej,
Brigita Bukovec, Armand Duplantis ...
Kvantna fizika nam tako razloži, da kljub temu, da delca (recimo odbijajoča protona v zvezdi) nimata dovolj energije za zlivanje,
vseeno obstaja verjetnost, da kvantno
"pretunelirata" skozi Coulombovo odbojno oviro in se združita - to je fuzija, ki sprosti veliko več
energije, kot je porabi. Prav ta kvantni fenomen omogoča,
da lahko fuzija v zvezdah poteka
že pri nižjih temperaturah, to je recimo pri dobrih 10 milijonih Kelvinov – kot se to dogaja recimo v jedru Sonca.
Po klasični fiziki bi potrebovali še veliko višje temperature in tlak,
da bi se ta jedra lahko dovolj približala, da bi se sploh lahko zlila v novo jedro
(ocenimo temperaturo fuzije brez tunelskega pojava;
tipična energija, ki jo morata premagati dva protona p-p, da se zlijeta, je cca E = e2/(4πεod)
= 1.44 MeV
na razdalji zlivanja, ki je cca d ≈ 1 fm;
če to povežemo s trkanjem protonov, torej s termično gibalno energijo 3kT/2 ≈ E, dobimo
za temperaturo fuzije neverjetnih T ≈ 2E/(3k) = 11 109 K - kar je kar cca 733 krat več od sedanjih
15 milijonov K
- to je le ocena, a vendar presenetljivo visoka, tudi če jo prepolovimo zaradi
centralnega trka, ko recimo vsakemu protonu pripade polovica kinetične energije).
V resnici za fuzijo stojita dva učinka.
Boltzmannova porazdelitev pove, kako verjetno je, da imata recimo dva delca določeno višjo energijo (hitrost)
in tako lahko pride prej do fuzije.
In že omenjeni tunelski pojav, ki določa, kako verjetno je, da bosta delca z dano energijo lahko pretunelirala skozi Coulombovo oviro
(bosta premagala odbojno silo in se približala na tako majhno razdaljo, ko že prevlada močna jedrska sila nad odbojno).
Ko združimo ta dva pojava, dobimo Gamowo okno – energijsko območje, kjer je fuzija najverjetnejša.

George Anthony Gamow (1904 - 1968) - ukrajinsko-ameriški fizik, astrofizik in kozmolog.
Razloži, zakaj v Soncu fuzija poteka tako počasi in pri nižjih temperaturah, kot to
določa klasična (pomanjkljiva) fizika - termodinamika.
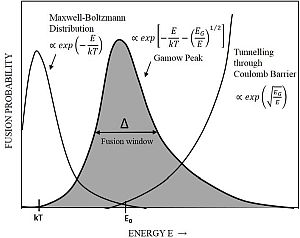
Po klasični fiziki skoraj ni možnosti, da bi se protoni zlili s prečkanjem Coulombove pregrade (odbojne sile) pri temperaturah,
za katere se običajno opazi, da povzročajo fuzijo, recimo v Soncu.
Fuzija v zvezdah podobnih Soncu je torej večinoma posledica dveh procesov,
termičnega gibanja nukleonov in kvantnega tuneliranja med nukleoni, delci.
Graf prikazuje
verjetnost tuneliranja (zapolnjena krivulja) kot funkcijo energije. Skrajno leva krivulja je
Maxwell-Boltzmannov faktor, skrajno desna pa Gamowov faktor.
'Δ' označuje Gamowovo okno - in je ∝ T5/6. T je temperatura v jedru zvezde.
Še sreča za Zemljo, življenje - fuzija v lahkih zvezdah je zelo počasna.
Zakaj?
Le zelo majhen delež protonov ima ustrezno energijo za zlivanje (Maxwell-Boltzmannova porazdelitev).
Večina trkov po klasični mehaniki tako ni dovolj energijskih za zlitje, zato je proces počasen,
a vendar ravno dovolj učinkovit zaradi kvantnega
tuneliranja med trki.
To efektivno pomeni, da Sonce porablja gorivo (vodik) zelo počasi.
Če bi bilo zlivanje pri višjih temperaturah (a zaradi okna Gamowa to pri Soncu ne pride v poštev),
bi Sonce izgorelo v milijonih, ne milijardah let.
Fizik George Gamow je rojeni Ukrajinec, ki je leta 1934 emigriral v ZDA.
Gamow je odkril razpad α prek tunelskega pojava in je raziskoval radioaktivni razpad atomskega jedra
(atomsko jedro je podal z modelom kapljice),
raziskoval je razvoj zvezd, je eden od očetov zvezdne nukleosinteze (fuzije),
razvil je nukleosintezo prapoka (nastanek prvih nukleonov) in je tudi zelo vplival na moderno genetiko.
Gamow je predpostavil (tudi zaradi idej Lemaîtrea, da so kozmični žarki "fosilno sevanje"),
da je v zgodnjem vesolju prevladovalo sevanje in ne snov, kar je privedlo
do, danes potrjene, teorije kozmičnega mikrovalovnega sevanja ozadja (CMB).
Večina kasnejših del v kozmologiji je utemeljena na Gamowi teoriji.
Vesolje spet pomaga kvantni mehaniki do novih spoznanj.
Kozmično sevanje je omogočilo odkritje novih delcev
(kot so pozitron, mion, pion), kar je dalo močne empirične dokaze za razvoj
kvantne teorije polja in kvantne elektrodinamike (QED).
Brez kvantne mehanike teh delcev ne bi mogli razumeti in obratno.
Pozitron (antielektron) kot prvi antidelec, je leta 1932 detektiral Carl Anderson
med preučevanjem kozmičnih žarkov (trki kozmičnih žarkov z atomskimi jedri Zemlje).
To je potrdilo Diracovo teorijo o obstoju antimaterije (razvije jo v letih 1928 - 1931),
ko je matematično napovedala obstoj pozitivno nabitega elektrona kot rešitev njegove
relativistične enačbe za elektron [
E = ±(p2c2 + m2c4)1/2 - enačbo poznamo
iz osnov relativnosti].
Pomemben pri interpretaciji (delec, antidelec) je tale dvojni predznak (±).
Meglična komora je bila postavljena v homogeno magnetno polje, ki povzroči ukrivljanje poti nabitih delcev.
Smer ukrivljanja pove, ali je delec pozitivno ali je negativno nabit, radij
ukrivitev pa pove ali sta delca enakih mas.
Odkritje miona in piona (prav tako iz kozmičnih žarkov)
je razširilo znanje o jedrskih silah in sprožilo razvoj kvantne teorije močnih interakcij.
Kozmični žarki imajo izjemno visoke energije.
Tuneliranje, parska kreacija, kvantna nestabilnost delcev – vse to so pojavi,
ki se jih da eksperimentalno opaziti pri interakciji kozmičnih žarkov z atmosfero našega planeta.
Še en nepričakovan rezultat nam vrne kvantna mehanika in sicer, da je naš
svet masno praktično prazen - kaj torej tehtamo - ali maso ali E/c2.
Podajmo ocene.
Tri kvarke (2 u in en d kvark) v protonu vežejo skupaj brezmasni gluoni.
Masa kvarkov pa prispeva komaj nekaj manj kot 1 % mase v protonu ali nevtronu.
Kje je potem skrita ostala energija, ki jo mi zaznavamo
kot maso (tehtamo)?
Ostalo (cca 99%) pride iz gluonske vezavne energije in kvantnih fluktuacij - ki vežejo recimo tri kvarke v proton.
Energijo gluona lahko ocenimo iz velikosti sistema preko Heisenbergove nedoločenosti. Upoštevamo,
da je brezmasni gluon zmožen prenašati močno silo med kvarki na razdalji
d = 1 fm = 10-15 m velikosti protona s hitrostjo svetlobe c preko valovanja v času
Δt = d/c.
Tako velja:
ΔpΔx ≥ ΔEΔt = ΔEd/c = h/(4π)
Za energijo ΔE dobimo tako oceno:
ΔE ≈ (c/d)h/(4π) = 197MeV ≈ 200 MeV. Enak rezultat bi dobili kar iz relativistične formule za brezmasni delec
E = pc.
Za tri kvarke bi tako energijo gluonov ocenili na cca 600 MeV.
Zgolj energija brezmasnih gluonov torej tvori že 2/3 tehtane mase protona.
Še komentar na to oceno.
čeprav proton sestavljajo 3 valenčni kvarki (uud), ti ne nosijo večine njegove energije.
Zaradi kvantnih fluktuacij in izmenjave gluonov, se znotraj protona ustvarjajo in uničujejo kvark-antikvark pari in gluoni.
A naša ocena je vse te dogodke zapakirala v efektivno
oceno energije gluonov na kvark.
Izračunajmo še kinetično energijo treh kvarkov. Izkaže se, da
kinetična energija lahkih kvarkov tvori cca 1/3 mase protona.
Energijo kvarka v protonu spet ocenimo preko načela nedoločenosti. Proton je sestavljen
iz treh kvarkov – za nedoločenost lege privzamemo kar dvojni premer protona
okrog 2d = 2 fm = 2 10-15 m
(to pomeni delno radialno
in tangentno gibanje kvarkov, saj
kvarki niso strogo omejeni na velikost protona,
ampak se gibajo v večjem obsegu zaradi močne interakcije z gluoni in drugimi kvarki). Sedaj
privzamemo za gibalno količino že kar znan Heisenbergov izraz
p ≈ h/(4π2d) in za kinetično energijo Ek ≈
pc (ker je mirovna
masa kvarka zelo majhna, velja pc >>
mqc2).
Kinetična energija enega kvarka je tako ocenjena
kar na okrog 100 MeV. Za vsoto treh kvarkov pa na okrog 300 MeV – kar je že zelo blizu 1/3 mirovne
energije protona mpc2 = 938.272 MeV.
če k tej oceni dodamo še energijo gluonov 600 MeV, dobimo skupaj
cca 900 MeV - to je dokaj groba ocena a v resnici zelo
didaktična. Torej nas že ti dve oceni pripeljeta do sklepa, da je
pri protonih, nevtronih zelo malo mirovne mase. Masa atomov se v resnici izraža iz
kinetične energije kvarkov (Ek/c2), to je 1/3 in večina (2/3) v energiji delcev polja močne jedrske sile,
v gluonih – ki so tudi brez mase. To so le poučne ocene, ki pa so zelo blizu realnim vrednostim.
Meritve v kombinaciji z izračuni kažejo, da je masa (mirovna) vseh treh kvarkov v protonu le okrog 9 MeV/c2
(up okrog 2.3 in down okrog 4.8 MeV/c2).
Naš svet je torej praktično prazen in masa, ki jo čutimo se v 99 % skriva v energijah nemasnih gluonov, ki vežejo kvarke v protone,
nevtrone in v
kinetični energiji zelo lahkih kvarkov - to kažejo meritve in natančnejši računi.
Smo torej v resnici kar energija deljena s hitrostjo svetlobe na kvadrat:
m ≈ E/c2.
To je rezultat, ki ga še pred 100 leti noben ne bi upal zagovarjati na izpitu iz fizike osnovnih delcev - noro!
V določenih režimih tistega časa z množičnimi
delovnimi taborišči za oporečnike (ideologija dialektičnega materializma je recimo zagovarjala večnost materije -
tudi mi smo se to tezo učili in se je celo preverjala na maturi)
so znanstveniki za podobne trditve, recimo iz kvantne teorije (spoznanja, da je masa le ena izmed oblik energije) bili tudi
preganjani ... Podajmo nekaj primerov iz bivše Sovjetske zveze in tudi iz takratne Nemčije, kar nekaj let sat bili zaveznici.
Boris Hessen je bil fizik in zgodovinar znanosti, umorjen je bil med Stalinovimi čistkami (1936).
Matvei P. Bronstein je razvil kvantno gravitacijo (bil je tudi zagovornik teorije velikega poka),
žal je bil tudi ubit v čistkah 1938; označen je bil za "sovražnika naroda".
Lev D. Landau je bil zagovornik moderne fizike, tudi zato je bil leta 1938 aretiran
- obtožen je bil protisovjetske propagande
(rešen je bil s posredovanjem fizika Kapice, zanj se je s pismom Stalinu zavzel tudi N. Bohr).
Morebiti je prav, da se spomnimo tudi na te tragične usode velikih raziskovalcev.
Danes so žal medijsko pozabljeni praktično od vseh centrov moči - pa se vsaj mi spomnimo nanje, saj so dali
življenje za resnico, kako deluje ta naš svet.
V tistem času pa so morali iz nacistične Nemčije in zasedene celinske Evrope
bežati tudi znanstveniki judovskega rodu (očitali so jim, poleg rasne manjvrednosti, še judovsko fiziko in matematiko
- kvantno mehaniko in relativnost).
Večina je našla zatočišče v Angliji ali ZDA. Zagotovo se je preganjanju Judov zoperstavil nemški matematik David Hilbert.
Nacionalsocialistom je v obraz povedal (ministru za izobraževanje Bernhardu Rustu 1934) –
da so z izgonom judovskih in ostalih svetovnonazorsko drugačnih matematikov
iz Göttingena praktično uničili inštitut za matematiko. Takrat so iz Göttingena, večinoma v ZDA,
odšli, bili izgnani: Edmund Landau, Richard Courant, Max Born, Felix Bernstein, Emmy Noether, Otto Blumenthal, Hermann Weyl …
Da ne pozabimo na zaslužne za razvoj kvantne kromodinamike.
Kvantna kromodinamika (QCD - quantum chromodynamics) je teorija, ki opisuje močne interakcije med osnovnimi delci,
imenovanimi kvarki in gluoni, ki tvorijo hadrone, kot so protoni in nevtroni.
Barva kvarka je abstrakten kvantni naboj (to je zgolj poimenovanje),
ki ga kvarki nosijo, podobno kot recimo električni naboj pri elektronih.

Kvarke so odkrili preko sipanja elektronov na nukleonih, recimo v samem protonu –
eksperimenti Roberta Hofstadterja so dokazali, da proton ni točkasto telo
(Hofstadterjev članek iz leta 1956, objavljenem v reviji Reviews of Modern Physics,
"Electron Scattering and Nuclear Structure - Elektronsko sipanje in jedrska struktura".).
Preko oblike sipalnega diagrama so ugotovili, da so gluoni nosilci močne sile med kvarki,
in da hkrati nastajajo v protonu kratkoživi pari kvark-antikvark. Silo med kvarki
se ponazori z izmenjavo gluonov (poenostavljeno povedano, to niso prosti delci,
ampak delujejo kot neke vrste vzmeti, lepilo ali 'glue' – po tem izrazu so gluoni
tudi dobili ime). Med samimi protoni, nevtroni, torej med vsemi nukleoni v jedru pa
se izmenjujejo večinoma pioni, lahko tudi rho mezoni, omega mezoni
(to so vsi mezoni, ki so tudi sestavljeni iz kvarka in antikvarka - ki pa ni nujno antidelec prisotnega kvarka).
Te sile razložimo podobno kot podajanje žoge med šolarji (in žoga šolarje na nek
način tudi veže skupaj) in to (žoganje) je možno le do določene razdalje –
do katere tudi deluje močna sila.
Od leve proti desni - očetje kvantne kromodinamike.
Murray Gell-Mann (1929 – 2019, predniki prihajajo iz Ukrajine, Judje, ameriški fizik,
leta 1964 je predlagal, da so hadroni sestavljeni iz treh osnovnih "delcev" - kvarkov).
George Zweig (1937, ameriški fizik in nevrobiolog, kvarku je dal ime "as" - mislil je, da so kvarki štirje - nekateri
so mnenja, da bi tudi on moral prejeti Nobelovo nagrado).
Richard F. Phillips Feynman (1918 - 1988, ameriški fizik in matematik, za sestavo hadronov je predlagal model partonov,
partoni so kvarki in gluoni skupaj, ki sestavljajo hadrone protone, nevtrone, mezone ...,
za vedenje subatomskih delcev se pogosto uporabljajo tudi znani Feynmanovi diagrami).
David Jonathan Gross (1941, ameriški fizik, tudi teoretik strun, uvedel je pojem "Asymptotic Freedom"
in opisuje pojav, da ko se kvarki približujejo zelo majhni razdalji - zaradi visoke energije,
postanejo njihovi medsebojni vplivi vse šibkejši, kot da bi "svobodno plavali" -
to je nasprotno intuiciji, a ključni pojem QCD).
Frank Anthony Wilczek (1951, ameriški teoretični fizik, matematik,
skupaj s kolegi je ugotovil, da
ko so kvarki zelo blizu skupaj, je močna sila med njimi šibka,
ko jih skušamo oddaljiti, se sila zelo poveča, to pomeni,
kvarkov ni mogoče izolirati,
to vodi v konfinement - to pomeni,
da ko vložiš dovolj energije, da bi kvarka "izvlekel" iz hadrona, se ta energija pretvori v nov par kvark-antikvark,
tako ne dobiš prostega kvarka, ampak nov delec, npr. mezon).
Hugh David Politzer (1941, je ameriški teoretični fizik, odkril "asymptotic freedom" neodvisno,
a skoraj istočasno kot David Gross in Frank Wilczek).
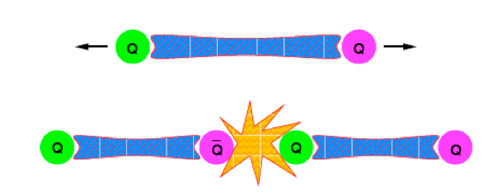
Ko se kvarka preveč oddaljita – se dovedena energija manifestira v novih dveh parih kvarkov - kvark, antikvark
(m = E/c2 - to je dovedena energija pri oddaljevanju, sila namreč med kvarkoma z razdaljo
ne pada; ko pa je razdalja dovolj velika, se dovedena energija, kot smo že omenili, pretvori v nov par kvarkov).
To je lep primer pretvorbe energije v materijo.
Znanstveniki, kot so Murray Gell-Mann (in George Zweig) za kvarkovsko teorijo, Richard Feynman za svojo kvantno kromodinamiko,
ter David Gross,
Frank Wilczek in Hideshi Politzer za razvoj teorije QCD (Quantum Chromodynamics),
so ključni za razumevanje, da je večina mase protona cca 99 % posledica
kinetične energije kvarkov in gluonske vezavne energije in kvantnih fluktuacij, močnih interakcij med njimi,
medtem ko samo majhen del mase cca 1 % izhaja
iz mase samih kvarkov. Kdo pa je izvedel meritve? Odgovor - Robert Hofstadter z ekipo.

Robert Hofstadter (1915 - 1990) -
ameriški fizik, izvede pionirske raziskave sipanja zelo hitrih elektronov
na atomskih jedrih, kar je pozneje pripeljalo do razlage zgradbe nukleonov (recimo protonov) in
do odkritja kvarkov kot osnovni delcev, ter do gluonov, to je nosilcev močne jedrske sile, ki vežejo tri kvarke v
protone, nevtrone.
Robert Hofstadter je
ameriški fizik, ki je z uporabo elektronskega sipanja (electron scattering)
kot eden prvih pokazal (članek iz leta 1956 - "Electron Scattering and Nuclear Structure
- Elektronsko sipanje in jedrska struktura"), da proton ni točkast, temveč ima razporejeno notranjo strukturo.
Tudi električni naboj ni enakomerno porazdeljen znotraj protona.
Ugotovil je torej, da proton ni elementarni delec, kar je takrat pomenilo velik preobrat.
Postavil je torej eksperimentalne temelje, ki so kasneje omogočili razvoj kvarkovskega modela.
Laserji - pot do gravitacijskih valov, LIGO



Nekateri očetje laserja - od leve proti desni.
Charles Hard Townes (1915 – 2015) - ameriški fizik, deloval je na področju kvantne elektronike,
ki je pripeljalo do izdelave
oscilatorjev in ojačevalnikov na osnovi načel maserja in laserja.
Arthur Leonard Schawlow (1921 – 1999, ameriški fizik, njegov osrednji prispevek je bila uporaba
dveh ogledal kot resonančne votline za uspešno delovanje maserjev od mikrovalovnih do vidnih valovnih dolžin - laserjev).
Theodore Harold Maiman (1927 – 2007, ameriški inženir in fizik, ki mu pripisujemo zasluge za izum prvega delujočega laserja,
lotil se je razvoja laserja na podlagi lastne zasnove s sintetičnim rubinskim kristalom -
16. maja 1960 je njegov rožnati rubinski laser v laboratorijih Hughes v Malibuju
v Kaliforniji oddal prvo koherentno svetlobo človeštvu v nesluteno uporabo ...).
Tudi razvoj laserjev (Light Amplification by Stimulated Emission of Radiation), danes se nam zdijo že samoumevni,
je omogočila kvantna mehanika. Danes nam brez laserjev živeti ni
(laserska kirurgija ..., laserski žarki prenašajo informacije na velike razdalje v optičnih vlaknih,
optični bralniki, 3D tiskanje in mikroobdelava, skenerji -
nepogrešljivi LIDAR (Light Detection And Ranging),
metalurgija, izdelava elektronike, CD, DVD, Blu-ray, zabava, kazalniki,
hladilni laserji, izjemni laserski žiroskopi, laserski pospeševalniki, laserski vodniki in umetne "zvezde",
za prilagajanje zrcal teleskopov, LIGO
detektorji, holografija ...).
Kako delujejo?
Einstein v svojem delu o kvantni teoriji svetlobe že leta 1917 poda koncept stimuliranega sevanja,
kar je bila osnova za kasnejši razvoj laserja.
Spontano in stimulirano sevanje lahko kombiniramo.
Poljuben atom recimo spontano preide v nižje energijsko stanje in tako odda foton.
Ta foton pa lahko sproži stimulirano sevanje drugih enakih atomov, kar pomeni, da se ustvarijo še drugi fotoni iste energije,
faze in smeri. Ta proces se večkrat ponovi med ogledaloma (resonančna votlina) in tako nastanejo koherentni svetlobni žarki — laser.
Te žarke, recimo širine D = 2 mm in λ = 530 nm lahko recimo zberemo v gorišču (f = 50 mm) leče,
na velikosti znane difrakcijske meje r ≈ f(λ/D) = 13 μm - kjer se torej zbere velika gostota energije. To lastnost tudi
pri laserjih s pridom uporabljamo,
recimo pri lokalnem taljenju železa,
ko lahko to dosežemo s cca 100 W moči,
kar je z belo svetlobo praktično
nemogoče. Za taljenje železa rabimo gostoto moči cca od
106 W/cm2 do 107 W/cm2 - odvisno od debeline.
A laser ima ogromen potencial za zelo široko uporabo.
Zaradi enoličnih interferenčnih vzorcev lahko z laserjem pomerimo tudi izjemno
majhne premike, razlike ... (LIGO).
Še zanimivost - laserski strokovnjak
Charles H. Townes poroča, da je več uglednih fizikov –
med njimi Niels Bohr, John von Neumann in Llewellyn Thomas – trdilo,
da maser krši Heisenbergovo načelo nedoločenosti in zato ne more delovati. Zelo so se motili - zanimiv nauk!
Leta 1964 so Charles H. Townes, Nikolaj Basov in Aleksandr Prohorov prejeli Nobelovo nagrado za fiziko,
»za temeljno delo na področju kvantne elektronike, ki je privedlo do konstrukcije oscilatorjev in ojačevalnikov,
ki temeljijo na načelu maser-laser«.
Charles Hard Townes in Arthur Leonard Schawlow sta skupaj razvila maser (Microwave Amplification by Stimulated Emission of Radiation)
leta 1958, ki je bil predhodnik laserja. Maser uporablja majhne vrednosti energije za dosego stimuliranega sevanja
- od tod tudi
mikrovalovi (GHz).
Schawlow je leta 1960 predlagal, da bi lahko maser prilagodili še za uporabo v vidnem delu
elektromagnetnega valovanja.
Theodore Maiman pa istega leta prvi izdela delujoči laser - uporabil je rubinov kristal kot aktivni medij
za stimulacijo.
To je
bil rezultat več desetletij teoretičnega in eksperimentalnega dela več znanstvenikov - tudi nekaterih, ki na koncu niso verjeli
lastnim teorijam (ironija znanosti).
Za detekcijo gravitacijskih valov (LIGO 2015) je bil potreben dolg razvoj izjemno natančnih senzorjev
tudi preko razvoja kvantnih tehnologij
- in laserji so nepogrešljivi del te izjemno uspešne zgodbe kvantne mehanike saj brez njih ne bi bilo LIGO detektorjev,
ki sta nam ( Livingston - Louisiana, Hanford - Washington, ZDA) z detekcijo gravitacijskih valov,
odprla novo okno v vesolje.
Interferometer LIGO (Laser Interferometer Gravitational-wave Observatory)
sestavljata dva pravokotna tunela (vsak je dolg kar L = 4 km, not je vakuum).
Do tunelov potuje laserski žarek, ki se razcepi na dva žarka (polprepustno zrcalo - 'beam splitter'), ki potujeta
do končnih zrcal, kjer se odbijeta nazaj.
Ko se žarka spet srečata, opazujemo morebitne motnje v svetlobnem vzorcu
(interferenco).
Če se razdalja do zrcal rahlo spremeni, se ta vzorec spremeni.
To nam pove, da se je prostor-čas deformiral. Detektorja sta v resnici
precej bolj zapleteno narejena (z več odboji, z dušenjem tresljajev, itn),
a dejstvo, da detektorja lahko pomerita razdaljo, premik ΔL ≈ 10-19 m - je izven vsake primerjave,
predstave.
To je premik, ki je 10 000-krat manjši od premera protona (blizu ocene velikosti kvarka) ali
kot da bi izmerili razdaljo do najbližje zvezde (4 svetlobna leta) natančno na debelino lasu.
Če vemo, kako se vsak trenutek trese ta naš planet, je to še dodaten argument, da je v ta projekt bilo vgrajeno
praktično vso človeško znanje. Dejanski premik zrcal 14. septembra 2015
je bil ΔL ≈ 4 10-18 m,
povzročil ga je trk dveh črnih lukenj (cca 36 in 29 mas Sonca) oddaljenih kar cca 1,3 milijarde svetlobnih let.
Detektorje so gradili praktično od rojstva naše
generacije (bilo je več konceptov) - in zdelo se je že, da iz te moke ne bo kruha ...,
a znanost in vztrajnost sta nas znova demantirala.
Večina očetov kvantne mehanike in kvantnih tehnologij je v naši zgodnji mladosti še
živela - a le redko smo slišali zanje (razen za Einsteina). Učili smo se o njihovih predrznih
sklepanjih, danes pa živimo od njihovega znanja, njihovih spoznaj, ki so nas pripeljale v
čudoviti novi svet modernih tehnologij, ki nam (lahko) izjemno lajšajo življenje.
No - sedaj se moramo še priučiti pasti vseh teh čudovitih naprav (kdaj nas zavedejo) in iz njih
potegniti kar se da veliko dobrega. Zdi se, da zanimanje mladih
za naravoslovje precej kopni - tudi zaradi lahkotnosti bivanja, ki ga omogočajo kvantne
dobrine (informatika na klik). V kaosu modernega sveta se lahko namreč tudi hitro zgodi -
da se vsa ta res kompleksna fizika in tehnologije izgubijo - ne bi bilo prvič v zgodovini
človeštva.
Eden od vrhuncev kvantne mehanike v 20. stoletju je bil uspešen model nukleosinteze (fuzije) atomov v zvezdah
- opis zlivanja lažjih jeder v
masivnejša in seveda sama nukleosinteza velikega poka – za helij, litij.

Hans Albrecht Bethe (2. julij 1906 - 6. marec 2005) - nemško-ameriški fizik.
Hans Bethe je leta 1939 opisal osnovne fuzijske procese v zvezdah (proton-proton veriga, CNO-cikel,
leta 1967 je dobil Nobelovo nagrado za ta izjemen uspeh).
George Gamow, Ralph Alpher in Robert Herman (1940-ih) so podali nukleosintezo v zgodnjem vesolju
(Big Bang nukleosinteza – za helij, litij itd.).
Končni model nukleosinteze elementov v zvezdah ima kratico "B2FH" po avtorjih.
B2FH članek iz leta 1957 so podpisali naslednji avtorji:
Burbidge (Margaret), Burbidge (Geoffrey), Fowler (William), Hoyle (Fred)
To so zaslužni avtorji za sistematičen opis nastanka elementov od H do Fe in naprej - masivnejši elementi od železa nastanejo
pri eksplozijah supernov in trkih zvezd (pri teh že zelo velikih atomih
namreč nukleosinteza rabi, zaradi razsežnosti jeder in posledično prevladujočega vpliva odbojne sile nad močno jedrsko,
več energije, kot jo vrne v okolje). Večji atomi tudi pogosteje postanejo nestabilni, vendar obstajajo izjeme.
Težja jedra potrebujejo več nevtronov kot protonov, da ostanejo stabilna (svinec-208 je primer stabilnega masivnejšega jedra,
ima 126 nevtronov in 82 protonov). Uran je radioaktiven in nestabilen, vendar, v primerjavi s supertežkimi umetnimi elementi, še zmeraj
spada med dolgožive elemente. Ima izjemno dolg razpolovni čas, zato je še vedno naravno prisoten na Zemlji.
Recimo uran-235 pa je atom primeren za fisijo - razpad, kar pomeni,
da se lahko razcepi med trkom z nevtronom. Uporablja se v jedrskih reaktorjih in žal tudi v bombah,
kjer se sprosti del energije, ki se je v njem akumulirala med fuzijo pri
eksplozijah supernov ali trkih nevtronskih zvezd.
Skupna masa razpadnih produktov urana je malenkost manjša kot začetna masa urana in
ta razlika v masah (Δm) se sproti v energijo po znani Einsteinovi enačbi:
ΔE = Δm·c2.
Leta 2017 so astronomi prvič neposredno opazili trk nevtronskih zvezd (dogodek GW170817, ki ga je zaznal LIGO, detektor
gravitacijskih valov) in opazili,
da med takimi dogodkih nastajajo zlato, platina, uran in drugi težki elementi.




Od leve proti desni.
Burbidge Margaret (1919 – 2020, angleška astronomka in astrofizičarka),
Burbidge Geoffrey (1925 - 2010, angleško-ameriški astronom, astrofizik in kozmolog),
Fowler William (1911 – 1995, ameriški fizik in astrofizik), Hoyle Fred (1915 – 2001,
angleški astronom, astrofizik, kozmolog, matematik, pisatelj in popularizator znanosti).
Končni model nukleosinteze (fuzije) elementov v zvezdah ima kratico "B2FH" po avtorjih,
slike zgoraj.
William Fowler je leta 1983 dobil Nobelovo nagrado za fiziko prav za svoje delo na področju nukleosinteze (B2FH),
a mnogi so mnenja, da bi jo moral dobiti še kdo (a saj vemo - žal krogle in medalje le redko zadenejo prave ...).
K temu poglavju pa zagotovo spada izjemna intuitivna misel Einsteina in že nekaterih njegovih
predhodnikov, da se recimo z oddajanjem svetlobe, mora ta energijski manko poznati
tudi na masi sistema, ki s sevanjem izgublja energijo (ali prirastek mase nekega sistema z absorpcijo svetlobe ali
ostalih oblik energije). Ta intuicija, ki je tudi delno posledica zakona o ohranjanju energije, je na koncu
odigrala eno ključnih vlog v drami iskanja enormnega vira energije zvezd.
Velika nemoč fizikov konec 19. stoletja se je kazala v dejstvu, da so geologi in biologi zagotovo vedeli, da je Zemlja
stara vsaj kakšno milijardo let in da je bistven prispevek k energiji Zemlje posledica izjemnega
izseva Sonca - a fiziki nikakor niso našli med znanimi viri energij (gravitacijsko sesedanje zvezd in posledično gretje zvezdne plinske
plazme, fosilna goriva - oksidacija, kemijsko gorenje, trki asteroidov ...)
takega vira, ki bi lahko svetil s Sončevim izsevom Lo = 3.827×1026 W
več kot nekaj 10 milijonov let.
Nekateri oholi fiziki so se v svoji samovšečnosti (v lastno obrambo) spravili kar z agresijo,
z žalitvami nad geologe in biologe.
Znameniti Lord Kelvin je tako napadel geologe, da so "soft" znanstveniki, ker so preko plastnic ocenili,
da je Zemlja stara blizu milijarde let, podobno oceno je dobil tudi Darwin preko modela razvoja vrst.

Albert Einstein (14. marec 1879 – 18. april 1955) - nemško-ameriški fizik in matematik, sin judovskih priseljencev.
Njegov vpliv na fiziko je bil izjemen - je soutemeljitelj posebne teorije relativnosti
in oče splošne teorije relativnosti ter znamenite enačbe E = m·c2 (s katero je nakazal pravilno pot, od kod zvezdam
toliko energije, da lahko svetijo milijarde let).
Za pravilno razlago fotoefekta prejme Nobelovo nagrado (dokončno kvantiziranje svetlobe, potrditev
Planckovega in Lenardovega prispevka, vpeljava fotonov z energijo E = hν je tako teoretično
kot eksperimentalno potrjena). A vse se je začelo s Fraunhoferjevimi absorpcijskimi črtami v spektru Sonca.
A. Einstein in sodobniki so po res dolgem, dolgem tuhtanju le doumeli (zelo je pomagala tudi nastajajoča
teorija relativnosti in sami zametki kvantne mehanike) in končno našli odrešilno bilko, razlago, od kod vendar zvezdam
toliko dolgožive energije. Predlagali so, najbolj natančno Einstein, da Sonce pretvori
del mase v energijo po znameniti formuli
ΔE = Δm·c2.
A A. Einstein takrat (1905) še ni poznal mehanizma, ki to omogoča - a je trdno tlakoval pot do razlage nukleosinteze
in masnega defekta.
Povzemimo bistveno idejo nukleosinteze, ki je bila najprej utemeljena z merjenjem atomskih mas
vodika in helija v laboratorijih, teoretično utemeljitev pa je dal že Einstein.
Velja torej, da je masa jedra (recimo helija) manjša kot seštevek posameznih mas (protonov), ker je del mase pretvorjen
preko močne jedrske sile
v negativno vezavno energijo atomskega jedra - ki je torej sedaj po zlitju neto nižja energija, kot pred zlitjem.
Zlivanje omogočata visok tlak, temperatura v sredicah zvezd
(v jedru Sonca je temperatura cca 15 milijonov K),
ki sta posledica gravitacijskega stiskanja
plazme in pozneje same sproščene energije med fuzijskimi dogodki.
Modeli kažejo, da ta energija Sonca, ki nas danes greje, rabi cca 200 000 let, da se iz jedra prebije do površja Sonca
in potem nekaj te energije v cca 8 minutah doseže Zemljo.
Pri nukleosintezi se večina energije sprosti v obliki kinetične energije nukleonov helija, sprošča pa se tudi
z gama sevanjem in tudi sami trki (pospešeno gibanje) ionov,
elektronov povzroča izdatno dodatno sevanje različnih valovnih dolžin.
Najprej se dogaja sevalni prenos energije - gama žarki rabijo recimo od 10.000 do 200.000 let (v povprečju 171 000 let) da iz sredice Sonca
prepotujejo cca 70 % polmera Sonca (gama fotoni se nenehno sipajo, absorbirajo in ponovno sproščajo v vse smeri
v gostem plinu elektronov in ionov - v plazmi).
Nato nastopi vzgon (v zgornji plasti Sonca debeli cca 200 000 km) - v zunanji plasti (fotosferi)
Sonca namreč temperatura že pade na cca 6000 K
(temperatura Sonca v globini 200 000 km pa je cca 2 milijona K - tako nastopi velik temperaturni gradient).
Konvekcijska cona prenosa energije (vzgon) potem v plazmi rabi le dneve do tedne, da doseže fotosfero.
Od fotosfere do Zemlje pa svetloba potrebuje le cca 8 minut ( t = 150 106 km/300 000 km/s ).

Sir Arthur Stanley Eddington (1882 - 1944) -
angleški fizik, astronom, astrofizik, matematik in popularizator znanosti.
Eddingtonovi odpravi sta slikali popolni Sončev mrk 29. maja 2019
iz otoka Principe (zahodna Afrika) in iz kraja Sobral (Brazilija) – nikjer ni bilo ravno idealno vreme,
a slike gravitacijskega "premika" zvezd ob popolnem mrku so bile odločilne za bodoči razvoj fizike.
Tako je pripomogel k uveljavitvi teorije relativnosti in Einsteinovih napovedi (odklon svetlobe ob Soncu, masivnih objektih)
- to je močno vplivalo
tudi na razvoj kvantne mehanike.
Angleški astrofizik Arthur Eddington je
leta 1920 je na predavanju pred Royal Society (in kasneje v članku) predlagal,
da zvezde črpajo energijo iz fuzije atomov, zlasti iz pretvorbe vodika v helij.
To je bila revolucionarna ideja, saj do takrat, kot smo že omenili, ni bilo jasno, od kod zvezde dobijo toliko
dolgožive energije. Takole je povedal:
"Če bi v notranjosti zvezd obstajal postopek, kjer se štirje atomi vodika združijo v en atom helija,
bi se sprostila ogromna količina energije."
Eddington je izračunal, da mora biti vir energije vsaj 1000× učinkovitejši od kemijskih reakcij.
Na podlagi spektroskopije
je sklepal, da so zvezde najverjetneje sestavljene pretežno iz vodika
(zvezde, meglice je skrbno spektroskopsko proučeval že omenjeni Sir William Huggins, nekoliko pozneje pa v doktorski disertaciji
1925 gospa Cecilia Helena Payne
ugotovi, da so zvezde sestavljene predvsem iz vodika in helija,
a njen prelomni zaključek so sprva zavrnili vodilni astrofiziki,
vključno s Henryjem Norrisom Russellom - a gospa je imela prav,
1956 je postala prva ženska, ki je bila imenovana za profesorico in predsednico oddelka na Harvardu).
Zato je logično domneval, da mora biti ravno vodik "gorivo" - a ni še imel eksperimentalnih meritev,
a te so kmalu prišle.
27. novembra 1919 je Francis Aston objavil preliminarne meritve mase atomov v 'Nature'.
A že na začetku leta 1920 izmeri, da je masa helijevega jedra (4He)
manjša od skupne mase štirih vodikovih jeder (protonov). Omenil je tudi energijski potencial - da se
pri tem procesu sprosti ogromna količina energije po znani formuli ΔE = Δmc2. A ni
omenjal, da se to dogaja v zvezdah.
19. julija 1920 Sir Arthur Eddington predava na srečanju
"British Association for the Advancement of Science" v Cardiffu.
V predavanju se neposredno sklicuje na Astonova odkritja in predlaga,
da se energija zvezd lahko pojasni s pretvorbo vodika v helij – kar pomeni, da masni defekt poganja zvezde v
izjemen in dolgotrajen izsev.
Ključni citat Eddingtona (1920):
"If, indeed, the sub-atomic energy in the stars is being freely used to maintain their radiation,
their radiation can be maintained for billions of years without difficulty...
I suggest that the stars are powered by the transformation of hydrogen into helium,
as indicated by Aston’s mass measurements."

Francis William Aston (1877 - 1945) -
angleški kemik in fizik (prvi izmeri da je masa jedra, recimo helija, manjša od mase
ločenih protonov, nevtronov - pot v praktično uporabo enačbe E = m·c2 in začetek poti v največjo skrivnost
fizike konca 19. stoletja, od kod zvezdam enormne količine energije).
Francis Aston leta 1922
prejme Nobelovo nagrado za svoje izjemne meritve. V predavanju na podelitvi je omenil (ponovil Eddingtonov sklep iz leta 2020),
da ta energija zlivanja 4 vodikovih jeder v helijevo jedro, zaradi masnega defekta, lahko pojasni izsev Sonca.
Arthur Eddington pa ni nikoli prejel Nobelove nagrade - baje je premalo
pomeril in premalo razvil teorijo.
Eddington je svojo idejo predstavil leta 1920 in objavil v knjigi The Internal Constitution of the Stars (1926).
To delo je postalo temeljna literatura za vse astrofizike v naslednjih desetletjih.
Mehanizem zlivanja lažjih atomskih jeder v masivnejša,
ki to omogoča, pa so torej dokončno utemeljili šele nekaj let pred drugo vojno (že omenili -
Hans Bethe leta 1939 proton-proton veriga in CNO-cikel). A idejo je dal Arthur Eddington, meritve
pa Francis Aston.
Bethe je izračunal, kako verjetni so koraki zlivanja in pokazal, da proizvedejo ravno dovolj energije za vzdrževanje Sončeve svetlosti.
Opišimo poenostavljen proces:
* dva protona ob trku tvorita devterij (D) + pozitron + nevtrino,
* devterij + proton tvorita helij-3 (3He) + gama žarek,
* dva helija-3 trčita v helij-4 (4He) + 2 protona (ki se vrneta v verigo).
Opisana veriga zlivanj in neto rezultat sta prikazana spodaj.
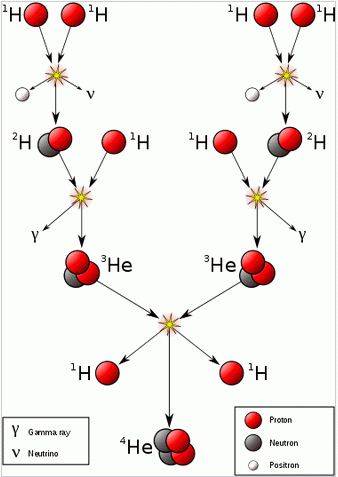
Shematični prikaz najpomembnejšega P-P I niza zlivanja vodika v helij v Sončevem jedru - razložil Bethe 1939.
Večina energije Sonca izhaja iz p–p (proton–proton) verige zlivanj vodika v helij:
4p => 4He + 2e+ + 2νe + ENERGIJA (Δmc2)
Od tega je kar 83.3 % Sončeve energije prav iz P-P I niza, ki sprosti 26.732 MeV energije (0.7 % mase
protonov
Δm = ΔE/c2
gre v energijo). Fuzija se seveda dogaja
v Sončevem jedru, znotraj območja - 0.25xRSonca - pri temperaturah okrog
14 milijonov Kelvinov in pri gostoti jedra kar
162.2 kg/dm3
(v povprečju se v jedru sprosti
L/(4πRje2)
~ nekaj 10 Wattov/m3,
v samem centru pa že blizu 300 W/m3, relativno malo - a je polmer
Rje jedra Sonca, kjer poteka fuzija, zelo velik -
okrog 28 polmerov Zemlje). Seveda – zvezdo drži skupaj lastna gravitacija,
ta stiska večinoma ioniziran plin v vročo kroglo – to je v našem primeru
lastna teža Sonca.
Izsev Sonca je
L = 3.828×1026 W, do Zemlje pride
j = L/(4πR2) = 1367 W/m2
(to je energija, ki nam daje življenje). Sonce zaradi fuzije vsako sekundo izgubi
4,26 milijonov ton mase (gre v izsev pri tvorbi težjih atomov) - izračunajte sami. Tudi v vesolju
ni nič zastonj – čeprav se to tako kdaj zdi ... in še dobro, da je tako!
Če Sonce vsako sekundo zaradi fuzije izgubi 4,26 milijona ton mase, koliko te mase pa
pripada sevanju, ki zadane vrh atmosfere Zemlje? Izračunajte sami - odgovor pa je rel. skromen,
le 1,94 kg fuzijske izgube mase Sonca na sekundo zadane Zemljo in od tega živi cel planet.
V enem dnevu je to sicer že kar cca 168 ton -
a ljudje porabimo kar cca 14 milijonov ton nafte/dan.
Torej 168 ton dnevne fuzije in to za celo Zemljo, je mačji kašelj glede na porabo zgolj
nafte za naše življenje, prevoze.
Problem je, da je energijski izkoristek nafte zelo majhen, nesnage pa ogromno v zraku, na površini, v vodah,
v našem telesu.
Torej ni čudno, da želimo na Zemlji fuzijo ukrotiti tudi za pridobivanje elektrike, toplote, za mobilnost ...
Za celo človeštvo, bi torej v enem dnevu, za enak ekvivalent fuzijske energije, rabili le okrog 1000 kg
fuzijskega goriva (kot to počne Sonce) -
v energijo pa bi se pretvorilo le okrog 7 kg porabljenega goriva (saj velja Δm ≈ 0,7 % mase protonov).
S tem bi pokrili večino porabe nafte na dan (to je cca 103,7 milijonov sodčkov).
No, na Zemlji ne mislimo čisto posnemati verige reakcij v Soncu. Reaktor ITER bi naj uporabljal drugačno verigo reakcij.
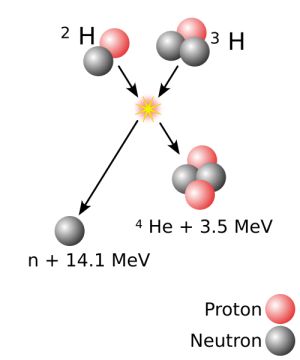
Najbolj obetavno in trenutno najbolj raziskano gorivo za komercialno fuzijo je mešanica dveh izotopov vodika:
- devterij (D, ali 2H) — stabilni vodikov izotop z enim protonom in enim nevtronom
- tritij (T, ali 3H) — radioaktivni izotop z enim protonom in dvema nevtronoma
Reakcija:
D + T => 4He + n + 17,6 MeV energije
Iz tega nastane helijevo jedro (4He), nevtron, in sprosti se 17,6 MeV energije.
Pri fuziji DT goriva se torej približno 0,375 % mase goriva spremeni v energijo na trk - zlivanje.
Devterij je tudi naravno prisoten.
Devterij (2H) najdemo v navadni vodi – približno 1 atom devterija na 6.000 vodikovih atomov.
To pomeni, da imamo ogromne zaloge devterija – praktično neomejen vir.
Tritij ni naraven — a ga lahko pridelamo.
Tritij (3H) je radioaktiven in se razgradi v ≈12 letih.
V naravi ga skoraj ni, a ga lahko proizvedemo znotraj fuzijskega reaktorja iz litija,
ki ga obstreljujemo s hitrimi nevtroni (n) samega reaktorja:
n (iz fuzije) + 6Li => 4He+3H + energija (+4,8 MeV)
- ali z litijem 7Li, ki ga je v naravi več, čez 90 %
n (iz fuzije) + 7Li => 4He+3H + n - energija (–2,5 MeV)
Torej: fuzija proizvaja lastno gorivo, preko hitrih nevtronov (n), ki razdelijo litij na tritij in helij – kar omogoča trajnost.
Litij pa najdemo v posebnih solinah (J. Amerika), v rudah, v oceanih.
Vrnimo se k začetkom kvantne mehanike.
Bethe se v svojem slavnem članku "Energy Production in Stars" (1939), kjer Bethe razloži proton-proton verigo in CNO-cikel,
neposredno sklicuje na prejšnje teoretične predloge, vključno z Eddingtonovo idejo o fuziji vodika v helij kot viru energije.
To je ena največjih uspešnih zgodb človeškega uma,
ki je razkrila, od kod zvezdam, Soncu toliko konstantne izsevane energije (recimo za 10
milijard let), ki je omogočila (omogoča) razvoj življenja
na Zemlji - naš nastanek, obstoj in razvoj, bodočnost - lahko, da nam bo fuzija pomagala odpraviti velike
ekološke težave.
Razlaga fuzije v zvezdah je hkrati razlaga povezave med kvantno mehaniko in energijsko bilanco zvezd,
planetov (ta energija tudi greje naš planet, omogoča tekočo vodo, poganja vodni krog na Zemlji ...), je pot do
fotosinteze - je torej povezava z življenjem.
Kako je mlada Dama razrešila skrivnost kemijske sestave večine zvezd in samega vesolja,
- v pomoč ji je bila ionizacijska enačba pridnega Gospoda Sahaja iz nižje kaste
in Boltzmanna enačba zasedenosti posameznih vzbujenih atomskih stanj, to je našega že omenjenega "tragičnega" junaka iz Devina.
Ker so v spektru Sonca zelo izrazite črte železa, kalcija, natrija ...
so praktično vsi fiziki menili, da to pomeni, da Sonce vsebuje veliko teh kovin.
A so se vsi po vrsti motili.
Podajmo najprej
Boltzmannovo porazdelitev po vzbujenih atomskih stanjih.
nj / n =
(gj / Z) ·
e-Ej / (kT)
Kjer so:
nj
= število atomov v vzbujenem stanju j (npr. n=3 za Hα)
n = vseh nevtralnih H atomov
gj = degeneracija stanja j
Ej = dovedena energija do vzbujenega stanja (npr. od n = 1 do n=3 je Ej = 12.09 eV)
Z = partitivna funkcija za nevtralni H
Uporaba
nam pove, kolikšen delež nevtralnih H atomov je v tretjem vzbujenem stanju, torej sposoben oddati Hα foton pri prehodu v
n=2.
Podajmo še enačbo, ki opisuje razmerje med številom ioniziranih
in nevtralnih atomov v plinu pri določeni temperaturi T in tlaku P.
To je
Saha-jeva ionizacijska enačba, ki se glasi:
(ni+1 · ne) / ni =
(2 Zi+1 / Zi) ·
[ (2π me k T) / h2 ]3/2 ·
e-χi / (kT)
Simboli in pomen:
ni =
število nevtralnih atomov v stanju i
ni+1 =
število ioniziranih atomov (en elektron manj)
ne =
število prostih elektronov
Zi ali gi =
statistična vsota (particijska funkcija) za stanje atoma/iona i-te ravni (v kvantni mehaniki je energijski nivo degeneriran,
če ustreza dvema ali več različnim merljivim stanjem kvantnega sistema )
Zi+1 ali gi+1 =
statistična vsota za ionizirano stanje (i+1) ravni
me =
masa elektrona
k = Boltzmannova konstanta
T = absolutna temperatura (v kelvinih)
h = Planckova konstanta
χi = εi+1 - εi =
ionizacijska energija potrebna za prehod iz stanja i v i+1
Enačbo nekateri tudi zapišejo z λth = h/(2π me k T)1/2 -
to je termična de Brogliejeva valovna dolžina elektrona.

Meghnad Saha (1893 – 1956) je bil indijski astrofizik in politik,
ki je pomagal zasnovati teorijo termične ionizacije. Njegova Sahova ionizacijska enačba je astronomom
omogočila natančno povezavo spektralnih razredov zvezd z njihovimi dejanskimi temperaturami.
Članek z naslovom "Ionization in the Solar Chromosphere" je bil objavljen leta 1920 v Philosophical Magazine:
https://www.saha.ac.in/web/images/library/digitised%20doc/papers/Page%2038.pdf
Brez nje Cecilia Payne-Gaposchkin ne bi mogla pravilno interpretirati, da Sonce sestavljata večinoma vodik in helij.
V času študija je bil Saha diskriminiran zaradi svojega družbenega položaja, a ga to ni ustavilo
(študentje so recimo nasprotovali, ker je jedel v isti jedilnici kot oni).
Njegova družina je namreč pripadala nižji kasti, kar je v Indiji pomenilo hudo družbeno diskriminacijo
(zato je bil skeptičen do hinduizma).
Študiral je na Presidency College v Kalkuti, kjer je bil sošolec slavnega fizika Satyendranatha
Bosea (poznana je Bose-Einsteinova statistika).

Cecilia Payne-Gaposchkin (rojena Cecilia Helena Payne, 1900 – 1979)
je bila ameriška astronomka in astrofizičarka britanskega rodu.
Njeno delo o sestavi vesolja in naravi spremenljivih zvezd je bilo temelj sodobne astrofizike.
V svoji doktorski disertaciji iz leta 1925 ("Stellar Atmospheres") je preko Saha-jeve ionizacijske enačbe
in Boltzmannove porazdelitve o zasedenosti posameznih vzbujenih stanj znotraj danega ionizacijskega stanja.
dokazala,
da so zvezde sestavljene predvsem iz vodika in helija.
Njen prelomni sklep so sprva zavrnili vodilni astrofiziki, vključno s Henryjem Norrisom Russellom,
ker je bil v nasprotju s takratno znanostjo, ki je trdila, da med Soncem in Zemljo
ni bistvenih elementarnih razlik
(to je bila nedokazana trditev na poenostavljeni interpretaciji spektrov - v bistvu
dogme v znanosti niso redkost).
Neodvisna opazovanja so sčasoma dokazala, da je imela prav.
Mentorja pri doktoratu mlade raziskovalke
Payne sta bila znamenita
gospoda - Harlow Shapley
(vodja Harvard College Observatory) — uradno njen doctoral advisor —
in v širšem znanstvenem kontekstu Henry Norris Russell, vpliven astronom takratnega časa.
Harlow Shapley jo je spodbudil pri raziskovanju in njenemu delu omogočil akademski okvir,
vendar ni bil povsem prepričan v popolno
interpretacijo njenih rezultatov glede sestave zvezd.
Na pritisk (predvsem Henryja Norrisa Russella) je v disertacijo dodala opombo / zadržek,
kjer je zapisala, da so ti rezultati verjetno nerealni
in
najbrž posledica napak v modelih ali nepopolnega razumevanja fizike zvezdnih atmosfer.
Z drugimi besedami - ni umaknila izračunov, je pa javno relativizirala njihov pomen.
Citat iz njene disertacije:
“The outstanding discrepancies between the astrophysical and terrestrial abundances
are displayed for hydrogen and helium.
The enormous abundance derived for these elements in the stellar atmosphere
is almost certainly not real.”
(Payne-Gaposchkin, Stellar Atmospheres, 1925, p. 188–189)
»Največja razhajanja med astrofizikalnimi in zemeljskimi vrednostmi razmerij
se pojavljajo pri vodiku in heliju;
izjemno visoka zastopanost, pripisana tema elementoma v zvezdnih atmosferah,
skoraj gotovo ni realna.«
Šele pozneje, okoli leta 1929, je Russell prišel
do istih zaključkov z neodvisnimi metodami in dejansko odpravil dvome — kasneje
pa tudi priznal, da je imel Payne-Gaposchkin prav,
čeprav je v praksi pogosto on sam dobil več priznanja za to spoznanje.
V prid mentorjema je vsaj to,
da sta vendar dovolila objavo (a s pridržkom).
A ta dilema o zaslugah v razmerjih mentor - študent, se v resnici ne da
v celoti razrešiti. Kaže pa ta zgodba tudi
na dejstvo, da mentorji precej redko v celoti
pregledajo in razumejo izdelek študenta ...

Črte Sončevega absorpcijskega spektra.
Zagotovo z lahkoto opazimo Fraunhoferjeve absorpcijske črte (zgornji spekter), ki so na sliki označene z naslednjimi črkami:
G (Ca črta 430,77 nm in železo 430,79 nm),
F (vodikova beta črta), b (železo in magnezij), E (železo),
D (helij, natrij), C (znamenita vodikova alfa črta) ... Ker so recimo črte železa zelo izrazite (G, b in E oznake),
so astronomi dolgo laično sklepali, da je v Soncu ogromno železa in da je Sonce
po masnem ali številčnem deležu elementov zelo podobno Zemlji. Kar pa je bila velika zmota (železa in ostalih masivnejših elementov od helija
je v Soncu zelo malo).
Zagato je, z veliko skepse kolegov, razrešila Dama Cecilia Helena Payne leta 1925.
Spodnji primerjalni spekter (odlično se ujema z zgornjim)
pa je nastal na zelo preprost način in sicer kar s spektroskopom na uklonsko mrežico s 600 razami na mm in s cca 0.2 mm široko vhodno
režo na tulcu dolgem 80 cm, usmerjenim v belo steno osvetljeno s soncem (a zaznamo vsaj 40
absorpcijskih črt). To vajo lahko ponovi vsak, ki bi se rad na lastne oči prepričal, kako je sestavljeno naše Sonce.
Cecilia Payne-Gaposchkin je pokazala, da so močne (izrazite) spektralne črte elementov lahko posledica fizikalnih razmer, ne pa nujno
velike količine teh elementov.
Zato je lahko pravilno sklepala, da Sonce sestavljata predvsem vodik in helij, čeprav so črte kovin zelo močne (izrazite).
Saha-jeva enačba sama po sebi ne določa količine posameznih elementov. Vendar pa je
Cecilia Helena Payne uporabila to enačbo v kombinaciji z analizo spektralnih črt, da je to ugotovila.
Kaj je pokazala analiza?
Saha-jeva enačba pokaže, kakšno je razmerje med ioniziranimi in nevtralnimi atomi elementa pri dani temperaturi.
Če želimo pravilno razložiti, zakaj so spektralne črte določenih elementov močne ali šibke, moramo vedeti,
kolikšen delež atomov je v višjem stanju za oddajo svetlobe - črt (nevtralni ali ionizirani atomi)
in koliko teh atomov je sploh prisotnih.
V ta namen pa je uporabila
Boltzmannovo porazdelitev, ki poda zasedenost posameznih vzbujenih stanj znotraj danega ionizacijskega stanja.
Razmišljanje mlade dame Payne-Gaposchkinove (takrat še
Cecilia Helena Payne) je temeljilo na naslednji logiki.
Črte so lahko izrazite zaradi ugodne ionizacije pri dani temperaturi in ne zato, ker je teh elementov veliko.
Ko je primerjala, koliko vodikovih atomov je potrebnih, da razložijo (celo šibkejše) črte vodika,
in koliko atomov železa bi bilo potrebnih za razlago izrazitih železovih črt, je ugotovila naslednje.
Da bi bile črte železa tako močne kot so, bi zadostovala zelo majhna količina železa pri danih pogojih, recimo na Soncu.
Nasprotno pa je za razlago spektralnih črt vodika potrebno neprimerno več vodika, seveda
ob upoštevanju temperature in stopnje ionizacije.
Iz tega je takrat izračunala, da mora biti razmerje elementov v Soncu približno:
- vodik (H) ≈90 % (številski delež),
- helij (He) ≈10 %,
- vsi ostali elementi skupaj < 1 %.
Rezultat se torej ne vidi neposredno v Saha-jevi enačbi, temveč v primerjavi izračunane gostote (n_e, n_H,
ki jo da Boltzmannova porazdelitev)
z opazovanimi spektralnimi črtami.
Cecilia Payne je v svoji znameniti doktorski disertaciji dejansko uporabila tako
Saha-jevo enačbo kot Boltzmannovo porazdelitev, da je razložila spektralne značilnosti zvezd in sestavo zvezdne atmosfere.
Obe enačbi sta bili ključni orodji, ki sta ji je omogočili pravilno razlago teh črt in pri ugotovitvi,
da Sonce ne more biti sestavljeno
večinoma iz težjih elementov – čeprav imajo ti močne (izrazite) spektralne črte (ki jih lahko vidimo tudi
s preprostim spektroskopom na uklonsko mrežico in ozko režo).
Pa ocenimo, koliko več je vodika kot železa na Soncu, na podlagi spektralnih črt Fe I in Hα.
Hα (656.3 nm) – prehod 3 => 2 (vodik) ,
Fe I črta (438.3 nm - Fraunhoferjeva e-linija, nekje so oznake d) – dokaj močna absorpcijska črta železa ,
T (Sonce) = 5770K ,
ne (elektronska gostota) je 1017 cm-3.
* Boltzmannova porazdelitev – zasedenost vzbujenega stanja
Za vodik (Hα, začetek je pri n = 3, potrebna energija za dvig na stanje n=3 je E3 = 12.09 eV), računi sledijo:
- osnovno stanje H, absolutna vrednost energije za n = 1: E1 = 13.6 eV
- energija potrebna za prehod iz stanja n = 1 na vbujeno stanje stanje n = 3:
En=3 = 13.6·(1-1/32) = 12.09 eV
g3 = 2n2 = 18, ZH ≈ 2 (partitivna funkcija)
Še komentar.
Partitivna funkcija je vsota vseh možnih energijskih stanj atoma, uteženim z Boltzmannovim faktorjem:
Z = ∑gie-Ei/(kT)
Kjer je
T temperatura,
Ei - energija stanja i,
gi - degeneracija stanja i (število načinov, kako je stanje lahko zasedeno),
(vodik pri tej temperaturi
ima zelo malo stanj, Z ≈ 2, železo pa ima 26 elektronov, polne d-orbitale, veliko možnih elektronskih konfiguracij, Z ≈ 1000)
n3/nH = (18/2)·e-(13.6-12.09)/(kT)
= 9·e-1.51/(8.617×10-5·5770)
= 9·e-3.04 ≈ 0.428
Sklep - približno 42.8 % nevtralnih H atomov je v n=3 stanju (ne povsem točno – v resnici je manj,
a uporabljamo poenostavljen model brez efektivnih potencialov).
To pomeni, da bo recimo Hα črta precej izrazita (prehod iz n = 2 v n = 3) in vidna, če bo vodika v deležu vseh atomov
veliko.
Za železo (Fe I črta pri 438.3 nm):
- ta črta prihaja iz stanja z Ej ≈ 2.2 eV
- gj ≈ 9, ZFeI ≈ 1000
nj/nFeI =
(9/1000)·e-2.2/(8.617×10-5·5770) = 0.009·e-4.42 ≈ 0.009·0.012 ≈ 1.1×10-4
Sklep - le približno 0.01 % nevtralnih Fe atomov je v tem stanju.
A začuda je ta črta vseeno dokaj izrazita -
Cecilia Payne je pokazala, da so močne (izrazite) spektralne črte nekaterih elementov lahko posledica fizikalnih razmer, ne pa nujno
velike količine teh elementov ali stanj (tak primer je v Soncu recimo precej redko železo, a Fe ima recimo 26 elektronov
in tako veliko energijskih stanj ...).
* Sahaeva enačba – koliko atomov je ioniziranih?
Za vodik (energija ionizacije je 13.6 eV).
Pri temperaturi 5770 K je delež ioniziranega vodika:
nH+·ne/nH ∝
T3/2·e-13.6/(kT) => e-27.34
≈ 1.4×10-12
Sklep - večina vodika na tej višini v fotosferi ni ionizirana, sledi sklep, da je Hα črta je močna.
Za železo je energija ionizacije 7.9 eV,
zapišimo sorazmernost (vrednost pred eksponentom je enaka):
e-7.9/(kT) = e-15.88 ≈ 1.25×10-7
Sklep - velika večina železa je ionizirana (Fe II), zelo malo ga je v obliki Fe I.
Ocena razmerja NFe/NH
Opazovana intenziteta črt kaže, da je Hα črta zelo močna, Fe I črte pa šibkejše.
Če povzamemo zgornje račune:
- veliko več vodikovih atomov je v pravem vzbujenem stanju.
- veliko več železa je ioniziranega (Fe II), zato manj prispeva k Fe I črtam.
Na podlagi teh izračunov in opazovanj dobimo razmerje:
NFe/NH = 1.4×10-12/1.25×10-7 ≈ 3×10-5
Tudi, če se lotimo izračuna za zelo izrazito Fe I črto pri 430,79 nm (Fraunhoferjeva G-linija), bi dobili praktično
enak rezultat.
Čeprav so železove črte vidne, njihova moč ne pomeni, da je železa veliko – pravzaprav je
na Soncu približno 30.000-krat več vodikovih atomov kot železovih,
Sahaeva in Boltzmannova enačba pojasnita, zakaj nekatere črte kljub temu izstopajo.
Številčni delež železa (Fe) v Soncu je približno 3×10-5.
To pomeni, da so na vsakih 100.000 atomov v Soncu,
približno le trije atomi železa. Masni delež želza v Soncu pa je cca 0.16 %.
A železove Fe I črte so dobro vidne, čeprav je železa malo, ker:
Fe ima izjemno število možnih prehodov – bogat spekter.
Tudi majhen delež nevtralnega Fe lahko povzroči močne absorpcijske črte.
Einsteinovi koeficienti (verjetnosti prehoda) za mnoge Fe I črte so veliki.
Črte so dodatno ojačane zaradi gostote v spodnji fotosferi, kjer so pogoji za absorpcijo ugodni.
Opišimo tri Einsteinove koeficiente.
Za prehod med dvema energetskima nivojema (nižji nivo 1 in višji nivo 2) obstajajo trije tipi prehodov.
1. Spontana emisija (oddajanje fotona), oznaka
A21
Gre za prehod iz višjega nivoja (2) na nižjega (1) brez zunanjega vpliva.
Odda se foton z energijo
hν = E2 - E1
.
Einsteinov A-koeficient je verjetnost (na časovno enoto), da bo atom spontano prešel z nivoja 2 na 1.
2. Stimulatna (sprožena) emisija, oznaka
B21
Prehod iz višjega na nižji nivo, ki ga sproži foton z energijo
hν
Povzroči emisijo dodatnega fotona (v fazi s prvim).
Einsteinov B21-koeficient - verjetnost na enoto časa in na enoto gostote energijskega spektra sevanja.
3. Absorpcija, oznaka
B12
Prehod iz nižjega na višji nivo ob absorpciji fotona.
Einsteinov B12-koeficient: verjetnost za absorpcijo fotona.
Zapišimo Einsteinove koeficiente:
A21 =
|μ21|2 × (64π4 ν3) / (3h c3)
- spontana emisija
μ21 je dipolni moment prehoda med nivojema 2 in 1.
B21 = A21c3 / (8πhν3) - sprožena emisija
B12 = B21 - absropcija, za električno dipolne prehode
Za konkretne vrednosti (npr. A21 za določen prehod železa), se uporabljajo baze podatkov, kot so:
NIST Atomic Spectra Database - https://www.nist.gov/pml/atomic-spectra-database.
Ali tudi Kuruczova baza podatkov in
VALD (Vienna Atomic Line Database) – priljubljena v astrofiziki.
Einstein je pokazal, da so koeficienti med seboj povezani:
A21/B21 = 8πhν3/c3
B12 = B21
To pomeni, da je verjetnost spontane emisije (A) neposredno povezana z
verjetnostjo sprožene emisije in absorpcije (B-koeficienti), ter s frekvenco prehoda.
Povedano je izpeljal tako, da je zahteval, da se pri ravnotežju ohrani Planckova funkcija za sevanje:
uν = ρ(ν) =
(8πhν3/c3)/(ehν/(kT) - 1)
uν ali ρ(ν) je spektralna gostota energije
(energija na enoto prostornine in na enoto frekvenčnega pasu),
v grobem velja uν ∝ E/(Vν).
Tako se je res zelo "počasi" zbistrila dolgo nejasna kvantna slika o sestavi zvezd, posredno tudi vesolja
- zvezde namreč nastajajo iz osnovnih gradnikov
vesolja kmalu po velikem poku (ideja katerega je takrat bila še povojih)
- in še zmeraj na kozmični ravni prevladujeta vodik in helij.
Lokalno - v točkah zmanjšanja entropije, kjer nastajajo zvezde - so sicer končni produkti zvezd
masivni elementi, a globalno, na kozmični ravni, se bistveno ni spremenilo razmerje vodik - helij.
Ostalih masivnejših elementov je še zmeraj skromno število, čeprav so le ti ključni gradniki našega telesa in Zemlje.
Še komentar.
Prvi, ki je verodostojno predlagal širitev vesolja na znanstveni osnovi, je bil
Georges Lemaître, belgijski duhovnik, fizik in astronom, leta 1927 v članku
"Homogeno vesolje s konstantno maso in rastočim polmerom, ki pojasnjuje radialne hitrosti ekstragalaktičnih meglic".
In počasi se je tudi zbistrila slika o razlogih za dolgoživ izsev nekaterih zvezd (recimo našega ljubega Sonca, kjer je vodik ključno gorivo) in
seveda se je skozi cca tri desetletja sestavil mozaik našega življenja, to je fizikalna kvantna zgodba,
kako in kje nastajajo težji elementi od vodika, helija
(v zvezdah pri fuziji, ob eksplozijah supernov, ob trkih zvezd ...). S stališča življenja se zdi
izjemno ugodno, da je poleg vodika, takoj po velikem poku nastalo le še cca 25 % helija ..., gre za masne deleže.
Torej po velikem poku ni bilo časa, vesolje se je namreč hitro širilo in tako ohlajalo, da bi nastali še ostali masivnejši elementi.
To bi najbrž pomenilo nastanek kratkoživih zvezd - kar pa za razvoj življenja kot ga poznamo, ni ugodno - saj se najbrž ne bi utegnilo razviti.
Ti izjemni masivnejši atomi, ki so počasi nastajali (nastajajo) v zvezdah iz vodika in helija, so:
kisik (ga dihamo, brez njega ni
učinkovite presnove - oksidacijo glukoze), ogljik (ogljikovodiki so osnova za večje organske molekule),
dušik, kalcij, kalij, klor, fluor, natrij, fosfor (DNA in RNA imata fosfatno hrbtenico,
je sestavni del molekule ATP – glavne energijske valute celic, celične membrane so narejene iz fosfolipidov ...),
žveplo, magnezij (sodeluje pri uravnavanju živčnih impulzov,
klorofil je magnezijeva kompleksna molekula, ki omogoča rastlinam in cianobakterijam zajem sončne energije
ter njeno pretvorbo v kemično obliko, kar je osnova življenja na Zemlji),
silicij, železo (prenaša kisik po našem telesu) ... in ostali gradniki našega planeta,
živih bitij, nas samih.
Nauk te izjemne primarne zgodbe stvarstva - o skromnem bogastvu masivnejših atomov v mladem vesolju in
potem počasi nastopi res dolg ples gravitacije, ki tvori (stiska) zvezde iz plinov (primarno sta to seveda vodik in helij)
in prašnih delcev in s tem tvori
težje atome preko fuzije, kjer se sprošča enormno energije, ki se lahko iz zvezd izseva tudi milijarde let (Sonce) in tako lahko
nastanejo kamniti planeti in kdaj tudi pogoji za nastanek življenja na njih, recimo rastlin, živali, človeka ...
- je na nek način podoben
razvoju človeka, vsakega od nas. Le človek, ki v mladosti NI zasipan z izobiljem, ampak s skromnostjo
in uravnoteženo izkušnjo ustvarjalnega preživetja, se lahko počasi razvije
v inovativnega posameznika, ki bo v sobivanju z drugimi ustvarjal pogoje za dostojno preživetje človeštva,
za naš razvoj. Človek, ki zmore in ustvarja:
ustvarja duhovne in materialne dobrine, od kamna in palice,
do modernih orodij; od nagonskega obnašanja, do samozavedanja in razmišljanja, učenja, prenosa kulture na mlajše rodove,
od preprostega sporazumevanja, do govora, pisave, knjige, tiska, šol, univerz, od izdelave očal, do
teleskopa, baterije, od pešpoti, cest, kočij, do vlakov, raket, elektrarn, računalnikov, od risanja na stene jam, do modernih kamer,
knjižnic, podatkovnih baz,
od jodlanja do telefona, kontroliranih elektromagnetnih valov za prenos govora, slik, informacij;
od preprostega merjenja razdalj s koraki, do zanesljivih meritev, kako daleč so planeti, zvezde, galaksije,
do ocen velikosti in starosti vesolja;
od lova do poljedelstva, od uporabe kamna do kovin, od vračev do moderne medicine, od lakote do moderne agronomije,
od darovanja prvorojencev, soljudi, do duhovnega preseganja zakonov džungle, do humanizma, umetnosti;
od ugibanj in govorjenja na pamet o Zemlji, vesolju, življenju,
do moderne znanosti, ko počasi odstiramo uganke, bistvena vprašanja ...
od kod in zakaj prihajamo in kaj nas tvori, zakaj lahko obstajamo;
od znanosti do poletov v vesolje ..., potrebno bo preživeti in nekoč se bo tako potrebno tudi odseliti na druge svetove,
ker bo naš planet postajal zaradi napihovanja Sonca prevroč ...
Od primerjav, z atomi skromnega začetka razvoja vesolja (začelo se je le vodikom in helijem), z razvojem človeka,
človeštva, se vrnimo spet nazaj k kvantni znanosti.
Kot smo omenili že na začetku,
je fotosinteza
osnova, srčika razvitega življenja - in je seveda tudi kvantni pojav
"par excellence", ki ga poganjajo kvanti svetlobe s Sonca. Svetloba razbije
vodo in ionizira vodik (spet kvantni pojav), pri tem se sprosti še molekula kisika O2.
Prosti elektroni in ionizirani vodiki pa se vežejo z molekulami CO2
in tako tvorijo sladkorje potrebne za rast rastlin, za življenje.
Sedaj, ko vemo, od kod masivnejši atomi (iz fuzije v zvezdah ...),
je čas, da o fotosintezi, temu osnovnemu procesu življenja na Zemlji, povemo še nekaj podrobnosti.
Cilj fotosinteze je torej pretvoriti svetlobno energijo sonca v kemično energijo v obliki sladkorjev
(ogljikovih hidratov), ki jih rastline in drugi fotosintetski organizmi uporabljajo za rast, razvoj in življenje,
živali pa jih pojemo ...
Fotosinteza poenostavljeno poteka po naslednji shemi:
Sonce da energijo,
kvanti svetlobe razbijejo molekule vode => voda kot donor
elektronov 12H2O + ogljikov dioksid
6CO2 = ogljikov hidrat, npr.
glukoza C6H12O6 + kisik 6O2 + voda 6H2O.
Rastline torej uporabljajo vodikove ione (H+) in elektrone (e-)
iz vode (H2O), da reducirajo CO2 v sladkorje. Kako poteka reakcija po razbitju vode:
6CO2 + 24H+ + 24e- + 6O2 =>
C6H12O6 + 6H2O + 6O2
V molekuli CO2 ima ogljik formalni naboj 0,
a je delno pozitiven zaradi vleka elektronov proti bolj elektronegativnima kisikoma.
To pomeni, da rade volje sprejme še kak negativen elektron.
Energija svetlobe je torej vložena zato, da "dvigne" elektrone ter vodikove ione iz vode in jih usmeri k CO2,
vodik in elektroni pa se tako neposredno porabijo za pretvorbo CO2 v sladkorje.
Kisik pa ni potreben naprej, zato se sprosti kot stranski produkt - tudi za dihanje živali v cca zadnjih
pol milijarde let.
Kisik, ki ga dihamo, pride torej iz H2O — ne iz CO2!
V resnici je proces fotosinteze malo bolj
zapleten - a gre za osnovni princip.
Ključna pri tem procesu je energija svetlobe in seveda ravno pravšnja temperatura na Zemlji, ki omogoča
tekočo vodo in tudi tvorbo kompleksnih organskih molekul.
Voda je potrebna za fotosintezo, a je tudi osnovna tekočina v celicah, je dobro topilo, je potrebna za sistem žil,
kjer voda transportira potrebne snovi za življenje, regulira tudi temperaturo, kemijske reakcije, hkrati
tudi čisti naša telesa - odstranjuje produkte presnove, prenove celic ...

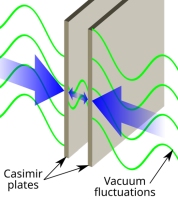

Nizozemska fizika Hendrik Casimir (1909 – 2000, levo) in Dirk Polder (1919 – 2001, desno)
v raziskovalnih laboratorijih Philips sta leta 1947 predlagala
obstoj sile med dvema polarizabilnima atomoma ter med takim atomom in prevodno ploščo;
ta posebna oblika se imenuje Casimir-Polderjeva sila. Po pogovoru z Nielsom Bohrom , ki je predlagal,
da je povezana z energijo ničelne točke, je Casimir leta 1948 sam oblikoval teorijo,
ki napoveduje silo med nevtralnima prevodnima ploščama.
Slednji pojav se imenuje Casimirjev učinek.
Končno je Lamoreaux leta 1997 s svojim neposrednim poskusom kvantitativno izmeril silo
z natančnostjo do 5 % od vrednosti, ki jo je napovedala teorija.
Nadaljnji poskusi so se približali natančnosti nekaj odstotkov.
Zelo poučen je tudi
Casimirjev efekt - morebiti tudi kozmološko. Fizik Hendrik Casimir je leta 1948 napovedal,
da se dve bližnji vzporedni kovinski plošči brez naboja privlačita. Pojav je posledica
vakuumskih fluktuacij v prostoru, to je virtualnih parov delcev-antidelcev (običajno je to elektromagnetno polje).
Vrzel med ploščama (efekt postane pomemben pri razdalji med ploščama 10 nm do 100 nm)
dopušča le specifične valovne dolžine za te virtualne delce (kot stoječe valovaje na struni – ne pozabimo,
kvantni delci se obnašajo tudi kot valovanje) in tako jih je v prostoru med ploščama manj kot zunaj.
Med ploščama je tako nižja energijska gostota, kar povzroči privlak.
Casimirov efekt je kvantno-poljski limit Van der Waalsovih sil –
ampak ima drugačen izvor, večji doseg in velja tudi v popolnem vakuumu brez dipolov.
Nekateri fizikalni modeli pravijo, da temeljni mikroskopski izvor Casimirjeve sile leži v Van der Waalsovih silah (vendar
van der Waalsova sila deluje na 10x krajših razdaljah).
Casimirova sila je lahko tudi odbojna, še posebej, če gre za fermionsko polje (ne klasično svetlobno),
ali če imamo posebne materiale in geometrijo.
Nekateri tako pri odbojni Casimirjevi sili iščejo temno
energijo (zaenkrat se zdi to dokaj optimistična smer iskanja – celo merljiva). Temna
energija namreč pospešuje širjenje vesolja.
Kvanta mehanika je prišla med nas relativno pozno in to z razvojem optike in astronomije, zelo počasi, "diskretno" in
nam je konec 19. in začetek 20. stoletja nepričakovano na široko odprla okno v skoraj zadnje kotičke vesolja, v razlage samih začetkov
vesolja (prostor-časa), v razlago, kje in zakaj nastajajo atomi, zakaj zvezde sploh svetijo, od kod prihaja življenje ...
Tudi odgovore na vse preostale enigme, ki jih trenutno ne znamo popolnoma razložiti, temna snov, temna energija,
ali v vesolju še kje drugje obstaja življenje, kako se bo razvijalo vesolje ..., nam bo v večji meri
razkrila kvantna mehanika, tudi izjemno zmogljivi pospeševalniki delcev in seveda še naprej same meritve vesolja
- brez njih (meritev) smo le
šarlatani.
Slovenija opazuje Sončev spekter - 2025
Kaj pa lahko storimo v tem letu kvantne mehanike 2025 dobrega za naše mlade?
Predlagamo spektroskop na tulec s tanko režo in uklonsko mrežico (in pogled v modro nebo
nam bo razkril sestavo Sonca).
Abeceda vesolja je sestavljena kar iz spektra svetlobe.
Ker je leto 2025
Mednarodno leto kvantne znanosti in tehnologije (IYQ2025) - se zdi zelo smiselno,
da dobi vsak učenec v Sloveniji priložnost opazovati Sončev spekter in v njem
tudi Fraunhoferjeve absorpcijske črte. Na tak način so tudi naši predniki določili kemijsko sestavo naše Zvezde,
ki nam daje življenje. To je bil začetek dolge in razburljive poti do razlage, zakaj Sonce lahko stabilno sveti
že skoraj 4,6 milijarde let in zakaj je sploh lahko nastalo življenje, ljudje. A poznate odgovore?

Shema spektroskopa, ki ga lahko naredijo na vsaki šoli, tudi vsak učenec. Zraven je podanih nekaj ocen,
kako se preslika spekter na očesno mrežnico in če vzamemo res grobo mejo ločljivosti mrežnice očesa
- 100 μm = 0.1 mm, bi načeloma lahko s pogledom skozi uklonsko mrežico opisanega spektroskopa
videli cca 30 absorpcijskih črt
v spektru Sonca. A vse je odvisno od posameznega človeka, očesa - kako natančno uspe razločiti barve med sabo (cca 2 nm),
kako oster vid ima
- a spektroskop je res učinkovit (ne glejte v Sonce, ampak zgolj v modro nebo,
še bolje v belo steno obsijano s soncem). Spekter lahko torej opazujemo neposredno z očesom skozi uklonsko mrežico (priporočam),
lahko ga slikamo (priporočam - potem je to že spektrometer) ali ga projiciramo na platno, a projekcija zahteva
nekaj več truda, temno komoro ... Najprej pa ga usmerite recimo v kako plinsko svetilo (neonsko luč, natrijevo luč, fluorescentno luč
- če jih še najdete),
kjer pa boste videli izrazite emisijske diskretne črte plina, plinov. Pogled v LED svetila je tudi zelo poučen,
lahko ga usmerite tudi v Luno - kaj opazite?
Še pomemben komentar k zgornji poenostavljeni skici.
Ko odprtino usmerimo proti beli steni (ali nebu),
gre odbita Sončeva svetloba skozi odprtino spektroskopa v vse smeri znotraj tubusa. To pomeni, da
je skoraj celotna uklonska mrežica enakomerno osvetljena.
Žarki tako sicer niso vzporedni, se pa dobro približamo
temu pogoju. Not bi lahko postavili zbiralno lečo z goriščem na vhodni reži - a za to v tem kontekstu zaznave
le močnejših Sončevih absorpcijskih črt ni potrebe.
Shema klasičnega spektrometra na uklonsko odbojno mrežico - slika levo.
Naš predlagan spektrometer na prepustno mrežico je veliko enostavnejši.
Shemi, kako spektrometer postavimo na teleskop, če bi koga to zanimalo ..., slika na sredi in desno.
Prvi spektroskopi/spektrometri so bili na prizme.
Vrednost predlagane vaje je, da res enostavno opazujemo zgodovinsko zelo pomemben
kvantni pojav absorpcije svetlobe v Sončevi atmosferi in delno v atmosferi Zemlje.
Vajo se da varno izvesti praktično na vseh šolah in to kar s pogledom v modro nebo (še bolje v belo steno obsijano s soncem)
skozi okno učilnice (a nikakor ne direktno v
Sonce). Nekaj nasvetov.
V ta namen potrebujemo:
- na stojalu pritrjen cca 80 cm dolg (znotraj potemnjen) tulec, ki je na sprednji strani
zaprt s pokrovčkom z režo široko cca 0,2 mm do 0.5 mm in dolgo recimo 5 cm (reža je lahko sestavljena
iz dveh britvic ali kar iz papirja z ostrim robom),
- na drugi strani tulca pa prilepimo uklonsko mrežico s 300 do 600 režami na mm (priporočamo 600 rež, ali del olupljenega
CD-ja), na tulec (bližje uklonski mrežici) pa lahko pritrdimo še karton proti direktni svetlobi z neba ali z bele stene.
Tulec z režo
usmerimo proti beli steni ali modremu nebu. Mrežica nameščena zadaj bo uklonila osvetljeno
režo v mavrični spekter in če se nekoliko potrudimo, lahko s prostim očesom opazimo nekatere
temnejše in širše Fraunhoferjeve absorpcijske črte - kot recimo kaže slika spodaj (večinoma lahko opazimo
le te črte, ki so označene s črkami).
Če šola nima uklonske mrežice, pa lahko uporabimo star CD, z lepilnim trakom odstranimo kovinsko
folijo in odrežemo v radialni smeri plastični del CD-ja z zunanjim lokom dolgim cca 5 cm.
CD ima vgravirane sledi gostote približno 625 na mm in te sledi nam služijo kot uklonska mrežica.

Na sliki so rezultati preprostega spektroskopa z ozko režo in uklonsko mrežico s 600 režami na mm.
Na vrhu je umerjen primerjalni spekter Fraunhoferjevih absorpcijskih spektralnih črt -
naš preprosto posnet spodnji spekter pa se odlično ujema
z zgornjo profesionalno podobo spektra z uradnimi oznakami izrazitejših absorpcijskih črt. Seveda ima naš
poenostavljen spektroskop (spektrometer) slabšo ločljivost - a dovolj dobro za pedagoške namene.
Tulec je bil usmerjen kar proti beli steni osvetljeni s soncem.
Brez težav bomo torej skozi uklonsko mrežico videli mavrico, Sončev spekter,
v njem pa kar nekaj absorpcijskih črt (nekoliko temnejših črt, v bistvu temnejšo režo multiplicirano
zaradi uklonske mrežice).
Zagotovo bomo na oko videli absorpcijske črte, ki so na sliki označene z naslednjimi črkami:
G (Ca črta 430,77 nm in železo 430,79 nm),
F (vodikova beta črta), b (železo in magnezij), E (železo),
D (helij, natrij), C (znamenita vodikova alfa črta), a (črto molekule kisika
O2, ki je posledica absorpcije naše atmosfere). Za O2 črto naše atmosfere v rdečem delu spektra velja,
da bo izrazitejša - če bomo opazovali nebo
ali bel zid, ko je Sonce že zelo nizko na nebu (zelo poučno - tudi za kako raziskovalno
nalogo). V resnici boste opazili v celotnem spektru se več absorpcijskih črt.
Temnejše črte so večinoma posledica
absorpcije svetlobe v atmosferi Sonca - tako lahko določimo, kateri elementi sestavljajo Sonce, kateri plini sestavljajo
atmosfero Sonca.
Atmosfero Sonca pa neposredno opazimo ob popolnem Sončevem mrku, ko Luna navidezno
prekrije Sončevo oblo - čudoviti prizori
(hkrati Vas tudi vabim na popolna Sončeva mrka, ki bosta 12. avg. 2026 in 2. avg. 2027 vidna v Evropi, v Španiji,
oz. v njeni bližini - počitnice v senci popolnega S. mrka, kaj je še lepšega).
Spekter se slika skozi mrežico (v tem primeru 600 rež na mm - občutljivost ISO100,
časi okrog od 1/100 s do 1/20 s (odvisno o pogojev, ure v dnevu). Zoom objektiv tukaj pride zelo prav - slikamo tako,
da na fotočip posnamemo celoten prvi
uklonski maksimum. Preko fotografiranja lahko s takim najbolj preprostim spektrometrom zaznamo kar čez 40
absorpcijskih črt.
Vodoravne črte so posledice grobe vhodne reže (narejena je bila kar iz papirja - v resnici pa nam
dokazujejo, potrjujejo, da res gledamo uklonsko sliko osvetljene reže). Če neposredno slikate režo,
boste na sliki brez težav opazili te robne anomalije reže - če seveda nimate idealne reže ... :)
Nekoliko krajši čas osvetlitve pomeni, da posnamemo več črt v modri in zeleni barvi,
z nekoliko daljšim časom osvetlitve pa ujamemo več črt v rdečem delu spektra.
Na robu rdečega dela spektra zagotovo lahko
ujamemo znamenito H-alfa (ali kar H-α) vodikovo
črto 656,3 nm (fotočipi imajo omejen spektralni, barvni doseg, občutljivost - sploh pri daljših valovnih dolžinah, na skrajnem robu
rdeče barve).
Vodikova H-alfa črta (oznaka C na spektru) nastane, preprosto povedano po Bohrovem modelu, ko elektron preskoči iz višje orbite n = 3
na nižjo orbito n = 2 (iz višjega energijskega nivoja na nižjega, n je glavno kvantno število).
Za vodikovo H-beta črto v modrem delu (486,1 nm, oznaka F na spektru) pa velja,
da elektron preskoči iz orbite n = 4 na nižjo orbito n = 2.
Vodika je v Soncu in tudi sicer v vesolju, največ - zato velikokrat Sonce
opazujemo prav skozi H-alfa teleskope in tako lahko opazimo izjemne površinske podrobnosti, pege, konvekcijske celice,
filamente, robne protuberance, izbruhe ... Sonce je torej izredno živahno - kako ne bi bilo, ko pa
se v njem vsako sekundo sprosti ΔE = 3.828×1026 J energije in
zato se mu zmanjša masa kar za Δm = ΔE/c2 = 4.26 milijard kg na sekundo
(to pomeni, da Sonce v cca šestih sekundah porabi ja Blejsko jezero mase).
Kako pa potem sploh lahko opazujemo Sonce v H-alfa svetlobi, če se ta absorbira v atmosferi Sonca?
V resnici se absorbira samo del te svetlobe. Glejte spodnji graf spektralne porazdelitve
svetlobe, ki prodre na Zemljo - ta del je rahlo nazobčan (padec števila fotonov zaradi absorpcije),
kar zaznamo kot temnejše črte v spektroskopu na tanko režo.
Večji del svetlobe pa seveda vseeno prodre skozi atmosfero Sonca in je tako H-alfa svetloba
ena najbolj znamenitih Sončevih spektralnih črt (valovnih dolžin - vodik
je tudi sicer osnovni gradnik vseh ostalih masivnejših atomov).

Vir slike Sonca v H-alfa svetlobi: https://www.reddit.com/r/Astronomy/
Hkrati pa, če imate H-alfa teleskop, lahko z učenci opazujete v H-alfa svetlobi (spektralni črti) še samo Sonce.
Ujeli boste imenitne robne protuberance, izbruhe, na površini pa filamente, pege, konvekcijske celice ...
To je odlična kombinirana vaja, ki večinoma ne zahteva drugega kot pogled skozi okno učilnice, sploh za ogled spektra
je to zagotovo čisto dovolj.
Kolikšna pa je gostota svetlobe v halfa svetlobi, v njeni bližini, recimo da teleskop prepušča
pasovno širino blizu 0.1 nm (zaokroženo)? Odgovorimo nekoliko pozneje.
Ali lahko opazimo tudi absorpcijo v atmosferi Zemlje? Kot smo že omenili - se da.
Če opazujemo nebo cca pol ure preden Sonce zaide,
opazimo v rdečem delu spektra še dodatno absorpcijsko črto pri cca 628 nm, ki jo v Zemeljski atmosferi
povzroči molekularni kisik O2 (ko je Sonce nižje, je pot svetlobe skozi atmosfero daljša
in je zato absorpcija Sončeve svetlobe zaradi molekul kisika O2 izrazitejša). Zelo poučno.
Pojavnost in izrazitost absorpcijskih črt (sploh vodikovih - njihova širina) v spektrih zvezd nam pove veliko
o temperaturi, starosti, velikosti, masi zvezd - na tak način tudi zvezde klasificiramo po glavnih spektralnih
tipih (O, B, A, F, G, K, M).
Sonce je tipa G (temperatura površja je cca 6000 K) - to so torej ne preveč vroče zvezde (podobna zvezda je tudi Kapela).
Najbolj vroče zvezde (več kot 30 000 K, modra barva) so tipa O
(recimo masivna zvezda Theta 1 Oriona v znamenitem trapezu zvezd, ki leži v Orionovi meglici M42).
Seveda lahko uporabite tudi mrežico s 300 režami, a so rezultati nekoliko slabši.
Lahko pa namesto klasične mrežice uporabite tudi CD disk brez kovinske folije (z lepilnim trakom jo brez težav
odstranimo) - ima nekje 625 rež na mm. A navadna šolska uklonska mrežica je za te namene enostavnejša za uporabo in
da izjemno kvalitetno sliko. A tudi z olupljenim CD - jem se da, sploh če odrežemo ustrezen kos, da ne
uporabljamo celega olupljenega CD-ja.
Še opomba.
Preproste ročne spektroskope lahko tudi kupite - kot učni pripomoček - tudi to je ena od možnosti.
A vsekakor priporočam tudi izdelavo spektroskopa na uklonsko mrežico in tanko režo. Če
nimate uklonske mrežice, pa se še zmeraj po šolah ali doma najdejo CD-ji, ki so tudi
primerni za tako imenitno vajo - več sledi.
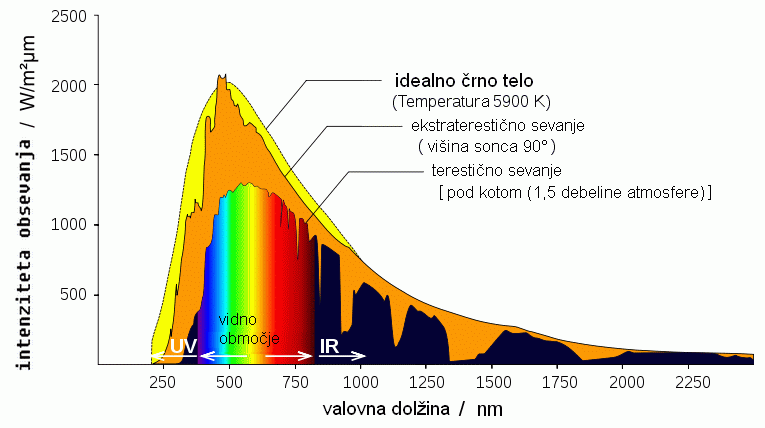
Pasovna širina ('bandwidth') tipičnega H-alfa teleskopa
je nekaj pod 0.1 nm - kolikšna je potem energijska gostota j = dL/dS te rdeče svetlobe, gre za ocene?
Gostoto obsevanja na valovno dolžino (dj/dλ) po valovnih dolžinah razberemo kar iz grafa zgoraj in pri H-alfa svetlobi
656,3 nm je
vrednost dj/dλ ≈ 1200 W/(m2μm) = 1.2 W/(m2nm). Velja za oceno na površini Zemlje
(spodnja krivulja od treh)
in iz tega podatka sledi ocena, da je gostota energijskega toka
vodikove H-alfa svetlobe (in njenih bližnjih sosed)
v tej pasovni širini j ≈ 0.1 nm*1.2 W/(m2nm) = 0.12 W/m2.
Kar je še zmeraj ogromna gostota energije - saj velja, da je
minimalna svetloba, ki jo lahko zazna človeško oko okoli 10-16 W/m2 (v pogojih, ko okolica ni
osvetljena). To pomeni, da v takem primeru
zadane paličico le nekaj fotonov - palčica je receptor na mrežnici očesa za nočni vid.
V praksi pa je ta meja precej višja, na primer, v osvetljenem okolju je ta meja (približno 10-14 W/m2).
Oko tudi ni enako občutljivo na vse valovne dolžine, najbolj je občutljivo na barvo
kjer Sonce oddaja največ svetlobe (Wienov zakon: λ = b/T)
- to je pri valovni dolžini 501.5 nm – kar je zeleni del vidnega spektra svetlobe. Vrnimo se k H-alfa svetlobi.
Če želimo oceniti še gostoto fotonov, lahko to vrednost delimo z energijo H-alfa fotona:
Efotona = hc/λ ≈ 6.626·10-34·3·108J/656 10-9 ≈ 3.03·10-19 J
Gostota fotonov na kvadratni meter na sekundo je torej:
N/(St) = 0.12 J/3.03·10-19 J (1/m2/s) ≈ 4·1017 fotonov/m2/s.
V Lunt H-alfa teleskop premera 35 mm tako prileti cca 1014 fotonov/s (to je še zmeraj ogromno).
H-α linija je dominantna v rdečem delu spektra Sončeve svetlobe, vendar v tem pasu ni prisotna zgolj črta vodika.
K tej
črti prispevajo tudi sevalni prispevki zaradi trkov - pospešenega gibanja nabitih delcev (toplotno sevanje) - a
obstajajo tudi šibkejše črte drugih atomov in ionov,
kot so helij, kisik, kalcij in še nekatere kovine, ki lahko prekrivajo ali vplivajo na spekter (a pri
protuberancah ne bistveno).
To je razlog - da ravno v tej H-α svetlobi vidimo na Soncu toliko izrednih podrobnosti, sploh
robne protuberance in izbruhe. Protuberanca je robni
gost plazemski oblak, ki izstopa iz Sončeve površine, vendar ostaja vezan na Sonce zaradi magnetnih sil
(se oblikuje po magnetnih silnicah).
Filament pa je dolga, nekoliko temnejša nitasta struktura, ki je v bistvu protuberanca,
ki je vidna na Sončevi površini (od zgoraj nad fotosfero). Zaradi nižje temperature (nima toliko dotoka energije)
je temnejša glede na fotosfero
(večinoma je sestavljena iz plazme).
Tudi širina spektralne črte (kot smo že omenili, Full Width at Half Maximum ali FWHM - širina pri polovični višini profila
črte) je odvisna od različnih dejavnikov (same hitrosti vira glede na opazovalca,
od temperature zvezde, saj le ta pomeni mero za termično gibanje nukleonov, tukaj so turbulentna gibanja plazme, atmosfere;
gostota plina in tlak določa tudi število trkov, sama ionizacija, tudi magnetna polja ...).
Tukaj je še Starkov efekt - pojav razširitve in razcepitve spektralnih črt zaradi prisotnosti električnega polja,
običajno zaradi bližnjih nabitih delcev (npr. elektronov in ionov) v plazmi ( je izrazit pri zelo vročih zvezdah tipa O in B,
pri belih pritlikavkah, velja ΔλStark ≈ w·Ne2/3).
Dopplerjev učinek se pojavi tako zaradi premikanja vira svetlobe (k in od opazovalca, kar razširi črto) in zaradi samega termičnega gibanja
nukleonov na ali ob zvezdi ter zaradi turbulenc ...
Kar pomeni, da bodo ti gibajoči atomi vplivali na svetlobo (sploh vodikovi, ki imajo najmanjšo maso in torej največje termične hitrosti).
Za termično gibanje delcev velja v povprečju povezava med kinetično energijo in absolutno temperaturo (srednja šola):
Ek = mv2/2 = 3kT/2 => v = (3kT/m)1/2,
m je masa, k je Boltzmannova konstanta, T je
absolutna temperatura plina, plazme Sonca, v je kvadratni povpreček hitrosti.
A pri Dopplerju je korektna naslednja (podobna) enačba hitrosti v = (2kT/m)1/2
- to pa pomeni, da se upošteva samo
Dopplerjev pojav za hitrost v smeri gledanja (torej le eno komponento hitrosti, recimo vx,
ki za nas povzroča Dopplerjev premik).
Številka 2 izhaja iz tega, da računamo standardni odmik v Gaussovem profilu – torej iz statistične obravnave komponentne hitrosti
[ f(vx) = (m/(2πkT))1/2e-mvx2/(2kT) ].
Dopplerjev premik za vodik je na Soncu:
Δλ = λov/c = (2kT/m)1/2λo/c ≈ 0.021 nm.
Z večanjem temperature se torej povprečna hitrost delcev povečuje. A to je kaotično premikanje v vse smeri
in
z večjim Dopplerjevim premikom se izrazito poveča širina spektralne črte (recimo H-alfa in H-beta).
Eden pomembnejših dejavnikov pa je tudi sam tlak.
Višji je tlak (sovpada z višjo temperaturo) pomeni več trkov med atomi ali ioni
(pogostejše interakcije), kar pa krajša življenjsko dobo vzbujenih stanj atomov
(v kvantnem smislu). S tem pa tudi večjo negotovost energije prehoda, kar po Heisenbergovem načelu povzroči širšo črto.
Če je življenjska doba kvantnega stanja (
Δt ) krajša (zaradi pogostejših trkov ), je energijska negotovost večja (
ΔE ), kar pomeni, da se prehod razmaže v širšo spektralno črto: ΔE ≥ h(rπΔt).
Skupna efektivna širina H-alfa črte pri Soncu je cca od 0.03 nm do 0.05 nm (odvisno od lokalnih pogojev na Soncu),
k tej širini zelo prispevajo tudi trki (tlak, oz. temperatura). Ostali prispevki so večinoma manj pomembni.
H-alfa absorpcijska črta (npr. iz fotosfere ali nižje kromosfere) je po navadi ožja (okoli 0.03–0.05 nm).
H-alfa emisijska črta (npr. iz protuberanc ali aktivnih regij v kromosferi) je lahko precej širša,
pogosto preko 0.1 nm, zaradi večje turbulence, višje temperature in posledično hitrih gibanj plazme.
Da se z večanjem temperature izrazito veča širina absorpcijskih črt vodika
se lepo vidi v primerjalnih spektrih različnih spektralnih tipov zvezd - vroče zvezde imajo izrazito širše
vodikove črte.

Preprost spektroskop na režo širine cca 0,2 mm in dolžine cca 6 cm, tubus (znotraj črn - mat), dolžine
cca 80 cm in na drugi strani uklonska mrežica cca 600 rež na mm.
Povejmo, da imajo prof. spektroskopi reže širin cca 0.02 mm ali celo manj.
Tulec se pritrdi na stojalo - recimo s selotejpom ...
Ko pogledamo nekoliko poševno skozi uklonsko mrežico in cev usmerimo v modro nebo ali
belo površino obsijano s soncem (nikakor pa ne direktno v Sonce) bomo opazili
spekter Sončeve svetlobe in znotraj spektra kar nekaj absorpcijskih (temnejših) črt.
To so v bistvu temnejše slike reže, ki jo je razklonila uklonska mrežica.
Lahko pa ta spekter tudi slikamo in našteli bomo vsaj 40 Fraunhoferjevih absorpcijskih spektralnih črt.
Časi slikanj so od okrog 1/100 s do 1/20 s (odvisno o pogojev, ure v dnevu in kateri del spektra želimo
podrobneje ujeti). Vir slik: splet.
Še nekaj izračunov dobljenih iz posnetka spektra.
Še prej pa podajmo opis ločljivosti (resolucije) spektroskopa na uklonsko mrežico (difrakcijsko mrežo, recimo da je njena
širina D = Nd, kjer je N število rež, d pa razdalja med njimi, v našem primeru je d = 0.001m/600 = 1.67 10-6 m).


Iz zgornje slike razberemo, da lahko uklonske vzorce ustvari ena sama reža ali dve in več rež ('slits').
Ko svetloba (v tem primeru ene valovne dolžine iz laserja) naleti na celoten niz enakih,
enako razmaknjenih in širokih rež, to je na uklonsko mrežico, se svetli vrhovi,
ki nastanejo zaradi konstruktivne interference valovanja (ojačitev) iz različnih rež,
nahajajo pod enakimi koti kot pri dveh režah. Vendar je vzorec glavnih interferenčnih črt
z več režami veliko ostrejši - ožji vrhovi. In prav to iščemo,
večjo razločljivost, ki je posledica več rež.
Opazujemo torej interferenco valovanja iz posameznih odprtin na razdalji d
- vrhove zaznamo kot spektralno črto višjih redov za naslednji geometrijski pogoj:
d*sin (α) = m*λ - snov srednje šole, za ojačitev mora biti razlika poti dveh valovanj
enaka mnogokratniku valovne dolžine, torej m*λ.
Pod sliko interferenc glede na število rež je podan še graf intenzitet svetlobe posameznih ojačitev
(kot ga recimo zazna ccd kamera).
Svetloba se torej uklanja na celotni mrežici dimenzije D (enako kot pri teleskopu s premerom objektiva D
- slika levo, z večjim premerom teleskopa
bomo ločili rec. tesnejše dvojne zvezde,
z večjo mrežico pa bomo ločili spektralne črte, ki so si bližje skupaj - to si tudi želimo).
Uklon na celotni mrežici je seveda ožji (≈ λ/D), kot ukloni na drobnih odprtinah mrežice dimenzije 's' (λ/s).
Svetloba pa se seveda zelo uklanja (kot smo ravno omenili)
tudi na samih drobnih odprtinah uklonske mrežice,
ki so na razdalji d, tako dobimo interferenčne proge - ta interferenčni uklon je seveda veliko večji (≈ λ/d) kot
uklon na celotni mrežici dimenzije D (tako so mrežice tudi dimenzionirane).
Slika na sredi prikazuje omenjeno interferenco preko intenzitete uklonjene in interferirane svetlobe
- vrhove zaznamo kot spektralno črto višjih redov za naslednji geometrijski pogoj:
d*sin (α) = m*λ - snov srednje šole, za ojačitev mora biti razlika poti dveh valovanj
enaka mnogokratniku valovne dolžine, torej m*λ.
Za majhne uklonske kote in prvi red uklona m = 1 velja kar pogoj d*α = λ.
A kakšna je sprememba valovne dolžine Δλ za uklon na mrežici z razdaljami d,
da bomo to zaznali
s spektrometrom, da bo sprememba vidna? Tudi to vprašanje ilustrira srednja slika
(polna krivulja in črtkana krivulja dveh bližnjih valovnih dolžin
λ in λ + Δλ )
in tudi desna slika prikazuje to spremembo. Ja - sprememba kota Δα za Δλ, mora biti velikostnega reda
ločljivosti celotne mrežice D. To je enaka logika kot pri tesnih dvozvezdjih - če je sprememba kota (zaradi spremembe valovne dolžine
Δλ) manjša
od kotne ločljivosti mrežice kot celote, te spremembe ne bomo zaznali.
Želimo si torej, da je sprememba kota (zaradi spremembe valovne dolžine
Δλ) velikostnega reda kotne ločljivosti mrežice (velikosti D) kot celote.
Povedano izrazimo še z enadžbami.
Ločljivost
je sposobnost spektroskopa, da ločimo med dvema zelo blizu ležečima valovnima dolžinama (spektralnima črtama).
Vemo, da je optična ločljivost za teleskope (posledica uklona svetlobe na objektivu) določena s premerom objektiva D
in valovno dolžino, in sicer iščemo kot α v radianih (pri tem kotu ima objektiv prvi interferenčni minimum),
ko recimo ločimo dve bližnji zvezdi - velja enačba
(faktor 1.22 smo zaokrožili na 1):
α ≈ λ/D.
Za uklonsko mrežico velja enako, gledamo širino
skozi katero pada vzporedna svetloba (za D velja: D = Nd).
Ločljivost take mrežice kot celote je αD = λ/D
(pri tem kotu ima mrežica širine D prvi interferenčni minimum, in če v ta minimum pade konstruktivna interferenca zaradi
uklona na več režah, jo lahko zaznamo, razločimo).
A zanima nas tudi, kolikšna je lahko sprememba kota Δα,
glede na spremembo valovne dolžine Δλ, ko bomo ločili ojačitev
naslednje (prejšnje) valovne dolžine (desna slika)
zaradi uklona in interference na sami mrežnični razdalji mali d (večinoma gledamo prvi red ojačitve m = 1). Ta je:
Δαd ≈ Δλ/d.
In ta dva kota morata biti primerljiva, da lahko ločimo naslednjo spektralno črto (da se ne prekrivata). Velja torej:
Δαd ≈ αD
Δλ/d = λ/D
Od koder sledi:
λ/Δλ = D/d = N = R
Vpeljali smo torej ločljivost spektroskopa na mrežico, ki jo označimo z R in velja:
R = λ/Δλ = N
N je število rež uklonske mrežice, kamor pada svetloba.
Pomembno je, da se zavedamo, da je ločljivost povezana s številom rež in tudi z valovno dolžino.
Pri vidnem delu elektromagnetnega valovanja večinoma ocenimo ločljivosti mrežice iz srednje
valovne dolžine vidnega dela spektra.
Omenimo še, da skozi vhodno režo svetloba osvetli celotno, nekaj cm široko, mrežico približno enakomerno,
- a svetloba žal ni čisto
vzporedna, kar je problem - a za naš namen bodo rezultati vseeno ugodni.
Pravi spektroskopi postavijo režo v gorišče zbiralne leče in tako na mrežico dejansko padejo
vzporedni žarki - a mi smo spektroskop res poenostavili. Če uklonski spekter projicirajo na zaslon,
ga tudi zberejo z zbiralno lečo - v našem primeru je to naredil fotoaparat na fotočipu.
Podajmo še primer (izračun ločljivosti) za naše oko, kjer je premer zenice D cca 5 mm in za mrežico 600 rež na mm.
N = n·D = (600zarez/mm)·5mm = 3000 zarez (rež)
Ločljivost za prvi uklonski red (m = 1) naše uklonske mrežice (R) je:
R = m·N = 1·3000 = 3000
Če na primer opazujemo svetlobo z valovno dolžino λ = 600 nm, potem je razločljiva sprememba valovne dolžine:
Δλ = 600 nm/3000 = 0.2 nm
Naša uklonska mrežica ima za oko ločljivost cca 0.2 nm, za fotoaparat s premerom objektiva recimo nekaj cm,
pa je ločljivost že blizu 0.02 nm.
Torej, problem naše uklonske mrežice ni teoretična ločljivost (ki je kar visoka),
ampak preprosta izvedba spektroskopa,
kjer je največji problem vhodna preširoka reža (kar smo že izračunali ob sliki). A v našem primeru tudi to zadostuje, bomo videli zakaj.
Vhodno režo bi sicer lahko še zožili, a bi potem izgubili veliko svetlobe - s tako napravo se potem težje opazuje.
Ker si želimo opazovati svetlobo vsaj na desetinko nanometra natančno, oz. profesionalni spektroskopi zagotovo na 1 nm/100 = 0.01 nm,
oziroma GRIS kar na 0.002 nm natančno,
si tudi želimo, da naša slika reže na očesni mrežnici ali na fotočipu ne presega
velikosti željene natančnosti (recimo 0.1 nm) s katero želimo slikati ali opazovati spekter.
A za šolske namene se bomo zadovoljili z resolucijo cca 1 nm na fotočipu in nekaj več na očesni mrežnici - kjer
je naš spektroskop na meji ločljivosti očesne mrežnice (izračuni ob sliki).
Problem velike slike reže (na očesni mrežnici, na čipu fotoaparata) je, da se črte med sabo prekrivajo.
A vendar vidimo nekaj črt?
Zakaj?
Ker so nekatere črte nekoliko širše in predvsem izrazitejše (temnejše - opazni so večji
padci gostote na zgornjem grafu jakosti spektra po valovnih dolžinah).
In ravno te izrazite padce (če so narazen vsaj dober nm) lahko vidimo ali še lepše slikamo tudi z našim
spektrometrom.
Tako z njim lahko ločimo recimo črti b4 (Mg - 516,7 nm) in b1 (Mg - 518,4 nm), narazen cca 1.7 nm ter
črti D3 (He - 587,6 nm) in D1 (Na - 589,6 nm), narazen cca 2 nm.
Tukaj je še vodikova črta gama (H-gama - 434.05 nm, oznaka f na spektru,
prehod iz n = 5 na n = 2) in Ca črta (430.77 nm, oznaka G na spektru), narazen cca 3.4 nm.
Kaj nam povedo številke iz obdelave fotografije.
Število pikslov (dolžina) celotnega spektra: Ns=1700
Velikost slike reže: Nreže = 8 pikslov
Zato je število ločljivih črt cca (zaokrožimo): Nč = 1700/8 ≈ 200
Na posnetku so barve od cca 410 nm do cca 660 nm (zaobjamemo torej λ_obseg = 660 nm - 410 nm = 250 nm).
Slika reže tako zaobjame približno Δλ = λ_obseg/Nč = 250 nm/200 ≈ 1.3 nm
Hkrati pa, če delimo dolžino spektra v pikslih (v našem primeru 1700) z zajetim razponom na sliki
(λ_obseg = λrdeča - λmodra ≈ 250 nm), potem dobimo:
1700 pix/250 nm ≈ 7 pix/nm
To je blizu velikosti reže, kar pomeni, da če bi bile spektralne črte ločene po cca 1 nm, bi jih kljub
prekrivanju videli cca 200. A črt je veliko več (na tisoče) in so zato veliko bolj skupaj in se zaradi
velikosti reže večinoma prekrivajo. A, kot smo že povedali, zaradi izrazitosti nekaterih (in oddaljenosti le teh za več kot 1 nm)
jih vseeno lahko naštejemo vsaj 40.
Če temu ne bi bilo tako - jih kemik William Hyde Wollaston leta 1802 ne bi videl 7.
Slaba ločljivost Newtonovega spektroskopa na režo in prizmo pa je najbrž razlog,
da že Newton ni opazil vsaj nekaj absorpcijskih črt v Sončevi svetlobi (lahko pa, da ni bil pozoren).
Torej - tak grob spektroskop (zaradi prekrivanja - preširoka reža za 0.8 m dolg tubus)
na našem posnetku ne more zaznati 200 črt.
A na posnetku sem jih preštel vsaj 40 (seveda izrazitejših) - kar je zelo
solidno glede na vložen trud.
Ta spektroskop je zdaleč najenostavnejši in tudi ni nobenih večjih težav z opažanjem ali
slikanjem absorpcijskih spektralnih črt.
Ni zelo natančen, je pa preprost in učinkovit pri uporabi, je praktično zastonj - in zato kar pravšnji za šole.
V nadaljevanju bomo omenili še kakšno izvedbo spektroskopa.
Obstaja tudi spektroskop na šivanko (iglo), pokaže precej več črt pri fotografiranju - a ni tako zelo enostaven,
kot to lahko preberemo na spletu.
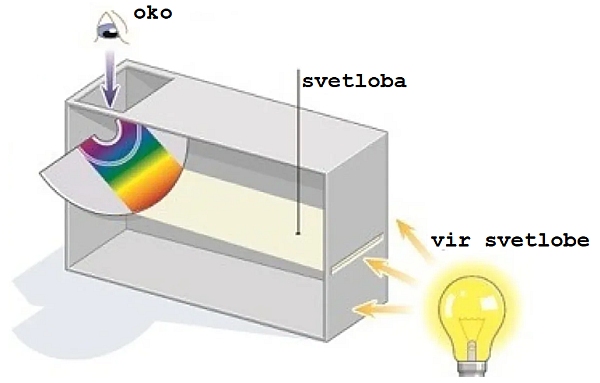
Še primer spektroskopa na CD - na odboj. Sam CD pa ima proge v plastiki (dobrih 625 na mm - po teh
progah se z laserjem zapisujejo digitalni podatki na CD - na kovinsko. oz. srebrno folijo) in
te proge uklanjajo svetlobo. A ta spektroskop še zdaleč ni tako
didaktično prepričljiv, enostaven, kot naš na uklonsko mrežico.
Sem testiral.

Spektroskop na šivanko (iglo), pokaže precej več črt pri fotografiranju - a ni tako zelo enostaven,
kot to lahko preberemo na spletu. Črn papir prepognemo kot kaže slika (desno od igle, ki jo zapičimo v papir).
Žarki s Sonca padajo v zgornjem primeru na šivanko z leve.
Pred slikanjem pregib stisnemo čisto skupaj, tako
nastane vertikalna pregrada in dela senco na desni strani pregiba. V tej senci posnamemo spekter
- to je spekter Sončeve svetlobe, ki se odbije od tanke
šivanke. Vse skupaj je dobro imeti v veliki škatli, z odprtino za slikanje in da svetloba pada zgolj na iglo.
A za šolske namene je spektroskop na tulec s tanko režo in mrežico veliko bolj učinkovit, enostaven za uporabo in
nazoren.
Za kake raziskovalne naloge pa se da seveda spektroskope zelo izpopolniti.
Na Gimnaziji Šentvid - Ljubljana smo tako naredili 2019 in še bolje 2025 (uporabili zavržene dele
prof. spektroskopa), spektroskop preko
heliostata, rezultati so res izjemni:
http://www2.arnes.si/~gljsentvid10/aktualno_2019.html in aktualno(_2025).html
Pokazali obiskovalcem na informativnih dnevih.
A tak pristop zahteva veliko časa, odrekanja.
Naš predlog spektroskopa na tulec s tanko režo in uklonsko mrežico (v letu kvantne mehanike 2025) pa ne.
In - z našim preprostim spektroskopom na uklonsko mrežico lahko tako v resnici že neposredno
opazujemo kar abecedo stvarstva iz katere se zapisuje čudovita zgodba o nastanku in življenju
vesolja, atomov, zvezd, planetov (potepuhov), časa, življenja.
Oglejte si tudi članek, ki je bil na to tematiko objavljen v astronomski reviji
Spika (nov. 2025).
Abeceda vesolja je sestavljena kar iz spektra svetlobe
Slovenija opazuje Sončev spekter - 2025
(Mednarodno leto kvantne mehanike)
(Vičar Zorko, revija Spika 11 [2025], strani 489 - 492) - 7,15 EUR
Zadnji velik uspeh kvantne mehanike je bilo odkritje Higgsovega bozona

Peter Ware Higgs (29. maj 1929 – 8. april 2024 - umre na dan Sončevega mrka) je bil britanski teoretični fizik,
profesor na Univerzi v Edinburghu in Nobelov nagrajenec za fiziko za svoje delo o masi subatomskih delcev - oče
Higgsovega bozona.
Higgsov bozon poznamo tudi pod imenom "Božji delec"!
Nekateri zavračajo to ime, spet
drugi predlagajo prav nasprotno poimenovanje ("Totally Secular Particle" ali kar »Masson«).
Ime "Božji delec" mu je dodelila istoimenska knjiga 'Božji delec: če je vesolje odgovor,
kaj je vprašanje? (The God Particle: If the Universe is the Answer, What is the Question?)',
ameriškega fizika Leona Ledermana, ki pa je dejansko želel, da ga imenujemo »Preklet delec«
(Goddamn particle – zaradi težavnosti odkrivanja), a si je urednik izprosil ime "Božji delec".
Na Boga so se sklicevali tako Newton, Faraday, Maxwell, Einstein ... tako da tako poimenovanje
zagotovo dodatno poudari zagato, kako težko je doumeti ter opisati dogajanje v naravi in samo
sosledje dogodkov v vesolju.
Higgsov bozon zelo hitro razpade - v času 1 zeptosekunde v druge delce – in kdo je Higgsovemu
bozonu dal »maso - energijo« (otroško vprašanje ali tudi ne in v tem kontekstu poimenovanje »Božji delec«
simbolično nekaterim veliko pomeni, drugim pač ne)? A bistveno je, da se ga da detektirati in
razumeti!?
Z uporabo dveh različnih metod odkrivanja so fiziki v CERN-u
(pospeševalnik protonov, to je hadronov: LHC - Large Hadron Collider) zaznali maso,
ki bi naj bila v območju Higgsovega bozona. Julija 2012 sta skupini sodelavcev
na detektorjih CMS in ATLAS neodvisno sporočili, da sta potrdili odkritje prej neznanega
bozona z maso med 125–127 GeV/c2, katerega lastnosti se s standardno deviacijo
5 sigma »ujemajo« s Higgsovim bozonom. Zato je večina raziskovalcev iz tega področja
prepričanih, da je Higgsov bozon odkrit!
Higgsov bozon je torej nosilec polja ( fiziki so vsakemu polju pripisali delce,
ker si drugače ne znajo (znamo) predstavljati delovanja med delci – spomnimo se na podajanje žoge, ko silo prenaša žoga,
ko jo primemo ali odvržemo ...).
Higgsov bozon v zgodnjem vesolju pripravi kvarke do sodelovanja, jih upočasni (na manjšo hitrost
od svetlobne) in s tem gre del energije v maso (materijo). Morebiti ni odveč primerjava, da je
Higgsov bozon nekaj takega v svetu osnovnih delcev, kot je pri ljudeh želja po sodelovanju
(to željo sicer težko definiramo, a deluje) - da torej delujemo kot skupnost, kajti drugače
iz nas ne bi bilo praktično nič. Smo ljudje, ker sodelujemo (prenašamo in dopolnjujemo kulturne
pridobitve iz roda v rod – govor, pisano besedo, izročilo, hrepenenje po presežnem, znanje,
umetnost, miselne in ročne spretnosti ..., no danes tudi nemo gledanje v ekrane,
pa še nekatere manj krepostne vrline imamo, recimo napuh ...). Torej ne begamo
v prazno, ampak se ustavimo (ustavi nas »Higgsov« bozon sodelovanja), premislimo
in skupaj delamo naprej. Higgsov bozon je imel torej podobno vlogo na začetku vesolja
in to pri tvorbi materije. Higgsov bozon je v resnici zelo težko slikovito razložiti,
sploh če nam šola v programu ne ponudi opisa koncepta polj v naravi – zato je nekdanji
angleški minister za znanost William Waldegrave leta 1993 celo podelil nagrado profesorju
Davidu Millerju iz UCL za najboljšo laično razlago Higgsovega bozona. Profesor David Miller
pravi takole. "Higgsovo polje" ima to lastnost - da maso lahko razumemo kot merilo upora
proti gibanju (za manjšo hitrost od svetlobne). "Higgsovo polje" je prof. prikazal kot sobo
fizikov, ki med seboj živahno klepetajo. Soba je torej polna ljudi, v prostor pa vstopi nov
znanstvenik in vznemirja - z vsakim korakom privablja nove občudovalce in vsi močno sodelujejo,
debatirajo z njimi - podpisuje avtograme ... Množica se še kar zbira okrog znanega znanstvenika,
obkrožen z novimi oboževalci, se zato zmeraj težje premika po sobi - v tej analogiji pridobi maso
zaradi "polja" oboževalcev, pri čemer vsak oboževalec deluje kot en sam Higgsov bozon. A v sobo
vstopi še en znanstvenik – tako se pojavita dve množici okoli različnih znanstvenikov, ena velika
in ena majhna. Če torej v sobo vstopi manj priljubljen (uspešen ali manj retorično spreten)
znanstvenik, se zbere okrog njega le majhna množica, nihče ne prosi za pozornost.
Lažje se premika po sobi - po analogiji je njegova interakcija z bozoni manjša,
zato ima manjšo maso.
Pa zaključimo z zanimivimi razmišljani - ki jih je porodila nad vse "muhasta" kvantna mehanika.
Eden takih, za mnoge spornih spoznanj, je verjetnostni opis sveta
kvantnih delcev - izračunamo lahko le verjetnost lege, gibalne količine ... v nekem času t.
Kvantna mehanika je statistična fizika in omogoča le izračun verjetnosti različnih izidov, ne pa točno določenih vrednosti.
Verjetnostni opis sveta
atomskih delcev je Einstein videl le kot začasno rešitev – njegov argument je bil:
»Bog je morda prebrisan, vendar ni zloben.«
Maxu Bornu pa je napisal, da je zagotovo prepričan,
da on (Bog) ne kocka. N. Bohr pa mu je odvrnil, da naj vendar ne ukazuje Bogu. No – (skoraj)
vsi so se sklicevali na Boga ... in vsak je verjel, da je na njegovi strani. Tudi, če ima
Einstein prav (da v ozadju ni kockanja), nam to prav nič ne pomaga pri opisu, meritvah sveta –
zmeraj nas bo spremljala nedoločenost lege in gibalne količine. V astronomiji (v svetu velikih
teles, na večji skali) pa nam postavlja omejitve tako hitrost svetlobe (opazujemo lahko le končno vidno obzorje
vesolja, od koder nas je še dohitela svetloba iz preteklosti), kot tudi ločljivost samih
inštrumentov,
tudi zaradi uklona svetlobe, spet kvantna mehanika ...
V grobem velja preprosta trditev - zmeraj le snov (recimo človek) gleda, opazuje
drugo snov - večinoma prejema odbito valovanje
ali direktno izsevano valovanje od druge snovi. A valovanju se
lahko valovna dolžina premakne zaradi Dopplerjevega pojava ali (in) gravitacijskega premika
(tudi gravitacijskih
valov). Na valovanje vpliva tudi vmesna snov, sipanje, uklon, absorpcija ...
A tisto kar šteje, niso zgolj omejitve (recimo
načelo nedoločenosti, zgolj verjetnostna porazdelitev delcev v prostoru in času), šteje to,
da se zavedamo obnašanja snovi, valovanj, naštetih omejitev. Zakaj? Ker tudi naštete omejitve
nosijo s sabo zelo
dragocene informacije. In prav to znanje, vedenje, zavedanje,
da lahko iz »nepopolnega« sveta potegnemo čim več koristnih informacij
pri iskanju resnice o nas in svetu, vesolju, je ključno.
In že do sedaj smo bili pri iskanju resnice nepričakovano zelo, zelo uspešni
(a zagotovo nas čaka še ogromno presenečenj).
In prav je, da se to res imenitno in skozi stoletja trdo prigarano znanje
prenese na mlade – seveda primarno preko šol (da se nit vedenj in radovednosti iz preteklosti v
bodočnost
ne prekine – kot se je žal že večkrat prekinila po svetu in tudi v Sloveniji).
Iz trenutnih spoznanj in iz zgodovine kvantne mehanike ter same astronomije je razvidno, da ta naš svet, tudi življenje,
tvorijo osnovni kvantni delci po zakonih, ki so nam kdaj težko razumljivi - a so
fiziki bili pri opisu osnovnih delcev narave vendar kar se da slikoviti. Recimo!?
Tako smo recimo gluonom, nosilcem močne jedrske sile, ki veže kvarke v naše sestavne dele (protone, nevtrone),
pripisali lastnost, da posredujejo barvno silo - to je le nomenklatura (lahko bi dali drugačne opise),
pa vendar, če sprejmemo ta opis, se postavlja zelo zanimivo in elementarno vprašanje - a se je vse začelo
z barvami, s svetlobo (" Fiat Lux! ")?
A prav taki kot so ti zakoni, omogočajo prav takšen svet na mali in veliki skali, kot ga živimo.
Človek se rad prepusti iluziji svobodne volje - da sam odloča o svoji usodi - ali res odločamo sami o svoji usodi,
mislih, dejanjih?
Nekaj tega upanja je nekaterim vlil Heisenbergov princip nedoločenosti.
A spet drugi so v njem videli še večji kaos,
ki pa vendar zmeraj uboga vzročne povezave preko množice interakcij,
le da jim, taki kot smo ljudje, ne zmoremo dosledno slediti.
A kombinacij v bioloških sistemih (tudi v naših telesih, glavah, v samih odnosih
med ljudmi, z ostalim svetom)
in v fizikalnih procesih našega okolja, vesolja je toliko,
da prav za vsakega ostane nekaj občutka "svobodne volje".
In pravijo, da ni pomembno ali je nekaj res, recimo trditev, da sami odločamo
o svojem življenju, pomembno je samo, da to verovanje deluje ...
Svoboda po Spinozi pomeni razumevanje nujnosti – modrost, s katero razumemo zakone narave,
in s tem sprejmemo svet takšen, kot je. Tudi Einstein se je večkrat skliceval na Spinozo.
Verjel je, da svobodna volja ne obstaja v klasičnem smislu – človek je del narave
in podrejen njenim zakonitostim.
A že, da se slehernik prebije do teh vprašanj, ni samoumevno - zahteva skupnost
na visoki ravni obratov pri poglobljenem prenosu znanja, vedenja na mlade generacije.
To človeštvu omogoča (žal pa ne nujno posamezniku) vedno nove premike v spoznavanju sveta,
vesolja in s tem tudi samega sebe.
Leto kvantne mehanike je spet tak čas, da pomislimo kako in zakaj smo tako narejeni in smo taki kot
smo - izjemna, a kdaj tudi zelo protislovna mentalna bitja.
Psihološka in kvantna nedoločenost naših izjemnih umskih sposobnosti in
samih dejanj so naša stalnica, ki jo doživljamo vsak dan, tudi v sanjah.
Dejanja sebe in sočloveka delimo na dobra in slaba, koristna in nekoristna, logična in nelogična,
humana in nehumana, na znanstvena
in neznanstvena,
na zakonita in nezakonita, krivične in poštene, legitimna in nelegitimna, duhovna in barbarska ...,
v resnici pa večinoma gledamo (to je nezavedno v nas)
na vse odločitve v luči lastnih koristi, iz lastne perspektive,
saj je taka narava življenja samega - tudi če to zanikamo in večinoma zanikamo, da sploh preživimo (tako
pravijo tudi psihologi in psihiatri, ki se dobro spoznajo na naše možgane) ...
So pa seveda redke izjeme in te izjeme peljejo ta naš "(Veliki) voz" zgodovine naprej - humanizem/znanost - med
njimi je astronomija ena vodilnih (kvantnih) lučk človeškega upanja in smisla.
Kdaj nam je ta realnost doživljanja in urejanja sveta
v ponos in nam daje smisel življenja (to doživljamo kot smisel),
kdaj se pa v tem svetu ne znajdemo, ker ga je v resnici težko razumeti ...,
sploh če družina, šola, družba, "prijatelji" ... odpovejo. A tudi na to moramo biti pripravljeni.
Svet se kdaj obrača na glavo, kar je danes prav, je jutri narobe ter obratno
in tudi to je resnica, bolje realnost tega sveta (tudi na nesrečo in kdaj na srečo v znanosti, zakaj? -
ko so pred 500 leti redki bistri in pogumni astronomi, takrat s strani Luthra poimenovani bedaki,
postavili vso astronomsko znanost na glavo - so jo obrnili ravno prav:).
In tudi kvantna mehanika je pred 100 leti postavila svet klasične fizike na glavo,
determinizem je zamenjala verjetnost, nedoločenost, tudi fizika energijskih skokov,
tukaj so pretvorbe mase v energijo sevanja, gibanja ... in obratno,
dojeli smo, da je naš svet masno skoraj praktično prazen (smo le meglica urnih majčkenih kvarkov) ...
A da ne bo pomote, še zdaleč ni vsaka znanstvena norost tudi genialnost!!!
IN na te čase, ko se vse postavi na glavo, je dobro biti pripravljen ...
Kako?
Tako da poznamo dogodke iz preteklosti in sedanjosti - tudi naravoslovna vedenja nam tukaj lahko še kako pomagajo
in da prenašamo veselje do življenja na bodoče generacije. To je edino kar šteje.
In vendar Leibniz optimistično pravi, da živimo v (na) najboljšem od vseh možnih svetov.
In kako mu lahko oporekamo?
Zorko Vičar
DODATEK
UMERITVENI GRAF

Tabela najizrazitejših Fraunhoferjevih absorpcijskih črt posameznih elementov in širina - tabela spodaj.
|
Oznaka |
izvor(at., mol.) |
valovna dolžina (nm) |
širina črte (nm) |
|
K |
Ca+ |
393,3682 (393,3666) |
2,0253 |
|
H |
Ca+ |
396,8492 (396,8468) |
1,5467 |
| |
Fe |
404,5825 |
0,1174 |
|
h (d
) |
H |
410,1748 (410,1735) |
0,3133 |
|
g |
Ca |
422,6740 (422,6728) |
0,1476 |
|
G |
Ca |
430,7741 |
|
|
G |
Fe |
430,7906 |
|
|
G' (g
) |
H |
434,0475 (434,0465) |
0,2855 |
|
e (ponekod d) |
Fe |
438,3547 (438,3557) |
0,1008 |
| |
Fe |
440,4761 |
0,0898 |
|
D |
Fe |
466,8140 |
|
|
F (b
) |
H |
486,1342 (486,1327) |
0,3680 |
|
c |
Fe |
495,7609 |
|
|
b4 |
Mg |
516,7327 (516,7343) |
0,0935 |
|
b4 |
Fe |
516,7491 |
|
|
b3 |
Fe |
516,8901 |
|
|
b2 |
Mg |
517,2698 (517,2699) |
0,1259 |
|
b1 |
Mg |
518,3619 (518,3618) |
0,1584 |
|
E2 |
Fe |
526,9541 |
|
|
D3 |
He |
587,5618 |
|
|
D2 |
Na |
588,9973 (588,9953) |
0,0752 |
|
D1 |
Na |
589,5940 (589,5923) |
0,0564 |
|
a
|
O2 (atmosfera Zemlje) |
627,6-628,7 |
|
|
C (a
) |
H |
656,2808 (656,2816) |
0,4020 |
|
B |
O2 (atmosfera Zemlje) |
686,7-688,4 |
|
|
A |
O2 (atmosfera Zemlje) |
759,4-762,1 |
|
.