Spodnji tekst je iz:
http://www.fiz.uni-lj.si/astro/mrk99/zgodovina.html
Sončevi mrki skozi zgodovino
Kratek pregled po kulturah
Kitajci
Najstarejši zapis o opazovanju Sončevega mrka najdemo v kitajskem tekstu
Šu Čing. Gre za mrk 22. oktobra 2137 pr.n.št., to je 1400 let pred opazovanji
kateregakoli drugega naroda. V zvezi s tem mrkom je znana zgodba o dvornih
astronomih Hiju in Hoju, ki sta bila predana pijači in nista skrbela za
koledar, kar je bila njuna dolžnost. Tako so se pomešali letni časi in
ko sta pozabila napovedati še Sončev mrk, jih je to stalo glavo. Kitajci
so tesno povezovali dogodke na Zemlji in na nebu in če je šlo kaj narobe,
so za to krivili vladarja. Razumljiv je zato takratni vladarjev ukaz o
opazovanju Sončevih mrkov: če nastopi prezgodaj, je treba astronome pobiti,
če prepozno, ravno tako. Ni znano, da bi kasneje še kak astronom doživel
usodo Hija in Hoja, pa tudi vladarji pred ljudstvom ne prevzemajo več take
odgovornosti.
Stara Kitajska se lahko pohvali tudi z izredno dolgo kontinuirano kroniko.
V Analih Luja, ki jih pripisujejo Konfuciju, so opisana opazovanja 34 Sončevih
mrkov med leti 722 in 481 pr.n.št. Od tega so jih uspeli 32 kronološko
identificirati. Tako so Sončevi mrki dragoceno pomagalo pri natančni dataciji
zgodovinskih dogodkov.
Egipčani
Egipčani so znanih po znanju geometrije. Njihove piramide imajo vse enako
obliko in so obrnjene po straneh neba. Natančno so tudi opazovali nebo,
saj je trenutek v letu, ko je bilo prvič mogoče opaziti Sirij na
jutranjem nebu oznanjal poplave Nila, ki so bile odločilne za poljedelstvo.
Njihov koledar je zato zelo točen, razteza pa se čez vsaj 3000 let. Vedeli
so na primer, da ima leto 365 dni in četrt. Kljub temu pa ne najdemo niti
enega samega zapisa o Sončevem mrku. Presenečenje je še večje, saj so jih
bližnji Babilonci opazovali mnogo. Možna razlaga je, da so bili Egipčani
zelo praktična civilizacija, Sončevi mrki pa brez pomena, saj faraon ni
bil podrejen dogodkom na nebu, ampak je bil on sam bog.
Babilonci
so povezovali dogodke na nebu s tistimi na Zemlji. Bogove so enačili s
telesi Osončja. Zato je razumljivo, da so bili takratni astronomi pravzaprav
astrologi. Da bi napovedali dogodke na Zemlji, so natančno opazovali nebo
in to zapisovali na glinaste tablice. Ko so kasneje preučevali svoje tekoče
zapise s starejšimi, so se iz astrologov spreminjali v astronome. Astronomija
kot znanost ima zato svoje začetke v Babilonu.
Babilonci so zabeležili vse mrke po letu 747 pr.n.št. Natančno so poznali
dolžino leta ter časa, ki ga Luna potrebuje za en obhod okoli Zemlje. Končno
so odkrili tudi periodo Sarosa, ki je odločilna za napovedovanje Sončevih
mrkov. Medsebojni položaji Zemlje, Lune in Sonca se ponovijo po 18 letih
in 10 dneh in 8 urah, torej bo vsakemu mrku čez 18 let sledil naslednji
mrk. Za letošnjim bo naslednji mrk iste Sarosove družine tako nastopil
21. avgusta 2017. Žal dolžina Sarosa ni enaka celemu številu dni. 8 dodatnih
ur pomeni, da ga ne bomo videli iz Evrope, ampak iz Združenih držav Amerike.
Za ponovitev mrka na skoraj istem kraju na Zemlji je treba počakati 3 Sarosove
periode. Za letošnjim bo naslednji mrk iste Sarosove družine v naši bližini,
to je v severni Afriki viden čez 54 let in en mesec, to je 12. septembra
2053.
Znanje o Sarosu se je kasneje preneslo Grkom, ti pa so ga posredovali
Aleksandrijski šoli in Rimljanom.
Pomembno je, da Babilonci sicer niso poznali gravitacijskega zakona
ali nebesne mehanike, do napovedovanja mrkov pa so vseeno prišli na empiričen
način, to je z analizo kronološko točnih zapisov preteklih pojavov. To
je osnova tudi današnji znanstveni metodi. Najprej zgradimo grob model,
za katerega sicer ne razumemo povsem, daje pa uporabne naapovedi. Šele
nato sledi eleganten del, ko ugotovljeno zakonitost uspemo razložiti z
uporabo osnovnih fizikalnih zakonov. V primeru mrkov je bil to Newtonov
gravitacijski zakon.
Grki
Prvi znan astronom je Tales in Mileta, ki mu pripisujejo pravilno napoved
mrka 28. maja 585 pr.n.št. Grki so vedeli, da je Sonce edini vir svetlobe
in da Luna le odbija Sončevo svetlobo. Seveda so poznali periodo
Sarosa, neodvisno od Babiloncev pa so ugotovili različno dolžino letnih
časov (pomlad traja 94, poletje 92, jesen 89 in zima 90 dni) in jo pravilno
razložili z različno oddaljenostjo Zemlje od Sonca. Aristotel je na osnovi
opazovanj Luninih mrkov pravilno sklepal, da je tako kot Luna tudi Zemlja
krogla (senca Zemlje, ki jo v času mrka meče na Luno je ukrivljena) in
določil razmerje njunih velikosti. Hiparh je zmeril tudi razdaljo do Lune
(v enotah Zemljine velikosti). Končno so Aleksandrijci določili Zemljino
velikost in dobili vrednost, ki je bila mnogo točnejša od podatka s katerim
se je Kolumb odpravil na pot proti Indiji (in odkril Ameriko).
Maji
Kot kaže so tudi Maji poznali dolžino Sarosa. To je presenetljivo, saj
se po 54 letih in enem mesecu mrk ne ponovi natančno na istem kraju. Letošnjemu
mrku v Evropi bo denimo čez 54 let sledil mrk v severni Afriki. Torej je
pomembno, da je velikost države določene kulture dovolj velik, da kronisti
lahko zabeležijo dovolj mrkov v isti družini Sarosov in nato odkrijejo
to zakonitost. Za Kitajce ali Asirce in Babilonce to velja, ni pa povsem
jasno, kako so do tega podatka prišli Maji, ki so poseljevali le majhen
teritorij polotoka Jukatan. Možno je, da jim je pomagala srečna okoliščina,
ko so se na Jukatanu zvrstili trije mrki v času približno stotih let.
Klasični mrki v zgodovini
Biblija nedvomno omenja Sončev mrk, ko v Amosu VIII,
9 beremo: "Storil bom, da bo Sonce opoldne zašlo in bo Zemljo na jasen
dan zagrnila tema." Po primerjavi z Babilonskim koledarjem ta mrk danes
z gotovostjo postavimo na 11. januar 689 pr.n.št., ko so v Jeruzalemu opazovali
skoraj popoln Sončev mrk.
Pesnik Arhiloh govori o tem, da je "Zevs, oče
bogov, spremenil poldne v noč in skril Sonce; in ljudi pahnil v strah."
V tem primeru gre za mrk 6. aprila 647 pr.n.št.,
ki je bil z otoka Tasosa, kjer je dalj časa živel Arhiloh, popoln okrog
10. ure dopoldne. To je tako najstarejši točno določen datum v grški
zgodovini.
Najbolj znan klasični mrk je v zvezi
z Lidijci in Medejci. Ti so se že 5 let bojevali in bojna sreča še ni bila
odločena. V šestem letu bojev pa se je, po zapisih Herodota, dan spremenil
v noč. Prihod mrka je na leto natančno napovedal že Tales iz Mileta. Ob
temi sta se vojski brž pobotali, mir pa utrdili s kraljevsko poroko. Gre
za mrk 28. maja 585 pr.n.št.
Križanje lahko povežemo s Sončevim mrkom 24. novembra
leta 29. Več o tem najdete v Humphreys, Colin J. in Waddington, W. G.,
"Dating the Crucifixion", Nature, Vol. 306, No. 5945, p.743-746, 22 December
1983.
Preroka Mohameda lahko povežemo z dvema Sončevima
mrkoma. Rodil se je leta 569/570 n.št., kar vemo po tem, da je bil 24.
novembra 569 viden popolni Sončev mrk. Njegov sin, Ibrahim, pa je umrl
27. januarja 632, na dan popolnega Sončevega
mrka. To so najprej razlagali kot božje znamenje. A Mohamed jih je zavrnil
z besedami "Sonce in Luna sta znaka bogov, njun mrk pa nima povezave z
rojstvom ali smrtjo ljudi". Uveljavitev tega mnenja je bila osnova za zavrnitev
astrologije.
Ob Sončevem mrku leta 1868 so v spektru Sončevih
prominenc odkrili element helij (Joseph Norman Lockyer, 27 let pred njegovim
odkritjem na Zemlji). Leta 1887 pa je avstrijski znanstvenik Theodor von
Oppolzer objavil podrobne izračune vseh mrkov med leti 1208 pr.n.št in
2162 n.št.
Einsteinova splošna teorija relativnosti, ki
je bila predlagana leta 1915, napoveduje, da se položaji zvezd v bližini
Sonca zaradi ukrivljenosti prostora navidezno razmaknejo do 1,75 ločne
sekunde. Meritve položaja zvezd, ki jih je napravil Arthur Eddington ob
Sončevem mrku 29. maja leta 1919 so to napoved
potrdila.
Pripravil T.Z.
Zgornji tekst je iz:
http://www.fiz.uni-lj.si/astro/mrk99/zgodovina.html
Kolumb in Lunin mrk
Sledi še poučna zgodba - sicer o Luninem mrku - kako je Kolumb
uporabil mrk za preživetje sebe in celotne posadke leta 1504 (dodal Z.V.).

Mladi Krištof Kolumb (Christopher Columbus, 1451-1506).
Krištof Kolumb (Christopher Columbus) je svoje zadnje četrto potovanje v "novi svet"
začel leta 1503, pristal je na današnji Jamajki.
Na otoku so doživeli polno hudih preizkušenj. Črvi so načeli njegovo ladjo in
popravljanje je
trajalo tja v leto 1504. Kolumbu je zmanjkovalo hrane. Problem je bil tudi ta, da so Jamajčani
na koncu zavrnili vse
prošnje za dodatno hrano.
Kolumb ni želel, da mornarji stradajo, umrejo. Naredil je nadvse pronicljiv načrt. Iz
navigacijskih tablic je razbral, da bo 29.2.1504 popoln Lunin mrk. Odločil se je, da bo na to
noč imel pogajanja z domačini.
Na srečanju je domačinom povedal, da Bog ni zadovoljen, ker z njim in mornarji ravnajo
tako slabo. Kot znamenje nezadovoljstva, bo Bog vzel Luno. Kmalu po teh besedah se je
začel Lunin mrk, Luna je postajala temnejša in rdečkasta.
To je zelo zaskrbelo Jamajčane, ki mrkov niso znali napovedovati, si jih razlagati, tudi z
opazovanji niso imeli izkušenj. Rotili so Kolumba, da naj vendar vrne Luno in da bodo imeli
na razpolago toliko hrane, kot si je bodo želeli. Kolumb je odgovoril, da se bo moral
pogovoriti z Bogom. Umaknil se je vstran in gledal peščeno uro, da je lahko ocenil čas konca
mrka. Malo pred koncem mrka, se je vrnil k Jamajčanom in napovedal, da jim bo Bog
vendarle vrnil Luno.

Ta in podobni dogodki kažejo, kako moč so imeli in imajo tisti, ki imajo znanje in razumejo
delovanje narave.
Čeprav je "novi svet" že bil odkrit, pa se vendar postavlja vprašanje, kakšen
bi bil današnji svet, če Kolumbu na Jamajki leta 1504 ne bi uspelo ugnati
domačinov s pomočjo Luninega mrka.

Lunin mrk posnet z 200 mm-skim objektivom.
Čas osvetlitve: 1 s; Kodak 200 ISO. Luna je prehajala iz Zemljine
polsence v senco. Posnetek je 21. januarja 2000 naredil Peter Mihor.
Aristotel je že okoli leta 330 pred našim štetjem trdil, da je Zemlja
okrogla, ker ima Zemljina senca ob Luninih mrkih okrogel obris.
Če zraven Lune narišemo krog, ki v razmerju ustreza dimenziji Zemlje
(Rz/Rl=3,7), potem opazimo, da se ukrivljenost Zemlje po pričakovanjih
kar dobro ujema s senco Zemlje na Luni. Seveda je potrebno upoštevati,
da senca Zemlje nima čisto enakih dimenzij kot sam planet Zemlja,
in da ukrivljenost sence na okrogli Luni ni enaka kot na ravni ploskvi.
To je le groba ocena razmerij.
Nekoliko natančneje in z boljšo metodo sta
razmerje Zemlja-Luna določila že v antični Grčiji Aristarh (živel je okoli
leta 270 pr. n. š) in kasneje Hiparh. Poglejmo Hiparhov premislek. Hiparh
je ugotovil, da v Zemljino senco lahko postavimo približno 8/3 Lun
(Luninih premerov). Kako je to ugotovil? Luna se med zvezdami giblje s
kotno hitrostjo približno 0.5 ločne stopinje na uro (30'). Hiparh je tudi
izmeril, da Luna potuje čez sredino Zemljine sence od začetka vhoda v
senco pa do začetka izhoda iz sence 8/3h. Če privzamemo za kotni premer
Lune 30', [ (8/3)*30' = 80' ] potem je kotni premer Zemljine sence 2β=80' in je razmerje med
kotoma Zemljine sence in Lune 80'/30'=8/3. To pa ni vse. V antiki so že
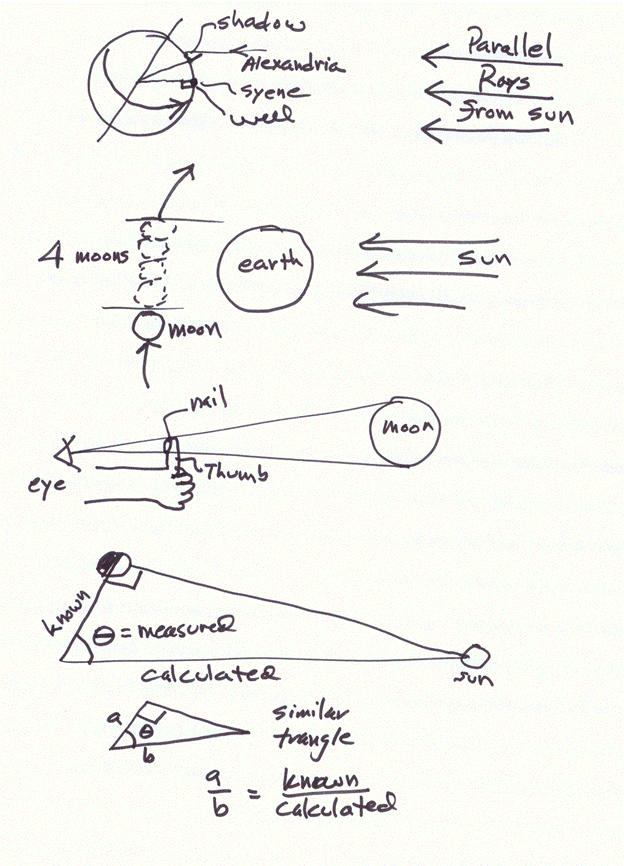
poznali polmer Zemlje, ki ga je določil Eratosten s pomočjo razdalje med
Aleksandrijo in Sieno (Asuanom) in vpadnih kotov Sončnih žarkov. V Sieni
je bil ta kot 0 stopinj glede na navpičnico, v Aleksandriji pa 7,2 stopinje.
Do te nadvse pronicljive rešitve je prišel, ko je izvedel, da namreč na
določen dan v Sieni padajo žarki v studenec navpično (Sonce je v zenitu),
torej ne delajo sence. Vrnimo se k mrku. Če bi torej poznali kot (2Pl)
pod katerim bi videli Zemljo z Lune, bi lahko izračunali razdaljo med
telesoma in polmer Lune. To je naredil Hiparh. Če pogledamo spodnjo sliko,
lahko iz nje razberemo, da med koti
α, β, Ps in Pl
velja zveza: α+β=Ps+Pl.
Kot β je 40' (določen je s pomočjo trajanja mrka),
α pa je približno kar
enak polovici zornega kota Sonca (15'). Danes vemo, da je kot Ps precej
manjši od vsote
α+β,
saj je premer Sonca približno 109 krat večji od
Zemljinega, hkrati pa je Sonce zelo daleč glede na razdaljo Zemlja-Luna.
Hiparh tega sicer ni mogel verodostojno dokazati
(pri računu astronomske
enote - razdalja Zemlja, Sonce -
se je pojavila velika napaka), a njegova domneva o velikosti kota Ps
je bila pravilna. Ker je torej kot Ps zelo majhen (
Ps << α+β)
v primerjavi z
α+β, ga
lahko zanemarimo, končni izraz za
Pl =α+β=55'.
Ker so koti majhni, velja: dl=Rz/Pl.
Kot Pl=55' moramo podati v radianih; rezultat je, razdalja Zemlja-Luna
dl=62Rz.
Rezultat je presenetljivo točen. Zaradi majhnih kotov velja tudi
razmerje: Rz/(4/3(2Rl))=Pl/β,
in končno dobimo za razmerje med polmerom Zemlje in Lune
vrednost: Rz/Rl=11/3=3,7.
Podatki za antiko in današnji podatki:
Antika Današnja vrednost
Rz=6247 km Rz=6378 km
Rl=3/11Rz=1700 km Rl=1738 km
dl=62*Rz=387000 km dl=384400 km (razdalja med Luno in Zemljo)
V antiki so torej preko Luninih mrkov dokaj dobro poznali
(izračunali) podatke o
dimenzijah med Zemljo in Luno, podatki o Soncu pa so bili nekoliko
slabše ocenjeni (razen Eratosten bi se naj zelo približal pravilni vrednosti).
To so bile tako rekoč prve ocene o tem, kako daleč so
pravzaprav vesoljska telesa.
Zorko Vičar
POVZETEK:

Če pogledamo zgornjo sliko,
lahko iz nje razberemo, da med koti
α, β, Ps in Pl
velja zveza: α+β=Ps+Pl.
Luna prepotuje 0.5 ločne stopinje na uro (30'), med mrkom potuje 8h/3 v senci in
opise kot 80'=(8/3)*30'.
Rz/Rl=3,7 = razmerje med kotoma Zemljine sence in Lune 80'/30'=8/3.
Kot β je 40' (določen je s pomočjo trajanja mrka),
α pa je približno kar
enak polovici zornega kota Sonca (15'). Danes vemo, da je kot Ps precej
manjši od vsote
α+β,
saj je premer Sonca približno 109 krat večji od
Zemljinega, hkrati pa je Sonce zelo daleč glede na razdaljo Zemlja-Luna.
Hiparh tega sicer ni mogel dokazati, a njegova domneva o velikosti kota Ps
je bila pravilna. Ker je torej kot Ps zelo majhen (
Ps << α+β)
v primerjavi z
α+β, ga
lahko zanemarimo,
končni izraz za
Pl =α+β=55'.
Ker so koti majhni, velja: dl=Rz/Pl.
Kot Pl=55' moramo podati v radianih; rezultat je, razdalja Zemlja-Luna
dl=62Rz.
Polmer Zemlje, je določil Eratosten s pomočjo razdalje med
Aleksandrijo in Sieno (Asuanom) in vpadnih kotov Sončnih žarkov.
Dodatek, vir 1:
http://www.physics.unlv.edu/~lenz/PHYS%20120.S09/history.htm
Aristarchus had used the following geometrical argument to deduce
the ratio of the distance of the moon from earth to the distance
of sun from earth. He did this by noting that when half the moon
was lit by light from the sun, the earth, moon, sun system formed
a right triangle. He measured the angle between Earth and Sun
and got 87° (the actual angle is closer to 89.85°)
and deduced that the sun was 20 times further from earth than the
moon. The actual value is about 400 times further or 80,000,000
miles.
Once the distance between earth and moon were known, it was easy
to estimate the diameter of the sun since during a solar eclipse,
the moon’s apparent size is just about the same as the apparent
size of the sun, that is they subtend the same angle in the sky.
Therefore the ratio of (moon’s diameter)/(sun’s diameter) =
(distance between earth-moon)/(distance between earth-sun).
Vir 2:
http://www.astro.umontreal.ca/~paulchar/grps/histoire/newsite/sp/great_moments_e.html
ca. 250 BC: The distance to the Sun
The first mathematically-based attempt at determining the
Sun-Earth distance is due to Aristarchus of Samos (ca. 310-230 BC).
The procedure followed by Aristarchus is illustrated on the diagram
below; form a triangle by connecting the Earth (E), Sun (S) and
Moon (M). At the first or third Moon quarter, the triangle so
described in a right-angle triangle (a=90°). The angle b can be
measured by an observer on Earth, which then allows the angle c
to be computed (c=90-b when a=90°). The ratio of the Earth-Moon
segment (EM) to the Earth-Sun segment (ES) is by definition equal
to sin(c) (in modern trigonometric parlance; Aristarchus expressed
this differently).
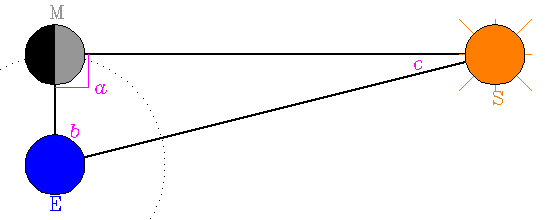
Aristarchus' geometric construction used to estimate the distance
to the Sun. The Earth-Sun-Moon triangle and sizes are not drawn to
scale.
While sound in theory, in practice this procedure is highly
inaccurate in the Earth/Sun/Moon case; this is because EM is
much smaller than ES, implying that b is very close to 90°,
so that c is in turn very small. This has the consequence that
a small measurement error on b translates in a large variation
in the ratio EM/ES (again in modern parlance, a measurement error
db is amplified by a factor 1/(sin c)^2, which is large when c is
very small). Aristarchus measured b=87°, while the true value is
in fact 89° 50 minutes. This may seem a small error, but because
of the large error amplification Aristarchus' value leads
to EM/ES=19, instead of the true value EM/ES=397. Nonetheless, Aristarchus' calculation was the first
to mathematically set the spatial scale of the cosmos.
Mrki skozi zgodovino
- Kitajci,
Egipčani,
Babilonci,
Grki,
Maji,
KLASIČNI MRKI V ZGODOVINI,
Biblija,
Arhiloh,
Lidijci in Medejci (Tales),
Križanje,
Prerok Mohamed,
Odkritje helija,
Kolumb in mrk, ...
Do sedaj je to stran obiskalo
 ljudi.
ljudi.
*
Glej tudi stran http://www.nosun.org/
* Soncni mrki v zgodovini

Nastanek Sončevega in Luninega mrka:
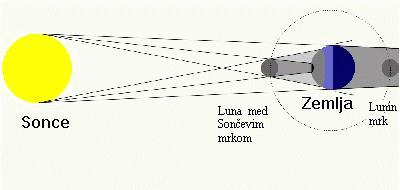
 Oglejte si tudi
prostorsko sliko in
Oglejte si tudi
prostorsko sliko in
animaciji nastanka:
-animacija Luninega mrka
-animacija Sončevega mrka
Kaj vse so nam odkrili Sončevi mrki?
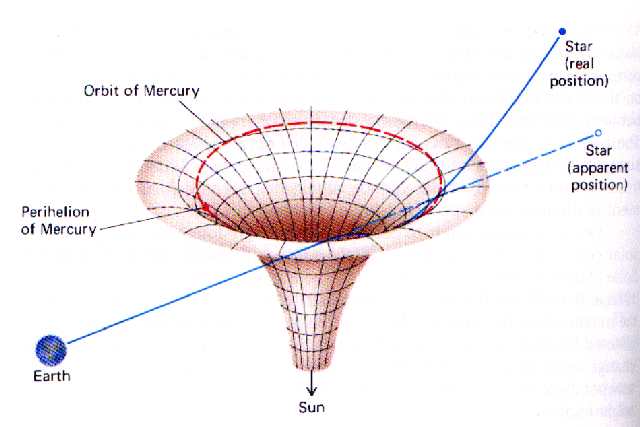


Razlaga animacije
Odklon svetlobe v gravitacijskem polju. Gravitacijsko polje
Sonca odkloni curek svetlobe z zvezde. Pri popolnem Sončevem
mrku, se zvezde, ki bi jih sicer videli tik ob Sončevem robu, zdijo
premaknjene proč od Sonca za 1,75 ločne sekunde. Opazovalec, ki ujame
žarek v svoj teleskop, vidi zvezdo iz katere prihaja
žarek na drugem mestu kot je v resnici.
Prva merjenja leta 1919 so v okviru dosegljive natančnosti potrdila napoved
Einsteinove splošne teorije relativnosti. Danes z radijskimi teleskopi
merijo odklon valov s treh kvazarjev in meritve so na del odstotka
natančne. Gravitacija (Einstein pa pravi, da masa in druge vrste energij ukrivljajo
prostor, ki je vir nelinearnega, pospešenega gibanja) torej vpliva na svetlobo podobno kot na masne delce,
recimo na kamen, ki ga vržemo poševno v zrak in se giblje krivo, po paraboli.
Animacijo je naredil Peter Mihor.

Kako Sonce spremeni sliko zvezdnega ozadja - po Einsteinu ukrivi prostor-čas -
efek se da spremljati recimo med Sončevim mrkom - a premiki so majhni!!!
Spekter in sestava Sonca.
Sončev svetlobni spekter je pri
določenih barvah
(valovnih dolžinah) temnejši.

Temnejše dele imenujemo Fraunhoferjeve
absorbcijske črte in so posledica absorpcije svetlobe, ki jo povzročajo
atomi in molekule v atmosferi Sonca (fotosferi). Ker pripadajo vsakemu
elementu
točno določene absorbcijske črte (barve), lahko iz lege črt v spektru
določimo
kemijsko sestavo zvezde. Spekter pa tudi pomaga pri določanju temperature
zvezd,
starosti zvezd, mase zvezd, hitrosti plinov, hitrosti zvezd ... in zato
zvezde delimo v spektralne tipe.
Glej tudi poglavje
SPEKTROGRAFIJA in
animacijo
nastanka črt.

Emisijski spekter atmosfere (kromosfere) Sonca, s pomočjo katerega
so odgkrili helij še preden so ga detektirali na Zemlji.
Tak spekter je moč posneti (v le nekaj sekundah) med Sončevim mrkom.
Nazaj na domačo
stran.









 Oglejte si tudi
prostorsko sliko in
Oglejte si tudi
prostorsko sliko in 





