Deseto poglavje
ISAAC NEWTON IN NJEGOVO DELO

Galileijeva, Keplerjeva in Huyghensova dela so bila stopnice, po katerih se je astronomija povzpela do veličastnega Newtonovega dognanja. Da bi ga popolnoma razumeli, bomo pospremili rojstvo in razvoj tega dognanja skozi življenje moža, ki nam ga je ustvaril. Pri tem se ne bomo oddaljili od glavnega predmeta pričujočega dela, kajti Newtonovo življenje, posvečeno izključno znanosti, je bilo tiho in mirno, brez velikih doživetij, čeprav se je rodil med angleško revolucijo, borbo med Karlorn I. in Cromwellovimi independenti in preživel šest vladarjev. Vse Newtonovo življenje je potekalo v treh angleških mestih in njihovi najbližnju okolici, v mestecu Granthamu v lincolnshirski grofiji, v vseučiliškem mestu Cambridgeu in v prestolnici države Londonu.

Kakšnih deset kilometrov južno od Granthama je majhen kraj Woolsthorpe. Tu so živeli Newtonovi predniki, mali farmarji, na svojem posestvu, v skromni, vendar pa za tiste čase udobni enonadstropni hiši. V njej se je rodil tudi Isaac Newton (4. I. 1643 do 31. III. 1727) na božični dan, t. j. 25. decembra 1642 po starem koledarju, ki je bil tedaj, pa tudi vse njegovo življenje na Angleškem v veljavi in uporabi. Newtonov oče, tudi Isaac, je umrl, preden se je rodil njegov edinec, ki je bil kakor Kepler sedemmesečni nedonošenček. Novorojenček je bil tako slaboten, da ni nihče, kdor ga je videl, verjel, da bo ostal pri življenju, še manj pa, da bo doživel 85. leto. Ko mu je bilo tri leta, se je njegova mati znova omožila in vzela duhovnika Barnaba Smitha iz bližnjega kraja, svojega prvorojenca pa je prepustila v varstvo svoji materi. Ko je drugič ovdovela, se je z otroki iz drugega zakona, dvema hčerkama in sinčkom, I. 1656 vrnila v Woolsthorpe. Medtem je njen najstarejši sin v bližnji vasi končal osnovno šolo, nato pa, od leta 1654 do 1657, obiskoval mkraljevsko šolo" v Granthamu. Leta 1658 ga je mati pridržala v Woolsthorpu, da bi ji pomagal gospodariti. To pa mu nikakor ni šlo izpod rok, kajti v Granthamu, kjer je stanoval v hiši lekarnarja Clarka, je rasel v družbi učenih ljudi, doktorjev, advokatov in duhovnikov, in v njem se je vzbudila Ijubezen do znanosti in hrepenenje po (128, 129) višji izobrazbi. Zato ga je njegov ujec, duhovnik William Ayscough poslal znova v Grantham, da bi se tam pripravil na univerzitetni študij.

Junija 1661 je bil Newton sprejet v Trinity College umiverze v Cambridgeu, kjer je bil tudi njegov ujec William končal svoj študij in obdržal prijateljske zveze z nekaterimi izmed tamkajšnjih profesorjev. S svojimi vrlinami in nenavadno nadarjenostjo je Newton vzbudil pozornost učiteljev, posebno profesorja Barrowa, in dosegel l. 1665 stopnjo bakalarja. Tedaj je moral šolanje prekiniti zaradi kuge, ki je od leta 1664' do 1667 razsajala po Angleškem in samo v Londonu pokosila okrog trideset tisoč ljudi. Na cambridgeski univerzi so nehali predavati, Newton pa je avgusta 1665 odšel v Woolsthorpe, kjer je skoraj nepretrgoma ostal do 25. marca 1667. Tako smo prišli do najvažnejšega razdobja v Newtonovem znanscvenem razvoju; pri tem razdobju se moramo dlje pomuditi.

Newton je prišel iz mračnih soban Trinity Collegea, iz šolskega reda i;n ozkih šolskih klopi, bled im utrujen v taplo naročje svaje rodbine, na čisti zrak in širne planjave svojega rojstnega kraja. Z izpitom za bakalarja je bilo končano prvo obdobje njegovega šolanja na univerzi; ta čas je izpopolnil svoje znanje latinščine, ki se je je učil že v Granthamu, tako da je lahko pisal v gladki latinščini, v svojem jedrnatem in natančnem znanstvenem slogu. Proučil .je Evklida, ki mu je postal vzor znanstvenega razmišljanja in razlage, seznanil se je s Kopernikovim sistemom, s trigonometrijo in drugimi novejšimi pridobitvami astronomije. Njegov učitelj Isaac Barrow (1630-1677), ki je dobro poznal grški jezik in izdal Evklidova, Arhimedova in Apolonijeva dela, ga je seznanil s klasiki grške znanosti, s Keplerjem in njegovo optiko in s svojim lastnim delom na tem področju. Tako je imel Newton že takrat dober pregled čez matematično znanje svojega časa. To je bilo znanje , ki ga je imel od drugih, učenje za izpit pa je bilo, kakor je še dandanes: človek si prisvaja tuje misli, misli s tujo glavo in vestno ponavlja tuje besede. V Woolsthorpu je začel Newton samostojno misliti ter strogo presojati svoje učitelje in predhodnike v znanosti. Ko je bral njihove knjige, je kmalu začutil, kako zelo jih umstveno prekaša. To pa ni pomenilo, da precenjuje sam sebe, temveč le, da se zaveda svojih velikanskih duševnih zmožnosti. Newton je bil velik henij in zato je dobro vedel, da svoje vrstnike in predhodnike visoko nadkriljuje, da so njegovi možgani v primeri z njihovimi mnogo popolneiši, njegov duhovni pogled globlji, njegova logika nezmotljivejša in njegove misli bolj krilate. Ob njihovih knjigah se je večkrat čudil, da so se sicer slavni možje zaman trudili najti tisto, kar je sam spoznal na prvi pogled.

Vse to je Newton čutil, ko se je v rojstnem kraju poglobil v matematiko in fizik,o ter z bistrim pogledom objel njune dotedanje prido hime, Bilo jih je precej in zelo so poglobile in razširile dognanja starih klasikov matematike. Matematika je bila že takrat znatno izpopolnila svoj jezik. Fibonacci, imenovan Leonardo Pizanski (1180-1250), je prinesel v Italijo indijsko - arabski način pisanja števil. Ko se je z uporaho črk za označevanje občih števil razvila algebra in ko so uvedli simbolične znake za njene operacije, so imeli na razpolago nepričakovano uporaben matematični jezik. Analitična geometrija, ki jo je osnoval Descartes, je povezala aritmetiko in geometrijo in omogočila računsko reševanje geometrijskih problemov. Analitična geometrija je neskončno rars'irila področje geometrije: Grki so poznali samo omejeno število geom'etrijskih krivulj, zdaj pa je vsaka poljubna enačba med koordinatama x in y pomenila po eno ravninsko krivuljo, tako da jih je bilo odslej neskončno mnogo. Če uporabimo tri koordinate, velja nekaj podobnega tudi za krivulje in ploskve v prostoru.

V dobi, o kateri govorimo, so Newtonovi vrstniki, pa tudi predhodniki, Cavalieri (1598-1647), Fermat (1601-1665), Roberval (1602 do 1675), dalje New.tonova rajaki, profesor oxfordske univerze Wallis (1616-1703), profesor edinburške univerze Gregory (1638-1675) in Newtonov učitelj Barrow začeli s svojimi deli posegatii na tisto področje matematike, ki se zdaj imenuje višja matematika. Ko so proučevali različ;ne k,rivulje, so ugotawljali njihove tangante, asimptote, obračajne m ekstremne točke ter računali doliine njihovih lokov in ploščine likov, ki jih omejujejo. Da bi rešili te probleme, so iznašli posamezne račune, ki pa so bili za razne krivulje različni in torej niso bili splošno velja vni in uporabljivi za vsako krivuljo. Tak splošno veljaven račutt je našel šele Newton, ne da bi mu bilo treba dolgo in naporno razmišljati.

Že v Woolsthorpu, kjer je ta razmišljanja 16. novembra l. 1665 prvikrat zabeležil, je spoznal, da gre pri vseh omenjenih problemih za dve osnovni nalogi. V kratki razlagi te Newtonove ideje bomo uporabili izraze in znake, ki jih danes uporabljamo v matematiki, ki pa se od Newtonovih nekoliko razlikujejo.

V našem sedanjem jeziku nam enačba
y = f (x)

pove, da je y funkcija neodvisne spremenljivke x. Če imamo x za absciso, y pa za ordinato točke, nam zgornja enačba predstavlja neko ravninsko krivuljo, geometrijsko podoao funkcije f (x). Newton svojih prvih razglabljanj ni zasnoval na takšnih geometrijskih predstavah, ampak na pojmih nauka o gibanju; tega nauka namreč ni razlikoval od geometrije, temveč je imel geometrijo za sestavni del mehanike. V mehaniki je neodvisna spremenljivka čas t. Kakor bomo videli iz vsega njegovega dela, je bil Newton predvsem naravoslovec. V naravi pa je (130,131) ćas res tista neodvisna spremenljivka, po kateri ugotavljamo zaporednost vseh sprememb in pojavov okrog nas na zemlji in na nebu. Čas teče nepretrgoma in nenehno in kot neodvisno spremenljivko ga uporabljamo pri opisovanju vseh naravnih pojavov. Opisati te pojave se pravi izraziti jih kot funkcije časa.

Oglejmo si torej enega izmed najpreprostejših naravnih pojavov , premočrtno gibanje materialne točke. Če z y zaznamujemo pot, ki jo napravi točka v času t = x, lahko enakomerno gibanje take točke izrazimo z obrazcem

y=vx,

kjer pomeni v stalno hitrost tega enakomernega gibanja. Če pa je gibamje, kakor pri proetem padu, enakomerno popešeno, je pot y takole advisna ad časa

y= gx²/2

kjer je g paspešek prostega pada. To je ugotovil že Galilei.

Vrnimo se zdaj k splošnemu primeru, kjer je ta odvisnost podana s katero koli f unkcijo f(x), o kateri predpostavljamo samo, da je zvezna. Potem je očitno tole. Pot, ki jo napravi točka v času x, t. j. njena oddaljenost od začetne lege, je enaka f(x). V času x+h, ki se razlikuje od prejšnjega za h, pa je ta oddaljenost f(x + h). V časovnem prirastku h je točka naredila pot f(x + h) - f(x). Povprečna hitrost gibajoče se točke v časovnem intervalu h je torej

(f(x + h) - f(x))/h

saj dobimo povprečno hitrost, če pot delimo s časom, ki je potreben zanjo. Če postavimo v zgornji izraz za h razne vrednosti, dobimo razne vrednosti hitrosti. Predpostavili smo, da se točka giblje zvezno, sicer pa se lahko giblje poljubno. Zato se bo tudi njena hitrost od trenutka do trenutka spreminjala; tudi te spremembe naj bodo zvezne, brez skokov. Kaj pa je potem dejanska hitrost točke v poljubnem trenutku x in kako jo bomo izračunali, ugotovili in izmerili? Ko se je ustavil ob tem vprašanju, je Newton zaslutil, da dobimo to hitrost, če si mislimo, da v gornjem ulomku interval h skrajšujemo, dokler ne izgine. To se zdi na prvi pogled protislovno in nesmiselno, kajti če v gornjem ulomku postavimo h = 0, sta števec in imenovalec hkrati nič in kaj potem? Newtona to ni ostrašilo. Vedel je, da vrednost ulomka ni odvisna od velikosti števca in imenovalca in da ju lahko delimo, ne da bi spremenili vrednost ulomka, s katerim koli, še tako velikim številom, da ju lahko torej zmanjšamo, kolikor hočemo. To svoje sklepanje je Newton verjetno uporabil tudi ob navedenih konkretnih prablemih Galileijeve mehanike. Storimo to tudi mi.

Pri prvem izmed navedenih problemov, kjer je bila

f(x) = vx

pri čemer je v konstanta, dobimo, če vstavimo v gornji obrazec

(f(x + h) - f(x))/h = (v(x + h) - vx)/h =v

torej stalno hitrost enakomernega gibanja.
Pri drugem problemu, kjer je bila

f(x)= px²/2
dobimo

(f(x + h) - f (x))/h = (p/2)( (x + h)² - x²) = (p/2)(2hx + h²) = px+ph/2

Če tukaj vstavimo h = 0, dobimo, da je hitrost pospešenega gibanja px, kar je ugotovil tudi Galilei.

Nato je Newton svojo splošno metodo uporabil tudi pri drugih najrazličnejših algebrajskih funkcijah y = f(x) in vedno uspel. Rezultat, svojega postopka je imenoval fluksijo in jo označeval z y', t. j. nad y je postavil piko [pozor - v html-ju bomo postavili namesto pike ']. V našem sedanjem matematičnem jeziku lahko Newtonovo operacijo izrazimo takole

y'=lim (f(x + h) - f(x))/h
h --> 0

to pa je osnovni obrazec diferencialnega računa. Dandanes pišemo namesto y'=dy/dx ali f'(x); tudi ne imenujemo te količine fluksijo, temveč, diferencialni kvocient ali odvod. Toda to so samo različni načini pisanja in različna imena. Sicer pa se Newtonov zelo prikladni način označevanja odvoda s piko uporablja danes v vektorski analizi, kadar gre za časovni odvod, na kakršnega je mislil Newton pri svojih prvih korakih na področju višje matematike.

Ko je tako s foronomijskimi razmišljanji prišel do pojma odvoda, ga je Newton uporabil tudi pri reševanju geometrijskih problemov. Če pomeni x absciso, y pa ordinato poljubne točke ravniske krivulj y = f(x), potem ni težko sprevideti, da nam količnik

(f(x + h) - f (x))/h

(132,133)

pomeni tangens kota, ki ga oklepata abscisna os in sekanta skozi točki y = f(x) in y = f(x + h) te krivulje. Zmanjšujmo h, dokler ne izgine. Tedaj preide sekanta v tangento krivulje v točki y = f(x). Zato pomeni f'(x) tanges kota med to tangento in abscisno osjo. Tako je Newton s čisto splošnim pravilom rešil tako tangentni problem kakor tudi druge probleme analitične geometrije. Če ima na primer ordinata y = f(x) v neki točki krivulje x, y maksimum ali minimum, je tangema v tisti točki vzporedna z abscisno osjo, odvod f'(x) pa je nič. Zato je lahko Newton s svojo metodo reševal probleme maksimuma in minimuma. Posrečilo pa se mu je tudi ugotoviti krivinski polmer v poljubni točki krivulje, ker je odkril, da je tudi ta polmer v bistvu odvod.

Hkrati, morda pa že prej, je Newton odkril še nekaj zelo pomembnega. Najhitreje bomo to razumeli, če bomo spet uporabili označbe, ki jih zdaj uporabljamo v višjii matematiki. Pač pa je priložena slika vzeta iz Newtonovih del.

Slika 27

Tu je poljubno načrtana ravninska krivulja ADB, ki v točki A seka abscisno os Ab. Izberimo si točko A za začetek koordinatnega sistema in vzemimo, da je

y = f(x) emačba krivuSje ADd. Potem je seveda
pri x=0 y=0.

Ploščino F(x) lika, ki ga omejujejo krivulja AD, ordinata DB = y in abscisa AB = x izražamo dandanes s temle integralom

F(x)=₀ò^xydx

Tudi ta ploščina je funkcija spremenljivke x, kakor smo zapisali. Poiščimo njen odvod! Najdemo ga, če izračunamo mejno vrednost količnika

(F(x+h)-F(x))/h
zah=0.

Naj nam na priloženi sliki daljica Bb pomeni prirastek h, ki je zapisan v gornjem količniku. Potem nam F(x + h) na zgornji sliki pomeni ploščino Abd DA, F(x) pa, kakor smo že rekli, ploščiano ABDA. Zato je števec zgornjega ulomka ploščinski element DF, ki je na sliki upodobljen kot lik BbdDB. Spremenimo ta lik, ki je zgoraj omejen z lokom Dd naše krivulje, v pravokotnik BbHKB z osnovnico Bb = h in višino BK = b. Potem je odvod F'(x) menja vrednost količnika

hb/h = b

če gre h proti nič. Očitno je, da se v tem primeru daljica b = KB približuje daljici BD = y = F'(x). Zato je

F'(x) = y = f(x)
Funkcija F(x) je torej tista funkcija, katere odvod je f(x).

Tako je prišel Newton do osnovnega stavka integralnega računa: Ugotavljanju funkcije F(x), ki jo je Newton imenoval fluento, pravimo zdaj integriranje. Integriranje je diferenciranju nasprotna operacija, kakor je dokazal Newton z gornjim sklepanjem. Z integriranjem se rešujejo razni geometrijski problemi. Kakor vidimo iz prejšnjih razglabljanj, se daju z integriranjem izračunati ploščine s krivuljami omejenih likov. Na tem problemu je Newton preizkusil svoje novo orodje, potem pa se je lotil tudi drugih nalog, tako računanja krivuljčnih lokov in računanja prostornin teles, ki jih obdajajo geometrijsko določene površine. Pri tem ni imel na razpolago popolnega matematičnega jezika, ki ga uporabljamo zdaj, pa tudi njegova razmiišljanja o mejnih prehodih in o drugih na novo nastalih pojmih niso bila vedno dovolj natančna. Potrebna so bila desetletja in stoletja, da so vse to dosegli. Zato pa je Newton z nedosegljivo intuicijo začutil in opazil vedno tisto, kar je bistveno in načelno. Tako je s svojiun fluksijskim računom, kakor ga je sam (134, 135) imenoval, sezidal temelj infinitezimalnega računa. Vse to je v glavnem naredil že, ko se je mudil v Woolsthorpu.

Skoraj nerazumljivo je, da je mladenič triindvajsetih let s svojim miselnim pogledom prodrl mnogo dalje kakor vsi njegovi vrstniki, ki so se ukvarjali z istimi problemi. Še bolj čudno pa je, da je Newton svoje velike izsledke zanemaril in se lotil drugih problemov. Že spomladi leta 1666 se je ukvarjal s čisto drugimi vprašanji.

Newtonov učitelj Barrow se je ukvarjal z optiko in predaval o njej, leta 1669 pa je bilo pripravljeno za tisk njegovo delo "Lectiones opticae"; nastalo je iz njegovih predavanj in izslo ob Newtonovem sodelovanju leta 1674. V tej razpravi je Barrow nadaljeval Keplerjevo delo in izpopolnil teorijo o lečah, toda kakor vsi njegovi vrstniki je imel tudi on čudne nazore o svetlobi. Nihče ni znal pravilno pojasmti, kako nastanejo mavrične barve, če gre sončna svetloba skozi prizmo. Mislili so, da nastane ta pojav zato, ker se soncna svetloba zgosca, ko gre skozi prizmo; ker pa vsi žarki nimajo enako dolge poti, se zgoste eni bolj, drugi manj. Zato so imeli rdeno barvo za najbolj zgosčeno, vijolično pa za najbolj razredčeno sončno svetlobo.

S to razlago pa Newton ni bil zadovoljen. Spoznal je, da se da vprašanje pravilno rešiti samo s poskusi. In odločil se je zanje. Bil je zelo spreten. Še ko se je učil v Granthamu, je naredil v hiši lekarnarja Clarka uro na vodni pogon; voda je kapljala iz majhne odprtmem enakomerno premikala kazalce. V Woolsthorpu je sam naredil zeio spretno sestavljeno in mojstrsko izdelano sončno uro in jo pritrdil na 'užni zid domače hiše. Po njegovi smrti so to uro hkrati s kamnom, na katerem je bila pritrjena, sneli in odnesli v London, v knjižnico Kra1'evske a društva, kjer je še dandanes. Ker je bil tako spreten, je Newton lahko izdelal tudi pripravo za optične poskuse.

Glavni del te Newtonove priprave je bila tristranična steklena prizma. Newton je znal dobro brusiti steklo in je prizmo geometrijsko pravilno izoblikoval. Potem je v svoji proti jugu obrnjeni sobi zaprl oknice in izvrtal vanje samo okroglo luknjico. Snop soncne svetlobe, ki je skozi to luknjico sijal v zatemnjeno sobo, je spustil skozi prizmo in ga prestregel na navpičnem belem zaslonu za njo. Na zaslonu se je prikazal pisan trak, v katerem se se dale dobro razločevati vse mavrične barve, rdeča, rumena, zelena, modra in vijolična. Ta trak je Newton imenoval spekter sončne svetlobe in tako mu pravimo še dandanes.

Da bi ugotovil, kako in zakaj nastane spekter, je Newton preluknjal zaslon, s katerim ga je prestregel, tako da so sijali skozi odprtino samo žarki določene barve, bodisi rdeče, bodisi rumene, zelene, modre ali vijolične. To enobarvno svetlobo je usmeril skozi drugo prizmo za zaslonom in jo prestregel z drugim zaslonom. Na tem zaslonu se ni prikazal spekter, temveč samo lisa iste barve, kakršno je imel svetlobni žarek, ki je sijal skozi luknjico v prvem zaslonu. Ta barva je bila torej elementarna, ker se ni dala več razstaviti. Druga prizma je svetlobni žarek pač prelomila, ne pa razklonila spet v druge sestavine.

Newton je natančno izmeril, kako prizma lomi posamezne vrste sončne svetlobe. Pokazalo se je, da je lomljivost posameznih vrst svetlobe različna; najmanj se lomi rdeča, najbolj pa vijolična. Newtonove raziskave so pokazale, da nastane spekter samo zato, ker se posamezni elementarni žarki sončne svetlobe različno lomijo, nikakor pa ne zato, ker so njihove poti skozi prizmo različno dolge.

Newton je torej s poskusi dognal, da je sončna svetloba sestavijena iz raznobarvnih žarkov, ki se različno lomijo. To je vzrok, zakaj prizma razkloni sončno svetlobo v elementarne žarke in barve, ki jih vidimo v spektru.

Ko je tako analiziral sončno svetlobo, jo je hotel Newton še sintetizirati; šel je torej po isti poti, kakor sto let pozneje Lavoisier pri svojih epohalnih kemijskih raziskovanjih. Ne vemo prav, ali je Newton tudi te poskuse končal že v Woolsthorpu ali šele po vrnitvi v Cambridge; za trdno je znano le, da jih je napravil v Cambridgeu z boljšo pripravo in jih tako vsaj preveril. Sicer pa to vprašanje ni važno in zato o njem ne bomo več govorili. Pač pa bomo kratko opisali še te njegove raziskave.

Newton je hotel s poskusi dognati, zakaj je sončna svetloba bela. Sklepal je, da njena belina ni nič drugega kakor mešanica vseh mavričnih barv. Da bi to nazorno dokazal, je sončno svetlobo, ki jo je razklonila njegova prizma, spet zbral z zbiralno lečo in tako spet dobil belo, barvo. Učinek je bil isti, če je lečo nadomestil s prizmo, popolnoma enako prvi, obrnjeno pa ravno narobe. Naposled je dognal, da za ta dokaz ne potrebuje ne druge prizme, ne zbiralne leče. Če je namreč prvo prizmo sukal okrog osi, vzporedne z lomečim robom, se je spekter na zaslonu premikat gor in dol. Če pa se je prizma hitro vrtela, so se na istem mestu zaslona menjavale vse mavrične barve. Ko je gledal v tisto mesto zaslona, so mu vse te barve druga za drugo hitele pred očmi in imel je vtis, da vidi belo barvo.

Mladi Newton, ki je v moških letih prekosil vse teoretike, je s temi raziskovanji dokazal, da je tudi imeniten eksperimentator.

V Woolsthorpu, nekako jeseni leta 1666, se je zbudila v Newtonu prva misel, iz katere se je rodilo njegovo najpomembnejše spoznanje, pojem težnosti. Kako se je to zgodilo, nam podrobneje poroča izdajatelj tretje izdaje Newtonovih "Načel" Pemberton, pa tudi francoski filozof Voltaire. Njemu je pripovedovala o tem Newtonova nečakinja gospa Conduit in torej ne gre za legendo. Newtonu je baje prvikrat šinila v (136,137) glavo misel o medsebojni privlačnosti nebesnih teles, ko je na svojem vrtu videl, da je zrelo jabolko padlo z jablane. Vprašal se je, zakaj je padlo, in odgovoril, da zaradi teže, ki ga je vlekla proti središču Zemlje. In spet se je vprašal, do kod sega ta privlačna sila teže, ki deluje tudi na najvišjih gorah. Naposled se je vprašal, ali sega morda vpliv težne sile celo do Lune.

0 tem se ni vprašal še nihče pred njim. In ko je Newton tako premišljeval, je pomislil na nekaj, kar je še mnogo tehtnejše: ali ni morda teža tista sila, ki vpliva na Luno, da kroži okrog Zemlje?

Tako je Newton načel in formuliral za vse svetovje pomemben problem. Ko ga je začel reševati, je prišel na povsem neraziskano podračje, kajti tedanja znanost še ni znala reševati tak5nih vprašanj o gibanju teles. Tako daleč se je razvila šele s Huyghensovimi deli o krivočrtnem gibanju.

Govorili smo že o tehle dveh Huyghensovih dognanjih: Če naj se telo enakomerno giblje po krogu, mora stalno vplivati nanj sila v smeri središča kroga.

Pospešek, ki ga ta sila neprestano daje krožečemu telesu, je

p=v²/r

Ta dognanja je Huyghens objavil leta 1673 torej sedem let potem, ko je Newton načel svoj problem. Do prvega dognanja je Newton prišel že, ko je svoj problem načenjal, ko pa ga je reševal, se je dokopal še do drugega, ni pa znano, kako. To lahko samo ugibamo. Kakor smo že povedali, je gvoj fluksijski račun že zgodaj uporabil, da je z njim iskal krivinske polmere ravninskih krivulj. O tem je napisal leta 1671 razpravo, ki pa je bila objavljena na podlagi ohranjenega rokopisa šele po njegovi smrti, leta 1736. Ker je imel Newton že l. 1666 prve pojme o krivinskem polmeru, je lahko prišel do zgornjega obrazca takole.

Najpreprosteje izračunamo krivinski polmer pri paraboli. Krivinski polmer v njenem temenu je enak njenemu parametru. Po Galileijevih raziskavah, ki jih je Newton poznal, se giblje telo, ki ga zalučamo v vodoravni smeri z začetno hitrostjo v, po paraboli s parametrom

v²/p

p je pri tem pospešek prostega pada. Če je začetna hitrost tolikšna, da je parameter parabole enak polmeru zemeljske oble r, če torej velja

v²/p = r,

potem se bo zalučano telo gihalo enakomerno po krogu s polmerom r. Pogoji za gibanje telesa bodo namreč po vsej njegovi poti enaki začetnim. Iz poslednje enačbe naravnost sledi tudi prejšnji t. j. Huyghensov obrazec.

To je samo en primer, kakor je mogel Newton dognati ta obrazec. Izpeljal pa ga je vsekakor, naj bo že kakor koli.

Če uporabimo ta obrazec pri Luni in zaznamujemo polmer Luninega tira z r, obhodno dobo Lune okrog Zemlje pa s T, dobimo, da je hitrost, s katero kroži Luna po svojem tiru

v = 2 pr/T

njen pospešek proti Zemlji pa

p = 4p²r/T²

S tem obrazcem je lahko Newton izračunal pospešek Lune proti Zemlji. Da bi dognal, ali res zemeljska teža povzroča ta pospešek, kakor je domneval, je moral ugotoviti, kako se vpliv zemeljske teže širi v prostoru.

Če bi si bil Newton ogledal planete, ki se zaradi podobnega vpliva Sonca gibljejo okrog Sanca, bi bil lahko iz tretjega Keplerjevega zakona zelo preprosto izpeljal zakon, po katerem se širi ta privlačna sila. Denimo, da se planeti gibljejo okrog Sonca po krogih, da je r polmer tira, T pa obhodna doba planeta. Tedaj dobimo njegov pospešek po gornjem obrazcu.

Po tretjem Keplerjevem zakonu velja, če vzamemo po prejšnji predpostavki za polmer r kroga kar veliko polos eliptičpega tira planeta,

r³/T²=k

kjer je k isto število za vse planete. Iz poslednjih dveh enačb pa sledi

p = 4p²k/r²
Če pišemo

4p²k = f

kjer je f isti za vse planete, dobimo

p = f/r²

(138, 139)

To pomeni, da imajo vsi planeti pospešek proti Soncu, ki pojema s kvadratom polmera planetnega tira.

Zdi se, da Newton ni šel po tej poti ali da se je vsaj obotavljal iz gornjih enačb sklepati na tako pomembne posledice glede gibanja planetov. Rad je imel stroge izpeljave in zato mu ni bilo prav nič všeč, da bi vso stvar nenatančno in grobo poenostavil in zamenjal eliptične planetne tire s krožnimi. To je prepustil drugim. In res, ko je Huyghens objavil svojo razpravo in v njej svoj obrazec za centripetalni pospešek, se je posrečilo Wrenu, Hooku in Halleyu, da so neodvisno drug od drugega iz Huyghensovega obrazca izpeljali zgornji obrazec za pospešek planetov. Niso se pa vprašali, kaj je vzrok tega pospeška.

Newton je lahko prišel do gornjega obrazca še drugače. Ko se je vprašal, kolikšna je zemeljska teža v čedalje večjih razdaljah od zemlje, se je morda spomnil na podoben primer, kako se svetloba širi v prostoru. Ko se širi iz svojega izvora na vse strani, gre svetloba skozi čedalje večje krogle, ki si jih mislimo v prostoru in ki imajo skupno središče v izvoru svetlobe. Ker so površine teh krogel sorazmerne kvadratom njihovih polmerov in je svetloba enakomerno porazdeljena po površini take krogle, pojema njena jakost s kvadratom razdalje od izvora r. Tako nekako je morda razmišljal tudi Newton in intuitivno dognal gornji obrazec. Veliki znanatveniki so svoja največja odkritja vnaprej zaslutili z intuicijo, ki je kakor ptica prehitela počasno korakanje kritičnega razmišljanja. Tudi ta Newtonov problem je rodila mladostna intuicija. Ne zanima pa nas toliko, kako je zgornje obrazce dognal, kolikor izredno pomembni izsledki, do katerih so mu pripomogli. Do teh izsledkov pridemo na kaj preprost način, kakor se pač rado zgodi, kadar je človek že blizu cilja.

Če zaznamujemo z R polmer zemeljske oble in z g pospešek prostega pada na površini Zemlje, potem je pospešek p, ki ga daje Zemlja Luni, oddaljeni od nje za r,

p = g R²/r²

kajti ta pospešek kot rečeno pojema s kvadratom oddaljenosti. Za ta pospešek smo dobili tudi izraz

p = 4p²r/T²

torej sledi iz obeh enačb

g = 4p²r³/R²T²

S tem obrazcem je poskusil Newton preveriti svojo veliko zamisel. Z njim lahko namreč iz polmera R zemeljske oble, polmera r Luninega tira in njene obhodne dobe T izračunamo pospešek prostega pada g na zemeljski površini in ga primerjamo s tistim, ki ga je Galilei ugotovil s svojimi poskusi.

Razumljivo je, da se Newton ni obotavljal narediti ta račun. V knjigah, ki jih je imel v Woolsthorpu, ni našel zanesljivih podatkov o številčnih vrednostih za R, r in T. Zato je po zgledu zemljepiscev in pomorščakov privzel, da je stopinja zemeljskega poldnevnika dolga 60 angleških milj in da je oddaljenost Lune od Zemlje 60 krat večja kakor polmer zemeljske oble. Za čas T je imel boljši podatek T = 27 d 7 h 43 m. Račup, ki ga je naredil s temi podatki, ni opravičil njegovega pričakovanja. Izračunani pospešek g je bil za celo sedmino manjši od dejanskega, tistega, ki ga je izmeril Galilei. Šele 16 let pozneje je Newton spoznal, zakaj se račun in poskus nista ujemala. Vzrok ni bil v obrazcu, ta je bil dober, pač pa v napačnem podatku za polmer zemeljske oble. Vse dotlej je Newton dvomil, ali je njegova ideja pravilna, in zato je ni nikomur zaupal.

Newton se je l. 1667 vrnil v Cambridge, končal tam svoj študij, dosegel vse tri akademske stopnje in postal 29. oktobra 1669 naslednik svojega učitelja Barrowa. Ta se je v Newtonovo korist odpovedal profesuri matematike, se vrnil k teologiji ter postal upravnik Trinity Collegea in kaplan kralja Karla II. Kot profesor je imel Newton majhne dohodke, 200 funtov letno, pa tudi majhne profesorske dolžnosti, tri ure predavanj na teden. Vseh trideset let, ko je bil profesor v Cambridgeu, niso zahtevali od njega nič več; zato se jc lahko popolnoma posvetil znanstvenemu delu.

Brž ko je doštudiral in se vživel v profesorski poklic, je začel obravnavati svoje velike zamisli, do katerih je prišel že v rojstnem kraju. Leta 1669 je napisal prvo matematično razpravo "De analysi per aequationes", v kateri je objavil svoj znani splošni binomski izrek in nekaj osnov svojega fluksijskega računa. To razpravo je daI svojemu učitelju Barrowu, ta pa jo je poslal Collinsu. Collins je imel tesne stike s člani hKraljevskega društva" in je imel takrat v Angliji podobno vlogo, kakor pred njim Mersenne v Franciji. Živahno si je namreč dopisoval z vsemi znanstveniki svoje deleže in bil nekakšen posredovalec med njimi. Svoji pošiljki je Barrow priložil pismo, v katerem je dejal, da je pisec razprave resda še zelo mlad in komaj dve leti magister, vendar pa mož izrednega uma. Kljub temu priporočilu Collins ni mogel doseči, da bi bila Newtonova razprava objavljena bodisi v publikacijah Kraljevskega društva ali kje drugje. Collins je vrnil razpravo piscu, obdržal pa je natančen prepis, ki so ga našli po njegovi smrti v njegovi (140, I41) zapugčini. Pozneje, ob sporu z Leibnizom, so lahko na podlagi tega prepisa dokazali, da je Newton prvi iznašel infinitezimalni račun. To Newtonovo. razpravo so natisnili šele leta 1711. Podobna usQda je doletela še eno Newtonovo razpravo, in sicer "Methodus fluxionum=<, napisano leta 1680. Tudi te Collins ni mogel spraviti v javnost; objavljena je bila leta 1736 v Newtonovih posmrtnih delih.

Newton s svojimi matematičnimi razpravami torej ni imel sreče in to je bila za matematiko velika škoda. Ko bi bile Newtonove razprave o pravem.času objavljene, bi bile zelo pospešile razvoj infiniteiimalnega računa, Newtonu pa bi 'bil iprihranjen nezaželeni spor z Leibnizom.

Več sreče je imel Newton s svojimi odkritji in iznajdbami v optiki. Že ko so prvič začeli uporabljati astronomske daljnoglede z lečami, refraktorje, kakor jim pravimo zdaj, se je pokaza'lo, da imajo razne napake. Ena največjih je bila kromatična disperzija leč, ki so jo odpravili šele pozneje, ko so sestavili akromatske leče. Konkavna zrcala nimajo te napake in italijanski jezuit Zucchi je že leta 1616 sestavil daljnogled z zrcalom. Vendar pa sta šele Gregory in Newton vpeljala v astronomijo take daljnoglede, ki jim pravimo zdaj ref lektorji. Bistvo ref lektorja je v tem, da konkavno zrcalo, ki je na dnu cevi daljnogleda, upodobi astronomski objekt v svojem gorišču, torej pred seboj, v cevi daljnogleda. Slika je zelo razločna, gre pa za to, kako naj namestimo povečalno lečo okularja, da bomo sliko videli. V ta namen je Gregory leta 1661 izvrtal v sredini zrcala luknjico, skozi katero se da z okularjem opazovati slika, ki jo prikaže veliko zrcalo in odbija konkavno zrcalce, pritrjeno v cevi onkraj gorišča velikega zrcala. Cassegrain je leta 1672 Gregoryjevo konkavno zrcalce nadomestil s konveksnim zrcalcem, pritrjenim tokraj gorišča velikega zrcala. Da bi pa velikega zrcala ne bilo treba vrtati, je Newton postavil v cev daljnogleda majhno ravno zrcalce, nagnjeno proti osi cevi v kotu 45°. To zrcalce je odbijalo žarke, ki so odsevali od velikega zrcala, v stran, tako da je bilo mogoče opazovati sliko skozi okular v plašču cevi. Iz kombinacije teh treh različnih vrst daljnogledov so se razvili naši sedanji veliki reflektorji, ki jih razen refraktorjev v astronomiji pogosto in uspešno uporabljajo.

Newton je leta 1668 sam izdelal manjši daljnogled te vrste, tri leta pozneje pa večjega, ki. ga je podaril Kraljevskemu društvu. Ta daljnogled še dandanes hranijo v društveni knjižnici. Na njem je napisano: "Iznašel ga je Sir Isaac Newton in ga izdelal z lastno roko."

Društvo je sprejelo Newtonov teleskop z velikim priznanjem in ga pokazalo kralju, Newtona pa je 11. avgusta 1672 izvolilo za rednega člana.

Tako je bil Newton, ko je komaj izpolnil devetindvajseto leto, sprejet med najbolj učene može Anglije. K temu odlikovanju mu je nedvomno pripomogel tudi njegov zaščitnik Barrow, ki je bil kraljev spovednik. Newton pa je hotel dokazati, da si je to čast zaslužil in da mu je niso izkazali po protekciji. To je lahko kmalu tudi storil. Tačas je bil končal raziskave in odkritja o sončni svetlobi ter napisal razpravo o njej in njenih raznobarvnih sestavinah. Zato je že 18. januarja 1672 poslal tajniku "Kraljevskoga društva" Oldenburgu pismo, v katerem je rečeno: "Prosim Vas, da mi sporočite, doklej bodo trajale seje Društva. Če bodo trajale še nekaj časa, pošljem Društvu v oceno poročilo 0 odkritju, ki me je tudi napotilo, da sem sestavil svoj teleskop. Ne dvomim, da bo Društvo cenilo moje odkritje še mnogo bolj kakor moj teleskop, saj gre po mojem mnenju za najvažnejše dosedanje dognanje o tem, kaj je svetloba." To razpravo je poslal tajniku Društva že 6. februarja 1672, v spremnem pismu pa ga je obvestil, da je začel svoje raziskave že leta 1666.

Ko so Newtonovo razpravo prvič prebrali, je bila sprejeta z odobravanjem. Društvu je bido v čast, da jo je objavilo v svojem glasilu "Transakcijah". Govorila je o velikih odkritjih, ki jih nihče ni mogel izpodbijati in za katera si razen Newtona nihče ni mogel lastiti zaslug. Vendar pa so se kmalu našli ljudje, ki so njegovo delo kritizirali in omalovaževali, zlasti še potem, ko je l. 1675 in 1676 objavil še dve razpravi o optiki. Glavni in najsrditejši njegov nasprotnik je bil Robert Hooke (1635-1703), tajnik Društva od l. 1678. Bil je sicer bistre glave in poln novih idej, ni pa imel dovolj matematične izobrazbe in nadarjenosti, da bi jih uresničil. Bil je tudi zelo častihlepen in prepirljiv. V boju proti Newtonu so se mu pridružili Huyghens, utemeljitelj valovne teorije o svetlobi, ter drugi manj pomembni angleški in francoski znanstveniki.

Rezultati Newtonovih poskusov so bili sicer res neovrgljivi, pač pa je bilo kaj lahko napadati njegove nazore o tem, kaj je svetloba, kar še dandanes ni popolnoma dognano. Možne so bile različne razlage, kakor so še zdaj, in znanstveniki so se lahko prerekali po mili volji. Cela štiri leta je moral Newton odgovarjati na napade in zavračati ugovore svojih nasprotnikov. Resda jim je pokazal moč svojega duha, toda dolgotrajni boj z njimi ga je izčrpal. Obžaloval je, da je v brezplodnem prerekanju tratil dragoceni čas. Sklenil je v bodoče molčati o optiki, vsaj dokler bo Hooke živ. Tako je tudi storil.

Prepir med Newtonom in njegovimi nasprotniki pa je imel tudi dobre strani. Newton si je pridobil v njem dragocenih izkušenj in se prekalil v pravega znanstvenika. Globlje kakor vsi njegovi vrstniki je spoznal, kako daleč lahko prodre znanost, kaj so hipoteze in kaj naravni zakoni. Slclenil je izogibati se vseh hipotez in pojasnjevati naravne pojave samo z dejanskimi in za razlago zadostnimi vzroki. Za enake posledice (142, 143) je treba po možnosti najti enake vzroke. Lastnosti teles, ki jih ne moremo ne povečati ne zmanjšati in ki jih imajo vsa raziskavi dostopna telesa, je treba imeti za splošne. V eksperimentalni fiziki je treba vse sklepe, do katerih smo prišli induktivno na podlagi pojavov, imeti za zanesljiwe aIi vsaj domnevati, da so zelo blizu resnici, če le ni nasprotnih predpostavk. To velja vse dotlej dokler ne najdemo drugih pojavov, ki te sklepe ali potrdijo ali pa nam povedo, da so izjemni.

Narava se pokorava svojim zakonom; ko jih spoznamo, lahko prodremo v njeno snovanje samo tako globoko, kakor seže pogled našega uma, globlje pa ne. Kje je meja, preko katere ne moremo?

Kakor o geometrijskih aksiomih tudi o nekaterih naravnih zakonih ne smemo dvomiti. Na podlagi takih osnovnih zakonov pridemo do vseh drugih z logičnim sklepanjem. Kar namreč velja za geometrijo, mora veljati tudi za gibanje, saj je geometriija samo del vede o gibanju.

Tako je Newton razločno videl pred seboj pot, po kateri je prišel dalje, kakor je slutil, čeprav ga je bilo strah meje, preko katere znanost ne more. Nehal je objavljati svoje razprave in odgovarjati na tuje, da se je lahko posvetil svojemu velikemu delu. Za to delo so bili potrebni velikanski duševni napori, saj je šlo za osnovne probleme narave.

Namen tega dela je bil: naravne pojave prevesti na matematične zakone. Newton je dal svojemu delu naslov "Philosophiae naturalis principia mathematica".

Predvsem je bilo treba razčistiti nekatere dotlej meglene pojme. Pred Newtonom znanstveniki niso imeli jasnih pojmov o sili, masi in teži. Maso so zamenjavali s težo teles. Newton je že v Woolsthorpu spoznal, da ima isto telo glede na svojo oddaljenost od središča Zemlje različen pospešek in da je torej tudi različno težko. Zato je vpeljal pojem mase, ki je kot bistvena znacilnost telesa nespremenljiva. Tako je pojem mase ločil od pojma teže. Težo je definiral kot produkt mase in pospeška prostega pada. Tako je prišel tudi do splošnega pojma sile kot produkta mase in pospeška telesa. Sila je vse tisto, kar povzroča pospešek, torej ne samo zemeljska teža, ampak tudi privlačnost vseh drugih nebesnih teles, vpliv magneta itd. Pri tem se ni treba spuščati v hipoteze o bistvu teh sil, o njihovih skritih vzrokih, o njihovem nastanku in načinu, kako delujejo, omejiti se je treba le na dejanske pojave, ki jih lahko opazujemo pri gibanju, in ugotavljati ter raziskovati samo te dejanske pojave.

Brž ko je razčistil osnovne pojme in jih izrazil z natančnimi definicijami, je začel Newton postavljati in oblikovati osnovne teze, zakone ali aksiome mehanike. Pri Galileiju je našel enega izmed teh zakonov, namreč zakon o vztrajnosti; svojega prednika pa je prekosil v tem, da je ta zakon doumel širše, spoznal njegov pomen in mu dal tole klasično obliko:

"Vsako telo vztraja v mirovanju ali enakomernem premočrtnem gibanju, če in dokler ga še kaksne sile ne prisilijo, da to svoje stanje spremeni."

Na ta zakon je kratko in jasno navezal svoj drugi zakon: "Sprememba gibalne količine je sorazmerna in istosmerna z vplivajočo silo."

V tem stavku in dodanem pojasnilu je tudi povedano, da je sila vektor, kakor bi rekli dandanes. Sila ima velikost, lego v prostoru in smer, sila je v prostoru usmerjena količina. Vse to je jasno izraženo v Newtonovi razlagi k drugemu zakonu, kjer pove, da se vplivi posameznih sil superponirajo po pravilu o paralelogramu, t. j. da se sile seštevajo kot vektorji.

Kot tretji osnovni zakon mehanike je Newton postavil zakon o akciji in reakciji, ki ga je izrazil takole:

"Akcija ima vedno nasprotno in enako reakcijo ali drugače povedano, medsebojna ucinka dveh teles sta si vedno enaka in nasprotno usmerjena."

Če telo pritiska na drugo telo ali ga, vleče, potem drugo telo z enako silo pritiska na prvo ali ga vleče. Če pritiskaš s prstom na kamen, tudi kamen z enako silo pritiska na prst.

Kakor je nekoč Evklid na svojih aksiomih sezidal celo geometrijo, tako je tudi Newton na teh treh zakonih kot temeljih spravil pod streho vso stavbo mehanike.

Vse probleme v svojem delu je rešil Newton z geometrijskimi, sintetičnimi metodami in se pri tem opiral na Evklida, čeprav je imel, ko je pisal "Načela", v rokah svoje orodje višje matematike. Vzrokov za to je bilo več. Eden je bil, da se je hotel ravnati po Evklidu. Drugi, da je bil Evklidov nauk vsem znanstvenikom dobro znan; uporabljati ga je pomenilo govoriti v običajnem jeziku, raba fluksijskega računa pa bi zahtevala znanje tega novega, še ne dovolj razvitega in zato neprepričljivega jezika. V novem jeziku se namreč tedaj še daleč ni dalo jasno izraziti, da so sile, hitrosti in premiki vektorji. V ta namen so bile mnogo primernejše geometrijske figure, ki to nazorno prikazujejo. Še v drugi polovici devetnajstega stoletja je mislil tako znani nemški znanstvenik Wilhelm Schell. Šele ob koncu tega stoletja, ko se je razvila vektorska analiza, se je posrečilo računati z vektorji, ne da bi jih bilo treba razstavljati v komponente kakor doslej.

Ker se je zgodilo to celih dve sto let potem, ko je Newton napisal svoje delo, svojega novega računa torej ni mogel uporabljati brez pridržkov. Res, da je v svojem delu kratko in mimogrede navedel osnovne (144, 145) misli infinitezimalnega računa, ki so ga privedle do njegovih velikih odkritij, kakor je rečeno v napisu na njegovem nagrobnem spomeniku. Ni pa uporabljal niti izrazov, niti označb fluksijskega računa, temveč jezik klasične geometrije.

Newton je napisal svoje delo v latinščini in ponazoril svoje stavke s figurami Evklidove geometrije. Ob tem veličastnem spomeniku znanosti. bomo poskusili povedati glavne mi5li njegovega stvari,telja v našem materinem jeziku in v jeziku naše vektorske analize, ki jih smiselno izraža.

Kakor smo že omenili, navaja Newton v začetku svojega dela splošne def inicije materije, mase, vztrajnosti, gibalne količine, sile, prostora, časa in drugih osnovnih pojmov mehanike. Ogledali si bomo samo nekatere teh definicij.

Najprej definira Newton maso kot mero za množino materije in sicer kot produkt njene gostote in prostornine. To pravzaprav ni definicija, marveč samo matematična zveza med maso, gostoto in prostornino. Kakor časa tako tudi mase ne moremo popolnoma zajeti z eno samo definicijo. Pač pa jo lahko enako kakor prostor in čas merimo z izbrano enoto in v tem smislu moramo razumeti njeno def inicijo.

Druga Newtonova def inicija se tiče pojma, ki ga Newton imenuje količino gibanja in definira kot produkt mase in hitrosti. Ta produkt tudi dandanes imenujemo gibalno količino ali krajše impulz.

Za tema dvema definicijama sledijo pojasnila, da je materija sposobna upirati se; zato vsako samo sebi prepuščeno telo vztraja v mirovanju ali enakomernam premačrtnem gihanju. Sila pa je vpliv, ki tako stanje telesa spremeni.

S svojim drugim aksiomom definira Newton silo kot časovno spremembo gibalne količine.

Da bi to povedali v našem sedanjem matematičnem jeziku, uporabljajo nekateri znanstveniki tale obrazec:

F = d(mv)/dt

kjer pomeni m maso, v hitrost, t čas in F silo.

Ta obrazec ne pove vsega, kar je Newton mislil. V njem so namreč same skalarne količine. Newton pa je razločno spoznal, da sta sila in hitrost vektorja, kar dokazujeta njegov drugi aksiom in priloženo pojasnilo. Da sta ti dve količini vektorja, je očitno izraženo v njegovih figurah. Zato je treba zgornjo enačbo, če naj res pove tisto, kar je Newton mislil, zamenjati s tremi skalarnimi ali pa tole vektorsko [poudarjeni simboli so vektorji]

F = d(mv)/dt

Če zapišemo časovni odvod tako, kakor ga je označeval Newton v svojem fluksijskem računu in kakor je dandanes navada v vektorskem računu, dobimo, ker je m konstanta, tole enačbo:

F = mdv/dt = mv'

To je osnovna enačba za gibanje materialne točke in osnovna enačba naše sedanje mehanike. V tej enačbi ni izražen samo drugi Newtonov zakon, marveč tudi prvi. Kadar je namreč F = 0, je v konstanten vektor, t. j. materialna točka se giblje enakomerno in premočrtno. Kakor je ugotovil Ernst Mach, je mogoče s tema dvema Newtonovima aksiomoma, z njegovim tretjim aksiomom in s stavki iz njegovega dela načelno rešiti vsak praktični problem mehanike, bodisi statike ali dinamike. Če zadenemo pri tem na težave, so vedno matematične, torej formalne, nikakor pa ne načelne.

Zato so Newtonovi aksiomi osnova klasične mehanike. Poskušali so jih zamenjati z drugimi, pa se je pokazalo, da so najnaravnejši temelji mehanike že zato, ker se je mehanika na njih razvila in iz njih zrasla. Na njih se da brez drugih pripomočkov zgraditi cela stavba klasične mehanike, kakor nam kaže na pr. moderni Bilimovičec učbenik mehanike.

Newtonova "Načela" ne raziskujejo samo gjbanja trdnih teles, marveč se ukvarjajo tudi z mehaniko tekočin in plinov ter z drugimi naravnimi pojavi. V njih so osnove nauka o valovanju, v njih je objavil Newton zvezo, ki jo je odkril med hitrostjo širjenja valovanja, nihajno dobo in valovno dolžino. Teorijo je uporabil pri valovanju na vodni površini in pri zvočnih valovih in izpeljal obrazec, kako je hitrost, s katero se širi zvok, odvisna od tlaka in gostote sredstva. To teorijo je šele 130 let pozneje izpopolnil Laplace. Newton je temeljito raziskoval tudi upor zraka in trenje pri gibanju. Zato naslov njegovega dela po pravici zajema tako široko področje.

Mnogo pomembnejše pa je bilo, da je Newton uporabil svojo teorijo za raziskovanje gibanja nebesnih teles; privedla ga je do zakona o splošni gravitaciji. To je storil v tretji knjigi svojega dela in v prilogi k njej, medtem ko se prvi dve knjigi ukvarjata s splošno teorijo o gibanju. Ko bomo govorili o velikih Newtonovih problemih, bomo pri vsakem povedali tisto, kar sodi v splošno teorijo, in tisto, kar sodi v uporabo. Vse pa bomo povedali v našem sedanjem matematičnem jeziku.

Drugi del druge knjige Newtonovih HNačela se ukvarja s središctnimi silami. Tako tudi dandanes imenujemo sile, ki so usmerjene proti določeni stalni točki v prostoru. Izberimo si to točko za začetek koordinatnega sistema. Sila naj deluje na neko materialno točko, ki ima krajevni vektor (146, 147) r. Potem je gibalna enačba te točke

mv' = F(r)ro

kjer pomeni r absolutno vrednost krajevnega vektorja r, ro pa enotni vektor v smeri vektorja r. Pri tem smo se glede na poznejšo uporabo omejilil na najvažnejši primer, da je namreč velikost središčne sile odvisna samo od oddaljenosti r materialne točke od središča sil.

Če zgornjo enačbo vektorsko pomnožimo z r, dobimo na desni strani nič, kajti rxr je kot produkt dveh kolinearnih vektorjev enak nič. Sledi torej

rxv' = 0

Ker velja

d(rxv)/dt = rxv'

je torej

d(rxv)/dt = 0

Tz tega sledi, da je

(rxv) = C

kjer pomeni C nek konstanten, od časa neodvisen vektor. Leva stran enačbe pomeni dvakratno ploščinsko hitrost naše materialne točke; ta ploščinska hitrost se ne spreminja.

Newton je to ugotovil z geometrijskim razglabljanjem in izrazil s sledečim stavkom. Če se lelo giblje pod vplivom središčne sile, je njegovo gibanje ravninsko in zveznica med telesom in središčem sil popiše v enakih časovnih presledkih enake ploščine.

Newtonove besede o ravninskem gibanju povedo tudi, da je ploščinska hitrost vektor, kakor je razvidno iz zgornje enačbe.

Ni težko sprevideti, da se da zgornji izrek tudi obrniti; Newton je v svojem naslednjem stavku to tudi storil.

Gornje ugotovitve je Newton uporabil za gibanje po krogu in izpeljal Huyghensov obrazec za centripetalni pospešek. Kakor smo že slišali, je bid Huyghensov dokaz za ta obrazec objavljen šele l. 1703. Nato je Newton predpostavil, da so tiri planetov krogi, in izpeljal obrazec, ki so ga že pred njim ugotovili Wren, Hooke in Halley; njihova imena v tem vrstnem redu navaja v svojem delu.

Potem se je Newton lotil sledeče naloge.

Telo se giblje po elipsi pod vplivom središčne sile, usmerjene proti enemu izmed gorišč; kolikšna je ta sila?

To nalogo je rešil Newton kakor vse druge s sintetično geometrijsko metodo. Predaleč bi zašli, pa tudi lahko ne bi bilo, če bi hoteli tu ponoviti njegovo sklepanje, ki razodeva nenavadno iznadljivost. Zato se bomo zadovoljili s tem, da bomo rešili nalogo z našimi sodobnimi pripomočki, ki nas privedejo do istega kakor Newtonovo sklepanje.

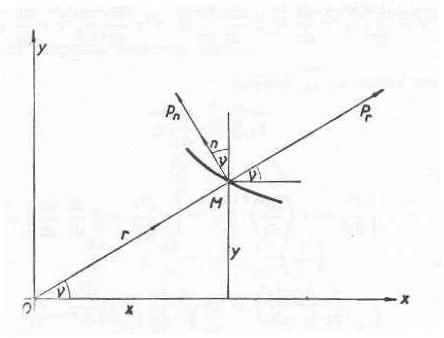
Oglejmo si v ta namen materialno točko, ki se poljubno giblje v ravnini. Izberimo si na tej ravnini, kakor je narisano na priloženi sliki, izhodišče 0 in os 0-X poljubnega koordinatnega sistema; z r in v označimo polarni koordinati točke M, kjer je v tem trenutku naša materialna točka.

Slika 28

Če zaznamujGmo z r krajevni vektor točke M, z ro pa enotni vektor iste smeri, lahko pišemo

r = rro

Če odvajamo po času t dobimo

r' = dr/dt = (dr/dt) ro + r (dro/dt) = r' ro + r ro'

(148, 149) Kakor vemo, je izraz na levi strani te enačbe vektor hitrosti

v=r'

naše materialne točke, ro' pa je vektor hitrosti, s katero se giblje krajišče enotnega vektorja, kadar se spreminja kot n. Če torej zaznamujemo z no enotni vektor, ki je pravokoten na vektorju ro in usmerjen v smislu rastočega n, velja

ro' = (dn/dt)no

in je torej

v = (dr/dt)ro + r(dn/dt)no

Časovni odvod tega izraza je

v' = (d²r/dt²)ro + (dr/dt)ro' + (dr/dt)(dn/dt)no + r(d²n/dt²)no + r(dn/dt)no'

Podobno kakor za ro dobimo

no' = -(dn/dt)ro

Zato je

v' = [d²r/dt² - r (dn/dt)²]ro + [r (d²n/dt²) + 2 (dr/dt)(dn/dt) ]no

Ker je

d(r²(dn/dt))/dt = 2r(dr/dt)(dn/dt) + r²(d²n/dt²)

dobimo

v' = [d²r/dt² - r (dn/dt)²]ro + (no/r)d(r²(dn/dt))/dt

Izraza

pr = d²r/dt² - r (dn/dt)²

pn = (1/r)d(r²(dn/dt))/dt

nam torej pomenita komponenti pospeška materialne točke v smeri vektorja ro oziroma vektorja no.

Vrnimo se zdaj k Newtonovi nalogi. Newton predpostavlja, da kaže sila proti gorišču elipse. Če postavimo izhodišče koordinatnega sistema v to gorišče, ima sila in s tem tudi pospešek materialne točke smer vektorja ro. Zato je pospešek pn v smeri no nič, tarej

d(r²(dn/dt))/dt = 0

Od tod sIedi

r²(dn/dt) = C

kjer je C od časa neodvisna konstanta. Ta konstanta nam pomeni dvakratno ploščinsko hitrost materialne točke, ki se giblje pod vplivom središčne sile. Ta točka ima po predpostavki sadno pospešek pr v smeri ro. Velikost tega pospeška poiščemo takole.
Ker velja

dr/dt = (dr/dn)(dn/dr)

dn/dt = C/r²

je

dr/dt = (C/r²)(dr/dn) = -C(d(1/r)/dn)

d²r/dt² = -C(d²(1/r)/dn²)(dn/dt) = -(C²/r²)(d²(1/r)/dn²)

Če postavimo to v obrazec za pr, dobimo

pr = -(C²/r²)[(1/r) + d²(1/r)/dn²]

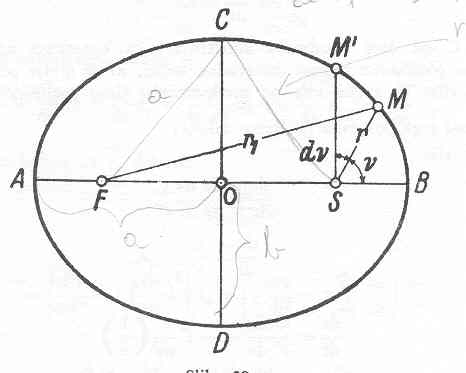
Newton predpostavlja, da se materialna točka giblje po elipsi, ki ima gorišče v točki S. Tako elipso vidimo na priloženi sliki.

Položimo v gorišče S te elipse izhodišče našega koordinatnega sistema in usmerimo njegovo os od S proti B. Potem sta polarni koordinati poljubne točke M na elipsi r in n, kakor smo jih tudi do sedaj zaznamovali. V teh koordinatah je treba izraziti enačbo elipse. Če označimo (150, 151) daljico, ki jo načrtamo od drugega elipsnega gorišča F do točke M, z rl, sledi iz definicije elipse

r+rl=2a,

kjer pomeni a veliko polos elipse. Če zaznamujemo z b malo polos, velja

OS = OF = (a² - b²)^1/2

Število
e=(a² - b²)^1/2/a

imenujemo numerično ekscentričnost elipse.

Slika 29

Lahko tudi pišemo

b² = a² - e²a²

Izraz

p = b²/a

se imenuje parameter elipse.

Iz trikotnika FMS, kjer je FS = 2ea, sledi po izreku o kosinusih trikotnikovih kotov

rl² = (2ea)² + r² + 4ear cos(n).

Ker je

rl = 2a - r,

dobimo

( 1 + e cos(n)) a r = a² - e²a² = b²,
t.j.

1/r=(1 + e cos(n))/p

To je enačba tira, po katerem se po predpostavki giblje materialna točka. Zdaj lahko izračunamo, kakšna mora biti središčna sila, če naj povzroči gibanje materialne točke po elipsi, ki jo določa zgornja enačba.

Iz te enačbe sledi

1/r= 1/p + (e/p) cos(n)

Zato je

d(1/r)/dn = - (e/p) sin(n)

d²(1/r)/dn² = - (e/p) cos(n)

torej

1/r + d²(1/r)/dn² = 1/p

Če postavimo to v zgornji obrazec za pospešek pr, dobimo

pr = - C²/(p r²)

Vidimo torej, da je velikost pospeška oziroma središčne sile odvisna samo od oddaljenosti r materialne točke od središča sil.

Uporabimo zdaj dobljene obrazce za gibanja planetov, ki potujejo po Keplerjevih elipsah s Soncem v skupnem gorišču. Iz zgornjih enačb sledi, da se morajo gibati po svojih tirih s stalno ploščinsko hitrostjo isto zahteva tudi drugi Keplerjev zakon. Zaznamujmo kakor prej z n in b polosi planetnega tira, s T pa obhodno dobo planeta okrog Sonca. V času T popiše krajevni vektor, ki kaže od Sonca k planetu, celo elipso planetovega tira s ploščino pab. Zato je dvojna ploščinska hitrost C planeta

C = 2pab/T

in ker smo imeli

p = b²/a

(152, 153)

dobimo, če postavimo ta dva izraza v zgornjo enačbo

pr = -4p²a³/(T²r²)

Po tretjem Keplerjevem zakonu je količnik a³/T² enak za vse planete, torej je tudi število

m = 4p²a³/T²

enako za vse planete. Zato je

pr = -m/r²

kjer znak minus pove, da je planet pospešen proti Soncu.

Do te enačbe je prišel Newton z geometrijsko raziskavo. Pove nam pa tole.

Vsak planet je vedno in povsod pospešen proti Soncu in velikost njegovega pospeška je obratno sorazmerna kvadratu njegove oddaljenosti od Sonca.

Do tu se Newtonovo razmišljanje sicer znatno razlikuje od razmišljanja njegovih predhodnikov, vendar pa le v tem, da velja za dejanske eliptične planetne tire. Newton pa je šel še naprej. Predvsem je rešil tudi nasprotno nalogo: središčni pospešek je obratno sorazmeren kvadratu oddaljenosti od središča sil, treba je najti pot teles ob danih začetnih pogojih. Ugotovil je, da je ta pot stožernica; ali je elipsa ali hiperbola ali parabola, je pa odvisno od začetnih pogojev.

Tudi te raziskave nam pričjo, kako rieprekosljivo spretno je Newton uporabljal Evklidovo geometrijo.

Ko je rešil te v prvi knjigi "Načel" navedene probleme, je v tretji knjigi navezal nanje svoja raziskovanja o gibanju nebesnih teles.

Slišali smo že, da je Newtonu že v mladih letih, ko se je mudil v rojstnem kraju, šinila v glavo misel, da sega zemeljska teža do Lune in da povzroča, da se Luna giblje okrog Zemlje. Njegovi tedanji računi pa tega niso potrdili in zato je svojo misel opustil. Morda bi jo bil za vedno zavrgel, da ga ni golo naključje spomnilo nanjo. Junija 1682 se je udeležil seje Kraljevskega društva. Preden so se zbrali vsi člani, se je pogovor sukal okrog raznih znanstvenih novosti. Eden izmed prlsotnih je pripovedoval o Picardovem merjenju Zemlje. Rezultati Picardovih meritev so se znatno razlikovali od podatkov o velikosti Zemlje, ki jih je bil Newton uporabil pri računanju v Woolsthorpu. Takoj ko je to slišal, je Newton pomislil, da s svojim računom morda zato ni prišel do pričakovanih rezultatov, ker prejšnji podatki niso bili pravilni. Potrpežljivo je počakal do konca seje, se vrnil domov in začel znova računati. Uorabil je svoj nekdanji obrazec

p = gR²/r²

kjer pomeni p pospešek Lune, r njeno oddaljenost od Zemlje, R polmer zemeljske oble in g pospešek prostega pada. Privzel je obrazec

p = 4p²a³/(T²r²)

to se pravi, svoje ugotovitve o gibanju planetov okrog Sonca je uporabil tudi za gibanje Lune okrog Zemlje, in dobil obrazec

g = 4p²a³/(T²R²)

torej isti kakor nekdaj v Woolsthorpu. Vstaviti pa je bilo treba natančnejše številčne vrednosti, ki so .bile zdaj na razpolago. Picard je dognal, da meri obseg zemeljskega poldnevnika 123,249.600 pariških čevljev, torej povpročni polmer zemeljske oble R = 19,615.000 čevljev. Za a in T je vzel Newton svoje stare podatke a = 60 R; T = 27 d 7 h 43 m.

Ko je primerjal novi podatek za R s svojim nekdanjim, je Newton na prvi pogled spoznal, da se bo z računom zdaj mnogo bolj približal pričakovanemu rezultatu kakor prej. To ga je tako razburilo, da ni mogel vstaviti številčnih vrednosti. To je zaupal nekemu prijatelju, ki je slučajno prišel k njemu. Iz računa je sledilo, da je pospešek prostega pada 15 čevljev 1 palec in 1 4/9 črte pariške mere na kvadratno sekundo. Huyghens pa je z opazovanjem nihala ugotovil skorajda isti pospešek 15 čevljev 1 palec l 7/9 črte. Ta skladnost je bila dokaz, da je bila Newtonova ideja pravilna. Z njo je Newton daleč prekosil svoje predhodnike.

Pri vsem svojem prejšnjem razmišljanju je Newton predpostavljal , da Sonce miruje, kakor je učil Kopernik. Zato je govoril o središcču Sonca kot o nepremičnem središču sil in na podlagi te predpostavke dobljene rezultate je uporabil za planete, analogno pa tudi za gibanje Lune okrog Zemlje. Čeprav je spoznal, da je ta predpostavka zelo blizu stvarnosti, jo je opustil pri nadaljnjih raziskavah, ki so ga privedla do tehle sklepov.

Luna ima pospešek proti Zemlji, ali kakor je rekel Newton, Luna teži proti Zemlji. Njen pospešek je posledica zemeljske privlačnosti, sila, ki ji daje ta pospešek, pa je po Newtonovi definiciji produkt pospeška (154, 155) in Lunine mase. Nekaj podobnega velja za gibanje planetov okrog Sonca. Sila, s katero Sonce vpliva na planet, je

P = mm/r²

kjer je m masa planeta.

Po Newtonovem načelu o akciji in reakciji privlači planet Sonce z enako in nasprotno usmerjeno silo. Ta sila mora biti produkt mase M Sonca in njegovega pospeška. Če torej vpeljemo novo konstanto f, ki jo določa enačba

f = m/M

t. j.

f = 4p²a³/(T²M)

dobimo za silo, s katero se privlačita Sonce in planet, tale izraz

P = fMm/r²

V obrazcu za f je količnik a³/T² po tretjem Keplerjevem zakonu za vse planete isti. Torej ima tudi v poslednjem izrazu f za vse planete cnako številčno vrednost; pokazalo se je, da velja isti f tudi za Luno in Zemljo ter za Jupitra in njegove lune. Zato je faktor f konstanta, ki velja za vse osončje in izraža splošno lastnost materije, nakopičene v tem delu vesoljstva.

Ko je Newton prišel do tega spoznanja, ga je razširil na vse vesoljstvo in spoznal, da velja zgornji obrazec za poljubna dva delca materije v vesoljstvu; to so potrdile tudi vse poznejše izkušnje. Newtonovo spoznanje je izraženo v temle zakonu:

Sleherni delec materije v vesoljstvu privlači vsak drug delec s silo, ki leži na zveznici teh dveh delcev in katere velikost je sorazmerna produktu mas ml in m2 teh delcev ter obratno sorazmerna kvadratu njune razdalje r.

Kolikšna je ta sila, nam pove obrazec

P = fm1m2/r²

pri čemer je f splošna konstanta.

To silo je Newton imenoval gravitacijsko. Zgornji zakon pa imenujemo splošni gravitacijski zakon.

Iz Newtonovega gravitacijskega zakona so sledila nova spoznanja. Mnogi dotlej nepojasnjeni naravni pojavi so se dali razložiti in opisati v eksaktnem jeziku matematike.

Povedali smo že, da je Newton v prvih dveh knjigah svojega dela razložil splošne zakone, v tretji pa njih uporabo za raziskovanje gibanja nebesnih teles. Še preden je dokončno napisal svoje delo, je odkril splošni gravitacijski zakon. Zato je že v prvih dveh knjigah upošteval, da ga bo pozneje uporabil, in je izpopolnil za to potrebno orodje. Zato je posebno skrbno proučil središčne sile in sicer prav take, ki pojemajo s kvadratom oddaljenosti od središča.

Dvanajsto poglavje prve knjige Newtonovih "Načel" govori o privlačnosti krogelnih teles s predpostavko, da ta privlačnost pojema s kvadratom oddaljenosti. Takoj v začetku poglavja dokazuje Newton tole.

Naj nam krog HJKLH predstavlja presek krogle z ravnino skozi poljubno točko P znotraj krogle in skozi njeno središče O. Površina krogle naj bo enakomerno obložena z materijo, to se pravi, naj bo homogena materialna krogelna lupina s konstantno površinsko gostoto r. Vprašajmo se, s kakšno silo bo ta lupina delovala na poljubno notranjo točko P, v kateri si mislimo enoto mase.

Kjer koli na krogli, denimo na kraju KL, omejimo s poljubnim robom majhen kos površine in ga označimo z Df1. Na njem je razporejena masa rDf1. Projicirajmo ta kos površine skozi točko P na nasprotno stran HJ krogle in označimo ploščino te projekcije z Df2. Na njej je masa rDf2.

Slika 30

(156, 157)

Če nenehoma zmanjšujemo ploskvico Df1, s tem pa tudi ploskvico Df2, tako da se točka L približuje točki K, točka J pa točki H, bo masa rDf1 privlačila točko P s silo, ki bo sorazmerna izrazu

rdf1/(KP²)

masa rDf2 pa s silo, sorazmerno izrazu

rdf2/(HP²)

Ploščini df1 in df2 pa sta v istem razmerju kakor kvadrata njunih razdalj KP in HP od točke P. Zato se njuna nasprotno usmerjena privleka uničujeta. Ker velja to za vsaka dva dela krogelne površine, katerih zveznica gre skozi P, materialna površina krogle sploh z nobeno silo ne deluje na točko P.

S tem preprostim Newtonovim sklepanjem sta njegova rojaka Priestley (1767) in Cavendish (1771) že pred Coulombom teoretično izpeljala zakon, ki mu pravimo Coulombov in ki govori o delovanju električne sile v prostoru. Tedaj je bilo že znano, da v notranjosti električno nabitega vodnika ni električnih sil. Če je tak vodnik popolna krogla in v bližini ni drugih vodnikov ali električnih nabojev, je zaradi simetrije elektrenina na njem enakomerno porazdeljena in njena površinska gostota povsod enaka. Priestley in Cavendish sta iskala zakon, kakšna mora biti električna sila zunaj krogelnega vodnika, da bi bila v vsaki točki znotraj njega nič. Uporabila sta zgornje Newtonovo sklepanje, kratko in malo obrnila Newtonov problem in tako ugotovila, da je električna sila obratno sorazmerna kvadratu oddaljenosti. Pozneje je Coulomb s poskusom dokazal tisto, kar je tako preprosto sledilo iz Newtonove razmišljave.

S podobnim razmišljanjem je Newton raziskal vpliv materialne krogelne lupine na poljubno materialno točko P zunaj krogle. Dognal je, da krogelna lupina privlači materialno točko prav tako, kakor če bi bila vsa masa lupine zgoščena v njenem težišču.

Na podlagi teh dveh izrekov ni bilo težko raziskati še druge primere. Eden izmed njih je privlek homogene materialne krcgle, t; j. take, ki je izpolnjena s povsod enako gosto snovjo. Če si jo mislimo sestavljeno iz neštetih homogenih krogelnih lupin, prav lahko ugotovimo, da privlači materialno točko P zunaj sebe tako, kakor če bi 'bi?a vsa masa zgoščena v središču. Če hočemo raziskati, kako vpliva taka krogla na poljubno točko P v svoji notranjosti, moramo ravnati takole. Označimo polmer krogle z R in razdelimo jo s koncentrično krogelno ploskvijo, ki gre skozi točko P', na dva dela. Notranji je polna krogla s polmerom r, zunanji pa votla krogla z notranjim polmerom r in zunanjim R. Če razstavimo to votlo kroglo na nešteto homogenih lupin, takoj spoznamo, da ne vpliva na točko P'. Enako storimo z notranjo krogio in spoznamo, da deluje na točko P', v kateri si mislimo enoto mase, s silo

fM/r²

kjer pomeni M maso notranje krogle, zgoščeno v mjenem središču. Ker je

M = 4pr³ r/3

je privlačna sila

4pf r r/3

in torej sorazmerna oddaljenosti točke P' od središča krogle. Sila , s katero privlači polna homogena krogla zunanjo materialno točko, torej pojema s kvadratom oddaljenosti r te točke od središča krogle; sila, s katero priylači krogla notranjo točko pa narašča z oddaljenostjo te točke od središča. Na površini krogle se torej naraščanje njenega privleka nezvezno spremeni.

Ko je vse to dognal, je Newton predpostavil, da gostota krogle p ni povsod enaka, marveč da je odvisna od oddaljenosti r. Tudi zdaj se je pokazalo, kar ni težko spoznati, da privlači krogla zunanjo točko s prav takšno silo, kakor če bi bila vsa masa M zgoščena v središču. Sila, s katero privlači notranjo točko, pa je odvisna od tega, kakšna je funkcija r = f(r), in se da, če je ta funkcija znana, izračunati z integralnim računom.

Newton je razširil svoje raziskave na medsebojno privlačnost dveh krogel, katerih gostota r je funkcija oddaljenosti od središča, in dognal, da se ti krogli privlačujeta, kakor da sta njuni masi zgoščeni v njunih središčih.

Vsa ta spoznanja so izredno važna za probleme o gibanju nebesnih teles. Vsi planeti imajo približno obliko krogle. Neznatne razlike v obliki je Newton pozneje upošteval. Dognal je tudi, da njihova gostota narašča, če se bližamo središču in da je odvisna od oddaljenosti od , središča. Zaradi vsega tega se medsebojno privlačujejo tako, kakor če bi imeli mase zgoščene v središčih. Zato lahko gibanje planetov prevedemo na gibanje materialnih točk, ki imajo mase posameznih planetov. To je tudi izhodišče za našo sedanjo nebesno mehaniko.

Vse te raziskave so pokazale, da je Newtonov obrazec ki povezuje pospešek prostega pada na zemeljski površini in pospešek Lune, veljaven kljub temu, da zemeljska privlačnost ne narašča, čim bliže smo središču Zemlje, marveč je največja na površini; to neenakomernost je Newton namreč že prej slutil in mu je delala preglavice, dokler je ni pojasnil.

V prvi knjigi njegovih "Načel" je objavljeno še eno, za raziskovanje gibanja nebesnih teles izredno važno dognanje, kii ga imenujemo zdaj Newtonov izrek o ohranitvi gibalne količine in o gibanju težišča. Ta izrek bomo izpeljali ob zgledu za gibanje dveh nebesnih teles, ki se medsebojno privlačujeta po Newtonovem gravitacijskem zakonu; pri tem splošnost izreka ne bo prav nič trpela, niti ne bomo povedali več, kakor je Newton mislil.

Oglejmo si dve nebesni telesi, n. pr. Sonce in enega izmed planetov. Zaznamujmo njuni masi z M oziroma m, njuna krajevna vektorja pa z R oziroma I. Lega planeta glede na Sonce je potem določena z vektorjem

r=I-R

vektorji hitrosti obeh teles pa s časovnima odvodoma

V = R'
v = I'

Če označimo z

ro = r/r

enotni vektor v smeri od Sonca proti planetu, je po Newtonovem zakonu sila, s katero Sonce privlačuje planet

-(fMm/r²)ro

sila, s katero planet privlačuje Sonce, pa

-(fMm/r²)ro

Ti dve sili sta po Newtonovem zakonu o akciji in reakciji enako veliki in nasprotno usmerjeni.

Gibalni enačbi za masi M in m sta torej

MV' = (fMm/r²)ro
mv' = -(fMm/r²)ro

Če ju seštejemo, dobimo

MV' + mv'= 0

in če integriramo.

MV + mv = B

kjer je B konstanten, od časa neodvisen vektor.

Izraza MV in mv nam po Newtonovi dešinicilji pomenita gibalni količini obeh teles. Zgornja enačba nam pove, da se vsota gibalnih količin ne spreminja, kakor koli se telesi gibljeta; (če ne delujejo nanju še kakšne druge, zunanje sile); to je Newtonov izrek o ohranitvi gibalne količine.

Krajevni vektor skupnega težišča abeh mas M in m je sorazmEren vektorju

S = MR+mI

Hitrost težišča je torej sorazmerna vektorju

S' = MR'+mI',

t. j.

S' = MV+mv,

Iz zgornjih enačb sledi

S' = B,

kjer je B konstanten vektor.

Ta enačba nam pove, da se giblje težišče v prostoru premočrtno in enakomerno.

Zgornja razmišljanja veljajo za poljubno število nebesnih teles, ker se njihove privlačne sile medsebojno uničujejo. Zato je Newton lahko izrekel še tale stavek.

Medsebojni vpliv dveh ali več nebesnih teles ne more spremeniti stanja mirovanja ali gibanja njihovega skupnega težišča; zato bo to težišče (če ni zunanjih sil ali ovir) ali mirovalo ali pa se bo gibalo enakomerno in premočrtno.

Newton je uporabil ta izrek za naše osončje in dejal:

(160, 161) Skupno težišče Sonca in planetov ali miruje ali pa se giblje enakomerno in premočrtno.

Sonce se neprestano giblje, vendar pa se le zelo malo oddaljuje od tega tezisca.

S tem spoznanjem se je Newton povzpel visoko nad Kopernika in nad mnenje vseh svojih vrstnikov.

Njegova nadaljnja. razglabljanja o problemu dveh teles nas privedelo do sledece ugotovnve.

Če delimo zgornji dve enačbi za gibanje mas M in m, prvo z M in drugo z m, in odštejemo prvo enačbo od druge, dobimo

v' - V' = -f(M+m)ro/r²;

ker pa je po prejšnjih enačbah

v' - V' = d²I/dt² - d²R/dt² = d²r/dt²

dobimo

m d²r/dt² = -f(M+m)ro/r².

Povedano v našem sedanjem jeziku je to diferencialna enačba za gibanje planeta okrog Sonca. Vidimo, da se planet giblje okrog Sonca, kakor če bi Sonce mirovalo, imelo pa maso (M + m) in privlačilo planet po Newtonovem zakonu.

Iz tega sledi, da se dve nebesni telesi gibljeta tudi drugo glede na drugo po elipsah. Iz teh relativnih gibanj lahko z zakonom o gibanju težišča izpeljemo njuno absolutno gibanje v prostoru in narobe. Ker deli težišče zveznico dveh nebesnih teles vedno v stalnem razmerju njunih mas, so si vsi ti tiri, v našem primeru elipse, med seboj podobni. Newton je to povedal z izrekom, ki velja ne glede na to, po kakšnem zakonu se telesi privlačujeta. Izrek se glasii:

Dve telesi, ki se privlačujeta, opisujeta akrog skupnega težišča ali pa drugo okrog drugega podobne geometrijske like.

Newton je v prvi knjigi svojih "Načel" predpostavil, da je središče sil nepremično. V našem primerur ko smatramo Sonce za to središče, nam zgornja enačba pove, da je Newtonova predpostavka opravičljiva, saj je masa planeta v primeri z maso Sonca tako majhna, da lahko M + m zamenjamo z M.

Da ni svojega računa tako poenostavil, bi bil Newton namesto enačbe

f = 4p²a³/(T²M)

ki smo jo izpeljali ob predpostavki, da Sonce miruje, dobil enačbo

f(m + M) = 4p²a³/T²

Ta enačba izraža zvezo med velikimi polosmi a planetnih tirov in njihovimi obhodnimi dobami T, ki ni popolnoma v skladu s tretjim Keplerjevim zakonom. Po tem zakonu je količnik

a³/T²

za vse planete isti, kar po zgarnji enačbi ne bi bilo res, saj je masa m in s tem vrednost tega količnika pri vsakem planetu drugačna. Ker pa so mase planetov v primeri z maso Sonca zelo majhne, lahko v zgornji enačbi m zanemarimo spričo M in tako tretji Keplerjev zakan vskladimo z zakoni nebesne mehanike.

Newton je maso planeta zanemaril spričo mase Sonca, da bi lahko ugotovil, kolikšen del sončne mase so mase tistih planetov, ki imajo lune.

Naj ima planet z maso m luno z maso ml, ki je v primeri z m. tako majhna, da jo lahko zanemarimo. Če zaznamujemo veliko polos tira, po katerem se giblje luna okrog planeta, z a1, njeno obhodno dobo pa s T1, velja enačba

f = 4p²a1³/(T1²m)

Z deljenjem dobimo iz poslednjih dveh enačb

m/M = (a1/a)³(T/T1)²

Po tem obrazcu se da izračunati razmerje med maso m planeta in maso M Sonca, če sta znani veliki polosi tirov planeta in njegove lune ter njuni odhodni dobi. Newton je to izračunal za vse planete, katerih lune so bile takrat znane. Če vzamemo maso Sonca za enoto, so po Newtonovih ugotovitvah mase Jupitra, Saturna in Zemlje

1/1067,1/3121,1/169282

Čeprav takrat paralaksa Sonca še ni bila natančno ugotovljena, je dobil Newton za masi dveh največjih planetov, Jupitra in Saturna, še dokaj pravilne vrednosti. Ob njih se je lahko prepričal, da se težišče osončja lahko samo za spoznanje premakne iz sončne oble.

Iz tega Newtonovega računa, s katerim je tako rekoč stehtal planete, so sledila še nova dognanja. Newtonov račun je pokazal, da so mase planetov v primeri z maso Sonca brez izjeme zelo majhne. Zato je vpliv njihove medsebojne privlačnosti neznaten, tako da je letni hod vsakega posameznega planeta skoraj prav takšen, kakršen bi bil, da ga privlačuje samo Sonce. Medsebojna privlačnost planetov se kot nekakšna majhna motnja očituje šele po daljših časovnih presledkih.

Newton se je zanimal tudi za te motnje. Ugotovil je, da Jupiter in Saturn znatneje vplivata drug na drugega, kadar sta blizu svoje konjunkcije, in da Sonce precej moti gibanje Lune okrog Zemlje. Ko je raziskoval te motnje, je pojasnil nekatere njihove posledice, ki so jih bili ugotovili empirično, z opazovanji, že pred njim in jih imenovali neenakosti. V svojem delu je Newton zgradil temelje za računanje planetnih motenj, ki je bilo potem skozi dve stoletji najvažnejši problem nebesne mehanike.

Oglejmo si le najpomembnejše Newtonove raziskave na tem področju.

Eno izmed vprašanj je bilo, kako se giblje Luna okrog Zemlje, če upostevamo tudi privlačnost Sonca. Ta privlačnost povzroča, da se giblje Luna drugače, kakor bi se morala, ko bi jo privlačevala samo Zemlja. S tem se je Newton lotil problema treh nebesnih teles, ki ga popolnoma in dokončno še do danes niso mogli rešiti in ki ga tako najbrž nikoli ne bo mogoče rešiti. Vendar pa se je Newtonu že pri tem prvem poskusu posrečilo razložiti nekatere izmed najvažnejših, že z opazovanji ugotovljenih neenakosti Luninega gibanja. Najpomembnejša ugotovitev se je tikala premikanja vozlov Luninega tira. Že stari aleksandrijci so vedeli, da je Lunin tir nagnjen proti ekliptiki v stalnem kotu, ki so ga znali izmeriti. Ta tir in ekliptika se sekata v dveh diametralnih točkah nebesne sfere, ki ju imenujemo vozla in o katerih smo že govorili. Aleksandrijci so vedeli, da se vozla pomikata retrogradno vzdolž ekliptike in jo obhodita približno v 18 letih. Vzrok tega pojava je bil popolnoma neznan, dokler ga ni ugotovil Newton. Na podlagi svojega gravitacijskega zakona pa je Newton popolnoma razjasnil, kako privlačna sila Sonca na Zemljo in Luno povzroča ta pojav.

Slišali smo že, da sta Huyghens in Newton s centrifugalno silo in sploščenostjo Zemlje razložila, zakaj je kazala Richerova ura v Cayenni drugače kakor v Parizu. Huyghens je sploščenost Zemlje izračunal tako, da je smatral zemeljsko težo spočetka za konstantno na površini Zemlje in jo potem zmanjšal za velikost centrifugalne sile, ki se menja z zem(jepisno širino in je največja na ekvatorju, na tečajih pa enaka nič. Zaznamujmo premer zemeljskega ekvatorja z a, s c pa razdaljo med obema tečajema, in imenujmo

n = (a-c)/a

razplošček Zemlje. Huyghens je našel n = 1/578 . Newton je šel v svojih "Načelih" še naprej. Na podlagi zakona o privlačnosti in izrekov, ki jih je navedel v prvi knjigi svojega dela, je izračunal tudi privlačnost sploščenega elipsoida in ob upoštevanju centrifugalne sile dobil, da je n = 1/230. Tako se je bolj ko Huyghens približal pravi vrednosti n=1/298

Z gravitacijskim zakonom je Newton lahko pojasnil še dva zelo pomembna naravna pojava, ki sta bila znana že prej, pa niso vedeli, kaj ju povzroča. Prvi je precesija točk enakonočja, znana in empirično raziskana že od Hiparhovih časov. Newton je združil svoje dognanje o sploščenosti Zemlje z razlago, zakaj se vozli Luninega tira premikajo, in na prvi pogled spoznal mehanizem precesije. V četrtem poglavju tretje knjige svojih "Načel" jo je na štirih straneh razložil takole.

Ko bi bila Zemlja popolna krogla, bi njena vrtilna os ne spremiojala smeri v prostoru, kajti rezultanta privlačnih sil Sonca, pa tudi Lune, na delce zemeljske snovi bi bila usmerjena skozi središče Zemlje. Opišimo torej okrog središča Zemlje kroglo z razdaljo zemeljskih tečajev kot premerom in izločimo tisti del Zemlje, ki leži znotraj te krogle i n ki za razlago premikanja zemeljske osi v prostoru ne pride v poštev. Ostane nam pas Zemljine nabrekline, ki je najdebelejši na ekvatorju, proti tečajema pa čedalje tanjši. Vsak delec snovi iz tega pasu kroži okrog zemeljske osi, Vsak tak delec lahko torej smatramo za Zemljino luno. Povedali smo, da privlačna sila Sonca na Zemljo in Luno premika ravnino Luninega tira; podobno deluje tudi na vsak delec Zemljinega pasu. Razlika je samo ta, da vozle tirov teh delcev nadomestujeta sečišči nebesnega ekvatorja z ekliptiko, t. j. točki enakonočja. Zato lahko sklepamo, da se bosta točki enakonočja premikali vzdolž ekliptike v nasprotnem smislu, kakor se vrti Zemlja; to pa je ravno precesija. Pri precesiji sodeluje ne le Sonce temveč tudi Luna in sicer zaradi svoje bližine še bolj kakor Sonce; njuna vpliva se seštevata in skupaj povzročata lunisolarno precesijo. (164, 165)

Tako je Newton pojasnil precesijo; popolna teorija tega pojava pa se je razvila šele v naslednjih dveh stoletjih. Iz teh razmišljanj je sledilo še nekaj važnega: ker se presek ravnine Zemljinega tira in ravnine Luninega tira premika in v 18 letih naredi obhod, se mora z isto periodo spreminjati tudi smer zemeljske osi v prostoru.

Drugi izmed omenjenih pojavov, ki ga je Newton v zvezi z zgoraj navedenimi razglabljanji pojasnil v svojih "Načelih", je bila že davno znana morska plima. Newton jo je pojasnil kot posledico privlačne sile Lune in Sonca na zemeljsko hidrosfero, in sicer na način, ki ga še dandanes uporabljamo za preprosto razlago tega pojava. S to Hstatično" teorijo je Nevton pojasnil osnovne pojave bibavice, delež Sonca in Lune, glavne periode in nepravilnosti plime, njene ekstreme v času sizigija in Luninih kvadratur, njeno povečanje v času enakonočja in kadar je Luna v perigeju. Ta teorija je bila izhodišče za poznejšo dinamično teorijo o plimi, ki je tudi kvantitativno razložila vse podrobnosti tega pojava.

Zadnje poglavje tretje knjige Newtonovega dela je posvečeno zvezdam repaticam. Konec leta 1680 se je prikazal na nebu bleščeč komet in seveda vzbudil pozornost vseh opazovalcev neba. Bil je eden izmed prvih glavnih objektov pet let prej ustanovljenega astronomskega observatorija v Greenwichu. Ustanovitelj in prvi upravnik tega observatorija je bil ktaljevski astronom John Flamsteed (1646-1719). Zasluge si je pridobil ne le z ustanovitvijo tega zavoda, ki je kmalu zaslovel po vsem svetu, marvec tudi z zelo natančnim in vestnim opazovanjem neba, saj je zbral gradivo za prvi veliki moderni zvezdni katalog, ki je izšel po njegovi smrti.

Flamsteed je opazoval omenjeni komet od 12. XII. 1680 do 5. II. 1681, Newton pa od 25. II. 1681 do 9. III. 1681. Newton je opazoval komet osebno, ker ga je imel za nov predmet, in problem svoje teorije. Na podlagi teh opazovanj in opazovanj svojih predhodnikov, zlasti še omenjenega Hevela, je prišel Newton do sledečih sklepov.

Kometi se gibljejo onstran Luninega tira in prihajajo iz medplanetnega prostora. Gibljejo se po stožernicah z goriščem v središču Sonca. Zveznice kometov s Soncem opisujejo ploščine, sorazmerne časovnim presledkom. Tiril kometov so tako splošcteni, da se le neznatno razlikujejo od parahol. Iz tega je sledilo, da se tudi kometi gibljejo po Newtonovem gravitacijskem zakonu pod vplivom sončne privlačnosti. To so potrdila vsa poznejša opazovanja.

Da bi se dale iz opazovanj ugotoviti poti kometov, je bilo treba rešiti tale geometrijski problem. Znane so tri časovno med seboj dovolj odaaljene lege kometa; ugotoviti je treba njegov tir, če predpostavljamo, da je parabola. Newton je rešil ta problem in tako zgradil temelj za računanje tirov nebesnih teles.

Newtonu se ni mudilo sporočiti svoja dognanja javnosti. Le tu in tam je povedal kaj o tem svojim prijateljem, ta čas pa je svojo teorijo dopolnjeval in izpopolnjeval. Morda bi bil to delal še leta in leta, da ga ni izpodbudil Halley.

Edmond Halley (1656-1742), sin industrijca iz londonske okolice, je že v mladih letih kazal veliko ljubezen in nadarjenost za matematiko in astronomijo. Bilo mu je komaj 20 let, ko je bila neka njegova razprava objavljena v bTransakcijah" Kraljevskega društva. Takoj nato ga je poslala angleška vlada na Sveto Heleno opazovat južno nebo in sestavit katalog njegovih zvezd. Ko je uspešno izpolnil to nalogo,,je bil l. 1678 sprejet v Kraljevsko društvo. Leta 1679 je obiskal tr Gdansku Hevela. Ta obisk,, pa tudi velika kometa, ki sta se prikazala, prvi že omenjeni l. 1680, in drugi, o katerem bomo še govorili, l. 1682, so mu vzbudili zanimanje za te nebesne pojave. Začel je razmišljati, kako bi iz podatkov, ki jih je dobil z opazovanjem, izračunal kometne tire. 0 tem je leta 1684 vprašal Newtona, ki pa mu je sporočil že dokončno rešitev problema in mu dovolil, da jo uporabi.

S tem pripomočkom se je Halleyju posrečilo dokazati periodičnost nekaterih kometov in povezati svoje ime z najsvetlejšim izmed njih. To je bil veliki komet, ki se je prikazal na nebu leta 1682. Na podlagi podatkov, kil jih je dobil z opazovanji, in z Newtonovo teorijo je Halley izračunal elemente kometovega tira, pri tem pa predpostavil, da je njegov tir parabola. Podobne račune je naredil tudi za druge komete, ki so jih opazovali že prej, če je le imel dovolj zanesljive podatke, da je lahko izraču_nal njihove parabolične tire. Rezultate svojih računov je l. 1705 objavil v HTransakcijah" Kraljevskega društva pod naslovom HAstronomiae cometicae SynopsisK. Tabela elementov raznih kometnih tirov je pokazala, da imajo kometi, ki so jih opazovali v letih 1531, 1607 in 1682, skoraj povsem enake tirne elemente, naklone tirov, astronomske dolžine perihelov in dvižnih vozlov in perihelne oddaljenosti. Halleyu je prišlo na misel, da so bile to periodične vrnitve istega kometa, ki približno v 75 letih obide Sonce in se ne giblje po paraboli, marveč po zaključeni eliptični poti. Ko je tako ugotovil obhodno dobo, je lahko po tretjem Keplerjevem zakonu izračunal veliko polos in vse elemente eliptičnega kometovega tira. Še en dokaz, da je ta komet res periodičen, je odkril, ko je posegel še za eno tako periodo nazaj, t. j. v leto 1456. Našel je zapisano, da se je tistega leta med bitko pri Beogradu prikazal na nebu bleščeč komet in enako prestrašil tako turško kakor tudi krščansko vojsko Ivana Hunyadyja, ki sta se tam bojevali.

Ko je tako astronomsko in zgodovinsko ugotovil obhodno dobo kometa, je lahko Halley napovedal, da se bo isti komet prikazal na (166, 167) nebu leta 1759, kar se je tudi zgodilo. Komet se je v redu prikazal tudi 1835. in 1910. leta.

Do danes se je posrečilo zgodovinsko dognati kakšnih trideset primerov, ko se je prikazal Halleyjev komet, in sicer vsa njegova zaporodna prikazovanja nazaj do 87. leta pred našim štetjem; ugotovljeno je tudi, da so ga videli 1. 240 pred našim štetjem. Ta komet, ki mu pravimo Halleyjev, je eno izmed najzanimivejših nebesnih teles. Tudi ta komet je dokaz, da drži Newtonov gravitacijski zakon.

Halley, ki je postal po Flamsteedovi smrti upravnik observatorija v Greenwichu in ga še bolj izpopolnil kakor njegov prednik, si je tudi sicer pridobil zasluge za astronomijo. Njegova raziskovanja zemeljskega magnetizma pa so bila važna za razvoj geofizike. Halley je astronomom pokazal, kako se da po prehodih Venere preko Sonca ugotoviti sončna paralaksa natančneje kakor prej. Ko je primerjal na novo ugotovljene lege zvezd stalnic s podatki Ptolemejevega uZbornika", se je prepričal, da so se Sirius, Aldebaran in Arcturus na zvezdnem nebu premaknili. Tako je dokazal, da zvezde stalnice ne zaslužijo imena, ki so jim ga dali stari zvezdoslovci.

Prijateljstvo med Newtonom in Halleyjem je bilo blagodejno tudi za Newtona. Kakor smo že omenili, je Halley spoznal, kako zelo važno je Newtonovo delo, in pregovoril je Newtona, da je svoje delo objavil. Newton ga je poslal Kraljevskemu društvu.

Na znameniti seji Društva 28. aprila 1686 je poročal o Newtonovem delu doktor Vincent, na seji 19. maja pa so sklenili tiskati ga na društvene stroške. Skrb za tiskanje so zaupali Hal'leyju. Ker pa društvo ni imelo dovolj denarja, mu je priskočil na pomoč Halley z lastnimi sredstvi. Delo, ki je dobilo predvideni naslov HPhilosophiae naturalis principia mathematica", je bilo dotiskano maja 1687. Glede datuma, kdaj je bila vsebina dela objavljena, si mnenja nasprotujejo. Eni menijo, da je bila objavljena že na seji Kraljevskega društva 28. aprila 1686, drugi pa, da šele takrat, ko je bilo delo dotiskano, torej leto dni pozneje.

Newtonova >,Načela" so po vsebini še dandanes med vsemi znanstvenimi deli na prvem mestu. Prvič zato, ker je v tem delu objavljen splošni naravni zakon, ki se mu pokorava vse vesoljstvo, drugič pa, ker se po tem zakonu uravnava gibanje vseh nebesnih teles z absolutno matematično natančnostjo, tako da ga lahko z računom spremljamo v daljno bodočnost in davno preteklost. Zato vidimo v Newtonovem delu še dandanes vrhunec eksaktnih znanosti, vzor pozitivne filozofije in veličasten dokaz, kako daleč sega moč duha. Ustvaritelja tega dela občudujemo kot najsijajnejši primer človeškega genija.

Ustavimo se za trenutek ob tem primeru. Lastnosti in sposobnosti genialnih ljudi so lahko samo človeške. Od sposobnosti drugih Ijudi se razlikujejo z živim utripanjem in popolno harmonijo; genialen človek ima več sposobnosti in nenavadnejše lastnosti. Glavna med njimi je genialna intuicija, jasnovidnost, ki sega dalje kakor pogled navadnega smrtnika, in dojema nove, neslutene probleme. Kakor smo videli, je bil Newton nedosegljivo jasnoviden že v mladih letih, ko je v duhu daleč pred seboj zaglectal tri velike probleme. Ni pa zadostovalo zaslutiti jih, treba se je bilo dokopati do njihove popolne, neovrgljive rešitve. Za to pa je bilo treba položiti temelje in zgraditi dve novi znanosti , infinitezimalni račun in racionalno mehaniko. In Newton je s svojim širokim filozofskim obzorjem, z neusmiljeno samokritiko in sistematičnim umstvenim delom tudi v tem daleč prekosil vse svoje predhodnike in vrstnike. Za to delo je bila potrebna temeljita zbranost misli, in Newton jo je dosegel tako, da se je odpovedal samemu sebi in vsemu svetu. Ves se je posvetil svoji znanosti in prav nič se ni zmenil za to, kaj bo svet mislil o njem in njegovem delu. Otresel se je slehernega častihlepja in hrepenenja po javnem priznanju, če ga je sploh kdaj imel. Po bridkih izkušnjah s svojimi optičnimi izsledki je javno priznanje z dna duše zaničeval. Zato ni niti s prstom ganil, da bi objavil svoja epohalna dela s področja višje matematike, čeprav mu je bilo to kot uglednemu članu Kraljevskega društva omogočeno. Pustil jih je, da so ležala neobjavljena v predalu njegove pisalne mize. Nehal je tudi objavljati kar koli s področja optike. Tako je zbral misli za svoje glavno delo in znal vložiti vanj višek svojih umstvenih sposobnosti.

Usoda je Newtonu namenila, da je ta vrhunec svojega znanstvenega poleta preživel za celih štirideset let in da je v domovini doživel zasluženo priznanje za svoje delo. Od leta 1688 je zastopal cambriško univerzo v angleškem arlamentu, Kraljevsko društvo pa ga je od leta P 1703 tja do njegove smrti vsako leto izvolilo za predsednika. Leta 1696 se je preselil v London, kjer je najprej kot inšpektor, od leta 1699 pa kot generalni intendant Kraljevske kovnice živel v izobidju, v hiši svoje nečakin'e Katarine, gospe Conduit, z letno lačo 2000 funtov. Vendar J 'P pa ves ta čas ni napisal ničesar, kar bi se dalo primerjati z njegovim glavnim delom; zadovoljil se je s tem, da je objavljal svoje dotlej neobjavljene starejše razprave, že objavljene pa ponovno izdajal in dopolnjeval. Leta 1704 je izdal svoje veliko delo "Optics", napisano v angleščini, v katerem opisuje svoje eksperimentalne izsledke na tem področju in razvija svojo emisijsko teorijo o svetlobi. Razen Optike sta bili natisnjeni še dve matematični razpravi uEnumeratio linearum tertii ordinis" in "De quadratura curvarum". Prva se ukvarja z razvrstitvijo krivulj tretjega reda, druga pa z uporabo fluksijskega računa za računanje ploščin likov ki jih oklepajo krivulje. Leta 1706 je izšla še latinska izdaja Optike, leta, 1707 "Arithmetica universalis", leta 1711 "Methodus differentialis" leta 1718 druga, (168, 169) leta 1721 pa tretja izdaja Optike v , angleščini. Tudi "Načela" so bila že pred njegovo smrtjo trikrat natisnjena, drugič leta 1713 in tretjič leta 1726. Skrb za ti dve izdaji je Newton zaupal svojima učencema Cotesu in Pembertonu in dodal vsaki izdaji samo nekaj spremnih besedi. Cotes je za drugo izdajo napisal obširen uvod.

Če upoštevamo, kaj vse je Newton ustvaril od leta 1666 do 1686 , torej v dvajsetih mladih l etih, se nam zdi, da je v naslednjih štiridesetih letih naredil bore malo. Često so se vpraševali kaj je bilo vzrok tega. Vzrokov je bilo več. Mlada leta so vredna več kakor stara in Newton se je v mladosti, ko je odkril gravitacijski zakon, vzpel tako visoko, da više ni mogel. Prav gotovo pa se mu po tem velikem problemu ni hotelo ukvarjati z nepomembnimi malenkostmi. Morda je tudi čutil, da njegova ustvarjalrost ni več takšna, kakor je bila nekdaj.

Od leta 1691 do 1693 je Newton bolehal za nespečnostjo, imgubo spomina in splošano dvševno razdvojonostjo; razdobje aned letl 1708 in 1716 pa mu je zagrenil prepir za prvenstvo v iznajdbi infinitezimalnega racuna.

Ta prepir je nastal takole. Gottfried Wilhelm Leibniz (1646 do 1716), potomec slovanske rodbine Lubenijec, veliki nemški filozof, ki se je od leta 1676 z velikim uspehom ukvarjal tudi z infinitezimalnim računom, je trdil, da je on odkril ta račun in ne Newton. Newton, ki je v prvi izdaji svojih "Načel" priznal Leibnizu njegove zasluge za razvoj infinitezimalnega računa in ki ni bil prav nič častihlepen, se je žečel izogniti prepiru. Toda vmešali so se še drugi angleški in nemški znanstveniki, ki so menili, da gre tu za narodno čast. Začel se je dolgotrajen spor, ki še dandanes ni čisto dognan. V tej pravdi je Leibniz pogorel. Anglezem se je posrečilo neovrgljivo dokazati ne le Newtonovo prednost, marveč tudi to, da je Leibniz po posredovanju omenjenih Collinsa in Oldenburga, tajnika Kraljevskega društva, prišel do prepisa prvih Newtonovih razprav o fluksijski teoriji, še preden so bile objavljene, in iz njih dobil navdih in vzpodbudo za svoje delo. Žal Leibniz ni sprevidel, kako neutemeljen in nepremišljen je bil njegov napad na Newtona. Ko bi mu bil pošteno priznal prvenstvo, bi se bil lahko še vedno skliceval na tisto, kar je sam ustvaril. Tega pa je bilo toliko, da nihče ne bi bil mogel tajiti njegovih velikih zaslug za razvoj infinitezimalnega računa. Kar se tega tiče, je bil Leibnizev odnos do Newtona podoben Kopernikovemu do Aristarha.

Šele na stara leta, ko jih je štel že blizu osemdeset, je Newton začel pešati in bolehati. Leta 1725 se je odpovedal mestu upravnika Kraljevske kovnice in se preselil v kraljevo letovišče Kensington, v okolici takratnega Londona. Vendar pa je skoraj še do zadnjega prcdsedoval sejam Kraljevskega društva. Seja dne 28. februarja 1727 je bila njegova zadnja. Ko se je po njej, 4. marca, vrnil domov v Kensington, je obležal in 29. marca 1727. umrl. Pokopali so ga v cerkvi, kjer kronajo angleške kralje, v Westminstrski opatiji, s častmi, ki so jih sicer deležni samo člani kraljeve rodbine. (170, 171)
================================================================================

1. KRATKA ZGODOVINA ASTRONOMIJE

2. Oglej si tudi izjemno zanimive odlomke iz različnih virov, kjer so opisani ljudje - raziskovalci, čas in dogodki ob nastanku velikih naravoslovnih odkritij.

Povzel Zorko Vičar

Nazaj na zgodovino.
Nazaj na domačo stran.