
TELESKOPI
|

|

|

|

|

|

|

|

|

|

|


|

|

|

|

|

|

|

|

|

|

|

 Vsebina te strani se v okviru časa in ustreznega gradiva dopolnjuje.
Vsebina te strani se v okviru časa in ustreznega gradiva dopolnjuje.

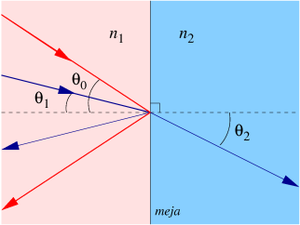
Izračunaj mejno magnitudo (ali premer objektiva teleskopa, če poznaš mejno magnitudo) s spodnjo formo. Vtipkaj premer objektiva v mm, klikni in dobil boš mejno magnitudo teleskopa.
1) Kakšen teleskop bi naj kupili? Kupili pa ga bomo vsekakor, saj imate(mo) doma že podobno "nepotrebno" navlako kot so minljivi: 2Xavto, 2XTV, 3XPC, obleke za nekaj 100000 SIT (nekaj 100 ali več EUR) ...
Ne kupite
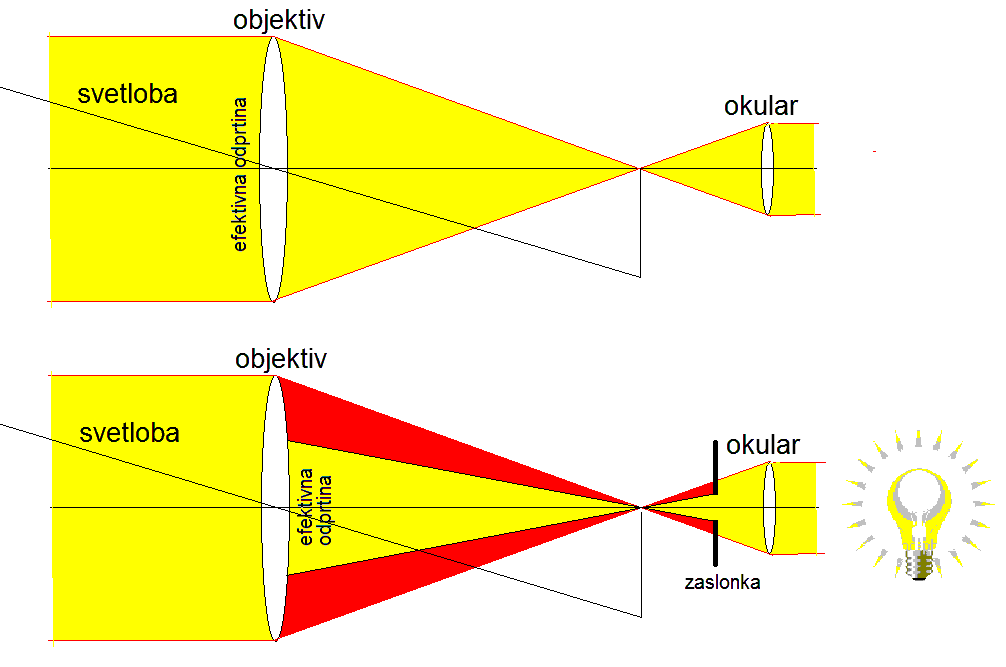
POVEČAVE (200X, 400X, ...), kupite TELESKOP, kar pomeni, kupite napravo s čim večjo vhodno odprtino, da zberete čim več svetlobe. Spomnite se samo, kako se zenica očesa razširi v temi. Dobro je, da nam teleskop približa objekte, še bolj pomembno pa je, da zbere čim več svetlobe milijone let oddaljenih objektov, tako da je slika le teh dovolj svetla, torej da objekte sploh lahko zaznamo, opazujemo.Kaj recimo pomeni napis (5", f/6,3) na teleskopu, ki bi ga jaz že priporočal.
5" je premer objektiva (vhodne odprtine)
v palcih ali "inčih" (D=5"=12,7cm), številka 6,3 pa je zaslonka teleskopa (f/D), f je goriščna razdalja teleskopa. Kvocient D/f=1/(f/D) je relativna odprtina teleskopa (v našem primeru je to 1/6,3). Večja relativna odprtina teleskopa da svetlejšo sliko. Zaslonka in relativna odprtina sta obratno sorazmerni količini (D/f=1/(f/D)=1/zaslonka).Če pomnožimo premer objektiva s številko 6,3 (zaslonko), dobimo goriščno razdaljo objektiva teleskopa (f= 6,3XD=6,3X12,7cm=80cm). Še enkrat, zaslonka je razmerje med goriščno razdaljo in premerom objektiva, tako kot pri fotoaparatu. Večja je odprtina teleskopa (pri enaki goriščni razdalji), manjša je zaslonka, večja je relativna odprtina, svetlejša je slika. Priporočam zaslonke med 5 in 10.
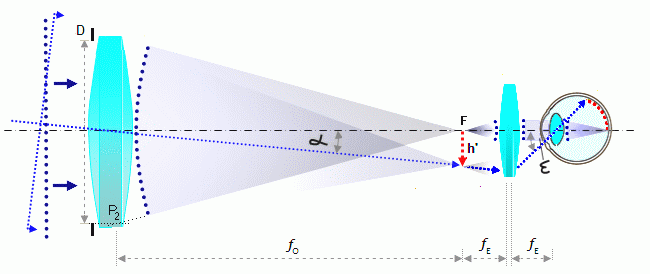
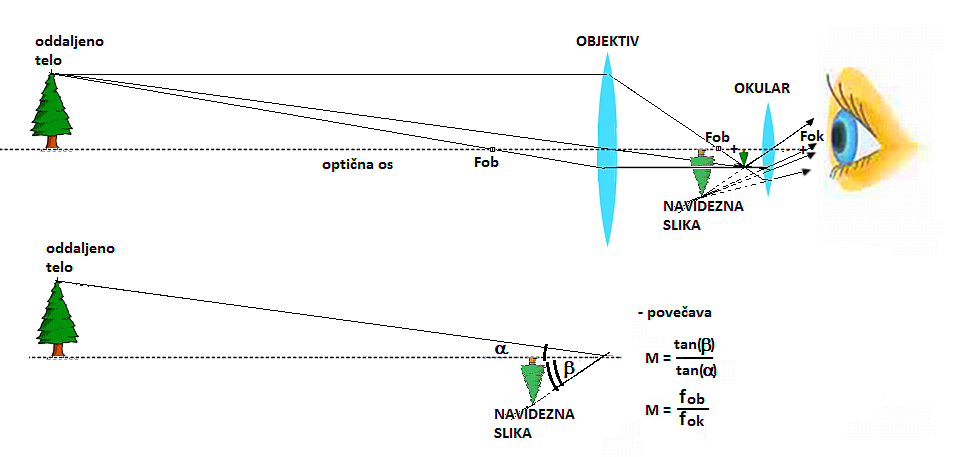
Povečava optičnih naprav je povezana z zornim kotom, pod katerim vidimo telo s prostim očesom in zornim kotom, pod katerim vidimo sliko telesa v okularju (lupi). Za povečavo teleskopa dobimo preprosto povezavo, ki je kar kvocient med goriščno razdaljo objektiva teleskopa in okularjem (povečava=f
ob/fok). Primer: za že navedeni teleskop priporočam tri okularje goriščnih razdalj 5mm, 12mm in 25mm. Povečave, ki jih tako dobim so: M1=fob/fok=800mm/5mm=160, M2=fob/fok=800mm/12mm=67, M3=fob/fok=800mm/25mm=32). Prvi povečavi (160 in 67, pri premeru objektiva D=5"=12,7cm) sta primerni za planete, Luno, Sončeve pege, dvojne zvezde in nekatere svetlejše planetarne meglice, kroglaste kopice ter galaksije. Tretja povečava (32) pa je namenjena svetlejšim obsežnim meglicam, razsutim kopicam in svetlejšim bližnjim galaksijam.Kako šibke objekte pa še lahko opazujemo s teleskopm? O tem v glavnem odloča premer objektiva, oziroma zaslonka.
Formulo, s katero ocenimo mejno magnitudo teleskopa (mejni sij teles, ki jih še zaznamo), smo že omenili:
m ≈ 2+5*log10D(mm)
Z besedami, mejna magnituda je dva
plus petkrat desetiški logaritem iz premera objektiva. Premer objektiva je podan v milimetrih, vendar se milimetri ne smejo upoštevati v računu.Primer za že navedeni teleskop (m ≈
2+5*log10127=12,5).Mejne magnitude za različne objektive:
|
D(premer v mm) |
30 |
50 |
70 |
100 |
150 |
200 |
250 |
1000 |
2000 |
5000 |
|
mejna magnituda |
9,4 |
10,5 |
11,2 |
12 |
12,9 |
13,5 |
14,0 |
17 |
18,5 |
20,5 |
Izpeljava enačbe za mejno magnitudo telesa, ki ga še vidimo skozi teleskop z odprtino premera D
Sij nebesnih telesNebesna telesa različno močno sijejo ("svetijo"), pravimo, da imajo različen sij. Siju ustreza gostota svetlobnega toka, ki ga oddaja vesoljsko telo in pade na Zemljino površje. Svetlobni tok prestrežemo z očesom ali kakim drugim svetlobnim merilnikom. Svetlobni tok merimo v vatih (W), njegovo gostoto pa v vatih na kvadratni meter (W/m2). V astronomiji uporabljamo za sij nekoliko drugačno enoto. Vesoljsko telo, od katerega prihaja na Zemljo svetlobni tok z gostoto 10-8 W/m2, ima sij prve magnitude, kar zapišemo 1m. Vesoljsko telo, od katerega prihaja svetlobni tok z gostoto 10-10 W/m2, pa ima sij šeste magnitude, kar zapišemo 6m. S prostim očesom zaznamo še vesoljska telesa s sijem 6m. Vesoljska telesa, ki jih s prostim očesom ne zaznamo, imajo sije: 7m, 8m, 9m ... Z daljnogledom, ki ima odprtino 10cm, vidimo še zvezde s sijem 12m. Odprtina tega daljnogleda je okoli 20-krat večja od odprtine zenice človeškega očesa pri nočnem opazovanju. Z najmočnejšimi daljnogledi zaznamo vesoljska telesa s sijem 24m. Vesoljska telesa, vidna s prostim očesom, imajo sij: 5m, 4m, 3m, 2m, 1m, 0m, -1m, -2m itn. Nekateri ob dobrih pogojih zaznajo tudi telesa sedme magnitude. Veliko je tudi odvisno od človeške starosti, z leti se namreč očesna zenica več ne odpre toliko kot v mladosti (mlademu se odpre do 7mm ali celo več), pa tudi mrežnica in leča očesa pešata.
Severnica ima sij 2,1m, zvezda Kapela 0,2m, Vega 0m, najsvetlejša zvezda na nočnem
nebu Sirij -1,5m, Venera v največjem siju -4,4m, Luna ob ščipu -13m,
najsvetlejše telo na nebu - Sonce pa kar (-27m).

Pogson je delal na observatorijih v Angliji in Indiji.
Do leta 1847 je izračunal tira dveh kometov.
Leta 1850 je pokazal, da je povprečna zvezda z navideznim sijem
1m približno stokrat svetlejša od povprečne zvezde, z magnitudo 6m,
ki je po Hiparhu še vidna s prostim očesom. Empirična povezava
med magnitudo in gostoto energijskega toka
je "Pogsonov zakon":
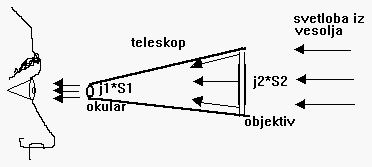
d1=dzenice=d=6mm,
m1=m
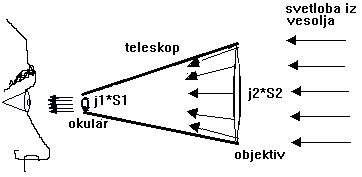
-ker (j1*S
očesa=j2*Sobjektiva ali j1*d2*π/4 =j2*D2*π/4 ), to pomeni, da v teleskop prihaja tista mejna gostota energijskega toka j2 , ki se v teleskopu zgosti na j1, energijski tok pa se pri tem ohranja (primerjava vodovodne cevi, ki se zoži, skoznjo teče enak vodni tok le hitrost se v ožjem delu poveča, v1*S1=v2*S2)-iz razmisleka sledi (D/d)2=10-2(m1-m)/5,
po logaritmiranju dobimo
m=5*log(D/d)+m1
-sledi končni izraz m=5*log
(D)-5*log6+6≈ 2+5*log(D)
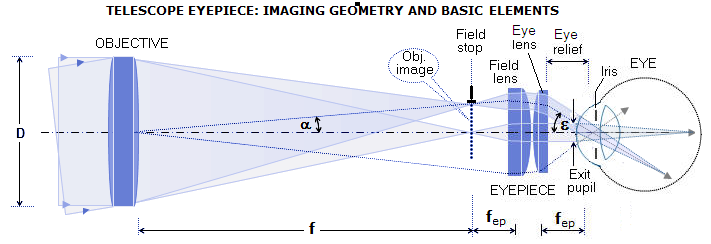
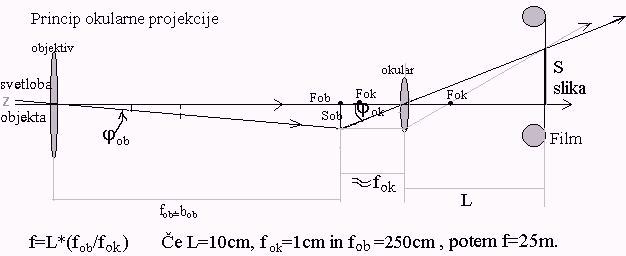
2) GEOMETRIJA NASTANKA SLIKE IN POVEČAVA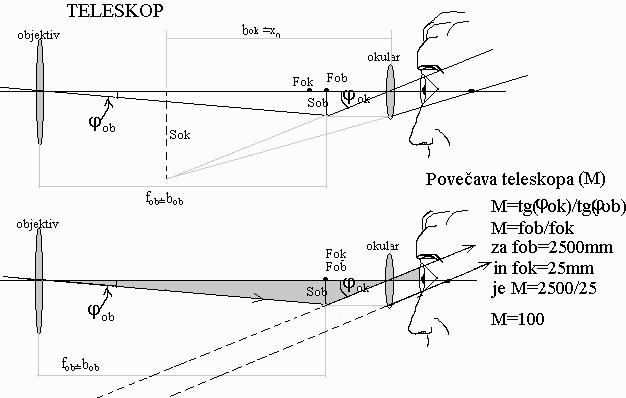
- povečava: M = fob / fok
- povečava = goriščna_razdalja_objektiva / goriščna_razdalja_okularja
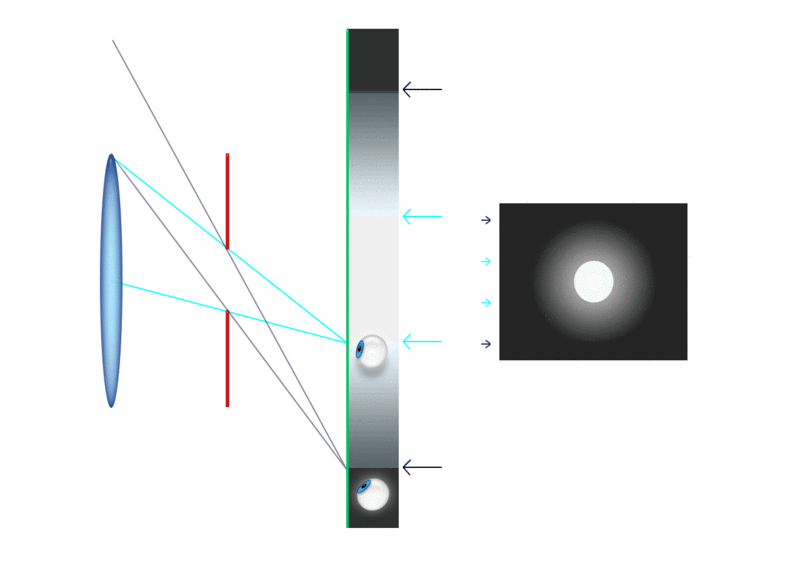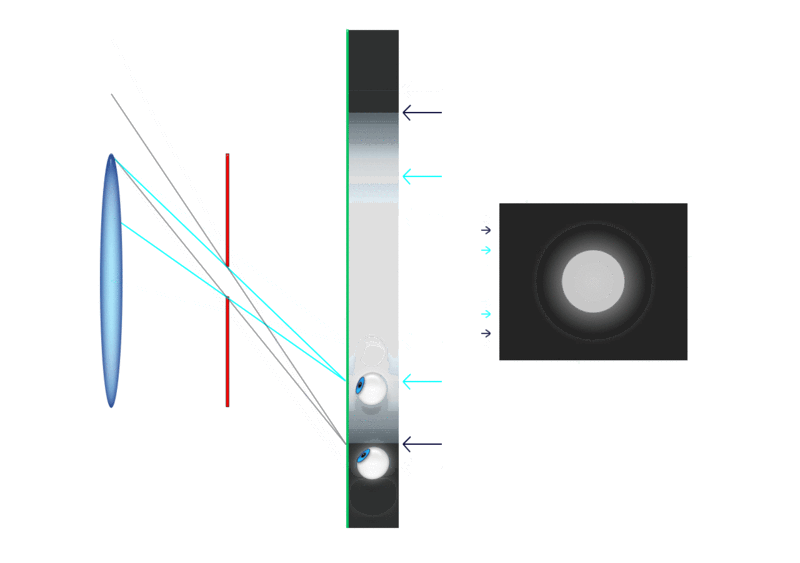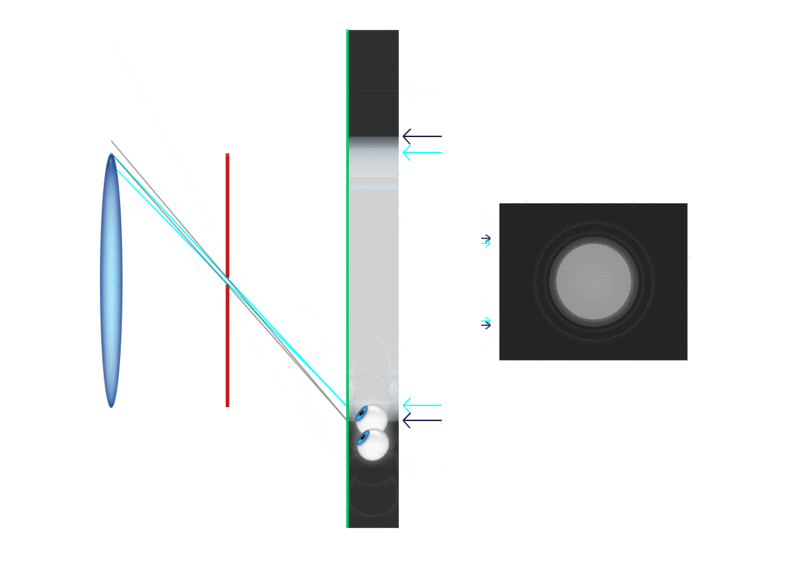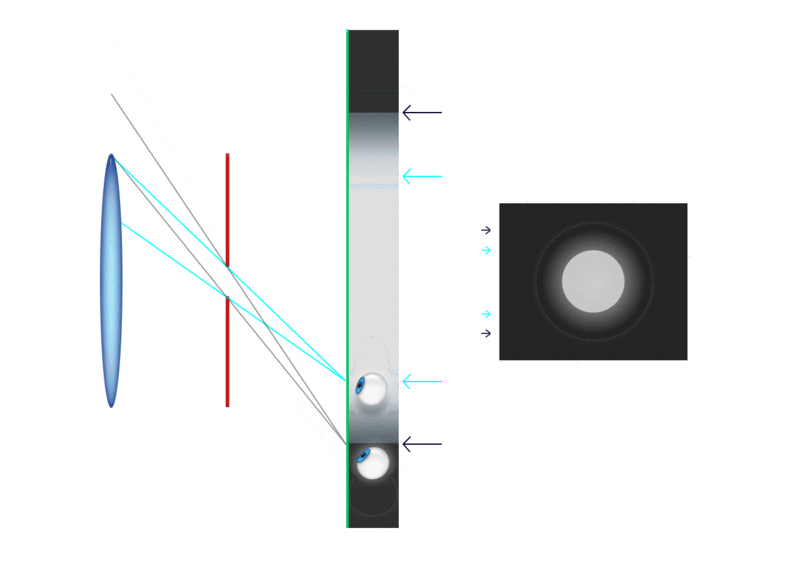
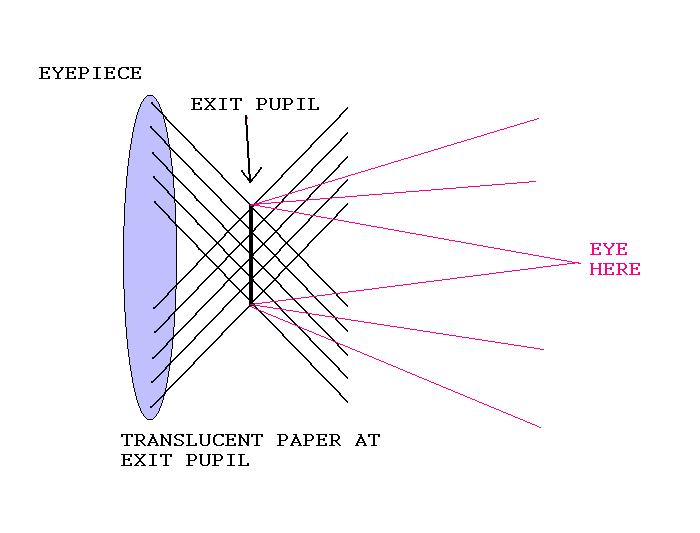
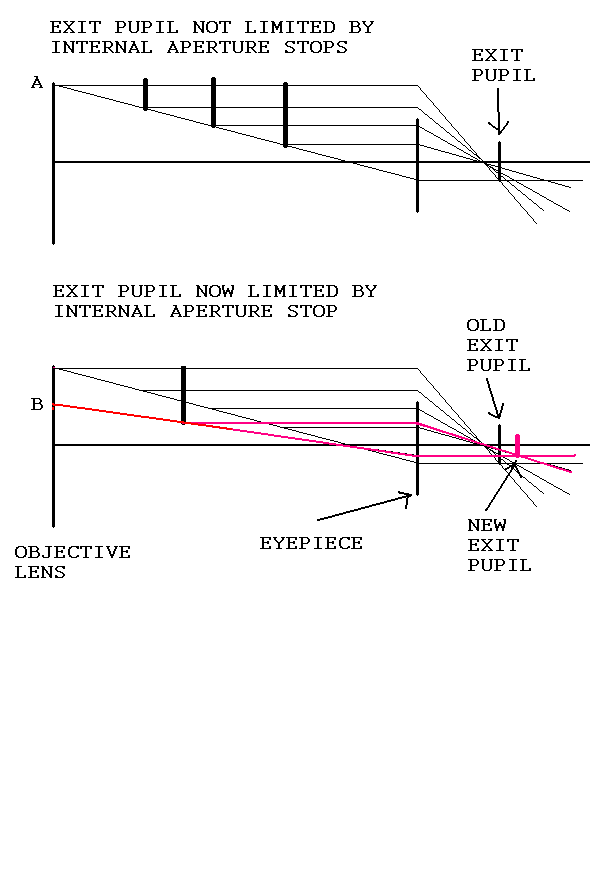
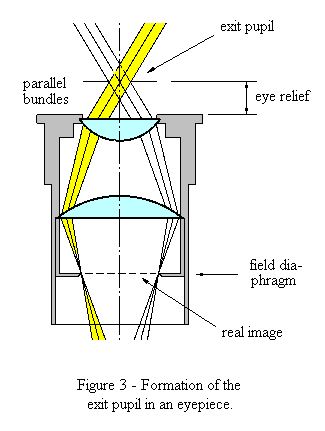
Vidno polje (zorni kot) teleskopa
Vidno polje človeškega očesa je okrog 46 stopinj
- kaj lahko sklepamo iz tega podatka
(recimo o vidnem polju okularjev)?
Zanimivost - japonski vrhunsko natrenirani piloti (druga vojna),
so imeli uporabno polje preko 110°, kar je bilo le malo manj od
maksimalnega (približno 140°). Kako je pri teleskopu z vidnim poljem?
Najprej zapišimo matematični izraz, nato pa ga bomo utemeljili.
vidno_polje = vidno_polje_okularja / povecava
(izraz v angleščini - true FOV: true Field Of View, dejansko vidno polje)
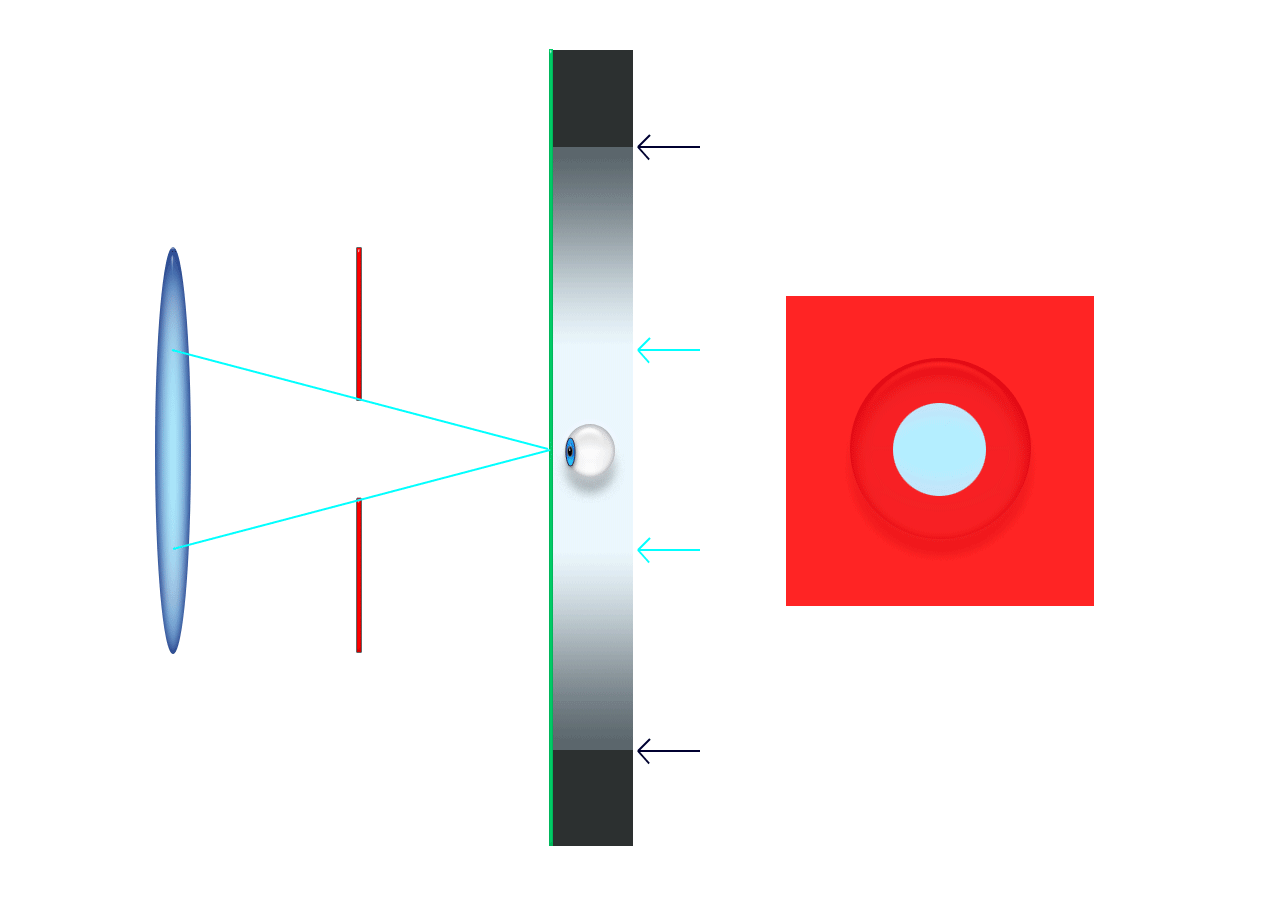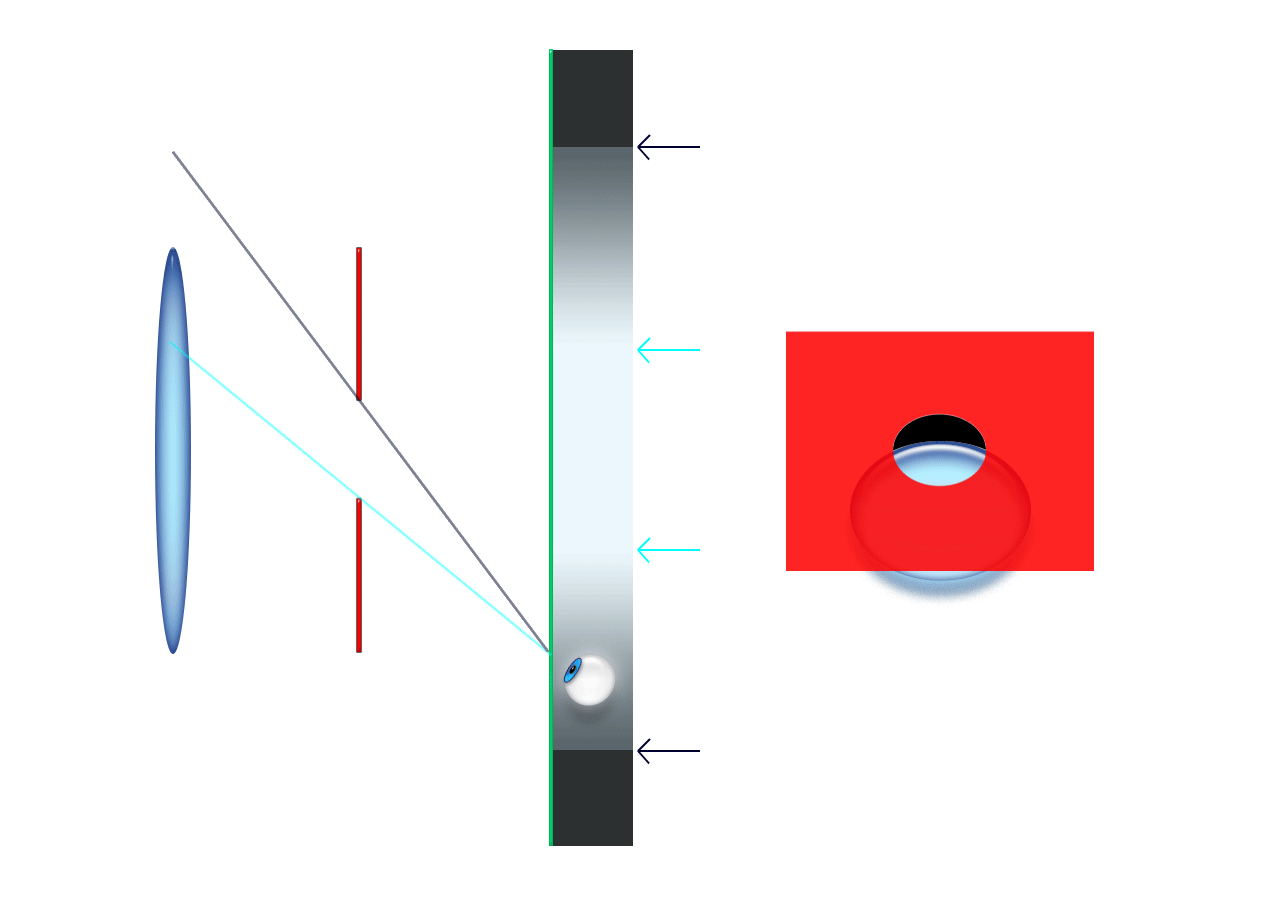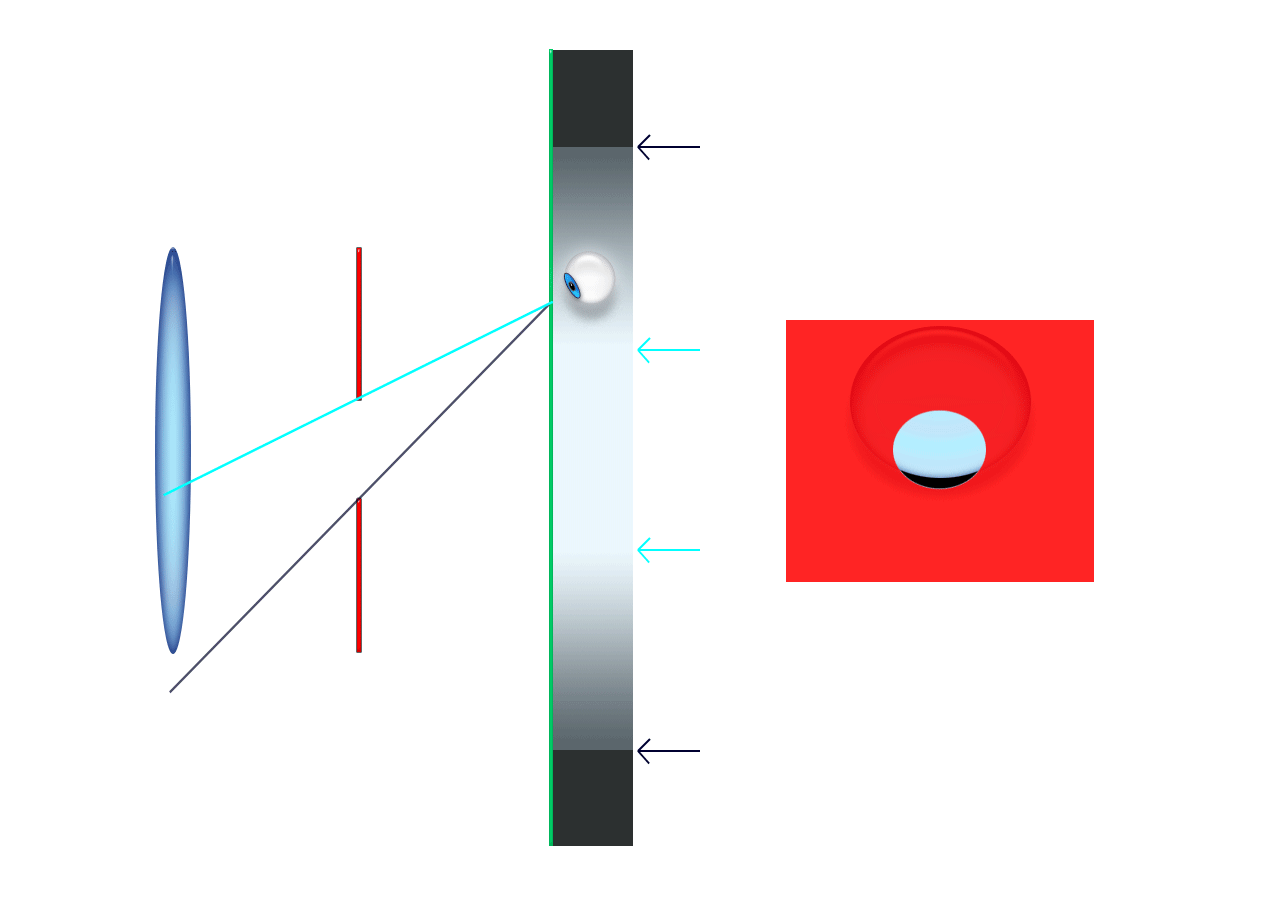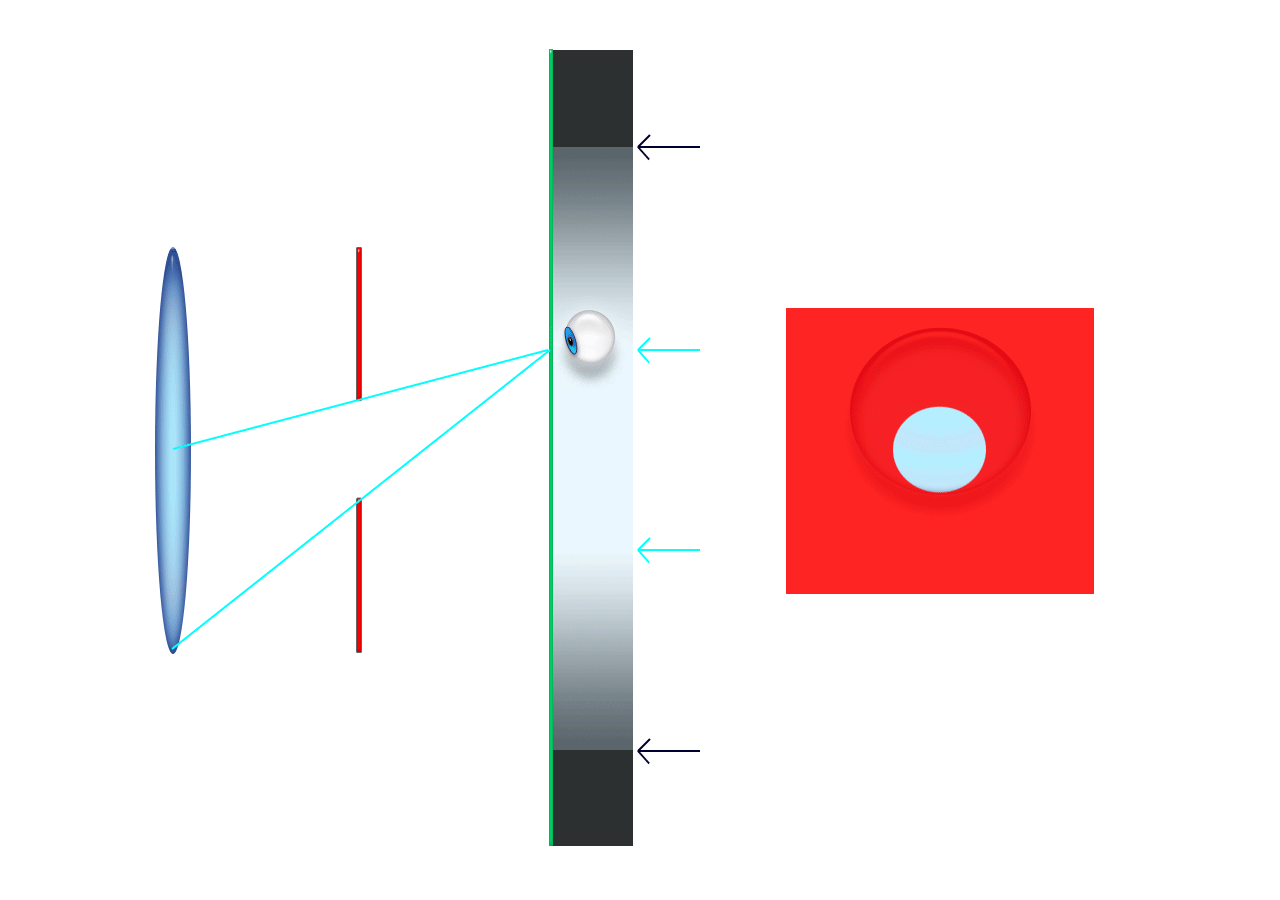
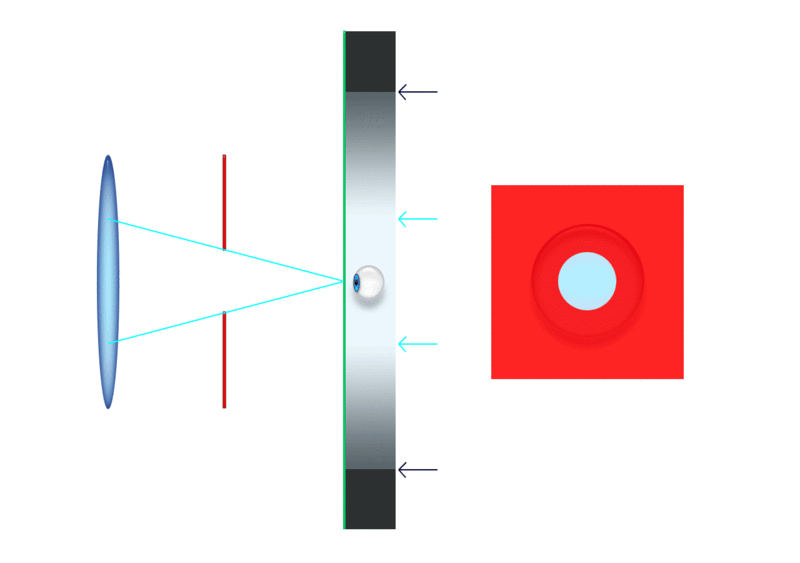
Do zgornjega izraza pridemo, če iz slike razberemo, kolikšna
je navečja slika Sob, ki jo lahko vidimo skozi okular.
Velja, glej sliko:
Sob = fok*tg(φok)
- φok = naj bo maksimalni kot, ki ga zmore
okular (okrog 50° za nižji cenovni razred,
Meade - Plossl - 25mm), v resnici je na sliki polovični kot in tudi slika
Sob je polovica maksimalne slike, ki jo lahko vidimo z danim okularjem.
Kako velika pa je slika Sob? Velja, glej sliko zgoraj,
Sob = fob*tg(φob)
Izraza za velikost slike izenačimo, saj to preslikava, ki jo opazujemo skozi okular,
fob*tg(φob) = fok*tg(φok)
Če predpostavimo, da je tg(φ) za majhne kote kar
kot φ v rad.
(to za okular gotovo ne velja, pa vendar
dobimo neko oceno), potem dobimo,
fob*φob = fok*φok
Od koder sledi, da je zorni kot, vidno polje
(vidno polje, pri dani povečavi M = fob / fok ) teleskopa
enako,
φob
= fok*φok/fob
= φok/(fob/fok)
= φok/M
Torej velja,
φob
= φok/povečava
Z besedami,
|
vidno_polje = vidno_polje_okularja / povecava
|
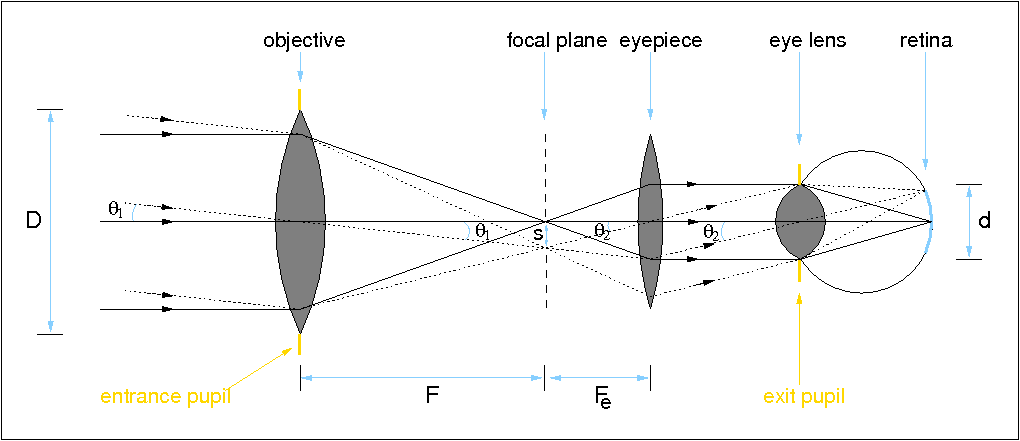



|

|

|

|

|

|

|
|

|
|
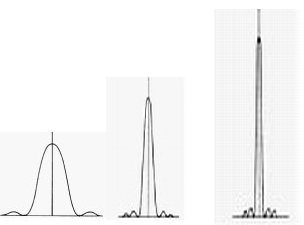
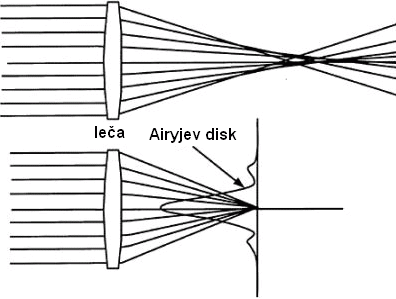
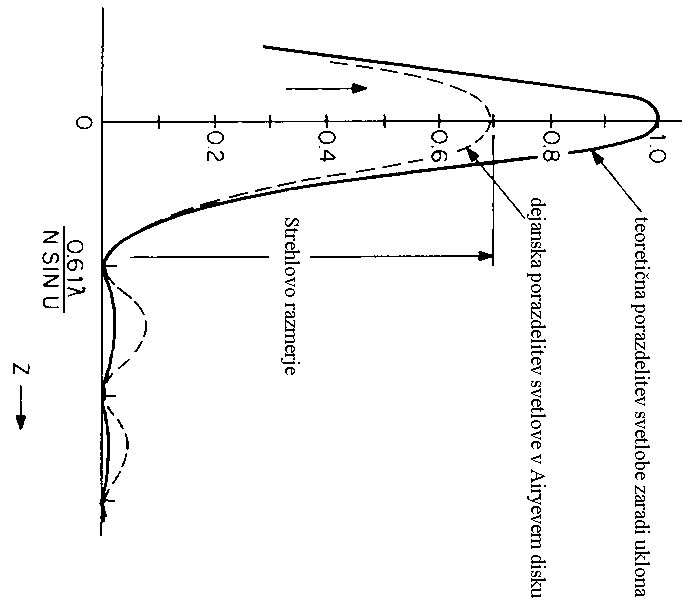
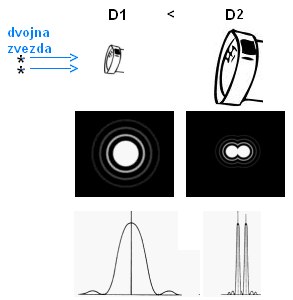
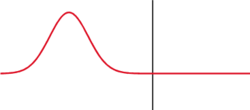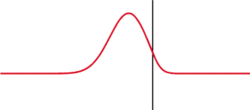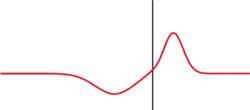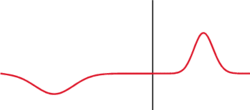
Zgornja slika je nenormirana (maksimalna višina ni 1)
- je simulacija realnega signala (slike zvzde) - diagram lahko tudi
razumemo kot stevilo fotonov (delcev svetlobe)
na delček površine slike. Pri večji odprtini je namreč teh fotonov več in zato je signal
višji (zvezda je svetlejša in ožja), a ožji glede na manjši premer objektiva.
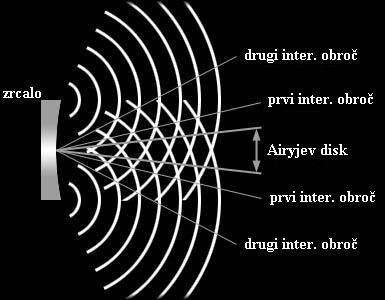
Preprosta izpeljava ločljivosti teleskopa,
optičnih naprav nasploh (tudi očesa)

|
|
|
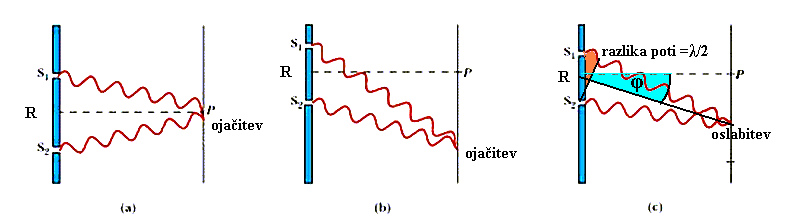
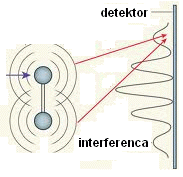
Zgornje slike pozna večina srednješolcev, saj z njihovo pomočjo izpeljejo kriterije za
interferenčne maksimume (razlika poti je enaka večkratniku valovne dolžine) in minimume
(razlika poti je enka lihemu večkratniku polovice valovne dolžine,
λ/2) dveh točkastih koherentnih izvorov valovanja na
razdalji R. Nekaj podobnega (interferenca) se dogaja s svetlobo v teleskopih, le da je tam
izpeljava ojačitev in oslabitev nekoliko bolj zapletena. Če zelo poenostavimo, dobimo za prvi
kot (φ) oslabitve obeh valovanj (kjer se srečajo
maksimumi in minimumi - valovanji se zato odštejeta), glede na simetralo, podobno vrednost,
kot je izraz za ločljivost teleskopa (1,22*
λ/D).
Za prvo oslabitev velja (za majhne kote je sinus kota kar enak kotu v radianih):
- razlika_poti = R*sin (φ) = R*
φ = (λ/2) ,
- iz česar sledi kot prve oslabitve, φ =
λ/(2*R) = λ/D
– rezultat blizu ločljivosti teleskopa,
- grobo (primerjalno) smo predpostavili, da je razdalja med izvoroma enaka kar polmeru (R)
zrcala.
Ta ocena je res čez palec, a omenili smo jo zato, ker se za
ločljivostjo optičnih naprav skriva
prav interferenca elektromagnetnega valovanja (svetlobe),
in ker je to tisti del fizike, ki se v
srednjih šolah še obravnava - naj bi se.
* Več najdete v članku

Testiranje enega izmed teleskopov, ki so jih šole prejele v MLA2009
(Airyjev disk, Strehlovo razmerje, ločljivost,
kontrast, primerjava teleskopov),
opazovanje in slikanje Saturna s spletno kamero, 7. in 8. april 2010
(Spika, mesec junij -6, leto 2010, strani 276 - 279)
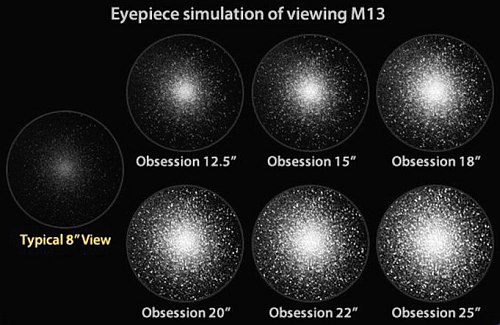

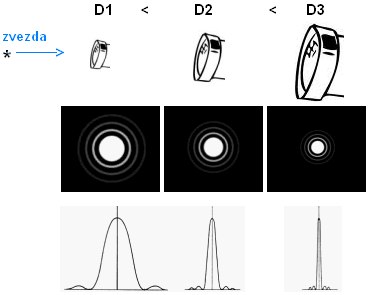
Primerjava podobe slike kroglaste kopice M13, pri različnih
premerih objektiva teleskopa in enaki povečavi.
Inča (") ali palec meri 25.4 mm. Pri D = 300 mm je preskok že očiten.
Primerjava med manjšimi in srednjimi teleskopi
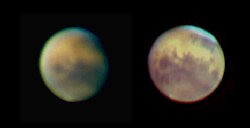
Primerjava podob Marsa med manjšim in večjim premerom
objektiva, recimo med 100 in 200 mm. Vir:
www.skyimaging.com/astronomy-equipment2.php.

Jupiter pri povečavi 100X v teleskopu 50 mm (levo, ločljivost teleskopa 2.8 ")
in 100 mm (desno, ločljivost teleskopa 1.4 "). Velikost premera objektiva
ni samo pomembna za svetlost slike, ampak tudi za ločljivost - večji je premer
objektiva, več podrobnosti vidimo, recimo na površini planetov, ločimo
več bližnjih zvezd, itn.
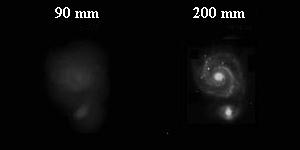
200 mm Newton se po kontrastu brez težav kosa z refraktorji premera okrog 100
mm, a nudi veliko več pri opazovanjih megličastih objektov. Slika kaže približno razliko
med opazovanjem para galaksij M51 in NGC 5195 (v obliki tolmuna - Whirlpool,
Vrtinec) v Lovskih psih (v bližini ojesa asterizma Veliki voz). Lord Rosse je leta 1845 na
umetniški podobi galaksije zelo natančno zabeležil spiralno strukturo M51 – to bi naj bil
prvi megličasti objekt, pri katerem so sploh opazili spiralne vzorce. Pri enaki povečavi
bosta sliki sicer enako veliki, a bo svetlost slike (gostota fotonov) pri 200 mm-skem
objektivu 4x višja kot pri 100 mm-skem, (200/100)2 = 4, kar se pri magnitudi
pozna »le« za 1.5, a oko to razliko še kako dobro zazna. Vemo kako opazna je razlika
med sijema Sirija in Vege (približno 1.5 magnitude) in ostalimi najsvetlejšimi zvezdami,
ali recimo med zvezdo Rigel in Belatriks v Orionu. A tudi pri planetih je povečava 400
(omogoča jo 200 mm Newton) - sploh pri Marsu - tista, ki večini razkrije vsaj nekaj
podrobnosti na planetu – medtem ko povečave do 200 (recimo refraktorji okrog 100
mm) pri večini pustijo vtis, da je Mars zgolj oranžna pikica. Je pa res, da je dober
»seeing«, ki omogoča povečave nad 200, redkost, mogoče je le nekaj takih dni v letu –
pa vendar.








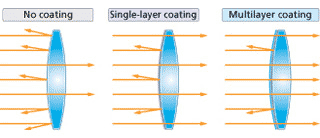
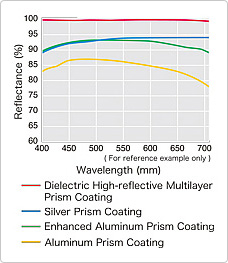
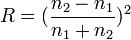
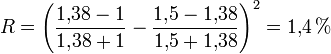



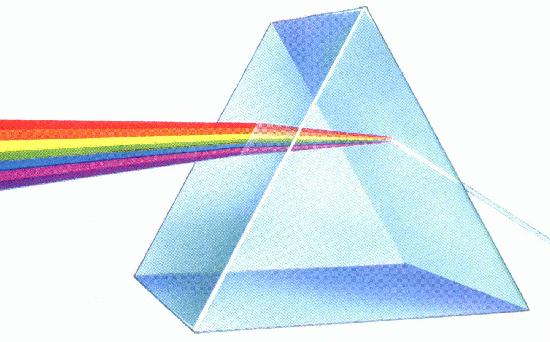
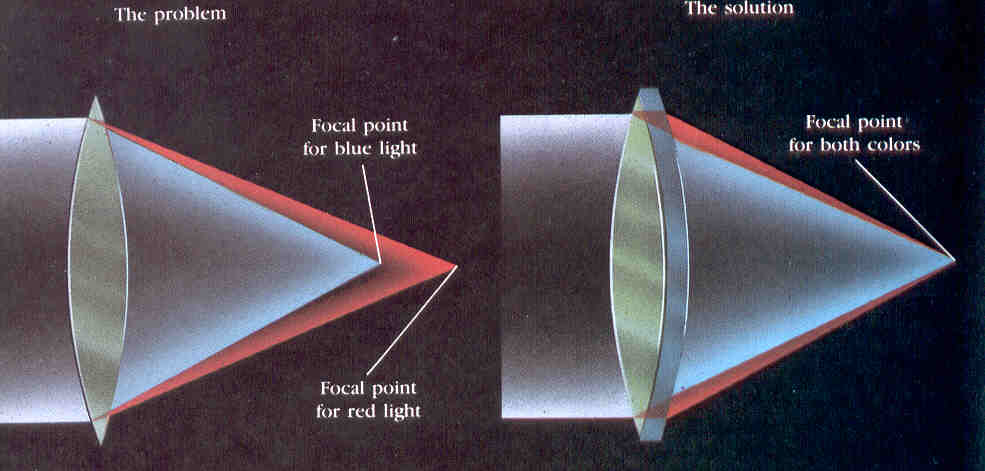
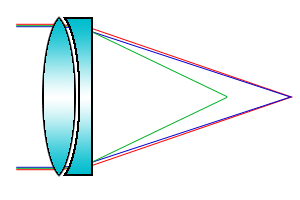
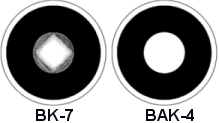
Vendar akromat še zmeraj ohrani nekaj barvne napake, slika zgoraj,
saj se v gorišču (fokusu) zbereta le rdeča in modra barva.
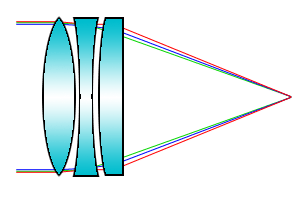
Boljša rešitev je objektiv s tremi ali večimi lečami, to je
apokromat (APOkromat, apochromat, kar APO), kjer se več barv zbere
v eni točki, gorišču.
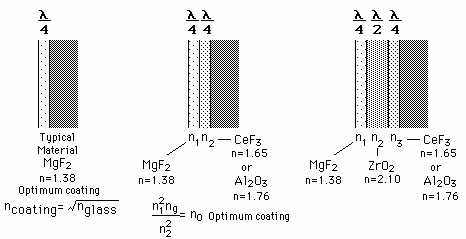
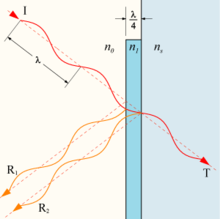
Shema večplastnih antirefleksnih nanosov (MC, Multi-coated Optics).
Vir: http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/antiref.html
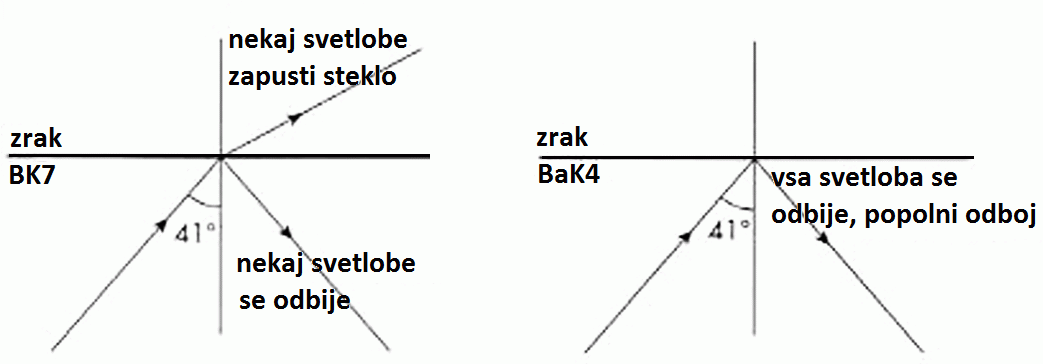
Naredimo še nekaj ocen o pomenu antirefleksnih slojev na
optičnih površinah.
V resnici so antirefleksni sloji (nanosi) na optiko
izjemnega pomena za astronomska opazovanja. Veliko pove že podatek,
da je daljnogled brez antirefleksnih nanosov
lahko tudi 2x slabši od daljnogleda
s kvalitetnimi antirefleksnimi nanosi.
Kaj to pomeni - da je recimo daljnogled z večplastnimi antirefleksnimi nanosi
z objektivom 50 mm, vsaj tako dober kot
daljnogled premera 70 mm brez antirefleksnih slojev.
Svetlobe prepuščata približno enako, a je kontrast pri 70 mm premera
(brez antirefleksnih nanosov)
bistveno slabši
zaradi notranjih odbojev.
Mnoge leče so zlepljene in med zlepljenima površinama tudi pride do odbojev,
a so zaradi manjše razlike obeh
lomnih količnikov ti odboji precej šibkejši.
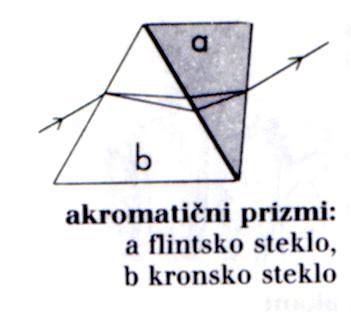
Objektiv ima za zmanjšanje barvne napake najmanj dve leči iz različnih lomnih količnikov
(dublet), boljši objektivi pa celo tri (triplet) ali več. Večinoma so leče zlepljene, ni pa nujno.
Zljepljene leče štejemo kot ene element.
Lepilo za leče je t. i.
kanadski balzam, imenovan tudi kanadski terpentin - ki je sestavina smole
kanadske jelke (Abies balsamea).
Terpentin je torej brezbarvna tekočina, ki se pridobiva z
destilacijo drevesne smole.
Leče lahko drži skupaj tudi posebno olje - površinska napetost.
Velikokrat leče ne morejo biti zlepljene, ker oblike površin tega ne dovoljujejo.
Kdaj pa zaradi različnih termičnih deformacij različnih stekel pride do
popačenja zlepljenega sistema leč - zato so mnogi sestavljeni objektivi nezlepljeni,
med lečami je zrak. To je danes manjši problem, saj so antirefleksni sloji
napredovali do učinkovitosti zgolj 0.25% odbite svetlobe.
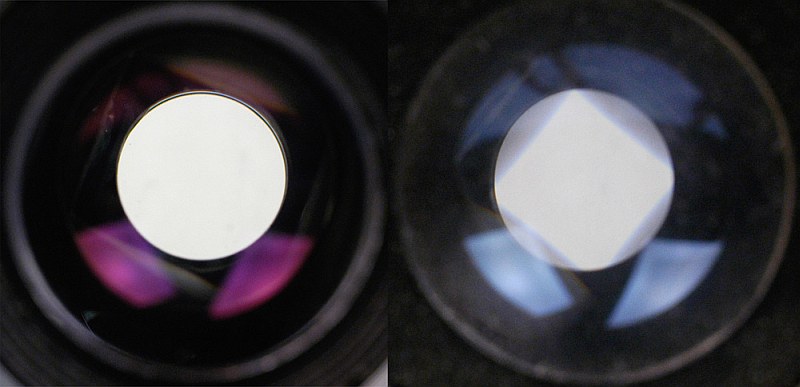
Število površin, ki jih svetloba prečka na svoji poti skozi daljnogled do naših
oči, je kar veliko - od 12 do 20 ali celo več optičnih površin. In na vsaki se, če ni
antirefleksnih slojev, zaradi
odboja izgubi vsaj 4% svetlobe.
Poglejmo primer za povprečen daljnogled s sedmimi elementi, torej s 14
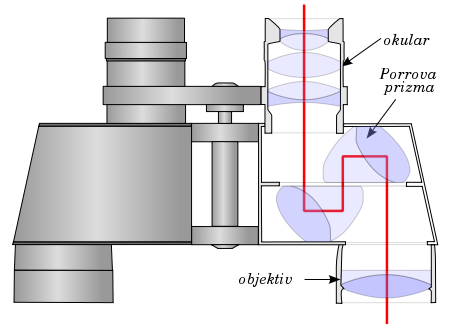
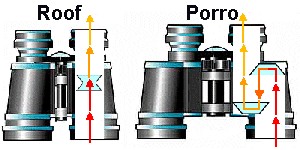
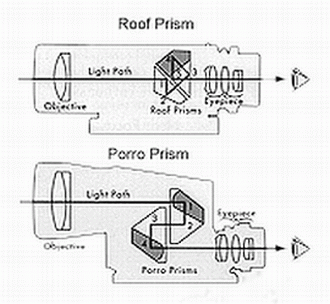
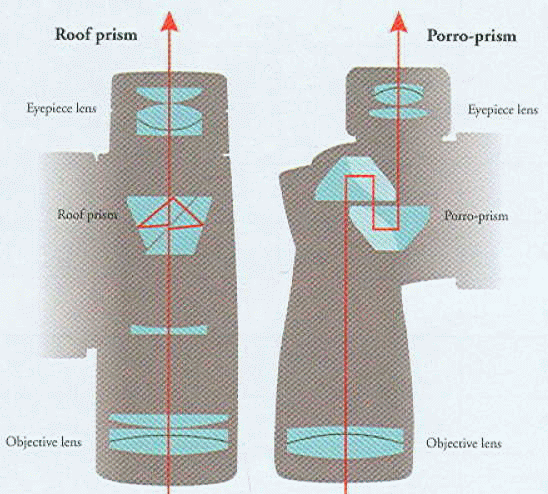
površinami. Naštejmo elemente (slike spodaj) - recimo dve nezlepljeni leči objektiva (dublet
ali celo triplet), 2 prizmi
in vsako svetloba prečka 2x in 3 leče okularja. Skupaj torej 7 elementov z dvema površinama
in tako dobimo teh 14 površin, ki jih svetloba prečka.
Pa poglejmo tri poučne primere o procentu izgubljene svetlobe (izgube žarkov, ki tvorijo sliko)
na poti skozi 14 ploskev optičnega sistema daljnogleda.
Daljnogled,
- brez antirefleksnih slojev (4% izgube na ploskev ali celo več),
- vse površine prevlečene z enoplastnim
antirefleksnim slojem debeline 1/4 valovne dolžine,
recimo z magnezijevim fluoridom, MgF2, n = 1.38,
(Fully Coated [FC] Optics, 1,4% izgube na ploskev),
- in
vse površine prevlečene z večplastnimi antirefleksnimi
nanosi [Fully-multi-coated (FMC) Optics, zgolj 0.25% odbite svetlobe na ploskev]
* Procent prepuščene svetlobe skozi 14 ploskev optičnega sistema brez antirefleksnih nanosov
je samo 100*(1-0.04)^14 = 56.5 %.
Izgubimo torej skoraj 44 % svetlobe
ki tvori sliko, oziroma velik del te izgubljene svetlobe pade v oko, a kot
odbita svetloba pod različnimi koti in s tem se zelo zmanjša kontrast slike.
* Procent prepuščene svetlobe skozi 14 ploskev optičnega sistema z enojnimi
antirefleksnimi nanosi (FC)
je kar 100*(1-0.014)^14 = 82.1 %.
Izgubimo torej 8 % svetlobe
ki tvori sliko. Rezultat je zelo obetaven.
* Procent prepuščene svetlobe skozi 14 ploskev optičnega sistema
z večplastnimi antirefleksnimi
nanosi (FMC)
je pa neverjetnih 100*(1-0.0025)^14 = 96.6 %.
Izgubimo torej samo dobre 3 % svetlobe
ki tvori sliko. Rezultat je praktično neverjeten.
No tudi cene take optike so neverjetne - 15x dražja optika od povprečnih
cen.
V resnici se izkaže, da so izgube koristne svetlobe nekoliko večje od
teoretičnih izračunov.
* Daljnogledi brez antirefleksnih slojev prepuščajo kvečjemu zgolj 50% svetlobe.
* "FC" optika ima izgube od 15-20%.
* "FMC" optika pa ima izgube okrog 8 %, lahko tudi manj.
V bistvu ni zelo velike razlike med "MC" in "FMC" optiko, razen seveda v ceni.
Pri "MC" optiki, ki stane do 100 EUR (daljnogledi do 70 mm),
ni največji problem
objektiv (ki ima na zunanji strani zaradi obstojnosti
samo en antirefleksni sloj),
ampak začuda
okular, ki bi vsaj na obeh površinah izstopne leče moral imeti večslojna premaza.
Zakaj?
V preosvetljenem okolju, ki smo si ga zaradi napačnega razumevanja
tehnološkega napredka ustvarili, je namreč
težko najti dovolj zasenčen opazovalni prostor.
Pri okularjih, ki imajo zgolj en antirefleksni nanos,
pa je svetloba iz okolice
zelo moteča (odbija se od oči v okular in delno nazaj v oči in direktna od okularja
v oči in spet delno nazaj v okular, ... - to se sevda zelo opazi
čez dan v slabih okularjih pri opazovanju Sonca, ko v okularjih vidimo
lastno oko). Ta problem se da delno odpraviti z ustrezimi
nastavki na okularjih (stranski senčili),
a večina daljnogledov teh nastavkov nima ...
Če se vrnemo k razliki med (FMC) optiko, ki ima na vseh površinah večplastne
antirefleksne nanose in optiko brez antirefleksnih nanosov ali samo s kakšnim
(C - Coated Optics),
je razmerje med obema svetlobnima tokoma iz okularja približno 2.
Ker je tok svetlobe sorazmeren s kvadratom premera objektiva, je FMC
daljnogled premera 50 mm ekvivalenten C daljnogledu prmera 70 mm, saj velja
- (koren iz 2) X 50 mm je približno 70 mm.
Iz teh ocen je tudi lažje razumeti, zakaj je tako velika
razlika v ceni med FMC in FC daljnogledi.
Ker pa je dobra MC optika (vsaj nekaj notranjih
površin ima večplastne antirefleksne nanose, ostale površine pa
enoplastne antirefleksne nanose) že zelo primerljiva
s FMC optiko - nima smisla zapravljati na stotine ali tisoče
EUR za FMC daljnoglede (razen seveda, če ...).
No kdaj se v ceni skriva tudi kvaliteta samih leč in
trajnost antirefleksnih slojev - kar pa je tudi izjemno pomembno.
Saj poznamo izrek - da nisem tako bogat, da bi kupoval poceni ...
Pomebno je tudi, da daljnogled onemogoča rošenje notranjih
površin leč in prizem.
 |  |

















|

|

|

|



|

|
|

|
|
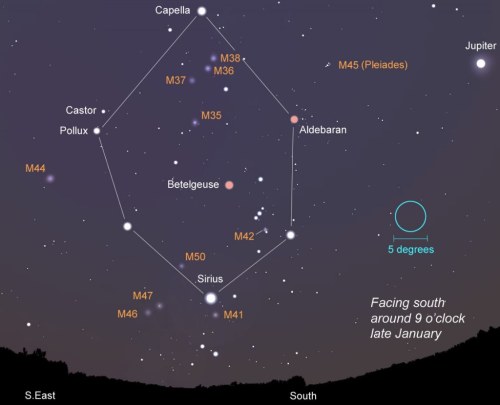
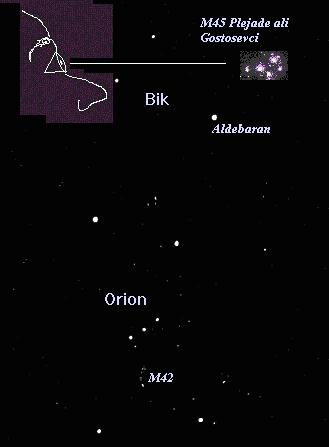
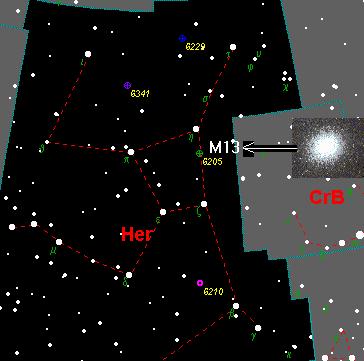
 POVEZAVA DO KARTE NEBESNIH OBJEKTOV MESSIERJEVA KATALOGA. |


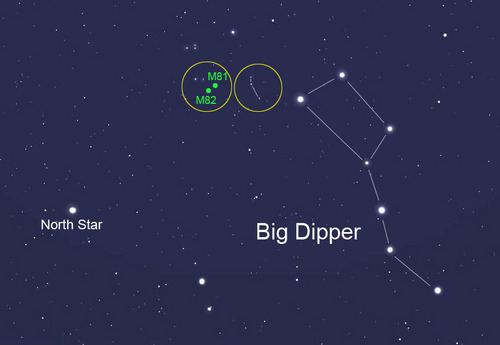





| a)________ |
b)________ |
zorni kot φ je podan v ločnih sekundah ["] in minutah [']
max.φ min.φ
Merkur 15" 5"
Venera 60" 10"
Mars 25" 3"
Jupiter 50" 30"
Saturn 20" 15"
(Sat. obroč) 40"
Uran 3,6"
Neptun 1,5"
Luna 30'
Sonce 30'