- gospoda nebesne mehanike

VIR I
Biografska enciklopedija znanosti in tehnike, Strani 91-93
[149] KEPLER, Johann nemški astronom
Rojen v Weil der Stadtu na Wurttemberškem 27. decembra 1571
Umr1 v Regensburgu na Bavarskem 15. novembra 1630
Keplerjeve elipse so pokončale grško astronomijo. Poteptale so nedotakljivost krožnega gibanja in zavrgle nebeške sfere, ki jih je pred dva tisoč leti postavil na nebo Evdoks [24] in jih je zadržal celo Kopernik. Posihmal so astronomi posnemali Keplerjev sestav Osončja, ne da bi ga bistveno dopolnili. (Keplerjeva jasnovidnost je bila omejena na Osončje. Za zvezde je mislil, da so vse na tankem, kake tri kilometre debelem obodu daleč zunaj osončja. V tem je hudo zaostajal za Brunom [138].)
VIR II
*** Koestler o Galileju in Keplerju -
zelo človeško (Mesečniki, Lunatiki)
VIR III
Fiziki 2 (strani 7-20) - Janez Strnad
"Johannes Kepler je opravil svoje življenjsko delo v duhovno in politično raztrganem in razklanem odlomku nemške zgodovine," preberemo v življenjepisu. Reformaciji v začetku 16. stoletja je proti koncu stoletja sledila protireformacija. Ne samo, da je vera po tej poti krojila Keplerjevo življenje, izdatno je nanj vplivala tudi neposredno. Kepler je bil vzgojen v protestantskem duhu in je bil globoko veren. Izbral si je augsburško različico protestantizma in pri njej vztrajal. Nasprotoval je skrajnemu stališču, ki so ga zastopali na Wurtternberškem. Tako je zašel med tabora. Kot protestant je moral zapustiti Gradec, Prago in Linz. Na drugi strani so ga wurttemberški protestanti izločili iz skupnosti in mu prepovedali, da bi se udeleževal obhajila. Med drugim so mu zamerili, da se je upiral njihovi togosti in jim zaradi nje napovedal nesrečo. Tubingensko univerzo je prosil, naj podpre njegovo prošnjo, da bi ga sprejeli nazaj v skupnost, a prošnja je bila zavrnjena. Pisma kažejo, da je to Keplerja globoko prizadelo. Katoliška gospoda pa mu je prizanašala zaradi njegovega ugleda in zato, ker ni skrival svojega nasprotovanja wurtternberškim protestantom. V astronomiji je sodeloval z jezuiti, ki so imeli v protireformaciji veliko vlogo, a je odklonil vsa vabila, naj se spreobrne. Ob vsem tem Kepler nikoli ni zašel v resne težave zaradi svojih astronomskih naukov.
Linz, v katerega se je vrnil z Wurttemberškega, so oblegali kmetje, ki so se uprli
prisilnemu spreobračanju in denarnim bremenom. Ob tem je zgorela tiskarna z delom
tiskanega gradiva. Zato je Kepler leta 1626 ženo in tri otroke zopet pustil v
Regensburgu in odpotoval v Ulm, kjer so bile možnosti za tiskanje boljše. Ko je tam
dokončal tisk novih astronomskih tablic, ki so jih po umrlem cesarju imenovali
Rudolfove, se je po letu dni odpravil k družini v Regensburg. Toda kmalu jo je spet
zapustil in odpotoval dalje v Prago, kjer je tablice izročil cesarju. Zopet so mu ponudili
ugodno mesto, če bi se spreobrnil, a Kepler je ponudbo enako kot prejšnje odklonil.
K sebi ga je brez pogojev verske narave sprejel vojskovodja lige Albrecht von
Wallenstein. Leta 1628 se je Kepler z družino preselil v Zagan v Šleziji, ki jo je
upravljal Wallenstein. Kepler mu je izdelal horoskop že leta 1608, na začetku njegove
poveljniške poti. Zdaj ga je Wallenstein večkrat prosil, naj horoskop dopolni. Po
njegovem mnenju so se napovedi prvega večinoma uresničile in je po tedanji navadi pričakoval,
da mu bodo nove napovedi koristile na poti do oblasti. Kepler se je izmikal,
češ da se vojskovodja ne sme bolj opirati na zvezde kot na svojo vojsko.
Že prej je
drugače kot Brahe - naročnike vselej opozoril na nezanesljivost horoskopov. V tistem
času pa je izrazito nasprotoval zlorabi astrologije v boju za oblast in Wallensteinu ni
ustregel, čeprav mu je ta ponujal bogato plačilo.
Več na naslovu: ejemcc_fiz.html#kepler2
VIR IV
Keplerjeva genialna ideja
Še zanimivost o izboru druge žene
Kmalu po smrti prve žene (s katero se baje nista najbolj razumela),
je dve leti iskal drugo ženo. Seznanil se je kar z 11-imi kandidatkami.
Iskanja se je lotil matematično in se pri tem hkrati držal ustaljenih
postopkov. Ta metoda je danes poznana kot problem poroke ali
tudi izbora najboljše tajnice in se med drugim predava pri
študiju moderne statistike in teorije odločanja.
42-letni Kepler se je na koncu poročil
s 24-letno Susanno Reuttinger - trije otroci (od šestih) iz tega zakona
so preživeli - odrasli.
Keplerjeva domneva
Keplerjeva domneva govori o najgostejšem
zlaganju krogel v trirazsežnem prostoru.
Po njej imata kubično ploskovno centrirano in šestkotniško
gosto pakiranje kot razporeditvi enako velikih krogel
v prostoru največjo srednjo gostoto. Gostota takšnih razporeditev
je malo več kot 74 %.
Domnevo je leta 1611 podal Johannes Kepler v delu O šestoglati snežinki
(Strena sue de nive sexangula). Kepler je začel raziskovati razporeditve
krogel med svojim dopisovanjem s Thomasom Harriotom leta 1606. Harriot je
bil prijatelj Walterja Raleigha, ki je postavil problem Harriotu o
najboljši razporeditvi topovskih krogel na ladijskih krovih. Harriot
je objavil delo o različnih vzorcih pakiranja leta 1591 in bil eden
od pionirjev teorije o atomih.
Domneva je (baje) dokazana komaj leta 2015.
Več na spodnji strani.
https://en.wikipedia.org/wiki/Kepler_conjecture
Kepler je zana tudi po zametkih integralnega
računa!
J. Kepler je znan tudi po Kepler-Poinsotovih poliedrih, manj znan pa je po zametkih integralskega
računa v Arhimedovem smislu. Kepler je namreč računal prostornine raznih teles,
med drugim tudi vinskih sodov,
kakršne so v njegovem času uporabljali v Avstriji. Kepler (1571--1630) je poznal Simpsonovo pravilo
za približno
računanje določenih integralov veliko prej kot Thomas Simpson (1710--1761).
NAŠ KOMENTAR - Kepler je bil vsaj 200 let pred časom, zakaj?
Kepler prišel do osnovnih zakonitosti nebesne mehanike in je s tem naredil odločilen korak do gravitacijskega zakona. Če smo odkriti, ga je že zapisal, a v posebni obliki. Pojem sile je bil takrat še zelo v povojih, sploh če vemo, da je Huygens »komaj« leta 1659 izpeljal izjemno pomemben izraz za centripetalno silo pri kroženju:
| Fc = m*v2/r |
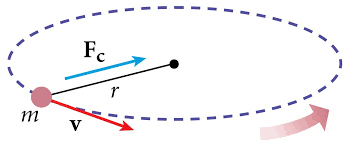
Centripetalna sila pri enakomernem kroženju:
Fc = m*v2/r = = mω2r = mr4π2/to2, 'to' je obhodni čas telesa z maso m na polmeru r od središča kroženja. Ta Huygensova enačba se izpelje v srednji šoli.
Huygensova formulacija centripetalne sile je seveda tudi skladna s poznejšo Newtonovo definicijo sile (2. zakon) in je pomenila izjemno pomemben korak pri študiju orbit v astronomiji. Je hkrati omogočila prehod iz tretjega Keplerjevega zakona (o gibanju planetov), na »inverzni kvadratni« zakon gravitacije (Fg ∝ 1/r2).
Taka odvisnost seveda zmeraj povzroči gibanje po stožnicah (krog, elipsa, parabola, hiperbola) - o tem pripoveduje prvi Keplerjev zakon. Preko kroženja planeta (poenostavitev) je pot do gravitacijskega zakona dokaj enostavna. Po Keplerju velja, tretji zakon, da je:
| to2 ∝ r3 |
- tako dobimo izraz, iz katerega izhaja, da je gravitacijska sila sorazmerna z obratno vrednostjo razdalje na kvadrat, sledi končni zapis:
Fg = mr4π2/to2 ∝ mr/r3. Iz zadnjega zapisa torej sledi, da je:
Fg ∝ m/r2.
Zadnji izraz predstavlja enega najpomembnejših opisov narave (odvisnot gravitacijske sile od razdalje), kar smo tudi iskali!!! Pot do končnega izraza Fg = GMm/r2 si oglejte v članku - Od Keplerja do Newtona
Še komentar zadnjega drznega sklepa!
Tukaj smo malo pogoljufali - saj je razdalja planeta do težišča, centra kroženja, nekoliko manjša od razdalje (r) planet - Sonce. A razlika je za planet zelo majhna in to je bila tudi neke vrste zgodovinska srečna okoliščine, saj je na koncu pripeljala do pravilnega sklepanja glede sile teže.
Drugi Keplerjev zakon se glasi - zveznica med Soncem in planetom opiše v enakih časovnih intervalih enake ploščine. Ohranja se torej ploščinska hitrost (zadaj je ohranitev vrtilne količine).
Ohranitev vrtilne količine velja recimo za nek sistem, na katerega je navor zunanjih sil enak nič (pri sistemu planet, Sonce to dokaj dobro velja in se zato vrtilna količina planeta, sistema, ohranja). Za točkasto telo, ki kroži z obodno hitrostjo v na polmeru r, je vrtilna količina kar L = mvr.

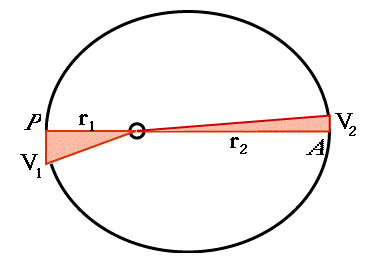
Od tod izhaja ohranitev ploščinske hitrosti - če ploščino definiramo za zelo kratek lok (Δφ*r) na polmeru r kot ΔS =Δφ*r*r/2 = Δlok*r/2 (približno ploščina trikotnika). Od tod sledi preprost dokaz, recimo da kar pogledamo vrtilni količini planeta v afeliju (odsončju) in periheliju (prisončju), za hitrost pa velja izraz v = Δlok/Δt = rΔφ/Δt:
mv1r1 = mv2r2
mr1Δφ1r1/Δt = mr2Δφ2r2/Δt
Δlok1r1 = Δlok2r2 ( maso in čas Δt smo okrajšali )
Končni dokaz je torej v enakosti ploščin:
ΔS1 = ΔS2
A izpeljava velja splošno za vse točke orbite. Ko je planet v prisončju (periheliju - najbližje Soncu) potuje najhitreje (v istem času opiše daljši lok) in je zato ploščinska hitrost enaka kot v afeliju, kjer planet posledično potuje počasneje (v istem času opiše krajši lok), saj je najdlje od Sonca.
Iz povedanega sledi enakost: v1r1 = v2r2,
kar Kepler dokaže (v svojem drugem zakonu), iz geometrije meritev, kot ohranitev ploščinskih hitrosti planeta - IZJEMNO!
Kepler je tako zapisal tudi zakon o ohranitvi vrtilne količine, čeprav je ta pojem bil vpeljan in je zaživel komaj v 18. in 19. stoletju. Bernoulli je v pismu iz leta 1744 zapisal "moment rotacijskega gibanja" in morda je to prvi koncept vrtilne količine, kot jo razumemo danes. Louis Poinsot pa je leta 1803 dokončno vpeljal vrtilno količino kot vektor pravokoten na ravnino rotacije in tudi pogoje za ohranitev vrtilne količine (the "conservation of moments") - kot ta fenomen razumemo še danes.
Kepler je bil torej oče, ne samo nebesne mehanike, ampak tudi mehanike nasploh. V njegovih zakonih se namreč skrivajo:
uporabna definicija sile, gravitacijska sila, vrtilna količina, ohranitev vrtilne količine,
- in to so zakoni podani v univerzalnih konceptih, torej veljavni povsod - čeprav se Kepler mnogih posledic svojih geometrijskih izpeljav še ni zavedal, ker koncepti moderne mehanike (sila, energija, gibalna in vrtilna količina ...) takrat še niso bili razviti, a jih je delno tudi sam slutil, soustvarjal (govoril je o moči, ki prebiva v Soncu, o delovanju teles na daljavo ...). So pa njegove geometrijske izpeljave tako dovršene (skladne z moderno fiziko), da so še danes temelj opisa dogajanj v Osončju, tudi povsod drugod v vesolju. Z njimi načrtujemo vesoljske polete, tirnice satelitov, računamo mrke, okultacije, konjunkcije, iščemo eksoplanete, tehtamo zvezde, "tehtamo" tudi skrivnostno temno snov, so vtkani v kozmologijo ...
Bil je torej veliki mojster daleč pred svojim časom.
Podobno analogijo (Keplerjevo genialnost) lahko v "modernem" času najdemo v Hendriku Antoonu Lorentzu, ki večino enačb, transformacij fizike relativnosti, zapiše že veliko pred letom 1905, preko Maxwellovih enačb, ko ohrani hitrost svetlobe konstantno za različne nepospešene opazovalne sisteme in seveda privzame, da povsod veljajo enaki fizikalni zakoni - kovarijantnost.
SKLEP
Kepler je bil zelo dolgo nekoliko prezrt znanstvenik (ni bil politično zanimiv - ker ni hotel postati žrtev politike ..., šlo mu je za resnico) - a kot začetnik nebesne mehanike, sodi med največje znanstvenike, genije človeškega rodu. Po njem so poimenovane misije v vesolje (teleskop Kepler za odkrivanje eksoplanetov, zvezda podobna Soncu Kepler-11 ima kar šest planetov), krater na Luni, na Marsu, asteroid, ... Na njegovih temeljih še danes gradi večina teoretične in praktične astronavtike (potovanja v vesolje, GPS) in tudi teoretične astronomije, tudi opazovalnih metod ...
Kepler je nekaj mesecev leta 1600 preživel tudi v dvorcu Kastelišče, Petanjci – Prekmurje, Slovenija (razlogi so tičali v hudih političnih nesoglasjih glede ekonomske prevlade v družbi – seveda pod krinko take ali drugačne zanemarljive razlike v veroizpovedi …).
Kako bi se Kepler znašel v našem "modernem" svetu, bi bil zadovoljen z našim splošnim znanjem astronomije?
Povzel:
Vičar Zorko
leto 2021
*** Delno je tekst navezava na - VK2020 Spika 1