Slovenija pod skupnim nebom
|

|
Slovenija pod skupnim nebom
|

|
J. Kepler »Astronomia nova« (1609), stran 285: "Ergo ellipsis est Planetae iter ..."
Do sedaj smo na krilih velike konjunkcije 2020 (srečanje Saturna in Jupitra zgolj
na razdalji desetine stopinje) preleteli pomen in lepoto spremljanja potovanja planetov
na nočnem nebu – Bojan pa je v ta namen sestavil nekaj imenitnih vaj. Tokrat pa si oglejmo
izjemen Keplerjev trud – in vztrajno dolgoletno iskanje prave ideje - kako iz Brahejevih
(in delno svojih) meritev lege planetov na nočnem nebu razrešiti uganko staro vsaj 10000 let.
Praktično noben ni tekmoval s Keplerjem, ker se sodobnikom še sanjalo ni, »kako prijeti
bika za roge« -
kako matematično obdelati meritve gibanja planetov po nočnem nebu.
Johannes Kepler in Tycho Brahe sta bila oba politična begunca – zatočišče sta našla
v Pragi pri cesarju Rudolfu II. Kepler je bil Brahejev pomočnik od leta 1600, bil je navdušen
nad njegovim delom in je nekoč pripomnil, da je Brahe mislil v kotnih sekundah. Brahe leta 1601 umre,
njegove meritve lege planetov pa tako podeduje njegov pomočnik, izjemen astronom in
matematik Johannes Kepler (vsaj zame največji genij vseh časov).
Genialna zamisel – preko Lege Marsa je Kepler našel obliko Zemljine tirnice
Kepler je seveda na začetku sprejemal Kopernikova krožna gibanja Zemlje in ostalih planetov – nakar
so ga same meritve končno le odvrnile od Kopernikove slike. Pri iskanju tirnice Zemlje je naletel
na razlike med krožnico Zemlje, ki jo je napovedoval Kopernik in tirnico
Zemlje (kmalu je ugotovil, da je to elipsa), ki je izhajala iz
Brahejevih in lastnih meritev gibanja Marsa napram Zemlji. Sledita izjemni sliki rojstva moderne
nebesne mehanike iz 24. poglavja Keplerjeve knjige »Astronomia nova«
(Nova astronomija iz leta
1609, stran 132 in del strani 133). A do zapisa tretjega Keplerjeva zakona je minilo še celih 9 let
iskanja. Če vam latinščina ni tuja, se lahko poglobite v tekst ob skicah. Vsi bistveni podatki,
ki jih bomo zapisali iz Keplerjeve knjige »Astronomia nova«, so iz teh dveh strani – preverite.

Vir:
https://archive.org/details/Astronomianovaa00Kepl
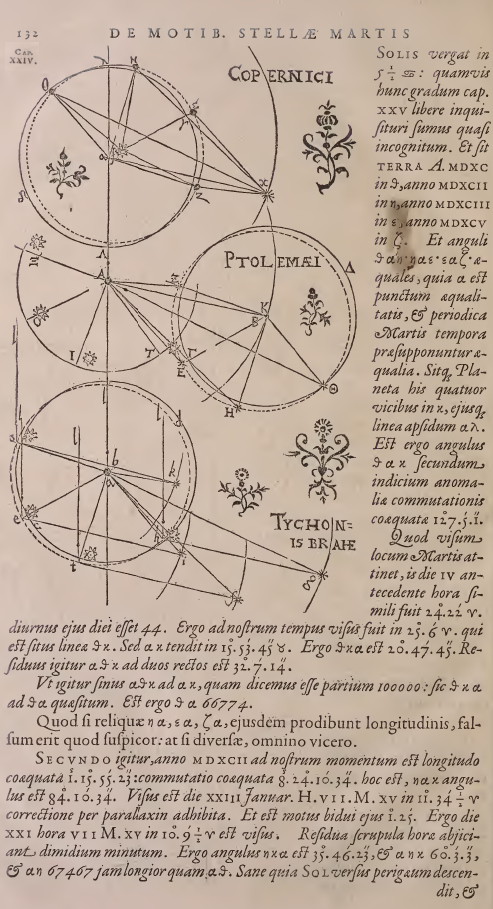
Osredotočili se bomo na skico poimenovano 'COPERNICI' (stran 132, kopija strani je zgoraj), ki (delno) izhaja iz Kopernikove slike Osončja (torej, ne na Brahejev in ne na Ptolemajev model »vesolja«, ki sta prikazana na isti strani). Slika se zdi nekoliko zapletena, a po Keplerjevi »pravi ideji« bomo zapopadli njeno preprostost in izjemen pomen.
Kepler je poznal obhodni čas Marsa okrog Sonca glede na zvezde (ta čas imenujemo tudi siderski čas), ki je bil takrat ocenjen na 687 dni (danes na 686.971 dni). Najprej je uporabil zelo zvito metodo iskanja Zemljine tirnice - orbite. Geometrijsko je iskal položaj Zemlje na njeni tirnici tako, da je narisal položaje Zemlje za datume, ko se je Mars po 687 dnevih spet vrnil v izbrano referenčno točko - ko je naredil en obhod okrog Sonca. Uporabil je tri Marsove cikle po 687 dni. V bistvu je iskal paralakso Marsa gledano iz Zemlje. Tako je dobil štiri točke na tirnici Zemlje. Še beseda o Zemlji. Obhod Zemlje okrog Sonca glede na zvezde traja 365.25636 dni, to je 20 min in 24.5 s dlje od tropskega koledarskega leta (razloga razlike se skriva v precesiji Zemlje). Kepler je privzel za Zemljo Kopernikovo krožno tirnico (na sliki je to polni krog), katere center je ekvant, ki je nekoliko odmaknjen od Sonca. A ko je iz Brahejevih meritev določal lege Marsa glede na zvezdno ozadje, je ugotovil, da iz Kopernikove Zemljine tirnice ne dobi enakih leg Marsa, ampak nekoliko izmaknjene. Če je torej hotel na sliki dobiti Brahejeve izmerjene lege Marsa, je moral Zemljo prestaviti na novo tirnico (na sliki je to črtkana orbita - tirnica). In kaj je sklepal iz novih leg Zemlje (leg na novi tirnici)? Na razpolago sta bili dve možnosti:
* - da tirnica Zemlje okrog središča ni napovedana Kopernikova krožnica, ampak neka
druga,
* - ali pa, da tirnica sploh ni krožnica ampak recimo neka druga stožnica
(bližal se je torej konec že od antike idealiziranih krožnic).
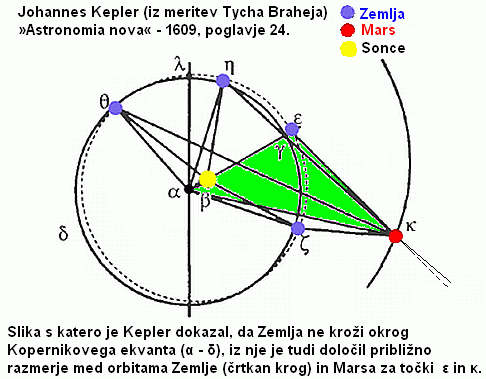
Kot bomo videli, se je izkazalo, da je tirnica v resnici elipsa s Soncem v enem izmed gorišč. A še prej se posvetimo izjemni Keplerjevi oceni razmerij relativnih razdalj od središča kroženja (takrat ekvanta) do Zemlje in Marsa. Še enkrat prerišimo skico z imenom »COPERNICI« in jo opremimo z barvami ter Keplerjevimi oznakami, da bo naše razmišljanje enostavnejše (skica spodaj).
Vir: https://archive.org/details/Astronomianovaa00Kepl
Obravnavajmo, s Keplerjevimi oznakami, trikotnik 'αεκ' (zeleno obarvana površina).
Kotu 'εκα' nasproti stranice 'αε'
je izmeril vrednost 42°21'30" in kotu 'κεα' nasproti stranice 'ακ'
vrednost 96°22'14".
Kapler ni poznal pravih oddaljenosti v Osončju, zato
je razdalji 'ακ' (ekvant – Mars) pripisal 100000 enot.
Z uporabo sinusnega
izreka [sin(εκα)/αε = sin(κεα)/ακ]
je ocenil razdaljo 'αε'
('ekvant – Zemlja') na vrednost αε = 67794 enot (sem preveril in drži do ±1/100000 natančno,
podatek nas kar začudi, kako natančni so bili izračuni že pred dobrimi 400 leti).
Kepler je izračunal
še ostale relativne razdalje do ekvanta:
αθ = 66774 enot
αη = 67467 enot
αε = 67794 enot
αζ = 67478 enot
Njegovi rezultati so pokazali razlike med dolžinami, ki bi jih pričakovali v primeru Kopernikove
krožnice – vse bi morale biti enake polmeru kroženja. To je pomenilo (poudarimo še enkrat),
bodisi da ekvant (α) ni središče Zemljine krožnice ali pa, da tirnica ni krog.
Njegovi prvi izračuni so bili že zelo blizu oceni pravilnih razmerij razdalj 'Sonce-Zemlja'
(67794 enot) , 'Sonce-Mars' (100000 enot) – to je bil (je) izjemen uspeh.
Ali so Keplerjeve skice omogočale take sklepe – ali so bile dovolj natančne? Ja so – in zakaj? Brahe je meril kote, kot smo že omenili, še brez teleskopa, a že zelo blizu ločljivosti človeškega očesa, ki znaša približno eno ločno minuto (1' = 1°/60). Za potrditev našega sklepanja, si oglejmo trikotnik 'γεκ', ki kaže paralakso, oziroma razliko med Kopernikovo predvideno krožnico in Keplerjevo tirnico določeno iz Brahejevih meritev. Kot 'εκγ' meri približno 3.5° = 3.5*60' = 210' (lahko sami preverite) in glede na natančnost meritev od 1' do 2' [ločni minuti], je to skica, ki ji gre popolnoma zaupati (napaka je okrog enega odstotka: 2/210).
To je bil velikanski dosežek za čase, ko so teleskopi bili še zgolj Keplerjeva želja (čeprav jih je teoretično že sam napovedal), zagotovo pa Braheju še nedosegljivi (Brahe je umrl leta 1601 - prvi uporabni daljnogledi so prišli v javno uporabo leta 1608 – zasnoval naj bi jih Hans Lippershey – a veliko je indicev, da jih je vojska uporabljala že leta prej).
Ena izmed lepših zgodb, kako bi naj Lippershey prišel na idejo za daljnogled pravi, da je v trgovini (delavnici) opazoval, poslušal, dva otroka med igranjem z lečami. Slišal je njuno komentiranje, da kako blizu je vremenska pristaniška vetrnica, če jo gledaš skozi dve leči. Tudi, če je zgodba zgolj mit pa je za mlade lahko imeniten izziv - in sicer, kako lahko mladi s svojo radovednostjo in hkrati ustvarjalno igro, prispevajo prvovrstne izume za celotno človeštvo. Vrnimo se k nebesni mehaniki.
Kot smo že omenili, se Tudi Kopernik ni prav dobro znašel s tirnico Marsa (gibanje je, podobno kot Ptolemaj, zapletel z epicikli). A Mars ima (kot vemo danes) precej ekscentrično tirnico (e = f/a = 0.0935±0.0001) napram Zemlji, ki ima ekscentričnost e = 0.01671022. Orbita - tirnica - Zemlje je torej zelo blizu krožnice. Tako je problem določitve pravilnih orbit planetov počakal (skozi tisočletja) na brihtnega Keplerja, ki pa mu je, z izjemnimi meritvami, k uspehu evidentno pomagal Brahe - kar pa seveda Kepler v knjigi večkrat jasno prizna, zapiše. Kepler tudi sicer spada med najbolj dobronamerne, poštene, garaške in seveda genialne znanstvenike celotne človeške zgodovine.
Če povzamemo.
Ko je torej Kepler izboljšal obliko Zemljine tirnice po metodi paralakse Marsa - jo tako
rekoč prvi pravilno določil (glede na natančnost meritev) - se je lotil Marsove poti s
precej ekscentrično lego (sedaj je poznal umerjen položaj opazovalca, tirnico Zemlje
okrog Sonca). A kot se je izkazalo, je prav zaradi ekscentričnosti Marsove tirnice, lažje
prišel do končne pravilne eliptične oblike.
Metoda in pot do tirnice Marsa je bila odprta.
Z enako metodo (paralakso), kot je ocenil tirnico Zemlje, je poiskal še razliko med tirnico
Marsa glede na napačno napovedano Kopernikovo krožnico - tokrat že z referenco v Soncu, to kažejo
naslednje skice. Pot do nebesne mehanike je bila tako na široko odprta avtocesta – po
kateri se še danes vozimo presenetljivim odkritjem nasproti.
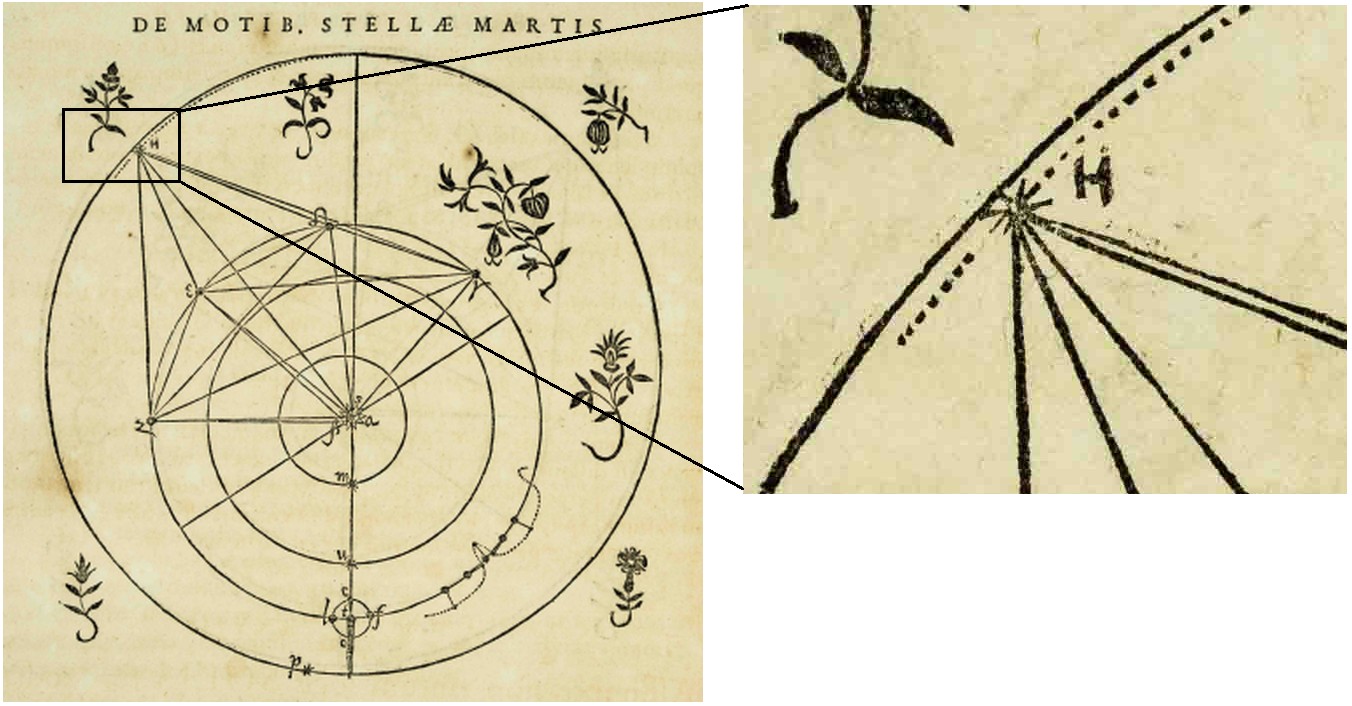
»Astronomia nova« - iz leta 1609, Stran 149, poglavje XXVII – odstopanje tirnice Marsa od krožnice.
Vir: https://archive.org/details/Astronomianovaa00Kepl
»Astronomia nova« iz leta 1609, Stran 248,
poglavje LI – določanje tirnice Marsa preko lege Zemlje z referenco v Soncu in nič več
v antičnem ekvantu.
Vir: https://archive.org/details/Astronomianovaa00Kepl
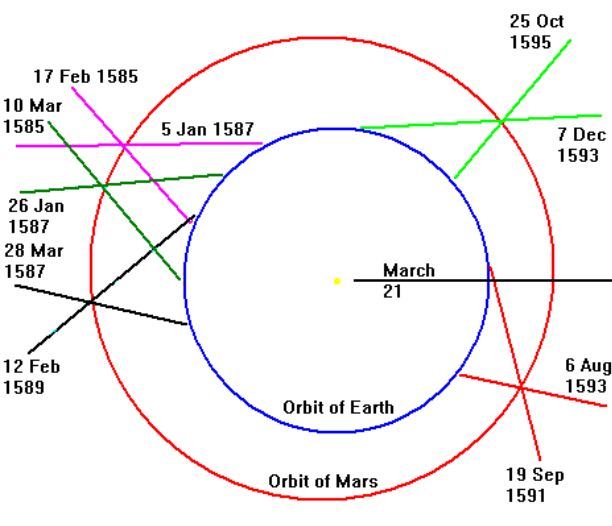
Slike paralaks Marsa gledano iz orbite Zemlje, po
večih obhodih Marsa okrog Sonca, ki trajajo po 687 dni.
Tam kjer se pari smeri Zemlja - Mars - zvezdno ozadje sekajo,
so točke na orbiti Marsa. Če je pri Zemlji imel Kepler še dileme o obliki
orbite, se je pri Marsu elipsa izkazala kot zadetek v polno.
Slika je modernizirana podoba Keplerjeve geometrije plesa Marsa (po
obhodih okrog Sonca)
na zvezdnem ozadju gledano z Zemlje. Obdobje od 17. feb. 1585
do 25. okt. 1595, skoraj 11 let - pet parov premic se seka
na orbiti Marsa (vsak par ima svojo barvo).
Keplerjeve slike seveda vsebujejo še povezave do Sonca, da je
potrdil goriščno lego. Najprej pa je določil orbito Zemlje in
seveda je računal z lastnimi relativnimi razdaljami - pravih ni poznal.
A to je zadostovalo za zapis nebesne mehanike.
Od Keplerja do Newtona
To je hkrati zametek poti do oblikovanja pojma gravitacijske sile,
Kepler jo poimenuje kar »magnetizem« (v kontekstu časa zelo brihtno). Teža je namreč tako
domača človeku, da je skoraj ne opazimo (to dilemo, da je teža, ki nas ljudi veže na Zemljo,
hkrati tudi sila s katero Sonce veže nase planete, je v bistvu v veliki meri razrešil Newton –
no potem pride Einstein ...). Glede samoumevne teže, ki jo čutimo na Zemlji, in je ne opazimo,
velja znana prispodoba - »da smo kot ribica, ki ne opazi oceana in ga ves čas
vsa zmedena išče, plava sem ter tja ..., ko ji povedo, da vendar tudi ona plava v oceanu,
odgovori, da ne, da je to vendar samo navadna voda in vsa razburjena plava naprej ...«.
In magnetna sila je bila v kontekstu časa za Keplerja prava prispodoba za moderno silo gravitacije (teže) – in Einstein jo je upravičeno nadomestil z ukrivljenostjo prostor-časa. Pojem sile se je takrat komaj počasi rojeval in nikakor ni samoumeven.
Keplerjev uvod v poglavje 33 se glasi: "Moč, ki premika planete prebiva v telesu Sonca ..." Kepler tudi navaja, da "moč [danes sila] slabi z razdaljo", in da je to podoben pojav kot pri »moči« svetlobe, ko se, z večanjem razdalje od svetila, žarki drug od drugega oddaljujejo in zato »moč« (gostota žarkov) pada. Tukaj je torej Kepler že na sledi inverznemu kvadratnemu zakonu gravitacije - izjemno. A tega eksplicitno ne zapiše, saj je bil matematični zapis sile pri krivem gibanju takrat še v povojih. A Kepler je pravilno sklepal, da je sila odvisna od razdalje (v svojem 3. zakonu čez 10 let to tudi implicitno zapiše, a je končno teoretično definicijo prepustil naslednikom, njegovo delo je nadaljevala veriga naravoslovcev vse do Newtona in seveda tudi naprej v današnji čas, zanamci pa se bodo morebiti smejali tem našim teorijam ..., vsekakor jim privoščimo).
Vrnimo se v Keplerjev svet. Po vseh preračunih, skicah, razmišljanjih, vmesnih rezultatih - po zavrnitvi krožnice, ko se je nekaj časa zdelo, da je tirnica Marsa poljuben oval - je Kepler na kocu le prišel do pravilne krivulje gibanja planetov (elipse), torej tudi do povezave med hitrostjo in oddaljenostjo planeta od Sonca (danes vemo, da tirnica ni ravno elipsa, saj le ta rotira okrog centralne mase in skozi čase nariše »cvet« - relativistični efekti, tudi motnje sosednjih teles). Čez 10 let pa je zapisal še povezavo med veliko polosjo elipse in obhodnim (siderskim) časom planeta med gibanjem okrog Sonca. Danes njegove sklepe (zakone) zapišemo z naslednjimi besedami.
I. Keplerjev zakon: Tirnica (pot) planeta je elipsa s Soncem v enem od gorišč.
II. Keplerjev zakon: Zveznica med Soncem in planetom opiše v enakih časovnih intervalih enake ploščine. Ohranja se torej ploščinska hitrost (vrtilna količina).
III. Keplerjev zakon : Kvadrat obhodnega časa (T) planeta je sorazmeren kubu velike polosi (a) elipse.
Nekateri zapišejo III. zakon tudi v obliki razmerij kvadratov časov in kubov polosi:
(T1/T2)2 = (a1/a2)3
Ali v obliki – da je količnik kvadrata siderične periode 'T' in kuba velike polosi elipse 'a'
za vse planete enak:
T2/a3 = konst.
Pri tretjem zakonu je najbolj korekten prvi zapis (sorazmernost med kvadratom obhoda in kubom velike polosi),
druga dva zapisa sta približna, a dokaj dobro veljata, ker je masa planetov 'm' precej manjša od mase Sonca
'M'. V splošnem pri dveh telesih velja, da potujeta okrog skupnega težišča in v tem primeru se danes tretji
Keplerjev zakon zapiše v pravilnejši Newtonovi verziji:
T2/a3 = 4π2/(G(M+m))
G je gravitacijska konstanta (G = 6.67*10-11m3kg-1s-2).
A ker ima večina planetov precej skromne mase 'm' (kot smo že omenili) napram masi Sonca M, je poenostavitev enačbe T2/a3 ≈ 4π2/(GM) v določenih okoliščinah smiselna.
S Keplerjem smo tako ljudje prejeli dragoceno vedenje, ki nam omogoča točna napovedovanja mrkov, navideznih prehodov Venere in Merkurja čez Sonce, okultacij, načrtovanje vesoljskih poletov, določanje mas v vesolju, oblikovanje kozmoloških modelov, napovedovanje dogodkov praktično milijone let v bodočnost ...
Naslednjič pa nakažemo pot do gravitacijskega zakona – in ne pozabimo, vse to zaradi potepuhov!
Zorko Vičar
Maj 2020 (zametek 2015)
Dodatki:
Po zavrnitvi krožnih in ovalnih orbit je Kepler zaključil, da mora biti Marsova orbita eliptična.
Na vrhu strani 285:
"Ergo ellipsis est Planetae iter; …
"(Torej je elipsa pot planeta [to je Marsove] poti;…)
Beri spodnji latinski tekst.

Vir: https://archive.org/details/Astronomianovaa00Kepl
Spodaj je še drugi Keplerjev zakon - zveznica med Soncem in planetom opiše v
enakih časovnih intervalih enake ploščine.
Ohranja se torej ploščinska hitrost (vrtilna količina).
Zapisan kot:
"Arcum ellipseos, cujus moras metitur area AKN, debere terminari in LK, ut sit AM."
"(Lok elipse, katerega trajanje je določeno [izmerjeno] s površino AKN,
je treba zaključiti v LK, tako da je [lok] AM.)"

Vir: https://archive.org/details/Astronomianovaa00Kepl
Tretji Keplerjev zakon:
Harmonices Mundi [Harmonija (ubranost) sveta], tiskana 1619,
stran 189: "Sed res est certissima exactissimaque quod proportio qua est inter binorum quorumcunque
Planetarum tempora periodica, sit pracise sesquialtera proportionis mediarum distantiarum, … "
Popolnoma gotovo pa je in natančno, da je delež med periodičnimi časi katerih koli dveh planetov
ravno "seskvialteralni" (sesquialteral)
delež [tj. Razmerje 3: 2 = 1.5] njune srednje razdalje, ... "),
Pri elipsi je to velika polos. Zapišimo povedano še z matematično simboliko.
T1 : T2 =
a11.5 : a21.5


Stran 189, zadnji odstavek.


