
AKTUALNO 2009
Stran se bo dopolnjevala v okviru razpoložljivega časa. Za vse morebitne napake in nerodnosti se že v naprej opravičujem.

Vir : Astronomy Picture of the Day via AGO.
translation into Slovenian by H. Mikuz.
[kolimacija|]





 |
 |





























































Rezultati pobude "Teleskop za vsako šolo"!
Razpis MŠŠ je bil dokončno izveden s 30. septembrom 2009.
Statistika pobude "Teleskop za vsako šolo" v %, MLA2009
-----------------------------------------------------------------------------
Št_kup_teleskopov st_šol izplen v %
----------------- ------ -----------
406 449 90.4% osnovne šole
113 165 68.5% srednje šole
7 28 25.0% Zavodi za izo. otrok s pos. potre.
---- ---- ------
Skupaj 526 642 81.9%
---------------------------------------------------------------------------

















































 Člani Atronomskega krožka Gimnazije Šentvid - Lj.
Člani Atronomskega krožka Gimnazije Šentvid - Lj.



































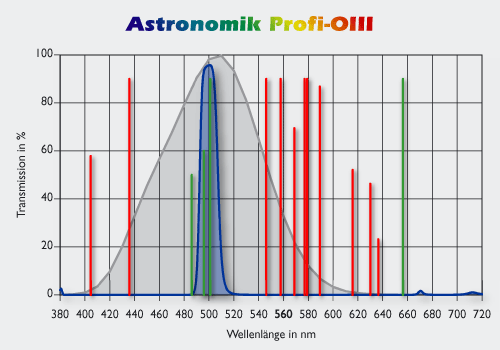
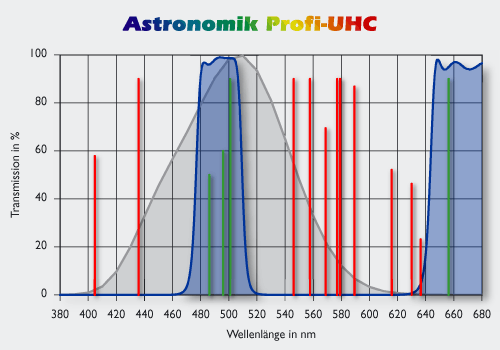



























































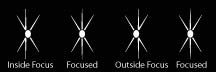





































































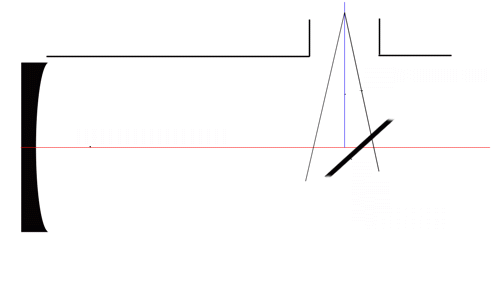
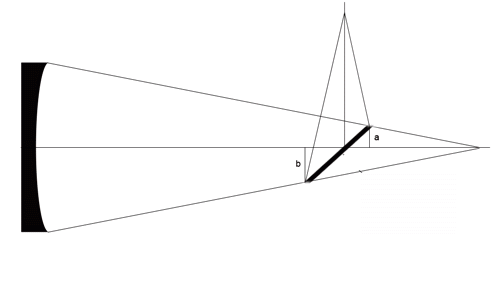

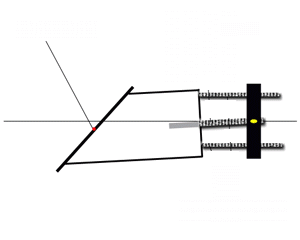
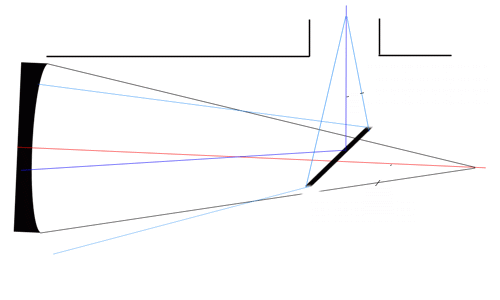

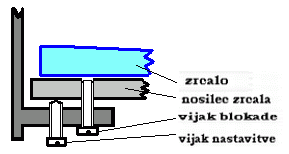
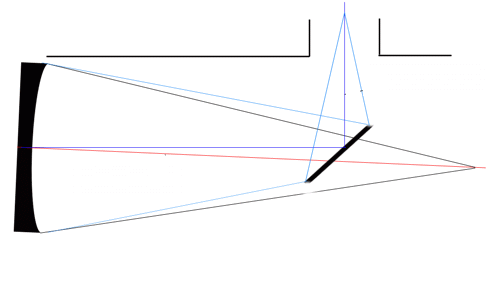

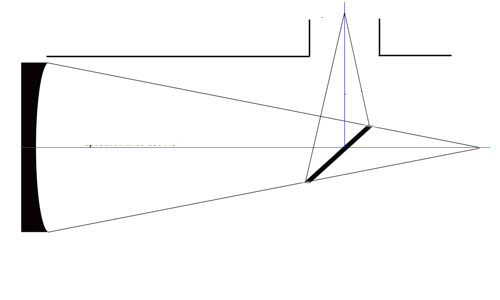




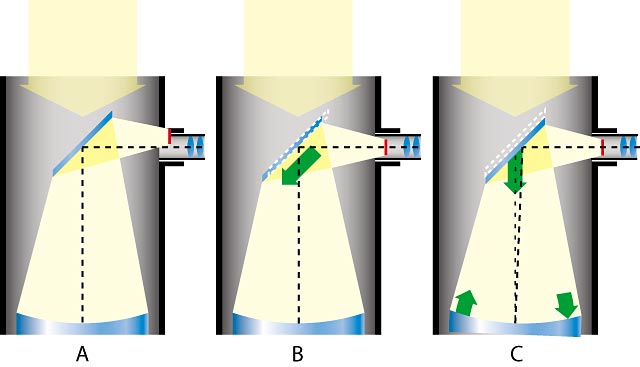
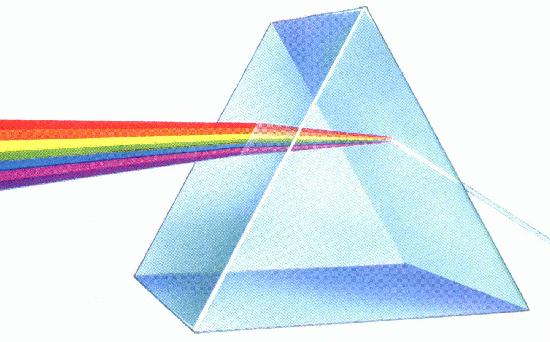
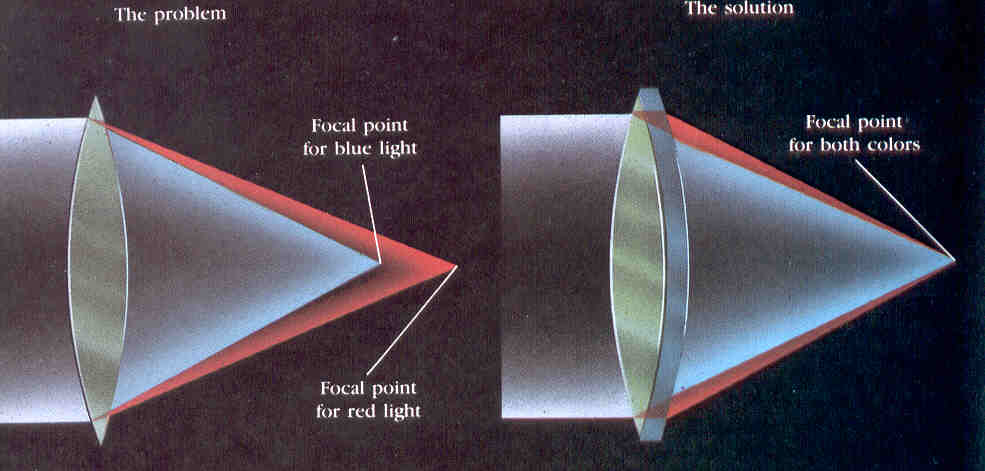
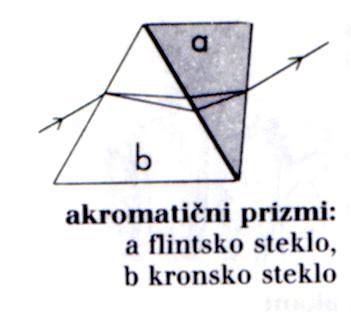
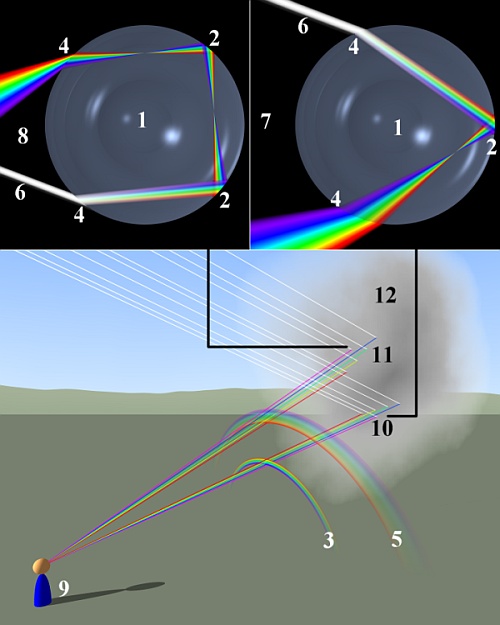
Princip delovanja akromatskih prizem in leč, bistvo sta dve
obratni prizmi (leči) z različnima lomnima količnikoma.
f/8.5 Ritchey-Chretien
![]()
f/10 Schmidt-Cassegrain

f/8 Classical Cassegrain

f/5 Newtonian

Primer dimenzioniranja teleskopa Newton D - premer pri. zrcala = 320 mm z - f/D svetlobna moč = 4 pl - polje linearnosti, odprtina (14-44 mm) = 32 mm (D/2 + Ft) - razdalja od optične osi do gorišča pravokotno izven tubusa Ft (ali FP) - točka gorišča izven tubusa = 75 mm --------- izračuni ------------------------------------- f - goriščna razdalja = D*z = 1280 mm d - dolžina cevi = D*z - (D/2 + Ft) = 1045 mm D2 - mala os sekundarnega eliptičnega zrcala D2 = ( (D/2 + Ft)/(D*z)*D ) + (pl*((D*z) - (D/2 + Ft))/(D*z) ) = 84,9 mm vidno polje = 2*(atan((pl/2)/(D*z) ) ) = 1,43 stopinje Prekrivanje sekundarca v % (izgube) = 100*(D2/D) = = 100 *((((D/2 + Ft)/(D*z)*D ) + (pl*((D*z) - (D/2 + Ft))/(D*z)))/D) = 27 %
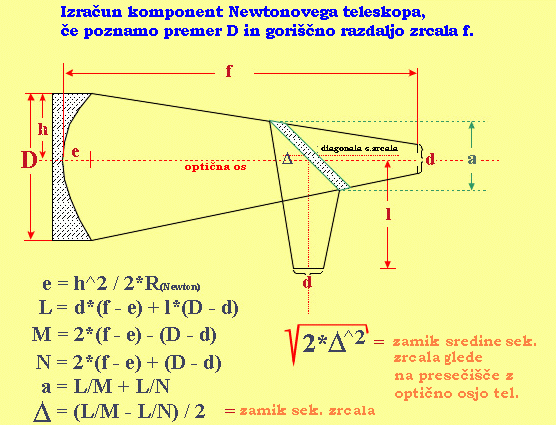
Stekla - katera so primerna za zrcala teleskopov ? --------------------------------------- - priporoča se majhen temperaturni koeficient 'a' linearnega raztezka (prostorskega = 3xa), da ne trpi oblika zrcala pri različnih temperaturah 1) Quartz (fused) silicijev dioksid obdelan na 2000° C, poseben postopek ... - zelo primeren za zrcala teleskopov 2) Pyrex (več sestavin, ena kombinacija je spodaj, je tudi ognjevarno) 74 SiO2, 13 Na2O, 10.5 CaO, 1.3 Al2O3, 0.3 K2O, 0.2 SO3, 0.2 MgO, 0.01 TiO2, 0.04 Fe2O3 73 SiO2, 14 Na2O, 9 CaO, 0.15 Al2O3, 0.03 K2O, 4 MgO, 0.02 TiO2, 0.1 Fe2O3 - primeren za zrcala teleskopov 3) Navadno steklo 50 do 70 % kremena (silicijev dioksid), kovinski oksidi v različnih količinah in včasih okrog 0,5 % žveplovega trioksida, ... - navadno steklo ni primerno za zrcala teleskopov -------------------------------------------------------- a=dL/(L*dt) Temperaturni koeficient linearnega raztezka (Coefficient of thermal expansion) navadno navajajo v milijoninkah na stopinjo Celzija. Vrednosti za stekla (×10^-6 /°C): steklo a ---------------- ---- Steklo (navadno) 8,5 Pyrex steklo 3,3 Quartz (fused) 0.59
+1972



+1974

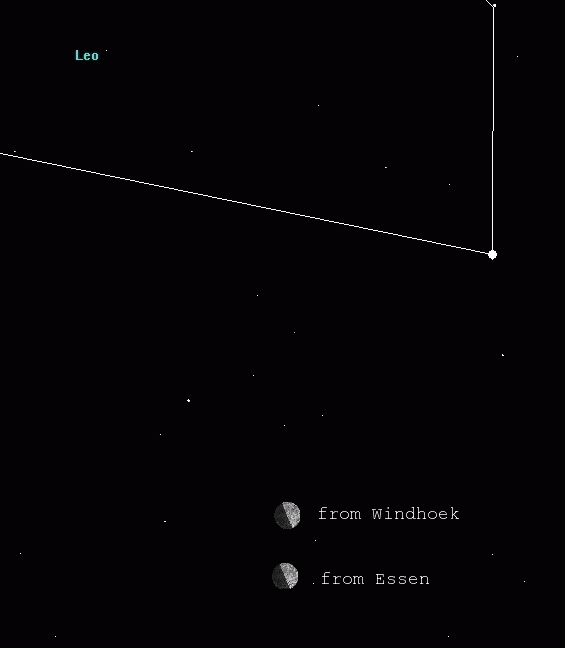
Razlaga slike:
Recimo, da smo bitja iz vesolja, iz kroglaste kopice M13 in iz Zemlje prejmemo zgornjo informacijo.
Kaj nam hočejo ti navadni smrtniki, Zemljani povedati?
Zgornje sporočilo je bilo odposlano iz
Zemlje, leta 1974, v smeri
kroglaste zvezden kopice
M13.
Med sprejemanjem še zmeraj največjega radijskega teleskopa
Arecibo - je bilo hkrati poslano zgornje sporočilo
(1's in 0's).
Ta poskus komunikacije z izvenzemeljskimi bitji je bil bolj
simbolne narave - človeštvo namreč redno na široko in naključno pošilja v Vesolje
radijske in televizijske signale.
Tudi če bi to sporočilo sprejeli v M 13, je le ta kopica tako daleč,
da bomo "morali" čakati 50000 let na odgovor morebitnih civilizacij iz M 13.
Seveda bi ta bitja morala zaznati in razumeti naše sporočilo.
Sporočilo podaja preprosta dejstva o človeški civilizaciji in
našem znanju: od leve proti desni so števila od 1 do 10, atoma
vodika in
ogljika,
nekaj zanimivih in pomembnih molekul,
DNA, opis človeka, osnove našega
Sončnega sistema in
osnove teleskopa, ki je poslal sporočilo.
Nekaj raziskovalcev izvenzemeljske inteligence
ravno "zdaj" sprejema mnoge osebe, ki lahko sodelujejo pri projektu iskanja, tako da
vključujejo (vključujemo) lastne računalnike v raziskovalno mrežo.
Glej tudi: http://antwrp.gsfc.nasa.gov/apod/
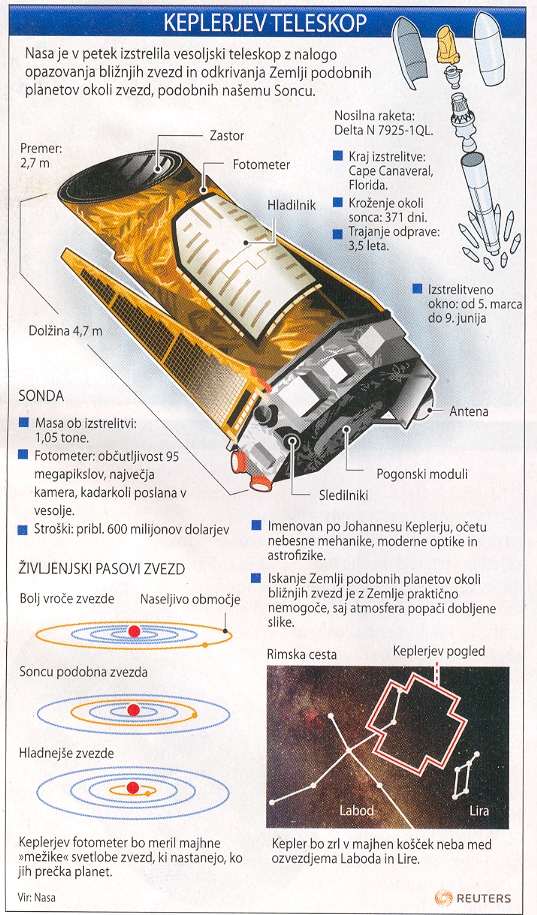
Kepler bo iskal Zemlji podobne planete
Znanstveniki nad podatke o 100.000 zvezdah
Oglej si film. Ne povedo, da so jih v to misijo popeljali
amaterji, ki so prvi odkrili planete zunaj Osončja!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Oglej si film o misiji "Kepler" - direktno youtube.
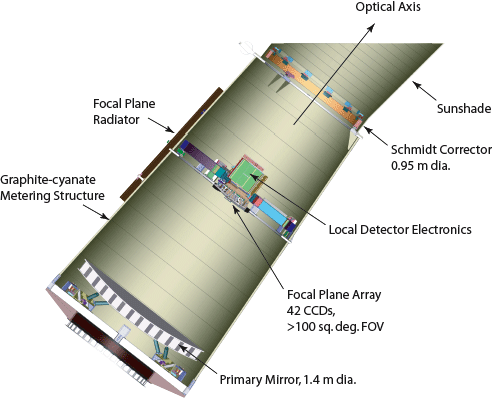

Organizacija NASA
Glavni partner Ball Aerospace & Technologies Corp.
Lansiran iz Space Launch Complex 17-B Cape Canaveral Air Force Station
Nosilna raketa Delta II (7925-10L)
Trajanje misije 3.5 let, ocenjujejo do 6 let (bomo videli)
Masa 1039 kg (večji osebni avto)
Tip orbite blizu Zemlje, heliocentrična orbita
Polmer orbite 1 AE
Orbitalna perioda 372.5 days
Valovne dolžine CCD 400-865 nm
Vhodna odprtina 0.95 m
Prmer zrcala 1,4 m
Velikost CCD kamere 0.708 m^2 - Največja kamera, ki je poletela v vesolje
42 CCD čipov (50cmx25cm z 2200 x 1024 svetlobnih elementov - pikslov,
27 mikrometrov veliki piksli),
- optika teleskopa je popačena, slika ni ostra,
pomembna je občutljivost za svetlobo, velikost slike je 10
loč. sekund, kar pomeni, da ena zvezda pade na 4 pixle,
(12*3600"/10 000 pixli = 4,3 "/pixel .... toje vsaj 2*2 pixla = 10"*10"),
zakaj je to dobro, da ena zvezda osvetli več pixlov, motnje
pa recimo le enega
- polovica čipa bo osvetljena z zvezdami primernimi za branje
- CCD je hlajen na - 40 °C
- CCD se prečita vsake 3 sekunde, samo piksli izbranih zvezd
se shranijo
- vsake 3 sekunde pa zato, da se piksli ne nasitijo zaradi
zvezd 9 magnitude
 - odstranjuje se tudi šum, napake zaradi kozmičnega sevanja, to traja
kar nekaj minut.
magnituda - svetlejše od 16,
(iz Ljubljane pridemo s teleskopom in CCD kamero komaj do 16 magnitude)
recimo zvezda kot Sonce, tip G2,
bo imela 12 magnitudo na razdalji
slabih 1000 sv. let, kar je 100 krat manj svetlobe, kot pri
zvezdah, ki jih vidimo komaj še s prostim očesom
Moč 2860 solarnih celic z močjo 1,1 kW, napetost 12 V
Cena 600 milijonov dolarjev (zamuja 2 leti, nesreča ves. taksija)
Kaj vsakih 30 minut bo izmeril svetlost 100000 zvezdam,
100 000 zvezd so izbrali po petih letih meritev izmed 4.5 milijona znotraj
polja meritev
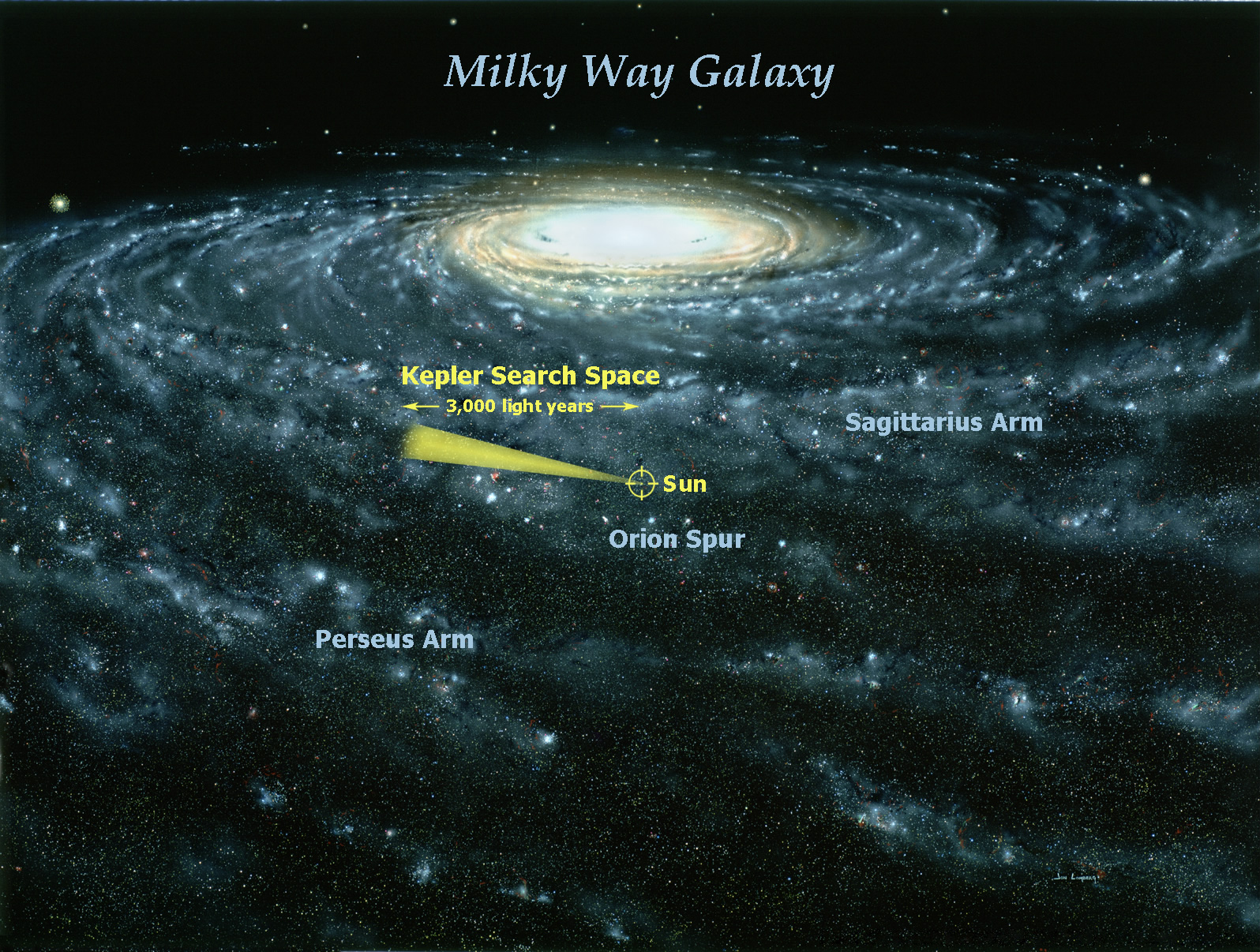
oddaljene med približno 600 in 3000 sv. let v Orionovem kraku naše galaksije
- področje med Liro in Labodom
(le 1% zvezd bližje od 600 sv. let,
tiste nad 3000 sv. let imajo premajhno razliko v svetilnosti),
- podatki se bodo enkrat na mesec 12 ur pošiljali na Zemljo, radijska zveza
- odstranjuje se tudi šum, napake zaradi kozmičnega sevanja, to traja
kar nekaj minut.
magnituda - svetlejše od 16,
(iz Ljubljane pridemo s teleskopom in CCD kamero komaj do 16 magnitude)
recimo zvezda kot Sonce, tip G2,
bo imela 12 magnitudo na razdalji
slabih 1000 sv. let, kar je 100 krat manj svetlobe, kot pri
zvezdah, ki jih vidimo komaj še s prostim očesom
Moč 2860 solarnih celic z močjo 1,1 kW, napetost 12 V
Cena 600 milijonov dolarjev (zamuja 2 leti, nesreča ves. taksija)
Kaj vsakih 30 minut bo izmeril svetlost 100000 zvezdam,
100 000 zvezd so izbrali po petih letih meritev izmed 4.5 milijona znotraj
polja meritev
oddaljene med približno 600 in 3000 sv. let v Orionovem kraku naše galaksije
- področje med Liro in Labodom
(le 1% zvezd bližje od 600 sv. let,
tiste nad 3000 sv. let imajo premajhno razliko v svetilnosti),
- podatki se bodo enkrat na mesec 12 ur pošiljali na Zemljo, radijska zveza
 - sprememba 1/10000, kot da bi hotel zaznati spremembo sija
avtomobilskega žarometa na veliki razdalji, ko leti mimo
žarometa muha
* - iz časa prehoda je mogoče izračunati orbito planeta in maso zvezde,
velikost planeta se oceni iz globine zmanjšanja sija (krivulje),
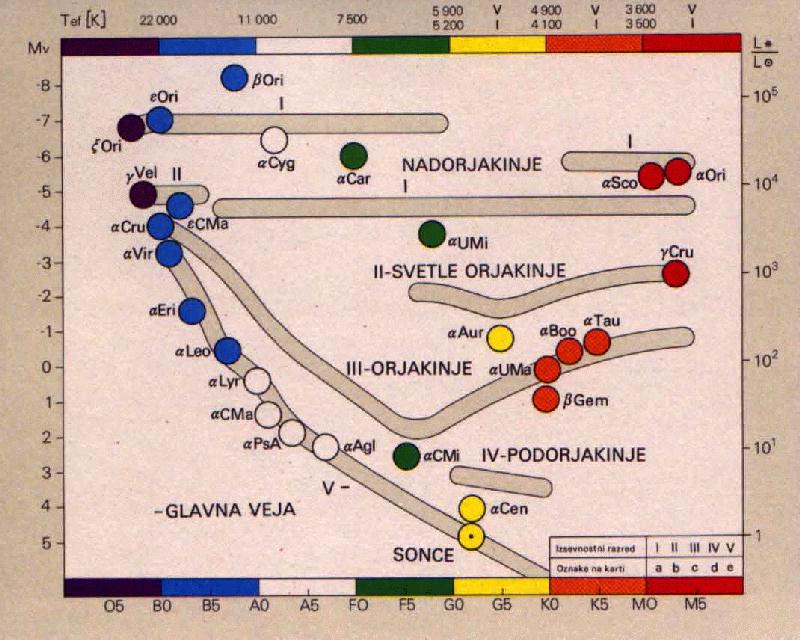
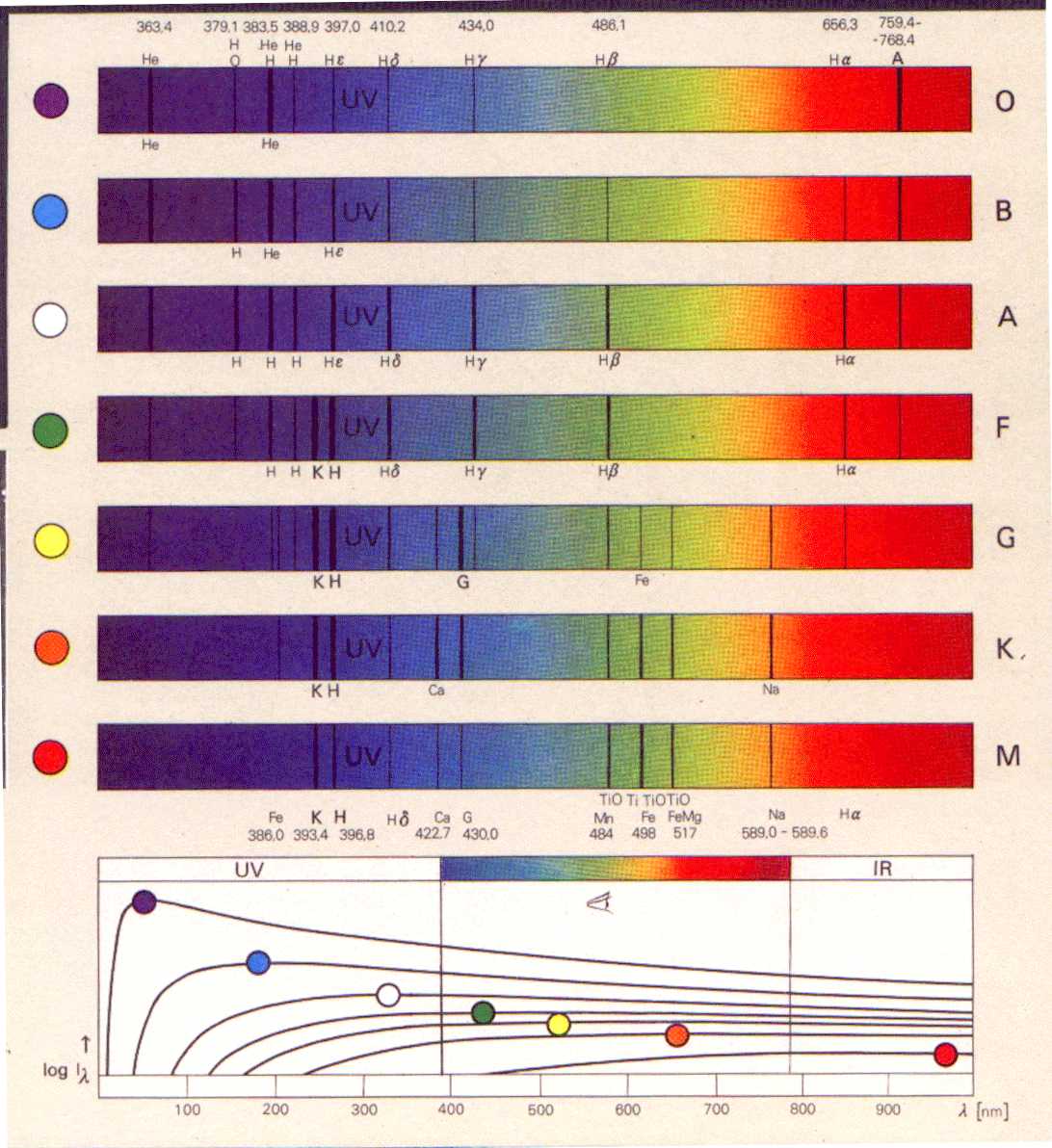
če poznamo še temperaturo zvezde (poznamo njen spektralni tip),
iz teh podatkov pa lahko izračunamo temperaturo planeta
(če je okoli 287 K, to je 14 °C, je ta planet kandidat za
življenje!!!!!!!!!!!!!)
Naselitveno področje (habitable zone)
- sprememba 1/10000, kot da bi hotel zaznati spremembo sija
avtomobilskega žarometa na veliki razdalji, ko leti mimo
žarometa muha
* - iz časa prehoda je mogoče izračunati orbito planeta in maso zvezde,
velikost planeta se oceni iz globine zmanjšanja sija (krivulje),
če poznamo še temperaturo zvezde (poznamo njen spektralni tip),
iz teh podatkov pa lahko izračunamo temperaturo planeta
(če je okoli 287 K, to je 14 °C, je ta planet kandidat za
življenje!!!!!!!!!!!!!)
Naselitveno področje (habitable zone)
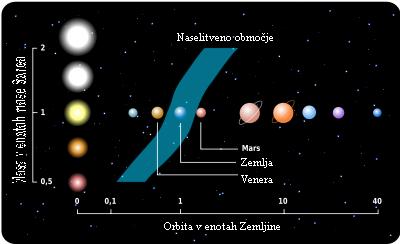
Območje naselitvene cone neke zvezde je:
Rnp = Rae(Lzve/Lson)1/2
*Glej tudi - Življenje v vesolju
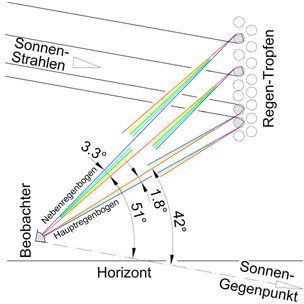
 Orbite naseltvene cone, glede na temperaturo zvezd.
Zorni kot - 12° (približno 2x daljnogled 7x50), v resnici polje 105 °^2
Cilj - najti okrog 480 Zemlji podobnih planetov
(to je ocena = 0.5%*100 000/100% = 500), samo okrog 0.5%
orbit bi naj ležalo v ravnini v katero gleda teleskop
Kepler (verjetnost v zornem polju stopinje je 1/180 = 0.0055 = 0.5%,
zaradi simetrije, iz Zemlje vidimo Sonce pod kotom 0.5 stopinje,
če bi bila zemlja bližje, bi se ta kot približal stopinji in
znotraj tega kota iščemo prehod planeta: ox),
približno ponovitev prehoda na leto, čez nekaj mesecev prvi
rezultati o prehodu večjih planetov - podobnih Jupitru ...
Prispodoba - naloga projekta je podobna nalogi, kot da bi
iz Zemlje iskali komarja na Luni, ki leti pred
žarometom avtomobila (svetlobni tok se zmanjša za
1/10000), do Lune pa je razdalja kar 60 polmerov Zemlje,
"iščemo torej komarje na Luni"
Jasno je le to, pravijo v Nasi:
"Kepler ne bo našel vesoljčka E. T.-ja, ampak bo pomagal najti E. T.-jev dom."
Zakaj taka lega, orientacija glede na Sonce, zakaj pokrov?
Orbite naseltvene cone, glede na temperaturo zvezd.
Zorni kot - 12° (približno 2x daljnogled 7x50), v resnici polje 105 °^2
Cilj - najti okrog 480 Zemlji podobnih planetov
(to je ocena = 0.5%*100 000/100% = 500), samo okrog 0.5%
orbit bi naj ležalo v ravnini v katero gleda teleskop
Kepler (verjetnost v zornem polju stopinje je 1/180 = 0.0055 = 0.5%,
zaradi simetrije, iz Zemlje vidimo Sonce pod kotom 0.5 stopinje,
če bi bila zemlja bližje, bi se ta kot približal stopinji in
znotraj tega kota iščemo prehod planeta: ox),
približno ponovitev prehoda na leto, čez nekaj mesecev prvi
rezultati o prehodu večjih planetov - podobnih Jupitru ...
Prispodoba - naloga projekta je podobna nalogi, kot da bi
iz Zemlje iskali komarja na Luni, ki leti pred
žarometom avtomobila (svetlobni tok se zmanjša za
1/10000), do Lune pa je razdalja kar 60 polmerov Zemlje,
"iščemo torej komarje na Luni"
Jasno je le to, pravijo v Nasi:
"Kepler ne bo našel vesoljčka E. T.-ja, ampak bo pomagal najti E. T.-jev dom."
Zakaj taka lega, orientacija glede na Sonce, zakaj pokrov?






















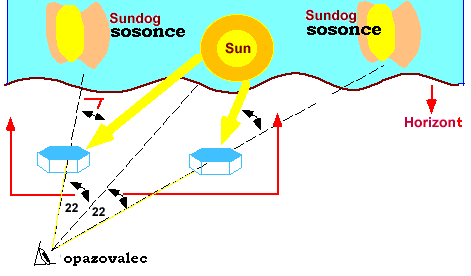
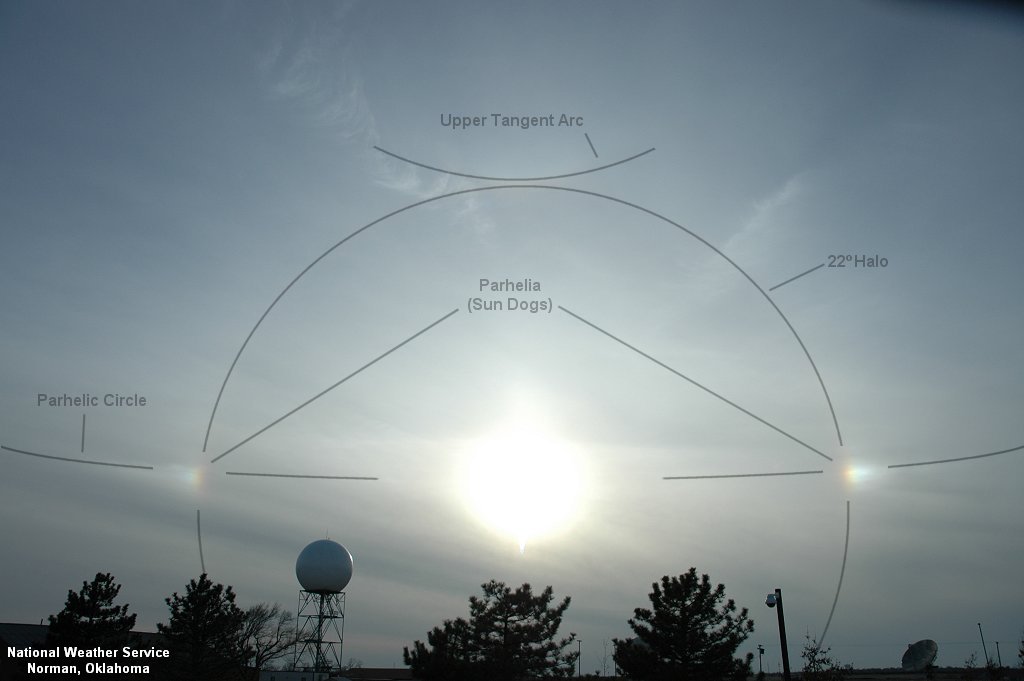
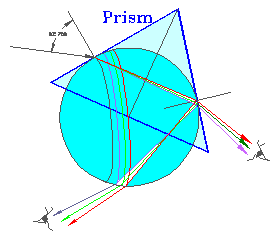
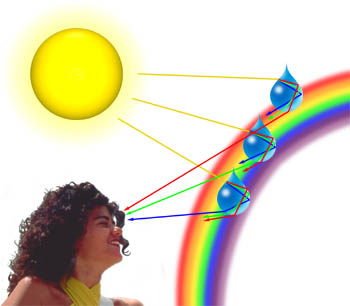




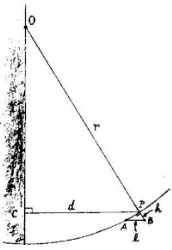
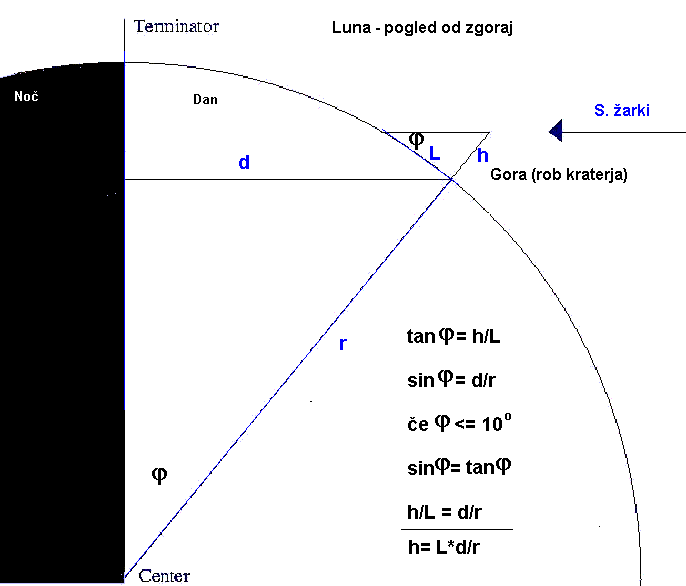
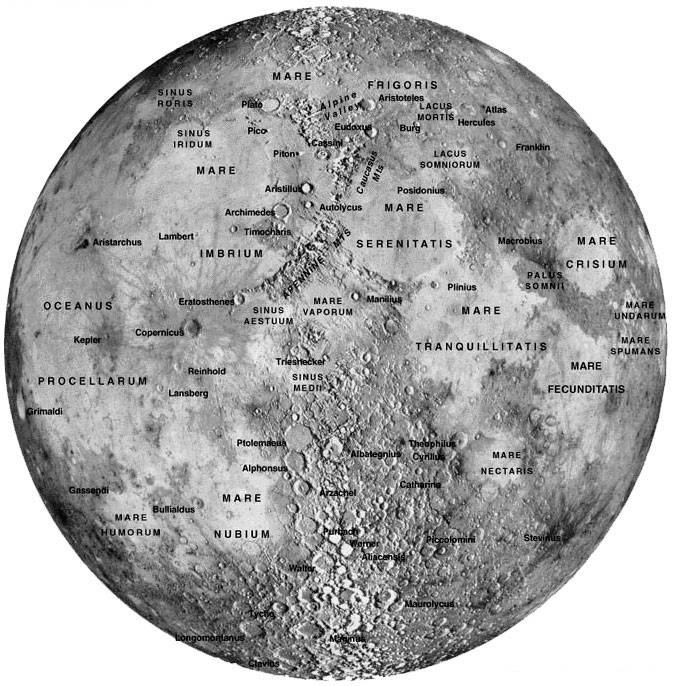
Geometrijsko korektna metoda
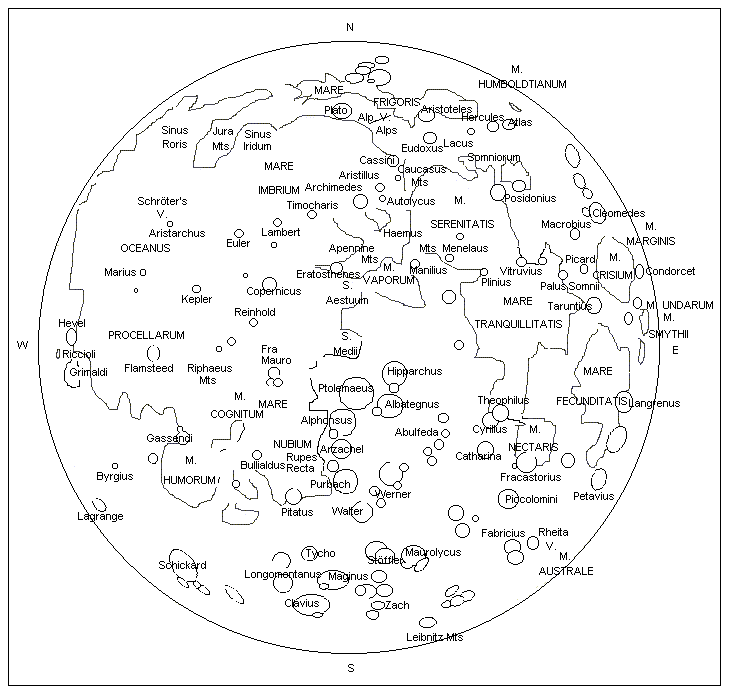
Določitev dolžine sence gore, kraterja na Luni z matematično eksaktno metodo A) Višina kraterja Ko merimo dolžino sence v svetlobnih elementih (pixlih) ali mm, je to le projekcija na ravnino pravokotno na smer našega pogleda, na sliko.Pravo dolžino izračunamo s pomočjo koordinat kraterja (selenografične koordinate), - podatke dobimo recimo na wikipediji. Izračunamo faktor nagiba in z njim pomnožimo izmerjeno dolžino L'. ls = lunina_širina_kraterja v ločnih stopinjah ld = lunina_dolžina_kraterja v ločnih stopinjah - za lažje razumevanje, na Zemlji podamo geografsjo šrino in dolžino nekega kraja, na Luni pa lunino dolžino in širino neke nekega kraja, kraterja, točke.
- za ponazoritev primerjave koordinat Zemlja-Luna povečaj sliko. 1 faktor_nagiba_korekcija = -------------------- cos(ls) * cos(ld) L = L''* faktor_nagiba_korekcija
----------------------- ** Bolj korekten faktor je (ker je Luna nekoliko nagnjena glede na opazovalca) 1 faktor_nagiba_korekcija = --------------------------- cos(ls - zs) * cos(ld - zd) -kjer sta ls in ld Lunine (selenografične) koordinate, zs in zd pa sta koordinati sub-zemljine točke (kjer daljica "Zmelja - Luna" prebada Luno). ------------------------- Veljavnost tega faktorja (pri velikih kotih) je potrebno preveriti? B) Določitev kota theta, pod katerim padajo žarki na krater, goro (izpeljava je spodaj)
x = sin(Bo)*sin(ls) + cos(Bo)*cos(ls)*sin(Co + ld) kot theta = arcsin(x) H = L * tan(theta) - višina kraterja, gore Kaj sta kota Co in Bo, kje jih dobimo: # Co: Colongitude of the Sun (*1 razlaga spodaj) # Bo: Subsolar point Lat (*2 razlaga spodaj) Kota Co in Bo dobimo na: http://www.lunar-occultations.com/rlo/ephemeris.htm
Slika za pomoč pri razumevanju pomena kotov. Za Luno velja, da (*2 Bo) subsolarna točka na Luni (to je točka kjer Luno prebada daljica, ki povezuje centra Lune in Sonca) ni nikoli več kot 1.5 st. nad ali pod Luninim ekvatorjem. Subsolarna točka na Luni je tista, v kateri je Sonce, če gledamo z Lune, v zenitu. Lunina dolžina se meri od centralnega meridiana (CM) proti vzhodu (to je pozitivna smer). Kot 90 st. minus lunina dolžina subsolarne točke je (*1 Co) lunina dolžina terminatorja, v angleščini se imenuje ta kot "Sun's selenographic colongitude". Terminator je področje med osvetljenim in neosvetljenim delom Lune. Ko je Sonce direktno nad vzhodnim robom Lune (prvi krajec), je lunina dolžina subsolarne točke +90 st., lunina dolžina terminatorja (Sun's selenographic colongitude) pa je 0 ločnih st. Lunina dolžina terminatorja narašča okrog 0.51 stopinje na uro. Lunina dolžina terminatorja se tako spreminja od 0 do 360° v približno 29.53 dneh. Pri polni Luni lunina dolžina terminatorja naraste na 90 st. zahodno; pri zadnjem krajcu na 180 st. in pri mladi Luni na 270 st. zahodno. http://www.pacifier.com/~tpope/Moon_Page.htm Sledijo primeri iz zgornje slike, datum 2009-01-05, posneto ob času 20 CET, 19 UT ------------------------------------------------------------------ Podatki in izračuni (brez upoštevanja koordinat sub-zemljine točke) -------------------- KRATER lun_sir° lun_dol° Co° Bo° x theta_rad H' km L' px korekcija H km H_resnična km Tycho 43.3 348.8 23.4 -0.7 0.145406309 0.145923633 3.363698794 16 1.400732003 4.711640549 4.8 Timocharis 26.7 346.9 23.4 -0.7 0.154235531 0.15485368 2.67958314 12 1.14926378 3.079547849 3.1 Copernicus 9.7 340 23.4 -0.7 0.056395701 0.056425638 3.231998965 40 1.079612486 3.489306436 3.8 Eratosten 14.5 348.7 23.4 -0.7 0.199867679 0.201222873 3.209675768 11 1.053319266 3.380813324 3.6 Autolycus * 30.7 1.5 23.4 -0.7 0.355764279 0.363731722 2.722647043 5 1.163389137 3.167497995 3.4 Aristillus * 33.9 1.2 23.4 -0.7 0.338678413 0.345511946 3.089354749 6 1.205065735 3.722875552 3.6 Rezultati 1 -------------------- KRATER H km H_resnična km (H_brez korekcij km) Tycho 4.7 4.8 (4.4) Timocharis 3.1 3.1 (3.1) Copernicus 3.5 3.8 (4.2) Eratosten 3.4 3.6 (3.7) Autolycus * 3.2 3.4 Aristillus * 3.7 3.6 Podatki in izračuni (z upoštevanjem koordinat sub-zemljine točke - rotacije Lune glede na Zemljo) zs =-6.8 st zd =-7 st --------------------------------------------------------------------------- KRATER lun_sir° lun_dol° Co° Bo° x theta_rad H' km L' px korekcija H km H_resniTycho 43.3 348.8 23.4 -0.7 0.145406309 0.145923633 3.363698794 16 1.563166779 5.258022207 4.8 Timocharis: 26.7 346.9 23.4 -0.7 0.154235531 0.15485368 2.67958314 12 1.206033573 3.231667228 3.1 Copernicus 9.7 340 23.4 -0.7 0.056395701 0.056425638 3.231998965 40 1.070382753 3.459475951 3.8 Eratosten 14.5 348.7 23.4 -0.7 0.199867679 0.201222873 3.209675768 11 1.076346737 3.454724039 3.6 Autolycus * 30.7 1.5 23.4 -0.7 0.355764279 0.363731722 2.722647043 5 1.274471382 3.469935739 3.4 Aristillus * 33.9 1.2 23.4 -0.7 0.338678413 0.345511946 3.089354749 6 1.332652178 4.117035334 3.6 Rezultati 2 -------------------- KRATER H km H_resnična km (H_brez korekcij km) Tycho 5.3 4.8 (4.4) Timocharis 3.2 3.1 (3.1) Copernicus 3.5 3.8 (4.2) Eratosten 3.5 3.6 (3.7) Autolycus * 3.5 3.4 Aristillus * 4.1 3.6 Zaključek Pri prvem ali zadnjem krajcu sta obe metodi dokaj blizu, napaka pa je večja tam, kjer so sence krajše in en svetlobni element (px) lahko pomeni 10 ali celo 20 procentov napake. Napaka pri prvi grobi metodi majhnih kotov se dodatno poveča, če je krater blizu terminatorja, takrat se poveča relativna vrednost sv. elementa za radaljo d, pri drugi metodi, geometrijsko eksaktni, pa je v tem primeru tudi problem majhnega kota, kjer je tudi čas pomemben (lunina dolžina terminatorja narašča okrog 0.51 stopinje na uro). Naši rezultati so tako uteženi najmanj z 10 % napako. Zelo pomembna je ostrina slike, višino bi lahko ocenjevali tudi vizualno s časom prehoda sence čez nitni križ (tako je meril Galilejo). Za osnovne šole je metoda majhnih kotov zelo primerna, učenci in učenke tako dobijo s preprosto metodo zelo primerne ocene višin gora, kraterjev in to na nebesnem objektu, na katerega načeloma nikoli ne bodo stopili. Ta igra senc in geometrije, človeškega uma, je lahko zelo poučna za razumevanje našega sveta glede na oddaljena telesa. Za srednjo šolo je geometrijska metoda sicer že mogoča a tudi na tem nivoju je potrebna previdnost (je pa dobra vaja za vektorske račune, kjer se najde tudi globlji in uporabni smisel matematike), zato naj za začetek uporabijo metodo majhnih kotov. Eksaktno metodo pa naj uporabijo zgolj mehanično za korekten izračun in s tem primerjavo rezultatov med metodama - seveda se tudi v srednji šoli da kaj povedati o prostorki geometriji. http://www.fourmilab.ch/earthview/lunarform/cratnear.html http://www.maguires.com/astronomy/lunar_craters2.htm
Izpeljava izrazov potrebnih za določanje višine kraterjev:Koordinate točke na krogli (sferi) in zapis krajevnega vektorja s širino in dolžino (lahko sta geografski ali poljubni koordinati na Luni, planetu, ...). Na Luni prav tako merimo koordinate od Luninega ekvatorja, ki oklepa kot približno 1,5 ločne stopinje z ekliptiko in od ničelnega, centralnega meridiana (CM), ki kaže proti Zemlji. Zapišimo koordinate krajevnega vektorja do gore, roba kraterja na Luni. Te koordinate se imenujejo tudi selenografske. Širino l na Luni bomo zamenjali z zapisom (ls). Dolžino j na Luni bomo zamenjali z zapisom (ld). Vektorje bomo zapisovali z krepko pisavo. Enotski vektor do točke T na Luni je torej r = R/R = (cos ls cos ld, cos ls sin ld, sin ls) Za Luno velja, da subsolarna točka na Luni (to je točka kjer Luno prebada daljica, ki povezuje centra Lune in Sonca) ni nikoli več kot 1.5 st. nad ali pod Luninim ekvatorjem. Subsolarna točka na Luni je tista, v kateri je Sonce, če gledamo z Lune, v zenitu.
Slika za pomoč pri razumevanju pomena kotov. Širino subsolarne točke na Luni bomo zamenjali z zapisom (Bo). Namesto dolžine subsolarne točke pa bomo uporabili kot 90 st. minus lunina dolžina subsolarne točke - to je v bistvu lunina dolžina terminatorja (Co). Nekatero to točko imenujejo tudi s tujko - "kolongituda sonca".
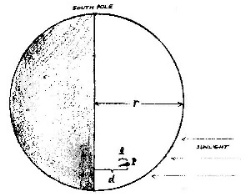
Enotski vektor do subsolarne točke na Luni je torej s = (cos Bo sin Co, cos Bo cos Co, sin Bo) Analogno enotskemu vektorju subsolarne (sub_sončne) točke, definiramo se sub_zemeljsko točko. To je točka na Luni iz katere bi videli Luno v zenitu, oziroma točka na površini Lune, ki leži na daljici Luna-Zemlja. ze = (cos zs cos zd, cos zs sin zd, sin zs) ----------------------------------------------------------------------- Sedaj imamo pripravljene vektorje za izračun višine objekta na Luni. Pomagajmo si s spodnjo sliko.
Naša naloga je določiti višino (H) gore, kraterja. Vse skupaj obravnavamo v (horizontalni) ravnini, ki je pravokotna na krajevni vektor, kateri teče od središča Lune, pa do gore (kraterja) na površini Lune. Iz slike vidimo, da višina gore, senca gore in žarek iz Sonca tvorijo pravokotni trikotnik. Če hočemo izračunati višino gore (H), moramo zato poznati dolžino sence (L) in kot (q) pod katerim pada svetloba na goro. Če poznamo L in q, lahko izračunamo H iz preproste zveze: H=L*tan q Kot q bomo izračunali s pomoćjo zgoraj opisanih vektorjev (r in s). Nato bomo rešili še en hud zalogaj, določili bomo dolžino L, kar pa ni čisto enostavno, saj mi v resnici vidimo, slikamo dolžino L', ki je projekcija sence gore pravokotno na smer Zemlja-Luna. Tukaj bomo zanemarili vpliv lege opazovalca ma Zemlji, in da smer Zemlja-Luna (obeh središč) ni čisto enaka smeri opazovalec - krater (gora) na Luni. Kot med enotskima vektorjena r in s je kar (90° - q), to je kot med vpadnimi žarki iz Sonca in krajevnim vektorjem do tiste točke, gore na Luni, ki ji hočemo določiti višino H. Za izračun kota q uporabimo kar skalarni produkt med vektorjema r in s: r*s = r*s*cos a = r*s*cos (90° - q), - ker je cos(90 - q) = sin q, - in ker je velikost vektorjev r in s po definiciji 1, - da je sin q = cos ls sin ld cos Bo cos Co + cos ls cos ld cos Bo sin Co + sin ls sin Bo, - sin q = cos ls cos Bo (sin ld cos Co + cos ld sin Co) + sin ls sin Bo, - ker velja, da je sin (x + y) = sin x cos y + cos x sin y pridemo do končnega izraza za q, sin q = sin ls sin Bo + cos ls cos Bo sin (ls + Co) q = arcsin(sin ls sin Bo + cos ls cos Bo sin (ls + Co)) Naša naloga bi bila sedaj skoraj končana, a sedaj moramo določiti še L iz meritve L'. V literaturi je več poti, ki pa so nekatere dvomljive narave. Poznamo vektor Zemlja-Luna (ze), in če bi poznali še vektor sence, bi lahko spet zadevo rešili s skalarnim produktom. Kako do vektorja Sence? Ena pot je vektorski produkt. Lahko pa si pomagamo tudi s trikotnikom vektorjev. Oglejmo si sliko trikotnika, ki pa naj bo sestavljena iz uteženih enotskih vektorjev (as in r). Kombinacija obeh nas pripelje do vektorja sence (L).
_____________ a = \/1+ (1/tan q)2 l = as - r l = (a cos Bo sin Co, a cos Bo cos Co, a sin Bo) - (cos ls cos ld, cos ls sin ld, sin ls) l = (a cos Bo sin Co - cos ls cos ld, a cos Bo cos Co - cos ls sin ld, a sin Bo - sin ls) - da dobimo enotski vektor sence moramo l deliti z dolžino, ki je kar l = 1/tan q
Sedaj naredimo skalarni produkt med vektorjema le in ze, iz produkta izrazimo kot (ks) in to je kot s sinusom katerga moramo deliti L', da dobimo dolžino sence L = L'/ sin ks. Višina kraterja je: H = L * tan q -------------------- Naredimo še ta zadnji korak: _____________ a = \/1+ (1/tan q)2 b = 1/l = tan q Enotski vektor sence je le. le = l/l = b l = b(a cos Bo sin Co - cos ls cos ld, a cos Bo cos Co - cos ls sin ld, a sin Bo - sin ls) ze = (cos zs cos zd, cos zs sin zd, sin zs) cos ks = le*ze = b( (a cos Bo sin Co - cos ls cos ld)(cos zs cos zd) + (a cos Bo cos Co - cos ls sin ld)(cos zs sin zd) + (a sin Bo - sin ls)(sin zs) ) ks = arccos( b( (a cos Bo sin Co - cos ls cos ld)(cos zs cos zd) + (a cos Bo cos Co - cos ls sin ld)(cos zs sin zd) + (a sin Bo - sin ls)(sin zs) ) ) L = L'/ sin ks. Višina kraterja je: H = L * tan q = (L'/ sin ks) * tan q
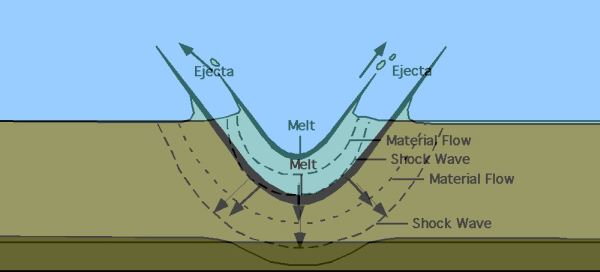
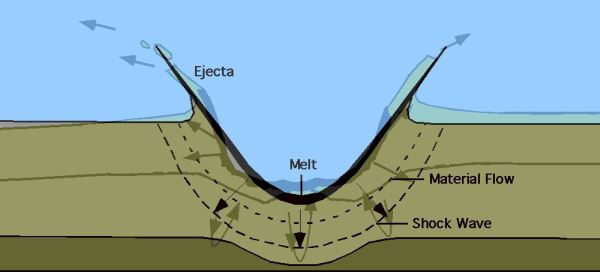
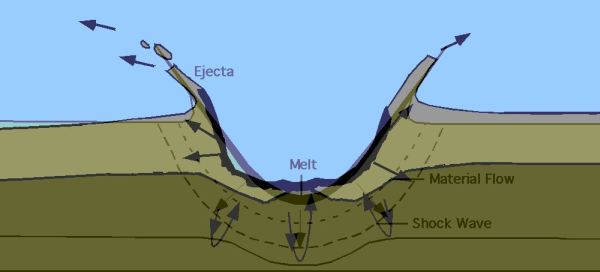
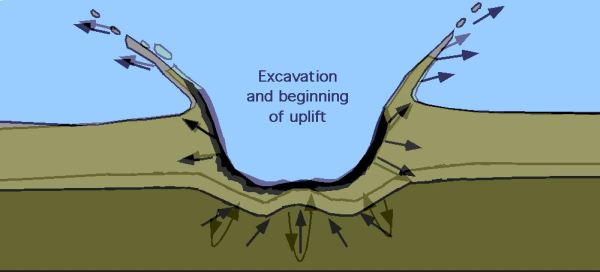
Sledi nekaj slik za boljšo prostorsko predstavo položaja Lune glede na Zemljeo in Sonce.Nastanek terminatorja (ločnica med dnevom in nočjo - zakaj ločnica ni ostra, se lepo vidi iz slike).
Libracija od strani.
Libracija od zgoraj. Iz: http://www.pacifier.com/~tpope/Moon_Page.htm





















Za astronomski krožek: ZORKO Vičar
E-POŠTA, RFC-822: Zorko.Vicar@guest.arnes.si