Spodaj so podatki za Observatorij Gimnazije Šentvid Ljubljana, dobljeni z omenjenimi orodji.
Šentvid pri Ljubljani (Prušnikova 98, lega observatorija Astronomskega krožka Gimnazije Šentvid-Ljubljana) Sferične koordinate / Gauss-Krugerjeve koordinate j, l (0 ' ") / Y[m](za-vz), X[m](ekvator-pol) x= 5106123 m Geografska širina: 46O 5' 54" (latitude) y= 5459091 m Geografska dolžina: 14O 28' 15" (longitude) Nadmorska višina 315m+20m(terasa)=335m (altitude). Podatke pripravil in določil: Zorko Vičar
Merjenje paralakse med prehodom Venere
Edmond Halley je leta 1716 predlagal, da bi prehod Venere uporabili za natančnejšo določitev razdalje Zemlja-Sonce Rz.
Slika zgoraj pojasni bistvo Halleyevega predloga.
Halley je predlagal naj se meri paralaksa Venere glede na Sonce
med prehodom čez Sonce, hkrati pa upošteva takratna ocena paralakse Sonca in tako
izračuna razdalja r od Zemlje do Venere med prehodom
(Kako določimo paralakso Venere glede na zvezde, kot qv,
bomo govorili v nadaljevanju,
direktno iz meritev to namreč ni mogoče).
Iz tretjega Keplerjevega zakona se nato
izračuna razdaljo Zemlja-Sonce Rz, to je astronomsko enoto AE. Meritve so uspele šele po Halleyevi smrti.
Odprave so poslali na različne konce sveta. S sabo so morale imeti natančne ure, kar je bil takrat
problem, ki so ga rešili šele izboljšani ladijski kronometri. Takrat so večinoma določali gegografsko dolžino
preko lege Lune, kar pa je bila precej nezanesljiva metoda.
Podrobnosti si lahko preberete na:
http://www.dsellers.demon.co.uk/venus/ven_ch8.htm.
Glej spodaj Halleyevo skico prehoda 1761, ki ga ni doživel.
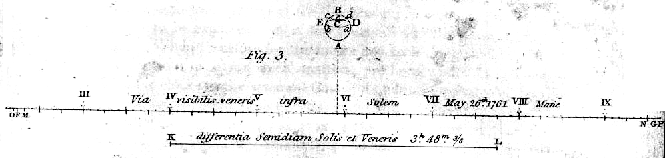
V letih 1761 in 1769, so opazovali
prehode Venere čez Sonce in merili relativno pralakso na Soncu.
Po nekaterih virih je meritve res natančno obdelal
šele Johann Franz Encke (1791-1865) v
prvi polovici 19. stoletja. To je bila za tiste čase kar dobra metoda za določitev
astronomske enote,
ki pa je dala za nekaj procentov večje vrednosti od današnjih meritev,
ki seveda ne temeljijo več na paralaksi pri
prehodih Venere. Predvsem preseneča velik časovni zamik med meritvami in obdelavo -
ja včasih ni bilo
računalnikov in računalniških paketov za računanje efemerid, ni bilo
Postgres, Oracle, MySql, ... podatkovnih baz. Takrat se je vse računalo peš z
logaritemskimi tablicami, vse na papirju,
z možgani kot procesorjem, gosjim peresom kot printerjem in "harddiskom".
Zato je bil Jurij Vega takrat s svojimi logaritmi
"bestseller" - a še živi pomen tega genija v našem zgodovinskem
spominu
(naredimo kaj, da bo v bodoče še bolj cenjen)?. Na Luni so prej po njemu poimenovali
krater, kot je dobil v Ljubljani spomenik. Slovenci smo res, kaj že!?
Glej tudi zgodbo o kronometru.
Glej tudi izračun iz opazovanj z leta 1769.
ali
http://www.vt-2004.org/Education/EduSheet3.html
ali
zelo didaktični stran http://skolor.nacka.se/samskolan/eaae/summerschools/TOV0.html
Spodaj je skrajšan tekst iz strani (meritve iz leta 1769 zbral Jean-Nicolas Delisle):
http://www.fiz.uni-lj.si/venera2004/izobrazevalne_pole/3/index.html
(http://www.vt-2004.org/Education/EduSheet3.html)
Dodan pa je komentar in nova slika, ki
zaobide nekoliko kompleksnejšo geometrijo izpeljave astronomske enote iz omenjene strani.
Spodnjo sliko bomo torej nadomestili z bolj preprostim premislekom.
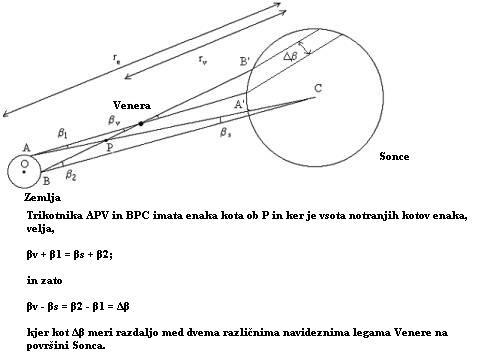
Na omenjeni strani (http://www.fiz.uni-lj.si/venera2004/izobrazevalne_pole/3/index.html)
se mogoče premalo poudarja, da razlika kotov Venerinih sledi
na združeni sliki Sonca ni absolutna paralaksa Venere glede na zvezde,
pač pa pralaksa Venere minus paralaksa
Sonca (premik glede na Sonce, center Sonca). Na strani ...venera2004... sta namreč sliki, ki
kažeta premaknjeno lego Venere in Sonca glede na "zvezdno" ozadje (sta pa glede na
spremljevalno skico napačno zamaknjeni),
nakar pa iz njiju naenkrat nastane samo premik Venere glede na Sonce, brez natančnejšega
pojasnjevanja zakaj.
Enačbe, ki so izpeljane sicer niso sporne,
a geometrija je (sploh za mlajše učence) nekoliko komplicirana, čeprav pravilna.
Tej geometriji (zgoraj, ali s klikom,
si jo lahko ogledate)
se bomo v nadaljevanju tega teksta izognili.
Poučna je tudi stran
http://www.vt-2004.org/Education/EduSheet2.html
ali
prevod
http://www.fiz.uni-lj.si/venera2004/izobrazevalne_pole/2/index.html
Če opazujemo
gibanje Venere med celotnim prehodom, lahko izrišemo njeno celotno
navidezno pot preko Sonca. Če opazujemo z mest A in B, bomo dobili dve
vzporedni črti (bolje poti). Razmik med črtama je relativni paralaktični premik
glede na center Sonca. Ta kot, ker je relativen, še ni dovolj za izračun razdalj,
ampak mu je potrebno še prišteti paralakso Sonca. Več v nadaljevanju.
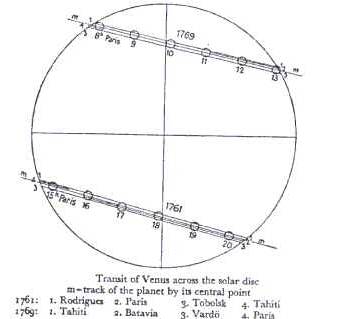
Sir Edmond Halley je predlagal širše zastavljeno akcijo za opazovanje
Venerinega prehoda v letih 1761 in 1769, Jean-Nicolas Delisle pa je skupaj
zbral dobljene rezultate. Te podatke bomo uporabil za izračun razdalje med Zemljo
in Soncem po prepostejši metodi, kjer so se vsi opazovalci nahajali na istem
poldnevniku. Opazovalci so bili zaradi natančnejše meritve na geografskih
širinah, čimbolj oddaljenih druga od druge. Zgoraj je skica meritev iz 6. junija leta 1761 in
iz 3. junija leta 1769.
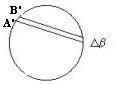
Kako določimo razdalja Δβ med dvemi opazovanimi potmi Venere preko Sonca?
Da direktno izračunamo Δβ, najprej
izmerimo premer Sonca DS, ter razdaljo Δβ med potema na risbi ali
fotografiji. Kotni premer Sonca znaša na Zemlji 30' (kar je ravno 0.5 ločne
stopinje). Iz razmerij dobimo
Δβ / 30' = A'B' / DS
torej
Δβ = (30') (A'B' / DS)
Vendar mora biti v naši enačbi kotni premer Sonca izražen v radianih. Zato
Δβ = (30 π / 10800) (A'B' / DS)
Δβ = (π /360) (A'B' / DS)
Izmerimo razdaljo med črtama 1 in 3 ter dobimo Δβ = 1.5 mm, premer Sonca na sliki (meritve iz 3. junija 1769) pa je DS = 70 mm, torej je,
Δβ = (π / 360)(1.5 / 70) = 0.00019 radianov (bolj natančna metoda nam da vrednost 0.00020 radianov)
Če izmerimo Δβ neposredno, naredimo
precejšnjo napako pri meritvi razdalje med črtama.
Uporabimo lahko natančnejšo metodo za
meritev Δβ
(glej Dodatek ).
Odprava kapitana Jamesa Cooka na Tahiti.
Na prvem potovanju z ladjo Endeavour je 3. junija 1769 na Tahitiju meril,
po navodilih Britanske Kraljeve družbe (Royal Society of Britain), prehod
Venere čez Sončevo ploskev. To potovanje je na žalost potekalo še brez
natančnega Harrisonovega kronometra, ki bi ga za ta primer najbolj rabil.
Geografsko dolžino je meril s pomočjo Luninih tablic.
Izbrani opazovalni kraji so bili pogosto zelo oddaljeni in potovanja so
bila v tistem času nevarna zaradi neugodnih vremenskih pogojev ter zaradi
številnih vojn med državami. Na Indijskem oceanu sta se npr. spopadali
Anglija in Francija. Poudaraiti je treba, da je bila znanstvena akcija,
organizirana ob Venerinem prehodu leta 1761 prva mednarodna akcija,
v celoti je bilo vanjo vključenih kar 130 znanstvenih ekspedicij po
celem svetu. Leta 1769 so znanstveniki opazovali pri Pondicheryju v
ču, na Sv. Domingu, v San Joseju v Kalifornijskem zalivu, v
Hudsonovem zalivu v Kanadi, na Tahitiju, Laponskem, v Jakutsku v
Siberiji… V celoti je bilo 151 opazovalcev na 77 različnih krajih.
Odprave so se soočale z različnimi problemi, zaradi katerih so bili
dobljeni rezultati včasih tudi slabši od pričakovanj.
Pralaktični premik Venere glede na zvezde in glede na Sonce.
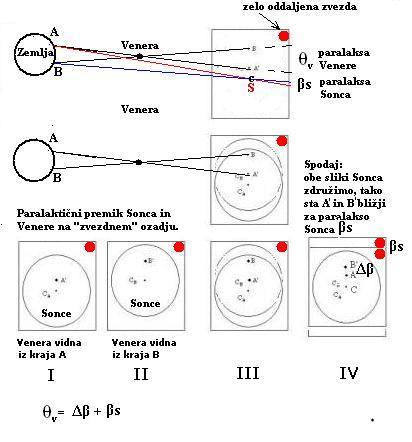
Skice, predvsem v tretji vrsti, kažejo položaj Venere in Sonca glede na zvezdno ozadje,
ki ga simbolično
predstavlja rdeča pika - zvezda, glede na opazovalca v krajih A in B. Seveda ni govora,
da bi lahko
v tistih časih, določili natančno lego Sonca glede na zvezde, paralakse Sonca pa tudi niso
poznali, saj so prav to iskali. Zato so morali skice Sonca prekriti s centroma, kar
pomeni, da se je pralaksa Venere na skici zmanjšala za pralakso Sonca. A tudi ta problem, kot
bomo videli, se da eleganto rešiti.
I in II - pralaktični premik Venere in Sonca glede na zvezde za kraja A in B
III - če obe sliki I in II združimo glede na zvezdno ozadje, dobimo paralakso Venere
qv
glede na zvezde
IV - ker absolutnega položaja Sonca glede na zvezde ne poznamo, sliki združimo glede na
center Sonca in tako odčitamo relativno paralakso Venere (Δβ) glede na Sonce,
ki je manjša za paralakoso Sonca (βs)
K relativnemu, res merljivemu, premiku (paralaksi) Δβ Venere glede na center Sonca,
moramo prišteti še paralakso Sonca βs, da bomo dobili resnično paralakso
Venere qv glede na oddaljene zvezde.
Ker paralakse Sonca βs
ne poznamo, jo bomo posredno potegnili iz tretjega Keplerjevega zakona in iz razmerij,
saj sta paralaktična kota sorazmerna z oddaljenostima Venere in Zemlje od Sonca.
qv = Δβ +βs;
kjer, še enkrat, kot Δβ meri razdaljo med dvema različnima navideznima legama Venere na površini Sonca. S preureditvijo zadnje enačbe dobimo
Δβ =βs
((qv /βs) - 1)
Naj bo Rz razdalja
med Zemljo in Soncem ter Rv razdalja med Venero in Soncem. Venerina
paralaksa je qv = AB / (Rz- Rv) in
Sončeva paralaksa je βs = AB / Rz, torej je
njun kvocient qv /βs = Rz / (Rz-
Rv). Zadnjo zvezo lahko nesemo v zgornjo enačbo in dobimo
Δβ =βs ((Rz / (Rz- Rv)) - 1) =βs Rv / (Rz- Rv)
Natančneje, lahko izrazimo Sončevo paralakso
βs = Δβ ((Rz / Rv) - 1)
Bodi pozoren na to, da
je Δβ relativni paralaktični premik glede na center Sonca,
to je kotna razdalja med dvema
vzporednima črtama.
Razmerje Rv
/ Rz lahko izračunamo iz
3. Keplerjevega zakona, saj
poznamo obhodna časa Venere (224.7 dni) in Zemlje (365.25 dni).
(Rz / Rv)3 = (365.25 / 224.7)2
zato
Rz / Rv = 1.38248
Zadnji rezultat lahko uporabimo v zvezi za Sončevo
paralakso in dobimo
βs = Δβ ((Rz / Rv) - 1) = Δβ (1.38248 - 1)
zato
βs = 0.38248 Δβ
In končno, ob uporabi definicije paralakse lahko
izračunamo razdaljo med Zemljo in Soncem Rz
Rz = AB /βs;
Potrebujemo torej razdaljo AB med dvema opazovalcema,
ki sta med prehodom izmerila Δβ.
Za demonstracijo zgoraj opisanih izračunov bomo
uporabili opazovalne podatke iz leta 1769, ki jih je v "A History of
Astronomy" objavil A. Pannekoek. Njegova knjiga prikazuje risbe in
tabele z izmerjenimi kontaktnimi časi, izmerjenimi na različnih
lokacijah v letih 1761 in 1769. Mi bomo uporabili podatke iz leta 1769 iz
opazovanj v krajih Vardö (Laponska) in Papeete (Tahiti).
sin ((φ1 + φ2) / 2) = (AB / 2) / R
Uporabljamo opazovanja iz leta 1769, iz krajev Vardö in
Tahiti, ki sta bili na področjih, od koder je bil prehod viden. Bodi
pozoren na to, da je bil v kraju Vardö polarni dan.
Vardö (Laponska) in Papeete (Tahiti) imata enako
geografsko dolžino, njuni širini pa sta 70° 21' S in 17° 32' J.
Geometrija je sedaj spremenjena.
φ = (90 - φ1) + 90 + φ2 = 127° 11'
Za polmer Zemlje vzamemo R = 6378 km, ter izračunamo
AB = 2 R sin(φ / 2) = 11425 km
Z uporabo Sončeve paralakse dobimo
βs = 0.38248 Δβ
in za razdaljo med Zemljo in Soncem Rz
Rz = AB /βs;
Podatki iz odprave leta 1769 nam dajo za Rz
Rz = 157 106 km
Natančna vrednost za razdaljo je Rz =
149.6 106 km. Z natančnejšo metodo za meritev Δβ
lahko dobimo točnejši rezultat.
Odštevanje časa do prehoda Venere.
Opazovanja leta 1769
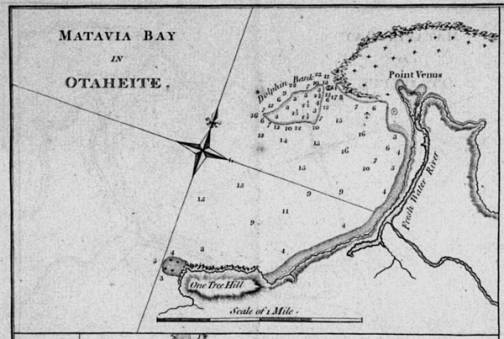
Venerina točka na Tahitiju je bila poimenovana v času prehoda.
Določitev razdalja D med opazovalcema v krajih A in B, za isti meridian
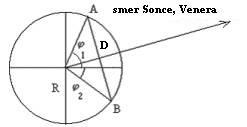
Razdaljo D=AB lahko izpeljemo iz znanih geografskih
širin obeh krajev. Na zgornjem diagramu
sta φ1 in φ2
geografski širini krajev A in B, R pa je polmer Zemlje.
http://www.venus-transit.de/1639/horrox.htm
PRIPRAVE NA PREHOD
Podobe Venere 24. maj 2004,
Astronomski krožek Gimnazije Šentvid - ADV Slovenija.
- oglej si film
Posnetke sta naredila Dejan Kolarič in Zorko Vičar 24. maj 2004,
digitalni fotoaparat Canon A60 je posodil Klemen Blokar.
Čudovit prizor 24. maja 2004 iz terase Gimnazije Šentvid.
Levo spodaj je Prokijon, zgoraj levo je Luna, desno od Lune sta Dvojčka, Polux in Kastor,
pod njima sta Saturn in Mars, desno
Venera nekaj stopinj nad obzorjem, pod njo nekoliko levo najvišji vrh Slovenije Triglav.
Spodnji sliki je Dejan sestavil iz šestih slik, slike je poravnal glede na zvezde.
Sledijo različni posnetki venere skozi teleskop MEADE LX200 10", f/10, ki kažejo na
migetanje atmosfere (refrakcija svetlobe v različno gosti atmosferi, v turbolentnih celcah ...),
ki pa nudi cel kup zanimivih barvnih oddtenkov
A) AVI FORMAT - posnetek Venere v nemirni atmosferi, 24.5.2004, zelo poučno.
Posnetek obdelal Dejan Kolarič.
Venera razbita na barve zaradi refrakcije v atmoisferi tik pred zahodom.
B) AVI FORMAT - posnetek Venere tik pred zahodom v nemirni atmosferi, 24.5.2004, zelo poučno.
VSI POSNETKI, TUDI FILMI, VENERE SO NASTALI NA NASLEDNJI NAčIN, glej spodnjo sliko, izjemno
preprosto a tudi izjemno učinkovito.
Venera nad Triglavom, 25. maj 2004, posnela Klemen Blokar in Zorko Vičar.
Animacija večerne poti Venere, zašla je vzhodno od Triglava, 25. maj 2004, posnela Klemen Blokar in Zorko Vičar.
GLEJ TUDI JAVASCRIPT ANIMACIJO, KI JE BOLJŠE KVALITETE.
Za astronomski krožek: ZORKO Vičar
E-POŠTA, RFC-822: Zorko.Vicar@guest.arnes.si