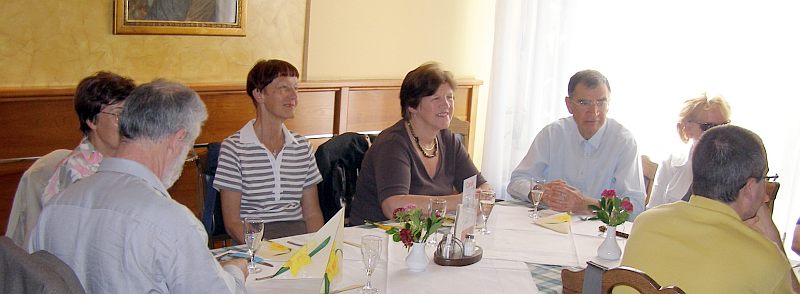PROGRAM ZA 3. OBDOBJE - ASTRONOMSKI KROŽEK Gimnazije Šentvid
Skupina Repatice in kometi
- astronomska predavanja in opazovanja pri AD Vega - Ljubljana
(2008/09)

Oktet predavateljev ADV: Andrej, Dejan, Gregor, Jure, Klemen, Matija, Peter, Zorko
Predstavitve: ppt, html, ...
URNIK, VSEBINA IN PREDAVATELJI ŠE NISO USKLAJENI - to je zgolj predlog!!!
- Uvodna ura - pogovor o programu ... [*]
- Pot na Mars (krivulja leta, čas, težave)
- Luna
- Zemlja
- Slovenski astronomi
- Astronomija na drugih valovnih dolžinah (infrardeča, ultravijolična, radijska ... ),
- Projekta Apollo in Orion
- Space Shuttle
- Rojstni hiši Jožeta Štefana, Josipa Plemlja (en dan)
- Exstrasolarni planeti
- Opazovanje na Toškem čelu
- Zanimive ideje za prihodnjo tehnologijo (vesoljsko dvigalo in podobno)
- Morebitna predavanja zunanjih gostov [z univerze, tujine, ..., ideje:
glaciolog dr. Peter Skvarča, T. Zwitter, A. Gomboc, D. Petrač, M. Prosen, ...]
----------------------------------------
Imenitno predavanje je izvedel (7.jan.2009) astronom
Rok Roškar iz Oddelka za astronomijo
Univerze v Washingtonu - University of Washington,
Department of Astronomy.
Kratka vsebina - zanimivosti o nastanku spiralnih galaksij;
kje se končajo diski, kako se spreminjajo krožnice zvezd in
kaj pravzaprav to pomeni za t.i. galaktično arheologijo in naše
dojemanje evolucije "lokalnega" vesolja ...
prikazano v kontekstu našega trenutnega znanja o kozmologiji in
nastanku vesolja nasploh, brez predstave o celoti,
podrobnosti ostanejo le podrobnosti, ...
Rokova predavanja so na:
-
http://www.astro.washington.edu/roskar/astronomy/sentvid.zip
včasih je problem med prenosom
power point prezentacij,
ki so narejene na macu, na PC (grafika se ne prikaže pravilno)
- v tem primeru glej pdf, nima filmčkov in podobnega...
Filmčka pa sta:
-
http://www.mpa-garching.mpg.de/aquarius/Aq-A-2-evolv-lowres.mp4
(prikaže temno snov od prasevanja do zdaj)
-
http://www.astro.washington.edu/roskar/astronomy/MW1hr.mpg
(nastanek naše galaksije)
-še nekaj drugih filmčkov iz Rokove raziskovalne skupine
se najde na
http://www.youtube.com/user/Nbodyshop


Zgornja slika pove o pridnosti in vztrajnosti več kot sto besed.
-
Obiski as. observatorija na Golovcu
- Tehnični muzej (Slovenija Bistra, ...)
- Rojstni hiša Jurija Vege (popoldne?), razstave o Hallersteinu - jezuit, a tudi misijonar, matematik, astronom, kartograf in mandarin
- Izdelava društvenega teleskopa
- Obisk reaktorja v Podgorici (alternativa je JE Krško)
- Pogovor o poljubnih temah - vprašanja, mi odgovarjamo [*]
- Podnebne spremembe
- Aktualni in bodoči dogodki na področju astronomije - astronavtike
(misije, tekoči - bodoči projekti, ESA, NASA, Rusija, Japonska, Kitajska,
Indija, kje je Slovenija - RAdial VElocities, GAIA, Hipparcos, Cassini,
projekt Kepler, itn)
- Astronomske novice
----
Sledijo predlogi iz prvega srečanja 8.10.2008 (študijsko leto 2008/2009).
- HDR (High Dynamic Range Photography) in
astrofotografija - praktični primeri (tudi v razredu, mlada Luna, M31)
- Detekcija nevtrinov
(Ker nevtrini interagirajo le šibko, je verjetnost za
njihovo interakcijo s snovjo zelo majhna.
Razpolovna debelina za absorpcijo nevtrinov v svincu je okrog enega svetlobnega leta.
Ker nevtrini interagirajo le šibko, je verjetnost za njihovo interakcijo s snovjo
zelo majhna. Razpolovna debelina za absorpcijo nevtrinov v svincu
je okrog enega svetlobnega leta. Vsak tip detektorja nevtrinov vsebuje veliko količino snovi
v podzemni jami in ta ga ščiti pred kozmičnim sevanjem.)
-
Sevanje kozmičnega ozadja
(mikrovalovi)
(Osnovno podobo prapoka - veliki pok - lahko danes vidimo v dejstvu, da se bolj oddaljene galaksije
hitreje oddaljujejo od bližnjih. Drugi pokazatelj prapoka je mikrovalovno sevanje kozmičnega
ozadja, precej oslabljeno sevanje, ki izvira iz časa kmalu po prapoku. To sevanje je izredno
enakomerno v vseh smereh. To posebnost sevanja so kozmologi poskusili pojasniti z začetnim
obdobjem hitrega napihnjenja, ki je sledilo prapoku, saj zelo oddaljeni predeli Vesolja
med sabo drugače niso mogli vplivati drug na drugega.)
- Pot od vodika v jedru zvezde do helija, kisika, dušika, železa, urana, planeta, do človeka.
- Merjenje razdalj
v vesolju (od antike do danes, paralaksa, supernove, rdeči premik, itn)
- Podnebne spremembe in teorije, modeli, ki zavračajo splošno sprejeto
in utemeljeno teorijo o vplivu toplogrednih plinov na podnebje
- Nobelovi nagrajenci in astronomija (težave pri korektnem izboru nagrajencev)
- Aktualna Nobelova nagrada za fiziko - nekateri odzivi iz Italije
- Opazovanja - poudarek na prostorski predstavi
(kje je objekt glede na našo galaksijo in Sonce)
- Hitrost svetlobe (priznana teorija, ki temelji na merjenjih
in teorije, ki oporekajo končnosti svetlobne hitrosti)
- Kako se odraža temna snov ob trkih galaksij
-
Električno vesolje 1
[Zorko in Gregor]
Predstavitev dosezkov teleskopa Hubble - 400 let po Galileju (MLA2009)
- kaj vse zmoremo, če sodelujemo in se učimo drug od drugega.
Električno vesolje - Kako je elektrika razsvetlila svet
Nagrada Aventis za leto 2006 - najprestižnejša nagrada za poljudnoznanstveno literaturo.
(DAVID BODANIS sodi poleg Stephena Hawkinga in Briana Greena med najuspešnejše
pisce poljudnoznanstvenih knjig. Doslej je napisal štiri dela, vsa so bila pri
bralcih izredno dobro sprejeta. Svojo kariero je začel kot profesor na Oxfordu,
trenutno pa kot strokovni svetovalec sodeluje z največjimi podjetji za tehnološki razvoj.
Sila elektrike je izjemno močna in neprenehoma deluje že 13 milijard let.
Čeprav je očem večino časa nevidna, so njeni učinki prisotni povsod. David Bodanis
je v knjigi Električno vesolje predstavil zgodovino znanstvenih odkritij, povezanih
z elektriko, in tako svojim bralcem odškrnil vrata v kraljestvo, ki vlada svetu,
v katerem živimo. Pri tem se je osredotočil predvsem na spoznanja 19. in 20. stoletja,
ki so omogočila izdelavo naprav, o katerih je človeštvo prej lahko le sanjalo)
- Umetno spreminjanje vremena
(zloraba vremena za parade, športne spektakle,
spreminjanje vremena za preprečitev orkanov, ujm, ...)
- Higgsov bozon ...
- xy
Seznam kaj kdo predava ||
Seznam kaj kdo predava - preliminarni datumi
FOTO GALERIJA 2008/2009
Sestavil mentor Zorko Vičar skupaj s člani AKGŠ & ADV in Kometi & repaticami
2008, Ljubljana
tel. 041 549 963 (Zorko)
Kontaktna oseba za UNI3
Franc Pavlovčič
Kolarjeva 25a
1000 Ljubljana
TELEFON: (01) 232 669 2
Nazaj na domačo stran.
Nekaj zanimivosti:


Obisk astronomske observatorija na Golovcu, 20. maj 2009.

Razdelitev teleskopkov firstcope-ov, MLA2009.

V kupoli observatorija Golovec.

Slika ne rabi komentarja - pogled.

Srce observatorija, 70 cm-ski teleskop Vega, slovenski prvak med teleskopi,
viličasta azimutna montaža je izdelana v Sloveniji (ima derotator CCD slike).
Vse udeležence je teleskop impresioniral, kupola pa deluje kot
svetišče - je znanstvena "kapela".
Študent Simon Kaučič (tel. 031 283347)
se je res lepo potrudil pri predstavitvi teleskopa in vaj, ki jih
izvajajo študentje (le teleskop je malo ponagajal).
Osnovni podatki o teleskopu Vega
http://astro.ago.uni-lj.si/vega/pmwiki.php?n=Main.TeleskopVega
- Zrcalo premer 70 cm, zerodur
- Primarno gorišče f=2.031m F/D=2.9 skala=0.914"/piksel
- Sekundarno gorišče, dvolečni korektor f=5.831m F/D=8.33 skala=0.319"/piksel
- Sekundarno gorišče (brez korektorja) f=5.562m F/D=8.0 skala=0.333"/piksel
- Koracni motorji PHYTRON Attach:ZSS_02.pdf


Prenos vrtenja iz motorja na veliko višinsko kolo.
Motor je spodaj desno, lepo se vidi prenos na veliko
zobato kolo, ki preko osi in valjčnih sklopk
s kotalnim trenjem poganja veliko višinsko kolo teleskopa
(valjčna sklopka objema, preko vzmeti, rob kolesa
z obeh strani).

Študent Simon kaže vaje in posnetke teleskopa Vega.

Sandi Brcar postavlja svoj motoriziran teleskop,
Newton, 8 palcev, f/5.
Velika pomanjkljivost observatorija je,
da nima vsaj amaterskega teleskopa
namenjenega za opazovanja obiskovalcev.
Čez dan bi jim tudi dobro služil Lunt ali
Coronado.

Kar dva sta potrebna, da se cev teleskopa
varno namesti na stojalo.
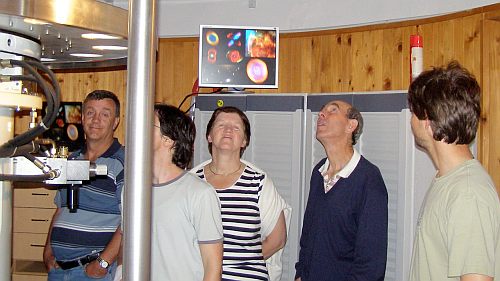
Druga skupina obišče observatorij, kupolo.




Med opazovanjem na dvorišču observatorija.
Saturn nam je priredil krasno predstavo,
vreme je bilo idealno, vzdušje pa tudi.
Hvala Sandiju za postavitev teleskopa.

Observatorij Golovec, nad njim kraljujeta Dvojčka,
nad kupolo pa ozvezdje Raka in prekrasna razsuta kopica
M44 - Jasli (se ne vidijo).
Slikano iz roke: Zorko vičar.


Gregor Vertačnik je iskal objekte s teleskopom,
ostali pa smo s prostimi
očmi iskali ozvezdja, z daljnogledom pa smo opazovali
razsuto kopico M44 - Jasli v Raku, nad kupolo teleskopa,
res lep prizor.
Obiski:
...
20.05. AD Vega S.Kaučič
25.05. OŠ Žalec S.Kaučič
26.05. Uvi 3. ziv. obdobje S.Kaučič
...
Končna ekskurzija, 27. maj 2009
- bil je lep deževen dana
- večina je videla kraje in muzeje prvič,
bili smo navdušeni nad videnim, nad prijaznostjo gostiteljev,
nad našimi svetovnimi astronomi, naravoslovci, pionirji
astronavtike - vse to gre večinoma mimo
izobraževalnega procesa, ekskurzij, itn ...
PROGRAM
1) Hallerstein - v Mengsu se ustavili od 8:30 do 10:20 dopoldne,
zjutraj (sprejel nas bo dir. muzeja)
2) Herman Potočnik - v Vitanje smo prišli ob 11:50 [dobra ura ..., Herman Potočnik
in še astronavt Baturin]
- ODLIČNO
3) Jurij Vega - v Zagorico, his. st. 12, ob 13:30 smo sli iz Vitanj,
ob 15:00 prispemo v Zagorico [ura]
4) Jozef Stefan (smo izpustili) - Koroska (Sv. Peter), problem je bil,
da sicer je na hisi spominska plosca
(hisa pa je v
privatni lasti in ni na ogled), ni pa nikjer na Koroskem
spominske sobe, razstave o nasem velikem fiziku,
cudno po Stefanu se imenuje naravni zakon, ima krater na Luni,
prvi je izracunal temperaturo Sonca, nima pa nikjer spominske
sobe, ...
Ferdinand Avguštin Hallerstein
Mengeš (Galerija mežnarija),
Muzej Mengeš, Trdinov trg 10, 1234 Mengeš,
Janez Škrlep: 031 395 719, muzej: 01 723 90 11
Herman Potočnik,
Spominsko središče Hermana Potočnika Noordunga,
Grajski trg 1, 3205 Vitanje,
Srečko Fijavž: 03 757 43 55, srecko.fijavz@vitanje.si
Jurija Vega,
Muzej Jurija Vege, Zagorica pri Dolskem 12, 1262 Dol pri Ljubljani,
Jože Pokovec: 01 564 72 76
Galerija slik
Ferdinand Avguštin Hallerstein

Pred cerkvijo v Mengšu nas je prijazno sprejel gospod Janez Škrlep.
Foto: g. Marko Skoberne

Odpravili smo se v bližnjo Galerijo mežnarijo.
Foto: g. Marko Skoberne

V galeriji je bila leta 2006 razstava posvečena
pomembnemu astronomu Ferdinandu Avguštinu Hallersteinu,
mladost je preživel v Mengšu
- jezuit, misijonar, matematik, astronom, kartograf
in mandarin, * 27. avgust 1703, Ljubljana, † 29. oktober 1774, Peking.
V Mengšu je hodil v osnovno šolo, v Ljubljani pa je dokončal
jezuitsko gimnazijo in študij filozofije. Tako kot mnogi njegovi
Leta 1734 se je v Judenburgu pripravljal na redovno zaobljubo,
nato pa odšel v Temišvar, kjer je vodil Kongregacijo smrtnega boja.
Želja postati misijonar se mu je uresničila leta 1735.
Pot na Kitajsko
Zaradi neugodnih razmer za misijonarje na Kitajskem se je
septembra 1735 sam ali skupaj z redovnim bratom, dunajskim
jezuitom Lambeckhovnom, ki mu je bil tudi sopotnik na nadaljnji
poti, odpravil preko Trsta v Genovo. Po dvotedenskem počitku sta
zapustila Genovo 30. oktobra z angleško trgovsko ladjo Penelope,
namenjeno v Lizbono na Portugalsko. Plovba mimo Balearskih otokov,
skozi Gibraltar in ob atlantski obali Pirenejskega polotoka ni
potekala brez težav. Laimbeckhoven in Hallerstein sta se morala
zadovoljiti s kajuto na krmi, ki sta jo delila s 15. drugimi
potniki. Hallersteina, ki ni bil vajen morja, je skoraj neprestano
mučila slabost. Čeprav so prispeli v Lizbono že 18. novembra,
sta morala ostati poldrugi dan v karanteni. Ko sta naslednji
popoldan vendarle stopila na trdna tla, so jima v lizbonskem
pristanišču priredili prijazen sprejem. Od profesorja matematike
na Univerzi v Lizboni, patra Emanuela De Camposa, je Hallerstein
izvedel za ponudbo enega od indijskih krajevnih vladarjev v mogulski
državi. Ta je poslal podkralju v Goo pismo, v katerem je prosil za
misijonarja, ki bi obvladal matematiko in astronomijo. Obljubil je,
da mu bo dal zgraditi hišo in cerkev in mu omogočil nemoteno
širjenje katoliške vere na svojem ozemlju. S pismom, napisanim v
perzijskem jeziku, je bil seznanjen tudi portugalski dvorni
astronom Giovanni Baptista Carbone (Battista), ki je poslal
generalu jezuitskega reda prošnjo, da bi omenjeno mesto zasedla
Hallerstein in Laimbeckhoven, ali vsaj eden od njiju.
Tudi Hallerstein sam se je ogrel, posebno še, ker je
tedaj na Kitajskem veljala prepoved misijonarskega dela.
V pismu je bratu sporočil, da je med potjo v Genovi izvedel
zelo spodbudne novice o širjenju krščanstva v južni Indiji.
Misijonar iz sicilske province, ki je 14 let deloval v
indijskem kraljevstvu Maduraj (to je bil po vsej verjetnosti
Francesco Tambini, generalni prokurator Indije, s katerim se
je Hallerstein srečal v Genovi), mu je povedal, da je v
misijonih v Maduraju, Misoru in drugod po Karnataki kakšnih
150 tisoč kristjanov, ki jih oskrbuje 28 jezuitskih misijonarjev.
Vsa njihova hrana sta le riž in voda in takšnega jedilnika se
morajo strogo držati, ker bi sicer razjezili spreobrnjence in
tudi preostale pogane. Vsako leto naj bi bili krstili vsaj 3
tisoč odraslih in veliko število njihovih otrok. Med čakanjem
odgovora iz Rima se je Hallerstein učil portugalščino in se
izpopolnjeval v astronomiji.
Po smrti kitajskega cesarja Yongzhenga sta se 24. aprila 1736
odpravila na Kitajsko. Vmesna postaja je bila portugalska
kolonija Goa, kjer je končno opravil slovesno zaobljubo.
Od tam je odpotoval naprej v Macao, od koder je bil 1.
marca 1739 poklican na kitajski dvor v Peking.
Delo na Kitajskem
V tem času je bil za cesarja imenovan Qianlong (1736-1796).
Hallerstein je sprva kot prisednik deloval v astronomskem
in matematičnem oddelku, po smrti vodje oddelka misijonarja
Ignaca Köglerja 3. junija 1746 pa je postal njegov predstojnik
in mandarin 5. stopnje. V tem času se je Hallerstein preko
misijonarja Gaubila, predstojnika francoskih jezuitov,
seznanil in tesno sodeloval s predstavniki ruske akademije
v Peterburgu. Po letih sodelovanja je 1762 postal njen častni
član, 1765 pa zunanji član te akademije. Po povabilu londonske
Kraljeve družbe pekinškim jezuitom o sodelovanju 1746 si je
Hallerstein začel dopisovati tudi z njo, dve leti kasneje pa
še s pariško akademijo.
V času njegovega službovanja na kitajskem dvoru je mnogo potoval
in pri tem zbiral podatke o pokrajinah in prebivalstvu. Na podlagi
statistike je ocenil število prebivalstva in njegov letni prirastek,
kar je takrat vzbudilo mnogo razprav v zahodnem svetu. V cesarskem
observatoriju je opravil številna opazovanja nebesnih pojavov,
lege planetov glede na zvezde, objavil zvezdni katalog in karto
zvezdnega neba.
V času portugalskega diplomatskega odposlanstva na Kitajskem
leta 1753 je bil Hallerstein njihov svetovalec in posrednik.
Po koncu obiska je postal mandarin 3. stopnje, sam cilj
zagotovitve portugalskih interesov v Macau, okrepitev
trgovskih stikov in zaščita misijonarjev pa ni bil dosežen.
Z leti je število misijonarjev na Kitajskem upadlo, 12.
novembra 1774, kmalu po njegovi smrti, pa je bil jezuitski
red na Kitajskem ukinjen.
Priznanja
Poimenovanja
Po njem se od 6. avgusta 2003 imenuje asteroid 15071
Hallerstein, ki so ga 24. januarja 1999 odkrili astronomi z
Observatorija Črni Vrh.
Delo
* Carte de Macao et ses environs (Karta Macaa in okolice, 1739)
* Popolne študije o astronomskih inštrumentih, 1744
* Observationes astronomicae ab anno 1717 ad annum 1752 (Astronomska opazovanja od leta 1717 do 1752, izdano na Dunaju 1768)
* I Hsiang Khao Chheng (zvezdni katalog, 1757)

G. Janez Škrlep nam je pripravil in komentiral
skoraj vso gradivo iz Hallersteinove razstave.

G. Janez Škrlep nam je živo pripovedoval o interesu Kitajcev
za Hallersteinovo življenje in delo, o stikih s
kitajskimi zgodovinarji, obiskih obeh delegacij. Še anekdota -
Hallerstein je na Kitajsko vzel tudi slovensko
pesmarico, a je nekaj časa niso našli,
nakar se je star kitajski arhivar spomnil, da jo je videl na
slovaškem oddelku - res tragikomično.
A važno je, da so našli "Hallersteinovo" slovensko pesmarico na
Kitajskem!
G. Janez je lepo predstavil metodo raziskovanja, kjer igrajo
pomembno vlogo tudi Hallersteinova pisma.
Bili smo navdušeni nad prezentacijo.

Izpis o datumu krsta.


Observatorij v Pekingu, kjer je deloval Hallerstein.


Naslovnica Hallersteinovih astronomskih tablic - efemerid iz leta 1757.
Vindobona je Duanj - mnogi to ime razumejo kot rimsko,
a zagotovo ima ime mesta Dunaj (Vindobona) korenine v
slovenščini (venetščini, vindi, ...).

Foto: g. Marko Skoberne
Herman Potočnik (22.12.1892 - 27.8.1929)
Leta 1929 izide knjiga našega rojaka Hermana Potočnika "Problem vožnje po vesolju",
eno ključnih del začetka astronavtike, nekateri mu
celo pripisujejo prvenstvo v načrtovanju geostacionarnega umetnega satelita.
Glej življenjepis Hermana Potočnika.

Družina Hermana Potočnika izvira iz Vitanja v Sloveniji. Oče Jožef Potočnik se je rodil leta 1841 v Razborju pri Slovenj Gradcu in je služboval kot zdravnik in visok mornariški častnik v Avstro-Ogrski mornarici. Mati Minka (Marija) se je rodila leta 1854 in je bila hči znanega trgovca z vinom Jožefa Kokošinka iz Maribora.
Oče je leta 1894 umrl, zato se je mati s štirimi otroki preselila na njegov dom, tako da je Herman otroštvo in obdobje osnovnega šolanja preživel v Mariboru. Imel je brata Adolfa in Gustava, oba sta bila mornariška častnika, ter sestro Franci.
V Mariboru je Potočnik obiskoval osnovno šolo. Kasneje je odšel v vojaški šoli v Fischau in v Hranice (na Moravskem). Šolanje mu je najbrž omogočil stric Heinrich, ki je bil poveljnik. Od leta 1910 do 1913 je študiral na vojaški tehniški akademiji v Mödlingu pri Dunaju in postal inženirijski poročnik.
Že naslednje leto je moral na fronto, kot strokovnjak za mostovne in železniške gradnje je deloval v Galiciji, Srbiji, Bosni, na soški fronti in naposled ob Piavi. Ker je zbolel za jetiko, so ga leta 1919 upokojili s stotniškim činom. Tedaj se je na Dunaju lotil študija strojništva, leta 1922 je absolviral, tri leta kasneje postal inženir - specialist za raketno tehniko. Naslednja štiri leta, ki so mu še preostala do smrti, je preživel na Dunaju in se je popolnoma posvetil načrtovanju prodora v vesolje.
Pri 36 letih je na Dunaju umrl zaradi pljučnice, tam so ga tudi pokopali. Osmrtnica, ki ni omenjala njegovega dela o vesoljski tehnologiji, je bila objavljena v mariborskem časopisu.
Spominsko središče
8. septembra 2006 se je v Vitanju, kjer je Herman preživel
nekaj otroških let in od koder je izhajala njegova mati, Minka,
odprlo spominsko središče temu pionirju astronavtike.
Priznanja
Poimenovanja
Po njem se imenujeta ulici v Ljubljani in Gradcu. Predlagali
so, da bi se
mednarodna vesoljska postaja imenovala po njem, vendar predlog
ni uspel.
Po njem se imenuje asteroid 19612 Noordung, odkrit 17.
julija 1999 na Observatoriju Črni Vrh.




V imenitnem spominskem središču
nas je toplo pozdravil gospod Srečko Fijavž (na desni) in
nas tudi kronološko vodil skozi Potočnikov čas in
razstavo.

Vitanje, kraj ujet med hribe - Pohorje, Konjiška gora.
Prelepa okolica.

V kulturnem domu smo si ogledali tudi
razstavo slik (iz postaje Mir) in odlične komentarja
ruskega astronavta dr. Jurija Baturina.

Ruski astronavt dr. Jurij Baturina - osebno je obiskal Vitanje.

Na poti do avtobusa smo ugibali strani neba (bil je deževen dan)
in ugibali ali vhod v cerkev res kaže proti zahodu,
oziroma oltar proti vzhodu.

Baron Jurij Vega (1754 - 1802):
matematik, posredno tudi astronoma, artilerijski častnik in balistik ...
Jurij Vega izda prvo knjigo tabel logaritmov in trigonometričnih
funkcij, ki so bile dolga leta (do razvoja računalnikov)
pomemben matematični pripomoček vsej znanosti.
Število pi izračuna na 140 mest. Prvi je pravilno rešil problem gibanja
telesa skozi tunel zvrtan skozi planet Zemljo, kar je enako projekciji
kroženja satelita na pravokotno ravnino. Po njem se tudi imenuje eden
izmed kraterjev na Luni. Oglej si karto Lune s
kraterjem Vega.
Oglej si tudi bankovec za 50 TOLARJEV.
Preberi Vegov življenjepis in delo
iz (http://vlado.fmf.uni-lj.si/sola/1995/vega/vega1.htm).
Preberi članek Vega in mase planetov (Janez S.)
Po Juriju Vegi se imenujejo tudi priznanja iz matematičnih tekmovanj (Vegova priznanja).
V ponedeljek 22.3.2004 ob 20. uri in 30. minut so odkrili spominsko plošče Juriju Vegi,
avtor Janez Pirnat, na Levstikovem trgu, Ljubljana.
Malo samokritike.
Na Luni so prej po njemu (Vegi) poimenovali krater, kot je dobil v Ljubljani
spominsko ploščo. Glej tudi podatke o
postavitvi plošče leta 2004.

Muzej Jurija Vege, Zagorica pri Dolskem 12, 1262 Dol pri Ljubljani,
Tel: 01 564 72 76
Gospodar Jože Pokovec (levo od monitorja zraven peči)
nam je imenitno predstavil
življenje in delo znamenitega Slovenca Jurija Vege.
Spominsk soba je lično urejena in ima tudi
multimedijsko predstavitev.
Gospod Jože je tudi povedal prisrčno zgodbo, kako sta se spet našla ukradena
sestra in Jurij Vega. Vega je sestro spoznal po podobici,
ki ji jo je podaril, ko je obiskoval šole v Ljubljani.


Baron Jurij Bartolomej Vega [júrij bartoloméj véga],
slovenski matematik, fizik, geodet, meteorolog, plemič in topniški častnik,
* 23. marec 1754,
Zagorica pri Dolskem, Kranjska, (danes Slovenija), † 26. september 1802, Nussdorf pri Dunaju.
Vega se je rodil v kmečki družini polgruntarja Jerneja Vege.
Tja se je iz bližnje Sv. Trojice preselil njegov ded. Njegov oče je umrl,
ko je bilo Juriju šest let. Osnovno znanje si je pridobil pri domačem duhovniku
in v Moravčah. Ko je dopolnil 13. let, je leta 1767 začel obiskovati 6. letne
jezuitske nižje študije (»gimnazijo«) v Ljubljani. Jezuiti so prav v njegovem
času začeli v zadnjih dveh humanitetnih letnikih dajati večji pomen matematično
naravoslovnim predmetom. Vega ju je obiskoval leta 1772 in 1773. Poleg matematike
in naravoslovnih znanosti so bili predmeti, ki jih je Vega poslušal: latinščina,
grščina, religija, nemščina, zgodovina, geografija.
Med leti 1769 in 1785 sta na liceju v Ljubljani poučevala fiziko Gregor Schoettl (1732-1777) in Anton Ambschel (1746-1821). Jezuitska gimnazija in kolegij z dijaškim domom sta v tem času stala pri cerkvi sv. Jakoba pod Ljubljanskim gradom. Kompleks kolegija okoli cerkve je zajemal današnjo šolo, Levstikov trg ter Gruberjevo in Virantovo hišo.
Gimnazijo je obiskovalo nad 500 učencev. Šolnine ni bilo. Študij na gimnaziji je bil v tistih časih stanovski privilegij, ki so ga kmečki sinovi, kot je bil Vega, težko pridobili. Siromašni dijaki niso mogli plačevati kolegija, zato so stanovali pri podpornikih v mestu. Ta usoda je doletela tudi Vego. Njegov sošolec je bil Linhart, ki je bil gojenec kolegija v letih 1771 in 1772.
Schoettlovi študentje so morali poznati veliko optičnih naprav, ki jih je profesor gotovo imel tudi v svojem fizikalnem kabinetu. Med optičnimi napravami so v popisu iz tega časa našteti: Newtonov, Gregoryjev in nizozemski daljnogled.
Po končani gimnaziji je Vega dve leti od 1774 do 1775 študiral še filozofijo na liceju v Ljubljani. Dveletni filozofski študij je takrat imel stolice za filozofijo, matematiko in fiziko. Leta 1775 je Vega z odličnim uspehom končal študij filozofije na liceju skupaj s Kranjcema F. Poglajenom in M. Kalanom. Po koncu študija se je Vega med 1775 in 1780 zaposlil kot inženir za rečno plovbo pri regulacijskih delih na Savi in Ljubljanici. Domnevamo, da je sodeloval z nekdanjim jezuitom Gruberjem pri zasnovi kanala med Gradom in Golovcem. Seznam vprašanj obširnega izpita Tentamen philosophicum se je ohranil in je dostopen v Matematični knjižnici v Ljubljani. Področja, s katerih so bili problemi pri izpitu, so bila: logika, algebra, metafizika, geometrija, trigonometrija, geodezija, stereometrija, geometrija krivulj, balistika in splošna in posebna fizika.
Vega na bankovcu za 50 tolarjev
Po službovanju v Ljubljani se je 7. aprila 1780 vpisal med topničarje cesarske armade na Dunaju. Ob tem je tudi spremenil svoj dotedanji priimek Veha v Vega. Po osnovnem usposabljanju je leta 1781 postal podporočnik in kmalu tudi učitelj matematike na topničarski šoli. Leta 1784, po izidu prvih dveh delov matematičnih predavanj, je napredoval v poročnika. Vega je napisal učbenik v štirih knjigah Predavanja o matematiki (Vorlesungen über die Mathematik). Prvi del je izšel leta 1782, drugi del 1784, tretji 1788 in četrti leta 1800. Njegovi učbeniki so vsebovali zanimive tabele. V drugem delu lahko najdemo izraze v zaprti obliki za sinuse mnogokratnikov 3. stopnje. Zapisani so v preprostih oblikah, s katerimi je lahko računati.
Leta 1781 se je Vega zavzemal za vpeljavo metrskega sistema v avstrijski habsburški monarhiji. Njegova zamisel ni prodrla in so jo uvedli šele kasneje leta 1871 za časa Franca Jožefa I.
Leta 1785 je pismeno zaprosil velikega mojstra brona Ignaza von Borna za sprejem v prostozidarsko ložo Zur wahren Eintracht. Usoda njegove prošnje ni znana, saj je Jožef II. kmalu zatem prepovedal tajne družbe.
Spominska znamka ob 250-letnici rojstva
Vega je leta 1786 prevzel profesuro na posebnem novoustanovljenem bombardirskem oddelku najboljših topničarjev avstrijskega poljskega topništva.
Leta 1787 se je poročil z malo plemkinjo Jožefo Swoboda (1771-1800) iz Budejovic na Češkem. Imela sta tri otroke.
Tik pred odhodom na bojišče je leta 1789 pripravil za tisk tretji del matematičnih predavanj, ki so govorila o mehaniki trdnin. Naslednje desetletje je bil topniški častnik in je večino svojega časa preživel na bojiščih po Evropi. Leta 1788 je služil pod poveljstvom avstrijskega kraljevega feldmaršala Gideona (1717-1790). Med 1789 in 1792 je kot stotnik sodeloval v bojih proti Turkom pri Beogradu. Njegovo poveljstvo nad možnarskimi baterijami je pripomoglo k padcu beograjske trdnjave.
Nato je služil na Moravskem. Leta 1793 se je za krajši čas znova vrnil k poučevanju matematike na Dunaju. Končno je kot major koalicijske vojske med leti 1793 in 1797 sodeloval v bojih proti francoskim revolucionarjem pod poveljstvom avstrijskega generala de Wurmserja (1724-1797). Boril se je pri Fort Luisu, Manheimu, Mainzu, Wiesbadnu, Kehlu in Dietzu. Leta 1795 je imel dva 13,6 kg (30 funtna) možnarja z dosegom do 2.998 m (3.280 jardov). Stari 27,2 kg (60-funtni) možnarji so imeli doseg le 1.791 m (1.960 jardov).
V Leipzigu je leta 1794 njegovo najpomembnejše delo, logaritmovniki Zakladnica vseh logaritmov (Thesaurus logarithmorum completus). Inženir Franc Allmer, častni član senata Tehniške univerze v Gradcu je v Muzeju Carla Friedricha Gaussa v Göttingenu našel Vegove logaritemske tablice točne na 10 desetiških mest. Gauss je to delo uporabljal pogosto in je v njih zapisal več svojih izračunov. Našel je tudi nekaj Vegovih napak pri številih, večjih od milijona. Junija 1797 je bil Vega poveljnik topniške obrambe v Mainzu ob Renu.
Vega je napisal vsaj šest znanstvenih člankov. Neredno življenje aktivnega vojaka je znanstveniku Vegi pogosto onemogočalo uporabo potrebnih virov, predvsem med 1789 in 1798. Kjub temu je objavil 17 matematičnih, fizikalnih in astronomskih del v več ponatisih, ki so mu prinesle sloves tudi zunaj avstrijskih meja.
Leta 1794 je postal dopisni član Velikobritanske kraljeve znanstvene družbe v Göttingenu, 1797 član akademije v Mainzu, 1798 član Fizikalno matematične družbe v Erfurtu, 1800 pa član Kraljeve družbe znanosti v Pragi in akademije v Berlinu. Po najvišjem vojaškem odlikovanju za zasluge je 22. avgusta 1800 dobil dedni baronski naslov, pravico do lastnega grba in čin podpolkovnika.
Svoja zadnja leta je preživel na Dunaju. Septembra 1802 so ga začeli pogrešati. Po nekaj dnevih iskanja so njegovo truplo našli v Donavi pri Dunaju. Policijsko poročilo je zaključilo, da se je zgodila nesreča. Vendar resnični vzrok smrti ostaja nepojasnjen.
Delo v matematiki
20. avgusta 1789 je Vega dosegel tedanji
svetovni rekord in izračunal število ? na 140 (137) decimalk. Ta račun je predložil
petrograjski akademiji v knjižici V. razprava, kjer je s svojo metodo našel v poprejšnjem de Lagnyjevem
(1660-1734) izračunu iz leta 1719 127 decimalk napako na 113. mestu. Rekord je obdržal 52 let do leta
1841, njegovo metodo pa še danes omenjajo. Njegov članek je akademija izdala šele šest let pozneje leta
1795. Vega je izpopolnil Machinovo enačbo iz 1706,
ki so ju verjetno dobili na podoben način kot John Wallis leta 1655 z razvitjem v neskončni
verižni ulomek, saj je prvi 6. sodi približek neskončnega verižnega ulomka za ?, drugi pa se
od prvega razlikuje v 9. členu in, ki se razlikujeta šele na 13. decimalki. Med temi japonskimi
matematiki so bili verjetno Seki Kova, imenovan tudi Takakazu (1640-1708), ki je leta 1700 našel
10 pravilnih mest, Takebe Hikodžiro Katahiro Kenko (1664-1739), ki je leta 1722 našel 42 (41 pravilnih)
mest za ?, Kamata Jošikijo (1678-1744), ki je leta 1730 našel 25 mest in Macunaga Jošisuke Riohicu,
(okoli 1639-1744), ki je leta 1739 našel 51 decimalk ?-ja z isto metodo kot Newton leta 1665 z vrsto arc sin (1/2) = pi/6.
kjer moramo za takšno točnost vzeti okoli 140 členov.
Delo v fiziki
Med boji proti Francozom je dokončal razpravo o Zemlji in splošni gravitaciji. Na fronti seveda ni imel možnosti uporabljati obsežnejših virov, temveč se je zanašal predvsem na svoj spomin. Razpravo so prebrali na Akademiji uporabnih znanosti v Erfurtu 2. januarja 1798. Istega leta so jo tudi natisnili pod imenom Matematično raziskovanje o smeri sile teže. Imela je 30 strani, ki so bile tudi v knjižni izdaji oštevilčene od 133 do 162. Domnevamo, da so bila vsaj na straneh od 1 do 133 tiskana dela drugih avtorjev. Razprava iz leta 1798 je bila zapisana v obliki vprašanj in odgovorov. Na koncu je naštel še osem vprašanj, ki so bila deloma napotki za nadaljnje raziskovanje po zgledu Newtonove Optike iz leta 1704, deloma pa posledica pomanjkanja strokovnih virov na fronti. Vegova razprava ni imela poljudnega uvoda, temveč se je takoj začela z enačbami. Na straneh 141 do 143 do bile natisnjene tabele. Najpomembnejše stvari, ki se jih je lotil v razpravi so: Zaradi vpliva sile teže se površina vode pri vrtenju kaže kot krivulja. Sila teže bi vplivala tudi na površino stolpa vode, položenega od pola do pola skozi središče Zemlje. Zaradi vrtenja nekdaj vroče stopljene Zemlje okoli svoje osi je njena oblika sploščena na polih. Po njem naj bi bilo razmerje premera Zemlje na polih in na ekvatorju 578/579, kar je bila za 0,16% prenizka vrednost in tako slabši približek od Newtonovega.
Na strani 156 je nanizal osem vprašanj, ki sledijo iz osnov nauka o (gravitacijskem) privlaku:
1. Kakšna je smer sile teže pri različni višini polov pri prostem, mirujočem, nevrtečem, popolnem elipsoidu enakomerne gostote in znane velikosti, mase in dolžine osi? (Upoštevamo le lastni privlak sile teže brez zunanjih motenj).
2. Kakšna je zveza med resnično višino polov in resnično (zemljepisno) širino?
3. Kakšna so razmerja med dolžinami enostavnega sekundnega nihala in z njim povezanim pospeškom sile teže na različnih (zemljepisnih) dolžinah?
4. Kolikšna je navidezna dolžina poldnevnika (meridiana) na različnih (zemljepisnih) dolžinah?
5. Kolikšna je ravnovesna površina vode v kanalu, postavljenem od enega do drugega pola takšnega elipsoida?
6. Kakšna je površina morij?
7. Če domnevamo, da se takšen popolnoma trden elipsoid enakomerno vrti, kakšni so potem odgovori na zgornja vprašanja?
8. Kakšni so vsi ti odgovori, če elipsoid ni sploščen, temveč podolgovat?
Leta 1800 je na Dunaju izšla razprava Poskus razkriti neko skrivnost v znanem nauku splošne gravitacije. Ta razprava je bila posvečena Albertu Saksonskemu, ki je pozneje Vego predlagal za viteški križec reda Marije Terezije. Obravnaval je »premočrtno centralno gibanje« telesa brez začetne hitrosti, ki pod vplivom gravitacijske sile, obratno sorazmerne s kvadratom razdalje, neovirano prileti v samo središče Zemlje. Razprava se navezuje na III. del matematičnih predavanj, kjer je Vega zapisal, da bo telo priletelo v središče z neskončno veliko hitrostjo in bo tam obtičalo s hitrostjo nič. Temu problemu je leta 1788 posvetil celo poglavje. Opisal je prosti pad telesa s površine proti središču Zemlje, če ni zračnega upora. Ugotovil je, da tir takšnega telesa ni parabola, temveč elipsa z najbolj oddaljenim goriščem v središču Zemlje. Takšna elipsa ima veliko ekscentričnost, kar ji daje videz parabole. Kakšno je nadaljnje gibanje telesa, se je vprašal Vega? Euler je v Scientia Motus menil, da se gibanje nadaljuje po zelo sploščeni elipsi s središčem Zemlje kot goriščem, zato se telo vrne, od koder je priletelo. Po Vegi Euler ni imel prav, saj telo v središču Zemlje izgubi vse gibanje, hitrost pa se mu poveča do neskončnosti. Po Francozu Simonu L'Huilierju (1750-1840), prejemniku nagrade pruske akademije znanosti leta 1786, neskončno velike in neskončno majhne količine niso možne in zato telo sploh ne more prileteti do središča Zemlje. V Dodatku k III. delu matematičnih predavanj iz leta 1790 je Vega predlagal spremembo Newtonovega splošnega gravitacijskega zakona, da bi odpravil težave pri računu prostega pada telesa skozi središče Zemlje. Ugotavljal je, da premočrtno centralno gibanje določa neki drug izrek centralne sile. Telo se ves čas vzdiguje nad središčem v dani smeri, tako med oddaljevanjem v nasprotni smeri, kot med vračanjem v izhodišče. Telo premočrtno niha na obeh straneh središča pod vplivom centralne sile. Pri enakih oddaljenostih od središča ima enako hitrost, saj je pospešek centralne sile funkcija potence oddaljenosti od središča. Potenca ima lahko cel ali racionalen, pozitiven ali negativen eksponent. Pri tem se je skliceval na delo profesorja Hindenburga, objavljeno v Leipziškem časopisu za čisto in uporabno matematiko. Leta 1800 je to zamisel opustil.
Odkril je računsko napako v svoji razpravi iz leta 1788 in dobil nov rezultat, po katerem telo leti skozi središče zemlje do razdalje, iz katere je vanj priletelo. Leta 1801 je dal na Dunaju natisniti latinsko delo Razprava o določitvi mase (masah) in razdalj nebesnih teles v Astronomskih Ephemeridah. Delo so natisnili tudi kot separat na 14. straneh. Na strani 15 in 16 je bil dodan popis njegovih dotedanjih del, vključno z najnovejšim. Vegova razprava je temeljila na drugi francoski izdaji Laplacovega Exposition du sisteme du monde. Poleg planetov je Vega izračunal tudi mase in oddaljenosti njihovih satelitov.
Čeprav je Vega s svojimi logaritmi zaslovel predvsem kot matematik, je bil večji del njegovih razprav in učbenikov posvečenih fiziki. Njegova dela v fiziki zajemajo vsa področja mehanike, predvsem teorijo gravitacije in z njo povezano astronomijo. Njegova fizika se tesno navezuje na licejska predavanja njegovega profesorja Schoettla. V zrelih letih ni bistveno spremenil svojih zamisli, ki jih je sprejel kot študent v Ljubljani. Zaradi prekinitve visokošolskega pouka fizike v Ljubljani med letom 1784 in 24. aprilom 1788 ter v 19. stoletju, Ljubljana pred drugo polovico 20. stoletja ni več obnovila kakovosti pouka fizike iz časa Vegovega študija.
Priznanja
Poimenovanja
Po njem so poimenovali:
* ljubljansko ulico (Vegova ulica),
* osnovno šolo v Moravčah
* idrijsko gimnazijo,
* krater na Luni (krater Vega),
* projekt veleposlaništva RS v ZDA in Ministrstva RS za visoko šolstvo, znanost in tehnologijo (projekt »Jurij Vega«),
* priznanje za mlade matematike (Vegovo priznanje),
* študentsko društvo MASS Vega klub,
* od 9. maja 2001 asteroid 14966 Jurijvega, ki ga je 30. julijja 1997 odkril Herman Mikuž na Observatoriju Črni Vrh.
Druge zanimivosti
Njegov rojstni dan, 23. marec, je bil izbran za občinski praznik Dola pri Ljubljani in Moravč
- to je tudi dan slovenskih topničarjev.
Mnogi ga postavljajo na 5. mesto (od desetih) najpomembnejših Slovencev v zgodovini.

Izbor 12-ih velikih mož slovenske zgodovine.

Foto: g. Marko Skoberne

Foto: g. Marko Skoberne
Avtor slik: Zorko Vičar,
nekaj slik pa je prispeval tudi g. Marko Skoberne.
Še zadnje dejanje leta 2008/09 (3. junij 2009)
- letno poročilo, zahvale, ...,
ob prijetni družbi in sproščenem pogovoru.


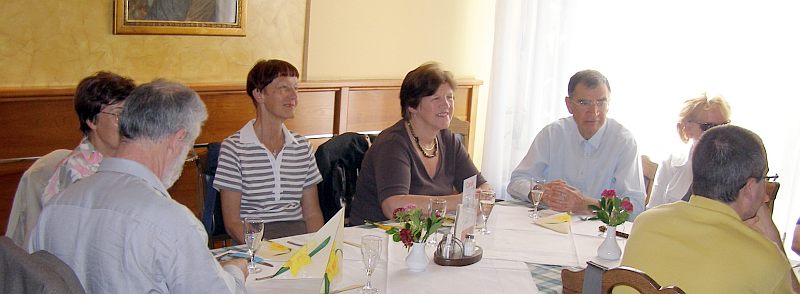


Foto: mentor Vičar Zorko