Zakaj astronomija
|

|
Zakaj astronomija
|

|
Uvod v kozmologijo in starost vesolja
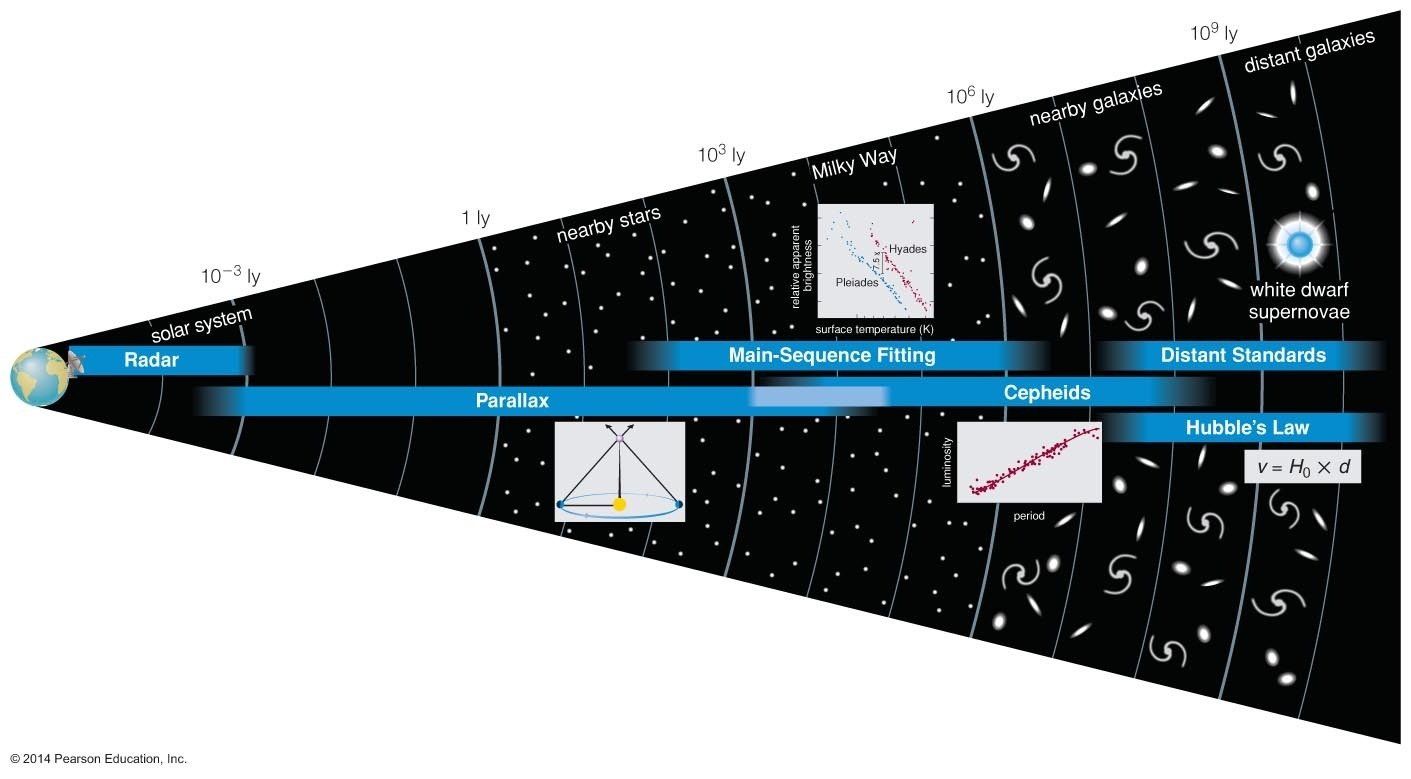
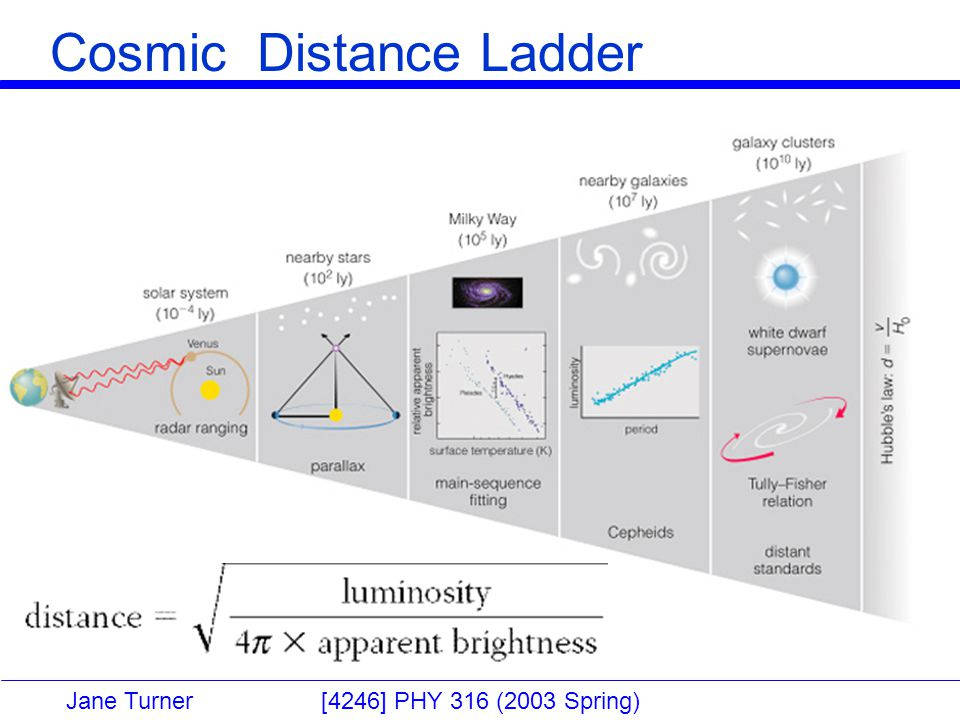
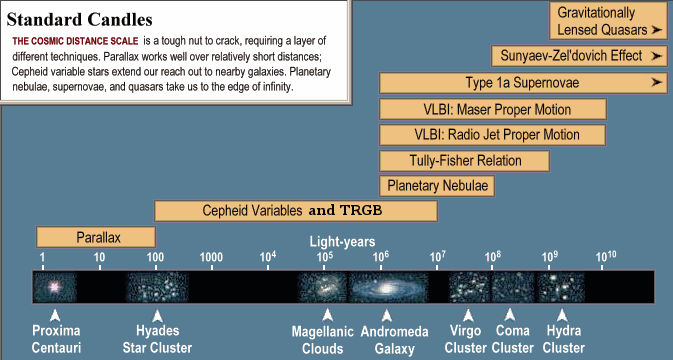
Ali se spustiti v kozmologijo in do katere globine? Zagotovo JA! Koliko časa posvetiti merjenjem razdalj v vesolju (paralaksa, Kefeide, supernove tipa Ia, Hubblov zakon v = Hd, mrki, Hertzsprung-Russllov diagram, gravitacijski valovi ...)?
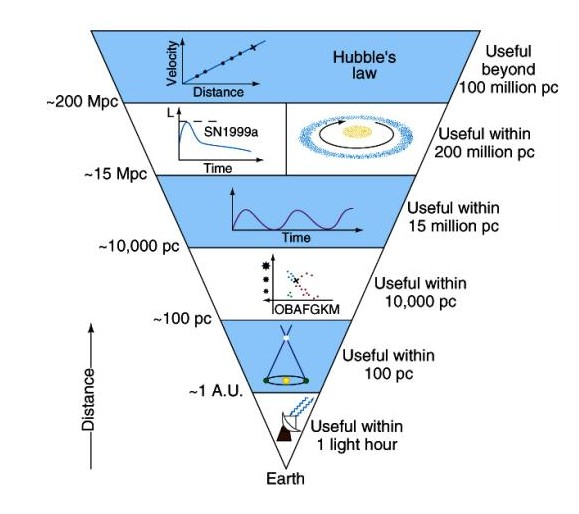
Metode merjenja razdalj v vesolju, od spodaj navzgor:
* radar (čas odboja em valovanja od telesa - do 1 svetlobne ure),
* paralaksa
(premik bližnje zvezde na ozadju med letnim
gibanjem Zemlje - do nekaj 100 svetlobnih let),
* HR diagram
(določimo navidezno magnitudo m in absolutno M – razdalja 10 pc, preko barvnega
indeksa iz HR diagrama – velja enačba: m – M = 5 log(d/10 pc), izhaja
iz Pogsonovega zakona:
j1/j1 = (d/10 pc)2 = 10-0,4(M-m) ),
metoda deluje do nekaj deset tisoč svetlobnih let,
*
Kefeide
(frekvenca spremembe sija zvezd Kefeid je povezana z absolutnim izsevom
d = (L/(4πj))1/2 ),
metoda deluje do 45 milijonov svetlobnih let,
* supernova tipa Ia zmeraj eksplodira z enakim izsevom
(tesni dvojni sistem bele pritlikavke, ki eksplodira, ker črpa snov iz
sosednje zvezde orjakinje), metoda deluje do dobrih 600 milijonov svetlobnih let,
*
na vrhu je
Hubblov zakon (d = v/H), uporaben do roba vidnega vesolja (milijarde svetlobnih let).
V Osončju (in oddaljenih dvojnih sistemih) pa
pridejo prav tudi Keplerjevi zakoni, tretji zakon:
to2/a3
= 4π2/(G(m1 + m2))
in (v antiki) tudi Lunini mrki ...
Parsek je razdalja, pod katero vidimo AE (razdalja Zemlja-Sonce 150 106 km)
pod kotom ene ločne sekunde in znaša 3,2616 svetlobnih let. Svetlobno leto
je razdalja, ki jo svetloba prepotuje v enem letu (1 sv. l. = c*t)
in znaša 9,46×1012 km (v vakuumu).
Vsekakor tega poglavja ne smemo ignorirati. Kot so pokazale meritve, se večina
galaksij v vesolju oddaljuje – svetloba se premakne proti rdeči barvi.
Hitrosti se meri preko Dopplerjevega pojava, rdečega premika
v/c = Δλ/λ = z.
Za velike hitrosti velja relativistična povezava: 1 + z = (1 + v/c)γ =
( (1 + v/c)/(1 - v/c) )1/2. Ko narišemo graf hitrosti (v) od razdalje (d),
dobimo znameniti Hubblov zakon: v = Hd. Če poznamo torej hitrost neke
zelo oddaljene galaksije (preko Dopplerja), lahko dokaj dobro ocenimo
njeno razdaljo. Meritve je izvajal Američan E. Hubble pred približno
100 leti. Med prvimi pa je videl povezavo med hitrostjo in razdaljo galaksij
župnik in fizik, Belgijec Georges Lemaître (na širjenje vesolja je sklepal
iz Einsteinovih enačb polja splošne teorije relativnosti in tudi iz meritev
Dopplerjevega premika spektralnih črt oddaljenih galaksij proti daljšim
valovnim dolžinam, rdeči premik – torej se galaksije oddaljujejo druga od
druge; o tem je leta 1922 pisal že ruski fizik A. Friedmann in sicer teoretično
preko ene izmed rešitev enačb splošne teorije relativnosti. Prve dokaze, meritve
rdečega premika »galaksij«, pa je že leta 1912 objavil Američan Vesto Melvin Slipher.
A takrat še niso vedeli, ni bilo dokazov, da ti objekti ležijo izven Rimske ceste.
To dokaže Hubble leta 1922, ko v Andromedini galaksiji M31 zazna utripajoče zvezde
kefeide in z njihovo pomočjo oceni oddaljenost galaksije (danes vemo, da je oddaljena
okrog 2,5 milijona svetlobnih let).
Leta 1927 je Lemaître objavil članek ("A homogeneous Universe of constant
mass and growing radius accounting for the radial velocity of extragalactic
nebulae" - "Homogeno vesolje konstantne mase in naraščajočega polmera
izračunanega iz radialne hitrosti izvengalaktičnih meglic").
Takrat Einstein ni sprejel Lemaîtrove matematike in je zavrnil
zamisel o širjenju vesolja. A Lemaître mu ni ostal dolžan in mu
takole odgovori: "Vos calculs sont corrects, mais votre physique est
abominable (Tvoja matematika je sicer pravilna, vendar je fizika nemogoča)."
Kdo je imel prav, se ve – Lemaître. Iz Hubble-Lemaîtrove konstante lahko
ocenimo zgornjo mejo starosti vesolja
t = 1/H = 1/(67,8(km/s)/Mpc) = 4,55 1017 s ≈ 14,4 milijard let
in ta enostavna ocena in sam podatek bo zagotovo mladim (recimo)
v veliko veselje (za eno izmed ocen H = 73,2 ± 0.3 km/s/Mpc pa je
starost vesolja 13,4 milijard let). Kozmologija bo vključena po delčkih
v ostala poglavja – tudi v razlago atomov, molekul, osnovnih delcev ...
Zapišimo Dopplerjev pojav (podaljšanje valovne dolžine svetlobe zaradi
oddaljevanja galaksij s hitrostjo v: Δλ = vλ/c ), oziroma rdeči premik
(z = v/c) s Hubblovim zakonom:
z = v/c = Δλ/λ = Hd/c
d = zc/H
Zadnji izraz velja za z = v/c < 0,1.
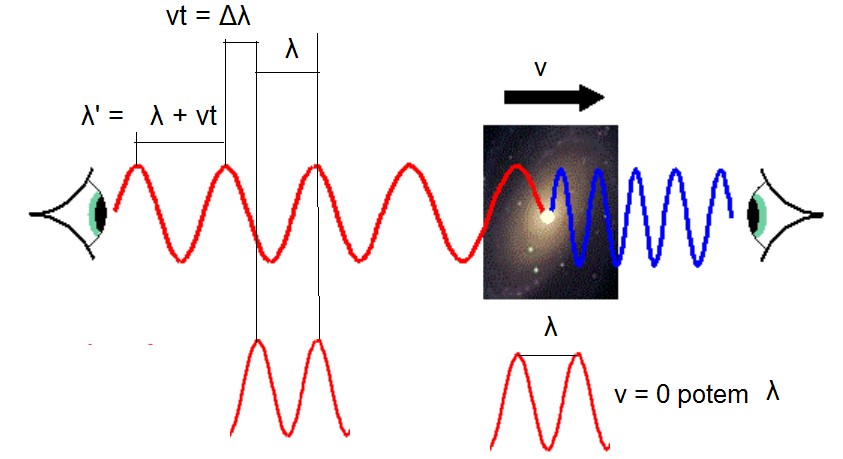

Dopplerjev pojav.
Prikaz, kako se spremeni valovna dolžina svetlobe, če se vir svetlobe
oddaljuje s hitrostjo "v" (valovna dolžina λ se podaljša v času t prehoda dveh
vrhov na
λ' = λ + Δλ = λ + vt,
na kratko pojav imenujemo tudi rdeči premik,
valovna dolžina rdeče barve je namreč največja v vidnem delu spektra em valovanja),
in
če se pa vir svetlobe približuje našemu očesu ali detektorju (v tem primeru
se valovna dožina λ zmanjša - na kratko pojav imenujemo tudi modri premik).
Dopplerjev pojav je ključen za kozmološka merjenja hitrosti in posredno tudi razdalj
v vesolju.
Izjemno pomembno vlogo igra tudi v dvojnih sistemih in še na mnogih področjih.
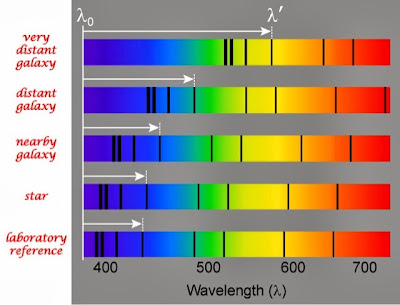
Zamiki absorbcijskih spektralnih črt so označeni z belimi dolžinami puščic -
zaradi večanja hitrosti oddaljenejših galaksij, je njihov
rdeči premik črt (podaljšanje valovne dožine) izrazitejši:
z = v/c = Δλ/λ
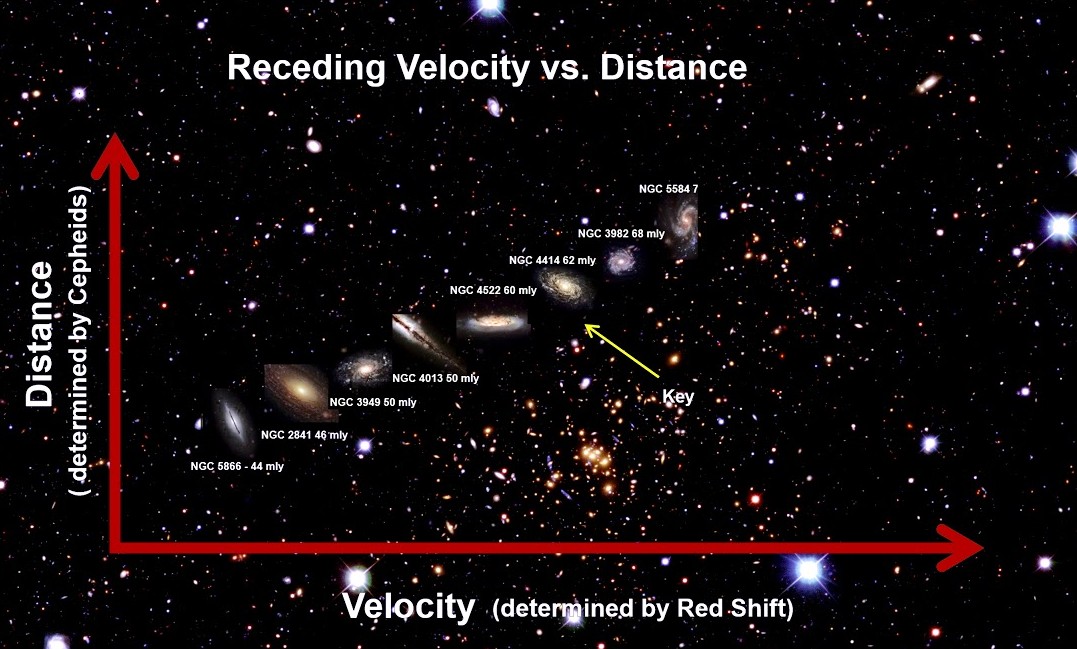
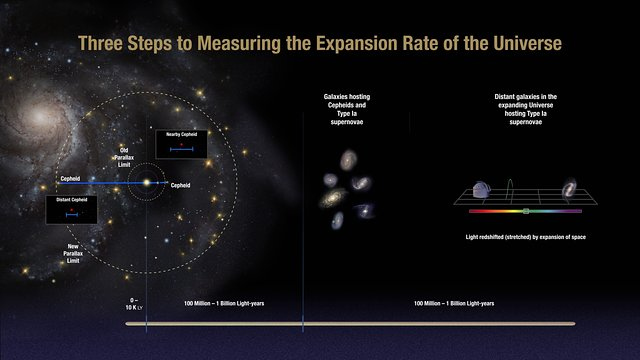
Meritve razdalj (d) do nekaterih galaksij preko izseva kefeid (frekvenca
utripanja kefeid je povezana z absolutnim izsevom L in velja:
d = (L/(4πj))1/2). Hitrost pa je določena preko Dopplerja
(rdečega premika z, velja: z = v/c = Δλ/λ).
Iz grafa razberemo Hubble-Lemaîtrov zakon: v = Hd ali d = v/H.
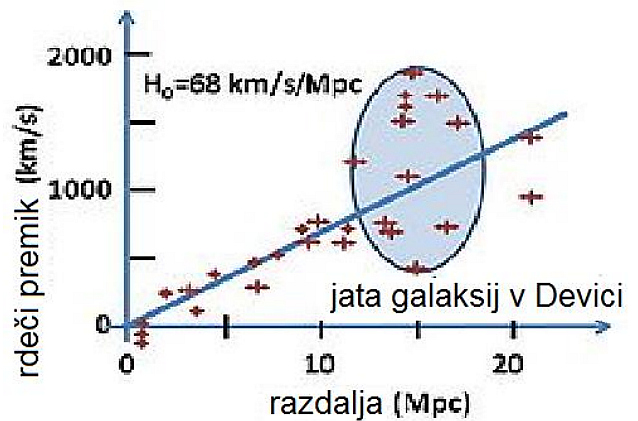
V 1920-tih sta Hubble in njegov asistent Milton Humason izmerila oddaljenosti
in rdeče premike nekaj ducatov galaksij (na sliki so zamiki absorpcijskih
spektralnih črt označeni z dolžino rjave puščice). Iz meritev sta razbrala
nekaj »čudnega«. Kot razmišlja Hubble leta 1929: "Bolj ko so galaksije oddaljene,
hitreje se oddaljujejo od nas." (zgoraj) To je danes znani Hubblov zakon:
V = Hd ali rdeči premik z = v/c = Hd/C (velja za z = v/c < 0,1).
Že leta 1927 pa Georges Lemaître (duhovnik in fizik) objavi svojo novo idejo,
da se vesolje širi (prvi izpelje Hubblov zakon in poda prvo opazovalno oceno
Hubble-Lemaîtrove konstante).

Levo Edwin Powell Hubble (20. nov. 1889 – 28. sep. 1953)
in desno
Georges Henri Joseph Édouard Lemaître ( 17. jul. 1894 – 20. jun. 1966).
Praktik in teoretik -
skupaj s sodelavci očeta moderne kozmologije - vede o
razvoju vesolja.
Razdalje do galaksij se meri preko paralakse, Kefeid, supernov tipa Ia ...
Hitrost pa se meri preko Dopplerjevega pojava, v veliki večini primerov
zaznamo rdeči premik
v = cΔλ/λ = cz.
Ko narišemo graf hitrosti v od razdalje
d, iz grafa razberemo znameniti Hubblov zakon: v = Hd.
Hubble-Lemaîtrovo konstanto se lahko oceni tudi iz sevanja mikrovalovnega
ozadja (iz fluktuacij - ki kažejo na starost vesolja in delež temne energije,
na gostoto materije - recimo iz Friedmannove enačbe za energijo (bomo izpeljali),
kjer je H = (dR/dt)/R, lahko določimo Hubblovo konstanto:
H2= 8πGρ/3 - kc2/R2 + Λc2/3).
Na tak način dobljena konstanta H,
se nekoliko razlikuje od direktnega merjenja preko hitrosti
in razdalj bližnjih galaksij (meritve se torej nadaljujejo in metode
izpopolnjujejo). Friedmannova enačba se nekako da razumeti iz
klasičnega energijskega zakona – to je lahko primerna tema za
kak seminar. Hubble-Lemaîtrova konstanta danes torej niha med
67 in 74 km/s/Mpc – meritve iz podatkov lokalnega vesolja in meritve na
podlagi zgodnjega vesolja (s pomočjo prasevanja) se torej razlikujejo
kar za okrog 10 %. Meritve in interpretacije Hubble-Lemaîtrove »konstante«
so torej v ospredju kozmoloških raziskav.
Astronomija in njeni vplivi na druge vede
V našem življenju je veliko več astronomije, kot je v resnici zaznamo
v babilonu medijskih dražljajev. Živimo s samoumevnim koledarjem, kako
bi živeli brez koledarja, teden ima 7 dni – zakaj; zakaj smo krog razdelili
na 360 stopinj - ker si je to številko nekdo kar izmislil, zakaj imamo 12 mesecev,
prestopna leta? A so že omenjeni samoumevni sateliti, GPS ...,
morebiti tehnologije v samem jedru nebesne mehanike in splošne teorije
relativnosti – tudi kak izračun in nepričakovan ekonomski vpliv teorije
relativnosti na družbo, smo že nakazali v uvodnih poglavjih. Slovenija
je 3. 9. 2020, z evropsko raketo napredne generacije Vega, izstrelila
tudi svoja prva satelita NemoHD in Trisat. Satelit visoke ločljivosti
NEMO-HD se je že izkazal za izjemno primernega za opazovanje površinskih
detajlov, tako kmetijskih površin, vegetacije, kot rek in ocen onesnaženosti,
snema videe dogajanj v večjih mestih, letališčih. Rezultati posnetkov, analiz,
bi lahko zelo popestrili pouk astronomije.
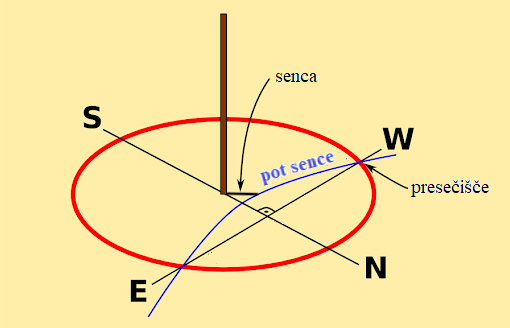
Astronomija in orientacije zgradb. Slika prikazuje sončni kompas
Vikingov – v resnici metodo, kako so naši predniki določali
smeri neba. Ta metoda je bila osnova za gradnjo hiš, templjev,
observatorijev v smeri vzhod – zahod, sever – jug. Pot vrha
sence navpične palice (gnomona) se označi s kamenčki,
s kredo ali kako drugače. Krivulja vrha sence je pri nas hiperbola;
senca vrha palice pa je v splošnem, glede na geografsko širino,
če pade na ravno površino, stožčasti presek - hiperbola,
elipsa ali na severnem, oz. južnem polu krog.
Kako pa določimo smeri neba iz poti (krivulje) sence?
Iz središča, ki ga določa palica, z vrvico narišemo krog,
ki 2x preseka pot sence. Smer obeh presečišč,
kroga in poti sence, je smer vzhod – zahod. Pravokotnica
na premico EW pa določa smer sever – jug. Vemo, da so mnoge
največje in najstarejše zgradbe (piramide, katedrale, observatoriji ...)
usmerjene v smeri vzhod – zahod pod stopinjo natančno
(res občudovanja vredno).
Dogodki na nebu, koledar in čas
Ne smemo pa spregledati pomena konjunkcij planetov, Lune, Sonca,
tudi okultacij – recimo Lune in zvezd (praktično večkrat na leto
lahko izvedemo kako meritev časa prekrivanja določene svetlejše
zvezde z Luno). Tukaj so prehodi Merkurja in Venere (z navideznim
prehodom Venere čez Sončevo ploskvico smo s pomočjo paralakse
(premika) Venere - preko opazovanj iz različnih krajev, določili
razdaljo Zemlja – Sonce, astronomsko enoto AE). Letni cikli,
letno gibanje Sonca, Lune, planetov, ozvezdij, vse to šteje pri
razumevanju nebesne mehanike, letnih časov, koledarja, tudi
arhitekture in sakralnih objektov, starih svetih krajev,
ki so v resnici bili prvi astronomski observatoriji –
gradbene mojstrovine kot observatoriji in koledarji določanja
prehodov med letnimi časi.
Koliko časa torej posvetiti koledarju, zakaj uporabljamo Sončev
koledar (zakaj štejemo prestopna leta pri gregorijanskem koledarju
nekoliko drugače kot pri julijanskem, v koliko letih se bo pri
gregorijanskem koledarju pojavila napaka enega dneva? Zadaj so
dokaj enostavni izračuni, lahko se izvedejo. Koliko povedati
o časovni enačbi, njen izvor se da delno prikazati z lučko in
kroglo, lahko se vsako leto izdela analema – slavna osmica lege Sonca
ob isti uri skozi celotno leto (zgolj z zaznambo vrha sence
palice ob isti uri dneva).
Ali preko slikanja Sonca (nad obzorjem) ob isti uri skozi vse leto
(v Spiki 5/2021 je objavljena krasna raziskovalna naloga
očeta Damijana in hčerke osnovnošolke Nike Dolenc).
Vsi ti pojmi na temo koledarjev
so namreč večini precej neznani in tozadevno se pojavlja kar
nekaj težav in nepotrebnih zavajanj (paradoksov, ki jih ni).
Vpelje se srednji Sončev čas, ki ga kažejo današnje ure in pravi
Sončev čas, ki ga kažejo Sončeve ure. Posebno pozornost se naj
torej posveti tropskemu ali Sončevemu letu, na katerem temelji
moderni koledar. Vpelje se tudi siderski ali zvezdni čas
(pove se, zakaj je zvezdni dan dolg 23 h 56 min, torej približno
za štiri minute krajši od srednjega Sončevega dneva po katerem
teče ritem našega življenja) ter sidersko ali zvezdno leto
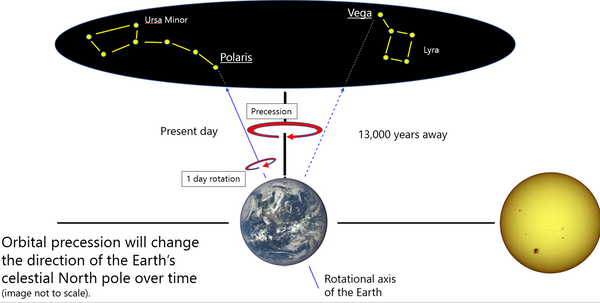
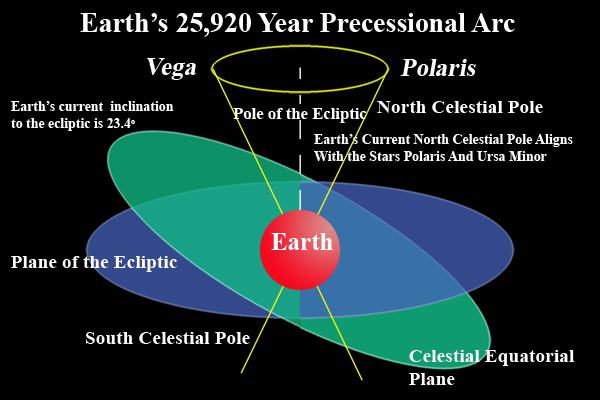
in razloži precesijo enakonočij ter njene posledice za koledar.

vir slike: wiki
Skica za razumevanje razlike med Sončevim in zvezdnim (siderskim) dnevom.
Ker Zemlja potuje okrog Sonca po elipsi je Sončev dan – čas med dvema
kulmicijama Sonca – za okrog 4 minute daljši od zvezdnega dneva (od časa
rotacije Zemlje glede na oddaljeno točko, zvezdo – glejte sliko). Zemlja
se od danega poldneva, do poldneva naslednjega dne, zaradi hkratnega
premika po tirnici okrog Sonca, mora zasukati še za okrog ene stopinje,
da Sonce spet kulminira, to pa traja še dodatne slabe 4 minute. Ker
je gibanje po elipsi neenakomerno, se zato tudi dolžina dneva na tirnici
nekoliko spreminja, zato smo definirali dolžino povprečnega (srednjega)
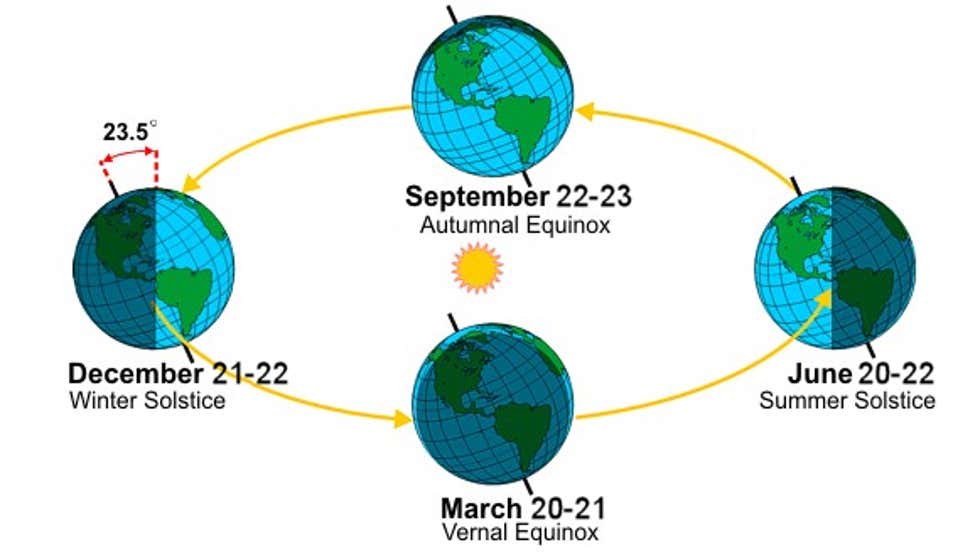
Sončevega dne. Drugi razlog je nagnjenost osi vrtenja Zemlje, sonce zato
med letom navidezno potuje pod (pozimi) in nad nebesnim ekvatorjem (poleti),
ob enakonočjih pa je v sečišču ravnin ekliptike in ekvatorja. To sta torej
glavna razloga, da se poldan na uri večinoma ne ujema s kulminacijo Sonca
(le 4x na leto in takrat se Sončeva ura dokaj dobro ujema z uro, ki
kaže srednji čas, včasih na mehanični ročni uri, danes večinoma na
mobilnem telefonu). Številne Sončne ure imajo zato vgravirane tabele
ali grafe časovne enačbe, ki uporabniku omogočajo popravek Sončevega
časa v srednji (linearni) čas.
Najprej je potrebno upoštevati, da se Zemlja ne zarotira v 24 urah okrog lastne osi, temveč v 23 urah, 56 minutah in 4,09 sekunde (glede na velike razdalje do zvezd). V enem letu Zemlja naredi 366 rotacij, vendar Sonce vzhaja in zahaja 365-krat; dodatna rotacija pomeni, da je zvezdni dan 3 minute in 55,91 sekunde krajši od povprečnega Sončevega dne. Medtem, ko ima zvezdni dan vedno enako dolžino, pa se dolžina Sončevega dneva, zaradi eliptične tirnice in nagnjenosti osi rotacije Zemlje, med letom spreminja.
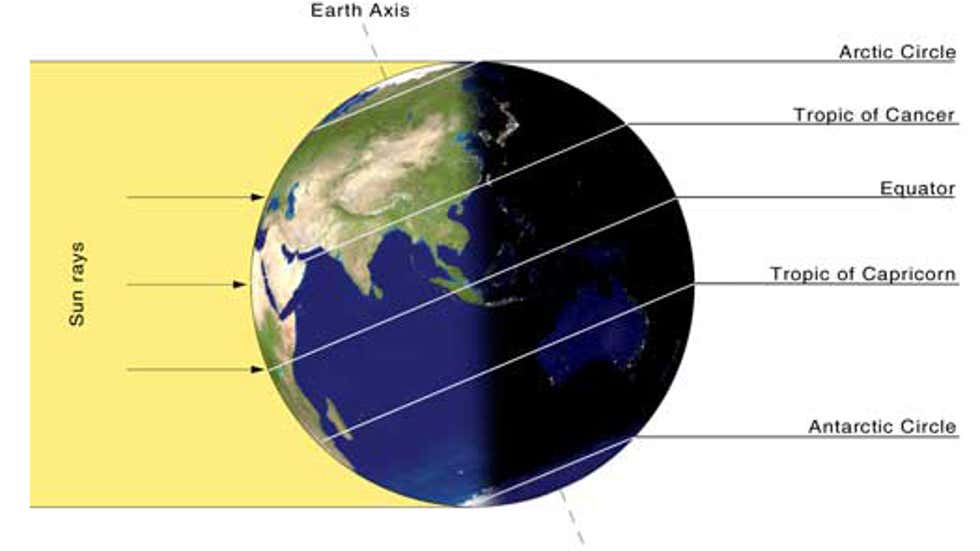
Recimo, da se opazovalec na severnem polu Zemlje vrti na ploščadi s časom rotacije 23 ur, 56 minut in 4,09 sekunde in sicer v smeri rotacije zvezdnega neba, da se kompenzira rotacijo Zemlje (tako se vrtijo tudi teleskopi med sledenjem zvezdam). Opazovalec bo videl negibne zvezde in Sonce, ki se gibljejo po »krogu« (približno 360 °/365,25 dni ≈ 0,9856 °/dan po ekliptiki med ozvezdji živalskega kroga, za toliko se mora dodatno zavrteti tudi Zemlja, kaj ji vzame približno 3 min 56 s, skupaj je to 24 h). Ravnina, ki določa ta krog Sonca, je ekliptika. Zaradi naklona zemeljske osi glede na ravnino orbite je ravnina ekliptike nagnjena glede na ravnino nebesnega ekvatorja za 23 ° 26 '21 .448 '' (natanko toliko kot os glede na orbitalno ravnino). Med letom opazovalec vidi, da se Sonce odmika od obzorja in dvigne na približno 23,44 ° nad nebesnim ekvatorjem in se nato spusti na približno -23,44 ° od nebesnega ekvatorja proti obzorju.
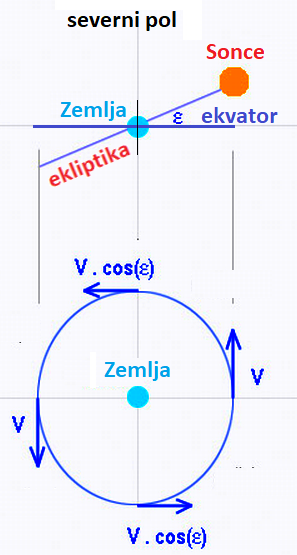
Tudi zgolj ob predpostavki, da se Sonce giblje s
konstantno hitrostjo po ekliptiki, se njegova
projekcija na ravnino ekvatorja vseeno ne premika
s konstantno hitrostjo (zakaj je to pomembno –
primer, ko Sonce kulminira, seka lokalni meridian,
je poldan, o tem pa odloča projekcija gibanja Sonca na
ekvator, ekvator pa je po definiciji pravokoten na os
rotacije Zemlje, projekcija pa seveda ne da enakomernega
gibanja – glejte sliko). Z malu truda lahko uganemo 4
projekcije na ekvator. V času solsticija je dejansko vektor
hitrosti vzporeden z ekvatorialno ravnino (hitrost projicirana
na ekvator je kar enka hitrosti V na ekliptiki), medtem ko je ob
enakonočjih vektor nagnjen za približno 23,44 ° (glejte sliko).
Ko se Sonce dviga ali pada (enakonočja) približno pod kotom ε = 23,44 °,
glede na nebesni ekvator, je projekcija njegove hitrosti V*cos (ε),
torej manjša od V (kot vemo pa se tudi hitrost V Zemlje, oziroma
navideznega gibanja Sonca na nebu spreminja zaradi eliptične orbite Žemlje).
Cikel se ponovi dvakrat na leto in je neodvisen od ge. širine opazovalca.
Zaradi naklona ekliptike torej sončna ura izgubi ali pridobi približno
20,3 sekunde na dan, odvisno od letnega časa. Zaradi tega efekta je
največja razlika od srednjega poldneva približno 9,8 minut.
Za oceno poglejmo še podaljšanje dneva v prisončju. Od 3. do 4. januarja je Zemlja v periheliju za 1,67 % bližje Soncu od povprečne razdalje, njena kotna hitrost pa je večja za 3,37%. Zaradi tega je dan 7,9 sekunde daljši od povprečja na ta datum. 0,0337 × 3 min 56 s /1 dan = 7,9 s V treh mesecih Sončeva ura nakopiči napako 7,6 minut zaradi ekscentričnosti orbite (neenakomerne hitrosti Zemlje na tirnici), kar vodi do nesimetrične oblike zanke (analeme – če slikamo Sonce, recimo vsak jasen dan ob 12. h – Sonce na sliki ne potuje samo navzgor in navzdol, ampak naredi osmico, saj kulminacija Sonca ne sovpada s povprečnim časom, ki ga merijo naše ure – to razliko pa opiše časovna enačba). Cikel se zaključi v enem obhodu Zemlje okrog Sonca (pravzaprav nekoliko prej, zaradi precesije Zemlje, enakonočij).
Zakasnitev 20,3 sekunde na dan, ki jo povzroča naklon ekliptike in 7,9 s zaradi ekscentričnosti tira, se sešteva proti božiču, ko skupaj prispevata okrog 30 sekund.
Kumulativni napaki 9,8 in 7,6 minut zaradi obeh učinkov se seštevata
približno kot sinusa datuma in je zato skupna napaka (odstopanje)
manjša od 17 minut.
Časovna enačba je torej v grobem vsota dveh »sinusnih« krivulj za obdobji
enega leta, oziroma šestih mesecev. Približno časovno enačbo E lahko
zapišemo kot:
E = 7,67 sin (g (N - 1)) - 9,87 sin (2 g (N - 81))
E je izražen v minutah, kjer so:
g = 360 °/ 365, če so koti izraženi v stopinjah,
g = 2 π / 365, če so koti izraženi v radianih.
Kjer je N zaporedna številka dneva v letu, na primer:
N = 1 za 1. jan., N = 2 za 2. jan., ..., N = 31 za 31. jan., N = 32 za 1. feb.
Izpeljava korektne enačbe presega srednješolsko poznavanje matematike.
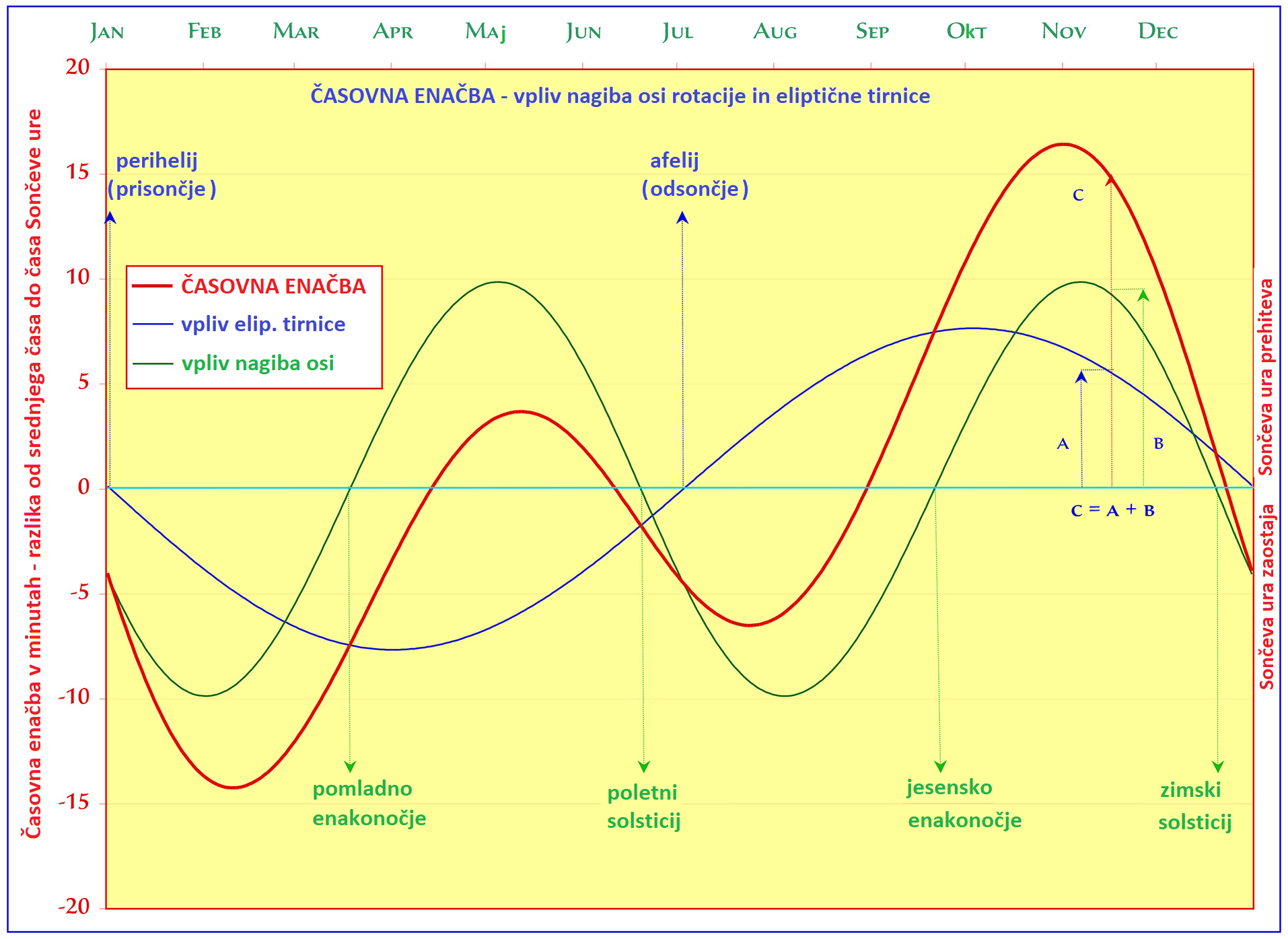
Časovna enačba v minutah (rdeča krivulja) – časovni odmik časa Sončeve
ure od povprečnega Sončevega časa, ki ga merijo naše linearne ure.
Z leti se, zaradi precesije, ta krivulja spreminja (tudi nagib osi se
rahlo spreminja, sama orbita, hitrost rotacije ...). Na grafu sta podana
še mejna primera:
1. Modra krivulja prikazuje odstopanje od srednjega časa zaradi neenakomernega
gibanja po elipsi (brez nagiba ekliptike).
2. Zelena krivulja pa zaradi nagiba ekliptike. Projekcija hitrosti (Sonca)
na nebesni ekvator nam razkrije krivuljo neenakomernega gibanja in torej
drugi razlog za odstopanje časa.
Oba vpliva skupaj pa se združita v časovni enačbi, v rdeči krivulji.
V resnici je to še ena posredna potrditev nagiba Zemljine osi in
eliptične tirnice preko Sončevega časa in linearnega časa, ki smo
ga vpeljali ljudje za konsistentno obravnavanje pojavov v prostoru
in času.

Analema ponazarja letni cikel Sončevega gibanja od 30. marca 2003
do 30. marca 2004 (slikano ob isti uri). V ospredju stojijo izjemni
korintski stebri antičnega templja.
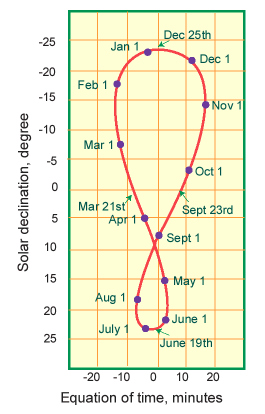
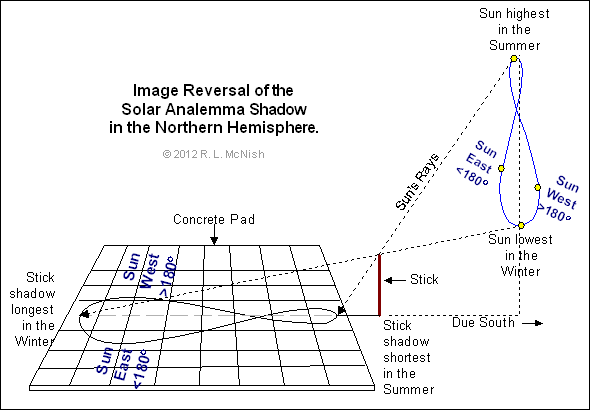
Analema pokoncne palice preko vrhov senc ob istem linearnem času (rec. 12:00) ob
različnih datumih skozi celo leto (leva slika).
Shema logike preslikava analeme v senco na površini Zemlje preko pokončne palice (slika desno).
Vir projekcije: https://calgary.rasc.ca/analemma.htm

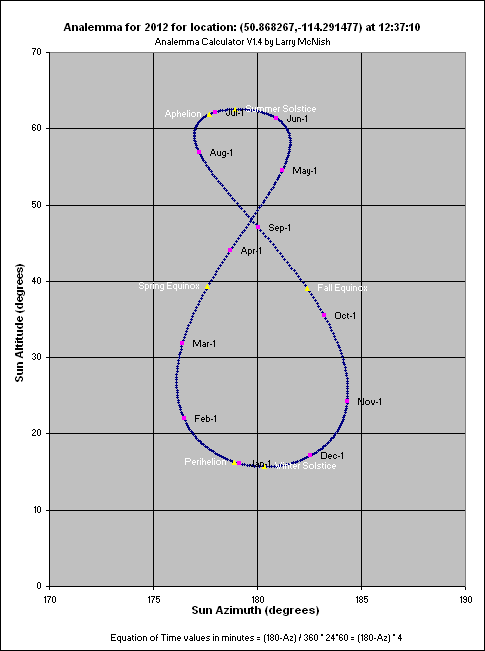
Analema iz senc na zidu (levo). Lega Sonca na nebu ob 12:37:10, lokacija je navedena na vrhu
grafa (slika desno). Vir: https://calgary.rasc.ca/analemma.htm
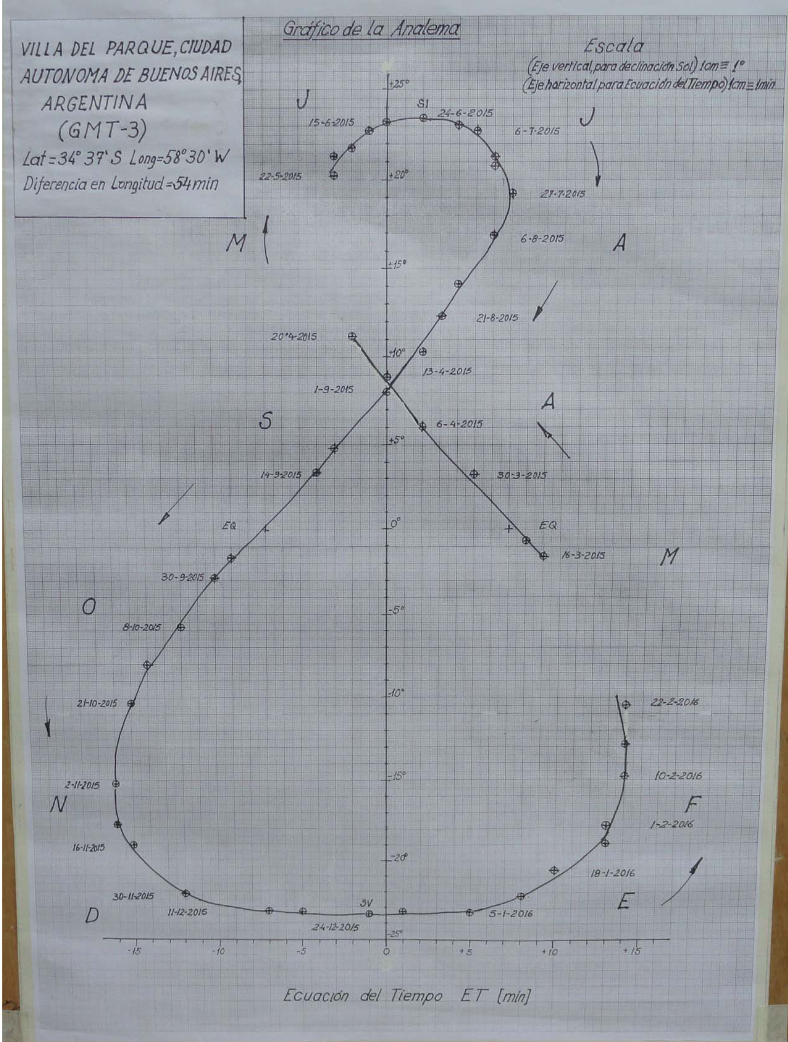
Analema iz senc pod ekvatorjem, Argentina - BUENOS AIRES
(tam je zima ob našem poletju, Sonce je nizko, zato šrši del analeme spodaj).
Vir: https://arxiv.org/ftp/arxiv/papers/1812/1812.10719.pdf
On times and shadows: the observational analemma (2015)
Alejandro Gangui
IAFE/Conicet and Universidad de Buenos Aires, Argentina
Cecilia Lastra
Instituto de Investigaciones CEFIEC, Universidad de Buenos Aires, Argentina
Fernando Karaseur
Instituto de Investigaciones CEFIEC, Universidad de Buenos Aires, Argentina
|
|
Koledar je sistem organiziranja datumov v daljšem obdobju. Po dogovoru
je dan najmanjša koledarska enota. V Evropi pa je osnova leto, cikel
višine Sonca. Merjenje delcev dneva pa je klasificirano kot merjenje časa.
Skozi celotno zgodovino človeštva, smo se bolj ali manj uspešno pomagali
z merjenjem časa preko cikličnih dogodkov na nebu, preko štetja zaporednih
dni, višine Sonca, z menjanjem ozvezdij, zvezd, na nebu, s ciklom Lune,
tudi kakega planeta, največkrat Venere ... Baje je na svetu okrog štirideset
koledarjev.
Astronomska osnova zahodnega koledarja
Glavni astronomski cikli so torej dan (na podlagi rotacije Zemlje okrog lastne osi),
leto (na podlagi potovanja Zemlje okrog Sonca, letnih časov) in mesec (na podlagi
potovanja Lune okoli Zemlje). Zapletenost koledarjev tiči v dejstvu, ker ti cikli
ne obsegajo celega števila dni, in ker časovno niso stabilni.
Oglejmo si težave s koledarjem. Siderski ali zvezdni dan (obrat Zemlje glede na
oddaljene zvezde) traja slabe 4 minute manj kot srednji Sončev dan, ki je dolg 24 ur.
Tako kot je dan definiran z zaporednimi kulminacijami Sonca (od poldneva do poldneva),
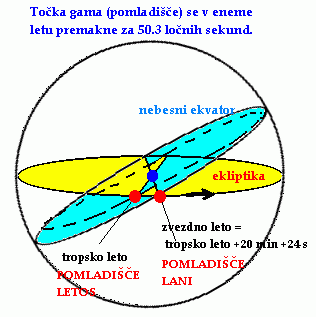
je tudi tropsko ali Sončevo leto definirano s sezonskim gibanjem Sonca. Leto je
v splošnem definirano s časom obhoda Zemlje okrog Sonca, a ker Zemlja precesira,
je tropsko leto (čas med dvema zaporednima prehodoma Sonca čez pomladišče)
za približno 20 minut krajše od zvezdnega leta in Sončev koledar mora upoštevati
sezonsko gibanje (višino) Sonca. Tropsko ali Sončevo leto traja približno
365.242189 srednjih Sončevih dni. Če poenostavimo, lahko rečemo, da je leto dolgo
365 povprečnih Sončevih dni in približno 6 ur (dobrih 11 minut manj, natančneje
11.248 minut, to pomeni da z julijanskim koledarjem prehitevamo višino sonca za en dan
že v 24*60 min/11.248 min = 128.0136548 letih).
To je bil tudi argument, da so se v prvem stoletju pr. Kr. odločili,
da bodo leta dolga 365 dni in vsako četrto leto (imenovano prestopno) za dan daljše,
torej dolgo 366 dni. V štirih letih se namreč nabere razlika približno enega dneva
(4X6 ur = 24 ur = 1 dan). Koledarsko reformo je leto 46 pr. n. št. izpeljal
J. Cezar (svetoval pa mu je imeniten astronom in matematik, Grk Sosigen).
Dogovorjeno je bilo, da so prestopna leta vsa tista, katerih letnica je deljiva
s štiri. To je bil julijanski koledar, ki je v večjem delu Evrope veljal do
16. stoletja, v Rusiji pa celo do leta 1918. Povedali smo že, da leto ne traja
točno 365 dni in 6 ur, ampak dobrih 11 minut manj, kar je naneslo do konca
16. stoletja že zamik desetih dni. V štiristo letih se namreč naberejo že dobri
trije dnevi preveč (približna ocena 400X11 min ), zato so leta 1582 odvzeli
10 dni, ki so se nabrala od uvedbe julijanskega koledarja in s tem uvedli
gregorijanski koledar.
Zakaj cca 10 dni razlike?
Veljavno krščansko datiranje velike noči je bilo definirano na Nicejskem koncilu leta 325
in večinoma temelji na starejšem judovskem koledarju in razmerju med polno
luno in enakonočjem.
Prej je bila velika noč v celoti povezana z judovskim verskim praznovanjem pashe (beg Judov iz Egipta,
Exodus - Izhod, glejte 2Mz 12,1-50)
in še danes ima to povezavo.
Nicejski koncil je prešel na julijanski sistem datiranja velike noči in takrat še ni bilo dovolj očitno,
da ima julijanski koledar napako (v cca 128 letih je prehiteval za en dan),
kar je pomenilo, da datum enakonočja sčasoma ni bil več usklajen z dejanskim dogodkom (z višino Sonca
na prvi pomladni dan). Če pogledamo razliko let 1582 in 325 ta znaša 1257 let in če to razliko delimo
s periodo 128, ki da napako enega dneva (izračunali zgoraj),
dobimo zamik (prehitevanje) že za 10 dni, saj velja:
(1582 - 325)/128.0136548 = 9.82 dni ≈ 10 dni.
In še o reformi koledarja - kdaj in kako stopi v veljavo gregorijanski koledar?
Četrtku 4. oktobra 1582 je sledil prvi dan gregorijanskega koledarja,
to je petek 15. oktobra 1582 (cikel prehoda med tedni ni bil prizadet).
Da se napaka ne bi spet ponovila (večala), so
Gregorijanski koledar dodatno korigirali tako,
da se v 400 letih odvzamejo že omenjeni trije dnevi. Ti trije dnevi se
odvzamejo tako, da se tri prestopna leta štejejo kot navadna. To so leta,
katerih letnice se pišejo z dvema ničlama na koncu (prehodi med stoletji)
in niso deljiva s 400. Zdaj tudi razumemo, zakaj sta leti 1600 in 2000
prestopni, leta 1700, 1800 in 1900 pa niso bila prestopna (so sicer deljiva
s 4 a ne s 400). Resnici na ljubo tudi gregorijanska korekcija ni rešila
težav s koledarjem, saj se bo napaka enega dneva spet nabrala v dobrih
3200 letih ( 400*11.248/(60*24) dni = 3.1244 dni na 400 let, napaka enega
dneva se pa spet pojavi, zaradi 0.1244 dni ostanka, v približno
400*1/0.1244 let = 3215,4 letih). Papež, po katerem se koledar tudi
imenuje, je reformo koledarja razglasil 24. februarja 1582 z bulo Inter
gravissimas in to v vili Mondragone v Frascatiju blizu Rima, o čemer
priča vgrajena plošča (reformo je pripravila posebna komisija na podlagi
predloga nemškega astronoma Christophera Claviusa in neapeljskega zdravnika,
astronoma in fizika Luigija Lilia).
|
|
Za konec omenimo še, da seveda obstaja več možnih rešitev za tropski
(Sončev) koledar, recimo Hajamov koledar (napako enega dneva baje doseže
v 5000 letih), trenutno najbolj natančen koledar je iranski (leta 1925
so precej zapleteno prenovili stari perzijski koledar - le na vsakih 3,8
milijona let kopiči enodnevno napako. A se je prehod iz julijanskega v
natančnejši koledar najlažje zgodil preko gregorijanske reforme. Pozna samo
tri dodatne izjeme na 400 let, glede na takrat utečen julijanski koledar
in zamik zgolj enega dneva v 3200 letih (zelo elegantna rešitev). So debate,
zakaj Evropa recimo ni prevzela Hajamovega koledarja – a gregorijanska reforma
je izjemna, saj ni zahtevala prehudih posegov v julijansko prakso (v staro
Sosigenovo antično reformo).
Se nadaljuje ...
Zorko Vičar
Korona pomlad 2021
DODATEK - merjenje razdalj v vesolju: