Zakaj astronomija
|

|
Zakaj astronomija
|

|
Einstein-Newton, kaj opazovati, optika, radijska astronomija,
oprema za mlade, sledi vprašanje - zakaj smo in koliko časa še bomo?
Zakaj je Einstein bolje opisal vesolje kot Newton
Ali učence soočimo z ukrivljenostjo prostor-časa (tukaj bi zagotovo prišel
prav Einsteinov miselni poskus s krovcem, ki ga je označil kot najsrečnejšo
misel svojega življenja), oziroma kaj storiti z efekti gravitacije (uklon
žarka, rdeči gravitacijski premik, »podaljšanje« časa, precesija perihelija,
gravitacijsko lečenje). Vsekakor je potrebno poudariti, da je koncept
gravitacijske sile napačen, saj fotoni nimajo mase, a se njihova pot
vseeno ukrivi ob masivnih zvezdah (kar lahko opazujemo ob popolnih
Sončevih mrkih), zato je Einsteinov koncept ukrivljenosti prostor-časa
veliko ustreznejši. Prostor-čas krivi energija, ki je lokalno v glavnem
zbrana v masi Zemlje, Sonca ...
(E = mc2). Tudi nobena sila ne more potovati neskončno hitro,
kar napačno privzame Newton (a tega Newtonu v kontekstu časa in takratnega
vedenja, ne gre zameriti). Skoraj vse o tem pojavu sledi v enem izmed nadaljevanj.
Ponovitev staroveških opazovanj (pred iznajdbo teleskopov)
Koliko priložnosti bi dali opazovanjem (ki so zmeraj odvisna od vremena
ali bi bilo prav, da je tudi učitelj prisoten pri opazovanjih – seveda ja ...,
kdaj to ni bilo samoumevno), kateri planet bi učenci lahko opazovali
s prostim očesom skozi tedne in mesece, ga vnašali na zvezdno karto,
da bi najhitreje prišli do razumevanja Nikolajeve,
Kopernikove (Aristarhove) in izboljšane Keplerjeve
slike Sončevega sistema (recimo, da bi zaznali očitno
retrogradno, vzvratno, gibanje planeta); ali učenci skozi
leto(a) vnašajo na karto vse s prostim očesom vidne planete,
tudi Luno, Sonce; ali je bolje, da se ozvezdja učimo v razredu
na papirju, ekranu ali raje preko neposrednih opazovanja pod
nebesno sfero (najbrž preko kombinacije obojega). Do katere mere
sta recimo programa »Stellarium« in »SkyChart/Cartes du Ciel«
lahko dober nadomestek astronomskih opazovanj?
Kje opazovati?
A se na opazovanja selimo v temne oddaljene kotičke (veliko logistike,
denarja in časa) ali se raje potrudimo na šolski terasi, igrišču,
učenci tudi doma ... (kljub svetlobi krajevnih luči, in ko to seveda
omogoča vreme) ali se za vsako ceno izogibati Luni, ko opazujemo
objekte globokega neba, ali se za ceno pretiranega poudarjanja
svetlobnega onesnaženja odreči opazovanjem ali jih opravimo kljub
lučem, in če je le mogoče, še v temnem okolju (te gromozanske
razlike med temnim in preosvetljenim nebom noben učenec ne bo
spregledal in zna biti zelo dobra izkušnja za bodoča ravnanja
in stališča naših učencev glede problematike svetlobnega
onesnaženja).
Optika in teleskop (Mala šola geometrijske optike, Spika 12/2022, strani 528 - 531)
Koliko povedati o optiki, odbojni in lomni zakon, koliko povezav
izpeljemo (enačba leče, zrcala, povečava, vidno polje, izstopna zenica, ...),
koliko časa posvetimo daljnogledom, teleskopom, kvaliteti optike, okularjem,
koliko očesu in svetlosti slike, izjemno pomembni ločljivosti, ali se takoj
navezati tudi na gravitacijsko lečenje; optika pri pouku fizike velikokrat
ostane nepokrita, a pri astronomiji kot izbirnem predmetu tudi ni ravno
ur na pretek – a vendar je ne smemo preskočiti. Optika so naše oči v vesolje.
Povzamemo nekatere bistvene lastnosti teleskopov.

Recimo, da valovne fronte svetlobe izhajajo iz točke.
V spodnjem za svetlobo delno prepustnem mediju (recimo voda, steklo) se valovne fronte širijo počasneje.
S tem se spremeni normalni vektor valovne fronte, ki ustreza lomu svetlobnega žarka.
Za lomni količnik svetlobe velja, da je hitrost "v" svetlobe v snovi
z lomnim količnikom n kar enaka: v = c/n. Kjer je c = 299 792 458 m/s hitrost svetlobe v vakuumu.
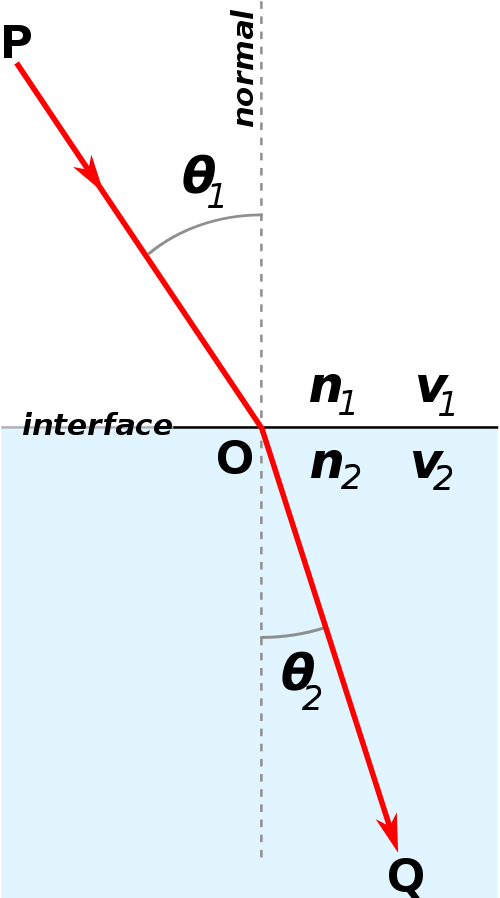
Za svetlobi velja torej lomni zakon:
n2/n1 = sin(θ1)/sin(θ2) = v1/v2
To je Snellov zakon (1621 ga odkrije Nizozemec Willebrord Snell van Royen).
Kako preslikati vzporedne žarke v točko? Prva ideja je optični sistem
iz večih prizem z različnim strankim kotom (strmino). Iz tega se rodi
ideja leče - a pot je bila ravno obratna (najprej smo "izumili" lećo).
Lečo si lahko pradstavljamo kot sistem sestavljen z neskončmo mnogo prizem.
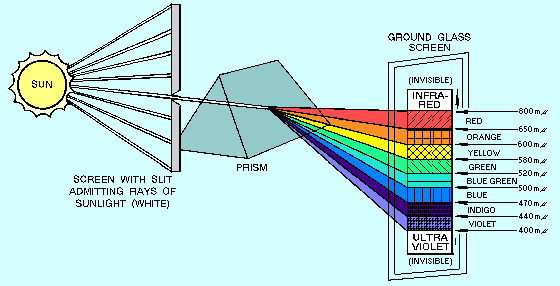
Problem loma svetlobe pa je, da je kot loma odvisen od valovne dolžine.
Najmanjši kot ima rdeča svetloba, ki ima v vidnem spektru najdaljšo valovno dolžino.
In ta efekt vsekakor nagaja pri optiki, lečah, saj ima vsaka valovna dolžina svoj fokus,
temu pravimo tudi bravna napaka. Preslikava ni enolična, ampak dobimo neostro sliko
v mavričnih barvah. Enote za valovne dolžine na desni pri barvah so nm (m// = nm).
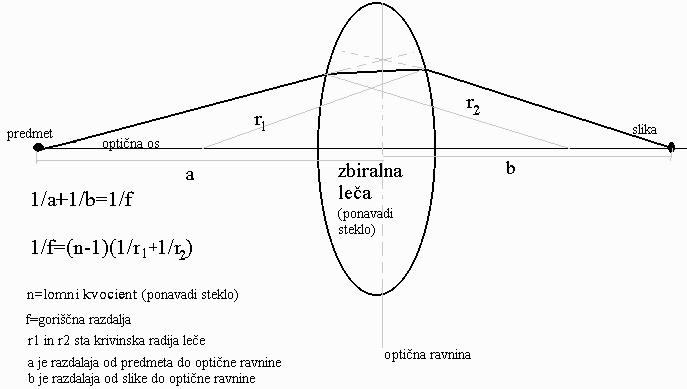
Zbiralna (konveksna) leča in izračun goriščne razdalje glede na lomni
količnik (n) stekla in krivinska radija (r1, r2)
obeh površin: 1/f = (n-1)(1/r1 + 1/r2).
Pri leči torej uporabimo - za tvorjenje slike - lastnost svetlobe, žarka, da se
pri vpadu (recimo iz zraka) na steklo ali katero drugo snov,
kjer je hitrost širjenja svetlobe manjša od hitrosti v zraku (ali brezzračnem prostoru), le ta
lomi proti vpadnici - pravokotnici na mejno ploskev "zrak - leča".
Snop vzporednih svetlobnih žarkov, ki vpada na konveksno lečo pod določenim kotom, se na drugi strani združi v eno točko, ki leži v goriščni ravnini. Če so svetlobni žarki vzporedni z optično osjo, se na drugi strani združijo v gorišču (F). Goriščna razdalja (f) je oddaljenost gorišč od leče (optične ravnine).
Zbiralna izbočena (konveksna) leča, zbiralno vbočeno (konkavno) zrcalo in razpršilna vbočena (konkavna) leča - preslikave.
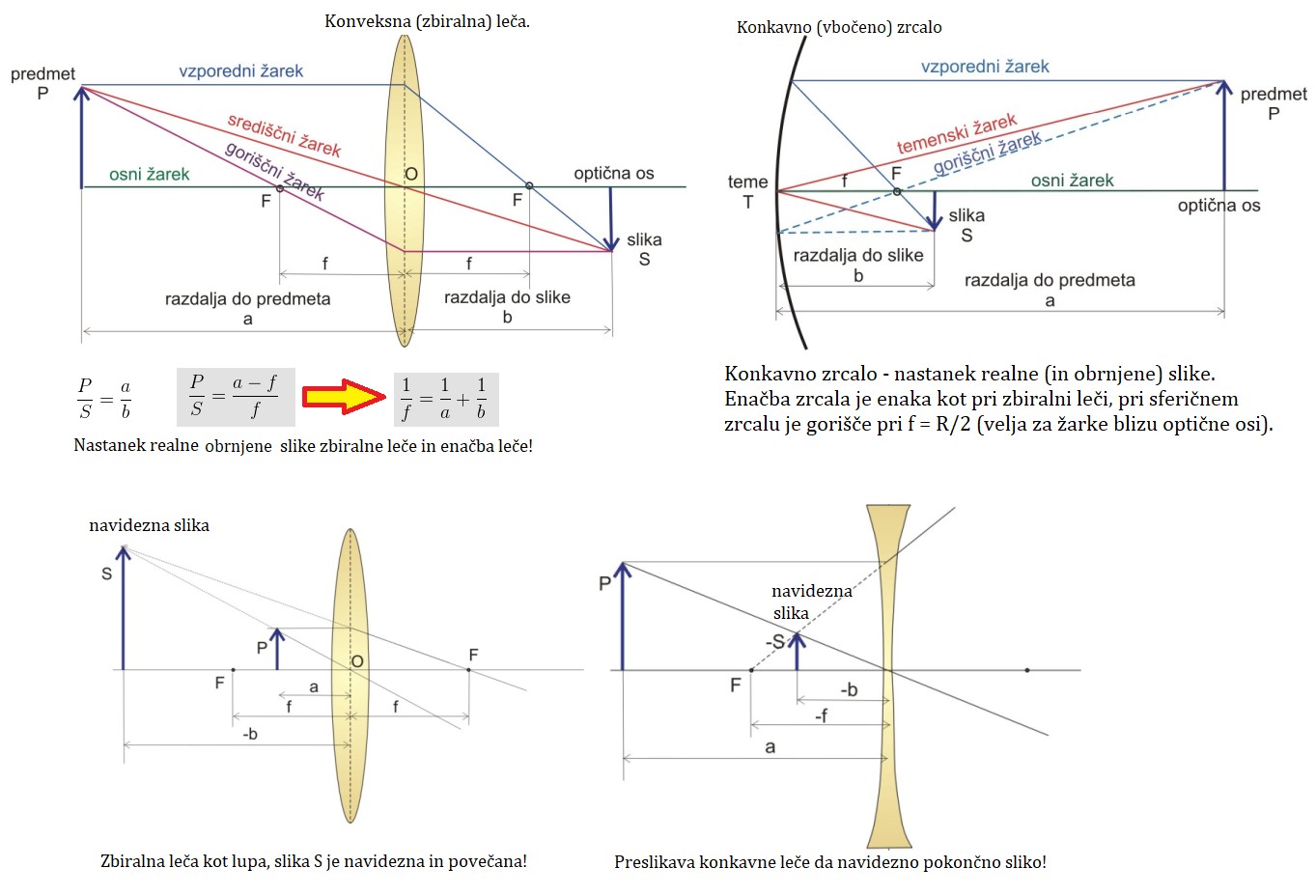
Osnove optike – konveksna (zbiralna) in konkavna (razpršilna) leča, konkavno
zrcalo, nastanek slik - preslikav! Leče so optične naprave, ki izkoriščajo
lom svetlobe. Pri vpadu svetlobe iz zraka na steklo ali katero drugo snov,
kjer je hitrost širjenja svetlobe manjša od hitrosti v zraku (ali brezzračnem prostoru)
se žarek lomi proti vpadnici - pravokotnici na mejno ploskev zrak - leča.
Zbiralna leča je recimo na sredini združen izsek dveh steklenih krogel.
Slika predmeta, ki jo dobimo s pomočjo zbiralne leče je lahko realna ali
navidezna. Realna slika je obrnjena in jo lahko fotografiramo (projiciramo
na film ali čip sestavljen iz svetlobnih elementov). Snop vzporednih
svetlobnih žarkov, ki vpada na konveksno lečo pod določenim kotom,
se na drugi strani združi v eno točko, ki leži v goriščni ravnini.
Če so svetlobni žarki vzporedni z optično osjo, se na drugi strani
združijo v gorišču (F). Goriščna razdalja (f) je oddaljenost gorišč
od leče. Konveksne leče uporabljamo za preslikave predmetov. Predmet
velikosti P postavimo na neko razdaljo a pred lečo (naj bo a > f).
Na razdalji b od leče dobimo realno obrnjeno sliko velikosti S.
Iz zgornje slike (podobnih trikotnikov) sledi, da sta povezavi med
P, S, f, a in b naslednji enačbi leče (enako velja za vbočeno zrcalo):
P/S = a/b in 1/f = 1/a + 1/b
V primeru, da je predmet P med lečo in goriščem F (naj bo a < f),
dobimo navidezno pokončno in povečano sliko S. Sedaj leča deluje kot lupa.
Teleskop je torej zbiralna leča, ki da realno sliko praktično v goriščni
ravnini (saj je razdalja »a« zelo velika in velja 1/a ≈ 0,
torej velja 1/f ≈ 1/b). Sliko lahko fotografiramo ali pogledamo
z zbiralno lečo (lupo), to je Keplerjev teleskop (lupo imenujemo v tem
primeru kar okular).
Konkavna leča je recimo sestavljena iz stekla vlitega med dvema rahlo
razmaknjenima kroglama. Razpršilna leča zmeraj da pomanjšano, pokončno
in navidezno sliko. Če uporabimo za okular razpršilno lečo, dobimo pokončno
sliko – Galilejev teleskop (ima pa nekoliko manjše vidno polje kot Keplerjev
teleskop). Razpršilno lečo je izumil znameniti srednjeveški učenjak Nikolaj
Kuzanski (z njo je začel korigirati kratkovidnost – tako je do danes pomagal
milijonom ljudi, otrok – tudi meni).
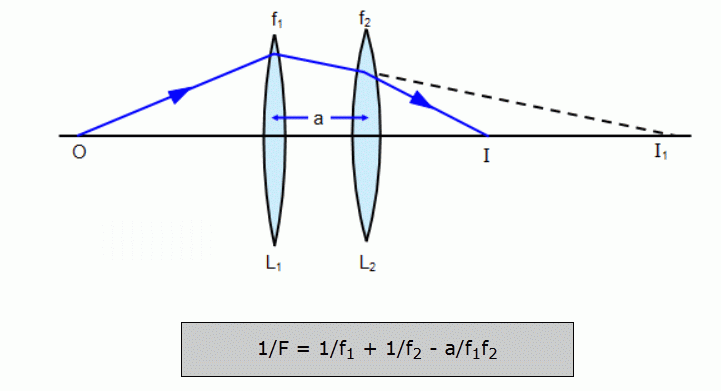
Recimo za dve konveksni leči na razdalji
a se efektivno gorišče obeh leč izračuna kot:
1/f = 1/f1 + 1/f2 - a/f1f2.
Vir: https://si.openprof.com/wb/opti%C4%8Dna_preslikava_-_le%C4%8De?ch=205
VELIKOST SLIKE
Kako izračunamo velikost slike v gorišču teleskopa, recimo Lune ali Sonca
(vidimo ju pod kotom φ = 0,5 °). Recimo, da ima teleskop goriščno razdaljo
f = 1 m. Pomagajmo si s sliko.
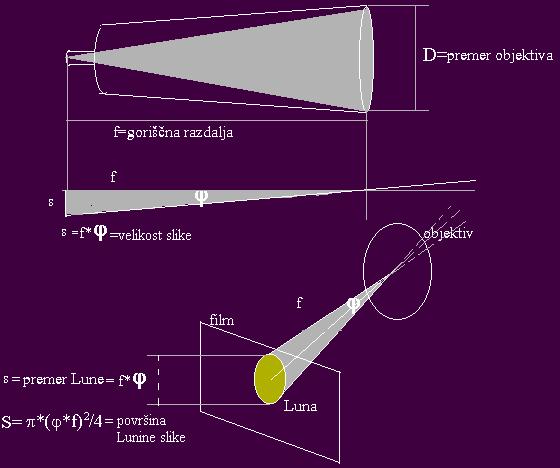
Ker so koti majhni, velja za velikost
slike S = (zorni kot v radianih)*(goriščna razdalja).
S = φf = 0,5 °(π/180 °)1000 mm = 8.73 mm. To je že spoštovanja vredna velikost slike, ki že razkrije veliko podrobnosti na Luni ali Soncu (tudi ob mrkih). Za navidezno majhne planete pa si pri takem teleskopu (f = 1 m) pomagamo s podaljšano goriščno razdaljo (ali z okularno projekcijo ali Barlowo lečo – tipično za planete rabimo 5 ali več m efektivne goriščne razdalje).
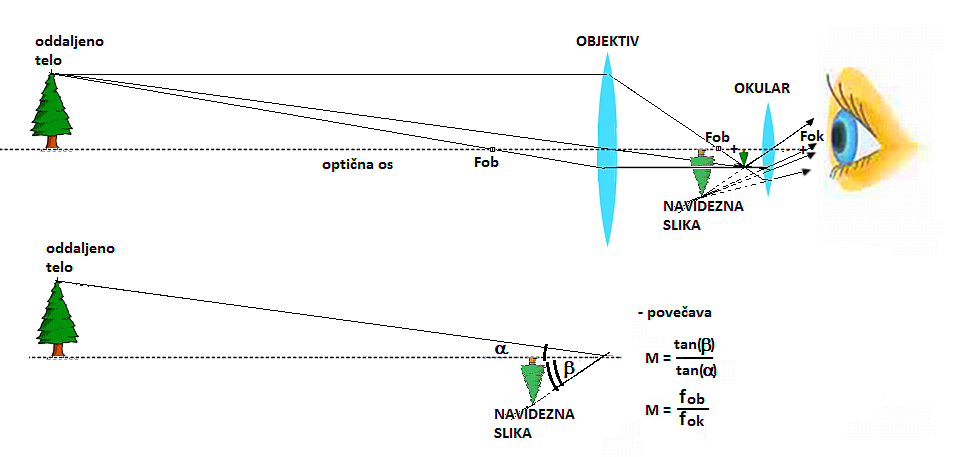
Skica preproste sheme teleskopa, refraktorja, princip - lom
svetlobe pri prehodu skozi zbiralne leče. Levo je zbiralna leča
kot objektiv (objektiv je lahko tudi vbočeno zrcalo, parabolično,
sferično ...), desno je zbiralna leča kot okular. Objektiv tvori
realno in obrnjeno sliko (mala obrnjena smrečica), okular pa deluje
kot lupa, ki to sliko še dodatno poveča (nastane navidezno povečana
smreka, tam kjer se stikajo črtkane premice preslikave). Leče teleskopov
so sestavljene iz različnih stekel (različnih lomnih količnikov), da se
tako zmanjša barvna napaka pri lomu svetlobe. Povečava teleskopa je kar
kvocient med goriščno razdaljo objektiva in okularja:
M = tan β/tan α = fob/fok.
Prvi daljnogledi so se pojavili (najbrž) kmalu po letu 1600 - Nizozemska
(najbolj znana začetnika opazovanja neba s teleskopi sta Simon Marius
1609 in Galileo Galilei 1610 – med njima se vname spor glede prvenstva
odkritja znamenitih Jupitrovih lun, imena jim da Marius: Io, Evropa,
Ganimed in Kalisto – te lune zaznamo že z manjšim teleskopom). Tudi
sama zgodba o odkritju teleskopa je zelo zgovorna, lahko bi jo opisali
kot pot od otroške igre do zvezd. Hans Lippershey, nizozemski brusilec
leč, je menda po naključju, ko je opazoval dva otroka, ki sta se igrala
z lečami v njegovi delavnici, že jeseni 1608 odkril teleskopski učinek,
do katerega pride, če pogledamo zaporedno skozi dve leči različnih goriščnih
razdalj. Torej znanosti ni brez igre in to je še en dokaz, kako pomembno je
svobodno ustvarjalno okolje za slehernega otroka, tudi za nas odrasle.
OPTIČNE NAPAKE

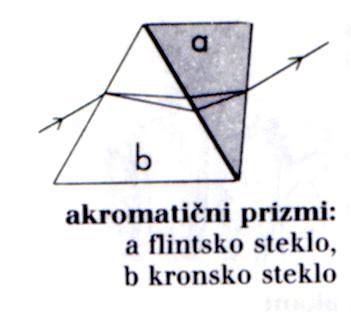
Kromatična aberacija - aberacija - barvna napaka, ki izhaja iz dejstva,
da se različne valovne dolžine svetlobe različno lomijo in se zato ne z
berejo v isti točki (gorišču). To napako se dokaj uspešno odpravi s
sestavljeno lečo iz različnih lomnih količnikov (recimo flintsko in
kronsko steklo).
Akromatik - achromatic, je objektiv, ki v točki (gorišču, fokusu)
zbere rdečo in modro svetlobo, vendar ne tudi preostalih barv
("sekundarnih" barv). To je soliden objektiv ali okular,
a še zmeraj se opazi precej barvne napake.
Apokromatik - apochromatic, apo objektiv je sestavljen iz najmanj
treh leč, posebnih stekel, tako da se zberejo rdeča, zelena in modra
svetloba v eni točki, gorišču in se s tem zmanjša delež "sekundarnih"
barv (ki se ne zberejo v gorišču) – to je zelo draga optika.
Poleg barvne napake, se pri preslikavi s pomočjo leče ali vbočenega zrcala
(zrcala nimajo barvne napake, odbojni zakon velja za vse valovne dolžine)
pojavlja še vrsto ostalih napak, ki so največkrat povezane s
povezane s slabo zbrušeno optiko, tudi s samo geometrijo zrcala (parabola, sfera, hiperbola ...).
Te napake so:
ukrivljenost polja – slike,
popačenje – distorzija, zelo moti koma – zvezde dobijo repke,
zgledajo kot kometki, astigmatizem – radialno ali tangentno raztegnjene
zvezde. Večina teh napak, razen barvne, na optični osi praktično izgine, ni vidna,
a žal se napake večajo proti robu polja.
Marsikatero od naštetih napak se da s kombinacijo različnih tako imenovanih korekcijskih
leč ("očal") odpraviti – a s tem zaradi odbojev in ostalih efektov izgubljamo svetlobo
in na koncu tudi ostrino ter kontrast slike.
Za planete (dvojne zvezde) je zato najboljši ortoskopski
Abbejev okular "le" s štirimi lečami, ki minimalno popačijo geometrijo
preslikave (sliko).
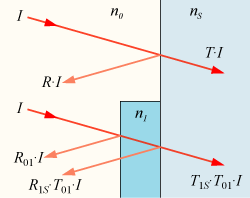
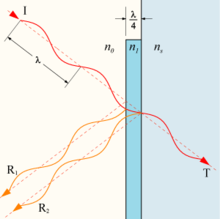
Leva slika kaže princip odboja z in brez antirefleksnega sloja.
Desna slika kaže interferenco na antirefleksnem sloju
debeline 1/4 valovne dolžine svetlobe.
PROBLEM ODBOJA SVETLOBE OD OPTIČNIH POVRŠIN
Ko svetloba pade na lečo, je gre večina skozi,
nekaj pa se je tudi odbije in ta odbita svetloba je izgubljena,
saj ne prispeva k svetlosti slike.
Kot bomo videli iz računov, se tipično na vsaki meji odbije okrog
4 % vpadne svetlobe. Zdi se malo, a če pomislimo, da so moderni objektivi
in še posebej okularji sestavljeni iz več leč,
se prepustnost zelo zmanjša.
Zato je danes večina leč naparjenih z antirefleksnimi sloji
debeline λ/4. Zakaj sloj debeline 1/4 valovne dolžine svetlobe? Odboj
od same leče je tako nasprotne faze z odbojem s površine antirefleksne plasti
(zaradi 1/4 zamika valovne dolžine) in se zato velik del odbitega valovanja
z obeh plasti oslabi, kar pa je še dodatna prednost pri odbojih znotraj
sistema leč. Poglejmo primere.
Koeficient refleksije (R) se računa po Augustin-Jean Fresnel-ovi
formuli
R = ((n2 - n1)/(n2 + n1))2
(ko so žarki praktično pravokotni na objektiv), n1
in n2 sta lomna količnika (recimo zraka in stekla).
Primer za lomni količnik kronskega stekla
n2 = 1.5 in zraka n1 = 1 (približek za zrak):
R = ((1.5-1)/(1.5+1))2 = (0.5/2.5)2 = (0.2)2 = 0.04,
to je odbojnost 4 %. Zdi se malo, a če pomislimo da so objektivi in okularji
sestavljeni iz več leč - se prepustnost zelo zmanjša. Pogosto se antirefleksni
sloj uporablja magnezijev fluorid
(MgF2, n1 = 1,38).
1/4 valovne dolžine debela AR plast ima tako dimenzije približno 100 nm
in zagotavlja odbojnosti 1.4 % - izračun je spodaj.
R = ((1.38 - 1)/(1.38 + 1) - (1.5 - 1.38 )/(1.5 + 1.38))2 = 1.4 %
* Procent prepuščene svetlobe skozi 14 ploskev optičnega sistema brez
antirefleksnih nanosov
je samo 100*(1-0.04)14 = 56.5 %.
Izgubimo torej skoraj 44 % svetlobe, ki tvori sliko, oziroma velik del
te izgubljene svetlobe pade v oko, a kot odbita svetloba pod različnimi
koti in s tem se zelo zmanjša kontrast slike.
* Procent prepuščene svetlobe skozi 14 ploskev optičnega sistema z
enojnimi antirefleksnimi nanosi (FC - Fully Coated) je kar
100*(1-0.014)14 = 82.1 %.
Izgubimo torej le 18 % svetlobe, ki tvori sliko. Rezultat je zelo obetaven.
* Procent prepuščene svetlobe skozi 14 ploskev optičnega sistema z večplastnimi
antirefleksnimi nanosi (FMC - Fully-multi-coated, zgolj 0.25 % odbite svetlobe)
je pa neverjetnih
100*(1-0.0025)14 = 96.6 %.
Izgubimo torej samo dobre 3 % svetlobe, ki tvori sliko. Rezultat
je praktično neverjeten.
No tudi cene take optike so neverjetne - 15x dražja optika od
povprečnih cen. A bolje
FC optika kot nič – FC daljnogledi do 80 mm premera objektivov
stanejo do 150 EUR
(20X80 FC so izjemni daljnogledi, recimo zornega polja 3.7 ° - FOV)!

Nazoren primer dobro (zgoraj) - brez težav pogledamo skozi optiko daljnogleda
in
slabo (spodaj) naparjene optike z
antirefleksnimi sloji - veliko odbojev od leč, objektiv je tako zatemnjen.
Če imamo objektiva premera 70 mm (FC - Fully Coated) -
daljnogled recimo s 14 optičnimi površinami, bomo izgubili okrog 18 % svetlobe,
ker tak optični sistem prepušča 82.1 % vpadle svetlobe (izračuni zgoraj).
FMC - Fully-multi-coated (zgolj 0.25 % odbite svetlobe) daljnogled
pa prepušča neverjetnih
100*(1-0.0025)14 = 96.6 % svetlobe - a je veliko dražji.
Kaj lahko storimo? Kupimo nekoliko večji daljnogled zgolj Fully Coated - recimo
80 mm - in še zmeraj bomo prihranili kar veliko denarja. Ali je bil ta naš sklep na pamet
pravšnji? Kot bomo videli, le delno, oziroma pri enaki izstopni zenici smo še
presegli pričakovanja.
Naredimo izračun.
Recimo, da iščemo nadomestilo za drag 2r = 70 mm FMC daljnogled, za večjega
FC, kolikšen premer 2R bi moral imeti ta drugi daljnogled?
Velja, da želimo enako število fotonov na mrežnici (j*S), to še zapišimo z gostoto svetlobnega
toka j in površino S ter prepustnostjo FC in FMC :
πR2j*FC = πr2j*FMC
Za polmer R nadomestnega daljnogleda po krajšanju tako dobimo izraz:
R = r(FMC/FC)1/2 = 35 mm*(96.6%/82.1%)1/2 = 37.965
mm
- za premer nadomestnega FC daljnogleda torej velja vrednost 2R = 76 mm
Torej, dovolj je že daljnogled FC 76 mm premera, da nadomestite FMC 70 mm.
Kupite torej soliden daljnogled 80 mm FC in boste zanj dali precej manj kot za
FMC 70 mm. Je pa res, da se razlika precej pozna na velikosti
in masi daljnogledov ter prenosljivosti. Velja za enaki izstopni zenici
(recimo daljnogleda 15x70 in 17x80, recimo 16x80 bo dal še veliko svetlejšo sliko).
Še vprašanje, za koliko se nam poveča gostota vpadnega energijskega toka (jR = ?) na mrežnico,
če imata daljnogleda enako izstopno zenico Sz
in različna premera objektiva (R > r)?
Pogljemo oba tokova fotonov na oko - velja:
jrSz = jobjektaSobjektiva_r
jRSz = jobjektaSobjektiva_R
Enačbi med sabo delimo in dobimo:
jR = jrSobjektiva_R/Sobjektiva_r
= jr(R/r)2
Če recimo opazujemo nebesne objekte najprej z daljnogledom 10x50 in potem pa z daljnogledom
16x80 - oba imata zenico 50 mm/10 = 80 mm/16 = 5 mm, potem - nam pade na mrežnico
pri 16x80 kar (R/r)2 = (80/50)2 = 2.56 x več svetlobe kot pri daljnogledu
10x50.
To je ogromno. Planetarnko meglico Helix v Vodnarju
recimo z daljnogledom 16x80 krasno razločimo, z daljnogledom
10x50 pa komaj ...
IZSTOPNA ZENICA (širina izstopnega snopa svetlobe iz okularja)
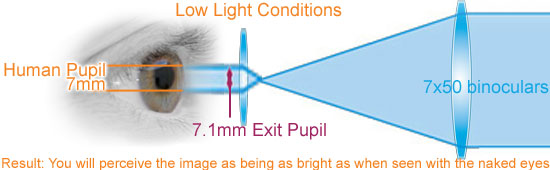

Izstopna zenica (izstopni snop svetlobe iz okularja) odloča o svetlosti
slike na mrežnici. Ko ponoči opazujemo temne nebesne objekte, recimo
planetarne meglice, si želimo kar se da svetlo sliko – veliko svetlobe
v očesu, veliko izstopno zenico teleskopa (če je možno, široko 7 mm,
kot je ponoči odprta zenica našega očesa). Izstopna zenica se izračuna
kot razmerje med premerom objektiva D in povečavo teleskopa M:
IZ = D/M = D(ffok/fob).
Teleskop s premerom D = 200 mm s povečavo 40x da izhodno zenico 5 mm
(IZ = 200 mm/40 = 5 mm,
kar je odlično za opazovanje večjih šibkejših objektov – recimo ostankov supernov).
Zenica očesa torej neposredno vpliva na najmanjšo, še smiselno povečavo, ki je enaka
razmerju med premerom objektiva in premerom zenice. Glej članek Zenica očesa: Spika,
april 2000, stran 183. Smiselne vrednosti so od 1 mm (za svetle planete,
Luno je ta meja 0,5 mm) do 7 mm (za megličaste objekte).

Vir slik o zenici:
http://www.nikon.com/products/sportoptics/how_to/guide/binoculars/basic/basic_05.htm
Človeška povprečna zenica se podnevi odpre približno 2mm in 7mm v temi.
Če uporabljate daljnogled z izstopno zenico nad 2mm pri dnevni svetlobi,
ne boste zaznali temnejše slike. Svetlost slike se torej ne bo spremenila,
če čez dan uporabljate daljnogleda z izstopnima zenicama 7 mm ali 2 mm.
Na drugi strani pa, če uporabljate daljnogled z majhno izstopno zenico
v temi, bo slika na mrežnici temnejša, kot če gledamo s prostim očesom.
No - v vsakem primeru pa bo slika (če gledamo z daljnogledom) na mrežnici
večja (kot pod katerim vidimo objekt bo večji) - kar pa vseeno poveča
zaznavanje podrobnosti. To pa so tudi razlogi za uporabo daljnogledov
(teleskopov), povečana in po možnosti maksimalno svetla slika ter
večja ločljivost slike. Pri astronomskih opazovanjih šibkih objektov
si torej želimo zenico veliko približno kot je velika zenica očesa
(celo do 8 mm pri mlajših in 5 mm pri starejših). A velika izstopna
zenica je smiselna samo, če opazujem res v temnem okolju -
brez svetlobnega onesnaženja.
Izstopna zenica 6 ali 7 v Mariboru, na obali, v Ljubljani ali okolici ...
je problematična prav zaradi svetlobnega onesnaženja, slika je zelo nekontrastna zaradi
sivine sipane umetne razsvetljave iz same atmosfere. Zenica 5 ali manj, pa ta efekt umetno osvetljne
atmosfere
v mestnem okolju nekoliko ublaži, ker je sama slika temnejša.
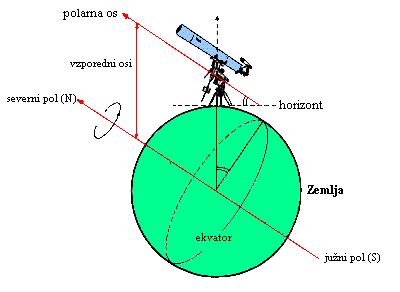
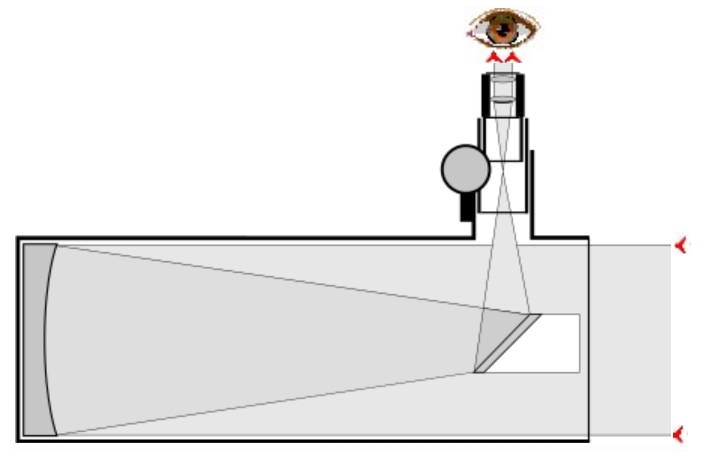
Leva slika - večinoma teleskop vrtimo okrog osi, ki je vzporedna z rotacijo
Zemlje (polarna montaža), da sledimo navideznemu vrtenju neba in tako ohranjamo
nebesni objekt v polju teleskopa.
Desna slika – primer najbolj preprostega reflektorja (tip Newton) – teleskopa
na vbočeno zrcalo (sfera, bolje parabola ...). Največji teleskopi na svetu
(in v orbitah)
so reflektorski – pri odboju svetlobe od zrcala ni barvne napake, kot se le ta
pojavlja pri objektivih sestavljenih iz leč (velike leče se tudi zaradi kastne
teže deformirajo).
MEJNA MAGNITUDA TELESKOPA
Na tem mestu izpeljimo enačbo za mejno magnitudo teleskopa
(izhajajmo iz Pogsonovega zakona
j1/j2 = 10-0,4(m1-m2) ).
Za premer očesne zenice v temi privzamimo vrednost 7 mm in za mejno magnitudo očesa
vrednost 5,7 m (še opomba - mnogi uporabljajo višje vrednosti za mejno magnitudo,
tja do 6,5 m ali tudi manjše 5 m).
VELJA TOREJ:
d1 = dzenice = d = 7 mm = 0,7 cm,
m1 = močesa = 5,7
D1 = D = Dteleskopa,
m2 = m = mobjekta
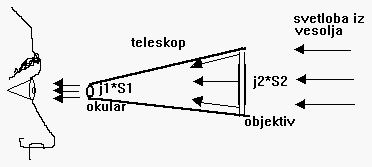
Ker velja ohranitev pretoka fotonov
( j1*Sočesa=j2*Sobjektiva ali
j1*d2*π/4 = j2*D2*π/4 ),
to pomeni, da v teleskop prihaja tista mejna gostota energijskega toka j2 ,
ki se v teleskopu zgosti na j1, energijski tok pa se pri tem ohranja
(primerjava
vodovodne cevi, ki se zoži, skoznjo teče enak vodni tok le hitrost se
v ožjem delu poveča, v1*S1 = v2*S2)
-iz opisanega razmisleka sledi (D/d)2 = 10-2(m1-m)/5,
po logaritmiranju dobimo
m = 5*log(D/d) + m1
m = 5*log(D) + m1 - 5*log(d)
- izvrednotimo neodvisen del enačbe m1 - 5*log(d) = 5.7 - 5*LOG(0.7) = 6.475
Sledi končni izraz za mejni sij nebesnih objektov
teleskopa s premerom objektiva D v cm:
m = 6,5+5*log(D)
Kjer je D premer objektiva teleskopa v cm. Teh ocen (formul) je več, ta je
dokaj realna. Za vajo ocenimo mejno magnitudo teleskopa s premerom D = 10 cm
(takega si lahko privošči vsak od nas), velja:
m = 6,5+5*log(10) = 6,5+5*1 = 11,5
S takim teleskopom lahko opazujemo že praktično vse
Messierjeve objekte (110 objektov, težave se lahko pojavijo pri M97, M76 ...).
Teleskop premera objektiva 20 cm pa ima mejno magnitudo blizu vrednosti
13 (teleskopi tipa Newton premera objektiva 20 cm so, glede na zmerno
ceno in še znosno prenosljivost ter solidno optično zmogljivost, zelo popularni
med zagnanimi amaterji).
LOČLJIVOST TELESKOPA
Pri teleskopih sta pomembna stabilna montaža (stojalo) in kar se da velik premer
objektiva, večji je, večja je ločljivost podob, ki jih opazujemo ali slikamo,
več svetlobe zbere objektiv in svetlejša je slika. Ločljivosti objektiva se
približno izračuna po formuli φ = 140/Dv_mm ['']. D je premer objektiva v mm.
Tako ima teleskop premera 140 mm ločljivost φ = 140''/140 = 1 '', to je ena
ločna sekunda. Ta podatek nam pove, da bomo recimo lahko med sabo ločili zvezde,
ki so narazen vsaj ločno sekundo. Večja je ločljivost več podrobnosti vidimo
na zvezdnem nebu, na planetih, Luni ... Korektna formula za ločljivost teleskopa
je φ = 1,22*λ/D,
odvisna je torej od premera objektiva D in valovne dolžine vpadne svetlobe λ.
Povečave teleskopa omejujeta dva faktorja, premer objektiva (večinoma se pri
teleskopih dopušča povečava do številke, ki je 2x premer objektiva v mm,
torej 200 mm-ski objektiv dopušča še smiselne povečave do okrog 400x)
in drugi faktor je nemirnost ozračja (različne gostote zraka, turbulence,
vetrovi, vzgon ... povzročijo lom svetlobe v različnih plasteh ozračja,
to vidimo kot migetanje in s tem neostro sliko).
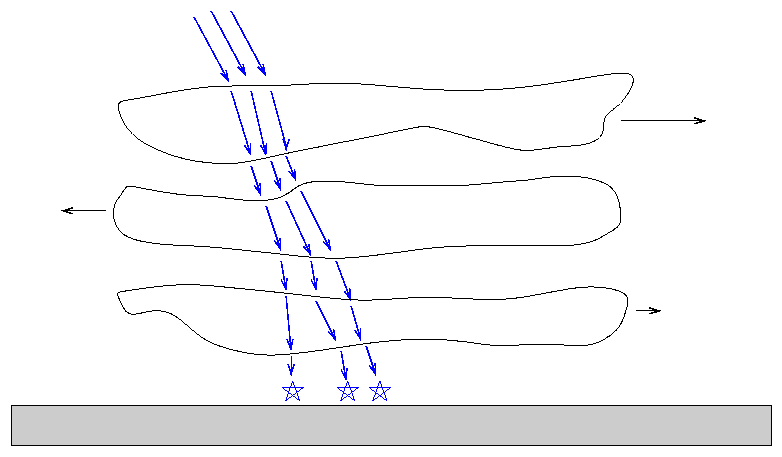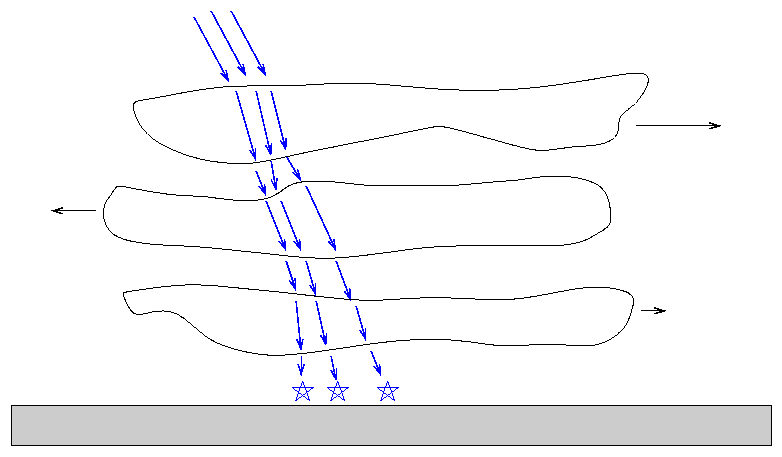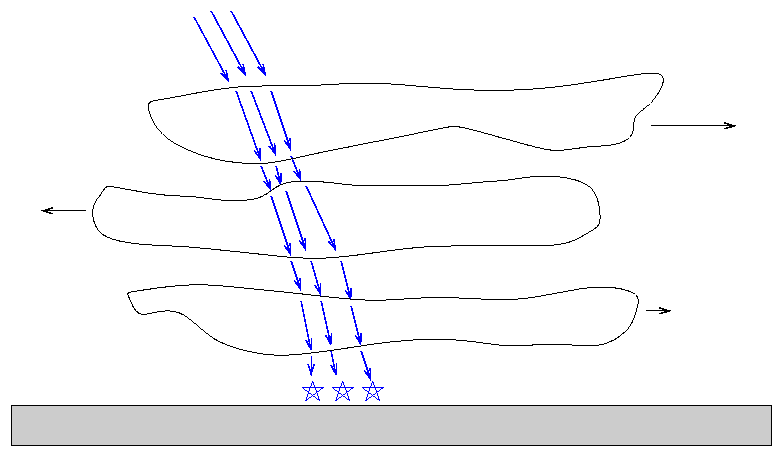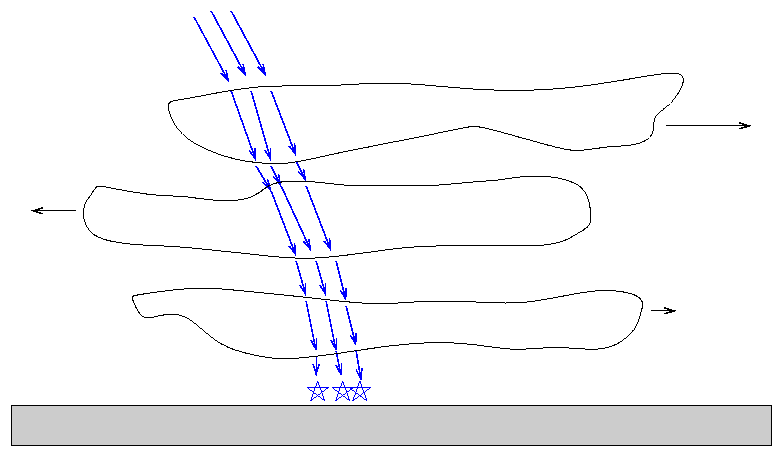
Pri zelo nemirnem ozračju
so smiselne povečave le okrog 100x, pri zelo stabilnih razmerah (v naših
krajih je to v mrzlem delu leta - večinoma februarja) pa so uporabne tudi
povečave do 600x (nekajkrat na leto). Zaradi motenj atmosfere, se poklicni
astronomi odločajo tudi za teleskope izstreljene v orbite nad atmosfero Zemlje.
Najbolj znan teleskop (do leta 2021) v orbiti Zemlje je Hubble
(HST - približno 539 km nad
površjem, premer zrcala je 2,4 m, goriščna razdalja pa kar 57,6 m, tip reflektor
Ritchey–Chrétien – njegovi rezultati so presegli vsa pričakovanja, z njim vidimo
praktično do vidnega horizonta vesolja, do območij, ki so od Zemlje oddaljene več
kot 13,4 milijarde svetlobnih let – torej vidimo v preteklost skoraj do začetkov
vesolja, glejte:
https://www.rmg.co.uk/stories/topics/what-has-hubble-space-telescope-discovered
).
Že skoraj od naše mladosti pa smo čakali na izstrelitev vesoljskega teleskopa James
Webb (JWST – premera 6,5 m, bo pa nameščen v Lagrangejevi točki L2, torej
na premici, ki jo določata središči Sonca in Zemlje, L2 leži za manjšo Zemljo).
No 25. 12. 2021 pa smo le dočakali uspešno izstrelitev teleskopa James
Webb, ki daje izjemne rezultate.
Največji teleskop gradi ESO v puščavi Atacama, Čile – ELT
(Extremely Large Telescope - 39.3 m premera).
Še glede goriščnega
razmerja teleskopov in vidnega (zornega) polja.
Kvocient med goriščno razdaljo f objektiva in
premerom D, se imenuje goriščno razmerje – tudi zaslonka ali
relativna odprtina 1/(f/D). Recimo - goriščno razmerje f/D = 5
pove, da teleskop spada med hitre, da ima veliko vidno polje in svetlo
sliko (a seveda manjšo s = φ*f) – pri fotografiranju so zato časi krajši.
Goriščno razmerje f/D = 5
ali manj tudi pomeni, da so taki teleskopi, same optične cevi krajše in s tem bolj
mobilne – in prav te lastnosti išče večina amaterjev. Goriščno razmerje
okrog f/D = 10 je večinoma značilno za refraktorje in skrajšane cevi
Ritchey–Chrétien ter katadioptrične teleskope Schmidt-Cassegrain, Maksutov,
Klevtsov (vsi ti teleskopi imajo skrajšane cevi na račun sekundarnega zrcala,
ki svetlobo odbije skozi središčno odprtino primarnega zrcala, objektiva –
razlikujejo se le po oblikah zrcal in katadioptrični še po načinu korekcije
preslikave z dodatnimi lečami).
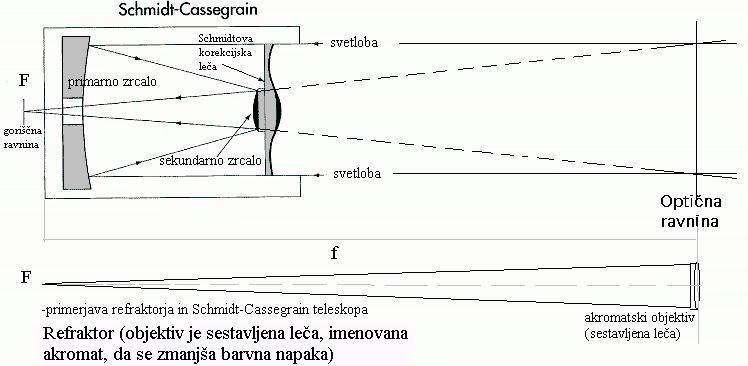
Katadioptrični teleskopi (Schmidt-Cassegrain, Maksutov, Klevtsov) imajo
skrajšane cevi na račun izbočenega sekundarnega zrcala, ki svetlobo odbije
skozi središčno odprtino primarnega zrcala, objektiva (navidezna optična
ravnina je zato precej pred cevjo). Razlikujejo se le po oblikah zrcal in
po načinu korekcije preslikave z dodatnimi lečami. Ritchey–Chrétien ima enako
zgradbo, le da nima korekcijskih leč (obe zrcali sta hiperbolične oblike)
- zato spada med teleskope z najmanj popačeno sliko, najmanj kome
(zvezdnih repkov).
Povejmo še, da je veliko lažje doseči večje povečave, kot manjše (zaradi zgradbe okularjev in želje po dovolj velikih poljih). Efektivno polje teleskopa (FOV - field of view) je kvocient med lastnim vidnim poljem okularja in povečavo. Primer za gorišče 750 mm in okular 25 mm z vidnim poljem 60 ° da efektivno polje teleskopa – za ta okular: FOV = 60 °/(750/25) = 60 °/30 = 2 °. Dve stopinji polja pri povečavi 30x je zelo razkošna podoba neba – v to polje lahko ujamemo skoraj celotno nam sosednjo galaksijo M31 v smeri ozvezdja Andromede, potem Plejade in tudi razkošne meglice in kopice Rimske ceste. Če ima tak teleskop premer objektiva D = 150 mm, dobimo tudi zelo svetlo sliko, saj ima goriščno razmerje f/D = 750 mm/150 mm = 5 in izstopno zenico 5 mm (150 mm/30 = 5 mm). Hkrati pa z okularjem gorišča 5 mm lahko dosežemo povečave M = 750 mm/5 mm = 150x – kar je že zelo spodobna povečava za planete, tesne dvojne zvezde, za Luno ...
Za zaključek tega hitrega pregleda optike, nakažimo še, kaj je v ozadju omejene ločljivosti teleskopov – zadaj je namreč univerzalni princip delovanja narave, to je valovanje. Svetloba (elektromagnetno valovanje) se namreč na objektivu ukloni in ti uklonski koti so manjši (kar je ugodno) na večjih objektivih in je zatorej pri večjih teleskopih slika zaradi interference (seštevanja uklonjenih valov svetlobe) manj deformirana, bolj jasna. Na oddaljenih zvezdah (razen na Soncu z uporabo filtrov) pa tudi s teleskopom ne moremo ujeti površinskih podrobnosti – zakaj se nam torej nekatere zvezde zdijo večje? Tiste, ki močneje svetijo, naredijo višji (širši) uklonski maksimum svetlobe na mrežnici (uklon na objektivu teleskopa in zenici očesa). Lepote nočnega zvezdnega neba so torej uklonski maksimumi valovanj, različno močnih točkastih izvirov svetlobe, zvezd na mrežnici (ne zveni romantično ali pač). To je seveda fizikalno-fiziološki pogled na vesolje, ki pa je s stališča razumevanja opazovanja vesolja ključen pri razlagi videnega, posnetega. Valovanje je v bistvu podlaga za vsakršno komunikacijo, tako med ljudmi in ostalo naravo (zvok, svetloba), kot med vesoljem in človekom (svetloba iz vesolja nam razkriva spektre zvezd, tudi eksoplanetov in s tem kemično sestavo oddaljenih svetov, ki jih fizično nikoli ne bomo dosegli, a vemo, da so sestavljeni iz enakih elementov kot življenje na Zemlji, tukaj je še izjemno pomemben Dopplerjev premik in sklepanje na širjenje vesolja in še in še bi lahko naštevali). Je pa danes zmeraj bolj očitno, da je tudi t. i. materija (osnovni delci, protoni, kvarki ..., torej tudi mi sami) večinoma odraz različne kombinacije »valovnih paketov«.
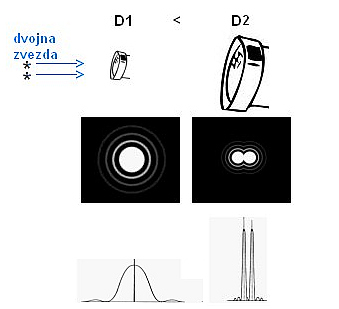
Zgornja slika prikazuje, zakaj z manjšimi teleskopi ne ločimo nekaterih tesnih
dvojnih zvezd, recimo Gama Andromede ali Epsilon Lire 1 in 2 ali na površini
planetov ne zaznamo nekaterih površinskih detajlov. Pri majhnih teleskopih
(premerih) je uklon svetlobe zvezd na objektivu tako velik, da se sliki tesnih
zvezd prekrijeta (prekrijeta se Airyjeva uklonska diska), pri večjih pa ne.
Zaključimo tole razglabljanje z ugotovitvijo, da je glavna prednost uporabe teleskopov za opazovanje nebesnih teles v primerjavi s prostim očesom ta, da s teleskopom vidimo telesa, ki jih s prostim očesom na vidimo (večja mejna magnituda, lahko jih tudi slikamo, pomerimo njihove spektre iz katerih izluščimo sestavo teles, temperaturo, hitrosti ...), in da zaradi večje povečave in premera objektiva teleskopa dosežemo veliko večjo ločljivost slike. Recimo ob Saturnu s prostim očesom ne zaznamo obročkov, prstanov, na Jupitru ne zaznamo atmosferskih prog, rdeče pege, večinoma tudi ne štirih Jupitrovih svetlejših lun, in še bi lahko naštevali izjemne podobe Sonca, Lune, meglic, kopic, galaksij, dvojnih zvezd, kometov, asteroidov ..., IN vse to nam omogočajo teleskopi.
Radijska astronomija
Kaj povedati o radijski astronomiji, zagotovo je zelo pomembna veja astronomije,
sploh pa je sestavljena (interferometrična) slika radijskih teleskopov veliko
ločljivejša od slike, ki jo dajo teleskopi v vidnem delu spektra, z njimi smo
ujeli akrecijske diske mladih planetnih sistemov (ALMA radijsko polje teleskopov
v Čilu), potem slika supermasivne črne luknje v jedru galaksije Messier
87 z maso reda velikosti nekaj milijard Sonc ... Vsekakor se iz te
tematike izvede vaja. Ker šole nimajo radijskih teleskopov, se lahko
pokaže Dopplerjev premik vodikove črte 21,106 cm različnih rokavov
naše galaksije iz meritev šentviškega radijskega teleskopa (ali kakega drugega).

Težko bi našli bolj pedagoško sliko, kot je tale slika HD 163296: curek iz zvezde
v nastajanju. Združuje vidno svetlobo izvrženega curka zvezde in sliko planetarnega
diska v radijskih valovih – kakšna moč, razločljivost radijske astronomije.
Nihče ni prepričan, da ve kako nastajajo taki curki med nastajanjem zvezd,
čeprav so nedavne slike mladega zvezdnega sistema HD 163296 precej nazorne.
Osrednja zvezda na predstavljeni sliki se še vedno oblikuje, vendar je že
obdana z vrtljivim diskom in navzven gibljivim curkom. Disk je prikazan v
radijskih valovih, ki jih je posnel Atacama Large Millimeter Array (ALMA)
v Čilu in prikazuje vrzeli, ki jih verjetno ustvarja gravitacija zelo mladih
planetov. Curek, prikazan v vidni svetlobi, ki ga je posnel zelo velik teleskop
(VLT, tudi v Čilu), iz središča diska izžene hitri plin - večinoma vodik.
Sistem se razteza na stotine krat večjo razdaljo od Zemlje do Sonca (AU).
Podrobnosti o teh novih opazovanjih se razlagajo kot podkrepitvena ugibanja,
da curke vsaj delno ustvarjajo in oblikujejo magnetna polja v vrtljivem
disku. Bodoča opazovanjih HD 163296 in drugih podobnih sistemov nastanka
zvezd lahko pomagajo pri ugotavljanju nastanka zvezd, planetov in življenja.
Vir: apod.
Oprema, ki jo priporočamo učencem
Ali učencem priporočimo nakup astronomske opreme, katere in kdaj? Vsekakor
to lahko storimo za manjše in srednje teleskope od 100 do 150 mm
(130 do 300 EUR) in sicer kmalu po uvodnih urah (a naj prej testirajo
šolsko opremo, da se lažje odločijo – a o morebitnem nakupu odločajo
učenci, brez vsake obveze). Krasno bi bilo, če bi se dalo opremo tudi
sposoditi na šoli.
Uvod v vprašanje: zakaj smo in koliko časa še bomo?
Koliko časa posvetiti eni najbolj vznemirljivih tem, ki privlači
večino mladih, tudi tiste, ki jih sama astronomija ne zanima toliko
- življenju v vesolju. Morebiti bi ta tema lahko bila celo jedro naših
prizadevanj pri predmetu astronomija.
Kajti če hočemo odgovoriti na to vprašanje, moramo vedeti, kako je nastala Zemlja
in kaj vse se je moralo zgoditi prej, da smo danes mi tukaj in
razmišljamo o vesolju ...
In
če je življenje tudi drugje v vesolju, zakaj
imamo težave z zaznavanjem le tega?
Ali kaj povedati o Drakovi enačbi?
Kateri so torej pogoji za »biti ali ne biti« v vesolju; to, da smo, ni
samoumevno? Ali je smiselno posebno poglavje - položaj Zemlje in človeka
v vesolju – naš odgovor je vsekakor JA. Ta sklop je multidisciplinaren.
Vanj - v ta kontekst spada tudi
huronska poledenitev, podnebne spremembe, vloga kisika, oksigenacija
Zemlje, časovnica nastanka življenja, rastlin, živali, vretenčarjev,
primatov - človeka.
O atmosferi, oceanih, seveda o Sončevi energiji kot o generatorju podnebja
na našem planetu in o bistvenem vplivu samega življenja na podnebje,
je potrebno govoriti celostno – to je podrobneje razdelano v naslednjih
poglavjih. Na tem mestu podajmo še informacijo o pozabljeni podnebni
katastrofi med letoma 1876 – 1878.
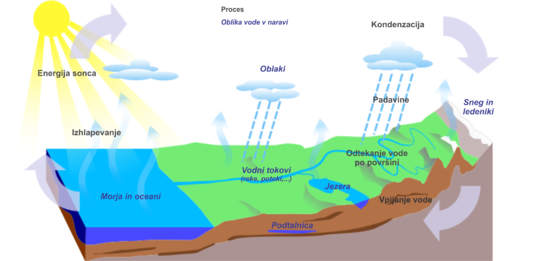
Shema kroženja vode v naravi - Sonce je glavni vir energije za ta izjemen proces,
ki ohranja naš planet v modrini življenja.
Oceani so stalen vir vodne pare, ki z njihovega površja neprenehoma izhlapeva.
Vode v oceanih je veliko več kot v ozračju (skupna masa vode v oceanih je približno
105-krat večja, kot je skupna masa vodne pare v ozračju). Ob primernih pogojih
vodna para v ozračju kondenzira in pade na tla v obliki padavin. Tako se lahko
vrne v oceane in tvori vodni krog. Na Zemlji so tudi ravno prave temperaturne
razmere
(temperature niso zelo daleč od temperature trojne točke vode), ki omogočajo
hkraten obstoj vodne pare, tekoče vode in ledu.
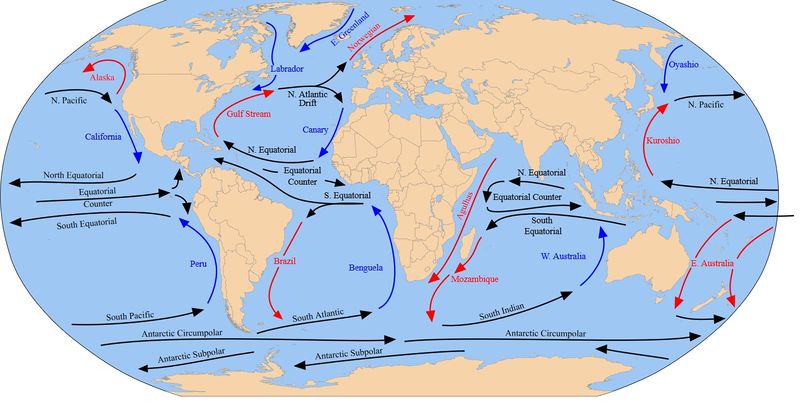
Oceanski površinski tokovi (so posledica vetrov, Coriolisove sile,
temperaturnih razlik ...) – so poleg Sonca, glavni generatorji
vremenskih dogajanj na Zemlji (zaradi vpliva vetra segajo 200 m
globoko, zaradi Coriolisove sile tudi do globine 1000 m in več –
obstajajo pa tudi globinski termohalinski tokovi do globine 3 km -
hladna, težja voda potone in se večinoma premika proti tropom).
Če se površinski tokovi zgolj rahlo spremenijo, lahko, zaradi
suše v prej deževnih pokrajinah, trpi do 4 milijarde ljudi.
Posledice nihanj oceanskih cirkulacij so bile včasih pogubne
za desetine milijonov ljudi. Voda nam vse da, a lahko tudi
vse vzame ...
Oceani so torej povzročili tudi veliko (skoraj globalno) sušo v
letih 1876 – 1878. Tihi ocen je predhodno zajelo dolgo obdobje
nizkih temperatur (1870 - 1876), kar je vplivalo na energijsko
bilanco globalne cirkulacije morskih tokov (le ti generirajo
smeri vetrov in s tem vreme, padavine). To dogajanje je oslabilo
zimski monsun v Indiji – ki je tako prejela manj padavin.
1877 pa se je zgodil preobrat, druga skrajnost, začne se vroče
obdobje nad Tihim oceanom (pojavijo se izraziti topli morski
tokovi proti Južni Ameriki - temperature morske površine so ostale
visoke kar 16 mesecev), kar pomeni začetek izrazitega El Nina,
ki prepreči kar dva monsuna v Aziji (topel oceanski tok, ki se
pojavi ob zahodnih obalah Južne Amerike, prinaša s sabo mokro
in deževno vreme ter poplave na sicer suhih območjih Južne Amerike,
a hkrati sušno obdobje na zahodnem delu Pacifika, v Aziji, Indoneziji ...).
V Pokrajini Šansi (Kitajska) od 1877 do 1878 ni padla niti kaplja dežja.
V Aziji je to bila najbolj obsežna suša v zadnjih 800 letih. Leta 1877
pa se je v severnem Atlantiku pojavila še dolgotrajna vroča anomalija
(topla voda), na območju Indijskega ocena pa je nastal t. i.
temperaturni dipol (ob obalah Somalije se je namreč ocen nadpovprečno segrel,
vode ob zahodnih obalah Avstralije pa so se izrazito ohladile). Nedavne
raziskave so pokazale, da se anomalije v temperaturah oceanske površinske
vode (od 2 do 8 °C višje temperature) pojavljajo v nepravilnih časovnih
presledkih 3 do 5 let (a v letih od 1875 do 1878 pa je prišlo celo do
sočasnih neljubih dogodkov, temperaturnih anomalij v vseh treh velikih
oceanih).
Podnebne razmere, ki so povzročile takratno veliko sušo in globalno lakoto,
so nastale zaradi naravnih variabilnosti in njihovega ponavljanja.
S kombincijo hidroloških vplivov, ki jih globalno segrevanje lahko še okrepi,
bi lahko ponovna sočasnost anomalij spet ogrozila svetovno varnost glede
preskrbe s hrano.
Primer pa kaže, da je naš planet, že pred zadnjimi brutalnimi posegi človeka
v okolje, bil globalno podnebno zelo ranljiv. A kot nam sporoča zgodovina
zadnjih nekaj tisoč let, se porušeni podnebni vzorci po nekaj letih spet
vrnejo v "utečene" cirkulacije (oceanski tokovi se stabilizirajo).
To kažejo tudi vzorci poselitev - kjer ni padavin ni civilizacij
in obratno. A na skali nekaj 1000 let se lokalni vremenski vzorci
lahko radikalno spremenijo - poznamo primere recimo iz severne Afrike,
Grenlandije, Južne Amerike. Velik del vplivov na vreme pripisujemo
nebesni mehaniki (obliki Zemljine tirnice), izsevu Sonca, vulkanski
dejavnosti, potresom - cunamijem, tudi seveda trkom z asteroidi in
zmeraj bolj življenju - človeku (tukaj je obdobje antropocena,
holocen naj bi se že končal). A kot smo že večkrat omenili, je
bistveno na vreme (atmosfero) vplival sam pojav življenja –
fotosinteza je dobesedno spremenila sestavo ozračja – na začetku
v ozračju praktično ni bilo kisika in s tem je življenje neposredno
trasiralo pot današnji klimi (trenutni »idilični« podobi našega
planeta – seveda preko izjemnih nihanj temperatur skozi zgodovino
in velikega števila izumrlih vrst).
Podobna podnebna katastrofa bi se lahko zgodila recimo v letih 1997-98 (El Nino, a se ne da po trajanju in intenzivnosti primerjati z dogodki iz let 1877-78). A se je tokrat globaliziran svet glede distribucije hrane le izkazal v pozitivni luči (dostava hrane, vode, v modernem svetu deluje globalno precej bolje kot pred 150 leti). Vprašanje pa je, kaj bi se zgodilo – če bi vsi trije oceani spet doživeli sočasno temperaturno anomalijo velikosti iz let 1870-78.

Od leta 1875 do 1878 so sočasne večletne suše v Aziji, Braziliji in Afriki,
imenovane Velika suša, povzročile ekstremno skromne pridelke, pomanjkanje hrane,
kar je povzročilo tako imenovano globalno lakoto, ki je imela za posledico do
50 milijonov smrtnih žrtev in dolgotrajne družbene posledice.
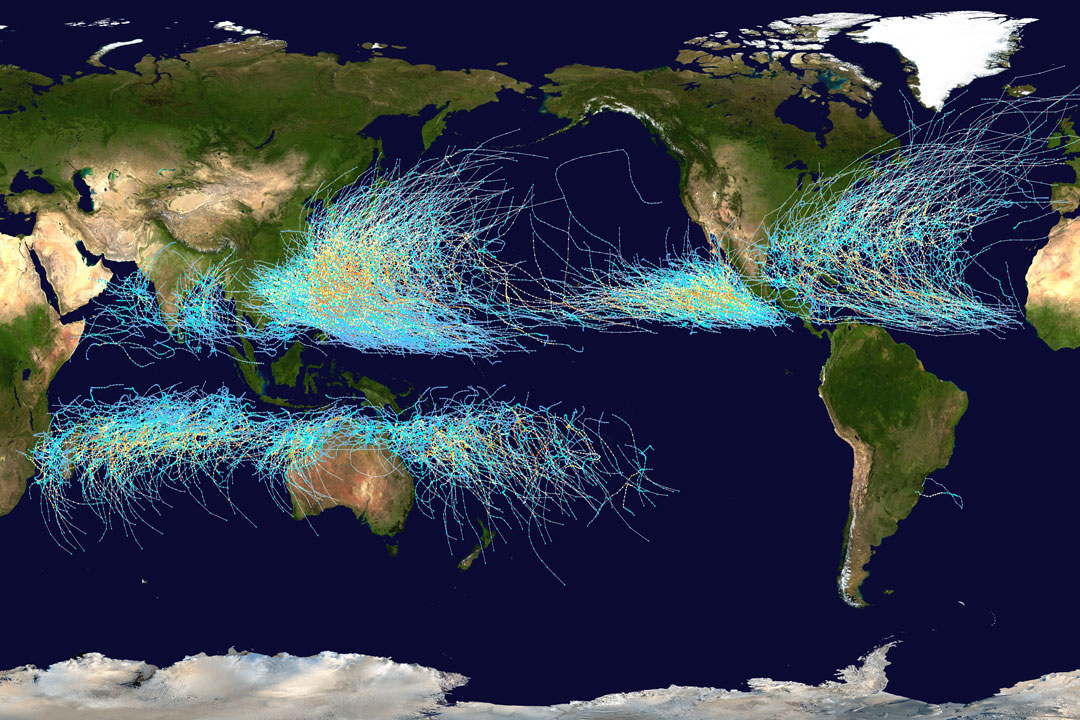
Vir: apod
Pot orkanov (Atlantik) in tajfunov (Tihi ocean). Karta prikazuje poti
vseh večjih neviht od 1985 do konca 2005. Ti izraziti cikloni se
običajno pojavljajo nad vodo (temperature vsaj okrog 27 °C),
saj jim izhlapevanje tople vode daje energijo. Cikloni tudi nikoli
ne prečkajo ali se le redko približajo Zemljinemu ekvatorju, saj
se tam Coriolisova sila zmanjša na ničlo (velja za horizontalne hitrosti) -
prav ta sila pa ciklone, rotacijo, tudi povzroča. Coriolisova sila pa tudi
posredno odkloni ciklonske poti proč od ekvatorja, beta efekt odkloni
ciklon proti zahodu in delno severno (na ekvatorju, kot smo že omenili,
pa se cikloni sploh ne morejo tvoriti). Orkani so v zadnjih 30 letih v
severnem Atlantiku v povprečju postali nekoliko močnejši, njihova moč
pa naj bi se še stopnjevala. Višje temperature pomenijo več energije
v zraku (mv2 ∝ kT), višje hitrosti vetrov, več vlage v zraku nad
vodnatimi predeli Zemlje, te oblake pa vetrovi prenesejo nad kopno ...,
področja brez prehoda vremenskih front pa tako postajajo še bolj suha.
Seveda moramo priznati, da napovedovanja vremena delno spada tudi pod teorijo
kaosa. Le ta proučuje obnašanje dinamičnih sistemov, ki so zelo občutljivi na
začetne pogoje (recimo na temperaturo, tlak, vlago ...), kjer je veliko
nelinearnosti – pogosto se kot primer navaja »metuljev učinek«
(To ugotovitev je matematik in meteorolog Edward Norton Lorenz
na predavanju leta 1972 slikovito povzel v vprašanju: »Ali lahko
utrip metuljevih kril v Braziliji sproži tornado v Teksasu?«).
Podobno velja za dinamične procese znotraj galaksij, akrecijskih
diskov, planetnih sistemov, pri napovedovanju nastanka življenja
tam daleč v času in prostoru. Majhne razlike v začetnih pogojih
(kot so recimo že tiste pri zaokroževanju pri računanju) ustvarijo
veliko razliko v napovedanem obnašanju takšnih dinamičnih sistemov,
kar na splošno vodi v nezmožnost dolgoročnega napovedovanja vremena
in ostalih kompleksnih dogajanj.
Tudi ta vidik znanosti je potrebno
predstaviti mladim. Tudi trki asteroidov v Zemljo so delno kaotični
procesi – vseh se ne da napovedati - zaradi stalnih motenj ostalih
teles v različnih orbitah. Sistem dveh teles večinoma znamo
rešiti – preko sil in ohranitvenih zakonov lahko dokaj solidno
napovemo njuno lego v bodočnosti (zato tudi zmoremo napovedovati
mrke stoletja naprej - tukaj se Sonce in Zemlja obravnavata ko
ločen sistem dveh teles, Luna pa zaradi manjše mase bistveno ne
vpliva na dinamiko obeh teles, je pa igralec pri mrkih – dolgoročno
temu seveda ni tako, vemo da Luna upočasnjuje čas rotacije Zemlje,
Zemlja pa Luno oddaljuje …, tukaj so še vplivi ostalih teles, planetov).
Pri sistemu več teles pa smo večinoma primorani na statistične prijeme,
poenostavitve, ko množico teles združimo v sisteme, ki jim določamo njihovo
notranjo dinamiko in večinoma zunanjo preko sil in energij, za pline uporabimo
plinsko enačbo …; recimo mešanici plinov - zraku – določimo hitrost in smer
gibanja preko vetra, hkrati pa njegovo temperaturo, tlak, gostoto kot rezultate
statistično opisanih dogajanj na nivoju atomov in molekul (a množica vplivov
na opazovani sistem, recimo na zrak, od zunaj in od znotraj je tako številna,
da nam recimo vremena - koliko bo recimo padavin in kje padlo iz tega zraka,
oblaka - ne uspe napovedati »zelo natančno« za več kot le nekaj dni – kljub
povečani zmogljivosti računalnikov; a vseeno meteorologija zelo pomaga ljudem,
recimo pri načrtovanju tedenskega življenja, pri gradnji infrastrukture pa le,
če upoštevamo meteorološke meritve (ekstreme, povratne dobe ...) - potem lahko
dosežemo tudi željeno varnost in trajnost izvedenih arhitekturnih posegov
v naravo – zadnje poplave v Ljubljani kažejo, da smo premalo pozorni na
upoštevanje meteoroloških ekstremov, ki jih lahko najde vsak učenec na spletu).
Zdi se, da je tudi velikan Jupiter na začetku razvoja Sončevega sistema zelo menjal
orbito, se približal Marsu in ga masno precej oskubil. Jupiter se je po simulacijah
premaknil navznoter do 1,5 AE od Sonca in se je nato zaradi nastajanja Saturna
sčasoma preselil navzven proti svoji trenutni lokaciji. Na tej poti je določil
porazdelitev snovi v notranjem Sončevem sistemu. Tako lahko pojasnimo
nepričakovano majhno maso Marsa in kompleksno sestavo asteroidnega pasu
(ki je zelo različen v sestavi, saj je Jupiter s sabo potegnil tudi
del stare snovi iz zunanjega dela planetne ravnine).
Se nadaljuje ...
Zorko Vičar
Korona pomlad 2021 (objavljeno mar. 2022),
v Spiki je bila objavljena nekoliko krajša verzija ...
DODATEK -....:
Še na kratko o oblakih, strelah in življenju
V oblakih se tvorijo različne oblike kondenzirane vlage. Običajno se v nevihtnem oblaku,
ena nad drugo, nahajajo različne oblike hidrometeorjev. Najniže so kapljice,
nad višino, na kateri je temperatura enaka ledišču, pa so podhlajene kapljice,
snežinke in drugi večji ledeni delci. Čisto na vrhu so manjši ledeni kristalčki.
Zdi se, da so v razvoju življenja, organskih molekul, pomembno vlogo odigrale tudi
razelektritve, strele (Miller–Ureyev poskus - ob zaključku poskusa je kar 15 odstotkov
ogljika iz mešanice tvorilo organske spojine, 2 odstotka ogljika pa aminokisline,
vsi ti produkti so gradniki življenja – tudi ponovljeni eksperimenti z drugačno
mešanico zraka so dali podobne rezultate). Kako nastanejo strele? Osnovni pogoj
za ločitev električnega naboja v oblaku je trenje, ki ga povzročajo močni vrtinci
znotraj kumulonimbusnega oblaka, katerih hitrosti znašajo 5-20 m/s ali več. Težja
ledena zrna v oblaku, ki padajo se hkrati drgnejo ob dvigajoče lahke ledene kristale
(ki so hkrati dipoli (+ -) ). Vemo, da so nevihtni oblaki posledica vzgona - topel
redkejši zrak se dviga, saj z višino temperatura večinoma pada, in če je v zraku dovolj
vlage, le ta kondenzira in nastane oblak, ki ga sestavljajo kapljice, lahki ledeni kristali,
večja ledena zrna. Večja ledena zrna pri preseganju določene mase začnejo padati -
ko se poruši ravnotežje med uporom vertikalnih vetrov in težo zrn. Lahki dvigajoči
kristali zaradi trenja (rahlih trkov) postanejo tako pozitivni, težja ledena padajoča
zrna pa negativna. Do prehoda nabojev (elektronov) prihaja, ker nekateri atomi in molekule
(snovi, kristali) manj vežejo elektronsko ovojnico nase kot drugi in ob stiku obeh delcev
(snovi) pride do prehoda elektronov. Ko se nakopiči dovolj ločenega naboja, se električna
napetost poveča do te mere, da pride do električnega preboja (izenačenja naboja preko
izrazitih tokov) – udara strele, pri kateri se zrak v prevodnem kanalu segreje tudi čez
50000 K – posledično hitro naraste tlak segretega zraka, kar slišimo kot grmenje, ki ga
seveda spremlja še bliskanje. Še fosforju, gradniku ATP in DNK ter strelah - Isaac Asimov
je fosfor nekoč imenoval "ozko grlo življenja", ker predstavlja 1 odstotek organizma,
vendar je prisoten le v 0,1 odstotku mineralov na Zemlji. Zadnje raziskave kažejo,
da visoke energije udara strel ustvarjajo preko fulguritov (staljene tvorbe zaradi
udarov strel v tla) spojine fosforja, ki so bile nekoč pogoste na Zemlji in so omogočale
preprosto življenje in še danes številni mikrobi uporabljajo to obliko vezanega fosforja
(Fe3P in CaHPO3).
Tudi dušik je gradnik beljakovin in DNK. Strele razbijejo dušikove molekule
in tudi poskrbijo, da nastanejo reaktivni dušikovi oksidi (NO in NO2).
Te okside so lahko
uporabljali zgodnji mikrobi (ko prostega kisika še ni bilo). Velik pomen imajo tudi vulkani
pri nastanku življenja – kemija vulkanov omogoča posebne oblike življenja (recimo nitasta
bakterija "lasje Venere", "Venus' hair") – vulkani so preko CO2
naš planet tudi rešili
dolge huronske poledenitve.
Coriolisova sila
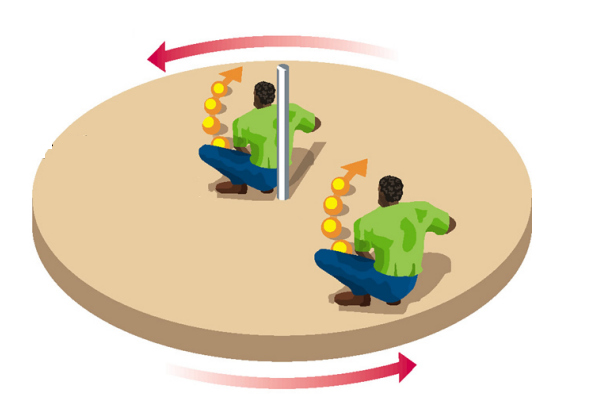
Coriolisova sila je sistemska sila na rotirajočem sistemu - na rotirajoči plošči
se recimo pot kotaleče žoge ukrivi.

Coriolisova sila je sistemska sila, ki jo čuti gibajoče telo na rotirajočem sistemu
(recimo atmosfera, vodni tokovi na Zemlji, zaradi te sile nastanejo tudi konvekcijski
vrtinci tekoče kovine v Zemljinem zunanjem jedru, ki jih poganja toplotni tok iz
notranjega jedra – pozitivna posledica je magnetno polje, ki varuje Zemljo pred
hitrim Sončevim vetrom nabitih delcev). Coriolisova sila deluje pravokotno na smer
gibanja (na severni polobli Zemlje desno od smeri gibanja). Če recimo hodimo po
rotirajoči plošči, se kar ne znajdemo, ker se nam tla spodmikajo – to zagato
slikovito ponazarja zgornja karikatura.
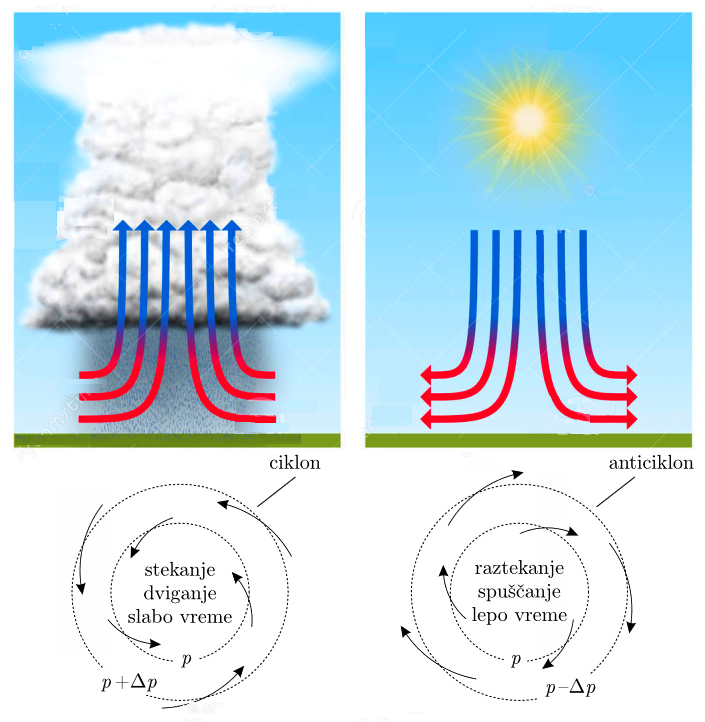
Coriolisova sila zavrtinči zrak v ciklonih v nasprotni smeri urinih
kazalcev – severna polobla (zrak se steka v središče ciklona z nizkim prtiskom,
ki se nato dvigne in vlažen zrak se v višinah z nizko temperaturo kondenzira,
privede tudi do razpenjanja in zato še do dodatnega ohlajanja, nastanejo oblaki
in velikokrat padavine – leva slika). Coriolisova sila na severni polobli
v anticiklonih zavrtinči zrak v smeri urinih kazalcev - v anticiklonih zrak
odteka vstran iz področja visokega pritiska, zato se zrak sredi anticiklona
spušča, stiska, posledično segreva in šuši in to je področje sončnega, jasnega
vremena (desna slika).
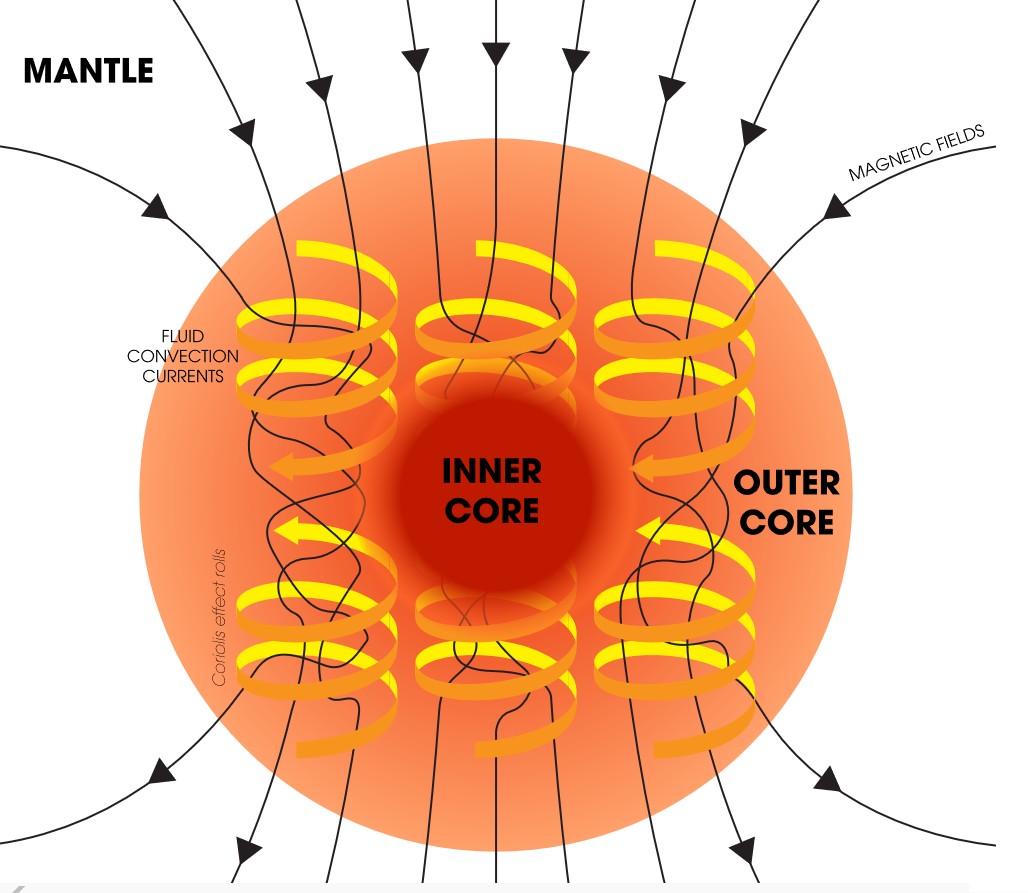
Vrtinčasto gibanje tekoče kovine (in s tem naboja) v zunanjem jedru zemlje povzroča
Coriolisova sila – posledica je magnetno polje.
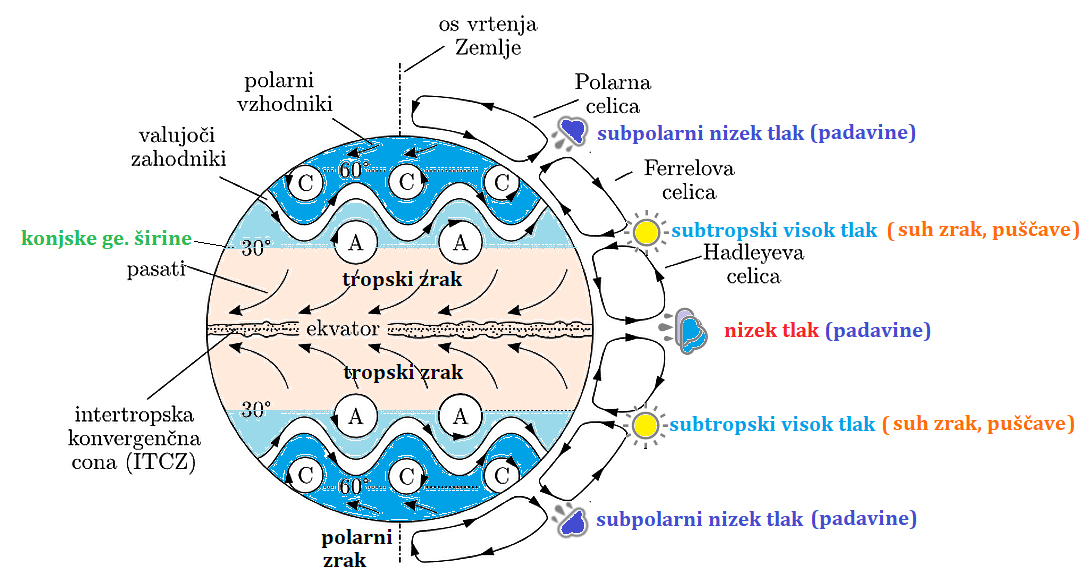
Groba shema globalne cirkulacije atmosfere. Oznaki C in A predstavljata ciklone (padavine,
nizek tlak – zrak se dviga, razpenja in vlaga kondenzira) in anticiklone (lepo vreme, visok
tlak – zrak odteka in se spušča, posledično se stiska, segreva in zato suši). Celoten
vremenski vzorec poganja seveda energija Sonca – na vrh atmosfere pade gostota energijskega
toka blizu 1400 W/m2. Od tega energijskega toka se globalno od Zemlje odbije okrog 30 %.
Območja v neposredni bližini ekvatorja prejmejo največ sončnega sevanja in so najtoplejša.
Tam se zrak pri tleh steka z obeh polobel ter se dviguje v tako imenovani intertropski
konvergenčni coni (angl. Intertropical Convergence Zone ali ITCZ). ITCZ je območje zelo
pogoste proste konvekcije, oblačnosti in posledično padavin. V ITCZ pade znaten delež
globalnih padavin na Zemlji. Lokacija ITCZ se spreminja glede na letne čase (v času
poletja na severni polobli je bolj severno, pozimi pa bolj južno), na njeno obliko
pa precej vpliva tudi razporeditev kopnega. Dviganje zraka v ITCZ povzroči, da v višinah
zrak odteka proti poloma. Zaradi Coriolisove sile, ki tok odklanja vstran (proti zahodu),
pa se tok proti poloma prekine in razklopi (pri približno ge. š. 30 °, to je t. i. konjska
zemljepisna širina), pri čemer nastanejo tri značilne celice. Hadleyeva celica je sestavljena
iz dviganja v ITCZ, toka zraka proti poloma v višinah, spuščanja zraka pri približno 30 ° ter
stekanja zraka proti ITCZ v spodnjih plasteh ozračja. Posledica stekanja so pasati.
To so prevladujoči dokaj stabilni severovzhodni in jugovzhodni prizemni vetrovi v
tropskih predelih, ki pihajo blizu tal od 30 ° ge. širine proti ekvatorju, oziroma
ITCZ in se obrnejo proti zahodu – Coriolisova sila (z njimi so pred stoletji Evropejci
jadrali v Ameriko, so tudi krmilni vetrovi za tropske nevihte, prenašajo tudi saharski
pesek, bogat z nitrati in fosfati, v vso Latinsko Ameriko, Karibsko morje ter v dele
jugovzhodne in jugozahodne Severne Amerike). Zaradi prevladujočega spuščanja zraka so
pri 30 ° velika območja puščav. Na primer, na severni polobli so Sahara, puščave
v Mehiki in ZDA ter Arabska puščava, na južni polobli pa Atakama (raj za astronome),
Namib, Kalahari ter puščave v Avstraliji. Polarna celica nastane v polarnih predelih,
pri čemer se nad poloma zrak spušča, pri približno 60 ° pa dviga (področje padavin),
vmes pa blizu tal pihajo polarni vzhodniki. Med Hadleyevo in polarno celico je
območje Ferrelove celice, v kateri prevladujejo valujoči zahodniki (spet zaradi
Coriolisove sile - strokovno pravimo valujočim zahodnikom Rossbyjevi valovi).
Ti valovi v zahodniku se imenujejo Rossbyjevi ali planetarni
valovi in njihova tipična valovna dolžina je nekaj tisoč kilometrov. Rossbyjevi
valovi se najpogosteje premikajo proti vzhodu, lahko pa so tudi stacionarni,
ko se nad nekim geografskim območjem dlje časa vzdržuje enaka vremenska situacija
(blokada).
Med valovi se na obeh straneh pojavljajo veliki vrtinci v toku zraka, pri čemer
se na polarni strani običajno pojavljajo cikloni, na ekvatorialni strani pa anticikloni.
V primerjavi s to idealizirano situacijo, je v realnosti globalna cirkulacija precej
bolj zapletena. Velik vpliv na cirkulacija ima kopno, ki lahko, prek vpliva orografije
ali zaradi različne temperature površja v primerjavi z oceani, precej spremeni globalni
tok zraka. Ogromen vpliv ima seveda tudi neenakomerna temperatura površin oceanov, ki
nastane zaradi gibanja vode - morskih tokov.
Konjske zemljepisne širine (zanimivo ime) so nekje med 25 ° in 35 ° ge. širine severno in južno od ekvatorja. Zanje je večinoma značilno sončno vreme, malo vetra in posledično zelo malo padavin. To je območje z visokim tlakom, kjer se razhajajo pasatni (severovzhodni) in zahodni vetrovi. Ena od razlag za tako ime je, da so se ladje (pred stoletji španske, portugalske ...) na tej zemljepisni širini brezveterja pogosto ustavile sredi oceana in tako kdaj zelo podaljšale potovanje. Posledično je pomanjkanje vode posadkam kdaj žal onemogočilo ohranjanje konj pri življenju (vozili so jih v Južno Ameriko) in so zato umirajoče živali metali v morje.
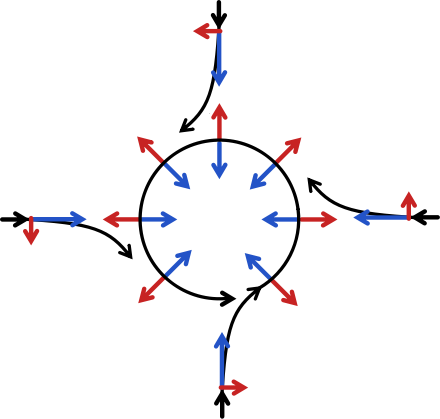

Shematski prikaz toka okoli območja nizkega tlaka na severni polobli (nastanek ciklona).
Sila gradienta tlaka je predstavljena z modrimi puščicami, Coriolisov pospešek (vedno
pravokoten na hitrost) pa z rdečimi puščicami. Tako se vzpostavi ravnovesje sil, ki
ustvari krožno gibanje ali ciklonski tok – to je v grobem ravnovesje med silo, ki kaže
proti središču in jo povzroča tlačna razlika (gradient) in Coriolisovo silo, ki deluje
stran od središča nizkega tlaka. Desno - sistem nizkega tlaka nad Islandijo (ciklon) se
vrti v nasprotni smeri urinega kazalca zaradi Coriolisove sile - sila zaradi gradienta
tlaka pa hoče zrak potisniti proti centru (tako se vzpostavi krožno ravnovesno gibanje).
Pri visokem tlaku, odtekanju zraka, lepo vreme (anticiklon), se smer rotacije obrne.
Južno od ekvatorja pa se cikloni vrtijo v smeri urinega kazalca.
Cikloni in anticikloni (tudi globalni oceanski tokovi) so torej še en dokaz rotacije Zemlje.
Rotacija Zemlje pa se da dokazati tudi preko zasuka ravnine nihanja – prvi je ta učinek uspešno
prikazal Foucault s svojim (Foucaultovim) nihalom leta 1851 v pariškem Panteonu (obiščite ga).
Rotacija Zemlje pa recimo med prostim padom povzroči tudi rahel zamik telesa
proti vzhodu.
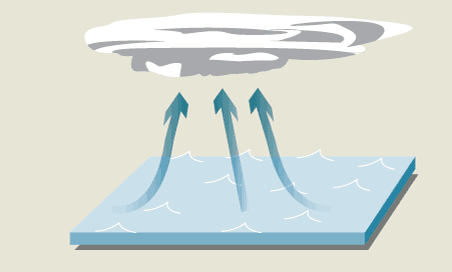
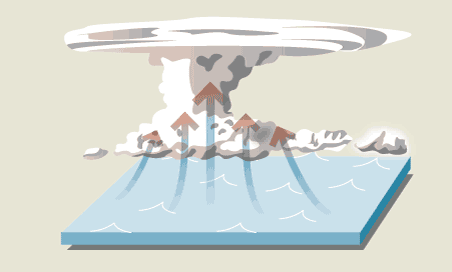
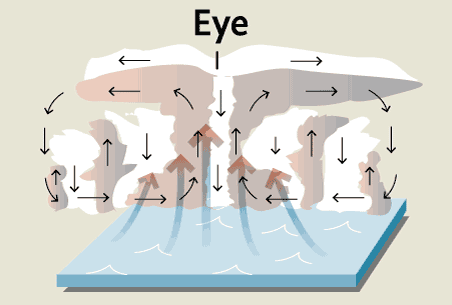
Tropski cikloni - tajfuni (orkani, hurikani, premerov od 150 km pa tudi več
kot 1000 km, celo 2000 km) se začnejo kot tropske nevihte, v območje nizkega
zračnega tlaka (tlak lahko dosega zgolj vrednosti 880 hPa) se zaradi tlačne
razlike steka zrak, ki se začne vrtinčiti (Coriolisova sila) in dvigati,
s sabo vleče toplo morsko paro – nastanejo oblaki (vlažen zrak se namreč
v višinah razpne, ohladi in posledično kondenzira). Močan veter vleče vlago
(energijo) iz oceanov. Nevihte torej pretvarjajo vlago v toploto, ki se sprošča
pri kondenzaciji. Toplota povzroči večji pretok zraka v središče nevihte, kar pa
povzroči izhlapevanje (nastane oko, lijak od 15 do 50 km premera, v katerem se
zrak spušča – in v samem očesu se ljudem zazdi, da je najhujše že mimo, a ni).
Vsa toplota in zrak, ki tečeta proti očesu ciklona (spiralno navzgor) ustvarita
super celico – tajfun, orkan ali hurikan. Tropski cikloni dosegajo hitrosti vetrov
do 300 km/h, sunki pa celo do 380 km/h (skoraj četrtino hitrosti zvoka).
V splošnem velja, da je Coriolisova sila vektorski produkt med kotno hitrostjo
in vektorjem hitrosti gibajočega se telesa na vrtečem sistemu - pomnožen z dvakrat
maso telesa:
Fco = acom = -2ωxvm,
negativni znak je značilen za sistemsko silo (enako velja za sistemsko centrifugalno silo,
ki jo recimo čutimo v avtu na ovinku,
Fcf = - mv2/r
in nas vleče iz ovinka, zato minus;
da pa sploh lahko nek sistem kroži, pa nanj deluje centripetalna sila, ki kaže proti središču
kroženja, za točkasto telo velja
Fc = mv2/r).
Severno od ekvatorja torej Coriolisova
sila deluje desno na smer gibanja, južno od ekvatorja pa levo.
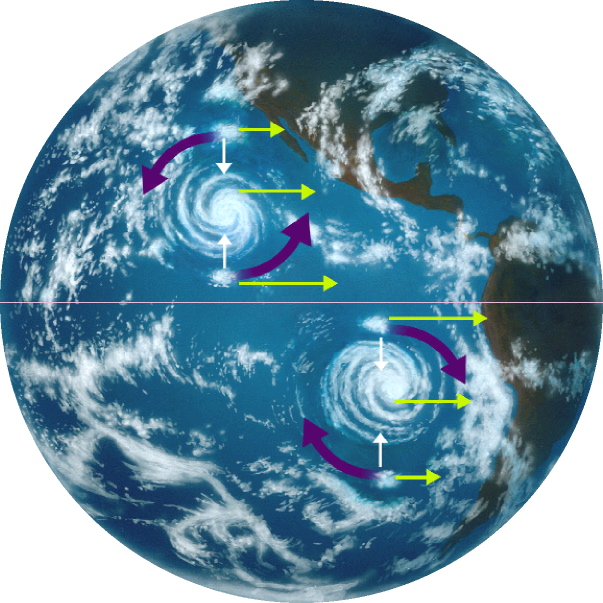
Severno od ekvatorja Coriolisova sila deluje desno na smer gibanja (cikloni se vrtijo
v nasprotni smeri urinih kazalcev), južno od ekvatorja pa levo (pod ekvatorjem se torej
cikloni vrtijo v smeri urinih kazalcev).
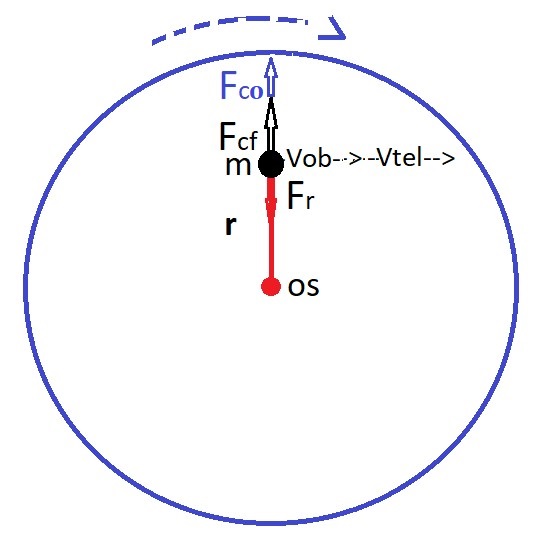
Vaja - oglejmo si Coriolisov pospešek zgolj pri krožnem gibanjem okoli osi vrtenja
na razdalji r, ko lahko za skupno hitrost seštejmo obhodno hitrost
vob in hitrost
telesa vtel glede na sistem, velja: v = vob + vtel.
Obhodna hitrost sistema na razdalji
r je:
vob = ωr.
Hitrost vstavimo v radialni pospešek, kaj dobimo:
ar = v2/r = (vob + vtel)2/r =
vob2/r + vtel2/r +
2vobvtel/r =
vob2/r + vtel2/r
+ 2ωvtel = ac + asis
+ aco
Sistemski pospešek je torej
asis = vtel2/r = ar -
vob2/r - 2ωvtel.
Kako interpretirati ta zapis? Na telo deluje centripetalna sila in
na vrtečem sistemu telo čuti še sistemski sili zaradi vrtenja
(prva je
večini poznana kot centrifugalna sila
Fcf = - mvob2/r
in druga je, zaradi
gibanja na vrtečem se sistemu, še Coriolisova sila
Fco = maco = - m2ωvtel
) –
obe sta pravokotni na hitrost. Splošna izpeljava je nekoliko bolj kompleksna
(iz pospeška, odvoda vektorskega izraza hitrosti sistema z dodatkom relativne
hitrosti
d(vtel + ωxr)/dt),
a na koncu je naš poseben rezultat enak splošnemu.
Korekten zapis Coriolisove sile je seveda vektorski:
Fco = acom = -2ωxvm = -2Ωxvm
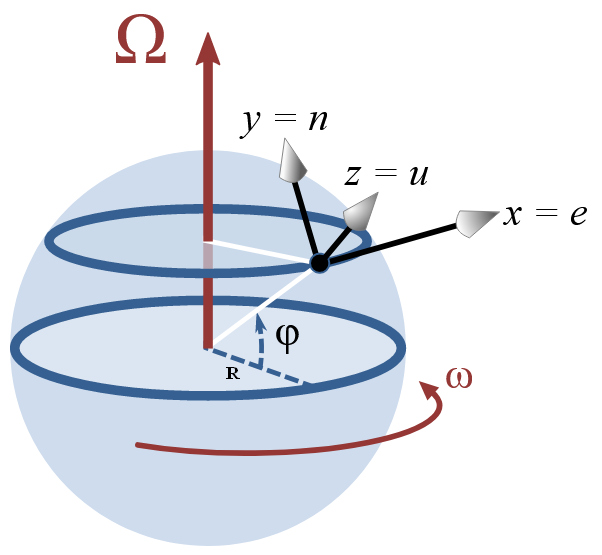
Koordinatni sistem na zemljepisni širini φ z x osjo vzhodno, y osjo severno in
osjo z navzgor (z smer je torej radialno navzven od središča krogle). Vektor kotne
hitrosti je Ω = ω(0, cos φ, sin φ)
in vektor hitrosti
v = (ve, vn, vu). Vektorski
produkt, oziroma pospešek aco pa se torej zapiše:
aco = -2Ωxv = 2ω(vnsin φ
– vucos φ, - vesin φ, vecos φ).
Če pa se telo giblje zgolj horizontalno (to je večinoma relevantno za globalne
zračne in morske tokove, sploh ker v vertikalni smeri dominira težni pospešek g),
je vu = 0 in je vektor pospeška (če je Coriolisov parameter f = 2ωsin φ):
aco = 2ωsin φ (vn, - ve)
= f(vn, - ve)
Za velikost vektorja za horizontalno hitrost torej velja:
aco = f (vn2 + ve2)1/2 = 2ωv sin(φ)
Kot drug poseben primer, si poglejmo še gibanje na ekvatorju
φ = 0 ° (sin 0 ° = 0 in cos 0 ° = 1). V tem primeru je vektor kotne hitrosti
Ω vzporeden s severno ali n-osjo in velja:
Ω = ω(0, 1, 0) in za pospešek dobimo
aco = -2Ωxv = 2ω(-vu, 0, ve)
V skladu s tem rezultatom gibanje proti vzhodu (to je v isti smeri
kot vrtenje sfere, Zemlje) povzroča pospešek navzgor, znan kot Eötvösov efekt,
gibanje navzgor pa pospešek proti zahodu, gibanje navzdol pa proti vzhodu (če
recimo telo spustimo iz določene višine, da prosto pada, se nekoliko premakne
proti vzhodu).
Na Zemlji (če je prisotno zgolj horizontalno gibanje) velja torej za Coriolisov
pospešek izraz, absolutna vrednost:
aco = 2ωv sin(φ)
- kjer je kot φ geografska širina kraja.
Na ekvatorju je torej horizontalna komponenta Coriolisove sile za zgolj
horizontalno gibanje enaka 0, a horizontalno gibanje (komponenta vzporedna
z ekvatorjem) vseeno na ekvatorju povzroči vertikalne pospeške.
Polmeri vrtincev, ki nastanejo zaradi Corolisove sile, so R = v/(2ω sin(φ)),
to velja za gibanje v horizontalni ravnini.
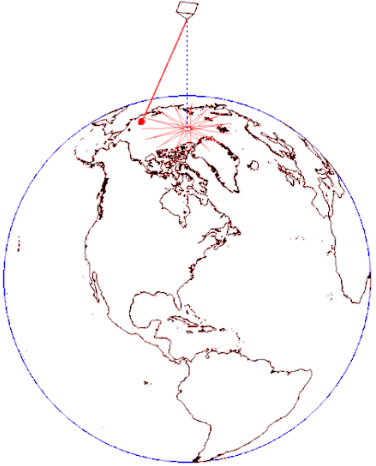

Ko računamo čas zasuka ravnine Foucaultovega nihala moramo torej upoštevati
geografsko širino in projekcijo kotne hitrosti. Za kotno hitrost Zemlje velja
ω = 2π/to, kjer čas rotacije Zemlje to = 23 ur 56 min 4 sek – glede na zvezde.
Velja ωsin(φ) = 2π/tn, od koder sledi, da ravnina nihala naredi zasuk v času
tn = to/sin(φ). Za Pariz velja tn = 31,8 ur, na polu pa kar en zvezdni dan:
23 ur 56 min 4 sek. Zasuk nihala, gledano iz Zemlje, pripišemo sistemski
Coriolisovi sili – opazovalec izven Zemlje pa bo vedel, da se ravnina nihanja ohranja,
zavrti pa se Zemlja.
Če se spomnimo še srednjeveških in antičnih pomislekov proti rotaciji
Zemlje - Hiparhov zadržek je bil, da bi, če Zemlja res rotira okrog lastne
osi in potuje še okrog Sonca, telo, ki ga vržemo v zrak, zaostajalo. Bil je
na sledi Coriolisovi sili, a tudi takratna predstava o zamiku predmeta, recimo
pri padanju, je bila nerealna (ni upoštevala vztrajnosti telesa, gibalne količine).