Zakaj astronomija
|

|
Zakaj astronomija
|

|
Kako do Keplerjevih zakonov
Ali kar napišemo Keplerjeve zakone na tablo, oz. v ppt predstavitve
ali morebiti vložimo dodatni trud in kaj povemo o dejstvu, da Kepler
ni poznal razdalj »Zemlja – Sonce – planeti« in je imel na razpolago
zgolj ideje Grkov, Kuzanskega, Kopernika ..., da planeti potujejo
po krožnicah okrog Sonca. Imel pa je tudi odlične (natančne in številne)
Brahejeve (delno tudi svoje)
meritve lege Marsa na nebu (glede na zvezde) in je le iz njih sklepal,
da take lege Zemlje in Marsa lahko razložimo le, če Zemlja in ostali
planeti potujejo po elipsah. Mnogi so prepričani, da je njegov geometrijski
dokaz (slika), vredna vsega občudovanja
(Michelangelo nebesne mehanike).
Računal je z relativnimi razdaljami in tako izpeljal znamenito povezavo med
obhodnim časom in veliko polosjo elipse planeta: T2 = konst*a3.
Ali torej uporabimo Keplerjeve skice iz 24. poglavja knjige
(»Astronomia nova« - Nova astronomija iz leta 1609 - kopija je tudi na spletu).
Ali bi to lahko bila ena izmed nadgradenj predmeta astronomija –
ODGOVOR JE VSEKAKOR JA! Če hočemo, da bodo mladi res razumeli,
kaj je počel Kepler 20 let, da je ukrotil nebesno mehaniko
(v zgolj 3 kratke, a odločilne zakone razumevanja vesolja).
Tretji zakon seveda lahko narišemo tudi v lineariziranem grafu
kjer y = T2 in x = a3 (lahko pa logaritem enačbe).
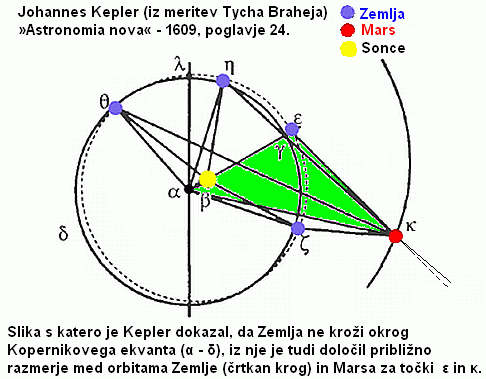
Modernizirana skica, s katero je Kepler geometrijsko
dokazal, da Zemlja ne kroži okrog
Kopernikovega ekvanta (α - δ).
Iz nje je tudi približno določil razmerje
med tirnicama Zemlje (črtkana orbita) in
Marsa za točki ε in κ na Zemljini in Marsovi
tirnici (zelen trikotnik). Iz ostalih trikotnikov pa
še vse ostale točke realne Zemljine tirnice (ζ,
η, λ, θ
).
Kepler je poznal obhodni čas Marsa okrog Sonca glede na zvezde
(ta čas imenujemo tudi siderski čas), ki je bil takrat ocenjen
na 687 dni (danes na 686.971 dni). Najprej je uporabil zelo
zvito metodo iskanja Zemljine tirnice - orbite. Geometrijsko
je iskal položaj Zemlje na njeni tirnici tako, da je narisal
položaje Zemlje za datume, ko se je Mars po 687 dnevih spet
vrnil v izbrano referenčno točko - ko je naredil en obhod
okrog Sonca. Uporabil je tri Marsove cikle po 687 dni.
V bistvu je iskal paralakso Marsa gledano iz Zemlje.
Tako je dobil štiri točke na tirnici Zemlje. Kepler
je privzel za Zemljo Kopernikovo krožno tirnico (na
sliki je to polni krog), katere center je ekvant, ki
je nekoliko odmaknjen od Sonca. A ko je iz Brahejevih
meritev določal lege Marsa glede na zvezdno ozadje,
je ugotovil, da iz Kopernikove Zemljine tirnice ne dobi
enakih leg Marsa, ampak nekoliko izmaknjene. Če je torej
hotel na sliki dobiti Brahejeve izmerjene lege Marsa, je moral
Zemljo prestaviti na novo tirnico (na sliki je to črtkana orbita
– tirnica, ki ustreza elipsi). Tako se je torej končalo obdobje
več tisočletne zmote - že od antike idealiziranih krožnic.
Tirnice planetov so elipse.
Svoje ugotovitve je strnil v tri zakone!
Keplerjevi zakoni
I. Keplerjev zakon: Tirnica (pot) planeta je elipsa s Soncem v enem od gorišč.
II. Keplerjev zakon: Zveznica med Soncem in planetom opiše v enakih časovnih
intervalih enake ploščine. Ohranja se torej ploščinska hitrost (vrtilna količina).
III. Keplerjev zakon : Kvadrat obhodnega časa (T)
planeta je sorazmeren kubu velike polosi; dokaj dobro velja
T2/a3 = konst.
V splošnem pri dveh telesih velja, da potujeta okrog skupnega težišča in
v tem primeru se danes tretji Keplerjev zakon zapiše v pravilnejši Newtonovi verziji:
T2/a3 = 4π2/(G(M+m))
G je gravitacijska konstanta (G = 6.67*10-11m3kg-1s-2).
Vaja za kroženje
Pri kroženju okrog težišča teles m1 in m2
izrazimo oba centripetalna pospeška
(r1 in r2
sta razdalji teles do težišča, r = r1 + r2 ) in ju seštejemo.
Gm2/r2 = 4π2r1/to2
Gm1/r2 = 4π2r2/to2
Rezultat za kroženje je pričakovan:
to2/r3
= 4π2/(G(m1 + m2))
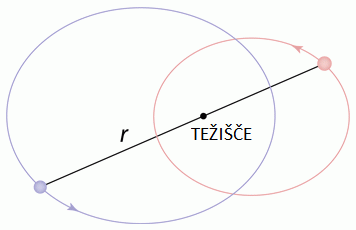
Gibanje dveh teles okoli skupnega težišča pod vplivom gravitacijske
sile.
Izpeljava korektnega III. Keplerjevega zakona za elipso je
nekoliko pretežka za srednjo šolo, lahko pa si jo radovedni
učenci pogledajo na spletu ali v učbeniku.
Uporaba Keplerjevih zakonov
3. Keplerjev zakon
(
to2/a3
= 4π2/(G(m1 + m2))
) lahko zagotovo uporabimo
za razlago iskanja eksoplanetov s pomočjo radialnih hitrosti. Preko povezav
za razmak a = r = rm + rM
zvezde in planeta ter težišča MrM = mrm,
obhodnega čas T,
izpeljemo povezavo za hitrost zvezde
(vM = m(2πG/T)1/3/(M + m)2/3) – glej Spiko 10,
2020. Pokažemo še graf najdenih eksoplanetov skozi leta z različnimi metodami
(za metodo radialnih hitrosti in prve uspešne rezultate, je bila podeljena
tudi Nobelova nagrada), določimo lahko še mase dvojnih sistemov, zvezd.
Zakon preoblikujemo preko vsote hitrosti vm + vM v naslednjo obliko:
m+M = T(vm + vM)3/(2πG) )
in izračunamo mase vsake zvezde posebej. Recimo iz povezave
m3/(m+M)2 = Tv3M/(2πG),
lahko uporabimo še zvezo mvm = MvM,
če seveda poznamo, oz. pomerimo hitrosti zvezd
vM in vm, recimo preko Dopplerjevega pojava,
vM = cΔλ/λ, c je hitrost svetlobe.
Veliko je odvisno od nagiba
ravnine kroženja dvojnega sistema, če gledamo pravokotno na ravnino kroženja in poznamo
razdaljo do sistema, se da hitrost zvezd meriti direktno preko časa in poti. Z obema
metodama (še z Dopplerjem) pa lahko sklepamo na nagib ravnine tirnic.
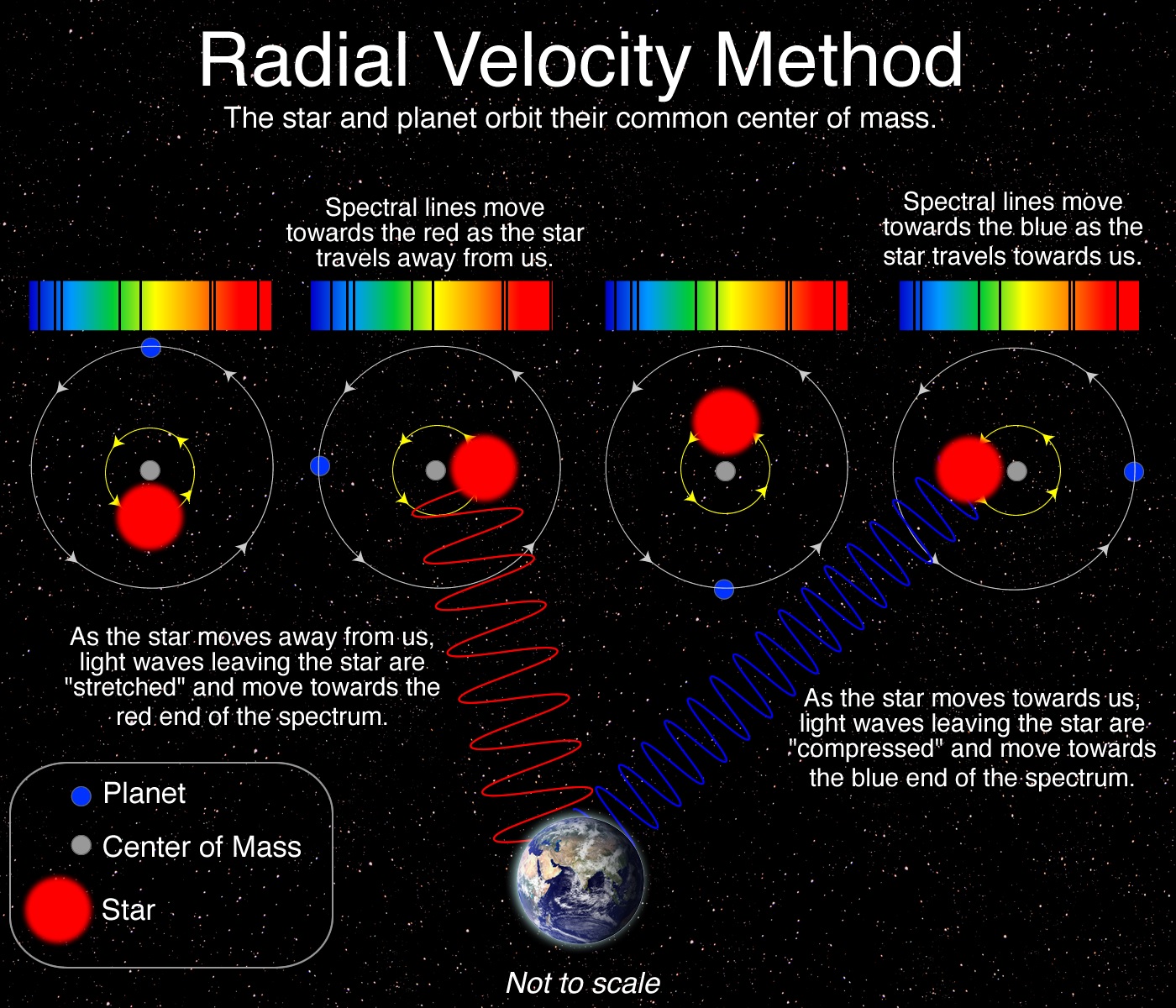
Pri iskanju eksoplanetov z metodo merjenja radialnih hitrosti
zvezde astronomi izkoriščajo dejstvo,
da se zvezda in planet gibljeta okoli skupnega
masnega težišča po Keplerjevih zakonih.
Če v svetlobi zvezde opazijo periodične premike spektralnih črt
zaradi Dopplerjevega pojava, lahko sklepajo, da okoli zvezde kroži planet,
pa čeprav ga neposredno ne vidijo. Iz periode lahko ocenijo tudi skupno maso
zvezde in planeta.
Keplerjevi zakoni res sežejo na številna področja astronomije
(vir: Las Cumbres Observatory).
Vir slike:
https://sciencesprings.wordpress.com/2018/05/04/from-mit-news-ushering-in-the-next-phase-of-exoplanet-discovery/radial-velocity-method-las-cumbres-observatory-2/
Vsekakor so
Keplerjevi zakoni tudi ustrezna pot do preproste izpeljave gravitacijskega zakona
in potem sledi nadgradnja 3. zakona v pravilnejšo obliko:
T2/a3 = 4π2/(G(M + m)), v kateri nastopa gravitacijska
konstanta G, ki je Kepler seveda še ni poznal.
Nikakor pa na
poti do gravitacijskega zakona ne smemo pozabiti na Huygensovo, »komaj« leta 1659
izpeljano, izjemno pomembno enačbo za centripetalno silo pri kroženju:
Fc = m*v2/r.
Pojem sile je bil takrat še v povojih. Ta Huygensova formulacija centripetalne sile
je skladna s poznejšo Newtonovo definicijo sile (2. zakon) in je pomenila izjemno
pomemben korak pri študiju orbit v astronomiji. Je hkrati omogočila prehod iz
tretjega Keplerjevega zakona (o gibanju planetov),
na »inverzni kvadratni« zakon gravitacije (Fg ∝ 1/r2).
Pomembno je torej, da vsaj na kratko kronološko in obvezno
preko raziskovalcev, pokažemo na razvoj astronomije in fizike.
Iz sosledij odkritij (recimo Kepler, Huygens, Newton ...)
bomo (bodo mladi) veliko lažje razumeli, zakaj je Kepler
že praktično izpeljal gravitacijski zakon, a tega ni vedel ...,
ker sila leta 1618 še ni bila dokončno definirana in izražena v
fizikalno-matematično korektnem zapisu. Kepler je govoril o moči,
magnetizmu, ki prebiva v telesu Sonca in tako nase vleče planete,
da potujejo po elipsah - v kontekstu časa Keplerjev koncept sploh
ni bil tako napak ...
Zagotovo je pri gibanju nebesnih teles, recimo kometov
v gravitaciji Sonca, potrebno poudariti, da če je telo gravitacijsko
vezano (Ek < - Ep), je njegova energija negativna (E = -GmM/(2a),
gibanje po elipsi ali krožnici), če je energija 0, se telo giblje
po paraboli (Ek = -Ep), in če je energija večja od 0, se telo giblje
po hiperboli (Ek > - Ep); vse te krivulje so dobro obdelane pri
matematiki in za vsako od njih se lahko poišče kak računski primer,
Morebiti se lahko omeni še virialni teorem (2Ek + Ep ≤ 0),
recimo za primer satelita, ki kroži okrog Zemlje (je stabilno vezan
v sistem) velja, mv2/R = GMm/R2, in ker je
E = mv2/2 - GMm/R = GMm/(2R) - GMm/R = -GmM/(2R) = Ep/2 = -Ek,
od koder sledi 2Ek + Ep ≤ 0 - to je virialni teorem, ki pravi,
da so telesa stabilno vezana v nek sistem (recimo v zvezdo),
če je vsota potencialne in dvojna vrednost kinetične energije
manjša ali enaka nič. Ker
virialni teorem velja tudi za zvezde in njihovo notranjo energijo,
lahko v tem kontekstu omenimo tudi Jeansovo maso
(iz zveze 3NkT < (3/5)GM2/R, kjer je
N število delcev,
Ep = -(3/5)GM2/R
potencialna energija oblaka
in Ek = 3NkT/2 kinetična energija plina,
delcev - ko velja 2Ek + Ep ≤ 0, od koder
sledi Jensova masa plina M > (5NkTR/G)1/2 ),
ki je potrebna za nastanek zvezde.
Tako združimo atomsko termodinamično sliko s stanjem velikih teles
(kinetična energija atomov, molekul nekega oblaka z maso M in polmerom R,
mora biti manjša
od polovice negativne potencialne energije oblaka – tako se plin (prah)
lahko začne krčiti, zaradi lastne gravitacije, v zvezdo, če je seveda
začetna masa recimo blizu Sončeve).
Teh nekaj primerov nazorno kaže, kaj se vse da izluščiti (določiti,
izračunati) iz enega samega "preprostega" Keplerjevega zakona, nadgrajenega
še z gravitacijskim zakonom.
Tako na razmeroma enostaven način vidimo, od kod astronomom
podatki o masah zelo oddaljenih zvezd, kako lahko
ugotavljajo ali je nek komet vezan na Sonce (in torej član
našega Osončja) ali pa je k nam pripotoval iz medzvezdja
(kot na primer komet Oumuamua), in kako lahko trdijo, da okrog
drugih zvezd potujejo eksoplaneti, pa čeprav jih (zaenkrat)
neposredno ne vidijo. To pa so danes, ko vsi dvomijo o vsem,
še kako pomembna spoznanja!
Če se slučajno v naše kraje, šole, še kdaj vrne izjemna naravoslovna gimnazija,
ki jo po nepotrebnem ukinil nek gospod ... tam okrog leta 1997 ...
bo astronomija in tudi sicer vsi ostali predmeti veliko lažje zadihali.
A veste, da so tudi profesorji družboslovci in humanisti zelo radi
poučevali naravoslovne oddelke!!! Ne govorim rad o zlatih časih –
a za mnoge pogumne gimnazije (mlade) so bili to zares zlati časi!

Slavni medzvezdni komet Oumuamua, ki nas je obiskal leta 2017,
je imel preveliko hitrost, da bi bil gravitacijsko
vezan na Sonce (njegova skupna energija je večja od nič!),
zato astronomi z gotovostjo vedo,
da je priletel iz medzvezdja (Vir: ESO/M. Kornmesser).
Sistem dveh teles
Vsekakor bi k temu poglavju lahko dodali še nekaj besed od dvojnih
sistem in akreciji (ko se iz večje zvezde – recimo orjakinje – pretaka
snov na sosednjo kompaktno zvezdo, recimo na belo pritlikavko in tako
lahko pride do eksplozije nove ali supernove – recimo supernova tipa Ia)
ter z upoštevanjem težavnosti, se opiše se logiko in pomen Lagrangeevih
točk, kjer lahko skupaj z dvojnim sistemom sinhrono potujejo manjša
telesa, tudi sateliti. Sonda SOHO (Solar and Heliospheric Observatory)
recimo kroži skupaj s sistemom Zemlja-Sonce v Lagrangeevi točki 1 in
ima tako cel čas odprt pogled za slikanje Sonca (Glejte sliko). Če
je to sistem dveh zvezd, se skozi točko L1 lahko pretaka tudi plazma
na drugo zvezdo (če sta zvezdi dovolj skupaj, tesni sistem in če ena
zvezda, njena plazma, sega nekoliko čez rob točke L1).
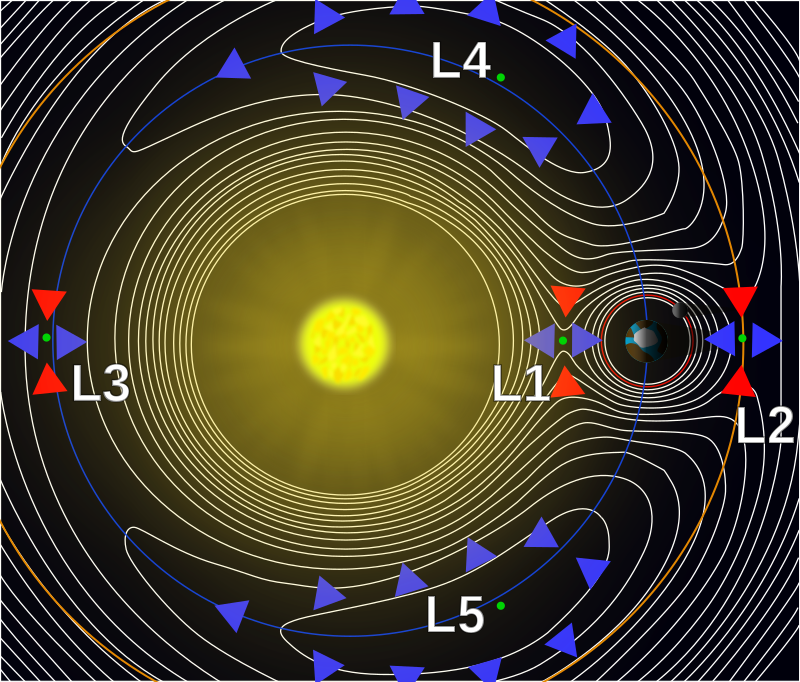
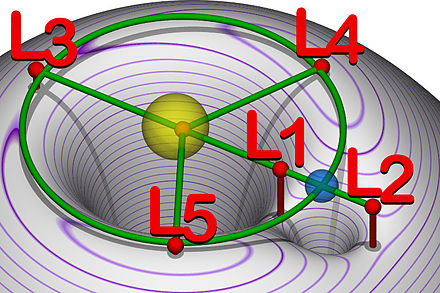
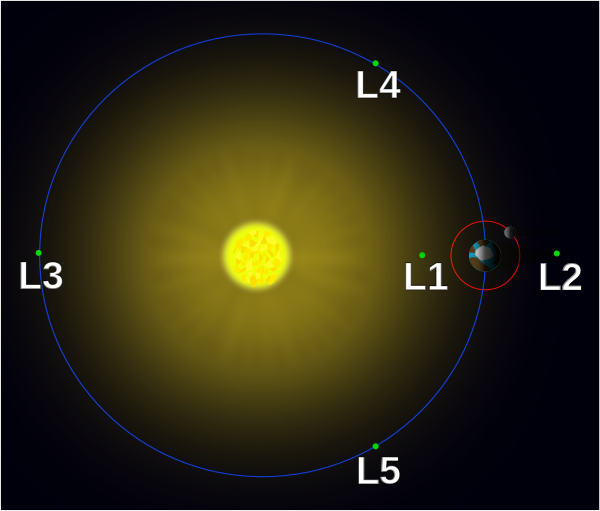
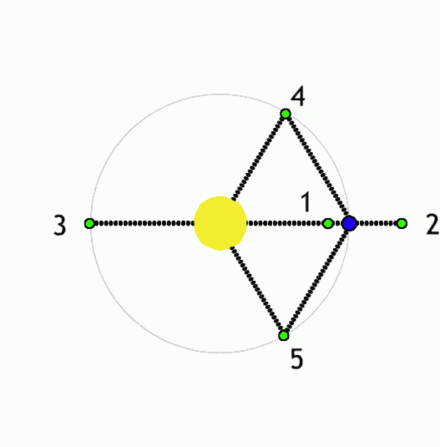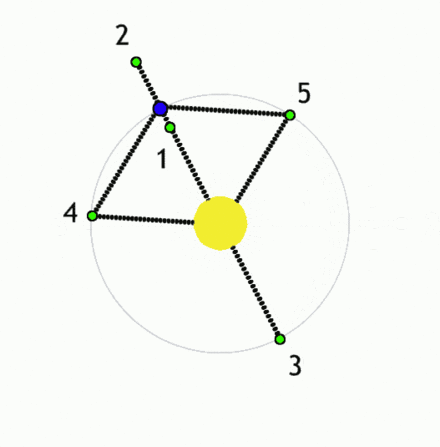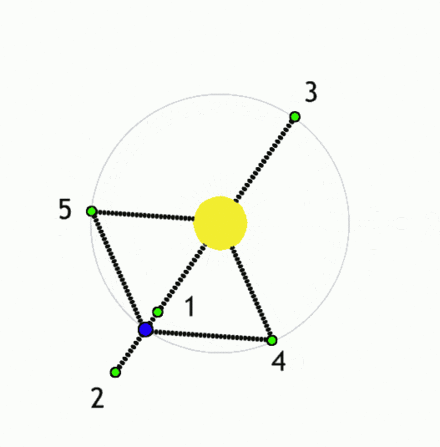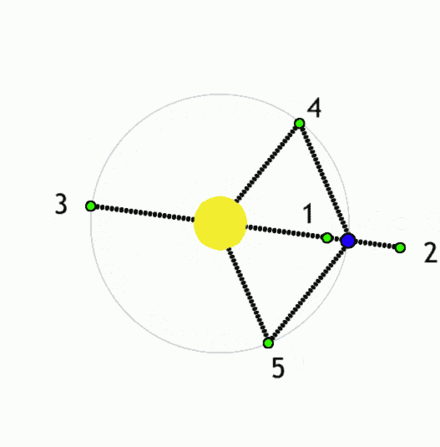
Dva pogleda na Lagrangeve točke med dvema telesoma (v tem primeru
med zvezdo in planetom), med katerima deluje gravitacijska sila.
V teh točkah je vsota sil na tretje telo (telo rotira skupaj s sistemom),
ki bi se znašlo tam, enaka nič
(vir: Wikipedia).
Recimo, da vas zanima opazovanje Sonca (na Zemlji so problem oblaki, noč, sama atmosfera).
Če se z raketo pripeljete v Lagrangevo točko L1, boste v tej poziciji, glede na sistem
Zemlja - Sonce, mirovali in tako lahko ves čas opazovali Sonce. V zvezdnem letu boste naredili
obhod okrog Sonca skupaj z Zemljo za svojim hrbtom ...
Po domače si lahko Lagrangeeve točke predstavljamo kot sile na majhno telo med
kroženjem v bližini dveh velikih teles, kjer so - sila zaradi rotacije in obe
gravitacijski sili - v ravnovesju (primer vrteče se gramofonske plošče, če nanjo
položimo majhno železno kroglico, bo sredobežna sila rotacije kroglico zabrisala
s plošče, če pa je v osi vrtenja plošče recimo magnet, bo le ta na določeni razdalji
r od središča zadržal kroglico na plošči, kjer se obe sili izničita; privlačna in
njej nasprotna sistemska sredobežna sila zaradi rotacije – tej točki lahko
rečemo stacionarna ali Lagrangeeva točka – ni pa to zelo stabilna lega).
Lagrangeeve točke se izračuna iz gravitacijskega potenciala in potenciala
zaradi rotacije ( Φgc = Φg + Φc
= -G( MN/|r-rN| + MK/|r-rK|)
- (ωr)2/2 ),
kjer sta rN in rK razdalji obeh centrov mas od težišča sistema
(N pomeni normalna
zvezda, K pa kompaktna, bela pritlikavka, nevtronska zvezda, črna luknja),
r pa razdalja od težišča dvojnega sistema, do poljubne točke v ravnini kroženja.
Sistem seveda kroži s Keplerjevo kotno hitrostjo
ω = (G(MN+MK)/a3)1/2.
V petih
Lagrangeevih točkah tako lahko sinhrono, skupaj s sistemom dveh teles, krožijo
manjša telesa – to so stacionarne točke (točke L1, L2 in L3 lahko sami izračunate
brez večjih težav, preko izenačitve sil obeh gravitacij in sredobežne sile,
seveda - vse je odvisno od obeh mas in razdalje med zvezdama ...). Če narišemo
sliko potenciala dveh velikih teles (recimo zvezd ali planeta in Sonca), dobimo
podobo dveh »posod« (simbolno) in točka L1 je področje, kjer se lahko pretaka
snov iz ene zvezde na drugo. Zgornji sliki predstavljata sistem Sonce – Zemlja.
V sistemu Zemlja, Luna so v L4 in L5 astronomi opazili zgoščena oblaka manjših teles.
Prav
tako vsebuje sistem Sonce-Jupiter v L4 in L5 asteroide imenovane Trojanci
(odkril jih je Wolf že leta 1906).

Do eksplozije supernove tipa Ia lahko pride zato,
ker se snov z normalne zvezde prek
Lagrangeve točke L1 (leži na zožitvi toka plazme) pretaka na bližnjo
belo pritlikavko.
Ko tej masa naraste prek Chandrasekharjeve
meje, na okrog
1.4 M☉, se bela pritlikavka pod
lastno težo sesede v nevtronsko zvezdo - eksplozija supernove tipa Ia
(vir: ESA/ATG medialab/C. Carreau).
Recimo supernove tipa Ia (naj bi zmeraj eksplodirale z enakim izsevom,
so torej standardni nebesni svetilniki, ki se zelo daleč vidijo) so
nam razkrile, da se vesolje širi pospešeno (pred kratkim so nam tako
razkrile zaenkrat skrivnostno temno energijo, celo okrog 70 % vse
energije vesolja). Supernova tipa Ia pa bi naj nastala v dvojnem
sistemu zvezd, kjer je ena od članic kompaktna bela pritlikavka,
na katero se preko točke L1 pretaka plazma s sosede in se tako
kompaktna zvezda počasi veča. Ko se poveča do Chandrasekharjeve
meje, na okrog
1.4 M☉ (2.765×1030 kg), eksplodira kot supernova
tipa Ia (elektroni in protoni se pod težo gravitacije združijo
v nevtrone: e- + p → νe + n,
sprosti se enormno energije, kar za
izsev okrog celotne galaksije, za okrog 5 milijard Sonc). Meritve
razdalj preko supernov tipa Ia (ki se izkažejo za temnejše od pričakovanj,
gledamo jih v preteklost) glede na oceno razdalje zaradi rdečega premika,
kažejo, da se vesolje vsaj v zadnji polovici življenja pospešeno širi
(in je tako supernova bila dlje od nas, kot smo to pričakovali iz
rdečega premika).
Se nadaljuje ...
Zorko Vičar
Korona pomlad 2021
DODATEK
POTEK POTENCIALA DVEH MASIVNIH NEBESNIH TELES
Φgc = Φg + Φc = -G( MN/|r-rN| + MK/|r-rK|) - (ωr)2/2
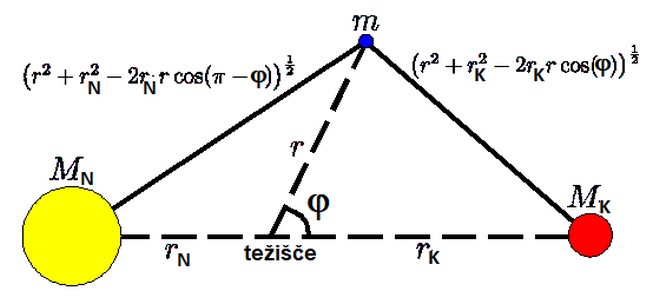
Velja:
cos(π - φ) = -cos(φ)
Velikost razlike vektorjev je:
|r-rN| = (r2 + rN2 - 2rrNcos(π - φ))1/2
= (r2 + rN2 + 2rrNcos(φ))1/2
|r-rK| =
(r2 + rK2 - 2rrKcos(φ))1/2
Potencial (4) lahko zapišemo tudi v naslednji obliki:
Φgc = -G( MN/(r2 + rN2 + 2rrNcos(φ ) )1/2 + MK/(r2 + rK2 - 2rrKcos(φ ) )1/2 ) - ω 2r2/2
Poiščimo lokalne stacionarne točke, z znanima pogojema, parcialna odvoda morata biti 0.
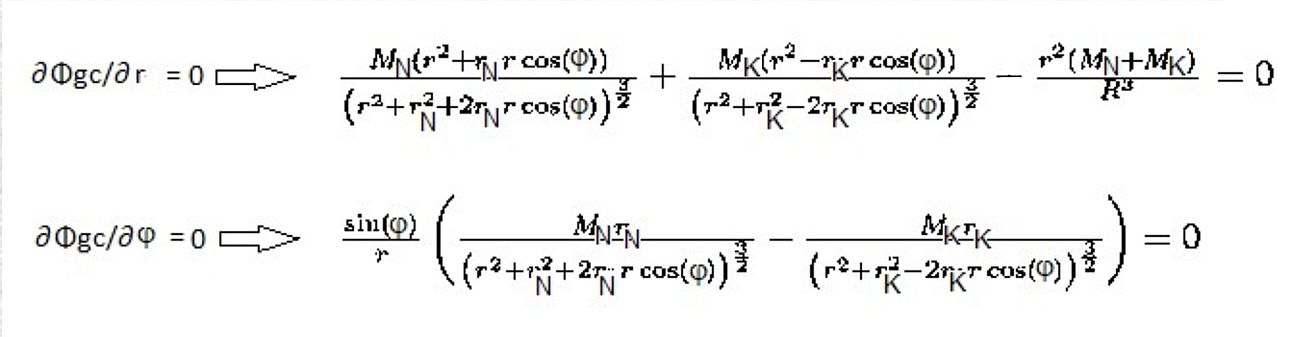
Rešitve zahtevajo numerično reševanje (velja: R = rN + rK,
za ω smo vstavili Keplerjevo vrednost
ω2 = G(MN+MK)/(rN + rK)3 ).
Odvod ∂
Φgc/∂
r=0, je po odvajanju pomnožen z r - tako se lažje najde rešitve. Seveda smo povsod okrajšali
gravitacijsko konstanto G.

Manjša telesa (zelena) v Lagrangeovih točkah ležijo v območju ravnovesja sil (recimo dveh zvezd).
V kateri koli drugi točki gravitacijske sile prevladajo in telesa se začnejo premikati
proti enemu od obeh masivnih teles, recimo proti zvezdama (lahko tudi izven sistema za točko L2).
Vir: WIKI