Zakaj astronomija - in zakaj tudi v šoli? (VI) Izsev in izračun polmera ter površinske temperature zvezd; kako dolgo zvezde zlivajo atome; pomen Lune za Zemljo; mrki in velikost ter razdalja do Lune, Sonca; Sončev mrk in potrditev Einsteinove splošne teorije relativnosti

Opazovanja in izsev ter izračun polmera ali površinske temperature zvezd
Posebej je potrebno poudariti, kako lahko recimo že s preprostimi opazovanji (ki jih tudi izvedemo) določimo magnitude zvezd, potem izračunamo še gostote svetlobnih tokov ( j = j_o*10^-0.4(m-mo) ), če poznamo razdaljo (preko kefeid ali paralakse ...), lahko izračunamo izsev L = j*S = σT⁴4πR² in preko temperature določimo še polmer zvezde R = R_☉(T_☉/T)²(L//L_☉)^1/2 in obratno.
Že v uvodu v astronomijo se poudari pomen sija zvezd in magnitude, kot to zaznajo človeške oči in seveda s tem fenomenom povezan Pogsonov zakon. Že stari Grki (Hiparh, Ptolomej) so razdelili zvezde po siju oziroma magnitudi - to je fiziološka enota za sij. Najsvetlejše so imenovali zvezde prve magnitude (m = 1 m), komaj vidne pa šeste magnitude (m = 6 m). Da bi stara razdelitev zvezd po njihovem siju ostala v veljavi in tudi fizikalno bolj praktično uporabna, so preko meritev poiskali zvezo med sijem in gostosto svetlobnega toka zvezde. Prve meritve segajo v leto 1856. Pogson je takrat odkril, da so zvezde prve magnitude približno 100 krat svetlejše od zvezd šeste magnitude (j₁(m=1)/j₂(m=6) = 100). Pogsonov zakon se tako glasi:
j₁/j₂=10^-0.4(m1-m2) = 100^-(m1-m2)/5
Izkaže se, da svetlobni tok z gostoto j = 2.518×10^-8 W/m² zaznamo kot sij magnitude 0. Seveda je potrebno poudariti pomen dvojnih zvezd, akrecije, pomen kefeid, opisati prenos energije v zvezdah in seveda nastanek zvezd.

Kako dolgo živijo zvezde?
Koliko povedati o življenju zvezd, planetov - vsaj toliko, da bomo razumeli nastanek težkih elementov, čas prebivanja zvezde na glavni veji Hertzsprung-Russllovega diagrama, tipe zvezd in barvo, končne faze razvoja zvezd (bele pritlikavke, nevtronske zvezde, črne luknje – preko eksplozij nove, supernove, hipernove ...). Potrebno je podati pomen zvezd, ki dolgo živijo (kako je izsev povezan za maso L = L_☉(M/M_☉)^3.5 in časom življenja zvezd, ko poteka fuzija v jedru zvezde t = 10¹⁰(M_☉/M)^2.5 let ). Poudarimo tudi izjemen pomen zvezd za nastanek planetov, sploh kamnitih in morebitnega življenja, izpelje se tirnica naselitvenega področja ( R_np = AE(L/L_☉)^1/2 ). Na tem mestu moramo torej nujno pojasniti, kaj je to Zlatolaskin pas, oziroma življenjski pas (naselitveno področje) okoli neke zvezde in kje se razteza pri različnih tipih zvezd (glejte recimo Spiko 2020/12).
Zagotovo se poda, po Stefanu, tudi izsev zvezde: L = j*S = σT⁴4πR²
in polmer zvezde: R = R_☉(T_☉/T)²(L//L_☉)^1/2 ali obratno.
To je lep primer, kaj vse lahko o oddaljenih zvezdah izvemo že s preprostimi opazovanji, ocenami magnitud (sija) in s preprosto, srednješolsko matematiko.

Površinske temperature zvezd in njihovi spektri
Do temperatur oddaljenih zvezd lahko pridemo preko več metod, recimo Wienovega zakona (T = 2897768,5 nm•K/λ, a metoda ni najbolj natančna), preko Stefanovega zakona ( L = j*S = σT⁴4πR² ) - a morano poznati polmer zvezde (kar se recimo da določiti pri dvojnih sistemih, če se zvezdi prekrivata ali če zvezdo prekrije eksoplanet, a tudi preko interferometrov je mogoče določiti polmere bližnjih zvezd in seveda poznati moramo razdaljo do zvezde). Temperature površine zvezd se še bolj natančno določajo preko intenzitete spektralnih absorpcijskih črt (višji energijski nivoji so zasedeni pri višjih temperaturah), ta metoda omogoča ocenjevanje temperatur dokaj natančno, do +/- 50 Kelvinov. Temperature površin zvezd se posredno določi tudi s fotometri, skozi različne filtre se meri gostota svetlobnega toka j, kar se pretvori v temperaturo s standardnimi modeli (recimo B modra svetloba 442 nm in V vidna svetloba 540 nm (zeleno-rumena), ko za barvni indeks velja B - V = -2.5log(j_B/j_V) in se izračuna temperatura zvezde preko enačbe T = 4600(1/(0.92(B - V) + 1.7) + 1/(0.92(B - V) + 0.62)) – to je Ballesterosova formula, obstaja še poenostavljena enačba T = (10000 K)/((B-V) + 1) in še veliko ostalih empiričnih enačb, glede na spektralne razrede zvezd). Ta metoda je zelo uporabna, če ni na voljo kvalitetnega spektra zvezd (recimo pri zvezdnih kroglastih kopicah); rezultati, dobljeni s to metodo, so natančni do +/- 100-200 K, metoda pa daje slabše rezultate za hladnejše zvezde. Zakaj je toliko besed posvečenih določanju temperature zvezd? Temperatura je, skupaj s spektrom, neke vrste prstni odtis zvezde. Drugi razlog se skriva v dejstvu, da se da relativno enostavno narediti slike, rec. kroglastih kopic, skozi dva filtra in določiti njihove temperature in narisati celo H-R diagram ... (za vajo z razredom bi bilo dovolj že, če se slika nekaj zvezd skozi B in V filtra in določi temperaturo, ter preveri rezultate iz katalogov).

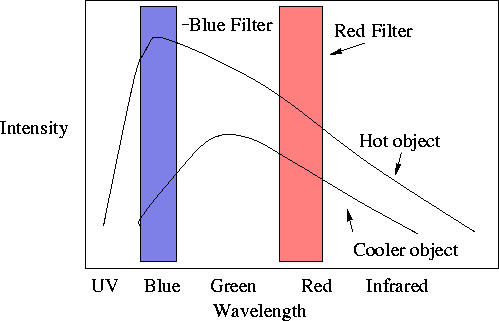
Planckov zakon – porazdelitev gostote energije izseva zvezd po valovnih dolžinah (»barvi«).

Pomen Lune za Zemljo
Plimovanje v sistemu Zemlja – Luna je zelo pomembno poglavje. Zaradi plimovanja se Luna oddaljuje od Zemlje, sama Zemlja pa posledično upočasnjuje (ta dinamika se da lepo razložiti brez računanja – za seminar pa se tudi kaj poračuna, zadaj je tudi razlaga, zakaj nam Luna kaže zmeraj bolj ali manj enak obraz ). To je lep primer ohranitve vrtilne količine sistema, hkrati pa nas opozarja na spremembo dolžine dneva in tozadevne »težave«, tudi vpliv na dolžine Sončevih mrkov. Lahko bi dodali še hipotezo o vplivu plimovanja na razvoj življenja na kopnem; pomen stabilnosti sistema »Zemlja – Luna - Sonce« za stabilnost podnebja, za razvoj kompleksnih živali, povratnih dob ekstremnih dogodkov (padavine, veter, ekstremne temperature, ...). Zelo enostavno se preko plimskih sil dokopljemo tudi do ocene Rocheove meje (mejna razdalja planet-luna pri kateri luna začne razpadati), ki torej določa (ne)stabilnost naravnih satelitov in na ta način lahko razložimo tudi nastanek Saturnovih prstanov.

Mrki in merjenje razdalj v antiki in hkrati mrki še v 20. stoletju pomagajo razumeti novo Einsteinovo mehaniko
Zagotovo je presenetljivo, kako moderna, predrzna in hkrati uspešna so bila razmišljanja in meritve naši antičnih očetov, Aristotel je pred približno 2350 leti utemeljeno trdil, da je Zemlja okrogla, ker ima ob Luninih mrkih Zemljina senca na površini Lune okrogel obris. Eratosten je pred 2260 leti s pomočjo razdalje med Aleksandrijo in Sieno (Asuanom) in vpadnih kotov Sončevih žarkov določil polmer Zemlje (računanje polmera iz loka in kota). Nekoliko pozneje in natančneje ter z boljšo metodo sta razmerje Zemlja-Luna določila še v antični Grčiji Aristarh in kasneje Hiparh. Izjemno natančen opazovalec, analitik in poznavalec kaldejske astronomije Hiparh, je pred približno 2160 leti s pomočjo trajanja Luninega mrka določil, da v Zemljino senco (med Luninim mrkom) lahko postavimo približno 8/3 Lun. Tako so v antiki že dokaj točno ocenili razdaljo Zemlja – Luna in sicer na 62 polmerov Zemlje. Ker so poznali velikost Zemlje, so tako lahko izračunali tudi velikost Lune. Aristarh pa je preko trikotnika Luna (prvi krajec Lune), Zemlja, Sonce ocenil razdaljo »Zemlja – Sonce« na 19 razdalj »Zemlja – Luna« (prava vrednost je sicer 397x več). V bistvu je bila to za tiste čase, glede na okorne metode merjenja kotov, drzna in izredno pomembna ocena. Zakaj? Iz te ocene izhaja, da je Sonce vsekakor veliko večje od Zemlje (takratna ocena je bila okrog 7x, današnja 109x). Zaradi tega rezultata so mnogi začeli razmišljati in se spraševati, kako pa lahko veliko večje Sonce kroži okrog majčkene Zemlje (danes vemo, da se rotacija dogaja okrog skupnega težišča)! V antiki so torej kar veliko razmišljali tudi o možnosti, da planeti (tudi naša Zemlja) potujejo okrog Sonca. Dokaj uspešno so že napovedovali mrke, poznali so že periodo sarosa (določili že Babilonci, ki so že tudi poznali »Pitagorov izrek«), to obdobje 18 tropskih let in 11,3 dni (ali 10,3 dni, odvisno od števila prestopnih let) in znaša 6585,66 dni, ko se spet približno ponovi lega Zemlje, Lune, Sonca na premici mrka (ali blizu, saj so telesa razsežna in ni nujna točna poravnava), ki leži v smeri presečišča ravnin gibanja Lune in Zemlje ... Zagotovo bi si morali učenci in profesorji skupaj ogledati Lunine mrke (teh se v Sloveniji vidi kar nekaj, tudi popolnih) in tudi delne Sončeve mrke. Tudi kako potovanje na ogled (vsaj bližnjega) popolnega Sončevega mrka ne bi bilo odveč (res so lahko tukaj problem finance, določene skrbi glede varnosti, a ogled takega mrka vključuje množico novih spoznanj, poleg astronomije je tukaj še geografija, zgodovina, sociologija – spoznavanje resnice o drugih kulturah na mestu samem in to šteje več kot vsa nakladanja in pretiravanja potrošniških medijev) ...
Kot smo že omenili in bomo še večkrat, pomen mrkov za zgodovinski razvoj astronomije, človeštva in znanosti nasploh, je izjemen. Einsteinova teorija splošne relativnosti je bila še dodatno potrjena preko Sončevega mrka 1919 (odklon svetlobe, zvezd, ob Soncu). Takrat so njegove izračune srejeli tudi najbolj konzervativni fiziki in tudi svetovna javnost. V antiki pa so Lunini mrki pomagali določiti razdaljo Zemlja-Luna in oceno velikosti Lune. To so bili prvi izjemni uspehi za drzne ocene, kako velik je Sončev sistem in pozneje Rimska cesta, vesolje. Tudi naši učenci lahko ob Luninem mrku ponovijo meritve antičnih učenjakov, izmerijo čas prehoda Lune čez Zemljino senco in tako podajo oceno velikosti Lune ter v drugem koraku določijo razdaljo Zemlja-Luna.

* Eno ključnih potrditev splošne teorije relativnosti je omogočil Sončev mrk 1919
Kot je v Antiki Lunin mrk pomagal določiti razdaljo Zemlja-Luna, oceno velikosti Lune, je Sončev mrk pomagal potrditi Einsteinovo splošno teorijo relativnosti. Torej, če se le da, si oglejte kak Lunin mrk in tudi po možnosti vsaj delni Sončev mrk – seveda, skupaj z učenci.

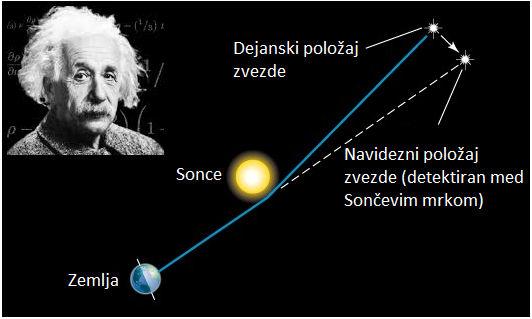
Slika: Kot odklona žarka iz prvotne smeri tik ob Soncu je po Einsteinu:
ϑ = 4GM/(c²R) = 1,75 ''
(če bo »slučajno« kdo od bralcev računal odmik, je rezultat potrebno iz radianov spremeniti v ločne sekunde: M = 1,99*10³⁰ kg je masa Sonca, R = 695700000 m polmer Sonca, c = 299792458 m/s = 3*10⁸ m/s hitrost svetlobe, G=6,67408*10^-11 m³·kg^-1·s^-2 gravitacijska konstanta). Izvor razmerij med količinami v formuli se da celo v srednji šoli do neke mere pojasniti, a samo do polovice Einsteinovega rezultata, preko poti fotona po hiperboli mimo Sonca. Nekaj podobnega, napako polovične vrednosti, je Einstein naredil leta 1911 in že drugi pred njim (Sodne), a je enačbo, preko splošne teorije relativnosti, korigiral leta 1915. O odklonu svetlobnih žarkov v gravitacijskem polju (zaradi teže) so razmišljali že mnogi pred Einsteinom – Newton, Laplace, Cavendish je izvedel račun, a brez objave. Prvi izračun odklona žarka v gravitacijskem polju Sonca pa je leta 1804 objavil že omenjeni nemški fizik in astronom Johhan Soldner (a z 2x premajhno vrednostjo). Med Sončevim mrkom, 29. maja leta 1919, je Einsteinovo napoved (1.75 loč. sekunde) odklona žarka zaradi gravitacije (bolje, zaradi ukrivljenosti prostora-časa) potrdil (približno) Sir Arthur Eddington (Eddingtonovi odpravi sta slikali mrk iz otoka Principe (zahodna Afrika) in iz kraja Sobral (Brazilija) – nikjer ni bilo ravno idealno vreme). Odmik svetlobe od prvotne smeri ob zvezdi lahko izračunamo tudi po znani enačbi za kot med asimptotami (velja za hiperbolo):
δ = 2sin^-1(1/e)
e=(a²+b²)^1/2/a; - je ekscentričnost (parametra a in b pa moramo izračunati iz ohranitve energije in vrtilne količine, Spika 1, 2018). Rezultat bo seveda za polovico premajhen ( ϑ = δ = 2GM/(c²R) = 0,875 '' (pravilen rezultat da splošna teorija relativnosti in znaša za Sonce okrog 1,75 '') ). Danes te odklone elektromagnetnega valovanja ob zvezdah natančno merijo s pomočjo kvazarjev v radijskem spektru, kar je veliko udobneje in natančneje.

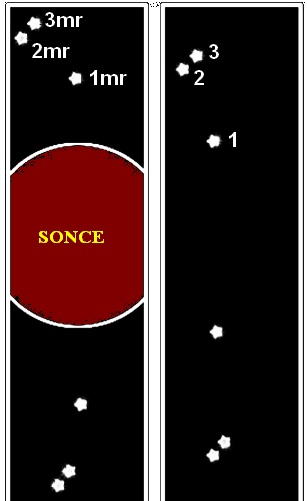
Položaj zvezd med in po mrku. Odmik med mrkom je 1.75 loč. sekunde, to je pričakovana vrednost za zvezde tik ob Soncu.

Uklon svetlobe ob masivnih galaksijah povzroča gravitacijsko lečenje, in tako vidimo še dlje v začetek vesolja.

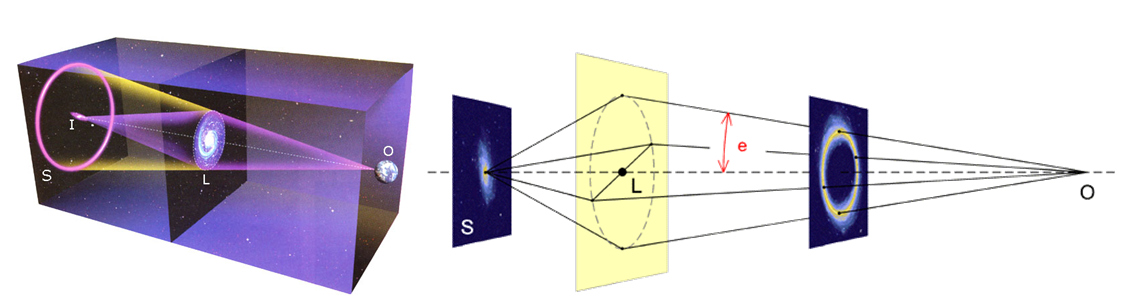
Iz zgornje geometrijske sheme lahko razberemo princip tvorbe slike gravitacijske leče (leča je lahko masivna galaksija, zvezda, ...). Kot osnovo privzamemo že omenjen izraz za odklon žarkov tik ob zvezdi, galaksiji. Odklona žarka iz smeri je: ϑ = 4GM/(c²R) .

Čarovnija vesolja. To isto supernovo AT 2016jka smo videli že trikrat - kdaj jo bomo videli četrtič? V primeru AT 2016jka ("SN rekviem"), se je eksplodirajoča zvezda slučajno nahajala za središčem jate galaksij (v tem primeru MACS J0138) in primerjava slik vesoljskega teleskopa Hubble pokaže, da smo jo videli trikrat. Te tri slike supernove so označene v krogih blizu spodnjega roba leve slike, posnete leta 2016. Na desnem posnetku, narejenem leta 2019, so krogi prazni, ker so vse tri slike ene supernove zbledele. Vendar računalniško modeliranje učinka leče jate kaže, da bi se morala na koncu v zgornjem krogu na desni sliki pojaviti četrta slika iste supernove. Toda kdaj? Najboljši modeli predvidevajo, da se bo to zgodilo leta 2037, vendar je ta datum negotov za približno dve leti zaradi nejasnosti v porazdelitvi mase jate in zgodovine svetlosti zvezdne eksplozije. Z izpopolnjenimi napovedmi in pozornim spremljanjem bodo Zemljani, živeči čez 16 let, morda lahko ujeli to četrto sliko – in morda naenkrat izvedeli več o jatah galaksij in supernovah. Vir: apod

Supernova rekviem (AT 2016jka - oddaljena okrog 10 milijard sv. let), vidna 2016 v kar treh preslikavah gravitacijskega lečenja jate galaksij MACS J0138 (jata je oddaljena 4 milijarde sv. let) - četrtič bi naj bila ista SN vidna okrog leta 2037 (zaradi daljše poti - glejte sliko). Slika je simbolična. Torej čakamo!!!

Če bo napoved uspela, bo to še ena velika potrditev verodostojnosti izračunov splošne teorije relativnosti in kar je najvažnejše - nova ocena, spoznanje, kako hitro se v resnici vesolje širi.

Gravitacijski (Einsteinov) rdeči premik

V tem kontekstu omenimo še, da gravitacija tudi svetlobi manjša energijo – če se foton oddaljuje od neke zvezde, se mu energija manjša, torej se mu valovna dolžina veča in manjša frekvenca. Valovno dolžino recimo v neskončnosti do masivnega telesa izračunamo podobno kot pri Dopplerju:
λ_∞ = λ(1 + z) = λ/(1 - 2GM/(Rc²))^1/2 = λ/(1 - v²/c²)^1/2
kjer hitrost v = (2GM/R)^1/2 lahko obravnavamo tudi kot ubežna hitrost. Gravitacijski (Einsteinov) rdeči premik se torej zapiše kot: λ_∞/λ = 1 + z = 1/(1 - 2GM/(Rc²))^1/2. Je neposredna posledica gravitacijske dilatacije časa, saj se frekvenca elektromagnetnega sevanja zmanjša pri prehodu na območje višjega gravitacijskega potenciala. Večinoma je ta prispevek za galaksije minimalen glede na efekt premikanja galaksij (klasični Doppler zaradi oddaljevanja galaksij). Člen '1 - 2GM/(Rc²)' se da v grobem razložiti z ubežno hitrostjo in dilatacijo časa (več v eni od naslednjih poglavij). Ta efekt spremembe frekvence, oz. valovne dolžine, se pa že dobro pozna pri nevtronskih zvezdah. Pri črnih luknjah pa svetloba sploh ne more uiti v prostor, pri polmeru r_s = 2GM/c², to je Schwarzschildov polmer, ko gre rdeči premik valovne dolžine proti neskončnosti.

Zakaj je Einstein bolje opisal vesolje kot Newton
Ali učence soočimo z ukrivljenostjo prostor-časa (tukaj bi zagotovo prišel prav Einsteinov miselni poskus s krovcem, ki ga je označil kot najsrečnejšo misel svojega življenja), oziroma kaj storiti z efekti gravitacije (uklon žarka, rdeči gravitacijski premik, »podaljšanje« časa, precesija perihelija, gravitacijsko lečenje). Vsekakor je potrebno poudariti, da je koncept gravitacijske sile napačen, saj fotoni nimajo mase, a se njihova pot vseeno ukrivi ob masivnih zvezdah (kar lahko opazujemo ob popolnih Sončevih mrkih), zato je Einsteinov koncept ukrivljenosti prostor-časa veliko ustreznejši. Prostor-čas krivi energija, ki je lokalno v glavnem zbrana v masi Zemlje, Sonca ... (E = mc²). Tudi nobena sila ne more potovati neskončno hitro, kar napačno privzame Newton (a tega Newtonu v kontekstu časa in takratnega vedenja, ne gre zameriti). Več o tem pojavu v naslednjih poglavjih.
Se nadaljuje ...

Zorko Vičar
Korona pomlad 2021 (objavljeno jan. 2022)

DODATEK -....: